Область техники
Настоящее изобретение относится к области обработки трехмерных тел в B-Rep представлении, а именно обработке трехмерных тел с использованием параллельных вычислений.
Предшествующий уровень техники
Из существующего уровня техники известны технические решения «Parameterizing a 3d modeled object for tessellation» [Заявка на патент № US2014184599, з. 28.12.2012 г.] и «Tessellation of a Parameterized 3D Modeled Object», заявка на патент № US2014184598, з. 28.12.2012 г.]. Оба технических решения описывают способы обработки трехмерных моделей для решения задач построения сеток (триангуляции).
При этом для решения задачи триангуляции не возникает необходимости преобразования объектов внутри тела в B-Rep представлении, например, геометрических объектов (поверхностей, кривых, точек), используемых соответствующими топологическими объектами (гранями, ребрами, вершинами). Соответственно, указанные технические решения не могут быть применены к случаям, когда такие преобразования к телу в B-Rep представлении необходимо применить. Заявляемое изобретение адресует подобные случаи.
Сущность изобретения
Задачей, на решение которой направлено заявляемое изобретение, является ускорение обработки трехмерных тел в B-Rep представлении за счет использования параллельных вычислений. B-Rep представление описывается с помощью структуры элементов, связных между собой (вершин, ребер, граней и др.). В силу связности элементов между собой (например, в замкнутом теле каждое ребро разделяется двумя гранями, а каждая вершина разделяется как минимум двумя ребрами) эффективное использование параллельных вычислений сильно затруднено (по причине сильной зависимости по данным).
Данная задача решается посредством обработки трехмерных тел в B-Rep представлении с использованием параллельных вычислений. Структуру B-Rep представления преобразуют в граф зависимостей между гранями тела, предварительно формируя массивы зависимостей между гранями на основании информации о связности граней через дочерние элементы (вершины или ребра тела в B-Rep представлении). Отношение «зависимости» между гранями Fi и Fj обозначает требование, что грань Fj может быть обработана только после грани Fi. При этом массивы зависимостей формируют в памяти вычислительного устройства, используя по меньшей мере идентификаторы граней и принадлежащих им вершин, а также идентификаторы вершин и граней, к которым принадлежит каждая вершина. После чего при необходимости оптимизируют граф, исключая в нем дублирующие зависимости, а параллельные вычисления применяют к обработке граней в полученном графе, обрабатывая каждую последующую грань после обработки всех граней, предшествующих ей в графе.
Также граф зависимостей между гранями тела может быть представлен в форме таблиц.
Параллельные вычисления ведут с одновременным использованием как минимум двух вычислительных устройств. Для повышения эффективности способа при наличии свободных мощностей вычислительной техники соответствующее вычислительное устройство анализирует наличие граней, незадействованных в обработке в данный момент времени, и при получении положительного отклика начинает их обработку. Под вычислительным устройством понимают любое устройство, способное производить вычисления. Примерами вычислительных устройств могут служить центральный процессор компьютера, ядро центрального процессора, гипер-поток ядра процессора, ядра и гипер-потоки со-процессора или графического ускорителя, узлы вычислительного кластера и т.д. При этом параллельные вычисления могут быть использованы на любом уровне вычислительной техники, например, с использованием векторных инструкций процессора, многопоточного программирования, программирования на системах с распределенной памятью (кластерах), на системах с использованием со-процессоров и графических ускорителей, а также с использованием произвольных комбинаций вышеперечисленных способов.
Под памятью понимают любой вид физического устройства или среды для хранения данных на вычислительном устройстве, включая регистры и кэш процессора, динамическую память с произвольным доступом (DRAM), статическую память с произвольным доступом (SRAM), любые виды запоминающих устройств (например, HDD и SSD).
Технически результатом, обеспечиваемым приведенной совокупностью признаков, является уменьшение времени обработки трехмерных тел в B-Rep представлении.
Описанный способ может применяться для конвертации трехмерных тел между различными форматами, восстановления, исправления и прочего изменения геометрических данных в трехмерных телах. Также экспертам в предметной области очевидно его применение к иным вариантам использования для обработки трехмерных тел, например, для решения задач визуализации, построения сеток и др.
Краткое описание чертежей
Сущность изобретения поясняется рисунками
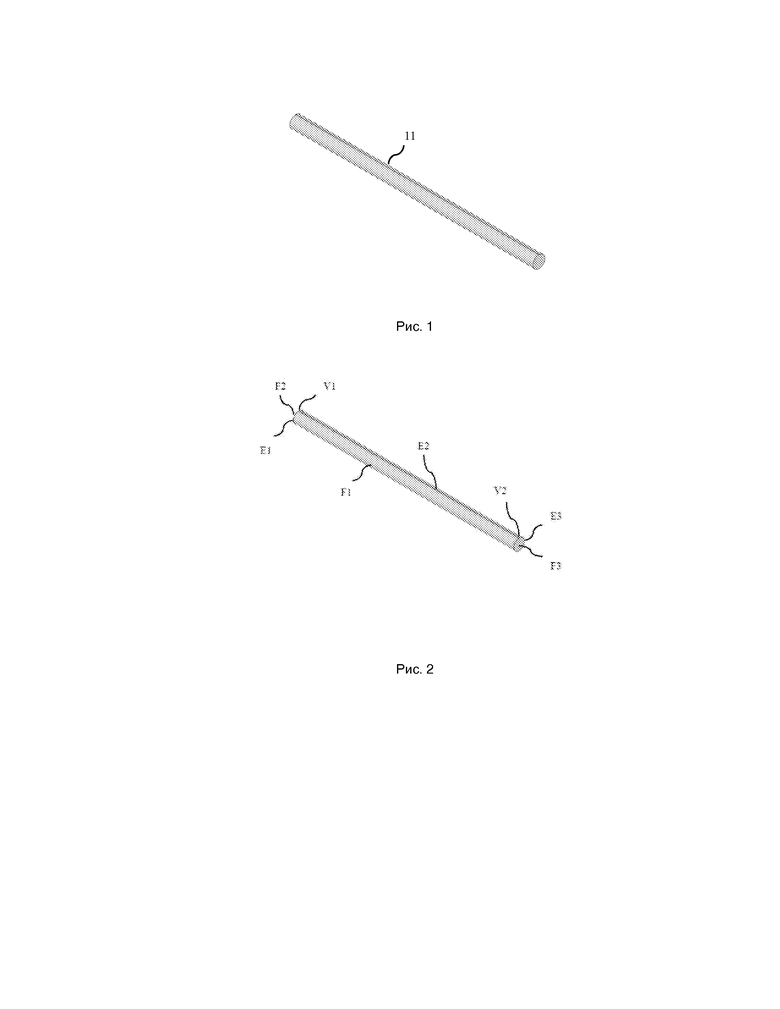
Рис. 1 - Тело, имеющее B-Rep представление (11). B-Rep (Boundary representation) - способ представления тела с помощью структуры данных, содержащей сведения о границах объема (вершинах, ребрах, гранях) и их соединении друг с другом [http://wap.ism-06-2.ru/shpora.php?razdel=5&id=402&].
Рис. 2 и 3 - B-Rep представление и его внутренняя структура. На рис. 2 и 3 использованы следующие обозначения:
V1, V2 - вершины;
E1, E2, E3 - ребра;
F1, F2, F3 - грани.
Рис. 4 - модель прямоугольного параллелепипеда в B-Rep представлении. На рис. 4 использованы следующие обозначения:
0, 1, …, 7 - вершины;
F0, F1,…, F5 - грани.
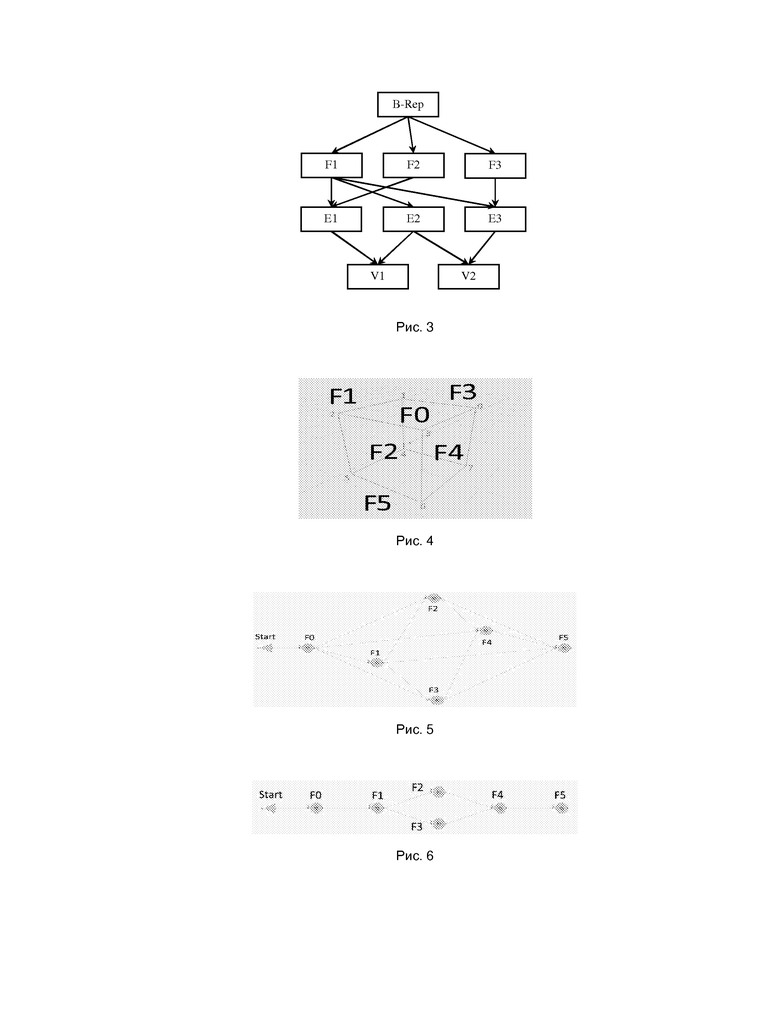
Рис. 5 и 6 - графы зависимостей граней тела, изображенного на рис. 4, полный и оптимизированный.
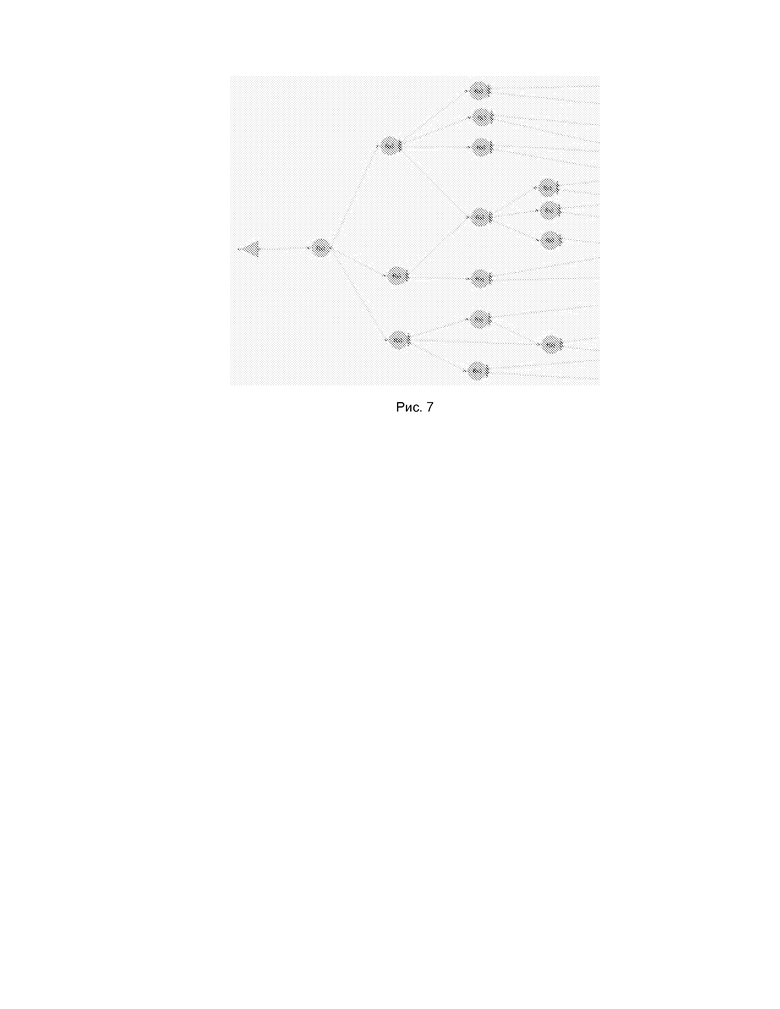
Рис.7 - пример фрагмента сложного графа зависимостей граней тела.
Подробное описание изобретения
Под элементами тела в B-Rep представлении (Рис. 2 и 3) понимаются грани, ребра, вершины. Элементы B-Rep представления упорядочены по иерархическому принципу (Рис. 3), где старшие элементы состоят из младших элементов. Например, каждая грань в рамках B-Rep представления состоит из ребер, а каждое ребро состоит из вершин. В зависимости от вида трехмерного тела иерархический принцип может применяться и к другим элементам B-Rep представления, таким как поверхности и кривые.
В качестве примера тела, иллюстрирующего применение способа, выбран прямоугольный параллелепипед (см. Рис. 4). Для тела в B-Rep представлении (Рис. 4) создаем набор элементов, составляющих данное представление и выстроенных по иерархическому принципу. Например, для тела в B-Rep представлении (Рис. 4) создаем массив вершин (V0-V7), массив граней (F0-F5), составляющих данное B-Rep представление (Рис. 4). Количество и содержание этих массивов зависит от конкретного трехмерного тела.
Затем одновременно создаем 2 таблицы:
1. Таблицу, содержащую номера всех граней и номера принадлежащих ей вершин (см. Табл. 1);
2. Таблицу, содержащую номера всех вершин и номера граней, к которым данная вершина принадлежит (см. Табл. 2).
Табл.1. Соответствие грани и номеров принадлежащих ей вершин
Табл.2. Соответствие вершины и номеров граней, к которым принадлежит данная вершина
После чего, используя данные таблиц (Табл. 1 и 2), формируем таблицу зависимостей между гранями (Табл. 3). Эта таблица выражает зависимость между «предшествующей» гранью (левый столбец) и «последующими» гранями (правый столбец). Термины «предшествующий» и «последующий» указывают на то, что любая «последующая» грань может быть обработана только после обработки всех «предшествующих» граней.
Табл.3. Таблица зависимостей между гранями
Далее для тела в B-Rep представлении формируем граф зависимостей граней, в котором ребра обозначают отношение зависимости «предшествующая» - «последующая» грань. На Рис.5 хорошо видно, что такой граф содержит избыточные ребра, например, между гранями F0 и F4 существуют три пути, соединяющих их: F0-F2-F4, F0-F3-F4 и F0-F4. Это обусловлено тем, что некоторые грани одновременно связаны с несколькими «предшествующими» гранями. Эта избыточность может увеличить время обработки тела, т.к. потребуются дополнительные проверки условия того, что все «предшествующие» грани были обработаны до начала обработки каждой «последующей» грани. Соответственно для того, чтобы ускорить процесс обработки, можно оптимизировать граф, то есть сократить зависимость грани от «предшествующих» ей граней до минимума. Оптимизируем граф, исключая для каждой грани те «предшествующие» грани, которые являются «предшествующими» для других «предшествующих» граней (см. Табл.4).
Табл.4. Таблица зависимостей между гранями
В примере выше, для F4 исключаем F0 как «предшествующую», т.к. F0 является «предшествующей» для F2 и F3, которые сами являются «предшествующими» к F4. На основании таблицы формируем оптимизированный граф (Рис. 6). После чего начинаем обработку в соответствии с оптимизированным графом. После завершения обработки F1 и при переходе к обработке «последующих» граней F2 и F3 (Рис. 6) возникает возможность применения параллельных вычислений в силу независимости обработки F2 и F3 друг от друга. Для повышения эффективности параллельных вычислений может быть использован способ, называемый «воровством задач» (от англ. “work stealing”).
Этот принцип может быть пояснен на следующем примере. Для больших сложных B-Rep тел ветвления в графе зависимостей (когда от одной «предшествующей» грани зависит множество «последующих») могут возникнуть произвольным образом. На рис. 7 приведен пример более сложного графа зависимостей со множеством ветвлений. Обязательное использование параллелизма при каждом таком ветвлении породило бы создание избыточного количества ВУ (например, количество вычислительных потоков, большее, чем количество ядер в центральном процессоре). Это привело бы к замедлению, а не ускорению вычислений, что, очевидно, не эффективно. Вместо такого «форсированного» параллелизма используют способ «воровства задач». Концепция «воровства задач» заключается в том, что каждое ВУ при завершении обработки своих имеющихся элементов (например, граней) пытается найти другие необработанные элементы. При этом может происходить отбирание («воровство») элементов у другого вычислительного устройства, над которыми оно уже начало работать. В заявленном способе реализация данной концепции состоит в том, что при обработке элементов B-Rep представления (граней) каждое работающее ВУ анализирует наличие элементов, незадействованных в обработке в данный момент времени, и при получении положительного отклика начинает обработку соответствующих элементов.
В зависимости от особенностей B-Rep представления или вычислительных алгоритмов реализация способа может быть основана на информации о связности граней посредством ребер, а не вершин.
Таким образом, данное изобретение ускоряет процесс обработки трехмерных тел в B-Rep представлении за счет использования параллельной обработки информации.
Изобретение относится к области обработки трехмерных тел, а именно обработке трехмерных тел с использованием параллельных вычислений. Техническим результатом является уменьшение времени обработки трехмерных тел в B-Rep представлении. Способ обработки трехмерных тел в B-Rep представлении с использованием параллельных вычислений, структуру B-Rep представления преобразуют в граф зависимостей между гранями тела, предварительно формируя массивы зависимостей между гранями на основании информации о связности граней через дочерние элементы, при этом массивы зависимостей формируют в памяти по меньшей мере из идентификаторов граней и принадлежащих им вершин, а также идентификаторов вершин и граней, к которым принадлежит каждая вершина, после чего при необходимости оптимизируют граф, исключая из него дублирующие зависимости, а параллельные вычисления применяют к обработке граней в полученном графе, обрабатывая каждую последующую грань после обработки всех граней, предшествующих ей в графе. 4 табл., 7 ил.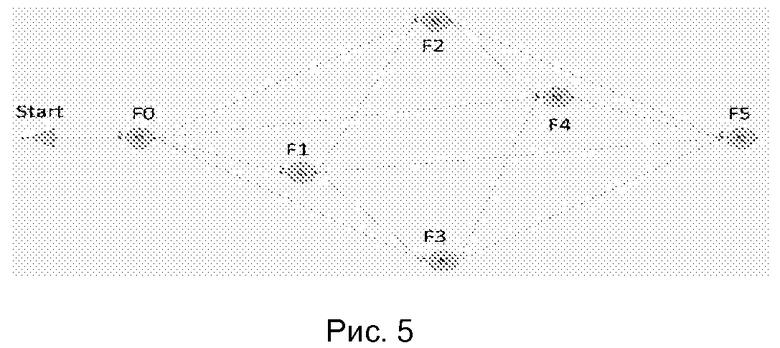
Способ обработки трехмерных тел в B-Rep представлении с использованием параллельных вычислений, отличающийся тем, что структуру B-Rep представления преобразуют в граф зависимостей между гранями тела, предварительно формируя массивы зависимостей между гранями на основании информации о связности граней через дочерние элементы, при этом массивы зависимостей формируют в памяти по меньшей мере из идентификаторов граней и принадлежащих им вершин, а также идентификаторов вершин и граней, к которым принадлежит каждая вершина, после чего при необходимости оптимизируют граф, исключая из него дублирующие зависимости, а параллельные вычисления применяют к обработке граней в полученном графе, обрабатывая каждую последующую грань после обработки всех граней, предшествующих ей в графе.
| US20140136151 A1, 15.05.2014 | |||
| US8994724 B2, 31.03.2015 | |||
| US20140184599 A1, 03.07.2014 | |||
| RU2011149310 A, 10.06.2013. |
Авторы
Даты
2016-09-10—Публикация
2015-05-18—Подача