Настоящее изобретение относится к области измерительной техники, в частности к способам детектирования электромагнитных волн терагерцового диапазона частот.
Известно, что диапазон терагерцового излучения находится между ИК- и СВЧ-диапазонами и занимает полосу 0,1-10 ТГц. В терагерцовом диапазоне лежит большое число частот резонансных возбуждений различных колебательных степеней свободы и переходов в конденсированных средах. В то же время терагерцовое излучение легко фокусируется и обладает большой проникающей способностью для целого ряда промышленных материалов, что создает возможность его использования для неразрушающей диагностики оптически непрозрачных предметов. Кроме того, в отличие от рентгеновского излучения, терагерцовые волны практически безвредны для живых организмов.
Проблемы генерации и детектирования электромагнитного излучения терагерцового диапазона в последнее время привлекают растущий интерес. С одной стороны, это объясняется уникальными перспективами применения терагерцового излучения в спектроскопии, неразрушающей диагностике биологических и медицинских объектов, системах связи и навигации (Chan W.L., Deibel J., and Mittleman D.M. // Rep. Prog. Phys. 2007. V. 70. P. 1325; Hattori T. and Sakamoto M. // Appl. Phys. Lett. 2007. V. 90, P. 261106). С другой стороны, освоение данного диапазона проходит довольно медленно, так как энергетическая эффективность действующих устройств по генерации и детектированию терагерцового излучения до сих пор не выше десятых долей процента (Kitaeva G. Kh. // Laser Physics Lett. 2008. V.5, No. 8. P.559). Поэтому поиск новых схем, а также новых самих физических принципов функционирования приборов в этой области чрезвычайно актуален.
В последнее десятилетие активно развиваются методы, основанные на перекачке энергии из оптического в терагерцовый диапазон (при генерации) и обратно (при детектировании). На сегодняшний день детектирование в терагерцовом диапазоне частот основано как на принципах детектирования оптического излучения, так и на принципах радиотехнического детектирования. На основе принципов радиотехники в настоящее время разрабатываются полевые транзисторы, способные детектировать терагерцовое излучение (R.F. Silverberg, S. Ali, A. Bier, B. Campano, T.C. Chen, E.S. Cheng, D.A. Cottingham, T.M. Crawford, T. Downes, F.M. Finkbeiner, D.J. Fixsen, D. Logan, S.S. Meyer, C. O'Dell, T. Perera, E.H. Sharp, P.T. Timbie, G.W. Wilson, Nuclear Instruments and Methods in Physics Research A, 520, 421 (2004)), а на основе оптических процессов - методы электрооптического детектирования (A. Nahata, A.S. Weling and T.F. Heinz, Appl. Phys. Lett. 69, 2321 (1996)), детектирования в фотопроводящих антеннах (R. Yano, H. Gotoh, Y. Hirayama, S. Miyashita, Y. Kadoya, T. Hattori, J. Appl. Phys. 97, 103103 (2005)) и фотоионизованных газах (N. Karpowicz, J. Dai, X. Lu, Y. Chen, M. Yamaguchi, H. Zhao, X.-C. Zhang, L. Zhang, C. Zhang, M. Price-Gallagher, C. Fletcher, O. Mamer, A. Lesimple and K. Johnson, Appl. Phys. Lett. 92, 011131 (2008)).
У каждого из известных на данный момент способов детектирования терагерцового излучения есть ряд своих существенных недостатков:
- для работы детекторов на основе полевых транзисторов необходимы низкие температуры, и, следовательно, громоздкие и энергозатратные системы охлаждения;
- фотопроводящие антенны, фотоионизированные газы, как и электрооптический метод, требуют для детектирования фемтосекундных лазеров, которые достаточно дороги и громоздки.
Наиболее близким к заявленному техническому решению - прототипом - является способ детектирования терагерцового излучения (Патент РФ ИЗ №2448399, опубл. 20.04.2012), заключающийся в направлении потока измеряемого терагерцового излучения на преобразователь с формированием в нем сигнала, регистрируемого детектором.
Недостатком известного способа является его сложность, обусловленная необходимостью дополнительного (до регистрации фотодетектором) преобразования сигнала, а именно фильтрации на поляризационной призме на новых частотах, смещенных относительно частоты накачки, сигнального оптического излучения, полученного на преобразователе (нелинейно-оптическом кристалле). Кроме того, прототип не свободен и от общих, характерных для метода электрооптического детектирования, недостатков, описанных выше.
Технический результат - упрощение детектирования электромагнитных волн в терагерцовом диапазоне частот.
Заявленный технический результат достигается тем, что в способе детектирования электромагнитных волн в терагерцовом диапазоне, заключающемся в направлении потока терагерцового излучения на преобразователь с формированием в последнем сигнала, регистрируемого детектором, в качестве преобразователя используют систему квантовых точек в матрице с терагерцовой прозрачностью, помещенную во внешнее магнитное поле с индукцией B=ħ×ν/g×µБ, в качестве детектора используют магнитометр, которым регистрируют изменение намагниченности системы квантовых точек под действием внешнего терагерцового излучения, а интенсивность последнего определяют как jвн=1/[g×µБ×n×b/ΔJ×(1+b×j0)-b], где В=0.1-10 Тл - индукция внешнего магнитного поля; ħ - 6.62·10-34 Дж·с - постоянная Планка; ν - частота регистрируемого излучения; g - безразмерный множитель Ланде; µБ - 9.27×10-24 Дж/Тл - магнетон Бора; jвн - интенсивность регистрируемого излучения; n - объемная плотность квантовых точек; b=c2/4πν3 - параметр, определяемый частотой; j0 - интенсивность фонового (теплового) терагерцового излучения, оптимально в матрице GaAs (арсенид галлия) формировать квантовые точки в виде сферических монокристаллов InAs (арсенид индия) с радиусом R так, что Rкр≤R≤2Rкр, где Rкр=2.23 (нм) - критический размер квантовой точки, необходимый для формирования одноэлектронного квантового уровня.
В основу заявленного способа положен принцип детектирования, основанный на связи магнитной восприимчивости системы квантовых точек с потоком внешнего терагерцового излучения. В каждой квантовой точке при определенных условиях имеется только одно связанное электронное состояние (Леденцов В.М., Устинов В.М., Щукин В.А., Копьев П.С., Алферов Ж.И., Бимберг Д. Гетероструктуры с квантовыми точками: получение, свойства, лазеры // ФТП, 32, 4, 385 (1998)). Во внешнем магнитном поле энергетический уровень связанного электрона испытывает зеемановское расщепление, обусловленное ориентацией его спина. Энергия этого расщепления в магнитных полях порядка (0.1-10) Тл как раз соответствует энергии фотонов терагерцового диапазона. Система электронных спинов во внешнем магнитном поле естественным образом приобретает магнитный момент, величина которого при тепловом равновесии обусловлена: 1) фактором магнитного расщепления, 2) плотностью квантовых точек и 3) температурой. Поток внешнего излучения с энергией, близкой к энергии зеемановского расщепления, пропорционального внешнему магнитному полю в указанном диапазоне, изменяет условия динамического равновесия распределения спинов и, тем самым, изменяет намагниченность системы. Величина этого изменения будет зависеть от интенсивности внешнего потока терагерцового излучения. Таким образом, возникает связь между легкоизмеряемым магнитометром изменением намагниченности системы и потоком терагерцового излучения, что и предлагается использовать для измерения последнего. Поскольку энергия упомянутых переходов пропорциональна внешнему магнитному полю, то измерения такого рода будут селективными, а не интегральными по частоте.
Для реализации предлагаемого способа не требуются сверхчувствительные магнитометры, основанные на эффекте Джозефсона и регистрирующие изменение магнитного поля порядка 10-16 Тл, так как здесь вполне достаточно широкораспространенных магнитометров, работающих на эффекте Холла и чувствующих изменение магнитного поля порядка 10-7 Тл (Абрамзон Г.В., Обоишев Ю.П. Индукционные измерительные преобразователи переменных магнитных полей. Л. 1984).
В настоящем способе используется явление формирования одноэлектронного квантового уровня в квантовых точках (КТ) в присутствии постоянного магнитного поля.
Известно, что энергия зеемановского расщепления энергетического уровня контролируется магнитным полем В (см. например, Физическая Энциклопедия, т. 3, 1992, М. сс. 77-78).
ΔE=ħω=|g|µBB,
где µB - магнетон Бора, a g - безразмерный множитель Ланде.
Эта энергия может быть такова, что переходы с переворотом спина между расщепленными подуровнями резонансны терагерцовому излучению. Это состояние электрона имеет ненулевой спиновый момент, что приводит к появлению намагниченности во внешнем поле. Тогда поглощение терагерцового излучения вызывает изменение намагниченности в связи с перераспределением равновесной населенности зеемановских подуровней.
Вначале рассчитывается волновая функция и определяется уровень энергии электрона, локализованного в преимущественно сферической КТ во внешнем магнитном поле. Основное внимание при этом уделяется преодолению «конфликта симметрий», навязываемых волновой функции граничными условиями (фактически - формой КТ), с одной стороны, и магнитным полем - с другой. Преодоление этого конфликта обеспечивается переходом от осесимметричных функций Эрмита, соответствующих отдельным уровням Ландау, к функциям Грина в магнитном поле, имеющим сферическую симметрию в окрестности центра. Условие непрерывности логарифмической производной на границе КТ и матрицы приводит к трансцендентному уравнению для энергии связанного состояния. Из него определяется и диапазон размеров КТ, в котором она остается идеальной, и величина зеемановского расщепления. Далее строится система уравнений, определяющих динамику чисел заполнения состояний с определенной ориентацией спина. Решение ее дает связь намагниченности системы КТ с потоком внешнего излучения.
Перейдем к построению волновой функции связанного в КТ электрона во внешнем магнитном поле. Пусть КТ является сферой радиуса R, создающая для электрона потенциальную яму U(r). Начало координат расположим в центре КТ. Вне ее электрон находится только в магнитном поле, так что уравнение Шредингера в этой области r>R имеет вид
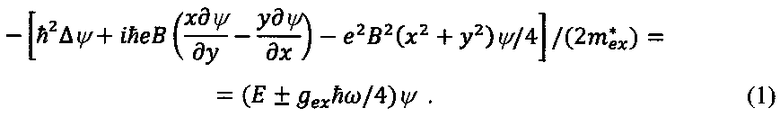
В левой части этого уравнении Δ - трехмерный оператор Лапласа, ħ - постоянная Планка, ψ - волновая функция, е - модуль заряда электрона, В - магнитная индукция, направленная по оси z (здесь и далее - система СИ), х и y - латеральные координаты, 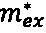 - эффективная масса электрона в материале матрицы. В правой части Е<0 - энергия связанного уровня, зависящая от магнитного поля,
- эффективная масса электрона в материале матрицы. В правой части Е<0 - энергия связанного уровня, зависящая от магнитного поля, 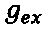 - фактор магнитного расщепления в материале матрицы, знак перед ним соответствует направлению спина электрона по или против магнитного поля соответственно, m - масса свободного электрона, ω=еВ/т - циклотронная частота для свободного электрона. Все последнее слагаемое в скобках в правой части - энергия взаимодействия спина электрона с магнитным полем в материале матрицы. Для представления потенциала магнитного поля выбрана симметричная калибровка. За нулевое значение энергии, как обычно в подобных случаях, принята энергия дна зоны проводимости матрицы.
- фактор магнитного расщепления в материале матрицы, знак перед ним соответствует направлению спина электрона по или против магнитного поля соответственно, m - масса свободного электрона, ω=еВ/т - циклотронная частота для свободного электрона. Все последнее слагаемое в скобках в правой части - энергия взаимодействия спина электрона с магнитным полем в материале матрицы. Для представления потенциала магнитного поля выбрана симметричная калибровка. За нулевое значение энергии, как обычно в подобных случаях, принята энергия дна зоны проводимости матрицы.
Остановимся теперь на выборе формы удерживающего потенциала КТ. Как правило, при наличии магнитного поля его аппроксимируют параболической потенциальной ямой. При этом и внутри ямы обычно решают двухмерную задачу для волновой функции. Именно такая форма потенциала позволяет сохранить структуру решения в магнитном поле, поскольку его эффективный потенциал также параболический. Это позволяет избежать «конфликта симметрий», навязываемых волновой функции формой потенциала магнитного поля, с одной стороны, и формой потенциальной ямы, с другой, и использовать для волновой функции обычные решения Ландау. Однако, при всех положительных чертах такого подхода, для идеальных КТ он не годится. Дело в том, что единственный уровень энергии в идеальной КТ лежит вблизи дна зоны проводимости матрицы и гораздо выше дна потенциальной ямы. Электрон с такой энергией является слабосвязанным и достаточно времени проводит вне ямы. Приближение же параболического потенциала приводит к полному удержанию электрона в яме («parabolic confinement»). Ясно, что так можно описывать лишь низколежащие уровни в потенциальной яме, которых в идеальной КТ просто нет.
Поэтому примем для потенциала КТ простейшее приближение ямы постоянной глубины (типа «miffin-tin»)

Это сразу приводит к описанному выше «конфликту симметрий». Волновая функция, соответствующая единственному связанному уровню в яме, имеет сферическую симметрию, подобную обычному s-состоянию в атоме. Стандартные же решения уравнения (1), соответствующие обычным уровням Ландау (функции Эрмита), имеют явно выраженную осевую симметрию. Преодолевается этот конфликт переходом от решений, связанных с отдельными уровнями Ландау, к функциям Грина уравнения (1):

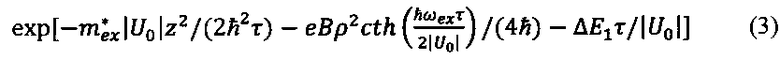
где р2=х2+y2 и

энергия связи электрона, т.е. разность энергии дна зоны проводимости матрицы в магнитном поле (первого уровня Ландау в матрице с учетом спинового расщепления) и собственной энергии связанного уровня. Здесь 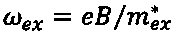 - циклотронная частота в материале матрицы. Подчеркнем, что это - решение именно однородного уравнения, т.к. нулевая точка исключена из области его определения r>R. Как и обычная функция Грина, (3) представляет собой ряд по собственным функциям дифференциального оператора в левой части (1), соответствующих отдельным уровням Ландау. В этом нетрудно убедиться, разложив сомножитель
- циклотронная частота в материале матрицы. Подчеркнем, что это - решение именно однородного уравнения, т.к. нулевая точка исключена из области его определения r>R. Как и обычная функция Грина, (3) представляет собой ряд по собственным функциям дифференциального оператора в левой части (1), соответствующих отдельным уровням Ландау. В этом нетрудно убедиться, разложив сомножитель
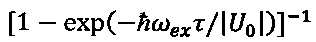
в ряд и проведя явное интегрирование.
Правая часть выражения (3) содержит интеграл типа Лапласа. Существенная область интегрирования в нем определяется окрестностью единственной точки перевала, причем характер перевальной оценки и, в конечном итоге, симметрию решения определяет именно положение этой точки. Решающее значение здесь имеет поведение второго слагаемого в экспоненте (3). В частности, если магнитное поле не слишком мало, а точка наблюдения лежит достаточно далеко от центра, точка экстремума экспоненты определяется формулой

Тогда гиперболический котангенс в (3) можно принять за 1, и для волновой функции получаем

где N′ - новое значение нормировочного коэффициента. Видим, что вдали от КТ решение явно осесимметрично, как и должно быть в чисто магнитном поле. Если, напротив, поле не слишком велико, а точка наблюдения лежит недалеко от центра, для положения экстремума экспоненты нетрудно получить
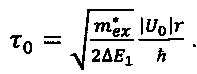
При этом гиперболический котангенс в (3) можно аппроксимировать как
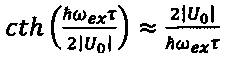
что дает для волновой функции

Таким образом, при любом конечном значении магнитного поля осевая симметрия волновой функции вдали от центральной точки переходит в сферическую симметрию в окрестности центра. Область координат, где один тип симметрии сменяет другой, зависит от значения магнитного поля. Чем больше последнее, тем ближе к центру лежит эта «переходная» область. Относительная величина магнитного поля определяется соотношением щели между уровнями Ландау (напомним, что достаточно сильное магнитное поле называют «квантующим») и глубиной потенциальной ямы. Для реально достижимых в лабораторных экспериментах стационарных магнитных полей ≤10 Тл и характерных значений эффективных масс 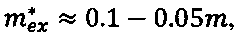 величина щели составляет ħωex~0.01-0.02 эВ, а типичная величина |U0|~0.5 эВ. Другими словами, реальные магнитные поля довольно малы. Поэтому практически вся идеальная КТ радиусом R~2-5 нм лежит в области сферической симметрии волновой функции. Именно таким образом разрешается «конфликт симметрий», подробно описанный выше. Отметим, что в окрестности КТ магнитное поле проявляет себя только тем, что создает осесимметричный стационарный поток вероятности, связанный с сомножителем exp(-ieBxy/2ħ).
величина щели составляет ħωex~0.01-0.02 эВ, а типичная величина |U0|~0.5 эВ. Другими словами, реальные магнитные поля довольно малы. Поэтому практически вся идеальная КТ радиусом R~2-5 нм лежит в области сферической симметрии волновой функции. Именно таким образом разрешается «конфликт симметрий», подробно описанный выше. Отметим, что в окрестности КТ магнитное поле проявляет себя только тем, что создает осесимметричный стационарный поток вероятности, связанный с сомножителем exp(-ieBxy/2ħ).
Внутри потенциальной ямы r<R, образованной КТ, уравнение Шредингера имеет вид (с учетом модели (2))

т.е. отличается от (1) только заменой некоторых постоянных: отрицательной энергии уровня Е на положительную величину |U0|+Е, а также эффективной массы электрона и фактора магнитного расщепления на соответствующие величины для материала КТ. Поэтому и решение (7) легко строится из (6) путем аналитического продолжения в область отрицательных значений ΔЕ1. При этом необходимо учесть и граничные условия в нуле

В результате волновая функция в (7) может быть записана в виде
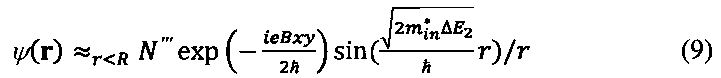
причем кинетическая энергия электрона в яме
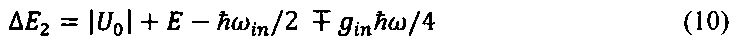
где  и
и 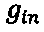 - соответственно циклотронная частота и фактор магнитного расщепления в материале КТ. Отметим, что физический смысл формул (4) и (10) абсолютно однотипен и по сути классический, несмотря на присутствие постоянной Планка. Дно зоны проводимости как в материале КТ, так и в матрице «поднимается» в магнитном поле за счет орбитального
- соответственно циклотронная частота и фактор магнитного расщепления в материале КТ. Отметим, что физический смысл формул (4) и (10) абсолютно однотипен и по сути классический, несмотря на присутствие постоянной Планка. Дно зоны проводимости как в материале КТ, так и в матрице «поднимается» в магнитном поле за счет орбитального 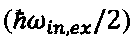 и сдвигается за счет спинового
и сдвигается за счет спинового 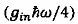 взаимодействия электронов с полем.
взаимодействия электронов с полем.
Уравнение для энергии уровня дает условие непрерывности логарифмической производной на границе областей
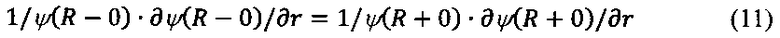
Подстановка (6) и (9) в это соотношение дает для энергии связанного уровня в магнитном поле
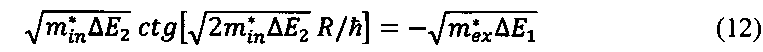
Из полученного выражения легко видеть, учитывая знак правой части, что первый связанный уровень (ΔЕ1=0) в отсутствие магнитного поля появится при превышении радиусом критического значения

Магнитное поле значительно меняет ситуацию, особенно для КТ околокритических размеров, что можно использовать для тонкого управления электронными состояниями.
Основная задача здесь - оценить величину зееманового расщепления энергии единственного связанного уровня Е(В) в идеальной КТ. Это можно сделать, численно решив уравнение (12). Данные по эффективным массам электронов и глубине потенциальной ямы для КТ из InAs в матрице GaAs достаточно воспроизводимы (|(U0|≈0.7 эВ, 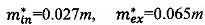 ). Для рассматриваемых материалов, согласно (13), критический размер кластера составляет Rcr≈2.23 нм. По мере роста размеров КТ фактор Ланде монотонно меняется от значения g=2, характерного для электрона в вакууме, к величине gin=-14.6, относящегося к среде («bulk semiconductor») InAs. Причина такого изменения - спин-орбитальное взаимодействие валентных электронов. В нашем случае, с одной стороны, в идеальной КТ может «удержаться» только электрон с нулевым орбитальным моментом, так что его g-фактор отклоняться от «свободного» значения не должен. Именно это, кстати, позволяет решать скалярные уравнения (1) и (7) вместо 8-компонентных матричных уравнений для волновой функции. Отметим, что добавка к Е энергии спина в правой части этих уравнений - отражение исходной двухкомпонентности уравнений Паули. С другой стороны, речь идет о слабосвязанном состоянии со значительным размером электронного облака, аналогичном, в некотором смысле, ридберговскому атому водорода. Электрон в таком состоянии ощутимо «чувствует» окружение. Это, видимо, должно сказываться и на факторе магнитного расщепления, подверженном множеству различных воздействий. Разумеется, более-менее однозначно оценить величину g-фактора может только эксперимент. Поэтому мы проведем расчеты для двух «полярных» случаев: gin=gех=2, как у электрона в вакууме, и gin=-14.6, gех=-0.44, как в объемных полупроводниках. Это позволит оценить диапазон характерных частот переходов между зеемановскими уровнями. Второй связанный уровень в КТ появляется при превышении ее размеров величины R≥2Rcr, т.е. ~4.46 нм в нашем случае. При этом КТ перестает быть идеальной, так что за эти размеры мы выходить не будем.
). Для рассматриваемых материалов, согласно (13), критический размер кластера составляет Rcr≈2.23 нм. По мере роста размеров КТ фактор Ланде монотонно меняется от значения g=2, характерного для электрона в вакууме, к величине gin=-14.6, относящегося к среде («bulk semiconductor») InAs. Причина такого изменения - спин-орбитальное взаимодействие валентных электронов. В нашем случае, с одной стороны, в идеальной КТ может «удержаться» только электрон с нулевым орбитальным моментом, так что его g-фактор отклоняться от «свободного» значения не должен. Именно это, кстати, позволяет решать скалярные уравнения (1) и (7) вместо 8-компонентных матричных уравнений для волновой функции. Отметим, что добавка к Е энергии спина в правой части этих уравнений - отражение исходной двухкомпонентности уравнений Паули. С другой стороны, речь идет о слабосвязанном состоянии со значительным размером электронного облака, аналогичном, в некотором смысле, ридберговскому атому водорода. Электрон в таком состоянии ощутимо «чувствует» окружение. Это, видимо, должно сказываться и на факторе магнитного расщепления, подверженном множеству различных воздействий. Разумеется, более-менее однозначно оценить величину g-фактора может только эксперимент. Поэтому мы проведем расчеты для двух «полярных» случаев: gin=gех=2, как у электрона в вакууме, и gin=-14.6, gех=-0.44, как в объемных полупроводниках. Это позволит оценить диапазон характерных частот переходов между зеемановскими уровнями. Второй связанный уровень в КТ появляется при превышении ее размеров величины R≥2Rcr, т.е. ~4.46 нм в нашем случае. При этом КТ перестает быть идеальной, так что за эти размеры мы выходить не будем.
Обратим внимание на «энергетическую инверсию» зеемановских уровней: при gin=gех=2 более устойчивым, как для свободного электрона, является состояние со спином против поля (соответственно с магнитным моментов вдоль поля), а при gin=-14.6, gex=-0.44 - наоборот. Это означает, что в тепловом равновесии система КТ в первом случае проявляет парамагнитные свойства, а во втором - диамагнитные. Величина такой индуцированной намагниченности зависит от плотности КТ, модулей g-факторов, индукции поля и температуры.
Осталось связать намагниченность системы КТ с температурой и внешним фоном терагерцового излучения. Пусть n - объемная плотность КТ, n+ и n- - соответственно плотность КТ с таким направлением спина, которое соответствует верхнему и нижнему уровням зееманового расщепления. Естественно,
n=n++n-
а объемная плотность модуля магнитного момента матрицы, заполненной квантовыми точками

Если энергия зееманового расщепления составляет ħw, то в тепловом равновесии, естественно,

где k - постоянная Больцмана, Т - абсолютная температура. Поэтому в тепловом равновесии намагниченность системы можно записать как
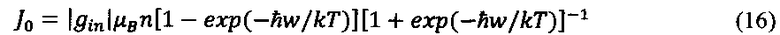
Будем считать, что динамическое равновесие КТ с определенной ориентацией спина поддерживается только за счет излучения и поглощения фотонов с энергией зеемановского расщепления. Ниже мы обсудим правомочность и роль такого допущения. Тогда уравнения, описывающие эволюцию спинового состояния КТ, можно записать в стандартном для двухуровневой системы виде
dn-/dt=n+(р+j·σ)-n-·j·σ
dn+/dt=n-·j·σ-n+(р+j·σ)
Здесь р - вероятность спонтанно излучения «зеемановского фотона», j - плотность потока таких фотонов ([j]=м-2·с-1), σ - сечения процесса вынужденного поглощения и излучения (они совпадают в соответствии с принципом детального равновесия). В установившемся режиме, естественно, n+ и n- постоянны, что дает для соотношения числа переходов

Отсюда, учитывая известное соотношение Эйнштена для отношения вероятностей спонтанного и вынужденного излучения
р/σ=w3/π2c2
мы можем связать плотность потока «зеемановских фотонов» с отношением КТ с различной ориентацией спина

и намагниченностью среды (14)

Теперь исходную намагниченность системы, находящейся в тепловом равновесии, когда динамическое равновесие системы КТ поддерживается за счет взаимодействия с «зеемановскими фотонами», а материал матрицы имеет окно прозрачности в терагерцовом диапазоне, можно (наряду с (16)) представить в виде

где j0 - не интересующая нас сейчас плотность потока фотонов теплового фона в равновесии
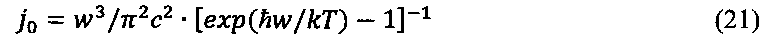
А при наличии внешнего потока фотонов jвн намагниченность системы КТ будет теперь
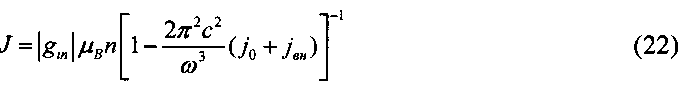
Таким образом, уменьшение намагниченности среды J0-J однозначно связано с превышением над равновесным потока фотонов данной частоты, что с учетом малости плотности потока тепловых фотонов j0 в сравнении с плотностью внешнего потока jвн позволяет записать
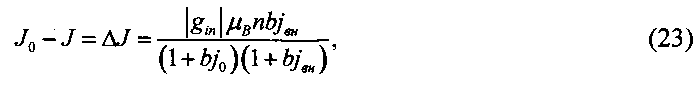
где 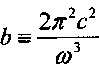 - параметр, зависящий от частоты внешнего потока.
- параметр, зависящий от частоты внешнего потока.
Из изложенного, преобразованием (19)-(23), следует, что в системе квантовых точек в матрице с терагерцовой прозрачностью, помещенной во внешнее магнитное поле с индукцией В=h×ν/g×µБ, под действием внешнего терагерцового излучения интенсивностью jm наблюдается изменение намагничеснности ΔJ, подчиняющееся зависимости
jвн=1/[g×µБ×n/ΔJ×(1+b×j0)-1]×b.
Выше показано, что оптимальная точность измерений достигается при формировании в матрице GaAs (арсенид галлия) квантовых точек в виде сферических монокристаллов InAs (арсенид индия) с радиусом R так, что Rкр≤R≤2Rкр,
При этом заявленный способ, в отличие от аналогов и прототипа, при реализации не требует:
- низких температур и громоздких и энергозатратных систем охлаждения;
- применения дорогих и громоздких фемтосекундных лазеров.
Таким образом, вышесказанное свидетельствует о том, что заявленный технический результат - упрощение детектирования электромагнитных волн в терагерцовом диапазоне частот - достигнут.
Анализ заявленного технического решения на соответствие условиям патентоспособности показал, что указанные в независимом пункте формулы признаки являются существенными и взаимосвязаны между собой с образованием устойчивой совокупности необходимых признаков, неизвестной на дату приоритета из уровня техники, и достаточной для получения требуемого сверхсуммарного технического результата.
Вышеизложенные сведения свидетельствуют о выполнении при использовании заявленного технического решения следующей совокупности условий:
- объект, воплощающий заявленное техническое решение, при его осуществлении относится к области измерительной техники, в частности к способам детектирования электромагнитных волн терагерцового диапазона частот;
- для заявленного объекта в том виде, как он охарактеризован в независимом пункте нижеизложенной формулы, подтверждена возможность его осуществления с помощью вышеописанных в заявке и известных из уровня техники на дату приоритета средств и методов;
- объект, воплощающий заявленное техническое решение, при его осуществлении способен обеспечить достижение усматриваемого заявителем технического результата.
Следовательно, заявленный объект соответствует требованиям условий патентоспособности «новизна», «изобретательский уровень» и «промышленная применимость» по действующему законодательству.
| название | год | авторы | номер документа |
|---|---|---|---|
| Детектор субмиллиметровых волн на основе квазинульмерной структуры с примесными комплексами A+e во внешнем магнитном поле | 2024 |
|
RU2832992C1 |
| СПОСОБ ПЕРЕКЛЮЧЕНИЯ БОЗОНОВ | 2010 |
|
RU2456671C2 |
| СПИНОВЫЙ ТРАНЗИСТОР | 2008 |
|
RU2387047C1 |
| ЧАСТОТНО-ПЕРЕСТРАИВАЕМЫЙ ИСТОЧНИК КОГЕРЕНТНОГО ИЗЛУЧЕНИЯ ДАЛЬНЕГО ИНФРАКРАСНОГО И ТЕРАГЕРЦОВОГО ДИАПАЗОНА НА ПОЛУПРОВОДНИКОВОЙ НАНОГЕТЕРОСТРУКТУРЕ | 2011 |
|
RU2478243C1 |
| Спиновая гетероструктура с составной активной областью с квантовыми точками | 2023 |
|
RU2822632C1 |
| ТВЕРДОТЕЛЬНЫЙ КВАНТОВЫЙ МАГНИТОМЕТР | 2024 |
|
RU2837487C1 |
| Квантовый сенсор на основе квантовой точки с примесным комплексом (A+e) во внешнем электрическом поле | 2023 |
|
RU2828816C1 |
| ТВЕРДОТЕЛЬНЫЙ МАЗЕР НА ЭЛЕКТРОНАХ ПРОВОДИМОСТИ | 2007 |
|
RU2351045C1 |
| СПОСОБ ФОРМИРОВАНИЯ СПИНОВЫХ ВОЛН | 2010 |
|
RU2477907C2 |
| СПОСОБ СОЗДАНИЯ ИНВЕРСНОЙ ЗАСЕЛЕННОСТИ ЯДЕРНЫХ УРОВНЕЙ В МАТЕРИАЛЕ АКТИВНОЙ СРЕДЫ И ИНИЦИИРОВАНИЯ ОДНОПРОХОДНОГО КОГЕРЕНТНОГО ГАММА - ИЗЛУЧЕНИЯ | 2015 |
|
RU2602769C1 |
Изобретение относится к области измерительной техники и касается способа детектирования электромагнитных волн в терагерцовом диапазоне. Способ включает в себя направление потока терагерцового излучения на преобразователь с формированием в последнем сигнала, регистрируемого детектором. В качестве преобразователя используют систему квантовых точек в матрице с терагерцовой прозрачностью, помещенную во внешнее магнитное поле с индукцией В=ħ×ν/g×µБ, в качестве детектора используют магнитометр, который регистрирует изменение намагниченности системы квантовых точек. Интенсивность излучения определяют как jвн=1/[g×µБ×n×b/ΔJ×(1+b·j0)-b], где В - индукция внешнего магнитного поля; ħ - постоянная Планка; ν - частота регистрируемого излучения; g - множитель Ланде; µБ - магнетон Бора; jвн - интенсивность регистрируемого излучения; n - объемная плотность квантовых точек; b=с2/4πν3 - параметр, определяемый частотой; j0 - интенсивность фонового (теплового) терагерцового излучения. Технический результат заключается в упрощении способа детектирования. 1 з.п. ф-лы.
1. Способ детектирования электромагнитных волн в терагерцовом диапазоне, заключающийся в направлении потока терагерцового излучения на преобразователь с формированием в последнем сигнала, регистрируемого детектором, отличающийся тем, что в качестве преобразователя используют систему квантовых точек в матрице с терагерцовой прозрачностью, помещенную во внешнее магнитное поле с индукцией
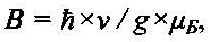
в качестве детектора используют магнитометр, которым регистрируют изменение намагниченности системы квантовых точек под действием внешнего терагерцового излучения, а интенсивность последнего определяют как
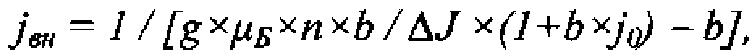
где В - индукция внешнего магнитного поля;
ΔJ - изменение намагниченности системы квантовых точек;
ħ - постоянная Планка;
ν - частота регистрируемого излучения;
g - безразмерный множитель Ланде;
µБ - магнетон Бора;
jвн - интенсивность регистрируемого излучения;
n - объемная плотность квантовых точек;
b=с2/4πν3 - параметр, определяемый частотой;
j0 - интенсивность фонового (теплового) терагерцового излучения;
с - скорость света.
2. Способ детектирования электромагнитных волн в терагерцовом диапазоне по п. 1, отличающийся тем, что в матрице GaAs (арсенид галлия) формируют квантовые точки в виде сферических монокристаллов InAs (арсенид индия) с радиусом R так, что
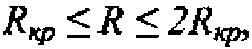
где Rкр - 2.23 (нм) - критический размер квантовой точки, необходимый для формирования одноэлектронного квантового уровня.
| СПОСОБ ДЕТЕКТИРОВАНИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ТЕРАГЕРЦОВОМ ДИАПАЗОНЕ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2009 |
|
RU2448399C2 |
| US 7170085 B2, 30.01.2007 | |||
| WO 2005031806 A2, 07.04.2005 | |||
| CN 102176463 A, 07.09.2011. | |||
Авторы
Даты
2016-10-10—Публикация
2015-05-13—Подача