Настоящее изобретение относится к кодированию аудиосигналов, и, в частности, к устройству для кодирования речевого сигнала с использованием ACELP в автокорреляционной области.
В кодировании речи посредством линейного предсказания с кодовым возбуждением (CELP), огибающая спектра (или эквивалентно, кратковременная временная структура) речевого сигнала описывается посредством модели линейного предсказания (LP) и остаток предсказания моделируется посредством долговременного предсказателя (предиктора) (LTP, также известного как адаптивная кодовая книга) и сигнала остатка, представленного посредством кодовой книги (также известной как фиксированная кодовая книга). Последняя, фиксированная кодовая книга, в общем, применяется как алгебраическая кодовая книга, где кодовая книга представлена посредством алгебраической формулы или алгоритма, в силу чего нет необходимости сохранять всю кодовую книгу, но только алгоритм, в то время как одновременно обеспечивается возможность для быстрого алгоритма поиска. Кодеки CELP, применяющие алгебраическую кодовую книгу для остатка, известны как кодеки линейного предсказания с алгебраическим кодовым возбуждением (ACELP) (см. [1], [2], [3], [4]).
В кодировании речи, использование алгебраической кодовой книги остатков является подходом выбора в основных кодеках, как, например, [17], [13], [18]. ACELP основывается на моделировании огибающей спектра посредством фильтра линейного предсказания (LP), собственной частоты речевых звуков посредством долговременного предсказателя (LTP) и остатка предсказания посредством алгебраической кодовой книги. Параметры LTP и алгебраической кодовой книги оптимизируются посредством алгоритма наименьших квадратов в перцепционной области, где перцепционная область определяется посредством фильтра.
Вычислительно наиболее сложной частью алгоритмов типа ACELP, узким местом, является оптимизация кодовой книги остатков. Единственным в текущее время известным оптимальным алгоритмом является исчерпывающий поиск по пространству размера Np для каждого подкадра, где в каждой точке, требуется оценка сложности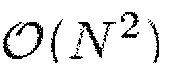 
. Так как обычными значениями являются длина подкадра N=64 (т.е. 5 мс) с p=8 импульсами, это имеет следствием более, чем 1020 операций в секунду. Ясно, что это не является жизнеспособным вариантом. Чтобы оставаться в рамках пределов сложности, установленных требованиями аппаратного обеспечения, подходы оптимизации кодовой книги должны работать с неоптимальными итеративными алгоритмами. Много таких алгоритмов и улучшений для процесса оптимизации было представлено в прошлом, например, [17], [19], [20], [21], [22].
Явным образом, оптимизация ACELP основывается на описании речевого сигнала x(n) как вывода модели линейного предсказания, так что оцененный речевой сигнал является
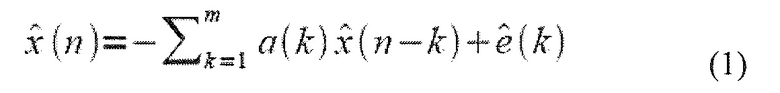
где a(k) являются коэффициентами LP и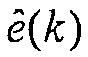 
является сигналом остатка. В векторной форме, это уравнение может быть выражено как
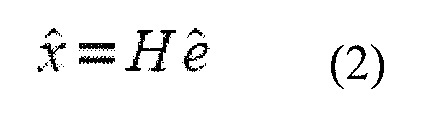
где матрица H определяется как нижнетреугольная матрица свертки Теплица с диагональю h(0) и нижними диагоналями h(1), ..., h(39) и вектор h(k) является импульсной характеристикой модели LP. Следует отметить, что в этой системе обозначений перцепционная модель (которая обычно соответствует взвешенной модели LP) пропущена, но предполагается, что перцепционная модель включена в импульсную характеристику h(k). Этот пропуск не имеет никакого влияния на общность результатов, но упрощает систему обозначений. Включение перцепционной модели применяется как в [1].
Соответствие модели измеряется посредством возведенной в квадрат ошибки. То есть,
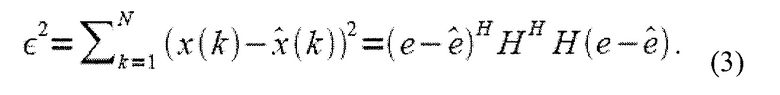
Эта возведенная в квадрат ошибка используется, чтобы находить оптимальные параметры модели. Здесь, предполагается, что LTP и кодовая книга импульсов оба используются, чтобы моделировать вектор e. Практическое применение может быть найдено в соответствующих публикациях (см. [1-4]).
На практике, вышеупомянутая мера соответствия может быть упрощена следующим образом. Пусть матрица B=HTH содержит корреляции h(n), пусть ck будет k-ым вектором фиксированной кодовой книги и положим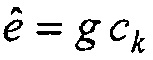 
, где g является коэффициентом усиления. Предположим, что g выбран оптимально, тогда кодовая книга ищется посредством максимизации критерия поиска
где d=HTx является вектором, содержащим корреляцию между целевым вектором и импульсной характеристикой h(n) и верхний индекс T обозначает транспонирование. Вектор d и матрица B вычисляются до поиска кодовой книги. Эта формула обычно используется в оптимизации как LTP, так и кодовой книги импульсов.
Большое количество исследований было инвестировано в оптимизацию использования вышеупомянутой формулы. Например,
1) Вычисляются только те элементы матрицы B, к которым фактически осуществляется доступ алгоритмом поиска. Или:
2) Алгоритм проб и ошибок поиска импульсов редуцируется к тому, что пробуются только такие векторы кодовой книги, которые имеют высокую вероятность успеха, на основе предыдущей проверки (см. например, [1, 5]).
Практические детали алгоритма ACELP относятся к концепции импульсной характеристики при расширении остатка нулями (ZIR). Эта концепция появляется при рассмотрении сигнала синтеза исходной области в сравнении с синтезированным остатком. Остаток кодируется в блоках, соответствующих размеру кадра или подкадра. Однако, при синтезе сигнала исходной области с помощью модели LP из Уравнения 1, остаток фиксированной длины будет иметь "хвост" бесконечной длины, соответствующий импульсной характеристике фильтра LP. То есть, хотя вектор кодовой книги остатков имеет конечную длину, он будет иметь влияние на сигнал синтеза значительно дальше текущего кадра или подкадра. Влияние кадра на будущее может вычисляться посредством расширения вектора кодовой книги с помощью нулей и вычисления вывода синтеза из Уравнения 1 для этого расширенного сигнала. Это расширение синтезированного сигнала известно как импульсная характеристика при расширении остатка нулями. Затем, чтобы учитывать влияние предыдущих кадров в кодировании текущего кадра, ZIR предыдущего кадра вычитается из цели текущего кадра. В кодировании текущего кадра, таким образом, рассматривается только та часть сигнала, которая не была уже смоделирована посредством предыдущего кадра.
На практике, ZIR учитывается следующим образом: Когда (под)кадр N-1 кодирован, квантованный остаток расширяется с помощью нулей до длины следующего (под)кадра N. Расширенный квантованный остаток фильтруется посредством LP, чтобы получать ZIR квантованного сигнала. ZIR квантованного сигнала затем вычитается из исходного (не квантованного) сигнала и этот модифицированный сигнал формирует целевой сигнал при кодировании (под)кадра N. Этим способом, все ошибки квантования, сделанные в (под)кадре N-1, будут учитываться при квантовании (под)кадра N. Эта практика значительно улучшает перцепционное качество выходного сигнала.
Однако было бы весьма предпочтительным, если бы были обеспечены дополнительные улучшенные концепции для кодирования аудио.
Задача настоящего изобретения состоит в том, чтобы обеспечить такие улучшенные концепции для кодирования аудиообъектов. Задача настоящего изобретения решается посредством устройства согласно пункту 1 формулы изобретения, посредством способа для кодирования согласно пункту 15 формулы изобретения, посредством декодера согласно пункту 16 формулы изобретения, посредством способа для декодирования согласно пункту 17 формулы изобретения, посредством системы согласно пункту 18 формулы изобретения, посредством способа согласно пункту 19 формулы изобретения и посредством компьютерной программы согласно пункту 20 формулы изобретения.
Обеспечивается устройство для кодирования речевого сигнала посредством определения вектора кодовой книги алгоритма кодирования речи. Устройство содержит модуль определения матрицы для определения автокорреляционной матрицы R, и модуль определения вектора кодовой книги для определения вектора кодовой книги в зависимости от автокорреляционной матрицы R. Модуль определения матрицы выполнен с возможностью определять автокорреляционную матрицу R посредством определения коэффициентов вектора для вектора r, при этом автокорреляционная матрица R содержит множество строк и множество столбцов, при этом вектор r обозначает один из столбцов или одну из строк автокорреляционной матрицы R, где R(i,j)=r(|i-j|), где R(i, j) обозначает коэффициенты автокорреляционной матрицы R, где i является первым индексом, обозначающим одну из множества строк автокорреляционной матрицы R, и где j является вторым индексом, обозначающим один из множества столбцов автокорреляционной матрицы R.
Устройство выполнено с возможностью использовать вектор кодовой книги, чтобы кодировать речевой сигнал. Например, устройство может генерировать кодированный речевой сигнал, так что кодированный речевой сигнал содержит множество коэффициентов линейного предсказания, указание собственной частоты речевых звуков (например, параметры основного тона), и указание вектора кодовой книги, например, индекс вектора кодовой книги.
Дополнительно, обеспечивается декодер для декодирования кодированного речевого сигнала, который кодирован посредством устройства согласно вышеописанному варианту осуществления, чтобы получать декодированный речевой сигнал.
Дополнительно обеспечивается система. Система содержит устройство согласно вышеописанному варианту осуществления для кодирования входного речевого сигнала, чтобы получать кодированный речевой сигнал. Дополнительно, система содержит декодер согласно вышеописанному варианту осуществления для декодирования кодированного речевого сигнала, чтобы получать декодированный речевой сигнал.
Обеспечиваются улучшенные концепции для целевой функции ACELP алгоритма кодирования речи, которые учитывают не только влияние импульсной характеристики предыдущего кадра на текущий кадр, но также влияние импульсной характеристики текущего кадра в следующем кадре, при оптимизации параметров текущего кадра. Некоторые варианты осуществления реализуют эти улучшения посредством изменения корреляционной матрицы, которая является центральной для стандартной оптимизации ACELP для автокорреляционной матрицы, которая имеет эрмитову теплицеву структуру. Посредством использования этой структуры, является возможным делать оптимизацию ACELP более эффективной в терминах как вычислительной сложности, так и требований к памяти. Одновременно, также применяемая перцепционная модель становится более согласующейся, и межкадровые зависимости могут избегаться, чтобы улучшать производительность под влиянием потери пакетов.
Кодирование речи с использованием парадигмы ACELP основывается на алгоритме наименьших квадратов в перцепционной области, где перцепционная область определяется посредством фильтра. Согласно вариантам осуществления, вычислительная сложность стандартного определения проблемы наименьших квадратов может уменьшаться посредством учета влияния импульсной характеристики при расширении остатка нулями в следующем кадре. Обеспеченные модификации вводят теплицеву структуру для корреляционной матрицы, появляющейся в целевой функции, которая упрощает структуру и уменьшает вычисления. Предложенные концепции уменьшают вычислительную сложность вплоть до 17% без уменьшения перцепционного качества.
Варианты осуществления основываются на обнаружении, что посредством незначительной модификации целевой функции, сложность в оптимизации кодовой книги остатков может быть дополнительно уменьшена. Это уменьшение в сложности приходит без уменьшения в перцепционном качестве. Как альтернатива, так как оптимизация остатка ACELP основывается на итеративных алгоритмах поиска, с представленной модификацией, является возможным увеличивать количество итераций без увеличения в сложности, и этим способом получать улучшенное перцепционное качество.
Как стандартная, так и модифицированная целевые функции моделируют восприятие и стараются минимизировать перцепционное искажение. Однако оптимальное решение для стандартного подхода не является необходимо оптимальным по отношению к модифицированной целевой функции и наоборот. Это одиночно не означает, что один подход будет лучше, чем другой, но аналитические аргументы действительно показывают, что модифицированная целевая функция является более согласующейся. Конкретно, в отличие от стандартной целевой функции, обеспеченные концепции трактуют все выборки внутри подкадра одинаково, с согласующимися и хорошо определенными перцепционными и сигнальными моделями.
В вариантах осуществления, предложенные модификации могут применяться так, что они изменяют только оптимизацию кодовой книги остатков. Это, поэтому, не изменяет структуру битового потока и может применяться обратно совместимым способом к существующим кодекам ACELP.
Дополнительно, обеспечивается способ для кодирования речевого сигнала посредством определения вектора кодовой книги алгоритма кодирования речи. Способ содержит:
- Определение автокорреляционной матрицы R. И:
- Определение вектора кодовой книги в зависимости от автокорреляционной матрицы R.
Определение автокорреляционной матрицы R содержит определение коэффициентов вектора для вектора r. Автокорреляционная матрица R содержит множество строк и множество столбцов. Вектор r обозначает один из столбцов или одну из строк автокорреляционной матрицы R, где
R(i,j)=r(|i-j|).
R(i, j) обозначает коэффициенты автокорреляционной матрицы R, где i является первым индексом, обозначающим одну из множества строк автокорреляционной матрицы R, и где j является вторым индексом, обозначающим один из множества столбцов автокорреляционной матрицы R.
Дополнительно, обеспечивается способ для декодирования кодированного речевого сигнала, который кодирован согласно способу для кодирования речевого сигнала согласно вышеописанному варианту осуществления, чтобы получать декодированный речевой сигнал.
Дополнительно, обеспечивается способ. Способ содержит:
Кодирование входного речевого сигнала согласно вышеописанному способу для кодирования речевого сигнала, чтобы получать кодированный речевой сигнал. И:
Декодирование кодированного речевого сигнала, чтобы получать декодированный речевой сигнал согласно вышеописанному способу для декодирования речевого сигнала.
Дополнительно, обеспечиваются компьютерные программы для осуществления вышеописанных способов, когда исполняются на компьютере или сигнальном процессоре.
Предпочтительные варианты осуществления обеспечиваются в зависимых пунктах формулы изобретения.
В последующем, варианты осуществления настоящего изобретения описываются более подробно со ссылкой на чертежи, на которых:
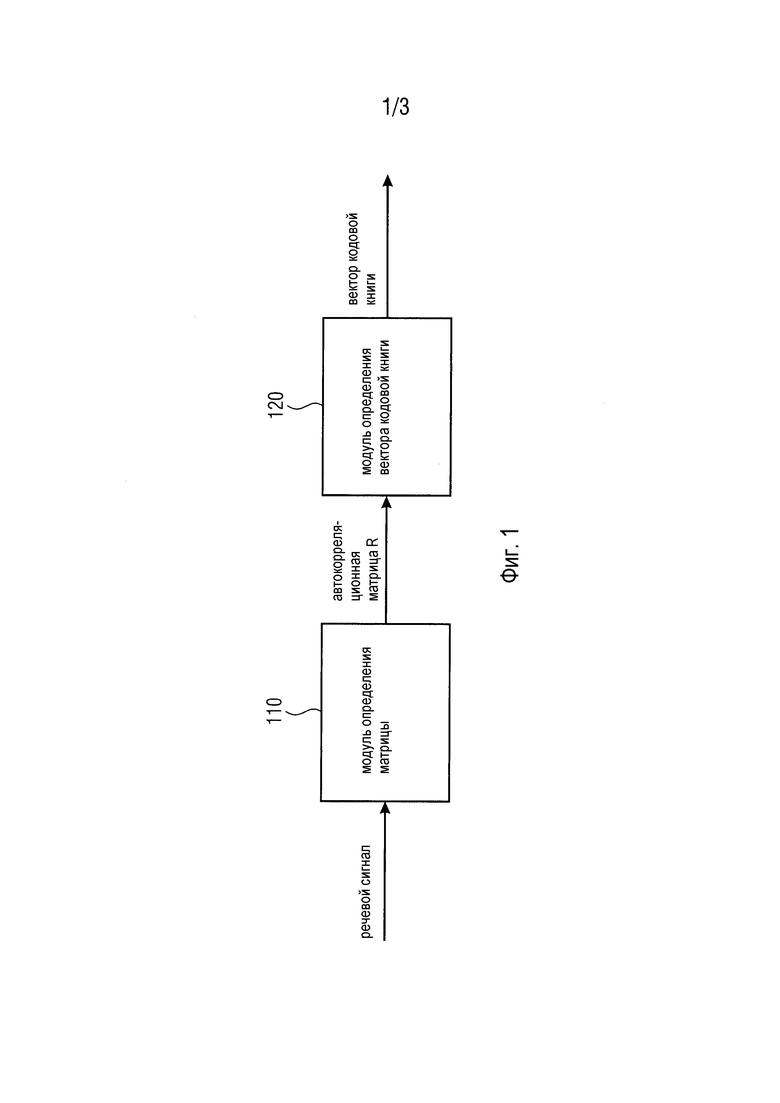
Фиг. 1 иллюстрирует устройство для кодирования речевого сигнала посредством определения вектора кодовой книги алгоритма кодирования речи согласно одному варианту осуществления,
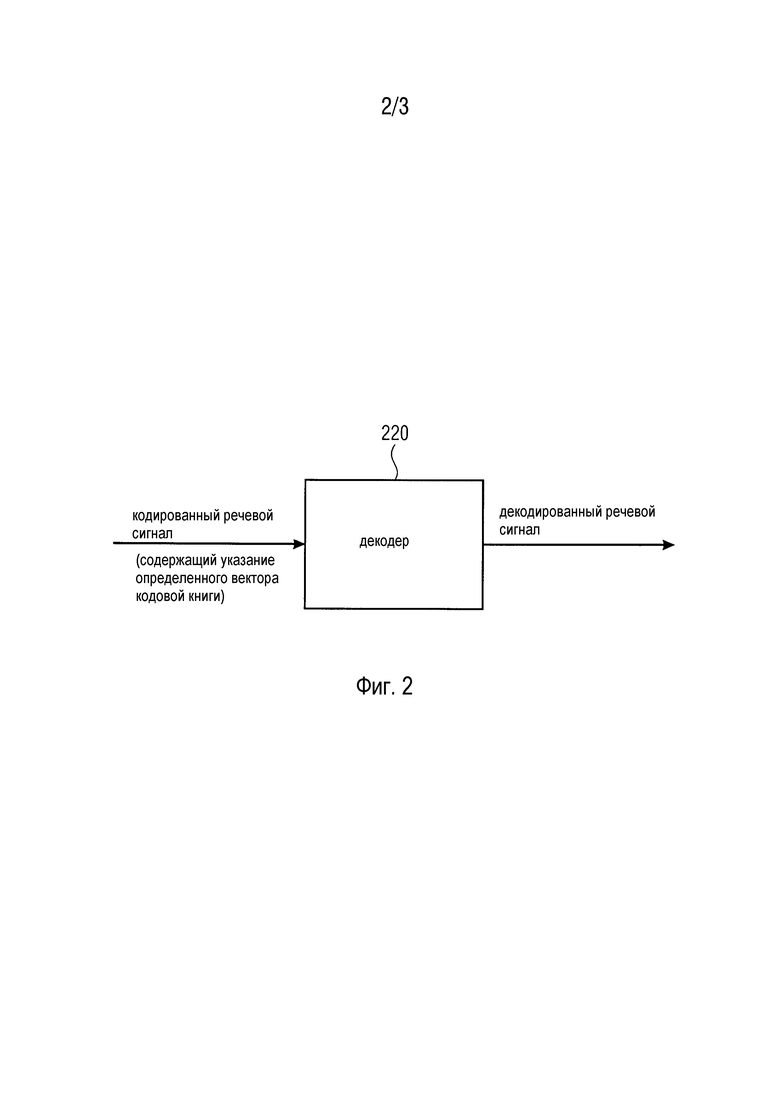
Фиг. 2 иллюстрирует декодер согласно одному варианту осуществления и декодер, и
Фиг. 3 иллюстрирует систему, содержащую устройство для кодирования речевого сигнала согласно одному варианту осуществления и декодер.
Фиг. 1 иллюстрирует устройство для кодирования речевого сигнала посредством определения вектора кодовой книги алгоритма кодирования речи согласно одному варианту осуществления.
Устройство содержит модуль (110) определения матрицы для определения автокорреляционной матрицы R, и модуль (120) определения вектора кодовой книги для определения вектора кодовой книги в зависимости от автокорреляционной матрицы R.
Модуль (110) определения матрицы выполнен с возможностью определять автокорреляционную матрицу R посредством определения коэффициентов вектора для вектора r.
Автокорреляционная матрица R содержит множество строк и множество столбцов, при этом вектор r обозначает один из столбцов или одну из строк автокорреляционной матрицы R, где R(i,j)=r(|i-j|).
R(i, j) обозначает коэффициенты автокорреляционной матрицы R, где i является первым индексом, обозначающим одну из множества строк автокорреляционной матрицы R, и где j является вторым индексом, обозначающим один из множества столбцов автокорреляционной матрицы R.
Устройство выполнено с возможностью использовать вектор кодовой книги, чтобы кодировать речевой сигнал. Например, устройство может генерировать кодированный речевой сигнал, так что кодированный речевой сигнал содержит множество коэффициентов линейного предсказания, указание собственной частоты речевых звуков (например, параметры основного тона), и указание вектора кодовой книги.
Например, согласно одному конкретному варианту осуществления для кодирования речевого сигнала, устройство может быть выполнено с возможностью определять множество коэффициентов линейного предсказания (a(k)) в зависимости от речевого сигнала. Дополнительно, устройство выполнено с возможностью определять сигнал остатка в зависимости от множества коэффициентов линейного предсказания (a(k)).
Дополнительно, модуль 110 определения матрицы может быть выполнен с возможностью определять автокорреляционную матрицу R в зависимости от сигнала остатка.
В последующем, описываются некоторые дополнительные варианты осуществления настоящего изобретения.
Возвращаясь уравнениям 3 и 4, где Уравнение 3 определяет возведенную в квадрат ошибку, показывающую соответствие перцепционной модели, как:
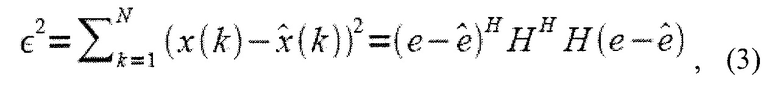
и где Уравнение 4
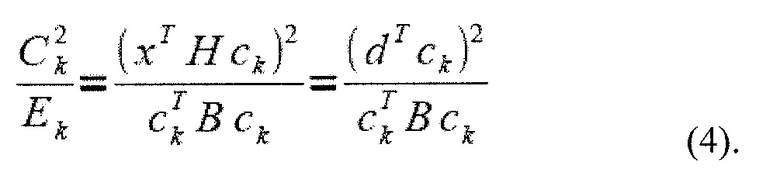
указывает критерий поиска, который подлежит максимизации.
Алгоритм ACELP центрируется около Уравнения 4, которое в свою очередь основывается на Уравнении 3.
Варианты осуществления основываются на обнаружении, что анализ этих уравнений выявляет, что значения квантованного остатка e(k) имеют очень разное влияние на энергию ошибки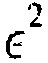 
в зависимости от индекса k. Например, при рассмотрении индексов k=1 и k=N, если единственное ненулевое значение кодовой книги остатков появляется при k=1, то энергия ошибки 
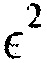сводится к:
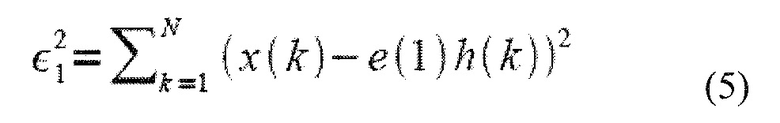
в то время как для k=N, энергия ошибки 
сводится к:
Другими словами, e(1) взвешивается с импульсной характеристикой h(k) в диапазоне от 1 до N, в то время как e(N) взвешивается только с h(1). В терминах спектрального взвешивания, это означает, что каждый e(k) взвешивается с разной спектральной весовой функцией, так что, в крайности, e(N) является линейно взвешенным. С позиции перцепционного моделирования, имеет смысл применять один и тот же перцепционный вес для всех выборок внутри кадра. Уравнение 3 должно, таким образом, быть расширено таким образом, чтобы оно учитывало ZIR в следующем кадре. Следует отметить, что здесь, среди прочего, различие с предшествующим уровнем техники состоит в том, что учитываются как ZIR из предыдущего кадра, так и ZIR в следующем кадре.
Пусть e(k) будет исходным, неквантованным остатком и 
квантованным остатком.
Дополнительно, пусть оба остатка будут ненулевыми в диапазоне от 1 до N и нулевыми в других местах. Тогда
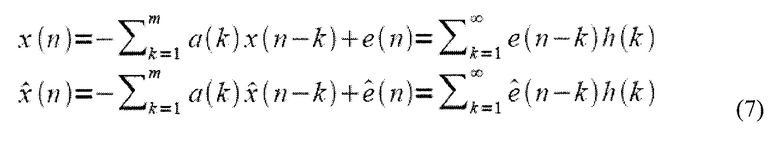
Эквивалентным образом, такие же отношения в матричной форме могут быть выражены как:
где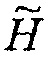 
является бесконечномерной матрицей свертки, соответствующей импульсной характеристике h(k). Подстановка в Уравнение 3 дает
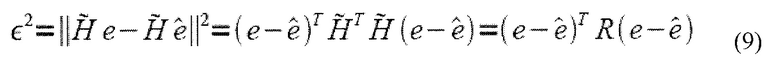
где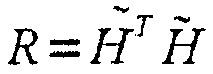 
является эрмитовой теплицевой матрицей конечного размера, соответствующей автокорреляции h(n). Посредством аналогичного вывода как для Уравнения 4, получается целевая функция:
Эта целевая функция очень подобна Уравнению 4. Основное различие состоит в том, что вместо корреляционной матрицы B, здесь эрмитова теплицева матрица R находится в знаменателе.
Как описано выше, эта новая формулировка имеет преимущество, что все выборки остатка e внутри кадра получат одно и то же перцепционное взвешивание. Однако, является важным, что эта формулировка вводит значительные преимущества для вычислительной сложности и требований к памяти также. Так как R является эрмитовой теплицевой матрицей, первый столбец r(0) .. r(N-1) определяет матрицу полностью. Другими словами, вместо сохранения полной матрицы NxN, является достаточным сохранять только Nx1 вектор r(k), что, таким образом, дает значительное сбережение в распределении памяти. Более того, вычислительная сложность также уменьшается, так как не является необходимым определять все NxN элементов, но только первый столбец Nx1. Также индексирование внутри матрицы является простым, так как элемент (i,j) может быть найден посредством R(i,j)=r(|i-j|).
Так как целевая функция в Уравнении 10 является, таким образом, аналогичной Уравнению 4, структура общего ACELP может сохраняться. Конкретно, любая из следующих операций может выполняться с любой целевой функцией, только с незначительными модификациями алгоритма:
1. Оптимизация задержки LTP (адаптивная кодовая книга)
2. Оптимизация кодовой книги импульсов для моделирования остатка (фиксированная кодовая книга)
3. Оптимизация усилений LTP и импульсов, либо раздельно, либо объединенно
4. Оптимизация любых других параметров, чья производительность может быть измерена посредством возведенной в квадрат ошибки из Уравнения 3.
Единственная часть, которая должна модифицироваться в стандартных приложениях ACELP, является обработка корреляционной матрицы B, которая заменяется матрицей R, также как цель, которая должна включать в себя ZIR в следующем кадре.
Некоторые варианты осуществления используют концепции настоящего изобретения посредством того, что, в любом месте в алгоритме ACELP, где появляется корреляционная матрица B, она заменяется автокорреляционной матрицей R. Если все экземпляры матрицы B пропускаются, то вычисление ее значения может избегаться.
Например, автокорреляционная матрица R определяется посредством определения коэффициентов первого столбца r(0), .., r(N-1) автокорреляционной матрицы R.
Матрица R определяется в Уравнении 9 посредством R=HTH, в силу чего ее элементы Rij=r(i-j) могут вычисляться посредством
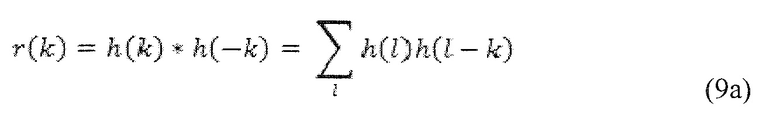
То есть, последовательность r(k) является автокорреляцией для h(k).
Часто, однако, r(k) может получаться посредством даже более эффективного средства. Конкретно, в стандартах кодирования речи, таких как AMR и G.718, последовательность h(k) является импульсной характеристикой фильтра линейного предсказания A(z), фильтрованного посредством перцепционной весовой функции W(z), которая используется, чтобы включать предыскажение. Другими словами, h(k) обозначает перцепционно взвешенную импульсную характеристику модели линейного предсказания.
Фильтр A(z) обычно оценивается из автокорреляции речевого сигнала rX(k), то есть, rX(k) является уже известным. Так как H(z)=A-1(u)W(z), то следует, что автокорреляционная последовательность r(k) может определяться посредством вычисления автокорреляции для w(k) посредством
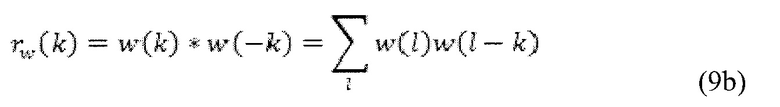
в силу чего автокорреляция для h(k) равняется
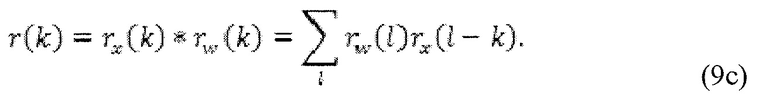
В зависимости от дизайна системы в целом, эти уравнения могут, в некоторых вариантах осуществления, модифицироваться соответственно.
Вектор кодовой книги из кодовой книги может тогда, например, определяться на основе автокорреляционной матрицы R. В частности, Уравнение 10 может, согласно некоторым вариантам осуществления, использоваться, чтобы определять вектор кодовой книги из кодовой книги.
В этом контексте, Уравнение 10 определяет целевую функцию в форме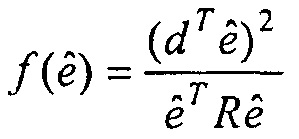 
, которая является в других отношениях такой же формой как в стандартах кодирования речи AMR и G.718, но так, что матрица R теперь имеет симметричную теплицеву структуру. Целевая функция является в своей основе нормализованной корреляцией между целевым вектором d и вектором кодовой книги 
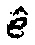и наилучший возможный вектор кодовой книги является тем, который дает наивысшее значение для нормализованной корреляции 
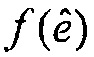, например, который максимизирует нормализованную корреляцию 
.
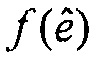Векторы кодовой книги могут, таким образом, оптимизироваться с помощью таких же подходов как в упомянутых стандартах. Конкретно, например, может применяться очень простой алгоритм для нахождения наилучшего вектора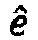 
алгебраической кодовой книги (т.е. фиксированной кодовой книги) для остатка, как описано ниже. Следует, однако, отметить, что значительные усилия были инвестированы в дизайн эффективных алгоритмов поиска (ср. AMR и G.718), и этот алгоритм поиска является только иллюстративным примером применения.
1. Определение начального вектора кодовой книги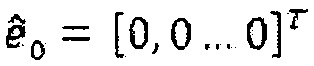 
и установка количества импульсов на p=0.
2. Установка начальной меры качества кодовой книги на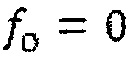 
.
3. Установка временной меры качества кодовой книги на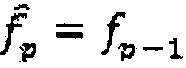 
.
4. Для каждого положения k в векторе кодовой книги
(i) Увеличение p на единицу.
(ii) Если положение k уже содержит отрицательный импульс, переход на этап vii.
(iii) Создание временного вектора кодовой книги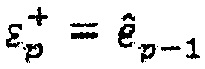 
и добавление положительного импульса в положении k.
(iv) Оценка качества временного вектора кодовой книги посредством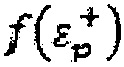 
.
(v) Если временный вектор кодовой книги лучше, чем любой из предыдущих,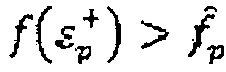 
, то сохранение этого вектора кодовой книги, установка 
и переход на следующую итерацию.
(vi) Если положение k уже содержит положительный импульс, переход на следующую итерацию.
(vii) Создание временного вектора кодовой книги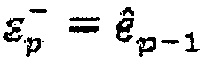 
и добавление отрицательного импульса в положении k.
(viii) Оценка качества временного вектора кодовой книги посредством 
.
(ix) Если временный вектор кодовой книги лучше, чем любой из предыдущих, 
, то сохранение этого вектора кодовой книги, установка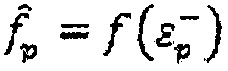 
и переход на следующую итерацию.
5. Определение вектора кодовой книги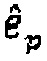 
, чтобы он был последним (то есть, наилучшим) из сохраненных векторов кодовой книги.
6. Если количество импульсов p достигло требуемое количество импульсов, то определение выходного вектора как 
, и остановка. В противном случае, продолжение на этапе 4.
Как уже указано, по сравнению со стандартными применениями ACELP, в некоторых вариантах осуществления, цель модифицируется так, что она включает в себя ZIR в следующем кадре.
Уравнение 1 описывает модель линейного предсказания, используемую в кодеках типа ACELP. Импульсная характеристика при расширении остатка нулями (ZIR, также иногда известная как отклик при отсутствии входного сигнала), указывает на вывод модели линейного предсказания, когда остаток текущего кадра (и все будущие кадры) устанавливается на нуль. ZIR может легко вычисляться посредством определения остатка, который является нулевым от положения N вперед как
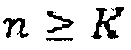
в силу чего ZIR может быть определена как
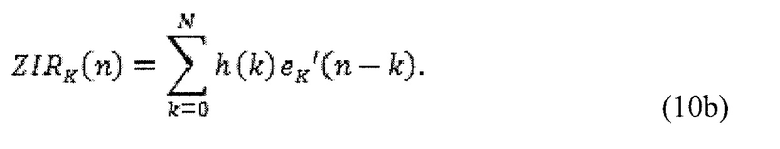
Посредством вычитания этой ZIR из входного сигнала, получается сигнал, который зависит от остатка только из текущего кадра вперед.
Эквивалентным образом, ZIR может определяться посредством фильтрации прошлого входного сигнала как
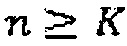
Входной сигнал, где ZIR была удалена, часто известен как цель и может определяться для кадра, который начинается в положении K как d(n)=x(n)-ZIRK(n). Эта цель в принципе в точности равна цели в стандартах AMR и G.718. При квантовании сигнала, квантованный сигнал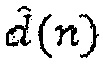 
сравнивается с d(n) для продолжительности кадра K≤n<K+N.
Обратно, остаток текущего кадра имеет влияние на следующие кадры, в силу чего он является полезным, чтобы рассматривать его влияние при квантовании сигнала, то есть, таким образом, может потребоваться оценивать разность 
также за текущим кадром, n > K+N. Однако, чтобы делать это, может потребоваться рассматривать влияние остатка текущего кадра только посредством установки остатков следующих кадров на нуль. Поэтому, может сравниваться ZIR для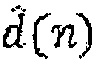 
в следующем кадре. Другими словами, получается модифицированная цель:
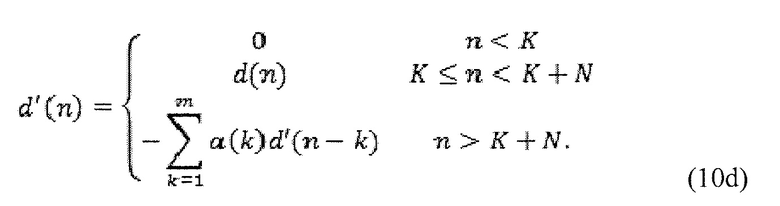
Эквивалентно, с использованием импульсной характеристики h(n) для A(z), тогда
Эта формула может быть записана в удобной матричной форме посредством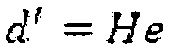 
, где H и e определены как в Уравнении 2. Можно видеть, что модифицированная цель является в точности x из Уравнения 2.
В вычислении матрицы R, отметим, что в теории, импульсная характеристика h(k) является бесконечной последовательностью, которая не является реализуемой в практической системе.
Однако является возможным либо
1) усечение или оконная обработка импульсной характеристики к конечной длине и определение автокорреляции усеченной импульсной характеристики, либо
2) вычисление спектра мощности импульсной характеристики с использованием спектров Фурье ассоциированного LP и перцепционных фильтров, и получать автокорреляцию посредством обратного преобразования Фурье.
Теперь, описывается расширение, использующее LTP.
Долговременный предсказатель (LTP) фактически является также линейным предсказателем.
Согласно одному варианту осуществления, модуль 110 определения матрицы может быть выполнен с возможностью определять автокорреляционную матрицу R в зависимости от перцепционно взвешенного линейного предсказателя, например, в зависимости от долговременного предсказателя.
LP и LTP могут свертываться в один объединенный предсказатель, который включает в себя как форму огибающей спектра, так и гармоническую структуру. Импульсная характеристика такого предсказателя будет очень длинной, в силу чего является даже более трудным управляться с предшествующим уровнем техники. Однако, если автокорреляция линейного предсказателя уже известна, то автокорреляция объединенного предсказателя может быть вычислена посредством простой фильтрации автокорреляции с использованием LTP вперед и назад, или с помощью аналогичной обработки в частотной области.
Отметим, что предыдущие способы, использующие LTP, имеют проблему, когда задержка LTP является более короткой, чем длина кадра, так как LTP будет вызывать цикл обратной связи внутри кадра. Преимущество включения LTP в целевую функцию состоит в том, что, когда задержка LTP является более короткой, чем длина кадра, то эта обратная связь явно учитывается в оптимизации.
В последующем, описывается расширение для быстрой оптимизации в некоррелированной области.
Центральной проблемой в дизайне систем ACELP является уменьшение вычислительной сложности. Системы ACELP являются сложными, так как фильтрация посредством LP вызывает усложненные корреляции между выборками остатков, которые описываются посредством матрицы B или в текущем контексте посредством матрицы R. Так как выборки e(n) являются коррелированными, не является возможным всего лишь квантовать e(n) с требуемой точностью, но должны пробоваться многие комбинации разных квантований с подходом проб и ошибок, чтобы найти наилучшее квантование по отношению к целевой функции из Уравнения 3 или 10, соответственно.
Посредством введения матрицы R, получается новая перспектива для этих корреляций. Именно, так как R имеет эрмитову теплицеву структуру, могут применяться несколько эффективных матричных разложений, таких как разложение по сингулярным значениям, разложение Холецкого или разложение Вандермонда матриц Ганкеля (матрицы Ганкеля являются перевернутыми матрицами Теплица, в силу чего одни и те же разложения могут применяться к матрицам Теплица и Ганкеля) (см. [6] и [7]). Пусть R=E D EH будет разложением для R, так что D является диагональной матрицей такого же размера и ранга что и R. Уравнение 9 может тогда быть модифицировано следующим образом:
где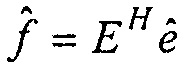 
. Так как D является диагональной, ошибка для каждой выборки f(k) является независимой от других выборок f(i). В Уравнении 10, предполагается, что вектор кодовой книги масштабирован посредством оптимального усиления, в силу чего новая целевая функция равняется
Здесь, выборки снова являются коррелированными (так как изменение квантования одной строки изменяет оптимальное усиление для всех строк), но в сравнении с Уравнением 10, влияние корреляции здесь является ограниченным. Однако, даже если корреляция учитывается, оптимизация этой целевой функции является намного более простой, чем оптимизация Уравнений 3 или 10.
С использованием этого подхода разложения, является возможным
1. применять любой стандартный способ скалярного или векторного квантования с требуемой точностью, или
2. использовать Уравнение 12 в качестве целевой функции с любым стандартным алгоритмом поиска импульсов ACELP.
Оба подхода дают почти оптимальное квантование по отношению к Уравнению 12. Так как стандартные способы квантования, в общем, не требуют каких-либо способов грубой силы (за исключением возможного цикла обратной связи по скорости), и так как матрица D является более простой, чем либо B, или R, оба способа квантования являются менее сложными, чем стандартные алгоритмы поиска импульсов ACELP. Основным источником вычислительной сложности в этом подходе является, таким образом, вычисление матричного разложения.
Некоторые варианты осуществления используют уравнение 12, чтобы определять вектор кодовой книги из кодовой книги. Например, существует несколько матричных факторизаций для R формы R=EHDE. Например,
(a) Разложение по собственным значениям может вычисляться, например, посредством использования научной библиотеки GNU (http://www.gnu.org/software/gsl/manual/html_node/Real-Symmetric-Matrices.html). Матрица R является вещественной и симметричной (также как теплицевой), в силу чего может использоваться функция "gsl_eigen_symm()", чтобы определять матрицы E и D. Другие варианты осуществления такого же разложения по собственным значениям являются легко доступными в литературе [6].
(b) Может использоваться факторизация Вандермонда матриц Теплица [7] с использованием алгоритма, описанного в [8]. Этот алгоритм возвращает матрицы E и D, так что E является матрицей Вандермонда, которая эквивалентна дискретному преобразованию Фурье с неравномерным распределением частот.
С использованием таких факторизаций, вектор e остатка может преобразовываться в область преобразования посредством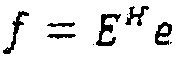 
или 
. В этих областях может применяться любой общий способ квантования, например,
1. Вектор 
может квантоваться посредством алгебраической кодовой книги в точности как в общих вариантах осуществления ACELP. Однако, так как элементы 
являются некоррелированными, усложненная функция поиска как в ACELP не является необходимой, но может применяться простой алгоритм, такой как
(a) Установка начального усиления на g=1
(b) Квантование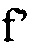 
посредством 
=округление (gf').
(c) Если количество импульсов в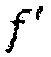 
больше, чем предварительно определенная величина p, 
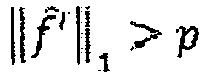, то увеличение усиления g и возвращение на этап b.
(d) В противном случае, если количество импульсов в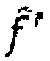 
меньше, чем предварительно определенная величина p, 
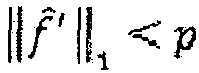, то уменьшение усиления g и возвращение на этап b.
(e) В противном случае, количество импульсов в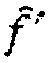 
равняется предварительно определенной величине p, 
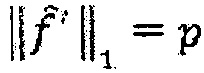, и обработка может останавливаться.
2. Арифметический кодер может использоваться аналогично кодеру, используемому в квантовании спектральных линий в TCX в стандартах AMR-WB+ или MPEG USAC.
Следует отметить, что, так как элементы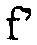 
являются ортогональными (как можно видеть из Уравнения 12) и они имеют один и тот же вес в целевой функции из Уравнения 12, они могут квантоваться отдельно, и с одним и тем же размером шага квантования. Это квантование будет автоматически находить оптимальное (наибольшее) значение целевой функции в Уравнении 12, которое является возможным с той точностью квантования. Другими словами, алгоритмы квантования, представленные выше, будут оба возвращать оптимальное квантование по отношению к Уравнению 12.
Это преимущество оптимальности связано с тем фактом, что элементы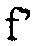 
могут обрабатываться отдельно. Если используется подход кодовой книги, где векторы кодовой книги ck являются нетривиальными (имеют более, чем один ненулевых элементов), то эти векторы кодовой книги более не будут иметь независимых элементов и преимущество матричной факторизации теряется.
Заметим, что факторизация Вандермонда матрицы Теплица может выбираться так, что матрица Вандермонда является матрицей преобразования Фурье, но с неравномерно распределенными частотами. Другими словами, матрица Вандермонда соответствует деформированному по частоте преобразованию Фурье. Следует, что в этом случае вектор f соответствует представлению частотной области сигнала остатка на деформированной частотной шкале (см. "свойство обмена корнями" в [8]).
Является важным отметить, что это следствие не является хорошо известным. На практике, этот результат утверждает, что если сигнал x фильтруется с помощью матрицы свертки C, то
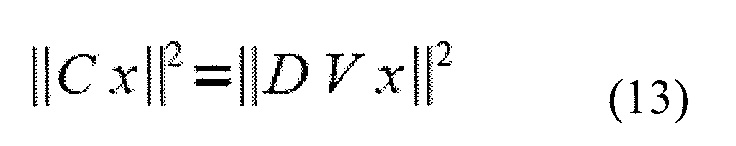
где V является (например, деформированным) преобразованием Фурье (которое является матрицей Вандермонда с элементами на единичном круге) и D является диагональной матрицей. То есть, если требуется измерить энергию фильтрованного сигнала, энергия деформированного по частоте сигнала может эквивалентно измеряться. В противоположность, любая оценка, которая должна делаться в деформированной области Фурье, может эквивалентно делаться в фильтрованной временной области. Вследствие двойственности времени и частоты, также существует эквивалентность между оконной обработкой временной области и деформированием по времени. Практическая проблема, однако, состоит в том, что нахождение матрицы свертки C, которая удовлетворяет вышеупомянутому отношению, является чувствительной к вычислениям проблемой, в силу чего вместо этого часто является более легким найти приближенные решения 
.
Отношение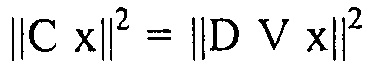 
может использоваться для определения вектора кодовой книги из кодовой книги.
Для этого, следует сначала отметить, что здесь, посредством H, вместо C будет обозначаться матрица свертки как в Уравнении 2. Если, затем, потребуется минимизировать шум квантования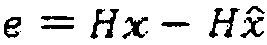 
, его энергия может быть измерена:
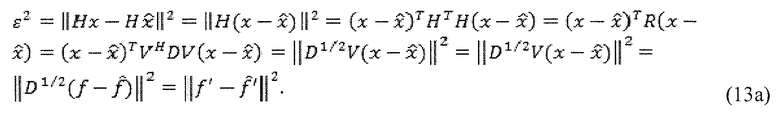
Теперь, описывается расширение для независимости по кадрам.
Когда кодированный речевой сигнал передается по несовершенным линиям передачи, таким как радиоволны, неизменно, пакеты данных иногда теряются. Если кадры зависят друг от друга, так что пакет N необходим, чтобы идеально декодировать N-1, то потеря пакета N-1 будет портить синтез обоих пакетов N-1 и N. Если, с другой стороны, кадры являются независимыми, то потеря пакета N-1 будет портить синтез только пакета N-1. Является, поэтому, важным разработать способы, которые являются свободными от зависимостей между кадрами.
В стандартных системах ACELP, основным источником зависимости между кадрами является LTP и до некоторой степени также LP. Конкретно, так как оба являются фильтрами бесконечной импульсной характеристики (IIR), поврежденный кадр будет вызывать "бесконечный" хвост поврежденных выборок. На практике, этот хвост может быть несколько кадров в длину, что является перцепционно раздражающим.
С использованием структуры текущего изобретения, реализуется путь, посредством которого генерируемая зависимость между кадрами может количественно выражаться посредством ZIR из текущего кадра в следующем. Чтобы избегать этой зависимости между кадрами, должны быть сделаны три модификации для стандартного ACELP.
1. При вычислении ZIR из предыдущего кадра в текущем (под)кадре, она должна вычисляться из исходного (не квантованного) остатка, расширенного с помощью нулей, не из квантованного остатка. Этим способом, ошибки квантования из предыдущего (под)кадра не будут распространяться в текущий (под)кадр.
2. При квантовании текущего кадра, должна учитываться ошибка в ZIR в следующем кадре между исходным и квантованным сигналами. Это может делаться посредством замены корреляционной матрицы B на автокорреляционную матрицу R, как описано выше. Это обеспечивает то, что ошибка в ZIR в следующем кадре минимизируется вместе с ошибкой внутри текущего кадра.
3. Так как распространение ошибки происходит вследствие обоих LP и LTP, оба компонента должны включаться в ZIR. Это является различием со стандартным подходом, где ZIR вычисляется только для LP.
Если ошибки квантования предыдущего кадра при квантовании текущего кадра не учитываются, эффективность в перцепционном качестве вывода теряется. Поэтому, является возможным выбирать учитывать предыдущие ошибки, когда не имеется никакого риска распространения ошибок. Например, стандартная система ACELP применяет разделение на кадры, где каждый 20 мс кадр подразделяется на 4 или 5 подкадров. LTP и остаток квантуются и кодируются отдельно для каждого подкадра, но весь кадр передается как один блок данных. Поэтому, индивидуальные подкадры не могут теряться, но только полные кадры. Следует, что требуется использовать независимые от кадров ZIR только на границах кадров, но ZIR могут использоваться с междкадровыми зависимостями между оставшимися подкадрами.
Варианты осуществления модифицируют стандартные алгоритмы ACELP посредством включения влияния импульсной характеристики текущего кадра в следующем кадре, в целевую функцию текущего кадра. В целевой функции проблемы оптимизации, эта модификация соответствует замене корреляционной матрицы на автокорреляционную матрицу, которая имеет эрмитову теплицеву структуру. Эта модификация имеет следующие преимущества:
1. Вычислительная сложность и требования к памяти уменьшаются вследствие добавленной эрмитовой теплицевой структуры автокорреляционной матрицы.
2. Одна и та же перцепционная модель будет применяться на всех выборках, что делает дизайн и настройку перцепционной модели более простыми, и ее применение более эффективным и согласующимся.
3. Корреляции между кадрами могут полностью избегаться в квантовании текущего кадра, посредством учета только неквантованной импульсной характеристики из предыдущего кадра и квантованной импульсной характеристики в следующем кадре. Это улучшает устойчивость систем, где ожидается потеря пакетов.
Фиг. 2 иллюстрирует декодер 220 для декодирования кодированного речевого сигнала, который кодирован посредством устройства согласно вышеописанному варианту осуществления, чтобы получать декодированный речевой сигнал. Декодер 220 выполнен с возможностью принимать кодированный речевой сигнал, при этом кодированный речевой сигнал содержит указание вектора кодовой книги, который определяется устройством для кодирования речевого сигнала согласно одному из вышеописанных вариантов осуществления, например, индекс определенного вектора кодовой книги. Дополнительно, декодер 220 выполнен с возможностью декодировать кодированный речевой сигнал, чтобы получать декодированный речевой сигнал в зависимости от вектора кодовой книги.
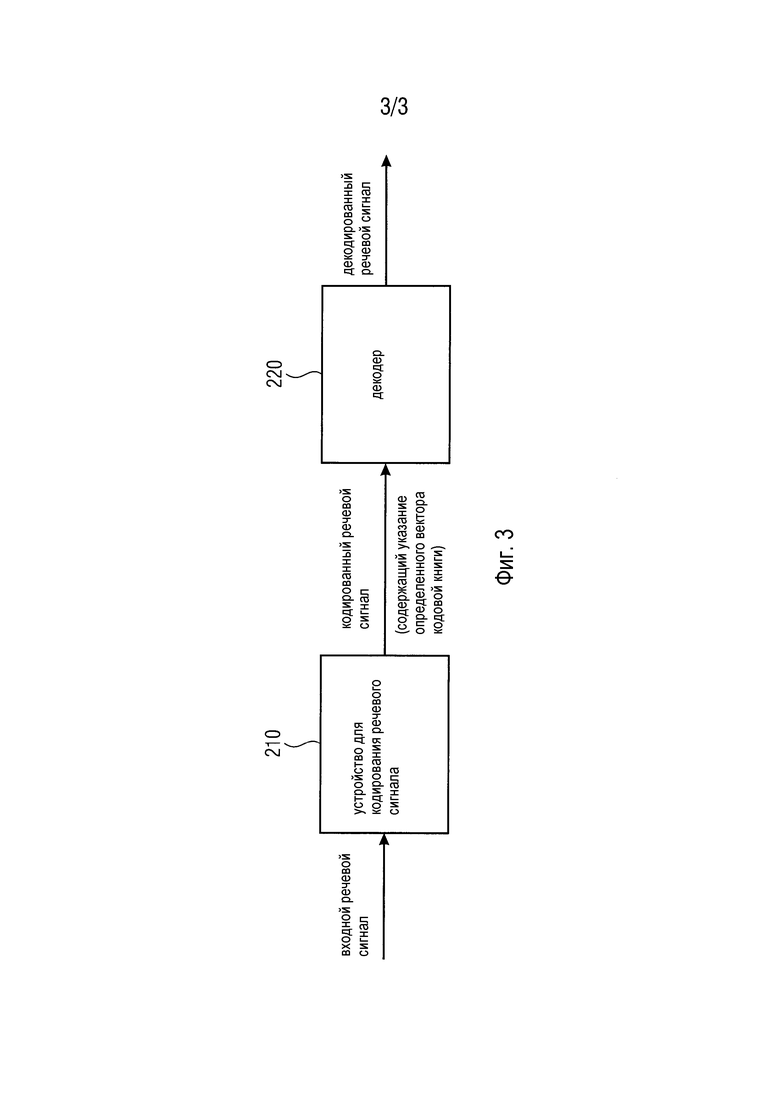
Фиг. 3 иллюстрирует систему согласно одному варианту осуществления. Система содержит устройство 210 согласно одному из вышеописанных вариантов осуществления для кодирования входного речевого сигнала, чтобы получать кодированный речевой сигнал. Кодированный речевой сигнал содержит указание определенного вектора кодовой книги, определенного посредством устройства 210 для кодирования речевого сигнала, например, он содержит индекс вектора кодовой книги. Дополнительно, система содержит декодер 220 согласно вышеописанному варианту осуществления для декодирования кодированного речевого сигнала, чтобы получать декодированный речевой сигнал. Декодер 220 выполнен с возможностью принимать кодированный речевой сигнал. Дополнительно, декодер 220 выполнен с возможностью декодировать кодированный речевой сигнал, чтобы получать декодированный речевой сигнал в зависимости от определенного вектора кодовой книги.
Хотя некоторые аспекты были описаны в контексте устройства, эти аспекты также представляют описание соответствующего способа, где блок или устройство соответствует этапу способа или признаку этапа способа. Аналогично, аспекты, описанные в контексте этапа способа, также представляют описание соответствующего блока или элемента или признака соответствующего устройства.
Новый разложенный сигнал может сохраняться в цифровом запоминающем носителе или может передаваться в среде передачи, такой как беспроводная среда передачи или проводная среда передачи, такая как сеть Интернет.
В зависимости от некоторых требований вариантов осуществления, варианты осуществления изобретения могут осуществляться в аппаратном обеспечении или в программном обеспечении. Вариант осуществления может выполняться с использованием цифрового запоминающего носителя, например, гибкого диска, DVD, CD, ROM, PROM, EPROM, EEPROM или флэш-памяти, имеющего электронно-считываемые сигналы управления, сохраненные на нем, которые взаимодействуют (или являются способными взаимодействовать) с программируемой компьютерной системой, так что выполняется соответствующий способ.
Некоторые варианты осуществления согласно изобретению содержат нетранзиторный носитель данных, имеющий электронно-считываемые сигналы управления, которые являются способными взаимодействовать с программируемой компьютерной системой, так что выполняется один из способов, здесь описанных.
В общем, варианты осуществления настоящего изобретения могут осуществляться как компьютерный программный продукт с программным кодом, при этом программный код является работоспособным для выполнения одного из способов, когда компьютерный программный продукт исполняется на компьютере. Программный код может, например, сохраняться на машиночитаемом носителе.
Другие варианты осуществления содержат компьютерную программу для выполнения одного из способов, здесь описанных, сохраненную на машиночитаемом носителе.
Другими словами, один вариант осуществления нового способа является, поэтому, компьютерной программой, имеющей программный код для выполнения одного из способов, здесь описанных, когда компьютерная программа исполняется на компьютере.
Дополнительный вариант осуществления новых способов является, поэтому, носителем данных (или цифровым запоминающим носителем, или машиночитаемым носителем), содержащим, записанную на нем, компьютерную программу для выполнения одного из способов, здесь описанных.
Дополнительный вариант осуществления нового способа является, поэтому, потоком данных или последовательностью сигналов, представляющей компьютерную программу для выполнения одного из способов, здесь описанных. Поток данных или последовательность сигналов может, например, быть выполнена с возможностью передаваться посредством соединения передачи данных, например, посредством сети Интернет.
Дополнительный вариант осуществления содержит средство обработки, например, компьютер, или программируемое логическое устройство, выполненное с возможностью или выполненное с возможностью выполнять один из способов, здесь описанных.
Дополнительный вариант осуществления содержит компьютер, имеющий, установленную на нем компьютерную программу для выполнения одного из способов, здесь описанных.
В некоторых вариантах осуществления, может использоваться программируемое логическое устройство (например, программируемая пользователем вентильная матрица), чтобы выполнять некоторые или все из функциональностей способов, здесь описанных. В некоторых вариантах осуществления, программируемая пользователем вентильная матрица может взаимодействовать с микропроцессором, чтобы выполнять один из способов, здесь описанных. В общем, способы предпочтительно выполняются посредством любого аппаратного устройства.
Вышеописанные варианты осуществления являются всего лишь иллюстративными для принципов настоящего изобретения. Следует понимать, что модификации и изменения компоновок и деталей, здесь описанных, должны быть очевидными для других специалистов в данной области техники. Предполагается, поэтому, что изобретение ограничено только посредством объема приложенной патентной формулы изобретения и не посредством конкретных деталей, представленных в качестве описания и объяснения вариантов осуществления отсюда.
Ссылки
[1] Salami, R. and Laflamme, C. and Bessette, B. and Adoul, J.P., "ITU-T G. 729 Annex A: reduced complexity 8 kb/s CS-ACELP codec for digital simultaneous voice and data", Communications Magazine, IEEE, vol 35, no 9, pp 56-63, 1997.
[2] 3GPP TS 26.190 V7.0.0, "Adaptive Multi-Rate (AMR-WB) speech codec", 2007.
[3] ITU-T G.718, "Frame error robust narrow-band and wideband embedded variable bit-rate coding of speech and audio from 8-32 kbit/s", 2008.
[4] Schroeder, M. and Atal, B., "Code-excited linear prediction (CELP): High-quality speech at very low bit rates", Acoustics, Speech, and Signal Processing, IEEE Int Conf, pp 937-940, 1985.
[5] Byun, K.J. and Jung, H.B. and Hahn, M. and Kim, K.S., "A fast ACELP codebook search method", Signal Processing, 2002 6th International Conference on, vol 1, pp 422-425, 2002.
[6] G. H. Golub and C. F. van Loan, "Matrix Computations", 3rd Edition, John Hopkins University Press, 1996.
[7] Boley, D.L. and Luk, F.T. and Vandevoorde, D., "Vandermonde factorization of a Hankel matrix", Scientific computing, pp 27-39, 1997.
[8] Bäckström, T. and Magi, C., "Properties of line spectrum pair polynomials - A review", Signal processing, vol. 86, no. 11, pp. 3286-3298, 2006.
[9] A. Härmä, M. Karjalainen, L. Savioja, V. Välimäki, U. Laine, and J. Huopaniemi, "Frequencywarped signal processing for audio applications", J. Audio Eng. Soc, vol. 48, no. 11, pp. 1011-1031, 2000.
[10] T. Laakso, V. Välimäki, M. Karjalainen, and U. Laine, "Splitting the unit delay [FIR/all pass filters design]", IEEE Signal Process. Mag., vol. 13, no. 1, pp. 30-60, 1996.
[11] J. Smith III and J. Abel, "Bark and ERB bilinear transforms", IEEE Trans. Speech Audio Process., vol. 7, no. 6, pp. 697-708, 1999.
[12] R. Schappelle, "The inverse of the confluent Vandermonde matrix", IEEE Trans. Autom. Control, vol. 17, no. 5, pp. 724-725, 1972.
[13] B. Bessette, R. Salami, R. Lefebvre, M. Jelinek, J. Rotola-Pukkila, J. Vainio, H. Mikkola, and K. Jarvinen, "The adaptive multirate wideband speech codec (AMR-WB)", Speech and Audio Processing, IEEE Transactions on, vol. 10, no. 8, pp. 620-636, 2002.
[14] M. Bosi and R. E. Goldberg, Introduction to Digital Audio Coding and Standards. Dordrecht, The Netherlands: Kluwer Academic Publishers, 2003.
[15] B. Edler, S. Disch, S. Bayer, G. Fuchs, and R. Geiger, "A time-warped MDCT approach to speech transform coding", in Proc 126th AES Convention, Munich, Germany, May 2009.
[16] J. Makhoul, "Linear prediction: A tutorial review", Proc. IEEE, vol. 63, no. 4, pp. 561-580, April 1975.
[17] J.-P. Adoul, P. Mabilleau, M. Delprat, and S. Morissette, "Fast CELP coding based on algebraic codes", in Acoustics, Speech, and Signal Processing, IEEE Int Conf (ICASSP'87), April 1987, pp. 1957-1960.
[18] ISO/IEC 23003-3:2012, "MPEG-D (MPEG audio technologies), Part 3: Unified speech and audio coding", 2012.
[19] F.-K. Chen and J.-F. Yang, "Maximum-take-precedence ACELP: a low complexity search method", in Acoustics, Speech, and Signal Processing, 2001. Proceedings.(ICASSP'01). 2001 IEEE International Conference on, vol. 2. IEEE, 2001, pp. 693-696.
[20] R.P. Kumar, "High computational performance in code exited linear prediction speech model using faster codebook search techniques", in Proceedings of the International Conference on Computing: Theory and Applications. IEEE Computer Society, 2007, pp. 458-462.
[21] N.K. Ha, "A fast search method of algebraic codebook by reordering search sequence", in Acoustics, Speech, and Signal Processing, 1999. Proceedings., 1999 IEEE International Conference on, vol. 1. IEEE, 1999, pp. 21-24.
[22] M.A. Ramirez and M. Gerken, "Efficient algebraic multipulse search", in Telecommunications Symposium, 1998. ITS'98 Proceedings. SBT/IEEE International. IEEE, 1998, pp. 231-236.
[23] ITU-T Recommendation G.191, "Software tool library 2009 user's manual", 2009.
[24] ITU-T Recommendation P.863, "Perceptual objective listening quality assessment", 2011.
[25] T. Thiede, W. Treurniet, R. Bitto, C. Schmidmer, T. Sporer, J. Beerends, C. Colomes, M. Keyhl, G. Stoll, K. Brandeburg et al., "PEAQ - the ITU standard for objective measurement of perceived audio quality", Journal of the Audio Engineering Society, vol. 48, 2012.
[26] ITU-R Recommendation BS. 1534-1, "Method for the subjective assessment of intermediate quality level of coding systems", 2003.
Изобретение относится к средствам для кодирования аудиосигнала. Технический результат заключается в повышении эффективности кодирования аудио. Устройство кодирования речевого сигнала посредством определения вектора кодовой книги алгоритма кодирования речи содержит модуль определения матрицы для определения автокорреляционной матрицы R и модуль определения вектора кодовой книги для определения вектора кодовой книги в зависимости от автокорреляционной матрицы R. Модуль определения матрицы выполнен с возможностью определять автокорреляционную матрицу R посредством определения коэффициентов вектора для вектора r, при этом автокорреляционная матрица R содержит множество строк и множество столбцов, при этом вектор r обозначает один из столбцов или одну из строк автокорреляционной матрицы R, где R(i, j)=r(|i-j|), где R(i, j) обозначает коэффициенты автокорреляционной матрицы R, где i является первым индексом, обозначающим одну из множества строк автокорреляционной матрицы R, и где j является вторым индексом, обозначающим один из множества столбцов автокорреляционной матрицы R. 12 н. и 12 з.п. ф-лы, 3 ил.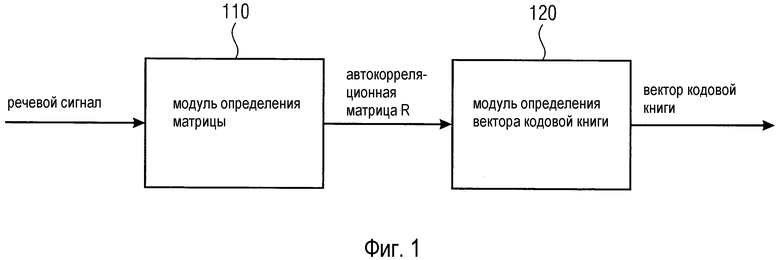
1. Устройство для кодирования речевого сигнала посредством определения вектора кодовой книги алгоритма кодирования речи, при этом устройство содержит:
модуль (110) определения матрицы для определения автокорреляционной матрицы R и
модуль (120) определения вектора кодовой книги для определения вектора кодовой книги в зависимости от автокорреляционной матрицы R,
при этом модуль (110) определения матрицы выполнен с возможностью определять автокорреляционную матрицу R посредством определения коэффициентов вектора для вектора r, при этом автокорреляционная матрица R содержит множество строк и множество столбцов, при этом вектор r обозначает один из столбцов или одну из строк автокорреляционной матрицы R, где
R(i,j)=r(|i-j|),
где R(i, j) обозначает коэффициенты автокорреляционной матрицы R, где i является первым индексом, обозначающим одну из множества строк автокорреляционной матрицы R, и где j является вторым индексом, обозначающим один из множества столбцов автокорреляционной матрицы R,
причем модуль (120) определения вектора кодовой книги выполнен с возможностью определения вектора кодовой книги посредством применения формулы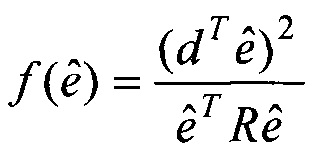 
,
где R является автокорреляционной матрицей и где 
является одним из векторов кодовой книги алгоритма кодирования речи, где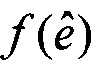 
является нормализованной корреляцией и где dT определяется согласно
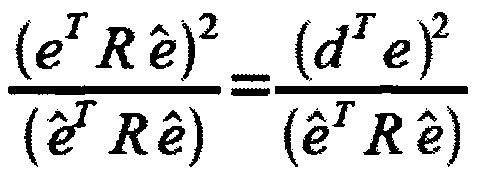
где е является исходным, неквантованным остаточным сигналом.
2. Устройство по п. 1, в котором модуль (120) определения вектора кодовой книги выполнен с возможностью определять тот вектор кодовой книги 
алгоритма кодирования речи, который максимизирует нормализованную корреляцию
.
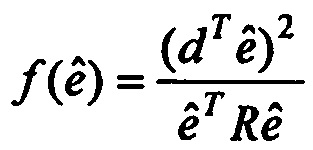3. Устройство по п. 1,
в котором модуль (110) определения матрицы выполнен с возможностью определять коэффициенты вектора для вектора r посредством применения формулы:
r(k) = h(k) * h(-k),
где h(k) обозначает перцепционно взвешенную импульсную характеристику модели линейного предсказания и где k является индексом, который является целым числом.
4. Устройство по п. 1, в котором модуль (110) определения матрицы выполнен с возможностью определять автокорреляционную матрицу R в зависимости от перцепционно взвешенного линейного предсказателя.
5. Устройство по п. 1, в котором модуль (120) определения вектора кодовой книги выполнен с возможностью разлагать автокорреляционную матрицу R посредством выполнения матричного разложения.
6. Устройство по п. 5, в котором модуль (120) определения вектора кодовой книги выполнен с возможностью выполнять матричное разложение, чтобы определять диагональную матрицу D для определения вектора кодовой книги.
7. Устройство по п. 6, в котором модуль (120) определения вектора кодовой книги выполнен с возможностью определять вектор кодовой книги посредством использования
,
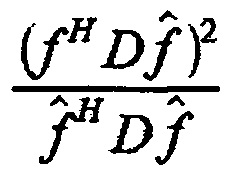где D является диагональной матрицей, где f является первым вектором и где 
является вторым вектором.
8. Устройство по п. 6, в котором модуль (120) определения вектора кодовой книги выполнен с возможностью выполнять факторизацию Вандермонда над автокорреляционной матрицей R, чтобы разлагать автокорреляционную матрицу R, чтобы выполнять матричное разложение, чтобы определять диагональную матрицу D для определения вектора кодовой книги.
9. Устройство по п. 6, в котором модуль (120) определения вектора кодовой книги выполнен с возможностью использовать уравнение
||Сх||2=||DVx||2,
чтобы определять вектор кодовой книги, где С обозначает матрицу свертки, где V обозначает преобразование Фурье и где х обозначает речевой сигнал.
10. Устройство по п. 6, в котором модуль (120) определения вектора кодовой книги выполнен с возможностью выполнять разложение по сингулярным значениям над автокорреляционной матрицей R, чтобы разлагать автокорреляционную матрицу R, чтобы выполнять матричное разложение, чтобы определять диагональную матрицу D для определения вектора кодовой книги.
11. Устройство по п. 6, в котором модуль (120) определения вектора кодовой книги выполнен с возможностью выполнять разложение Холецкого над автокорреляционной матрицей R, чтобы разлагать автокорреляционную матрицу R, чтобы выполнять матричное разложение, чтобы определять диагональную матрицу D для определения вектора кодовой книги.
12. Устройство по п. 1, в котором модуль (120) определения вектора кодовой книги выполнен с возможностью определять вектор кодовой книги в зависимости от нулевой импульсной характеристики речевого сигнала.
13. Устройство по п. 1, в котором устройство является кодером для кодирования речевого сигнала посредством использования кодирования речи на основе линейного предсказания с алгебраическим кодовым возбуждением и
в котором модуль (120) определения вектора кодовой книги выполнен с возможностью определять вектор кодовой книги на основе автокорреляционной матрицы R как вектор кодовой книги алгебраической кодовой книги.
14. Устройство для кодирования речевого сигнала посредством определения вектора кодовой книги алгоритма кодирования речи, при этом устройство содержит:
модуль (110) определения матрицы для определения автокорреляционной матрицы R и
модуль (120) определения вектора кодовой книги для определения вектора кодовой книги в зависимости от автокорреляционной матрицы R,
при этом модуль (110) определения матрицы выполнен с возможностью определять автокорреляционную матрицу R посредством определения коэффициентов вектора для вектора r, при этом автокорреляционная матрица R содержит множество строк и множество столбцов, при этом вектор r обозначает один из столбцов или одну из строк автокорреляционной матрицы R, где
R(i,j)=r(|i-j|),
где R(i, j) обозначает коэффициенты автокорреляционной матрицы R, где i является первым индексом, обозначающим одну из множества строк автокорреляционной матрицы R, и где j является вторым индексом, обозначающим один из множества столбцов автокорреляционной матрицы R,
причем модуль (120) определения вектора кодовой книги выполнен с возможностью разлагать автокорреляционную матрицу R посредством выполнения матричного разложения,
причем модуль (120) определения вектора кодовой книги выполнен с возможностью выполнять матричное разложение, чтобы определять диагональную матрицу D для определения вектора кодовой книги, и
причем модуль (120) определения вектора кодовой книги выполнен с возможностью определять вектор кодовой книги посредством использования
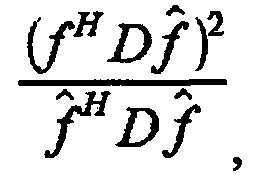
где D является диагональной матрицей, где f является первым вектором и где 
является вторым вектором.
15. Устройство для кодирования речевого сигнала посредством определения вектора кодовой книги алгоритма кодирования речи, при этом устройство содержит:
модуль (110) определения матрицы для определения автокорреляционной матрицы R и
модуль (120) определения вектора кодовой книги для определения вектора кодовой книги в зависимости от автокорреляционной матрицы R,
при этом модуль (110) определения матрицы выполнен с возможностью определять автокорреляционную матрицу R посредством определения коэффициентов вектора для вектора r, при этом автокорреляционная матрица R содержит множество строк и множество столбцов, при этом вектор r обозначает один из столбцов или одну из строк автокорреляционной матрицы R, где
R(i,j)=r(|i-j|),
где R(i, j) обозначает коэффициенты автокорреляционной матрицы R, где i является первым индексом, обозначающим одну из множества строк автокорреляционной матрицы R, и где j является вторым индексом, обозначающим один из множества столбцов автокорреляционной матрицы R,
причем модуль (120) определения вектора кодовой книги выполнен с возможностью разлагать автокорреляционную матрицу R посредством выполнения матричного разложения,
причем модуль (120) определения вектора кодовой книги выполнен с возможностью выполнять матричное разложение, чтобы определять диагональную матрицу D для определения вектора кодовой книги, и
причем модуль (120) определения вектора кодовой книги выполнен с возможностью выполнять факторизацию Вандермонда над автокорреляционной матрицей R, чтобы разлагать автокорреляционную матрицу R, чтобы выполнять матричное разложение, чтобы определять диагональную матрицу D для определения вектора кодовой книги.
16. Система для кодирования речевого сигнала посредством определения вектора кодовой книги алгоритма кодирования речи и для декодирования кодированного речевого сигнала, чтобы получать декодированный речевой сигнал, содержащая:
устройство (210) по одному из пп. 1-15 для кодирования входного речевого сигнала, чтобы получать кодированный речевой сигнал, и
декодер (220) для декодирования кодированного речевого сигнала, чтобы получать декодированный речевой сигнал,
причем декодер (220) выполнен с возможностью принимать кодированный речевой сигнал, причем кодированный речевой сигнал содержит указание вектора кодовой книги, определенного устройством по одному из пп. 1-15,
причем декодер (220) выполнен с возможностью декодировать кодированный речевой сигнал для получения декодированного речевого сигнала в зависимости от вектора кодовой книги.
17. Способ кодирования речевого сигнала посредством определения вектора кодовой книги алгоритма кодирования речи, при этом способ содержит:
определение автокорреляционной матрицы R и
определение вектора кодовой книги в зависимости от автокорреляционной матрицы R,
при этом определение автокорреляционной матрицы R содержит определение коэффициентов вектора для вектора r, при этом автокорреляционная матрица R содержит множество строк и множество столбцов, при этом вектор r обозначает один из столбцов или одну из строк автокорреляционной матрицы R, где
R(i,j)=r(|i-j|),
где R(i, j) обозначает коэффициенты автокорреляционной матрицы R, где i является первым индексом, обозначающим одну из множества строк автокорреляционной матрицы R, и где j является вторым индексом, обозначающим один из множества столбцов автокорреляционной матрицы R,
причем определение вектора кодовой книги выполняется посредством применения формулы
,
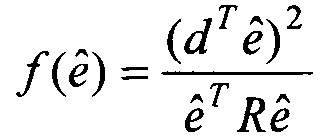где R является автокорреляционной матрицей и где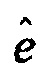 
является одним из векторов кодовой книги алгоритма кодирования речи, где 
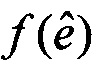является нормализованной корреляцией и где dT определяется согласно
,
где е является исходным, неквантованным остаточным сигналом.
18. Способ кодирования речевого сигнала посредством определения вектора кодовой книги алгоритма кодирования речи, при этом способ содержит:
определение автокорреляционной матрицы R и
определение вектора кодовой книги в зависимости от автокорреляционной матрицы R,
при этом определение автокорреляционной матрицы R содержит определение коэффициентов вектора для вектора r, при этом автокорреляционная матрица R содержит множество строк и множество столбцов, при этом вектор r обозначает один из столбцов или одну из строк автокорреляционной матрицы R, где
R(i,j)=r(|i-j|),
где R(i, j) обозначает коэффициенты автокорреляционной матрицы R, где i является первым индексом, обозначающим одну из множества строк автокорреляционной матрицы R, и где j является вторым индексом, обозначающим один из множества столбцов автокорреляционной матрицы R,
причем разложение автокорреляционной матрицы R выполняется посредством выполнения матричного разложения,
причем выполнение матричного разложения выполняется, чтобы определять диагональную матрицу D для определения вектора кодовой книги, и
причем определение вектора кодовой книги выполняется посредством использования
,
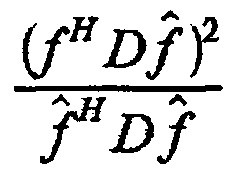где D является диагональной матрицей, где f является первым вектором и где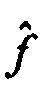 
является вторым вектором.
19. Способ кодирования речевого сигнала посредством определения вектора кодовой книги алгоритма кодирования речи, при этом способ содержит:
определение автокорреляционной матрицы R и
определение вектора кодовой книги в зависимости от автокорреляционной матрицы R,
при этом определение автокорреляционной матрицы R содержит определение коэффициентов вектора для вектора r, при этом автокорреляционная матрица R содержит множество строк и множество столбцов, при этом вектор r обозначает один из столбцов или одну из строк автокорреляционной матрицы R, где
R(i,j)=r(|i-j |),
где R(i, j) обозначает коэффициенты автокорреляционной матрицы R, где i является первым индексом, обозначающим одну из множества строк автокорреляционной матрицы R, и где j является вторым индексом, обозначающим один из множества столбцов автокорреляционной матрицы R,
причем разложение автокорреляционной матрицы R выполняется посредством выполнения матричного разложения,
причем выполнение матричного разложения выполняется, чтобы определять диагональную матрицу D для определения вектора кодовой книги, и
причем выполнение матричного разложения, чтобы определять диагональную матрицу D для определения вектора кодовой книги, выполняется посредством выполнения факторизации Вандермонда над автокорреляционной матрицей R, чтобы разлагать автокорреляционную матрицу R.
20. Способ для кодирования входного речевого сигнала посредством определения вектора кодовой книги алгоритма кодирования речи и для декодирования кодированного речевого сигнала, чтобы получать декодированный речевой сигнал, содержащий:
кодирование входного речевого сигнала согласно способу по одному из пп. 17-19, чтобы получать кодированный речевой сигнал, причем кодированный речевой сигнал содержит указание вектора кодовой книги, и
декодирование кодированного речевого сигнала, чтобы получать декодированный речевой сигнал, в зависимости от вектора кодовой книги.
21. Компьютерно-читаемый носитель, содержащий компьютерную программу для осуществления способа по п. 17, когда исполняется на компьютере или сигнальном процессоре.
22. Компьютерно-читаемый носитель, содержащий компьютерную программу для осуществления способа по п. 18, когда исполняется на компьютере или сигнальном процессоре.
23. Компьютерно-читаемый носитель, содержащий компьютерную программу для осуществления способа по п. 19, когда исполняется на компьютере или сигнальном процессоре.
24. Компьютерно-читаемый носитель, содержащий компьютерную программу для осуществления способа по п. 20, когда исполняется на компьютере или сигнальном процессоре.
| US 5265167 A, 23.11.1993 | |||
| Дорожная спиртовая кухня | 1918 |
|
SU98A1 |
| EP 1833047 A1, 12.09.2007 | |||
| Способ приготовления лака | 1924 |
|
SU2011A1 |
| RU 2010151983 A, 27.06.2012. | |||
