Варианты осуществления настоящего изобретения относятся к кодеру для кодирования аудиосигнала для получения потока данных и к декодеру для декодирования потока данных для получения аудиосигнала. Дополнительные варианты осуществления относятся к соответствующему способу кодирования аудиосигнала и декодирования потока данных. Дополнительный вариант осуществления относится к компьютерной программе, выполняющей этапы способов кодирования и/или декодирования.
Аудиосигнал, который должен быть закодирован, может представлять собой, например, речевой сигнал; т.е. кодер соответствует речевому кодеру, и декодер соответствует речевому декодеру. Наиболее часто используемой парадигмой в кодировании речи является алгебраическое линейное предсказание с мультикодовым управлением (ACELP), которое используется в таких стандартах, как семейство AMR, G.718 и MPEG USAC. Оно основано на моделировании речи с использованием модели источника, состоящей из линейного прогноза (LP) для моделирования огибающей спектра, долговременного прогноза (LTP) для моделирования основной частоты и алгебраической кодовой книги для разности. Параметры кодовой книги оптимизированы в области перцепционно взвешенного синтеза. Перцепционная модель основана на фильтре, посредством чего отображение разности на взвешенный вывод описывается комбинацией линейного прогноза и взвешенного фильтра.
Наибольшая часть вычислительной сложности в кодеках ACELP тратится на выбор элемента алгебраической кодовой книги, что происходит при квантовании разности. Отображение области разности в область взвешенного синтеза по существу представляет собой умножение на матрицу размера N x N, где N - длина вектора. Вследствие этого отображения, с точки зрения отношения сигнала к шуму (SNR) взвешенного вывода, разностные отсчеты коррелированы и не могут быть квантованы независимо. Из этого следует, что каждый потенциальный вектор кодовой книги должен быть оценен явно в области взвешенного синтеза, чтобы определить наилучший элемент. Этот подход известен как алгоритм анализа посредством синтеза. Оптимальная производительность возможна только при поиске перебором кодовой книги. Размер кодовой книги зависит от битовой скорости, но при заданной битовой скорости B имеется 2B элементов для оценки при общей сложности O(2BN2), что явно нереалистично, когда B больше или равно 11. Таким образом, в практических кодеках используют неоптимальное квантование, которое балансирует между сложностью и качеством. Были представлены несколько из этих итеративных алгоритмов для нахождения наилучшего квантования, которые ограничивают сложность за счет точности. Чтобы преодолеть это ограничение, необходим новый подход.
Задача настоящего изобретения состоит в том, чтобы обеспечить концепцию для кодирования и декодирования аудиосигналов, избегая упомянутых выше недостатков.
Задача решена посредством независимых пунктов формулы изобретения.
Первый вариант осуществления обеспечивает кодер для кодирования аудиосигнала в поток данных. Кодер содержит модуль (линейного или долговременного) предсказания, модуль разложения на множители, преобразователь и стадию квантования и кодирования. Модуль предсказания выполнен с возможностью анализировать аудиосигнал, чтобы получить коэффициенты (линейного или долговременного) предсказания, описывающие огибающую спектра аудиосигнала или основную частоту аудиосигнала, и подвергнуть аудиосигнал функции анализирующей фильтрации, зависящей от коэффициентов предсказания, чтобы выдать разностный сигнал аудиосигнала. Модуль разложения на множители выполнен с возможностью применять матричное разложение на множители к автокорреляционной или ковариационной матрице функции синтезирующей фильтрации, заданной коэффициентами предсказания, чтобы получить матрицы, разложенные на множители. Преобразователь выполненным с возможностью преобразовывать разностный сигнал на основе матриц, разложенных на множители, чтобы получить преобразованный разностный сигнал. Стадия квантования и кодирования выполнена с возможностью квантовать преобразованный разностный сигнал, чтобы получить квантованный преобразованный разностный сигнал или закодированный квантованный преобразованный разностный сигнал.
Другой вариант осуществления обеспечивает декодер для декодирования потока данных в аудиосигнал. Декодер содержит стадию декодирования, обратный преобразователь и стадию синтеза. Стадия декодирования выполнена с возможностью выдавать преобразованный разностный сигнал на основе входящего квантованного преобразованного разностного сигнала или на основе входящего закодированного квантованного преобразованного разностного сигнала. Обратный преобразователь выполнен с возможностью обратно преобразовывать разностный сигнал из преобразованного разностного сигнала на основе матриц, разложенных на множители, полученных в результате матричного разложения на множители автокорреляционной или ковариационной матрицы функции синтезирующей фильтрации, заданной коэффициентами предсказания, описывающими огибающую спектра аудиосигнала или основную частоту аудиосигнала, чтобы получить матрицы разложения на множители. Стадия синтеза выполнена с возможностью синтезировать аудиосигнал на основе разностного сигнала посредством использования функции синтезирующей фильтрации, заданной коэффициентами предсказания.
Как видно на основе этих двух вариантов осуществления, кодирование и декодирование представляют собой двухэтапные процессы, что делает эту концепцию сопоставимой с кодированием ACELP. Первый этап дает возможность квантования синтеза относительно огибающей спектра или основной частоты, в то время как вторая стадия дает возможность (прямого) квантования или синтеза разностного сигнала, также называемого сигналом возбуждения, и представления сигнала после фильтрации сигнала с помощью огибающей спектра или основной частоты аудиосигнала. Кроме того, аналогично кодированию ACELP, квантование разностного сигнала или сигнала возбуждения соответствует задаче оптимизации, причем целевая функция задачи оптимизации в соответствии с раскрытыми здесь идеями в значительной степени отличается от кодирования ACELP. Более подробно, идеи настоящего изобретения основаны на принципе, что матричное разложение на множители используется для декорреляции целевой функции задачи оптимизации, посредством чего можно избежать дорогих вычислительных итераций и гарантировать оптимальную производительность. Матричное разложение на множители, которое является центральным этапом изложенных вариантов осуществления, включено в вариант осуществления кодера, и предпочтительно, но не обязательно, может быть включено в вариант осуществления декодера.
Матричное разложение на множители может быть основано на различных методиках, например на разложении по собственным значениям, на разложении на множители Вандермонда или на любом другом разложении на множители, причем для каждой выбранной методики разложение разлагает на множители матрицу, например, автокорреляционную или ковариационную матрицу функции синтезирующей фильтрации, заданной коэффициентами (линейного или долговременного) предсказания, которые обнаружены посредством первой аудиоинформацией на первой стадии (линейного предсказания или долговременного предсказания) кодирования или декодирования.
В соответствии с другим вариантом осуществления модуль разложения на множители разлагает на множители функцию синтезирующей фильтрации, содержащую коэффициенты предсказания, которые сохранены с использованием матрицы, или разлагает на множители взвешенную версию матрицы функции синтезирующей фильтрации. Например, разложение на множители может быть выполнено при помощи матрицы V Вандермонда, диагональной матрицы D и преобразованной сопряженной версии матрицы V* Вандермонда. Матрица Вандермонда может быть разложена на множители с использованием формулы R=V*DV или C=V*DV, причем матрица автокорреляции R или ковариационная матрица C заданы преобразованной сопряженной версией матрицы функции H* синтезирующей фильтрации и регулярной версией матрицы H функции синтеза, т.е. R =H*H или C=H*H.
В соответствии с дополнительным вариантом осуществления преобразователь, исходя из ранее определенной диагональной матрицы D и ранее определенной матрицы Вандермонда V, преобразовывает разностный сигнал x в преобразованный разностный сигнал y с использованием формулы y=D1/2Vx или формула y=DVx.
В соответствии с дополнительным вариантом осуществления стадия квантования и кодирования теперь может квантовать преобразованный разностный сигнал y, чтобы получить квантованный преобразованный разностный сигнал 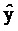 . Это преобразование представляет собой задачу оптимизации, как описано выше, причем используется целевая функция
. Это преобразование представляет собой задачу оптимизации, как описано выше, причем используется целевая функция 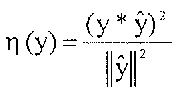 . При этом выгодно, чтобы эта целевая функция имела уменьшенную сложность по сравнению с целевыми функциями, используемыми для других способов кодирования или декодирования, такими как целевая функция, используемая в кодере ACELP.
. При этом выгодно, чтобы эта целевая функция имела уменьшенную сложность по сравнению с целевыми функциями, используемыми для других способов кодирования или декодирования, такими как целевая функция, используемая в кодере ACELP.
В соответствии с вариантом осуществления декодер принимает матрицы, разложенные на множители, от кодера, например, вместе с потоком данных, или в соответствии с другим вариантом осуществления декодер содержит опциональный модуль разложения на множители, который выполняет матричное разложение на множители. В соответствии с предпочтительным вариантом осуществления декодер принимает матрицы, разложенные на множители, непосредственно и отклоняет коэффициенты предсказания от этих матриц, разложенных на множители, поскольку матрицы имеют свое начало координат в коэффициентах предсказания (см. кодер). Этот вариант осуществления позволяет дополнительно уменьшить сложность декодера.
Дополнительные варианты осуществления обеспечивают соответствующие способы кодирования аудиосигнала в поток данных и декодирования потока данных в аудиосигнал. В соответствии с дополнительным вариантом осуществления способ кодирования, а также способ декодирования могут быть выполнены или по меньшей мере частично выполнены процессором, таким как центральный процессор компьютера.
Варианты осуществления настоящего изобретения будут описаны со ссылкой на приложенные чертежи.
Фиг. 1А показывает блок-схему кодера для кодирования аудиосигнала в соответствии с первым вариантом осуществления;
Фиг. 1В показывает блок-схему последовательности операций соответствующего способа кодирования аудиосигнала в соответствии с первым вариантом осуществления;
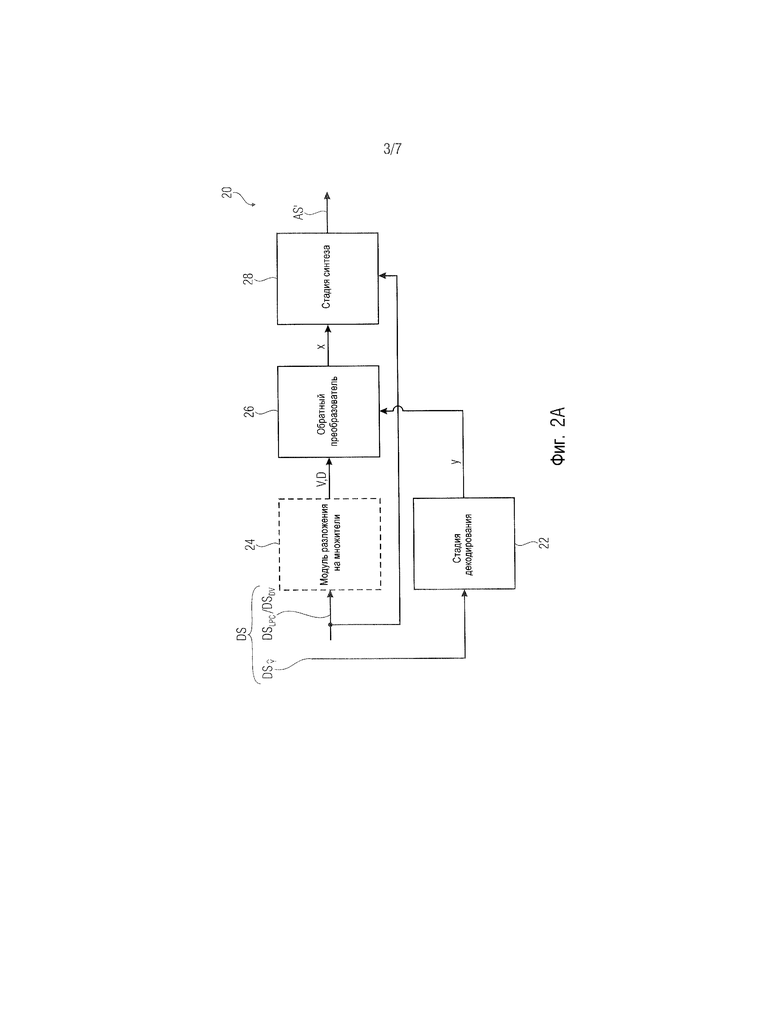
Фиг. 2А показывает блок-схему декодера для декодирования потока данных в соответствии со вторым вариантом осуществления;
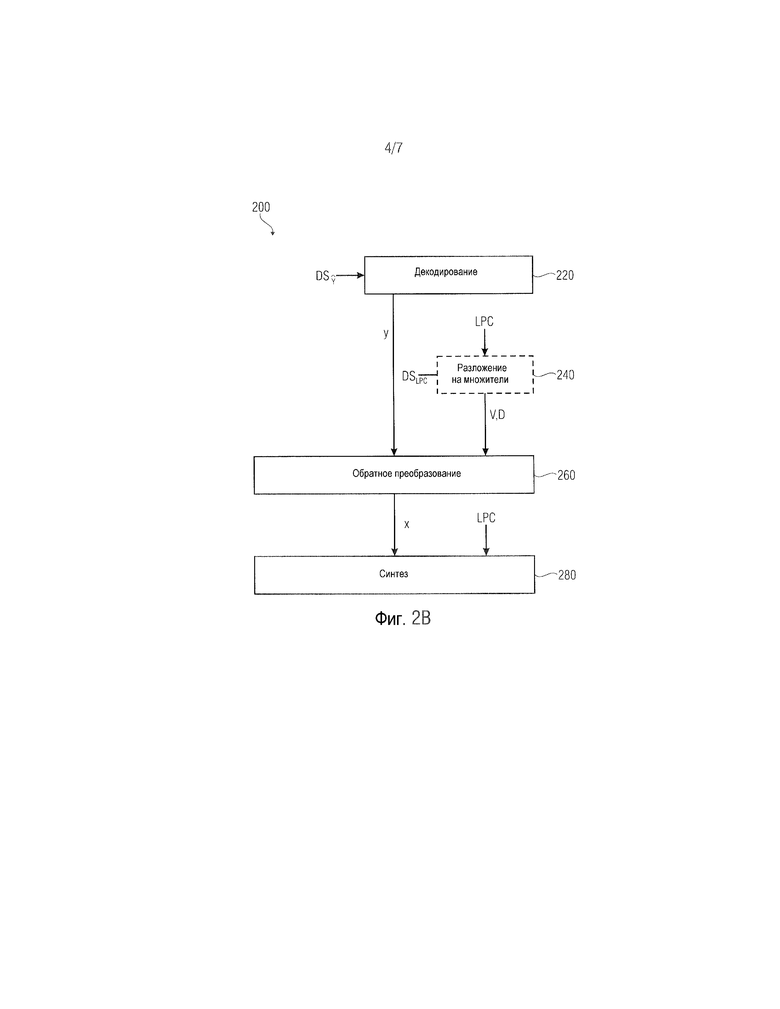
Фиг. 2В показывает блок-схему последовательности операций соответствующего способа декодирования потока данных в соответствии со вторым вариантом осуществления;
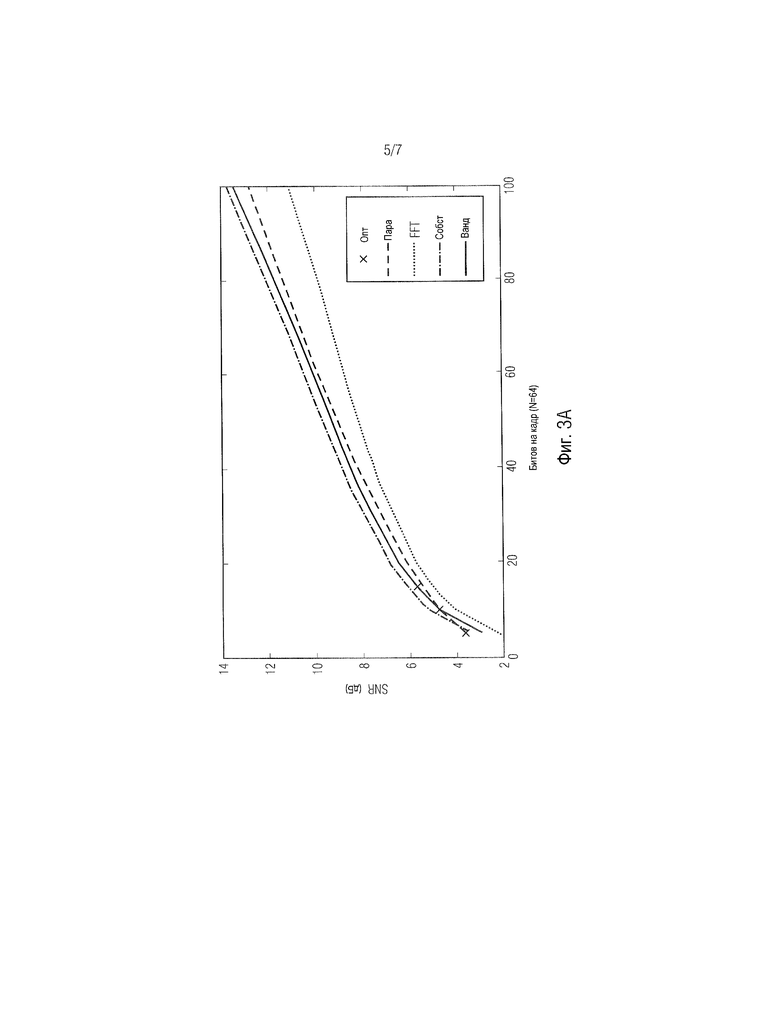
Фиг. 3А показывает схему, иллюстрирующую среднее перцепционное соотношение сигнал/шум как функцию битов на кадр для различных способов квантования;
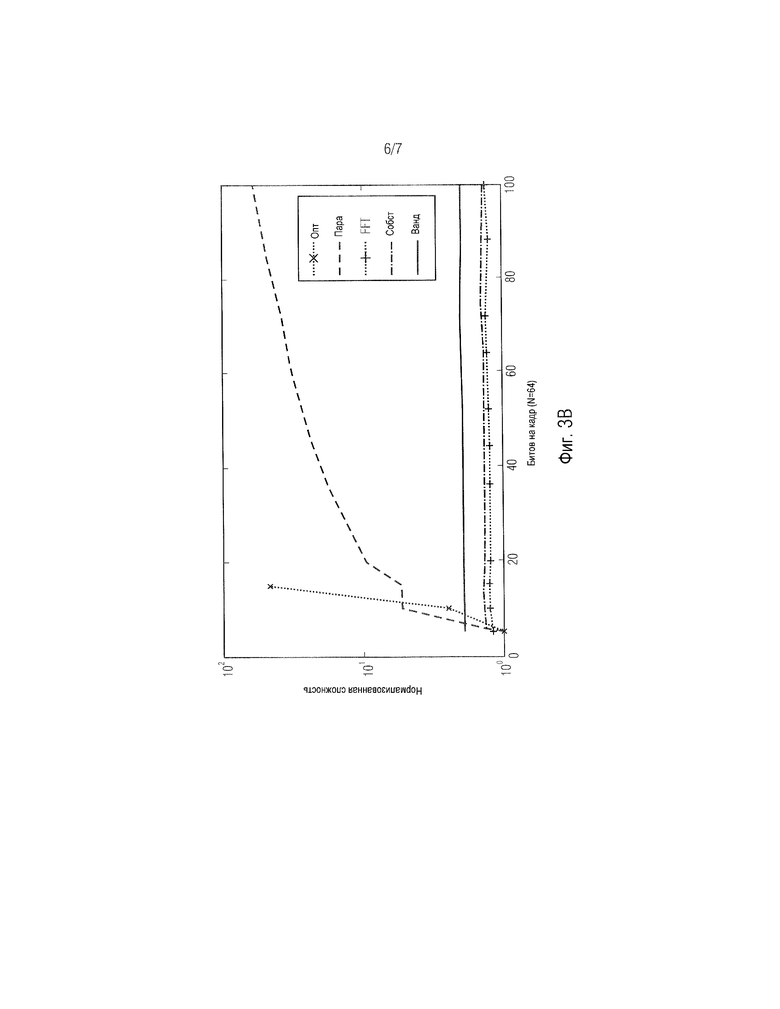
Фиг. 3В показывает схему, иллюстрирующую нормализованное время выполнения разных способов квантования как функцию битов на кадр; и
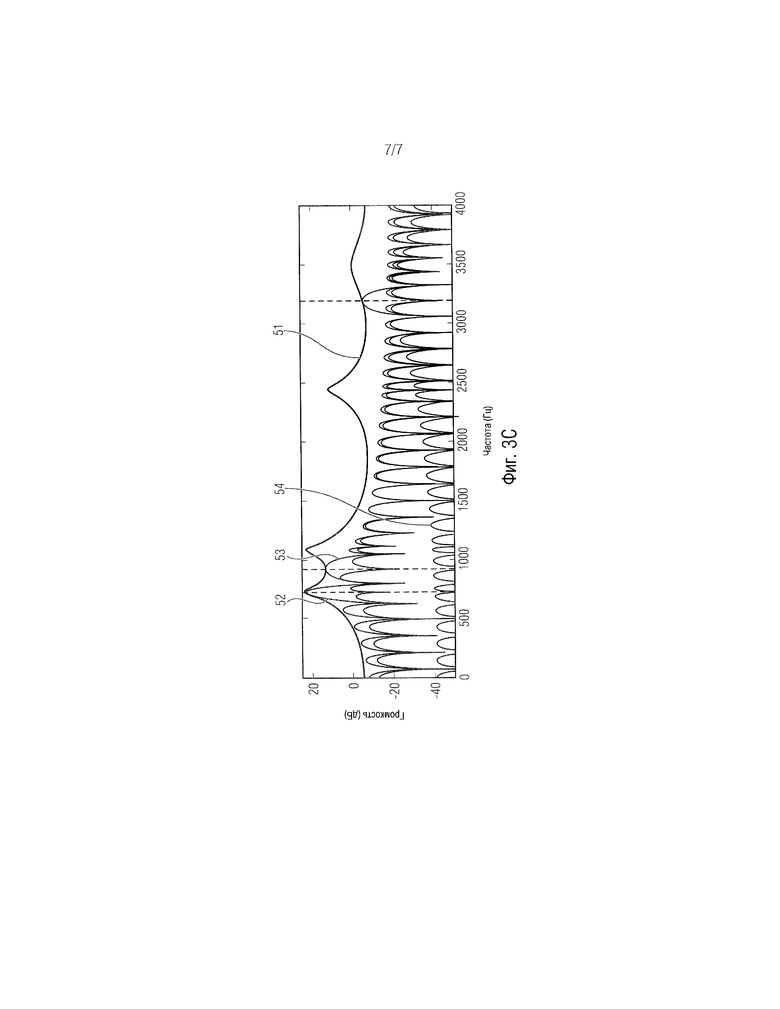
Фиг. 3С показывает схему, иллюстрирующую характеристики преобразования Вандермонда.
Варианты осуществления настоящего изобретения будут далее подробно описаны со ссылкой на приложенные чертежи. В настоящем документе одинаковые ссылочные номера присвоены объектам, имеющим одинаковую или сходную функцию, и поэтому их описание является взаимозаменяем или взаимно применимым.
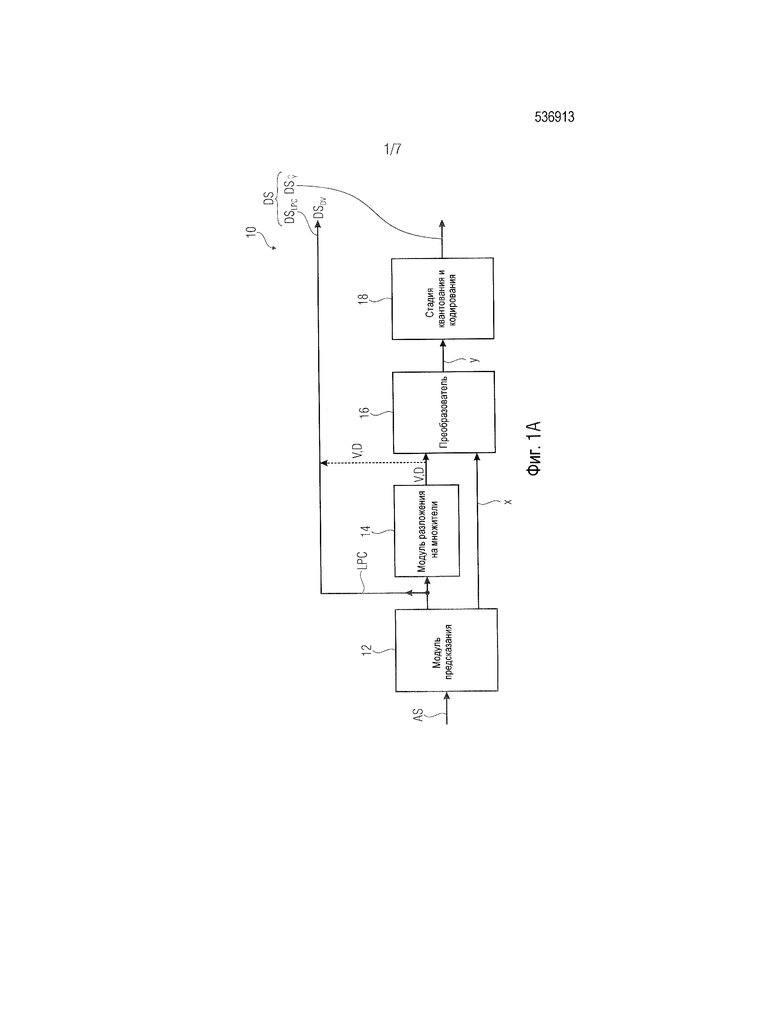
Фиг. 1А показывает кодер 10 в базовой конфигурации. Кодер 10 содержит модуль 12 предсказания, реализованный здесь как модуль 12 линейного предсказания, а также модуль 14 разложения на множители, преобразователь 16 и стадию 18 квантования и кодирования.
Модуль 12 линейного предсказания размещен на входе, чтобы принимать аудиосигнал AS, предпочтительно цифровой аудиосигнал, такой как сигнал с импульсно-кодовой модуляцией (PCM). Модуль 12 линейного предсказания соединен с модулем 14 разложения на множители и с выходом кодера (см. ссылочный номер DSLPC/DSDV, через так называемый LPC-канал LPC). Кроме того, модуль 12 линейного предсказания соединен с преобразователем 16 через так называемый разностный канал. Наоборот, преобразователь 16 (в дополнение к разностному каналу) соединен с модулем 14 разложения на множители на своей входной стороне. На своей выходной стороне преобразователь соединен со стадией квантования и кодирования, причем стадия 18 квантования и кодирования соединена с выходом (см. ссылочный номер DSŷ). Эти два потока DSLPC/DSDV данных и DSŷ формируют выходной поток DS данных.
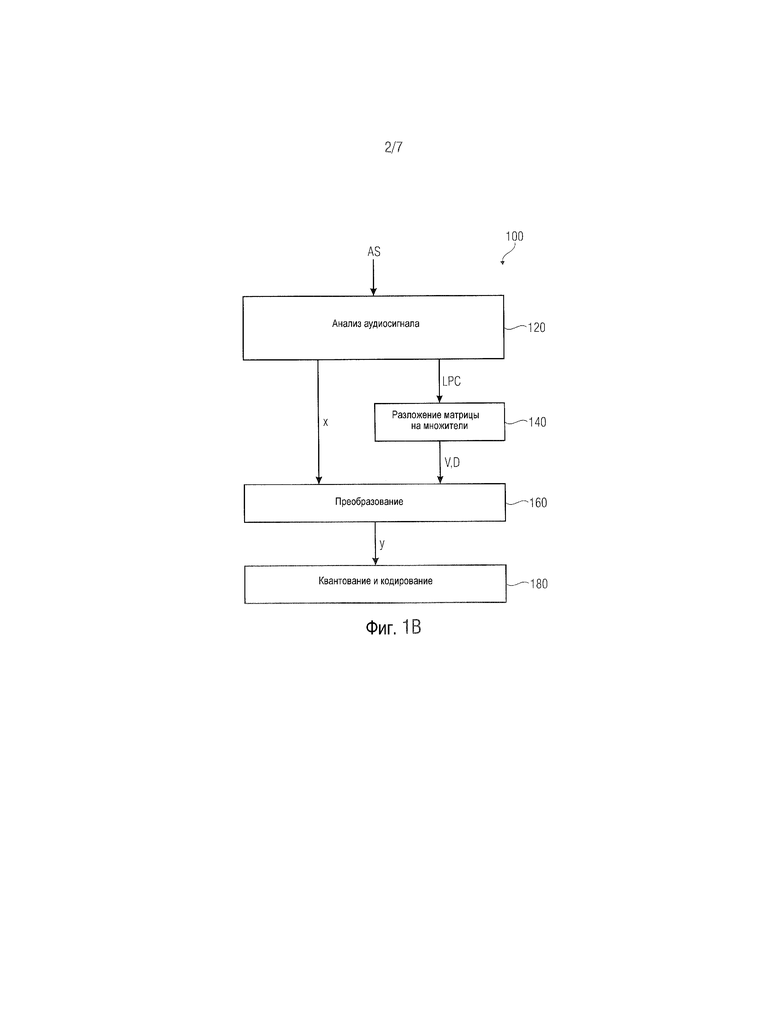
Ниже будет описана функциональность кодера 10, причем дополнительные ссылки делаются на фиг. 1В, описывающую способ 100 кодирования. Как видно в соответствии с фиг. 1В, основной метод 100 кодирования аудиосигнала AS в поток DS данных содержит четыре основных этапа 120, 140, 160 и 180, которые выполняются элементами 12, 14, 16 и 18. На первом этапе 120 модуль 12 линейного предсказания анализирует аудиосигнал AS, чтобы получить коэффициенты линейного предсказания LPC. Коэффициенты линейного предсказания LPC описывают огибающую спектра аудиосигнала AS, что позволяет впоследствии синтезировать основной аудиосигнал с использованием так называемой функции синтезирующей фильтрации H. Функция синтезирующей фильтрации H может содержать нагруженные значения функции синтезирующей фильтрации, заданные коэффициентами LPC. Коэффициенты линейного предсказания LPC выдаются модулю 14 разложения на множители с использованием LPC-канала LPC, а также передаются на выход кодера 10. Модуль 12 линейного предсказания 12, кроме того, подвергает аудиосигнал AS функции анализирующей фильтрации H, которая задана коэффициентами линейного предсказания LPC. Этот процесс является взаимно дополняющим по отношению к синтезу аудиосигнала на основе коэффициентов LPC, выполняемому декодером. Результатом этого подэтапа является разностный сигнал x, выдаваемый преобразователю 16 без части сигнала, описываемой функцией фильтрации H. Следует отметить, что этот этап выполняется по кадрам, т.е. аудиосигнал AS, имеющий амплитуду и временную область, делится или подвергается дискретизации на временные промежутки (отсчеты), например, имеющие продолжительность 5 мс, и квантуется в частотной области.
Следующим этапом является преобразование разностного сигнала x (см. этап 160 способа), выполняемое преобразователем 16. Преобразователь 16 выполнен с возможностью преобразовывать разностный сигнал x, чтобы получить преобразованный разностный сигнал y, выдаваемый на стадию 18 квантования и кодирования. Например, преобразование 160 может быть основано на формуле y=D1/2Vx или на формуле y=DVx, где матрицы D и V обеспечиваются модулем 14 разложения на множители. Таким образом, преобразование разностного сигнала x основано по меньшей мере на двух матрицах V, разложенных на множители, в качестве примера называемой матрицей Вандермонда, и D, в качестве примера называемой диагональной матрицей.
Применяемое разложение матрицы на множители может быть свободно выбрано, например, как разложение по собственным значениям, разложение на множители Вандермонда, разложение Холецкого и т.п. Разложение Вандермонда может использоваться в качестве разложения на множители симметричных, положительно-определенных матриц Теплица, таких как автокорреляционные матрицы, на произведение матриц Вандермонда V и V*. Для автокорреляционной матрицы в целевой функции это соответствует дискретному преобразованию Фурье с неравномерным частотным разрешением, которое обычно называют преобразованием Вандермонда. Этот этап 140 разложения матрицы на множители, выполняемый модулем 14 разложения на множители и представляющий фундаментальную часть изобретения, будет подробно описан после описания функциональности стадии 18 квантования и кодирования.
Стадия 18 квантования и кодирования квантует преобразованный разностный сигнал y, принятый от преобразователя 16, чтобы получить квантованный преобразованный разностный сигнал ŷ. Этот преобразованный квантованный разностный сигнал ŷ выдается как часть потока DSŷ данных. Следует отметить, что весь поток DS данных содержит часть LPC, обозначаемую как DSLPC/DSDV и часть ŷ, обозначаемую как DSŷ.
Квантование разностного сигнала преобразования y может быть выполнено, например, с использованием целевой функции, например, в терминах 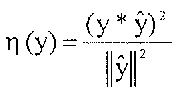 . По сравнению с типичной целевой функцией кодера ACELP эта целевая функция имеет уменьшенную сложность, в результате чего кодирование обеспечивает преимущество, состоящее в повышенной производительности. Это повышение производительности может использоваться для кодирования аудиосигналов AS, имеющих более высокое разрешение, или для сокращения необходимых ресурсов
. По сравнению с типичной целевой функцией кодера ACELP эта целевая функция имеет уменьшенную сложность, в результате чего кодирование обеспечивает преимущество, состоящее в повышенной производительности. Это повышение производительности может использоваться для кодирования аудиосигналов AS, имеющих более высокое разрешение, или для сокращения необходимых ресурсов
Следует отметить, что сигнал DSŷ может являться закодированным сигналом, причем кодирование выполнено посредством стадии 18 квантования и кодирования. Таким образом, в соответствии с дополнительными вариантами осуществления стадия 18 квантования и кодирования может содержать кодер, который может быть выполнен с возможностью выполнять арифметическое кодирование. Стадия 18 квантования и кодирования может использовать линейные шаги квантования (т.е. равные расстояния) или переменные, например, логарифмические шаги квантования. В качестве альтернативы кодер может быть выполнен с возможностью выполнять другое энтропийное кодирование (без потерь), в котором длина кода варьирует как функция вероятности сингулярных входных сигналов AS. Таким образом, для получения оптимальной длины кода альтернативным вариантом может являться обнаружение вероятности входных сигналов на основе огибающей синтеза и, таким образом, на основе коэффициентов LPC. Таким образом, стадия квантования и кодирования также может иметь вход для LPC-канала.
Ниже будут описаны предпосылки, позволяющие сократить сложности целевой функции 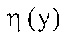 . Как упомянуто выше, улучшенное кодирование основано на этапе разложения 140 матрицы на множители, выполняемом модулем 14 разложения на множители. Модуль 14 разложения на множители разлагает на множители матрицу, например, автокорреляционную матрицу R или ковариационную матрицу C функции синтезирующей фильтрации H, заданной коэффициентами линейного предсказания LPC (см. LPC-канал). Результатом этого разложения на множители являются две матрицы, разложенные на множители, например, матрица Вандермонда V и диагональная матрица D, представляющие первоначальную матрицу H, включающую в себя сингулярные коэффициенты LPC. Вследствие этого отсчеты разностного сигнала x являются декоррелированными. Из этого следует, что прямое квантование (см. этап 180) разностного сигнала преобразования является оптимальным квантованием, посредством чего вычислительная сложность почти не зависит от скорости передачи. В сравнении с традиционным подходом к оптимизации кодирования ACELP кодовая книга должна балансировать между вычислительной сложностью и точностью, особенно при высоких скоростях передачи. Таким образом, действительно описаны предпосылки, исходя из тезисов кодирования ACELP.
. Как упомянуто выше, улучшенное кодирование основано на этапе разложения 140 матрицы на множители, выполняемом модулем 14 разложения на множители. Модуль 14 разложения на множители разлагает на множители матрицу, например, автокорреляционную матрицу R или ковариационную матрицу C функции синтезирующей фильтрации H, заданной коэффициентами линейного предсказания LPC (см. LPC-канал). Результатом этого разложения на множители являются две матрицы, разложенные на множители, например, матрица Вандермонда V и диагональная матрица D, представляющие первоначальную матрицу H, включающую в себя сингулярные коэффициенты LPC. Вследствие этого отсчеты разностного сигнала x являются декоррелированными. Из этого следует, что прямое квантование (см. этап 180) разностного сигнала преобразования является оптимальным квантованием, посредством чего вычислительная сложность почти не зависит от скорости передачи. В сравнении с традиционным подходом к оптимизации кодирования ACELP кодовая книга должна балансировать между вычислительной сложностью и точностью, особенно при высоких скоростях передачи. Таким образом, действительно описаны предпосылки, исходя из тезисов кодирования ACELP.
Традиционная целевая функция ACELP принимает форму ковариационной матрицы. В соответствии с улучшенными подходами имеется альтернативная целевая функция, которая использует автокорреляционную матрицу взвешенной функции синтеза. Кодеки, основанные на ACELP, оптимизировали соотношение сигнал/шум (SNR) в области перцепционно взвешенного синтеза. Целевая функция может быть выражена как
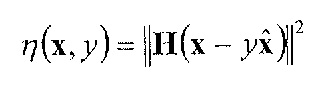 (1)
(1)
где x - целевая разность, 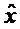 - квантованная разность, H - матрица свертки, соответствующая взвешенному синтезирующему фильтру, и γ - масштабный коэффициент усиления. Чтобы найти оптимальное квантование
- квантованная разность, H - матрица свертки, соответствующая взвешенному синтезирующему фильтру, и γ - масштабный коэффициент усиления. Чтобы найти оптимальное квантование 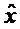 , стандартный подход должен найти оптимальное значение γ, обозначаемое γ*, в нуле производной η(x, γ). Посредством вставки оптимального значения γ* в уравнение (1) получается новая целевая функция:
, стандартный подход должен найти оптимальное значение γ, обозначаемое γ*, в нуле производной η(x, γ). Посредством вставки оптимального значения γ* в уравнение (1) получается новая целевая функция:
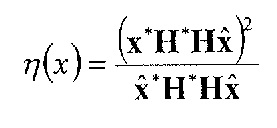 (2)
(2)
где H* преобразованная сопряженная версия синтеза с помощью функции H.
Следует отметить, что при традиционном подходе H является квадратной нижней треугольной матрицей свертки, посредством чего ковариационная матрица C=H*H является симметричной ковариационной матрицей. Замена нижней треугольной матрицы на полноразмерную матрицу свертки, посредством чего матрица автокорреляции R=H*H является симметричной матрицей Теплица, соответствует другой корреляции взвешенного синтезирующего фильтра. Эта замена дает значительные сокращение сложности с минимальным воздействием на качество.
Модуль 14 линейного предсказания может использовать обе матрицы, а именно ковариационную матрицу C или автокорреляционную матрицу R для разложения матрицы на множители. Описание ниже сделано при условии, что автокорреляция R используется для изменения целевой функции на разложение матрицы на множители, зависящее от коэффициентов LPC. Симметричные положительно определенные матрицы Теплица, такие как R, могут быть разложены как
R=V*DV (3)
через несколько способов, в том числе разложение по собственным значениям. Здесь V* - преобразованная-сопряженная версия матрицы Вандермонда V. В традиционном подходе с использованием ковариационной матрицы C может быть применено другое разложение на множители, такое как сингулярное разложение C=USV.
Для автокорреляционной матрицы может использоваться альтернативное разложение на множители, называемое здесь разложением на множители Вандермонда, которое имеет также форму уравнения (3). Разложение на множители Вандермонда представляет собой новую концепцию, дающую возможность разложения/преобразования. Матрица Вандермонда имеет V со значением 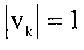 и
и
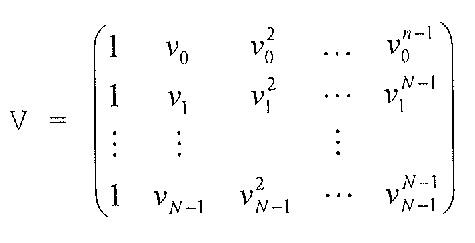 (4)
(4)
и D - диагональная матрица со строго положительными элементами. Разложение может быть вычислено с произвольной точностью со сложностью O(N3). Прямое разложение обычно имеет вычислительную сложность O(N^3), но здесь она может быть уменьшена до O(N^2), или, если приблизительное разложение на множители является достаточным, то сложность может быть уменьшена до O(N jog N). Для выбранного разложения может быть определено
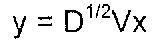 и
и 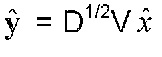 (5)
(5)
где x=V-1D-1/2y, и посредством вставки в уравнение (2) может быть получено
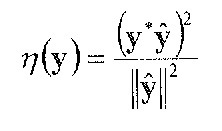 (6)
(6)
Следует отметить, что здесь отсчеты y не коррелированы друг с другом, и упомянутая выше целевая функция представляет собой не что иное, как нормализованную корреляция между целевой и квантованной разностью. Из этого следует, что отсчеты y могут быть независимо квантованы, и если точность всех отсчетов одинакова, то это квантование приводит к наилучшей возможной точности.
В случае разложения на множители Вандермонда, поскольку V имеет значение 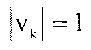 , оно соответствует дискретному преобразованию Фурье с неравномерным частотным разрешением, и элементы y соответствуют частотному компоненту разности. Кроме того, умножение на диагональную матрицу D соответствует масштабированию частотных полос, и из этого следует, что y является представлением частотной области разности.
, оно соответствует дискретному преобразованию Фурье с неравномерным частотным разрешением, и элементы y соответствуют частотному компоненту разности. Кроме того, умножение на диагональную матрицу D соответствует масштабированию частотных полос, и из этого следует, что y является представлением частотной области разности.
Напротив, разложение по собственным значениям имеет физическую интерпретацию, только когда длина окна приближается к бесконечности, когда разложение по собственным значениям и преобразование Фурье совпадают. Конечная длина разложения по собственным значениям, таким образом, свободно относится к представлению частоты сигнала, но маркировка компонентов по частотам затруднительная. Однако, разложение по собственным значениям, как известно, является оптимальным основанием, посредством чего оно может в некоторых случаях дать наилучшую производительность.
Исходя из этих двух матриц V и D, разложенных на множители, преобразователь 16 выполняет преобразование 160, в результате чего разностный сигнал x преобразовывается с использованием декоррелированного вектора, заданного уравнением (5).
При условии, что x является не коррелированным белым шумом, отсчеты Vx также будут иметь одинаковое ожидание энергии. В результате этого могут использоваться арифметический кодер или кодер, использующие алгебраическую кодовую книгу для кодирования значений. Однако квантование Vx не является оптимальным относительно целевой функции, поскольку это опускает диагональную матрицу D1/2. С другой стороны, полное преобразование y=D1/2Vx включает в себя масштабирование посредством диагональной матрицы D, и это изменяет ожидание энергии отсчетов y. Создание алгебраической кодовой книги с неоднородной дисперсией не является тривиальным. Таким образом, возможен вариант использовать арифметическую кодовую книгу вместо того, чтобы получить оптимальный расход битов. Тогда арифметическое кодирование может быть задано точно, как раскрыто в [14].
Следует отметить, что, если используется разложение, такое как преобразование Вандермонда или другое комплексное преобразование, действительная и мнимая части являются независимыми случайными переменными. Если дисперсия комплексной переменной равна σ2, то действительная и мнимая части имеют дисперсию σ2/2. Разложения с действительными величинами, такие как разложение по собственным значениям, обеспечивают только действительные значения, посредством чего разделение действительной и мнимой частей не является необходимым. Для более высокой производительности с преобразованиями с комплексными величинами могут быть применены традиционные способы арифметического кодирования комплексных значений.
В соответствии с описанным выше вариантом осуществления коэффициенты предсказания LPC (см. DSLPC) выдаются как сигналы LSF (сигналы с линейным частотным спектром), причем это альтернативный вариант выдать коэффициенты предсказания LPC в матрицах V и D, разложенных на множители (см. DSDV). Этот альтернативный вариант обозначается прерывистой линией, помеченной V,D, и указанием, что DSDV получается из выхода модуля 14 разложения на множители.
Таким образом, другой вариант осуществления изобретения относится к потоку данных (DS), содержащему коэффициенты предсказания LPC в форме двух матриц (DSVD), разложенных на множители.
Со ссылкой на фиг. 2 будут описаны декодер 20 и соответствующий способ 200 декодирования.
Фиг. 2А показывает декодер 20, содержащий стадию 22 декодирования, факультативный модуль 24 разложения на множители, обратный преобразователь 26 и стадию 28 синтеза. Стадия 22 декодирования, а также модуль 24 разложения на множители размещены на входе декодера 20 и, таким образом, выполнены с возможностью принимать поток DS данных. Более подробно, первая часть потока DS данных, а именно коэффициенты линейного предсказания, обеспечиваются факультативному модулю 24 разложения на множители (см. DSLPC/DSDV), причем вторая часть, а именно квантованный разностный сигнал преобразования 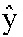 или закодированный квантованный преобразованный разностный сигнал
или закодированный квантованный преобразованный разностный сигнал 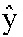 обеспечивается стадии 22 кодирования (см. DSŷ). Стадия 28 синтеза размещена на выходе декодера 20 и выполнена с возможностью выдавать аудиосигнал AS', подобный, но не равный аудиосигналу AS.
обеспечивается стадии 22 кодирования (см. DSŷ). Стадия 28 синтеза размещена на выходе декодера 20 и выполнена с возможностью выдавать аудиосигнал AS', подобный, но не равный аудиосигналу AS.
Синтез аудиосигнала AS' основан на коэффициентах LPC (см. DSLPC/DSDV) и основан на разностном сигнале x. Таким образом, стадия 28 синтеза соединена со входом для приема сигнала DSLPC и с обратным преобразователем 26, обеспечивающим разностный сигнал x. Обратный преобразователь 26 вычисляет разностный сигнал x на основе преобразованного разностного сигнала y и на основе по меньшей мере двух матриц V и D, разложенных на множители. Таким образом, обратный преобразователь 26 имеет по меньшей мере два входа, а именно первый для приема V и D, например, от модуля 24 разложения на множители, и один для приема преобразованного разностного сигнала y от стадии декодера.
Ниже будет подробно описана функциональность декодера 20 со ссылкой на соответствующий способ 200, проиллюстрированный на фиг. 2В. Декодер 20 принимает поток DS данных (от кодера). Этот сигнал DS данных позволяет декодеру 20 синтезировать аудиосигнал AS', причем часть потока данных, называемая DSLPC/DSDV, дает возможность синтезировать основной сигнал, и причем часть, называемая DSŷ, дает возможность синтезировать подробную часть аудиосигнала AS'. На первом этапе 220 стадия 22 декодера декодирует входящий сигнал DSŷ и выдает преобразованный разностный сигнал y обратному преобразователю 26 (см. этап 260).
Параллельно или последовательно модуль 24 разложения на множители выполняет разложение на множители (см. этап 240). Как описано относительно этапа 140, модуль 24 разложения на множители применяет разложение на множители к автокорреляционной матрице R или ковариационной матрице C функции синтезирующей фильтрации H, т.е. это разложение на множители, используемое декодером 20, подобно или почти подобно разложению на множители, описанному в контексте кодирования (см. способ 100), и, таким образом, может представлять собой разложение по собственным значениям или разложение на множители Холецкого, как описано выше. Здесь функция синтезирующей фильтрации H отклонена от входящего потока DSLPC/DSDV данных. Кроме того, модуль 24 разложения на множители выдает две матрицы V и D, разложенные на множители, обратному преобразователю 26.
На основе двух матриц V и D обратный преобразователь 26 обратно преобразовывает разностный сигнал x из преобразованного разностного сигнала y и выдает x стадии 28 синтеза (см. этап 280). Стадия 28 синтеза синтезирует аудиосигнал AS' на основе разностного сигнала x, а также на основе коэффициентов LPC, принятых как поток DSLPC/DSDV данных. Следует отметить, что аудиосигнал AS' подобен, но не равен аудиосигналу AS, поскольку квантование, выполненное кодером 10, не является квантованием без потерь.
В соответствии с другим вариантом осуществления матрицы V и D, разложенные на множители, могут быть обеспечены обратному преобразователю 26 от другого объекта, например, непосредственно от кодера 10 (как часть потока данных). Таким образом, модуль 24 разложения на множители декодера 20, а также этап 240 разложения матрицы на множители, являются факультативными объектами/этапами, и, таким образом, проиллюстрированы пунктирными линиями. Здесь может быть альтернативный вариант, в котором коэффициенты предсказания LPC (на основе которых выполняется синтез 280) могут быть выведены из входящих матриц V и D, разложенных на множители. Другими словами, это означает, что поток DS данных содержит DSŷ и матрицы V и D (т.е. DSDV) вместо DSŷ и DSLPC.
Повышение производительности описанного выше кодирования (а также декодирования) описаны ниже относительно Фиг. 3А и 3В.
Фиг. 3А показывает схему, иллюстрирующую среднее перцепционное соотношение сигнал/шум как функцию битов, используемых для кодирования принимаемой длины, и равных 64 кадрам. В схеме проиллюстрированы пять кривых для пяти разных подходов квантования, причем два подхода, а именно, оптимальное квантование и попарное итерационное квантование представляют собой традиционные подходы. Формула (1) формирует основу этого сравнения. В качестве сравнения производительности квантования предложенного способа декорреляции с традиционным представлением временной области разностного сигнала кодек ACELP был реализован следующим образом. Входной сигнал был подвергнут повторной дискретизации до 12,8 кГц, и линейный предсказатель был оценен с окном Хэмминга длиной 32 мс, центрированным в каждом кадре. Затем была вычислена разность предсказания для кадров длиной 5 мс, соответствующих субкадру кодека AMR-WB. Долговременный прогноз был оптимизирован с помощью целочисленных задержек между 32 и 150 отсчетами с полным перебором. Оптимальное значение использовалось для коэффициента усиления LTP без квантования.
Предыскажение с фильтром (1-0.68z-1) было применено ко входному сигналу и при синтезе, как в AMR-WB. Примененное перцепционное взвешивание составляло A(0.92z-1), где A(z) - фильтр с линейным предсказанием.
Чтобы оценить производительность, необходимо сравнить предложенное квантование с традиционными подходами (оптимальным квантованием и попарным итерационным квантованием). Чаще всего используемые подходы делят разностный сигнал кадра длиной 64 кадра на четыре перемежающихся дорожки. Этот подход был применен с двумя способами, а именно с подходом оптимального квантования (см. "Опт"), в котором все комбинации опробуются с полным перебором, или с попарным итерационным квантованием (см. "Пара"), в котором два импульса последовательно добавлялись посредством опробования их на каждой возможной позиции.
Первый из способов становится невыполнимо сложным в вычислительном отношении для скоростей передачи выше 15 битов за кадр, в то время как последний является субоптимальным. Следует отметить, что последний их них также более сложен, чем способы предшествующего уровня техники, применяемые в таких кодеках, как AMR-WB, но, таким образом, он также наиболее вероятно получает более хорошее соотношение сигнал/шум. Традиционные способы сравниваются с описанными выше алгоритмами для квантования.
Квантование Вандермонда (см. "Ванд") преобразовывает разностный вектор x как y=D1/2Vx, где матрицы V и D получены из разложения на множители Вандермонда, и квантование использует арифметический кодер. Квантование по собственным значениям (см. "Собст") является подобным квантованию Вандермонда, но матрицы V и D получены посредством разложения по собственным значениям. Кроме того, также может быть применено квантование FFT (см. "FFT"), т.е. в соответствии с дополнительным вариантом осуществления комбинация окон с использованием фильтров при преобразовании y=D1/2Vx может использоваться вместо дискретного преобразования Фурье (DFT), дискретного косинусного преобразования (DCT), модифицированного дискретного косинусного преобразования (MDCT) или других преобразований в алгоритмах обработки сигналов. Взято быстрое преобразование Фурье (FFT) разностного сигнала, причем применен тот же самый арифметический кодер, как для квантования Вандермонда. Подход FFT, очевидно, дает низкое качество, поскольку известно, что важно принимать во внимание корреляцию между отсчетами в уравнении (2). Таким образом, это квантование является нижним ориентиром.
Демонстрация производительности описанного способа проиллюстрирована на фиг. 3А, оценивающей среднее долгосрочное перцепционное соотношение сигнал/шум и сложность способов, заданных уравнением (1). Можно ясно видеть, что, как и ожидалось, квантование в области FFT дает наихудшее соотношение сигнал/шум. Низкая производительность может быть приписана тому факту, что это квантование не принимает во внимание корреляцию между разностными отсчетами. Кроме того, это может быть заявлено, что оптимальное квантование разностных сигналов во временной области равно попарной оптимизации при 5 и 10 битах на кадр, поскольку на этих скоростях передачи они имеют только 1 или 2 импульса, посредством чего способы точно одинаковы. Для 15 битов за кадр оптимальный способ немного лучше, чем попарная оптимизация, как и ожидалось.
При 10 битах на кадр и выше квантование в области Вандермонда лучше, чем квантование во временной области, и квантование в области собственных значений на один шаг лучше, чем квантование в области Вандермонда. При 5 битах на кадр производительность арифметических кодеров быстро уменьшается, наиболее вероятно потому, что они, как известно, являются субоптимальными для очень разреженных сигналов.
Заметим также, что попарный способ начинает отклоняться от попарного способа при более чем 80 битах на кадр. Неофициальные эксперименты показывают, что эта тенденция увеличивается при более высоких скоростях передачи, в результате чего, в конечном счете, способ FFT и попарный способ достигают подобного соотношения сигнал/шум, значительно ниже, чем способ Вандермонда и способ собственных значений. Напротив, способ собственных значений и способ Вандермонда продолжаются как более или менее линейные функции скорости передачи. Способ собственных значений всякий раз приблизительно на 0,36 дБ лучше, чем способ Вандермонда. Гипотеза состоит в том, что по меньшей мере часть этого различия объясняется разделением действительной и комплексной частей в арифметическом кодере. Для оптимальной производительности должны действительная и комплексная части должны быть закодированы совместно.
Фиг. 3В показывает измерение времени выполнения каждого подхода на каждой скорости передачи для иллюстрации оценки сложности разных алгоритмов. Можно заметить, что сложность оптимального подхода во временной области (см. "Опт") очень быстро увеличивается уже при низких скоростях передачи. Попарная оптимизация разности во временной области (см "Пара"), в свою очередь, линейно увеличивается как функция скорости передачи. Следует отметить, что способы предшествующего уровня техники ограничивают сложность попарного подхода, в результате чего она становится постоянной для высоких скоростей передачи, хотя конкурентоспособные результаты соотношения сигнал/шум эксперимента, проиллюстрированного на фиг. 3a, не могут быть достигнуты с такими пределами. Кроме того, оба подхода декорреляции (см. "Собст" и "Ванд"), а также подход FFT (см "FFT"), приблизительно постоянны при всех скоростях передачи. Преобразование Вандермонда имеет в описанной выше реализации примерно на 50% более высокую сложность, чем способ собственных значений, но причина этого может быть описана с использованием высоко оптимизированной версии собственных значений, обеспеченной посредством MATLAB, тогда как разложение на множители Вандермонда не является оптимальной реализацией. Однако важно, что при скорости передачи 100 битов на кадр попарный оптимизированный ACELP примерно в 30 и 50 раз сложнее, чем алгоритм Вандермонда и алгоритм на основе собственных значений, соответственно. Только способ FFT быстрее, чем способ собственных значений, но поскольку соотношение сигнал/шум у способа FFT является плохим, это нежизнеспособный вариант.
В итоге, описанный выше способ обладает двумя значительными преимуществами. Во-первых, при применении квантования в перцепционной области улучшается перцепционное соотношение сигнал/шум. Во-вторых, поскольку разностный сигнал является декоррелированным (относительно целевой функции), квантование может быть применено непосредственно, без очень сложного цикла анализа-синтеза. Из этого следует, что вычислительная сложность предложенного способа является почти постоянной относительно скоростей передачи, тогда как традиционный подход становится все более и более сложным с увеличением скорости передачи.
Представленный выше подход полностью неработоспособен с традиционными способами кодирования речи и аудиокодирования. Более конкретно, декорреляция целевой функции может быть применена в режиме ACELP таких кодов, как MPEG USAC или AMR-WB+, без ограничения на присутствие в кодеке других инструментов. Методы, которыми применяются способы базовой полосы частот или расширения полосы частот, останутся такими же методами, которыми выполняются долгосрочное предсказание, улучшение форманты, постфильтрация басов и т.д. в ACELP, не требуются изменения, и методы, которыми реализованы разные режимы кодирования (например, ACELP и TCX), и переключение между этими режимами не будут затронуты декорреляцией целевой функции.
С другой стороны, очевидно, что все инструменты (т.е., по меньшей мере все реализации ACELP), которые используют одну и ту же целевую функцию (см. уравнение (1)) могут быть легко переформулированы для использования преимущества декорреляции. Таким образом, в соответствии с дополнительным вариантом осуществления, декорреляция может быть применена, например, к долговременному вкладу предсказания, и, таким образом, коэффициенты усиления могут быть вычислены с использованием декоррелированного сигнала.
Кроме того, поскольку представленной областью преобразования является представление частотной области, классические способы кодеков для речи и аудиокодеки в частотной области также могут быть применены к этой новой области в соответствии с дополнительными вариантами осуществления. В соответствии со специальным вариантом осуществления при квантовании спектральных линий мертвая зона может быть применена для увеличения эффективности. В соответствии с другим вариантом осуществления может быть применено заполнение шумом, чтобы избежать спектральных провалов.
Хотя описанный выше вариант осуществления кодирования (см. Фиг. 1А и 1В) был описан в контексте кодера, использующего модуль линейного предсказания, следует отметить, что модуль предсказания также может быть выполнен с возможностью содержать модуль долговременного предсказания для определения коэффициентов долговременного предсказания, описывающих основную частоту аудиосигнала AS, фильтрации аудиосигнала AS на основе функции фильтрации, определенной коэффициентами долговременного предсказания и выдачи разностного сигнала x для последующей обработки. В соответствии с дополнительным вариантом осуществления модуль предсказания может представлять собой комбинацию модуля линейного предсказания и модуля долговременного предсказания.
Ясно, что предложенное преобразование может быть легко применено к другим задачам при обработке речи и обработке аудиоданных, таким как улучшение речи. Во-первых, способы на основе подпространства основаны на разложении по собственным значениям или сингулярном разложении сигнала. Поскольку представленный подход основан на подобных разложениях, способы улучшения речи, основанные на анализе подпространства, могут быть адаптированы к предложенной области в соответствии с дополнительным вариантом осуществления. Отличие от традиционных способов подпространства состоит в том, когда применяется модель сигнала, основанная на линейном предсказании и работе с окнами в разностной области, такая, как применяется в ACELP. Напротив, традиционные способы подпространства применяют накладывающиеся окна, которые фиксированы во времени (неадаптивные).
Во-вторых, декорреляция на основе декорреляции Вандермонда обеспечивает частотную область, подобную обеспеченной посредством дискретного преобразования Фурье, косинусного преобразования или других подобных преобразований. Любой алгоритм обработки речи, который обычно выполняется в преобразовании Фурье, косинусном преобразовании или подобной области преобразования, таким образом, может быть применен с минимальными модификациями также в областях преобразования описанного выше подхода. Таким образом, может быть применено улучшение речи, использующее спектральное вычитание в области преобразования, т.е. это означает, что в соответствии с дополнительными вариантами осуществления предложенное преобразование может использоваться при улучшении речи или аудиосигнала, например, со способом спектрального вычитания, анализа подпространства или их производных и модификаций. При этом преимуществом является то, что этот подход использует такую же работу с окнами, как ACELP, поэтому алгоритм улучшения речи может быть тесно интегрирован в речевой кодек. Кроме того, окно ACELP имеет более низкую алгоритмическую задержку, чем используемые в традиционном анализе подпространства. Следовательно, таким образом, работа с окнами основана на модели сигнала с более высокой производительностью.
Что касается уравнения (5), которое используется для преобразователя 14, т.е. на этапе 140, следует отметить, что его создание также может быть другим, например, в форме y=DVx.
В соответствии с дополнительным вариантом осуществления кодер 10 может содержать упаковщик на выходе, выполненный с возможностью упаковывать два потока DSLPC/DSDV и DSŷ данных в общий пакет DS. Наоборот, декодер 20 может содержать распаковщик, выполненный с возможностью разбивать поток DS данных на два пакета DSLPC/DSDV и DSŷ.
Хотя некоторые аспекты были описаны в контексте устройства, ясно, что эти аспекты также представляют описание соответствующего способа, причем блок или устройство соответствуют этапу способа или признаку этапа способа. Аналогичным образом, аспекты, описанные в контексте этапа способа, также представляют описание соответствующего блока или элемента, или признака соответствующего устройства. Некоторые или все этапы способа могут быть исполнены посредством (или с использованием) аппаратного устройства, такого как, например, микропроцессор, программируемый компьютер или электронная схема. В некоторых вариантах осуществления некоторый один или более наиважнейших этапов способа могут быть исполнены таким устройством.
Закодированный аудиосигнал изобретения может быть сохранен на цифровом запоминающем носителе или может быть передан на передающем носителе, таком как беспроводной передающий носитель или проводной передающий носитель, например Интернет.
В зависимости от некоторых требований реализации варианты осуществления изобретения могут быть реализованы в аппаратных средствах или в программном обеспечении. Реализация может быть выполнена с использованием цифрового запоминающего носителя, например, гибкого диска, DVD, Blu-ray, CD, ПЗУ (ROM), ППЗУ (PROM), СППЗУ (EPROM), ЭСППЗУ (EEPROM) или флэш-память, имеющего сохраненные на нем читаемые электронным образом управляющие сигналы, которые взаимодействуют (или способны взаимодействовать) с программируемой компьютерной системой, в результате чего выполняется соответствующий способ. Таким образом, цифровой запоминающий носитель может являться машиночитаемым.
Некоторые варианты осуществления в соответствии с изобретением содержат носитель данных, имеющий читаемые электронным образом управляющие сигналы, которые способны взаимодействовать с программируемой компьютерной системой, в результате чего выполняется один из описанных здесь способов.
Обычно варианты осуществления настоящего изобретения могут быть реализованы как компьютерный программный продукт с программным кодом, программный код может выполнять один из способов, когда компьютерный программный продукт выполняется на компьютере. Программный код, например, может быть сохранен на машиночитаемом носителе.
Другие варианты осуществления содержат компьютерную программу для выполнения одного из описанных здесь способов, сохраненную на машиночитаемом носителе.
Другими словами, вариант осуществления способа изобретения, таким образом, представляет собой компьютерную программу, имеющую программный код для выполнения одного из описанных здесь способов, когда компьютерная программа выполняется на компьютере.
Дополнительный вариант осуществления способов изобретения, таким образом, представляет собой носитель данных (или цифровой запоминающий носитель, или машиночитаемый носитель), содержащий записанную на нем компьютерную программу для выполнения одного из описанных здесь способов. Носитель данных, цифровой запоминающий носитель или носитель с записанными данными обычно являются материальными и/или непереходными.
Дополнительный вариант осуществления способа изобретения, таким образом, представляет собой поток данных или последовательность сигналов, представляющих компьютерную программу для выполнения одного из описанных здесь способов. Поток данных или последовательность сигналов, например, могут быть выполнены с возможностью передаваться через соединение передачи данных, например, через Интернет.
Дополнительный вариант осуществления содержит средство обработки, например, компьютер или программируемое логическое устройство, выполненное с возможностью выполнять один из описанных здесь способов.
Дополнительный вариант осуществления содержит компьютер, имеющий установленную на нем компьютерную программу для выполнения одного из описанных здесь способов.
Дополнительный вариант осуществления в соответствии с изобретением содержит устройство или систему, выполненные с возможностью переносить (например, электронным или оптическим образом) компьютерную программу для выполнения одного из описанных здесь способов на приемник. Приемник, например, может представлять собой компьютер, устройство мобильной связи, запоминающее устройство и т.п. Устройство или система, например, могут содержать файловый сервер для переноса компьютерной программы на приемник.
В некоторых вариантах осуществления программируемое логическое устройство (например, программируемая пользователем вентильная матрица) может использоваться для выполнения некоторой или всей функциональности описанных здесь способов. В некоторых вариантах осуществления программируемая пользователем вентильная матрица может взаимодействовать с микропроцессором для выполнения одного из описанных здесь способов. Обычно способы предпочтительно выполняются любым аппаратным устройством.
Описанные выше идеи будет обсуждены ниже в другой формулировке и с некоторыми дополнительными подробностями, что может помочь осветить уровень техники. Преобразование Вандермонда было недавно представлено как частотно-временное преобразование, которое в отличие от дискретного преобразования Фурье также выполняет декорреляцию сигнала. Хотя приблизительная или асимптотическая декорреляция, обеспечиваемая преобразованием Фурье, во многих случаях является достаточной, ее производительность является неадекватной в приложениях, которые используют короткие окна. Преобразование Вандермонда, таким образом, будет полезно в приложениях обработки речи и обработки аудиоданных, которые должны использовать короткие окна для анализа, поскольку входной сигнал варьируется быстро в течение времени. Такие приложения часто используются на устройствах мобильной связи с ограниченной вычислительной способностью, посредством чего эффективные вычисления имеют первостепенную важность.
Реализация преобразования Вандермонда, однако, оказалась значительным усилием: она требует передовые численные инструменты, производительность которых оптимизирована для сложности и точности. Этот вклад предоставляет базовое решение этой задачи, включающее в себя оценку производительности. Ключевые термины: частотно-временные преобразования, декорреляция, матрица Вандермонда, матрица Теплица, дискретное преобразование Фурье с неравномерным частотным разрешением.
Дискретное преобразование Фурье представляет собой один из самых фундаментальных инструментов в цифровой обработке сигналов. Оно обеспечивает физически обоснованное представление входного сигнала в форме частотных компонентов. Поскольку быстрое преобразование Фурье (FFT) также вычисляет дискретное преобразование с очень низкой вычислительной сложностью O(N log N), оно стало одним из самых важных инструментов цифровой обработки сигналов.
Несмотря на похвалы, дискретное преобразование Фурье имеет недостаток: оно не делает компоненты сигнала полностью декоррелированными (для численного примера см. раздел 4). Только когда длина преобразования сходится в бесконечности, компоненты действительно становятся ортогональными. Такая приблизительная декорреляция является достаточно хорошей во многих приложениях. Однако приложения, которые используют относительно малые преобразования, такие как многие алгоритмы обработки речи и аудиоданных, точность этого приближения ограничивают общую эффективность алгоритмов. Например, стандарт кодирования речи AMR-WB использует окна с длиной N=64. Практика показала, что производительность дискретного преобразования Фурье в этом случае недостаточна, и, следовательно, большинство широко распространенных речевых кодеков используют кодирование во временной области.
Фиг. 3С показывает характеристики преобразования Вандермонда; толстая линия с пометкой 51 иллюстрирует спектр Фурье (с равномерным частотным разрешением) сигнала, и линии 52, 53 и 54 являются ответом фильтров полосы пропускания трех выбранных частот, отфильтрованных с помощью входного сигнала. Шаг разложения на множители Вандермонда равен 64.
Естественно, имеется много преобразований, которые обеспечивают декорреляцию входного сигнала, таких как преобразование Карунена-Лоэва (KLT). Однако компоненты преобразования KLT являются абстрактными объектами без физической интерпретации, столь же простой, как для преобразования Фурье. Физически обоснованное представление, с другой стороны, дает возможность прямой реализации физически обоснованных критериев в способы обработки. Таким образом, требуется преобразование, которое обеспечивает и физическую интерпретацию, и декорреляцию.
Мы недавно представили преобразование, называемое преобразованием Вандермонда, которое имеет обе из этих предпочтительных характеристик. Оно основано на разложении эрмитовой матрицы Теплица на произведение диагональной матрицы и матрицы Вандермонда. Это разложение на множители фактически также известно как параметризация Каратеодори ковариационных матриц и очень похоже на разложение на множители Вандермонда матриц Ханкеля.
Для особого случая положительно определенных эрмитовых матриц Теплица разложение на множители Вандермонда будет соответствовать дискретному преобразованию Фурье с неравномерным частотным разрешением. Другими словами, это частотно-временное преобразование, которое обеспечивает компоненты сигнала, дискретизированные в частотах, которые не обязательно однородно распределены. Преобразование Вандермонда, таким образом, обеспечивает оба желаемые свойства: декорреляцию и физическую интерпретацию.
Хотя существование и свойства преобразования Вандермонда были аналитически продемонстрированы, цель текущей работы состоит в том, чтобы, во-первых, собрать и документировать существующие практические алгоритмы для преобразований Вандермонда. Эти способы появились в самых разных областях, включающих в себя численную алгебру, численный анализ, системную идентификацию, частотно-временной анализ и обработку сигналов, посредством чего их часто трудно найти. Таким образом, эта статья делает обзор способов, которые обеспечивают объединенную платформу для анализа и обсуждения результатов. Во-вторых, мы обеспечиваем численные примеры как основу для дополнительной оценки производительности разных способов.
Этот раздел представляет краткое введение в преобразования Вандермонда. Для более всестороннего обоснования и описания приложений, к которым мы обратимся.
Матрица Вандермонда V задана скалярами νk как
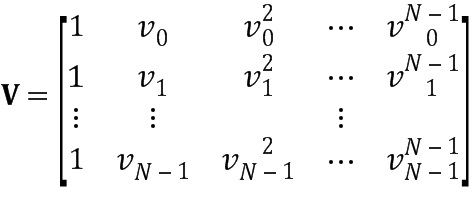 (1z)
(1z)
Она является матрицей полного ранга, если скаляры νk различны (νk ≠ νh для k ≠ h), и ее обратная матрица имеет явную формулу.
Симметричная матрица Теплица T задана скалярами τk как
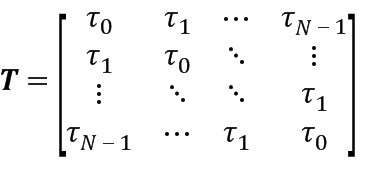 (2z)
(2z)
Если T положительно определена, то она может быть разложена на множители как
T=V*ΛV, (3z)
где Λ - диагональная матрица с действительными и строго положительными элементами λkk > 0, и все экспоненциальные ряды V находятся на единичной окружности νk=exp(iβk). Эта форма также известна как параметризация Каратеодори матрицы Теплица.
Мы представляем здесь два использования для преобразования Вандермонда: либо как декоррелирующее преобразование, либо как замена для матрицы свертки. Рассмотрим сначала сигнал x, который имеет автокорреляционную матрицу E[xx*]=Rx. Поскольку автокорреляционная матрица представляет собой положительно определенную, симметричную матрицу Теплица, мы можем разложить ее на множители как R=V*ΛV. Из этого следует, что если мы применяем преобразование
yd=V-*x, (4z)
где V-* - обратная эрмитова матрица матрицы V, тогда автокорреляционная матрица yd представляет собой
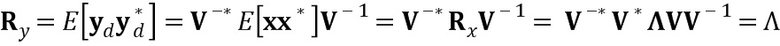 . (5z)
. (5z)
Преобразованный сигнал yd, таким образом, является некоррелированным. Обратное преобразование представляет собой
x=V*yd. (6z)
В качестве эвристического описания мы можем сказать, что прямое преобразование V-* содержит в своей k-й строке фильтр, полоса пропускания которого находится на частоте -βk, и выход полосы заграждения для x имеет низкую энергию. Более конкретно, спектральная форма выхода близка к AR-фильтру с одиночным полюсом на единичной окружности. Следует отметить, что поскольку этот набор фильтров является адаптивным к сигналу, мы рассматриваем здесь выход фильтра, а не частотную характеристику основных функций.
Обратное преобразование V*, в свою очередь, имеет экспоненциальный ряд в его столбцах, в результате чего x является взвешенной суммой экспоненциального ряда. Другими словами, преобразование представляет собой частотно-временное преобразование с неравномерным разрешением. Фиг. 3С демонстрирует дискретный (с равномерным разрешением) спектр Фурье входного сигнала x и частотные характеристики выбранных строк V-*.
Преобразование Вандермонда для оценки сигнала в свернутой области может быть создано следующим образом. Пусть C - матрица свертки, и x - входной сигнал. Рассмотрим случай, когда наша цель состоит в том, чтобы оценить свернутый сигнал yc=Cx. Такая оценка появляется, например, в речевых кодеках, использующих ACELP, когда энергия погрешности квантования оценивается в перцепционной области и когда отображение на перцепционную область описывается фильтром.
Энергия yc представляет собой
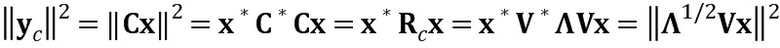 . (7z)
. (7z)
Энергия yc, таким образом, равна энергии преобразованного и масштабированного сигнала
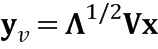 . (8z)
. (8z)
Мы можем, таким образом, эквивалентно оценить энергию сигнала в свернутом или преобразованном представлении. 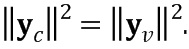 Обратное преобразование, очевидно
Обратное преобразование, очевидно
x=V-1Λ-1/2yv. (9z)
Прямое преобразование V имеет экспоненциальный ряд в своих строках, посредством чего оно представляет собой свернутое преобразование Фурье. Его обратное преобразование V-1 имеет в своих столбцах фильтры с полосами пропускания на βk. В этой форме частотная характеристика набора фильтров равна дискретному преобразованию Фурье. Только обратное преобразование использует то, что обычно рассматривается как искажение компонентов, чтобы позволить совершенное воссоздание.
Для использования преобразований Вандермонда нам нужны эффективные алгоритмы для определения, а также применения преобразований. В этом разделе мы обсудим доступные алгоритмы. Начнем с применения преобразований, поскольку это более непосредственная задача.
Умножение матриц V и V* является непосредственным и может быть реализовано со сложностью O(N2). Для уменьшения требований для хранения покажем здесь алгоритмы, в которых экспоненты 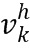 не нужно явно оценивать для h > 1. А именно, если y=Vx, и элементы x представляют собой ξk, то элементы ηk от y могут быть определены с рекурсией
не нужно явно оценивать для h > 1. А именно, если y=Vx, и элементы x представляют собой ξk, то элементы ηk от y могут быть определены с рекурсией
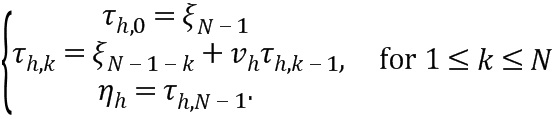 (10z)
(10z)
здесь τh,k - временный скаляр, для которого должно храниться только текущее значение. Полная рекурсия имеет N шагов для N компонентов, посредством чего общая сложность составляет O (N2), и хранение постоянно. Подобный алгоритм может быть легко написан для y=V*x.
Умножение обратных матриц Вандермонда V-1 и V-* является немного более сложной задачей, но, к счастью, относительно эффективные методы уже доступны из публикаций. Алгоритмы являются простыми для реализации, и как для x=V-1y, так и для x=V-*y сложность составляет O(N2), и хранение линейно O(N). Однако алгоритм включает в себя подразделение на каждом шаге, которое во многих архитектурах имеет высокие постоянные затраты.
Хотя описанные выше алгоритмы для умножения на обратные матрицы являются точными в аналитическом смысле, практические реализации численно неустойчивы для больших N. В нашем опыте вычисления с матрицами вплоть до размера N∼ 64 иногда возможны, но за этими пределами численная нестабильность делает эти алгоритмы бесполезными как таковые. Практическим решением является упорядочение Leja корней νk, что эквивалентно исключению Гаусса с выбором ведущего элемента столбца. Основная идея упорядочения Leja состоит в том, чтобы переупорядочить корни таким образом, что расстояние корня νk до его предшественников 0... (k - 1) максимизируется. Посредством такого переупорядочения знаменатели, появляющиеся в алгоритме, максимизируются, и значения промежуточных переменных минимизируются, посредством чего вклады погрешностей отсечения также минимизируются. Реализация упорядочения Leja является простой и может быть достигнута со сложностью O(N2) и хранением O(N).
Заключительным препятствием тогда является получение разложения на множители, то есть, корней νk и, при необходимости, диагональных значений λkk. Мы знаем, что корни могут быть получены посредством решения
Ra=[1 1... 1]T, (11z)
где a имеет элементы αk. Тогда ν0=1, и остальные корни ν1... νN представляют собой корни полиномиала 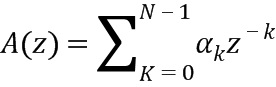 . Мы можем легко показать, что это эквивалентно решению системы Ханкеля
. Мы можем легко показать, что это эквивалентно решению системы Ханкеля
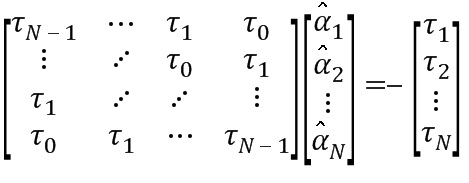 (12z)
(12z)
где 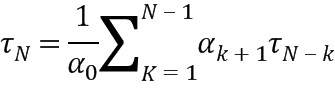 . Тогда корни νk являются корнями
. Тогда корни νk являются корнями 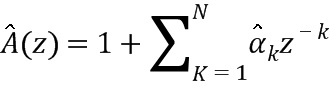 .
.
Поскольку разложение на множители первоначальной системы Теплица уравнения Eq. 11z эквивалентно уравнению Eq. 12z, мы можем использовать быстрый алгоритм для разложения на множители матриц Ханкеля. Этот алгоритм возвращает тридиагональную матрицу, собственные значения которой соответствуют корням 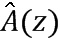 . Собственные значения тогда могут быть получены со сложностью O(N2) посредством применения LR-алгоритма, или со сложностью O(N3) посредством стандартного несимметричного QR-алгоритма. Корни, полученные таким образом, являются приближениями, посредством чего они могут находиться немного смещенными с единичной окружности. Тогда полезно нормализовать абсолютное значение корней к единице и выполнить уточнение с помощью 2 или 3 итераций метода Ньютона. Полный процесс имеет вычислительную сложность O(N2).
. Собственные значения тогда могут быть получены со сложностью O(N2) посредством применения LR-алгоритма, или со сложностью O(N3) посредством стандартного несимметричного QR-алгоритма. Корни, полученные таким образом, являются приближениями, посредством чего они могут находиться немного смещенными с единичной окружности. Тогда полезно нормализовать абсолютное значение корней к единице и выполнить уточнение с помощью 2 или 3 итераций метода Ньютона. Полный процесс имеет вычислительную сложность O(N2).
Последним этапом в разложении на множители является получение диагональных значений Λ. Заметим, что
Re=V*ΛVe=V*λ, (13z)
где e=[1 0... 0]T, и λ - вектор, содержащий диагональные значения Λ. Другими словами, посредством вычисления
λ=V-*(Re) (14z)
мы получаем диагональные значения λkk. Эта инверсия может быть вычислена с помощью описанных выше способов, посредством чего диагональные значения получаются со сложностью O(N2).
Таким образом, имеются следующие этапы, требуемые для разложения на множители матрицы R.
1. Решить уравнение Eq. 11z с использованием алгоритма Левинсона-Дарбина или других классических способов.
2. Расширить последовательность автокорреляции посредством 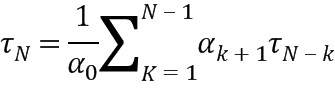 .
.
3. Применить алгоритм тридиагонализации к последовательности τk.
4. Решить собственные значения νk с использованием либо LR-алгоритма, либо симметричного QR-алгоритма.
5. Уточнить местоположения корней посредством масштабирования νk до единицы и нескольких итераций метода Ньютона.
6. Определить диагональные значения λkk с использованием уравнения Eq. 14z.
Приступим к численному примеру, который демонстрирует используемые концепции. Здесь матрица C - матрица свертки, соответствующая тривиальному фильтру 1+z-1, матрица R - ее автокорреляция, матрица V - соответствующая матрица Вандермонда, полученная с помощью алгоритма из раздела 3, матрица F - матрица дискретного преобразования Фурье, и матрицы ΛV and ΛF демонстрируют точность диагонализации двух преобразований. Мы можем, таким образом, определить

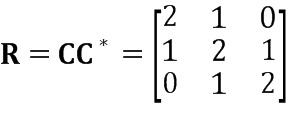 , (15z)
, (15z)
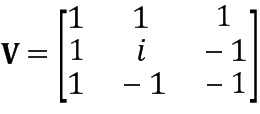 ,
, 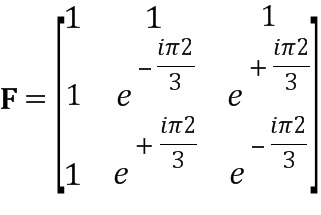
посредством чего мы можем оценить диагонализацию с помощью
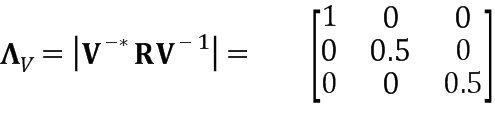 (16z)
(16z)
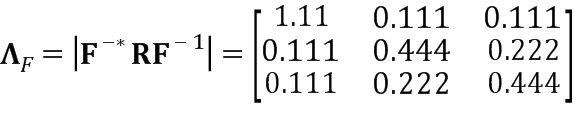
Здесь мы можем видеть, что с помощью преобразования Вандермонда мы получаем совершенно диагональную матрицу ΛV. Производительность дискретного преобразования Фурье далека от оптимальной, поскольку не диагональные значения явно не равны нулю. Как количественный показатель производительности мы можем вычислить отношение абсолютных сумм не диагональных и диагональных значений, которое равно нулю для разложения на множители Вандермонда и равно 0,444 для преобразования Фурье.
Затем мы можем продолжить оценивать реализации, описанные в разделе 3. Мы реализовали каждый алгоритм в MATLAB с целью обеспечения базовой производительности, с которыми могут быть сравнены будущие работы, и нахождения возможных узких мест по производительности. Рассмотрим производительность с точки зрения сложности и точности.
Чтобы определить производительность разложения на множители, сравним разложение на множители Вандермонда с дискретным преобразованием Фурье и преобразованием Карунена-Лоэва, последнее из которых применяется с разложением по собственным значениям. Мы применили разложение на множители Вандермонда с использованием двух способов: во-первых, алгоритма, описанного в этой статье (V1), и, во-вторых, подхода, описанного с использованием встроенной функции поиска корней, обеспеченной посредством MATLAB (V2). Поскольку эта функция MATLAB представляет собой точно настроенный универсальный алгоритм, мы ожидали бы получить точные результаты, но с более высокой сложностью, чем наш специальный алгоритм.
В качестве данных для всех наших экспериментов мы использовали множество речевых, аудио- и микшированных звуковых отсчетов, используемых при оценке стандарта MPEG USAC, с частотой дискретизации 12,8 кГц. Отсчеты аудио были обработаны с помощью оконной функции с окнами Хэмминга до желаемой длины, и были вычислены их автокорреляции. Чтобы удостовериться, что автокорреляционные матрицы являются положительно определенными, главная диагональ была умножена на (1+10-5).
Для количественных показателей производительности мы использовали вычислительную сложность в терминах нормализованного времени выполнения и точность в терминах того, насколько близка  к диагональной матрице, с измерением посредством отношения абсолютных сумм не диагональных и диагональных элементов. Результаты перечислены в таблицах 1 и 2.
к диагональной матрице, с измерением посредством отношения абсолютных сумм не диагональных и диагональных элементов. Результаты перечислены в таблицах 1 и 2.
Сложность алгоритмов разложения на множители для разных длин окна N в терминах нормализованного времени выполнения
Точность алгоритмов разложения на множители для разных длин окна N в терминах log10 от отношения абсолютных сумм недиагональных и диагональных элементов матрицы 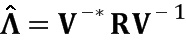
Следует отметить, что здесь нет смысла сравнить времена выполнения между алгоритмами, только увеличение сложности как функция размера кадра, поскольку встроенные функции MATLAB были реализованы на языке, отличающемся от наших собственных алгоритмов. Мы видим, что сложность предложенного алгоритма V1 увеличивается со скоростью, сопоставимой с KLT, в то время как сложность алгоритма, использующего функции поиска корней MATLAB V2, увеличивается больше. Точность предложенного алгоритма разложения на множители V1 еще не является оптимальной. Однако, поскольку функция поиска корней MATLAB V2 приводит к точности, сопоставимой с KLT, мы приходим к заключению, что улучшения возможны посредством алгоритмических улучшений.
Второй эксперимент представляет собой применение преобразований для определения точности и сложности. Сначала мы применяем уравнения Eq. 4z и Eq. 9z, сложности которых перечислены в таблице 3. Здесь мы видим, что умножение матриц KLT и встроенного решения матричных систем MATLAB V2 имеют приблизительно одинаковую скорость увеличения сложности, в то время как предложенные способы для Eq. 4z и Eq. 9z имеют намного меньшее увеличение. Алгоритм FFT естественно быстрее, чем все другие подходы.
Наконец, чтобы получить точность решений Вандермонда, мы последовательно применяем прямое и обратное преобразование. Евклидовы расстояния между первоначальными и воссозданными векторами перечислены в таблице 4. Мы можем заметить, во-первых, что алгоритмы FFT и KLT являются, как и ожидалось, самыми точными, поскольку они основаны на ортонормальных преобразованиях. Во-вторых, мы видим, что точность предложенного алгоритма V1 немного ниже, чем встроенное решение MATLAB V2, но оба алгоритма обеспечивают достаточную точность.
Мы представили подробности реализации декорреляции частотно-временных преобразований с использованием разложения на множители Вандермонда с целью рассмотрения доступных алгоритмов, а также обеспечения базовой производительности для дальнейшего развития. Хотя алгоритмы были теоретически доступны из предыдущих работ, оказалось, что достижение работающей системы требует
Сложность решений Вандермонда для разных длин окна N в терминах нормализованного времени выполнения. Здесь 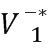 и
и 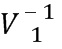 обозначают решения уравнений Eq. 4z и Eq. 9z с помощью соответствующих предложенных алгоритмов
обозначают решения уравнений Eq. 4z и Eq. 9z с помощью соответствующих предложенных алгоритмов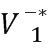
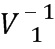
Точность прямого и обратного преобразований, измеренная как log10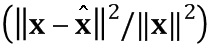 , где
, где 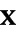 и
и 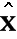 - первоначальный и воссозданный векторы
- первоначальный и воссозданный векторы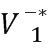
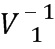
значительных усилий. Основными проблемами являются численная точность и вычислительная сложность. Эксперименты подтверждают, что способы доступны со сложностью O(N2), хотя получение низкой сложности одновременно с численной устойчивостью является проблемой. Однако, поскольку универсальные реализации MATLAB обеспечивают точные решения, мы утверждаем, что получение высокой точности возможно с помощью дальнейшей настройки реализации.
В заключение, наши эксперименты показывают, что для решений Вандермонда предложенные алгоритмы имеют хорошую точность и достаточно низкую сложность. Для разложения на множители специальное разложение на множители действительно дает более хорошую декорреляцию, чем FFT, при умеренной сложности, но по поводу точности имеются возможности для улучшений. Встроенные реализации MATLAB дают удовлетворительную точность, которая приводит нас к заключению, что точные алгоритмы со сложностью O(N2) могут быть реализованы.
Описанные выше варианты осуществления являются лишь иллюстративными для принципов настоящего изобретения. Подразумевается, что модификации и изменения описанных здесь конфигураций и подробностей будут очевидны для специалистов в области техники. Таким образом, изобретение ограничено только объемом следующей формулы изобретения, а не конкретными деталями, представленными посредством описания и объяснения вариантов осуществления настоящего изобретения.
ЛИТЕРАТУРА
[1] B. Bessette, R. Salami, R. Lefebvre, M. Jelinek, J. Rotola-Pukkila, J. Vainio, H. Mikkola, and K. Järvinen, ʺThe adaptive multirate wideband speech codec (AMR-WB)," Speech and Audio Processing, IEEE Transactions on, vol. 10, no. 8, pp. 620-636, 2002.
[2] ITU-T G.718, ʺFrame error robust narrow-band and wideband embedded variable bit-rate coding of speech and audio from 8-32 kbit/s," 2008.
[3] M. Neuendorf, P. Gournay, M. Multrus, J. Lecomte, B. Bessette, R. Geiger, S. Bayer, G. Fuchs, J. Hilpert, N. Rettelbach, R. Salami, G. Schuller, R. Lefebvre, and B. Grill, ʺUnied speech and audio coding scheme forhigh quality at low bitrates," in Acoustics, Speech and Signal Processing. ICASSP 2009. IEEE Int Conf, 2009, pp. 1-4.
[4] J.-P. Adoul, P. Mabilleau, M. Delprat, and S. Morissette, ʺFast CELP coding based on algebraic codes," in Acoustics, Speech, and Signal Processing, IEEE International Conference on ICASSP'87., vol. 12. IEEE, 1987, pp. 1957-1960.
[5] C. Laamme, J. Adoul, H. Su, and S. Morissette, ʺOn reducing computational complexity of codebook search in CELP coder through the use of algebraic codes," in Acoustics, Speech, and Signal Processing, 1990. ICASSP-90., 1990 International Conference on. IEEE, 1990, pp. 177-180.
[6] F.-K. Chen and J.-F. Yang, ʺMaximum-take-precedence ACELP: a low complexity search method," in Acoustics, Speech, and Signal Processing, 2001. Proceedings.(ICASSP'01). 2001 IEEE International Conference on, vol. 2. IEEE, 2001, pp. 693-696.
[7] K. J. Byun, H. B. Jung, M. Hahn, and K. S. Kim, ʺA fast ACELP codebook search method," in Signal Processing, 2002 6th International Conference on, vol. 1. IEEE, 2002, pp. 422-425. [8] N. K. Ha, \A fast search method of algebraic codebook by reordering search sequence," in Acoustics, Speech, and Signal Processing, 1999. Proceedings., 1999 IEEE International Conference on, vol. 1. IEEE, 1999, pp. 21-24.
[9] M. A. Ramirez and M. Gerken, ʺEfficient algebraic multipulse search," in Telecommunications Symposium, 1998. ITS'98 Proceedings. SBT/IEEE International. IEEE, 1998, pp. 231-236.
[10] T. Bäckström, ʺComputationally efficient objective function for algebraic codebook optimization in ACELP," in Interspeech 2013, August 2013.
[11] |ʺVandermonde factorization of Toeplitz matrices and applications in filtering and warping," IEEE Trans. Signal Process., vol. 61, no. 24, pp. 6257-6263, 2013.
[12] G. H. Golub and C. F. van Loan, Matrix Computations, 3rd ed. John Hopkins University Press, 1996.
[13] T. Bäckström, J. Fischer, and D. Boley, ʺImplementation and evaluation of the Vandermonde transform," in submitted to EUSIPCO 2014 (22nd European Signal Processing Conference 2014) (EUSIPCO 2014), Lisbon, Portugal, Sep. 2014.
[14] T. Bäckström, G. Fuchs, M. Multrus, and M. Dietz, ʺLinear prediction based audio coding using improved probability distribution estimation," US Provisional Patent US 61/665 485, 6, 2013.
[15] K. Hermus, P. Wambacq et al., \A review of signal subspace speech enhancement and its application to noise robust speech recognition," EURASIP Journal on Applied Signal Processing, vol. 2007, no. 1, pp. 195-195, 2007.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО И СПОСОБ ДЛЯ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ АУДИОСИГНАЛА С ИСПОЛЬЗОВАНИЕМ ВЫРОВНЕННОЙ ЧАСТИ ОПЕРЕЖАЮЩЕГО ПРОСМОТРА | 2012 |
|
RU2574849C2 |
| КОДЕР АУДИОСИГНАЛА, ДЕКОДЕР АУДИОСИГНАЛА, СПОСОБ КОДИРОВАНИЯ ИЛИ ДЕКОДИРОВАНИЯ АУДИОСИГНАЛА С УДАЛЕНИЕМ АЛИАСИНГА (НАЛОЖЕНИЯ СПЕКТРОВ) | 2010 |
|
RU2591011C2 |
| УСТРОЙСТВО ДЛЯ КОДИРОВАНИЯ РЕЧЕВОГО СИГНАЛА С ИСПОЛЬЗОВАНИЕМ ACELP В АВТОКОРРЕЛЯЦИОННОЙ ОБЛАСТИ | 2013 |
|
RU2636126C2 |
| СПОСОБЫ, УСТРОЙСТВА И СИСТЕМЫ ДЛЯ УЛУЧШЕНИЯ УНИФИЦИРОВАННОГО ДЕКОДИРОВАНИЯ И КОДИРОВАНИЯ РЕЧИ И ЗВУКА | 2018 |
|
RU2779265C2 |
| АУДИОКОДЕР И АУДИОДЕКОДЕР ДЛЯ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ ОТСЧЕТОВ АУДИОСИГНАЛА | 2009 |
|
RU2515704C2 |
| АУДИОКОДЕР ДЛЯ КОДИРОВАНИЯ АУДИОСИГНАЛА, ИМЕЮЩЕГО ИМПУЛЬСОПОДОБНУЮ И СТАЦИОНАРНУЮ СОСТАВЛЯЮЩИЕ, СПОСОБЫ КОДИРОВАНИЯ, ДЕКОДЕР, СПОСОБ ДЕКОДИРОВАНИЯ И КОДИРОВАННЫЙ АУДИОСИГНАЛ | 2008 |
|
RU2439721C2 |
| АУДИОКОДЕР И ДЕКОДЕР | 2015 |
|
RU2696292C2 |
| УСТРОЙСТВО И СПОСОБ ДЕКОДИРОВАНИЯ КОДИРОВАННОГО ЗВУКОВОГО СИГНАЛА | 2009 |
|
RU2483366C2 |
| КОДЕР И ДЕКОДЕР АУДИОСИГНАЛА, ИСПОЛЬЗУЮЩИЕ ПРОЦЕССОР ЧАСТОТНОЙ ОБЛАСТИ С ЗАПОЛНЕНИЕМ ПРОМЕЖУТКА В ПОЛНОЙ ПОЛОСЕ И ПРОЦЕССОР ВРЕМЕННОЙ ОБЛАСТИ | 2015 |
|
RU2671997C2 |
| ОСНОВАННОЕ НА ЛИНЕЙНОМ ПРЕДСКАЗАНИИ КОДИРОВАНИЕ АУДИО С ИСПОЛЬЗОВАНИЕМ УЛУЧШЕННОЙ ОЦЕНКИ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ | 2013 |
|
RU2651187C2 |
Изобретение относится к средствам для кодирования и декодирования. Технический результат заключается в повышении эффективности кодирования. Кодер для кодирования аудиосигнала в поток данных содержит модуль предсказания, модуль разложения на множители, преобразователь и каскад квантования и кодирования. Модуль предсказания выполнен с возможностью анализировать аудиосигнал, чтобы получить коэффициенты предсказания, описывающие спектральный аналог аудиосигнала или основную частоту аудиосигнала, и подвергнуть аудиосигнал функции анализирующей фильтрации, зависящей от коэффициентов предсказания, чтобы выдать разностный сигнал аудиосигнала. Модуль разложения на множители выполнен с возможностью применять матричное разложение на множители к автокорреляционной или ковариационной матрице функции синтезирующей фильтрации, заданной коэффициентами предсказания. Преобразователь выполнен с возможностью преобразовывать разностный сигнал на основе матриц, разложенных на множители. Каскад квантования и декодирования выполнен с возможностью квантовать преобразованный разностный сигнал, чтобы получить квантованный преобразованный разностный сигнал или закодированный квантованный преобразованный разностный сигнал. 7 н. и 16 з.п. ф-лы, 7 ил., 4 табл.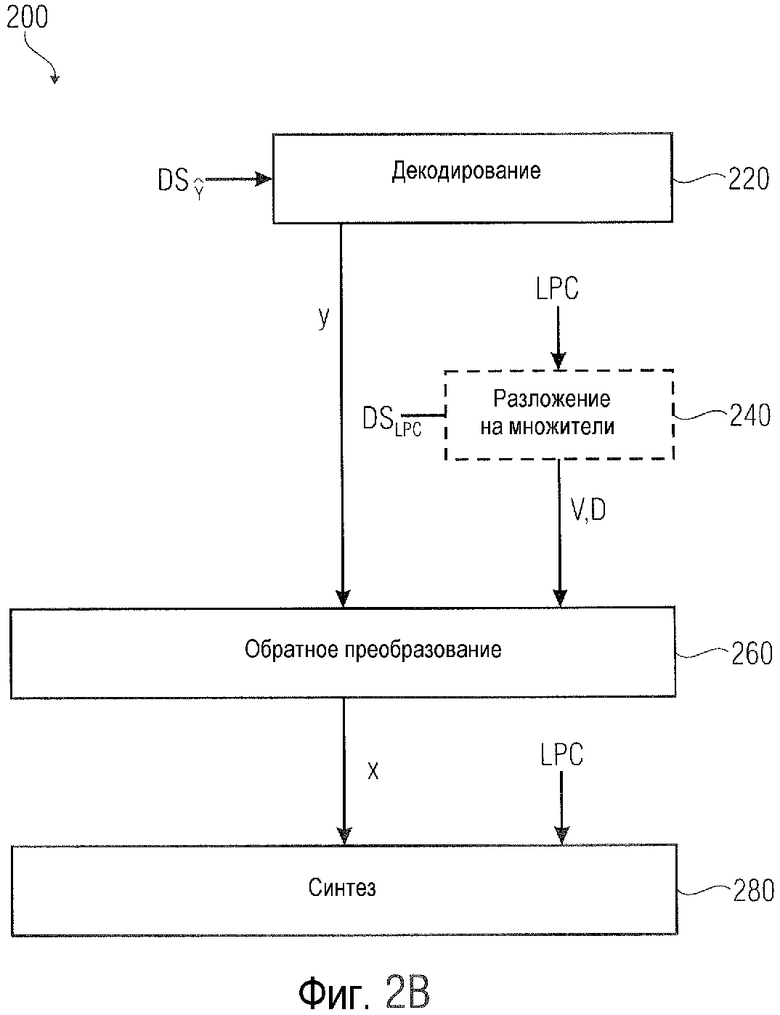
1. Кодер (10) для кодирования аудиосигнала (AS) в поток (DS) данных, содержащий:
модуль (12) предсказания, выполненный с возможностью анализировать аудиосигнал (AS), чтобы получить коэффициенты (LPC) предсказания, описывающие огибающую спектра аудиосигнала (AS) или основную частоту аудиосигнала (AS), и подвергнуть аудиосигнал (AS) функции (H) анализирующей фильтрации, зависящей от коэффициентов (LPC) предсказания, чтобы выдать разностный сигнал (x) аудиосигнала (AS);
модуль (14) разложения на множители, выполненный с возможностью применять матричное разложение на множители к автокорреляционной или ковариационной матрице (R, C) функции (H) синтезирующей фильтрации, заданной коэффициентами (LPC) предсказания, чтобы получить матрицы (V, D), разложенные на множители;
преобразователь (16), выполненный с возможностью преобразовывать разностный сигнал (x) на основе матриц (V, D), разложенных на множители, чтобы получить преобразованный разностный сигнал (y); и
каскад (18) квантования и кодирования, выполненный с возможностью квантовать преобразованный разностный сигнал (y), чтобы получить квантованный преобразованный разностный сигнал (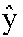 ), и содержащий модуль энтропийного кодирования, имеющий вход для коэффициентов (LPC) предсказания и выполненный с возможностью выполнять энтропийное кодирование квантованного преобразованного разностного сигнала (
), и содержащий модуль энтропийного кодирования, имеющий вход для коэффициентов (LPC) предсказания и выполненный с возможностью выполнять энтропийное кодирование квантованного преобразованного разностного сигнала (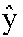 ) с обнаружением вероятности на основе коэффициентов (LPC) предсказания, чтобы получить закодированный квантованный преобразованный разностный сигнал (
) с обнаружением вероятности на основе коэффициентов (LPC) предсказания, чтобы получить закодированный квантованный преобразованный разностный сигнал (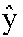 ).
).
2. Кодер (10) по п. 1, в котором функция (H) синтезирующей фильтрации задана матрицей (H), содержащей взвешенные значения функции (H) синтезирующей фильтрации.
3. Кодер (10) по п. 1, в котором модуль (14) разложения на множители вычисляет автокорреляционную или ковариационную матрицу (R, C) на основе произведения преобразованной сопряженной версии функции (H*) синтезирующей фильтрации и регулярной версии функции (H) синтезирующей фильтрации;
4. Кодер (10) по п. 1, в котором модуль (14) разложения на множители разлагает на множители автокорреляционную или ковариационную матрицу (R, C) на основе формулы C=V*DV или на основе формулы R=V*DV,
где V - матрица Вандермонда, V* - преобразованная сопряженная версия матрицы Вандермонда, и D - диагональная матрица со строго положительными элементами.
5. Кодер (10) по п. 4, в котором модуль (14) разложения на множители выполнен с возможностью выполнять разложение на множители Вандермонда.
6. Кодер (10) по п. 1, в котором модуль (14) разложения на множители выполнен с возможностью выполнять разложение по собственным значениям и/или разложение на множители Холецкого.
7. Кодер (10) по п. 4, в котором преобразователь (16) преобразовывает разностный сигнал (x) на основе формулы y=D1/2Vx или на основе формулы y=DVx.
8. Кодер (10) по п. 1, в котором каскад (18) квантования и кодирования квантует преобразованный разностный сигнал (y), чтобы получить квантованный преобразованный разностный сигнал (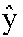 ), на основе целевой функции
), на основе целевой функции 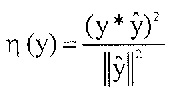 .
.
9. Кодер (10) по п. 1, в котором каскад (18) квантования и кодирования содержит средство для оптимизации квантования посредством применения заполнения шумом, чтобы обеспечить заполненное шумом спектральное представление аудиосигнала (AS), разностного сигнала (x) или преобразованного разностного сигнала (y), или посредством оптимизации квантованного преобразованного разностного сигнала (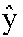 ) относительно мертвых зон или относительно других параметров квантования.
) относительно мертвых зон или относительно других параметров квантования.
10. Кодер (10) по п. 1, в котором преобразование разностного сигнала (x) является преобразованием из временной области разностного сигнала (x) в частотную область преобразованного разностного сигнала (y).
11. Кодер (10) по п. 1, в котором каскад квантования и кодирования содержит кодер, выполненный с возможностью выполнять кодирование квантованного преобразованного разностного сигнала (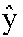 ), чтобы получить закодированный квантованный преобразованный разностный сигнал (
), чтобы получить закодированный квантованный преобразованный разностный сигнал (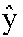 ').
').
12. Кодер (10) по п. 11, в котором кодирование, выполняемое кодером, находится вне группы, содержащей арифметическое кодирование.
13. Кодер (10) по п. 11, в котором кодер (10) дополнительно содержит упаковщик, выполненный с возможностью упаковывать закодированный квантованный преобразованный разностный сигнал (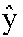 ') и коэффициенты (LPC) предсказания в поток (DS) данных для выдачи кодером (10).
') и коэффициенты (LPC) предсказания в поток (DS) данных для выдачи кодером (10).
14. Кодер (10) по п. 1, в котором модуль (12) предсказания содержит модуль линейного предсказания (и/или модуль долговременного предсказания).
15. Способ (100) кодирования аудиосигнала (AS) в поток (DS) данных, причем способ содержит этапы, на которых:
анализируют (120) аудиосигнал (AS), чтобы получить коэффициенты (LPC) предсказания, описывающие огибающую спектра аудиосигнала (AS) или основную частоту аудиосигнала (AS), и подвергают аудиосигнал (AS) функции (H) анализирующей фильтрации, зависящей от коэффициентов (LPC) предсказания, чтобы выдать разностный сигнал (x) аудиосигнала (AS);
применяют (140) матричное разложение на множители к автокорреляционной или ковариационной матрице (R, C) функции (H) синтезирующей фильтрации, заданной коэффициентами (LPC) предсказания, чтобы получить матрицы (V, D), разложенные на множители;
преобразовывают (160) разностный сигнал (x) на основе матриц (V, D), разложенных на множители, чтобы получить преобразованный разностный сигнал (y); и
квантуют и кодируют (180) преобразованный разностный сигнал (y), чтобы получить квантованный преобразованный разностный сигнал (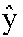 ), и выполняют энтропийное кодирование с использованием коэффициентов (LPC) предсказания квантованного преобразованного разностного сигнала (
), и выполняют энтропийное кодирование с использованием коэффициентов (LPC) предсказания квантованного преобразованного разностного сигнала (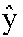 ) с обнаружением вероятности на основе коэффициентов (LPC) предсказания, чтобы получить закодированный квантованный преобразованный разностный сигнал (
) с обнаружением вероятности на основе коэффициентов (LPC) предсказания, чтобы получить закодированный квантованный преобразованный разностный сигнал (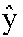 ).
).
16. Применение способа (100) по п. 15 вместо дискретного преобразования Фурье, дискретного косинусного преобразования, модифицированного дискретного косинусного преобразования в алгоритмах обработки сигналов.
17. Декодер (20) для декодирования потока (DS) данных в аудиосигнал (AS'), содержащий:
каскад (22) декодирования, выполненный с возможностью выдавать преобразованный разностный сигнал (y) на основе входящего закодированного квантованного преобразованного разностного сигнала (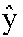 ) с использованием энтропийного декодирования с обнаружением вероятности на основе коэффициентов (LPC) предсказания, описывающих огибающую спектра аудиосигнала (AS) или основную частоту аудиосигнала (AS);
) с использованием энтропийного декодирования с обнаружением вероятности на основе коэффициентов (LPC) предсказания, описывающих огибающую спектра аудиосигнала (AS) или основную частоту аудиосигнала (AS);
обратный преобразователь (26), выполненный с возможностью обратно преобразовывать разностный сигнал (x) из преобразованного разностного сигнала (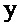 ) на основе матриц (V, D), разложенных на множители, представляющих результат матричного разложения на множители автокорреляционной или ковариационной матрицы (R, C) функции (H) синтезирующей фильтрации, заданной упомянутыми коэффициентами (LPC) предсказания; и
) на основе матриц (V, D), разложенных на множители, представляющих результат матричного разложения на множители автокорреляционной или ковариационной матрицы (R, C) функции (H) синтезирующей фильтрации, заданной упомянутыми коэффициентами (LPC) предсказания; и
каскад (28) синтеза, выполненный с возможностью синтезировать аудиосигнал (AS') на основе разностного сигнала (x) посредством использования функции (H) синтезирующей фильтрации, заданной коэффициентами (LPC) предсказания.
18. Декодер (20) по п. 17, причем декодер (20) содержит модуль (24) разложения на множители, выполненный с возможностью применять матричное разложение на множители к автокорреляционной или ковариационной матрице (R, C) функции (H) синтезирующей фильтрации, заданной входящими коэффициентами (LPC) предсказания, чтобы получить матрицы (V, D), разложенные на множители.
19. Декодер (20) по п. 17, причем декодер (20) содержит генератор коэффициентов предсказания, выполненный с возможностью отклонять коэффициенты (LPC) предсказания на основе входящих матриц (V, D), разложенных на множители.
20. Декодер (20) по п. 17, в котором каскад (22) декодирования выполняет декодирование на основе известных правил кодирования и/или параметров кодирования, отклоненных от входящих правил кодирования и/или параметров кодирования.
21. Способ (200) декодирования потока (DS) данных в аудиосигнал (AS'), причем способ содержит этапы, на которых:
выдают (220) преобразованный разностный сигнал (y) на основе входящего закодированного квантованного преобразованного разностного сигнала (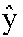 ) с использованием энтропийного декодирования с обнаружением вероятности на основе коэффициентов (LPC) предсказания, описывающих огибающую спектра аудиосигнала (AS) или основную частоту аудиосигнала (AS);
) с использованием энтропийного декодирования с обнаружением вероятности на основе коэффициентов (LPC) предсказания, описывающих огибающую спектра аудиосигнала (AS) или основную частоту аудиосигнала (AS);
применяют (240) матричное разложение на множители к автокорреляционной или ковариационной матрице (R, C) функции (H) синтезирующей фильтрации, заданной коэффициентами (LPC) предсказания;
описывают (240) огибающую спектра аудиосигнала (AS) или основную частоту аудиосигнала (AS), чтобы получить матрицы (V, D), разложенные на множители;
обратно преобразовывают (260) разностный сигнал (x) из подвергнутого обратному преобразованию разностного сигнала (y) на основе матриц (V, D), разложенных на множители; и
синтезируют (280) аудиосигнал (AS') на основе разностного сигнала (x) посредством использования функции (H) синтезирующей фильтрации, заданной коэффициентами (LPC) предсказания.
22. Машиночитаемый цифровой запоминающий носитель, хранящий сохраненную на нем компьютерную программу, имеющую программный код для выполнения при его работе на компьютере способа (100, 200) по п. 15.
23. Машиночитаемый цифровой запоминающий носитель, хранящий сохраненную на нем компьютерную программу, имеющую программный код для выполнения при его работе на компьютере способа (100, 200) по п. 21.
| TOM BACKSTROM, "Vandermonde Factorization of Toeplitz Matrices and Applications in Filtering and Warping", IEEE TRANSACTIONS ON SIGNAL PROCESSING, vol | |||
| Устройство для сортировки каменного угля | 1921 |
|
SU61A1 |
| Пишущая машина для тюркско-арабского шрифта | 1922 |
|
SU24A1 |
| US 5495556 A1, 27.02.1996 | |||
| Изложница с суживающимся книзу сечением и с вертикально перемещающимся днищем | 1924 |
|
SU2012A1 |
| EP 1396841 B1, 27.02.2008 | |||
| US 7065486 B1, 20.06.2006 | |||
| АУДИОКОДЕР ДЛЯ КОДИРОВАНИЯ АУДИОСИГНАЛА, ИМЕЮЩЕГО ИМПУЛЬСОПОДОБНУЮ И СТАЦИОНАРНУЮ СОСТАВЛЯЮЩИЕ, СПОСОБЫ КОДИРОВАНИЯ, ДЕКОДЕР, СПОСОБ ДЕКОДИРОВАНИЯ И КОДИРОВАННЫЙ АУДИОСИГНАЛ | 2008 |
|
RU2439721C2 |
Авторы
Даты
2018-07-25—Публикация
2015-03-03—Подача