Заявленное изобретение относится к области электросвязи и информационных технологий, а именно к сжатию оцифрованных изображений.
Заявленное изобретение может быть использовано для снижения требований к скорости передачи изображений и к емкости запоминающих устройств, используемых для хранения изображений.
Существующие в настоящее время стандарты сжатия видеоданных, например MPEG-1, 2, 4, Н-263, Н-264, предусматривают выполнение следующих типовых этапов преобразования: кодирование цветового пространства изображения; разделение цветовых компонент на блоки фиксированного размера (4×4, 8×8, 16×16, 32×32, 64×64); выполнение над каждым блоком операции двумерного дискретного косинусного преобразования (ДКП-2); квантование коэффициентов ДКП-2 с последующим энтропийным кодированием. Эффект сжатия достигается за счет того, что после выполнения ДКП-2 большая часть коэффициентов принимает значение, близкое к нулю. В связи с этим квантованные блоки коэффициентов содержат большое количество нулевых элементов, что обеспечивает высокий коэффициент сжатия на этапе энтропийного кодирования. Недостатком указанных стандартов является необходимость разделения исходного изображения на блоки меньшего размера. Это приводит к существенному недостатку - возникновению артефакта блочности, который проявляется в наличии видимых границ между блоками пикселей на декодированных изображениях. Данное обстоятельство существенно ухудшает зрительное восприятие изображений при увеличении коэффициента сжатия. Подробно использование ДКП-2 для сжатия изображений описано в стандарте ISO/IEC 10918-1: 1993.
Известен также способ и устройство для кодирования и декодирования изображения и способ и устройство для декодирования изображения с помощью адаптивного порядка сканирования коэффициентов по патенту РФ 2518935 МПК H04N от 10.06.2014, заключающийся в том, что на передающей стороне исходное изображение разделяют на блоки меньшего размера, выполняют над указанными блоками ДКП-2, квантуют их и выполняют энтропийное кодирование над квантованными коэффициентами, отличающийся использованием адаптивного порядка сканирования коэффициентов ДКП-2 путем проецирования коэффициентов на ось под углом α (равен 0, 45 или 90 градусов) к опорной оси и кодированием с помощью энтропийного кодирования о заранее заданном угле α и отсканированных коэффициентах.
Недостатком данного способа-аналога является ограниченное число вариантов сканирования коэффициентов, которое определяется заранее заданным углом α, что приводит либо к снижению коэффициента сжатия при заданном качестве восстановленных изображений, либо к снижению качества восстановления при увеличении коэффициента сжатия. Кроме того, поскольку ДКП-2 выполняют над блоками меньшего размера, чем сжимаемое изображение, то сохраняется недостаток, связанный с эффектом блочности при восстановлении изображений на приеме.
Другой способ сжатия основывается на субполосном преобразовании изображения с последующим устранением межполосной избыточности. Субполосное преобразование подробно рассмотрено в книге В.П. Воробьев, В.Г. Грибунин "Теория и практика вейвлет-преобразования". - С-Петербург, ВУС, 1999. Используя субполосное преобразование, изображение преобразуют в набор субполос, каждая из которых представляет собой матрицу коэффициентов преобразования. В качестве субполосного преобразования используют вейвлет-разложение по схеме Малла. В этом случае используется реализация вейвлет-преобразования в виде зеркального фильтра с ядром, вид которого определяется используемым вейвлет-базисом. Адаптация заключается в выборе низкочастотной либо высокочастотной составляющей зеркального фильтра по каждой субполосе.
Данный аналог за счет адаптивного выбора частотных составляющих субполос обеспечивает повышение коэффициента сжатия по сравнению с методами, в которых выбор частотных составляющих субполос является фиксированным.
Недостатком указанного аналога является то, что при сжатии изображения используют неизменный вейвлет-базис, что не позволяет обеспечивать требуемый коэффициент сжатия при кодировании всего многообразия различных изображений.
Наиболее близким по своей технической сущности к заявленному способу кодирования оцифрованных изображений является способ кодирования оцифрованных изображений с использованием дискретного вейвлет-преобразования адаптивно-определенного базиса по патенту RU 2429541 С2, МПК G06T 9/20 (2006/1) от 02.09.2009. Способ-прототип кодирования оцифрованных изображений заключается в том, что исходное изображение разбивают на блоки и для упомянутых блоков выполняют дискретное вейвлет-преобразование с использованием вейвлет-базисов, которые были определены адаптивно на этапе адаптивного кодирования.
Способ-прототип кодирования оцифрованных изображений обеспечивает снижение требований к скорости передачи изображений и к емкости запоминающих устройств на основе повышения коэффициента сжатия за счет выбора оптимального вейвлет-базиса из библиотеки.
Общая схема способа-прототипа представлена на фиг. 1. На передающей стороне входное изображение 1 подвергают преобразованию цветовых пространств на этапе 2, результатом которого являются матрицы пикселов, соответствующие цветовым пространствам изображения (например, матрица яркости, матрица контрастности и матрица цветности). Каждую из этих матриц передают на этап 3 дискретизации изображения, на котором его сегментируют и формируют блоки исходного изображения (далее по тексту - БИИ). Затем выполняют этап 4 адаптивного кодирования с использованием методов статистического, корреляционного и спектрального анализа, для чего адаптивно определяют вейвлет-базисы для БИИ, выполняют дискретное вейвлет-преобразование (далее по тексту - ДВП), а также выполняют другие действия по кодированию БИИ. Способ определения вейвлет-базиса может быть как одним для всех БИИ, так и различаться от блока к блоку. Кроме того, при расчете коэффициентов ДВП субполос БИИ для каждой из этих субполос может быть использован свой вейвлет-базис. На завершающем этапе 5 формируют битовый поток изображения. Полученные последовательности бит для каждого из БИИ дополняют служебной информацией (например, информацией о размерах блоков, размерах изображения, используемых вейвлет-базисах и т.д.) и объединяют в битовый поток изображения. Окончание этапа 5 означает завершение компрессии входного изображения 1 и результирующая битовая последовательность на этапе 6 может быть записана запоминающим устройством или передана по каналу связи.
В способе-прототипе предусмотрено несколько вариантов адаптивного определения вейвлет-базисов для БИИ: на основе расчета характеристики БИИ; на основе расчета характеристики субполос БИИ; на основе оценки восстановления блоков изображения. При этом каждый из указанных вариантов предполагает выбор оптимального вейвлет-базиса из библиотеки базисов.
При необходимости восстановления изображения записанную или переданную последовательность бит подвергают декомпрессии. На этапе 7 декомпрессии анализируют битовый поток изображения, извлекают служебную информацию и выделяют последовательности бит, соответствующие кодированным коэффициентам ДВП для БИИ. Полученная служебная информация и последовательности бит позволяют осуществить декодирование на этапе 8 и обратное ДВП для соответствующих базисных функций на этапе 9 для того, чтобы в результате получить блоки восстановленного изображения. Полученные на этапе 9 блоки восстановленного изображения в соответствии со служебной информацией на этапе 10 объединяют в матрицы цветовых пространств восстановленного изображения. После того как все матрицы изображения восстановлены, наступает этап преобразования цветовых пространств 11, представляющий собой восстановленное изображение в виде матриц требуемого цветового пространства. Результатом декомпрессии является восстановленное изображение 12.
Особенностью способа-прототипа является то, что выбор оптимального вейвлет-базиса осуществляют из библиотеки вейвлет-базисов ограниченного объема. Поскольку разнообразие сжимаемых изображений бесконечно велико, а объем библиотеки вейвлет-базисов ограничен, то возможны случаи, когда выбранный вейвлет-базис для сжатия текущего БИИ будет неоптимальным. Это, в свою очередь, приводит либо к снижению качества восстановленных на приеме изображений, либо к снижению коэффициента сжатия.
Недостатком ближайшего аналога (прототипа) является ограниченный набор вейвлет-базисов, из которого выбирают оптимальный, что приводит к снижению эффективности сжатия (коэффициента сжатия).
Целью заявленного технического решения является разработка способа кодирования цифрового изображения, обеспечивающего повышение коэффициента сжатия без снижения качества восстановленного на приеме изображения за счет исключения предварительно сформированной библиотеки вейвлет-базисов и формирования базиса ортогонального преобразования непосредственно из самого БИИ.
Указанный технический результат в заявленном способе кодирования оцифрованных изображений с использованием адаптивного ортогонального преобразования достигается тем, что в известном способе кодирования, заключающемся в преобразовании цифрового пространства цифрового изображения, разделении изображения на блоки размером P×N элементов, адаптивном кодировании каждого блока размером P×N элементов, формировании битового потока, согласно изобретению адаптивное кодирование выполняют путем определения базиса ортогонального преобразования и для упомянутых блоков выполняется двумерное ортогональное преобразование с использованием базиса ортогонального преобразования, который был определен адаптивно на этапе адаптивного кодирования, дополнительно определение базиса ортогонального преобразования выполняют путем вычисления правосторонней матрицы ортогонального преобразования размером N×N элементов и левосторонней матрицы ортогонального преобразования размером P×Pэлементов, а для вычисления правосторонней матрицы ортогонального преобразования предварительно назначают величину коэффициента mp, кратную N, причем mp<<N, и формируют нулевую матрицу WP размером N×N элементов, затем вычисляют  корреляционных матриц Xi, i=1, 2, …,
корреляционных матриц Xi, i=1, 2, …,  по формулe
по формулe 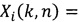
 ; k, n=1, 2, …, mp, где Xi(k,n) - k-ый, n-ый элемент i-ой корреляционной матрицы; а(j,k+(i-1)mp) - элемент блока исходного изображения размером P×N элементов, расположенный в j-ой строке и k+(i-1)mp столбце; a(j,n+(i-1)mp - элемент блока исходного изображения размером P×N элементов, расположенный в j-ой строке и n+(i-1)mp столбце, затем, используя QR-алгоритм вычисления собственных векторов и собственных чисел квадратной симметрической матрицы, для каждой матрицы Xi, i=1, 2, …,
; k, n=1, 2, …, mp, где Xi(k,n) - k-ый, n-ый элемент i-ой корреляционной матрицы; а(j,k+(i-1)mp) - элемент блока исходного изображения размером P×N элементов, расположенный в j-ой строке и k+(i-1)mp столбце; a(j,n+(i-1)mp - элемент блока исходного изображения размером P×N элементов, расположенный в j-ой строке и n+(i-1)mp столбце, затем, используя QR-алгоритм вычисления собственных векторов и собственных чисел квадратной симметрической матрицы, для каждой матрицы Xi, i=1, 2, …,  , вычисляют матрицу собственных векторов Vi и диагональную матрицу собственных чисел [diagλ]i, i=1, 2, …,
, вычисляют матрицу собственных векторов Vi и диагональную матрицу собственных чисел [diagλ]i, i=1, 2, …,  , такие, что Xi=Vi[diagλ]i, причем abs(λi(1,1))>abs(λi(2,2))>,…,>abs(λi(j,j))>,…,>abs(λi(mp,mp)), где λi(j,j) - j-ый, j-ый элемент i-ой диагональной матрицы собственных чисел [diagλ]i, после чего присваивают элементам матрицы WP размером N×N элементов элементы матриц собственных векторов Vi, i=1, 2, …,
, такие, что Xi=Vi[diagλ]i, причем abs(λi(1,1))>abs(λi(2,2))>,…,>abs(λi(j,j))>,…,>abs(λi(mp,mp)), где λi(j,j) - j-ый, j-ый элемент i-ой диагональной матрицы собственных чисел [diagλ]i, после чего присваивают элементам матрицы WP размером N×N элементов элементы матриц собственных векторов Vi, i=1, 2, …, 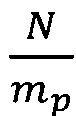 по формуле WP(k+(i-1)mp, i+(j-1)mp)=Vi(k,j), k=1, 2, …, mp; i=1, 2, …,
по формуле WP(k+(i-1)mp, i+(j-1)mp)=Vi(k,j), k=1, 2, …, mp; i=1, 2, …,  ; j=1, 2, …, mp, а для вычисления левосторонней матрицы ортогонального преобразования предварительно назначают величину коэффициента ml, кратную Р, причем ml<<P, и формируют нулевую матрицу WL размером P×P элементов, затем вычисляют
; j=1, 2, …, mp, а для вычисления левосторонней матрицы ортогонального преобразования предварительно назначают величину коэффициента ml, кратную Р, причем ml<<P, и формируют нулевую матрицу WL размером P×P элементов, затем вычисляют 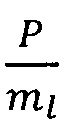 корреляционных матриц Yi, i=1, 2, …,
корреляционных матриц Yi, i=1, 2, …,  по формуле
по формуле  ; k, n=1, 2, …, ml, где Yi (k, n) - k-ый, n-ый элемент i-ой корреляционной матрицы; a(k+(i-1)ml,j) - элемент блока исходного изображения размером P×N элементов, расположенный в k+(i-1)ml строке и в j-ом столбце; а(n+(i-1)ml,j) - элемент блока исходного изображения размером P×N элементов, расположенный в n+(i-1)ml строке и в j-ой строке, затем, используя QR-алгоритм вычисления собственных векторов и собственных чисел квадратной симметрической матрицы, для каждой матрицы Yi, i=1, 2, …,
; k, n=1, 2, …, ml, где Yi (k, n) - k-ый, n-ый элемент i-ой корреляционной матрицы; a(k+(i-1)ml,j) - элемент блока исходного изображения размером P×N элементов, расположенный в k+(i-1)ml строке и в j-ом столбце; а(n+(i-1)ml,j) - элемент блока исходного изображения размером P×N элементов, расположенный в n+(i-1)ml строке и в j-ой строке, затем, используя QR-алгоритм вычисления собственных векторов и собственных чисел квадратной симметрической матрицы, для каждой матрицы Yi, i=1, 2, …, 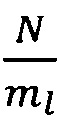 , вычисляют матрицу собственных векторов Ui и диагональную матрицу собственных чисел [diagϒ]i, i=1, 2, …,
, вычисляют матрицу собственных векторов Ui и диагональную матрицу собственных чисел [diagϒ]i, i=1, 2, …,  , такие, что Yi=Ui[diagϒ]i, причем abs(ϒi(1,1))>abs(ϒi(2,2))>,…,>abs(ϒi(j,j))>,…,>abs(ϒi(mp,mp)), где ϒi(j,j) - j-ый, j-ый элемент i-ой диагональной матрицы собственных чисел [diagϒ]i, после чего присваивают элементам матрицы WL размером P×P элементов элементы матриц собственных векторов Ui, i=1, 2, …,
, такие, что Yi=Ui[diagϒ]i, причем abs(ϒi(1,1))>abs(ϒi(2,2))>,…,>abs(ϒi(j,j))>,…,>abs(ϒi(mp,mp)), где ϒi(j,j) - j-ый, j-ый элемент i-ой диагональной матрицы собственных чисел [diagϒ]i, после чего присваивают элементам матрицы WL размером P×P элементов элементы матриц собственных векторов Ui, i=1, 2, …, 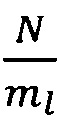 по формуле WL(i+(j-1)ml,k+(i-1)ml)=Ui(k,j), k=1, 2, …, ml; i=1, 2, …,
по формуле WL(i+(j-1)ml,k+(i-1)ml)=Ui(k,j), k=1, 2, …, ml; i=1, 2, …,  ; j=1, 2, …, ml, после этого выполняют двумерное ортогональное преобразование блока исходного изображения размером P×N элементов по формуле С=WL⋅A⋅WP, где С - матрица коэффициентов двумерного ортогонального преобразования размером P×N элементов; WL - левосторонняя матрица ортогонального преобразования размером P×P элементов; WP - правосторонняя матрица ортогонального преобразования размером N×N элементов; A - матрица блока исходного изображения размером P×N элементов.
; j=1, 2, …, ml, после этого выполняют двумерное ортогональное преобразование блока исходного изображения размером P×N элементов по формуле С=WL⋅A⋅WP, где С - матрица коэффициентов двумерного ортогонального преобразования размером P×N элементов; WL - левосторонняя матрица ортогонального преобразования размером P×P элементов; WP - правосторонняя матрица ортогонального преобразования размером N×N элементов; A - матрица блока исходного изображения размером P×N элементов.
В предлагаемом способе кодирования оцифрованных изображений с использованием адаптивного ортогонального преобразования определение базиса ортогонального преобразования выполняют на основе матрицы блока исходного изображения размером P×N элементов, при этом не требуется предварительного создания библиотеки базисов. Поэтому новая совокупность действий при выполнении кодирования оцифрованных изображений с использованием адаптивного ортогонального преобразования позволяет либо улучшить качество восстанавливаемых на приеме изображений, либо повысить коэффициент их сжатия за счет адаптивного вычисления базиса на основе кодируемого изображения.
Заявленный способ поясняется чертежами, на которых показаны:
фиг. 1 - общая схема компрессии и декомпрессии в ближайшем аналоге (прототипе);
фиг. 2 - этапы адаптивного кодирования заявленного способа преобразования;
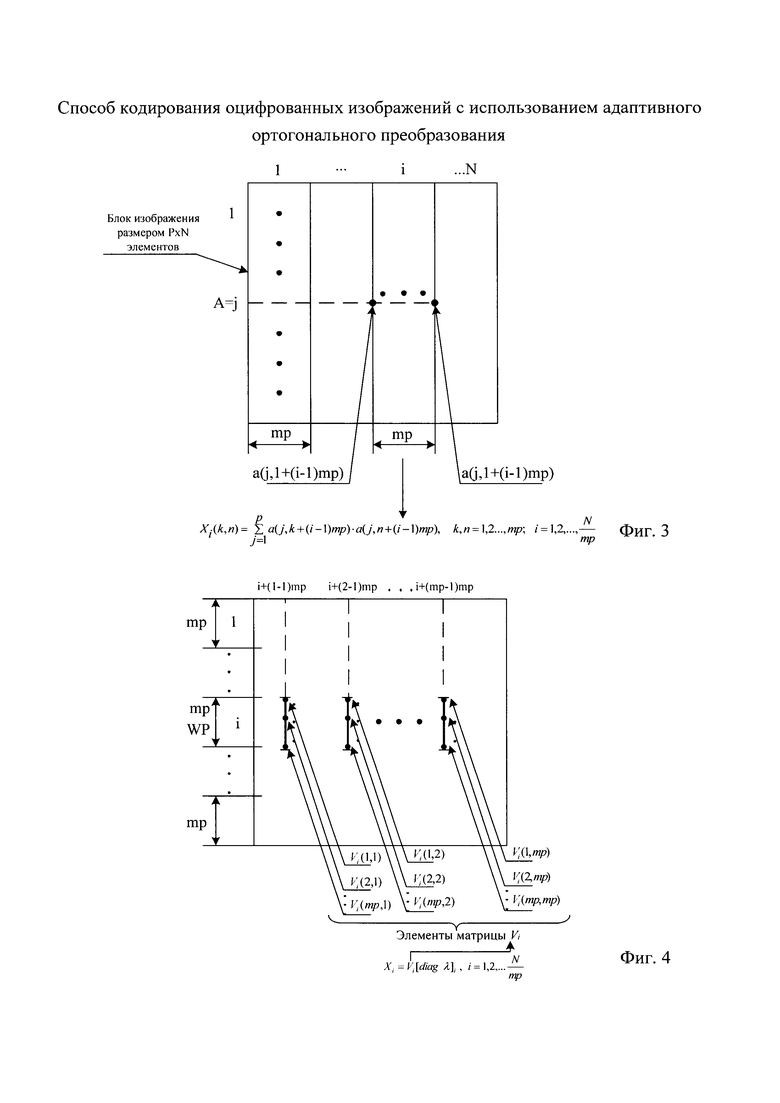
фиг. 3 - этапы вычисления правосторонней матрицы ортогонального преобразования;
фиг. 4 - присвоение элементам матрицы WP размеров N×N элементов матриц собственных векторов Vi, i=1, 2, … ;
;
фиг. 5 - этапы вычисления левосторонней матрицы ортогонального преобразования;
фиг. 6 - формирование i-й корреляционной матрицы левосторонней матрицы ортогонального преобразования размером P×P элементов;
фиг. 7 - пример исходного изображения размером 1080×1920 пикселей;
фиг. 8 - фрагмент восстановленного изображения при использовании алгоритма JPEG;
фиг. 9 - фрагмент восстановленного изображения при использовании алгоритма JPEG-2000;
фиг. 10 - фрагмент восстановленного изображения при использовании заявленного способа.
Реализация заявленного способа заключается в преобразовании цифрового пространства цифрового изображения, разделении изображения на блоки размером P×N элементов, адаптивном кодировании каждого блока размером P×N элементов, формировании битового потока и отличается от способа-прототипа выполнением этапа адаптивного кодирования при компрессии изображения. Фиг. 2 иллюстрирует этапы адаптивного кодирования заявленного способа преобразования. На фиг. 2 БИИ 1, представленный матрицей A размером P×N элементов, используется для расчета базиса ортогонального преобразования в виде правосторонней матрицы ортогонального преобразования - WP размером N×N элементов и левосторонней матрицы ортогонального преобразования - WL размером P×P элементов. Вычисление матриц WP и WL осуществляют на этапах 2 и 3, соответственно. После вычисления матриц WP и WL на этапе 4 выполняют двумерное ортогональное преобразование, в результате которого вычисляют коэффициенты двумерного ортогонального преобразования в виде матрицы С размером P×N элементов в соответствии с выражением С=WL⋅A⋅WP.
Этапы вычисления правосторонней матрицы ортогонального преобразования показаны на фиг. 3. Исходными данными для расчета матрицы WP размером N×N элементов является БИИ 1 в виде матрицы A размером P×N элементов и коэффициент mp, который определяет число ненулевых элементов в каждом столбце матрицы WP размером N×N элементов. На этапе 2, используя элементы a(i,j), i=1, 2, …, Р; j=1, 2, …, N, матрицы A вычисляют корреляционные матрицы Xi, i=1, 2, …,  по формуле
по формуле  (см. фиг. 6); k, n=1, 2, …, mp. Затем, на этапе 3, для найденных матриц Xi, i=1, 2, …,
(см. фиг. 6); k, n=1, 2, …, mp. Затем, на этапе 3, для найденных матриц Xi, i=1, 2, …,  вычисляют матрицы собственных векторов Vi и диагональные матрицы собственных чисел [diagλ]i, i=1, 2, …,
вычисляют матрицы собственных векторов Vi и диагональные матрицы собственных чисел [diagλ]i, i=1, 2, …,  . Вычисление матриц собственных векторов и диагональных матриц собственных чисел можно осуществить так, как это показано в работе [Б. Парлет Симметричные проблемы собственных значений. Численные методы: Пер. с англ. - М, 1983. 384 с]. На 4 этапе присваивают элементам предварительно сформированной нулевой матрицы WP размером N×N элементов элементы матриц собственных векторов Vi, i=1, 2, …,
. Вычисление матриц собственных векторов и диагональных матриц собственных чисел можно осуществить так, как это показано в работе [Б. Парлет Симметричные проблемы собственных значений. Численные методы: Пер. с англ. - М, 1983. 384 с]. На 4 этапе присваивают элементам предварительно сформированной нулевой матрицы WP размером N×N элементов элементы матриц собственных векторов Vi, i=1, 2, …,  в соответствии с выражением WP(k+(i-1)mp, i+(j-1)mp)=Vi(k,j), k=1, 2, …, mp; i=1, 2, …,
в соответствии с выражением WP(k+(i-1)mp, i+(j-1)mp)=Vi(k,j), k=1, 2, …, mp; i=1, 2, …,  ; j=1, 2, …, mp. Присвоение элементам матрицы WP размеров N×N элементов матриц собственных векторов Vi, i=1, 2, …
; j=1, 2, …, mp. Присвоение элементам матрицы WP размеров N×N элементов матриц собственных векторов Vi, i=1, 2, … показано на фиг. 4.
показано на фиг. 4.
Этапы вычисления левосторонней матрицы ортогонального преобразования показаны на фиг. 5. Исходными данными для расчета матрицы WL размером Р×Р элементов является БИИ 1 в виде матрицы A размером P×N элементов и параметр ml, который определяет число ненулевых элементов в каждой строке матрицы WL размером P×P элементов. На этапе 2, используя элементы a(i,j), i=1, 2, …, Р; j=1, 2, …, N, матрицы A вычисляют корреляционные матрицы Yi, i=1, 2, …,  по формуле
по формуле  ; k, n=1, 2, …, ml. Затем, на этапе 3, для найденных матриц Yi, i=1, 2, …,
; k, n=1, 2, …, ml. Затем, на этапе 3, для найденных матриц Yi, i=1, 2, …, 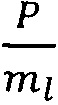 вычисляют матрицы собственных векторов Ui и диагональные матрицы собственных чисел [diagϒ]i, i=1, 2, …,
вычисляют матрицы собственных векторов Ui и диагональные матрицы собственных чисел [diagϒ]i, i=1, 2, …,  . На 4 этапе присваивают элементам предварительно сформированной нулевой матрицы WL размером Р×Р элементов элементы матриц собственных векторов Ui, i=1, 2, …,
. На 4 этапе присваивают элементам предварительно сформированной нулевой матрицы WL размером Р×Р элементов элементы матриц собственных векторов Ui, i=1, 2, …, 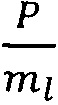 в соответствии с выражением WL(i+(j-1)ml, k+(i-1)ml)=Ui(k,j), k=1, 2, …, ml; k=1, 2, …,
в соответствии с выражением WL(i+(j-1)ml, k+(i-1)ml)=Ui(k,j), k=1, 2, …, ml; k=1, 2, …,  ; j=1, 2, …, ml.
; j=1, 2, …, ml.
Проверка эффективности заявленного способа кодирования оцифрованных изображений с использованием адаптивного ортогонального преобразования проводилась методом имитационного моделирования.
В качестве исходного было использовано монохромное изображение с 256 уровнями серого размером 1080×1920 пикселей. Пример исходного изображения показан на фиг. 7. Результаты имитационного моделирования представлены в таблице 1.

В ходе моделирования оценка качества восстановленных изображений осуществлялась путем расчета пикового отношения сигнал/шум (PSNR) и визуальным просмотром. Расчет PSNR осуществлялся в соответствии с выражением  , где P - число строк блока исходного изображения; N - число столбцов блока исходного изображения; A(i,j) - элемент блока исходного изображения размером P×N элементов, расположенный в i-ой строке и j-ом столбце;
, где P - число строк блока исходного изображения; N - число столбцов блока исходного изображения; A(i,j) - элемент блока исходного изображения размером P×N элементов, расположенный в i-ой строке и j-ом столбце;  - элемент блока восстановленного изображения размером P×N элементов, расположенный в i-ой строке и j-ом столбце. Представленные в табл. 1 значения PSNR получены при сжатии исходного изображения в 100 раз. Кроме заявленного способа в таблице 1 представлены результаты вычисления PSNR при использовании известных стандартов сжатия неподвижных изображений JPEG и JPEG-2000. Анализ результатов показывает, что заявленный способ характеризуется превышением величины PSNR на 5,1 [дБ] по сравнению с алгоритмом JPEG и на 2,5 [дБ] по сравнению с алгоритмом JPEG-2000.
- элемент блока восстановленного изображения размером P×N элементов, расположенный в i-ой строке и j-ом столбце. Представленные в табл. 1 значения PSNR получены при сжатии исходного изображения в 100 раз. Кроме заявленного способа в таблице 1 представлены результаты вычисления PSNR при использовании известных стандартов сжатия неподвижных изображений JPEG и JPEG-2000. Анализ результатов показывает, что заявленный способ характеризуется превышением величины PSNR на 5,1 [дБ] по сравнению с алгоритмом JPEG и на 2,5 [дБ] по сравнению с алгоритмом JPEG-2000.
Визуальный анализ качества восстановленных изображений показал, что изображения, полученные на основе заявленного способа, не имеют артефактов в виде блочности (см. фиг. 8), характерных для алгоритма JPEG, и артифактов в виде выделения фоновых участков, характерных для алгоритма JPEG-2000 (см. фиг. 9). Фрагмент восстановленного изображения на основе заявленного способа представлен на фиг. 10. Анализ представленного изображения свидетельствует об отсутствии указанных артефактов.
Таким образом, в заявленном способе кодирования оцифрованных изображений с использованием адаптивного ортогонального преобразования обеспечивается повышение качества восстановленных изображений при заданном коэффициенте сжатия по сравнению с известными.




Изобретение относится к области электросвязи и информационных технологий и предназначено для использования в сетях передачи видеоизображений, в частности при необходимости сжатия оцифрованных видеоизображений. Техническим результатом является повышение коэффициента сжатия без снижения качества восстановленного на приеме изображения за счет исключения предварительно сформированной библиотеки вейвлет-базисов и формирования базиса ортогонального преобразования непосредственно из самого блока исходного изображения. Предложен способ кодирования цифрового изображения. Согласно способу преобразуют цифровое пространство цифрового изображения, разделяют изображение на блоки размером P×N элементов, адаптивно кодируют каждый блок размером P×N элементов, формируют битовый поток. При этом адаптивное кодирование выполняют путем определения базиса ортогонального преобразования, причем для определения базиса ортогонального преобразования вычисляют правостороннюю матрицу ортогонального преобразования размером N×N и левостороннюю матрицу ортогонального преобразования размером Р×Р элементов. 1 з.п. ф-лы, 10 ил., 1 табл.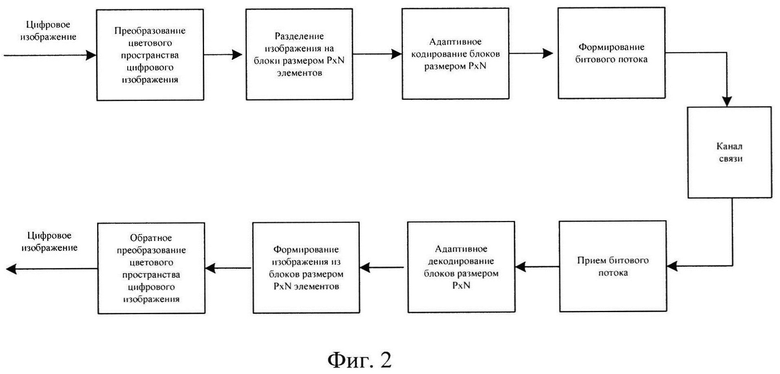
1. Способ кодирования цифрового изображения, заключающийся в том, что преобразуют цифровое пространство цифрового изображения, разделяют изображение на блоки размером P×N элементов, адаптивно кодируют каждый блок размером P×N элементов, формируют битовый поток, отличающийся тем, что адаптивное кодирование выполняют путем определения базиса ортогонального преобразования, причем для определения базиса ортогонального преобразования вычисляют правостороннюю матрицу ортогонального преобразования размером N×N и левостороннюю матрицу ортогонального преобразования размером Р×Р элементов и затем для упомянутых блоков размером P×N элементов выполняют двумерное ортогональное преобразование с использованием ранее определенного базиса ортогонального преобразования, а для вычисления правосторонней матрицы ортогонального преобразования предварительно назначают величину коэффициента mp, кратную N, причем mp<<N, и формируют нулевую матрицу WP размером N×N элементов, затем вычисляют  корреляционных матриц Xi,
корреляционных матриц Xi, 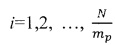 по формуле
по формуле 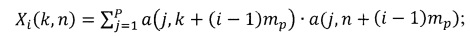 k, n=1, 2, … mp, где Xi(k,n) - k-ый, n-ый элемент i-ой корреляционной матрицы; a(j,k+(i-1)mp) - элемент блока исходного изображения, расположенный в j-ой строке и в k+(i-1)mp столбце; a(j,n+(i-1)mp - элемент изображения, расположенный в j-ой строке и в n+(i-1)mp столбце, затем с использованием QR-алгоритма вычисления собственных векторов и собственных чисел квадратной симметрической матрицы для каждой корреляционной матрицы Xi,
k, n=1, 2, … mp, где Xi(k,n) - k-ый, n-ый элемент i-ой корреляционной матрицы; a(j,k+(i-1)mp) - элемент блока исходного изображения, расположенный в j-ой строке и в k+(i-1)mp столбце; a(j,n+(i-1)mp - элемент изображения, расположенный в j-ой строке и в n+(i-1)mp столбце, затем с использованием QR-алгоритма вычисления собственных векторов и собственных чисел квадратной симметрической матрицы для каждой корреляционной матрицы Xi, 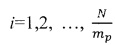 вычисляют матрицу собственных векторов Vi и диагональную матрицу собственных чисел [diagλ]i,
вычисляют матрицу собственных векторов Vi и диагональную матрицу собственных чисел [diagλ]i, 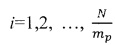 , такие, что Xi=Vi[diagλ]i, причем (abs(λi(1,1))>abs(λ1(2,2))>, …, >abs(λi(j,j))>, …, >abs(λi(mp,mp)), где λi(j,j) - j-ый, j-ый элемент i-ой диагональной матрицы собственных чисел [diagλ]i, после чего присваивают элементам матрицы WP размером N×N элементов элементы матриц собственных векторов Vi,
, такие, что Xi=Vi[diagλ]i, причем (abs(λi(1,1))>abs(λ1(2,2))>, …, >abs(λi(j,j))>, …, >abs(λi(mp,mp)), где λi(j,j) - j-ый, j-ый элемент i-ой диагональной матрицы собственных чисел [diagλ]i, после чего присваивают элементам матрицы WP размером N×N элементов элементы матриц собственных векторов Vi, 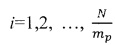 в соответствии с выражением WP(k+(i+1)mp, i+(j-1)mp)=Vi(k,j), k=1, 2, …, mp;
в соответствии с выражением WP(k+(i+1)mp, i+(j-1)mp)=Vi(k,j), k=1, 2, …, mp; 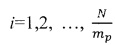 , j=1, 2, …, mp, а для вычисления левосторонней матрицы ортогонального преобразования предварительно назначают величину коэффициента
, j=1, 2, …, mp, а для вычисления левосторонней матрицы ортогонального преобразования предварительно назначают величину коэффициента кратную Р, причем
кратную Р, причем 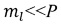 , и формируют нулевую матрицу WL размером Р×Р элементов, затем вычисляют
, и формируют нулевую матрицу WL размером Р×Р элементов, затем вычисляют  корреляционных матриц Yi,
корреляционных матриц Yi, 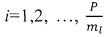 по формуле
по формуле 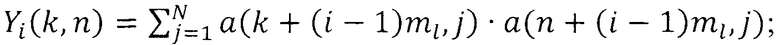 k,
k,  где Yi(k,n) - k-ый, n-ый элемент i-ой корреляционной матрицы;
где Yi(k,n) - k-ый, n-ый элемент i-ой корреляционной матрицы;  - элемент блока исходного изображения, расположенный в
- элемент блока исходного изображения, расположенный в  строке и в j-ом столбце;
строке и в j-ом столбце; 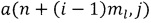 - элемент блока исходного изображения, расположенный в
- элемент блока исходного изображения, расположенный в  строке и в j-ом столбце, затем с использованием QR-алгоритма вычисления собственных векторов и собственных чисел квадратной симметрической матрицы для каждой матрицы Yi,
строке и в j-ом столбце, затем с использованием QR-алгоритма вычисления собственных векторов и собственных чисел квадратной симметрической матрицы для каждой матрицы Yi,  вычисляют матрицу собственных векторов Ui и диагональную матрицу собственных чисел
вычисляют матрицу собственных векторов Ui и диагональную матрицу собственных чисел 
 такие, что
такие, что  причем
причем  где
где 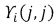 - j-ый, j-ый элемент i-ой диагональной матрицы собственных чисел
- j-ый, j-ый элемент i-ой диагональной матрицы собственных чисел  после чего присваивают элементам матрицы WL размером Р×Р элементов элементы матриц собственных векторов Ui,
после чего присваивают элементам матрицы WL размером Р×Р элементов элементы матриц собственных векторов Ui,  в соответствии с выражением
в соответствии с выражением  ,
, 

2. Способ по п. 1, отличающийся тем, что двумерное ортогональное преобразование блока исходного изображения размером P×N элементов выполняют в соответствии с выражением С=WL⋅А⋅WP, где С - матрица коэффициентов двумерного ортогонального преобразования размером P×N элементов; WL - левосторонняя матрица ортогонального преобразования размером Р×Р элементов; WP - правосторонняя матрица ортогонального преобразования размером N×N элементов; А - матрица блока исходного изображения размером P×N элементов.
| СПОСОБ КОДИРОВАНИЯ ОЦИФРОВАННЫХ ИЗОБРАЖЕНИЙ С ИСПОЛЬЗОВАНИЕМ ДИСКРЕТНОГО ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ АДАПТИВНО ОПРЕДЕЛЕННОГО БАЗИСА | 2009 |
|
RU2429541C2 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ ИЗОБРАЖЕНИЯ И СПОСОБ И УСТРОЙСТВО ДЛЯ ДЕКОДИРОВАНИЯ ИЗОБРАЖЕНИЯ С ПОМОЩЬЮ АДАПТИВНОГО ПОРЯДКА СКАНИРОВАНИЯ КОЭФФИЦИЕНТОВ | 2011 |
|
RU2518935C1 |
| СПОСОБ КОДИРОВАНИЯ ИЗОБРАЖЕНИЯ И СПОСОБ ДЕКОДИРОВАНИЯ ИЗОБРАЖЕНИЯ | 2010 |
|
RU2528144C1 |
| Проволочный канат | 1972 |
|
SU500306A1 |
| US 5351083 A, 27.09.1994 | |||
| US 6282555 B1, 28.08.2001 | |||
| Изложница с суживающимся книзу сечением и с вертикально перемещающимся днищем | 1924 |
|
SU2012A1 |
Авторы
Даты
2018-02-19—Публикация
2017-03-27—Подача