Изобретение относится к измерительной технике и может быть использовано для бесконтактного определения положения вала механического узла.
Известен абсолютный угловой энкодер, построенный на рефлексивном коде Грея [Пат. №2632058 А, США, МПК 7 Н03М 1/00, Н04В 14/04, Н04В 14/02, H01J 31/04, Н03М 13/00, H01J 31/00. Pulsecodecommunication / FrankGray; патентообладатель BellTelephoneLaborInc"; заявл. 13 ноября 1947; опубл. 17 марта 1953].
Суть данного устройства заключается в том, что при реализации n-разрядного энкодера на поверхность растрового диска наносится n кодирующих дорожек, каждая из которых отвечает за формирование кода соответствующего разряда.
Кодирующие дорожки формируются таким образом, чтобы коды, соответствующие двум соседним угловым положениям растра, отличались только в одном разряде. Такой способ кодирования обеспечивает длину кода равную 1 и, как следствие, обеспечивает высокую помехозащищенность.
Недостатком такого энкодера является применение нескольких кодирующих дорожек, что ограничивает область применения энкодера, так как, при его реализации, используется вся поверхность растрового диска, а в случае применения растра, работающего на просвет, источники и приемники излучения оказываются механически не связанными, что приводит к снижению технологичности конструкции. В свою очередь, применение отражающего растрового диска приводит к необходимости высокой точности относительного расположения растра и оптопар, работающих на отражения и делает конструкцию не применимой в условиях вибраций.
Известен оптический энкодер, описанный в патенте Спеддинга Н.Б. [Пат. №264738, Новая Зеландия, МПК 7 G01B 11/26, G01B 5/24. A position encoder / Spedding Norman Bruce; патентообладатель «INDUSTRIAL RESEARCH LIMITED» - заявл. 20 октября 1994; опубл. 2 февраля 1996], который содержит n оптических пар (где n - разрядность энкодера), распределенных равномерно с угловым шагом 360/n, растровый диск с одной кодирующей дорожкой в виде чередующихся прозрачных и непрозрачных секторов.
При этом максимальное количество прозрачных секторов cmax в зависимости от разрядности энкодера определяют выражением:
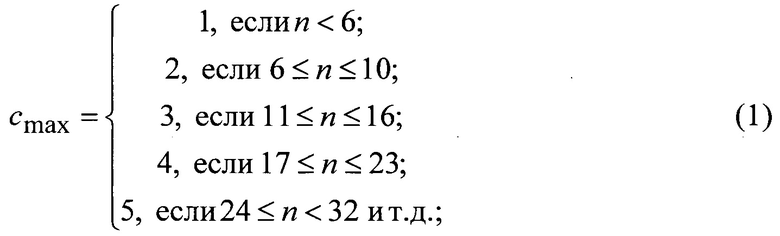
где n - разрядность энкодера (количество используемых оптопар).
Угловой размер прозрачных секторов рассчитывают по выражению:

где c - принятое количество прозрачных секторов;
i=1…cmax - номер сектора;
αi - угловой размер i-го сектора,
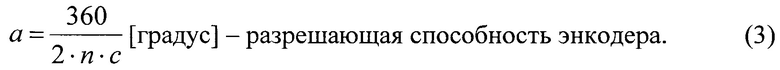
Угловой размер β непрозрачных секторов вычисляют по выражению:

где s - натуральное число.
Информация с датчика выводится виде параллельного кода, который определяет значение угла.
Недостатком такого энкодера является низкая разрешающая способность по сравнению с многодорожечным энкодером. Например, при разрядности энкодера 5, обеспечивают разрешающую способность 36 градусов, при максимально возможной 360/25=11.25 градуса, при разрядности 8 - 11.25 (максимально достижимая - 360/28=1.40625 градуса) и т.д.
Технической задачей предлагаемого изобретения является увеличение разрешающей способности энкодера при сохранении разрядности.
Указанный технический результат достигается тем, что в известном энкодере, содержащем n оптических пар (где n - разрядность энкодера), которые распределены равномерно с угловым шагом 360/n, растровый диск с одной кодирующей дорожкой в виде чередующихся прозрачных и непрозрачных секторов, прозрачные и непрозрачные сектора формируются путем комбинации точной и грубой шкал.
Сущность предлагаемого технического решения, заключается следующем.
На кодирующей дорожке, представляющей собой чередующиеся прозрачные и непрозрачные сектора, размещают точную и грубую шкалы. При этом грубая шкала, представляет собой непрозрачный сектор с угловым размером 720/n градусов и прозрачный сектора с угловым размером 360/n градусов, который примыкает к непрозрачному при движении почасовой стрелке. Точная шкала с угловым размером 360(1-3/n) градусов содержит n-3 части с угловым размером 360/n градусов. Каждую часть формируют по последовательности значений соответствующего разряда модифицированного n-3-разрядного кода. При этом при этом старшему разряду ставят в соответствие часть, расположенную рядом с прозрачным сектором основной шкалы, младшему - часть, расположенную рядом с непрозрачным сектором основной шкалы; нулю ставят в соответствие прозрачный сектор с угловым размером а, где а - разрешающая способность энкодера, единице - непрозрачный. Разрешающую способность энкодера рассчитывают по выражению:
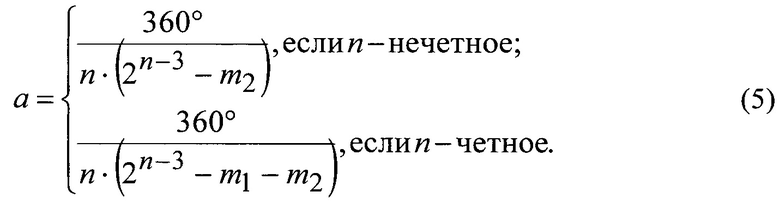
Модифицированный n-3-разрядный код получают путем исключения из 2n-3 возможных значений известного n-3-разрядного двоичного кода, при четных n больших или равных 6, m1 кода вида:
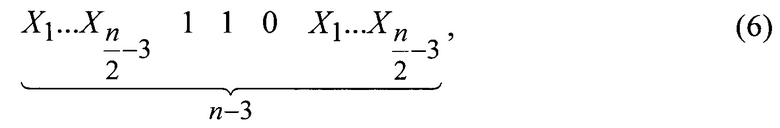
где 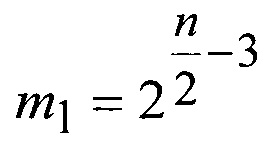 , а также, при n больших или равных 7, одного любого кода из каждой пары вида:
, а также, при n больших или равных 7, одного любого кода из каждой пары вида:
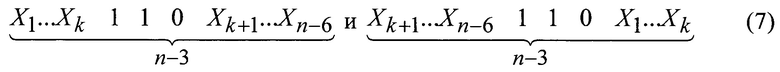
где k - целое число от 0 до n-6.
Общее количество m2 пар вида (7) определяют выражением:

Абсолютный оптический однооборотный угловой энкодер содержит n оптических пар (где n - разрядность энкодера), которые распределены равномерно с угловым шагом 360/n, растровый диск с одной кодирующей дорожкой в виде чередующихся прозрачных и непрозрачных секторов, причем прозрачные и непрозрачные сектора формируются путем комбинации точной и грубой шкал.
Изобретение поясняется рисунками на фиг. 1-8.
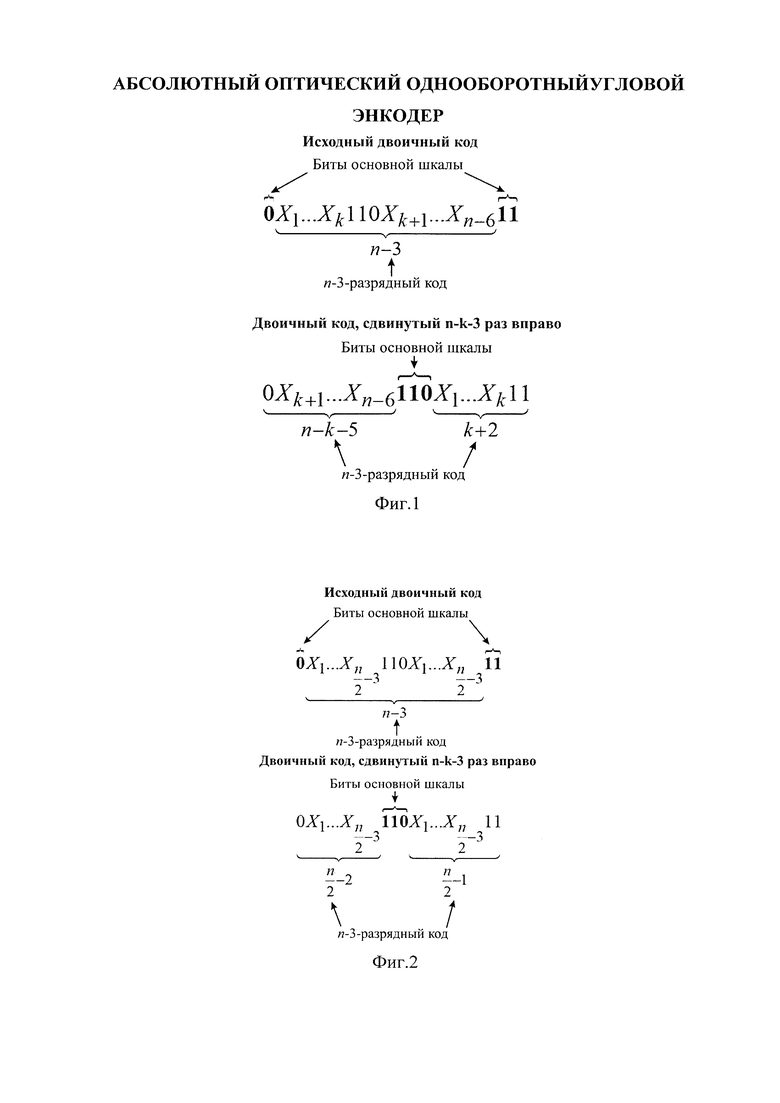
На фигурах 1 и 2 приведено формирование двоичных кодов на выходе энкодера при наличии цепочек 110.
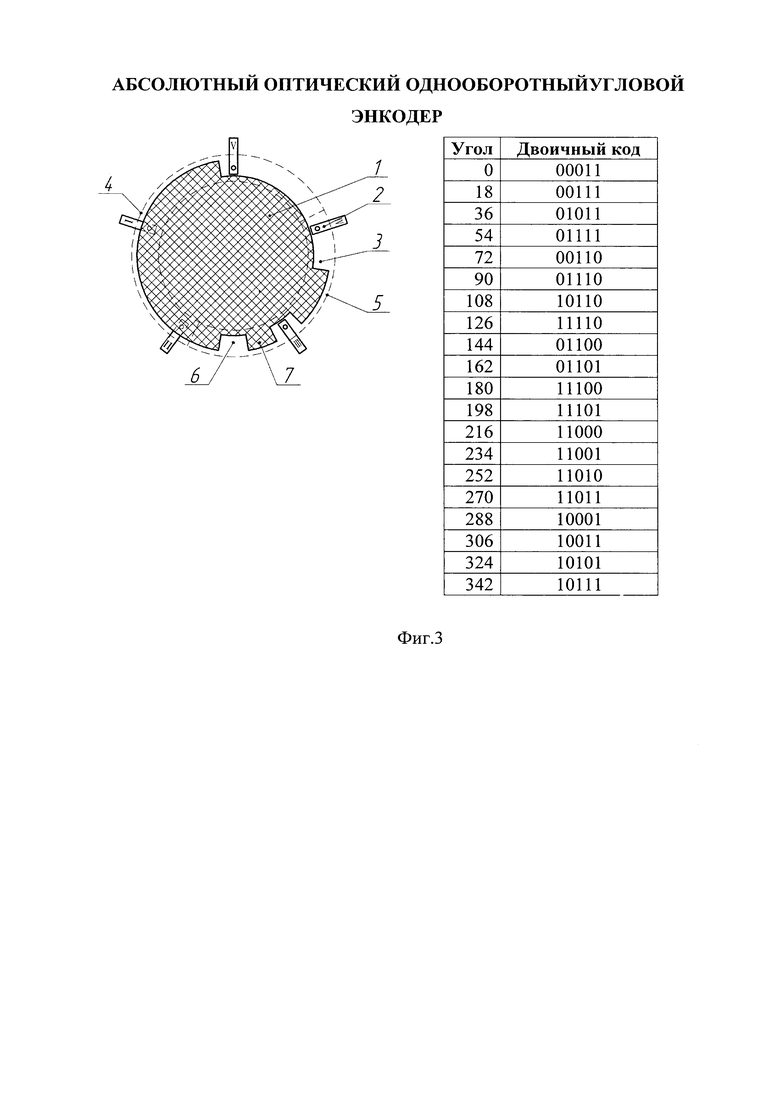
На фигуре 3 приведен пример реализации пятиразрядного энкодера.
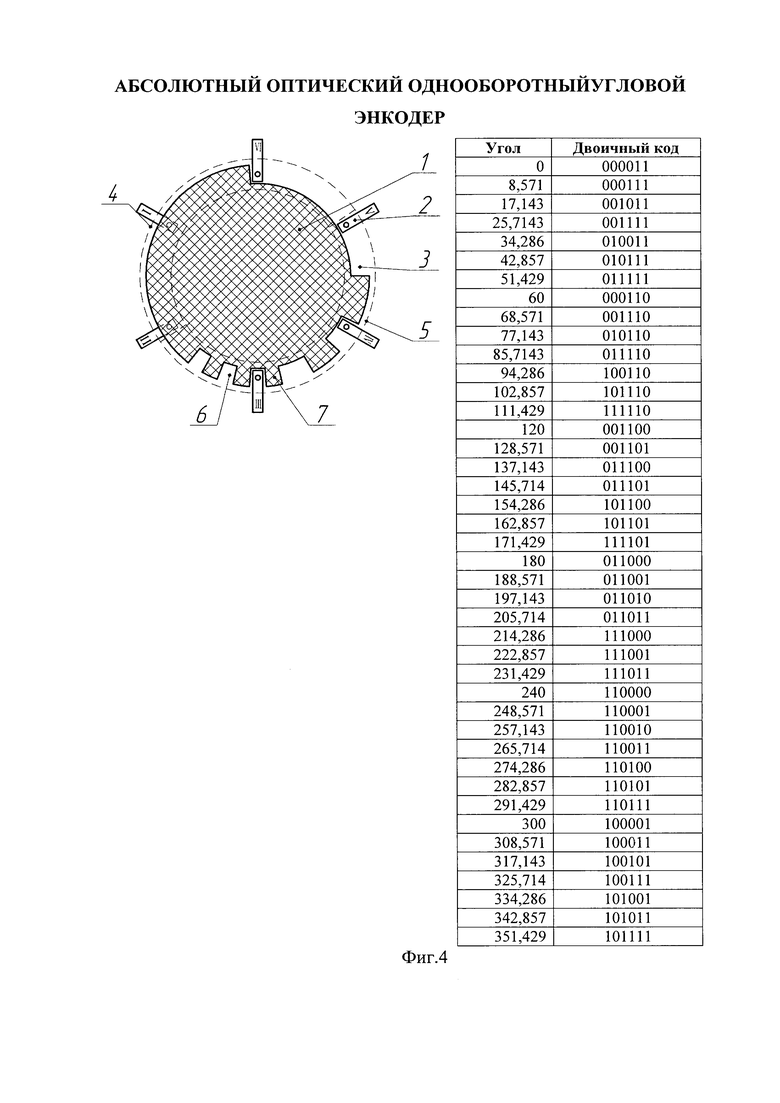
На фигуре 4 приведен пример реализации шестиразрядного энкодера.
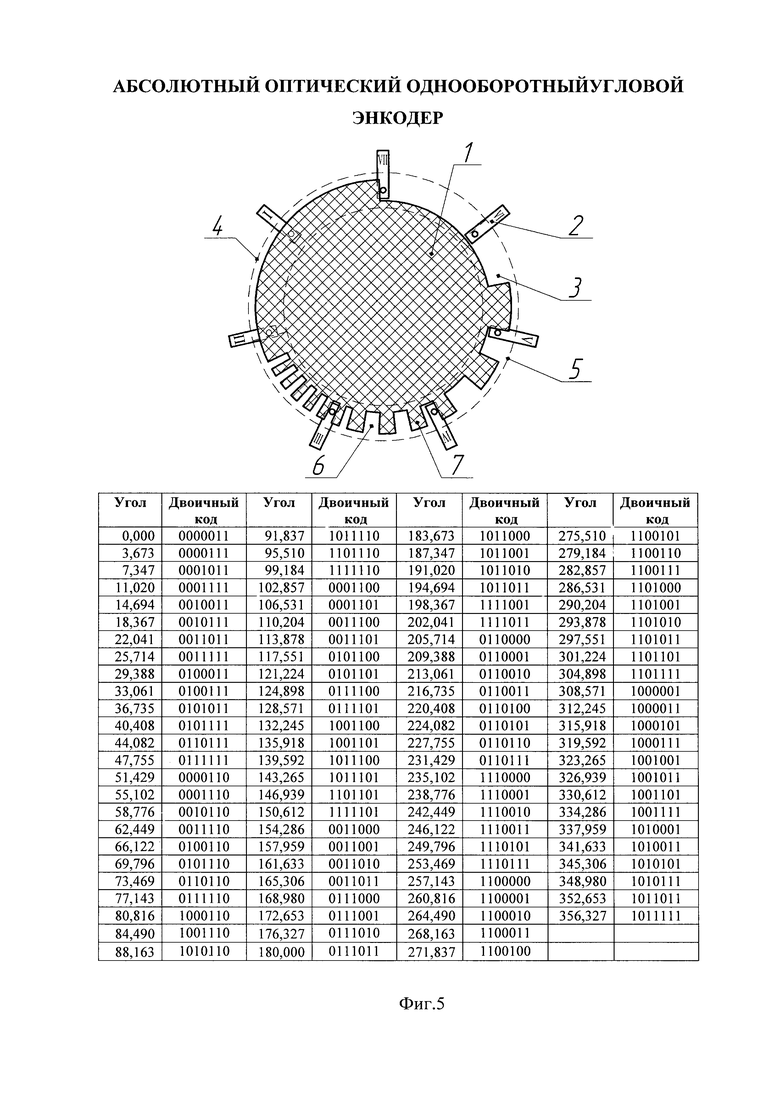
На фигуре 5 приведен пример реализации семиразрядного энкодера.
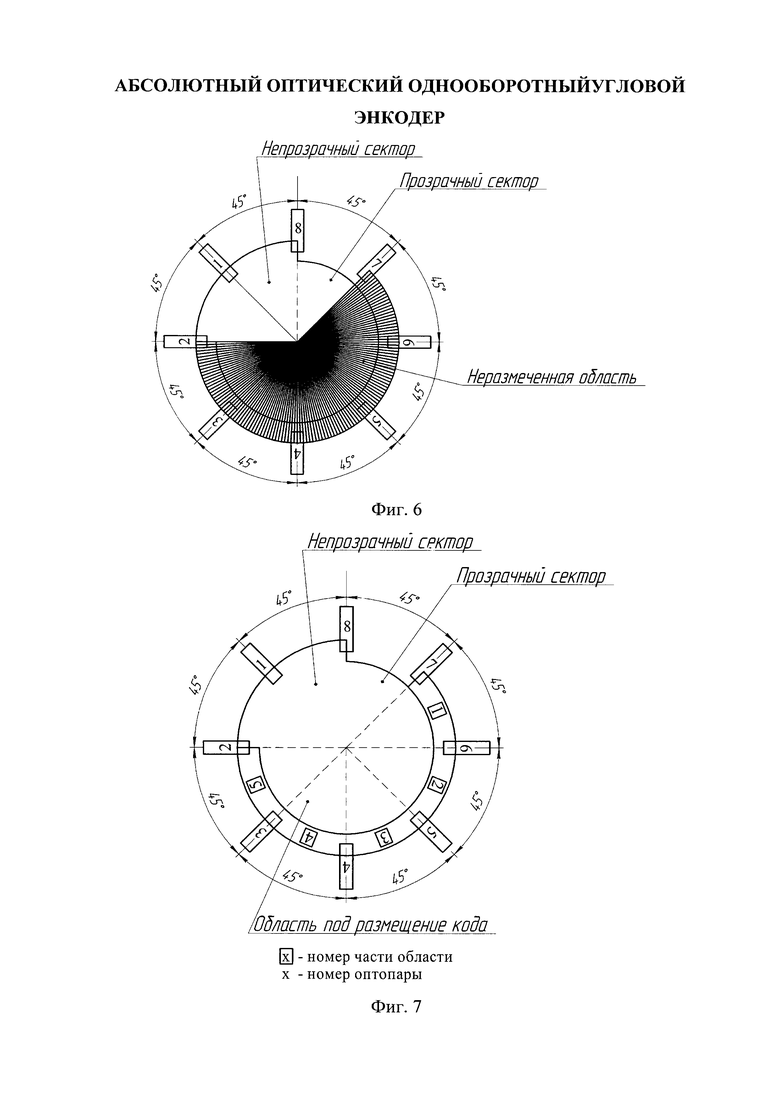
На фигуре 6 приведено расположение оптопар, растровый диск с грубой шкалой и несформированной точной шкалой для восьмиразрядного энкодера.
На фигуре 7 приведено расположение оптопар, растровый диск с грубой шкалой и несформированной точной шкалой, разделенной на пять частей, для восьмиразрядного энкодера.
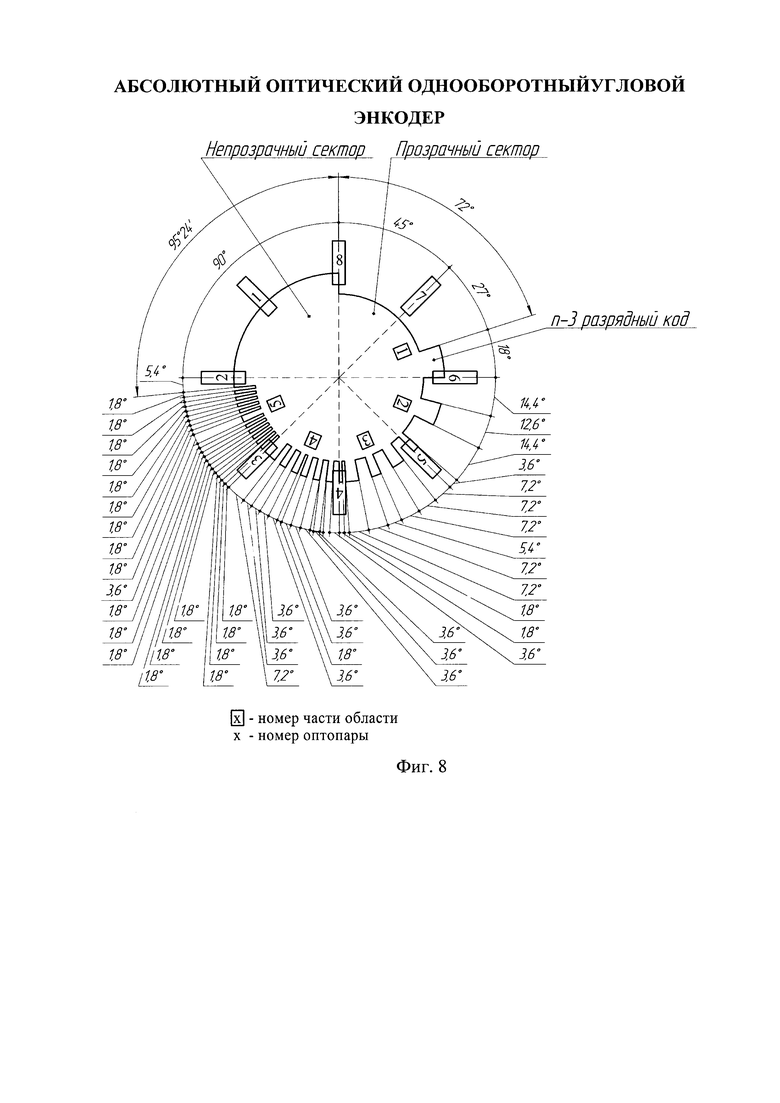
На фигуре 8 приведен пример реализации восьмиразрядного энкодера с указанием основных конструктивных размеров.
Абсолютный оптический однооборотный угловой энкодер, содержит n оптических пар 2 (где n - разрядность энкодера), которые распределены равномерно с угловым шагом 360/n, растровый диск 1 с одной кодирующей дорожкой 3 в виде чередующихся прозрачных 6 и непрозрачных секторов 7, причем прозрачные и непрозрачные сектора формируются путем комбинации точной 5 и грубой 4 шкал.
Работа энкодера в соответствии с вышеприведенным описанием поясняется следующим образом.
Кодирование углового положения с точностью до 360/n градусов, может быть реализовано с помощью трех последовательно расположенных оптопар, третья из которых в пределах поворота на угол 360/n градусов остается постоянно открытой, две другие - постоянно закрыты.
Это позволяет определить угловое положение растра qГ с точностью до 360/n градусов по следующему алгоритму:
1. Считывается код с n - оптопар.
2. Считанный код подвергается s раз кольцевому сдвигу вправо, пока два младших разряда не примут значения единицы, а старший ноль.
3. Приняв за нулевое положение растра такое, что при отсутствии сдвигов старший бит в считанном с оптопар коде равен 0, а два младших 1, и считая положительным вращение против часовой стрелки, угловое положение растра qГ определяется выражением:

При определении углового положения qГ неиспользуемыми оказываются (n-3) оптопар.
Таким образом, задействовав неиспользуемые оптопары, путем формирования кодирующей последовательности на свободной части растра, можно обеспечить повышение разрешения энкодера. При этом следует учитывать, что в (n-3)-разрядном коде, считываемым с этих оптопар необходимо исключить те, которые содержат последовательность 110, так как при выполнении сдвиговых операций для определения qГ, это приводит к неоднозначности определения значения s. То есть возможно более одного значения s, при которых старший разряд имеет значение 0, а два младших 1 (фиг. 1).
В связи с этим, для исключения неоднозначности при определении s, необходимо в парах (n-3)-разрядных кодов вида (7) исключить по одному коду и при определении s считать исключенный код запрещенным.
Следует отметить, что для четных n, существуют такие (n-3)-разрядные коды, содержащие цепочки 110, которые при различных значений s, переходят сами в себя (фиг. 2). Такие коды также необходимо исключить.
Оставшиеся значения кодов позволяют уточнить угловое положение растра, определенное по грубой шкале значением s, в (2n-3-m2) раз для нечетных n, и в (2n-3-m1-m2) раз - для четных n, и обеспечить разрешающую способность в соответствии с выражением (5). Внешний вид кодирующих дисков для n равных 5, 6, 7 приведен на фигурах. 3-5.
Определение точного углового положения q, при использовании такой кодирующей последовательности реализуется по следующему алгоритму:
1. Считывается код с n - оптопар.
2. Считанный код подвергается s раз кольцевому сдвигу вправо, пока два младших разряда не примут значения единицы, а старший ноль. При этом (n-3)-разрядный двоичный код, расположенный между старшим разрядом и двумя младшими, не должен иметь запрещенное значение.
3. Определяется номер j (n-3)-разрядного модифицированного кода в соответствии с принятой последовательностью расположения при формировании растра. При этом первому коду присваивается номер 0.
4. Рассчитывается точное значение углового положения растра q по выражению:

Для пояснения последовательности формирования энкодера, рассмотрим пример расчета 8-ми разрядного энкодера.
При разрядности n, равной 8, оптопары будут распределены равномерно по периметру растра с угловым шагом:
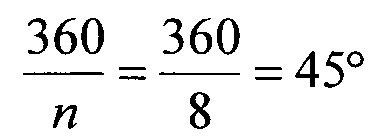 .
.
Рассчитаем угловые размеры прозрачного и непрозрачного секторов основной шкалы.
Угловой размер непрозрачного сектора основной шкалы составит:
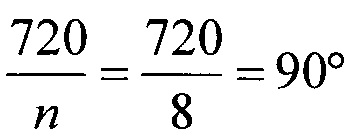 .
.
Угловой размер прозрачного сектора основной шкалы составит:
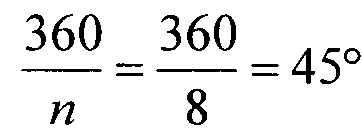 .
.
Угловой размер части кодирующего диска под размещение n-3 разрядного кода составит:
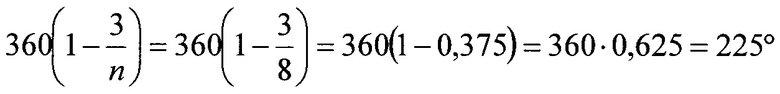 .
.
Кодирующий диск без (n-3)-разрядного кода и расположение оптопар приведены на фиг. 6.
Рассчитаем структуру и угловые элементы части диска под размещение n-3 разрядного кода:
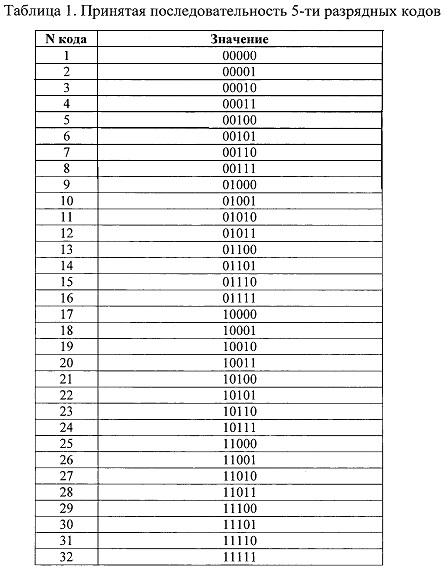
1. Сформируем последовательность кодов, содержащую 2n-3 кода, соответствующих (n-3)-разрядному двоичному коду.
В данном случае разрядность кода равна:
8-3=5.
Количество кодов составит:
28-3=25=32,
В качестве последовательности кодов примем последовательность значений обычного прямого двоичного 5-ти разрядного кода. Принятая последовательность для расчетов приведена в таблице 1.
2. Так как принятое значение n, равное 8, четное и больше 6. Из полученной последовательности исключим m1 код вида (6).
Для данного случая m1 равно:
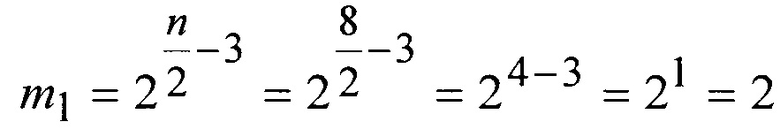 .
.
Количество позиций Xi при n, равном 8, имеет значение:
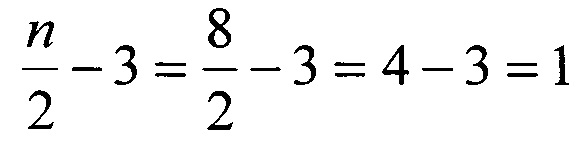 .
.
Таким образом, Xi могут принимать значения, приведенные в таблице 2.

Следовательно, из последовательности, приведенной в таблице 2 необходимо исключить коды, приведенные в таблице 3.

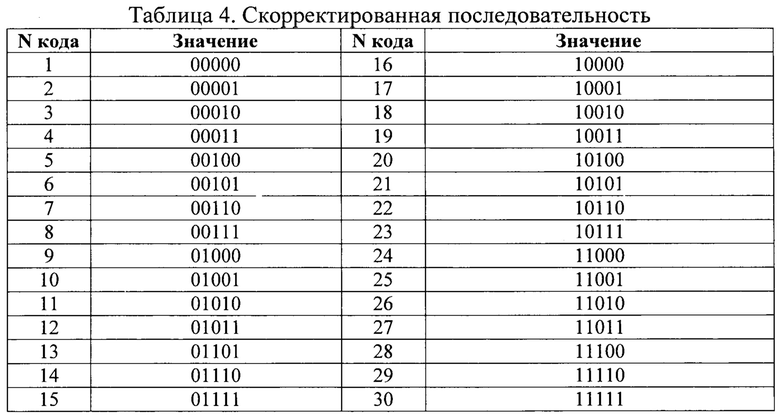
Таким образом с корректированная последовательность кодов примет вид, приведенный в таблице 4.
3. Так как принятое значение n, равное 8, больше 7. Из полученной последовательности исключим m2 пар вида (7).
Та как n - четное, m2 равно:
m2=(n-5)⋅2n-7-2n/2-4=(8-5)⋅28-7-28/2-4=3⋅21-24-4=3⋅2-20=6-1=5.
Количество позиций Xi при n, равном 8, имеет значение:
n-6=8-6=2.
Таким образом, Xi могут принимать значения, приведенные в таблице 5.

В свою очередь, k, при n равном 8, принимает значения 0, 1, 2.
Следовательно, из последовательности, приведенной в таблице 4 необходимо исключить по одному коду из каждой пары в таблице 6.
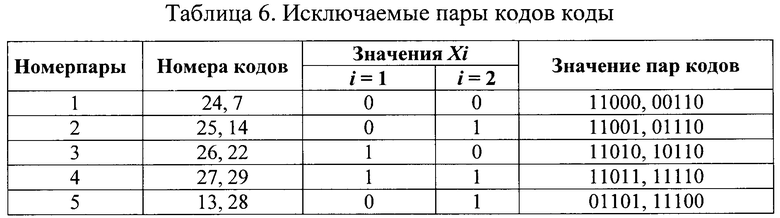
Из каждой пары исключим по одному коду, приведенному в таблице 7.

Оставшиеся коды, приведенные в таблице 8, добавим в исходную последовательность кодов.

Таким образом, скорректированная последовательность кодов примет вид в соответствии с таблицей 9.

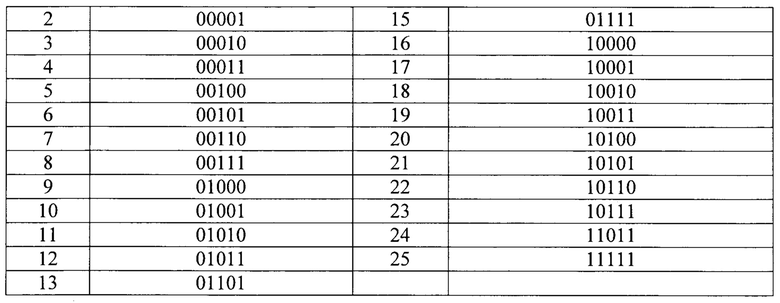
4. При реализации кодирующего диска сохраним исходную последовательность кодов, таким образом последовательность значений для каждого разряда примет вид согласно таблице 10.
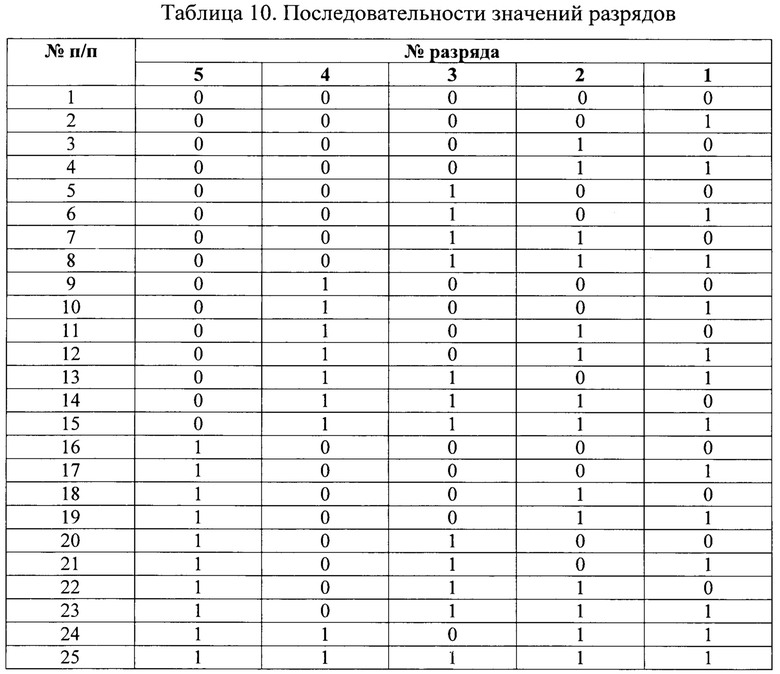
5. Разобьем неразмеченную часть кодирующего диска на n-3 равных частей. При n равном 8, размер одной части составит:
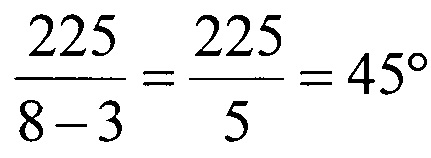 .
.
Таким образом, кодирующий диск примет вид на фиг. 7.
Определим разрешающую способность а энкодера и угловой размер цифры n-3-разрядного кода.
Так как n, равное 8, четное разрешающая способность примет значение:
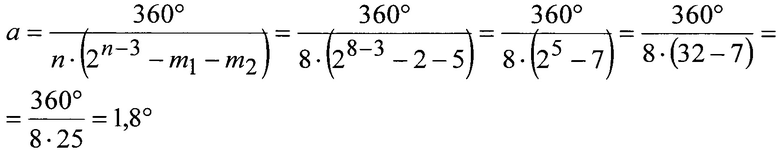
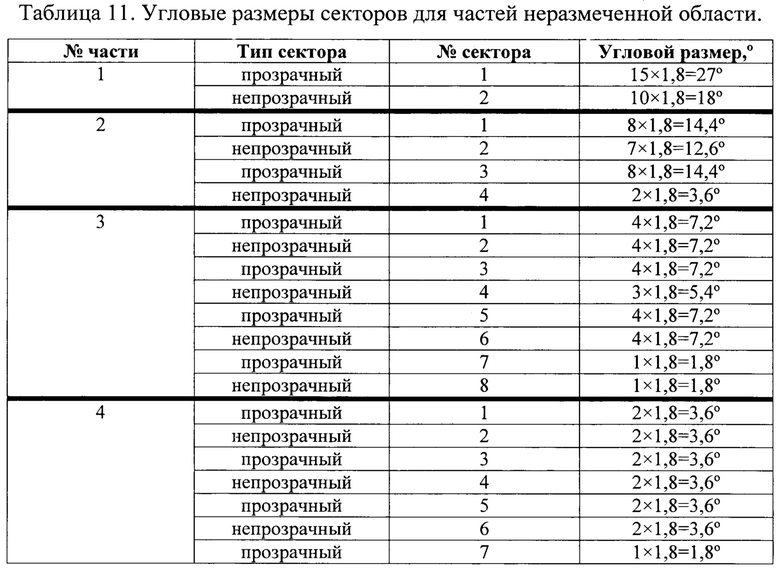
Определим угловые размеры прозрачных и непрозрачных секторов для каждой части неразмеченной области, приняв одной цифре последовательности значений разрядов угловой размер равный 1,8°. Результаты расчета приведены в таблице 11.
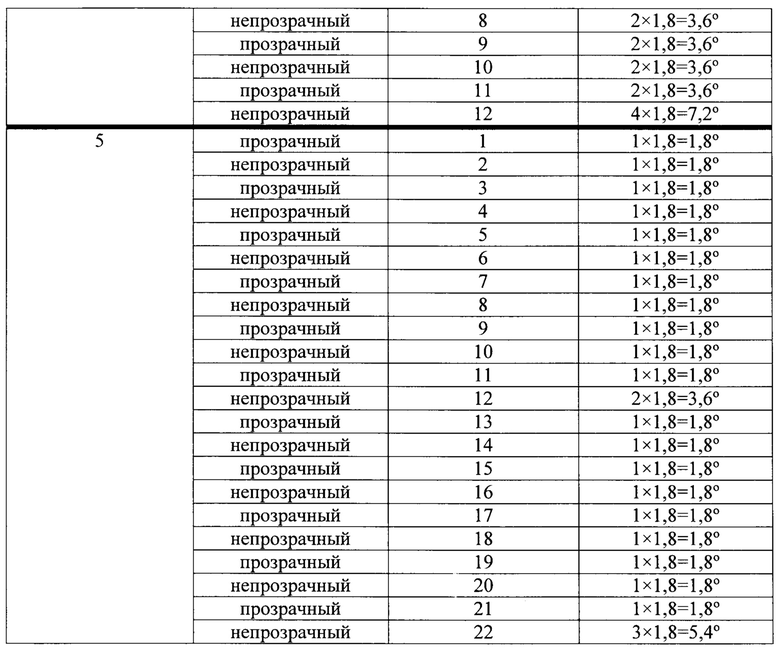
Примечания:
1. Нумерация частей неразмеченной области начинается от прозрачного сектора основной шкалы к непрозрачному.
2. Нумерация секторов для части неразмеченной области начинается от прозрачного сектора основной шкалы к непрозрачному.
Поставив в соответствие старшему разряду часть, расположенную рядом с прозрачным сектором основной шкалы, младшему - часть, расположенную рядом с непрозрачным сектором основной шкалы, окончательно получим одну из реализаций кодирующего диска с одной дорожкой, приведенный на фиг. 8.
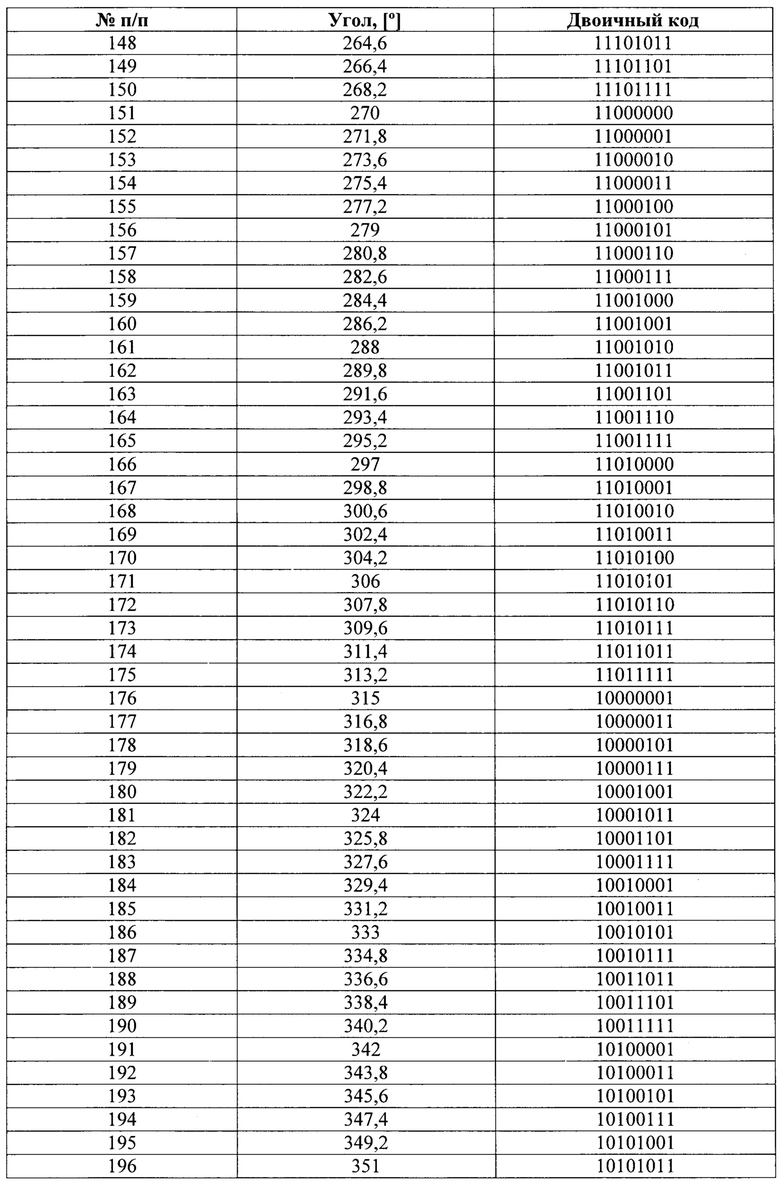
Коды значений углового положения диска для различных угловых положений приведен в таблице 12.
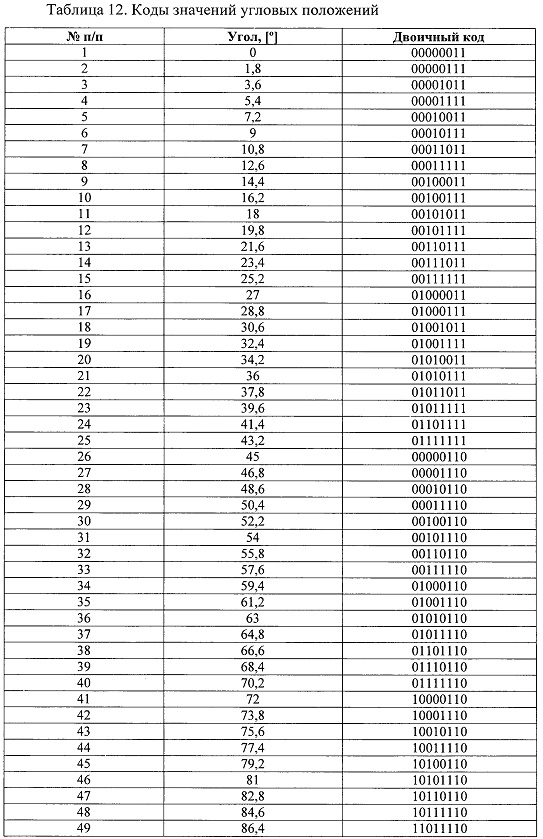
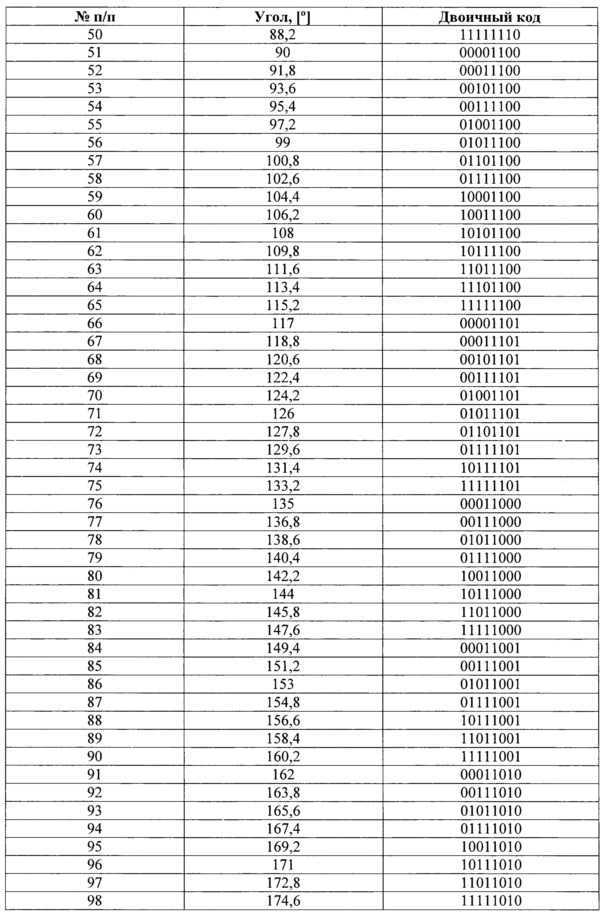
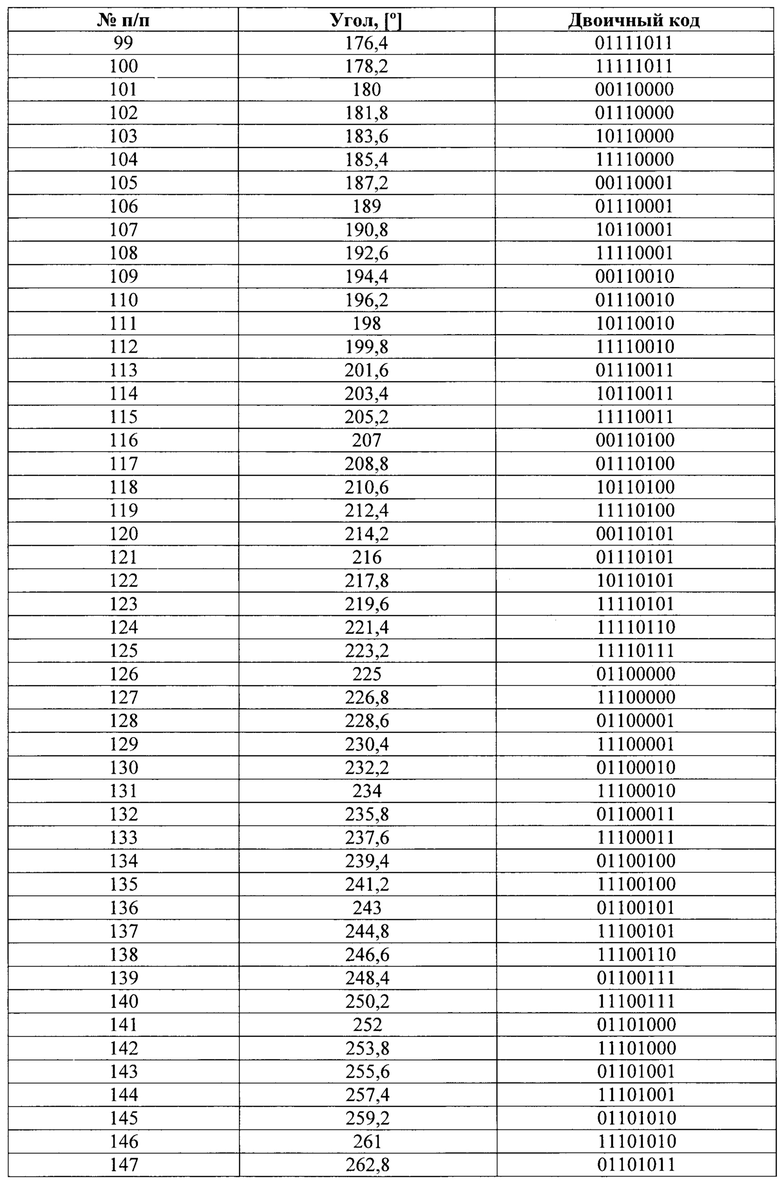

Следует отметить, что при n, равном 8, возможны другие реализации кодирующего диска, которые могут быть получены при исключении любых других значений кодов на этапе 3, а также при изменении последовательности итогового набора кодов на этапе 4.
При этом любые другие отбрасываемые значения и произвольная последовательность сортировки итогового набора кодов принципиального значения не имеют и приводят к положительному результату.
Данные варианты реализации могут варьироваться из конструктивных или иных соображений, при решении конкретной прикладной задачи применения однооборотного однодорожечного абсолютного энкодера, в том числе и для реализации энкодеров линейного перемещения.
Сопоставляя выражение для разрешающей способности известного энкодера (2) и предлагаемого (5), видно, что данный энкодер обеспечивает увеличение разрешающей способности в W раз:
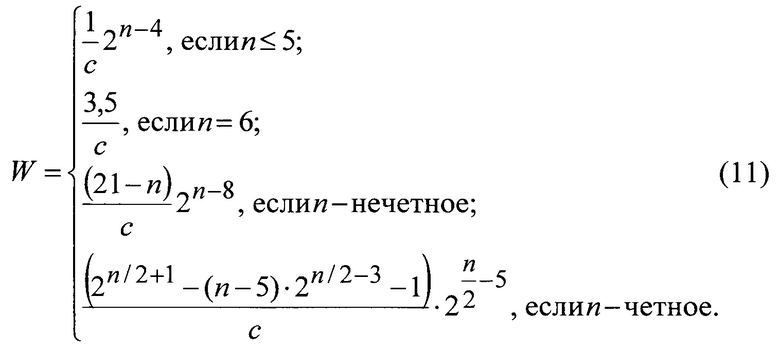
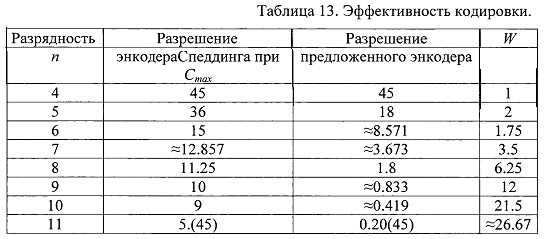
По сравнению с известным энкодером, при n больше 4 разрешающая способность предложенного энкодера увеличивается (таблица 13).
Таким образом, применение кодирующей дорожки, сформированной путем комбинации грубой и точной шкал позволяет повысить разрешающую способность однодорожечного энкодера.
| название | год | авторы | номер документа |
|---|---|---|---|
| Абсолютный оптический однооборотный угловой энкодер | 2017 |
|
RU2645880C1 |
| Устройство определения угла поворота | 2023 |
|
RU2805303C1 |
| РАСТРОВО-КОДОВЫЙ ПРЕОБРАЗОВАТЕЛЬ УГЛОВЫХ ПЕРЕМЕЩЕНИЙ | 1991 |
|
RU2027206C1 |
| СПОСОБ ИЗМЕРЕНИЯ УГЛА ПОВОРОТА И УСТРОЙСТВО ЕГО РЕАЛИЗУЮЩЕЕ | 2019 |
|
RU2720052C1 |
| Способ построения углового преобразователя абсолютного типа | 2016 |
|
RU2634329C1 |
| КОДОВАЯ ШКАЛА | 2012 |
|
RU2490790C1 |
| КОДОВАЯ ШКАЛА | 2012 |
|
RU2497275C1 |
| КОДОВАЯ ШКАЛА | 2014 |
|
RU2560782C1 |
| КОДОВАЯ ШКАЛА | 2016 |
|
RU2658188C2 |
| Эталон единицы плоского угла | 2016 |
|
RU2637727C1 |
Изобретение относится к измерительной технике и может быть использовано для бесконтактного определения положения вала механического узла. Абсолютный оптический однооборотный угловой энкодер, содержит n оптических пар (где n - разрядность энкодера), которые распределены равномерно с угловым шагом 360/n, растровый диск с одной кодирующей дорожкой в виде чередующихся прозрачных и непрозрачных секторов, причем прозрачные и непрозрачные сектора формируются путем комбинации точной и грубой шкал. Технический результат - повышение разрешающей способности однодорожечного энкодера. 13 табл., 8 ил.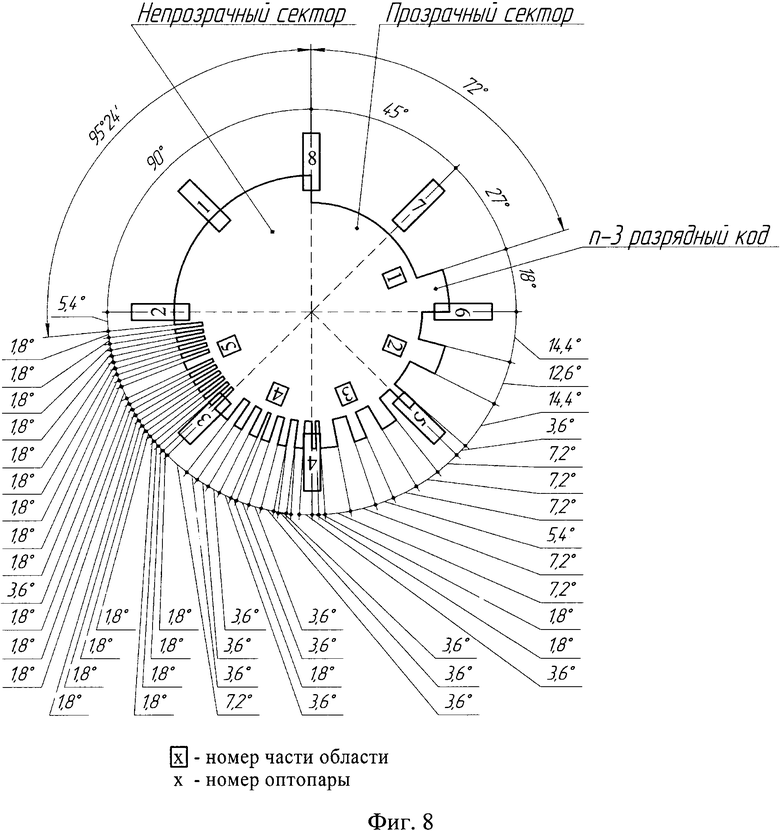
Абсолютный оптический однооборотный угловой энкодер, содержащий n оптических пар (где n - разрядность энкодера), которые распределены равномерно с угловым шагом 360/n, растровый диск с одной кодирующей дорожкой в виде чередующихся прозрачных и непрозрачных секторов, отличающийся тем, что прозрачные и непрозрачные сектора формируются путем комбинации точной и грубой шкал.
| US 4421980 A, 20.12.1983 | |||
| US 4786803 A1, 22.11.1988 | |||
| CN 104677394 A, 03.06.2015 | |||
| US 4691101 A, 01.09.1987. |
Авторы
Даты
2018-04-23—Публикация
2017-01-17—Подача