Изобретение относится к измерительной технике и может быть использовано для бесконтактного определения положения вала механического узла.
Известен энкодер, реализованный на рефлексивном коде Грея [Пат. №2632058 A, США, МПК7 H03M 1/00, H04B 14/04, H04B 14/02, H01J 31/04, H03M 13/00, H01J 31/00. Pulse code communication / Frank Gray; патентообладатель Bell Telephone Labor Inc"; заявл. 13 ноября 1947; опубл. 17 марта 1953].
Суть данного изобретения заключается в том, что при реализации n-разрядного энкодера на поверхность растрового диска наносится n кодирующих дорожек, каждая из которых отвечает за формирование кеда соответствующего разряда.
Кодирующие дорожки формируются таким образом, чтобы коды, соответствующие двум соседним угловым положениям растра, отличались только в одном разряде. Такой способ кодирования обеспечивает длину кода равную 1 и, как следствие, обеспечивает высокую помехозащищенность.
Недостатком такого энкодера является применение нескольких кодирующих дорожек, что ограничивает область применения энкодера, так как, при его реализации, используется вся поверхность растрового диска, а в случае применения растра, работающего на просвет, источники и приемники излучения оказываются механически не связанными, что приводит к снижению технологичности конструкции. В свою очередь, применение отражающего растрового диска приводит к необходимости высокой точности относительного расположения растра и оптопар, работающих на отражения, и делает конструкцию не применимой в условиях вибраций.
Известен оптический энкодер, описанный в патенте Спеддинга Н.Б. [Пат. №264738, Новая Зеландия, МПК7 G01B 11/26, G01B 5/24. A position encoder / Spedding Norman Bruce; патентообладатель «INDUSTRIAL RESEARCH LIMITED» - заявл. 20 октября 1994; опубл. 2 февраля 1996], который содержит n оптических пар (где n - разрядность энкодера), распределенных равномерно с угловым шагом 360/n, растровый диск с одной кодирующей дорожкой в виде чередующихся прозрачных и непрозрачных секторов.
При этом максимальное количество прозрачных секторов cmax в зависимости от разрядности энкодера определяют выражением
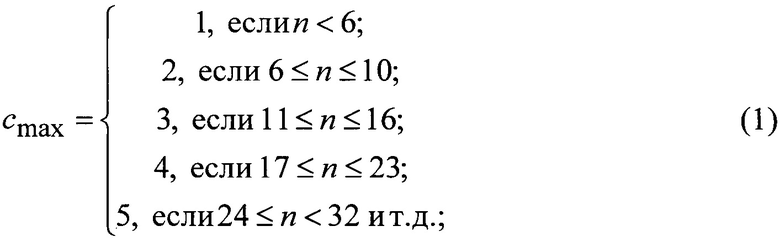
где n - разрядность энкодера (количество используемых оптопар).
Угловой размер прозрачных секторов рассчитывают по выражению

где c - принятое количество прозрачных секторов;
i=1…cmax - номер сектора;
αi - угловой размер i-го сектора,
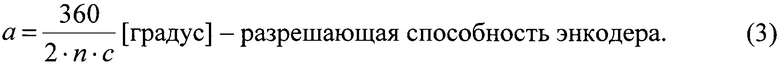
Угловой размер непрозрачных секторов вычисляют по выражению

где s - натуральное число.
Информация с датчика выводится в виде параллельного кода, который определяет значение угла.
Недостатком такого энкодера является низкая разрешающая способность по сравнению с многодорожечным энкодером. Например, при разрядности энкодера 5, обеспечивают разрешающую способность 36 градусов, при максимально возможной 360/25=11.25 градуса, при разрядности 8 - 11.25 (максимально достижимая - 360/28=1.40625 градуса) и т.д.
Технической задачей предлагаемого изобретения является разработка энкодера с максимальной разрешающей способностью для разрядности n, при использовании только одной кодирующей дорожки.
Технический результат достигается тем, что в известном энкодере, содержащем n-оптопар, где n - разрядность энкодера, и растровый диск с одной кодирующей дорожкой, оптопары располагают с одинаковым шагом a, где a, равное 360/2n, - разрешающая способность энкодера, а кодирующую дорожку формируют в соответствии с двоичной последовательностью длиной m=2n, при этом каждой цифре последовательности соответствует угловой размер a, нулю ставится в соответствии непрозрачный сектор, единице прозрачный - или наоборот.
Сущность предлагаемого технического решения заключается в том, что двоичную последовательность длиной m формируют следующим образом:
1. Формируют группы цепочек, состоящие из нулей, обрамленные с каждой стороны единицами:
- первая группа содержит одну цепочку из n нулей и одну цепочку из (n-2) нулей;
- последующие группы содержат 2b-2 цепочек из (n-b) нулей, где b принимает значения от 3 до n-1;
2. Для каждой группы цепочек формируется набор дополнений:
- для первой группы четыре дополнения вида (0x, 1x, x1, х0), где x показывает место сопряжения дополнения с цепочкой;
- для второй и первой группы восемь дополнений вида (00х, 01х, 10х, 11х, х00, х01, х10, х11);
- для i-ой и предшествующих групп 2i+1 дополнений вида (хС и Сх), где C - двоичное b-разрядное число.
3. Цепочку из n нулей располагают в старших битах двоичной последовательности, таким образом, чтобы единица, стоящая слева, оказалась в младшем байте кодирующей последовательности.
4. Последовательно добавляют возможные неиспользованные дополнения и цепочки. В процессе подстановки исключают цепочки и дополнения, образованные автоматически. При этом запрещается подсоединять к сформированной части последовательности те цепочки и дополнения, которые приводят к необходимости использования цепочек или дополнений отсутствующих в имеющимся наборе. По завершению заполнения всех битов кодирующей последовательности, все группы цепочек и дополнений должны быть полностью задействованы.
Абсолютный оптический однооборотный угловой энкодер содержит n оптопар, где n - разрядность энкодера, растровый диск с одной кодирующей дорожкой, состоящей из последовательно расположенных прозрачных и непрозрачных секторов, причем оптопары располагают с одинаковым шагом a, где a, равное 360/2n, - разрешающая способность энкодера, а кодирующую дорожку формируют в соответствии с двоичной последовательностью длиной m=2n, при этом каждой цифре последовательности соответствует угловой размер a, нулю ставится в соответствии непрозрачный сектор, единице прозрачный - или наоборот.
Изобретение поясняется фиг. 1 и 2.
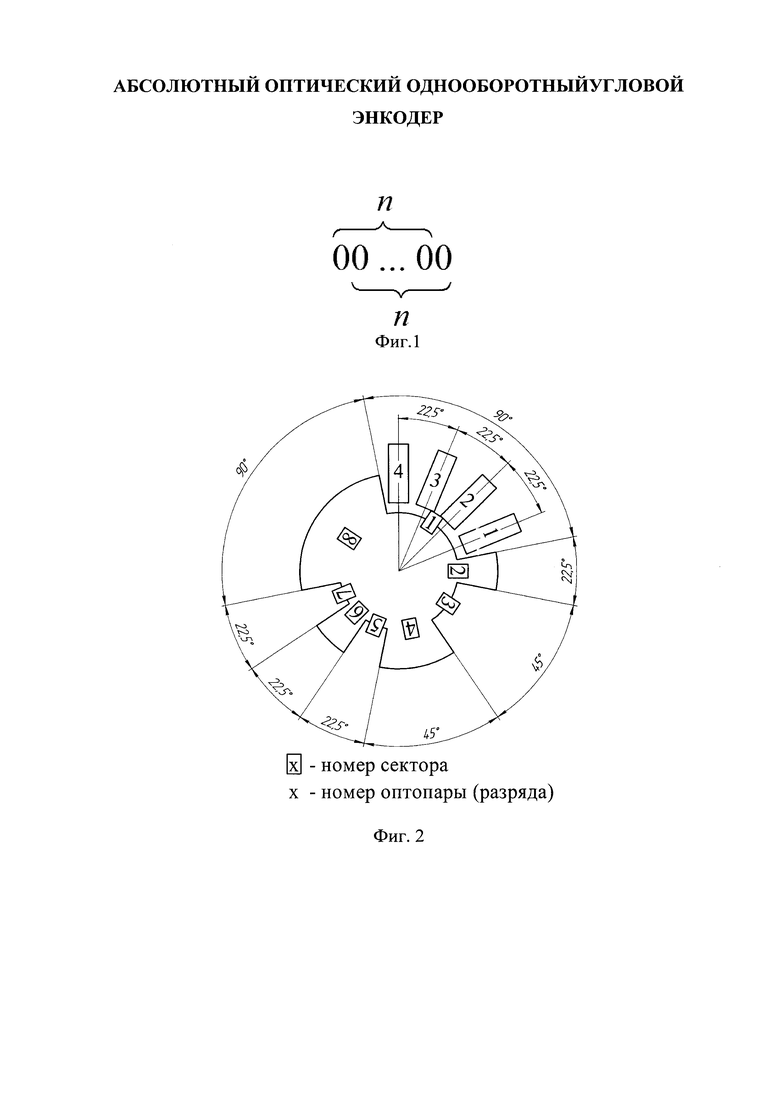
На фиг. 1 приведено формирование кода энкодера при длине цепочки, содержащей нули, больше n.
На фиг. 2 приведен пример реализации четырехразрядного энкодера с основными конструктивными параметрами.
Абсолютный оптический однооборотный угловой энкодер содержит n оптопар 2, где n - разрядность энкодера, растровый диск 1 с одной кодирующей дорожкой 3, состоящей из последовательно расположенных прозрачных 4 и непрозрачных 5 секторов, причем оптопары 2 располагают с одинаковым шагом a, где a, равное 360/2n, - разрешающая способность энкодера, а кодирующую дорожку 3 формируют в соответствии с двоичной последовательностью длиной m=2n, при этом каждой цифре последовательности соответствует угловой размер a, нулю ставится в соответствии непрозрачный сектор, единице прозрачный - или наоборот.
Работа энкодера в соответствии с вышеприведенным описанием поясняется следующим образом.
Для реализации однооборотного абсолютного энкодера, обладающего максимальным разрешением при разрядности n, необходимо, чтобы за полный оборот растра наблюдались все возможные значения n-разрядного двоичного кода, считанные с приемников оптического излучения.
Так как оптопары имеют угловой шаг расположения, равный разрешающей способности энкодера, то двоичная последовательность, используемая для формирования кодирующей дорожки, должна содержать в себе все возможные n-разрядные коды.
В частности, для реализации кода 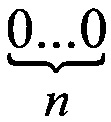 необходимо, чтобы кодирующая последовательность содержала хотя бы одну цепочку вида
необходимо, чтобы кодирующая последовательность содержала хотя бы одну цепочку вида 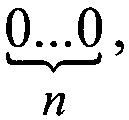 с другой стороны такая цепочка должна быть только одна, иначе на полном обороте будет наблюдаться повторение кода
с другой стороны такая цепочка должна быть только одна, иначе на полном обороте будет наблюдаться повторение кода 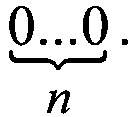 В то же время, для исключения повторения указанного кода, количество последовательно расположенных нулей не должно превышать n (фиг. 1).
В то же время, для исключения повторения указанного кода, количество последовательно расположенных нулей не должно превышать n (фиг. 1).
Таким образом, цепочка 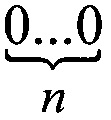 должна быть с двух сторон обрамлена единицами и примет вид
должна быть с двух сторон обрамлена единицами и примет вид 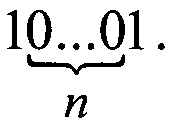
Полученная цепочка, помимо кода 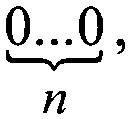 автоматически реализует коды:
автоматически реализует коды: 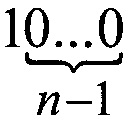 и
и 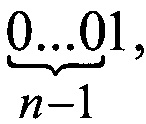 следовательно, в кодирующей последовательности должна отсутствовать дополнительная цепочка вида
следовательно, в кодирующей последовательности должна отсутствовать дополнительная цепочка вида 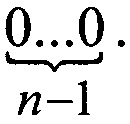 При этом необходимость реализации кода вида
При этом необходимость реализации кода вида 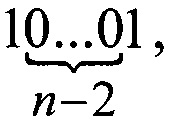 требует наличие хотя бы одной цепочки вида
требует наличие хотя бы одной цепочки вида 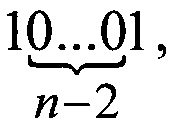 так как указанный код не может быть реализован с помощью цепочки
так как указанный код не может быть реализован с помощью цепочки 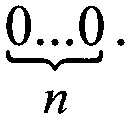
С другой стороны, учитывая тот факт, что кодов 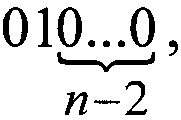
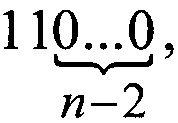
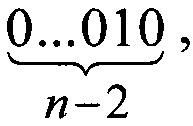
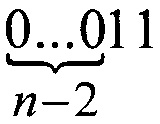 всего четыре и они реализуются с помощью цепочек
всего четыре и они реализуются с помощью цепочек 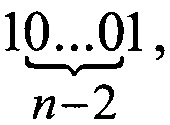
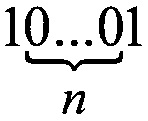 путем добавления дополнений (0x, 1x, x1, х0), то можно утверждать, что цепочка вида
путем добавления дополнений (0x, 1x, x1, х0), то можно утверждать, что цепочка вида 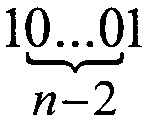 также только одна.
также только одна.
Таким образом, в кодирующей последовательности выделяется первая группа цепочек и дополнений к ним.
Продолжая аналогичные рассуждения, по вопросу реализации кодов 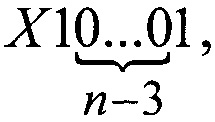
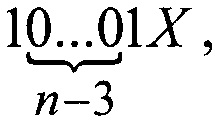
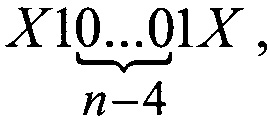
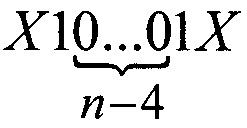 и так далее, можно показать необходимость существования других групп цепочек, которые содержат 2b-2 цепочек из (n-b) нулей, где b принимает значения от 3 до n-1, и дополнений вида (хС и Сх), где C - двоичное b-разрядное число.
и так далее, можно показать необходимость существования других групп цепочек, которые содержат 2b-2 цепочек из (n-b) нулей, где b принимает значения от 3 до n-1, и дополнений вида (хС и Сх), где C - двоичное b-разрядное число.
Следовательно, двоичная последовательность, содержащая описанные цепочки и дополнения, будет содержать все возможные значение n-разрядного двоичного кода и, как следствие, исключает возможность повторения кодов на полном обороте.
Последующее декодирование углового положения с полученного таким образом энкодера реализуется с помощью таблицы кодов.
Следует отметить, что инверсия полученной двоичной последовательности также может быть использована для построения энкодера.
Это объясняется следующим. Если принять, что некоторому угловому положению кодирующего диска соответствует двоичный код S(α), то для любых целых j∈[1(360/a-1)] должно выполняться условие отсутствия повторения кодов:
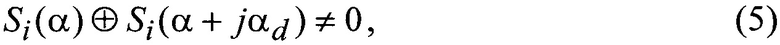
где (- побитовая операция «ИСКЛЮЧАЮЩЕЕ-ИЛИ»;
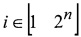 - номер двоичного кода Si(α).
- номер двоичного кода Si(α).
Учитывая свойство побитовой операции «ИСКЛЮЧАЮЩЕЕ-ИЛИ»:
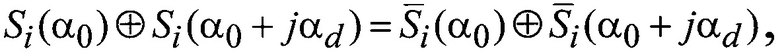
видно, что коды 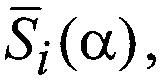 соответствующие инвертирующей последовательности, также будут удовлетворять условию (5).
соответствующие инвертирующей последовательности, также будут удовлетворять условию (5).
Таким образом, при реализации кодирующего диска n-разрядного энкодера, в соответствие нулю можно ставить как прозрачный, так и непрозрачный сектор, соответственно единице - непрозрачный или прозрачный сектор.
Для пояснения принципа формирования кодирующей последовательности, рассмотрим пример для n равного 4.
При разрядности энкодера n равном 4, разрешающая способность a составит:
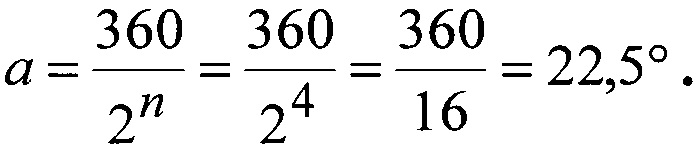
Таким образом, угловой шаг расположения оптопар составит 22,5°.
При n равном 4 двоична последовательность для формирования кодирующей дорожки примет длину m
m=24=16.
Сформируем группы цепочек, состоящие из нулей, обрамленные с каждой стороны единицами.
Для n равного 4, b может принимать значения от 3 до 4-1, то есть имеет только одно значение 3. Следовательно, получим две группы цепочек. При этом в первой группе содержится две цепочки: 100001 и 1001, а во второй - 2b-2=23-2=21=2 цепочки вида 101.
Сформируем наборы дополнений:
- для первой группы получим четыре дополнения: 0x, 1x, x1, х0;
- для первой и второй группы - восемь дополнений: 00х, 01х, 10х, 11х, х00, х01, х10, х11.
Разместим цепочку 100001 в старших битах кодирующей последовательности, таким образом, чтобы единица, стоящая слева, оказалась в младшем байте кодирующей последовательности. В итоге получим
где x - неопределенное значение.
Дополним справа полученную последовательность третьим дополнением х0 из первой группы. В результате получим
Так как при этом в разрядах 12 и 11 сформировалась последовательность, которая может соответствовать как цепочке 1001, так и цепочке 101, то оказывается использованным дополнение второй группы 00х.
Таким образом, в оставшийся набор цепочек и дополнений содержит
- цепочку первой группы 1001;
- цепочки второй группы 101, 101;
- дополнения первой группы 0x, 1x, x1;
- дополнения второй группы 01х, 10х, 11х, х00, x01, x10, x11.
Дополним дополнение первой группы х0 на позиции 11 до дополнения второй группы х00. В результате получим
Оставшийся набор цепочек и дополнений содержит:
- цепочку первой группы 1001;
- цепочки второй группы 101, 101;
- дополнения первой группы 0x, 1x, x1;
- дополнения второй группы 01х, 10х, 11х, х01, х10, x11.
Так как в наборе имеются только цепочки 1001, 101 и 101, то последовательность на позициях 12-10 может быть только частью цепочки 1001. Следовательно, цепочка 1001 располагается в позициях 12-9 и кодирующая последовательность имеет вид
Оставшийся набор цепочек и дополнений содержит
- цепочки второй группы 101, 101;
- дополнения первой группы 0x, 1x, x1;
- дополнения второй группы 01х, 10х, 11x, x01, x10, x11.
Так как к цепочке 1001 (позиции 12-9) слева примыкает дополнение первой группы 0х (позиция 13). Следовательно, оставшийся набор цепочек и дополнений содержит
- цепочки второй группы 101, 101;
- дополнения первой группы 1x, x1;
- дополнения второй группы 01x, 10х, 11х, x01, x10, x11.
Так как для цепочки 1001 (позиции 12-9) доступно только дополнение x1 из первой группы, то кодирующая последовательность примет вид
- цепочки второй группы 101, 101;
- дополнения первой группы 1х;
- дополнения второй группы 01x, 10х, 11x, x01, x10, x11.
Так как для цепочки 100001 (позиции 16-12, 1) слева доступно только дополнение первой группы 1х, то кодирующая последовательность примет вид
Оставшийся набор
- цепочки второй группы 101, 101;
- дополнения второй группы 01x, 10х, 11x, x01, x10, x11.
Для цепочки 1001 (позиции 12-9) доступны только дополнения второй группы х10 и x11. Дополним эту цепочку первым дополнением. В итоге получим
Оставшийся набор
- цепочки второй группы 101, 101;
- дополнения второй группы 01x, 10х, 11x, x01, x11.
Последовательность на позициях 8 и 7 может быть только частью одной из цепочек 101. Таким образом, кодирующая последовательность примет вид
Оставшийся набор
- цепочки второй группы 101;
- дополнения второй группы 01x, 10х, 11x, x01, x11.
Из кодирующей последовательности видно, что цепочка 101 (позиции 8-6) имеет дополнение второй группы: 01x. То есть оставшийся набор содержит
- цепочки второй группы 101;
- дополнения второй группы 10х, 11x, x01, x11.
Так как цепочка 100001 (позиции 16-12, 1) из оставшегося набора может иметь только дополнение 11х, то кодирующая последовательность имеет вид
Оставшийся набор
- цепочки второй группы 101;
- дополнения второй группы 10х, x01, x11.
С другой стороны, цепочка 101 (позиции 8-6) не может иметь дополнение x11, так как в этом случае неиспользованной остаются цепочка 101 при сформированной кодирующей последовательности. Таким образом ей доступна только цепочка х01. Следовательно, кодирующая последовательность примет вид
Оставшийся набор
- цепочки второй группы 101;
- дополнения второй группы 10х, x11.
Оставшаяся цепочка 101 реализуется на позициях 6-4, при этом она имеет дополнение слева 10х, а справа - x11 и весь набор цепочек и дополнений оказывается использованным при сформированной кодирующей последовательности.
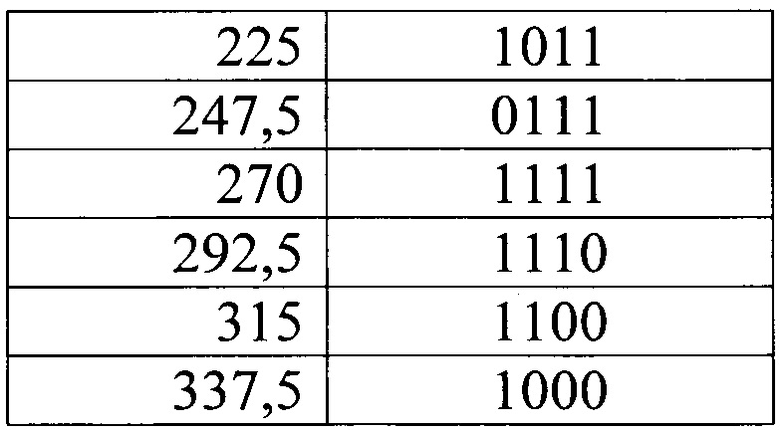
Определим угловые размеры секторов кодирующей дорожки, приняв за угловой размер одной цифры двоичной последовательности a=22,5°. Нулю сопоставим прозрачный сектор, единице - непрозрачный, нумерацию секторов произведем по часовой стрелке. Результаты расчета приведены в таблице 1.
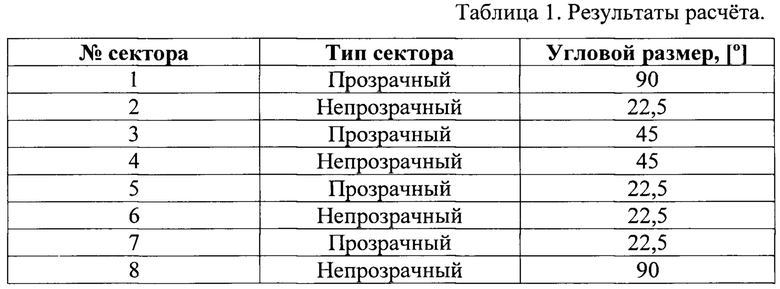
Окончательно получим одну из реализаций растра с одной дорожкой, приведенную на фиг. 2. Коды угловых положений для данной реализации растра приведены в таблице 2.
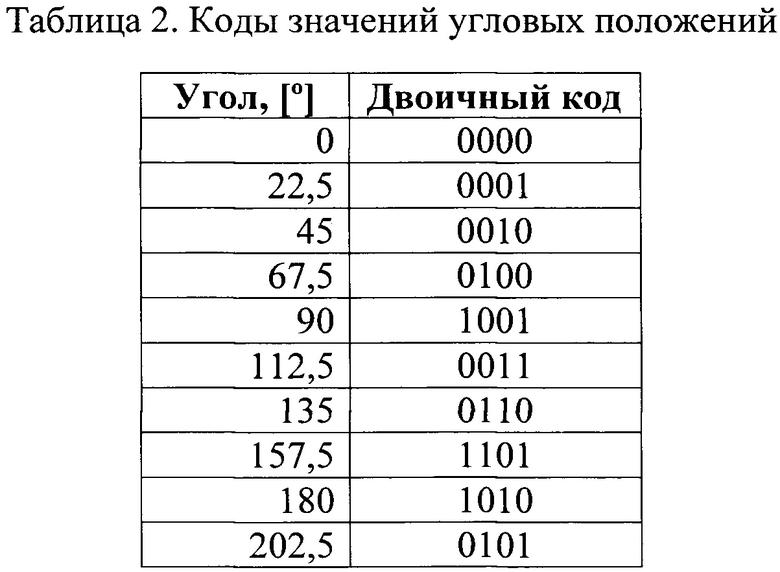
Следует отметить, что при n равном 4, возможны другие реализации кодирующего диска, которые могут быть получены при другой последовательности примыкания дополнений.
При этом любые другие варианты формирования кодирующей последовательности принципиального значения не имеют и приводят к положительному результату. Эти варианты реализации могут варьироваться из конструктивных или иных соображений, при решении конкретной прикладной задачи применения однооборотного однодорожечного абсолютного энкодера, в том числе и для реализации энкодеров линейного перемещения.
Таким образом, расположение оптопар с угловым шагом a и применение кодирующей дорожки, сформированной по двоичной последовательности длиной m позволяет получить энкодер с максимальным разрешением для разрядности n.
| название | год | авторы | номер документа |
|---|---|---|---|
| Абсолютный оптический однооборотный угловой энкодер | 2017 |
|
RU2651637C1 |
| Устройство определения угла поворота | 2023 |
|
RU2805303C1 |
| СПОСОБ ИЗМЕРЕНИЯ УГЛА ПОВОРОТА И УСТРОЙСТВО ЕГО РЕАЛИЗУЮЩЕЕ | 2019 |
|
RU2720052C1 |
| РЕКУРСИВНАЯ КОДОВАЯ ШКАЛА | 2010 |
|
RU2444126C1 |
| СПОСОБ РАСПОЗНАВАНИЯ ИДЕНТИФИКАЦИОННОЙ МАРКИРОВКИ АМПУЛ | 2014 |
|
RU2572387C1 |
| РЕКУРСИВНАЯ КОДОВАЯ ШКАЛА | 2011 |
|
RU2450437C1 |
| СПОСОБЫ И УСТРОЙСТВА ДЛЯ ПЕРЕДАЧИ И ОБРАБОТКИ ДАННЫХ, УСТРОЙСТВО СЕТЕВОЙ СТОРОНЫ И ТЕРМИНАЛ | 2018 |
|
RU2743100C1 |
| РАСТРОВО-КОДОВЫЙ ПРЕОБРАЗОВАТЕЛЬ УГЛОВЫХ ПЕРЕМЕЩЕНИЙ | 1991 |
|
RU2027206C1 |
| СПОСОБ ПОМЕХОУСТОЙЧИВОГО СЖАТИЯ ДАННЫХ ДЛЯ ПЕРЕДАЧИ И ХРАНЕНИЯ ИНФОРМАЦИИ | 2021 |
|
RU2840261C2 |
| РЕКУРСИВНАЯ КОДОВАЯ ШКАЛА | 2010 |
|
RU2434323C1 |
Изобретение относится к измерительной технике и может быть использовано для бесконтактного определения положения вала электродвигателя. Абсолютный оптический однооборотный угловой энкодер содержит n оптопар, где n - разрядность энкодера, растровый диск с одной кодирующей дорожкой, состоящей из последовательно расположенных прозрачных и непрозрачных секторов, причем оптопары располагают с одинаковым шагом a, где a, равное 360/2n, - разрешающая способность энкодера, а кодирующую дорожку формируют в соответствии с двоичной последовательностью длиной m=2n, при этом каждой цифре последовательности соответствует угловой размер a, нулю ставится в соответствии непрозрачный сектор, единице прозрачный - или наоборот. Технический результат - максимальное разрешение для разрядности n энкодера. 2 ил., 2 табл.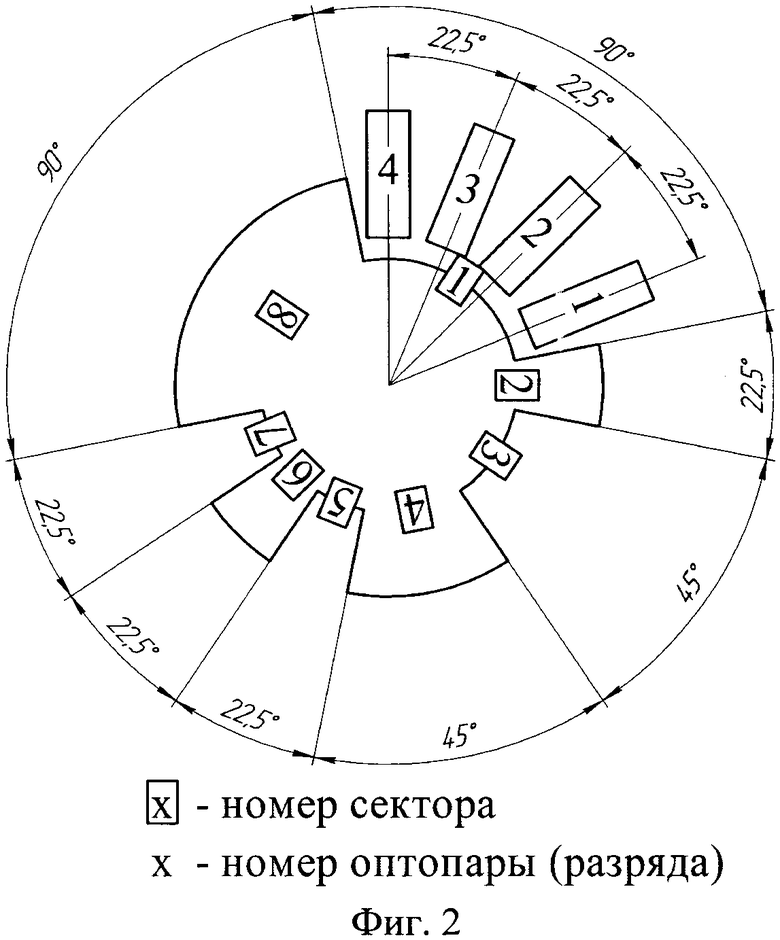
Абсолютный оптический однооборотный угловой энкодер, содержащий n оптических пар, где n - разрядность энкодера, и растровый диск с одной кодирующей дорожкой, отличающийся тем, что оптопары распределены с одинаковым шагом а, где а, равное 360/2n, - разрешающая способность энкодера, а кодирующая дорожка сформирована в соответствии с двоичной последовательностью длиной m равной 2n, при этом каждой цифре последовательности соответствует угловой размер а, нулю ставится в соответствии непрозрачный сектор, единице прозрачный - или наоборот.
| АБСОЛЮТНЫЙ ДАТЧИК УГЛА ПОВОРОТА | 2010 |
|
RU2436037C1 |
| US 9427872 B1, 30.08.2016 | |||
| US 20160003645 A1, 07.01.2016 | |||
| US 20070187582 A1, 16.08.2007. | |||
Авторы
Даты
2018-02-28—Публикация
2017-01-17—Подача