Изобретение относится к способам испытаний полупроводниковых приборов на стойкость к воздействию тяжелых заряженных частиц (ТЗЧ, или ионов) различных энергий космического пространства (КП) по результатам испытаний на стойкость к воздействию ионизирующих излучений (ИИ) моделирующих установок: 1) к импульсному реакторному гамма-нейтронному излучению; 2) импульсному рентгеновскому излучению электрофизических установок (генераторов рентгеновского излучения, линейных ускорителей, циклотронов); 3) ускорителей заряженных частиц; 4) импульсного лазерного излучения, с использованием коэффициентов относительной эффективности (КОЭ) заданных уровней ИИ к излучениям моделирующих установок (МУ).
Особое место при исследовании стойкости больших интегральных схем (БИС) технологии «комплементарные структуры «металл-диэлектрик-полупроводник» - на - диэлектрике» (КМОП/КНД, далее МДП) занимают эффекты отказов от единичных сбоев SEE (Single event effect) /1-3/.
Эффекты SEE подразделяются на «мягкие» и «жесткие» ошибки. Остаточные «жесткие» ошибки проявляются комплексно.
Источниками SEE в чувствительных объемах БИС являются протоны высоких энергий, электроны и ТЗЧ, которые с определенной вероятностью могут вызвать ядерные реакции с последующей ионизацией материала осколками деления, и ТЗЧ, которые вызывают «воронки заряда» вдоль трека распространения, что создает, в свою очередь, или переходный процесс или постоянные деструктивные эффекты.
Известен способ определения стойкости полупроводниковых приборов к электронному или протонному излучениям КП, заключающийся в облучении приборов электронным или протонным пучком на линейном ускорителе или циклотроне и измерении параметров до и после облучения /4/.
Недостатком указанного способа является высокая стоимость подобных испытаний и малая доступность установок, создающих протоны (электроны) определенного энергетического диапазона.
Испытания элементной компонентной базы (ЭКБ) на ускорителях, формирующих ТЗЧ, в соответствии с процедурой, представленной на Фиг. 1, позволяют установить абсолютное значение поперечного сечения 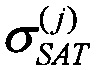 в [см2] для SEE, которое является характеристикой чувствительности (стойкости) испытываемой БИС при облучении моноэнергетическим и мононаправленным пучком частиц j-го сорта (Фиг. 2):
в [см2] для SEE, которое является характеристикой чувствительности (стойкости) испытываемой БИС при облучении моноэнергетическим и мононаправленным пучком частиц j-го сорта (Фиг. 2):

где ν - количество (или частота, с-1) SEE, возникающих в БИС при облучении; N(j)=Ф×cosθ - количество (или интенсивность) частиц данного типа из их общего потока FI (или общей плотности потока, см-2⋅с-1), см-2, который падает под углом θ на поверхность элемента ЭКБ, имеющего площадь S (Фиг. 3). Энергетические характеристики частиц ускорителей наиболее близки к характеристикам ТЗЧ КП и, как правило, имеют высокую проникающую способность. Такие испытания позволяют установить наиболее точные абсолютные значения сечения 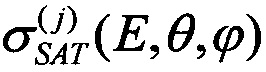 для SEE при воздействии частиц j-го сорта в зависимости от их энергии и углов падения (полярного θ и азимутального ϕ) и могут быть непосредственно использованы для прогнозирования количества или частоты SEE ν при воздействии изотропных ((θ, ϕ=const) потоков ТЗЧ разного сорта и энергии по формуле:
для SEE при воздействии частиц j-го сорта в зависимости от их энергии и углов падения (полярного θ и азимутального ϕ) и могут быть непосредственно использованы для прогнозирования количества или частоты SEE ν при воздействии изотропных ((θ, ϕ=const) потоков ТЗЧ разного сорта и энергии по формуле:
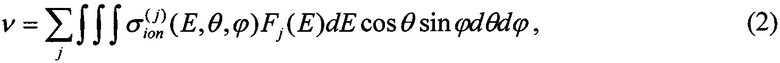
где Fj(E) - дифференциальный энергетический спектр направленного потока, в единицах [см-2⋅стеррад-1(МэВ/нуклон)-1], или плотности потока в единицах [см-2⋅ср-1(МэВ/нуклон)-1⋅с-1], частиц j-го сорта. Здесь «ср» - означает стеррадиан (единица телесного угла).
Определение значений 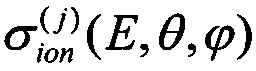 на ускорителях частиц в зависимости от нескольких параметров (сорта частиц, их энергии и углов падения) требует значительных временных и материальных затрат и поэтому существуют затруднения в непосредственном применении на практике для оценки радиационной стойкости (PC) элементов ЭКБ, предназначенных для бортовой радиоэлектронной аппаратуры (РЭА) космического аппарата (КА). Для оптимизации процесса испытаний и сокращения их объема до «разумных» пределов могут быть использованы моделирующие установки (МУ), в том числе исследовательский ядерный реактор (ИЯР) и электрофизические установки (ЭФУ), генерирующие импульсное рентгеновское излучение (РИ).
на ускорителях частиц в зависимости от нескольких параметров (сорта частиц, их энергии и углов падения) требует значительных временных и материальных затрат и поэтому существуют затруднения в непосредственном применении на практике для оценки радиационной стойкости (PC) элементов ЭКБ, предназначенных для бортовой радиоэлектронной аппаратуры (РЭА) космического аппарата (КА). Для оптимизации процесса испытаний и сокращения их объема до «разумных» пределов могут быть использованы моделирующие установки (МУ), в том числе исследовательский ядерный реактор (ИЯР) и электрофизические установки (ЭФУ), генерирующие импульсное рентгеновское излучение (РИ).
С целью удешевления испытаний эквивалентную поглощенную дозу гамма-рентгеновского излучения ИЯР или рентгеновского излучения ЭФУ со спектром RS определяют с использованием метода, изложенного в /8/.
Существующие тенденции разработки и изготовления БИС (т.е. сокращение размеров приборов, потребляемой мощности, увеличение линейного разрешения, увеличение объема памяти и быстродействия) могут только увеличить чувствительность к эффектам SEE. Это легко можно увидеть, если представить прибор простым конденсатором (C), в который проникает ионизирующая частица, создающая нестационарный заряд Qt, в результате чего изменяется напряжение в нагрузке (т.е. логическое состояние). Эффект SEE наблюдается, если линейные потери энергии частиц LET>Qcrit - величины «критического заряда». При уменьшении активной области такого прибора, ее емкость также уменьшается и тот же самый заряд способствует появлению эффектов SEE. Прибор по толщине в основном остается неизмененным, подвергаются изменениям только длина и ширина прибора. Если будем рассматривать транзисторную структуру МДП в виде чипа квадратной конфигурации LxL, то критический заряд QC, достаточный для изменения логического состояния такого прибора, будет пропорционален квадрату размера L. Модель «критического заряда» QC /7/ пригодна для анализа SEE для интегральных микросхем (ИМС) ряда технологий (включая NMOS, CMOS/объемный, CMOS/SOS, i2L, GaAs, ECL, CMOS/SOI, биполярный VHSIC). Этот критический заряд приводит непосредственно к переключению из состояния логической «1» в состояние логического «0» или изменению логического состояния (конверсии), но он может быть меньше, чем полный радиационно-индуцированный заряд Qt, из-за длины трека ТЗЧ в чувствительном объеме структуры МДП, который используется в модели «хорды» s (Фиг. 3). Хорда минимальна при нормальном падении ТЗЧ на лицевую или инверсную поверхность чипа структуры МДП и принимает максимальное значение smax, когда является пространственной диагональю чипа в виде параллелепипеда (Фиг. 3). Существенно то, что QC является разницей между зарядом Qt в узле и минимальным зарядом, необходимым для усиления и последующей конверсии. Для линейных потерь энергии частиц (Linear Energy Transfer) LETL можно записать:
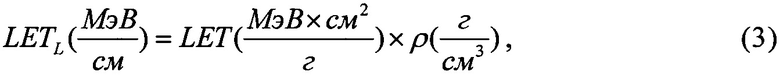
где LET - массовые потери энергии ТЗЧ; ρ - плотность материала M, тогда полные потери энергии на длине хорды выделенного чувствительного объема структуры МДП составят

Здесь длина максимальной хорды SMAX транзисторной структуры дается в [см]. Для более корректной оценки генерации зарядов необходимо располагать данными о следующих константах: 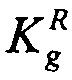 - постоянной генерации носителей заряда, [Кл см-3⋅рад-1(M)];
- постоянной генерации носителей заряда, [Кл см-3⋅рад-1(M)]; 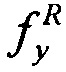 - предельному значению доли нерекомбинированного радиационно-индуцированного заряда;
- предельному значению доли нерекомбинированного радиационно-индуцированного заряда; 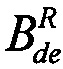 - фактору дозового накопления гамма-рентгеновского излучения моделирующей установки со спектром квантов RS, а
- фактору дозового накопления гамма-рентгеновского излучения моделирующей установки со спектром квантов RS, а 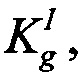
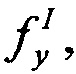
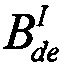 - такие же константы для ионов КП. В большинстве измерений эти величины не могут быть селектированы без принятия определенных допущений /5/.
- такие же константы для ионов КП. В большинстве измерений эти величины не могут быть селектированы без принятия определенных допущений /5/.
В табл. 1 приведены пределы изменения величины LET, при которых требуется анализ тех или иных видов излучений КП. Как следует из таблицы, при LET>100 МэВ⋅см2/мг схема считается стойкой и анализа не требуется.

Одна из классических интерпретаций состоит в том, что общая острота кривых поперечного сечения зависит от вариации межячеечной чувствительности к эффектам SEE /9/. Такая интерпретация несомненно более подходит для нерегулярных схем, таких, например, как логические схемы. Однако в случае БИС памяти, такой как статическое запоминающее устройство SRAM (Static Random Access Memory) или динамическое запоминающее устройство DRAM (Dynamic Random Access Memory), тщательное рассмотрение экспериментальных данных включает в большей степени роль внутреннего содержания ячеек, нежели межячеечных различий.
Наиболее близким по технической сущности и принятым за прототип является экспериментально разработанный способ прогнозирования интенсивности сбоев БИС в полях ИИ КП, предложенный в /6/.
В прототипе в качестве альтернативной гипотезы, объясняющей наличие значительной кривизны в области примыкающей к критическому «пороговому» значению LETTH, в том числе вариации чувствительности БИС к эффектам SEE в пределах одной ячейки, было описано как зависящее от позиционирования («posicion-dependence»), внутренне усиление эффекта SEE. Однако так как эти термины используют разработчики схем для других целей, и поскольку терминология «эффективность собранного заряда» («sharge-collection efficiency») имеет специфическую историю и механистическую импликацию, был введен термин «эффективность» («efficient»). Намерением здесь являлось использование термина, который свойственен всем технологиям, независимо от того, является ли «усиление» (в контексте «gain») большим или меньшим единицы.
В /6/ ввели концепцию эффективности при проверке чувствительности БИС к эффектам SEE, которую можно определить из кривой поперечного сечения. Это приводит к зависимости эффективности вероятности и демонстрирует, каким образом распределение вероятности можно представить графически как функцию фракции чувствительной области. Кривая эффективности может быть также определена путем воздействия импульсного лазера или воздействием ионного микропучка, или путем компьютерной симуляции. Эти кривые позволяют с другой стороны получить информацию о расчете чувствительности к эффектам SEE в качестве критерия добротности («figure of merit» FOM - Добротность есть величина, используемая для характеристики производительности устройства, системы или метода, по отношению к его альтернативе). В результате был проверен диапазон применимости этого метода и получено заключение, что он может быть использован в пределах более чем восьми порядков величины амплитуды индуцированных КП сбоев для геосинхронной орбиты.
В соответствии с ним была принята концепция «эффективности заряда» как мера эффективности индуцированного заряда для создания эффектов сбоя от единичной частицы. Эффективность измерена для чувствительности к эффектам SEE в пределах одной ячейки. Эффективность - это корреляция между местом положения входа частицы (single even (SE) stricke location) и актуальной чувствительностью к сбоям - т.е. отношение физической геометрии прибора к реакции схемы.
Она иллюстрирует, каким образом может быть определена зависимость эффективности из стандартных данных поперечного сечения эффектов SEE для тяжелых ионов или импульсного лазера, и показано, каким образом она может быть рассчитана из комбинации данных о собранном заряде и анализе схемы. Принимают допущение о величине критического заряда QC, необходимого для генерации эффекта SEE. Критический заряд, соответствующий энерговыделению LET, соответствует величине 50% поперечного сечения насыщения σSAT и ограничен номинальной толщиной прибора /9/ (используют коэффициент преобразования 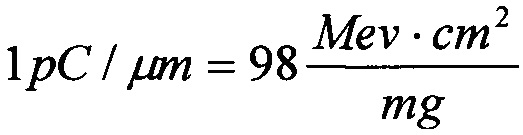 ). График зависимости
). График зависимости 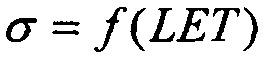 поперечного сечения в области насыщения σSAT аппроксимируют для данных с использованием логарифмически нормального закона или закона распределения Вейбулла. Принимают, что эффективность SEE максимальна, если значение поперечного сечения составляет 50% от предельного значения L0,5=LET(σ=0,5σSAT). Значение максимальной эффективности SEE определяют, как
поперечного сечения в области насыщения σSAT аппроксимируют для данных с использованием логарифмически нормального закона или закона распределения Вейбулла. Принимают, что эффективность SEE максимальна, если значение поперечного сечения составляет 50% от предельного значения L0,5=LET(σ=0,5σSAT). Значение максимальной эффективности SEE определяют, как 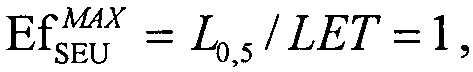 и, естественно, она изменяется как 1/LET. На Фиг. 4. показана аппроксимация логарифмически-нормальным законом зависимости эффективности SEE при моделировании лазерным импульсом от относительной величины площади сбора заряда /6/. На Фиг. 5. приведена типичная кривая аппроксимации зависимости
и, естественно, она изменяется как 1/LET. На Фиг. 4. показана аппроксимация логарифмически-нормальным законом зависимости эффективности SEE при моделировании лазерным импульсом от относительной величины площади сбора заряда /6/. На Фиг. 5. приведена типичная кривая аппроксимации зависимости 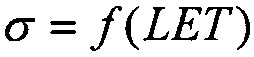 законом распределения Вейбулла (заметные расхождения с экспериментальными данными в области больших значений LET /6/.
законом распределения Вейбулла (заметные расхождения с экспериментальными данными в области больших значений LET /6/.
Кривые поперечного сечения и эффективности могут быть лучше аппроксимированы с использованием сглаживающего логарифмически-нормального распределения (L-n) вследствие того, что логарифмически-нормальное распределение (Фиг. 4) по сравнению с вейбулловским более соответствует физике прибора /10/.
Отметим, что лог-нормальное распределение (L-n) имеет меньшее количество параметров, чем распределение Вейбулла. Если использовать аппроксимацию кривой поперечных сечений, то лог-нормальное распределение менее выгодно в области малых значений LET. Такое поведение приборов характерно для режима отсечки при высокой эффективности. Расчетные значения интенсивности сбоев на 1-2% больше или меньше при использовании распределения Вейбулла для описания кривой поперечных сечений вместо лог-нормального распределения.
Интенсивность сбоев может быть определена с использованием цифрового представления о характеристиках «добротности» (FOM) и значений, определенных из данных по поперечным сечениям или из симуляции в смешанном режиме.
Кривую эффективности также используют для прогнозирования интенсивности сбоев с включением статистик достоверности эффективности. Скорейшим путем является предварительный расчет значения LET0,25, при котором поперечное сечение равно 25% от предельного значения поперечного сечения σ0,25=0,25σSAT, и объединение его напрямую с предельным значением поперечно сечения при расчете FOM.
На Фиг. 6. показана зависимость интенсивности сбоев (SEE) от добротности (FOM) /11/. На Фиг. 7. представлены зависимости поперечного сечения SEE, распределения эффективности и аппроксимирующей функции интегрального логарифмически-нормального закона распределения от LET для ИМС IDT 71 256 (R-MOS) /6/.
В более сложных методах кривую поперечного сечения аппроксимируют, и из этой аппроксимации определяют параметры FOM. Медианное значение σ0,5=0,5σSAT или L0,5 (или «средний» параметр "m") экстрагируется из анализа схемы, классического критического заряда QC наряду с предполагаемым процессом эффективности накопленного заряда. Из анализа аппроксимации кривой L-n распределения эффективности (как показано на Фиг. 7) может быть экстрагировано стандартное отклонение (параметр "s").
По этим двум параметрам конструируют FOM:
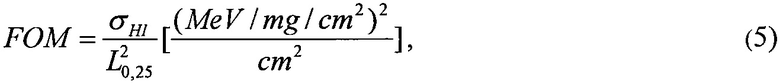
где σHI - предельное значение поперечного сечения на один бит; L0,25 - значение LET, при котором σ на уровне 25% предельного значения поперечного сечения /11/-/14/. Для L-n распределения L0,25=m-0,674s.
Известно несколько критических обзоров, посвященных применению FOM /15/-/18/. С использованием предельного поперечного сечения и L0,25 разработчик может рассчитать интенсивность сбоев для стандартной орбиты, геосинхронной или минимума солнечной активности, как это показано на Фиг. 5. Этот рисунок заимствован из /11/, в которой было отмечено, что точки, относящиеся к ложным, лежат правее прямоугольного участка графика. В диапазоне, простирающимся в область более низких значений LET, очевидно получается аппроксимация квадратичной функцией.
Интенсивность сбоев, проинтегрированная по модели IRPP (Integrated Rectangular Parallel-Piped), имеет основную форму (форма Bredford) /19/
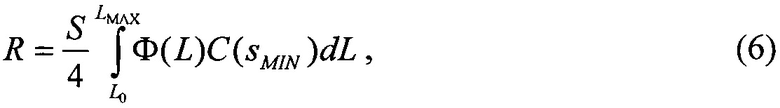
где R - интенсивность сбоев в ячейке, sMIN=Ес/ρ⋅LET [см] - минимальная длина хорды (пространственной диагонали) в чувствительном объеме транзисторной структуры, Ес=22,5Qc [МэВ] - критическое значение энергии генерации SEE, [Qc]=nКл - размерность критического заряда, [Ес]=МэВ - размерность критической энергии, S - площадь поверхности [см2], L0 - минимальное значение 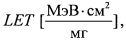 достаточное для генерации сбоев, Ф(L) - дифференциальный спектр
достаточное для генерации сбоев, Ф(L) - дифференциальный спектр 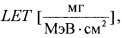 LMAX - максимальное значение LET в спектре Ф(L), C - интегральное распределение длины пути, ρ - плотность материала
LMAX - максимальное значение LET в спектре Ф(L), C - интегральное распределение длины пути, ρ - плотность материала 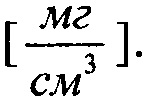 Сбои можно наблюдать, когда длина хорды ассоциируется с LET (или L) большим чем sMIN.
Сбои можно наблюдать, когда длина хорды ассоциируется с LET (или L) большим чем sMIN.
При этом принимают, что прибор имеет уникальный критический заряд, QC, больше которого наблюдается сбой, и постоянную толщину, а, такую, что QC соответствует уникальному значению эффективного значения LET. График основного поперечного сечения в зависимости от эффективного значения LET вводится ступенчатой функцией. Можно переобозначить равенство (6) в виде понятия LC, т.е. критического значения LET,

где 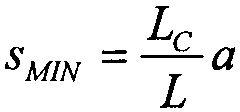 и L0=LCa/sMAX.
и L0=LCa/sMAX.
Величину LC определяют минимальным значением L, при котором частица может вызвать сбой при нормальном падении через ячейку, т.е. пути длиной а. Налетающий поток может генерировать сбои при заданном значении L, если длина пути больше чем LC/L в величинах а. При больших значениях L путь укорачивается. Минимальное значение L, при котором генерируются сбои, соответствует максимально возможной длине пути (sMAX). Это значение получается при L=L0. Для случаев вблизи минимального значения L, которые могут вызвать сбои, соответствующие длины пути очень длинные, соответственно больше чем LCa/L.
Экспериментально кривая поперечных сечений никогда не демонстрирует вид ступенчатой функции, которая ассоциируется с простыми трактовками, приведенными выше; она постоянно демонстрирует постепенное плавное увеличение выше так называемого «порогового значения» LETTH. В /6/ приведены доводы, что диапазон чувствительности к сбоям демонстрирует различные механизмы усиления собранного заряда. В работе /20/, например, содержатся выражения для чувствительности, в виде зависимости от толщины, которая здесь выступает в качестве альтернативы.
Несмотря на то что требуется рассматривать прибор, как имеющий различные области с различной эффективностью, необходимо рассматривать полную ячейку, если рассчитывать накопление энергии, которая проистекает из полного пути частицы в ячейках. Поэтому накопленный заряд в КП в большой степени определяется распределением пути в IRPP.
Поэтому далее в /6/ рассматривают энергию, которая должна быть накоплена на таком особенном пути на кривой зависимости поперечного сечения от LET для инициирования сбоев. Часть кривой с низкими значениями поперечного сечения подразумевает запасенную энергию меньше чем 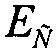 вследствие процесса усиления (gain). LET в этом случае соответствует точке на кривой поперечного сечения, и ее выделяют, помечая из окружающих значений LET те, которые учитываются в расчете интенсивности сбоев. Окружающие точки называют Le, а лабораторное эффективное значение L. Запасенная энергия, вызывающая сбой, в этом случае будет равна
вследствие процесса усиления (gain). LET в этом случае соответствует точке на кривой поперечного сечения, и ее выделяют, помечая из окружающих значений LET те, которые учитываются в расчете интенсивности сбоев. Окружающие точки называют Le, а лабораторное эффективное значение L. Запасенная энергия, вызывающая сбой, в этом случае будет равна 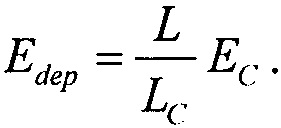 При малых L значение Edep меньше чем
При малых L значение Edep меньше чем 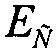 вследствие экстремального значения усиления, которое было, LQ, минимальное значение Le, при котором можно наблюдать сбои, может также изменяться. При низких значениях L величина Edep может быть меньше
вследствие экстремального значения усиления, которое было, LQ, минимальное значение Le, при котором можно наблюдать сбои, может также изменяться. При низких значениях L величина Edep может быть меньше 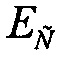 вследствие механизма усиления. В /6/ введена функция g(L) для определения функции усиления в зависимости от L для выражения зависимости усиления от L. Она является функционалом, из которого проистекает функция поперечного сечения. Отсюда проистекают условия применения полной функции Вейбулла или L-n функции.
вследствие механизма усиления. В /6/ введена функция g(L) для определения функции усиления в зависимости от L для выражения зависимости усиления от L. Она является функционалом, из которого проистекает функция поперечного сечения. Отсюда проистекают условия применения полной функции Вейбулла или L-n функции.
Если используют L-n функцию для описания данных, приведенных для малых значений L вблизи отсечки, то применяют эту функцию совместно с нижним пределом L в интегральном распределении L. Это может привести к 1-2% улучшению результатов расчетов, однако, очень не на много улучшается прогноз интенсивности сбоев /21/:
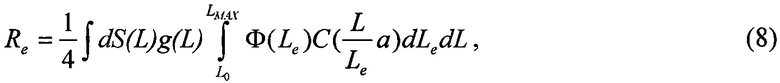
где L0=La/sMAX; sMIN=L/Lea; g(L) - распределение Вейбулла или L-n, dS(L) - дифференциальный элемент площади, соответствующий g(L). Интегрирование по dS(L) является независимым от других членов, что приводит к соотношению
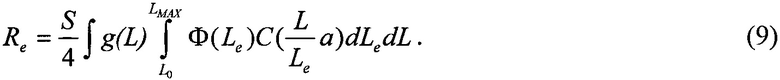
Соответствующее уравнение может быть получено с использованием интегрального распределения 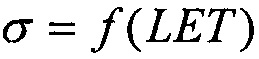 и дифференциального распределения длин хорд /9/.
и дифференциального распределения длин хорд /9/.
Этот результат является идентичным тому, который получается при принебрежении вариаций внутри ячейки при оценке чувствительности к SEE /9/.
В результате выполненной в /6/ перепроверке стандартного метода представления чувствительного объема в виде IRPP для расчета интенсивности SEE в допущении, что вероятность сбоев зависит от положения бита на поверхности, было сделано заключение, что является нецелесообразным переформулировка IRPP.
В /6/ экспериментальная зависимость 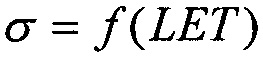 начинается при LET=0 из начала координат (0,0) (Фиг. 7). Поэтому аппроксимация зависимости
начинается при LET=0 из начала координат (0,0) (Фиг. 7). Поэтому аппроксимация зависимости 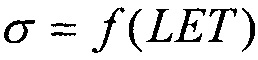 теоретическим L-n законом распределения учитывает этот факт, а экстрагированные параметры распределения включают эту информацию.
теоретическим L-n законом распределения учитывает этот факт, а экстрагированные параметры распределения включают эту информацию.
Сборка UTMC "Summit" была тестирована 17.05.2000 на чувствительность к отказам от SEE и интенсивность отказов на циклотроне "88-inch Cyclotron" Lawrence Berkeley Laboratory.
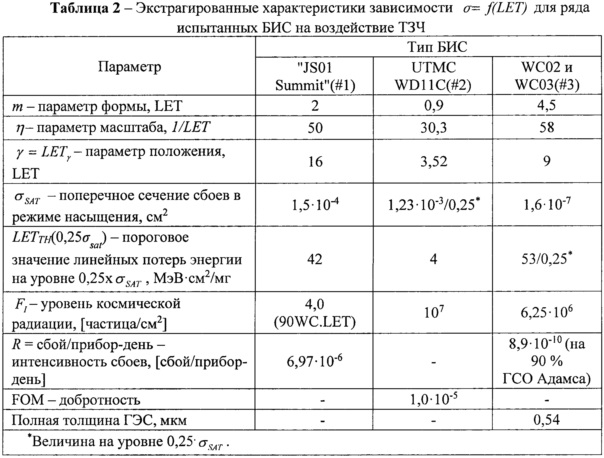
Однако представленные на Фиг. 8 результаты тестирования БИС вентильных матриц "JS01 Summit", изготовленных по технологии UTMC 0,6 μm Commercial RadHard™ (CRH), дают минимальное значение поперечного сечения σMIN=10-7 см2/бит, а параметры аппроксимирующего интегрального закона распределения Вейбулла дают параметр положения 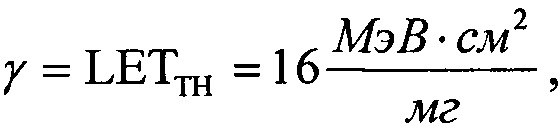 ниже которого интегральная функция
ниже которого интегральная функция
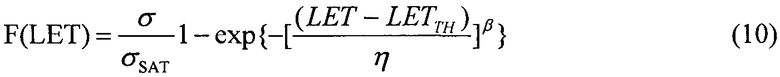
не определена (характеристики зависимости 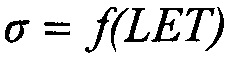 приведены в табл. 2). На том же циклотроне проводились квалификационные испытания на чувствительность к SEE ИМС параллельно-последовательного преобразователя (serializer) UTMC WD11C 3.3V LVDS на воздействие ТЗЧ, или ионов. Данные по чувствительности к эффектам SEE были собраны 14.04.2003 и показаны на Фиг. 9.
приведены в табл. 2). На том же циклотроне проводились квалификационные испытания на чувствительность к SEE ИМС параллельно-последовательного преобразователя (serializer) UTMC WD11C 3.3V LVDS на воздействие ТЗЧ, или ионов. Данные по чувствительности к эффектам SEE были собраны 14.04.2003 и показаны на Фиг. 9.
Минимальное значение поперечного сечения на графике также составляет σMIN=10-7 см2/бит, в то время как параметр 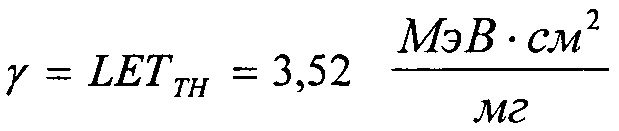 (табл. 2). В тех же условиях 10.07.2003 были проведены исследования чувствительности ИМС 4 Мбит SRAM фирмы "Aeroflex PIC" (WC02 и WC03) к эффектам SEE на 88-дюймовом циклотроне LBNL (Фиг. 10). Аналогично σMIN=10-14 см2/бит, а
(табл. 2). В тех же условиях 10.07.2003 были проведены исследования чувствительности ИМС 4 Мбит SRAM фирмы "Aeroflex PIC" (WC02 и WC03) к эффектам SEE на 88-дюймовом циклотроне LBNL (Фиг. 10). Аналогично σMIN=10-14 см2/бит, а 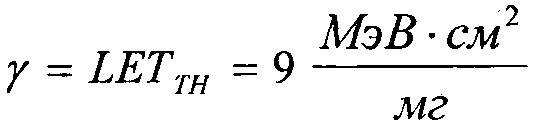 (табл. 2). Альтернативой модели эффективности является представление о дополнительном локальном формировании накопленного заряда за счет воздействия таких факторов, как атмосферные нейтроны, «эффект упаковки» и естественная фоновая радиоактивность, действующие помимо ионизирующего излучения космического пространства, в том числе на поверхности Земли и на активном участке вывода космического аппарата на орбиту. В области малых значений относительного изменения σ/σSAT справедливо аппроксимировать функцию F(LET) экспоненциальным распределением. Если границей нечувствительности к SEE считать значение
(табл. 2). Альтернативой модели эффективности является представление о дополнительном локальном формировании накопленного заряда за счет воздействия таких факторов, как атмосферные нейтроны, «эффект упаковки» и естественная фоновая радиоактивность, действующие помимо ионизирующего излучения космического пространства, в том числе на поверхности Земли и на активном участке вывода космического аппарата на орбиту. В области малых значений относительного изменения σ/σSAT справедливо аппроксимировать функцию F(LET) экспоненциальным распределением. Если границей нечувствительности к SEE считать значение 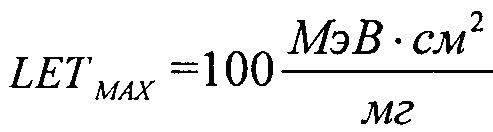 (табл. 1), то при
(табл. 1), то при 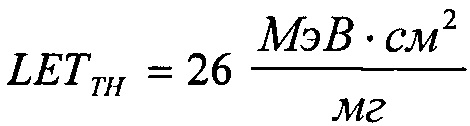 приращение интенсивности отказа за счет учета дополнительного заряда
приращение интенсивности отказа за счет учета дополнительного заряда 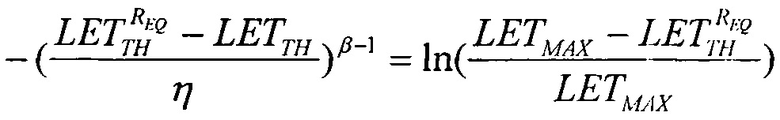 дает изменение суммарной интенсивности сбоев ΔZΣ(LET)=1,3%, что приводит к изменению функции распределения SEE ΔF(LET)=0,4%. Анализ взаимодействия единичных частиц с ЧО с привлечением микродозиметрического подхода дает обоснование как линейному участку на зависимости интенсивности сбоев от флюенса частиц (т.е. величины обратной σ), так и наличию при определенных условиях выхода на участок насыщения σSAT. При этом разумным представляется принять распределение таких SEE на участке 0<LET<LETTH в виде равномерного закона распределения.
дает изменение суммарной интенсивности сбоев ΔZΣ(LET)=1,3%, что приводит к изменению функции распределения SEE ΔF(LET)=0,4%. Анализ взаимодействия единичных частиц с ЧО с привлечением микродозиметрического подхода дает обоснование как линейному участку на зависимости интенсивности сбоев от флюенса частиц (т.е. величины обратной σ), так и наличию при определенных условиях выхода на участок насыщения σSAT. При этом разумным представляется принять распределение таких SEE на участке 0<LET<LETTH в виде равномерного закона распределения.
На Фиг. 11 показана зависимость интенсивности SEE Z(LET) при аппроксимации функции σ(LET) трехпраметрическим законом распределения Вейбулла 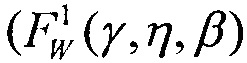 при γ=LETTH, двухпарметрическим законом распределения Вейбулла
при γ=LETTH, двухпарметрическим законом распределения Вейбулла 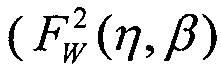 при γ=0, экспоненциальным законом распределения при Z(LET)=λ на участке 0<LET<LETTH и равномерным законом распределения (FU(LET)) с
при γ=0, экспоненциальным законом распределения при Z(LET)=λ на участке 0<LET<LETTH и равномерным законом распределения (FU(LET)) с 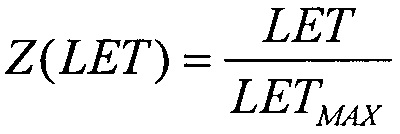 на том же участке. На Фиг. 12 показана зависимость изменения поперечного сечения SEE [см2] от
на том же участке. На Фиг. 12 показана зависимость изменения поперечного сечения SEE [см2] от 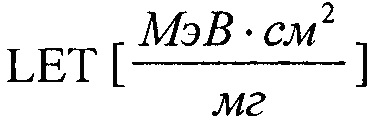 при аппроксимации единичной функции распределения (F1(LET), трехпраметрическим законом распределения Вейбулла
при аппроксимации единичной функции распределения (F1(LET), трехпраметрическим законом распределения Вейбулла 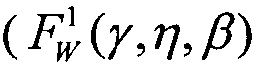 при γ=LETTH, двухпарметрическим законом распределения Вейбулла
при γ=LETTH, двухпарметрическим законом распределения Вейбулла 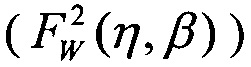 при γ=0, двухпараметрическим законом распределения Вейбулла (FW(η,β)) γ=0 по модели эффективности /6/, при комбинированном законе распределения (Вейбулла + равномерным законом распределения
при γ=0, двухпараметрическим законом распределения Вейбулла (FW(η,β)) γ=0 по модели эффективности /6/, при комбинированном законе распределения (Вейбулла + равномерным законом распределения 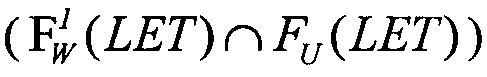 на участке 0<LET<LETMAX.
на участке 0<LET<LETMAX.
В методе /6/, принятом за прототип, не учитывается «предыстория» поведения ИМС до попадания в область LETTH, например нахождение ИМС на поверхности Земли или на активном участке траектории вывода КА. Кроме этого, имеется проблема «умолчания» поведения кривой 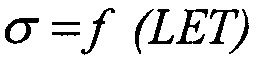 в области малых значений LET и наличие ненулевого значения параметра положения.
в области малых значений LET и наличие ненулевого значения параметра положения.
Техническим результатом предлагаемого способа оценки стойкости элементов цифровой техники к эффектам сбоев от воздействия единичных частиц является повышение точности определения характеристик зависимости поперечного сечения эффектов единичных сбоев (SEE) от LET, а также определение минимального значения флюенса частиц FMIN, достаточного для генерации эффектов SEE.
Технический результат достигается тем, что в способе оценки стойкости элементов цифровой электроники к эффектам сбоев от воздействия единичных частиц космического пространства путем определения минимального значения потока частиц, соответствующего отличному от нулевого значения сечению сбоев в области малых значений линейной передачи энергии частицами, для чего получают экспериментальную зависимость величины сечения сбоев от величины линейных потерь энергии частиц, аппроксимируют эту зависимость теоретическим многопараметрическим законом распределения, экстрагируют параметры этого распределения, определяют пороговое значение линейных потерь энергии единичных частиц, соответствующего минимальному значению сечения сбоя, определяют максимальное значение сечения сбоев в режиме насыщения и минимальное значение потока частиц, а затем реализуют сопоставление минимальных значений потоков частиц, полученных с использованием следующих математических моделей:
1) в качестве теоретического многопараметрического интегрального закона распределения сечения сбоя для значений, больших величины порогового значения линейных потерь принимают трехпараметрический закон распределения Вейбулла, а для значений, меньших величины порогового значения линейных потерь, но больших величины их нулевого значения, принимают равномерный закон распределения, учитывающий «предысторию» возможности появления единичных сбоев, полагают в качестве критерия равными интенсивности сбоев и определяют сечения сбоев и минимальное значение потока частиц;
2) для вейбулловского и равномерного законов распределения принимают в качестве критерия равными между собой интегральные функции распределения и определяют сечения сбоев и минимальное значение потока частиц;
3) для порогового значения линейных потерь энергии частиц принимают в качестве критерия комбинированную величину интенсивности сбоев, которую определяют в виде суммы величин интенсивности сбоев для равномерного и вейбулловского законов распределения, определяют сечения сбоев и минимальное значение потока частиц;
4) для вейбулловского и равномерного законов распределения определяют величины ресурсов, а в качестве скорректированной величины ресурса для порогового значения линейных потерь энергии частиц принимают в качестве критерия произведение указанных ресурсов, определяют сечения сбоев и минимальное значение потока частиц;
5) принимают в качестве критерия равными интегральные функции распределения сбоев для вейбулловского и равномерного законов распределения, а затем определяют скорректированную пороговую величину линейных потерь энергии частиц, определяемую в виде линейного соотношения соответствующих величин для указанных законов, определяют сечения сбоев и минимальное значение потока частиц;
6) определяют в качестве критерия скорректированный ресурс как произведение ресурсов для вейбулловского и равномерного законов распределения, затем определяют параметры скорректированного закона распределения и получают скорректированное значение минимального потока частиц, определяют сечения сбоев и минимальное значение потока частиц;
7) в качестве критерия равными принимают ресурсы, определенные для вейбулловского и равномерного законов распределения, определяют параметры скорректированного закона распределения, определяют сечения сбоев и минимальное значение потока частиц;
из полученного набора данных выбирают минимальное значение потока частиц (наихудший случай).
Изобретение иллюстрируется следующими чертежами.
Фиг. 1. Схема процедуры оценки зависимости вероятности сбоев от эффектов SEE от флюенса ТЗЧ /22/.
Фиг. 2. Типичная зависимость поперечного сечения SEE σ [см2] от линейных потерь энергии 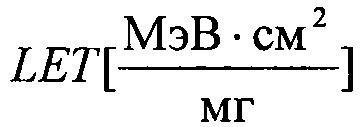 в Si от ионов Fe /8/.
в Si от ионов Fe /8/.
Фиг. 3. Исходная структура чувствительного объема транзистора МОП для расчета LET.
Фиг. 4. Аппроксимация логарифмически-нормальным законом зависимости эффективности SEE при моделировании лазерным импульсом от относительной величины площади сбора заряда /6/.
Efficacy - эффективность
Cumulative relative area - относительная площадь сбора заряда
Фиг. 5. Типичная кривая аппроксимации зависимости 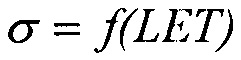 законом распределения Вейбулла (заметные расхождения с экспериментальными данными в области больших значений LET /6/.
законом распределения Вейбулла (заметные расхождения с экспериментальными данными в области больших значений LET /6/.
Фиг. 6. Зависимость интенсивности сбоев (R) от добротности (FOM) /11/
Rate - интенсивность
Calc - расчетные данные
Upset rate - интенсивность сбоев
Figure of merit - добротность
Фиг. 7. Зависимости поперечного сечения SEE, распределения эффективности и аппроксимирующей функции интегрального логарифмически-нормального закона распределения от LET для ИМС IDT 71 256 (R-MOS) /6/.
Фиг 8. Экспериментальные данные и аппроксимация L-n распределением результатов тестирования сборки UTMC "Summit" 17.05.2000 на чувствительность к отказам от SEE и интенсивность отказов на циклотроне "88-inch Cyclotron" Lawrence Berkeley National Laboratory (LBNL).
Cross Section/Device, cm2/bit - поперечное сечение/прибор, см2/бит
Log norm - аппроксимация L-n распределением
Comulative - интегральное L-n распределение
Efficacy - эффективность
Фиг. 9. Результаты испытания 14.04.2003 на чувствительность к SEE ИМС параллельно-последовательного преобразователя (serializer) UTMC WD11C 3.3V LVDS на воздействие ТЗЧ на циклотроне "88-inch Cyclotron" LBNL.
SEU (SEE) Cross Section, cm2/bit - поперечное сечение, см2/бит
Weibull fit - аппроксимайия законом Вейбулла
S/N… - серийный номер
Фиг. 10. Результаты исследования чувствительности 10.07.2003 ИМС 4 Мбит SRAM фирмы "Aeroflex PIC" (WC02 и WC03) к эффектам SEE на циклотроне "88-inch Cyclotron" LBNL.
Cross Section, cm2/bit - поперечное сечение, см2/бит
Weibull fit - аппроксимайия законом Вейбулла
Part… - номер образца
Фиг. 11. Зависимость интенсивности SEE Z(LET) при аппроксимации функции σ(LET) трехпраметрическим законом распределения Вейбулла 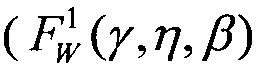 при γ=LETTH, двухпарметрическим законом распределения Вейбулла
при γ=LETTH, двухпарметрическим законом распределения Вейбулла 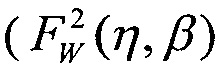 при γ=0, экспоненциальным законом распределения при Z(LET)=λ на участке 0<LET<LETTH и равномерным законом распределения (FU(LET)) с
при γ=0, экспоненциальным законом распределения при Z(LET)=λ на участке 0<LET<LETTH и равномерным законом распределения (FU(LET)) с 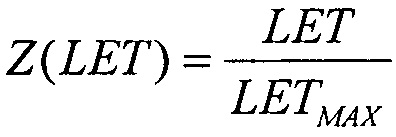 на том же участке.
на том же участке.
Фиг. 12. Зависимость изменения поперечного сечения SEE [см2] от 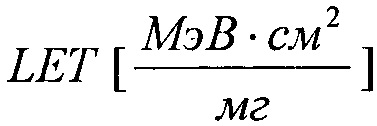 при аппроксимации единичной функции распределения (F1(LET), трехпраметрическим законом распределения Вейбулла
при аппроксимации единичной функции распределения (F1(LET), трехпраметрическим законом распределения Вейбулла 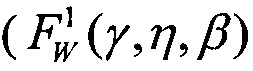 при γ=LETTH, двухпарметрическим законом распределения Вейбулла
при γ=LETTH, двухпарметрическим законом распределения Вейбулла 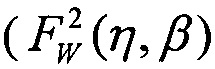 при γ=0, двухпараметрическим законом распределения Вейбулла (FW(η, β)) γ=0 по модели эффективности /6/, при комбинированном законе распределения (Вейбулла + равномерным законом распределения
при γ=0, двухпараметрическим законом распределения Вейбулла (FW(η, β)) γ=0 по модели эффективности /6/, при комбинированном законе распределения (Вейбулла + равномерным законом распределения 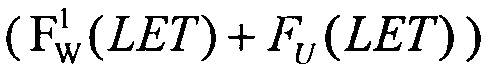 на участке 0<LET<LETMAX.
на участке 0<LET<LETMAX.
Предлагаемый способ реализуется следующим образом.
На моделирующей установке (МУ) или имитационными методами (ИМ) экспериментально снимают зависимость поперечного сечения σ эффектов SEE от величины LET. В качестве моделирующих установок используют импульсные источники, такие, например, как импульсные ядерные реакторы, электрофизические установки, генерирующие импульсное X-Ray, циклотроны протонного излучения и т.п. /22/, /23/. ИМ реализуют с помощью импульсного лазерного излучения /24/ или методами компьютерного моделирования /25/. Полученную зависимость 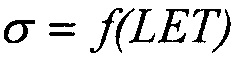 далее аппроксимируют теоретическим интегральным многопараметрическим законом распределения, экстрагируют параметры этого распределения, определяют пороговое значение LETTH, соответствующее минимальному значению поперечного сечения SEE σMIN, определяют максимальное значения поперечного сечения в режиме насыщения σSAT. Затем определяют значения потока частиц FMIN, соответствующего отличному от нулевому значению поперечному сечению σMIN. В качестве теоретического многопараметрического интегрального закона распределения поперечного сечения SEE для значений LET, больших величины порогового значения LETTH принимают трехпараметрический закон распределения Вейбулла
далее аппроксимируют теоретическим интегральным многопараметрическим законом распределения, экстрагируют параметры этого распределения, определяют пороговое значение LETTH, соответствующее минимальному значению поперечного сечения SEE σMIN, определяют максимальное значения поперечного сечения в режиме насыщения σSAT. Затем определяют значения потока частиц FMIN, соответствующего отличному от нулевому значению поперечному сечению σMIN. В качестве теоретического многопараметрического интегрального закона распределения поперечного сечения SEE для значений LET, больших величины порогового значения LETTH принимают трехпараметрический закон распределения Вейбулла
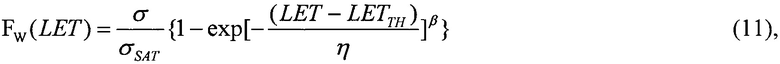
где LETTH=γ - параметр положения, η - параметр масштаба, β - параметр формы, а для значений LET, меньших величины порогового значения LETTH, но больших величины их нулевого значения, принимают интегральный закон распределения, учитывающий «предысторию» возможности появления единичных сбоев SEE.
Для диапазона 0<LET<LETMAX в качестве плотности исходного распределения поперечного сечения принимают равномерное распределение

с верхним граничным значением 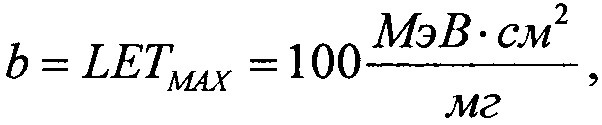 равным максимальному значению величины линейной передачи энергии, выше которой испытания на стойкость к воздействию SEE рекомендуется не проводить, a=0 - нижнее граничное значение, а интегральный закон распределения поперечного сечения сбоев SEE в этом диапазоне задают в виде
равным максимальному значению величины линейной передачи энергии, выше которой испытания на стойкость к воздействию SEE рекомендуется не проводить, a=0 - нижнее граничное значение, а интегральный закон распределения поперечного сечения сбоев SEE в этом диапазоне задают в виде 
Затем реализуют критерии сопоставления этих двух распределений для значения LETTH, получают на основании этого скорректированное значение 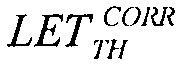 и соответствующие ему поперечные сечения
и соответствующие ему поперечные сечения 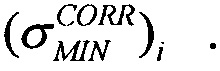 Затем находят соответствующие значения потока частиц (FMIN)i, соответствующие отличному от нулевого значения поперечному сечению
Затем находят соответствующие значения потока частиц (FMIN)i, соответствующие отличному от нулевого значения поперечному сечению  В приведенных ниже примерах величина поперечного сечения сбоев SEE σМАХ=10 см2.
В приведенных ниже примерах величина поперечного сечения сбоев SEE σМАХ=10 см2.
Для первого критерия для значения LET=LETTH величины интенсивности поперечного сечения сбоев для равномерного и вейбулловского законов распределения поперечного сечения сбоев принимают равными между собой, ZU=ZW, считая их непрерывными величинами. В свою очередь, для равномерного закона распределения поперечного сечения сбоев SEE функцию интенсивности сбоев выбирают в виде
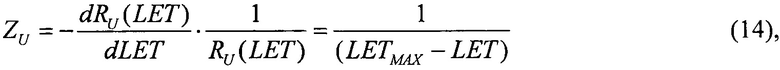
где R(LET)=1-F(LET) - функция ресурса, для вейбулловского закона распределения поперечного сечения сбоев SEE функцию интенсивности SEE - в виде
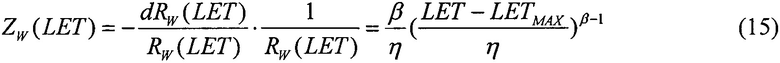
Для второго критерия принимают равными интегральные функции распределения сбоев 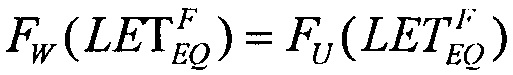 для вейбулловского и равномерного распределений в виде соотношения
для вейбулловского и равномерного распределений в виде соотношения
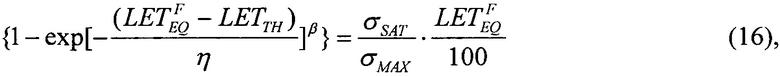
которое в асимптотике 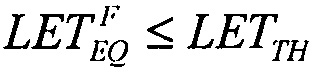 дает единственное значение
дает единственное значение 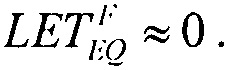 При равенстве
При равенстве 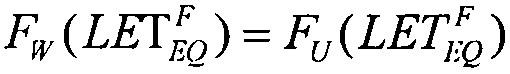 реализуют соотношение вида
реализуют соотношение вида 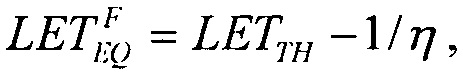 которое позволяет оценить
которое позволяет оценить 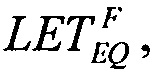
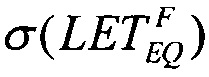 и
и 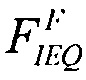 при определении функции распределения FW(LET) в диапазоне изменения LET от LETTH до +∝.
при определении функции распределения FW(LET) в диапазоне изменения LET от LETTH до +∝.
В качестве третьего критерия принимают комбинированную величину интенсивности сбоев ZΣ(LET), которую определяют в виде суммы интенсивности SEE равномерного (14) и вейбулловского (15) законов распределения поперечного сечения сбоев.
В качестве четвертого критерия для всех значений LET величины ресурса для равномерного закона распределения поперечного сечения сбоев SEE RU(LET) в виде
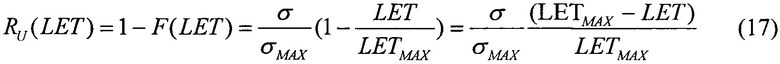
и для вейбулловского закона распределения поперечного сечения сбоев SEE RW(LET) в виде
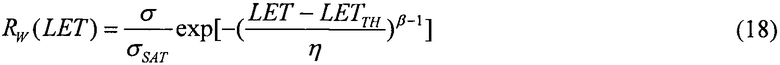
принимают в качестве результирующей величины ресурса RΣ(LET) произведение ресурсов для равномерного распределения и распределения Вейбулла поперечных сечений сбоев

или в виде
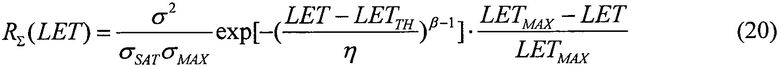
В качестве пятого критерия равными принимают интегральные функции распределения сбоев для вейбулловского и равномерного законов распределения 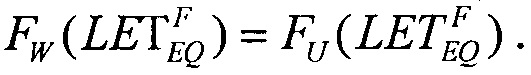 Для диапазона изменения LET от нуля до +∝ представляют
Для диапазона изменения LET от нуля до +∝ представляют 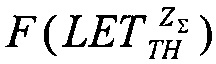 также в виде
также в виде
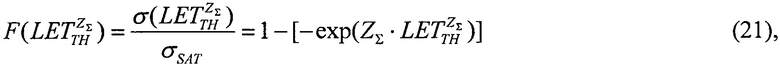
затем, следуя процедуре линеаризации преобразуют ее к форме линейного соотношения Y=X+В, где его члены Y, X, В определены в
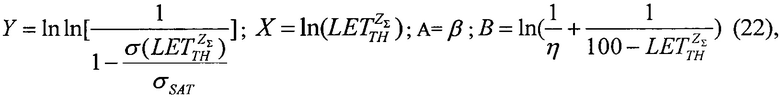
после чего, при применении численных методов решения в качестве выходных данных определяют значения 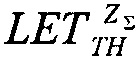 и
и 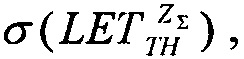 а также величину
а также величину 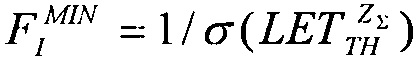 - минимального потока частиц, достаточного для генерации SEE.
- минимального потока частиц, достаточного для генерации SEE.
В указанное линейное соотношение подставляют соответствующие значения 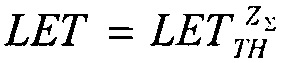 и при Y=0 полученное равенство
и при Y=0 полученное равенство
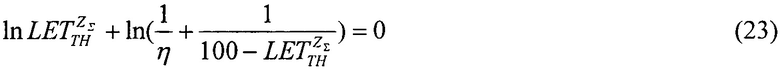
преобразуют к виду квадратного уравнения ax2+bx+c=0

где a=1, 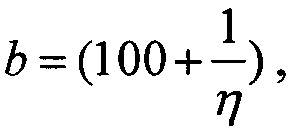
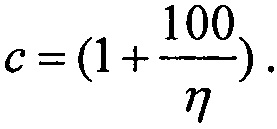
Для шестого критерия определяют скорректированный ресурс как произведение ресурсов для равномерного и вейбулловского законов распределения RΣ(LET)=RU(LET)⋅RW(LET), интегральную функцию распределения FΣ(LET) поперечных сечений SEE представляют в виде
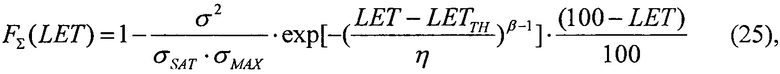
которую относительно 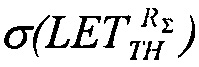 преобразуют в квадратное уравнение вида ax2+bx+c=0
преобразуют в квадратное уравнение вида ax2+bx+c=0
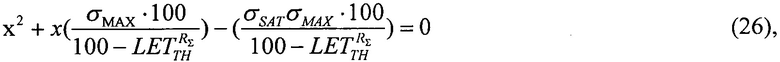
где 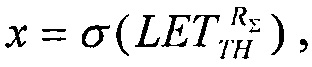 a=1,
a=1, 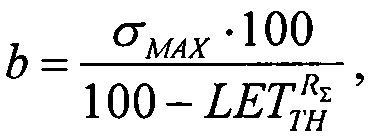
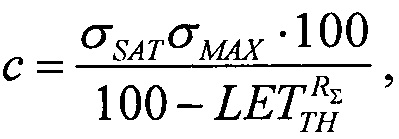 решая которое при подстановке экспериментально полученных данных
решая которое при подстановке экспериментально полученных данных 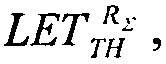 σSAT, σMAX получают значение
σSAT, σMAX получают значение 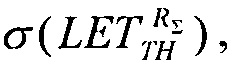 в то время как обратная величина позволяет определить минимальную величину потока частиц, достаточных для генерации SEE.
в то время как обратная величина позволяет определить минимальную величину потока частиц, достаточных для генерации SEE.
В качестве седьмого критерия равными принимают значения ресурсов для равномерного закона распределения поперечного сечения сбоев RU(LET) в виде (17) и для вейбулловского закона распределения (18) в виде (19) 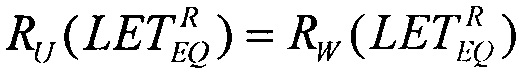
или соотношение
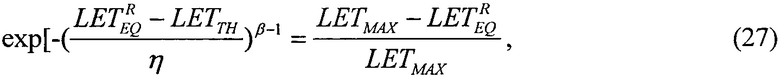
которое преобразуют в
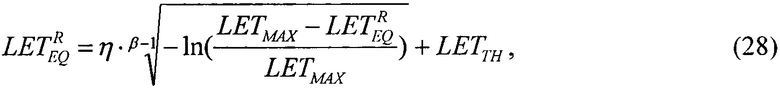
которое решают численными методами и находят значение 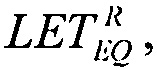 соответствующее значение
соответствующее значение 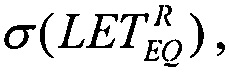 обратную величину
обратную величину 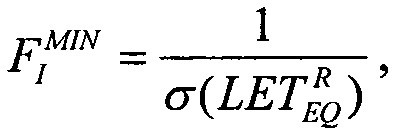 соответствующую минимальному значению потока частиц, достаточных для генерации SEE.
соответствующую минимальному значению потока частиц, достаточных для генерации SEE.
Из полученного набора значений потоков частиц вызывающих SEE выбирают наименьшее значение, соответствующее наихудшему случаю и считают это значение уровнем стойкости интегральной сборки.
Пример конкретной реализации.
Способ оценки стойкости элементов цифровой электроники к эффектам сбоев от воздействия единичных частиц (SEE) космического пространства (КП) в области малых значений линейной передачи энергии (LET) реализуют путем получения экспериментальной зависимости величины поперечного сечения SEE от величины LET на моделирующих установках или имитационными методами, последующей аппроксимации этой зависимости теоретическим многопараметрическим интегральным законом распределения, экстракцией параметров этого распределения, определения порогового значения величины передачи энергии LETTH, соответствующее минимальному значению поперечного сечения SEE σMIN; определение максимального значения поперечного сечения SEE в режиме насыщения σSAT, минимального значения поперечного сечения SEE σMIN, соответствующего пороговому значению величины передачи энергии LETTH, и определение потока частиц FMIN соответствующего отличному от нулевого значения поперечному сечению сбоев σMIN.
В качестве теоретического закона распределения поперечного сечения для LET>LETTH принимают трехпараметрический закон распределения Вейбулла (11) с параметрами: LETTH=γ - параметр положения, η - параметр масштаба, β - параметр формы. Для диапазона LET больше нуля, но меньше LETMAX в качестве плотности исходного распределения поперечного сечения принимают равномерное распределение (12) с верхним граничным значением константы 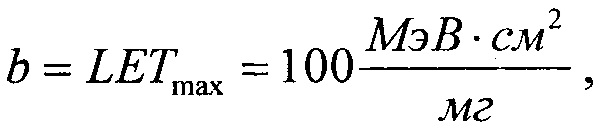 равным максимальному значению величины LET, выше которой испытания на стойкость к воздействию SEE рекомендуется не проводить, нижним граничным значением константы а=0, а интегральный закон распределения поперечного сечения сбоев SEE в этом диапазоне задают в виде (13).
равным максимальному значению величины LET, выше которой испытания на стойкость к воздействию SEE рекомендуется не проводить, нижним граничным значением константы а=0, а интегральный закон распределения поперечного сечения сбоев SEE в этом диапазоне задают в виде (13).
В качестве первого критерия непрерывности для значения LET=LETTH величины интенсивности сбоев SEE для равномерного закона распределения поперечных сечений сбоев SEE и вейбулловского законов распределения поперечных сечений сбоев SEE принимают равными между собой, ZU=ZW, считая их непрерывными величинами. Для равномерного закона распределения функцию интенсивности параметрического отказа выбирают в виде (14), где R(LET)=1-F(LET) - функция ресурса, для вейбулловского - в виде (15). Приравнивая (14) к (15) и разрешая относительно 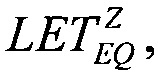 получают оценки значений
получают оценки значений 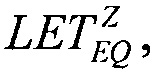
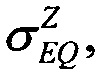
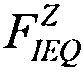 и приращения Δσ/σSAT для ИМС из табл. 2: "JS01 Summit" (обозначена #1), UTMC WD11C (обозначена #2) и WC02 и WC03 (обозначена #3) (табл. 3).
и приращения Δσ/σSAT для ИМС из табл. 2: "JS01 Summit" (обозначена #1), UTMC WD11C (обозначена #2) и WC02 и WC03 (обозначена #3) (табл. 3).

Для второго критерия непрерывности принимают равными интегральные функции распределения сбоев 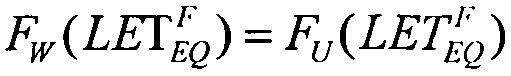 для вейбулловского и равномерного распределений в виде соотношения (16), которое в асимптотике
для вейбулловского и равномерного распределений в виде соотношения (16), которое в асимптотике 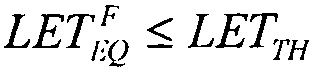 дает единственное значение
дает единственное значение 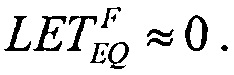 При равенстве
При равенстве 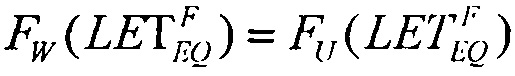 реализуют соотношение вида
реализуют соотношение вида 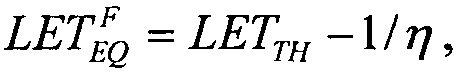 которое позволяет оценить
которое позволяет оценить 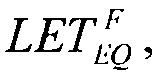
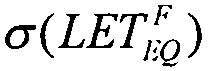 и
и 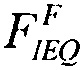 при определении функции распределения FW(LET) в диапазоне изменения LET от LETTH до +∝. (табл. 4).
при определении функции распределения FW(LET) в диапазоне изменения LET от LETTH до +∝. (табл. 4).

В качестве третьего критерия аддитивности комбинированную величину интенсивности сбоев ZΣ(LET) определяют в виде суммы (14) и (15). Разрешая это равенство относительно величины 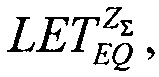 оценивают величину
оценивают величину 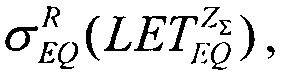 приращение величины Δσ/σSAT (%) и значение минимального потока частиц
приращение величины Δσ/σSAT (%) и значение минимального потока частиц 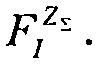 Для ИМС #3, можно например, получить равенство
Для ИМС #3, можно например, получить равенство 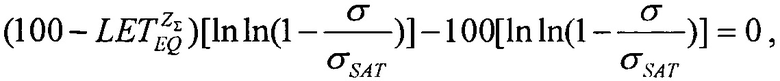 разрешая которое относительно
разрешая которое относительно 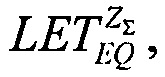 можно получить оценку, равную
можно получить оценку, равную 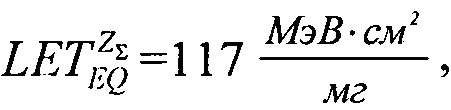 которая не является физически обоснованной в рамках определения функции FU(LET) и превышает значение
которая не является физически обоснованной в рамках определения функции FU(LET) и превышает значение 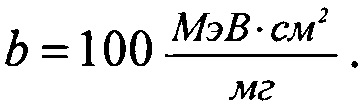 Поэтому принимают
Поэтому принимают 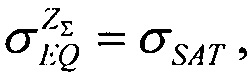
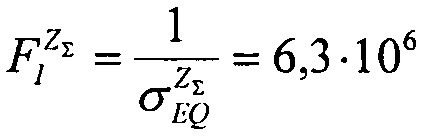 частиц, Δσ/σSAT (%)=0.
частиц, Δσ/σSAT (%)=0.
Третий критерий для таких исходных данных не применим, т.к. интенсивность потока выше, максимальной интенсивности, которую имеет смысл оценивать.
В качестве четвертого аддитивности для всех значений LET величины ресурса для равномерного закона распределения поперечного сечения сбоев SEE RU(LET) в виде (17) и для вейбулловского закона распределения RW(LET) в виде (18) принимают в качестве суммарной величины ресурса RΣ(LET) произведение ресурсов для равномерного закона распределения поперечного сечения сбоев SEE и закона распределения поперечного сечения сбоев SEE Вейбулла (19). В случае «суммарного» (кумулятивного) ресурса RΣ(LETTH)=RU(LETTH)⋅RW(LETTH) интегральную функцию распределения FΣ(LET) поперечных сечений SEE представляют в виде (25), которую относительно 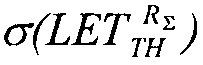 преобразуют в квадратное уравнение вида (26) ax2+bx+c=0, где
преобразуют в квадратное уравнение вида (26) ax2+bx+c=0, где 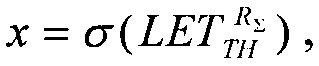 a=1,
a=1, 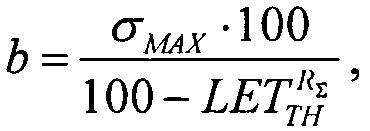
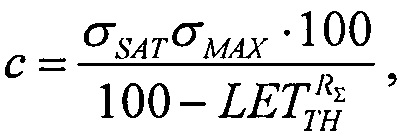 решая которое при подстановке экспериментально полученных данных
решая которое при подстановке экспериментально полученных данных 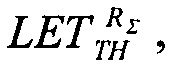 σSAT, σMAX получают значение
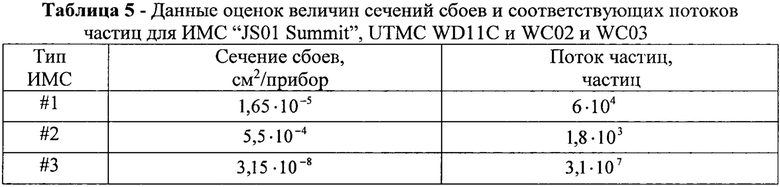
σSAT, σMAX получают значение 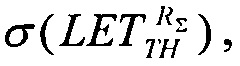 в то время как обратная величина позволяет определить минимальную величину потока частиц, достаточных для генерации SEE. В табл. 5 приведены данные оценок величин сечений сбоев и соответствующих потоков частиц для ИМС "JS01 Summit", UTMC WD11C и WC02 и WC03 (данные табл. 2).
в то время как обратная величина позволяет определить минимальную величину потока частиц, достаточных для генерации SEE. В табл. 5 приведены данные оценок величин сечений сбоев и соответствующих потоков частиц для ИМС "JS01 Summit", UTMC WD11C и WC02 и WC03 (данные табл. 2).
В качестве пятого критерия равными принимают интегральные функции распределения сбоев для вейбулловского и равномерного законов распределения 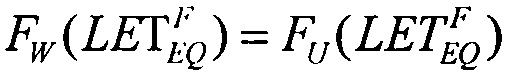 и определяют скорректированную пороговую величину линейных потерь энергии частиц (22), а затем определяют сечение сбоев и минимальное значение потока частиц.
и определяют скорректированную пороговую величину линейных потерь энергии частиц (22), а затем определяют сечение сбоев и минимальное значение потока частиц.
В табл. 6 приведены данные оценок величин сечений сбоев и соответствующего потока частиц 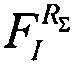 для ИМС "JS01 Summit", UTMC WD11C и WC02 и WC03 при определении суммарной интенсивности сбоев
для ИМС "JS01 Summit", UTMC WD11C и WC02 и WC03 при определении суммарной интенсивности сбоев

Для шестого критерия определяют скорректированный ресурс как произведение ресурсов для равномерного и вейбулловского законов распределения RΣ(LET)=RU(LET)⋅RW(LET), интегральную функцию распределения FΣ(LET) поперечных сечений SEE представляют в виде (25), которую относительно 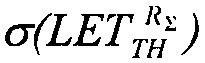 преобразуют в квадратное уравнение вида ax2+bx+c=0
преобразуют в квадратное уравнение вида ax2+bx+c=0
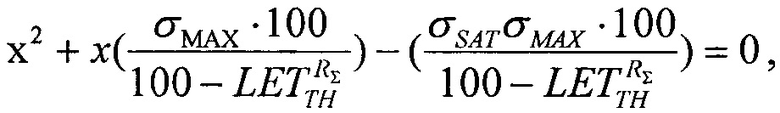
где 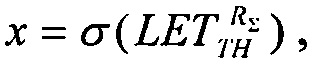 a=1,
a=1, 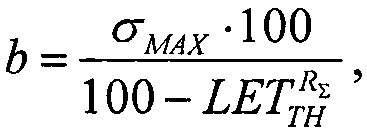
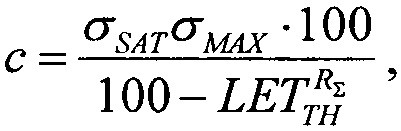 решая которое при подстановке экспериментально полученных данных
решая которое при подстановке экспериментально полученных данных 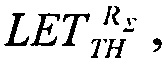 σSAT, σMAX получают значение
σSAT, σMAX получают значение 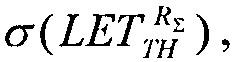 в то время как обратная величина позволяет определить минимальную величину потока частиц, достаточных для генерации SEE. В табл. 7 приведены данные оценок сечений сбоев и соответствующих потоков частиц для ИМС "JS01 Summit", UTMC WD11C и WC02 и WC03 при определении суммарной интенсивности сбоев
в то время как обратная величина позволяет определить минимальную величину потока частиц, достаточных для генерации SEE. В табл. 7 приведены данные оценок сечений сбоев и соответствующих потоков частиц для ИМС "JS01 Summit", UTMC WD11C и WC02 и WC03 при определении суммарной интенсивности сбоев

Для седьмого критерия непрерывности равными принимают значения ресурсов для равномерного закона распределения RU(LET) в виде (17) и для вейбулловского закона распределения в виде (18), а 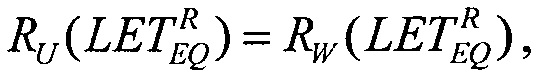 в котором для
в котором для 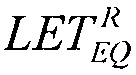 выполняется равенство ресурсов для равномерного и вейбулловского распределений, которое преобразуют в трансцендентное уравнение
выполняется равенство ресурсов для равномерного и вейбулловского распределений, которое преобразуют в трансцендентное уравнение 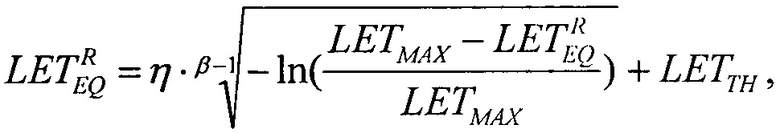 которое решают численными методами и находят значение
которое решают численными методами и находят значение 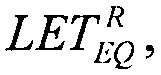 соответствующее значение
соответствующее значение 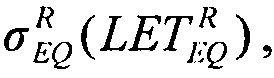 обратную величину
обратную величину 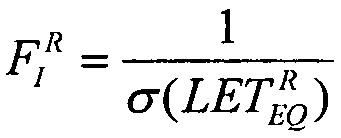 - минимального значения потока частиц, достаточных для генерации SEE. В табл. 8 приведены данные оценок величин сечений сбоев и соответствующих потоков частиц для ИМС "JS01 Summit", UTMC WD11C и WC02 и WC03.
- минимального значения потока частиц, достаточных для генерации SEE. В табл. 8 приведены данные оценок величин сечений сбоев и соответствующих потоков частиц для ИМС "JS01 Summit", UTMC WD11C и WC02 и WC03.

В зависимости от выбора критерия равенства: интенсивностей сбоев; комбинированной велиичны интенсивности сбоев «куммулятивной» функции распределения ресурса; равенства функций распределения ресурса; равенства интегральных функций рапределения поперечных сечений сбоев, по результатам экстракции параметров определяют соответствующие значения скорректированных значений пороговых величин линейной передачи энергии, интенсивностей сбоев, величин поперечных сечений, а обратные значения последних принимают равными минимальным значениям потоков частиц, достаточным для генерации SEE, из которых выбирают минимальное значение (табл. 3-табл. 8). В табл. 9 приведены результаты сравнения минимальных значений потоков частиц для всех рассмотренных критериев равенства показателей законов распределения сбоев для ИМС #1, #2 и #3 из табл. 3-табл. 8 и результаты оценки эффективности согласно /6/.
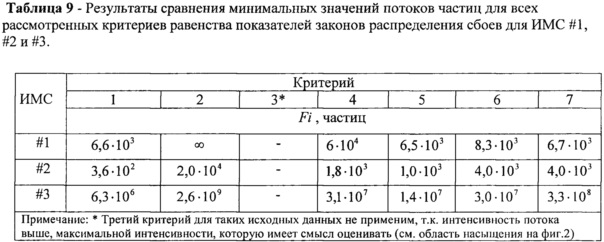
Как видно из таблицы 9, для ИМС #1 минимальное значение потока частиц, необходимое для возникновения эффектов SEE, выбираем по критерию 5; для ИМС #2 и #3 по критерию 1.
В результате реализации этого технического решения получен технический результат предлагаемого способа, состоящий в повышение точности определения характеристик зависимости поперечного сечения эффектов SEE от LET, а также определение минимального значения флюенса частиц FMIN, достаточного для генерации эффектов SEE в зависимости от выбранного критерия сопоставления предыстории реакции ИМС на воздействие сопутствующих выводу на орбиту ионизирующих излучений и эффектов SEE, сопровождающих пребывание космического аппарата на заданной орбите.
Литература
1. Benedetto J., Eaton P., Avery K., Mavis D., Gadlage M., Turdinger Т., Dodd P.E., Vizkelethy G. Heavy ion-induced digital single-event transient in deep submicron processes // IEEE Transactions on Nuclear Science, Dec. 2004. - Vol. 51. - No. 6. - P. 3480.
2. Martin Denton, European Organization for Nuclear Research. CERN Training, April 10-12, 2000 "Radiation effects on electronic componente and circuits for LHC", Radiation Effects on Electronic Component and Circuits, First course: Radiation Effects on Electronic Component; Second course: Radiation Effect on Electronics Circuits, CERN-EP-ATE/CEA Sacaly DAPHNIA, Internet.
3. Titus L., Johnson G.H., Schrimpf R.D., Galloway K.F. Single event burnout of power bipolar junction transistors // IEEE Transactions on Nuclear Science, 1991. - Vol. NS-38. - No. 6. - Pp. 1315-1322, 1991.
4. Edmonds L.D., Bames C.E., Scheick L.Z. Space Radiation Effects in Microelectronics. JPC Publikation 00-06 // Passadena, California: Jet Propulsion Laboratory, California Institute of Technology, National Aeronautics and Space Administration, May 2000.
5. Качемцев A.H., Киселев B.К., Торохов С.Л. «Способ испытаний полупроводниковых БИС технологии КМОП/КНД на стойкость к эффектам единичных сбоев от воздействия тяжелых заряженных частиц космического пространства» / Патент № RU 2495446 C2, с приоритетом от 17.10.2011, опубл. 10.10.2013, Бюл. №28.
6. Petersen E.L., Pouget V., Massengill L.W., Buchner S.P. and McCorrow D. Rate Predictions for Single-Event Effects - Critique II // IEEE Transactions on Nuclear Science, Dec. 2005. - Vol. NS-52. - No. 6. - Pp. 2158-2164.
7. Robinson P., Lee W., Aguero R., Gabriel S. Anomalies due to single event upsets // Journal of Spacecraft of Spacecraft and Rockets, Mar-Apr 1994. - Vol. 31. - No. 2. - Pp. 166-171.
8. LaBel, K. Single event effects specification // radhome.gsfc.nasa.gov/radhome/papers/seespec.htm, 1993. Last updated: Dr. Holbert's EEE460 Course, January 18, 2006.
9. Petersen E.L., Pickel J.C., Adams J.H., Jr., and Smith E.C. Rare predictions for single event effects - A critique // IEEE Transactions on Nuclear Science, Dec. 1992. - Vol. NS-39. - No. 6. - Pp. 1577-1599.
10. Messengill L.W., Alles M.L., Kerns S.E., and Jones K.L. Effects of process parameter distributions and ion strike locations on SEE cross-sections data // IEEE Transactions on Nuclear Science, Dec. 1993. - Vol. NS-40 / -No. 6. - Pp. 1804-1811.
11. Petersen E.L., Shapiro P., Adams J.H., and Burke E.A. The SEE Figure of merit and proton upset rate calculations // IEEE Transactions on Nuclear Science, Dec. 1995. - Vol. NS-42. - No. 6. - Pp. 2550-2562.
12. Petersen E.L., Langworthy J.B., and Diehl S.E. Suggested single even upset figure of merit // IEEE Transactions on Nuclear Science, Dec. 1983. - Vol. NS-30. - No. 6. - Pp. 4533-4539.
13. Petersen E.L., Pickel J.C., Smith E.C., Rudek P.J., and Letaw J.R. Geometical factors in SEE Rate Calculations // IEEE Transactions on Nuclear Science, Dec. 1993. - Vol. NS-40. - No. 6. - Pp. 1888-1909.
14. Petersen E.L. SEE rate calculations using the effective flux aPproach and generalized Fig. of merit aPproximation // IEEE Transactions on Nuclear Science, Dec. 1995. - Vol. NS-42. - No. 6. - Pp. 1995-2003.
15. Barak J., Reed R.A., and LaBel K.A. On the Fig. of merit model and SEE rate calculations // IEEE Transactions on Nuclear Science, Dec. 1999. - Vol. NS-46. - No. 6. - Pp. 1504-1510.
16. Edmonds L.D. Proton SEE cross-sections derived from hevy ion test data // IEEE Transactions on Nuclear Science, Oct. 2000. - Vol. NS-46. - No. 5. - Pp. 1713-1728.
17. Hiemstra D.M. and Blackmore E.W. LET spectra of proton energy levels from 50 to 500 MeV and their effectiveness for single event effects characterization of microelectronics // IEEE Transactions on Nuclear Science, Dec. 2002. - Vol. NS-50. - No. 6. - Pp. 2245-2250.
18. Normand E. Extension of the FOM method - Proton SEL and atmospheric neutron SEE // IEEE Transactions on Nuclear Science, Dec. 2004. - Vol. NS-51. - No. 6. - Pp. 3494-3504.
19. Petersen E.L., Shapiro P., Adams J.H., and Burke E.A. Calculation of cosmic-ray induced soft upsets and scaling in VLSI devices // IEEE Transactions on Nuclear Science, Dec. 1982. - Vol. NS-29. - No. 6. - Pp. 2055-2063.
20. Petersen E.L. Interpretation of heavy ion cross-section measurement // 11. Petersen E.L., Shapiro P., Adams J.H., and Burke E.A. The SEE Figure of merit and proton upset rate calculations // IEEE Transactions on Nuclear Science, Jun. 1996. - Vol. NS-43. - No. 3. - Pp. 952-959.
21. Petersen E.L. Predictions and observations of SEE rates in space // 11. Petersen E.L., Shapiro P., Adams J.H., and Burke E.A. The SEE Figure of merit and proton upset rate calculations // IEEE Transactions on Nuclear Science, Dec. 1997. - Vol. NS-44. - No. 6. - Pp. 2174-2187.
22. "Space Radiation Effects on Microelectronics", NASA Jet Propulsion].
23. Buchner S., Kang K., Krening D., Lannan G. and Schneiderwind R. Dependence of the SEE window of vulnerability of a logic circuit on magnitude of deposited charge // IEEE Transaction on Nuclear Science, Dec. 1993. - Vol. NS-40. - No. 6. - Pp. 1853-1857.
24. Buchner S., Howard Jr. J., Poivey C., McMorrow D., Peace R.L. Pulsed-laser testing methodology for single event transients in linear devices // IEEE Transactions on Nuclear Science, Dec. 2004. - Vol. 51. - No. 6. - Pp. 3716-3722.
25. Huhtinen M. and Faccio F. Computational method to estimate single event upset rates in an accelerator environment / CERN, http://www.cern.ch/Atlas/GROUPS/FRONTEND/WWW/SEE.pdf.NIM A450 (2000) 155.
ПОЯСНЯЮЩИЕ МАТЕРИАЛЫ
ПРИЛОЖЕНИЕ «A»: ЛИНЕАРИЗАЦИЯ ЗАКОНА РАСПРЕДЕЛЕНИЯ ВЕЙБУЛЛА
При задании ФР Вейбулла в форме (11) функция «ресурса» может быть представлена с учетом (3) в виде
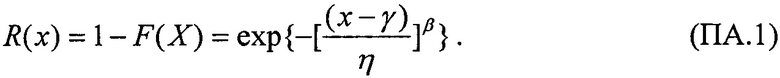
Натуральный логарифм «ресурса» имеет вид:

С использованием свойств натурального логарифма преобразуем (ПА2) в виде:

Взятие двойного логарифма от (ПА3) преобразует равенство в виде:
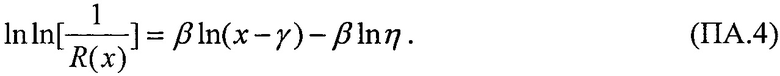
Введем в (ПА4) новые обозначения:

После этих преобразований соотношение (ПА.1) сведено к линейному виду:

На Фиг. ПА1 приведена линеаризированная функция распределения Вейбулла в виде (ПА.6) в координатах (Y,Z).
Если принять значение величины Z=ln(х-γ)=0, то значение функции Y(Z)=B=-βlnη. Из наклона прямой Y(Z)=AZ+В определяют параметр формы
β=A=arctgϕ, где угол ϕ определяет степень наклона прямой к оси Z. Тогда значение параметра формы определиться из равенства

При этом значение случайной величины х=γ, т.е. параметру положения.
На Фиг. ПА.2 показана деформация исходного распределения 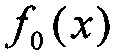 радиационно-критического параметра (РКП) при ступенчатом изменении внешней радиационной нагрузки (Envirimental Stress (ES)) (n=1, 2, 3…). Показаны также смещения математического ожидания μ(x) и дисперсии σ(х) и левой и правой границ областей изменения РКП. Так как и математическое ожидание μ(x)=Е(х), так и дисперсия D(x)=σ(х) являются с одной стороны функцией
радиационно-критического параметра (РКП) при ступенчатом изменении внешней радиационной нагрузки (Envirimental Stress (ES)) (n=1, 2, 3…). Показаны также смещения математического ожидания μ(x) и дисперсии σ(х) и левой и правой границ областей изменения РКП. Так как и математическое ожидание μ(x)=Е(х), так и дисперсия D(x)=σ(х) являются с одной стороны функцией 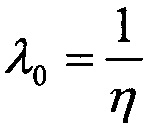 и параметра формы m, то рост как параметра масштаба η, так и параметра формы m приводит к асимметричной деформации исходной плотности распределения
и параметра формы m, то рост как параметра масштаба η, так и параметра формы m приводит к асимметричной деформации исходной плотности распределения 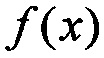 при увеличении радиационной нагрузки к левому крылу распределения, как это демонстрирует график на фиг. ПА2.
при увеличении радиационной нагрузки к левому крылу распределения, как это демонстрирует график на фиг. ПА2.
Значения случайной величины (х-γ), интегральной вероятности F(x), функции Y(x) в точках, близких к местам пересечения зависимости Y=AZ+В осей Y и Z приведены в табл. ПА.1.

Метод выбора критериев отказа реализуется следующим образом:
1) в качестве интегральной функции распределения F(x) случайной величины выбирают ее относительное изменение 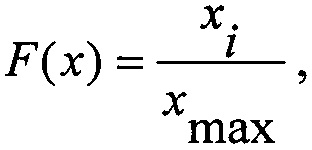 где xi - значения контролируемой величины на i-м шаге (уровне) физического воздействия, а xmax - ее максимальное значение на полигоне измерений. Эта величина должна быть ограничена «снизу» на уровне
где xi - значения контролируемой величины на i-м шаге (уровне) физического воздействия, а xmax - ее максимальное значение на полигоне измерений. Эта величина должна быть ограничена «снизу» на уровне 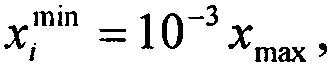 а «сверху» - на уровне
а «сверху» - на уровне 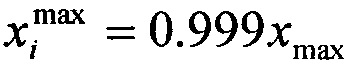 для возможности линеаризации теоретического закона распределения (см. данные табл. ПА.1);
для возможности линеаризации теоретического закона распределения (см. данные табл. ПА.1);
2) в качестве теоретического закона распределения принят закон распределения Вейбулла, который характерен для описания процессов, характеризующийся деградацией (повышением внутренней энтропии);
3) производят измерения независимых выборок с изменением уровня физической нагрузки ES, по крайней мере, при двух уровнях ES, если этой нагрузкой, как в нашем примере является величина плотности потока частиц КП или LET частиц, или при одном или нескольких уровнях ES, если нагрузкой является доза ИИ или флюенс частиц;
4) определяют параметры распределения Вейбулла путем линеаризации;
5) подставляют в соотношение (10) исходное значение плотности функции Вейбулла с найденными значениями параметров γ, η, β и ΔR для соответствующих уровней нагрузки ES (включая «нулевой», т.е. исходное состояние);
6) численными методами определяют зависимость параметра β и η от нагрузки ES;
7) используя соотношение (ПА.3), определяют изменение относительной величины ΔF(z, η, β)=1-ΔR(z, η, β) где 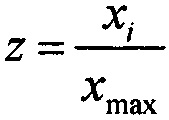 на прогнозируемый уровень нагрузки.
на прогнозируемый уровень нагрузки.
На Фиг. ПА.3 показано примерное изменение интенсивности параметрического отказа объекта исследования при деградационных процессах от уровня воздействия физической нагрузки.
ПРИЛОЖЕНИЕ «Б»: РАДИАЦИОННЫЕ ЭФФЕКТЫ В ИМС ОТ ОТДЕЛЬНЫХ ЯДЕРНЫХ ЧАСТИЦ
Космическое излучение может являться источником ИИ высоких энергий. Первичное ИИ КП разделяют на галактическое космическое излучение (ГКИ) и солнечное космическое излучение (СКИ), отдельно выделяют солнечный ветер (СВ) и радиационные пояса Земли (РПЗ), искусственные (ИРПЗ) и естественные (ЕРПЗ).
Появление ГКИ в окрестностях Солнечной системы происходит следующим образом. Частицы с очень большой энергией покидают звездную материю. Это могут быть не только легкие, но и тяжелые, возникающие в результате термоядерного синтеза элементы. Они мигрируют из пространства с высокой плотностью в окружающее межзвездное пространство. Часть ионов попадает в мощные электромагнитные поля, существующие в КП, и ускоряется до сверхвысоких энергий, после чего покидает область взаимодействия с этими полями. Эти частицы мигрируют в КП и частично долетают в околосолнечное пространство. Особенно большие потоки частиц возникают при взрыве сверхновых звезд. Далее эти частицы взаимодействуют с ядрами атомов воздуха. Они имеют очень высокую энергию, до 1018 эВ. ГКИ изотропно распределено в пространстве и приходит в околоземное пространство со всех направлений. На Фиг. ПБ.1 показан энергетический спектр ГКИ.
СКИ излучение возникает из-за хромосферных вспышек. В состав СКИ входят многие элементы, но их интенсивность резко падает с увеличением атомного номера. Максимальная энергия обычно составляет несколько сот МэВ, но при мощных вспышках достигает значений 1-20 ГэВ. В результате извержений в хромосфере ускоряются протоны и альфа-частицы вплоть до энергий 109 эВ. Плотность потока излучения зависит от уровня солнечной активности. Так, в годы высокой активности число вспышек достигает десяти, а в годы малой активности - одна или даже ни одной. Увеличение солнечной активности наблюдается периодически, примерно 1 раз в 10 лет, и плотность потоак частиц в такие годы возрастает по сравнению с обычной на 2-4 порядка. Наибольшая плотность потока была зафиксирована после вспышки 4 августа 1972 года, 7⋅104 част/(см2⋅с⋅стеррад) для энергий, больших чем 107 эВ. Солнечное космическое излучение состоит в основном из протонов, причем наблюдаются протоны с энергией около 50 ГэВ с плотностью потока 2⋅106 час(см2⋅с⋅стеррадр), а протоны с энергией в интервале от 10 до 100 МэВ до 109 част/(см2⋅с⋅стеррад).
Солнечный ветер представляет собой поток плазмы солнечной короны в пространство. Это в основном протоны и электроны, а также в небольшом количестве ядра гелия и ионы кислорода, кремния, серы, железа. Составляющие солнечный ветер заряженные частицы движутся по спиралеобразным траекториям в магнитном поле Солнца, которое к тому же вращается.
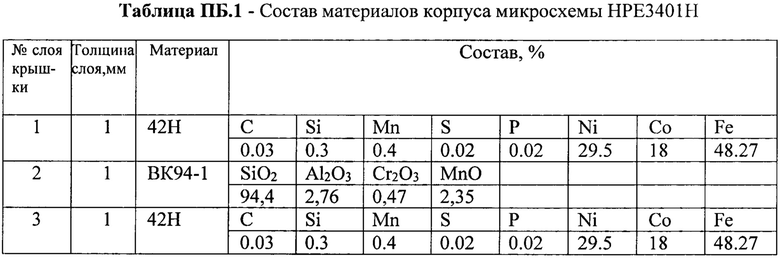
Заряженные частицы (протоны, электроны, альфа-частицы и ионы или ядра тяжелых элементов), захватываемые и удерживаемые в течение длительного времени магнитным полем Земли, образуют радиационные пояса Земли (РПЗ). РПЗ подразделяются на естественные (ЕРПЗ) и искусственные (ИРПЗ). Они являются составляющими ГКИ, СКИ, солнечного ветра, а также это вторичные частицы, возникающие в результате взаимодействия первичного излучения с атмосферой Земли. Эти частицы попадают в магнитные ловушки и под действием силы Лоренца движутся по спиральной траектории по меридианам. Так, протон с энергией 100 МэВ имеет период колебаний 0,3 с, а время его удержания в ловушке составляет 100 лет. Радиационные пояса дрейфуют по долготе. Различают внешний и внутренний ЕРПЗ, причем энергия частиц во внутреннем поясе больше, так как там больше и магнитное поле. На фиг. ПБ.2 и ПБ.3 показаны спектры протонов и электронов. Видно, что на высоте 10000 км энергия протонов может достигать 100 МэВ, а у поверхности - 40 МэВ с плотностью потока 107 част/см2⋅с /ПБ.1]. Так как космическое излучение изотропно во всех направлениях, такие протоны могут проникать сквозь оконное стекло, воздух комнаты и взаимодействовать с корпусом микросхемы. Для широкого класса микросхем используются металлокерамические корпуса. Крышка корпуса микросхемы НРЕ3401Н, например, представляет собой слой сплава 42Н, слой керамики ВК94-1, слой сплава 42Н, каждый слой толщиной 1 мм. Состав сплава 42Н и керамики ВК94-1 приведен в табл. ПБ.1. Пространство между крышкой и поверхностью схемы заполнено аргоном при нормальном давлении. Расстояние от крышки корпуса до поверхности схемы равно 0,5 мм.
Протон, налетая на корпус микросхемы, может взаимодействовать с материалом корпуса. Например, может произойти захват протона атомами Fe, Co, Ni, Mn, Cr, в результате образуются нестабильные изотопы, которые могут распадаться с образованием альфа-частиц. Атомы материала схемы, выбитые альфа-частицами, образуют кластеры, размер которых может оказаться сравним с размерами активных областей приборов. Для моделирования таких процессов была использована программа, аналогичная TRIM-95, работающая с использованием метода Монте-Карло.
Крышка корпуса толщиной 3 мм состояла из трех слоев: 1 - сплав 42Н толщиной 1 мм, 2 - керамика ВК94-1 толщиной 1 мм, 3 - сплав 42Н толщиной 1 мм. Расстояние от крышки корпуса до поверхности схемы 1 мм, среда заполнена аргоном. Рассматривается взаимодействие протонов с материалом корпуса последовательно в одной точке нормально к поверхности корпуса.
Расчет проводился в следующей последовательности.
1. Протоны с энергией 40 МэВ налетали на металлокерамический корпус ИМС;
2. Образовавшиеся в результате взаимодействия протонов и Co60 нижнего слоя крышки корпуса ИМС α-частицы пролетают слой Ar, заполняющий пространство между крышкой корпуса и рабочей поверхностью схемы;
3. Взаимодействие пролетевших через аргон α-частиц с защитным окислом и металлизацией схемы;
4. Взаимодействие атомов Si, выбитых из нижнего слоя SiO2, с приборным слоем.
На Фиг. ПБ.1 представлены проекции треков в плоскости XZ: а) протонов после прохождения ими металлокерамического корпуса ИМС; б) α-частиц, образовавшихся в результате взаимодействия протонов и 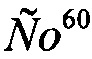 в Ar; в) α-частиц, преодолевших пространство от корпуса до рабочей поверхности схемы; г) Si, выбитого из слоев SiO2 схемы α-частцами и достигшего приборного слоя.
в Ar; в) α-частиц, преодолевших пространство от корпуса до рабочей поверхности схемы; г) Si, выбитого из слоев SiO2 схемы α-частцами и достигшего приборного слоя.
Плотность потока падающего излучения 107 част/см2⋅с, что при площади поверности корпуса 100 мкм2 означает, что за 1 с на поверхность корпуса может попасть около 10 протонов с энергией 40 МэВ.
При расчете считалось, что протоны падают последовательно в одну точку корпуса, а α-частицы образуются в нижнем слое, т.е. в сплаве 42Н. и все рассматривавшиеся протоны вызвали появление α-частиц. Следует отметить, что по мере пересечения пространства крышки корпуса и инертного газа частицы практически изотропно распределяются и по поверхности схемы. Таким образом, в результате взаимодействия с 5000 протонов образуется 5000 α-частиц, и поверхности схемы достигает 4356 α-частиц с энергией порядка 20 МэВ. Далее оценивалось количество атомов Si, выбитых их нижнего слоя SiO2, их энергии и направления движения. На следующем этапе по результатам расчета, взятых из файла данных Collision, рассчитывалось количество выбитых атомов, попавших в приборный слой и оценивались средние размеры кластеров радиационных дефектов (КРД), образовавшихся в результате такого взаимодействия. При оценке размеров КРД считалось, что кластер образуют частицы, расстояние между которыми менее 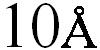 . Не рассматривалось влияние атомов кислорода, который тоже может быть выбит из нижнего слоя SiO2.
. Не рассматривалось влияние атомов кислорода, который тоже может быть выбит из нижнего слоя SiO2.
Таким образом, в результате моделирования было получено, что сами α-частицы попадают в приборный слой с вероятностью 0,06, плотность их распределения в приборном слое 38 частиц/мкм2⋅с, а образующиеся КРД достигать размеров 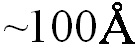 хотя бы в одном направлении.
хотя бы в одном направлении.
На Фиг. ПБ.2 представлены энергетические потери на ионизацию для всех этапов расчета.
Энергетические потери на ионизацию составили 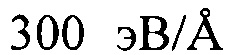 в Si и
в Si и 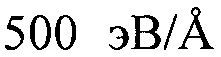 в сапфире.
в сапфире.
Впервые на практике с радиационными эффектами в ИМС от SEE столкнулись при анализе случайных ошибок в динамических оперативных запоминающих устройств (ОЗУ) /ПБ.1/. Оказалось, что потеря отдельных информационных битов в динамических ОЗУ связана с ионизационными потерями от отдельных α-частиц из-за естественной радиоактивности конструкционных материалов, α-частицы, попадая в 40 ячеек памяти, стирают информационный заряд на запоминающих конденсаторах. В дальнейшем были обнаружены новые эффекты (сбои и отказы) от SEE частиц практически во всех типах ИМС.
Наиболее остро данная проблема встала перед ИМС, используемыми в электронной аппаратуре КА. Применение БИС и СБИС в бортовой электронной аппаратуре КА приводит к возникновению периодических отказов и сбоев в них из-за воздействия протонов и ионов РПЗ, 14 февраля 1996 г. в геостационарном спутнике GOES-8 (США) было обнаружено 4 сбоя в узле ОЗУ системы управления ориентацией /ПБ.2/. Количество сбоев существенно увеличивается в момент солнечных вспышек, так одна из самых больших солнечных вспышек была зафиксирована в октябре 1989 г., которая привела к функциональным отказам многих бортовых систем КА. Использование КМОП ИС с высокой чувствительность к эффекту защелкивания от отдельных ядерных частиц приводит в ряде случаев к полной потере КА. Так, КА ESA ERS-1, запущенный в 1991 г., просуществовал всего 5 дней из-за выхода из строя источников питания вследствие резкого возрастания тока потребления из-за эффекта защелкивания в используемых КМОП ОЗУ NEC 64.
Впервые о возможности существования эффектов от SEE, которые потенциально могут ограничить степень интеграции микросхем, было указано в работах /ПБ.3, ПБ.4/. первое упоминание о возможности появления сбоев в цифровых устройствах электронной аппаратуры КА было в 1985 году.
Анализ достигнутых результатов позволяет заметить, что они соответствуют мировому уровню в части исследований эффектов объемной ионизации от SEE в цифровых ИС. Более того, работы по моделированию отказов ИМС из-за структурных повреждений и дозовых эффектов появились ранее, чем аналогичные работы на Западе.
Появление «неожиданных» сигналов как кратковременных, так и за счет изменения отдельных разрядов информации в ряде случаев может привести к "зависанию" всей электронной системы, выход из которого возможен только с использованием специальной процедуры.
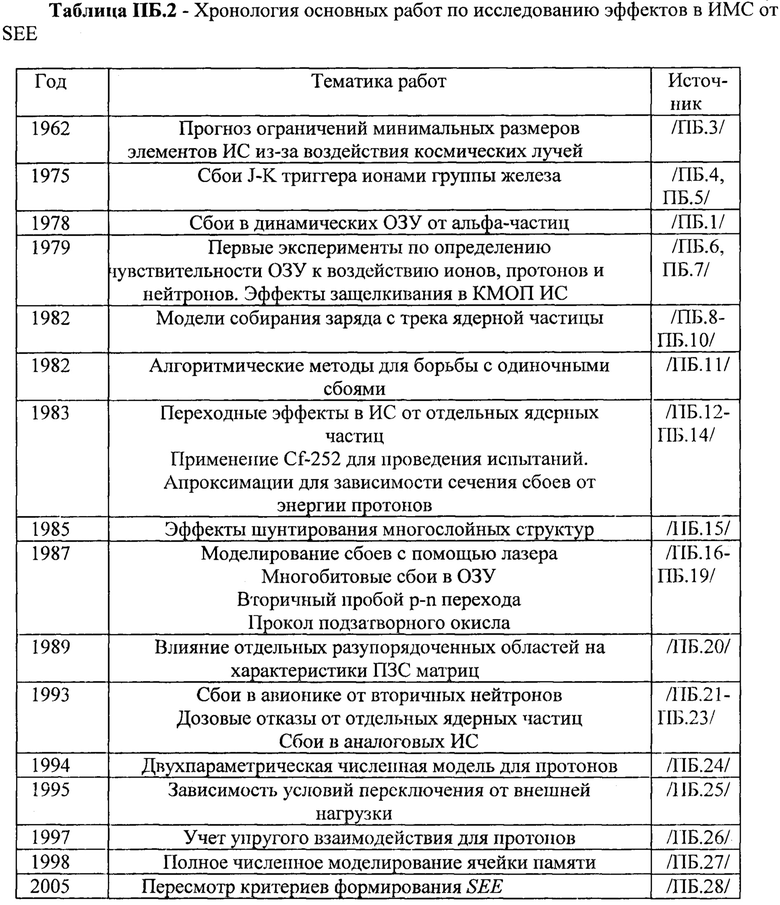
Литература к «ПРИЛОЖЕНИЮ «Б»»
ПБ.1. May Т.С. Woods М.Н. New Physical Mechanism for Soft Errors in Dynamic Memories. - Proc. Reliability Phys, Symp. 1978, p. 2-7.
ПБ.2. Ritter J.C. Spacecraft anomalies and future trends. - 1996 IEEE NSREC IEEE Nucl. and Space Radiation Conference. Short Course. Indian Wells, California, 1998. P. I-1-I-52.
ПБ.3. Wallmark J.T., Marcus S.M. Minimum size and maximum packing density of non-redudant semiconductor devices. - IRE Proc., 1962, v. 50, p. 286-291.
ПБ.4. Устойчивое к радиации статическое оперативное запоминающее устройство с низким напряжением питания ядра http://kit-e.ru/redirect.php?link=http://www.baesystems.com/ProductsServices/bae_prod_eis_monolithic16Bsram.html.
ПБ.5. Сравнение радиационной стойкости FLASH и SRAM-микросхем - http://kit-e.ru/redirect.php?link=http://wvvw.actel.com/products/solutions/ser/.
ПБ.6. Guenzer C.S., Wolicki E.A., Alias R.G. Single event upset of dynamic RAMs by neutrons and protons. - IEEE Trans. On Nucl. Sci. 1979, v. NS-26, №6, p. 5048-5051.
ПБ.7. Benedetto J.M., Eaton P.H., Mavis D.G., Gadlage M., Turfinger T. Digital Single Evet Trasient Trends With Technology Node Scaling // IEEE Transaction on Nuclear Science, Dec. 2006. - Vol. 53. - No. 6. - Pp. 3462-3465.
ПБ.8. Benedetto J.M., Eaton P.H., Mavis D.J., Gadlage M. and Turflinger T. Variation of digital SET pulse widths and the implications for single event hardening of advanced CMOS processes // IEEE Trans. Nucl. Sci., Dec. 2005. - Vol. NS-52. No. 6. - Pp. 2114-2119.
ПБ.9. J. Benedetto J., P. Eaton P., K. Avery K., D. Mavis D., M. Gadlage M., and T. Turflinger T. Heavy ion induced digital single-event transients in deep submicron processes // IEEE Trans. Nucl. Sci., Dec. 2004. - Vol. NS-51. No. 6. - Pp. 3480-3485. [ПБ.10]. Eaton P., Benedetto J., Mavis D., Avery K., Sibley M., Gadlage M., and Turflinger T. Single event transient pulse width measurements using a variable temporal latch technique // IEEE Trans. Nucl. Sci., Dec. 2004. - Vol. NS-51. - No. 6. - Pp. 3365-3368.
ПБ.10. Campbell A.B. Upsets in error detection and correction integrated circuits. IEEE Transactions on Nuclear Scince, 1982, NS-29, №6, p. 2076-2081.
ПБ.11. Diehl S.E., et al. Considerations for single event immune VLSI logic. IEEE Transactions on Nuclear Scince, 1985, NS-30, №6, p. 4501-4506.
ПБ.12. Stephen J.H., et al. Cosmic ray simulation experiments for the study of single event upsets and latch - up in CMOS memories. IEEE Transactions on Nuclear Scince, 1983, NS-30, №6, p. 4464-4469.
ПБ.13. Bendel W.L., Petersen E.L. Proton Upsets in Orbit. - IEEE Transactions on Nuclear Scince, 1983, NS-30, №6, p. 4115-4120.
ПБ.14. Buecher S.P., et al. Laser simulation of singke event upsets. - IEEE Transactions on Nuclear Scince, 1985, NS-32, №6, p. 1228-1234.
ПБ.15. Hohl J.H., Galloway K.F. Analytical model for the single event burnout of power MOSFETs - IEEE Transactions on Nuclear Scince, 1987, NS-34, №6, p. 1275-1282.
ПБ.16. Wrobel T.F. On heavy ign induced hard-errors in dielectric structers. - IEEE Transactions on Nuclear Scince, 1987, NS-34, №6, p. 1262-1268.
ПБ.17. Martin R.C., et al. The size effect et ion charge tracks on single event multiplr - bit upset. - IEEE Transactions on Nuclear Scince, 1987, NS-34, №6, p. 1305-1311.
ПБ.18. Агаханян T.M., Аствацатурьян E.P., Скоробогатов П.К., Чумаков А.И. Радиационная стойкость интегральных микросхем. - Микроэлектроника, 1980, т. 9, №3, с. 195-201.
ПБ.19. Аствацатурьян Е.Р., Големинов Н.Г., Крамер-Агеев Е.А., Чумаков А.И. Особенности появления сбоев в элементах БИС под действием ионизирующего излучения. - СЭ. Серия 3. Микроэлектроника, 1981, вып. 2(39), с. 55-58.
ПБ.20. Аствацатурьян Е.Р., Големинов Н.Г., Крамер-Агеев Е.А., Чумаков А.И. Влияние статистического характера взаимодействия ионизирующего излучения с веществом на катастрофические отказы элементов БИС. - СЭ. Серия 3. Микроэлектроника, 1981, вып. 2(39), с. 59-63.
ПБ.21. Агаханян Т.М., Аствацатурьян Е.Р., Чумаков А.И. Особенности использования БИС и сверхБИС в аппаратуре ядерного физического эксперимента. - Электронные приборы и схемы для экспериментальной физики / Под ред. Т.М. Агаханяна. - М.: Энергоатомиздат, 1983, с. 3-9.
ПБ.22. Агаханян Т.М., Аствацатурьян Е.Р., Скоробогатов П.К, Чумаков А.И. Физические ограничения на стойкость биполярных полупроводниковых структур в ИМС повышенной степени интеграции к дестабилизирующим воздействиям. Микроэлектроника, 1984, т. 13, вып. 5, с. 389-396.
ПБ.23. Adell Р.С., Schrimpf R.D., Holmas W.T., Boch J., Stacey J., Ribero P., Sternberg A., Galloway K.F. Total-dose and single-event effects in DC/DC converter control circuitry // IEEE Transactions on Nuclear Science, Dec. 2003. - Vol. 50. - No. 6. - Pp. 1867-1872.
ПБ.24. Adel P.C., Schrimpf R.D., Choi B.K., Holmas W.T., Attwood J.P., Cirba C.R., Galloway K.F. Total-dose and single-event effects in switching DC/DC power converter // IEEE Transactions on Nuclear Science, Dec. 2003. - Vol. 49. - No. 6. - Pp. 3217-3221.
ПБ.25. Buchner S., McMorrow D., Sternberg A.L., Massenagill L., Peace R.L., Maher M. Single-event transical characterization of as LM119 voltage comparator: As aPproach to SET model validation using a pulsed laser // IEEE Transactions on Nuclear Science, Jun. 2002. - Vol. 49. - No. 3. - Pp. 1502-1508.
ПБ.26. Buchner S., Howard Jr. J., Poivey C., McMorrow D., Peace R.L. Pulsed-laser testing methodology for single event transients in linear devices // IEEE Transactions on Nuclear Science, Dec. 2004. - Vol. 51. - No. 6. - Pp. 3716-3722.
ПБ.27. Peace R.L., Sternberg A.L., Boulghassoul Y., Massengill L.W., Bushner S., McMorow D., Walsh D.S., Hash G.L., LaLumondiere S.D., Moss S.C. Comparison of SETs in bipolar linear circuits generated with a ion micro beam, laser light and circuits simulation // IEEE Transactions on Nuclear Science, Dec. 2002. - Vol. 49. - No. 6. - Pp. 3163-3170.
ПБ.28. Petersen E.L., Pouget V., Massengill L.W., Buchner S.P. and McCorrow D. Rate Predictions for Single-Event Effects - Critique II // IEEE Transactions on Nuclear Science, Dec. 2005. - Vol. NS-52. - No. 6. - Pp. 2158-2164.
ПРИЛОЖЕНИЕ «В»: ОБОСНОВАНИЕ ВИДА ЗАВИСИМОСТИ ПОПЕРЕЧНОГО СЕЧЕНИЯ СБОЕВ ОТ ЕДИНИЧНЫХ ЧАСТИЦ ОТ ВЕЛИЧИНЫ ЛИНЕЙНОЙ ПЕРЕДАЧИ ЭНЕРГИИ LET
Для решения задачи о попадании ТЗЧ в чувствительный объем (ЧО) транзисторной структуры (ТС) необходимо рассматривать вероятность попаданий в заданный объем в функции от числа попаданий

где x - число взаимодействий частиц с объемом заданной величины; λ - интенсивность попаданий; Q - нормировочный множитель; FI - поток частиц (ионов).
Нормировка, выполненная при х=1 и FI=10-7 частиц⋅см-2 дает значение константы в законе распределения Q=2,425⋅10-21 см2⋅частиц-1
В общем случае для реализации единичного сбоя следует выполнить условие

где V - объем, в котором выделяется энергия частицы, приводящая к эффекту единичного сбоя (SEE);
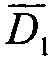 - средняя по чувствительному объему энергия (поглощенная доза), приводящая к (SEE);
- средняя по чувствительному объему энергия (поглощенная доза), приводящая к (SEE);
D - полная доза, выделенная в чувствительном объеме при пролете частицы;
ξ - радиационно-критический параметр.
Микродозиметрический подход позволяет исследовать общие закономерности эффектов единичных сбоев, он не в состоянии дать достаточно корректный прогноз для реальных БИС в заданных условиях облучения, ограничиваясь лишь вероятностным представлением для описания единичных сбоев.
Увеличение флуктуаций величины радиационного эффекта в объеме V, связанных с актами единичного энерговыделения от отдельных частиц, можно представить в виде двух физических процессов:
- непрерывное поглощение энергии;
- порционное (распределение энергии по совокупности элементов).
В качестве системы однотипных элементов приведем пример больших интегральных схем (БИС) на основе базовых матричных кристаллов (БМК), а также БИС с регулярной структурой (например, запоминающие устройства (ЗУ) с размерной организацией записи/считывания).
Для большого числа событий плотность вероятности образования кластера при взаимодействии нейтрона с чувствительным объемом может быть задана распределением Вейбулла, характерным для описания процессов с нарастающей деградацией. Тогда плотность вероятности образования n эффектов SEE будет равна
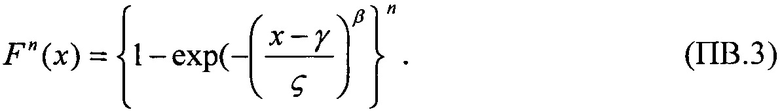
Накопление SEE следует рассматривать в виде случайного процесса с интенсивностью λ(FI, z), где FI - флюенс частиц, z - реальное энерговыделение в ЧО V. Приращение числа отказов Δe можно ввести соотношением

В свою очередь, интенсивность процесса накопления SEE пропорциональна числу элементов в структуре, чувствительность которых к этому виду отказов является функцией флюенса частиц и энергии, выделившейся в объеме V

Начальное количество чувствительных к выделенной энергии элементов равно ϕ(z). Тогда изменение во времени числа элементов будет определяться соотношением
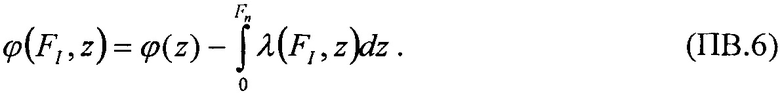
Подставляя (ПВ.5) в (ПВ.6), можно получить
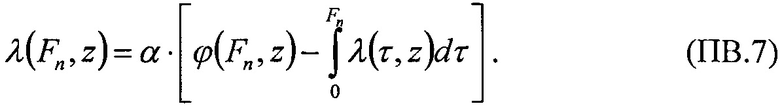
Равенству (ПВ.7) удовлетворяет решение для интенсивности отказов в виде
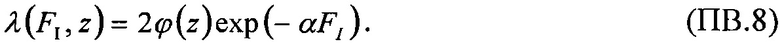
Интегрируя Δe(FI) по флюенсу частиц, получим
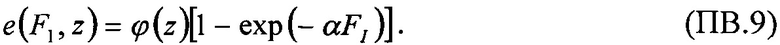
Откуда следует, что при достаточно большом FI число SEE, вызванных единичными частицами, стремится к числу элементов в структуре, в которых выделилась энергия определенной величины. Соответственно, для малых значений флюенса число сбившихся элементов определяется только малой долей от числа элементов, в которых реализовалось критическое энерговыделение.
Рассмотрим подробнее указанное обстоятельство.
Выделенная энергия распределена по совокупности элементов и может быть определена функцией ς, которую необходимо ввести в (ПВ.9)
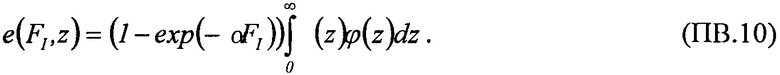
Здесь ϕ(z) имеет смысл распределения элементов по выделившейся в них энергии, а ς(z), по сути, означает число взаимодействий, в которых реализовано энерговыделение (z, z+dz).
Начальное количество чувствительных к выделенной энергии элементов равно ϕ(z)
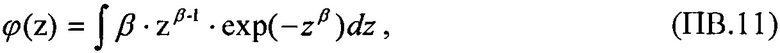
где β - параметр формы распределения Вейбулла, β=2 для редких взаимодействий закон Пуассона), β=4 для большого числа событий (закон Гаусса). Интегрирование ведется от 0 до максимального значения передачи энергии в спектре LET.
Функцию ς(z) можно переобозначить
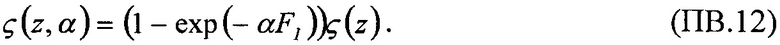
Тогда

Равенство (ПВ.13) характерно для описания количественно малых эффектов. Величина g(z, α, FI) - вероятность того, что пролетающая через объем V частица выделяет энергию в пределах (z, z+dz). Если акты взаимодействия есть достаточно редкие события, то в качестве функции распределения энергии можно ввести функцию, основанную на законе Пуассона
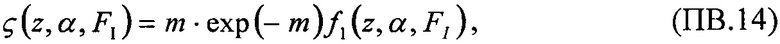
здесь m - число событий, т.е. пересечений частицей ЧО V, 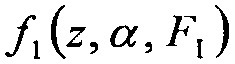 - плотность вероятности того, что частица передает энергию в пределах ЧО объема, или энергетический спектр частицы на входе в ЧО в случае, если пробег атома смещения не превышает линейного размера области V.
- плотность вероятности того, что частица передает энергию в пределах ЧО объема, или энергетический спектр частицы на входе в ЧО в случае, если пробег атома смещения не превышает линейного размера области V.
Назовем 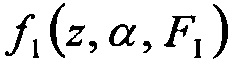 - спектром одиночного события. Функцию (ПВ.14) можно для малого числа m привести к виду
- спектром одиночного события. Функцию (ПВ.14) можно для малого числа m привести к виду
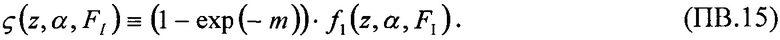
Здесь m имеет смысл среднего числа взаимодействий в ЧО в единицу времени. Для малого m (m<<1) получим
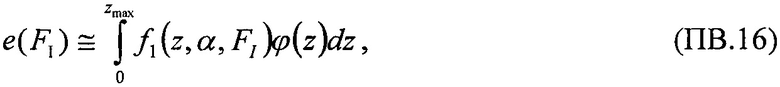
т.е. частота образования SEE (интенсивность) определяется вероятностью реализации в спектре одиночного события в определенном числе элементов критического значения энергии z*.
Это означает, что при малом флюенсе частиц, когда SEE достаточно редки, увеличение числа актов выделения критической энергии в критическом объеме, или увеличение вероятности сбоев пропорционально дозе поглощенного излучения (флюенсу частиц).
Вот почему на участке изменения LET 0<LET<LETTH корректна аппроксимация зависимости 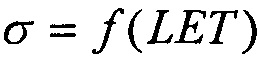 интегральной функцией равномерного распределения FU(LET).
интегральной функцией равномерного распределения FU(LET).
При большом числе событий соотношения (ПВ.15) и (ПВ.16) не корректны, т.к. нельзя точно указать, при каком взаимодействии произошел сбой. Определенно можно говорить, что это событие произошло бы с ростом энерговыделения и числа событий, т.е. пересечений ЧО частицей, а следования и ориентация выделенного направления в кластере по траектории минимальной длины.
Для большого числа событий изменение во времени числа элементов будет определяться соотношением

Можно ввести среднее число событий для энергетического спектра (z, zmax)
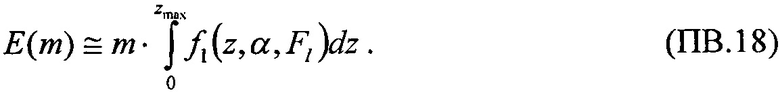
Если в процессе взаимодействия реализуется хотя бы SEE, то (ПВ.18) можно представить в виде
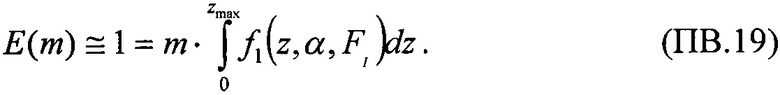
Это возможно при m→∝ и z→∝, если принять эти условия, то функция распределения в (ПВ.14) должна иметь вид дельта-функции δ(zmax). В этом случае соотношение (ПВ.19) можно представить в виде

В результате получается, что наступает насыщение при больших флюенсах и число повреждений не зависит от флюенса частиц. Оно определяется только плотностью распределения максимальной энергии zmax по элементам регулярной структуры.
Следствием этого являются:
1. С ростом числа элементов структуры число повреждений возрастает.
2. Для конкретной компановки БИС существует предельная энергия zc. ниже которой SEE не реализуются. Если в спектре zc>zmax, то эффект не реализуется. Так как процесс накопления повреждений есть случайный процесс, при анализе корреляции не рассматриваем.
При zc<<zmax распределение ϕ(z) можно представить в виде δ-функции, а при росте числа однотипных элементов n величина e(FI) согласно (ПВ.9) неограниченно возрастает.
3. Рост степени интеграции увеличивает вероятность повреждения единичной частицей. В этом случае из (ПВ.9) следует

так как закон Пуассона здесь не применим. Учитывая смысл величины α как среднего числа повреждений на единицу флюенса частиц, ЧО V, легко понять, что α связана с флюенсом частиц FI и при его росте

Для "счетного" режима (m<<1) из (ПВ.10), (ПВ.15), (ПВ.19) получим
 4VA
4VA
Если в пределах области выделившейся энергии в соответствии с распределением ς(z, α, FI) имеются слабые флюктуации энерговыделения, то при достаточно большом спектре одиночных событий

Равенство (ПВ.21) указывает на то, что не все элементы из совокупности n могут иметь эффект SEE. Если «сбился» лишь один элемент из n, то ϕ(zC)=1 (ПВ.23) и (ПВ.24) совпадают.
Отсюда следует, что при малых значениях флюенса FI при zC≈zmax существует зависимость e(FI) от флюенса (косвенно от m).
Если

то для m=α⋅FI сбоев/(частиц⋅см-2) при e(FI)=0,63 событий/(частиц⋅см-2) (событие - это выделение в ЧО критической энергии zC) и α=1 частица-1⋅см2, т.е. FI=1/m=1/1=1 частиц⋅см-2. Для α=10 частица-1⋅см2 FI=10-1 частиц⋅см-2. Для α=107 частица-1⋅см2 получится характерное значение флюенса частиц FI=10-7 частиц⋅см-2.
Если плотность треков частиц составляет ϕT(FI), то при топологическом размере чувствительного элемента БИС L×L вероятность попадания частицы в площадку размером L×L составляет

Для технологии 3 мкм и ϕT(FI)=1 трек⋅см-2/(частиц⋅см-2) PS=9⋅(10-8-10-9). При этом использована модель «площадки»: флюенс частиц падает нормально к планарной транзисторной структуре.
Если интерес представляет интенсивность отказов в одной ячейке e(FI)=1 сбой/(частиц⋅см-2) при α=107 частица-1⋅см2 этому значению соответствует величина плотности треков частиц ϕT(FI)=1 трек/(частиц⋅см-2) для реальных условий (одна частица создает один трек), что дает величину флюенса FI=10-7 частиц⋅см-2. Увеличение степени интеграции n приводит к снижению величины достаточного флюенса в n раз и росту интенсивности отказов

где e1(FI)=1 сбой/(частиц⋅см-2).
В случае насыщения можно использовать следующее суммарное соотношение для одной структуры
e(FI)≈1 сбой/(частиц⋅см-2)=α=107 частиц-1⋅см2~10-7 частиц⋅см-2
Для КМОП БИС на основе БМК за параметр 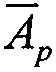 принимаем среднюю площадь
принимаем среднюю площадь

при  - длине кристалла, b - ширине кристалла, h - высоте кристалла. Тогда средний размер кристалла
- длине кристалла, b - ширине кристалла, h - высоте кристалла. Тогда средний размер кристалла 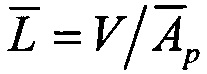 где V - объем ЧО.
где V - объем ЧО.
Можно ввести число поврежденных структур на единицу флюенса, или так называемое сечение SEE σSEU
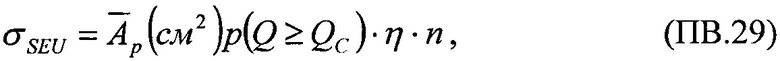
где p(Q>QC) - вероятность того, что размер собранного заряда превысит критическую величину в ЧО, достаточную для появления эффекта SEE, η - степень использования базовых элементов БИС БМК, n - число вентилей на кристалл.
Для оценки флюенса, приводящего к единичному сбою ТС, необходимо использовать «сечение сбоев»

При облучении материалов, входящих в состав БИС технологии МОП, возникает комплекс ионизационных эффектов, связанных с особенностями энергорвыделения, интенсивности, различием спектральных и энергетических характеристик ионизирующего излучения и параметрам облучаемой БИС. Сюда, к последним, следует отнести: степень интеграции, технологические характеристики, электрофизические характеристики. Например, при интеграции 10-103 мкм-3 при облучении тяжелыми частицами, энергия которых выше 1-10 МэВ, энерговыделение носит неравновесный характер, т.е. отношение приращения энергии к пороговой ΔE/E0≥1. В случае больших объемов такие частицы наряду с другими видами ионизирующего излучения (рентгеновское, гамма- и электронное излучение) создают в объеме ИС равновесное энерговыделение. Причем считается, что γ-кванты и высокоэнергетические электроны (Ee≥1 МэВ) создаюют однородное энерговыделение, т.е. ΔE/E0<<1, d(ΔE)/dx≈0, а при рентгеновском и низкоэнергетическом электронном излучениях может возникнуть необходимость учета неоднородности распределения энергии по объему образца, т.е.

ПРИЛОЖЕНИЕ «Г»: ЗАВИСИМОСТЬ ПОПЕРЕЧНОГО СЕЧЕНИЯ ЭФФЕКТОВ SEE/SEE ОТ ЛИНЕЙНЫХ ПОТЕРЬ ЭНЕРГИИ LET ТЯЖЕЛЫХ ЗАРЯЖЕННЫХ
Особая ситуация при построении графиков зависимости поперечного сечения эффектов SEE/SEE от линейных потерь энергии LET при исследовании чувствительности БИС/СБИС к факторам космического пространства (КП), в частности к воздействию тяжелых заряженных частиц (ТЗЧ), или тяжелых ионов, складывается вблизи порогового значения LETTH, соответствующего накоплению критического заряда QC в пределах чувствительного объема (ЧО) исследуемого прибора.
Причина этого обстоятельства состоит в том, что, во-первых, помимо эффектов SEE/SEE возможно присутствие дополнительных эффектов, таких как сбор заряда из смежных ТС при пересечении частицей нескольких структур, эффект MBU (передачи энергии через кросс-соединения), ионизация от атмосферных нейтронов при прохождении аппаратуры в составе КА активного участка разгонной траектории, и т.п.
Особенность дополнительных соображений на этот счет состоит в том, что даже в отсутствии прямого воздействия ионизирующих излучений (ИИ), именно в лабораторных условиях - «лежа на столе» БИС/СБИС подвергается воздействию космических ливней, воздействию атмосферных нейтронов, протонов и т.п. Таким образом, на зависимости поперечного сечения от величины LET значение поперечного сечения σTH при значении LETTH не равно нулю.
Исходя из этого можно сделать ряд следующих допущений:
1) при LET<LETTH величина поперечного сечения эффектов SEE/SEE не равна нулю;
2) зависимость поперечного сечения сбоев σ от величины LET в диапазоне изменения последней 0<LET<LETTH подчиняется равномерному закону распределения случайной величины;
3) величина возможного изменения спектра величин линейной передачи энергии LET ограничена сверху значением 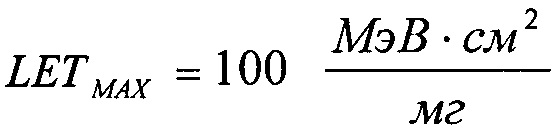 (при значении которой исключается необходимость исследования зависимости поперечного сечения);
(при значении которой исключается необходимость исследования зависимости поперечного сечения);
4) в диапазоне изменения 0<LET<LETTH величина вероятности случайного отказа Fd(LET) остается неизменной в среднем величиной (не учитываются все возможные вариации интенсивности ионизирующей способности ИИ КП на уровне Земли).
В силу сделанных предположений зависимость поперечного сечения от величины линейной передачи энергии можно ввести на участке 0<LET<LETMAX может быть введена дифференциальной функцией распределения (pdf) в виде
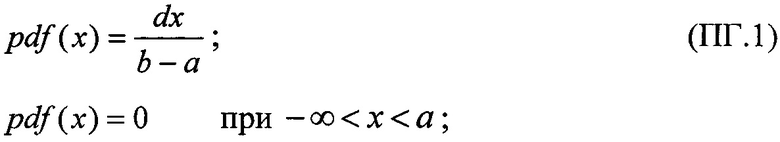
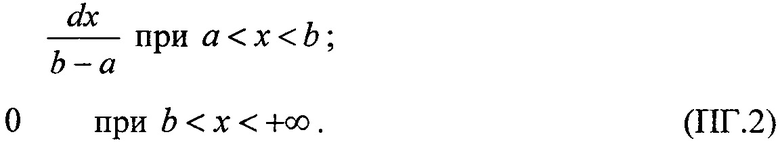
Интегральная функция равномерного распределения
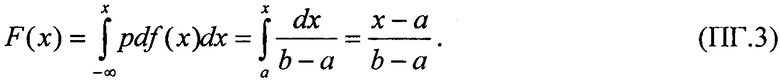
Интенсивность параметрического отказа в общем виде определяется для произвольного распределения случайной величины соотношением

где такая форма записи определяет относительное изменение ресурса по отношению к его значению для заданной случайной величины x. Связь между ресурсом R(x) (вероятностью сохранения работоспособности) и вероятностью ее отказа F(x) определяется простым соотношением
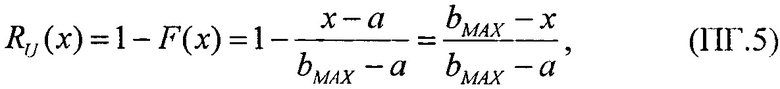
Так как для равномерного распределения первая производная от ресурса равна

то интенсивность отказа может быть определена для этого распределения в виде
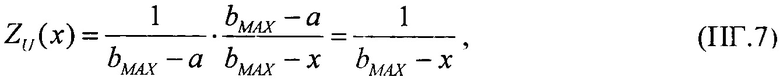
Известно, что для распределения Вейбулла, которое является основной аппроксимацией зависимости поперечного сечения эффектов SEE/SEE от линейных потерь энергии, интенсивность отказов может быть определена соотношением

Следствие 1: Суммарная интенсивность сбоев.
Суммарная интенсивность отказов на всем интервале изменений значения линейных потерь энергии может быть определена как сумма аддитивных интенсивностей
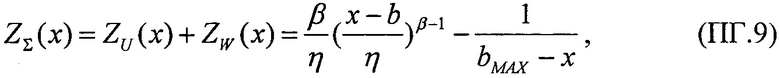
При х=LET, b=LETMAX комбинированная величина интенсивности отказа может быть определена в виде
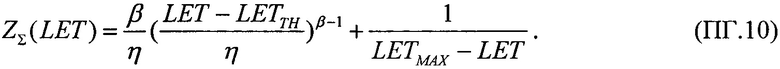
Так как суммарная величина ресурса равна произведению ресурсов для равномерного распределения и распределения Вейбулла

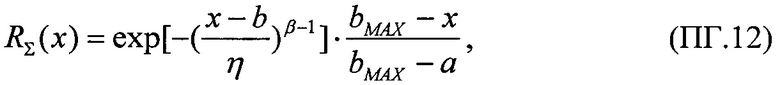
При a=0, x=LET, b=LETTH (12), 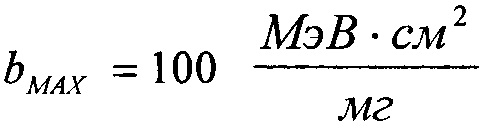 при LET=0 суммарный ресурс равен
при LET=0 суммарный ресурс равен

т.к. функция Вейбулла равна нулю на интервале 0<LET<LETTH, а функция равномерного распределения на этом интервале отлична от нуля и равна максимальному значению 1 при отсутствии воздействия частиц ИИ (LET=0).
Следствие 2: Зависимость 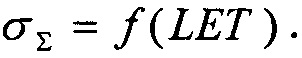
Если говорить о зависимости 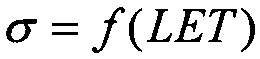 на всем интервале изменения линейной передачи энергии, то
на всем интервале изменения линейной передачи энергии, то
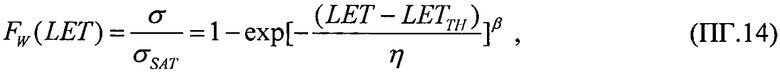
которую можно линеаризировать к виду (ПА.4)-(ПА.6) (Приложение «Л»)
Y=AX+B,
где
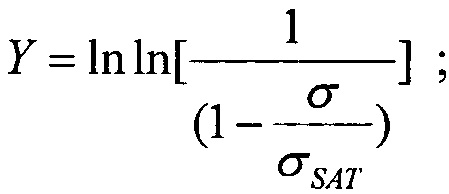
X=ln(LET-LETTH);
A=β;
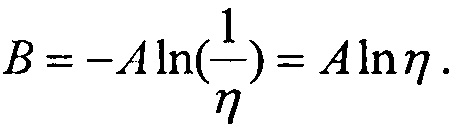
Ту же величину для равномерного распределения можно представить вместо (ПГ.5) в виде
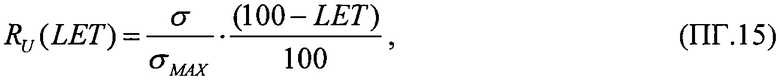
где 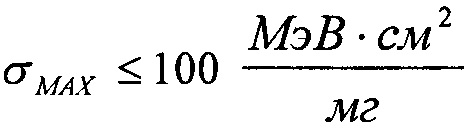 (см. табл. 1).
(см. табл. 1).
Суммарное («кумулятивное») значение функции ресурса для представления зависимости 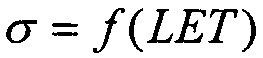 будет равно
будет равно
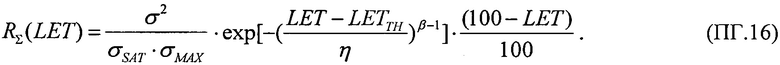
Тогда
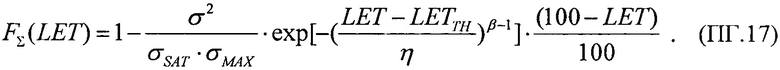
Это соотношение также можно представить в виде линейной функции вида (ИГ.6), где
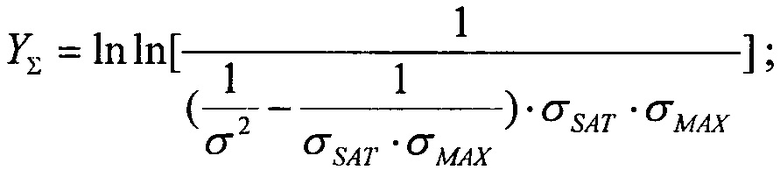
X=ln(LET-LETTH)+ln(100-LET);
A=(β-1);
B=A⋅lnη+ln(100).
Поскольку 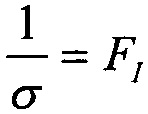 флюенсу частиц, то
флюенсу частиц, то 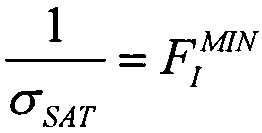 - соответствует минимальному флюенсу частиц, а
- соответствует минимальному флюенсу частиц, а 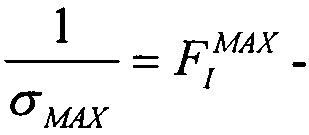
При LET=LETTH величина (ПГ.12) равна максимальному флюенсу частиц для условий «приземного» воздействия. В точке LETTH (ПГ.12)
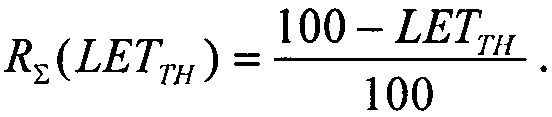
Следствие 3: Равенство ресурсов 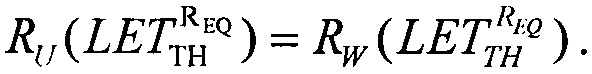
В точке 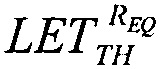 должно выполняется равенство
должно выполняется равенство 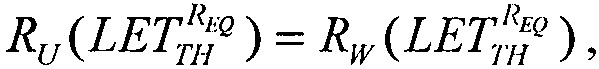 что позволяет записать с учетом (ПГ.5) и (ПГ.8) соотношение
что позволяет записать с учетом (ПГ.5) и (ПГ.8) соотношение
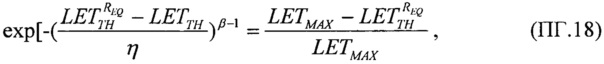
После процедуры логарифмирования по основанию натурального логарифма получим
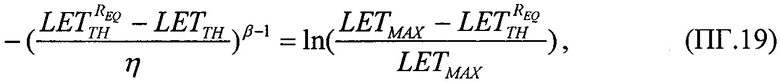
После ряда несложных преобразований (ПГ.19) преобразуется в
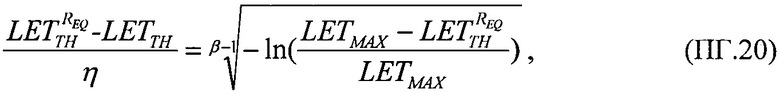
Наконец,
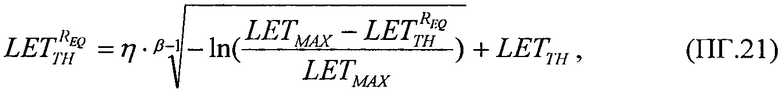
При 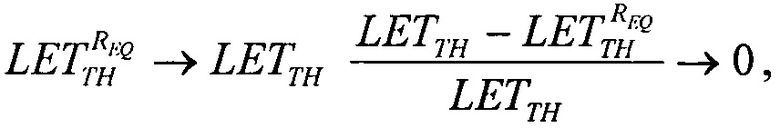 ln(~0)→0,
ln(~0)→0, 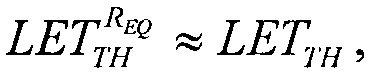 а величина интенсивности для равномерного распределения равна
а величина интенсивности для равномерного распределения равна
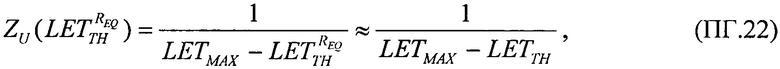
При β=1 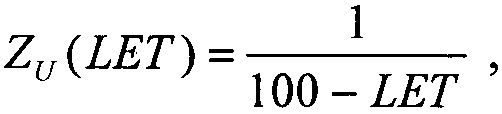 а
а 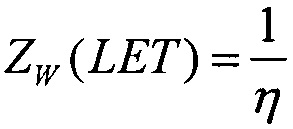 из (ПГ.8).
из (ПГ.8).
Тогда
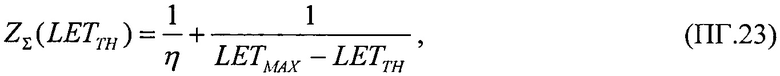
Таким образом, интенсивность отказов в этом случае обратно пропорциональна величине η и смещена на аддитивную постоянную величину 1/(LETMAX-LETTH). При 0<LET<LETTH первое слагаемое по определению равно нулю, если распределение FW определено в границах LETTH<LET<∝. При экспонециальном распределении также 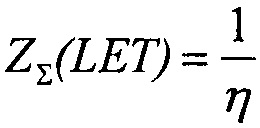 и ZΣ(LETTH) соответствует (ПГ.23). При определении распределения FE в границах 0<LET<∝ при LET=0 из (ПГ.10) получим интенсивность суммарного распределения FU+FE
и ZΣ(LETTH) соответствует (ПГ.23). При определении распределения FE в границах 0<LET<∝ при LET=0 из (ПГ.10) получим интенсивность суммарного распределения FU+FE

Следствие 4: Равенство распределений поперечных сечений сбоев 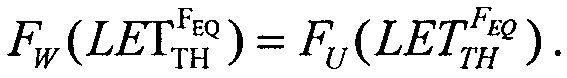
В точке 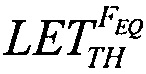 может выполняться равенство распределений поперечного сечения
может выполняться равенство распределений поперечного сечения
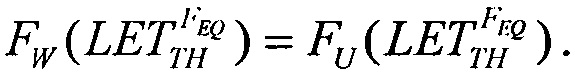 Тогда выполняется соотношение
Тогда выполняется соотношение
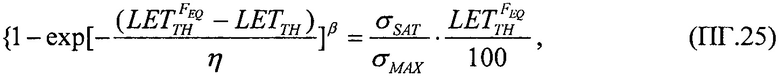
которое после ряда преобразований можно привести к виду
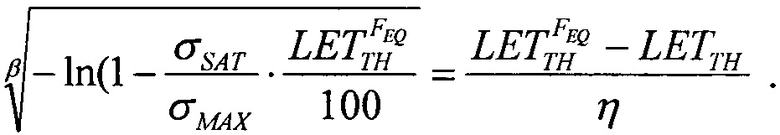
В асимптотике 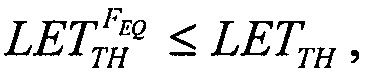 для их близких величин можно считать
для их близких величин можно считать 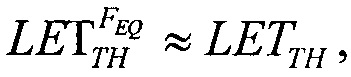 тогда
тогда
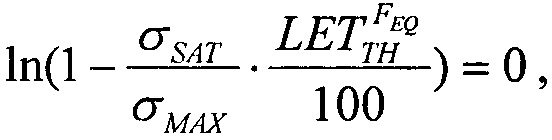
тогда 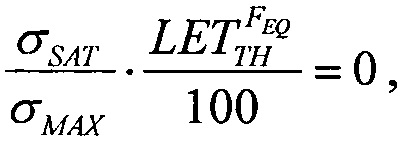 что дает единственное значение
что дает единственное значение 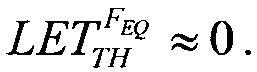
Для интенсивности отказов при 10% воздействии солнечного ветра можно использовать соотношение

где R - интенсивность SEE в единицах [сбой/(бит-день)]. σSAT - поперечное сечение насыщения SEE в [мкм2], a LETTH - пороговое значение LET в единицах [пКл/мкм].
Для большинства практических случаев интенсивность отказов в (ПГ.26) может быть определена с использованием аппроксимирующего выражения для σSAT=ab, (a, b>c) a - длина, b - ширина и c - толщина ЧО ТС в [мкм], L - топологический размер, в [мкм]
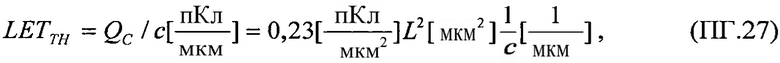
Приведенное соотношение применимо для многих приложений. Это соотношение допускает разброс в оценке добротности (FOM) с величиной до 5 раз и поправочным коэффициентом в 3,5 для приборов на GaAs.
В случае суммарной интенсивности (I) SEE (ПГ.9) при 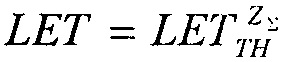 из (ПГ.10) следует при определении FW в интервале LETTH<LET<∝
из (ПГ.10) следует при определении FW в интервале LETTH<LET<∝
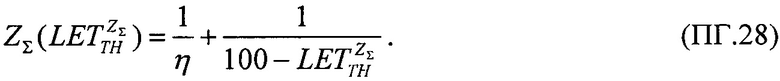
С другой стороны, функция распределения поперечных сечений сбоев в этом случае равна
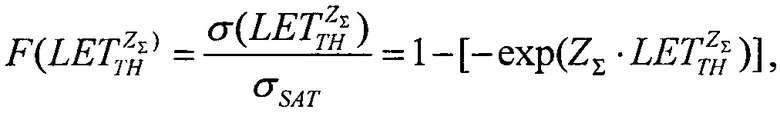
которую, следуя процедуре линеаризации (Приложение «А»), можно преобразовать к виду
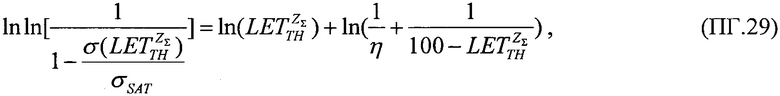
линейного соотношения Y=X+В, где
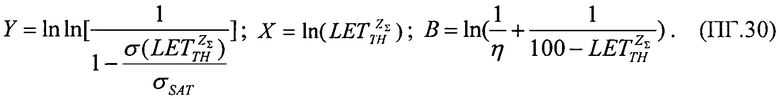
При применении численных методов решения (ПГ.28) выходными данными являются 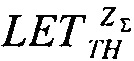 и
и 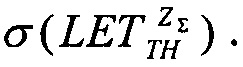 Величина
Величина 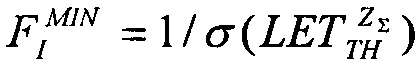 - минимальный поток частиц, достаточный для генерации SEE. Подставляя соответствующие значения
- минимальный поток частиц, достаточный для генерации SEE. Подставляя соответствующие значения 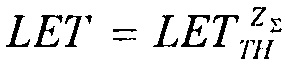 и σSAT в (ПГ.26) можно оценить интенсивность сбоев. Пусть Y=0 в (ПГ.30), отсюда
и σSAT в (ПГ.26) можно оценить интенсивность сбоев. Пусть Y=0 в (ПГ.30), отсюда

где обозначено для упрощения 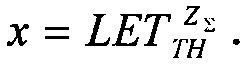 Равенство (ПГ.31) можно преобразовать к виду квадратного уравнения ax2+bx+c=0
Равенство (ПГ.31) можно преобразовать к виду квадратного уравнения ax2+bx+c=0
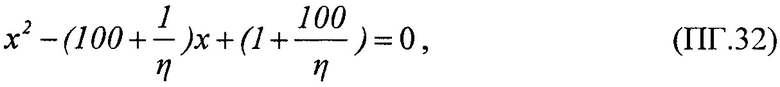
где a=1, 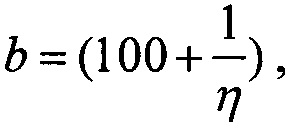
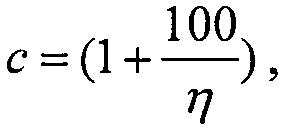 решение которого имеет вид
решение которого имеет вид

Подстановка в (ПГ.32) ряда значений параметра масштаба 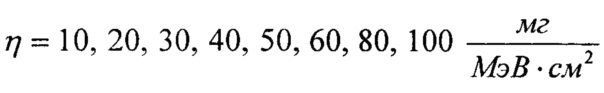 дает два практически не зависящих от величины η корня уравнения: x1=0,02…0,06 и х2=99,94…99,99, что позволяет утверждать, что поперечное сечение SEE может принимать значение 0,63 σSAT либо при очень круто восходящей зависимости
дает два практически не зависящих от величины η корня уравнения: x1=0,02…0,06 и х2=99,94…99,99, что позволяет утверждать, что поперечное сечение SEE может принимать значение 0,63 σSAT либо при очень круто восходящей зависимости 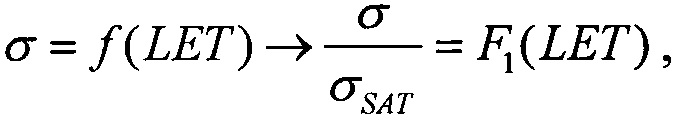 либо при пологой
либо при пологой 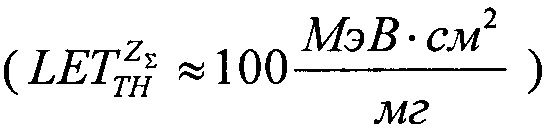 (Фиг. ПГ.1).
(Фиг. ПГ.1).
В случае «суммарного» (кумулятивного) ресурса (II) (ПГ.16) интегральную функцию распределения поперечных сечений SEE представляют в виде (ПГ.17), разрешая которую относительно 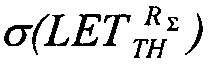 можно также получить квадратное уравнение вида ax2+bx+c=0
можно также получить квадратное уравнение вида ax2+bx+c=0
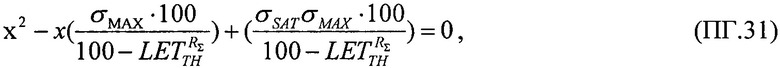
где 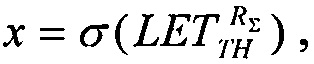 a=1,
a=1, 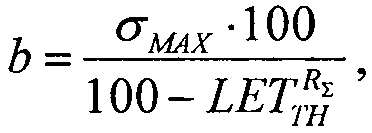
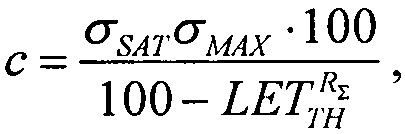 решение которого дается также в виде (ПГ.31). Подставляя экспериментально полученные данные
решение которого дается также в виде (ПГ.31). Подставляя экспериментально полученные данные 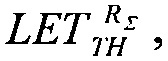 σSAT, σMAX можно определить значение
σSAT, σMAX можно определить значение 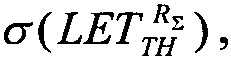 а величина обратная позволяет определить минимальную величину потока частиц, достаточных для генерации SEE.
а величина обратная позволяет определить минимальную величину потока частиц, достаточных для генерации SEE.
В случае равных ресурсов (III) (ПГ.18) величина 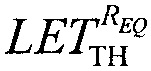 определяется (ПГ.21), при этом
определяется (ПГ.21), при этом 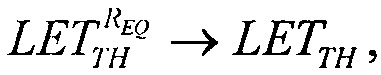 а
а 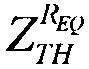 определяется (ПГ.23).
определяется (ПГ.23).
В случае равных интегральных распределений поперечных сечений сбоев (IV) выполняют соотношение (ПГ.25) откуда следует 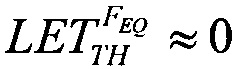 при определении FW(LET) в диапазоне 0<LET<∝.
при определении FW(LET) в диапазоне 0<LET<∝.
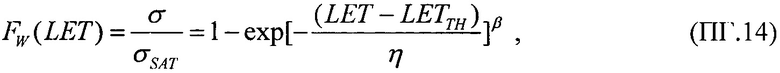
которую можно линеаризировать к виду (Приложение «А»)
Y=AX+B,
где
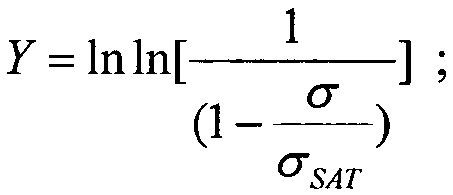
X=ln(LET-LETTH);
A=β;
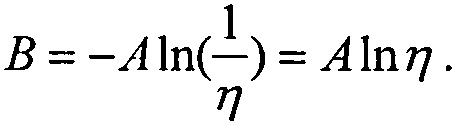
Ту же величину для равномерного распределения можно представить вместо (ПГ.5) в виде
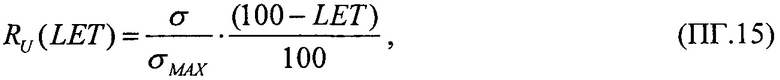
где 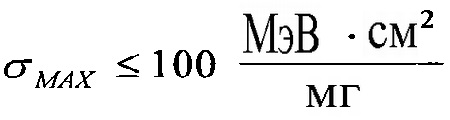 (см. табл. 1).
(см. табл. 1).
Суммарное («кумулятивное») значение функции ресурса для представления зависимости 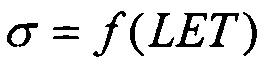 будет равно
будет равно
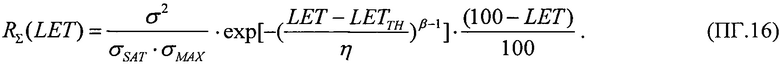
Тогда,
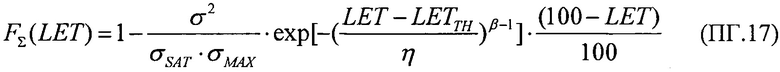
Это соотношение также можно представить в виде линейной функции вида (ПА.4), где
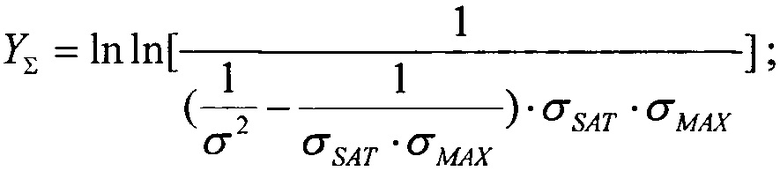
X=ln(LET-LETTH)+ln(100-LET);
A=(β-1);
B=A⋅lnη+ln(100).
Поскольку 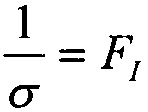 флюенсу частиц, то
флюенсу частиц, то 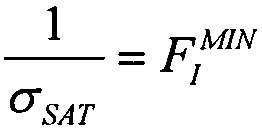 - соответствует минимальному флюенсу частиц, а
- соответствует минимальному флюенсу частиц, а 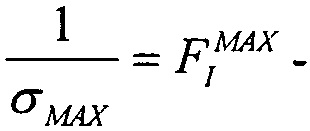
При LET=LETTH величина (ПГ.12) равна максимальному флюенсу частиц для условий «приземного» воздействия. В точке LETTH (ПГ.12)
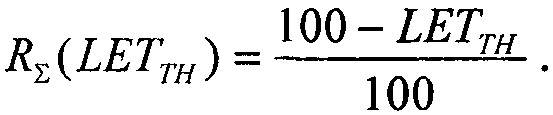
Следствие 3: Равенство ресурсов 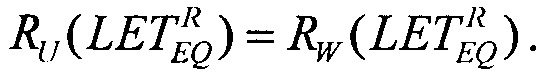
В точке 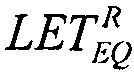 должно выполняется равенство
должно выполняется равенство 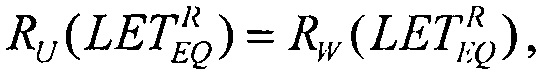 что позволяет записать с учетом (ПГ.5) и (ПГ.8) соотношение
что позволяет записать с учетом (ПГ.5) и (ПГ.8) соотношение
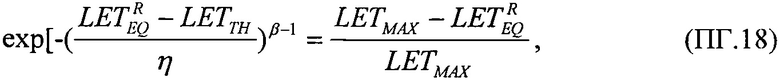
После процедуры логарифмирования по основанию натурального логарифма получим
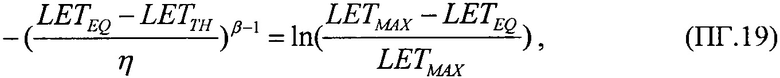
После ряда несложных преобразований (ПГ. 19) преобразуется в
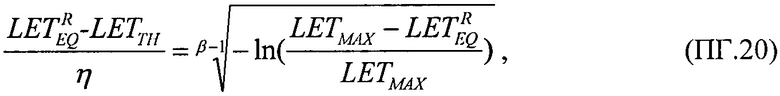
Наконец,
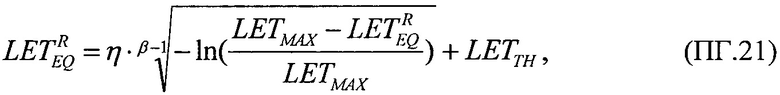
При 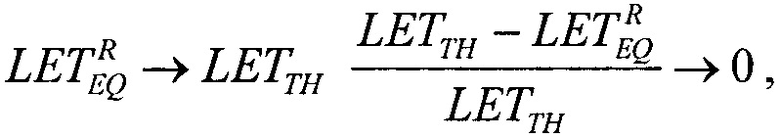 ln(~0)→0,
ln(~0)→0, 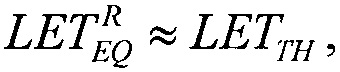 а величина интенсивности для равномерного распределения равна
а величина интенсивности для равномерного распределения равна
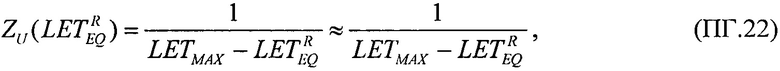
При β=1 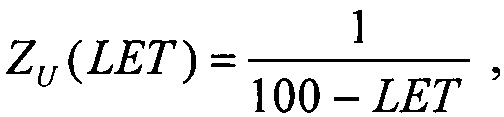 а
а 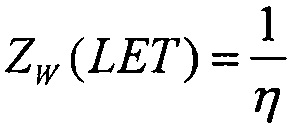 из (ПГ.8).
из (ПГ.8).
Тогда
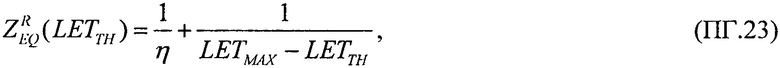
Таким образом, интенсивность отказов в этом случае обратно пропорциональна величине η и смещена на аддитивную постоянную величину 1/(LETMAX-LETTH). При 0<LET<LETTH первое слагаемое по определению равно нулю, если распределение FW определено в границах LETTH<LET<∝. При экспонециальном распределении также 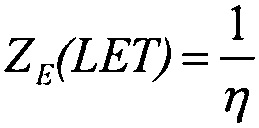 и ZΣ(LETTH) соответствует (ПГ.23). При определении распределения FE в границах 0<LET<∝ при LET=0 из (ПГ.10) получают интенсивность суммарного распределения FU∩FE
и ZΣ(LETTH) соответствует (ПГ.23). При определении распределения FE в границах 0<LET<∝ при LET=0 из (ПГ.10) получают интенсивность суммарного распределения FU∩FE

Следствие 4: Равенство распределений сбоев 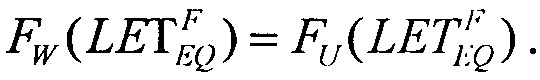
В точке 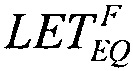 может выполняться равенство распределений поперечного сечения
может выполняться равенство распределений поперечного сечения
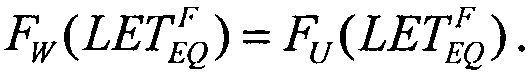 Тогда выполняется соотношение
Тогда выполняется соотношение
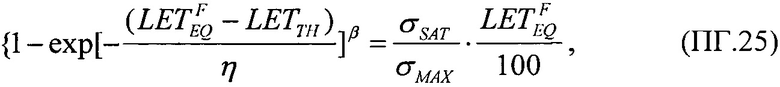
которое после ряда преобразований приводят к виду
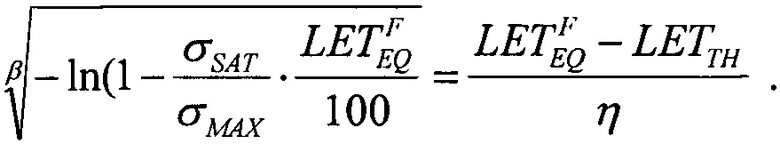
В асимптотике 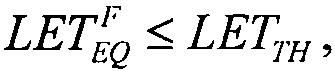 для их близких величин можно считать
для их близких величин можно считать 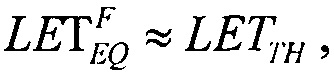 тогда
тогда
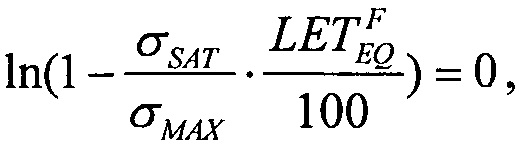
тогда 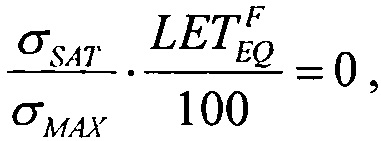 что дает единственное значение
что дает единственное значение 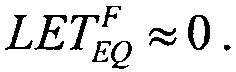
Для интенсивности отказов при 10% воздействии солнечного ветра используют использовать соотношение

где R - интенсивность SEE в единицах [сбой/(бит-день)]. σsat - поперечное сечение насыщения SEE в [мкм2], a LETTH - пороговое значение LET в единицах [пКл/мкм].
Для большинства практических случаев интенсивность отказов в (ПГ.26) определяют с использованием аппроксимирующего выражения для σSAT=ab, (a, b>c) a - длина, b - ширина и c - толщина ЧО ТС в [мкм], L - топологический размер, в [мкм]
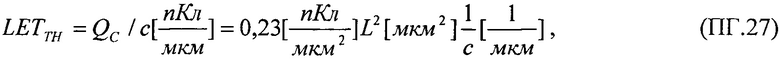
Приведенное соотношение применимо для многих приложений. Это соотношение допускает разброс в оценке добротности (FOM) с величиной до 5 раз и поправочным коэффициентом в 3,5 для приборов на GaAs.
В случае суммарной интенсивности (I) SEE (ПГ.9) при 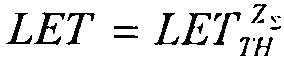 из (ПГ.10) следует при определении FW в интервале LETTH<LET<∝
из (ПГ.10) следует при определении FW в интервале LETTH<LET<∝
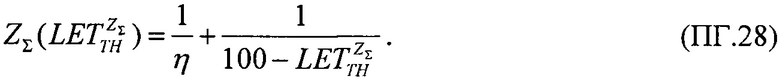
С другой стороны, функция распределения ошибок в этом случае равна
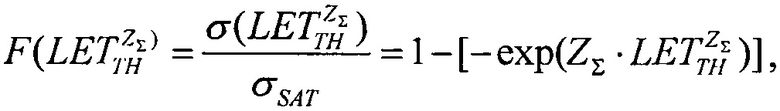
которую, следуя процедуре линеаризации (Приложение «А») преобразуют к виду
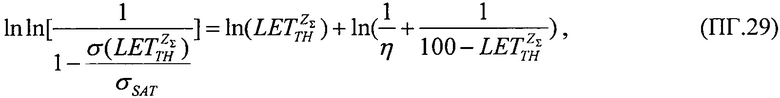
линейного соотношения Y=Х+В, где
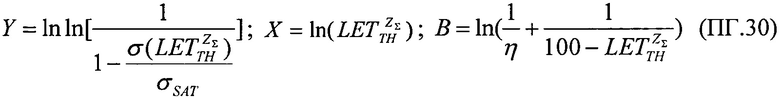
При применении численных методов решения (ПГ.28) выходными данными являются 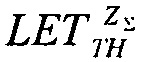 и
и 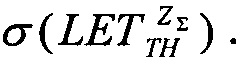 Величина
Величина 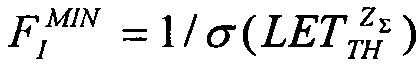 - минимальный поток частиц, достаточный для генерации SEE, подставляя соответствующие значения
- минимальный поток частиц, достаточный для генерации SEE, подставляя соответствующие значения 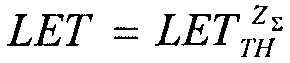 и σSAT в (ПГ.26) оценивают интенсивность сбоев. Пусть Y=0 в (ПГ.30), отсюда
и σSAT в (ПГ.26) оценивают интенсивность сбоев. Пусть Y=0 в (ПГ.30), отсюда

где обозначено для упрощения 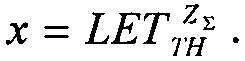 Равенство (ПГ.31) преобразуют к виду квадратного уравнения ax2+bx+c=0
Равенство (ПГ.31) преобразуют к виду квадратного уравнения ax2+bx+c=0
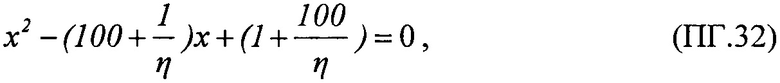
где a=1, 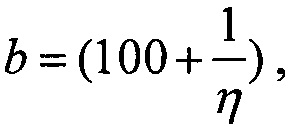
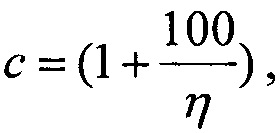 решение которого получают в виде
решение которого получают в виде

Подстановка в (ПГ.32) ряда значений параметра масштаба 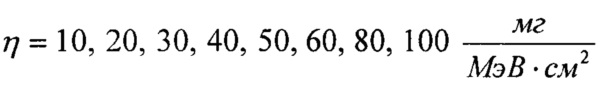 дает два практически не зависящих от величины η корня уравнения: x1=0,02…0,06 и x2=99,94…99,99, что позволяет утверждать, что поперечное сечение может принимать значение 0,63 σSAT либо при очень круто восходящей зависимости
дает два практически не зависящих от величины η корня уравнения: x1=0,02…0,06 и x2=99,94…99,99, что позволяет утверждать, что поперечное сечение может принимать значение 0,63 σSAT либо при очень круто восходящей зависимости 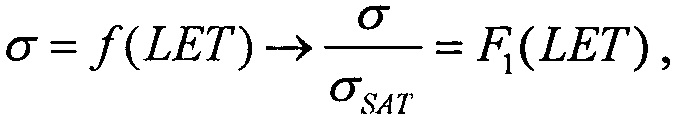 либо при пологой
либо при пологой 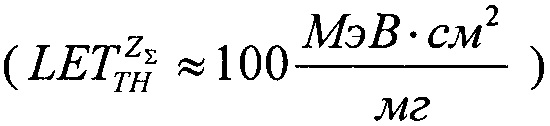 (Фиг. ПГ.1).
(Фиг. ПГ.1).
В случае «суммарного» (кумулятивного) ресурса (II) (ПГ.16) интегральную функцию распределения поперечных сечений SEE представляют в виде (ПГ.17), разрешая которую относительно 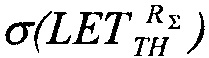 также получают квадратное уравнение вида ax2+bx+c=0:
также получают квадратное уравнение вида ax2+bx+c=0:
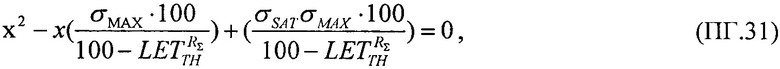
где 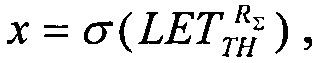 a=1,
a=1, 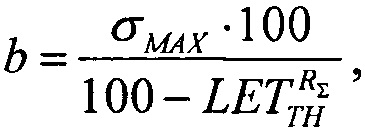
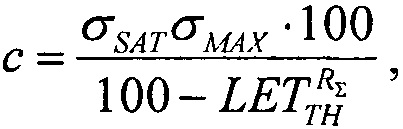 решение которого также получают в виде (ПГ.31). Подставляя экспериментально полученные данные
решение которого также получают в виде (ПГ.31). Подставляя экспериментально полученные данные 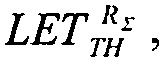 σSAT, σМАХ, определяют значение
σSAT, σМАХ, определяют значение 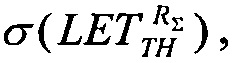 а величина обратная позволяет определить минимальную величину потока частиц, достаточных для генерации SEE.
а величина обратная позволяет определить минимальную величину потока частиц, достаточных для генерации SEE.
В случае равных ресурсов (III) (ПГ.18) величину 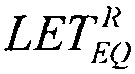 определяют из (ПГ.21), при этом
определяют из (ПГ.21), при этом 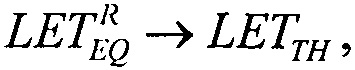 а
а 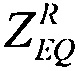 определяют из (ПГ.23).
определяют из (ПГ.23).
В случае равных интегральных распределений вероятности сбоев (IV) выполняют соотношение (ПГ.25) откуда следует 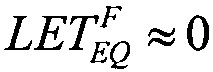 при определении FW(LET) в диапазоне 0<LET<∝.
при определении FW(LET) в диапазоне 0<LET<∝.
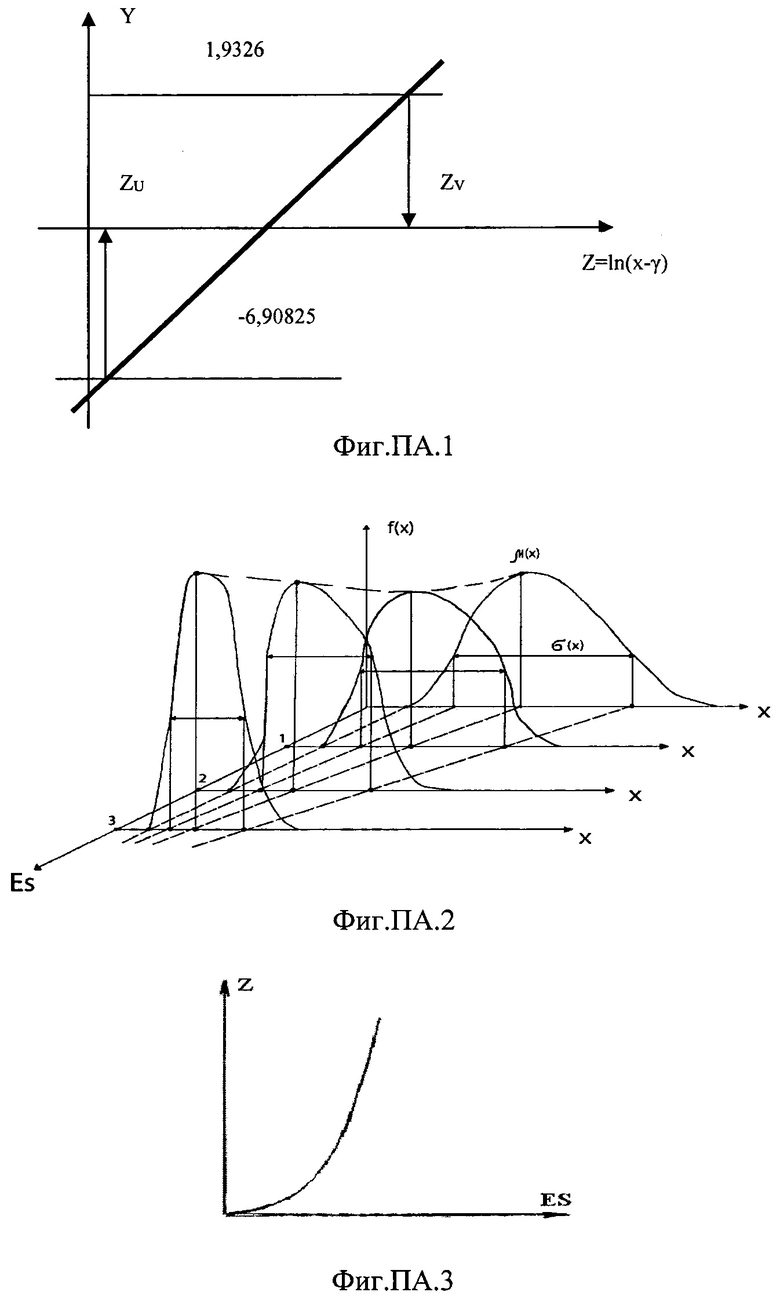
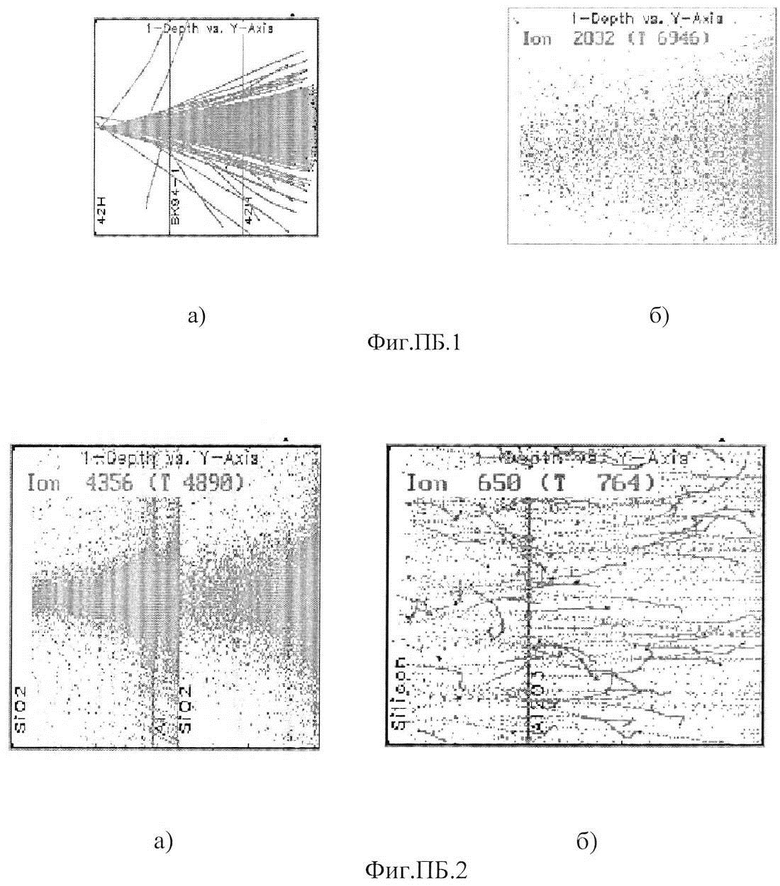
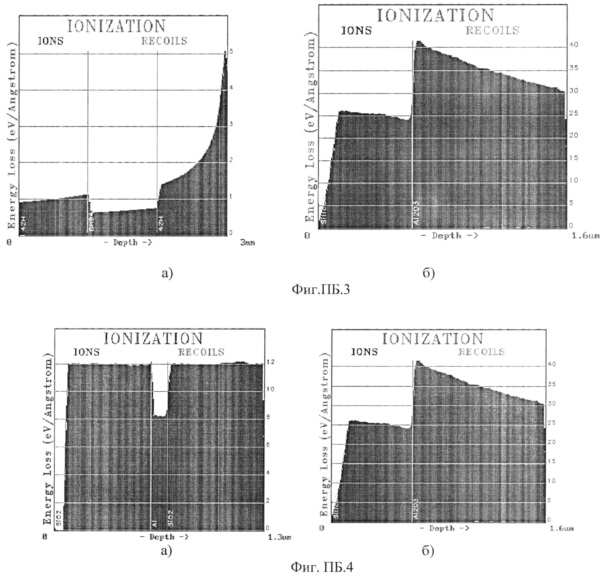
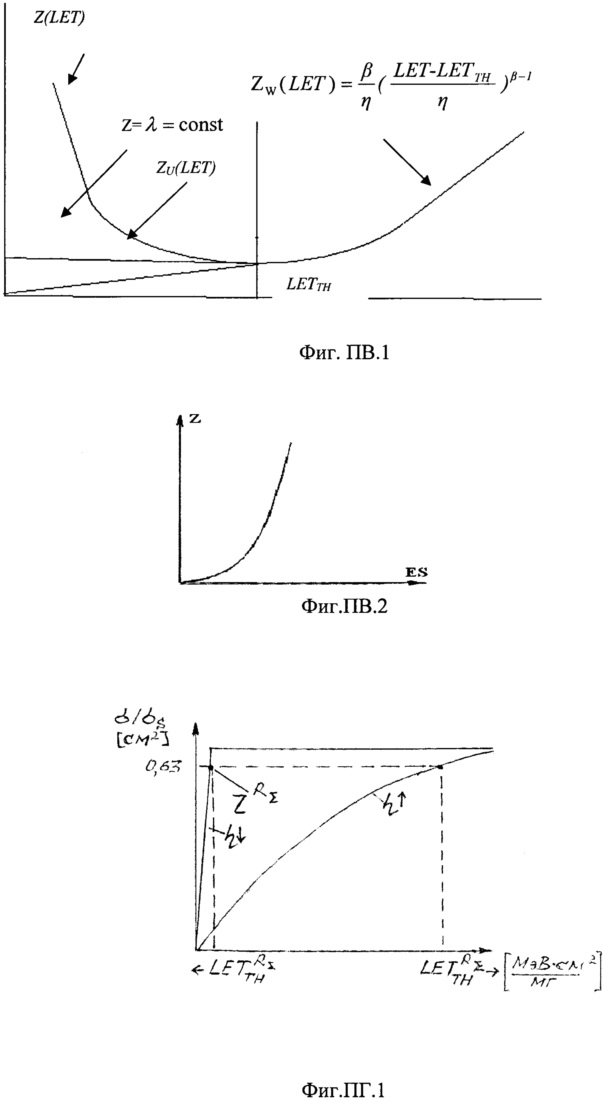
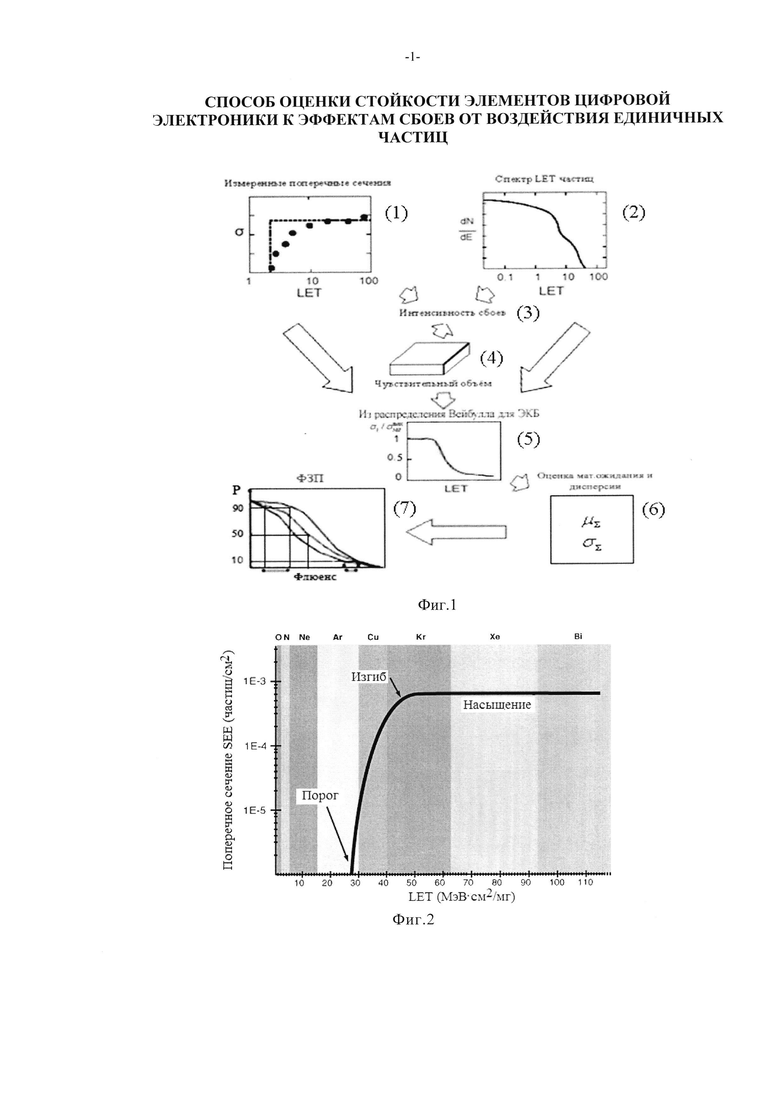
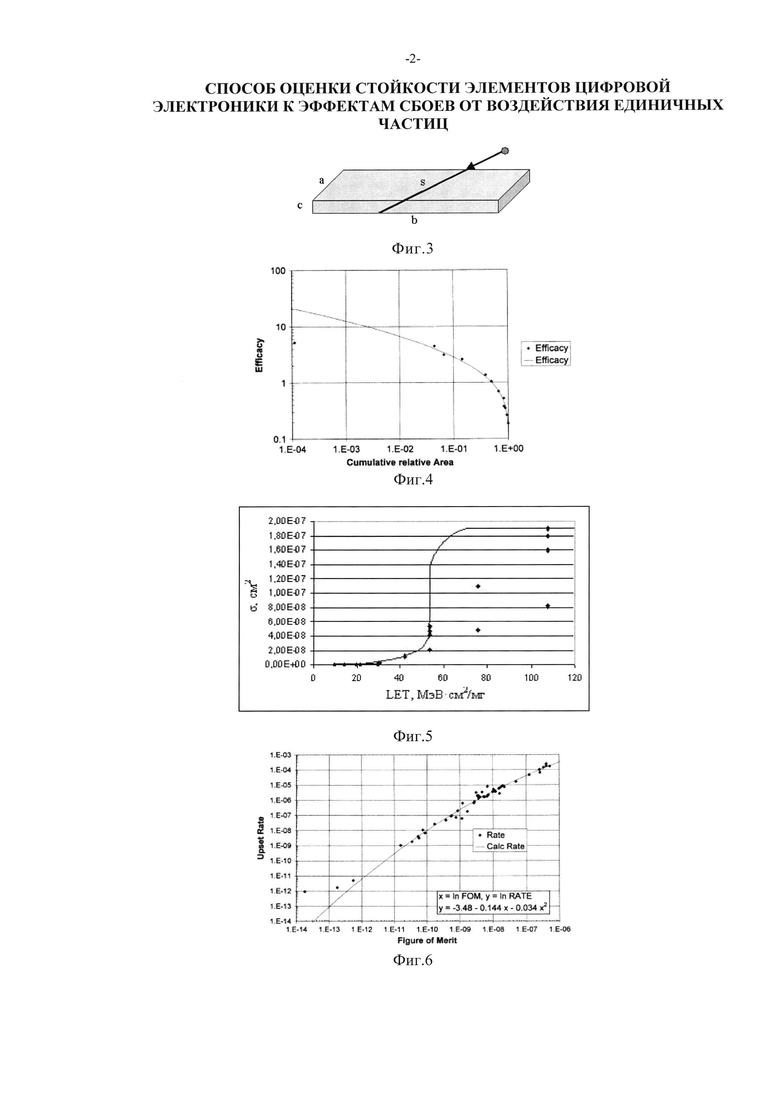
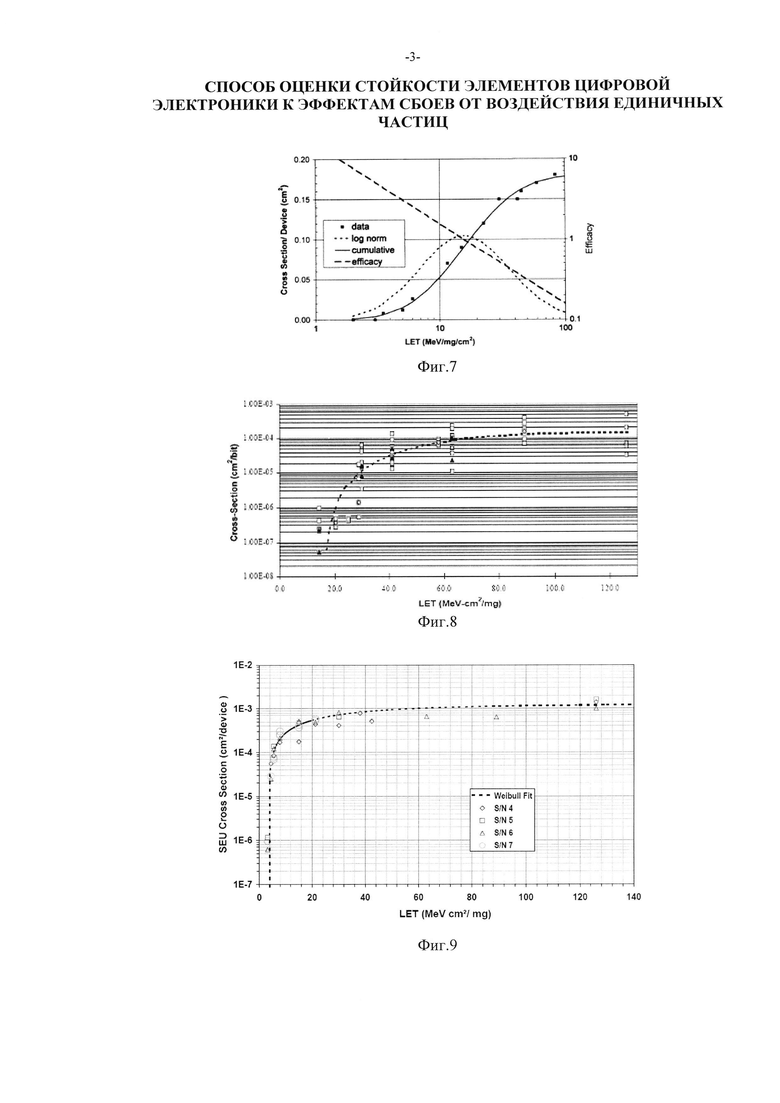
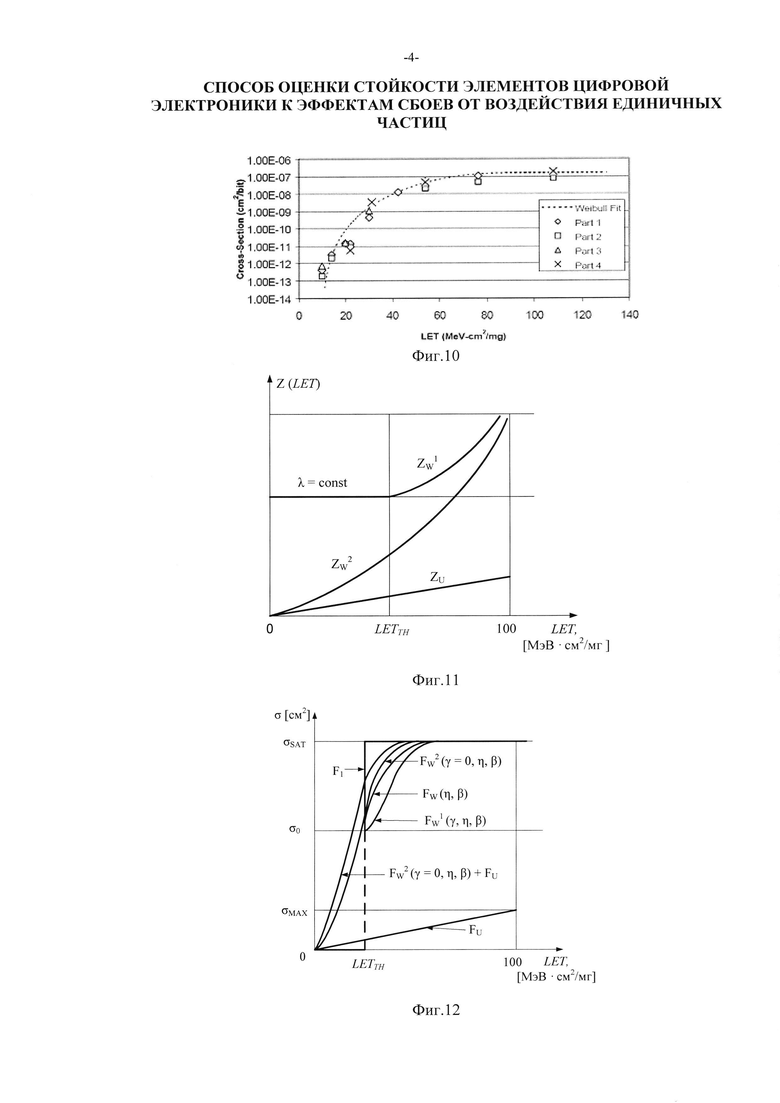
Изобретение относится к способам испытаний полупроводниковых приборов на стойкость к воздействию тяжелых заряженных частиц различных энергий космического пространства (КП). В способе оценки стойкости элементов цифровой электроники к эффектам сбоев от воздействия единичных частиц КП определяется минимальное значение потока частиц, соответствующее отличному от нулевого значения сечению сбоев в области малых значений линейной передачи энергии (LET). Получают экспериментальную зависимость величины сечения сбоев от величины LET, аппроксимируют эту зависимость теоретическим многопараметрическим законом распределения, экстрагируют параметры этого распределения, определяют пороговое значение LET единичных частиц, соответствующее минимальному значению сечения сбоя. В данном способе используются семь вариантов математических моделей. Из полученного набора данных выбирают минимальное значение потока частиц. Техническим результатом является повышение точности характеристик зависимости поперечного сечения эффектов единичных сбоев (SEE) от LET, а также определение минимального значения флюенса частиц, достаточного для генерации эффектов SEE. 12 ил., 9 табл.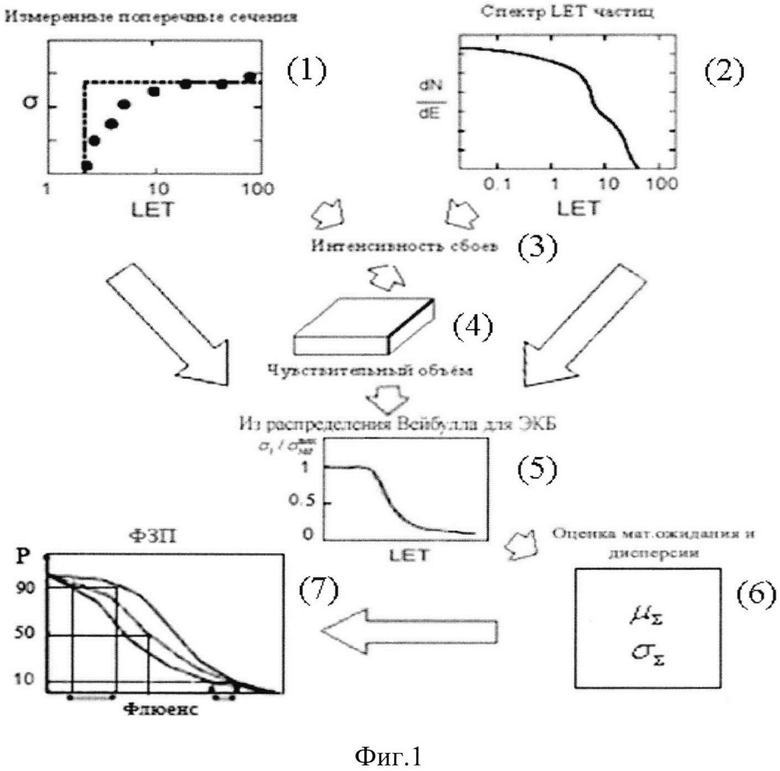
Способ оценки стойкости элементов цифровой электроники к эффектам сбоев от воздействия единичных частиц космического пространства путем определения минимального значения потока частиц, соответствующего отличному от нулевого значения сечению сбоев в области малых значений линейной передачи энергии частицами, для чего получают экспериментальную зависимость величины сечения сбоев от величины линейных потерь энергии частиц, аппроксимируют эту зависимость теоретическим многопараметрическим законом распределения, экстрагируют параметры этого распределения, определяют пороговое значение линейных потерь энергии единичных частиц, соответствующего минимальному значению сечения сбоя, определяют максимальное значение сечения сбоев в режиме насыщения и минимальное значение потока частиц, отличается тем что реализуют сопоставление минимальных значений потоков частиц, полученных с использованием следующих математических моделей:
1) в качестве теоретического многопараметрического интегрального закона распределения сечения сбоя для значений, больших величины порогового значения линейных потерь принимают трехпараметрический закон распределения Вейбулла, а для значений, меньших величины порогового значения линейных потерь, но больших величины их нулевого значения, принимают равномерный закон распределения, учитывающий «предысторию» возможности появления единичных сбоев, полагают в качестве критерия равными интенсивности сбоев и определяют сечения сбоев и минимальное значение потока частиц;
2) для Вейбуловского и равномерного законов распределения принимают в качестве критерия равными между собой интегральные функции распределения и определяют сечения сбоев и минимальное значение потока частиц;
3) для порогового значения линейных потерь энергии частиц принимают в качестве критерия комбинированную величину интенсивности сбоев, которую определяют в виде суммы величин интенсивности сбоев для равномерного и Вейбулловского законов распределения, определяют сечения сбоев и минимальное значение потока частиц;
4) для Вейбулловского и равномерного законов распределения определяют величины ресурсов, а в качестве скорректированной величины ресурса для порогового значения линейных потерь энергии частиц принимают в качестве критерия произведение указанных ресурсов, определяют сечения сбоев и минимальное значение потока частиц;
5) принимают в качестве критерия равными интегральные функции распределения сбоев для Вейбулловского и равномерного законов распределения, а затем определяют скорректированную пороговую величину линейных потерь энергии частиц, определяемую в виде линейного соотношения соответствующих величин для указанных законов, определяют сечения сбоев и минимальное значение потока частиц;
6) определяют в качестве критерия скорректированный ресурс как произведение ресурсов для Вейбулловского и равномерного законов распределения, затем определяют параметры скорректированного закона распределения и получают скорректированное значение минимального потока частиц, определяют сечения сбоев и минимальное значение потока частиц;
7) в качестве критерия равными принимают ресурсы, определенные для Вейбулловского и равномерного законов распределения, определяют параметры скорректированного закона распределения, определяют сечения сбоев и минимальное значение потока частиц;
из полученного набора данных выбирают минимальное значение потока частиц (наихудший случай).
| СПОСОБ ОЦЕНКИ СТОЙКОСТИ ЦИФРОВОЙ ЭЛЕКТРОННОЙ АППАРАТУРЫ К ВОЗДЕЙСТВИЮ ИОНИЗИРУЮЩИХ ИЗЛУЧЕНИЙ (ВАРИАНТЫ) | 2014 |
|
RU2578053C1 |
| СПОСОБ ИСПЫТАНИЙ ПОЛУПРОВОДНИКОВЫХ БИС ТЕХНОЛОГИИ КМОП/КНД НА СТОЙКОСТЬ К ЭФФЕКТАМ ЕДИНИЧНЫХ СБОЕВ ОТ ВОЗДЕЙСТВИЯ ТЯЖЕЛЫХ ЗАРЯЖЕННЫХ ЧАСТИЦ КОСМИЧЕСКОГО ПРОСТРАНСТВА | 2011 |
|
RU2495446C2 |
| E.L | |||
| Petersen et al "Rate Predictions for Single-Event Critique II", IEEE Transactions on Nuclear Science, Vol.52, No.6, December 2005, pp.2158-2167 | |||
| US 8346497 B2, 01.01.2013. | |||
Авторы
Даты
2018-06-13—Публикация
2016-12-26—Подача