СПОСОБ ОПРЕДЕЛЕНИЯ СТОЙКОСТИ ЭЛЕКТРОННЫХ КОМПОНЕНТОВ И БЛОКОВ РАДИОЭЛЕКТРОННОЙ АППАРАТУРЫ К ВОЗДЕЙСТВИЮ ИОНИЗИРУЮЩИХ ИЗЛУЧЕНИЙ Российский патент 2014 года по МПК H01L21/66 

Изобретение относится к области испытаний сложно-функциональной аппаратуры (СФА) специального назначения (например, космического («Space») и военного назначения («Military»)), к которой предъявляются повышенные требования по устойчивости к сбоям или потери работоспособности, вызванным воздействием радиации. С развитием полупроводниковых технологий, когда постоянно уменьшаются размеры и напряжение питания интегральных микросхем (ИМС), а тактовая частота растет, задача повышения радиационной стойкости становится важной и для производителей коммерческой микроэлектроники. Ее решение требует принятия мер на всех уровнях разработки ИМС: синтеза и верификации, трассировки шин питания, конструирования библиотечных элементов схем, технологического процесса изготовления.

При испытаниях узлов, блоков, приборов, а, тем более, целых систем специального назначения, проблема испытаний на радиационную стойкость (PC) не имеет в настоящее время типовых решений. Это связано с некоторыми объективными и принципиально не устранимыми физическими ограничениями. Основные причины такой ситуации заключаются в следующем:

- ограниченные возможности моделирующих установок (невозможность обеспечения равномерного и однородного облучения при экстремальных уровнях нагружения);

- влияние объекта испытаний на поля нагружения моделирующих установок;

- значительные перерывы во времени между воздействиями различных факторов ионизирующего излучения (ИИ) при пофакторном их моделировании;

- локальная неоднородность и не синхронность во времени энерговыделения от различных видов ИИ (отсутствие синэнергетического эффекта);

- малая статистика из-за ограниченных выборок тестируемых образцов.

Известны способы оценки PC радиоэлектронной аппаратуры (РЭА) и составляющей ее электронной компонентной базы (ЭКБ), основанные на статистической обработке экспериментальных данных (вероятностные методы) /1-4/, основанные на статистической обработке результатов экспериментальных исследований PC конечных (ограниченных) выборок облучавшихся объектов. Однако, выбор определяющего радиационно-критического параметра (РКП) в качестве критерия PC не всегда является физически обоснованным, т.е. в качестве объекта анализа используют интегральные параметры (ток потребления, рабочая частота цифровых ИМС и т.п.), которые неоднозначно отражают взаимодействие ИИ с материалами электронной техники, и не учитывают вклада сложных статистических процессов на границах раздела (интерфейсов) материалов электронной техники с различными физико-электрическими и химическими свойствами, в том числе, с различным примесно-дефектным составом (ПДС).

Для оценки стойкости аппаратуры автоматики космических аппаратов (КА) в ряде случаев используют экспериментальные методы определения критических значений сечений σ_SAT единичных сбоев (single event effect, или SEE) в ИМС (или обратимых нарушений функционирования цифровой электроники) в зависимости от величин линейных потерь энергии LET в 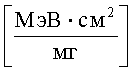тяжелых заряженных частиц (ТЗЧ). По результатам таких измерений на дорогостоящих ускорителях протонов или ионов ТЗЧ определяют допустимые потоки частиц по схеме /5/ (Фиг.1). Для порогового значения LET_TH величина 1/σ_i(LET_TH) для; i-го вида ТЗЧ является минимальным допустимым потоком частиц φ_MIN, при котором возможен эффект единичных сбоев. В процедуре оценки PC аппаратуры используют для аппроксимации зависимости σ_i/σ_SAT=f(LET) закон распределения Вейбулла, по которому интенсивность отказов (функция риска) зависит от уровня радиационного воздействия, а параметр формы m коррелирует с характером физических процессов, происходящих в электронных приборах при воздействии ИИ (Фиг.2) (см. Приложение «А»). Однако такой подход не применялся до настоящего времени для различных видов радиационных воздействий: импульсного ИИ, ИИ ядерных энергетических установок и т.п.

При проведении испытаний СФА при экстремальных уровнях воздействия результаты испытаний фактически «недостоверны». Кроме того, окончательный характер зачетных испытаний, нестабильность технологий изготовления комплектующих изделий, утрата контроля за качеством и стабильностью изготовления материалов - все это приводит к снижению гарантии подтверждения достигнутых уровней PC для каждого из изготовленных приборов. В этой ситуации основной вопрос формулируется очень просто: как обеспечить выполнение требований ТУ и ТЗ на прибор при ограниченном наборе экспериментальных данных? В более общем смысле проблема состоит в получении любым путем зависимости вероятности параметрического или функционального отказа прибора от уровня воздействующего ИИ, то есть в построении физического закона поражения (ФЗП).

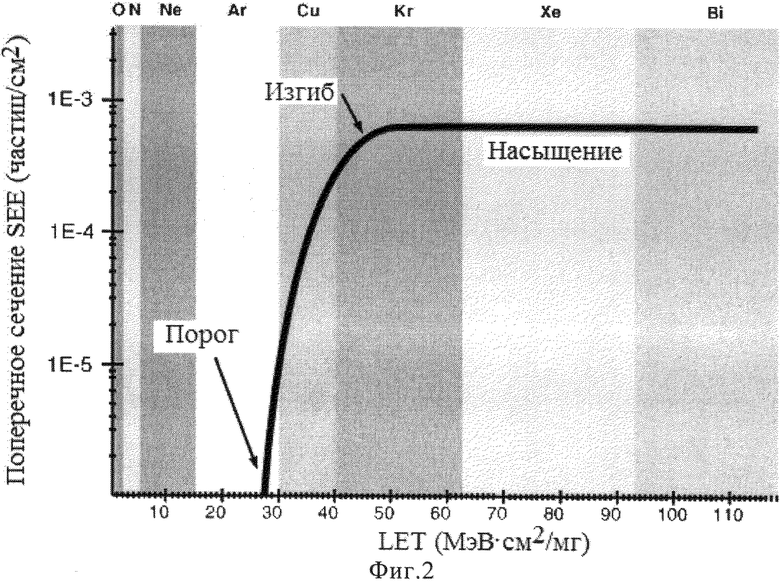
Наиболее близким по технической сущности и принятым за прототип является разработанный способ построения ФЗП с доверительными границами и без их учета, предложенный в /4/. Графически этот способ проиллюстрирован на Фиг.3. 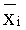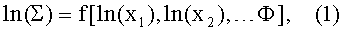Для реализации этого способа для определения сохранения работоспособности без использования доверительных границ предпринимают следующие шаги: 1) для каждого независимого режима отказа объекта модель границ безопасности для некоторого РКП ∑ определяют как функцию независимых переменных x_i, которые распределены по допущению по закону распределения Вейбулла со средним значением и стандартным отклонением s_i в виде

где Ф является мерой радиационного воздействия и она не зависит от случайной переменной; 2) затем преобразуют среднее значение и стандартное отклонение распределенной по закону Вейбулла величины x_i в аналогичные значения нормированной случайной величины ln(x_i); 3) производят разложение величины ln(∑) в ряд Тейлора около среднего значения величины ln(x_i); 4) вычисляют вероятность сохранения работоспособности для каждого значения режима повреждения с помощью соотношения

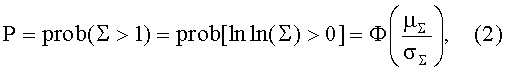
где 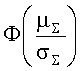является обобщенной стандартной функцией нормального распределения (квантилью), µ_∑ - математическое ожидание РКП, σ_∑ - среднее квадратичное отклонение величины РКП; 5) комбинируют определенные режимы повреждения k, для определения сохранения работоспособности, в систему оценки уровней сохранения работоспособности при допущении функциональной независимости режимов повреждения и допущений, что статистически они действуют последовательно, можно записать

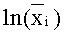
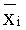
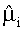
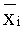
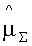
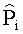
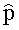
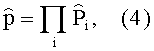
При учете доверительных границ помимо шагов 1)-5) выполняют следующее: 6) производят расчет среднего значения и стандартного отклонения несмещенной оценки среднего , где является случайной переменной, представляющей выборку среднего значения величины x_i. Для этой несимметричной оценки, которую называют выполняют оценку ее среднего значения и стандартного отклонения; 7) производят разложение величины lnln(∑) в ряд Тейлора около среднего значения µ_i и извлекают коэффициенты разложения β_i; 8) при допущении о том, что несмещенная оценка логарифмических границ безопасности имеет ту же функциональную зависимость lnln(∑), что и выборочное среднее в виде ln(x_i) производят разложение несимметричной оценки в ряд Тейлора в окрестностях µ_i; 9) рассчитывают среднее и стандартное отклонение вероятности сохранения работоспособности; 10) комбинируя индивидуальную вероятность сохранения работоспособности с вероятностью сохранения работоспособности всего объекта , рассчитывают ее среднее и стандартное отклонение для модели последовательного соединения составных частей

11) рассчитывают параметры функции плотности распределения величины ; 12) рассчитывают доверительные границы р_дов, а доверие d есть вероятность того, что превышает заданную границу p₀.

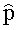
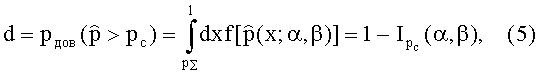
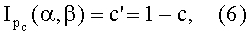
Интегральное β-распределение 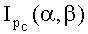табулировано в /5/, где p_c дается для ряда значений α и β и c', а c - доверительная вероятность и необходимость приведения исходных распределений РКП к логарифмически-нормальному виду.

Недостатками способа /4/, выбранного в качестве прототипа являются:

- сложный математический аппарат, используемый для обработки экспериментальных данных;

- использование в качестве теоретического закона распределения экспериментальных данных нормального (Гауссова) закона распределения и необходимость приведения в дальнейшем исходных РКП к логарифмически-нормальному виду, что требует использования представительных выборок (более 25-50 измерений);

- отсутствие учета того обстоятельства, что воздействие ИИ на ЭКБ и блоки РЭА в целом приводят к зависимости интенсивности параметрического отказа РКП и функционального отказа РЭА в целом от уровня радиационной нагрузки.

Техническим результатом предлагаемого способа является повышение достоверности определения стойкости электронных компонентов и блоков РЭА к воздействию ИИ по результатам испытаний ограниченной выборки ЭКБ, субблоков РАЭ или всего прибора в целом (далее объекта), а также учет и сравнение полученных данных с данными по стойкости ЭКБ из справочной литературы, требованиями ТЗ и критериальными значениями РКП, а также определение наиболее значимого вида ИИ по его влиянию на уровень стойкости объекта.

Технический результат достигается тем, что в способе определения стойкости электронных компонентов и блоков радиоэлектронной аппаратуры к воздействию ИИ путем построения зависимости функции распределения вероятности параметрической или функциональной работоспособности от уровня радиационной нагрузки x и определения критического уровня воздействия ИИ по заданному уровню этой вероятности. С целью определения функции распределения вероятности параметрической или функциональной работоспособности для малых выборок облучаемых объектов (физического закона поражения, ФЗП), используют доверительный интервал или трехпараметрическую функцию распределения Вейбулла. Внутренние границы этого интервала (u - нижняя и v - верхняя) получают на основе обработки экспериментальных данных по облучению выборки размером п, внешние границы (U - нижняя и V - верхняя) задают из общих физических представлений, определяющими из которых является уровень отсутствия наблюдаемых критических изменений и незначительное, на 20-30%, превышение требований по стойкости объектов к воздействию ИИ. В выбранных границах (U, V) вводят экспериментально полученную интегральную функцию распределения нижних допустимых уровней стойкости к различным видам ИИ в форме

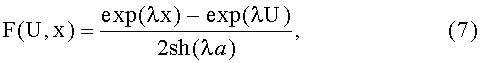
определяют скорость изменения вероятности параметрических или функциональных отказов (интенсивность изменения параметрического ресурса) путем решения трансцендентного уравнения

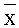
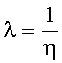
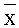
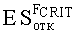
где: a - полуширина интервала [U, V], - среднее арифметическое значение уровней стойкости объектов в выборке; - интенсивность параметрических отказов; η - параметр масштаба эквивалентного распределения Вейбулла. Затем строят семейство графиков зависимости функции распределения F(U, x) от различных видов ионизирующих излучений (флюенса нейтронов F_n; величины полной поглощенной дозы ИИ D_ИИ; мощности экспозиционной дозы ИИ P_ИИ; флюенса ТЗЧ Ф_ион; величины линейных потерь энергии (LET) (для аппаратуры, размещаемой на КА) и т.п.) при фиксированных значениях , по построенным графикам определяют уровень радиационной нагрузки , при котором вероятность отказа прибора составляет F_CRIT, или ресурс сохранения работоспособности R_СОХР=1-F_CRIT.

Для повышения информативности вероятностной оценки стойкости объектов к воздействию различных видов ИИ; в качестве ФЗП вместо F(U, x) из соотношения (7) используют трехпараметрическое распределение Вейбулла

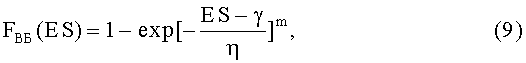
где ES - уровень радиационной нагрузки, F_ВБ(ES) - вероятность параметрического или функционального отказа в зависимости от величины уровня радиационной нагрузки ES, η - параметр масштаба, m - параметр формы, γ - параметр положения, вероятность 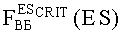парметрического или функционального отказа при критическом уровне радиационной нагрузки ES_CRIT, критическое значение ES_CRIT определяют путем обработки экспериментальных данных с использованием закона распределения Вейбулла, а для случая параметрического отказа значения РКП задают в относительных единицах, или процентах.

Для оценки стойкости к воздействию ИИ СФА по результатам обработки экспериментальных данных с использованием экспоненциального закона распределения или распределения Вейбулла для составных частей объекта, математическое ожидание (МО) µ_∑ для СФА определяют с использованием соотношения (ПБ.14) (Приложение «Б»)

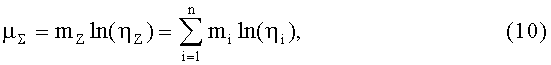
где m_i - экспериментально полученный параметр формы распределения Вейбулла для ФЗП отдельного элемента (субблока), η_i - соответствующий параметр масштаба распределения Вейбулла, а в случае ФЗП в экспоненциальном виде параметр формы m_i принимают равным единице, а интенсивность отказов λ_i=1/η_i, m_Z - параметр формы распределения Вейбулла для СФА, η_Z - параметр масштаба распределения Вейбулла для СФА.

Еще одной целью предлагаемого способа является определение по результатам обработки экспериментальных данных наиболее значимого вида ИИ по его влиянию на уровень стойкости СФА. Величины радиационной нагрузки ES в виде флюенса нейтронов, мощности дозы ИИ, линейных потерь энергии пересчитывают в единицы эквивалентной полной поглощенной дозы ИИ (TID) по критерию 1 Мэв-экв., производят построение ФЗП для каждого из видов ИИ на общем графике зависимости F_ВБ(ES), туда же, при необходимости, наносят гистограмму плотности распределения комплектующих СФА электронных компонентов по одному из видов ИИ, а по результатам сопоставления видовых ФЗП судят о стойкости всей СФА в целом к тому или иному виду ИИ.

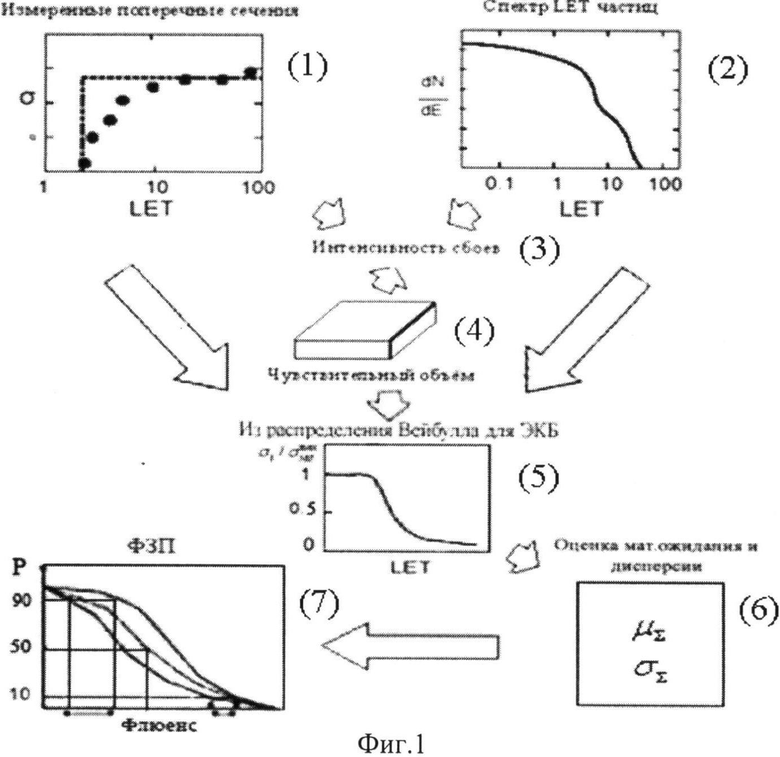
На Фиг.1 приведено схематическое представление процедуры оценки интенсивности сбоев и параметрической вероятности сохранения работоспособности электронных устройств КА /6/:

(1) - Измеренные поперечные сечения SEE;

(2) - Спектр линейных потерь энергии ТЗЧ;

(3) - Интенсивность сбоев БИС;

(4) - Чувствительный объем транзистора структуры «металл-оксид-полупроводник»;

(5) - Зависимость относительного поперечного сечения SEE в относительных единицах 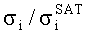от LET для i-го элемента ЭКБ ( - сечение насыщения);

(6) - Оценка математического ожидания и дисперсии;

(7) - Построение ФЗП.

На Фиг.2 представлена типичная зависимость поперечного сечения SEE от LET для различных ТЗЧ. По оси Y: Поперечное сечение SEE (см²); по оси X: LET (МэВ·см²/мг).

На Фиг.3 показана функция зависимости вероятности сохранения работоспособности объекта R (ресурса) от уровня радиационной нагрузки ES (Enviroment Radiation Stress)

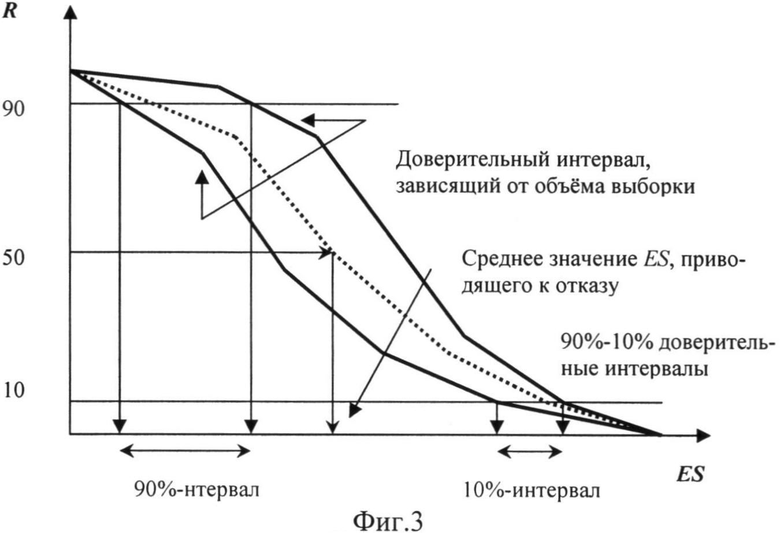
На Фиг.4 приведены ФЗП для блоков РЭА типового спутника от «тиристорного эффекта» (LATCHUP), выгорания от переходных ионизационных процессов рентгеновского и гамма-излучения (TREE BURNOUT), выгорания от эффектов системно-генерированного электромагнитного импульса (SGEMP BURNOUT), деградации от флюенса нейтронов (NEUTRON DEGRADATION), и эффектов полной поглощенной дозы (TOTAL DOSE). Для сопоставления на рисунке все виды воздействий приведены к единицам флюенса рентгеновского излучения в единицах log₁₀ (X-Ray Fluence).

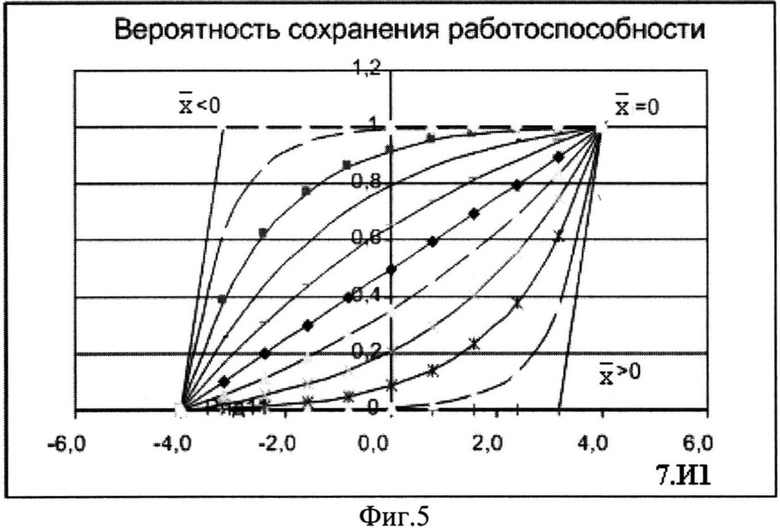
На Фиг.5. представлено семейство зависимостей функции распределения F(U, x) от фактора 7.И1 при фиксированном значении , V и U=const для блоков B1 №1, №2 прибора «А». Отношение является параметром, значение - изменяется от -1 до +1 через 0,2.

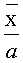
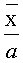
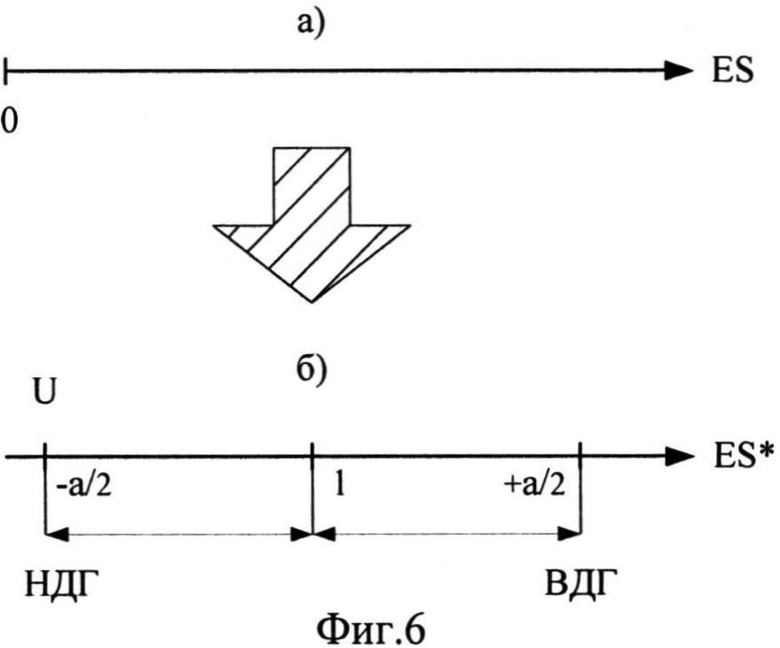
На Фиг.6 показана процедура перенормировки масштаба по оси радиационной нагрузки ES в ES^∗ при использовании интегральной функции распределения нижних допустимых уровней стойкости U к различным видам ИИ в форме (7). НДГ - нижняя допустимая граница стойкости к фактору 7.И1; ВДГ - верхняя допустимая граница стойкости к фактору 7.И1.

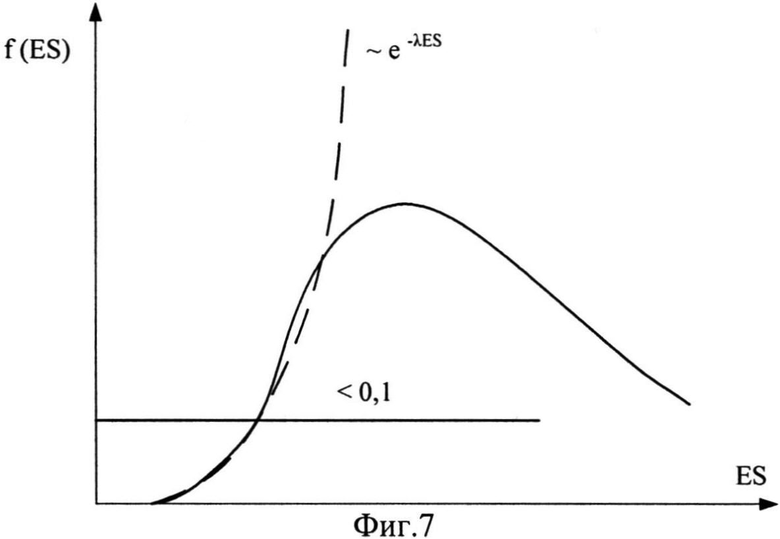
На Фиг.7 показана возможность использования, в области малых значений вероятности, в качестве аппроксимирующей функции плотности распределения вероятности параметрического или функционального отказа f(ES) экспоненциальной функции f(ES)=C exp(λ·ES): сплошная линия - реальная асимметричная функция; пунктирная - экспоненциальная.

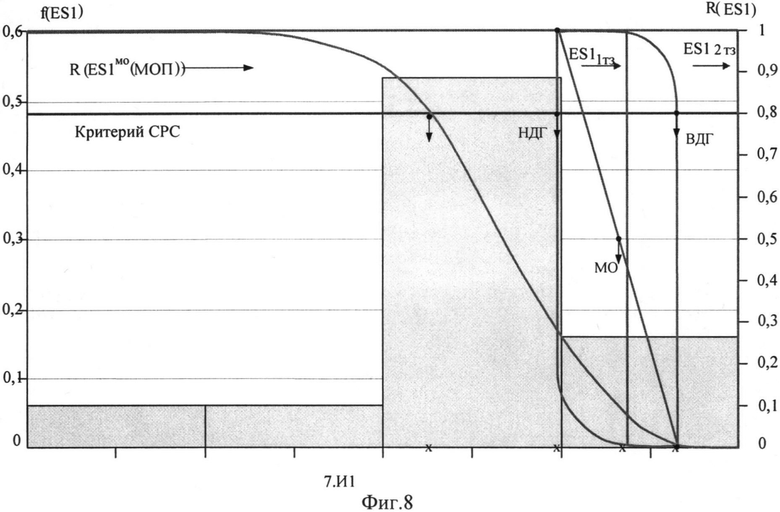
На Фиг.8 представлен интегральный закон распределения уровня PC (ФЗП) в зависимости от величины фактора 7.И1 для блоков В1 №1, №2 прибора «А»: R(ES1(МОП)) - параметрическая вероятность сохранения работоспособности по литературным данным МОП ЭКБ; ES_1ТЗ и ES_2TЗ - уровни стойкости по ТЗ к воздействию фактора 7.И1; СРС - критерий сохранения работоспособности по уровню R(ES1(МОП))=0,8.

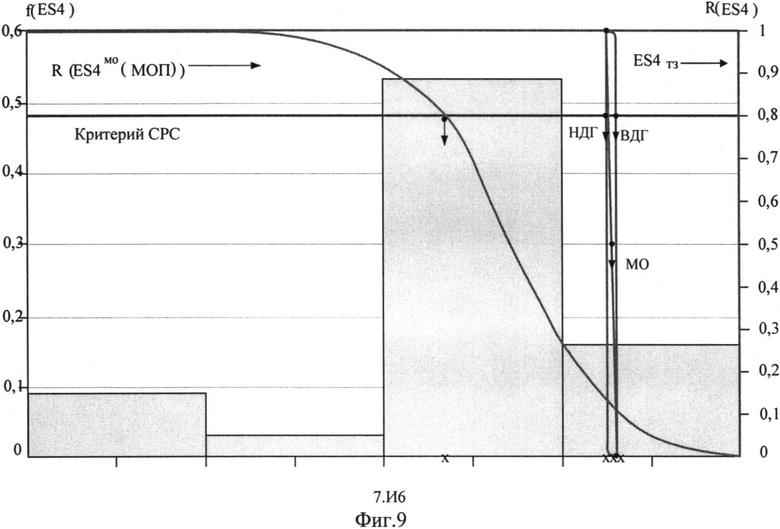
На Фиг.9 представлен интегральный закон распределения уровня PC (ФЗП) для прибора «А», полученный по результатам анализа перечня МОП ЭКБ, входящей в состав комплектующих прибора, при воздействии фактора 7.И6, а также ФЗП, полученный по результатам экспериментальных исследований на МУ блоков и узлов прибора «А» и на воздействие 7.И6 (Значком «ES4_ТЗ» помечено значение фактора 7.И6, требуемое по ТЗ).

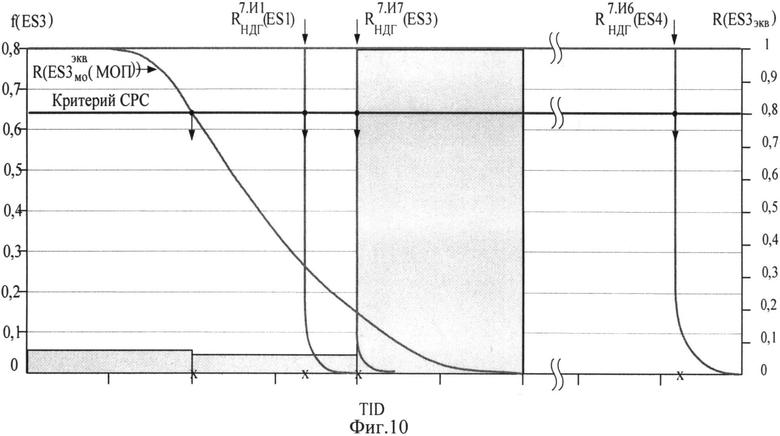
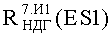
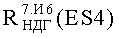
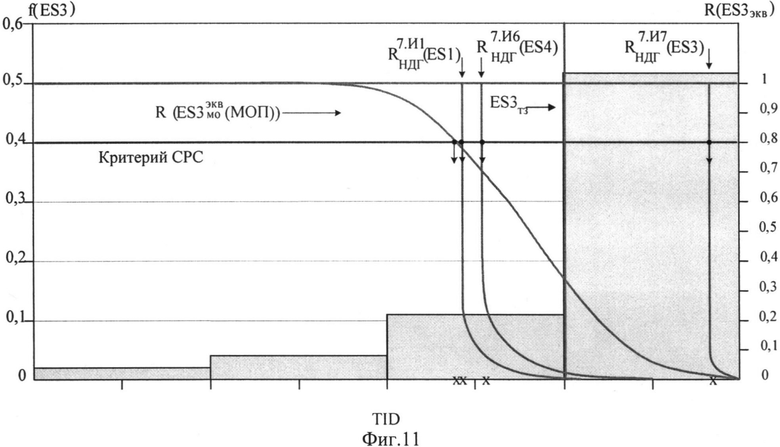
На Фиг.10 представлен интегральный закон распределения уровня PC (ФЗП) для прибора «А», полученный по результатам анализа перечня МОП ЭКБ, входящей в состав комплектующих прибора, при воздействии TID, а также ФЗП, полученные по результатам экспериментальных исследований на МУ блоков и узлов прибора «А» на воздействие фактора 7.И1, в единицах эквивалентной TID, на воздействие фактора в единицах эквивалентной TID (рав. (12)) и на воздействие 7.И7.

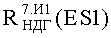
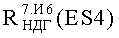
На Фиг.11 представлен интегральный закон распределения уровня PC (ФЗП) для прибора «Б», полученный по результатам анализа перечня МОП ЭКБ, входящей в состав комплектующих прибора, при воздействии TID, а также ФЗП, полученные по результатам экспериментальных исследований на МУ блоков и узлов прибора «Б» на воздействие фактора , фактор 7.И1 в единицах эквивалентной TID, на воздействие фактора 7.И6 , фактор 7.И6 в единицах TID (рав. (12)) и на воздействие фактора 7.И7 (Значком «ES3_ТЗ» помечено значение фактора 7.И7, требуемое по ТЗ).

Фиг.12. Функция риска, моделируемая распределением Вейбулла с различными значениями параметра формы m=α.

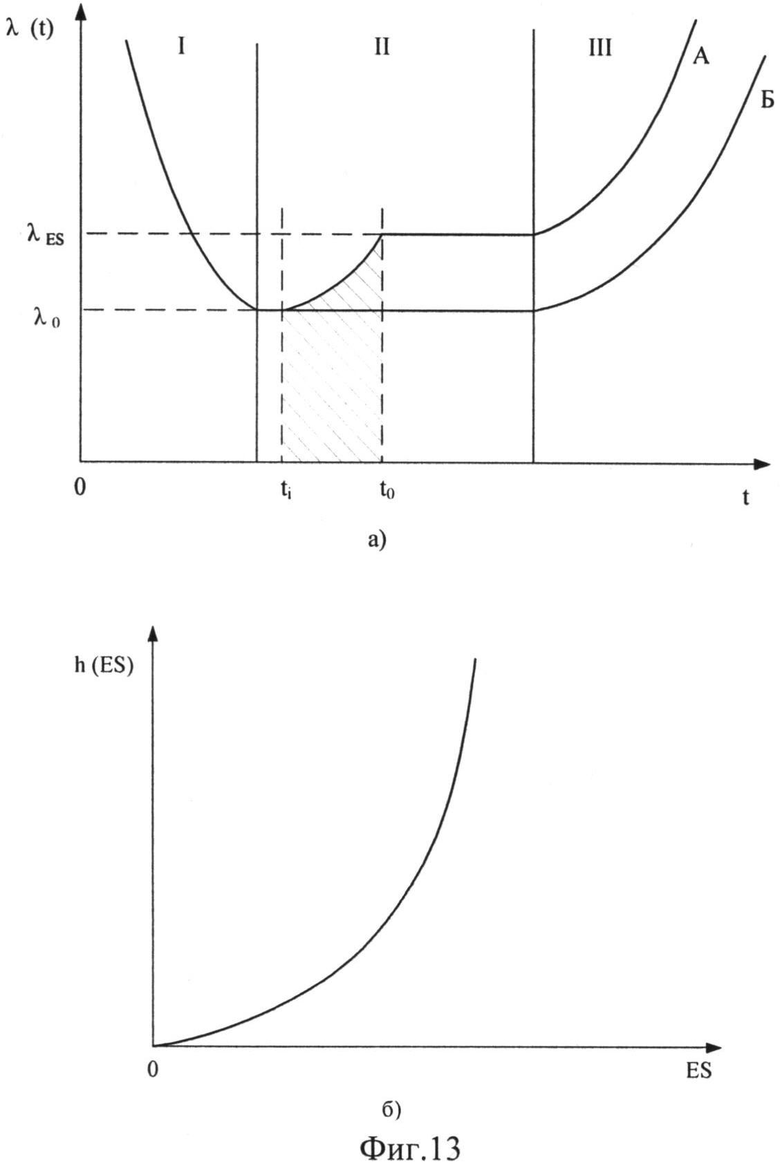
Фиг.13. Интенсивность отказов, моделируемая распределением Вейбулла для различных условий эксплуатация: а) зависимость λ(t) во времени в отсутствие «А» и при наличии «Б» радиационной нагрузки; б) зависимость интенсивности отказов h(ES) от уровней радиационной нагрузки. Здесь: «I» - область приработки; «II» - область нормальной эксплуатации; «III» - область старения (износа); t_i - время начала действия радиационной нагрузки; t_о - время завершения действия радиационной нагрузки.

Предлагаемый способ реализуется следующим образом.

Предлагаемый расчетно-экспериментальный способ основан на использовании понятия доверительного интервала. С целью определения функции распределения вероятности параметрического или функционального отказа для малых выборок облучаемых объектов (физического закона поражения, ФЗП) используют доверительный интервал или трехпараметрическую функцию распределения Вейбулла, внутренние границы которого (u - нижняя и v - верхняя), получены на основе обработки экспериментальных данных по облучению выборки размером n, внешние границы (U - нижняя и V - верхняя) задают из общих физических представлений, определяющими из которых является уровень отсутствия наблюдаемых критических изменений (уровень стойкости ЭКБ) и незначительное превышение (на 20-30%) требований ТЗ, связанное, главным образом, с максимальным значением дозиметрической погрешности δ_ES. При таком предлагаемом способе введения функции распределения уровня PC по образцам оказалось, что вид функции распределения не зависит от ширины доверительного интервала (U-u) и (V-v), который определяется верхними (V,v) и нижними (U, u) границами интервала экспериментально измеренных величин (v-u) и интервала их изменения для ожидаемой генеральной совокупности (V-U). Вводят экспериментально полученную интегральную функцию распределения нижних допустимых уровней стойкости к различным видам ИИ в форме (7) (дифференциальная плотность распределения f(ES)~exp(λ·ES) на Фиг.7), определяют скорость изменения вероятности параметрических или функциональных отказов (интенсивность изменения параметрического ресурса) путем решения трансцендентного уравнения (8). Такой вид функции распределения обусловлен малой выборкой испытуемых объектов одного типа, что предполагает использование информационного критерия Шеннона-Бриллюена, согласно которому ранжирование законов распределения по степени минимальной информативности (негоэнтропийный критерий) реализуется следующим образом: 1) равномерное распределение; 2) экспоненциальное распределение; 3) распределение Пуассона; 4) нормальный закон (распределение Гаусса) и т.д. В нашем случае (7) был выбран экспоненциальный закон распределения случайной величины.

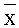
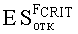
Затем строят семейство графиков зависимости функции распределения F(U,x) от различных видов ионизирующих излучений (фактора 7.И1; величины фактора 7.И7; фактора 7.И6; флюенса ТЗЧ; Ф_ион величины линейных потерь энергии (LET) (для аппаратуры, размещаемой на КА) и т.п.) при фиксированных значениях уровня радиационной нагрузки , определяющего параметрическое изменение радиационно-критического параметра или функциональный отказ (Фиг.5). По построенным графикам определяют уровень радиационной нагрузки , при котором вероятность отказа прибора составляет F_CRIT, или ресурс сохранения работоспособности R_СОХР=1-F_CRIT.

По построенным графикам определяется уровень радиационной нагрузки , при котором вероятность отказа прибора составляет F_ОТК=0,2, или ресурс сохранения работоспособности (СРС) R_СОХР=1-F_ОТК=0,8. Такой критерий получил широкое распространение при оценке вероятности сохранения работоспособности объектов в России и США в условиях специального применения.

На Фиг.5 по оси x=ES откладывают нормированное значение радиационной нагрузки в единицах ES^∗=ES/(U+a/2) (Фиг.6), что предполагает по окончании всех процедур выполнение обратной перенормировки. При допустимом уровне радиационной нагрузки ES_CRIT, определяющем вероятность сохранения работоспособности объекта на уровне R_СОХР=0,8 аппроксимация интегральной функции распределения экспоненциальной зависимостью (7) является правомерной (Фиг.7).

Для повышения информативности вероятностной оценки стойкости объектов к воздействию различных видов ИИ, в качестве ФЗП используют трехпараметрическое распределение Вейбулла (9), где ES - уровень радиационной нагрузки, F_ВБ(ES) - вероятность параметрического или функционального отказа в зависимости от величины уровня радиационной нагрузки ES, η - параметр масштаба, m - параметр формы, γ - параметр положения. Вероятность F_ВБ(ES) параметрического или функционального отказа на уровне ES_CRIT воздействующего ИИ определяют путем обработки экспериментальных данных с использованием закона распределения Вейбулла, а для случая параметрического отказа значения РКП задают в относительных единицах, или процентах.

Под ES здесь принимают следующие виды ИИ:

1) ES1 = фактор 7.И1;

2) ES2 = флюенс ТЗЧ Ф_ион;

3) ES3 = фактор 7.И7;

4) ES4 = фактор 7.И6;

5) ES5 = LET в 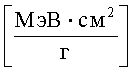(для аппаратуры, размещаемой на КА).

С целью оценки стойкости к воздействию ИИ СФА по результатам обработки экспериментальных данных с использованием экспоненциального закона распределения или распределения Вейбулла для составных частей объекта, МО µ_∑ для СФА определяют с использованием соотношения (ПБ.14) (Приложение «Б»), где m_i - экспериментально полученный параметр формы распределения Вейбулла для ФЗП отдельного элемента (субблока), η_i - параметр масштаба распределения Вейбулла, а в случае ФЗП в экспоненциальном виде параметр формы mi принимают равным единице, а интенсивность отказов λ_i=1/η_i.

Из (9), при известных значениях экспериментальных данных, определяют вероятность параметрического отказа на уровне 0,2 - 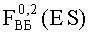, полученную путем обработки экспериментальных данных с использованием закона распределения Вейбулла.

При необходимости, на следующем этапе определяют вероятность для совокупности отдельных составляющих прибора (блоков, субблоков) и сравнивают полученное значение с оценкой величины для всего прибора в целом (табл.1).

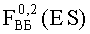
С целью определения наиболее значимого вида ИИ по его влиянию на уровень стойкости величины радиационной нагрузки ES в виде факторов 7.И1, 7.И6, линейных потерь энергии пересчитывают в единицы эквивалентной поглощенной дозы ИИ (77D) по критерию 1 Мэв-экв., производят построение ФЗП для каждого из видов ИИ на общем графике зависимости F_ВБ(ES), туда же, при необходимости, наносят гистограмму плотности распределения комплектующих СФА электронных компонентов по одному из видов ИИ, а по результатам сопоставления видовых ФЗП судят о стойкости всей СФА в целом к тому или иному виду ИИ.

Пример конкретной реализации способа.

Пример конкретной реализации способа.

Ниже приводятся результаты применения способа, описание которого приведено выше, для оценки стойкости прибора «А» и его составных частей, испытания которых на PC проводились в автономном режиме: блоков В1 и макетов блока P1.

Вначале исследовались данные, полученные по результатам облучения двух блоков В1 №1, №2 прибора «А» и двух приборов «А» №1, №2 в целом на двух различных моделирующих установках (МУ), соответственно. Критериальным параметром являлось сохранение работоспособности и отсутствие эффектов TREE. Уровню радиационного нагружения для блоков В1 соответствует фактор 7.И1, равный величине 10×1Ус, а для приборов - фактор 7.И6 величиной, равной 4,25×4Ус. Используя ФЗП, определили вероятность сохранения работоспособности прибора (ресурс) с учетом воздействия ИИ МУ. 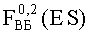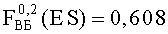В результате расчетов была получена вероятность параметрического отказа для условий облучения блоков В1 на первой установке из соотношения (9), которая составляет 0,12, - для условий облучения двух приборов на второй установке.

Далее исследовалась параметрическая работоспособность макетов блока Р1 прибора «А» №1, №2 и два прибора «А» в целом №3, №4 после воздействия импульсного излучения. В качестве критериальных параметров были выбраны усредненные токи и изменение частоты (см. табл.1). Согласно экспериментам макет блока Р1 должен сохранять работоспособность после воздействия смешанного излучения факторов 7.И1 и 7.И7 величиной 4,2×3Ус и 2,0×3Ус, соответственно. В результате расчетов были определены значения вероятности параметрического отказа 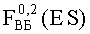, полученные из (9), которые составляют 0,68 и 0,75 - для двух приборов «А» и 0,738, 0,741 и 0,74 - для макетов Р1 для трех критериальных параметров.

Результаты расчетов работоспособности прибора «А» приведены в табл.1.

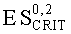
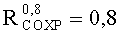
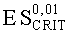
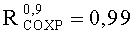
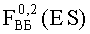
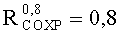
В табл.1 приведены значения нижней допустимой границы (НДГ) уровня стойкости по соответствующему уровню радиационной нагрузки , рассчитанные для вероятности сохранения работоспособности , значения НДГ уровня стойкости по соответствующему уровню радиационной нагрузки , рассчитанные для вероятности сохранения работоспособности , а также уровень радиации из критерия для прибора «А», блоков В1 и макетов Р1 для вероятности сохранения работоспособности .

В табл.1 содержатся следующие обозначения:

- уровень соответствующей радиационной нагрузки i (i=1, 3, 4), при котором наступает параметрический (катастрофический) отказ на уровне вероятности отказа F_CRIT=0,2;

m - параметр формы распределения Вейбулла;

λ - интенсивность параметрического (катастрофического) отказа;

η - параметр масштаба распределения Вейбулла;

- уровень соответствующей радиационной нагрузки i (i=1, 3, 4), при котором наступает параметрический (катастрофический) отказ на уровне вероятности отказа F_CRIT=0,99;

- вероятность сохранения работоспособности (ресурса), определенная с использованием закона распределения Вейбулла для .

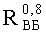
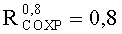
На Фиг.8 представлен интегральный закон распределения уровня PC (ФЗП) в зависимости от величины фактора 7.И1 для блоков B1 №1, №2 прибора «А».

Затем с учетом полученных данных (см. табл.1) для макета блока Р1 были определены математические ожидания из соотношения (10). Так как исходное распределение имело вид экспоненциального распределения (7), то параметр формы для всех радиационно-критических параметров принимался равным единице.

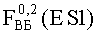
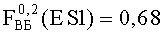
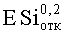
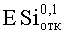
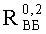
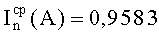
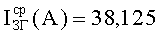
С другой стороны, используя (ПБ.12) (Приложение «Б»), и выполняя двойное потенцирование (ПБ.12) с учетом (10), получим вероятность параметрического отказа для всего прибора «А» с использованием критерия из (9), которая составляет 0,668. В табл.1 соответствующее значение, полученное для условий облучения всего прибора равно . Таким образом, имеется достаточно хорошее совпадение значений вероятностей параметрического отказа, полученное как с учетом испытаний макета блока P1 прибора, так и всего прибора в целом.

Таблица 1 - Результаты оценки радиационной чувствительности прибора «А» к воздействиям ИИ МУ Наименованию объекта испытаний Уровень рад. нагружения Наименование критериального параметра m λ η Прибор «А» Блок В 1 (№1, №2) ES1^max=2×1Ус сохранение работоспособности 1,8×1Ус 0,4 6,7 (-12) 1,5 (11) 1,62×1Ус 0,120 Прибор «А» (№1, №2) ES1^max=4,1×5Ус 2,65×5Ус 0,4 29,70 0,033 7,21×3Ус 0,680 2,8×5Ус   24,36 0,041 2,16×3Ус 0,750 Прибор «А» (№3, №4) ES4=4,3×6Ус сохранение работоспособности и отсутствие ложного срабатывания 3,69×6Ус 0,4 0,78 1,282 1,2×4Ус 0,608 Прибор «А» Макет Р1 (№1, №2) ES1^max=4,2×5Ус 2,15×5Ус 0,4 10,72 0,093 4,2×1Ус 0,738 ЕS3=0,8×5Ус 0,5×2Ус   0,36 2,770 0,79×1Ус 0,741 Δf=10,5 0,5×2Ус   0,64 1,562 1,0×1Ус 0,740 *) В круглых скобках приведены показатели степени по основанию 10 где: m_i - параметр формы, η_i - параметр масштаба распределения Вейбулла для каждого испытанного устройства.

Такая же процедура была применена для оценки PC к воздействию факторов 7.И7 и 7.И6 (см. табл.1). Для каждого вида ИИ можно построить зависимость F(U, x)=f(ES) (Фиг.9 и Фиг.10), аналогичную, приведенной на Фиг.8. График зависимости имеет тот же вид, а координатная сетка определяется видом воздействующего фактора и экспериментальными данными. 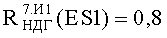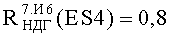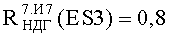Если во внимание принимается НДГ вероятности сохранения параметрической (катастрофической) работоспособности прибора (блока, субблока) R(U, x)=1-F(U, x)=f(ES), то для каждого из видов ESi осуществляют построение зависимости вида R(U, ES)=f(ES) для аналога, представленного на Фиг.8, и выполняют оценку НДГ вероятности сохранения работоспособности по фактору 7.И1, по фактору 7.И6 и по фактору 7.И7 (см. табл.2), откуда определяются значения уровней ИИ в абсолютных и относительных единицах измерения.

В табл.2 приведены также величины соответствующих значений уровней стойкости в абсолютных единицах и их отклонения от значений МО эквивалентного фактора 7.И7 для ЭКБ из справочной литературы (МОП) в единицах TID от математического ожидания уровня PC по каждому из факторов ИИ

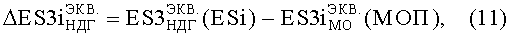
а также оценки этих уровней для верхней допустимой границы (ВДГ) - . Для расчета для фактора 7.И1 со средней энергией спектра E_7.И1≈1 МэВ использовали рекомендации /7/, а для расчета использовали соотношение

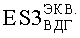
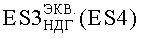
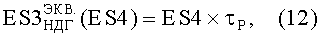
где τ_P - длительность импульса ИИ на первой установке.

На Фиг.10 приведен интегральный ФЗП для прибора «А», полученный по результатам анализа перечня МОП ЭКБ, входящей в состав комплектующих прибора, при воздействии фактора 7.И7, а также ФЗП, полученные по результатам экспериментальных исследований на МУ блоков и узлов прибора «А» на воздействие фактора 7.И1 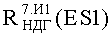в единицах эквивалентной TID, на воздействие фактора 7.И6 в единицах TID (рав. (12)) и на воздействие фактора 7.И7. На Фиг.11 приведен ФЗП для прибора «Б», полученный с использованием предлагаемого способа. Сравнение результатов, приведенных на Фиг.10 и Фиг.11 показывает, что ФЗП, полученный по результатам оценки PC ЭКБ из анализа справочных данных и ФЗП, полученные по результатам выполненных экспериментальных исследований уровня PC приборов и блоков на МУ по факторам 7.И1, 7.И6 и 7.И7, в целом совпадают для условия равенства максимальной плотности вероятности сохранения работоспособности (ресурса) dR/d(ES) комплектующей прибор ЭКБ от уровня воздействия ИИ и нижней допустимой границей ФЗП для каждого вида ИИ (Фиг.8-11).

Фактором, определяющем уровень PC для двух приборов, подвергавшихся анализу, является 7.И1. Порядок чередования по степени радиационного воздействия факторов ИИ для прибора «А» следующий: (1) - 7.И1; (2) - 7.И7; (3) - 7.И6, для прибора «Б»: (1) - 7.И1; (2) - 7.И6; (3) - 7.И7. В целом полученная картина аналогична приведенной на Фиг.4 в /4/ для факторов космического пространства и импульсного ИИ, воздействующих на аппаратуру КА.

Обращает на себя внимание тот факт, что ФЗП по фактору 7.И7 для прибора «Б» имеет НДГ порядка 0,685×6Ус, которая близка к максимальному уровню стойкости 1,0×6Ус по этому фактору для примененной ЭКБ. У прибора «А» НДГ по этому фактору имеет значение 0,155×6Ус, которое близко к минимальному уровню стойкости 0,1×6Ус по этому фактору для примененной ЭКБ. Указанное обстоятельство связано с различными сроками разработки приборов, что, по-видимому, определяет качество ЭКБ и методы оценки стойкости ее к эффектам от воздействия фактора 7.И7, в том числе возможный «технологический дрейф» уровня PC однотипной ЭКБ.

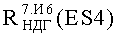
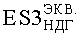
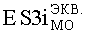
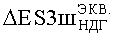
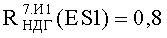
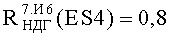
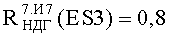
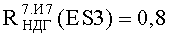
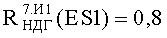
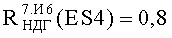
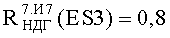
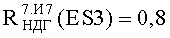
Различия в положении на Фиг.10 и на Фиг.11 ФЗП связано со специально разработанными схемотехническими решениями для прибора «А», предотвращающими эффекты TREE. Насыщенность прибора «Б» цифровой ЭКБ приводит к снижению стойкости к переходным эффектам от импульса ИИ до уровня 1,0×1Ус-1,0×3Ус по фактору 7.И6 и большей зависимости итогового результата от собственного уровня стойкости к этому фактору отдельных ИМС и исполнительных каскадов.

Таблица 2 - Результаты оценки чувствительности приборов «А» и «Б» к воздействиям спецфакторов Наименовали с объекта испытаний Уровень рад. нагружения Критериальный параметр Значение Значение Значение Значение Прибор «А» ES1^max Нижняя допустимая граница 1,875×2Ус 2,35×3Ус 0,275×6Ус +1,85×3Ус ES4^max Нижняя допустимая граница 39×6Ус 40,5×6Ус 42×6Ус +38,9×6УС ES3^max Нижняя допустимая граница 0,12×6Ус 0,13×6Ус 0,155×6Ус +0,104×6Ус ES3^max Нижняя допустимая граница - 0,53×3Ус - - Прибор «Б» ES1^max Нижняя допустимая граница 1,3×3Ус - - 0,8×3Ус ES4^max Нижняя допустимая граница 0,687×6% 0,742×6Ус 0,89×6Ус 0,587×6Ус ES3^max Нижняя допустимая граница 1,67×3Ус - - +1,17×3Ус ES3^max Нижняя допустимая граница - 0,5×3Ус - -

Приведенная в табл.1 величина 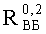- вероятность сохранения работоспособности (ресурса), определенная с использованием закона распределения Вейбулла из экспериментальных зависимостей для всех экспериментов с положительным эффектом имеет значение в интервале 0,68-0,75, которые достаточно близки директивному значению 0,8, которое использовалось при проведении настоящего анализа. Предложенный способ позволяет при заданных уровнях радиационного нагружения определить вероятность сохранения работоспособности объектов, отсутствия эффектов TREE по результатам испытания отдельных узлов и блоков и использовании критериев параметрического и функционального отказа.

С использованием разработанного единого методического подхода получены соотношения, которые используются для получения зависимости вероятности параметрического или функционального отказа от величины воздействующего ИИ - физического закона поражения (ФЗП) как с учетом, так и без учета доверительного интервала.

Приложение «А»: Применение распределения Вейбулла

Распределение Вейбулла названо в честь шведского исследователя Валодди Вейбулла (Waloddi Weibull), применявшего это распределение для описания времен отказов разного типа в теории надежности.

Если вероятность отказа меняется с течением времени, применяется распределение Вейбулла. Данное распределение определено для положительных значений параметров η, m и γ, которые называются соответственно параметрами масштаба, формы и положения.

Параметр положения γ. Обычно распределение Вейбулла сосредоточено на полуоси от 0 до бесконечности. Если вместо границы 0 ввести параметр γ, что часто бывает необходимо на практике, то возникает так называемое трехпараметрическое распределение Вейбулла.

Параметр формы m является своеобразным индикатором изнашиваемости объекта или образования в нем остаточных дефектов структуры и сохраняет свое значение в области изменения случайной величины, в которой характер дефектов является стабильным и однородным.

Параметр масштаба η определяет ширину плотности распределения случайной величины.

Плотность распределения Вейбулла:

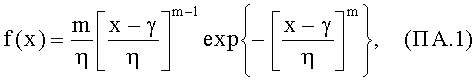
при γ<x, η>0, m>0

Функция распределения (ФР) Вейбулла:

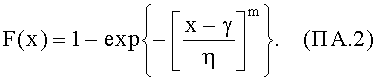
Функция надежности. Функция надежности вычисляется с помощью функции распределения Вейбулла по формуле:

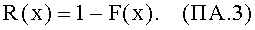
Кумулятивная функция риска:

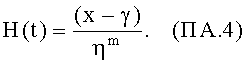
Функция риска (интенсивности). Функция риска описывает вероятность отказа в течение малого промежутка времени при условии, что до этого момента отказа не произошло. На основе распределения Вейбулла получается функция риска (интенсивности отказов) следующего вида:

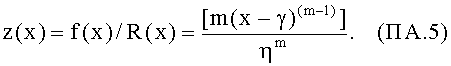
В формулах для функции интенсивности и кумулятивной функции риска использованы те же обозначения, что и в приведенных выше выражениях для функций плотности и надежности.

В общем виде функция интенсивности отказов записывается в виде:

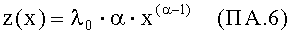
где λ₀>0 и α>0 - некоторые численные параметры.

Здесь λ₀ - интенсивность отказов, соответствующая нормальной эксплуатации объекта (т.е. m=α=1). В случае применения этой функции к условиям воздействия ИИ вместо аргумента x в (ПА.5-ПА.6) следует подставить значение величины радиационной нагрузки ES. Связь величины с шириной распределения Вейбулла определяется соотношением λ₀=1/η^m, а параметр m=α.

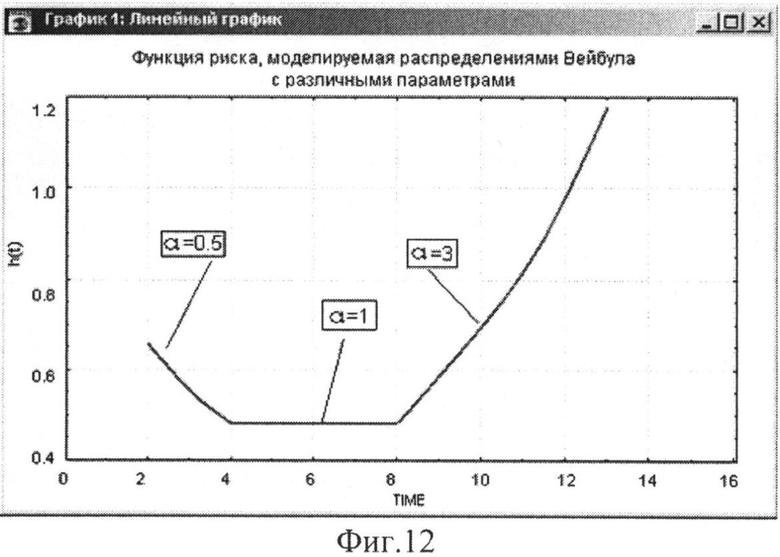
При α=1 функция риска равна константе, что соответствует нормальной эксплуатации объекта (см. формулы).

При α<1 функция риска убывает, что соответствует приработке объекта.

При α>1 функция риска возрастает, что соответствует старению объекта.

Функция риска представлена на Фиг.12.

Следует обратить внимание на три области значений параметра α (Фиг.12):

I. α<1; II. α=1; III. α>1. В первой области «I» функция риска убывает (период настройки или приработки), во второй области «II» функция риска равна константе (область нормальной работы), в третьей области «III» функция риска возрастает (область старения). В случае использования закона распределения Вейбулла в теории надежности эти области представлены на Фиг.13-а) зависимостью вида «А». При воздействии радиационной нагрузки ES в пределах временной области «II» с началом по оси времени в момент t_i и завершением в момент времени t₀ величина интенсивности отказов λ(t) не является константой, а меняется по закону (ПА.6), как показано на Фиг.12-а) зависимостью вида «Б». Тот факт, что при воздействии радиационной нагрузки функция риска (интенсивности отказов) зависит от уровня ES в соответствии с соотношением (ПА.5) показан на Фиг.12-б). Важно, что все периоды эксплуатации можно описать одним и тем же семейством распределения. В этом и состоит идея использования распределения Вейбулла.

Приложение «Б»: Оценка параметров ФЗП для СФА по результатам обработки экспериментальных данных для составных частей

Представление функции повреждения без доверительных границ эквивалентно допущению, что верно заданы выборки среднего и стандартного отклонения случайных переменных при их простой оценке. Во внимание принимают следующие шаги для определения сохранения работоспособности без использования доверительных границ:

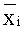
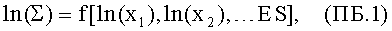
1) для каждого независимого режима отказа системы определяется модель границ безопасности ∑ как функция независимых переменных x_i, которые распределены по допущению по закону распределения Вейбулла со средним значением и стандартным отклонением s_i. Введем их в виде

где ES является мерой радиационного воздействия и она не зависит от случайной переменной.

2) преобразование среднего значения и стандартного отклонения распределенной по закону Вейбулла величины x_i в аналогичные значения нормированной случайной величины ln(x_i) проводят с использованием соотношения

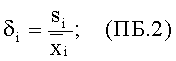
- коэффициент вариации;

- математическое ожидание генеральной совокупности;

- квадрат дисперсии генеральной совокупности.

3) разлагают ln(∑) в ряд Тейлора около среднего значения величины ln(x_i), a именно, µ_i,

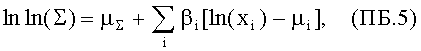
выражают параметры µ_∑ и β_i через соотношения

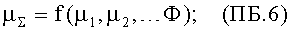
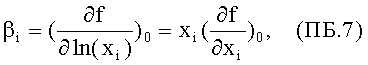
где коэффициенты β_i преобразованы, исходя из равенств ln(x_i)=µ_i или x_i=ехр(µ_i). Если важный функциональный критерий задан в форме произведений соответствующих случайных величин

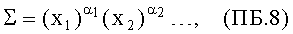
то подстановка такой случайной величины в равенство (ПБ.5) дает точное согласие. Так как равенство (ПБ.5) является линейной комбинацией нормальных случайных переменных, т.е. ln(x_i), то ln(∑) является также нормальной величиной со своим уровнем аппроксимации, своим средним значением µ_∑ и стандартным отклонением

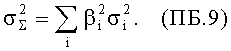
1) получают вероятность сохранения работоспособности для каждого значения режима повреждения с помощью соотношения

где Ф(х) является обобщенной стандартной функцией нормального распределения (квантилью)

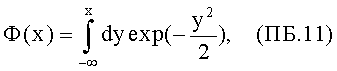
которая табулирована, например, в /5/. Таким образом, Р относят к нормальному распределению, что вытекает из того, что ln(x_i) является нормальным распределением, а представление lnln(∑) в виде суммы нормальных случайных переменных делает lnln(∑) также нормально распределенным.

5) комбинируют определенные виды повреждения для определения сохранения работоспособности в систему оценки уровней сохранения работоспособности при допущении функциональной независимости видов повреждения, и допускают, что статистически они действуют последовательно, что позволяет записать

Если соотношение (ПБ.5) сравнить с линеаризированной формой интегрального закона распределения Вейбулла

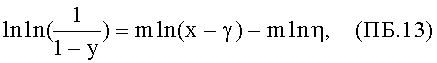
то следует принять, что для объекта, состоящего из n единиц, математическое ожидание среднего для всего объекта может быть определено из суммы произведений параметров формы на логарифм натуральный параметра масштаба для каждой составляющей единицы

,

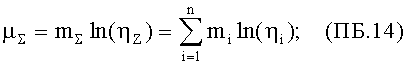
где:

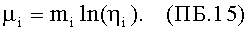
С учетом (ПБ.14) и (ПБ.15) из (ПБ.5) следует, что

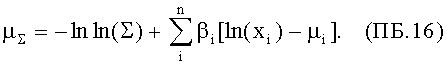
Тогда

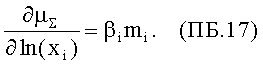
Окончательно получим

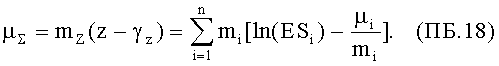
Если

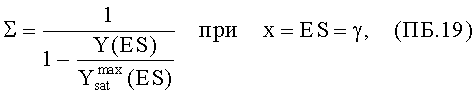
то выполняя двойное потенцирование (ПБ.18) с учетом (ПБ.5), получим для всего КА

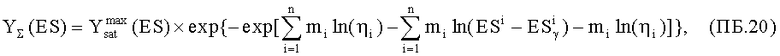
а - максимальное значение РКП из всех рассмотренных для субблоков (ЭКБ), - пороговое значение РКП для уровня для каждого из субблоков (ЭКБ).

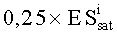
Литература

1. Rickets L.W. Fundamentals of Nuclear Hardening of Electronic Equipment. - N.Y. Willey-Ntranscience, 1973.

2. Никифоров А.Ю., Телец В.А., Яшанин И.Б. и др. Способ разбраковки КМОП микросхем, изготовленных на КНД структурах, по стойкости к радиационному воздействию // Патент РФ №2364880 от 20.08.09 г.

3. Виноградова О.М., Копнов П.В., Фомичев В.В., Яшанин И.Б. Автоматизированная информационная система «Статистическая обработка результатов радиационной отбраковки микросхем» // Свидетельство об официальной регистрации программы для ЭВМ №2007614627 от 06.11.07 г.

4. Clement D.C. and Jonson J.W. TRW Defense and Space Group Satellite Survivability Estimates. // IEEE Transactions on Nuclear Science, Dec. 1981. - vol. NS-28. - No.6. - pp.4199-4203.

5. Bagge Carl and Rothman David. A First-Order Methodology for Cflculating Probabbility of Mission Success, 31 Januar 1999, DNA 4843F.

6. LaBel, K. Single event effects specification // radhome.gsfc.nasa.gov/radhome/papers/seespec.htm.

7. Бутин В.И., Зинченко В.Ф., Романенко А.А. Система радиационных испытаний изделий электронной техники: Монография / Владимир: Владимирский государственный университет, 2003. - 188 с.

Изобретение относится к области испытаний сложно-функциональной аппаратуры. Сущность изобретения заключается в том, что используют трехпараметрическое распределение Вейбулла или доверительный интервал, внутренние границы которого (U - нижняя и V - верхняя) получают на основе обработки экспериментальных данных по облучению выборки размером n, внешние границы (U - нижняя и V - верхняя) задают из общих физических представлений, определяющими из которых является уровень отсутствия наблюдаемых критических изменений и незначительное, на 20-30%, превышение требований по стойкости объектов к воздействию ИИ, в выбранных границах (U, V) вводят экспериментально полученную интегральную функцию распределения нижних допустимых уровней стойкости к различным видам ИИ, определяют скорость изменения вероятности параметрических или функциональных отказов (интенсивность изменения параметрического ресурса), затем строят семейство графиков зависимости функции распределения F(U, x) от различных видов ионизирующих излучений (флюенса нейтронов (F_n); мощности дозы гамма-рентгеновского излучения (P_γ-X-Rey); полной поглощенной дозы (D_γ-X-Ray); флюенса тяжелых заряженных частиц (ТЗЧ) Ф_ион; величины линейных потерь энергии (LET) (для аппаратуры, размещаемой на космическом аппарате (КА) и т.п.) при фиксированных значениях , по построенным графикам определяют уровень радиационной нагрузки , при котором вероятность отказа прибора составляет F_CRIT, или ресурс сохранения работоспособности R_СОХР=1-F_CRIT. Технический результат - повышение достоверности определения стойкости электронных компонентов и блоков РЭА к воздействию ионизирующего излучения. 3 з.п. ф-лы, 13 ил., 2 табл.

1. Способ определения стойкости электронных компонентов и блоков радиоэлектронной аппаратуры к воздействию ионизирующих излучений (ИИ) путем построения зависимости функции распределения вероятности параметрической или функциональной работоспособности от уровня радиационной нагрузки x и определения критического уровня воздействия ИИ по заданному уровню этой вероятности, отличающийся тем, что, с целью определения функции распределения вероятности параметрической или функциональной работоспособности, для малых выборок облучаемых объектов (физического закона поражения, ФЗП) используют трехпараметрическое распределение Вейбулла или доверительный интервал, внутренние границы которого (u - нижняя и v - верхняя) получают на основе обработки экспериментальных данных по облучению выборки размером n, внешние границы (U - нижняя и V - верхняя) задают из общих физических представлений, определяющими из которых является уровень отсутствия наблюдаемых критических изменений и незначительное, на 20-30%, превышение требований по стойкости объектов к воздействию ИИ, в выбранных границах (U, V) вводят экспериментально полученную интегральную функцию распределения нижних допустимых уровней стойкости к различным видам ИИ в форме

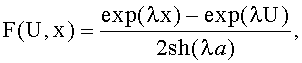
определяют скорость изменения вероятности параметрических или функциональных отказов (интенсивность изменения параметрического ресурса) путем решения трансцендентного уравнения

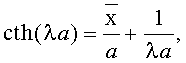
где a - полуширина интервала [U, V];
- среднее арифметическое значение уровней стойкости объектов в выборке;
- интенсивность параметрических отказов;
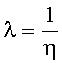
η - параметр масштаба эквивалентного распределения Вейбулла,
затем строят семейство графиков зависимости функции распределения F(U, x) от различных видов ионизирующих излучений (флюенса нейтронов (F_n); мощности дозы гамма-рентгеновского излучения (P_γ-X-Rey); полной поглощенной дозы (D_γ-X-Ray); флюенса тяжелых заряженных частиц (ТЗЧ) Ф_ион; величины линейных потерь энергии (LET) (для аппаратуры, размещаемой на космическом аппарате (КА)) и т.п.) при фиксированных значениях , по построенным графикам определяют уровень радиационной нагрузки , при котором вероятность отказа прибора составляет F_CRIT, или ресурс сохранения работоспособности R_СОХР=1-F_CRIT.

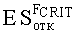
2. Способ по п.1, отличающийся тем, что, с целью повышения информативности вероятностной оценки стойкости объектов к воздействию различных видов ИИ, в качестве ФЗП используют трехпараметрическое распределение Вейбулла

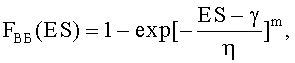
где ES - уровень радиационной нагрузки;
F_ВБ(ES) - вероятность параметрического или функционального отказа в зависимости от величины уровня радиационной нагрузки ES;
η - параметр масштаба;
m - параметр формы;
γ - параметр положения,
для деградационных эффектов, определяющих ФЗП, вероятность 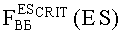параметрического или функционального отказа при критическом уровне радиационной нагрузки ES_CRIT, критическое значение ES_CRIT определяют путем обработки экспериментальных данных с использованием закона распределения Вейбулла, а для случая параметрического отказа значения радиационно-критических параметров (РКП) задают в относительных единицах, или процентах.

3. Способ по п.2, отличающийся тем, что для оценки стойкости к воздействию ИИ сложно-функциональной аппаратуры (СФА) по результатам обработки экспериментальных данных с использованием экспоненциального закона распределения или распределения Вейбулла для составных частей объекта, математическое ожидание (МО) µ_∑ для СФА определяют с использованием соотношения

где m_i - экспериментально полученный параметр формы распределения Вейбулла для ФЗП отдельного элемента (субблока);
η_i - параметр масштаба распределения Вейбулла,
а в случае ФЗП в экспоненциальном виде параметр формы m_i принимают равным единице, а интенсивность отказов λ_i=1/η_i;
m_Z - параметр формы распределения Вейбулла для СФА;
η_Z - параметр масштаба распределения Вейбулла для СФА.

4. Способ по п.2, отличающийся тем, что, с целью определения наиболее значимого вида ИИ по его влиянию на уровень стойкости, величины радиационной нагрузки ES в виде флюенса нейтронов, мощности дозы ИИ, линейных потерь энергии, пересчитывают в единицы эквивалентной полной поглощенной дозы ИИ по критерию 1 Мэв-экв., производят построение ФЗП для каждого из видов ИИ на общем графике зависимости F_ВБ(ES), туда же, при необходимости, наносят гистограмму плотности распределения комплектующих СФА электронных компонентов по одному из видов ИИ, а по результатам сопоставления видовых ФЗП судят о стойкости всей СФА в целом к тому или иному виду ИИ.