Изобретение относится к способам оценки сечений радиационно-индуцированных сбоев в элементах статических оперативных запоминающих устройств (СОЗУ), выполненных по комплементарной металл-оксид-проводник (КМОП) технологии (КМОП СОЗУ) при воздействии потоков нейтронов с энергией до 14 МэВ, и может использоваться для определения сечения сбоев в конкретных радиационных условиях, а также параметра сбоеустойчивости интегральной микросхемы для прогнозирования сечения сбоев при любых видах спектрально-энергетической характеристики нейтронных потоков с энергией до 14 МэВ.
Для расчета одиночных радиационных эффектов, возникающих при воздействии нейтронов, обычно используют модель вторичных частиц, рожденных путем взаимодействия нейтронов внешней среды и материалов микросхемы. Поскольку именно вторичные заряженные частицы имеют ионизирующую способность, которой не имеют первичные нейтроны, их учет необходим для оценки устойчивости микросхем к одиночным радиационным эффектам.
Известен способ определения частоты сбоев в ИМС при воздействии потоков нейтронов на основе экспериментально определенных сечений с помощью генераторов моноэнергичных нейтронов, моноэнергичных протонов и нейтронов сплошного спектра [JEDEC standard: Measurement and Reporting of Alpha Particle and Terrestrial Cosmic Ray-Induced Soft Errors in Semiconductor Devices. August 2006. (Стандарт ассоциации инженеров электронных приборов (JEDEC) № JESD89A. Измерение и описание мягких ошибок в полупроводниковых приборах при воздействии альфа-частиц и наземных компонентов космических лучей. 2006)]. Для моноэнергичных нейтронов способ предлагает использовать частоту событий в стационарном потоке нейтронов, которая связана с сечением сбоев согласно выражению:
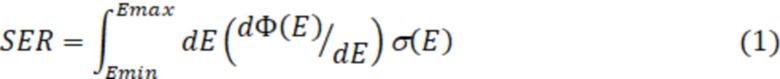
где  дифференциальная плотность потока нейтронов [МэВ-1⋅см-2⋅с-1], σ(Е) - сечение сбоев микросхемы при потоке нейтронов с энергией E. Вид функции σ(Е) метод предлагает аппроксимировать функцией Вейбулла, вид которой приведен ниже:
дифференциальная плотность потока нейтронов [МэВ-1⋅см-2⋅с-1], σ(Е) - сечение сбоев микросхемы при потоке нейтронов с энергией E. Вид функции σ(Е) метод предлагает аппроксимировать функцией Вейбулла, вид которой приведен ниже:

где σнас - параметр верхней асимптоты графика функции, Е0 - параметр порога начальной энергии сбоя, W и S - другие параметры, определяющие форму кривой функции. Частота сбоев SER в общем случае связана с сечением сбоя о следующим соотношением

где Ф это плотность потока нейтронов [см-2с-1], σ - сечение сбоев при таком стационарном потоке [см2]. Использование модели вторичных частиц данный способ не предполагает.
Недостатками этого способа являются, во-первых, трудоемкость проведения оценок, обусловленная сложностью задачи оптимизации функции зависимости сечения сбоя от энергии или ЛПЭ (линейных потерь энергии) исходящей частицы с помощью функции Вейбулла с четырьмя параметрами относительно небольшого набора точек, в результате которой возможно получение нескольких эффективных наборов параметров с большим различием в значениях от набора к набору; и во-вторых, отсутствие возможности использования в методе данных, полученных на источниках протяженного спектра нейтронов, например, нейтронов спектра деления.
Известен также способ оценки сечения одиночных сбоев в КМОП СОЗУ при воздействии потоков нейтронов произвольного спектра [М.М. Арманов, А.С. Кустов, О.В. Ткачев, К.Д. Кокшарова / Оценка сечения одиночных сбоев в статическом ОЗУ для произвольного спектра нейтронов по результатам, полученным на нейтронном генераторе // Вопросы атомной науки и техники. Сер: Физика радиационного воздействия на радиоэлектронную аппаратуру. 2021. Вып. 3. С 17-21.] заключающийся в оценке зависимости сечения сбоев согласно выражению:

где ƒ2, ƒ1 это некоторые энергетические спектры нейтронов, а P2 и Р1 определяются выражением
P(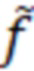 ,LETth)=
,LETth)=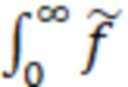 (LET)*exp (-
(LET)*exp (- dLET
dLET
где, (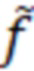 ,LET) это реализация модели вторичных заряженных частиц в виде функции, рассчитанной для кремния программой ПРИЗМА, LETth - порог чувствительности к сбою по ЛПЭ, характеризующий сбоеустойчивость микросхемы.
,LET) это реализация модели вторичных заряженных частиц в виде функции, рассчитанной для кремния программой ПРИЗМА, LETth - порог чувствительности к сбою по ЛПЭ, характеризующий сбоеустойчивость микросхемы.
Недостатком этого способа является метод перехода к ЛПЭ-спектру, который основан на расчете спектров вторичных заряженных частиц на основе кремниевой мишени без учета материального состава микросхемы. Такие методы нечувствительны к изменению состава ЛПЭ-спектра вторичных частиц при изменении угла падения пучка нейтронов на пластину микросхемы. Другим недостатком способа является отсутствие явного метода определения порогового параметра чувствительности микросхемы LETth.
Также известен способ прогнозирования сечения сбоев при воздействии нейтронов некоторой энергии или спектра энергий, в рамках которого сечение сбоя микросхемы при воздействии нейтронов с некоторой энергией En определяется согласно выражению
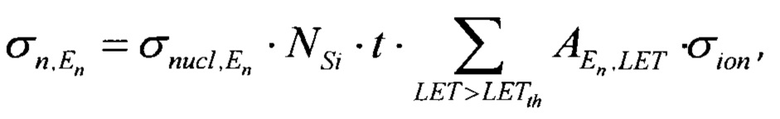
где  - суммарное сечение упругих и неупругих взаимодействий нейтрона с энергией
- суммарное сечение упругих и неупругих взаимодействий нейтрона с энергией 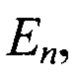
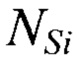 - плотность атомов кремния, t - объем ядерных взаимодействий,
- плотность атомов кремния, t - объем ядерных взаимодействий, 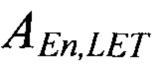 - вероятность достижения ЛПЭ равной LET вторичным ядром,
- вероятность достижения ЛПЭ равной LET вторичным ядром, 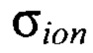 - сечение насыщения сбоев от некоторого иона. При наличии экспериментально определенного сечения на нейтронах с энергией 14 МэВ, можно записать следующее выражение
- сечение насыщения сбоев от некоторого иона. При наличии экспериментально определенного сечения на нейтронах с энергией 14 МэВ, можно записать следующее выражение

где параметры 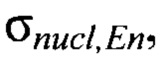 и
и 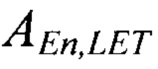 могут быть вычислены путем Монте-Карло моделирования. Авторы используют Монте-Карло симулятор на основе GEANT [GEANT4. Инструмент для моделирования прохождения частиц через вещество, https://geant4.web.cern.ch - электронный ресурс] для реализации модели вторичных заряженных частиц. С помощью вышеуказанного выражения можно оценить параметр LETth, который и будет являться характеристикой чувствительности микросхемы. [С. Weulersse et al., "Applicability and extrapolation model for SEE characterization using 14 MeV neutron," in Proc. Eur. Conf. Radiat. Effects Compon. Syst., Bremen, Germany, 2016.].
могут быть вычислены путем Монте-Карло моделирования. Авторы используют Монте-Карло симулятор на основе GEANT [GEANT4. Инструмент для моделирования прохождения частиц через вещество, https://geant4.web.cern.ch - электронный ресурс] для реализации модели вторичных заряженных частиц. С помощью вышеуказанного выражения можно оценить параметр LETth, который и будет являться характеристикой чувствительности микросхемы. [С. Weulersse et al., "Applicability and extrapolation model for SEE characterization using 14 MeV neutron," in Proc. Eur. Conf. Radiat. Effects Compon. Syst., Bremen, Germany, 2016.].
Недостатками описанного способа являются, во-первых, использование мишени из кремния, и во-вторых, наличие неопределенных параметров в выражении для сечения сбоев, а именно t и σion, которые могут быть как дополнительными параметрами модели, которые требуют экстракции путем анализа экспериментальных данных, так и отдельно оцениваемыми факторами, усложняющими применение способа в целом.
Известен также способ оценки сечения сбоев, в рамках которого количество событий при воздействии флюенса нейтронов в некоторых реальных условиях Фr(Er) в микросхеме можно оценить с помощью выражения:
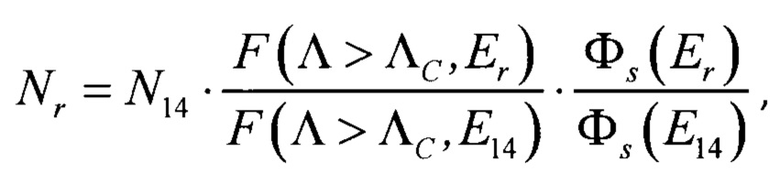
где Nr - это количество сбоев при воздействии нейтронов случайного спектра, N14 - количество сбоев при воздействии нейтронов с энергией 14 МэВ, Фs(Е14), Фs(Er) - потоки вторичных частиц при облучении нейтронов соответствующих спектров. Е(Λ, Е14), F(Λ, Er) - нормированные функции ЛПЭ-спектра нейтронов с энергией 14 МэВ и нейтронов случайного спектра соответственно. ΛC - некоторый параметр, определяемый для микросхемы и аналогичный LETth в перечисленных ранее способах.
Выражение для оценки количества сбоев N, приведенное выше, можно переписать для оценки сечений сбоев воспользовавшись соотношением σ=N/Ф, где σ - сечение сбоев микросхемы при данном флюенсе Ф нейтронов. Функции Е(Λ, En) имеют смысл нормированных на единицу ЛПЭ-спектров вторичных частиц, которые образовались в результате воздействия первичных нейтронов с мишенью, методом Монте-Карло при помощи программ на основе GEANT, и являются реализацией модели потоков вторичных частиц. [И.В. Елушов. Оценка стойкости элементов СОЗУ к одиночным сбоям при воздействии высокоэнергичных нейтронов. Технологии электромагнитной совместимости, 2019. Вып. №69. №2. С 6-12.]. Данное техническое решение принято в качестве прототипа.
Недостатками прототипа являются, во-первых, отсутствие явного метода определения параметра сбоеустойчивости микросхемы ΛC, и во-вторых, отсутствие методических рекомендаций, описывающих, в каком случае следует использовать кремний и оксид кремния в качестве мишени для расчета ЛПЭ-спектров вторичных частиц.
Для устранения недостатков прототипа следует использовать геометрическую модель микросхемы с указанием материалов ее составных частей в качестве мишени в рамках численного расчета. Для этого задается мишень в виде структуры из плоских однородных слоев в форме параллелепипеда, где один кремниевый слой является детектором частиц.
Предложенный способ предполагает наличие единственного параметра сбоеустойчивости ΛC, определяемого с помощью расчета на основе экспериментальных значений сечения сбоев и имеющего физический смысл значения порога ЛПЭ вторичной частицы, выше которого наступает сбой (здесь и далее подразумевается ЛПЭ в кремнии). Для этого требуются две серии экспериментов, одна из которых получена на генераторах нейтронов с энергией 14 МэВ, другая - на нейтронах произвольного спектра, близкого к спектру деления урана-235.
Техническим результатом изобретения является повышение достоверности расчетно-экспериментальной оценки сечения сбоев в микросхемах КМОП СОЗУ, возникающих при воздействии потоков нейтронов с произвольной энергетической характеристикой в диапазоне до 14 МэВ, за счет использования трехмерной модели микросхемы, состоящей из плоских слоев натуральной толщины из материалов кремния и оксида кремния, и позволяющая учитывать зависимость ЛПЭ-спектров вторичных заряженных частиц от угла падения нейтронов относительно плоскости пластины микросхемы при расчете методом Монте-Карло параметров модели вторичных заряженных частиц.
Технический результат достигается тем, что с помощью численного расчета методом Монте-Карло получают реализацию модели вторичных заряженных частиц, рассчитанной с использованием геометрической модели микросхемы в виде плоских слоев, состоящих из кремния или оксида кремния, и имеющих толщину соразмерную топологическим слоям исследуемой микросхемы; затем, при использовании ее в рамках расчетно-экспериментального метода оценки сечений сбоев путем определения параметра чувствительности микросхемы определяют ΛC и ЛПЭ-спектров вторичных частиц в реальных условиях.
Способ включает в себя следующие этапы.
1. Получают экспериментальных значений сечения сбоев изделия с использованием доступных источников нейтронов.
На данном этапе проводится экспериментальная оценка сечений сбоев на доступных источниках нейтронов. Для определения параметра сбоеустойчивости необходимо исследование с использованием минимум двух типов источников нейтронов, одним из которых должен быть источник нейтронов с энергией 14 МэВ, другой может иметь сплошной спектр нейтронов с энергией до 14 МэВ. Дополнительное исследование с помощью третьего источника нейтронов позволит провести верификацию модели и получить дополнительные оценки, тем самым сделав прогноз точнее.
2. Формируют упрощенную геометрическую модель микросхемы, используемой в качестве мишени.
На данном этапе создают геометрическую модель микросхемы с учетом химического состава материалов и толщин основных топологических слоев, соответствующих технологии изготовления. Модель строится по следующим правилам:
• в качестве материалов используют кремний или оксид кремния;
• модель микросхемы состоит из тонких слоев в форме параллелепипеда;
• каждому слою соответствует один материал;
• толщина слоя соответствует топологическому размеру соответствующего топологического слоя микросхемы;
• длина и ширина слоя выбираются свободно, но и длина, и ширина по отдельности должны быть не меньше пробега исследуемых вторичных частиц в данном материале - при расчете с энергиями нейтронов до 14 МэВ рекомендуется использовать длину и толщину равные не менее 2 мм;
• один из слоев называется детектором, он имеет кремний в качестве материала и располагается в пределах топологического слоя, в котором выполнены активные элементы печатной платы;
3. Проводят расчеты по модели вторичных заряженных частиц для условий экспериментального облучения, а также для отличающихся по спектральному составу условий.
На данном этапе реализуют модели вторичных частиц в виде функций F(Λ), которые имеют физический смысл интегрального ЛПЭ-спектра, нормированного на единицу, при этом значение функции F(ΛC) будет эквивалентно доле частиц, для которых справедливо Λ>ΛC, где ΛC - критическое значение ЛПЭ и параметр сбоеустойчивости изделия. Модель потоков вторичных частиц зависит от состава и геометрии микросхемы, от направления падения нейтронов и от их энергии. Этот пункт повторяется столько же раз, сколько есть независимых экспериментальных оценок, и отдельно для расчета с учетом реальных условий.
Расчет по модели вторичных частиц реализуют с помощью численного моделирования взаимодействий нейтронов с мишенью в виде модели микросхемы методом Монте-Карло, для каждой из вторичных частиц получают набор значений: типа частицы (наименования и массы изотопа для тяжелых ядер), ее начальной энергии, ее потерю энергии в детекторе и направления движения в момент возникновения, пересечения или остановки движения в объеме слоя-детектора. Реализация модели вторичных частиц, таким образом, заключается в составлении списка с характеристиками всех вторичных частиц, полученных для некоторого численного расчета. В дальнейшем для определения вида F(Λ) производится отбор частиц.
Отбор частиц проводят по следующим признакам:
• отбор вторичных частиц по признаку способности к ионизации - наличию кулоновского заряда - таких как ионы, протоны, дейтроны; электроны являются исключением и в модель не входят ввиду малой ионизирующей способности;
• дальнейший отбор вторичных частиц по начальной энергии, которая должна быть не меньше 10 кэВ.
Построение функции F(Λ) включает в себя следующие этапы:
• для каждой отобранной частицы, за исключением альфа-частиц, протонов и дейтронов, установить значение ЛПЭ, равное значению ЛПЭ соответствующей частицы в кремнии с энергией, равной начальной энергии частицы;
• для альфа-частиц, протонов и дейтронов установить значение ЛПЭ, равное максимальному ЛПЭ частицы в пределах трека внутри слоя-детектора;
• объединение всех значений ЛПЭ в один список (массив значений, столбец таблицы и т.д.), размер списка должен соответствовать количеству частиц;
• сортировка списка от меньших значений ЛПЭ к большим;
• отброс частиц, ЛПЭ которых оказывается менее 0.035 МэВ/мкм или 0.168 МэВ⋅см2/мг;
• создание функции на основе сортированного списка, где аргументом является значение ЛПЭ, а значением функции - количество частиц, меньшее или равное значению аргумента;
• нормировка функции: максимум функции должен быть равен 1, а интервал допустимых значений функции не выходить за пределы от 1 до 0.
Примеры графиков функций F(Λ) представлены на изображениях с фиг. 1 по фиг. 6.
4. Рассчитывают R-функции и определяют значение параметра ΛC.
На данном этапе рассчитанные функции F(Λ) используют для получения R-функций. Вид функции R определяется индивидуально для каждой задачи, и включает в себя функции для экспериментальных (Fexp) и прогнозируемых (Fr) условий согласно выражению:
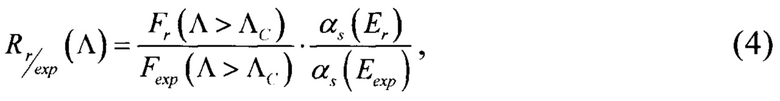
где, α - отношение числа вторичных заряженных частиц Фs к первичному числу нейтронов Фn, определяемое выражением:

в котором Ei - i-й спектр нейтронов, падающих на мишень согласно выбранному направлению.
С помощью R-функции однозначно определяется параметр сбоеустойчивости ΛC, при этом используются оценки сбоев, полученные при экспериментальной проверке. Определение ΛC проводится согласно выражению
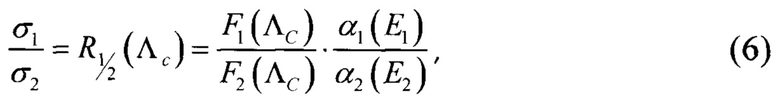
где σ1, σ2 соответствуют экспериментальным сечениям сбоев, полученным на установках со спектрально-энергетическими характеристиками Ф(1) и Ф(E2). Если экспериментальных данных больше, проводят оценки ΛC для каждой пары из списка σ1, σ2, …, σn, впоследствии из этих значений выбирается наименьшее. Следуя способу, в качестве одного из источников нейтронов используюь генератор нейтронов с энергией 14 МэВ, на котором требуется получить значение σ14, в качестве другого - непрерывный спектр, близкий к спектру распада урана-235, на котором требуется получить значение σf. Таким образом, выражение (6), путем подстановки раскрытого с помощью (4) выражения для R(Λ) принимает вид

откуда ΛC может быть определено методом последовательных приближений или графически, с использованием средств компьютерное визуализации.
5. Определяют сечения сбоев для прогнозируемых условий.
Сечение сбоев в прогнозируемых условиях определяют согласно выражению
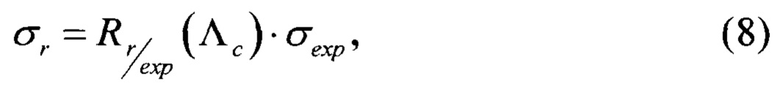
где σr - это сечение сбоев для реальных условий, которое находится путем произведения сечения σexp сбоев в условиях эксперимента на значение функции R в точке ΛC. R-функция при этом имеет вид (4), где в качестве Fr используется функция, полученная для нейтронов прогнозируемых условий, а в качестве Fexp используется функция, соответствующая нейтронам экспериментальной установки, в результате которого было получено значение σexp. Подставив полученное на предыдущем пункте расчета значение  получают итоговое выражение для сечения сбоев в прогнозируемых условиях
получают итоговое выражение для сечения сбоев в прогнозируемых условиях

где в качестве σexp выбирают любое из двух экспериментальных сечений, использованных в выражении для ΛC, используя также соответствующий расчетный спектр Fexp(Λ) и значения Фn(Eexp), Фs(Eexp).
Пример реализации способа.
Допустим, что имеются два типономинала микросхем СОЗУ, с условными наименованиями ИМС1 и ПМС2. Также имеются значения сечения сбоев (на микросхему), определенные экспериментально с использованием генератора нейтронов с энергией 14 МэВ и реакторного спектра, близкого к спектру деления, отмеченные в таблице 1 как и Ср соответственно.

Создаются модели микросхем, состоящие из нескольких плоских слоев. Для простоты будем считать, что модель для двух микросхем будет одинакова и состоит из трех слоев согласно таблице 2.

При этом также опишем условия эксперимента и прогнозируемые условия. Пусть все воздействия нейтронов на ИМС1 будут осуществляться со стороны слоя 1, а все воздействия на ИМС2 со стороны слоя 3.
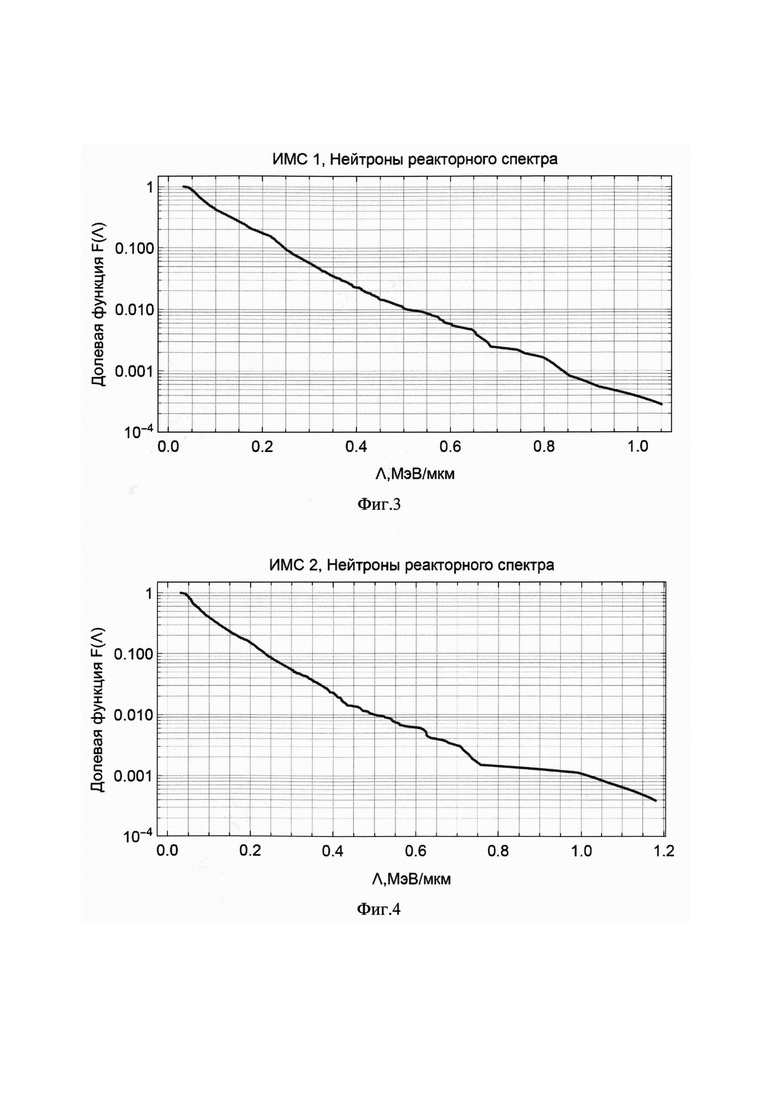
1) Необходимо установить вид функции F(Λ). Для этого путем Монте-Карло расчета создается модель вторичных частиц для каждой микросхемы и каждого типа нейтронных воздействий, включая нейтронов прогнозируемых условий. Таким образом, требуется определить вид F(Λ) для трех видов воздействий: нейтронов с энергией 14 МэВ (см Фиг. 1, Фиг. 2), нейтронов реакторного спектра (см Фиг. 3, Фиг. 4) и нейтронов прогнозируемых условий (см Фиг. 5, Фиг. 6), для двух типов микросхем. Итого шесть функций.
2) Значения параметров сбоеустойчивости ΛC можно определить графически. Им будет соответствовать значение Λ в точке пересечения кривой R(Λ) с уровнем σR. Для этого воспользуемся рассчитанными функциями F(Λ) (Фиг. 1, Фиг. 2, Фиг. 3, Фиг. 4), а также выражением (7). Отношения первичных нейтронов Фn и вторичных частиц Фs из численного расчета занесем в таблицу 3:

Выражение для R(Λ) для микросхем ИМС1 и ИМС2 будет иметь вид

При этом для микросхемы ИМС1 в качестве F14(Λ) и Fƒ(Λ) будут использованы функции на рис. Фиг. 1 и Фиг. 3 соответственно, а для микросхемы ИМС2 - функции на Фиг. 2 и Фиг. 4.
Оценка значений с помощью графиков (Фиг. 7, Фиг. 8) для микросхем ИМС1 и ПМС2 составила 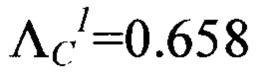 МэВ/мкм и
МэВ/мкм и  МэВ/мкм соответственно. Примечание: в спорных ситуациях на пологих участках функции следует выбирать наименьшее значение Λ для сохранения консервативности оценки.
МэВ/мкм соответственно. Примечание: в спорных ситуациях на пологих участках функции следует выбирать наименьшее значение Λ для сохранения консервативности оценки.
3) Сечение сбоев при воздействии прогнозируемого спектра определяется согласно выражению (9), где Fr(ΛC), - функция, которая рассчитана с учетом реальных условий воздействия нейтронов (Фиг. 5, Фиг. 6), σexp - экспериментальное значение; можно выбрать одно из двух экспериментальных сечений: при воздействии нейтронов с энергией 14 МэВ и при воздействии реакторных нейтронов: на результат оценки этот выбор не повлияет. При значениях количества частиц Фn (Er)=109 и Фs (Er)=3.67⋅103 получим:
для ИМС1:
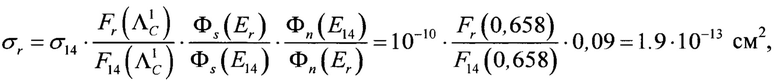
для ИМС2:

| название | год | авторы | номер документа |
|---|---|---|---|
| Способ расчетно-экспериментальной оценки радиационной стойкости интегральных схем к воздействию отдельных заряженных частиц, основанный на локальном лазерном облучении | 2017 |
|
RU2661556C1 |
| Способ оценки стойкости элементов цифровой электроники к эффектам сбоев от воздействия единичных частиц | 2016 |
|
RU2657327C1 |
| СПОСОБ ЭЛЕМЕНТНОГО АНАЛИЗА СРЕД И РЕАЛИЗУЮЩЕЕ ЕГО УСТРОЙСТВО | 2011 |
|
RU2478934C2 |
| СПОСОБ ОЦЕНКИ СТОЙКОСТИ ЦИФРОВОЙ ЭЛЕКТРОННОЙ АППАРАТУРЫ К ВОЗДЕЙСТВИЮ ИОНИЗИРУЮЩИХ ИЗЛУЧЕНИЙ (ВАРИАНТЫ) | 2014 |
|
RU2578053C1 |
| Способ регистрации нейтронов и устройство для его осуществления | 2017 |
|
RU2663683C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ГЕОМЕТРИИ ТРЕЩИНЫ ПОДЗЕМНОГО ПЛАСТА (ВАРИАНТЫ) И СПОСОБ МОДЕЛИРОВАНИЯ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ТРЕЩИНЫ ПОДЗЕМНОГО ПЛАСТА | 2009 |
|
RU2483210C2 |
| СПОСОБ АНАЛИЗА ЭЛЕМЕНТОВ И ОТНОШЕНИЙ МАСС ЭЛЕМЕНТОВ ТКАНИ И СПОСОБ ПОСТРОЕНИЯ ГЕОМЕТРИЧЕСКОЙ МОДЕЛИ НА ОСНОВЕ МЕДИЦИНСКОГО ИЗОБРАЖЕНИЯ | 2017 |
|
RU2736917C1 |
| СПОСОБ ИМИТАЦИОННОГО ТЕСТИРОВАНИЯ СТОЙКОСТИ ПРИБОРНОЙ СТРУКТУРЫ К ОБЛУЧЕНИЮ БЫСТРЫМИ НЕЙТРОНАМИ (ВАРИАНТЫ) | 2016 |
|
RU2638107C1 |
| Устройство моделирования на пучках тяжелых ионов высокой энергии полей смешанного излучения для целей экспериментальной радиобиологии | 2021 |
|
RU2761376C1 |
| ТРИГГЕР КОМПЛЕМЕНТАРНОЙ МЕТАЛЛ-ОКСИД-ПОЛУПРОВОДНИКОВОЙ СТРУКТУРЫ МИКРОСХЕМЫ | 2013 |
|
RU2541894C1 |



Изобретение относится к способам оценки сечений радиационно-индуцированных сбоев в микросхемах статической памяти при воздействии потоков нейтронов произвольного спектра до 14 МэВ и может быть использовано в рамках мероприятий по обеспечению сбоеустойчивости аппаратуры, определенной к эксплуатации в условиях воздействий нейтронных потоков с произвольным спектрально-энергетическим составом в диапазоне до 14 МэВ путем расчетно-экспериментальной оценки на основе пересчета экспериментальных сечений сбоев, полученных с помощью доступных источников нейтронов, на сечение сбоев в прогнозируемых условиях при эксплуатации. Сущность: для каждого воздействия потоков нейтронов с помощью Монте-Карло симулятора определяется реализация модели вторичных частиц, по ней определяются спектры линейных потерь энергии вторичных заряженных частиц, для получения которой задается модель микросхемы в виде нескольких плоских однородных слоев из кремния либо оксида кремния, толщина которых близка к толщине топологических слоев микросхемы, позволяющие определить пороговое значение сбоя по линейным потерям энергии, являющееся параметром модели сбоеустойчивости микросхемы, и определить сечение сбоев микросхемы в прогнозируемых условиях. 3 табл., 8 ил.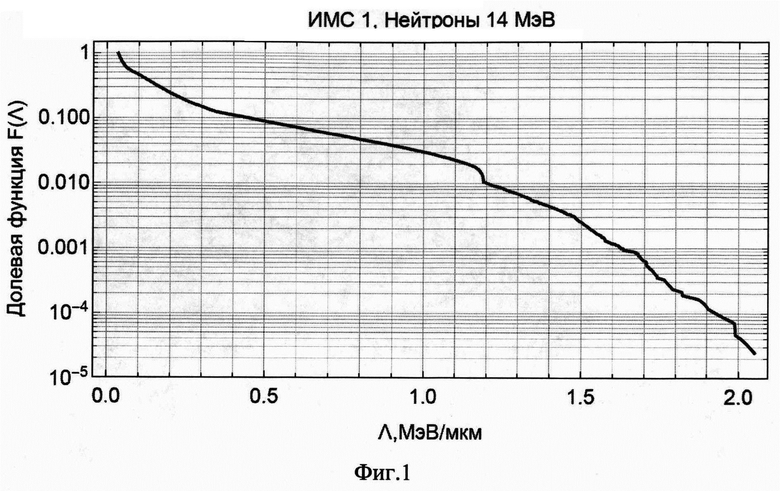
Способ оценки сечения сбоев в микросхемах статических оперативных запоминающих устройств, выполненных по комплементарной металл-оксид-проводник технологии, при воздействии потоков нейтронов в диапазоне энергий до 14 МэВ, включающий в себя реализацию модели потоков вторичных частиц методом Монте-Карло в виде спектров линейных потерь энергии вторичных частиц и использование двух серий экспериментальных значений сечения сбоев для источников нейтронов, один из которых генерирует нейтроны с энергией 14 МэВ и второй источник нейтронов непрерывного спектра, близкого к спектру деления урана-235, для определения порогового значения линейных потерь энергии эффекта одиночного сбоя, являющегося параметром устойчивости микросхемы, отличающийся тем, что создают модель микросхемы, состоящей из плоских однородных слоев из кремния либо оксида кремния и детектора частиц в виде слоя кремния, соответствующего толщине топологического слоя микросхемы, в котором выполнены транзисторы, с помощью которой проводят реализацию модели потоков вторичных частиц в виде нормированных интегральных спектров вторичных частиц, соответствующую условиям эксперимента (Fexp1, Fexp2, …) и прогнозируемым условиям Fr, а также расчетному количеству вторичных частиц Фs(En), полученных при воздействии от первичных нейтронов количеством Фn(En); после чего численно или графически определяют значение ΛC с помощью выражения

где σ14, σƒ - экспериментально определенные сечения для микросхемы на генераторе нейтронов с энергией 14 МэВ и источнике нейтронов, близком к спектру деления соответственно, функции F14 и Fƒ - рассчитаны согласно условиям экспериментов на источнике нейтронов с энергией 14 МэВ и источнике сплошного спектра соответственно, после чего, используя определенное значение  , рассчитывают сечение сбоев в прогнозируемых условиях σr с использованием одного из экспериментально определенных сечений сбоев σexp согласно выражению
, рассчитывают сечение сбоев в прогнозируемых условиях σr с использованием одного из экспериментально определенных сечений сбоев σexp согласно выражению

где Fr(Λ), Fexp(Λ) - нормированные интегральные спектры вторичных заряженных частиц для прогнозируемых условий и условий эксперимента, в котором было получено значение σexp соответственно, Фs(Er), Фs(Eexp) - количества вторичных заряженных частиц, полученных в результате воздействия на мишень количества нейтронов Фn(Er), Фn(Eexp) спектров прогнозируемых условий и экспериментальной установки соответственно.
| Способ оценки стойкости элементов цифровой электроники к эффектам сбоев от воздействия единичных частиц | 2016 |
|
RU2657327C1 |
| Устройство для радиационного облучения и испытания надежности объектов авиакосмического назначения к воздействию потоков нейтронов с использованием синхроциклотрона | 2021 |
|
RU2761406C1 |
| US 2020005957 A1, 02.01.2020 | |||
| US 2015060686 A1, 05.03.2015. | |||
Авторы
Даты
2023-01-19—Публикация
2022-07-28—Подача