Изобретение относится к области исследования радиационной стойкости полупроводниковых приборов (ППП) и интегральных схем, и в большей степени интегральных микросхем (ИМС) с последовательной и комбинационной обработкой логических сигналов. Оно относится к экспериментальным исследованиям, выполняемым как на моделирующих условия воздействия ионизирующих излучений (ИИ) установках, непосредственно воспроизводящих их виды, называемыми моделирующими установками (МУ), так и на установках, количественно воспроизводящих сходные радиационным эффекты, называемыми имитирующими установками (ИУ). К числу последних, например, относят импульсные лазерные источники.
В современной электронной промышленности разработчики ИМС имеют драматический опыт увеличения как плотности транзисторных структур, так и рабочей частоты. Одной из существенных причин такого роста является уменьшение топологического размера приборов, входящих в состав ИМС. Топологический размер относится к длине затвора транзисторов технологии «Комплементарной Металл-Оксид-Полупроводник» (КМОП).
Изобретение относится, в том числе и к ИМС, пригодным для применения в условиях космического пространства (КП), таких, как спутники, межпланетные полеты или рабочий космический челнок. Предметом обсуждения является неблагоприятное воздействие факторов КП на чипы ИМС, проявляющееся, во-первых, в эффектах от полной поглощенной дозы от воздействия ИИ (Total Ionizing Doze = TID) вследствие торможения электронов и протонов, а, во-вторых, в эффектах единичных сбоев, или сбоев от единичных частиц, (Single Event Upset = SEU) вследствие взаимодействия с космическими лучами (тяжелые заряженные частицы (ТЗЧ) высокой энергии), протоны и нейтроны высоких энергий. Из всех этих эффектов SEUs представляют наибольшую вызванную радиацией опасность, которую надо избегать для объектов микроэлектроники в КП. Рассматривают эффекты, касающиеся потерь энергии, сбора заряда и сбоев из-за прохождения космическими лучами полупроводниковых структур в ИМС. Если ион высоких энергий проходит через все материалы, он теряет энергию из-за взаимодействия с материалами. Энергия иона теряется, во-первых, из-за взаимодействия иона с орбитальными электронами материала, на ионизацию материала и формирование трека электронно-дырочных пар (ehp). Скорость, с которой ион теряет энергию, исторически называется «мощностью торможения» (dE/dx). Дифференциальная энергия dE измеряется в единицах [МэВ], тогда как толщина материала измеряется в единицах массовой толщины [мг/см2]. Термин LET (линейная передача энергии) чаще используется вместо «мощности торможения». В кремнии для создания одной eph требуется энергия 3,6 эВ. При плотности кремния 2,42 г/см3 один микрон линейной толщины преобразуется в 0,242 мг/см2 массовой. Также заряд электрона равен 1,6.10-7 пКл. Отсюда для образования заряда dQ в кремнии в треке длиной L при торможении заряженной частицы «мощность торможения» LET образует заряд:
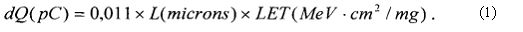
Таким образом, ион с LET порядка 100 MeV-cm2/mg создает заряд примерно 1 пКл вдоль его трека.
В объемном кремнии eph не являются значимыми, т.к. они, в конце концов, рекомбинируют. При наличии электрического поля, однако, eph достаточно быстро разделяются посредством дрейфа в направлении, противоположном направлению поля и могут быть достаточно быстро собраны каким-нибудь источником напряжения, создающим поле. В ИМС на объемном кремнии такое электрическое поле приложено вдоль p-n-перехода в приборах. Каждый и любой из сигналов на выводе ИМС обычно изолирован от источника VDD одним или большим числом таких переходов (сток транзистора р-МОП) и изолирован от общей точки («земли») VSS одним или большим числом таких переходов (сток транзистора n-МОП).
Фиг. 1 иллюстрирует эффект прохождения иона через переход стока в транзисторе n-МОП. Фиг. 1 демонстрирует поперечное сечение перехода стока (10), имеющего n+-сток n-МОП (12), диффундирующий в p- (epi) пленку (14) p+-подложки ((16) n-МОП). Переход (20) изолирует вывод схемы для положительного источника питания (+V) от напряжения подложки (VSS). Ион пролетает через переход (10) и создает трек (20) электронно-дырочных пар, которым соответствует символ «-» для электронов и «+» для дырок. Электронно-дырочные пары, в свою очередь, создают плазму, контур которой напоминает воронку заряда (22).
Указанные компоненты тока наблюдаются в качестве сигналов на выводах ИМС при наличии электрического поля на переходе и воронки разделенных свободных зарядов электронов и дырок. Исходя из конструкции на Фиг. 1 электроны собираются на узле схемы, а дырки на узле подложки, в результате протекает отрицательный импульс тока в диффузионном узле n-МОП, который приводит к «разряду» (уменьшению) напряжения сигнала.
Этот дополнительный ток является короткоживущим, завершающимся примерно через 100-200 пс.
Запаздывающая компонента тока генерируется вследствие диффузии электронов и дырок из области, где электрическое поле равно нулю. Эти заряды могли бы в отсутствии рекомбинации достичь области, где существует поле, и где они могут рекомбинировать. Эта запаздывающая компонента могла бы достигать длительности нескольких сотен наносекунд.
Небольшой заряд собирается в области p+-подложки, т.к. скорость рекомбинации здесь выше из-за более высокой концентрации примеси. Если напряжение питания на стоке n-МОП равно нулю, электрическое поле, по сути, равно нулю и не наблюдается существенного увеличения собранного заряда.
Сходные процессы наблюдаются в окрестностях стока p-МОП, сформированного диффузией примеси в n-карман и смещенного источником VDD. В этом случае присутствует электрическое поле, даже если напряжение источника смещения равно нулю. Толщина области сбора в этом случае много меньше (в лучшем случае половина толщины кармана), т.к. переход «карман-подложка» постоянно смещен в обратном направлении и также может собирать индуцированный заряд.
Нейтроны и протоны высоких энергий, как известно, вызывают схожие эффекты непосредственно непрямым способом через ядерные реакции с кремнием. В этом случае, тяжелые ионы отдачи сопутствующих продуктов пролетают через переходы и формируют импульс тока из собранного заряда. В КП протоны высоких энергий порождаются, главным образом, из захваченных радиационными поясами протонов и из солнечных вспышек. Для высотной авиации и нейтроны и протоны высоких энергий связаны с продуктами реакций, сформированных в космических ливнях, когда космические ТЗЧ подвергаются ядерным реакциям в атмосфере.
Компоненты добавочного стороннего тока, описанные выше, ответственные за эффекты SEUs, наблюдались в схемах на космических орбитах в течение последних 10-15 лет. Более замечательно то, что SEUs обнаруживают в статических триггерах (latchs) и SRAM (Static Random Acces Memory). Эффект появления квазистационарного тока определяется зависимостью реакции от схемы, которая, в свою очередь, определяется величиной заряда, собранного в узле сигнала. По существу, величина емкости узла сигнала определяет (в первом случае), насколько велико падение напряжения dV, которое является результатом собранного заряда dQ в соответствии с равенством 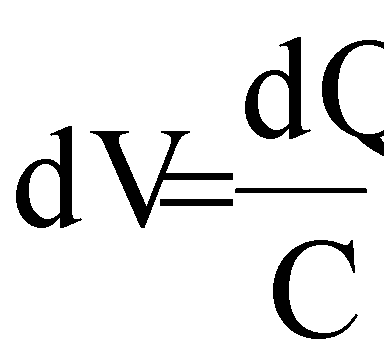 . Это является верным только в предположении, что схема очень слабо рассеивает заряд в течение последующих сотен пикосекунд). Высокая проводимость транзисторов смягчает этот эффект, так как они рассеивают этот заряд более быстро. Более важная для триггеров и SRAM положительная петля обратной связи по усилению обуславливает «опрокидывание» данных (
. Это является верным только в предположении, что схема очень слабо рассеивает заряд в течение последующих сотен пикосекунд). Высокая проводимость транзисторов смягчает этот эффект, так как они рассеивают этот заряд более быстро. Более важная для триггеров и SRAM положительная петля обратной связи по усилению обуславливает «опрокидывание» данных (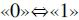 ) в том случае, когда собранный заряд достигает критического значения QCRIT, а напряжение на узле питания возрастает до критического значения. Более детальное обсуждение этих эффектов и, в частности, откликов схем SRAM, можно найти в [1].
) в том случае, когда собранный заряд достигает критического значения QCRIT, а напряжение на узле питания возрастает до критического значения. Более детальное обсуждение этих эффектов и, в частности, откликов схем SRAM, можно найти в [1].
SEUs становятся более проблематичными при дальнейшим уменьшением топологического размера. Топологичекий размер следующих поколений не радиационно-стойких коммерческих ИМС уменьшился за последние годы от 1 мкм до 0,13 мкм (в настоящее время) и непрерывно уменьшается до перспективных 0,05 мкм. Для получения этого сокращения в промышленности было использовано несколько моделей масштабирования, включая латеральное (боковое) масштабирование, где масштабируется только длина затвора, масштабировании постоянного напряжения питания, когда VDD остается константой, и масштабирование постоянного электрического поля, где VDD уменьшается с уменьшением толщины подзатворного оксида для поддержания постоянной величины электрического поля в транзисторе. Модель масштабирования электрического поля является доказанным фактом для большинства практических применений, поскольку она пригодна для описания большинства отрицательных эффектов большого электрического поля (пробой подзатворного диэлектрика и «горячие» электроны).
По данным [2] длительности переходных импульсов SET (Single Event Transient) и поперечные сечения ошибок как функции технологических решений (0,25, 0,18 и 0,13 µm) и как функции рабочего напряжения (2,00, 1,50, 1,25 и 1,00 В) при фиксированном значении LET=60 MeV·cm2/mg показывают существенное увеличение длительности импульса SET с сокращением топологического размера и сопутствующим уменьшением номинального рабочего напряжения и значимого увеличения длительности импульса SET, если приборы функционируют при напряжении, которое ниже нижней допустимой границы рабочих напряжений по спецификации на каждую из рассмотренных технологий. Там же содержатся результаты исследований традиционных ячеек памяти DICE (Dual Interlocked Storage Cell = двойная взаимоблокирующая ячейка памяти) для проверки соответствия с результатами измерений по методу PDTL (Programmable Delay Temporal Latch = PDTL, или программируемой задержки, или временнОй «защелки») зависимости поперечных сечений SET от напряжения функционирования. Результаты измерений по цепям DICE, в общем, соответствуют данным по методу PDTL, т.е. большинство переходных процессов фиксируются при уменьшении номинального напряжения, что трактуется, таким образом, что эффективность фиксации эффектов SETs в ячейках DICE «улучшается» вследствие более длинных импульсов SET. Основываясь на результатах [2] определено, что длительности импульсов SET являются прямой пропорциональной функцией номинального рабочего напряжения и могут потенциально непрерывно увеличиваться с уменьшением топологических размеров вследствие соответствующего уменьшения номинального рабочего напряжения. Это приводит к потенциальной «двойной борьбе фронтов» в соответствующих технологиях, так что, высокие рабочие частоты комбинируются с длительностью протяженных импульсов SET. Прогресс в будущих приборах в сторону подавления SET связан с использованием таких технологий как временная «защелка» [2] для технологий объемного кремния (bulk/epi Si), «кремния-на-изоляторе» (Silicon-On-Insulator = SOI) и/или необходимости разрабатывать основы для серьезного рассмотрения возможности изготовления приборов с низкой интенсивностью SET, пригодных для прикладных специальных интегральных схем (Application Specific Integrated Circuit = ASIC).
Для масштабирования постоянного электрического поля, включая все физические размеры прибора (такие, как длина затвора L, ширина затвора W и толщина оксида затвора TOX), когда они сокращаются, приложенное напряжение питания VDD и пороговое напряжение транзистора VTH уменьшаются пропорционально. Это приводит в результате к пропорциональному уменьшению тока стока (ID), емкости нагрузки (C) и пропорциональному уменьшению емкости узла затвора 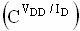 . Самый маленький ток транзистора для постоянного масштабируемого поля требует, чтобы плотность тока металлизации (относительно тока электромигации) уменьшалась с меньшей скоростью, чем масштабирование по постоянному напряжению, при котором ток транзистора остается постоянным. Далее, для систем с малой мощностью, масштабирующих постоянное поле (в которых шкала VDD пропорциональна), это есть только одна рассматриваемая возможность, так как это является, по существу (квадрат масштабирования), результатом малой мощности рассеивания.
. Самый маленький ток транзистора для постоянного масштабируемого поля требует, чтобы плотность тока металлизации (относительно тока электромигации) уменьшалась с меньшей скоростью, чем масштабирование по постоянному напряжению, при котором ток транзистора остается постоянным. Далее, для систем с малой мощностью, масштабирующих постоянное поле (в которых шкала VDD пропорциональна), это есть только одна рассматриваемая возможность, так как это является, по существу (квадрат масштабирования), результатом малой мощности рассеивания.
Орбитальная микроэлектроника обычно отстает от ее наземных коммерческих дубликатов на одно или два поколения, так как большинство шагов технологического процесса требует обеспечения требований по радиационной стойкости к TID от излучений КП. Большинство радиационно-стойких ИМС могут быть изготовлены с технологическим размером 0,8…0,7 мкм. SEU в статических триггерах и SRAM могут проявляться в устройствах с топологическими нормами меньше 10 мкм и для критического заряда для сбоивших схем, величиной ниже 1 пКл (ориентировочно для частиц с LET не ниже, чем 1 MeV-cm2/mg). Так как площадь поперечного сечения попадания ТЗЧ в 20 раз меньше, интегральный флюенс космических лучей с LET>1 MeV-cm2/mg в 1000 раз больше флюенса частиц с LET=20 MeV-cm2/mg для геостационарной орбиты. Это предполагает, что интенсивность ошибок от эффектов SEU (на один бит) увеличивается в 50 раз. Так как технология 0,18 мкм имеет, вероятно, в 20 раз больше триггеров, чем технология 0,8 мкм, интенсивность отказов целой ИМС этом случае в 1000 раз больше.
Для оценки стойкости ППП и ИМС к воздействию ИИ КП используют методы испытаний на ускорителях заряженных частиц, например, протонов, где с помощью подбора мишеней формируют необходимый «коктейль» из ТЗЧ [3].
При использовании имитационных методов (ИМ), как правило, используют пикосекундные импульсные лазеры с длиной волны 800-1500 нм [4].
Ограничения, касающиеся применения ИМ на основе облучения импульсным лазером, касаются экранировки поверхности чипа ИМС металлизацией и необходимостью точного подбора энергии лазерного импульса для получения равенства контролируемых выходных электрических характеристик ППП и ИМС.
Однако импульсное лазерное воздействие позволяет обнаружить новые эффекты, которые не фиксируются при проведении радиационных экспериментов на МУ: это позиционирование сбоев на поверхности чипа ИМС и задержка развития процесса сбоя во времени, связанная с работой генератора тактовой частоты [5, 6]. В этом смысле лазерные ИМ являются важными дополнительными условиями для построения зависимостей поперечного сечения эффектов SEU как функции величины LET.
На основе кулонометрического способа измерения электрофизических параметров [7] и устройства, его реализующего [8], предложен способ определения коэффициента относительной эффективности и эквивалентной дозы источника рентгеновского излучения получения коэффициента относительной эффективности (КОЭ), или в зарубежной литературе RDEF (Relative Dose Enhancement Factor) [9]. RDEF устанавливает связь между поглощенной эквивалентной дозой рентгеновского (гамма-) излучения с эквивалентной энергией 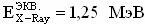 (средняя энергия спектра эталонного нуклида Co60) и величиной порогового значения линейной передачи энергии LETTH. При этом величина индуцированного радиацией критического заряда QC в треке иона и в чувствительном объеме транзисторной гетероструктуры технологии «металл-оксид-полупроводник» (МОП) остается равной
(средняя энергия спектра эталонного нуклида Co60) и величиной порогового значения линейной передачи энергии LETTH. При этом величина индуцированного радиацией критического заряда QC в треке иона и в чувствительном объеме транзисторной гетероструктуры технологии «металл-оксид-полупроводник» (МОП) остается равной
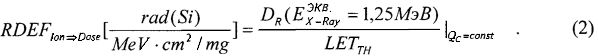
При имитации эффектов SEU импульсным лазерным излучением также можно ввести понятие RDEF
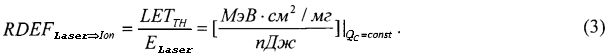
Тогда

Предыдущие решения устранения проблем SEU были сфокусированы на разработках SRAM и статических триггеров. Несмотря на то, что большинство рассмотренных работ было сфокусировано на статических триггерах для использования в ASIC, тем не менее, эти результаты могут быть распространены на разработки SRAM.
Один из таких триггеров описан в [10]. Эти разработки триггеров используют методы перекрестной изоляции, гарантирующие, что состояние триггеров не изменится при попадании ТЗЧ в любой из критических узлов.
Другая разработка представлена в [11]. Эта разработка в виде триггера DICE, также не может изменять логическое состояние при попадании частицы в единичный узел.
Каждый из этих триггеров может быть переключен, по-видимому, если единичная частица космического излучения проникает в ИМС в узком слое, расположенном в угле параллельно поверхности и вместе с этим пересекает, по крайней мере, два p-n-перехода. Геометрическое поперечное сечение для этого случая, хотя и мало, но может быть весьма существенным для применений на околоземных орбитах.
Отдельно от проблемы генерации SEUs в затворе и области подложки, космическое излучение может индуцировать процессы SETs в комбинаторной логике, в системе глобального времени и глобальных линиях контроля на уровне схем. SETs генерирует минимум эффектов в технологиях 0,8 мкм и 0,7 мкм, т.к. скорость распространения сигналов в этих схемах недостаточна для распространения SETs длительностью 100…200 пс на заметном расстоянии в пределах схемы. Однако, чем меньшее значение имеют технологические размеры будущих разработок (и их стойкость) для околоземных применений, тем более незначимыми становятся эффекты SETs для нормальных сигналов.
На Фиг. 2 приведен график зависимости критической длительности переходного импульса, необходимого для распространения SET без затухания через бесконечно длинную цепочку инверторов от технологического размера. Если длина импульса меньше, чем критическая длительность импульса, присущая инерциальная задержка вентиля вызывает затухание переходного единичного события. Эффект SET завершается в кристалле после прохождения пяти вентилей. Если длительность импульса равна или больше критической длительности, SET однозначно распространяется в вентилях как нормальный рабочий сигнал. Эффекты SETs, длительностью больше, чем критическая длительность, распространяется через все вентили без затухания; SETs, длительность которых равна половине критической длительности, затухает в первом вентиле; SETs с промежуточной длительностью распространяется через переменное число ступеней.
График на Фиг. 2 является результатом моделирования с использованием параметров SPICE для различных топологических норм (показанных в виде точек на графике) в диапазоне от 1,2 мкм (1200 нм) и 0,13 мкм (130 нм). Генерированный ряд параметров модели SPICE был получен, исходя из известных параметров модели между 1,2 мкм и 0,7 мкм, включительно. Были использованы правила сохранности электрического поля для генерации модели и размеры транзистора для прогнозирования параметров модели в малых топологических размеров. Масштабированные значения различных критических параметров (VDD, VTH и TOX) были сопоставлены с опубликованными в [12]. Непрерывная кривая содержит смоделированные точки, пунктирная линия экстраполировала точки на 0,05 мкм (50 нм), проектную топологическую норму коммерческих технологий 2012 г. Как обсуждалось выше, длительность процессов SETs составляет 100…200 пс. График на Фиг. 2 подтверждает тот факт, что через одно или два поколения орбитальных систем микроэлектронной аппаратуры, в которой применяются ИМС с топологическими нормами меньше 0,35 мкм, эффекты SETs не будут затухать в пределах вентилей схем, а будут распространяться как обычные рабочие сигналы схемы. Это будет иметь серьезные, если не катастрофические последствия для схем последовательного доступа.
На Фиг. 3 приведена топология компоновки для схемы последовательного доступа (30). Схема (30) имеет первичный триггер (32), блок комбинационной логики (34) и вторичный триггер (36). На этой иллюстрации триггеры (32) и (36) реализуют функции D-триггеров. Данные первого триггера (32) обычно поступают на вход комбинационной логики по заднему фронту синхроимпульса, который вырабатывает схема синхронизации времени. С выхода комбинаторной логики (34) сигнал поддерживает вход второго триггера (36) в течение всего времени, пока не придет следующий задний фронт импульса синхронизации. По заднему фронту этого импульса второй триггер запоминает любые данные, поступившие к этому времени на его вход и выполняет изменение состояния с переходом в режим ожидания.
Если в это время в комбинаторную логику (34) попадает ТЗЧ и логика является пригодной для распространения переходного процесса, то в конечном итоге SET появляется на входе второго триггера (36), что может быть воспринято как полезный (истинный) сигнал. Который из этих двух, полезный или SET, будет запомнен, зависит от времени их поступления и заднего фронта синхросигнала.
Фиг. 4 демонстрирует временную диаграмму, иллюстрирующую соотношение во времени для случая, когда истинные данные игнорируются, а позитивные SET ошибочно поступают на вход второго триггера. На Фиг. 5 синхросигнал (50) и четыре различных сигнала SET (52-58) иллюстрируют четыре разных случая, когда сигнал SET может совпасть с задним фронтом сигнала времени (50).
Переходный процесс может быть некорректно интерпретирован как полезный сигнал и впоследствии запомнен в триггере, если он длиннее периода времени, установленного для времени переключения перед задним фронтом синхросигнала и времени удержания после заднего фронта импульса синхросигнала. На Фиг. 5 первый из серии сигналов SET (52) наблюдается до указанного интервала, и поэтому не может быть переключен во второй триггер. Следующий сигнал SET (58) наблюдается после этого интервала, и поэтому опять не дает результата в изменение состояния триггера. Однако, второй и третий сигналы SET (54) и (56) приходят с некоторым опережением или запаздыванием, соответственно, по отношению к сигналу переключения, что приводит к ошибочному запоминанию сигнала SET во втором триггере.
Рисунок Фиг. 6 показывает еще одну временную диаграмму, иллюстрирующую временное соотношение для других типов SET, которые вызывают запись неправильных данных в триггер. В этом случае SET наблюдаются в пределах синхросигнала. Рисунок Фиг. 6 демонстрирует сигнал данных (60), нормальный синхросигнал (62), и три различных синхросигнала (64-68), которые искажены SET (обозначены пунктирной линией для каждого случая).
Истинные данные (60) удовлетворяют временам установки и поддержания вблизи заднего фронта синхроимпульса в случае его корректной работы, как это соответствует сигналу (62). Синхросигнал (64) содержит отрицательный вклад от SET по линии тактового сигнала, которая смещает задний фронт синхросигнала в сторону опережения сигнала данных. В результате будет запомнено низкое значение «0» сигнала данных (60). Синхросигнал (66) демонстрирует промежуточное расположение сигнала «1» SET относительно сигнала «1» данных. Синхросигнал не вызывает проблем, так как он поступил и действует после данных высокого уровня и может быть запомнен, пока сигнал данных остается на уровне «1». Синхросигнал (68) содержит положительный SET вблизи заднего фронта сигнала данных (60). Синхросигнал (68) вызывает в триггере сохранение ошибочного сигнала низкого уровня в противоположность предварительно запомненному сигналу высокого уровня. Отметим, что не является проблемой совмещение SET с задним фронтом сигнала данных. Данные триггера могут быть искажены при любом состоянии сигнала на линии синхронизации, когда задний фронт импульса SET следует после заднего фронта сигнала данных.
Различные интенсивности отказов в схемах прямого доступа (т.е. SEU в триггерах и SET в комбинаторной логике) зависят от частоты синхросигналов [3]. Изменение состояния наблюдается в триггерах только тогда, когда частота низкая, и триггер находится в состоянии удержания. Т.к. синхросигнал соответствует менее 50% всего времени, то интенсивность SEU не зависит от частоты. Напротив, SET, которые создаются в комбинаторной логике, могут быть накоплены, если они по какому-нибудь входу триггера совпадут с задним фронтом синхросигнала, а число таких совпадений будет расти линейно с ростом частоты синхросигнала. Таким образом, интенсивность SEU не зависит от частоты синхросигнала, в то время, как интенсивность SET прямо пропорциональна частоте синхросигнала. Это соотношение в интенсивности ошибок может быть проиллюстрировано экспериментально с использованием импульсного лазерного облучения тестовых структур, когда измеряются различные интенсивности ошибок в зависимости от частоты синхросигналов [13].
Это соотношение интенсивности ошибок смешивает проблемы SET с проблемой сжатия топологического размера в технологии ИМС. Результат сжатия топологического размера и уменьшения времени задержки в затворе позволяет схемам работать с большими частотами синхросигналов. Поставляет вклад переходных ошибок в целую схему не только каждый комбинаторный вентиль (до тех пор, пока переходные процессы не затухают), но и увеличивается так же вероятность накопления (вследствие большей частоты синхросигнала).
Для данных, обрабатываемых в условиях воздействия SETs, необходимо ввести ограничения на механизмы моделирования процессов распространения электрического заряда [14] и разработки аналитических способов определения интенсивности ошибок в приборах с различным топологическим размером.
Наиболее близким к предлагаемому техническому решению (прототипом) является способ прогнозирования интенсивности сбоев от эффектов SEU/SEE в цифровой аппаратуре, основанный на принятии «концепции эффективности заряда» как меры эффективности радиационно-индуцированного заряда (РИЗ) [15]. Этот способ позволяет получить уточненные статистическими методами обработки экспериментальных данных отклонения от аппроксимирующей ступенчатой функции зависимости поперечного сечения сбоев от величины LET в области малых значений и получить оценки величины порогового значения LETTH с использованием цифрового представления о характеристиках (figure merit = FOM) и значений, определенных из данных по поперечным сечениям или из симуляции в смешанном режиме: экспериментально полученной зависимости σ=f(LET) для ТЗЧ и данных по облучению импульсным лазерным излучением. Величину LETTH используют для оценок значения сечения насыщения σSAT, критического флюенса ионов FCRIT и интенсивности сбоев R.
Недостатком способа является то обстоятельство, что эффективность измерена для чувствительности к эффектам SEU в пределах одной ячейки структуры МОП. Кроме того, способ не предусматривает определение эквивалентных уровней ИИ импульсного источника гамма-рентгеновского излучения, что не позволяет использовать его для моделирования эффектов SEU/SEE на импульсных источниках гамма-нейтронного излучения, определения уровня бессбойной работы (УБР) и установления взаимнооднозначного соответствия между УБР и LETTH.
Предложенное техническое решение основано на концепции сохранения уровня критического заряда, вызывающего эффекты SEU и SET, что позволяет распространить эту идеологию и на данные из спецификации полупроводниковых приборов и ИМС. Так для импульсных диодов и диодов СВЧ в спецификации на прибор прямо указана величина заряда переключения из одного логического состояния в другое. В спецификации на полупроводниковые приборы и ИМС приводят данные о временах переключения 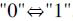 , токи переключения
, токи переключения 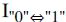 , напряжения в состоянии логических «0» и «1», V0L и V0H, соответственно. Эти данные могут быть использованы для вычисления величины критического заряда QC.
, напряжения в состоянии логических «0» и «1», V0L и V0H, соответственно. Эти данные могут быть использованы для вычисления величины критического заряда QC.
При пренебрежении этими процессами формирования критического заряда, возникает безусловная необходимость применения технологии подавления ошибок, вызванных SEU и SET.
Предложенное техническое решение имеет отношение к ИМС, в частности, как к схемам последовательной логики (SL), так и к схемам комбинаторной (комбинационной) логики (CL).
Техническим результатом изобретений является повышение достоверности оценки стойкости цифровой электронной аппаратуры к воздействию ИИ, в частности, оценки уровня бессбойной работы (УБР) и соответствующей ему величины TID, путем обеспечения независимо от условий облучения однозначной связи между результатами испытаний на моделирующих импульсные ИИ установках, результатами имитационного моделирования, в том числе с использованием импульсного лазерного излучения, и данных спецификаций на ППП и ИМС о динамических параметрах.
Технический результат достигается путем сопоставления и конверсии различных данных по стойкости к дозовым эффектам при статическом или импульсном облучении на МУ, по стойкости к эффектам мощности дозы при импульсном облучении на МУ, по стойкости к воздействию импульсного лазерного излучения при ИМ эффектов мощности дозы, по стойкости к низкоинтенсивному излучению факторов КП и по данным спецификаций о динамических параметрах ППП и ИМС на основе общей концепции, основанной на представлении о равенстве величин критического заряда QC, который вызывает в чувствительном объеме νS возникновение сторонних токов, вызывающих эффекты SEU и SET в цифровых электронных схемах.
Данная задача решается созданием вариантов способа оценки стойкости цифровой электронной аппаратуры к воздействию ионизирующих излучений на основе предложенной концепции.
Поставленная задача (вариант 1) решается тем, что для определения уровня бессбойной работы (УБР) блока или всего устройства радиоэлектронной аппаратуры (РЭА), в целом, содержащей в своем составе цифровые интегральные микросхемы (ИМС), по результатам экспериментальных исследований на моделирующих установках (МУ), в известном способе оценки стойкости цифровой электронной аппаратуры к воздействию ИИ путем использования экспериментально полученных данных при моделировании РИЗ в БИС/СБИС технологии КМОП/КНД с использованием генерации сторонних токов от импульсных источников ионизирующего излучения (ИИИ), в качестве которых используют сопутствующее гамма-излучение импульсного ядерного ректора (ИЯР) или гамма-рентгеновское излучение электрофизических установок (ЭФУ) (линейных импульсных ускорителей и/или рентгеновских установок) и от воздействия ТЗЧ космического пространства, затем с использованием соответствующих значений коэффициентов относительной эффективности 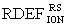 между эквивалентной дозой DRS гамма-рентгеновского излучения со спектром RS (Radiation Stress) и
между эквивалентной дозой DRS гамма-рентгеновского излучения со спектром RS (Radiation Stress) и 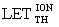 ионов (ТЗЧ),
ионов (ТЗЧ), 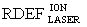 определяют величину эквивалентной дозы DRS и по известной длительности импульса ИИ τP определяют УБР.
определяют величину эквивалентной дозы DRS и по известной длительности импульса ИИ τP определяют УБР.
Кроме того, для определения поперечного сечения сбоев цифрового устройства, анализируют структурную схему радиоэлектронного устройства, определяют величины отдельных парциальных поперечных сечений сбоев 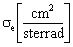 для каждого цифрового элемента схемы, суммарное поперечное сечение σΣ для однотипных элементов последовательной и комбинационной логики, усредненное поперечное сечение σD для элементов последовательной и комбинационной логики, полное сечение σTOT для всего цифрового устройства.
для каждого цифрового элемента схемы, суммарное поперечное сечение σΣ для однотипных элементов последовательной и комбинационной логики, усредненное поперечное сечение σD для элементов последовательной и комбинационной логики, полное сечение σTOT для всего цифрового устройства.
Кроме того, для сокращения числа испытаний, величину полного поперечного сечения сбоев вводят с учетом числа цифровых бистабильных триггеров DFF.
Кроме того, для сокращения числа испытаний на установках, моделирующих воздействие ТЗЧ, для определения единичного сечения сбоев σe для однотипных элементов схемы, для большинства практических случаев интенсивность сбоев определяют с использованием аппроксимирующего выражения для поперечного сечения насыщения σSAT=ab, (a, b>с) и критического порогового значения линейной передачи энергии (массовых потерь) 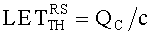
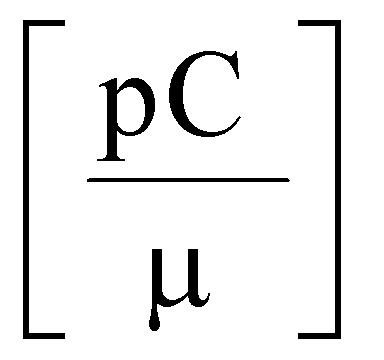 , где c - толщина полупроводниковой пластины, а и b - размеры чипа структуры, в мкм, а QC - величина критического радиационно-индуцированного (РИЗ), вызывающего сбои в работе логических устройств.
, где c - толщина полупроводниковой пластины, а и b - размеры чипа структуры, в мкм, а QC - величина критического радиационно-индуцированного (РИЗ), вызывающего сбои в работе логических устройств.
Кроме того, для учета частотной зависимости эффектов SEU в комбинационной логике, величину парциального сечения сбоев 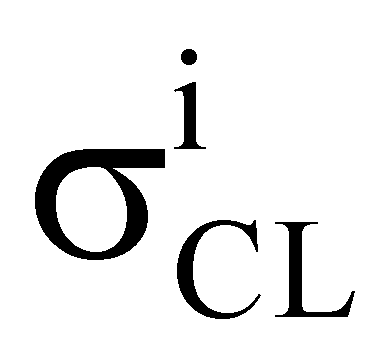 однотипных элементов комбинационной логики вводят с учетом тактовой частоты (частоты синхронизации).
однотипных элементов комбинационной логики вводят с учетом тактовой частоты (частоты синхронизации).
Кроме того, для учета частотной зависимости эффектов SEU в элементах комбинационной и последовательной логики, для учета зависимости поперечного сечения сбоев для однотипных элементов комбинационной логики от частоты синхронизации на аппроксимирующей зависимости поперечного сечения сбоев для однотипных элементов комбинационной логики 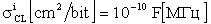 определяют по заданной частоте синхроимпульсов и
определяют по заданной частоте синхроимпульсов и 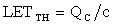 , в
, в  , величину сечения сбоев для однотипных элементов последовательной логики определяют с использованием соотношения
, величину сечения сбоев для однотипных элементов последовательной логики определяют с использованием соотношения
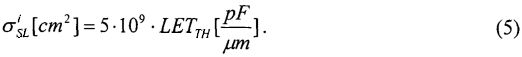
Кроме того, для унификации результатов оценки чувствительности к эффектам SEU элементов комбинационной и последовательной логики, для определения суммарного поперечного сечения сбоев для элементов последовательной и комбинационной логик поперечное сечение сбоев σSL для элементов последовательной логики определяют из 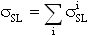 , где
, где 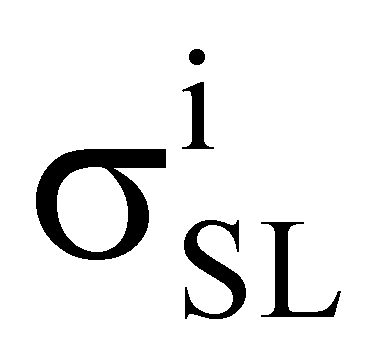 - парциальное поперечное сечение ошибок i-го элемента, и поперечное сечение сбоев σCL для элементов комбинационной логики определяют
- парциальное поперечное сечение ошибок i-го элемента, и поперечное сечение сбоев σCL для элементов комбинационной логики определяют 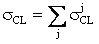 , где
, где  - парциальное поперечное сечение ошибок j-го элемента, суммарное сечение ошибок схемы последовательной логики σΣ находят с использованием соотношения
- парциальное поперечное сечение ошибок j-го элемента, суммарное сечение ошибок схемы последовательной логики σΣ находят с использованием соотношения
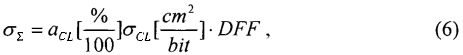
где: a CL - процентный состав схем комбинаторной логики; DFF - число фиксирующих элементов (триггеров) в схеме, а полное сечение сбоев в схеме определяют с использованием соотношения
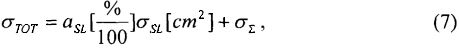
Кроме того, что для получения результата оценки эквивалентной дозы для эталонного спектра нуклидного источника Co60, исходя из спектра линейной передачи энергии 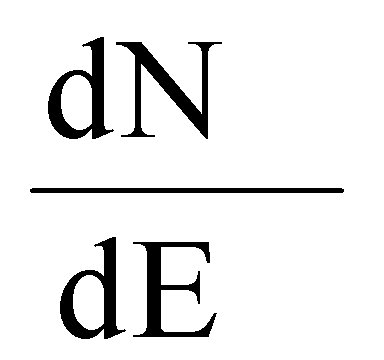 , чувствительного объема νS типовой транзисторной структуры отдельного цифрового элемента и максимального значения величины пространственной диагонали sMAX (хорды) чувствительного объема, определяют пороговое значение линейной передачи энергии LETTH и величину интенсивности сбоев
, чувствительного объема νS типовой транзисторной структуры отдельного цифрового элемента и максимального значения величины пространственной диагонали sMAX (хорды) чувствительного объема, определяют пороговое значение линейной передачи энергии LETTH и величину интенсивности сбоев 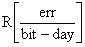 , определяют КОЭ
, определяют КОЭ 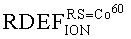
Кроме того, для оценки интенсивности сбоев от эффектов SEU, для получения экспериментальной зависимости поперечного сечения сбоев блоков РЭА или ИМС от LET вида 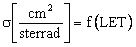 , на соответствующей МУ, воспроизводящей пучки ионов (ТЗЧ), выполняют облучение объектов исследования в диапазоне заданных флюенсов ТЗЧ из спектра LET вида
, на соответствующей МУ, воспроизводящей пучки ионов (ТЗЧ), выполняют облучение объектов исследования в диапазоне заданных флюенсов ТЗЧ из спектра LET вида 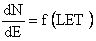 , где dN/dE - распределение числа ТЗЧ по энергиям, определяют чувствительный объем νS транзисторной гетероструктуры, в котором формируется критический заряд QC, определяют максимальный размер хорды sMAX (пространственной диагонали) в модели чувствительного объема (ЧО) в виде параллелепипеда (Rectangular Parallel Piped = RPF) из s2=a
2+b2+с2, где a=b=L - топологический размер ЧО элемента, с=t - толщина гетероструктуры в ЧО, определяют пороговое значение LETTH на зависимости
, где dN/dE - распределение числа ТЗЧ по энергиям, определяют чувствительный объем νS транзисторной гетероструктуры, в котором формируется критический заряд QC, определяют максимальный размер хорды sMAX (пространственной диагонали) в модели чувствительного объема (ЧО) в виде параллелепипеда (Rectangular Parallel Piped = RPF) из s2=a
2+b2+с2, где a=b=L - топологический размер ЧО элемента, с=t - толщина гетероструктуры в ЧО, определяют пороговое значение LETTH на зависимости 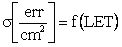 для полного телесного угла, интенсивность сбоев определяют с использованием соотношения
для полного телесного угла, интенсивность сбоев определяют с использованием соотношения
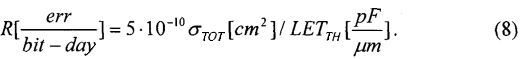
Кроме того, для конверсии результатов экспериментальной оценки чувствительности к эффектам SEU цифровой аппаратуры при испытаниях на установках ИЯР и ЭФУ, моделирующих воздействие ТЗЧ по эффекту идентичности критического заряда QC, определяют величину коэффициента относительной эффективности 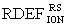 в единицах
в единицах 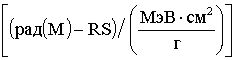 , где M - полупроводниковый материал в ЧО транзисторной структуры, а величину эквивалентной дозы гамма-излучения DRS(γ-кв.RS-экв.-(M)) определяют из соотношения
, где M - полупроводниковый материал в ЧО транзисторной структуры, а величину эквивалентной дозы гамма-излучения DRS(γ-кв.RS-экв.-(M)) определяют из соотношения

Кроме того, для реализации эксперимента на импульсном ядерном реакторе (ИЯР) или электрофизической установке (ЭФУ), генерирующих импульсное гамма-рентгеновское излучение, при известной длительности импульса гамма-рентгеновских квантов источника эталонного ИИ τP, для цифровой аппаратуры определяют мощность дозы 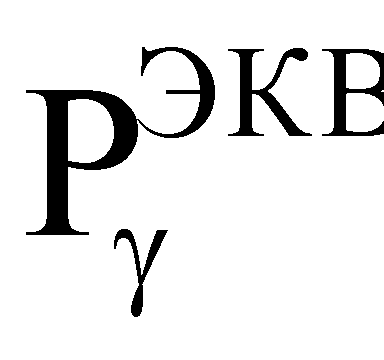 ИИ из отношения эквивалентной поглощенной дозы к длительности этого импульса
ИИ из отношения эквивалентной поглощенной дозы к длительности этого импульса
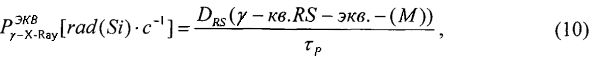
которую принимают равной УБР.
Данная задача также решается по варианту 2, в котором декорпусированный кристалл (чип) гетероэпитаксиальной структуры полупроводникового прибора (ППП) или ИМС облучают импульсным лазерным источником, определяют критическую пороговую энергию  сбоев, для определения величины УБР ППП или ИМС при эквивалентном по величине критического заряда QC воздействии импульсного ИИ с энергией квантов ~1 МэВ-экв.(М), оценку порогового значения
сбоев, для определения величины УБР ППП или ИМС при эквивалентном по величине критического заряда QC воздействии импульсного ИИ с энергией квантов ~1 МэВ-экв.(М), оценку порогового значения  производят при воздействии импульсного лазерного излучения (ИЛИ), затем с использованием соответствующих значений коэффициентов относительной эффективности
производят при воздействии импульсного лазерного излучения (ИЛИ), затем с использованием соответствующих значений коэффициентов относительной эффективности 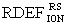 между эффективной дозой DRS гамма-рентгеновского излучения со спектром RS и
между эффективной дозой DRS гамма-рентгеновского излучения со спектром RS и 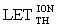 ТЗЧ (ионов),
ТЗЧ (ионов), 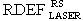 между энергией сбоев
между энергией сбоев 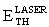 от лазерного импульса и эффективной дозой DRS гамма-рентгеновского излучения, определяют величину эквивалентного критического заряда QC, величину интенсивности сбоев R, величину эффективной дозы DRS и по известной длительности импульса ИИ τP определяют УБР.
от лазерного импульса и эффективной дозой DRS гамма-рентгеновского излучения, определяют величину эквивалентного критического заряда QC, величину интенсивности сбоев R, величину эффективной дозы DRS и по известной длительности импульса ИИ τP определяют УБР.
Кроме того, для получения адекватных с воздействием ТЗЧ условий, при использовании имитационных методов (ИМ) с помощью ИЛИ гетероструктуру чипа ППП или ИМС облучают пикосекундным импульсом лазерного источника с длительностью не более 350 пс и длиной волны в диапазоне 800-1500 нм.
Кроме того, для получения эквивалентной величины критического заряда QC, который вызывает в критическом объеме νS возникновение сторонних токов, вызывающих эффекты SEU и SET, для реализации фотоионизации ЧО транзисторных структур, используют значение 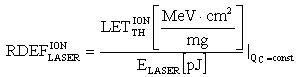 , устанавливающего связь между результатом облучения объекта с использованием ТЗЧ и ИЛИ, и
, устанавливающего связь между результатом облучения объекта с использованием ТЗЧ и ИЛИ, и 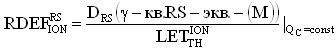 , устанавливающего связь между результатом облучения объекта с использованием импульсного ионизирующего излучения (ИИИ) и ТЗЧ, получают значение
, устанавливающего связь между результатом облучения объекта с использованием импульсного ионизирующего излучения (ИИИ) и ТЗЧ, получают значение 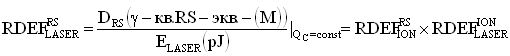 , с использованием которого, в свою очередь, определяют величину эффективной поглощенной дозы гамма-рентгеновского излучения DRS(γ - кв.RS-экв.-(М)) эталонного источника Co60 для материала (М) (например, в качестве M=Si, SiO2) и при известной длительности импульса гамма-квантов источника эталонного ИИ τP УБР цифровой аппаратуры определяют из отношения эквивалентной поглощенной дозы к длительности этого импульса
, с использованием которого, в свою очередь, определяют величину эффективной поглощенной дозы гамма-рентгеновского излучения DRS(γ - кв.RS-экв.-(М)) эталонного источника Co60 для материала (М) (например, в качестве M=Si, SiO2) и при известной длительности импульса гамма-квантов источника эталонного ИИ τP УБР цифровой аппаратуры определяют из отношения эквивалентной поглощенной дозы к длительности этого импульса
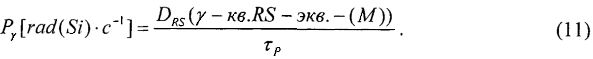
Кроме того, для фиксации эффективности ИМ, при использовании ИМ с помощью импульсного лазерного источника фиксируют критическую пороговую энергию  сбоев в единицах [pJ].
сбоев в единицах [pJ].
Кроме того, для конверсии результатов ИМ, значение величины 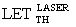 определяют с использованием соотношения
определяют с использованием соотношения

Кроме того, для фиксации эффективности ИМ, величину 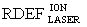 для длины волны лазерного излучения λLASER=800-1500 nm принимают равной
для длины волны лазерного излучения λLASER=800-1500 nm принимают равной
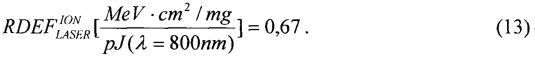
Кроме того, для преобразования результатов ИМ в эвивалентное воздействие ТЗЧ, величину эквивалентного значения 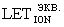 определяют из
определяют из
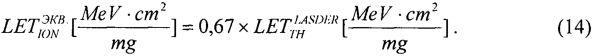
Кроме того, для определения УБР при ИМ, в единицах, эквивалентных воздействию источников импульсного ИИ, с использованием
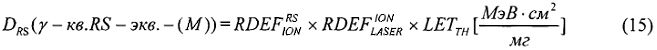
определяют величину эквивалентной полной поглощенной дозы гамма-квантов DRS(γ-кв.RS-экв.-(M)) и при известной длительности импульса гамма-квантов источника эталонного ионизирующего излучения τP УБР цифровой аппаратуры определяют (11) Pγ[rad(Si)·c-1].
Кроме того, для использования инженерных методов оценки интенсивности сбоев от эффектов ТЗЧ, преобразуют 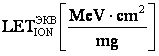 в
в 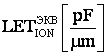 .
.
Данная задача решается также по варианту 3 тем, что определяют уровень бессбойной работы (УБР) по результатам использования динамических электрических параметров спецификации на элементы ЭКБ, для получения эквивалентной величины критического заряда 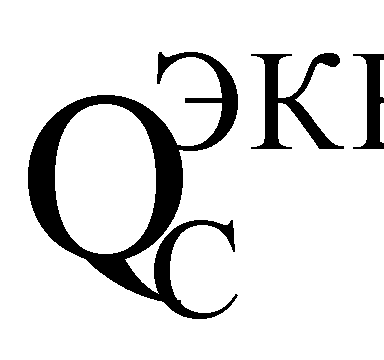 , который вызывает в ЧО νS возникновение сторонних токов, генерирующих эффекты SEU и SET в цифровых электронных схемах, в способе оценки стойкости цифровой аппаратуры к воздействию ИИ используют данные о значении динамических электрических параметров спецификаций на элементы ЭКБ.
, который вызывает в ЧО νS возникновение сторонних токов, генерирующих эффекты SEU и SET в цифровых электронных схемах, в способе оценки стойкости цифровой аппаратуры к воздействию ИИ используют данные о значении динамических электрических параметров спецификаций на элементы ЭКБ.
Кроме того, для определения эквивалентного значения 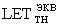 по величине эквивалентного критического заряда
по величине эквивалентного критического заряда 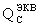 , в качестве динамического параметра используют времена переключения из одного логического состояния в другое
, в качестве динамического параметра используют времена переключения из одного логического состояния в другое 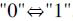 и соответствующее значение напряжения питания ИМС.
и соответствующее значение напряжения питания ИМС.
Кроме того, для определения эквивалентного значения 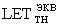 по величине эквивалентного критического заряда
по величине эквивалентного критического заряда 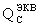 , соответствующего воздействию «ионного коктейля», в качестве динамического параметра используют так же уровни выходных напряжений логических состояний V0L и V0H и соответствующее значение емкости на выходе контролируемого сигнала.
, соответствующего воздействию «ионного коктейля», в качестве динамического параметра используют так же уровни выходных напряжений логических состояний V0L и V0H и соответствующее значение емкости на выходе контролируемого сигнала.
Кроме того, для определения эквивалентного значения 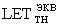 по величине эквивалентного критического заряда
по величине эквивалентного критического заряда 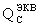 , соответствующего воздействию «ионного коктейля», в качестве динамического параметра используют прямые данные о заряде переключения QПЕР между этими логическими состояниями.
, соответствующего воздействию «ионного коктейля», в качестве динамического параметра используют прямые данные о заряде переключения QПЕР между этими логическими состояниями.
Кроме того, для определения эквивалентного значения 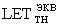 по величине эквивалентного критического заряда
по величине эквивалентного критического заряда 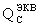 , соответствующего воздействию «ионного коктейля», используют соотношение
, соответствующего воздействию «ионного коктейля», используют соотношение
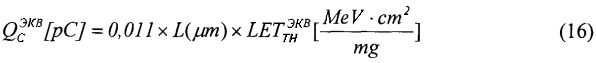
или 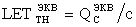 , и затем определяют эквивалентное значение
, и затем определяют эквивалентное значение 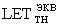 .
.
Кроме того, для конверсии величин динамических параметров переключений в эффективное значение УБР от воздействия ИИ со спектром RS, с использованием соответствующих значений коэффициентов относительной эффективности 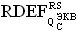 между эквивалентной дозой DRS гамма-рентгеновского излучения со спектром RS и
между эквивалентной дозой DRS гамма-рентгеновского излучения со спектром RS и 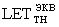 , соответствующей генерации эквивалентного заряда от параметров динамических переключений логических состояний определяют величину эквивалентной дозы DRS и по известной длительности τP импульса ИИ эквивалентного источника определяют УБР.
, соответствующей генерации эквивалентного заряда от параметров динамических переключений логических состояний определяют величину эквивалентной дозы DRS и по известной длительности τP импульса ИИ эквивалентного источника определяют УБР.
Данная задача решается также по варианту 4 тем, что для определения уровня бессбойной работы (УБР) БИС/СБИС при воздействии эквивалентного импульсного источника ионизирующего излучения с энергией квантов 1,25 МэВ-экв.(М), производят выборочно оценку порогового значения линейной передачи энергии (LETTH) либо из прямых измерений зависимости поперечного сечения сбоев от величины LET, либо при воздействии импульсного лазерного излучения, либо из данных о значении таких электрических параметров спецификации на элементы ЭКБ, как времена переключения из одного логического состояния в другое 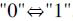 , или уровни выходных напряжений логических состояний VOL и V0H, либо из данных о заряде переключения QПЕР. между этими состояниями, затем с использованием соответствующих значений коэффициентов относительной эффективности
, или уровни выходных напряжений логических состояний VOL и V0H, либо из данных о заряде переключения QПЕР. между этими состояниями, затем с использованием соответствующих значений коэффициентов относительной эффективности 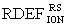 между эквивалентной дозой гамма-рентгеновского излучения DRS и
между эквивалентной дозой гамма-рентгеновского излучения DRS и 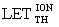 ,
, 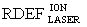 между энергией сбоев от лазерного импульса
между энергией сбоев от лазерного импульса  и
и 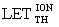 ,
, 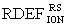 между эффективной дозой гамма-рентгеновского излучения DRS и
между эффективной дозой гамма-рентгеновского излучения DRS и 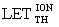 ,
, 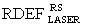 между энергией сбоев от лазерного импульса
между энергией сбоев от лазерного импульса  и эффективной дозой гамма-рентгеновского излучения DRS, определяют величину эквивалентной дозы DRS и по известной величине длительности импульса ИИ τP определяют УБР.
и эффективной дозой гамма-рентгеновского излучения DRS, определяют величину эквивалентной дозы DRS и по известной величине длительности импульса ИИ τP определяют УБР.
Заявляемые изобретения связаны единым изобретательским замыслом и представляют собой способ оценки стойкости цифровой электронной аппаратуры к воздействию ИИ, в частности, величин УБР и TID.
Изобретение проиллюстрировано следующими рисунками:
Фиг. 1. Поперечное сечение p-n-перехода, сформированного на кремниевой подложке. Эффект прохождения иона через переход «сток-тело» в транзисторе n-МОП

Фиг. 2. График логарифмической зависимости длительности переходного импульса, необходимого для распространения SET без затухания через бесконечно протяженную цепочку инвертеров как функция топологического размера [17].
Фиг. 3. Блок-схема компоновки последовательной логики [17].

Фиг. 4. Два процесса сбоя (опрокидывания). (A) прямое попадание в элемент памяти или последовательной логики и (B) при попадании в комбинированную логику создается SET, который попадает при распространении в элемент памяти или последовательной логики.
Combinational Logick Network - устройство комбинаторной логики
PRE - триггер с фиксацией состояния
SET - переходный процесс от воздействия единичной частицы
SEU - эффект переключения (изменения логического состояния) под действием единичной частицы
Фиг. 5. Временная диаграмма, иллюстрирующая соотношение во времени для случая, когда истинные данные игнорируются, а позитивные SET ошибочно поступают на вход второго триггера (46).

Фиг. 6. Временная диаграмма, иллюстрирующая ситуацию, когда SET на диаграмме синхросигнала может привести к ошибке запоминания.

Фиг. 7. Зависимость интенсивности сбоев в устройствах последовательной логики (Flip-Flop [17]) и комбинационной логики (тестовые чипы DICE [18]) и их взаимное соответствие.

Фиг. 8. Сравнение данных по воздействию ТЗЧ на две тестовые схемы. Черная линия соответствует поперечному сечению в насыщении для чипа D-триггеров. Более светлая - это линейная аппроксимация данных для DICE. Точка для 1 МГц для D-триггеров совпала точно, хотя чип находился в рабочем состоянии.

Фиг. 9. Три варианта оценки УБР цифровых ИМС
Фиг. 10. Исходная структура чувствительного объема транзистора МОП для расчета LET.
Фиг. 11. Схематическое представление процедуры оценки интенсивности сбоев и параметрической вероятности сохранения работоспособности электронных устройств КА /6/.
Фиг. 12. Типичная зависимость поперечного сечения SEE от LET для различных ТЗЧ. По оси Y: Поперечное сечение SEE (см2); по оси X: LET (МэВ·см2/мг).
Фиг. 13. Типичный спектр ТЗЧ. По оси Y: флюенс частиц [частиц/м2- стеррад·с], по оси X: 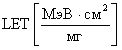 .
.
Фиг. 14. Поперечное сечение исследовавшихся структур КМОП/КНС. Фиг. 15. Линеаризированная функция распределения Вейбулла в виде зависимости от Y=fln(LET-LETγ)
Фиг. 16. Зависимость сечения насыщения сбоев от линейных потерь энергии.
В соответствии с заявленным должны быть описаны отличительные признаки (specific to structural features) и/или методологические шаги (способ реализации), это следует понимать так, что изобретение, определяемое в дополнительных звеньях (claims = претензии), не является ограниченным отличительными признаками или способом реализации. Напротив, отличительные признаки и способ реализации являются открытыми как предпочтительная форма использования заявляемых звеньев.
Предлагаемый способ реализуется по общему алгоритму определения УБР с использованием трех основных вариантов и одного обобщенного (Фиг. 9) в зависимости от объема имеющейся информации:
Способ по варианту 1 реализуют следующим образом.
Поставленная задача (вариант 1) решается тем, что для определения уровня бессбойной работы (УБР) блока или всего устройства радиоэлектронной аппаратуры (РЭА), в целом, содержащей в своем составе цифровые интегральные микросхемы (ИМС), по результатам экспериментальных исследований на моделирующих установках (МУ), в известном способе оценки стойкости цифровой электронной аппаратуры к воздействию ИИ путем использования экспериментально полученных данных при моделировании РИЗ в БИС/СБИС технологии КМОП/КНД по генерации сторонних токов от импульсных источников ионизирующего излучения (ИИИ). В качестве ИИИ используют сопутствующее гамма-излучение импульсного ядерного ректора (ИЯР) или гамма-рентгеновское излучение электрофизических установок (ЭФУ) (линейных импульсных ускорителей и/или рентгеновских установок) и воздействие ТЗЧ ускорителей заряженных частиц. Затем с использованием соответствующих значений коэффициентов относительной эффективности 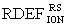 между эквивалентной дозой DRS гамма-рентгеновского излучения со спектром RS (Radiation Stress) и
между эквивалентной дозой DRS гамма-рентгеновского излучения со спектром RS (Radiation Stress) и 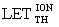 ионов (ТЗЧ),
ионов (ТЗЧ), 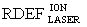 определяют величину эквивалентной дозы DRS (9) и по известной длительности импульса ИИ τP определяют УБР (10).
определяют величину эквивалентной дозы DRS (9) и по известной длительности импульса ИИ τP определяют УБР (10).
Для определения поперечного сечения сбоев цифрового устройства, анализируют структурную схему радиоэлектронного устройства, определяют величины отдельных парциальных поперечных сечений сбоев (5) 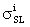 и
и 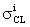 для каждого цифрового элемента схемы последовательной и комбинационной логики, суммарное поперечное сечение (6) σΣ для однотипных элементов последовательной и комбинационной логики, усредненное поперечное сечение σD для элементов последовательной и комбинационной логики, полное сечение (7) σTOT для всего цифрового устройства.
для каждого цифрового элемента схемы последовательной и комбинационной логики, суммарное поперечное сечение (6) σΣ для однотипных элементов последовательной и комбинационной логики, усредненное поперечное сечение σD для элементов последовательной и комбинационной логики, полное сечение (7) σTOT для всего цифрового устройства.
Для сокращения числа испытаний, величину полного поперечного сечения сбоев вводят с учетом числа цифровых бистабильных триггеров DFF.
Для сокращения числа испытаний на установках, моделирующих воздействие ТЗЧ, для определения единичного сечения сбоев σе для однотипных элементов схемы, для большинства практических случаев интенсивность сбоев определяют с использованием аппроксимирующего выражения для поперечного сечения насыщения σSAT=ab, (a, b>с) и критического порогового значения линейной передачи энергии (массовых потерь) 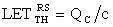 , в
, в 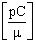 , где c - толщина полупроводниковой пластины, а и b - размеры чипа структуры, в мкм, a QC - величина критического радиационно-индуцированного (РИЗ), вызывающего сбои в работе логических устройств.
, где c - толщина полупроводниковой пластины, а и b - размеры чипа структуры, в мкм, a QC - величина критического радиационно-индуцированного (РИЗ), вызывающего сбои в работе логических устройств.
Для учета частотной зависимости эффектов SEU в комбинационной логике, величину парциального сечения сбоев 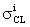 однотипных элементов комбинационной логики вводят с учетом тактовой частоты (частоты синхронизации).
однотипных элементов комбинационной логики вводят с учетом тактовой частоты (частоты синхронизации).
Для учета частотной зависимости эффектов SEU в элементах комбинационной и последовательной логики, для учета зависимости поперечного сечения сбоев для однотипных элементов комбинационной логики от частоты синхронизации на аппроксимирующей зависимости поперечного сечения сбоев для однотипных элементов комбинационной логики 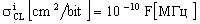 определяют по заданной частоте синхроимпульсов и
определяют по заданной частоте синхроимпульсов и 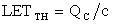 , в
, в  , величину сечения сбоев для однотипных элементов последовательной логики определяют с использованием соотношения (5).
, величину сечения сбоев для однотипных элементов последовательной логики определяют с использованием соотношения (5).
Для унификации результатов оценки чувствительности к эффектам SEU элементов комбинационной и последовательной логики, для определения суммарного поперечного сечения сбоев для элементов последовательной и комбинационной логик поперечное сечение сбоев σSL для элементов последовательной логики определяют из 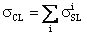 , где
, где 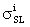 - парциальное поперечное сечение ошибок i-го элемента, и поперечное сечение сбоев σCL для элементов комбинационной логики определяют
- парциальное поперечное сечение ошибок i-го элемента, и поперечное сечение сбоев σCL для элементов комбинационной логики определяют 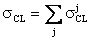 , где
, где 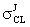 - парциальное поперечное сечение ошибок j-го элемента, суммарное сечение ошибок схемы последовательной логики σΣ находят с использованием соотношения (6).
- парциальное поперечное сечение ошибок j-го элемента, суммарное сечение ошибок схемы последовательной логики σΣ находят с использованием соотношения (6).
Полное сечение сбоев в схеме определяют с использованием соотношения (7).
Для получения результата оценки эквивалентной дозы для эталонного спектра нуклидного источника Со60, исходя из спектра линейной передачи энергии 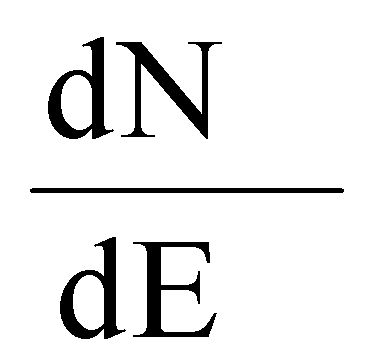 , чувствительного объема νS типовой транзисторной структуры отдельного цифрового элемента и максимального значения величины пространственной диагонали sMAX (хорды) чувствительного объема, определяют пороговое значение линейной передачи энергии LETTH и величину интенсивности сбоев
, чувствительного объема νS типовой транзисторной структуры отдельного цифрового элемента и максимального значения величины пространственной диагонали sMAX (хорды) чувствительного объема, определяют пороговое значение линейной передачи энергии LETTH и величину интенсивности сбоев 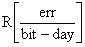 , определяют КОЭ
, определяют КОЭ 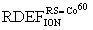 для порогового значения LETTH и полной поглощенной дозы TID эквивалентного источника гамма-квантов Co60 со средней энергией квантов RS=1,25 МэВ и определяют величину TID.
для порогового значения LETTH и полной поглощенной дозы TID эквивалентного источника гамма-квантов Co60 со средней энергией квантов RS=1,25 МэВ и определяют величину TID.
Для оценки интенсивности сбоев от эффектов SEU, для получения экспериментальной зависимости поперечного сечения сбоев блоков РЭА или ИМС от LET вида 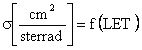 , на соответствующей МУ, воспроизводящей пучки ионов (ТЗЧ), выполняют облучение объектов исследования в диапазоне заданных флюенсов ТЗЧ из спектра LET вида
, на соответствующей МУ, воспроизводящей пучки ионов (ТЗЧ), выполняют облучение объектов исследования в диапазоне заданных флюенсов ТЗЧ из спектра LET вида 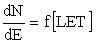 , где dN/dE - распределение числа ТЗЧ по энергиям. Затем определяют чувствительный объем (ЧО) νS транзисторной гетероструктуры, в котором формируется критический заряд QC, определяют максимальный размер хорды sMAX (пространственной диагонали) в модели ЧО в виде параллелепипеда (Rectangular Parallel Piped = RPP) из s2=а
2+b2+с2, где a=b=L - топологический размер ЧО элемента, с=t - толщина гетероструктуры в ЧО, определяют пороговое значение LETTH на зависимости
, где dN/dE - распределение числа ТЗЧ по энергиям. Затем определяют чувствительный объем (ЧО) νS транзисторной гетероструктуры, в котором формируется критический заряд QC, определяют максимальный размер хорды sMAX (пространственной диагонали) в модели ЧО в виде параллелепипеда (Rectangular Parallel Piped = RPP) из s2=а
2+b2+с2, где a=b=L - топологический размер ЧО элемента, с=t - толщина гетероструктуры в ЧО, определяют пороговое значение LETTH на зависимости 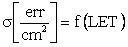 для полного телесного угла. Интенсивность сбоев определяют с использованием соотношения (8).
для полного телесного угла. Интенсивность сбоев определяют с использованием соотношения (8).
Для конверсии результатов экспериментальной оценки чувствительности к эффектам SEU цифровой аппаратуры при испытаниях на установках ИЯР и ЭФУ, моделирующих воздействие ТЗЧ по эффекту идентичности критического заряда QC, определяют величину коэффициента относительной эффективности 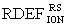 в единицах
в единицах 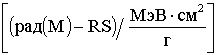 , где M - полупроводниковый материал в ЧО транзисторной структуры. Величину эквивалентной дозы гамма-излучения DRS(γ-кв.RS-экв.-(М)) определяют из соотношения (9).
, где M - полупроводниковый материал в ЧО транзисторной структуры. Величину эквивалентной дозы гамма-излучения DRS(γ-кв.RS-экв.-(М)) определяют из соотношения (9).
Для реализации эксперимента на импульсном ядерном реакторе (ИЯР) или электрофизической установке (ЭФУ), генерирующих импульсное гамма-рентгеновское излучение, при известной длительности импульса гамма-рентгеновских квантов источника эталонного ИИ τP для цифровой аппаратуры определяют мощность дозы 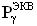 ИИ из отношения (10) эквивалентной поглощенной дозы к длительности этого импульса. Эту величину принимают равной УБР.
ИИ из отношения (10) эквивалентной поглощенной дозы к длительности этого импульса. Эту величину принимают равной УБР.
Данная задача также решается по варианту 2, в котором декорпусированный кристалл (чип) гетероэпитаксиальной структуры полупроводникового прибора (ППП) или ИМС облучают импульсным лазерным источником, определяют критическую пороговую энергию  сбоев. Для определения величины УБР ППП или ИМС при эквивалентном по величине критического заряда QC воздействии импульсного ИИ с энергией квантов ~1 МэВ-экв.(М), оценку порогового значения
сбоев. Для определения величины УБР ППП или ИМС при эквивалентном по величине критического заряда QC воздействии импульсного ИИ с энергией квантов ~1 МэВ-экв.(М), оценку порогового значения 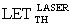 производят при воздействии импульсного лазерного излучения (ИЛИ), затем с использованием соответствующих значений коэффициентов относительной эффективности
производят при воздействии импульсного лазерного излучения (ИЛИ), затем с использованием соответствующих значений коэффициентов относительной эффективности 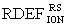 между эффективной дозой DRS гамма-рентгеновского излучения со спектром RS и
между эффективной дозой DRS гамма-рентгеновского излучения со спектром RS и 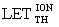 ТЗЧ (ионов),
ТЗЧ (ионов), 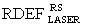 между энергией сбоев
между энергией сбоев  от лазерного импульса и эффективной дозой DRS гамма-рентгеновского излучения, определяют величину эквивалентного критического заряда QC, величину интенсивности сбоев R, величину эффективной дозы DRS и по известной длительности импульса ИИ τP определяют (10) УБР.
от лазерного импульса и эффективной дозой DRS гамма-рентгеновского излучения, определяют величину эквивалентного критического заряда QC, величину интенсивности сбоев R, величину эффективной дозы DRS и по известной длительности импульса ИИ τP определяют (10) УБР.
Для получения адекватных с воздействием ТЗЧ условий, при использовании имитационных методов (ИМ) с помощью ИЛИ гетероструктуру чипа ППП или ИМС облучают пикосекундным импульсом лазерного источника с длительностью не более 350 пс и длиной волны в диапазоне 800-1500 нм.
Для получения эквивалентной величины критического заряда QC, который вызывает в ЧО объеме νS возникновение сторонних токов, вызывающих эффекты SEU и SET, для реализации фотоионизации ЧО транзисторных структур, используют значение 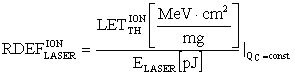 , устанавливающего связь между результатом облучения объекта с использованием ТЗЧ и ИЛИ, и
, устанавливающего связь между результатом облучения объекта с использованием ТЗЧ и ИЛИ, и 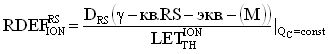 , устанавливающего связь между результатом облучения объекта с использованием импульсного ионизирующего излучения (ИИИ) и ТЗЧ, получают значение
, устанавливающего связь между результатом облучения объекта с использованием импульсного ионизирующего излучения (ИИИ) и ТЗЧ, получают значение 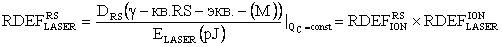 , с использованием которого, в свою очередь, определяют величину эффективной поглощенной дозы гамма-рентгеновского излучения DRS(γ-кв.RS-экв.-(M)) эталонного источника Co60 для материала (М) (например, в качестве M=Si, SiO2) и при известной длительности импульса гамма-квантов источника эталонного ИИ τP УБР цифровой аппаратуры определяют из отношения эквивалентной поглощенной дозы к длительности этого импульса (11).
, с использованием которого, в свою очередь, определяют величину эффективной поглощенной дозы гамма-рентгеновского излучения DRS(γ-кв.RS-экв.-(M)) эталонного источника Co60 для материала (М) (например, в качестве M=Si, SiO2) и при известной длительности импульса гамма-квантов источника эталонного ИИ τP УБР цифровой аппаратуры определяют из отношения эквивалентной поглощенной дозы к длительности этого импульса (11).
Для фиксации эффективности ИМ, при использовании ИМ с помощью импульсного лазерного источника фиксируют критическую пороговую энергию  сбоев в единицах [pJ].
сбоев в единицах [pJ].
Для конверсии результатов ИМ, значение величины 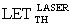 определяют с использованием соотношения (12).
определяют с использованием соотношения (12).
Для фиксации эффективности ИМ, величину 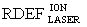 для длины волны лазерного излучения λLASER=800-1500 nm принимают равной (13).
для длины волны лазерного излучения λLASER=800-1500 nm принимают равной (13).
Для преобразования результатов ИМ в эквивалентное воздействие ТЗЧ, величину эквивалентного значения 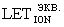 определяют из (14).
определяют из (14).
Для определения УБР при ИМ, в единицах, эквивалентных воздействию источников импульсного ИИ, с использованием (15) определяют величину эквивалентной полной поглощенной дозы гамма-квантов DRS(γ-кв.RS-экв.-(М))и при известной длительности импульса гамма-квантов источника эталонного ионизирующего излучения τP УБР цифровой аппаратуры определяют (11) Рγ[rad(Si)·с-1].
Для использования инженерных методов оценки интенсивности сбоев от эффектов ТЗЧ, преобразуют 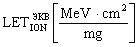 в
в 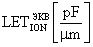 .
.
Данная задача решается также по варианту 3 тем, что определяют уровень бессбойной работы (УБР) по результатам использования динамических электрических параметров спецификации на элементы ЭКБ. Для получения эквивалентной величины критического заряда 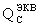 , который вызывает в ЧО νS возникновение сторонних токов, генерирующих эффекты SEU и SET в цифровых электронных схемах, используют данные о значении динамических электрических параметров спецификаций на элементы ЭКБ.
, который вызывает в ЧО νS возникновение сторонних токов, генерирующих эффекты SEU и SET в цифровых электронных схемах, используют данные о значении динамических электрических параметров спецификаций на элементы ЭКБ.
Для определения эквивалентного значения 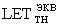 по величине эквивалентного критического заряда
по величине эквивалентного критического заряда 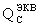 , в качестве динамического параметра используют времена переключения из одного логического состояния в другое
, в качестве динамического параметра используют времена переключения из одного логического состояния в другое 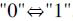 и соответствующее значение напряжения питания ИМС.
и соответствующее значение напряжения питания ИМС.
Для определения эквивалентного значения 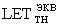 по величине эквивалентного критического заряда
по величине эквивалентного критического заряда 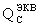 , соответствующего воздействию «ионного коктейля», в качестве динамического параметра используют так же уровни выходных напряжений логических состояний V0L и V0H и соответствующее значение емкости на выходе контролируемого сигнала.
, соответствующего воздействию «ионного коктейля», в качестве динамического параметра используют так же уровни выходных напряжений логических состояний V0L и V0H и соответствующее значение емкости на выходе контролируемого сигнала.
Для определения эквивалентного значения 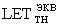 по величине эквивалентного критического заряда
по величине эквивалентного критического заряда 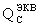 , соответствующего воздействию «ионного коктейля», в качестве динамического параметра используют прямые данные о заряде переключения QПЕР между этими логическими состояниями.
, соответствующего воздействию «ионного коктейля», в качестве динамического параметра используют прямые данные о заряде переключения QПЕР между этими логическими состояниями.
Для определения эквивалентного значения 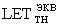 по величине эквивалентного критического заряда
по величине эквивалентного критического заряда 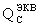 , соответствующего воздействию «ионного коктейля», используют соотношение (16) или
, соответствующего воздействию «ионного коктейля», используют соотношение (16) или 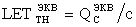 . Затем определяют эквивалентное значение
. Затем определяют эквивалентное значение 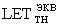 .
.
Для конверсии величин динамических параметров переключений в эффективное значение УБР от воздействия ИИ со спектром RS, с использованием соответствующих значений коэффициентов относительной эффективности 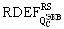 между эквивалентной дозой DRS гамма-рентгеновского излучения со спектром RS и
между эквивалентной дозой DRS гамма-рентгеновского излучения со спектром RS и 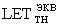 , соответствующей генерации эквивалентного заряда от параметров динамических переключений логических состояний, определяют величину эквивалентной дозы DRS и по известной длительности τP импульса ИИ эквивалентного источника определяют (10) УБР.
, соответствующей генерации эквивалентного заряда от параметров динамических переключений логических состояний, определяют величину эквивалентной дозы DRS и по известной длительности τP импульса ИИ эквивалентного источника определяют (10) УБР.
Данная задача решается также по варианту 4 тем, что в известном способе оценки стойкости цифровой электронной аппаратуры к воздействию ИИ путем использования экспериментально полученных данных при моделировании РИЗ в БИС/СБИС технологии КМОП/КНД от воздействия ТЗЧ КП, от воздействия ИЛИ пикосекундного диапазона, для определения уровня бессбойной работы (УБР) БИС/СБИС при воздействии эквивалентного импульсного источника ионизирующего излучения с энергией квантов 1,25 МэВ-экв. (М), производят выборочно оценку порогового значения линейной передачи энергии (LETTH) либо из прямых измерений зависимости поперечного сечения сбоев от величины LET по варианту 1, либо при воздействии импульсного лазерного излучения по варианту 2, либо из данных о значении динамических электрических параметров спецификации на (datasheet) элементы ЭКБ, или уровни выходных напряжений логических состояний VOL и V0H, либо из данных о заряде переключения QПЕР. между этими состояниями. Затем с использованием соответствующих значений КОЭ: 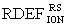 между эквивалентной дозой гамма-рентгеновского излучения DRS и
между эквивалентной дозой гамма-рентгеновского излучения DRS и 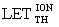 ,
, 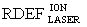 между энергией сбоев от лазерного импульса
между энергией сбоев от лазерного импульса  и
и 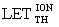 ,
, 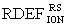 между эффективной дозой гамма-рентгеновского излучения DRS и
между эффективной дозой гамма-рентгеновского излучения DRS и 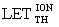 ,
, 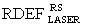 между энергией сбоев от лазерного импульса
между энергией сбоев от лазерного импульса  и эффективной дозой гамма-рентгеновского излучения DRS, определяют величину эквивалентной дозы DRS. По известной величине длительности импульса ИИ τP определяют (10) УБР.
и эффективной дозой гамма-рентгеновского излучения DRS, определяют величину эквивалентной дозы DRS. По известной величине длительности импульса ИИ τP определяют (10) УБР.
Пример конкретной реализации.
1. Примеры по варианту 1. Определения УБР по результатам экспериментальных исследований зависимости поперечного сечения сбоев от величины линейной передачи энергии σ=f(LET) для ТЗЧ из заданного ионного «коктейля».
А. Критический заряд.
Существующие тенденции (т.е. сокращение размеров приборов, потребляемой мощности, увеличение линейного разрешения, увеличение объема памяти и быстродействия) увеличивают чувствительность к эффектам SEU. Это легко можно понять, если представить прибор простым конденсатором (С), в который проникает ионизирующая частица, создающая заряд Q, в результате чего изменяется напряжение (т.е. логическое состояние). Эффект SEU наблюдается, если LET>Qcrit.
При уменьшении активной области такого прибора, ее емкость также уменьшается и тот же самый заряд способствует появлению эффектов SEU. Прибор по толщине в основном остается неизмененным, подвергаются изменениям только длина и ширина прибора. Если будем рассматривать перспективный прибор с чипом квадратной конфигурации L×L и толщиной чипа с, то критический заряд, достаточный для изменения логического состояния такого прибора, будет пропорционален квадрату размера L.
Robinson et al. [19] представили критический заряд для ИМС ряда технологий (включая NMOS, CMOS/объемный, CMOS/SOS, i2L, GaAs, ECL, CMOS/SOI VHSIC биполярный):
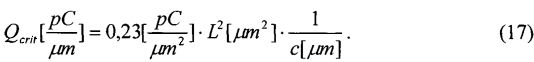
Этот критический заряд приводит непосредственно к переключению из состояния логической «1» в состояние логического «О» или изменению логического состояния (контрверсии), но он меньше, чем полный радиационно-индуцированный заряд в ЧО. Существенно то, что Qcrit является разницей между накопленным зарядом в узле и минимальным зарядом, необходимым для усиления и последующей коррекции [20]. В схемах SRAM Qcrit зависит не только от величины собранного заряда, но и от скорости изменения импульса во времени.
Элементарная модель SEU может быть сформулирована с использованием представлений о LET с использованием той же толщины прибора в виде прямоугольного параллелепипеда (IRPP). Она основана на вычислении поглощенной энергии Edep, представлении траектории частицы, пролетающей через объем прибора в виде поперечной хорды.
Накопленный заряд зависит от энергии образования электронно-дырочной пары wehp

где q=1,60022×10-19 Coulombs/e, а значения wehp для ряда элементов приведены в табл. 1.
Используя эти данные, можно произвести в первом приближении расчет LET, минимально необходимой для создания SEU (алгоритм приведен ниже).
Ниже приведена процедура оценки величины LET для параллелепипеда с размерами а, b, c, где c - толщина прибора (Фиг. 10). Минимальное значение LET соответствует максимальному значению длины хорды smax, которая является диагональю параллелепипеда

Минимальное значение LET будет соответствовать случаю, для которого сбой может быть рассчитан из соотношения:

Можно рассчитать минимальную длину smin, которую частица должна пройти с заданными LET для создания эффекта SEU

Частицы создают сбои под углом от θс-π/2: имеется два потенциальных случая (при LETC<LETTH)
1. Если LET>LETC, то под всеми углами падения реализуются сбои.
2. Если LET<LETC, то существует критический угол θC, при котором наблюдаются сбои. Интенсивность сбоев была определена как число ошибок в день на чип, [errors/day-chip] или число ошибок в день на бит [errors/bit-day]. Скорость ошибок радиационно-стойких схем составляет порядка 10-8 [errors/bit-day], а нерадиационно-стойких - на несколько порядков больше по величине.
Можно выделить несколько основных этапов в расчете эффектов SEU [21], проиллюстрированных на Фиг. 11:
(4) - Определение ЧО транзистора структуры МОП;
(5) - Определение зависимости относительного поперечного сечения эффектов SEE в 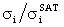 в [отн. ед.] от LET для i-го элемента ЭКБ (
в [отн. ед.] от LET для i-го элемента ЭКБ (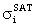 - сечение насыщения);
- сечение насыщения);
(6) - Оценка математического ожидания µ и дисперсии D;
(7) - Построение физического закона поражения (ФЗП) для всей цифровой схемы.
(1). Измерение поперечного сечения σ эффектов SEU/SEE в зависимости от LET для каждого из образцов на ускорителе заряженных частиц или источнике импульсного ИИ [15]. Поперечное сечение сбоев прибора (в смысле ИМС или транзисторной структуры) определяется как отношение числа сбоев к флюенсу частиц 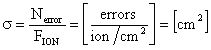 . Экспериментально зависимость поперечного сечения определяют как функции энергии частиц в виде LET (Фиг. 12).
. Экспериментально зависимость поперечного сечения определяют как функции энергии частиц в виде LET (Фиг. 12).
(2) - Определение спектра линейных потерь энергии LET для ТЗЧ производят для заданного, исходя из реальных условий существования цифровой аппаратуры, спектра «ионного коктейля» (Фиг. 13).
(3) - Оценка интенсивности сбоев Rerr ИМС. На этом этапе интегрируют поперечное сечение и чувствительный объем прибора со спектром LET (соотношение (6)).
(4) - Определение ЧО транзистора структуры МОП. ЧО меньше чем реальный физический объем прибора. ЧО определяют для SEE только для ТЗЧ ионов и протонов, так же, как для эффектов SEL («тиристорных эффектов»). Для гамма- и рентгеновского излучения эти понятия совпадают (ЧО, такая, например, как «островок» в n-канальном транзисторе МОП в p-кармане структуры КМОП/КНД, расширяется до геометрических размеров всего транзистора МОП). Геометрия чувствительного объема и критический заряд являются наиболее сложными параметрами для определения.
(5) - Представление зависимость относительного поперечного сечения SEE в относительных единицах 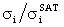 от LET для i-го элемента ЭКБ (определение
от LET для i-го элемента ЭКБ (определение 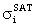 - сечения насыщения и порогового значения LETTH, определение критического значения флюенса частиц
- сечения насыщения и порогового значения LETTH, определение критического значения флюенса частиц 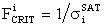 ), аппроксимация зависимости трехпараметрическим распределением Вейбулла [22], оценка параметров распределения (γ-положения, η-масштаба, β-формы) для каждой i-й ИМС;
), аппроксимация зависимости трехпараметрическим распределением Вейбулла [22], оценка параметров распределения (γ-положения, η-масштаба, β-формы) для каждой i-й ИМС;
(6) - Оценка математического ожидания µi и дисперсии Di для каждой i-й ИМС, определение µ и D для всей схемы в целом с использованием [21].
(7) - Построение физического закона поражения (ФЗП) для всей цифровой схемы [22].
Ниже приведен пример расчета сравнительной величины LET для структур КМОП «объемной» кремниевой технологии (v) и технологии КМОП/КНС. Величина LET для v-технологии принята за 1.
Исходными данными являются:
- равенство напряжения смещения;
- равенство емкости подзатворного узла;
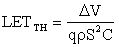 ;
;
q - заряд электрона;
ρ - плотность полупроводникового материала;
V - напряжение смещения;
S2=2а 2+с2 - квадрат хорды; а=b - квадратная топология транзисторов МОП;
C - емкость подзатворного диэлектрика.

Соотношения для оценки интенсивности отказов SEU получены с использованием функции распределения поперечного сечения отказов прибора от длины хорды. После интегрирования потока и поперечного сечения в диапазоне энергий (LET) была получена формула для интенсивности отказов при 10% воздействии (9), где Rerr - интенсивность SEU в единицах 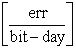 ; σSAT - поперечное сечение насыщения SEU в (µm2), a LETcrit - критическое значение LET в единицах [рС/µm].
; σSAT - поперечное сечение насыщения SEU в (µm2), a LETcrit - критическое значение LET в единицах [рС/µm].
Для большинства практических случаев интенсивность отказов в приведенном выше соотношении может быть определена с использованием аппроксимирующего выражения для σSAT=ab, (a, b>с) и
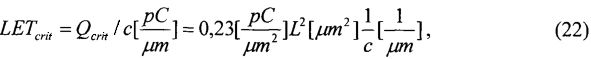
где c - толщина кремниевой пластины, а а и b - ее размеры в мкм. Приведенное соотношение применимо для многих приложений. Пример оценки Rerr приведен в табл. 2. Это соотношение допускает разброс в оценке качества (Figure of Merit = FOM) с величиной до 5 раз и поправочный коэффициент в 3,5 для приборов на GaAs.
Основные параметры структур МОП в составе исследовавшихся БИС, которые были проанализированы, приведены на Фиг. 14 и в табл. ПА2 и табл. ПА3 из [16].
Соотношение (18) с учетом 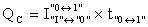 (20) и (21) можно представить в виде:
(20) и (21) можно представить в виде:
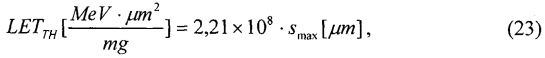
или
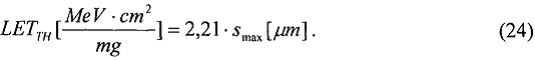
Результаты оценки чувствительности структур МОП к эффектам SEU/SEE для КП сведены в табл. 2. Из данных табл. 2 следует, что транзисторы малой мощности подвержены эффектам SEE от ТЗЧ только под определенным углом падения ТЗЧ. С другой стороны воздействие ТЗЧ можно моделировать воздействием импульсного рентгеновского или гамма-излучения [16]. Необходимо только понимать, что в этом случае ионизации подвергается весь объем транзистора структуры МОП, в то время как при воздействии ТЗЧ в ЧО генерируется «нить» заряда, расположенная локально в пределах объема выделенного прямоугольника (Фиг. 13).

Индексом «1)» в отмечены значения LETTH, которые свидетельствуют о чувствительности структур МДП данного класса мощности к SEE от ТЗЧ. Индексом «2)» отмечены структуры МОП, не требующие анализа на чувствительность к SEE. Это означает, что транзисторы малой мощности подвержены эффектам SEE от ТЗЧ только под определенным углом падения ТЗЧ. Индексом «3)» отмечена возможность тотальной ионизации транзисторных структур независимо от величины LETTH. Критерии оценки чувствительность приборов к действию факторов КП приняты из табл. 3 [16].
В табл. 2 в последнем столбце показана возможность тотальной ионизации транзисторных структур независимо от величины LETTH. Аппроксимируя зависимость на Фиг. 12 поперечного сечения чувствительности приборов к воздействию ионов от LET ступенчатой функцией, определим для случая LET<LETTH достаточный для образования сбоев флюенс частиц в пределах до 6×10-4 част./см2, или от 1 до 6×104 част./мкм2.
Б. Результаты оценки стойкости аппаратуры КА к эффектам SEU/SEE и SEL по результатам экспериментальных исследований комплектующих ИМС на источнике ТЗЧ.
Рассматривали гипотетический КА, в состав электронной аппаратуры которого включены все типы ИМС, которые были испытаны на ускорителе заряженных частиц. Обработка данных результатов измерения зависимости σ=f(LET) с использованием аппроксимации законом Вейбулла приведена в табл. 3 и 4 с учетом модели «критического заряда», рассмотренной выше.
Для всех типов ИМС, приведенных в таблице, сечение насыщения сбоев рассчитывалось по формулам (5)-(7), остальные параметры были получены исходя из квалификационных испытаний.
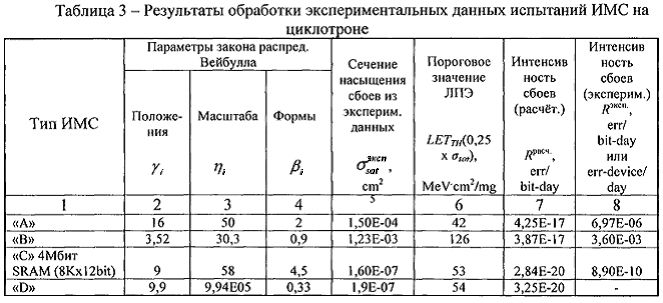
Был использован алгоритм получения значений параметров для ИМС типа «D», в основе которого лежит линеаризация закона распределения Вейбулла. По экспериментальным данным зависимости σ=f(LET) была построена линеаризированная функция распределения Вейбулла в виде Y=f(ln(LET-LETγ)) (Фиг. 15) и зависимость сечения сбоев от линейных потерь энергии σ=f(LET) (Фиг. 16).
Из наклона прямой Y(Z)=AZ+B на Фиг. 15 определяют параметр формы β=А=arctgφ, где угол φ определяет степень наклона прямой к оси Z. Из Фиг. 15 параметр формы η=0.33. Если Y(Z)=В при Z=0, тогда значение постоянной В из графика линеаризированной функции Вейбулла составляет -13,81. Параметр масштаба равен η=9,9·105.
Из графика зависимости сечения сбоев от LET определяют пороговое значение линейных потерь энергии на уровне σ=0,25σsat. При σ=4,75·10-8 cm2 значение LETTH=54 MeV·cm2/mg. Таким образом, определены все параметры ИМС типа «D». Теперь по (8) можно рассчитать интенсивность сбоев R=3,25·10-20 сбой/бит-день.
После определения всех параметров ИМС, составляющих электронную аппаратуру KA, и с учетом 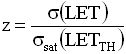 , для всего устройства можно записать:
, для всего устройства можно записать:
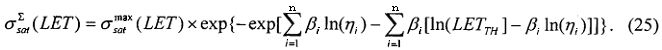
В результате вычислений по (25) с учетом данных табл. 3 и табл. 4 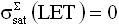 . Величина
. Величина 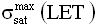 принята максимальной из всех возможных значений для полученных в ходе экспериментов с 6-ю типами ИМС. Максимальные значения параметров масштаба 7, получены для ИМС «D», что свидетельствует о сдвиге максимума плотности распределения σ(LET) в область более высоких значений аргумента (более тяжелых ионов), и об уменьшении значения σsati для конкретной ИМС. Значения LETTH>120 МэВ/см2-мг свидетельствует об отсутствии необходимости проведения испытаний на устойчивость к воздействию эффектов SEE. Отсюда следует:
принята максимальной из всех возможных значений для полученных в ходе экспериментов с 6-ю типами ИМС. Максимальные значения параметров масштаба 7, получены для ИМС «D», что свидетельствует о сдвиге максимума плотности распределения σ(LET) в область более высоких значений аргумента (более тяжелых ионов), и об уменьшении значения σsati для конкретной ИМС. Значения LETTH>120 МэВ/см2-мг свидетельствует об отсутствии необходимости проведения испытаний на устойчивость к воздействию эффектов SEE. Отсюда следует:

1) Величина критического флюенса частиц для гипотетической аппаратуры КА в этом случае составит
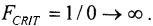
2) Расчеты математического ожидания для всей системы из
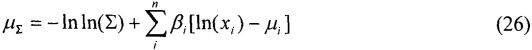
с учетом (27)
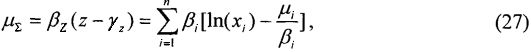
где βZ - параметр формы для всей системы в целом, γZ - параметр положения для всей системы в целом, z - случайная величина (в том числе, уровень радиационной нагрузки), позволяют представить связь между значением lnlnΣ,
где 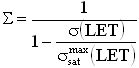 , его математическим ожиданием
, его математическим ожиданием 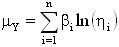 , и дисперсией
, и дисперсией 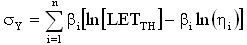 , в виде
, в виде
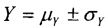
по аналогии с (29)
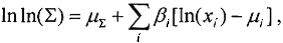
полученным разложением ln(Σ) в ряд Тейлора около среднего значения величины ln(xi), а именно, µi. Из данных табл. 4, следует, что верхняя оценка значения функции YV=118, а нижняя оценка - YU= -30. Как следует из данных табл. 5 в этом случае при значении YV величина аргумента X=ln(LET-LETγ)→∞, а при YU величина X→0.

Это значит, что при YV величина LET→∞, а при YU величина LET→0, что означает, что LET=LETγ, т.е. параметру положения. Отсюда следует, что максимальный флюенс частиц, приводящий к эффектам типа SEE от действия ТЗЧ для значения YU равен величине FUV=1/ехр(3,5)=3,6×10-2 см-2, а то же значение для FUU=1/ехр(16)=5,3×10-4 (см. табл. 3 и табл. 4).
Тогда нижняя допустимая граница флюенса частиц заключена в интервале
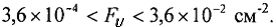
Отношение µY/σ=0,5774. В соответствии с
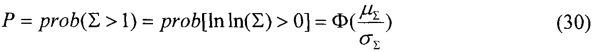
получим вероятность сохранения работоспособности P для каждого значения режима повреждения с помощью соотношения (28), где Ф(х) является обобщенной стандартной функцией нормального распределения (квантилью)

которая табулирована, например, в [23]. Таким образом, P относят к нормальному распределению, что вытекает из того, что ln(xi) является нормальным распределением, а представление lnln(Σ) в виде суммы нормально распределенных случайных переменных делает lnln(Σ) также нормально распределенным. Вероятность сохранения работоспособности КА с такими ЭРИ из (29) равна квантили нормального распределения
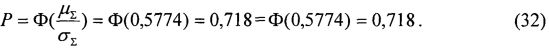
Таким образом, всю процедуру оценки интенсивности сбоев и параметрической вероятности сохранения работоспособности электронных устройств КА, описанную выше, можно представить в виде следующей блок-схемы (Фиг. 11).
В. Оценка эквивалентной поглощенной дозы DR источника ИИИ и УБР для моделирования эффектов SEU/SEE.
Ниже анализируется чувствительность БИС технологии КМОП/КНД к возможности появления SEE с использованием предложенной выше процедуры.
Для этого используют два способа. Первый из них (В. 1) предусматривает использование зависимости поперечного сечения сбоев для всей аппаратуры на Фиг. 16. Второй способ (В. 2) предусматривает использование расчетных соотношений для определения порогового значения LETTH (Фиг. 9)
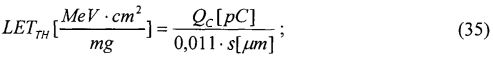
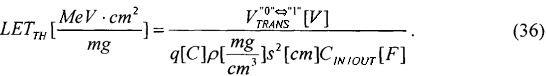
При расчете по способу (В. 1) используют алгоритм, показанный на Фиг. 9, реализованный в Приложении «А». Результаты оценок содержатся в табл. ПА.3 Приложения «А».
При расчете по способу (В. 2) используя значения LETTH из табл. 2 и подставляя их значения в (5) для smax=28,4 мкм и соответствующих значений RDEF из табл. ПА.2 Приложения «А», получают с учетом критериев табл. 3 [16] значения эквивалентных доз DR(γ-кв.1МэВ-экв.-(Si)), которые сведены в табл. ПБ.1 Приложения «Б».
Величина 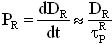 , где
, где 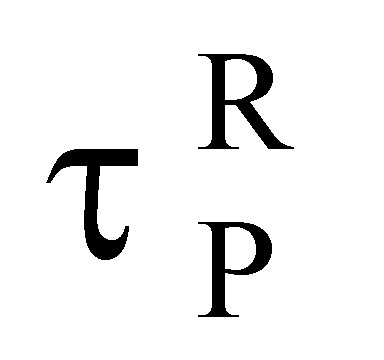 - длительность импульса МУ, PR - предельная мощность дозы для квантов с энергией ~1 МэВ, обеспечивающая эквивалентную ионизацию ЧО для плотности потока Fcrit=1,9·106 част. см-2 (или УБР).
- длительность импульса МУ, PR - предельная мощность дозы для квантов с энергией ~1 МэВ, обеспечивающая эквивалентную ионизацию ЧО для плотности потока Fcrit=1,9·106 част. см-2 (или УБР).
С целью повышения достоверности определения интегральной величины констант 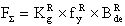 [16] ее значение рассчитывают из соотношения (ПА. 10), которое в дальнейшем используют для определения величин
[16] ее значение рассчитывают из соотношения (ПА. 10), которое в дальнейшем используют для определения величин 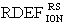 и эквивалентной дозы DR(γ-кв.RS-экв.-(М)) моделирующего SEE в БИС технологии КМОП/КНД аналогичной технологии и конструктива источника гамма-рентгеновского излучения. Так при подстановке в (ПА.10) данных, соответствующих структурам («L»↓↑) и («М»↓↑): KΣ и
и эквивалентной дозы DR(γ-кв.RS-экв.-(М)) моделирующего SEE в БИС технологии КМОП/КНД аналогичной технологии и конструктива источника гамма-рентгеновского излучения. Так при подстановке в (ПА.10) данных, соответствующих структурам («L»↓↑) и («М»↓↑): KΣ и 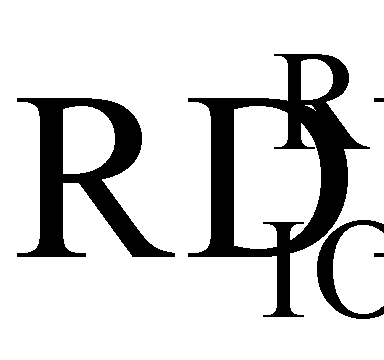 из табл. ПА. 11 Приложения «A»; a=L, b=B, smax из табл. 2, c=tПС=3,5·10-5 см; w=3,6·10-6 МэВ;
из табл. ПА. 11 Приложения «A»; a=L, b=B, smax из табл. 2, c=tПС=3,5·10-5 см; w=3,6·10-6 МэВ; 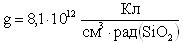 ; LETTH из (22), получают расчетные значения DR или PR для аналогичных структур МДП по конструкции и электрическим режимам эксплуатации. При smax=28,8 мкм, L=17,5 мкм, B=3 мкм величина
; LETTH из (22), получают расчетные значения DR или PR для аналогичных структур МДП по конструкции и электрическим режимам эксплуатации. При smax=28,8 мкм, L=17,5 мкм, B=3 мкм величина  , а величина
, а величина 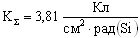 для структур («L»↓↑) и
для структур («L»↓↑) и 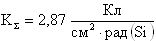 для структур («M»↓↑).
для структур («M»↓↑).
Пример реализации по Варианту 2 определения величины УБР при использовании ИМ с помощью импульсного лазерного излучения
Для определения величины УБР при использовании ИМ с помощью импульсного лазерного излучения гетероструктуру чипа ППП или ИМС облучают пикосекундным импульсом лазерного источника с длительностью не более 350 пс и длиной волны в диапазоне 800-1500 нм, фиксируют критическую пороговую энергию  сбоев при воздействии импульсного лазерного излучения, определяют значение величины
сбоев при воздействии импульсного лазерного излучения, определяют значение величины  с использованием из соотношения (3)
с использованием из соотношения (3) 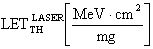 , величину
, величину  определяют из соотношения
определяют из соотношения 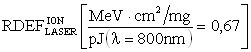 [14]. В табл. 6 приведены значения переводных
[14]. В табл. 6 приведены значения переводных 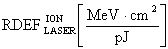 для трех значении длин волн импульсного пикосекундного лазера: λ=590 nm, 600 nm, 800 nm для ИМС IDT 71256 (R-MOS) SRAM [14].
для трех значении длин волн импульсного пикосекундного лазера: λ=590 nm, 600 nm, 800 nm для ИМС IDT 71256 (R-MOS) SRAM [14].
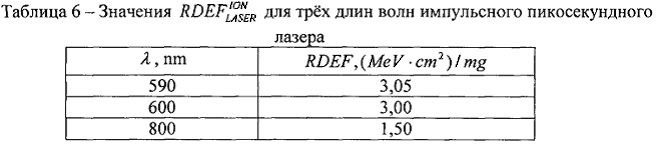
Для λ=800 nm величина 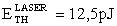 (ИМС IDT 71256 (R-MOS) SRAM), величина
(ИМС IDT 71256 (R-MOS) SRAM), величина 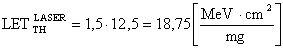 , а величину эквивалентного значения
, а величину эквивалентного значения 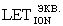 определяют из (14)
определяют из (14) 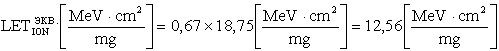 , и с учетом данных о σTOT[cm2]=1,26·10-5 cm2 (5V HM-6504 4K CMOS RAM, среднее значение сбоев
, и с учетом данных о σTOT[cm2]=1,26·10-5 cm2 (5V HM-6504 4K CMOS RAM, среднее значение сбоев 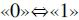 ) и
) и 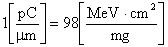 [14], и smax[µm] определяют величину интенсивности сбоев
[14], и smax[µm] определяют величину интенсивности сбоев 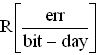 из (9)
из (9)
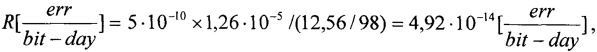
а для информационной емкости ИМС 256 К интенсивность составит 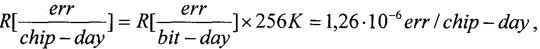 что соответствует lerr-chip/3,45 year. С использованием
что соответствует lerr-chip/3,45 year. С использованием
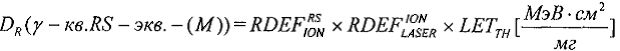
определяют величину эквивалентной полной поглощенной дозы гамма-квантов 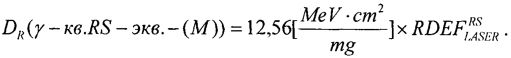 Для транзисторов малой мощности «L» из табл. ПА.2 значение
Для транзисторов малой мощности «L» из табл. ПА.2 значение  для источника X-Ray(10keV) и
для источника X-Ray(10keV) и 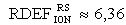 , и для источника Co60(1,25MeV) получают
, и для источника Co60(1,25MeV) получают 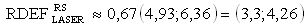 , соответственно, при ориентации структуры "↑↕" по отношению к падающему излучению. Тогда DR(γ-кв.RS-экв.-(М))=41,4…5,35rad(Si), и при известной длительности импульса гамма-квантов источника эталонного ионизирующего излучения τP УБР цифровой аппаратуры определяют
, соответственно, при ориентации структуры "↑↕" по отношению к падающему излучению. Тогда DR(γ-кв.RS-экв.-(М))=41,4…5,35rad(Si), и при известной длительности импульса гамма-квантов источника эталонного ионизирующего излучения τP УБР цифровой аппаратуры определяют
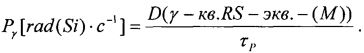
Величину УБР можно рассчитать двумя способами: 1) с использованием времени пролета ионов через ЧО; 2) по времени набора эквивалентной дозы на МУ. При использовании времени пролета ионов так же рассматривают два случая: а) продольный пролет (" ") в приборном слое транзисторных структур ИМС; б) поперек ("↑↓")приборного слоя. Время пролета равно
") в приборном слое транзисторных структур ИМС; б) поперек ("↑↓")приборного слоя. Время пролета равно 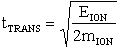 , где EION[J] - энергия иона, mION[g] - масса иона.
, где EION[J] - энергия иона, mION[g] - масса иона.
В табл. 10 приведены данные, используемы при определении скорости типичного «коктейля» ионов. Для получения наименьшего значения tTRANS необходима максимальная энергия EION при минимальной массе mION. Поэтому в табл. 7 приведены данные оценки скорости ионов He и Au.
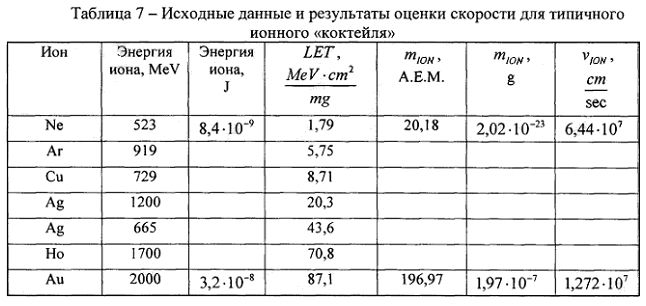
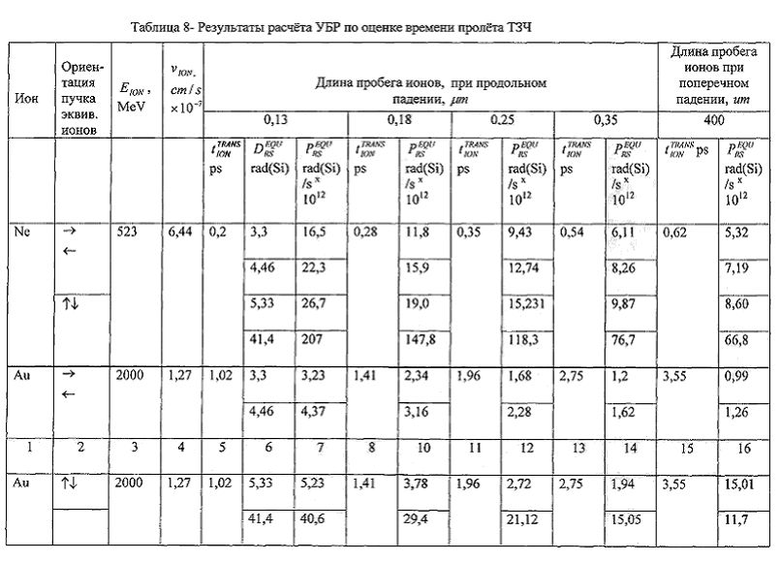
В табл. 8 сведены результаты расчета УБР по оценке времени пролета двух ТЗЧ для современных технологий МОП.
Пример реализации по варианту 3 определения величины УБР путем использования официальных данных спецификаций на полупроводниковые приборы и ИМС.
В качестве объекта анализа выбрали ИМС НХ6656 Honeywel′s SOI RAM технологии RICMOS™ IV (Radiation Insensive CMOS) с организацией 32K×8 bit. Из данных спецификации на ИМС величины входных емкостей ИМС равны CIN=7pF, выходных COUT=9pF. Уровень переключения логических состояний по напряжению 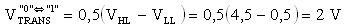 . Критический заряд переключения равен
. Критический заряд переключения равен 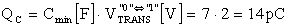 . Для определения величины хорды использовали эмпирическую формулу QC=0,35[рС]·s2[µm2], откуда
. Для определения величины хорды использовали эмпирическую формулу QC=0,35[рС]·s2[µm2], откуда 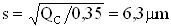 . Для определения величины порогового значения LETTH использовали (36), при подстановке численных значений
. Для определения величины порогового значения LETTH использовали (36), при подстановке численных значений
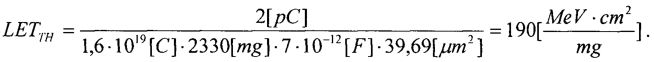
Величина 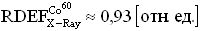 , величина
, величина 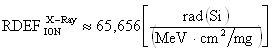 из (8). Тогда эквивалентная доза квантов эталонного источника Co60 составит
из (8). Тогда эквивалентная доза квантов эталонного источника Co60 составит 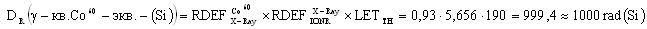 .
.
При длительности импульса тестового источника X-Ray τP≈1µS величина УБР составит 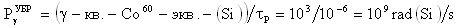 .
.
Таким образом, результаты исследований радиационной стойкости к воздействию гамма-рентгеновского излучения ИЯР и ЭФУ могут быть использованы для определения стойкости к SEE от ТЗЧ с применением соответствующих коэффициентов RDEF. Поэтому предложенный способ, предполагающий только облучение гамма-рентгеновским излучением ИЯР или ЭФУ, позволяет существенно снизить стоимость испытаний, уменьшить их объем и повысить достоверность результатов испытаний.
Установлена зависимость эквивалентной дозы гамма-рентгеновского излучения ИЯР или ЭФУ по критерию эквивалентности критического РИЗ QC с величиной 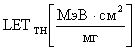 , что позволяет выбирать режимы испытаний БИС технологии КМОП/КНД с учетом конструктивных особенностей и электрического режима эксплуатации на основании как расчетных, так и экспериментальных значений
, что позволяет выбирать режимы испытаний БИС технологии КМОП/КНД с учетом конструктивных особенностей и электрического режима эксплуатации на основании как расчетных, так и экспериментальных значений 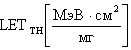 .
.
Величина эквивалентной дозы гамма-рентгеновского излучения ИЯР или ЭФУ приведена к энергии квантов Eγ,X-Ray=1 МэВ-экв., что позволяет использовать МУ с произвольным спектром FS ИИ.
ПРИЛОЖЕНИЕ «А»: Оценка эквивалентной поглощенной дозы DR источника ИИИ и УБР для моделирования эффектов SEU/SEE с использованием зависимости поперечного сечения сбоев для всей аппаратуры.
Пусть в аппаратуре КА содержится a
SL=40% однотипных ИМС последовательной логики и a
SL=60% схем комбинаторной логики, выполненных по стандартной технологии КМОП. Число схем последовательной логики Ni=1000 ед., число схем комбинаторной логики NJ=DFF=114 ед. Частота синхронизации F=10 МГц. Суммарное сечение сбоев для элементов последовательной логики составит 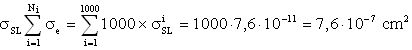 , суммарное сечение сбоев для элементов комбинаторной логики составит с учетом зависимости сечения от частоты
, суммарное сечение сбоев для элементов комбинаторной логики составит с учетом зависимости сечения от частоты 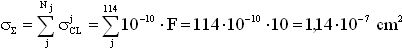 . Полное сечение для всей аппаратуры KA равно σTOTσSL+σΣ=(0,76+1,14)·10-7=1,9·10-7 cm2. Из зависимости σ=f(LET) на Фиг. 16 следует, что ее аппроксимация ступенчатой функцией дает для σSAT=σTOT=1,9·10-7 cm2 значение LETTH=53 MeV·cm2/mg.
. Полное сечение для всей аппаратуры KA равно σTOTσSL+σΣ=(0,76+1,14)·10-7=1,9·10-7 cm2. Из зависимости σ=f(LET) на Фиг. 16 следует, что ее аппроксимация ступенчатой функцией дает для σSAT=σTOT=1,9·10-7 cm2 значение LETTH=53 MeV·cm2/mg.
Вместо облучения полупроводниковых БИС технологии КМОП/КНД электронным, протонным излучением или потоком ТЗЧ для моделирования SEE ограниченную выборку БИС облучают импульсным гамма-нейтронным ионизирующим излучением ИЯР или импульсным рентгеновским излучением ЭФУ с эквивалентной дозой, вызывающей равную с ТЗЧ генерацию РИЗ Qt в ЧО БИС. Средняя энергия гамма-нейтронного излучения ИЯР или рентгеновского излучения ЭФУ выбирается 1,0-3,0 МэВ [16].
Для определения эквивалентной дозы DR(γ-кв.RS-экв.-(М)) излучений ИЯР или ЭФУ, вызывающей в материале (М) равную с линейными потерями энергии LETTH для ТЗЧ величину РИЗ Qt в диапазоне LETTH от единиц до сотни МэВ·см2/мг используют значение коэффициента RDEF дозы рентгеновского или гамма-излучения по отношению к величине LETTH из (2).
При эквивалентной ионизации полного объема структуры МОП от гамма-рентгеновского излучения ИИ и локального объема от ионов КП можно рассчитать эквивалентную дозу гамма-рентгеновского излучения DR, обеспечивающую такую же ионизацию, как и критическая плотность потока (доза) ионов
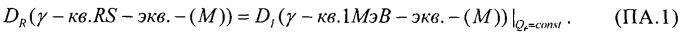
Здесь «RS» спектр ИИ (Radiation Spectrum) МУ, a «M» - материал, в котором поглощается энергия ИИ (M∝Si или M∝SiO2). Равенство (32) также представляют в виде
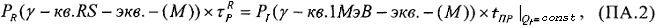
где PR,I - мощность поглощенной дозы соответствующих источников ИИ; 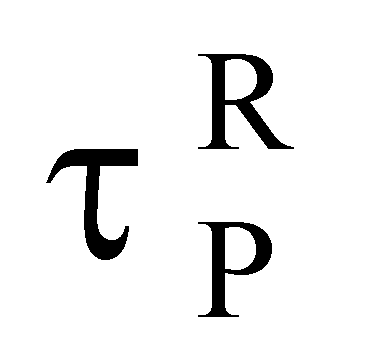 - длительность импульса ИИ МУ; tПР. - время пролета ТЗЧ через чувствительный объем, которое определяют из соотношения
- длительность импульса ИИ МУ; tПР. - время пролета ТЗЧ через чувствительный объем, которое определяют из соотношения

где E - энергия ТЗЧ; mЧ - масса ТЗЧ; smax - максимальная длина хорды в чувствительном объеме вдоль трека первичной частицы. При изотропном распределении частиц в пространстве время пролета будет варьироваться в зависимости от длины хорды, которая изменяется от толщины приборного слоя tПС при нормальном падении частиц до значения smax при практически продольном распространении частиц в тонком слое. Дозу DI из (ПА.1) определяют соотношением
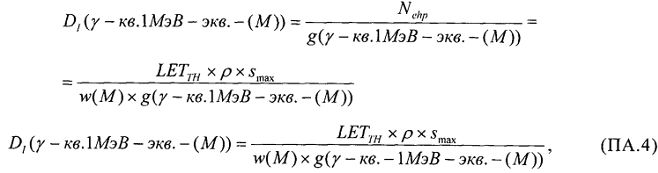
Величина эквивалентной мощности дозы равна отношению (ПА.2) к (ПА.1)
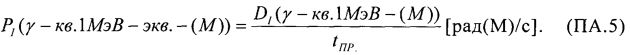
Согласование полной поглощенной дозы импульсного ИИ DR(γ-кв.RS-(M)) в структуре МДП от МУ со спектром RS с эквивалентной дозой от воздействия ТЗЧ DI(γ-кв.1МэВ-экв.-(M)) из (ПА.4) производят с использованием соотношения (ПА.6)
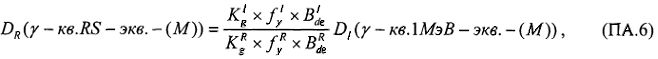
Величину константы 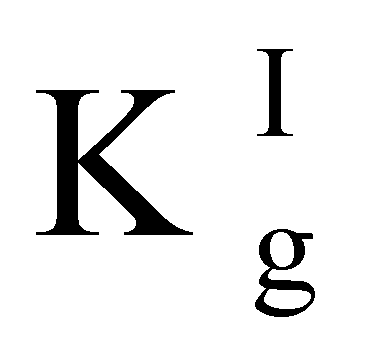 можно получить, отнеся величину критического заряда Qcrit=QC, создаваемую ТЗЧ в ЧО структуры МДП, к величине поглощенной дозы DI от воздействующей ТЗЧ:
можно получить, отнеся величину критического заряда Qcrit=QC, создаваемую ТЗЧ в ЧО структуры МДП, к величине поглощенной дозы DI от воздействующей ТЗЧ:
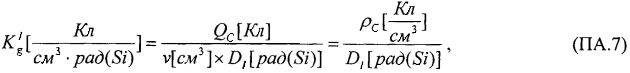
где: ρc - плотность критического заряда; ν=a×b×c=A×tПС - объем ЧО; A=a×b - площадь поверхности ЧО; tПС=с=smin - толщина приборного слоя (Фиг. 14). Величину QC принимают с учетом (2) из (ПА.7)
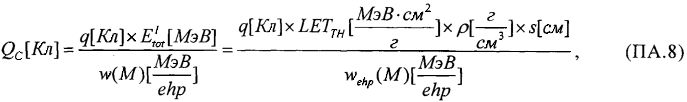
где s - соответствует длине пространственной хорды при падении единичной ТЗЧ под произвольными углами к лицевой (инверсной) поверхности чипа структуры (Фиг. 10). Величину поглощенной дозы от одной ТЗЧ принимают приведенной к всему объему ЧО при произвольном значении длины хорды 5:
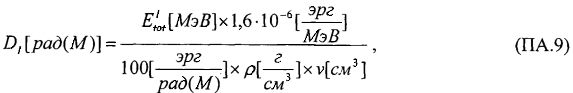
Подставляя (ПА.8) и (ПА.9) в (ПА.4), получают
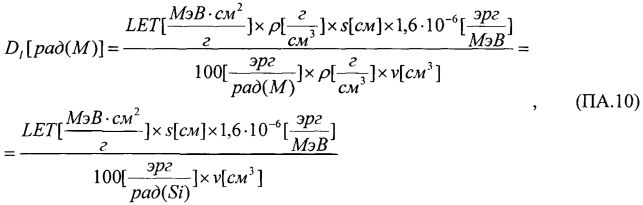
а величину константы 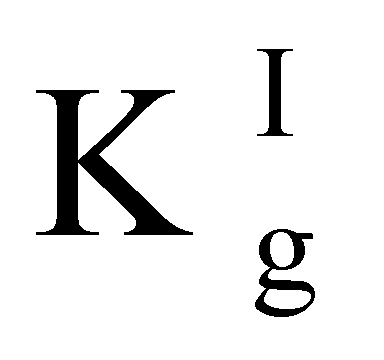 из (36) при подстановке (37) и (39) в виде
из (36) при подстановке (37) и (39) в виде

Аналогичное равенство можно записать для мощностей доз PR(γ-экв.RS-(M)) и PI(γ-1МэВ-экв.-(M)).
В (ПА.6) можно принять 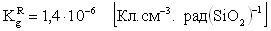 для источника рентгеновского излучения 10 кэВ и
для источника рентгеновского излучения 10 кэВ и 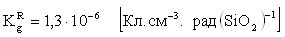 для нуклидного источника Co60 [16].
для нуклидного источника Co60 [16].
При известных значениях параметров структур МОП и геометрических параметров может быть выполнена коррекция результатов облучения на одном источнике на условия облучения на другом и ввести на основании (2) и (ПА.1) понятие коэффициента относительной эффективности (RDEF) [9]
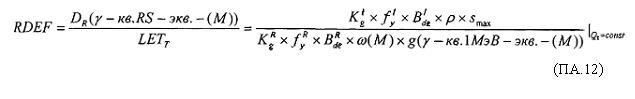
в единицах 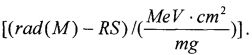
На основании этих данных можно определить значения 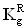 ,
, 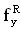 ,
, 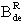 , а также преобразовать их в соответствующие значения для нуклидного источника Co60:
, а также преобразовать их в соответствующие значения для нуклидного источника Co60: 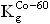 ,
, 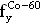 ,
, 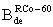 (табл. ПА.1).
(табл. ПА.1).
При расчете констант 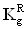 ,
, 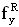 ,
, 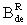 принимают следующие значения констант: ρ=2,33 [g/cm3] для Si;
принимают следующие значения констант: ρ=2,33 [g/cm3] для Si; 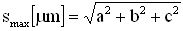 - максимальное значение хорды в чипе структуры МДП; а - ширина чипа структуры МДП; b - длина чипа; с - высота чипа, [µm];
- максимальное значение хорды в чипе структуры МДП; а - ширина чипа структуры МДП; b - длина чипа; с - высота чипа, [µm]; 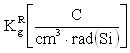 - постоянную генерации радиационно-индуцированных носителей заряда для МУ и одиночной ТЗЧ, предельное значение доли нерекомбинированного радиационно-индуцированного заряда в структуре МДП при воздействии излучения МУ и одиночной ТЗЧ в присутствии приложенного электрического поля напряженностью Е, [MV·cm-1], из табл. ПА.1 Приложения «А» [16];
- постоянную генерации радиационно-индуцированных носителей заряда для МУ и одиночной ТЗЧ, предельное значение доли нерекомбинированного радиационно-индуцированного заряда в структуре МДП при воздействии излучения МУ и одиночной ТЗЧ в присутствии приложенного электрического поля напряженностью Е, [MV·cm-1], из табл. ПА.1 Приложения «А» [16]; 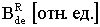 - фактор дозового накопления в структуре КНД гамма-рентгеновского излучения МУ со спектром квантов RS и одиночной ТЗЧ из табл. ПА.1 Приложения «А» [16].
- фактор дозового накопления в структуре КНД гамма-рентгеновского излучения МУ со спектром квантов RS и одиночной ТЗЧ из табл. ПА.1 Приложения «А» [16].
Для учета кинетики накопления и релаксации заряда радиационно-индуцированных носителей в электрическом поле величину коэффициента 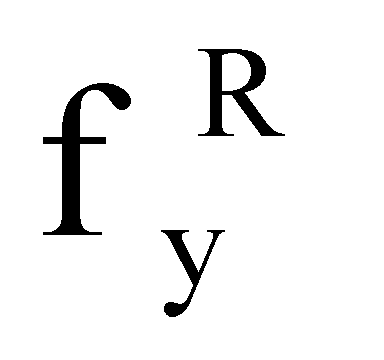 определяют для энергии рентгеновских квантов EX-Ray=10-300 кэВ и для энергии гамма-рентгеновских квантов ИЯР или рентгеновских квантов ЭФУ с энергией ЕЯР,Х-Ray=1…6 МэВ [16]. Для учета конструктивных особенностей транзисторной структуры КНД, для оценки величины фактора дозового накопления ВЦ используют зависимость величины
определяют для энергии рентгеновских квантов EX-Ray=10-300 кэВ и для энергии гамма-рентгеновских квантов ИЯР или рентгеновских квантов ЭФУ с энергией ЕЯР,Х-Ray=1…6 МэВ [16]. Для учета конструктивных особенностей транзисторной структуры КНД, для оценки величины фактора дозового накопления ВЦ используют зависимость величины 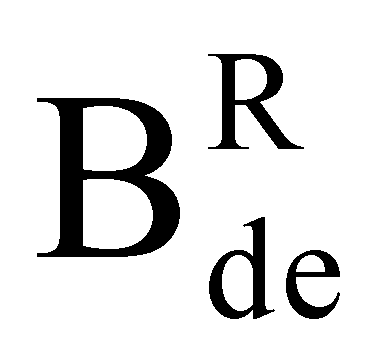 от толщины подзатворного оксида tox для энергии квантов 10 кэВ и напряженности электрического поля E=1…6 МВ·см-1 [16]. Для ИИ ИЯР, ЭФУ, одиночной ТЗЧ с энергией квантов ЕИЯР,ЭФУ,ТЗЧ≥1 МэВ принимают величину
от толщины подзатворного оксида tox для энергии квантов 10 кэВ и напряженности электрического поля E=1…6 МВ·см-1 [16]. Для ИИ ИЯР, ЭФУ, одиночной ТЗЧ с энергией квантов ЕИЯР,ЭФУ,ТЗЧ≥1 МэВ принимают величину 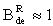 .
.
При изготовлении диэлектрика подзатворного оксида структуры МДП на основе диоксида кремния (M=SiO2) константы радиационной генерации в нем электронно-дырочных пар принимают равными 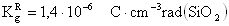 для источника рентгеновского излучения с энергией 10 кэВ и
для источника рентгеновского излучения с энергией 10 кэВ и 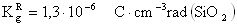 для ИЯР или ЭФУ. Величину
для ИЯР или ЭФУ. Величину 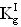 для ТЗЧ вычисляют с использованием соотношения (ПА.23) Приложения «А» [16], а величины
для ТЗЧ вычисляют с использованием соотношения (ПА.23) Приложения «А» [16], а величины 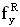 и
и 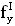 для соответствующих значений энергий из соотношений, приведенных в табл. ПА.1 Приложения «А» [16].
для соответствующих значений энергий из соотношений, приведенных в табл. ПА.1 Приложения «А» [16].
Данные по расчету величины RDEF для рентгеновского излучения ЭФУ с энергией квантов 10 KeV кэВ, ТЗЧ с 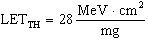 , для источников гамма-рентгеновского излучения ИЯР, гамма-квантов нуклидного источника Co60 приведены в табл. 4 [16] для транзисторных структур МДП различного класса мощности: низкой (low - «L»); средней (middle - «M»); большой (big - «B»).
, для источников гамма-рентгеновского излучения ИЯР, гамма-квантов нуклидного источника Co60 приведены в табл. 4 [16] для транзисторных структур МДП различного класса мощности: низкой (low - «L»); средней (middle - «M»); большой (big - «B»).
Для определения 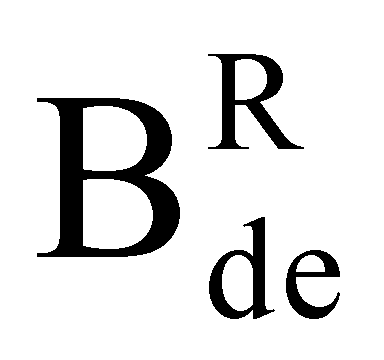 и
и 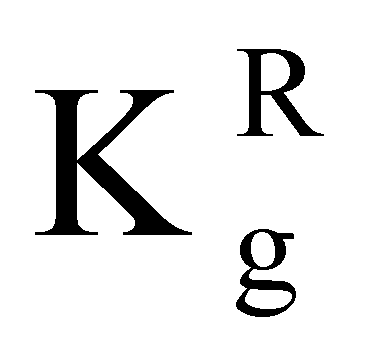 удобнее использовать тестовые транзисторы МДП при аналогичных параметрах А и tox, что и у транзисторов МДП основной схемы.
удобнее использовать тестовые транзисторы МДП при аналогичных параметрах А и tox, что и у транзисторов МДП основной схемы.


В табл. ПА.2 приведены значения RDEF и переводного множителя 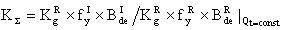 (ПА.12) для двух источников ИИ: Х-Ray и ИЯР (Co60) с энергией гамма-квантов Eγ-кв.≥1 MeV для транзисторных структур МДП различного класса мощности: низкой (low - «L»); средней (middle - «М»); большой (big - «В»).
(ПА.12) для двух источников ИИ: Х-Ray и ИЯР (Co60) с энергией гамма-квантов Eγ-кв.≥1 MeV для транзисторных структур МДП различного класса мощности: низкой (low - «L»); средней (middle - «М»); большой (big - «В»).
Результаты оценки чувствительности аппаратуры КА из экспериментальной зависимости на Фиг. 16 к эффектам SEU/SEE сведены в табл. ПА.3.


Аппроксимируя зависимость на Фиг. 16 поперечного сечения σ[cm2] чувствительности приборов к SEE от ТЗЧ от 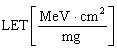 ступенчатой функцией, определяют поток частиц для случая LET<LETTH, достаточный для образования SEE.
ступенчатой функцией, определяют поток частиц для случая LET<LETTH, достаточный для образования SEE.
Для этого используют то обстоятельство, что поперечное сечение At ЧО структур МДП мощности «Z» и «М» по данным табл. 3 равно поперечному сечению σSEE(LETTH) для SEE на Фиг. 12, т.е. At=L×В=σSEE(LETTH). Обратная величина сечения σSEE(LETTH) позволяет оценить величину критического потока частиц, для которого только одна частица с вероятностью 1 попадает в ЧО структуры МДП. С использованием данных табл. 3 E=17,5 мкм=1,75·10-3 см и B=3,0 мкм=3,0·10-4 см оценка величины сечения дает значение σSEE(LETTH)=5,25·10-7 см2, а величина критического флюенса частиц равна Fcrit=1,9·106 част·см-2.
ПРИЛОЖЕНИЕ «Б»: Оценка эквивалентной поглощенной дозы DR источника ИИИ и УБР для моделирования эффектов SEU/SEE с использованием расчетных соотношений для определения порогового значения LETTH
Используя эти данные, можно произвести в первом приближении расчет порогового значения LETTH, минимально необходимой для создания SEU/SEE..
Минимальное значение LETTH будет соответствовать случаю, для которого сбой может быть рассчитан из соотношения (2) в виде:

Тогда равенство (ПА.4) можно записать в виде:
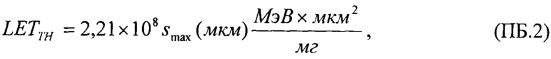
или
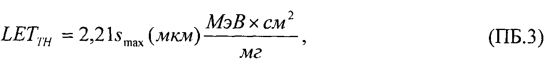
или
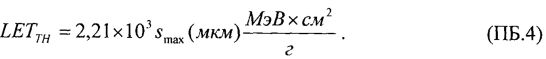
На Фиг. 9 приведены наиболее распространенные формы соотношений для определения порогового значения LETTH для широкого класса топологических размеров современных структур МОП
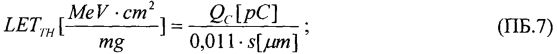
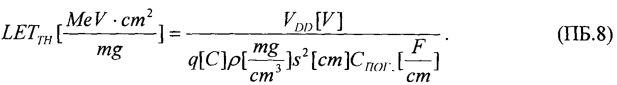
При этом сохраняется равенство радиационно-индуцированного заряда Qt в чувствительном объеме БИС при воздействии как излучения МУ, так и линейных потерь энергии LET.
При расчете по варианту (В.2) используют значения LETTH из табл. 2 и, подставляя их значения в (5) для smax=28,4 мкм и соответствующих значений RDEF из табл. ПА.2 Приложения «А», получают с учетом критериев табл. 3 [16] значения эквивалентных доз DR(γ-кв.МэВ-экв.-(Si)), которые сведены в табл. ПБ.1. Величина 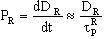 , где
, где 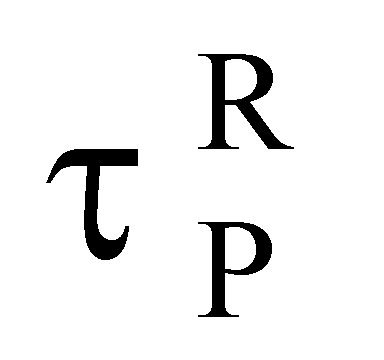 - длительность импульса МУ, PR - предельная мощность дозы для квантов с энергией ~1 МэВ, обеспечивающая эквивалентную ионизацию ЧО для плотности потока Fcrit=1,9·106 част.см-2 (или УБР).
- длительность импульса МУ, PR - предельная мощность дозы для квантов с энергией ~1 МэВ, обеспечивающая эквивалентную ионизацию ЧО для плотности потока Fcrit=1,9·106 част.см-2 (или УБР).

С целью повышения достоверности определения интегральной величины констант 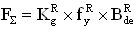 ее значение рассчитывают из соотношения (ПА.11), которое в дальнейшем используют для определения величин RDEF и эквивалентной дозы DR(γ-кв.RS-экв.-(М)) моделирующего SEE источника гамма-рентгеновского излучения БИС технологии КМОП/КНД аналогичной технологии и конструктива. Так при подстановке в (ПА.11) данных, соответствующих структурам («L»↓↑) и («M»↓↑): KΣ и RDEF из табл. ПА.2 Приложения «A»; a=L, b=B, smax из табл. 5, c=tПС=3,5·10-5 см; w=3,6·10-6 МэВ;
ее значение рассчитывают из соотношения (ПА.11), которое в дальнейшем используют для определения величин RDEF и эквивалентной дозы DR(γ-кв.RS-экв.-(М)) моделирующего SEE источника гамма-рентгеновского излучения БИС технологии КМОП/КНД аналогичной технологии и конструктива. Так при подстановке в (ПА.11) данных, соответствующих структурам («L»↓↑) и («M»↓↑): KΣ и RDEF из табл. ПА.2 Приложения «A»; a=L, b=B, smax из табл. 5, c=tПС=3,5·10-5 см; w=3,6·10-6 МэВ; 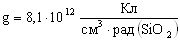 ; LETTH из (ПА.29) Приложения «А» [16], получают расчетные значения DR или PR для аналогичных структур МДП по конструкции и электрическим режимам эксплуатации. При smax=28,8 мкм, L=17,5 мкм, B=3 мкм величина
; LETTH из (ПА.29) Приложения «А» [16], получают расчетные значения DR или PR для аналогичных структур МДП по конструкции и электрическим режимам эксплуатации. При smax=28,8 мкм, L=17,5 мкм, B=3 мкм величина 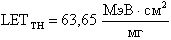 , а величина
, а величина 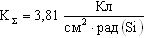 для структур («L»↓↑) и
для структур («L»↓↑) и 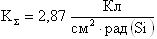 для структур («M4»↓↑).
для структур («M4»↓↑).
Перечень цитированных источников
1. Dodd Р.Е., Sexton F.W. "Critical Charge Concepts for CMOS SRAMs" // IEEE Transaction on Nuclear Science, Vol. 42.-No. 6. - December 1995. - pp. 1764-1771.
2. Benedetto J.M., Eaton P.H., Mavis D.G., Gadlage M., Turfinger T. Digital Single Evet Trasient Trends With Technology Node Scaling // IEEE Transaction on Nuclear Science, Dec. 2006. - vol. 53. - No. 6. - pp. 3462-3465.
3. Berg M., Wang J.-J., Ladbury R., Buchner S., Kim H., LaBel K., Phan A. and Friendlich M. An Analysis of Single Event Upset Dependencies on High Frequency and Architectural Implementations within Actel RTAX-S Family Field Programmable Gate Arrays / IEEE Transactions on Nuclear Science, Dec. 2005. - Vol. NS-52. - No. 6. - pp. 3569-3574.
4. Chugg A.M., Jones R., Moutre M.J., Duncan P.H., Sorensen R. Harboe, Mattisson S., Larsson S., Fitzgerald R. and O′Shea T. Laser Simulation of Single Event Effects in Pulse Width Modulators / IEEE Transactions on Nuclear Science, Dec. 2005. - Vol. NS-52. - No. 6. - pp. 2487-2494.
5. Ferlet-Cavoris V., Paillet P., McMorrow D., Torres A., Gaillardin M., Melinger J.S., Knudson A.R., Cambell A.B., Schwank J.R., Vizkelethy G., Shaneyfelt M.R., Hirose K., Faynot O., Jahan C., Tosti L. Direct Measurement of Transient Pulses Induxed by Laser and Heavy Ion Irradiation in Deca-Nanometr Devices // IEEE Transactions on Nuclear Science, Dec. 2005. - Vol. 52. - No. 6. - pp. 2104-2113.
6. McMorrow D., Melinger J.S., Bucher S., Scott T., Brown R.D., Haddad N.F. Application of pulsed laser for evacuation and optimization of SEU-Hard designs // IEEE Transactions on Nuclear Science, Jun. 2000. - vol. 47. - No. 3. - p. 559.
7. Кабальнов Ю.А., Качемцев A.H., Киселев В.К. Способ кулонометрического измерения электрических параметров наноструктур транзистора n-МОП в технологиях КМОП/КНС и КМОП/КНИ / Патент на изобретение RU 2439745 C1 с приорит. от 18.10.2010.
8. Качемцев А.Н., Киселев В.К., Палицына Т.А. Устройство для кулонометрического измерения электрофизических параметров наностуктур транзистора n-МОП в технологиях КМОП/КНС и КМОП/КНИ / Патент на изобретение RU 2456627 C1 с приорит. от 31.11.2011.
9. Качемцев А.Н., Киселев В.К., Скупов В.Д., Торохов С.Л. Способ определения коэффициента относительной эффективности и эквивалентной дозы источника рентгеновского излучения / Патент на изобретение RU 2480861 C1 с приорит. от 31.08.2011.
10. Dooley J.G. SEU Immune Latch for Gate Arrey, Standarte Cell and other ASIC Application / US. Pat. No. 531070.
11. Galin T., Nicolaidis M. and Velazco R. Upset Hardened Memory Design for Submicron CMOS Technology / IEEE on Transactions, Vol. 43. - No. 6. - December 1996. - pp. 2874-2878.
12. U.S.A. National Technology Roadmap for Semiconductors.
13. Busher S.M., Daze D., Brown D., McMorrow D. аnd Melinger J. Comparision of Error Rates in Combinatorial and Sequential Logic // IEEE on Nuclear Science, Vol. 44. - No. 6. - December 1997. - pp. 2209-2216.
14. Gadlage M.J., Eaton P.H., Benedetto J.M. and Turfinger T.L. Comarison of Heavy Ion and Proton Inducced Combinatorial and Sequental Logic Error Rates in a Deep Submicron Process / IEEE Transactions on Nuclear Science, vol. NS-52. - No. 6. - Dec. 2005. - pp. 2120-2124.
15. Petrsen E.L., Pouget V., Messengill L.W., Buchner S.P. and McMorrow D. Rate Predictions for Single-Event Effecs - Critique II / IEEE Nransactions on Nuclear Science, Dec. 2005. - Vol. 52. - No. 6. - pp. 2158-2167.
16. Качемцев A.H., Киселев В.К., Торохов С.Л. Способ испытаний полупроводниковых БИС технологии КМОП/КНД на стойкость к эффектам единичных сбоев от воздействия тяжелых заряженных частиц (ТЗЧ) // Патент на изобретение RU 2495446 C2 с приорит. от 17.10.2011.
17. Buchner S., Baze M., Brown D. McMorrow D. and Melinger J. Comparision of Error Rates in Combinatorial and Sequental Logic / IEEE Transactions on Nuclear Science, Dec. 2004. - Vol. NS-51. - No. 6. - pp / 3480-3485.
18. Benedetto J., Eaton P., Avery K., Mavis K., Gadlage M., Turfinger T., Dodd P. and Vizkelethyd G. Heavy Ion Induced Digital Single-Event Transients in Deep Submicron Processes / IEEE Transactions on Nuclear Science, Dec. 2004. - Vol. NS-51. - No. 6. pp. 3480-3485.
19. Robinson P., Lee W., Aguero R., Gabriel S. Anomalies Due to Single Event Upsets / Journal of Spacekraft and Rockets, Mar-Apr., Mar.-Apr. 1994. - Vol. 31. - No. 2 - pp. 166-171.
20. Pickel J.C., Blanford J.T. Cosmic Ray Induced Errors in MOS Memory Cells / IEEE Transactions on Nuclear Science, Dec. 1978. - Vol. NS-25. - No. 6. - pp. 1166-1171.
21. LaBel K. Single Event Effects Specification″, radhome.gsfc.nasa.gov/radhome/papers/seespec.htm, 1993.
22. Качемцев A.H., Киселев B.K., Корсакова Н.Г. Способ определения стойкости электронных компонентов и блоков радиоэлектронной аппаратуры к воздействию ионизирующих излучений / Патент на изобретение RU 2504862 C1 с приорит. от 17.07.2012.
23. Гнеденко Б.Б., Беляев Ю.К., Соловьев А.Д. Математические методы в теории надежности. - М.: Наука. Главная ред. ФМЛ. 1965. - 524 с.
24. Dozier С.М., Brown D.B. The Use of Low Energy X-Ray for Device Testing - a Comparision Whith Co-60 Radiation // IEEE Transactions on Nuclear Science, 1975. - Vol. NS-30. - No. 6. pp. 4382-4387.
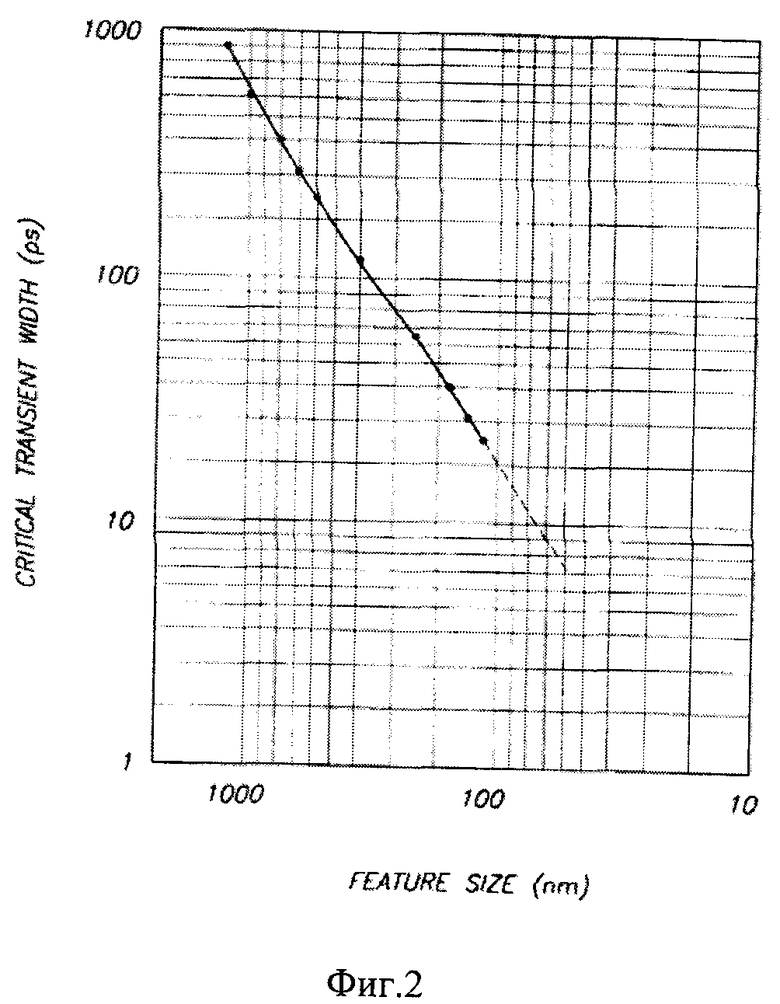
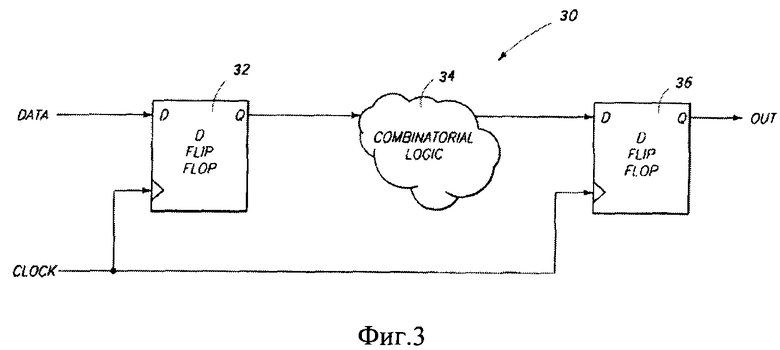
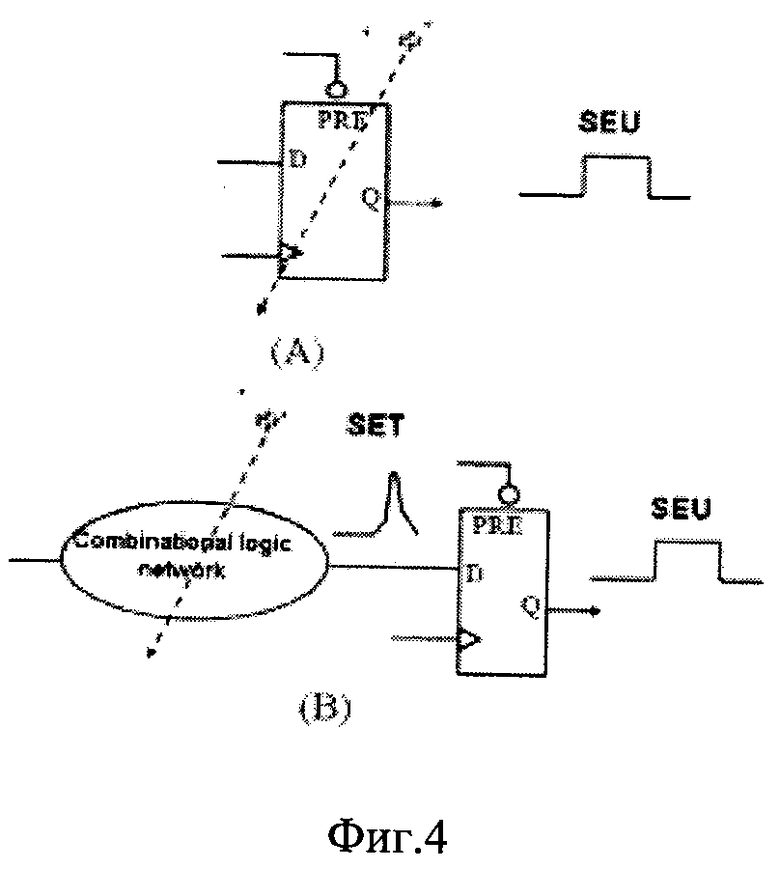
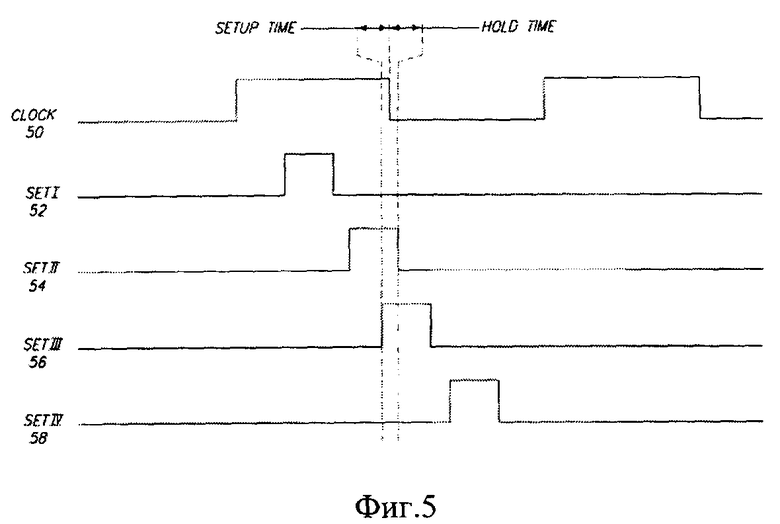
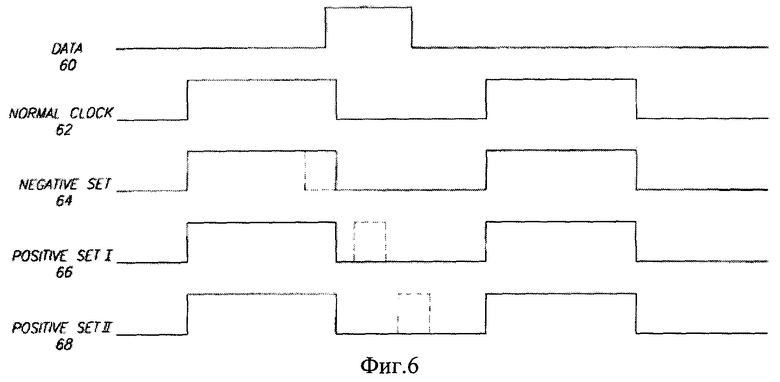
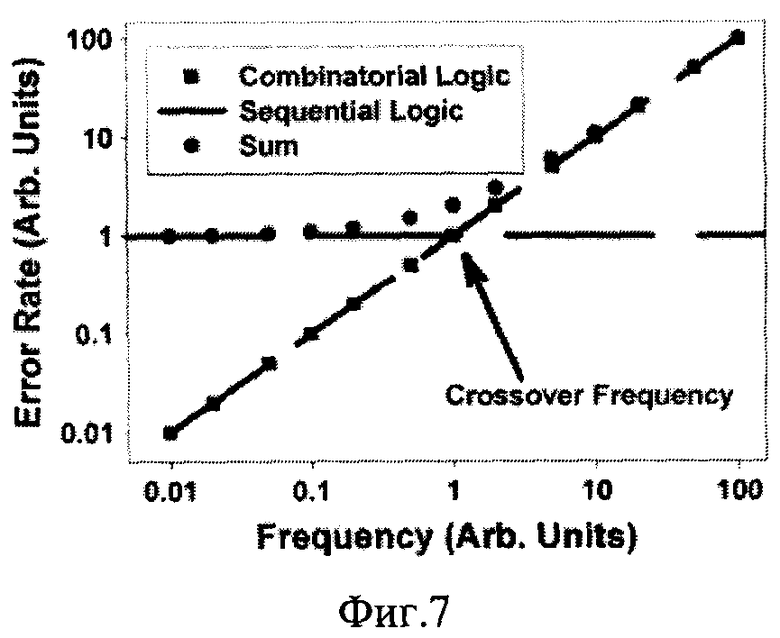
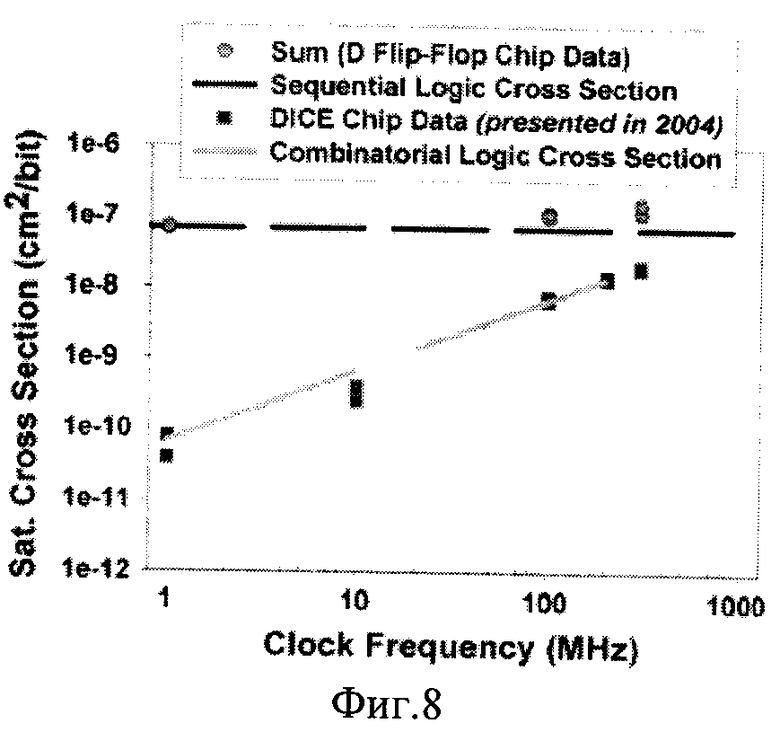
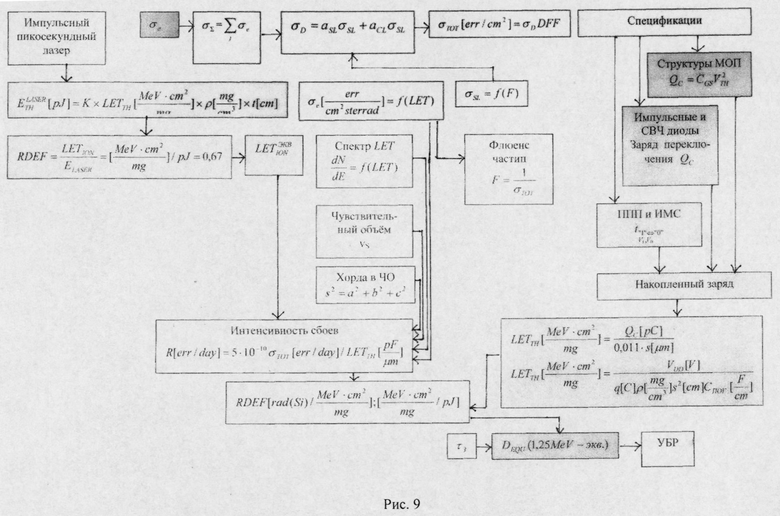
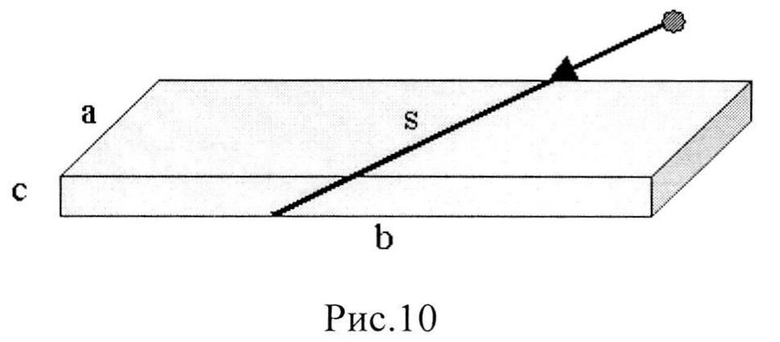
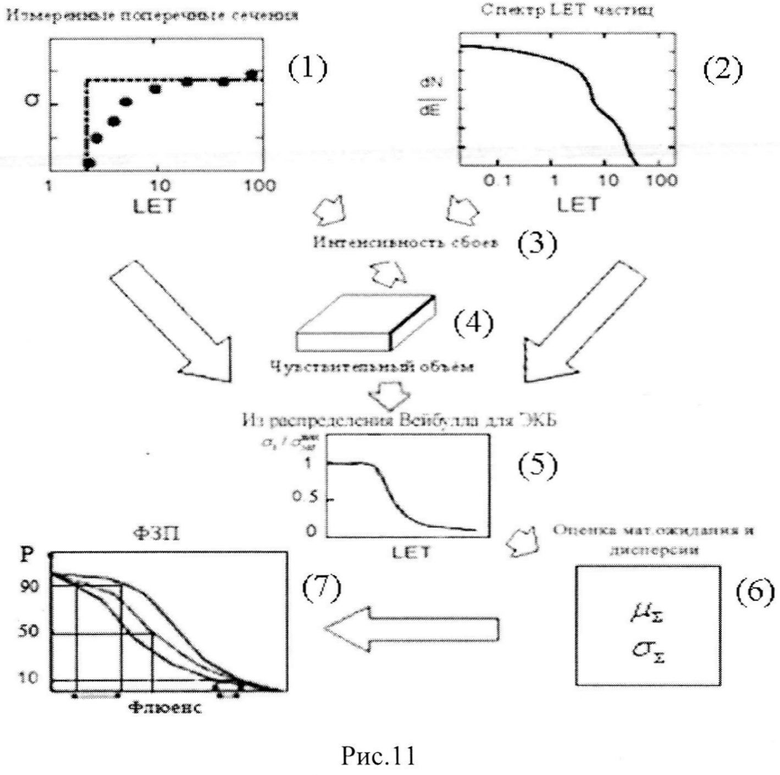
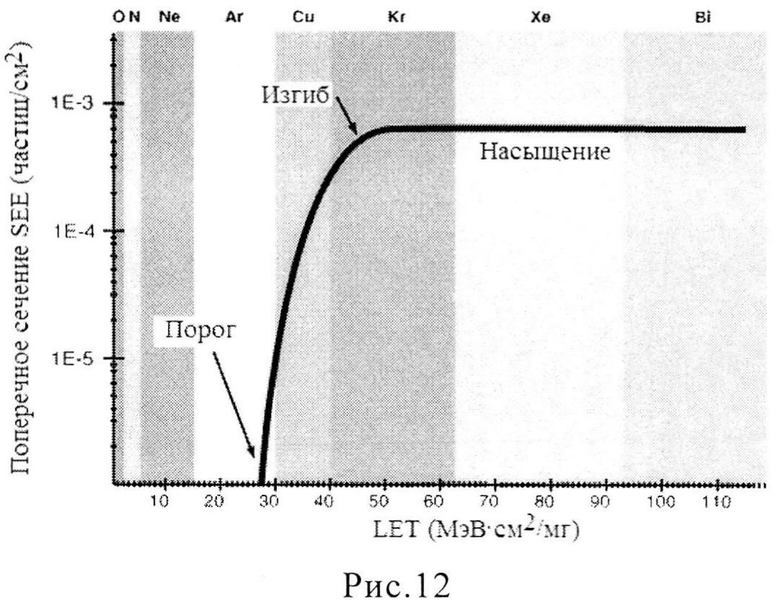
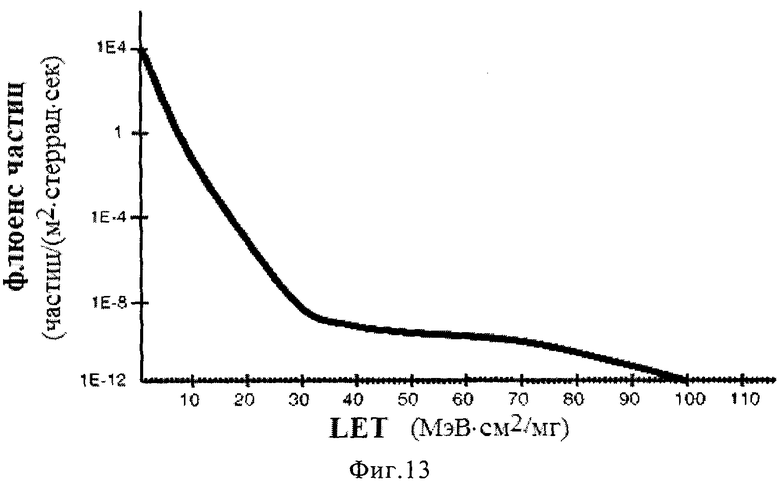
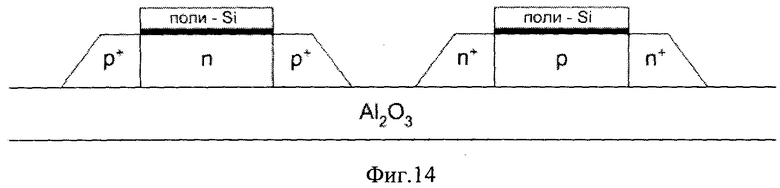
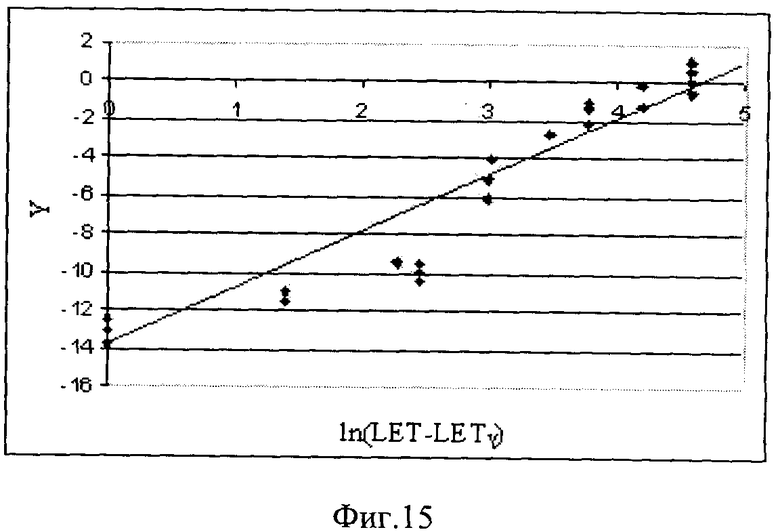
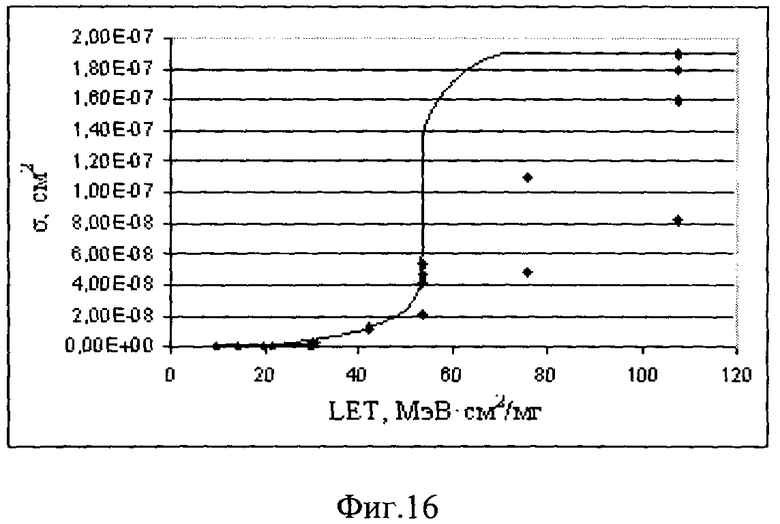
Изобретение относится к области исследования радиационной стойкости полупроводниковых приборов (ППП) и интегральных схем, и в большей степени интегральных микросхем (ИМС) с последовательной и комбинационной обработкой логических сигналов. Сущность изобретения заключается в том, что путем сопоставления и конверсии различных данных по стойкости к дозовым эффектам при статическом или импульсном облучении на моделирующих установках (МУ), по стойкости к эффектам мощности дозы при импульсном облучении на МУ, по стойкости к воздействию эффектов мощности дозы ИЛИ при имитационном моделировании, по стойкости к низкоинтенсивному излучению факторов космического пространства (КП) и по данным спецификаций о динамических параметрах ППП и ИМС на основе общей концепции генерации критического заряда в чувствительном объеме νS, вызывающего эффекты SEU и SET в цифровых электронных схемах. 4 н. и 23 з.п. ф-лы, 16 ил., 12 табл.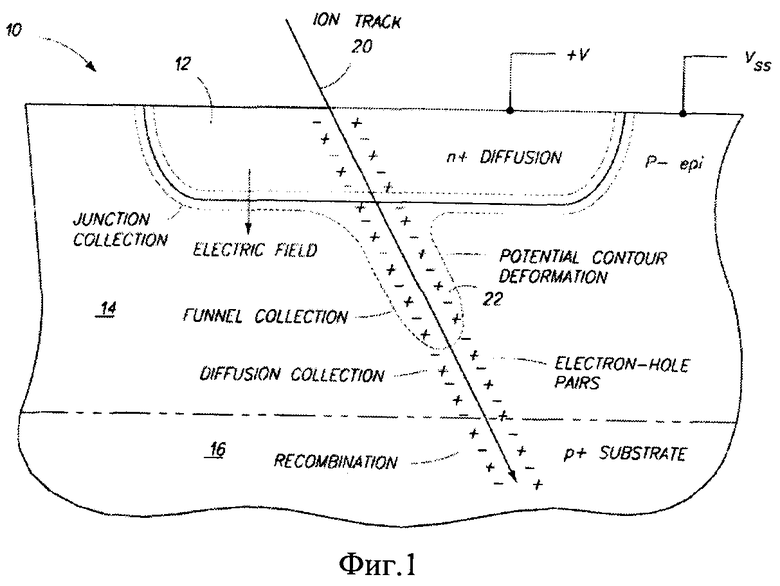
1. Способ оценки стойкости цифровой электронной аппаратуры к воздействию ионизирующих излучений (вариант 1), в котором выполняют экспериментальные исследования зависимости поперечного сечения сбоев от величины линейной передачи энергии σ=f(LET) для каждой тяжелой заряженной частицы (ТЗЧ) из заданного ионного «коктейля», определяют из этой зависимости значения поперечного сечения насыщения сбоев σSAT, определяют минимальный поток ТЗЧ, вызывающий эффекты сбоев, определяют пороговую величину линейных потерь энергии, LEТTH, соответствующей величине σSAT, определяют величину критического заряда QC генерации эффекта сбоя, которые используют для оценки величины интенсивности сбоев RSEU, отличающийся тем, что для определения уровня бессбойной работы (УБР) блока или всего устройства радиоэлектронной аппаратуры (РЭА), в целом, содержащей в своем составе цифровые интегральные микросхемы (ИМС), по результатам экспериментальных исследований на моделирующих установках (МУ) определяют коэффициент относительной эффективности (КОЭ) 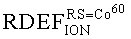
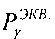 для МУ, которая соответствует уровню бессбойной работы (УБР).
для МУ, которая соответствует уровню бессбойной работы (УБР).
2. Способ по п. 1, отличающийся тем, что для определения поперечного сечения сбоев цифрового устройства анализируют структурную схему радиоэлектронного устройства, определяют величины отдельных парциальных поперечных сечений сбоев 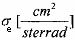 для каждого цифрового элемента схемы, суммарное поперечное сечение σΣ для однотипных элементов последовательной и комбинационной логики, усредненное поперечное сечение σD для элементов последовательной и комбинационной логики, полное сечение σTOT для всего цифрового устройства.
для каждого цифрового элемента схемы, суммарное поперечное сечение σΣ для однотипных элементов последовательной и комбинационной логики, усредненное поперечное сечение σD для элементов последовательной и комбинационной логики, полное сечение σTOT для всего цифрового устройства.
3. Способ по п. 2, отличающийся тем, что для сокращения числа испытаний, величину полного поперечного сечения сбоев вводят с учетом числа цифровых бистабильных триггеров DFF.
4. Способ по п. 2, отличающийся тем, что для сокращения числа испытаний на установках, моделирующих воздействие ТЗЧ, для определения единичного сечения сбоев σе для однотипных элементов схемы, для большинства практических случаев интенсивность сбоев определяют с использованием аппроксимирующего выражения для поперечного сечения насыщения σSAT=ab, (a, b>с) и критического порогового значения линейной передачи энергии (массовых потерь) 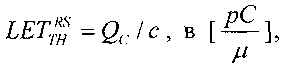 где c - толщина полупроводниковой пластины, a и b - размеры чипа структуры, в мкм, a QC - величина критического радиационно-индуцированного (РИЗ), вызывающего сбои в работе логических устройств.
где c - толщина полупроводниковой пластины, a и b - размеры чипа структуры, в мкм, a QC - величина критического радиационно-индуцированного (РИЗ), вызывающего сбои в работе логических устройств.
5. Способ по п. 2, отличающийся тем, что для учета частотной зависимости эффектов SEU в комбинационной логике величину парциального сечения сбоев 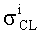
6. Способ по п. 5, отличающийся тем, что для учета частотной зависимости эффектов SEU в элементах комбинационной и последовательной логики, для учета зависимости поперечного сечения сбоев для однотипных элементов комбинационной логики от частоты синхронизации на аппроксимирующей зависимости поперечного сечения сбоев для однотипных элементов комбинационной логики 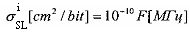 величину
величину 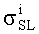
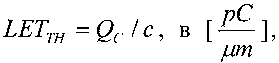 величину сечения сбоев для однотипных элементов последовательной логики определяют с использованием соотношения
величину сечения сбоев для однотипных элементов последовательной логики определяют с использованием соотношения
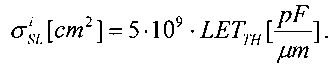
7. Способ по любому из пп. 3 или 6, отличающийся тем, что для унификации результатов оценки чувствительности к эффектам SEU элементов комбинационной и последовательной логики, для определения суммарного поперечного сечения сбоев для элементов последовательной и комбинационной логик поперечное сечение сбоев σSL для элементов последовательной логики определяют из 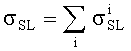
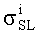
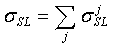
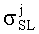
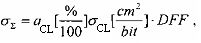
где a
CL - процентный состав схем комбинаторной логики; DFF - число фиксирующих элементов (триггеров) в схеме, а полное сечение сбоев в схеме определяют с использованием соотношения
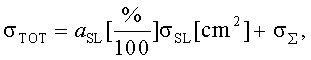
8. Способ по п. 1, отличающийся тем, что для получения результата оценки эквивалентной дозы для эталонного спектра нуклидного источника Co60, исходя из спектра линейной передачи энергии 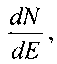 чувствительного объема νS типовой транзисторной структуры отдельного цифрового элемента и максимального значения величины пространственной диагонали sMAX (хорды) чувствительного объема, определяют пороговое значение линейной передачи энергии LETTH и величину интенсивности сбоев
чувствительного объема νS типовой транзисторной структуры отдельного цифрового элемента и максимального значения величины пространственной диагонали sMAX (хорды) чувствительного объема, определяют пороговое значение линейной передачи энергии LETTH и величину интенсивности сбоев 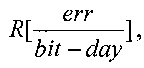 определяют КОЭ
определяют КОЭ 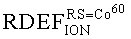
9. Способ по п. 8, отличающийся тем, что для оценки интенсивности сбоев от эффектов SEU, для получения экспериментальной зависимости поперечного сечения сбоев блоков РЭА или ИМС от LET вида 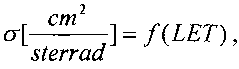 на соответствующей МУ, воспроизводящей пучки ионов (ТЗЧ), выполняют облучение объектов исследования в диапазоне заданных флюенсов ТЗЧ из спектра LET вида
на соответствующей МУ, воспроизводящей пучки ионов (ТЗЧ), выполняют облучение объектов исследования в диапазоне заданных флюенсов ТЗЧ из спектра LET вида 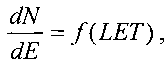 где dN/dE - распределение числа ТЗЧ по энергиям, определяют чувствительный объем νS транзисторной гетероструктуры, в котором формируется критический заряд Qc, определяют максимальный размер хорды sMAX (пространственной диагонали) в модели чувствительного объема (ЧО) в виде параллелепипеда {Rectangular Parallel Piped=RPР) из s2=a
2+b2+c2, где a=b=L - топологический размер ЧО элемента, c=t - толщина гетероструктуры в ЧО, определяют пороговое значение LETTH на зависимости
где dN/dE - распределение числа ТЗЧ по энергиям, определяют чувствительный объем νS транзисторной гетероструктуры, в котором формируется критический заряд Qc, определяют максимальный размер хорды sMAX (пространственной диагонали) в модели чувствительного объема (ЧО) в виде параллелепипеда {Rectangular Parallel Piped=RPР) из s2=a
2+b2+c2, где a=b=L - топологический размер ЧО элемента, c=t - толщина гетероструктуры в ЧО, определяют пороговое значение LETTH на зависимости 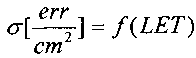 для полного телесного угла, интенсивность сбоев определяют с использованием соотношения
для полного телесного угла, интенсивность сбоев определяют с использованием соотношения
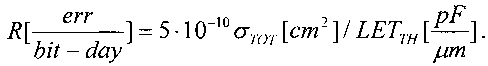
10. Способ по п. 1, отличающийся тем, что для конверсии результатов экспериментальной оценки чувствительности к эффектам SEU цифровой аппаратуры при испытаниях на установках ИЯР и ЭФУ, моделирующих воздействие ТЗЧ по эффекту идентичности критического заряда QC, определяют величину коэффициента относительной эффективности 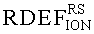
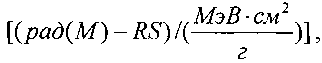 где M - полупроводниковый материал в ЧО транзисторной структуры, а величину эквивалентной дозы гамма-излучения DRS(γ - кв.RS-экв.-(М)) определяют из соотношения
где M - полупроводниковый материал в ЧО транзисторной структуры, а величину эквивалентной дозы гамма-излучения DRS(γ - кв.RS-экв.-(М)) определяют из соотношения
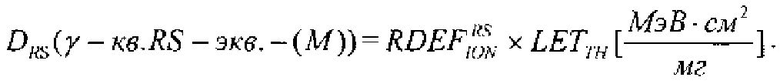
11. Способ по п. 10, отличающийся тем, что для реализации эксперимента на импульсном ядерном реакторе (ИЯР) или электрофизической установке (ЭФУ), генерирующих импульсное гамма-рентгеновское излучение, при известной длительности импульса гамма-рентгеновских квантов источника эталонного ИИ τP для цифровой аппаратуры определяют мощность дозы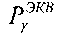 ИИ из отношения эквивалентной поглощенной дозы к длительности этого импульса
ИИ из отношения эквивалентной поглощенной дозы к длительности этого импульса
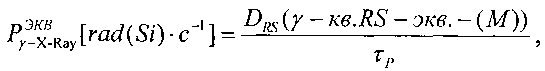
которую принимают равной УБР.
12. Способ оценки стойкости цифровой электронной аппаратуры к воздействию ионизирующих излучений (вариант 2), в котором декорпусированный кристалл (чип) гетероэпитаксиальной структуры полупроводникового прибора (ППП) или ИМС облучают импульсным лазерным источником, определяют критическую пороговую энергию 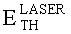
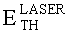
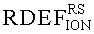
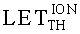
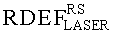
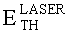
13. Способ по п. 12, отличающийся тем, что для оценки интенсивности сбоев при ИМ, с учетом данных о σТОТ[cm2], sMAX[µm] на зависимости σ[cm2]=f(LET) определяют величину интенсивности сбоев с использованием соотношения
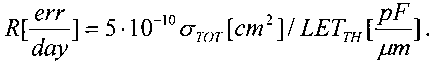
14. Способ по п. 12, отличающийся тем, что для получения адекватных с воздействием ТЗЧ условий, при использовании имитационных методов (ИМ) с помощью ИЛИ гетероструктуру чипа ППП или ИМС облучают пикосекундным импульсом лазерного источника с длительностью не более 350 пс и длиной волны в диапазоне 800-1500 нм.
15. Способ по п. 12., отличающийся тем, что для получения эквивалентной величины критического заряда Qc, который вызывает в критическом объеме νS возникновение сторонних токов, вызывающих эффекты SEU и SET, для реализации фотоионизации ЧО транзисторных структур, используют значение 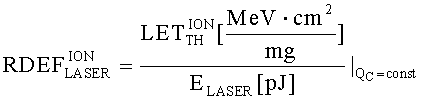
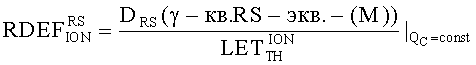
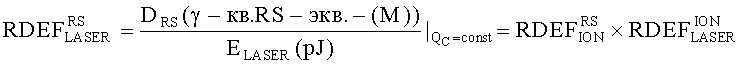
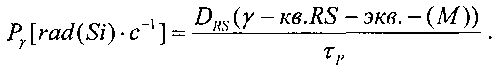
16. Способ по п. 15, отличающийся тем, что для фиксации эффективности ИМ, при использовании ИМ с помощью импульсного лазерного источника фиксируют критическую пороговую энергию 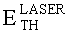
17. Способ по п. 15, отличающийся тем, что для конверсии результатов ИМ, значение величины 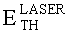
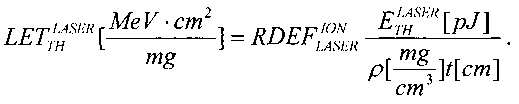
18. Способ по п. 17, отличающийся тем, что с целью фиксации эффективности ИМ, величину 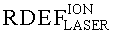
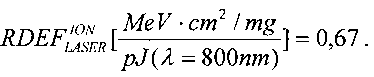
19. Способ по п. 18, отличающийся тем, что для преобразования результатов ИМ в эвивалентное воздействие ТЗЧ, величину эквивалентного значения 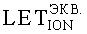
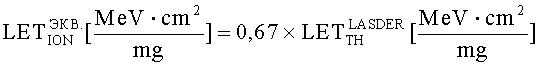
20. Способ по п. 19, отличающийся тем, что для определения УБР при ИМ, в единицах, эквивалентных воздействию источников импульсного ИИ, с использованием
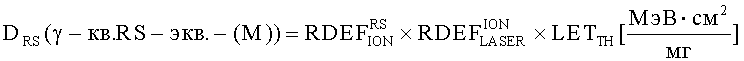
определяют величину эквивалентной полной поглощенной дозы гамма-квантов DRS(γ-кв.RS-экв.-(М)) и при известной длительности импульса гамма-квантов источника эталонного ионизирующего излучения τP УБР цифровой аппаратуры определяют
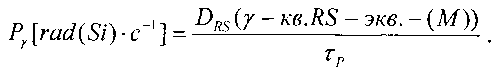
21. Способ по любому из пп. 12 или 19, отличающийся тем, что для использования инженерных методов оценки интенсивности сбоев от эффектов ТЗЧ, преобразуют
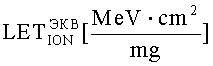
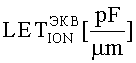
22. Способ оценки стойкости цифровой электронной аппаратуры к воздействию ионизирующих излучений (вариант 3), отличающийся тем, что определяют уровень бессбойной работы (УБР) по результатам использования динамических электрических параметров спецификации на элементы ЭКБ для получения эквивалентной величины критического заряда 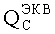
23. Способ по п. 22, отличающийся тем, что для определения эквивалентного значения 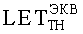
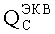
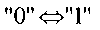 и соответствующее значение напряжения питания ИМС.
и соответствующее значение напряжения питания ИМС.
24. Способ по п. 22, отличающийся тем, что для определения эквивалентного значения 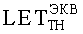
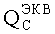
25. Способ по п. 22, отличающийся тем, что для определения эквивалентного значения 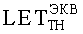
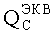
26. Способ по любому из пп. 23, 24, 25, отличающийся тем, что для определения эквивалентного значения 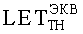
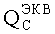
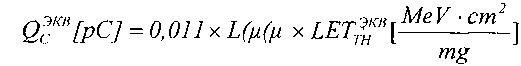
или 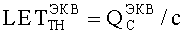
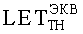
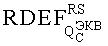
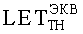
27. Способ оценки стойкости цифровой электронной аппаратуры к воздействию ионизирующих излучений (вариант 4) путем использования экспериментально полученных данных при моделировании РИЗ в БИС/СБИС технологии КМОП/КНД от воздействия ТЗЧ КП, от воздействия ИЛИ пикосекундного диапазона, отличающийся тем, что для определения уровня бессбойной работы (УБР) БИС/СБИС при воздействии эквивалентного импульсного источника ионизирующего излучения с энергией квантов 1,25 МэВ-экв.(М), производят выборочно оценку порогового значения линейной передачи энергии (LETТН), производят либо из прямых измерений зависимости поперечного сечения сбоев от величины LET, либо при воздействии импульсного лазерного излучения, либо из данных о значении таких электрических параметров спецификации на элементы ЭКБ, как времена переключения из одного логического состояния в другое 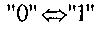 , или уровни выходных напряжений логических состояний VOL и V0H, либо из данных о заряде переключения QПЕР. между этими состояниями, затем с использованием соответствующих значений коэффициентов относительной эффективности
, или уровни выходных напряжений логических состояний VOL и V0H, либо из данных о заряде переключения QПЕР. между этими состояниями, затем с использованием соответствующих значений коэффициентов относительной эффективности 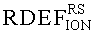
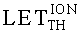
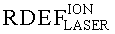
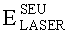
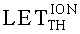
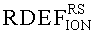
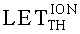
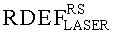
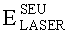
| E | |||
| L | |||
| Petersen et al "Rate Predictions for Single-Event Effects-Critique II" | |||
| IEEE Transactions on Nuclear Science, Vol | |||
| Устройство для устранения мешающего действия зажигательной электрической системы двигателей внутреннего сгорания на радиоприем | 1922 |
|
SU52A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Способ предохранения от окисления металлических приборов, укрепляемых на дюралюминиевых поверхностях летательных аппаратов | 1924 |
|
SU2158A1 |
| СПОСОБ ИСПЫТАНИЙ ПОЛУПРОВОДНИКОВЫХ БИС ТЕХНОЛОГИИ КМОП/КНД НА СТОЙКОСТЬ К ЭФФЕКТАМ ЕДИНИЧНЫХ СБОЕВ ОТ ВОЗДЕЙСТВИЯ ТЯЖЕЛЫХ ЗАРЯЖЕННЫХ ЧАСТИЦ КОСМИЧЕСКОГО ПРОСТРАНСТВА | 2011 |
|
RU2495446C2 |
| RU 95103986 A1, 27.07.1996 | |||
| US 8346497 B2, 01.01.2013. | |||
Авторы
Даты
2016-03-20—Публикация
2014-09-22—Подача