Изобретение относится к измерительной технике, в частности к аналого-цифровому преобразованию, а именно к кодовым шкалам цифровых преобразователей угла (ЦПУ).
ЦПУ используются в различных технических системах самого широкого назначения. Естественно, что надежность работы преобразователя влияет на надежность работы всей системы. Основными компонентами ЦПУ являются кодовая шкала и считывающие элементы. В процессе работы ЦПУ возможны выходы из строя считывающих элементов. В этом случае информация со шкалы будет считываться с ошибками. Для компенсации таких ошибок ЦПУ снабжаются дополнительными (корректирующими) считывающими элементами, число которых определяется разрядностью шкалы и кратностью исправляемых ошибок. Решение данной задачи базируется на использовании теории кодов, исправляющих ошибки. Наиболее подходящими кодовыми шкалами, в которых могут быть применены корректирующие коды, являются псевдослучайные кодовые шкалы.
Известна псевдослучайная кодовая шкала (см. Ожиганов А.А., Лукьянов В.Д. Кодовые шкалы на основе рекуррентных последовательностей для преобразователей перемещений повышенной информационной надежности // Датчики и системы. - Москва, 2012. - №2. - С. 13-17) - [1], содержащая информационную дорожку, выполненную в виде градаций псевдослучайной двоичной последовательности максимальной длины периода М=2n-1, построенной посредством примитивного многочлена h(x) степени n, где n - разрядность шкалы, n информационных считывающих элементов, размещенных вдоль информационной дорожки с угловыми шагами, кратными величине кванта шкалы δ=360°/М, с возможностью получения с них М различных n разрядных кодовых комбинаций (см. Ожиганов А.А. Алгоритм размещения считывающих элементов на псевдослучайной кодовой шкале // Изв. вузов СССР. Приборостроение, 1994. Т. 37. №2. С. 22-27) - [2], k корректирующих считывающих элементов, размещенных вдоль информационной дорожки с возможностью получения с них совместно с n информационными считывающими элементами М различных (n+k) - разрядных кодовых комбинаций, представляющих собой код Хемминга с обнаружением и исправлением одиночной ошибки.
Недостатком такой шкалы является низкая информационная надежность, поскольку в ней не обеспечена возможность не только исправления, но даже и обнаружения двойных ошибок.
Наиболее близким по техническому решению и выбранному авторами за прототип является псевдослучайная кодовая шкала (см. Псевдослучайная кодовая шкала. Патент RU 2510572 С1, МПК Н03М 1/24. Опубликовано: 27.03.2014. Бюл. №9) - [3], содержащая информационную дорожку, выполненную в виде градаций псевдослучайной двоичной последовательности максимальной длины периода М=2n-1, построенной посредством примитивного многочлена h(x) степени n, где n - разрядность шкалы, n информационных считывающих элементов, размещенных вдоль информационной дорожки с угловыми шагами, кратными величине кванта шкалы δ=360°/М, с возможностью получения с них М различных n разрядных кодовых комбинаций, k корректирующих считывающих элементов, размещенных вдоль информационной дорожки с возможностью получения с них совместно с n информационными считывающими элементами М различных (n+k) - разрядных кодовых комбинаций, представляющих собой код Хемминга с обнаружением и исправлением одиночной ошибки, контрольный считывающий элемент, размещенный вдоль информационной дорожки с возможностью получения с него совместно с (n+k) считывающими элементами М различных (n+k+1) - разрядных кодовых комбинаций, представляющих собой код Хемминга с исправлением одиночной и обнаружением двойной ошибки, выходы n информационных считывающих элементов, выходы k корректирующих считывающих элементов и выход контрольного считывающего элемента являются выходами псевдослучайной кодовой шкалы.
Недостатком прототипа является невысокая информационная надежность, поскольку в ней не обеспечена возможность исправления двойных ошибок.
В предлагаемом изобретении решается задача повышения информационной надежности псевдослучайной кодовой шкалы за счет формирования с нее корректирующих кодов с исправлением двойных ошибок.
Для достижения технического результата псевдослучайная кодовая шкала содержит информационную дорожку, выполненную в виде градаций псевдослучайной двоичной последовательности максимальной длины периода М=2n-1, построенной посредством примитивного многочлена h(x) степени n, где n - разрядность шкалы, n информационных и k+1 корректирующих считывающих элементов, размещенных вдоль информационной дорожки с угловыми шагами, кратными величине кванта шкалы δ=360°/М, с возможностью получения с них М различных (n+k+1) - разрядных кодовых комбинаций, представляющих собой корректирующий код с исправлением одиночной и обнаружением двойной ошибки, kд дополнительных корректирующих считывающих элементов, размещенных вдоль информационной дорожки с угловыми шагами, кратными величине кванта шкалы δ, с возможностью получения с них совместно с (n+k+1) считывающими элементами М различных (n+k+kд+1) - разрядных кодовых комбинаций, представляющих собой корректирующий код с исправлением двойной ошибки, выходы считывающих элементов являются выходами псевдослучайной кодовой шкалы.
Новым в предлагаемом изобретении является:
- снабжение псевдослучайной кодовой шкалы kд дополнительными корректирующими считывающими элементами;
- соответствующее размещение всех считывающих элементов вдоль информационной дорожки с угловыми шагами, кратными величине кванта шкалы δ, с возможностью получения с них М различных (n+k+kд+1) - разрядных кодовых комбинаций, представляющих собой корректирующий код с обнаружением и исправлением двойных ошибок.
Совокупность существенных признаков в предлагаемом изобретении позволила повысить информационную надежность псевдослучайной кодовой шкалы.
В результате этого можно сделать вывод о том, что предлагаемое изобретение обладает изобретательским уровнем и позволяет получить технический результат.
Изобретение является новым, так как из уровня техники по доступным источникам информации не выявлено аналогов с подобной совокупностью признаков.
Изобретение является промышленно применимым, так как может быть использовано во всех областях, где требуется высокоточное позиционное определение углового положения объекта с использованием цифровых преобразователей угла повышенной информационной надежности на основе заявляемых псевдослучайных кодовых шкал.
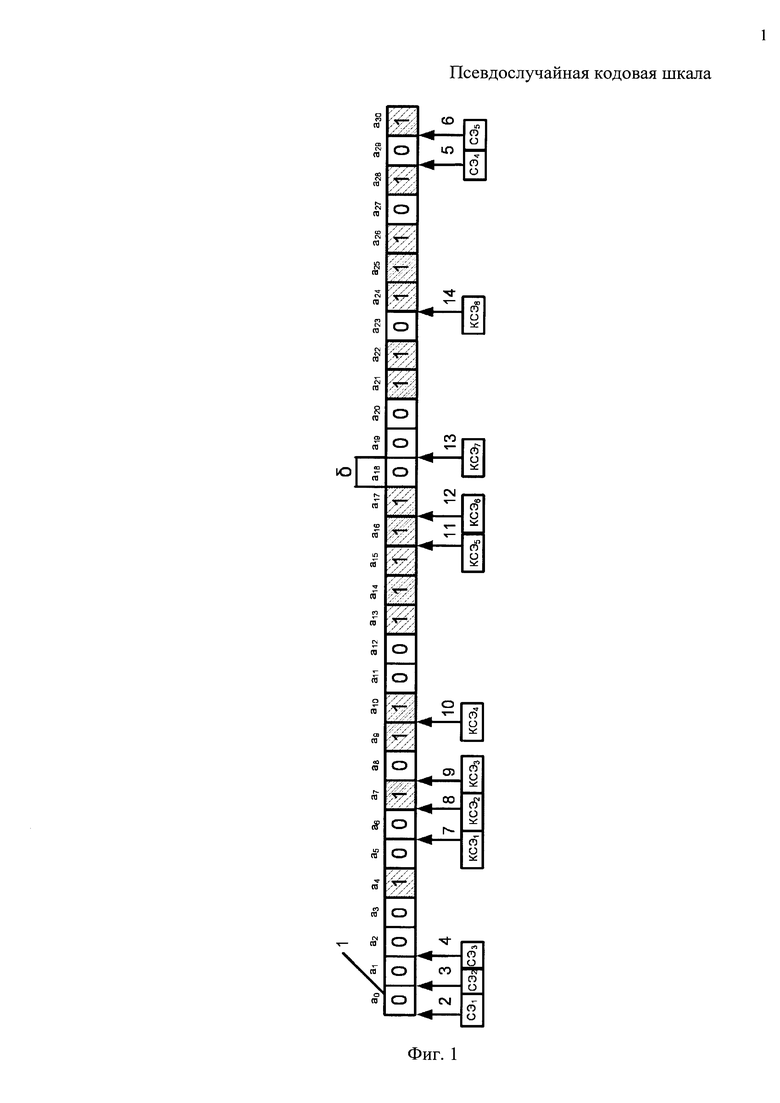
Предлагаемое изобретение поясняется фиг. 1, где показана линейная развертка круговой пятиразрядной псевдослучайной кодовой шкалы.
Заявляемая псевдослучайная кодовая шкала содержит информационную кодовую дорожку 1, информационные считывающие элементы 2, 3, 4, 5, 6 (n=5), корректирующие считывающие элементы 7, 8, 9, 10, 11, 12, 13, 14 (k=8).
Для пояснения сути изобретения приведем некоторые теоретические предпосылки.
В [1, 2 и 3], а также в (см. Ожиганов А.А. Псевдослучайные кодовые шкалы // Изв. вузов СССР. Приборостроение, 1987. Т. 30. №2. С. 40-43) - [4] рассмотрены использованные в изобретении кодовые шкалы, получившие название псевдослучайные (ПСКШ), и строящиеся на основе теории М-последовательностей. ПСКШ имеют всего одну информационную кодовую дорожку, выполненную в соответствии с символами М - последовательности а=а0а1…аМ-1 и n информационных считывающих элементов (СЭ), размещенных вдоль дорожки. Считывающие элементы дают возможность получить при полном обороте шкалы М=2n-1 различных n-разрядных кодовых комбинаций, что обеспечивает разрешающую способность ПСКШ δ=360°/М. В общем виде задача размещения информационных СЭ на ПСКШ решена в [2].
Для генерации М-последовательности с периодом М=2n-1 используется примитивный неприводимый многочлен h(x) степени n с коэффициентами поля Галуа GF(2) (см. Макуильямс Ф.Д., Слоан Н.Д. Псевдослучайные последовательности и таблицы // ТИИЭР. 1976. Т. 64. №12. С. 80-95) - [5], т.е.
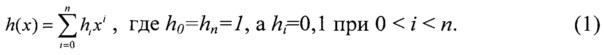
Символы М-последовательности an+j удовлетворяют рекуррентному выражению
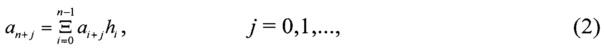
где знак  означает суммирование по модулю два, а индексы при символах М-последовательности берутся по модулю М. Начальные значения символов М-последовательности a0a1…an-1 могут выбираться произвольно, за исключением нулевой комбинации. Для определенности при построении круговой ПСКШ символы М-последовательности a0a1…aM-1 отображаются на информационной дорожке по ходу часовой стрелки.
означает суммирование по модулю два, а индексы при символах М-последовательности берутся по модулю М. Начальные значения символов М-последовательности a0a1…an-1 могут выбираться произвольно, за исключением нулевой комбинации. Для определенности при построении круговой ПСКШ символы М-последовательности a0a1…aM-1 отображаются на информационной дорожке по ходу часовой стрелки.
М-последовательности относятся к классу циклических кодов и могут задаваться с помощью порождающего многочлена g(x)=(xM+1)/h(x), где h(x) определяется в соответствии с выражением (1), М=2n-1.
Для каждой М-последовательности длины М существует ровно М различных циклических сдвигов, которые могут быть получены путем умножения порождающего многочлена g(x) на xj, где j=0,1,…,М-1.
Поскольку ПСКШ строятся в соответствии с символами М-последовательности, можно путем циклических сдвигов определить порядок размещения на шкале n информационных считывающих элементов, т.е. m-му СЭ, m=1,2,…,n, ставится в соответствие jm-й циклический сдвиг 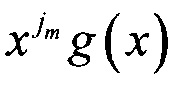 М-последовательности.
М-последовательности.
Тогда многочлен, определяющий порядок размещения n информационных СЭ на шкале, имеет вид:
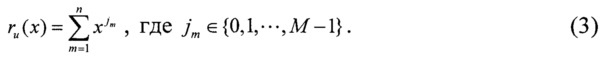
Положив j1=0, согласно полинома (3) получим положения 2-го, 3-го, …, n-го информационных СЭ, смещенные относительно первого СЭ на j2,j3,…,jn квантов информационной дорожки шкалы соответственно.
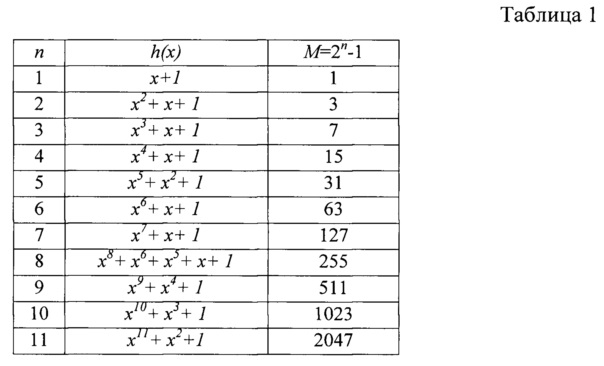
В табл. 1 приведены многочлены h(x) до n=11 включительно, которые могут быть использованы для генерации соответствующих М-последовательностей [5].
Поясним вариант построения ПСКШ, приведенной на фиг. 1.
В примере для простоты принято n=5 и соответственно из табл. 1 выбран примитивный неприводимый многочлен h(х)=x5+х2+1, где h0=h2=h5=1, h1=h3=h4=0. Здесь период М-последовательности М=25-1=31, а сама М-последовательность a=a0a1… а29а30=0000100101100111110001101110101. При начальных значениях М-последовательности a0=a1=a2=a3=0, а4=1 остальные символы последовательности получены в соответствии с рекуррентным соотношением (2), которое в данном примере имеет вид a5+j=a2+j⊕aj, j=0,1,…,25. Размещение пяти информационных считывающих элементов СЭ1 (на фиг. позиция 2), СЭ2 (на фиг. позиция 3), СЭ3 (на фиг. позиция 4), СЭ4 (на фиг. позиция 5) и СЭ5 (на фиг. позиция 6) вдоль информационной дорожки шкалы задано согласно (3) многочленом ru(х)=1+х+х2+х29+х30.
При построении информационной дорожки 1 М-последовательность с периодом М=31 должна быть нанесена на шкалу в виде пассивных (нули М-последовательности) и активных (единицы М-последовательности) участков информационной дорожки, например, по ходу часовой стрелки, причем на информационную дорожку шкалы наносится только один период М-последовательности. М-последовательность с периодом М=2n-1 определяет число квантов информационной дорожки шкалы, которое в данном примере равно М=31. Отсюда величина кванта δ=360°/М=360°/31=11,6129032280645°. Информационные считывающие элементы, числом 5, должны быть размещены вдоль информационной дорожки согласно r(х) с угловым шагом, кратным величине кванта шкалы δ, например, по ходу часовой стрелки. Причем, СЭ1 устанавливается точно в начало шкалы, СЭ2 - со сдвигом на 1 квант относительно начала шкалы, СЭ3 - со сдвигом на 2 кванта относительно начала шкалы, СЭ4 - со сдвигом на 29 квантов относительно начала шкалы, а СЭ5 - со сдвигом на 30 квантов относительно начала шкалы. Отметим, что возможны и другие варианты размещения информационных СЭ вдоль дорожки шкалы [2].
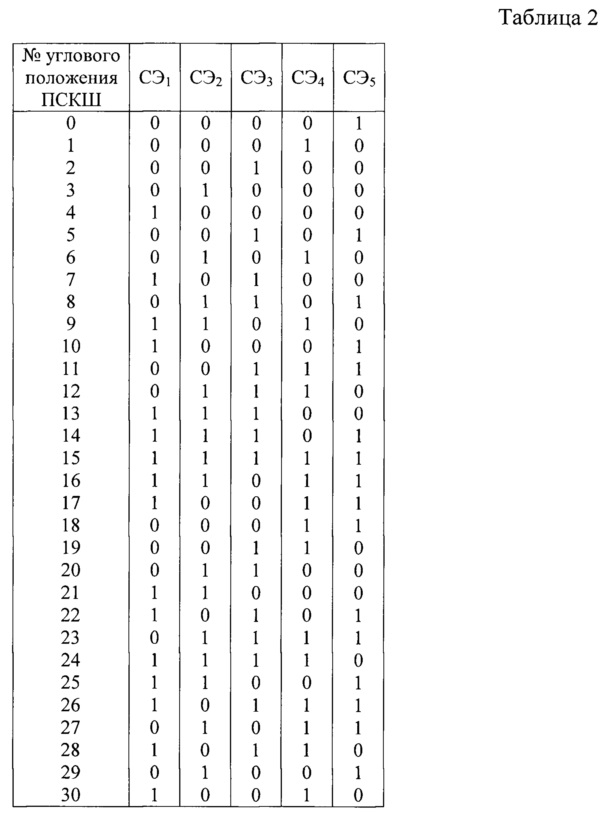
Последовательно фиксируя информационными СЭ пятиразрядную кодовую комбинацию при перемещении шкалы на один квант против хода часовой стрелки, получаем 31 различную пятиразрядную кодовую комбинацию. Эти кодовые комбинации, соответствующие 31 различному угловому положению ПСКШ, приведены в табл. 2.
Технический результат изобретения (повышение информационной надежности) достигается за счет использования циклических корректирующих кодов с исправлением двойных ошибок известных по:
Блейхут Р. Теория и практика кодов, контролирующих ошибки: Пер. с англ. - М.: Мир, 1986. - 576 с. - [6];
Питерсон У., Уэлдон Э. Коды, исправляющие ошибки: Пер. с англ. - М.: Мир, 1976. - 594 с. - [7];
Теория кодирования / Т. Касани, Н. Такура, Е. Ивадари, Я. Инагаки: Пер. с япон. - М.: Мир, 1978. - 576 с. - [8].
Для того чтобы корректирующий код обладал возможностью исправления двойных ошибок, его минимальное кодовое расстояние должно быть не менее 5, т.е. d≥5. Методы формирования корректирующих кодов с d≥5 подробно рассмотрены в [6, 7, 8] и другой доступной литературе по теории кодирования.
В нашем примере число информационных символов n=5 (это пятиразрядный код, который снимается с 5 информационных СЭ).
Для получения корректирующего кода с d≥5 выбирается образующий многочлен циклического кода g(x)=1+x+x3+х4+х8 с числом значащих членов, равным 5.
Далее, посредством образующего многочлена g(x)=1+x+x3+x4+x8 формируется образующая матрица циклического корректирующего кода

Для каждого столбца матрицы G определяются номера циклических сдвигов М - последовательности, используемые для нахождения мест установки на шкале СЭ.
Тогда многочлен размещения корректирующих СЭ будет иметь вид (определен по столбцам 4÷11) rк(х)=х6+х7+х8+х10+х16+х17+х19+х24.
Многочлен размещения как информационных, так и корректирующих СЭ r(х)=ru(х)+rк(х)=1+х+х2+х6+х7+х8+х10+х16+х17+х19+х24+х29+х30.
Следовательно, корректирующие СЭ, числом 8, должны быть размещены вдоль информационной дорожки согласно rк(х) с угловыми шагами, кратными величине кванта шкалы δ, например, по ходу часовой стрелки. Причем, КСЭ1 устанавливается относительно начала шкалы со сдвигом на 6 квантов, КСЭ2 - со сдвигом на 7 квантов, КСЭ3 - со сдвигом на 8 квантов, КСЭ4 - со сдвигом на 10 квантов, КСЭ5 - со сдвигом на 16 квантов, КСЭ6 - со сдвигом на 17 квантов, КСЭ7 - со сдвигом на 19 квантов, a KCЭ8 - со сдвигом на 24 кванта.
Размещение СЭ, определенное согласно приведенной процедуре, не является единственно возможным, поскольку любая нетривиальная линейная комбинация строк матрицы G определяет блоковый код с аналогичными характеристиками.
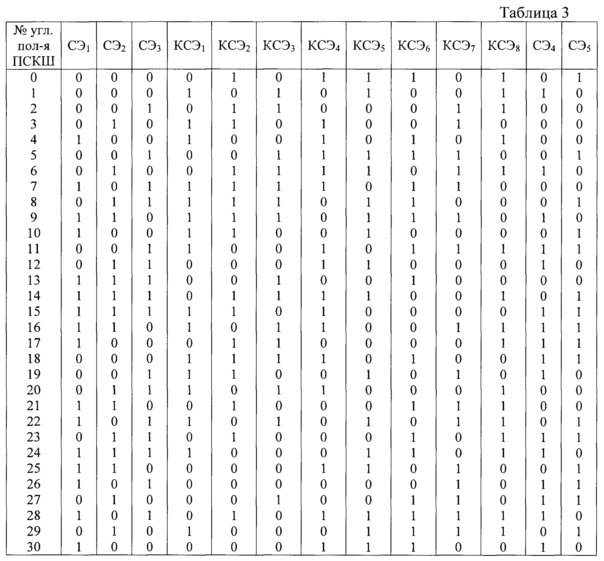
Последовательно фиксируя информационными и корректирующими СЭ тринадцатиразрядную кодовую комбинацию при перемещении шкалы на один квант против хода часовой стрелки, получаем 31 различную тринадцатиразрядную кодовую комбинацию циклического корректирующего кода с минимальным кодовым расстоянием d=5. Известно [6, 7, 8], что такой код позволяет исправлять двойную ошибку. Эти кодовые комбинации, соответствующие 31 различному угловому положению ПСКШ, приведены в табл. 3.
Таким образом, в предлагаемом изобретении решена задача повышения информационной надежности ПСКШ за счет формирования с нее корректирующих кодов с исправлением двойных ошибок. Как отмечалось ранее, под ошибкой в работе ЦПУ на основе ПСКШ в рассматриваемом изобретении понимается выход из строя считывающих элементов. Еще одним применением изобретения является его использование там, где информация с ЦПУ на основе ПСКШ должна непосредственно передаваться в устройство обработки по каналу связи, подверженному помехам.
Предлагаемая ПСКШ может быть положена в основу построения ЦПУ повышенной информационной надежности. В свою очередь, такие преобразователи целесообразно использовать в различных системах управления летательными аппаратами или технике специального назначения, где обеспечение надежности их работы является первостепенным требованием.
Литература
1. Ожиганов А.А., Лукьянов В.Д. Кодовые шкалы на основе рекуррентных последовательностей для преобразователей перемещений повышенной информационной надежности // Датчики и системы. - Москва, 2012. - №2. - С. 13-17.
2. Ожиганов А.А. Алгоритм размещения считывающих элементов на псевдослучайной кодовой шкале // Изв. вузов СССР. Приборостроение, 1994. Т. 37. №2. С. 22-27.
3. Псевдослучайная кодовая шкала. Патент RU 2510572 С1, МПК Н03М 1/24. Опубликовано: 27.03.2014. Бюл. №9. - Прототип.
4. Ожиганов А.А. Псевдослучайные кодовые шкалы // Изв. вузов СССР. Приборостроение, 1987. Т. 30. №2. С. 40-43.
5. Макуильямс Ф.Д., Слоан Н.Д. Псевдослучайные последовательности и таблицы // ТИИЭР. 1976. Т. 64. №12. С. 80-95.
6. Блейхут Р. Теория и практика кодов, контролирующих ошибки: Пер. с англ. - М.: Мир, 1986. - 576 с.
7. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки: Пер. с англ. - М.: Мир, 1976. - 594 с.
8. Теория кодирования / Т. Касани, Н. Такура, Е. Ивадари, Я. Инагаки: Пер. с япон. - М.: Мир, 1978. - 576 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| Псевдослучайная кодовая шкала | 2019 |
|
RU2709666C1 |
| Псевдослучайная кодовая шкала | 2021 |
|
RU2761058C1 |
| Псевдослучайная кодовая шкала | 2022 |
|
RU2777832C1 |
| ПСЕВДОСЛУЧАЙНАЯ КОДОВАЯ ШКАЛА | 2012 |
|
RU2510572C1 |
| ПРЕОБРАЗОВАТЕЛЬ УГОЛ-КОД | 2013 |
|
RU2530336C1 |
| КОДОВАЯ ШКАЛА | 2014 |
|
RU2560782C1 |
| РЕКУРСИВНАЯ КОДОВАЯ ШКАЛА | 2010 |
|
RU2434323C1 |
| РЕКУРСИВНАЯ КОДОВАЯ ШКАЛА | 2011 |
|
RU2446557C1 |
| РЕКУРСИВНАЯ КОДОВАЯ ШКАЛА | 2010 |
|
RU2444126C1 |
| Кодовая шкала | 2015 |
|
RU2612622C1 |
Изобретение относится к измерительной технике, в частности к аналого-цифровому преобразованию, а именно к кодовым шкалам преобразователей угла поворота вала в код. Техническим результатом является повышение информационной надежности псевдослучайной кодовой шкалы за счет формирования с нее корректирующего кода с исправлением двойных ошибок. Устройство содержит информационную дорожку, выполненную в виде градаций псевдослучайной двоичной последовательности максимальной длины периода М=2n-1, построенной посредством примитивного многочлена h(x) степени n, где n - разрядность шкалы, n информационных и k+1 корректирующих считывающих элементов, размещенных вдоль информационной дорожки с угловыми шагами, кратными величине кванта шкалы δ=360°/М, с возможностью получения с них М различных (n+k+1) - разрядных кодовых комбинаций, представляющих собой корректирующий код с исправлением одиночной и обнаружением двойной ошибки, kд дополнительных корректирующих считывающих элементов, размещенных вдоль информационной дорожки с угловыми шагами, кратными величине кванта шкалы δ, с возможностью получения с них совместно с (n+k+1) считывающими элементами М различных (n+k+kд+1) - разрядных кодовых комбинаций, представляющих собой корректирующий код с исправлением двойной ошибки, выходы считывающих элементов являются выходами псевдослучайной кодовой шкалы. 1 ил., 3 табл.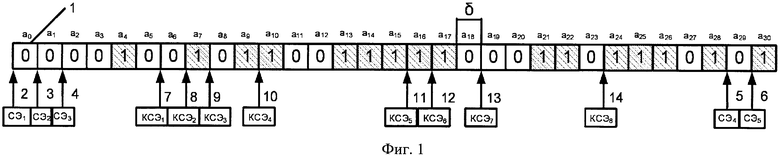
Псевдослучайная кодовая шкала, содержащая информационную дорожку, выполненную в виде градаций псевдослучайной двоичной последовательности максимальной длины периода М=2n-1, построенной посредством примитивного многочлена h(x) степени n, где n - разрядность шкалы, n информационных и k+1 корректирующих считывающих элементов, размещенных вдоль информационной дорожки с угловыми шагами, кратными величине кванта шкалы δ=360°/М, с возможностью получения с них М различных (n+k+1)-разрядных кодовых комбинаций, представляющих собой корректирующий код с исправлением одиночной и обнаружением двойной ошибки, отличающаяся тем, что псевдослучайная кодовая шкала снабжена kд дополнительными корректирующими считывающими элементами, размещенными вдоль информационной дорожки с угловыми шагами, кратными величине кванта шкалы δ, с возможностью получения с них совместно с (n+k+1) считывающими элементами М различных (n+k+kд+1)-разрядных кодовых комбинаций, представляющих собой корректирующий код с исправлением двойной ошибки, выходы считывающих элементов являются выходами псевдослучайной кодовой шкалы.
| ПСЕВДОСЛУЧАЙНАЯ КОДОВАЯ ШКАЛА | 2012 |
|
RU2510572C1 |
| РЕКУРСИВНАЯ КОДОВАЯ ШКАЛА | 2010 |
|
RU2434323C1 |
| РЕКУРСИВНАЯ КОДОВАЯ ШКАЛА | 2010 |
|
RU2444126C1 |
| Преобразователь перемещения в код системы остаточных классов | 1984 |
|
SU1259487A1 |
| US 2006249665 A1, 09.11.2006 | |||
| US 5900930 A, 04.05.1999 | |||
| US 4342025 A, 27.07.1982. | |||
Авторы
Даты
2018-07-06—Публикация
2017-03-10—Подача