Изобретение относится к наглядным учебным пособиям по физике. Оно может быть использовано в учебном процессе при изучении нелинейных процессов и, в частности, нелинейных колебательных движений. В данном случае для исследования зависимости порога устойчивости перевернутого маятника от частоты колебаний его опоры, а также для демонстрации явления параметрического резонанса.
Жесткий маятник, подвес которого совершает принудительные колебания в вертикальном направлении, в зависимости от частоты и амплитуды вынужденных колебаний точки подвеса, может совершать большое число разнообразных видов движения. Некоторые движения этой простой механической системы оказываются неожиданно сложными. Поведение такого маятника интенсивно изучается. Он вызывает неослабевающий интерес не только как пробный камень новых методов исследования нелинейных систем, но и потому, что дифференциальное уравнение маятника часто встречается в самых разных проблемах современной физики. Механические аналоги различных нелинейных физических систем допускают непосредственную визуализацию их временной динамики, что очень полезно для понимания специфики поведения сложных систем.
Известно техническое решение [H.J.T. Smith, J.A. Blackburn, «Experimental study of an inverted pendulum», American Journal of Physics, 60, 909 (1992)], реализующее демонстрацию поведения перевернутого маятника Капицы. Колебания опоры математического маятника производится с частотой, обеспечивающей устойчивое положение равновесия маятника в перевернутом положении. Недостатками данного устройства являются:
- жесткая связь опоры маятника с грузом математического маятника, что мешает наглядности эксперимента и приводит к неточности определения параметров колебаний;
- при воздействии вибрации опорной точки, необходимой для обеспечения устойчивости в перевернутом положении, в стержне возникает переменное напряжение больше чем в L/a, раз превосходящее по величине напряжение вызванное силой тяжести груза на конце стержня, где L-длина стержня маятника, а - амплитуда колебаний подвеса. Такая сила вызовет продольный изгиб в стержне, который вблизи резонансных частот создаст поперечные колебания стержня с амплитудой, переходящей за допустимые пределы. Это приведет к нарушению устойчивого равновесия перевернутого маятника. [П.Л. Капица, «Маятник с вибрирующим подвесом», Успехи физических наук, 44, 7-20 (1951)].
Существует прибор [М. М. Michaelis «Stroboscopic study of the inverted pendulum», American Journal of Physics 53, 1079 (1985)], также демонстрирующий движение перевернутого маятника. Реализацию перевернутого маятника достигают путем замены лезвия электролобзика на две связанные между собой алюминиевые пластины - короткую и длинную. Короткая одним концом устанавливается жестко в паз лезвия, а длинная крепится ко второму концу короткой так, чтобы она могла свободно вращаться относительно их общей оси, она и выполняет роль маятника Капицы длиной L (длина длинной пластины).
Недостатками данного устройства являются:
- меньшая наглядность физического маятника по сравнению с математическим; - в данной демонстрации не видна зависимость устойчивости маятника от значения частоты;
- крепеж маятника и возникающие напряжения в пластинах вносят ошибки в параметры колебаний.
Известно также [HARVARD UNIVERSITY, Harvard Natural Sciences Lectures Demonstrations, - https://sciencedemonstrations.fas.harvard.edu/presentations/inverted-pendulum»] устройство того же назначения. В Гарвардском университете для демонстрации нелинейных колебаний используют физический маятник в виде однородной полосы, жестко закрепленной перпендикулярно наружной поверхности внешнего кольца подшипниковой опоры, выполненной с возможностью вращения подшипниковой опоры вокруг оси вертикально вибрирующей опоры маятника с изменением ориентации полосы в вертикальной плоскости. Вибрацию опоры маятника в вертикальном положении осуществляют с помощью электролобзика. Сначала поднимают маятник и включают вибрацию высокой частоты. Показывают устойчивость перевернутого маятника путем нажатия на него рукой. Потом осуществляют вибрацию на низкой частоте, при этом амплитуда колебаний резко увеличивается и при приложении небольшой силы маятник падает и продолжает качаться возле нижнего положения равновесия.
Недостатками указанного устройства являются:
- использование физического маятника, что менее наглядно, чем математический маятник;
- жесткая связь маятника с опорой снижает точность определения параметров колебаний маятника;
- не показана зависимость устойчивого равновесия от частоты колебаний опорной точки.
Целью настоящего изобретения являлась разработка способов демонстрации и исследования движения математического маятника при продольных колебаниях его подвеса и устройства для их осуществления, которые позволяли бы наглядно изучать процессы нелинейного колебательного движения математического маятника при его различном положении в пространстве.
Техническая задача - создание устройства, обеспечивающего возможность движения груза математического маятника под действием силы тяжести в условиях отсутствии жесткой связи груза с подвесом при различном положении подвеса в пространстве, с возможностью наблюдения изменения амплитуды и частоты нелинейного колебательного движения груза при изменении частоты и амплитуды механических продольных колебаний его подвеса, при визуально различимом изменении параметров движения груза от положения устойчивого равновесия в верхней точке до положения устойчивого равновесия груза в нижней точке, с фиксацией величины амплитуды его колебаний.
Ожидаемым техническим результатом являлась возможность наблюдения нелинейных колебаний груза математического маятника в зависимости от частоты и амплитуды продольных колебаний его подвеса, с определением частоты, соответствующей как явлению параметрического резонанса, так и порогу устойчивости перевернутого положения маятника.
Поставленная задача была решена созданием устройства согласно изобретению для демонстрации и исследования движения математического маятника при продольных колебаниях его подвеса, содержащее маятник в виде груза на нерастяжимом подвесе, соединенном с источником его продольных механических колебаний, отличающегося тем, что содержит:
- тороид, выполненный вращением образующей окружности вокруг оси тороида, лежащей в плоскости этой окружности и не пересекающей ее, в виде полого кольца из твердого оптически прозрачного материала, имеющего в паре с металлическим материалом низкий коэффициент трения покоя;
- груз в виде металлического шара, помещенного во внутреннюю полость указанного полого кольца тороида с минимальным зазором, обеспечивающим возможность свободного перемещения груза внутри кольца;
- две внешние к тороиду опоры, жестко закрепленные на наружной поверхности двух диаметрально противолежащих участков тороида и имеющие оси поворота опор, соосные между собой в вертикальной плоскости, проходящей через центр тороида перпендикулярно оси тороида, и обеспечивающие возможности синхронного возвратно-поступательного движения опор вверх-вниз при вертикальном положении кольца тороида и поворота тороида с опорами вокруг указанных осей на угол 360°;
- источник механических колебаний, соединенный с указанными двумя опорами с возможностью обеспечения колебаний тороида в вертикальной плоскости с заданной амплитудой и частотой, и при этом:
- тороид на его наружной поверхности снабжен кольцевой шкалой для визуального наблюдения угла отклонения груза от положения его устойчивого равновесия в верхней и в нижней точках кольца тороида;
- функцию виртуального нерастяжимого подвеса выполняет радиус движения груза внутри кольца тороида относительно центра тороида.
При этом согласно изобретению целесообразно, чтобы кольцо тороида было выполнено из стекла, а кольцевая шкала была тарирована в единицах, позволяющих измерять соответствующую амплитуду отклонений груза относительно нижней и верхней точек его устойчивого равновесия в кольце тороида.
Поставленная задача была решена также созданием способа демонстрации и исследования движения математического маятника в условиях земного тяготения при продольных колебаниях его подвеса, в котором груз на подвесе подвергают воздействию механических колебаний, отличающегося тем, что с помощью указанного выше устройства согласно изобретению, в условиях наблюдения визуально различимого положения груза, связанного с нерастяжимым виртуальным подвесом, производят следующие манипуляции:
- обеспечивают механические колебания подвеса с грузом в вертикальной плоскости на различной частоте, приводящей сначала груз в положение его устойчивого равновесия в нижней точке кольца тороида, а затем частоту колебаний увеличивают до достижения частоты, при которой происходит резкое увеличение амплитуды колебаний груза в кольце, что свидетельствует о наступлении параметрического резонанса маятника, и последующее падение величины амплитуды груза, что свидетельствует о выходе маятника из состояния параметрического резонанса;
- при достижении частоты продольных колебаний тороида Ω, определяемой по формуле
Ω>(2gR)1/2/A,
где:
g - ускорение свободного падения, м/сек2;
R - заданная длина виртуального подвеса, м, равная радиусу движения груза внутри кольца тороида относительно центра тороида: R=r1+r2, где r1 - внутренний радиус кольца тороида, м, r2 - радиус груза, м;
А - заданная амплитуда продольных колебаний тороида в вертикальной плоскости, м, и при этом величина 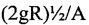 является расчетной для заданных размеров тороида, груза и заданных величин амплитуды колебаний тороида, маятник, переводят из нижнего положения в перевернутое положение путем поворота тороида с опорами на осях опор на 180°, и затем поддерживают указанную выше частоту механических колебаний в течение времени наблюдения колебания груза при устойчивом равновесии маятника в перевернутом положении;
является расчетной для заданных размеров тороида, груза и заданных величин амплитуды колебаний тороида, маятник, переводят из нижнего положения в перевернутое положение путем поворота тороида с опорами на осях опор на 180°, и затем поддерживают указанную выше частоту механических колебаний в течение времени наблюдения колебания груза при устойчивом равновесии маятника в перевернутом положении;
- плавно уменьшают частоту механических колебаний, фиксируя частоту и амплитуду колебаний груза при самопроизвольной потере его положения устойчивого равновесия в перевернутом положении маятника с падением в его нижнее положение в кольце тороида, и фиксируют частоту 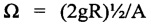 , при которой положение устойчивого равновесия груза возникает в нижней точке тороида.
, при которой положение устойчивого равновесия груза возникает в нижней точке тороида.
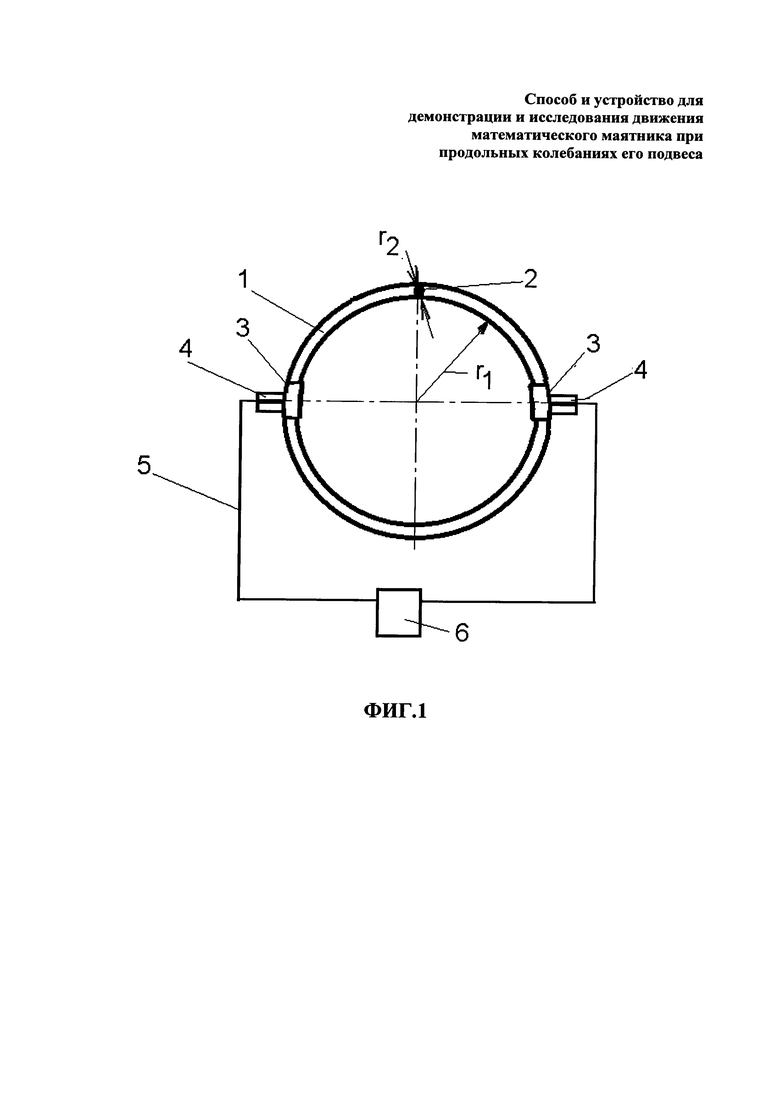
В дальнейшем изобретение поясняется примерами осуществления способа демонстрации и исследования движения математического маятника при продольных колебаниях его подвеса согласно изобретению, что реализовано в устройстве для демонстрации и исследования движения математического маятника в условиях земного тяготения при продольных колебаниях его подвеса, которое поясняется прилагаемым чертежом Фиг. 1, на котором представлен вид спереди схемы устройства согласно изобретению. При этом приведенные примеры осуществления способа согласно изобретению и устройства согласно изобретению не являются исчерпывающими, не выходят за рамки формулы изобретения и не ограничивают возможности реализации изобретения.
Устройство, содержит маятник в виде груза с подвесом, соединенным с источником его продольных механических колебаний. Устройство содержит подвес в форме тороида 1, выполненного вращением образующей окружности вокруг оси тороида, лежащей в плоскости этой окружности и не пересекающей ее, в виде полого кольца из твердого оптически прозрачного материала, имеющего в паре с металлическим материалом низкий коэффициент трения покоя. Груз выполнен в виде металлического шарика 2, помещенного во внутреннюю полость указанного полого кольца тороида 1 с возможностью его свободного перемещения в кольце. Две опоры 3, жестко закрепленные на наружной поверхности двух диаметрально противолежащих участков тороида 1 и имеющие оси поворота опор, например, с помощью подшипниковых опор 4, соосные между собой в горизонтальной плоскости, проходящей через ось вращения тороида 1 при вертикальном положении кольца тороида, и обеспечивающие возможность поворота тороида на осях указанных опор на угол 360°. Указанные опоры 4 соединены стержнями 5 с источником механических колебаний 6, с возможностью обеспечения возвратно-поступательного движения опор в вертикальной плоскости вверх-вниз при положении тороида в вертикальной плоскости. При этом кольцо тороида на его наружной поверхности снабжено кольцевой угловой шкалой, приспособленной для визуальной фиксации положения груза внутри кольца при механических колебаниях тороида.
Таким образом, устройство согласно изобретению для демонстрации и исследования движения математического маятника в условиях земного тяготения при продольных колебаниях его подвеса представляло собой устройство для воплощения классического нелинейного математического маятника в стандартном и перевернутом положениях, являющееся альтернативой конструкции маятника Капицы и позволяющее наглядно демонстрировать эффект параметрического резонанса и экспериментально исследовать параметры устойчивости маятника в перевернутом положении по критерию его устойчивости.
Согласно изобретению, способ демонстрации и исследования движения математического маятника в условиях земного тяготения при продольных колебаниях его подвеса был реализован с помощью описанного выше устройства, согласно изобретению, в условиях наблюдения визуально различимого положения груза 2 во внутренней полости тороида 1, и при этом тороид 1, содержащий размещенный в нем груз 2 и установленный в опорах 3 и 4 в вертикальном положении, подвергали воздействию механических колебаний в вертикальной плоскости с различной частотой и амплитудой с использованием генератора механических колебаний и производят описанные ниже манипуляции:
- обеспечивают механические колебания подвеса с грузом в вертикальной плоскости на различной частоте, приводящей сначала груз в положение его устойчивого равновесия в нижней точке кольца тороида, а затем частоту колебаний увеличивают до достижения частоты, при которой происходит резкое увеличение амплитуды колебаний груза в кольце, что свидетельствует о наступлении параметрического резонанса маятника, и последующее падение величины амплитуды груза, что свидетельствует о выходе маятника из состояния параметрического резонанса;
- при достижении частоты продольных колебаний тороида Ω, определяемой по формуле
Ω>(2gR)1/2/A,
где:
g - ускорение свободного падения, м/сек2;
R - заданная длина виртуального подвеса, м, равная радиусу движения груза внутри кольца тороида относительно центра тороида: R=r1+r2, где r1 - внутренний радиус кольца тороида, м, r2 - радиус груза, м;
А - заданная амплитуда продольных колебаний тороида в вертикальной плоскости, м, и при этом величина 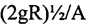 является расчетной для заданных размеров тороида, груза и заданных величин амплитуды колебаний тороида, маятник, переводят из нижнего положения в перевернутое положение путем поворота тороида с опорами на осях опор на 180°, и затем поддерживают указанную выше частоту механических колебаний в течение времени наблюдения колебания груза при устойчивом равновесии маятника в перевернутом положении;
является расчетной для заданных размеров тороида, груза и заданных величин амплитуды колебаний тороида, маятник, переводят из нижнего положения в перевернутое положение путем поворота тороида с опорами на осях опор на 180°, и затем поддерживают указанную выше частоту механических колебаний в течение времени наблюдения колебания груза при устойчивом равновесии маятника в перевернутом положении;
- плавно уменьшают частоту механических колебаний, фиксируя частоту и амплитуду колебаний груза при самопроизвольной потере его положения устойчивого равновесия в перевернутом положении маятника с падением в его нижнее положение в кольце тороида, и фиксируют частоту 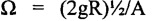 , при которых положение устойчивого равновесия груза возникает в нижней точке тороида.
, при которых положение устойчивого равновесия груза возникает в нижней точке тороида.
После проведения демонстрации нелинейных колебаний математического маятника в его различных положениях и получения результатов фиксации значений частоты и амплитуды колебаний груза маятника при заданных значениях частоты и амплитуды колебаний его подвеса было признано целесообразным сопоставить эти результаты с теоретическими выкладками о параметрах движения математического маятника и условий устойчивого равновесия в перевернутом положении.
В настоящем изобретении предложен способ и устройство для демонстрации и исследования движения математического маятника, представляющее собой воплощение классической системы нелинейного математического маятника для стандартного и перевернутого положений, являющееся альтернативой конструкции маятника Капицы и позволяющее наглядно демонстрировать эффект параметрического резонанса и экспериментально исследовать параметры устойчивости маятника по критерию устойчивости. Известно, что в простейшем случае критерий устойчивого равновесия в верхнем положении выражается в виде неравенства, в которое входят длина математического маятника - L, частота вертикальных вибраций точки подвеса - Ω, амплитуда вибраций - А и, наконец, ускорение свободного падения - g, а именно,

Наш вариант классической нелинейной системы позволит непосредственно наблюдать, как изменение частоты Ω, при постоянной амплитуде А нарушает критерий (1), лишая маятник устойчивого «перевернутого» положения равновесия. Рассмотрим гладкую изнутри тороидальную трубку, по которой может без трения скользить тяжелый шарик. Пусть диаметр шарика r2 чуть меньше внутреннего диаметра трубки и одновременно много меньше внутреннего радиуса тороида r2. Тогда длина виртуального подвеса R=r1+r2. В исходном состоянии трубка строго вертикальна. Введем прямоугольную систему координат OXYZ, ее начало совпадает с центром трубки, ось ОХ направлена вертикально вниз, ось OY горизонтальна и направлена направо, а ось OZ - горизонтальна и направлена на нас. Тогда положение шарика, находящегося внутри трубки, будет характеризоваться двумя его координатами x(t) и y(t), которые при неподвижном центре трубки связаны соотношением X2+Y2=R2.
Пусть плоскость трубки совпадает с вертикальной плоскостью OXY, а ее центр движется по вертикали по закону X(t)=AcosΩt. Положение шарика относительно трубки будем характеризовать углом поворота θ(t) радиуса трубки, проведенного из ее центра в точку мгновенного нахождения шарика относительно вертикальной оси ОХ. Координаты шарика относительно неподвижной системы координат получим тогда в виде
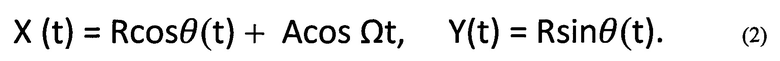
Уравнение движения шарика запишем относительно неинерциальной системы отсчета, связанной с вертикально колеблющейся с большой частотой трубкой. Тогда помимо сил давления со стороны стенок трубки, направленных в центр трубки, и вертикально направленной силы тяжести на него «будет действовать» еще и сила инерции, направленная вертикально и равная
mAΩ2cosΩt,
где m - масса шарика.
Уравнение моментов, записанное относительно оси, связанной с центром трубки и параллельной оси OZ, получим в виде
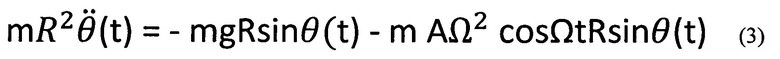
или после сокращения левой и правой части уравнения (3) на mR2
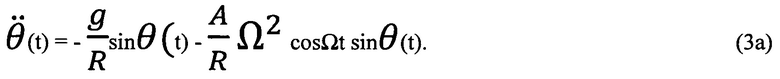
Решение нелинейного уравнения (3а), являющегося обобщением уравнения математического маятника, будем искать, следуя подходу Капицы. Поскольку уравнение (3а), - уравнение Матье, не имеет точного решения в общепринятом смысле, получим его приближенное решение, руководствуясь характерными физическими особенностями системы и ограничениями, наложенными на ее движение. Первое важное ограничение движения состоит в том, что по условию задачи выполняется неравенство A«R, поэтому впоследствии ограничимся в уравнении лишь главными вкладами по этому отношению. Кроме того, будем искать общее решение системы (3а) в виде суперпозиции двух независимых, характеризуемых принципиально различными масштабами временных изменений движений, - «быстрого», определяемого большой частоте Ω вибраций-колебаний центра трубки, и «медленного», на фоне которого и происходит «быстрое», но существенно меньшей амплитуды.
С учетом сказанного решение уравнения (3а) представим в виде
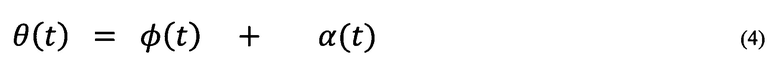
где 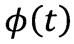 - «медленная» и α(t) - «быстрая» составляющие общего движения системы.
- «медленная» и α(t) - «быстрая» составляющие общего движения системы.
Тогда, очевидно,
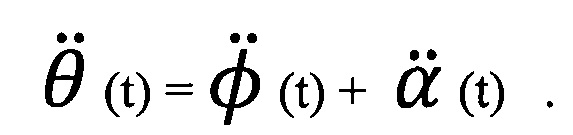
Представим далее величину α (t) в виде
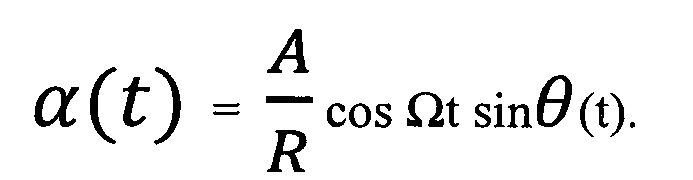
Тогда в рамках используемого приближения
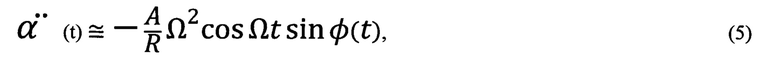
т.е. «быстрые» колебания малой амплитуды происходят на фоне временной квази - статичности «медленной» величины 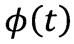 (вклад которой в θ(t) является определяющим).
(вклад которой в θ(t) является определяющим).
Очевидно,
sinθ(t)=sin[ϕ(t)+α(t)]=sinϕ cosα+cosϕ sinα.
Учитывая малость отношения 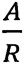 , используем известные разложения
, используем известные разложения 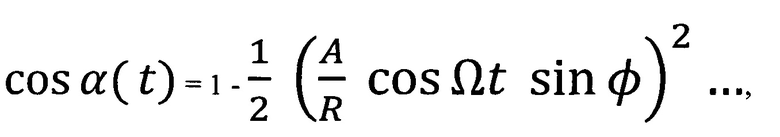 и
и 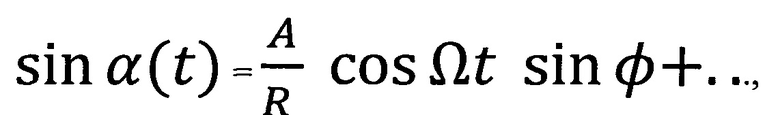
где в том же приближении мы произвели замену аргументов θ на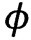 .
.
Таким образом, ограничиваясь основным (линейным) по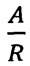 приближением, получим
приближением, получим
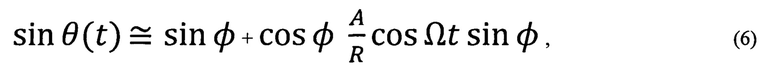
Уравнение (3а) преобразуем к виду
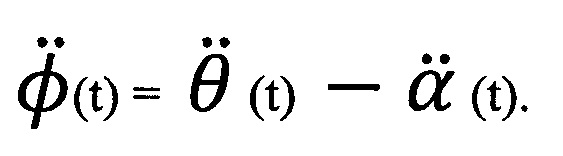
Используя уравнения (3а), (5) и (6), получим
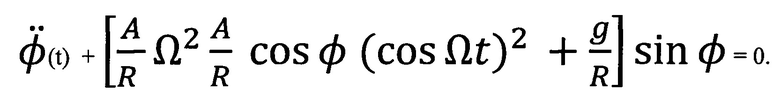
Усредняя, наконец, выражение в квадратной скобке по периоду быстрых колебаний-вибраций, получим дифференциальное уравнение для «медленной» составляющей общего движения 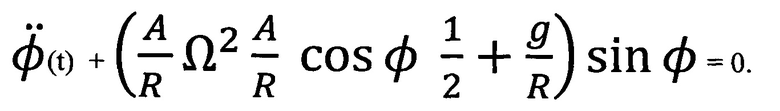
Если теперь определить стандартным образом эффективную потенциальную энергию 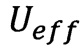 ,отвечающую величине
,отвечающую величине 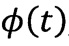 , при помощи соотношения
, при помощи соотношения
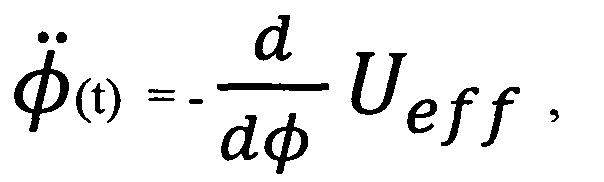
то эффективная потенциальная энергия 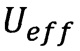 (зависящая от
(зависящая от 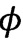 часть) примет вид
часть) примет вид
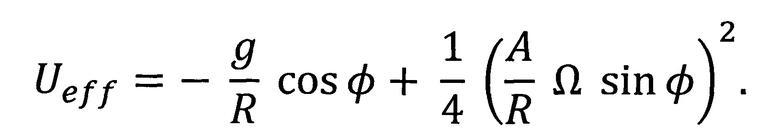
Дифференцируя эффективную потенциальную энергию 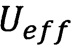 по
по 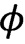 , получим три равновесных положения системы
, получим три равновесных положения системы 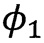 ,
, 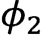 и
и 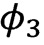 (отсчитываемой по или против часовой стрелки)
(отсчитываемой по или против часовой стрелки)
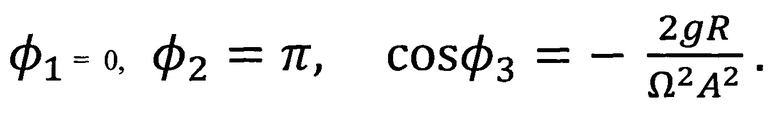
Очевидно, третье соотношение имеет смысл тогда, когда задающие движение системы параметры удовлетворяют неравенству

Дифференцируя функцию 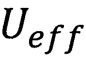 дважды по величине
дважды по величине 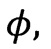
получим, что решение 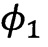 - 0 устойчиво всегда, решение
- 0 устойчиво всегда, решение 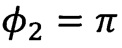 будет устойчивым только при выполнении неравенства (7), решение
будет устойчивым только при выполнении неравенства (7), решение 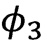 всегда неустойчиво.
всегда неустойчиво.
Таким образом, при выполнении условия (7) возникает устойчивое равновесие перевернутого маятника.
Тем самым, в настоящем изобретении предложена конструкция маятника, являющаяся альтернативной конструкции общепринятого маятника Капицы. Данная конструкция обладает несомненным преимуществом перед классической конструкцией, так как не имеет жесткого крепления груза маятника и точки подвеса, что исключает появление неконтролируемых напряжений изгиба, существенно влияющих на характер движения маятника, что особенно существенно при больших частотах колебаний подвеса.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ и устройство для демонстрации и исследования движения ансамбля математических маятников при продольных колебаниях его подвеса | 2017 |
|
RU2658788C1 |
| Устройство для изучения вращательного движения неголономных систем | 2018 |
|
RU2704359C1 |
| СПОСОБ МОДЕЛИРОВАНИЯ ПАРАМЕТРИЧЕСКИХ КОЛЕБАНИЙ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ (ВАРИАНТЫ) | 2020 |
|
RU2748870C1 |
| СПОСОБ РЕГУЛИРОВАНИЯ ЖЕСТКОСТИ ВИБРОЗАЩИТНОЙ СИСТЕМЫ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2011 |
|
RU2475658C2 |
| Учебный прибор по механике | 1990 |
|
SU1774370A1 |
| Способ возбуждения колебаний и устройство для его осуществления | 2015 |
|
RU2669163C2 |
| Способ определения собственных частот колебаний механической системы с помощью вращающегося маятника | 2015 |
|
RU2647513C2 |
| СПОСОБ ПЛАНИРУЮЩЕГО ПОЛЕТА И ЛЕТАТЕЛЬНЫЙ АППАРАТ ДЛЯ ОСУЩЕСТВЛЕНИЯ СПОСОБА | 2008 |
|
RU2397109C2 |
| УСТРОЙСТВО ДЛЯ ИЗУЧЕНИЯ ЗАКОНОВ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ | 2006 |
|
RU2309462C1 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ПРИСОЕДИНЕННЫХ МАСС, МОМЕНТОВ ИНЕРЦИИ И ДЕМПФИРОВАНИЯ МОДЕЛЕЙ СУДОВ МЕТОДАМИ ИХ СВОБОДНЫХ КОЛЕБАНИЙ В ЖИДКОСТИ | 2009 |
|
RU2425343C1 |
Предложено устройство для демонстрации и исследования движения математического маятника при продольных колебаниях его подвеса, содержащее маятник в виде груза с подвесом, соединенным с источником его продольных механических колебаний. Подвес в форме тороида, выполненного вращением образующей окружности вокруг оси тороида, лежащей в плоскости этой окружности и не пересекающей ее, в виде полого кольца из твердого оптически прозрачного материала, имеющего в паре с металлическим материалом низкий коэффициент трения. Груз выполнен в виде металлического шарика, помещенного во внутреннюю полость указанного полого кольца тороида и свободно перемещающегося в кольце. Две опоры, жестко закрепленные на наружной поверхности двух диаметрально противолежащих участков тороида и имеющие оси поворота опор, соосные между собой в горизонтальной плоскости, проходящей через ось вращения тороида при вертикальном положении кольца тороида, и обеспечивающие возможность поворота тороида на осях указанных опор на угол 360°. Источник механических колебаний, соединенный с указанными опорами, имеет возможность обеспечивать возвратно-поступательное движение опор в вертикальной плоскости вверх-вниз при ориентации тороида в вертикальной плоскости. При использовании представленного маятника предложены способы исследования зависимости порога устойчивости перевернутого маятника от частоты колебаний его опоры, а также для демонстрации явления параметрического резонанса. 2 н. и 1 з.п. ф-лы, 1 ил.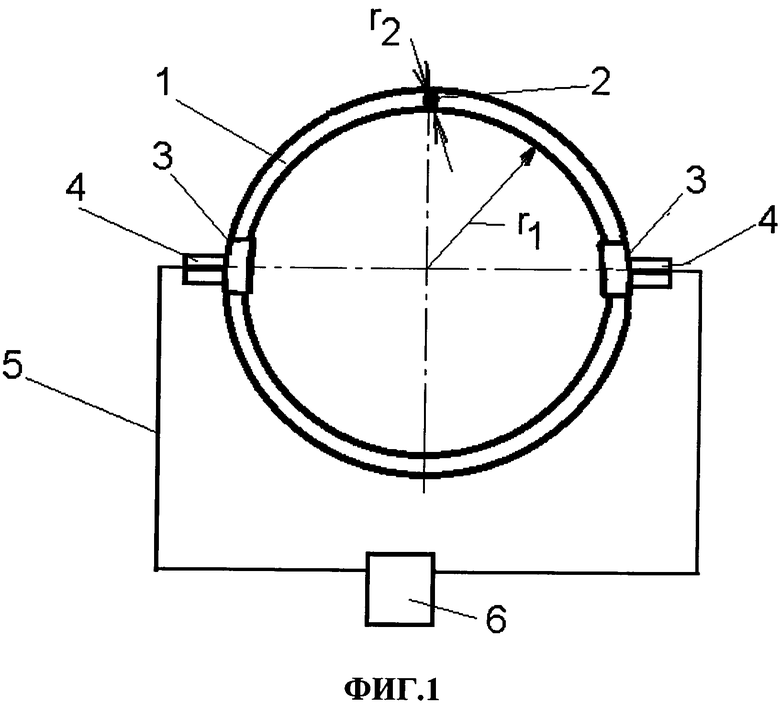
1. Устройство для демонстрации и исследования параметров движения математического маятника при продольных колебаниях его подвеса, содержащее маятник в виде груза с подвесом, соединенным с источником его продольных механических колебаний, отличающееся тем, что содержит:
- подвес в форме тороида, выполненного вращением образующей окружности вокруг оси тороида, лежащей в плоскости этой окружности и не пересекающей ее, в виде полого кольца из твердого оптически прозрачного материала, имеющего в паре с металлическим материалом низкий коэффициент трения покоя;
- груз в виде металлического шара, помещенный во внутреннюю полость указанного полого кольца тороида с возможностью его свободного перемещения в кольце;
- две опоры, жестко закрепленные на наружной поверхности двух диаметрально противолежащих участках тороида и имеющие оси поворота опор, соосные между собой в горизонтальной плоскости, проходящей через ось вращения тороида при вертикальном положении кольца тороида, и обеспечивающие возможность поворота тороида на осях указанных опор на угол 360°;
- источник механических колебаний, соединенный с указанными опорами с возможностью обеспечения возвратно-поступательного движения опор в вертикальной плоскости вверх-вниз при положении тороида в вертикальной плоскости,
и при этом:
- тороид на его наружной поверхности снабжен кольцевой угловой шкалой для визуального наблюдения угла отклонения груза от положения его устойчивого равновесия в верхней и нижней точках кольца тороида;
- функцию виртуального нерастяжимого подвеса выполняет радиус движения груза внутри кольца тороида относительно центра тороида, равный сумме внутреннего радиуса, тороида и радиуса груза.
2. Устройство по п. 1, отличающееся тем, что указанное кольцо тороида выполнено из стекла.
3. Способ демонстрации и исследования параметров движения математического маятника при продольных колебаниях его подвеса, в котором груз на подвесе подвергают воздействию механических колебаний, отличающийся тем, что с помощью устройства по любому из пп. 1, 2 в условиях наблюдения визуально различимого положения груза, связанного с нерастяжимым виртуальным подвесом, производят следующие манипуляции:
- обеспечивают механические колебания подвеса с грузом в вертикальной плоскости на различной частоте, приводящей сначала груз в положение его устойчивого равновесия в нижней точке кольца тороида, а затем частоту колебаний увеличивают до достижения частоты, при которой происходит резкое увеличение амплитуды колебаний груза в кольце, что свидетельствует о наступлении параметрического резонанса маятника, и последующее падение величины амплитуды груза, что свидетельствует о выходе маятника из состояния параметрического резонанса;
- при достижении частоты продольных колебаний тороида Ω, определяемой по формуле
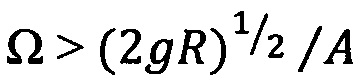 ,
,
где:
g - ускорение свободного падения, м/сек2;
R - заданная длина виртуального подвеса, м, равная радиусу движения груза внутри кольца тороида относительно центра тороида: R=r1+r2, где r1 - внутренний радиус кольца тороида, м, r2 - радиус груза, м;
А - заданная амплитуда продольных колебаний тороида в вертикальной плоскости, м,
и при этом величина 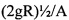 является расчетной для заданных размеров тороида, груза и заданных величин амплитуды колебаний тороида,
является расчетной для заданных размеров тороида, груза и заданных величин амплитуды колебаний тороида,
маятник переводят из нижнего положения в перевернутое положение путем поворота тороида с опорами на осях опор на 180° и затем поддерживают указанную выше частоту механических колебаний в течение времени наблюдения колебания груза при устойчивом равновесии маятника в перевернутом положении;
- плавно уменьшают частоту механических колебаний, фиксируя частоту и амплитуду колебаний груза при самопроизвольной потере его положения устойчивого равновесия в перевернутом положении маятника с падением в его нижнее положение в кольце тороида, и фиксируют частоту 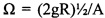 , при которой положение устойчивого равновесия груза возникает в нижней точке тороида.
, при которой положение устойчивого равновесия груза возникает в нижней точке тороида.
| УЧЕБНЫЙ ПРИБОР ПО ФИЗИКЕ | 1991 |
|
RU2017228C1 |
| ПРИБОР ДЛЯ ИЗУЧЕНИЯ ЗАКОНОВ МЕХАНИКИ | 2011 |
|
RU2473974C1 |
| УСТАНОВКА ДЛЯ ИССЛЕДОВАНИЯ НЕОДНОРОДНОГО МАГНИТНОГО ПОЛЯ | 2006 |
|
RU2321895C1 |
| Учебный прибор по физике В.А.Чернышева | 1985 |
|
SU1273976A1 |
| Учебная установка по физике | 1991 |
|
SU1831716A3 |
| JP 2004219676 A, 05.08.2004 | |||
| US 3424960 A1, 28.01.1969 | |||
| CN 101158613 A, 09.04.2008 | |||
| CN 201035796 Y, 12.03.2008 | |||
| Учебный прибор по математике | 1978 |
|
SU930340A1 |
Авторы
Даты
2018-08-15—Публикация
2017-07-17—Подача