Изобретение относится к вычислительной технике и предназначено для генерации идеальных троичных псевдослучайных последовательностей (ИТП), т.е. последовательностей с идеальной периодической автокорреляционной функцией (ПАКФ), применяемых для синхронизации, оценки и измерения параметров в системах фиксированной и мобильной связи, а также в радиолокации и навигации.
Практическое значение идеальных троичных последовательностей (ИТП) состоит в том, что они с успехом заменяют отсутствие идеальных двоичных последовательностей для длин N>4. Другим достоинством ИТП является то, что их длина N может быть сколько угодно большой. В этом они обладают преимуществом по сравнению с получившими широкое применение идеальными многофазными последовательностями Франка (Frank), Задова-Чу (Zadoff-Chu), Милевского (Milewski) и их различными модификациями, у которых объем алфавита с ростом их длины увеличивается. Платой за это является отличный от единицы пик-фактор передаваемого сигнала, а также энергетические потери при обработке в приемнике, обусловленные наличием нулей.
Заметим, что при передаче нули могут попеременно (через период) замещаться соответственно единицами или минус единицами, обеспечивая тем самым единичный пик-фактор. В этом случае для реализации нулевых боковых лепестков на выходе корреляционного приемника время интегрирования должно быть равным четному числу периодов последовательности.
В настоящее время известны различные семейства идеальных троичных последовательностей: KR 20160067992 (А) - 2016-06-14, GB 1518997 (А) - 1978-07-26, ЕР 0492325 (А2) - 1992-07-01, SU 1244658 (A1) - 1986-07-15, US 3414894 (A) - 1968-12-03, US 3264623 (A) - 1966-08-02, GB 792294 (A) - 1958-03-26, (Ипатов В.И. Периодические дискретные сигналы с оптимальными корреляционными свойствами. - М.: Радио и связь, 1992 и Fan P. and Darnell М. Sequence Design for Communications Applications. - RSP-John Wiley & Sons Inc., London, 1996). Наибольшее распространение получили семейства ИТП Ипатова длины (pmk-1)/(pm-1), p≥3, m≥1 и k≥3 - нечетно, ИТП Хохолдта-Джастесена (Hoholdt-Justesen) длины (2mk-1)/(2m-1), m≥1 и k≥3 - нечетно и составные (комбинированные) троичные последовательности, являющиеся посимвольным произведением двух ИТП с взаимно простыми длинами или произведением ИТП и идеальной двоичной последовательности 1 1 1 -1 длины 4. Помимо отличного от единицы пик-фактора другим недостатком этих ИТП является их разреженность на числовой оси с ростом длины. Поэтому актуальна задача нахождения новых идеальных троичных последовательностей с приемлемыми значениями пик-фактора.
Прототипом предлагаемого изобретения является устройство генерации периодической ИТП (Ипатов В.И. Периодические дискретные сигналы с оптимальными корреляционными свойствами. - М.: Радио и связь, 1992, Стр. 70 и Ипатов В.И. Широкополосные системы и кодовое разделение сигналов. Принципы и приложения. - М.: Техносфера. 2007, Стр. 279), состоящее из последовательно соединенных генератора q-ичной m-последовательности длины qk-1, q=pm, m≥1 и k≥3 - нечетно, блока преобразователя, выполняющего операцию преобразования входного ненулевого символа (ненулевого элемента поля GF(q)) в символ двузначного мультипликативного характера, значением которого есть -1 или 1, а нулевого символа (нулевого элемента поля GF(q)) соответственно в нуль, выход которого подключен к первому входу умножителя, второй вход которого подключен к выходу блока генератора меандра.
Блок схема устройства строится в соответствии с полученным В.П. Ипатовым выражением для общего члена этих последовательностей:
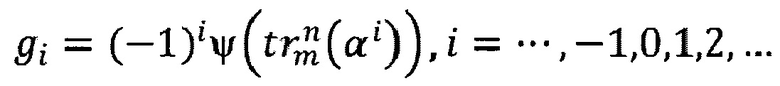
где 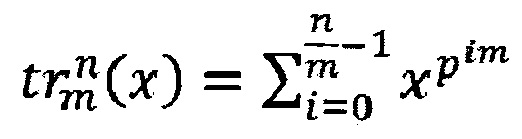 - след элемента x из поля Галуа GF(pn) относительно поля GF(pm), n=mk, m≥1 и k≥3 - нечетно, ψ - двузначный мультипликативный характер поля GF(pm), α - примитивный элемент поля GF(pn).
- след элемента x из поля Галуа GF(pn) относительно поля GF(pm), n=mk, m≥1 и k≥3 - нечетно, ψ - двузначный мультипликативный характер поля GF(pm), α - примитивный элемент поля GF(pn).
Напомним, что двузначным мультипликативным характером поля GF(q) является отображение мультипликативной группы GF*(q) основного поля (т.е. всех q-1 ненулевых элементов поля) на множество {-1, 1} вида 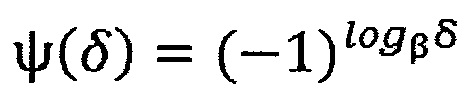 , δ ∈ GF(q), β - примитивный элемент поля GF(q). Очевидно, что logβδ принимает одно из значений 0, 1, 2, …, q-2. В случае ИТП Ипатова q=pm и мультипликативный характер для нулевого элемента поля δ=0 доопределен до нуля.
, δ ∈ GF(q), β - примитивный элемент поля GF(q). Очевидно, что logβδ принимает одно из значений 0, 1, 2, …, q-2. В случае ИТП Ипатова q=pm и мультипликативный характер для нулевого элемента поля δ=0 доопределен до нуля.
Принцип работы и блок-схема генератора q-ичной m-последовательности длины qk-1 подробно описаны в литературе и в частности в книгах (Ипатов В.И. Периодические дискретные сигналы с оптимальными корреляционными свойствами. - М.: Радио и связь, 1992 и Fan Р. и Darnell М. Sequence Design for Communications Applications. - RSP-John Wiley & Sons Inc., London, 1996, Golomb, S.W., Gong, G. Signal Design for Good Correlation. - for Wireless Communication, Cryptography and Radar. - Cambridge University Press, USA, 2005 и др.).
Преобразователь, в котором осуществляется вычисление двузначного мультипликативного характера элемента поля Галуа, можно реализовать с помощью различных устройств. В частности, для этой цели может быть использовано устройство непосредственного вычисления двузначного мультипликативного характера любого ненулевого элемента поля GF(q) (В.П. Ипатов, В.И. Корниевский, О.И. Корнилов, В.Д. Платонов. Устройство для определения двузначного характера элементов конечного поля, SU 1244658). Однако такая реализация требует значительные аппаратные и временные ресурсы. С другой стороны, конструкция преобразователя может быть существенно упрощена за счет использования заранее вычисленной таблицы отображения ненулевых pm элементов xj в один из символов {-1,0,1}, реализованной посредством постоянного запоминающего устройства (ПЗУ), как это предложено в работе (Ипатов В.И. Периодические дискретные сигналы с оптимальными корреляционными свойствами. - М.: Радио и связь, 1992).
Техническим результатом предлагаемого изобретения является генерация новых ИТП нечетной длины N1N2, где N1=(pmk-1)/(pm-1), m≥1, k≥3 - нечетно и 
Для этого предлагается генератор периодических идеальных троичных последовательностей, состоящий из последовательно соединенных генератора q-ичной m-последовательности длины qk-1, q=pm, m≥1 и k≥3 - нечетно и преобразователя, выполняющего операцию отображения выходного ненулевого q-ичного символа m-последовательности в символ двузначного мультипликативного характера, значением которого есть -1 или 1, а нулевого элемента этой последовательности соответственно в нуль, умножителя, первый вход которого подключен к выходу преобразователя, а второй вход подключен к выходу блока формирования сигнала меандра единичной амплитуды, отличающегося тем, что преобразователь состоит из последовательно соединенных формирователя адреса, вход которого является входом преобразователя, перепрограммируемого постоянного запоминающего устройства и кодопреобразователя, выход которого является выходом преобразователя, который осуществляет отображение символа q-ичной m-последовательности по правилу

где bi - q-ичный выходной символ генератора m-последовательности, i=…-1,0,1,2,…, zi=logβbi, bi≠0, β - примитивный элемент поля GF(q),  - последовательность, образованная из (pm-1)/N2 периодов идеальной троичной последовательности а длины N2, при этом преобразователь выполнен в виде последовательно соединенных формирователя адреса, преобразующего q-ичное число в
- последовательность, образованная из (pm-1)/N2 периодов идеальной троичной последовательности а длины N2, при этом преобразователь выполнен в виде последовательно соединенных формирователя адреса, преобразующего q-ичное число в 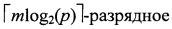 двоичное число (двоичный адрес), ППЗУ объема q×2, по адресам которого записана таблица соответствия символа bi∈GF(pm) двухразрядному двоичному числу, принимающему значение 10, если ƒ(bi)=1, значение 01, если ƒ(bi)=-1 и значение 00, если ƒ(bi)=0, и кодопреобразователя двухразрядного двоичного числа в символ троичного кода {-1,0,1}. Здесь
двоичное число (двоичный адрес), ППЗУ объема q×2, по адресам которого записана таблица соответствия символа bi∈GF(pm) двухразрядному двоичному числу, принимающему значение 10, если ƒ(bi)=1, значение 01, если ƒ(bi)=-1 и значение 00, если ƒ(bi)=0, и кодопреобразователя двухразрядного двоичного числа в символ троичного кода {-1,0,1}. Здесь 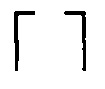 обозначает операцию округления числа к большему.
обозначает операцию округления числа к большему.
Предлагаемое изобретение основывается на методе построения ИТП нечетной длины N1N2, где N1=(pmk-1)/(pm-1),  описанном в работе (Е.И. Кренгель. Построение новых идеальных троичных последовательностей. - Сборник докладов 19-й международной конференции "Цифровая обработка сигналов и ее применение", 29-31 марта, 2017, Стр. 61-65). Запись
описанном в работе (Е.И. Кренгель. Построение новых идеальных троичных последовательностей. - Сборник докладов 19-й международной конференции "Цифровая обработка сигналов и ее применение", 29-31 марта, 2017, Стр. 61-65). Запись 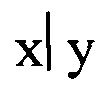 обозначает x делит y.
обозначает x делит y.
Пусть d есть p-ичная m-последовательность длины pmk-1 с элементами
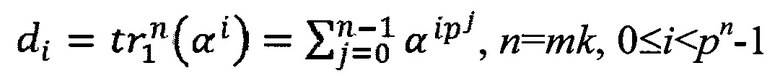
и b есть q-ичная m-последовательность длины pmk-1 с элементами
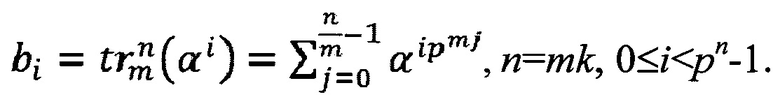
Рассмотрим матрицу декомпозиции последовательности d, состоящую из Т=(pn-1)/(pm-1) строк и pm-1 столбцов. Строками этой матрицы являются последовательности из всех нулей или циклические сдвиги некоторой короткой p-ичной m-последовательности длины pm-1. Значения этих сдвигов определяются последовательностью
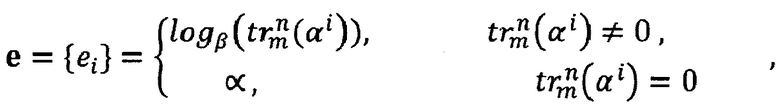
где 0≤i<T, а символ ∞ указывает на последовательность из всех нулей. В литературе (Games, R.A. Crosscorrelation of m-sequences and GMW sequences with the same primitive polynomial. - Discrete Applied Mathematics, 12, pp. 139-146, 1985) последовательность e получила название последовательности сдвигов.
Согласно (Е.И. Кренгель. Построение новых идеальных троичных последовательностей. - Сборник докладов 19-й международной конференции "Цифровая обработка сигналов и ее применение", 29-31 марта, 2017, Стр. 61-65) алгоритм построения новых ИТП длины N1N2 состоит из следующих шагов.
1. Для некоторой ИТП а нечетной длины N2, выбираем параметры р, m≥1, k≥3, где  и примитивный полином степени n=km над GF(p).
и примитивный полином степени n=km над GF(p).
2. Вычисляем последовательность сдвигов е длины N1=(pn-1)/(pm-1) p-ичной m-последовательности d длины pmk-1, соответствующей выбранному полиному.
3. Строим матрицу V порядка N1×N2, i - строка которой определяются как
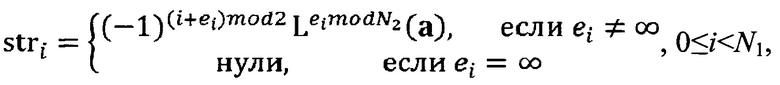
где Ls(а) - оператор циклического сдвига последовательности а влево на s разрядов.
4. Распаковываем матрицу V по столбцам в последовательность v, которая и является новой ИТП длины N1N2.
Анализ показывает, что если (N1,N2)=1, то длина новых ИТП совпадает с длиной составных ИТП. В противном случае, т.е. при (N1,N2)≠1, их длина может совпадать с длиной ИТП Ипатова или быть уникальной. Однако в любом случае полученные последовательности отличаются от известных ИТП, т.е. являются новыми. В этой связи необходимо отметить, что если последовательность a={1}, то последовательность v совпадает с ИТП Ипатова. Пик-фактор этих последовательностей равен произведению пик-факторов идеальной троичной последовательности длины N1 и идеальной троичной последовательности длины N2. Поскольку N1 существенно больше N2, то пик-фактор (и соответственно энергетические потери) новой последовательности будет главным образом определяться пик-фактором идеальной троичной последовательности длины N2.
Для генерации периодических ИТП поступим следующим образом. Образуем из (pm-1)/N2 периодов последовательности а последовательность 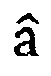 длины pm-1. Тогда с учетом того, что последовательность сдвигов {ei} по сути есть последовательность логарифмов Т первых элементов q-ичной m-последовательности b длины pn-1, а также bi+T=βbi, общий член полученной в соответствие с этим алгоритмом периодической троичной последовательности v', образованной из (pm-1)/N2 периодов ИТП v длины N1N2, может быть представлен как
длины pm-1. Тогда с учетом того, что последовательность сдвигов {ei} по сути есть последовательность логарифмов Т первых элементов q-ичной m-последовательности b длины pn-1, а также bi+T=βbi, общий член полученной в соответствие с этим алгоритмом периодической троичной последовательности v', образованной из (pm-1)/N2 периодов ИТП v длины N1N2, может быть представлен как
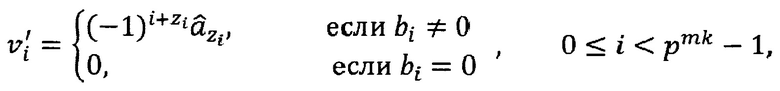
где zi=logβbi, bi≠0, причем zi=ei при всех 0≤i<Т.
Положим

Окончательно имеем  Вычисление f(bi) можно существенно упростить, если вместо таблицы логарифмов использовать таблицу, ставящую в соответствие символу bi∈GF(pm) двухразрядное двоичное число, принимающее значение 10, если ƒ(bi)=1, значение 01, если ƒ(bi)=-1 и значение 00, если ƒ(bi)=0.
Вычисление f(bi) можно существенно упростить, если вместо таблицы логарифмов использовать таблицу, ставящую в соответствие символу bi∈GF(pm) двухразрядное двоичное число, принимающее значение 10, если ƒ(bi)=1, значение 01, если ƒ(bi)=-1 и значение 00, если ƒ(bi)=0.
Известно, что элемент с поля GF(q), q=pm может быть представлен в виде суммы cm-1βm-1+cm-2βm-1+…c0, где ci∈GF(p), а β - примитивный элемент поля GF(pm). Поэтому любому элементу с из GF(pm) можно поставить в соответствии m-разрядное p-ичное число вида (cm-1, cm-2, … c0,). В двоичном виде это число состоит из 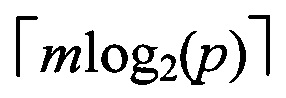 разрядов и соответственно равно (cm-1pm-1+cm-2pm-1+…с0)2. С учетом этого таблица отображения может быть реализована с помощью перепрограммируемого постоянного запоминающего устройства (ППЗУ) объемом pm×2, адресным входом в которые служит двоичное представление элемента с из GF(pm).
разрядов и соответственно равно (cm-1pm-1+cm-2pm-1+…с0)2. С учетом этого таблица отображения может быть реализована с помощью перепрограммируемого постоянного запоминающего устройства (ППЗУ) объемом pm×2, адресным входом в которые служит двоичное представление элемента с из GF(pm).
Наличие ППЗУ обусловлено возможностью смены генерируемой ИТП за счет выбора другой ИТП а без изменения вида m-последовательности. В результате блок преобразователя будет состоять из последовательно соединенных формирователя адреса, преобразующее m-разрядное p-ичное представление элемента поля GF(q) на выходе генератора q-ичной m-последовательности в 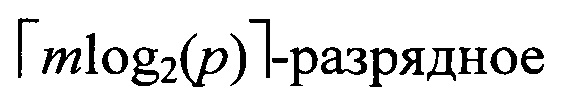 двоичное число, блока памяти объема q×2 и кодопреобразователя двухразрядного двоичного числа в символ троичного кода {-1,0,1}. Заметим, что в случае q=p адресом для ППЗУ является непосредственно значение символа с. Поэтому формирователь адреса в блоке преобразователя отсутствует.
двоичное число, блока памяти объема q×2 и кодопреобразователя двухразрядного двоичного числа в символ троичного кода {-1,0,1}. Заметим, что в случае q=p адресом для ППЗУ является непосредственно значение символа с. Поэтому формирователь адреса в блоке преобразователя отсутствует.
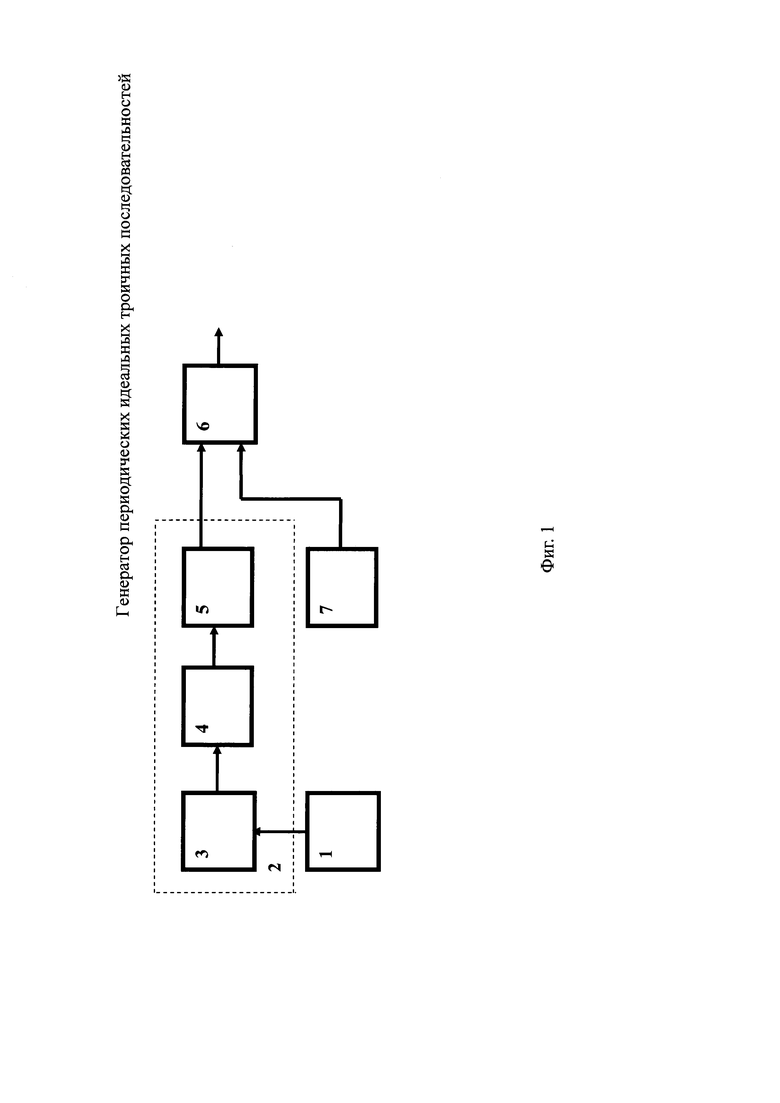
Блок-схема генератора периодических идеальных троичных последовательностей представлена на Фиг. 1. Генератор содержит последовательно соединенные генератор 1 q-ичной m-последовательности длины qk-1, q=pm, m≥1 и k≥3 - нечетно и преобразователь 2 q-ичного символа m-последовательности в символ троичного кода, состоящий из последовательно соединенных формирователя адреса 3, ППЗУ 4 и кодопреобразователя 5 двухразрядного двоичного кода в символ троичного кода, выход которого подключен к первому входу умножителя 6 и генератора меандра единичной амплитуды 7, выход которого подключен к второму входу умножителя 6.
Устройство работает следующим образом. Предварительно в регистр сдвига генератора 1, охваченного цепью линейной обратной связи по модулю q, записывается некоторое ненулевое k-разрядное q-ичное число. Обычно это единица. На вход генератора 1 поступают тактовые импульсы с частотой ƒt. На каждом такте информация в регистре сдвига сдвигается на разряд вправо, а в его самый младший q-ичный разряд записывается следующий q-ичный символ, являющийся выходным символом генератора 1. Этот символ bi в виде m-разрядного p-ичного числа поступает на вход формирователя адреса 3 преобразователя 2, формирующего из этого числа 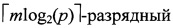 двоичный адрес. Из ППЗУ 4 по этому адресу считывается 2-х разрядное двоичное число со значением 10, если ƒ(bi)=1, значением 01, если ƒ(bi)=-1 и значением 00, если ƒ(bi)=0. С выхода ППЗУ 4 это двоичное число поступает на вход кодопреобразователя 5, в котором происходит преобразование двухразрядного двоичного числа в символ троичного кода {-1,0,1} по правилу: 10→1, 01→-1 и 00→0. Далее в умножителе 6 значение троичного символа перемножается с сигналом меандра, формируемого на выходе генератора меандра единичной амплитуды 7 периода ft/2. В результате на выходе умножителя 6 образуется новая периодическая ИТП. Следует подчеркнуть, что применение ППЗУ в схеме генератора идеальных троичных последовательностей позволяет реализовать смену генерируемой ИТП за счет смены последовательности а, определяющей содержимое ППЗУ.
двоичный адрес. Из ППЗУ 4 по этому адресу считывается 2-х разрядное двоичное число со значением 10, если ƒ(bi)=1, значением 01, если ƒ(bi)=-1 и значением 00, если ƒ(bi)=0. С выхода ППЗУ 4 это двоичное число поступает на вход кодопреобразователя 5, в котором происходит преобразование двухразрядного двоичного числа в символ троичного кода {-1,0,1} по правилу: 10→1, 01→-1 и 00→0. Далее в умножителе 6 значение троичного символа перемножается с сигналом меандра, формируемого на выходе генератора меандра единичной амплитуды 7 периода ft/2. В результате на выходе умножителя 6 образуется новая периодическая ИТП. Следует подчеркнуть, что применение ППЗУ в схеме генератора идеальных троичных последовательностей позволяет реализовать смену генерируемой ИТП за счет смены последовательности а, определяющей содержимое ППЗУ.
Предлагаемое изобретение может быть реализовано на соответствующей элементной базе по типовым технологиям. При этом существуют различные схемы реализации кодопреобразователя двухразрядного двоичного кода в символ троичного кода. В частности, для этого могут быть использованы цифро-аналоговый преобразователь (ЦАП) или вычитатель, выполненный на операционном усилителе (ОУ).
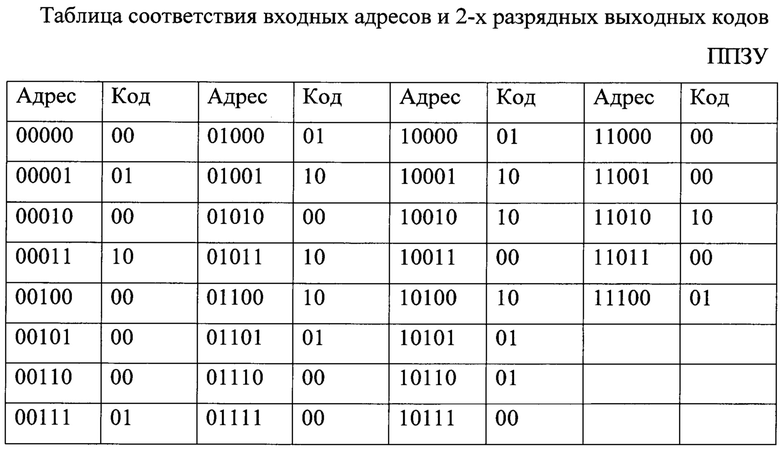
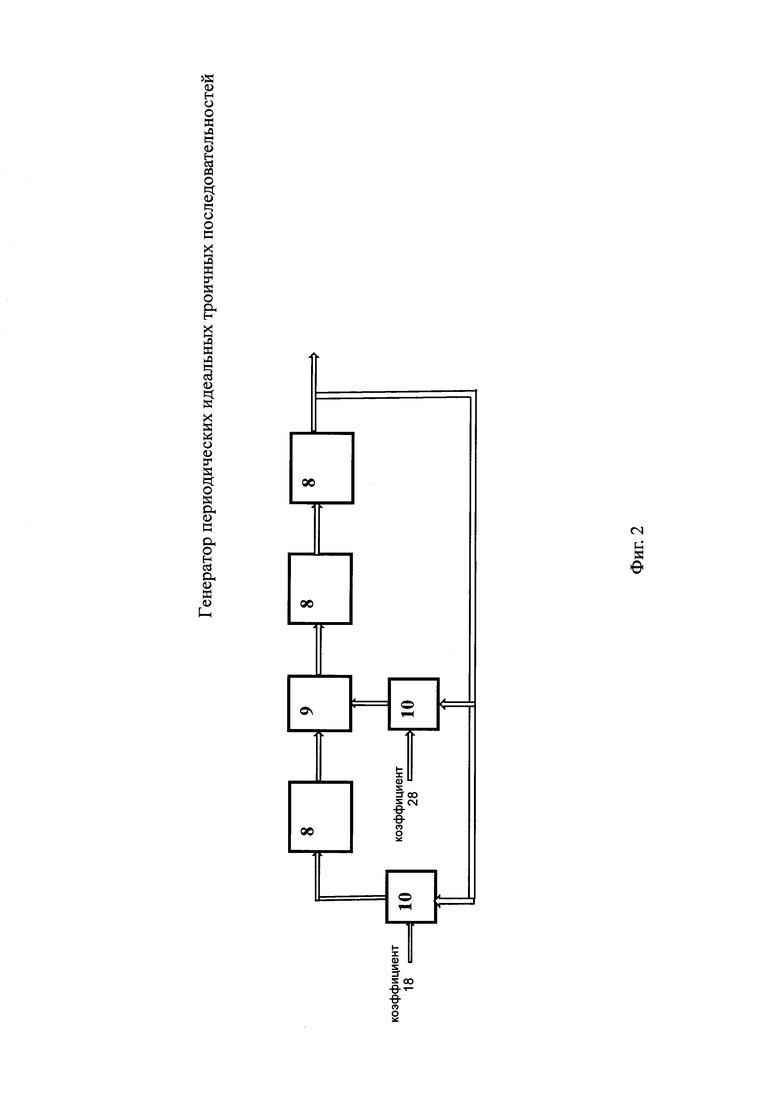
В качестве иллюстрации реализации генератора периодических идеальных троичных последовательностей рассмотрим следующий пример. Пусть p=29, n=3, k=3, m=1. Соответствующая длина m-последовательности равна 24388, а ее матрица декомпозиция имеет порядок 871×28. Выберем примитивный полином 3-й степени над GF(29) х3+х+11, а ИТП а=-1 -1 0 -1 0 0 1. Отсюда получаем, что N1=871, N2=7 и N=6097. При этом пик-фактор полученной ИТП длины 6097 равен 1,81. Поскольку m=1, то в качестве адреса для ППЗУ можем непосредственно использовать значение выходного символа генератора m-последовательности, т.е. преобразователь адреса в этом случае не требуется. На Фиг. 2 представлена блок-схема генератора m-последовательности над GF(29) длины 24388, состоящего из 3-х разрядного регистра сдвига с линейной обратной связью, выполненного по схеме Галуа. В качестве разрядов регистра используются 29-ричные элементы задержки 8 на один такт, умножение 29-ричного значения выхода генератора m-последовательности на коэффициенты 18 и 28, рассчитанные в соответствии с приведенным выше примером, по модулю 29 выполняется в соответствующих умножителях 10, а сложение чисел по модулю 29 выполняется в сумматоре 9. В качестве начального состояния регистра сдвига выбирается любое ненулевое 3-х разрядное 29-ричное число.
Ниже приведена Таблица соответствия входных адресов и 2-х разрядных выходных кодов ППЗУ, определяющая его структуру.
| название | год | авторы | номер документа |
|---|---|---|---|
| Генератор периодических псевдослучайных двоичных последовательностей сложной структуры с корреляционными свойствами, близкими к идеальным | 2018 |
|
RU2694439C1 |
| Генератор периодических псевдослучайных двоичных последовательностей сложной структуры | 2018 |
|
RU2690765C1 |
| Устройство для диагностирования цифровых объектов | 1989 |
|
SU1705829A1 |
| СПОСОБ ГЕНЕРАЦИИ И ПРОВЕРКИ ПОДЛИННОСТИ ЭЛЕКТРОННОЙ ЦИФРОВОЙ ПОДПИСИ, ЗАВЕРЯЮЩЕЙ ЭЛЕКТРОННЫЙ ДОКУМЕНТ | 2008 |
|
RU2392736C1 |
| СПОСОБ АКУСТИЧЕСКОГО КАРОТАЖА | 1990 |
|
RU2012018C1 |
| Устройство для определения двузначного характера элементов конечного поля @ | 1985 |
|
SU1312568A1 |
| Кодек квазициклического кода | 1986 |
|
SU1349010A1 |
| СПОСОБ ТРАНСЛЯЦИОННОГО УСЛОЖНЕНИЯ НЕЛИНЕЙНЫХ РЕКУРРЕНТНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ В ВИДЕ КОДОВ КВАДРАТИЧНЫХ ВЫЧЕТОВ, СУЩЕСТВУЮЩИХ В ПРОСТЫХ ПОЛЯХ ГАЛУА GF(p), И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2017 |
|
RU2669506C1 |
| Устройство для определения двузначного характера элементов конечного поля | 1984 |
|
SU1244658A1 |
| Устройство для цифрового формирования сигналов с амплитудно-фазовой модуляцией | 1980 |
|
SU919144A1 |
Изобретение относится к вычислительной технике и предназначено для генерации периодических идеальных троичных последовательностей (ИТП), являющихся последовательностями с идеальной периодической автокорреляционной функцией, и может быть использовано в системах фиксированной и мобильной связи, в радиолокации и навигации. Техническим результатом является генерация новых ИТП нечетной длины N1N2, где N1=(pmk-1)/(pm-1), m≥1, k≥3 - нечетно и 2N2│(pm-1). Устройство содержит генератор q-ичной m-последовательности длины qk-1, q=pm, m≥1 и k≥3 – нечетно, преобразователь, состоящий из последовательно соединенных формирователя адреса, перепрограммируемого постоянного запоминающего устройства и кодопреобразователя, умножитель, блок формирования сигнала меандра единичной амплитуды. 2 ил., 1 табл.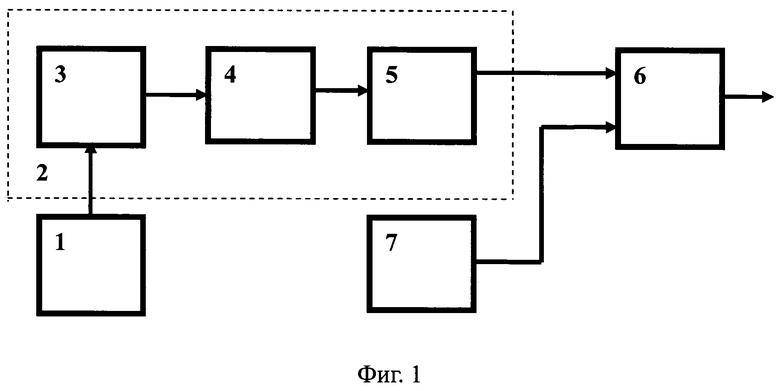
Генератор периодических идеальных троичных последовательностей, состоящий из последовательно соединенных генератора q-ичной m-последовательности длины qk-1, q=pm, m≥1 и k≥3 - нечетно и преобразователя, выполняющего операцию отображения выходного ненулевого q-ичного символа m-последовательности в символ двузначного мультипликативного характера, значение которого есть -1 или 1, а нулевого элемента этой последовательности соответственно в нуль, умножителя, первый вход которого подключен к выходу преобразователя, а второй вход подключен к выходу блока формирования сигнала меандра единичной амплитуды, отличающийся тем, что преобразователь состоит из последовательно соединенных формирователя адреса, вход которого является входом преобразователя, перепрограммируемого постоянного запоминающего устройства и кодопреобразователя, выход которого является выходом преобразователя, который осуществляет отображение символа q-ичной m-последовательности по правилу

где bi - q-ичный выходной символ генератора m-последовательности, 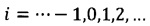 , zi=logβbi, bi≠0, β - примитивный элемент поля GF(q),
, zi=logβbi, bi≠0, β - примитивный элемент поля GF(q),  - последовательность, образованная из (pm-1)/N2 периодов идеальной троичной последовательности а длины N2, при этом преобразователь выполнен в виде последовательно соединенных формирователя адреса, преобразующего q-ичное число в ⎡mlog2(p)⎤-разрядное двоичное число (двоичный адрес), ППЗУ объема q×2, по адресам которого записана таблица соответствия символа bi∈GF(pm) двухразрядному двоичному числу, принимающему значение 10, если ƒ(bi)=1, значение 01, если ƒ(bi)=-1 и значение 00, если ƒ(bi)=0, и кодопреобразователя двухразрядного двоичного числа в символ троичного кода {-1,0,1}.
- последовательность, образованная из (pm-1)/N2 периодов идеальной троичной последовательности а длины N2, при этом преобразователь выполнен в виде последовательно соединенных формирователя адреса, преобразующего q-ичное число в ⎡mlog2(p)⎤-разрядное двоичное число (двоичный адрес), ППЗУ объема q×2, по адресам которого записана таблица соответствия символа bi∈GF(pm) двухразрядному двоичному числу, принимающему значение 10, если ƒ(bi)=1, значение 01, если ƒ(bi)=-1 и значение 00, если ƒ(bi)=0, и кодопреобразователя двухразрядного двоичного числа в символ троичного кода {-1,0,1}.
| US 2015098345 A1, 09.04.2015 | |||
| US 2011170697 A1, 14.07.2011 | |||
| US 2007085715 A1, 19.04.2007 | |||
| US 2005184888 A1, 25.08.2005 | |||
| СПОСОБ ПЕРЕДАЧИ ДИСКРЕТНОЙ ИНФОРМАЦИИ | 2006 |
|
RU2344544C2 |
| Устройство для определения двузначного характера элементов конечного поля | 1984 |
|
SU1244658A1 |
Авторы
Даты
2018-08-28—Публикация
2017-08-17—Подача