Изобретение относится к вычислительной технике и предназначено для генерации псевдослучайных двоичных последовательностей сложной структуры с почти идеальной автокорреляцией (с нулевой зоной автокорреляции N/2), используемых в широкополосных системах связи, в радарах с непрерывным излучением, а также в криптографии. Последовательность длины N называется почти идеальной, если ее периодическая автокорреляционная функция при всех ненулевых сдвигах кроме одного равна нулю. Последовательностями с нулевой зоной автокорреляции D называют последовательностями, имеющими нулевые значения боковых выбросов периодической автокорреляционной функции (ПАКФ) в некоторой зоне τ≤D относительно нулевого сдвига. Двоичную последовательность четной длины называют сбалансированной, если число нулей (единиц) в ней равно числу единиц (минус единиц) и почти сбалансированной, если разность между числом единиц и нулей по модулю равно двум.
В настоящее время известны различные генераторы псевдослучайных двоичных последовательностей (RU 2642351 (С1) - 2018-01-24, KR 20160067992 (А) - 2016-06-14, GB 1518997 (А) - 1978-07-26, ЕР 0492325 (А2) - 1992-07-01, RU 2013802 (А) - 1994-05-30, SU 1265973 (А1) - 1986-10-23, US 2018011691 (А1) - 2018-01-11, ES 2644485 (Т3) - 2017-11-29, CN 107683502 (А) - 2018-02-09, US 9813181 B2, Ипатов В.И. Периодические дискретные сигналы с оптимальными корреляционными свойствами. – М.: Радио и связь, 1992, Fan Р. and Darnell М. Sequence Design for Communications Applications. - RSP-John Wiley & Sons Inc., London, 1996 и др.) с хорошими корреляционными свойствами. В частности, в литературе описаны почти сбалансированные (ПС) почти идеальные двоичные последовательности (ПИДП) длины 2(pm+1), где р>2 простое число, а m≥1 целое 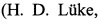 Н. D. Schotten, Н. Hadinejad-Mahram. Binary and quadriphase sequences with optimal autocorrelation properties: survey. - IEEE Transaction on Information Theory, vol. IT-49, No. 12, pp. 3271-3282, 2003), и почти идеальные троичные последовательности (ПИТП) с алфавитом {1,-1,0} длины 4(pm+1), (pm-l≡0 (mod 4), имеющие четыре нуля и равное число единиц и минус единиц (Кренгель Е.И. Конструирование почти идеальных и нечетно-идеальных троичных последовательностей. - журнал «Радиотехника», №9, 2006, стр. 8-12). ПИТП длины 4(pm+1) при замене нулей на последовательность 1 -1 1 -1 преобразуются по существу в сбалансированную ПИДП с малыми энергетическими потерями при обработке в несогласованном фильтре в приемнике. Полученные с помощью такого метода двоичные последовательности получили название несогласованных ПИДП (НПИДП) (Кренгель Е.И. Несогласованные почти идеальные двоичные последовательности. - журнал «Цифровая обработка сигналов», №4, 2006, стр. 44-47). НПИДП относятся к нелинейным псевдослучайным двоичным последовательностям сложной структуры, характеризуемой высоким значением линейной сложности. Линейная сложность является одной из важных характеристик двоичных последовательностей и численно равна наименьшей длине регистра сдвига с обратными связями, генерирующего эту последовательность.
Н. D. Schotten, Н. Hadinejad-Mahram. Binary and quadriphase sequences with optimal autocorrelation properties: survey. - IEEE Transaction on Information Theory, vol. IT-49, No. 12, pp. 3271-3282, 2003), и почти идеальные троичные последовательности (ПИТП) с алфавитом {1,-1,0} длины 4(pm+1), (pm-l≡0 (mod 4), имеющие четыре нуля и равное число единиц и минус единиц (Кренгель Е.И. Конструирование почти идеальных и нечетно-идеальных троичных последовательностей. - журнал «Радиотехника», №9, 2006, стр. 8-12). ПИТП длины 4(pm+1) при замене нулей на последовательность 1 -1 1 -1 преобразуются по существу в сбалансированную ПИДП с малыми энергетическими потерями при обработке в несогласованном фильтре в приемнике. Полученные с помощью такого метода двоичные последовательности получили название несогласованных ПИДП (НПИДП) (Кренгель Е.И. Несогласованные почти идеальные двоичные последовательности. - журнал «Цифровая обработка сигналов», №4, 2006, стр. 44-47). НПИДП относятся к нелинейным псевдослучайным двоичным последовательностям сложной структуры, характеризуемой высоким значением линейной сложности. Линейная сложность является одной из важных характеристик двоичных последовательностей и численно равна наименьшей длине регистра сдвига с обратными связями, генерирующего эту последовательность.
В работе (Edemskiy V., Minin A. About the linear complexity of the almost perfect sequences. - International Journal of Communications, Vol.1, 2016, pp. 223-226) было доказано, что линейная сложность L ПИДП длины 2(pm+1) и НПИДП длины 4(pm+1) равна соответственно 2(pm+1) и 3(pm+1), т.е. больше или равна 75% их длины, ограничивающей сверху величину линейной сложности последовательности.
Математическое определение этих последовательностей дано в (Кренгель Е.И. Конструирование почти идеальных и нечетно-идеальных троичных последовательностей. - журнал «Радиотехника», №9, 2006, стр. 8-12, Кренгель Е.И. Несогласованные почти идеальные двоичные последовательности. - журнал «Цифровая обработка сигналов», №4, 2006, стр. 44-47).
Пусть р>2 есть простое, и α есть примитивный элемент поля GF(pn), где n=2m, m≥1. Пусть β есть примитивный элемент поля GF(pm) и Т=(pn-1)/(pm-1)=pm+1. Тогда последовательность w, задаваемая правилом

где
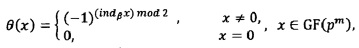
есть ПИТП длины 2(pm+l) с пиковыми значениями 2pm и числом нулевых элементов 2.
Здесь  - след элемента x GF(pn) относительно GF(pm), a indβx - индекс (логарифм) х по основанию β. При замещении 2-х равноотстоящих на Т нулей в последовательности w единицами или минус единицами мы получим ПИДП длины 2(pm+1).
- след элемента x GF(pn) относительно GF(pm), a indβx - индекс (логарифм) х по основанию β. При замещении 2-х равноотстоящих на Т нулей в последовательности w единицами или минус единицами мы получим ПИДП длины 2(pm+1).
Пусть р>2 - простое число, и а - примитивный элемент поля Галуа GF(pn), где n=2m, m≥1, такие, что pm-1 кратно 4. Пусть β - примитивный элемент поля Галуа GF(pm) и Т=(pn-l)/(pm-l)=pm+1. Тогда последовательность v, задаваемая правилом
 i=0, 1, …4T-1,
i=0, 1, …4T-1,
где


есть ПИТП длины 4(pm+1) с пиковыми значениями ACF(0)=-ACF(2T)=4pm и числом нулевых элементов 4. Здесь ⎣ u ⎦ есть max {n⎪n≤u, n - целое}, то есть ⎣и ⎦ есть операция округления числа к меньшему. При замещении 4-х равноотстоящих на Т нулей в последовательности ν на одну из трех двоичных последовательностей 1 1 1 1, -1 -1 -1 -1 или 1 -1 1 -1 мы получим НПИДП. Причем, в последнем случае последовательность будет сбалансированная, т.е. с равным числом -1 и 1, а при переходе к двоичному алфавиту {0,1} соответственно с равным числом 1 и 0. Обозначим полученную двоичную последовательность через v'.
В работе (Кренгель Е.И. Новые идеальные 4-фазные и 8-фазные последовательности с нулями. - журнал «Радиотехника», №5, 2007, стр. 3-8) описаны два варианта реализации генератора ПИТП длины 4(pm+1) с 4-мя нулями. В первом варианте генератор ПИТП длины 4(pm+1) состоит из генератора m-последовательности над Галуа GF(pm) длины pn-1 и блока вычисления функции ψ(x). Во втором варианте генератор ПИТП длины 4(pm+1) строится на основе ПЗУ объема 2(pm+l)x2, в котором хранятся троичные символы {-1, 0, 1}, и счетчика на 2(pm+1). Причем, через каждые 2(pm+1) тактов выходные символы инвертируются. Очевидно, что при переходе от ПИТП к НПИДП этот вариант генератора упрощается, поскольку в этом случае объем ПЗУ уменьшается в два раза до 2(pm+1)x1.
В первом варианте вычисление символов НПИДП производится посредством соответствующего генератора m-последовательности над GF(pm) длины pn-1, выход которого соединен с входом блока вычисления функции ψ(x). Генератор m-последовательности над GF(pm) длины pn-1 представляет собой регистр сдвига длины из n ячеек, содержащих символы поля Галуа GF(pm) (pm-ичные целые числа), охваченный линейной обратной связью по модулю pm. Основная сложность реализации первого варианта генератора НПИДП связана с вычислением дискретного логарифма х по основанию примитивного элемента β. Поэтому наибольшее быстродействие достигается при использовании таблиц, содержащих логарифмы всех pm элементов из GF(pm). Объем таблиц в этом случае максимален и составляет pm слов длиной приблизительно m⎡(log2p)⎤ бит, что почти в m⎡(log2p)⎤/4 раз превышает длину генерируемой двоичной последовательности. Здесь ⎡u⎤ есть min {n ⎟ n≥ u, n - целое}, т.е. ⎡u⎤ есть операция округления числа u к большему.
Для уменьшения объема памяти можно упростить блок вычисления функции ψ(xj) за счет использования таблицы отображения pm элементов х поля GF(pm) в соответствующий двоичный символ последовательности v' по следующему правилу: х→ψ(x), x≠0, а ψ(0) равно 1 или 0. В результате длина слова в таблице отображения равна 1 биту. Эта таблица может быть реализована с помощью ПЗУ объемом pm×1, адресным входом в которое является двоичное представление элемента x∈GF(pm) на выходе генератора m-последовательности над GF(pm). В этом случае генератор НПИДП длины 4(pm+1) состоит из последовательно соединенных генератора m-последовательности над GF(pm), блока преобразования (БП), отображающего выходной символ генератора m-последовательности виде m р-ичных коэффициентов в m⎡log2p⎤-разрядное двоичное число, являющееся адресным входом ПЗУ объемом pm × 1 бит.
Основным недостатком первого варианта является сложность разработки и реализация генератора m-последовательности над GF(pm), поскольку операции умножения и сложения в нем выполняются над элементами в поле Галуа GF(pm), что является достаточно трудоемкой задачей, требующей значительного числа операций. Кроме того, для больших значений р и m велика вероятность, что отсутствуют таблицы с характеристическими или примитивными полиномами с такими параметрами.
Второй тип генератора состоит из последовательно соединенных счетчика на 2(pm+1), устройства управления и ПЗУ объема 2(pm+1)×1, которое содержит 2(pm+1) первых двоичных символов НПИДП. По существу, это просто управляемая память, в которой значение выходного бита инвертируется через каждые 2(pm+1). Такой вариант генератора функционально намного проще, но требует в два раза больший объем памяти, что при достаточно больших длинах НПИДП будет намного более затратным.
Уменьшение сложности разработки и реализации генератора m-последовательности над GF(pm) длины pn-1 для n=2m осуществляется посредством его замены генератором из m=n/2 сдвинутых относительно друг друга на Т разрядов копий m-последовательности над GF(p) длины pn-1. Очевидно, что выполнение операций умножения над GF(p) значительно проще, чем над GF(pm). Кроме того, использование m сдвинутых копий m-последовательности над GF(p) позволяет распараллелить процесс формирования символа m-последовательности над GF(pm), что приводит к повышению быстродействия генератора m-последовательности над GF(pm) длины pn-1. Идея синтеза генератора m-последовательности над GF(pm) длины pn-1 посредством генерации m сдвинутых на (pn-1)/(pm-1) разрядов копий m-последовательности над GF(p) длины pn-1 в качестве вектора координат с последующим его скалярным умножением на базис {β0, β1,…, βm-1} поля GF(pm) над GF(p) в обобщенном виде была представлена в работе (G. Gong, G.Z. Xiao. Synthesis and uniqueness of m-sequences over GF(qn) as n-phase sequences over GF(q). - IEEE Trans. Commun. 42 (8), 1994, pp. 2501-2505).
Подобного рода генераторы в настоящее время используются в системах связи с псевдослучайной перестройкой рабочей частоты (ППРЧ), а также в криптографии (Y.-P. Hong and H.-Y. Song. Frequency /time hopping sequences with large linear complexities. - Coding and Cryptography, Vol. 3969 of the series LNCS, 2006, pp. 386-396).
Для отображения m-разрядного p-ичного числа на выходе генератора сдвинутых копий (ГСК) m-последовательности над GF(p) длины pn-1 в двоичное число, соответствующее функции ψ(х), согласно (G. Gong, G.Z. Xiao. Synthesis and uniqueness of m-sequences over GF(qn) as n-phase sequences over GF(q). - IEEE Trans. Commun. 42 (8), 1994, pp. 2501-2505) поступим следующим образом. pm-1 различным ненулевым наборам (ai,m-1 ai,m-2,… ai0,) m разрядных p-ичных чисел на выходе ГСК, соответствующим элементам поля Галуа αTi, i=0,l,…,pm-2, поставим в соответствие двоичную последовательность (1- (-1)⎣(i mod 4)/2⎦)/2 и запишем ее по адресам двоичного числа (ai,m-1pm-1 + ai,m-2pm-2 + ai0)2 в ПЗУ. Соответственно m-разрядному числу 00…0 поставим в соответствие число 1 или 0, которое записывается в ПЗУ по нулевому адресу. В результате на выходе ПЗУ формируется несбалансированная НПИДП, поскольку разность между числом единиц и нулей в этом случае равна 4. Очевидно, для формирования сбалансированной НПИДП необходимо каждые Т тактов изменять считываемый по нулевому адресу символ на противоположный. Следует отметить, что при несогласованной фильтрации на вход коррелятора приемника поступает НПИДП v' с алфавитом {1, -1}, а в качестве весовой последовательности в нем используется ПИТП v с символами {1, -1, 0}.
С учетом вышеизложенного технический результат изобретения состоит в уменьшении сложности разработки и реализации, а также повышении быстродействия генераторов периодических псевдослучайных двоичных последовательностей сложной структуры за счет замены генератора m-последовательности над GF(pm) длины (pn-1) с арифметикой в GF(pm), генератором сдвинутых относительно друг друга на Т символов копий m-последовательности) над GF(p) длины pn-1 с арифметикой в GF(p).
Указанный результат для НПИДП длины 4(pm+1) с неравным числом единиц и нулей достигается генератором периодических псевдослучайных двоичных последовательностей сложной структуры, содержащим генератор m-последовательности (ГМП) 1 над GF(pm) длины pn-1, где n=2m, (pm-l)≡0 (mod 4), с арифметикой в GF(pm), блок преобразования (БП) m-разрядного p-ичного числа в m⎡(log2p)⎤-разрядное двоичное число, двоичные выходы которого соединены с соответствующими адресными входами ПЗУ объемом pm × 1 бит, отличающимся тем, что ГМП над GF(pm) длины pn-1 реализован в виде последовательно соединенных генератора m-последовательности длины pn-1, состоящего из n разрядного регистра сдвига p-ичных чисел, выходные разряды которого подключены к входам блока скалярного перемножения (БСП), осуществляющего скалярное перемножения n-разрядного вектора состояний регистра сдвига на вектор из коэффициентов характеристического полинома m-последовательности над GF(p) длины pn-1, при этом выход БСП подключен к входу регистра сдвига, и блока умножения на матрицу (БУМ) р-ичных чисел порядка n×m, первый столбец которой соответствует нулевому сдвигу и равен (1 0 0…0)T, соответственно i-столбец этой матрицы соответствует сдвигу m-последовательности на (i-1)(pm+l), i=2,…,m, при этом n входов БУМ соединены с соответствующими выходами разрядов регистра сдвига, a m выходов БУМ подключены к m входам БП. Здесь верхний индекс T над вектором-строкой (1 0 0…0) обозначает операцию транспонирования.
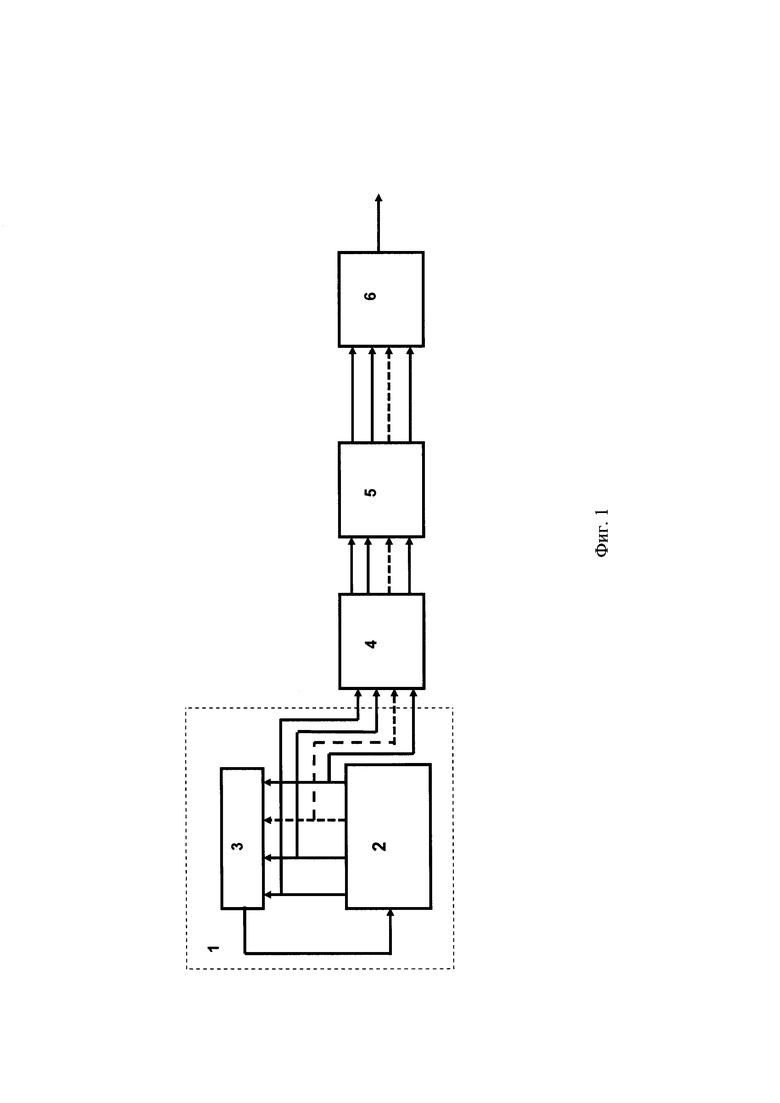
Блок-схема генератора периодических псевдослучайных двоичных последовательностей сложной структуры длины 4(pm+1) с неравным числом единиц и нулей представлена на Фиг. 1. Устройство содержит генератор m-последовательности 1 над GF(p) длины pn-1, состоящий из n-разрядного регистра сдвига p-ичных чисел 2 и БСП 3, осуществляющего скалярное перемножения n-разрядного вектора состояний регистра 2 на вектор из коэффициентов характеристического полинома m-последовательности, выход которого подключен к входу регистра сдвига 2, блок умножения на матрицу (БУМ) сдвиговых p-ичных коэффициентов порядка n×m 4, n входов которого соединены с соответствующими выходами разрядов регистра сдвига 2, БП m-разрядного p-ичного числа в m⎡(log2p)⎤-разрядное двоичное 5, m входов которого соединены с соответствующими m выходами БУМ 4 и ПЗУ 6 объема pm×1 бит, адресные входы которого подключены к m⎡(log2p)⎤ двоичным выходам БП 5.
Генератор работает следующим образом. Предварительно в регистр сдвига 2 записывается некоторое ненулевое число. Обычно это единица. На вход генератора 1 поступают тактовые импульсы с частотой ft. На каждом такте информация в регистре 2 сдвигается на разряд вправо, а в его самый младший р-ичный разряд записывается следующий p-ичный символ, появляющийся на выходе БСП 3. В БУМ 4 происходит умножение n-разрядного p-ичного вектора содержимого регистра 2 на матрицу сдвиговых коэффициентов порядка n×m, при этом используется арифметика в поле Галуа GF(p), которая эквивалентна арифметике по модулю р. Полученное в БУМ 4 m-разрядное p-ичное число поступает в БП 5, где из р-ичного преобразуется в двоичное и служит адресом, по которому из ПЗУ 6 извлекается текущий двоичный символ НПИДП. В результате на выходе ПЗУ 6 периодически появляются все символы НПИДП.
В соответствии с описанным выше преобразованием несбалансированной НПИДП в сбалансированную НПИДП генератор периодических псевдослучайных двоичных последовательностей сложной структуры длины 4(pm+1) с равным числом единиц и нулей отличается от описанного выше генератора периодических псевдослучайных двоичных последовательностей сложной структуры (Фиг. 1) введением последовательно соединенных дешифратора нуля и прореживателя единиц, а также двухвходового элемента ИЛИ, подключенного по первому входу к выходу прореживателя единиц, а по второму входу - к выходу ПЗУ, при этом вход дешифратора нуля соединен с выходом БП. В результате на выходе прореживателя единиц формируется последовательность периода 2(pm+1), состоящая из одной единицы и 2pm+1 нулей. Начало периода этой последовательности совпадает с появлением нулевой комбинации на выходе БП. При этом предполагается, что по нулевому адресу в ПЗУ хранится 0.
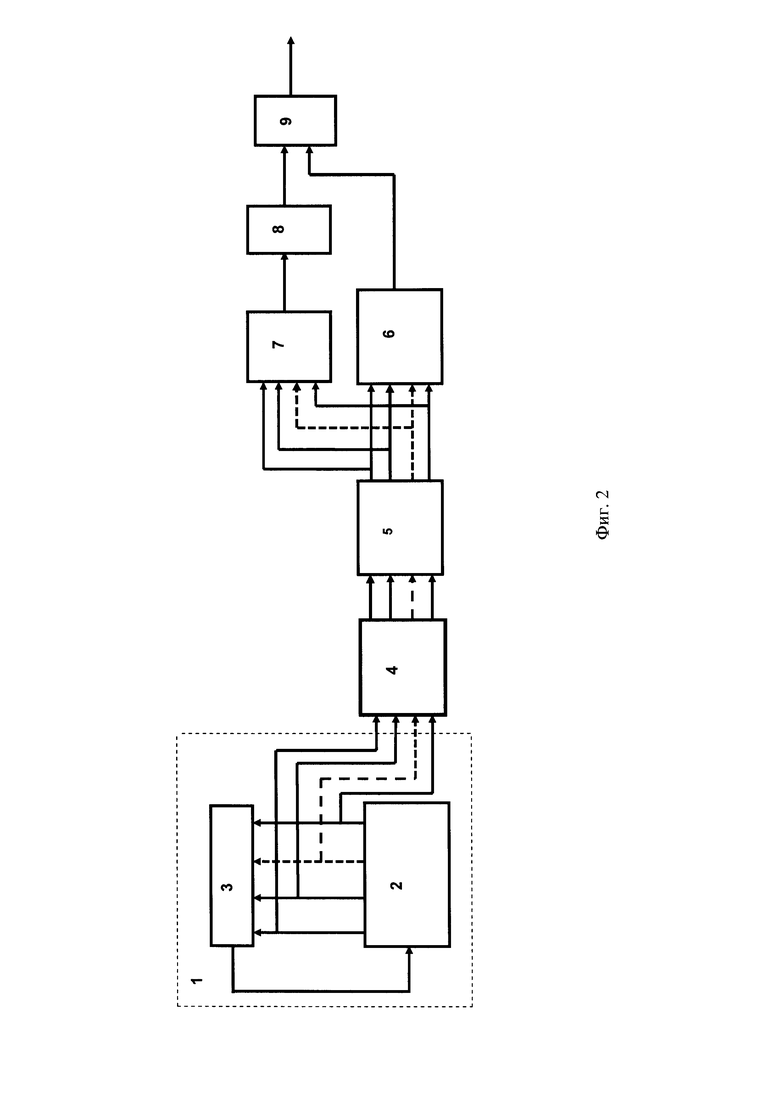
Блок-схема генератора периодических псевдослучайных двоичных последовательностей сложной структуры длины 4(pm+1) с равным числом единиц и нулей (сбалансированной несогласованной почти идеальной двоичной последовательности) представлена на Фиг. 2. Устройство содержит генератор m-последовательности 1 над GF(p) длины pn-1, состоящий из p-разрядного регистра сдвига р-ичных чисел 2 и БСП 3, осуществляющего скалярное перемножение n-разрядного вектора состояний регистра 2 на вектор из коэффициентов характеристического полинома m-последовательности, выход которого подключен к входу регистра сдвига 2, БУМ 4 сдвиговых p-ичных коэффициентов порядка n×m, n входов которого соединены с соответствующими выходами разрядов регистра 2, блок преобразования (БП) m-разрядного р-ичного числа в m⎡(log2p)⎤-разрядное двоичное 5, m входов которого соединены с соответствующими m выходами БУМ 4, a m⎡(log2p)⎤ двоичных выходов БП 5 с адресными входами ПЗУ 6 и дешифратором нуля 7, подключенного к входу прореживателя единиц 8, и двухвходовый элемент ИЛИ 9, подключенный по первому входу к выходу прореживателя 8, а по второму входу - к выходу ПЗУ 6.
Работа этого генератора происходит аналогично описанному выше генератору периодических псевдослучайных двоичных последовательностей сложной структуры длины 4(pm+1), представленному на Фиг. 1. Первоначально в регистр сдвига 2 также записывается некоторое ненулевое число. Полученное в БУМ 4 m-разрядное р-ичное число поступает в БП 5, где из p-ичного формируется двоичный адрес чтения символа из ПЗУ 6, и в дешифратор нуля 7, где оно дешифрируется. В случае нулевой комбинации на выходе БП на выходе дешифратора нуля 7 появляется единица, а в случае всех ненулевых комбинаций - нуль. Таким образом, на выходе дешифратора 7 формируется последовательность из одной единицы и pm нулей с периодом pm+1. Прореживатель единиц 8 осуществляет обнуление каждой второй появляющейся на его входе единицы, формируя на своем выходе последовательность из одной единицы и 2pm+1 нулей с периодом 2(pm+1). В элементе ИЛИ 9 происходит объединение выходных двоичных сигналов ПЗУ и прореживателя единиц 8. В результате на выходе элемента ИЛИ 9 появляются символы периодической сбалансированной НПИДП.
Для иллюстрации работы предлагаемого изобретения рассмотрим конструкцию генератора периодических псевдослучайных двоичных последовательностей сложной структуры длины 104 с неравным числом единиц и нулей. В этом случае р=5, n=4, m=2 и Т=26. Выбираем характеристический полином степени 4 над GF(5) вида f(x)=x4+x2+2x+2. Функциональная блок-схема генератора периодических последовательностей НПИДП длины 104 изображена на Фиг. 3. ГСК включает ГМП над полем GF(5) длины N=54-1=624, выполненный на регистре сдвига длины 4 с вынесенными сумматорами по mod 5 в схеме обратной связи (тип Фибоначчи), и БУМ с размером матрицы 4×2.
Первый столбец этой матрицы имеет вид (1 0 0 0)T. Поэтому практически берется выход первого (младшего) разряда регистра сдвига генератора m-последовательности. Вторая строка находится из следующих соображений. Примитивным нормализованным полиномом (старший коэффициент равен единице), двойственным к f(x), является F(x)=x4+х3+3х2+3. Согласно работе
(Питерсон У. Коды, исправляющие ошибки. - Москва, изд-во «Мир», 1964) последовательность состояний генератора m-последовательности длины 624, выполненного на основе примитивного полинома F(x) по схеме с встроенными сумматорами (по схема Галуа), будет определять всю совокупность векторов, необходимых для получения любого сдвига этой же (с точностью до фиксированного множителя) m-последовательности, но выполненной на основе по схеме с вынесенными сумматорам на основе полинома f(x). Рассмотрим m- последовательность, получаемую на выходе первого (младшего) разряда ГМП.
Циклическому сдвигу этой m-последовательности влево на T=26 будет соответствовать состояние генератора m-последовательности с полиномом F(х) по схеме Галуа при его сдвиге на 26*23=598 относительно начального состояния 1 0 0 0. В результате расчета находим, что этому сдвигу соответствует состояние 0 3 0 2. В результате матрица сдвиговых коэффициентов равна 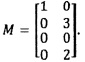
В Таблице ниже представлена структура данных ПЗУ генератора НПИДП длины 104.

Здесь А означает адрес ПЗУ, а Б - бит данных. В результате на выходе генератора получаем периодическую НПИДП длины 104 вида: 1 1 1 0 1 1 0 1 1 1 1 1 1 0 0 0 0 0 0 1 1 0 1 0 1 1 1 0 1 1 0 1 0 1 1 1 0 1 1 1 0 0 0 0 1 1 0 1 0 0 1 1 0 0 0 1 0 0 1 0 0 0 0 0 0 1 1 1 1 0 1 0 0 1 0 1 0 0 0 1 0 0 1 0 1 0 0 0 1 0 0 0 1 1 1 0 0 0 1 0 1 1 0 0 с линейной сложностью L=3Т=78.
Регистр сдвига 2 генератора m-последовательности 1 состоит из последовательно соединенных 4-х 5-ричных элементов задержки на один такт 10, БСП состоит из трех умножителей 11, в которых осуществляется умножение по модулю 5 содержимого соответствующих разрядов регистра сдвига 2 на коэффициенты 4, 3 и 3, и сумматора 12 по модулю 5, а БУМ соответственно состоит из двух умножителей 11, в которых выполняется умножение по модулю 5 содержимого 2-го и 4-го разрядов регистра сдвига 2 соответственно на коэффициенты 3 и 2, и сумматора 12 по модулю 5.
Предлагаемое изобретение может быть реализовано на соответствующей элементной базе по типовым технологиям.
| название | год | авторы | номер документа |
|---|---|---|---|
| Генератор периодических псевдослучайных двоичных последовательностей сложной структуры с корреляционными свойствами, близкими к идеальным | 2018 |
|
RU2694439C1 |
| Генератор периодических идеальных троичных последовательностей | 2017 |
|
RU2665290C1 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2021 |
|
RU2776346C1 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2020 |
|
RU2740339C1 |
| СПОСОБ СУММИРОВАНИЯ ЧИСЕЛ | 1998 |
|
RU2145113C1 |
| СПОСОБ ФОРМИРОВАНИЯ ПСЕВДОСЛУЧАЙНЫХ СИГНАЛОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2021 |
|
RU2769539C1 |
| УСТРОЙСТВО ДЛЯ ГЕНЕРАЦИИ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ | 2020 |
|
RU2761766C1 |
| ГЕНЕРАТОР НЕЛИНЕЙНЫХ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ | 2014 |
|
RU2549524C1 |
| УСТРОЙСТВО ЭЛЕКТРОННОГО СМЕЩЕНИЯ ЧАСТОТЫ | 1989 |
|
SU1840230A1 |
| УСТРОЙСТВО ФОРМИРОВАНИЯ ТРИПЛЕКСНЫХ ЧИСЕЛ | 2023 |
|
RU2812412C1 |

Изобретение относится к вычислительной технике. Технический результат заключается в повышении быстродействия генератора псевдослучайных двоичных последовательностей сложной структуры. Устройство содержит генератор m-последовательности длины (ГМП) над GF(pm) длины pn-1, где n=2m, (pm-l)≡0 (mod 4), с арифметикой в GF(pm), блок преобразования (БП) выходного символа m-последовательности в виде m р-ичных коэффициентов в ⎡m(log2p)⎤-разрядное двоичное число, двоичные выходы которого соединены с соответствующими адресными входами ПЗУ объемом pm×1 бит. ГМП над GF(pm) длины pn-1 реализован в виде последовательно соединенных генератора m-последовательности над GF(p) длины pn-1, состоящего из n разрядного регистра сдвига p-ичных чисел, выходные разряды которого подключены к входам блока скалярного перемножения (БСП), при этом выход БСП подключен к входу регистра сдвига, и блока умножения на матрицу (БУМ) р-ичных чисел порядка n×m, первый столбец которой соответствует нулевому сдвигу и равен (1 0 0…0)T, соответственно, i-столбец этой матрицы соответствует сдвигу m-последовательности на (i-1)(pm+1), 1=2,…,m, при этом n входов БУМ соединены с соответствующими выходами разрядов регистра сдвига, а m выходов БУМ подключены к m входам БП m-разрядного р-ичного числа в двоичное, причем введены последовательно соединенные дешифратор нуля и прореживателя единиц, а также двухвходовой элемент ИЛИ, подключенный по первому входу к выходу прореживателя единиц, а по второму входу - к выходу ПЗУ, при этом вход дешифратора нуля соединен с выходом БП. 1 з.п. ф-лы, 3 ил., 1 табл.
1. Генератор периодических псевдослучайных двоичных последовательностей сложной структуры, содержащий генератор m-последовательности (ГМП) над GF(pm) длины рn-1, где n=2m, (pm-1)≡0 (mod 4), с арифметикой в GF(pm), блок преобразования (БП) выходного символа m-последовательности в виде m p-ичных коэффициентов в ⎡m(lоg2p)⎤ - разрядное двоичное число, двоичные выходы которого соединены с соответствующими адресными входами ПЗУ объемом рm×1 бит, отличающийся тем, что ГМП над GF(pm) длины рn-1 реализован в виде последовательно соединенных генератора m-последовательности над GF(p) длины рn-1, состоящего из n разрядного регистра сдвига p-ичных чисел, выходные разряды которого подключены к входам блока скалярного перемножения (БСП), осуществляющего скалярное перемножение n-разрядного вектора состояний регистра сдвига на вектор из коэффициентов характеристического полинома m-последовательности, при этом выход БСП подключен к входу регистра сдвига, и блока умножения на матрицу (БУМ) р-ичных чисел порядка n×m, первый столбец которой соответствует нулевому сдвигу и равен (1 0 0 …0)T, соответственно, i-столбец этой матрицы соответствует сдвигу m-последовательности на (i-l)(pm+1), i=2,…,m, при этом n входов БУМ соединены с соответствующими выходами разрядов регистра сдвига, а m выходов БУМ подключены к m входам БП m-разрядного p-ичного числа в двоичное.
2. Генератор периодических псевдослучайных двоичных последовательностей сложной структуры по п. 1, отличающийся введением последовательно соединенных дешифратора нуля и прореживателя единиц, а также двухвходового элемента ИЛИ, подключенного по первому входу к выходу прореживателя единиц, а по второму входу - к выходу ПЗУ, при этом вход дешифратора нуля соединен с выходом БП.
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ | 2010 |
|
RU2446444C1 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ N-РАЗРЯДНЫХ ДВОИЧНЫХ ЧИСЕЛ | 1994 |
|
RU2080651C1 |
| Способ получения цианистых соединений | 1924 |
|
SU2018A1 |
| РЕГУЛЯТОР ВЯЗКОСТИ ДЛЯ ПОЛИВОЧНЫХ МАШИН | 1944 |
|
SU67872A1 |
| Устройство для погружения и извлечения ряда свай вдавливанием | 1979 |
|
SU887728A1 |
Авторы
Даты
2019-06-05—Публикация
2018-07-27—Подача