Общая область техники
Изобретение относится к анализу распространения трещин в механических деталях. Эти детали в основном предназначены для летательных аппаратов, но могут быть любым механическим компонентом. Распространение определяют в рамках усталостного распространения при помощи последовательности циклов нагрузки.
В частности, изобретение относится к методам и системам моделирования, определения и интерполяции коэффициента интенсивности напряжений (называемого в дальнейшем КИН) в моделированной цифровым способом детали, которую необходимо анализировать. Изобретение относится также к методам и системам вычисления срока службы анализируемой детали.
Коэффициент КИН разлагается на три величины, обозначенные KI, KII и KIII, соответствующие модам открытия трещины, плоского сдвига и антиплоского сдвига.
Настоящее описание представлено для KI, но его можно применять и для других величин.
Цифровые методы распространения трещины являются очень эффективными. Например, расширенные методы конечных элементов (XFEM) или метод податливости при трещинообразовании позволяют надежно прогнозировать пути распространения трещины, а также вычислять коэффициенты КИН вдоль фронта трещины.
Однако вычисление срока службы при распространении трещины обычно не входит в сферу торговых правил или является несовместимым с промышленными требованиями.
По этой причине в авиационной промышленности разработали свое собственное правило вычисления срока службы, которое работает на основании специальной постобработки результатов, полученных при цифровом моделировании распространения трещины.
Для данного размера трещины и, следовательно, для данной точки фронта трещины коэффициент КИН является величиной, характеризующей интенсивность нагрузки вблизи вершины трещины. В зависимости от амплитуды этой величины во время цикла усталостной нагрузки трещина будет распространяться более или менее быстро.
Именно цифровое моделирование распространения трещины предназначено для получения значений КИН вдоль фронта трещины и для разных длин трещины.
На основании этого списка значений кодексы вычисления срока службы должны обеспечивать предсказание срока службы при распространении трещины.
Тем не менее, с учетом вычислительных ресурсов шаги распространения, то есть итерации вычисления цифровых моделей, не могут быть слишком малыми, следовательно, моделирование можно осуществлять не для всех длин трещины.
Чтобы успешно вычислять срок службы, необходимо интерполировать коэффициенты КИН между шагами моделируемого распространения. Следовательно, необходимо иметь эффективный метод интерполяции, чтобы предсказанные сроки службы были релевантными.
Уровень техники
Следует напомнить, что в данном случае рассматривается моделирование трещины при усталостной нагрузке, то есть моделирование развития трещины при приложении нескольких циклов нагрузки.
Методы 3D-моделирования трещинообразования, как правило, осуществляемые при помощи конечных элементов, позволяют получать коэффициенты КИН вдоль фронта трещины на каждом шаге распространения, а также характеризующие ее геометрические данные (координаты узлов фронта трещины и поверхностей и узлов, связанных с одним из берегов трещины). На практике при вычислении срока службы используют только максимальный коэффициент КИН вдоль фронта трещины для каждого шага распространения (см. на фиг. 1 единственную точку Р1, Р2, Р3, Р4 на каждой из кривых линий, которая отображает каждый фронт трещины F1, F2, F3, F4 с различным шагом распространения). Чтобы иметь возможность использовать эти значения КИН, следует привести их в согласование с соответствующей длиной трещины.
Затем при помощи линейной интерполяции между точками табуляции получают точки между каждым табулированным значением.
Этот метод интерполяции коэффициентов КИН имеет два основных недостатка.
Первый из них состоит в том, что указанный в формуляре коэффициент КИН является максимальным коэффициентом КИН вдоль фронта трещины для каждого шага распространения. Иначе говоря, совершенно не обязательно, что указан КИН, соответствующий одной и той же точке фронта (точки на фиг. 1 относятся к разным местам фронта трещины). Таким образом, в этом методе не учитывают трехмерную геометрию трещины и ее изменение в течение времени, которое неизбежно влияет на изменение коэффициента КИН.
Второй недостаток состоит в том, что этот метод не позволяет проверить, является ли шаг распространения достаточно малым. Было установлено, что, если шаг распространения является слишком большим, сроки службы при распространении трещины не могут быть окончательными.
Кроме того, существует последняя слабость этого подхода, связанная с геометрией трещины, которую необходимо учитывать и которая может быть сложной (например, разветвленной). Действительно, трещине присуща трехмерная структура, поэтому возникает проблема определения «длины трещины». Это значительно ограничивает возможность применения этого метода.
Для вычисления распространения трещин существуют теоретические методы.
Например, метод весовых функций позволяет вычислять коэффициенты интенсивности напряжения КИН на основании поля напряжения не затронутой трещиной структуры и геометрии трещины (см. например, ссылки [1], [2] и [3] - ссылки приведены в конце описания). Однако этот метод ограничен простыми случаями, что препятствует его широкому применению.
Так называемые методы «возмущений» являются более сложными с точки зрения математики, но позволяют полуаналитически определять поведение трещины, а также стабильность фронта (см. ссылку [4]). Однако основная часть разработок может быть применима только при предположении как минимум полубесконечной среды.
Раскрытие изобретения
Изобретением предложен способ оценки коэффициента интенсивности напряжений в детали, моделированной цифровым путем, в рамках моделирования распространения усталостной трещины, содержащий следующие этапы:
- (Е2): при помощи цифрового моделирования анализируемой детали получают множество моделированных значений в разных точках анализируемой детали, при этом указанное множество моделированных значений включает в себя для разных моделированных шагов распространения трехмерной трещины, которая появляется на цифровой модели детали, совокупность моделированных значений коэффициента интенсивности напряжений в соответствующих точках, положение этих точек и данные, относящиеся к треснутой поверхности (координаты узлов и сторон трехмерных элементов, определяющие один из берегов трещины, при этом стороны элементов можно сохранить в виде таблицы взаимосвязи),
- (Е3): для каждого шага распространения и для совокупности моделированных для него значений определяют, с одной стороны, преобразованное значение эффективной амплитуды общего эквивалентного коэффициента интенсивности напряжений, соответствующего коэффициенту интенсивности напряжений плоской трещины с прямым фронтом и, с другой стороны, преобразованную длину рассматриваемой эквивалентной трещины, при этом указанные преобразованные значения определяют посредством уравнивания энергии, рассеиваемой в трехмерной трещине цифровой модели, и энергии, рассеиваемой в трещине стандартной модели плоской трещины с прямым фронтом, при этом сами значения энергии определяют в зависимости от коэффициентов интенсивности напряжений,
- (Е4): интерполируют преобразованные значения эффективной амплитуды общего эквивалентного коэффициента интенсивности напряжений между двумя последовательными преобразованными длинами (а) трещины,
- (Е5): сохраняют преобразованные значения эффективной амплитуды общего эквивалентного коэффициента интенсивности напряжений, интерполированные с соответствующими длинами трещины.
Таким образом, речь идет об общем способе, эквивалентном «в плане термодинамики» с методом плоской трещины с прямым фронтом. Создают понятие длины, имеющее физический смысл, что позволяет преодолеть вышеупомянутые ограничения.
Представленный способ применяют при помощи системы, содержащей блок обработки данных.
Изобретение имеет также следующие отличительные признаки, рассматриваемые отдельно или в комбинации:
- на этапе интерполяции применяют кусочно-линейную интерполяцию,
- на этапе интерполяции применяют интерполяцию посредством минимизации энергии кривизны,
- этап интерполяции включает в себя следующие подэтапы:
интерполяция с применением линейной интерполяции,
интерполяция с применением интерполяции посредством минимизации энергии кривизны, при этом оба вида интерполяции являются взаимозаменяемыми,
вычисление по меньшей мере одной величины, характеризующей разность значений амплитуды коэффициента интенсивности напряжений между двумя интерполяциями, при этом указанную разность вычисляют строго между двумя значениями длины трещины, соответствующими двум последовательным шагам,
сравнение указанной величины, характеризующей разность, с заранее определенным порогом,
если величина, характеризующая разность, превышает порог, генерируют команду на вычисление, на основании цифровой модели анализируемой детали, значений коэффициента интенсивности напряжений (КИН) вдоль нового моделированного фронта и значений положения трещины между двумя последовательными шагами,
- перед этапом (Е2) получения способ включает в себя этап (Е1) вычисления с применением моделирования методом конечных элементов (или расширенным методом конечных элементов) на последовательных шагах изменения трещины в анализируемой детали, при этом указанное моделирование осуществляет блок обработки,
- цифровые данные на этапе (Е2) получения данных получают посредством моделирования методом конечных элементов или моделирования расширенным методом конечных элементов,
- для этапа (Е3) определения первый набор данных позволяет узнать эффективную амплитуду степени восстановления энергии ΔG при помощи следующих отношений:
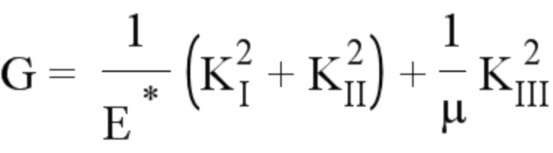

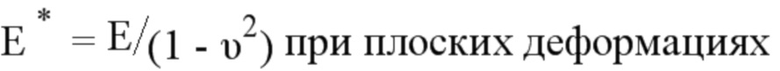
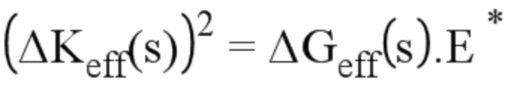
где KI, KII и KIII являются соответственно коэффициентами КИН, соответствующими модам открытия трещины, плоского сдвига и антиплоского сдвига, ΔKeff (s) является эффективной амплитудой коэффициента интенсивности напряжений, ΔGeff является эффективной амплитудой степени восстановления энергии, s является криволинейной абсциссой вдоль фронта трещины, E является модулем Юнга, μ является модулем сдвига, E* является эквивалентным модулем Юнга, ν является коэффициентом Пуассона,
второй набор данных позволяет узнать инкремент dSurf треснутой поверхности на единицу длины фронта трещины,
эти определения позволяют получить значение рассеянной энергии:

при этом рассеянную энергию уравнивают с рассеянной энергией стандартной модели плоской трещины с прямым фронтом, которую можно выразить следующим образом:
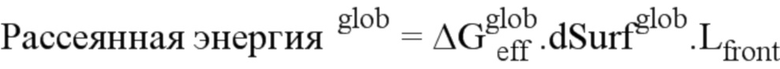
где обозначение glob относится к этой стандартной модели, а Lfront является длиной фронта трещины,
при этом, благодаря моделированию при помощи закона Париса с параметрами закрытия трещины Элбера, устанавливают связь между dSurfglob и 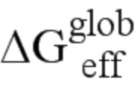
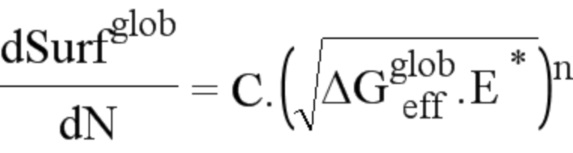
где С и n являются коэффициентами Париса,
при этом, уравнивая две рассеянные энергии, получаем:

при этом при помощи отношений между ΔGeff и ΔKeff, определяют 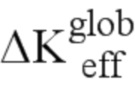 и определяют Surfglob, то есть преобразованную длину а эквивалентной трещины.
и определяют Surfglob, то есть преобразованную длину а эквивалентной трещины.
В частности, первый набор данных содержит значения коэффициента интенсивности напряжений в соответствующих точках на фронте трещины и их соответствующее положение, а второй набор данных содержит данные, относящиеся к треснутой поверхности.
Объектом изобретения является также способ оценки срока службы детали, моделированной цифровым методом, в котором применяют вычисление срока службы с использованием преобразованных значений эффективной амплитуды общего эквивалентного коэффициента интенсивности напряжений, интерполированных в зависимости от эквивалентной длины трещины при помощи описанного выше способа.
Объектом изобретения является также система, содержащая блок обработки, содержащий средства вычисления и память, при этом блок выполнен с возможностью осуществления описанного выше способа оценки срока службы при распространении усталостной трещины.
Объектом изобретения является также компьютерный программный продукт, выполненный с возможностью применения описанной выше системой и содержащий команды для осуществления описанного выше способа оценки срока службы.
Краткое описание чертежей
Другие признаки, задачи и преимущества изобретения будут более очевидны из нижеследующего описания, представленного в качестве иллюстративного и не ограничительного примера со ссылками на прилагаемые чертежи, на которых:
фиг. 1 - фронт трещины для разных шагов распространения;
фиг. 2 - система, позволяющая осуществлять изобретение;
фиг. 3 - анализируемая деталь;
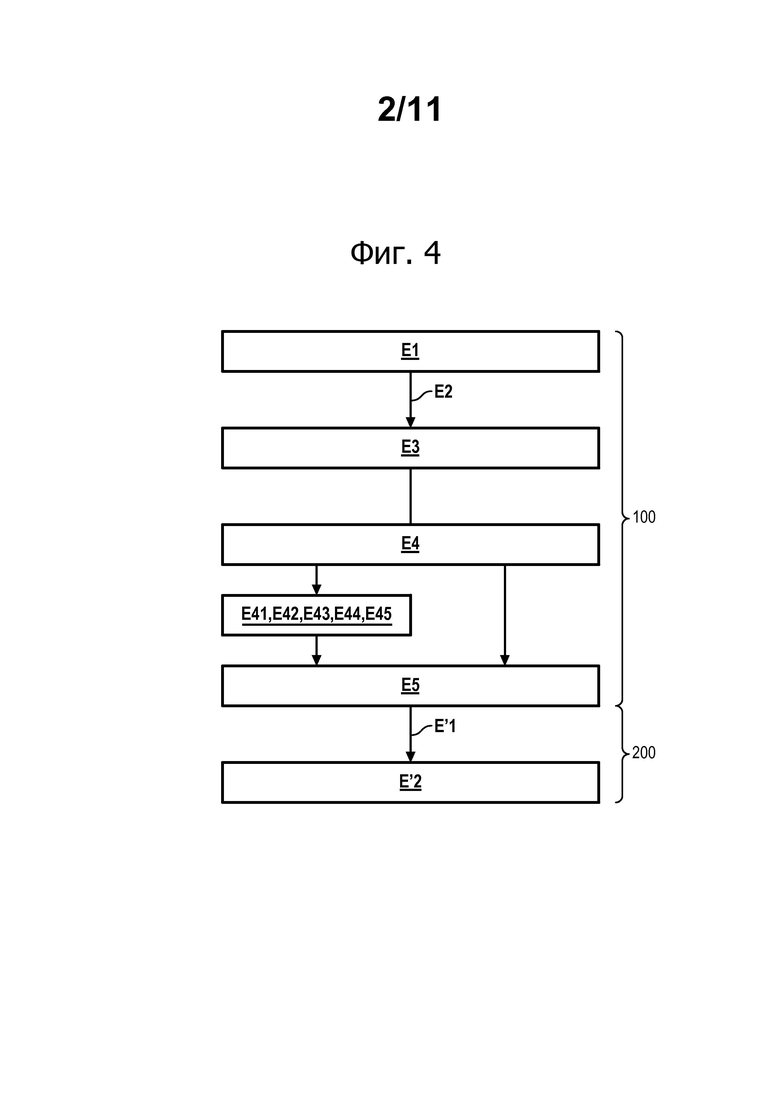
фиг. 4 иллюстрирует два способа и соответствующие варианты осуществления в соответствии с изобретением;
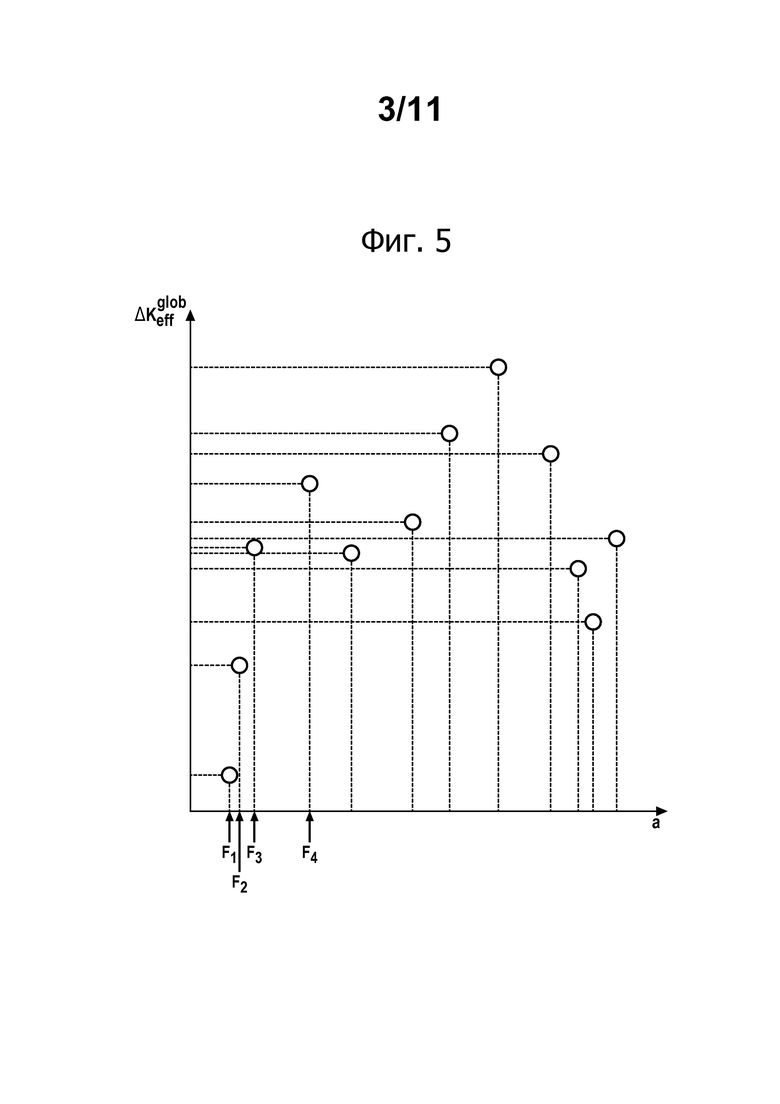
фиг. 5 - точки, преобразованные эквивалентно плоской трещине с прямым фронтом из трехмерной трещины в соответствии с теорией энергетической эквивалентности посредством термодинамического анализа;
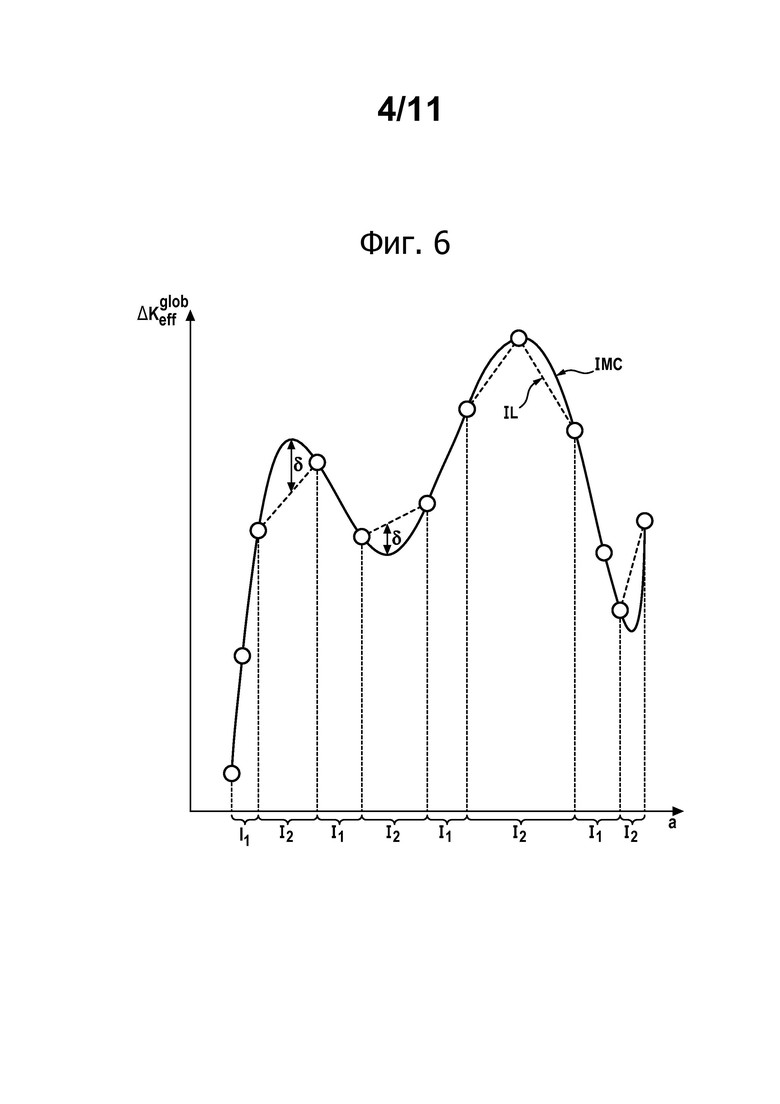
фиг. 6 - эти же точки при двух методах интерполяции: кусочно-линейной и с минимизацией энергии кривизны;
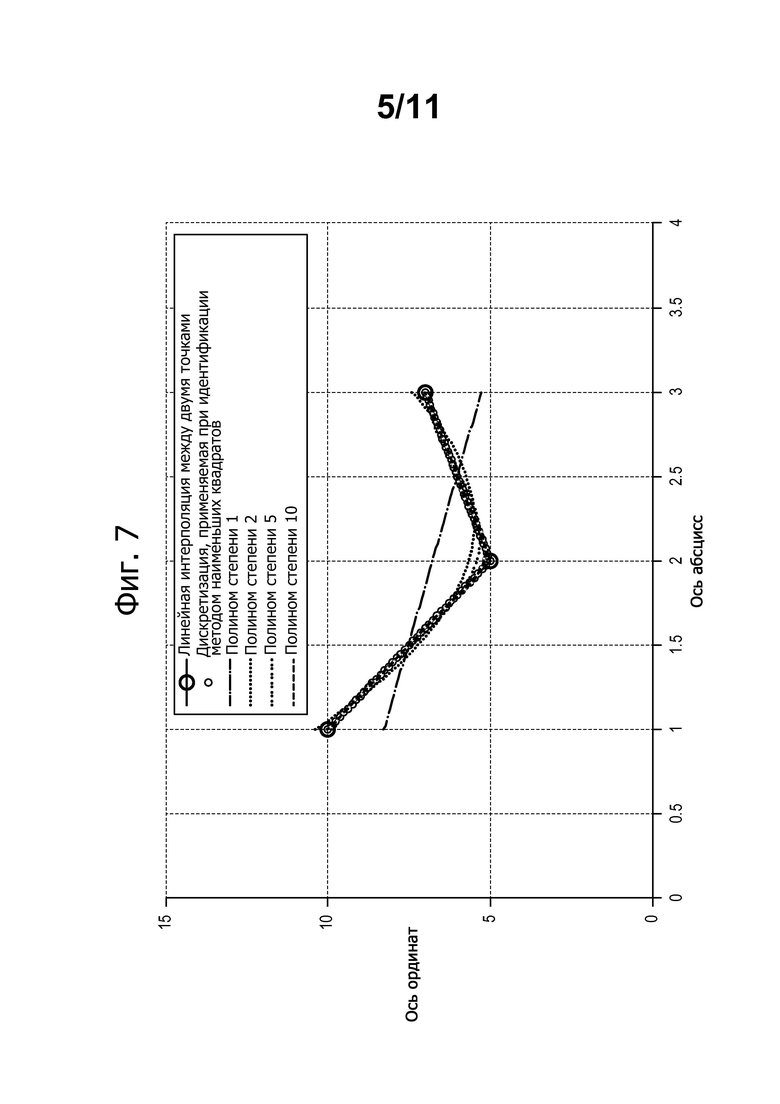
фиг. 7 - изменение полиномиальной интерполяции в соответствии со степенью полинома;
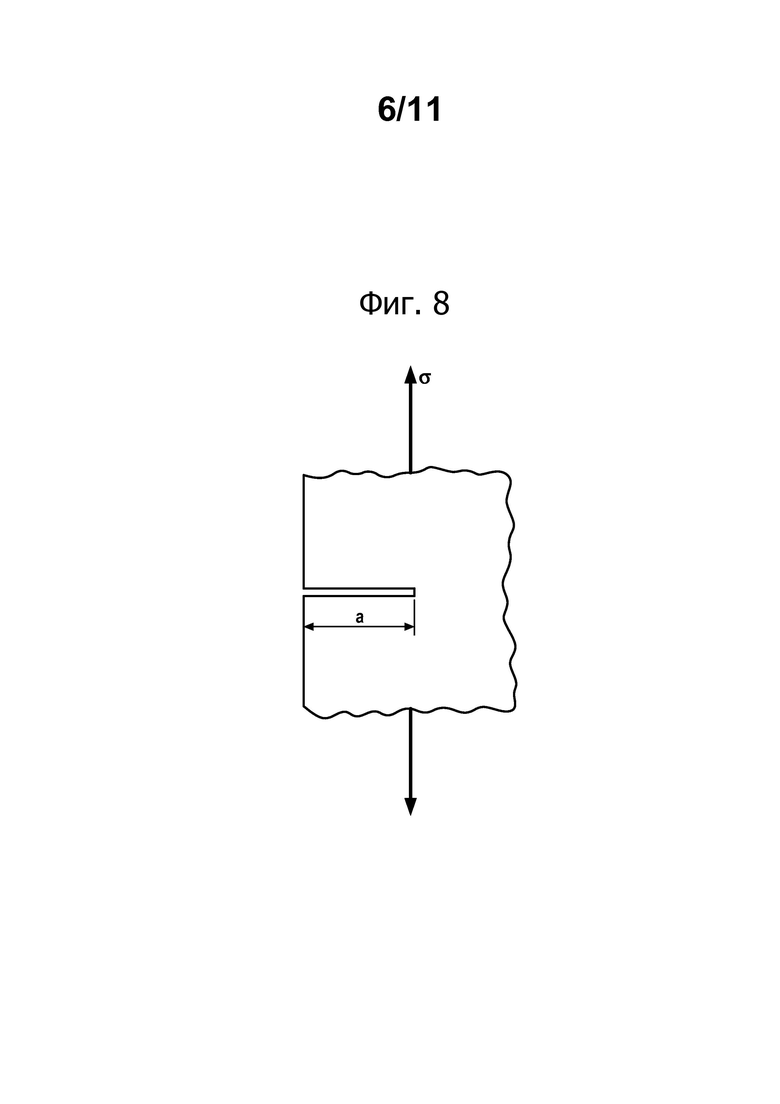
фиг. 8 - схематичный вид плоской трещины с прямым фронтом;
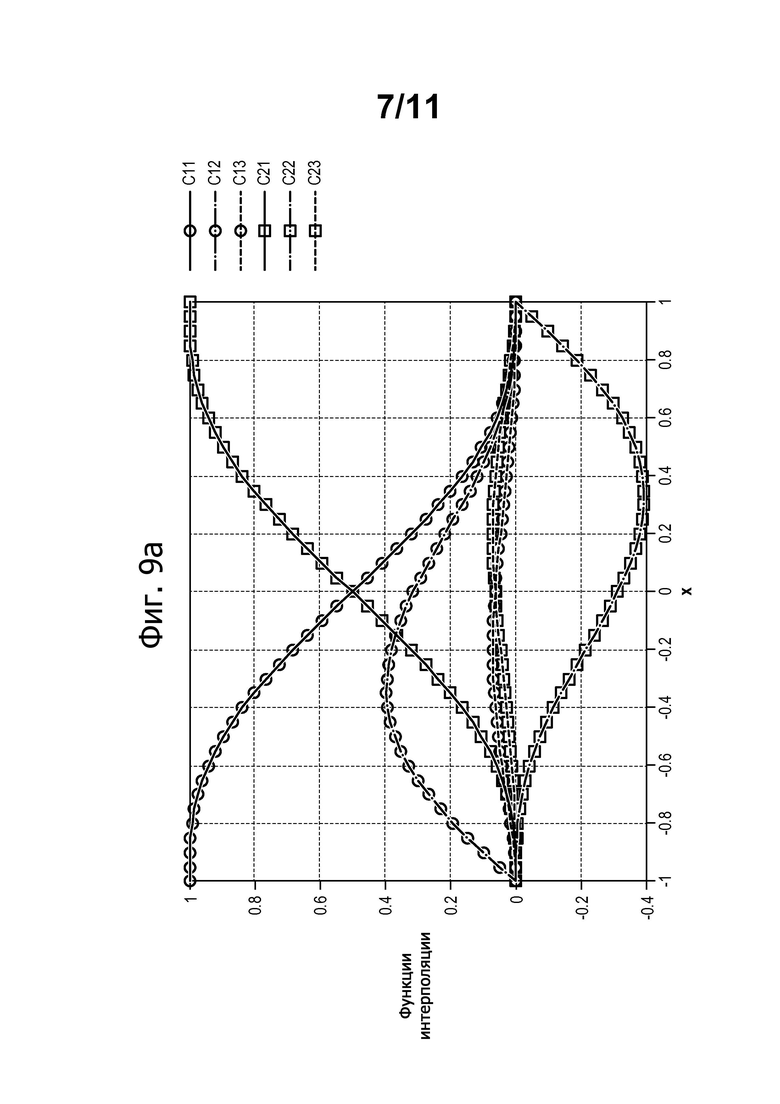
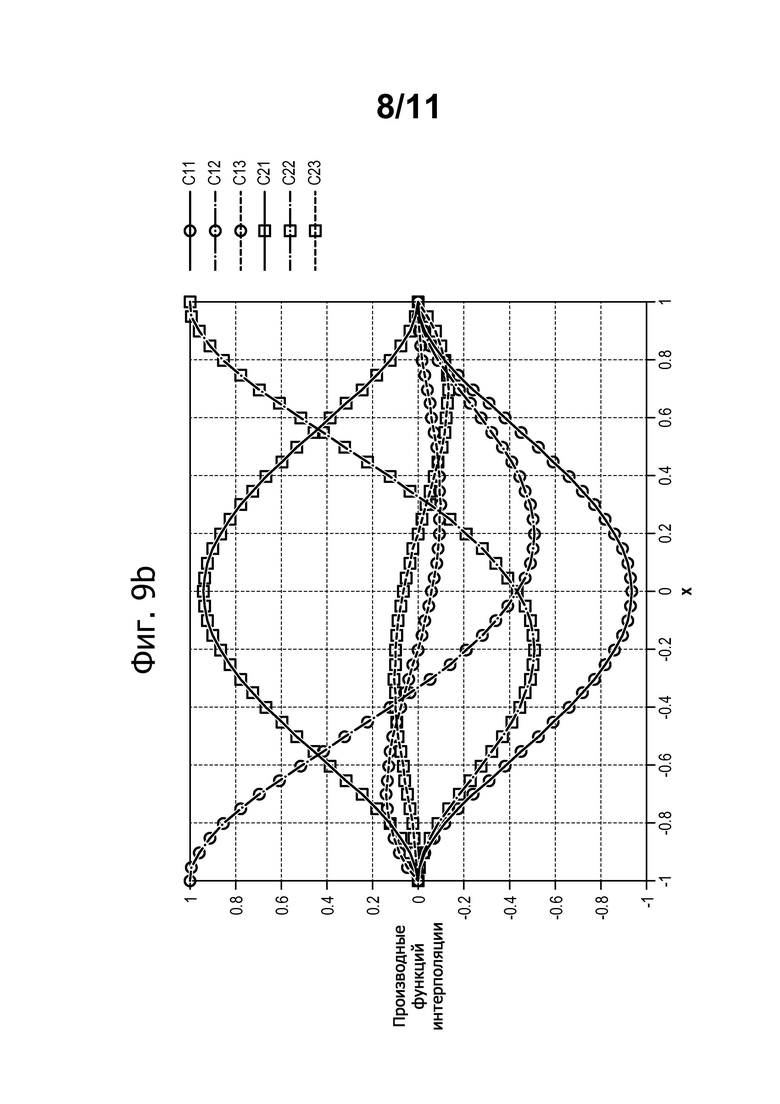
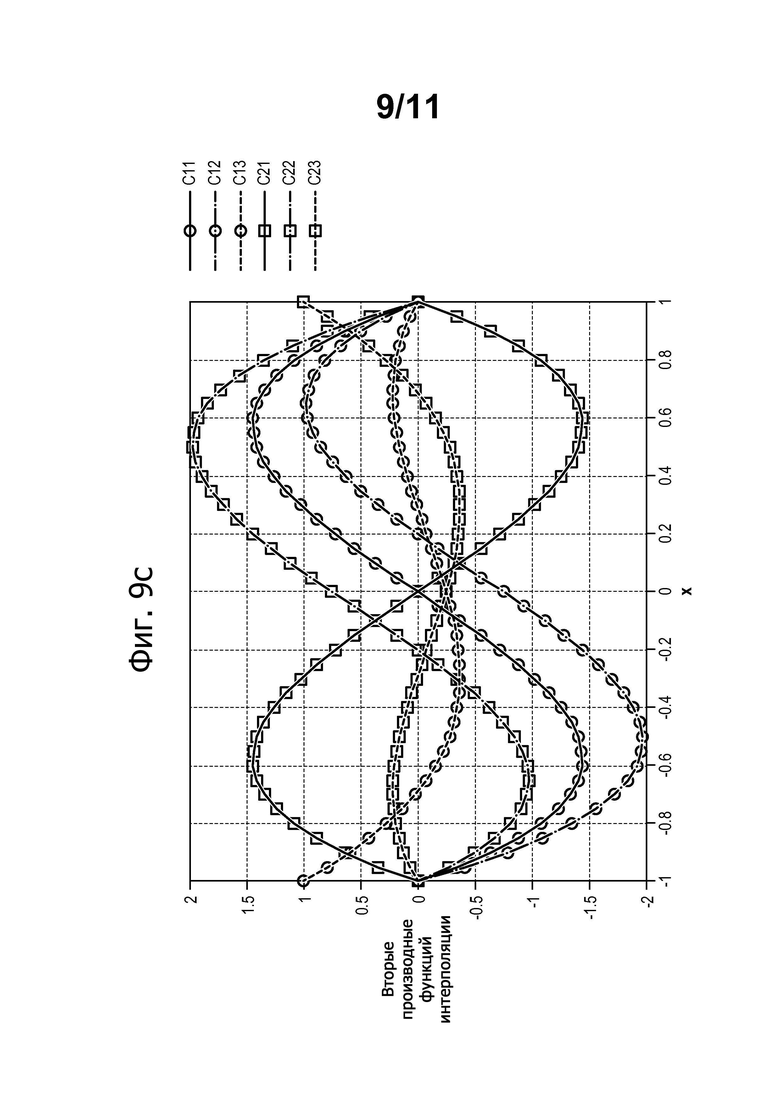
фиг. 9а-9с - функции одномерной формы, полученные посредством обобщения конечных элементов и служащие для вычисления энергии кривизны;
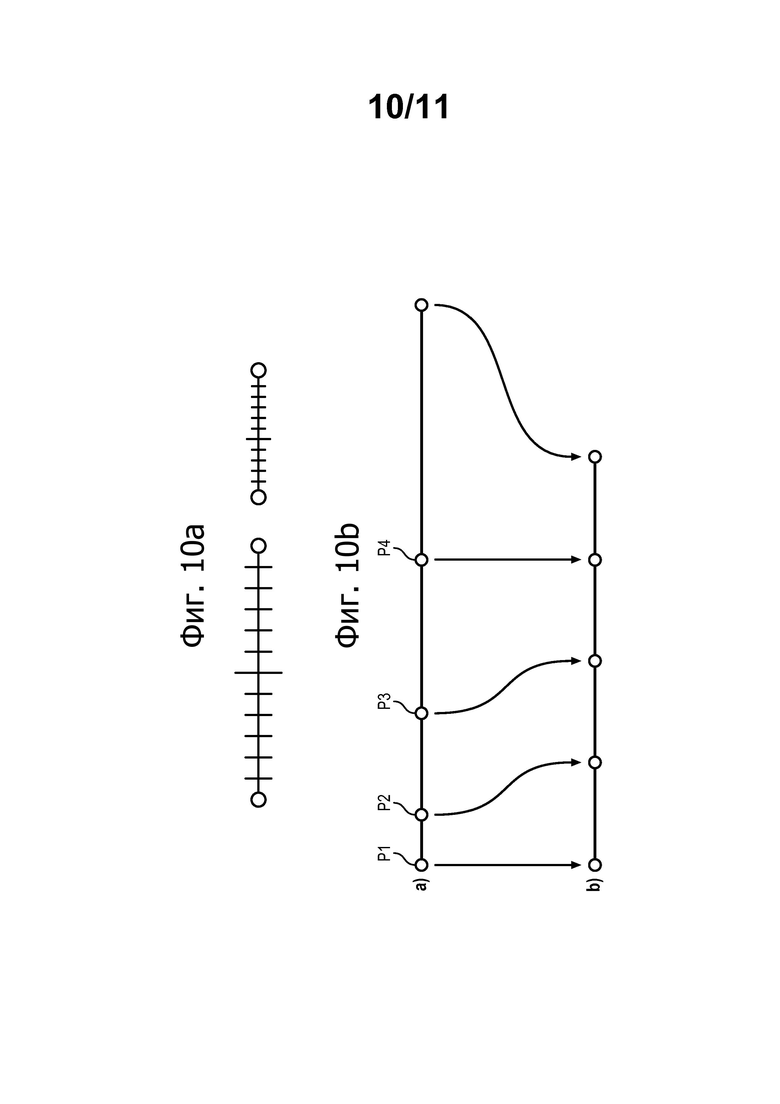
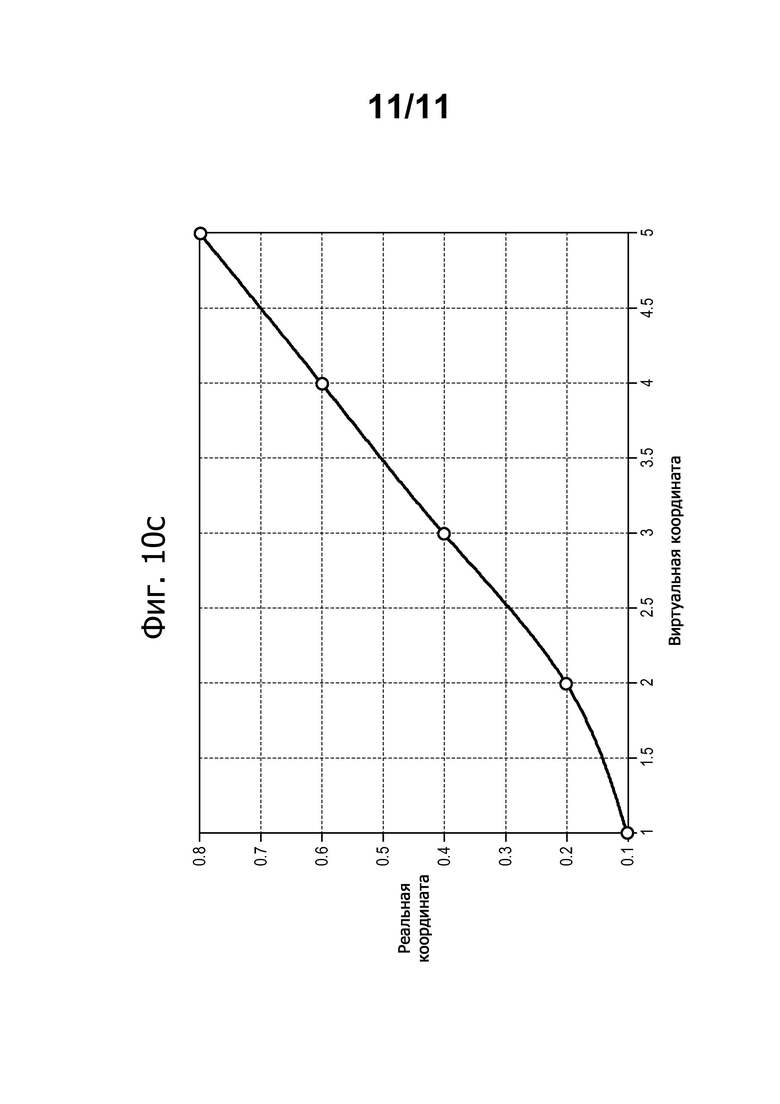
фиг. 10а-10с иллюстрируют изменение отображения для сглаживания метрик.
Подробное описание
На фиг. 2 показана система 10 интерполяции значений коэффициентов K интенсивности напряжений (КИН) анализируемой детали 20, которая моделирована цифровым методом. Как было указано во вступлении, коэффициент КИН K разлагается на три параметра KI, KII, KIII. Описание будет касаться только KI.
Анализируемая деталь 20 является деталью, которая предназначена для использования в авиации и для которой необходимо иметь возможность оценивать срок службы. Как правило, показанная на фиг. 3 деталь 20 является лопаткой компрессора или турбины, диском двигателя, фланцем, креплением двигателя, картером. Этот список представлен в качестве примера, поскольку для осуществления способа тип детали не имеет значения.
Система 10 содержит блок 12 обработки данных, например, компьютер или сервер, который имеет средства 14 вычисления, выполненные с возможностью осуществления способа, который будет подробно описан ниже, и предпочтительно имеет также память 16. Средства 14 вычисления могут представлять собой, например, вычислительное устройство типа процессора, микропроцессора, микроконтроллера и т.д. Память 16 может представлять собой, например, жесткий диск, запоминающее устройство типа флэш-памяти или удаленное пространство хранения типа «облака».
Блок 12 обработки данных может быть также выполнен с возможностью осуществлять цифровое моделирование, такое как моделирование при помощи конечных элементов, анализируемой детали 20. Моделирование методом конечных элементов позволяет получать для каждого шага распространения данные, относящиеся к указанной детали и к распространению трещины.
В частности, для каждого шага распространения можно получать значения КИН в соответствующих точках и положение этих точек, как правило, вдоль фронта трещины. Положения представляют собой, например, координаты узлов сетки, образующей фронт трещины. Можно получать данные, относящиеся к треснутой поверхности: кроме координат узлов, поверхности трехмерных элементов, образующие одну среди поверхностей трещины. Эти данные хранятся в виде таблицы взаимосвязи, классически применяемой в рамках метода конечных элементов. Можно также получать другие данные, такие как сетка треснутой поверхности, а также сетка фронта.
Далее со ссылками на фиг. 4 следует описание способа 100 интерполяции значений КИН трехмерной трещины, моделированной при помощи конечных элементов.
Этот способ 100 предпочтительно применяют также, чтобы улучшить интерполяцию коэффициентов КИН. Это будет описано ниже.
На первом этапе Е1 на анализируемой детали 20 осуществляют цифровое моделирование. Это моделирование позволяет получить вышеупомянутые данные.
В предпочтительном варианте выполнения это моделирование осуществляют при помощи метода конечных элементов или расширенного метода конечных элементов.
Этот этап Е1 осуществляет либо блок 12 обработки данных системы, либо другая система.
В обоих случаях блок 12 обработки данных системы осуществляет этап Е2 получения данных (созданных на этапе Е1). В частности, для каждого моделированного фронта трещины определяют первый набор данных, который включает в себя значения КИН в соответствующих точках на фронте трещины и их соответствующее положение, и второй набор данных, который включает в себя указанные выше данные, относящиеся к треснутой поверхности (координаты узлов, определяющие фронт трещины, а также поверхностную сетку одной из поверхностей трещины, например, таблицу взаимосвязи поверхностей соответствующих трехмерных элементов). Располагая множеством моделированных фронтов на разных шагах, можно, таким образом, получить множество наборов первых и вторых данных.
На самом деле речь идет о первом этапе способа интерполяции, поскольку этап Е1 моделирования не обязательно осуществляют для последующей интерполяции.
На этапе Е3 проблему геометрии трещины в трех измерениях сводят к проблеме плоской трещины с прямым фронтом. Плоская трещина с прямым фронтом является стандартной моделью, известной специалисту в данной области. Для этого получают термодинамическую эквивалентность, основанную на равенстве рассеиваемой энергии между двумя моделями. Физическое обоснование приведено ниже.
Первый закон термодинамики для трансформации фронта бесконечно малой трещины, дает в выражении в виде плотности энергии на единицу длины фронта трещины:
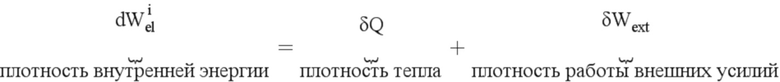
Второй закон термодинамики позволяет выразить необратимость трансформации:

Плотность рассеянной энергии всегда является положительной. Член dSurf представляет приращение треснутой поверхности на единицу длины фронта трещины в ходе бесконечно малой трансформации. Эта величина является однородной по длине: в некотором роде речь идет о приращении длины трещины в «термодинамическом» смысле термина. Таким образом, появляется «физическая» величина, которую можно учитывать для осуществления интерполяции, имеющей физический смысл.
Указанные выше элементы позволяют сделать первоначальную проблему трехмерного трещинообразования эквивалентной проблеме распространения плоской трещины с прямым фронтом при плоской упругости. В более общем смысле можно рассмотреть случай адаптированной упругости, то есть материал уже мог быть сначала подвергнут пластической деформации, но распространение трещины происходит при циклическом усталостном упругом нагружении.
Температурное поле может изменяться с течением времени, но температурное поле не подвержено пространственному изменению. Следовательно, усталостный цикл связывают с температурой.
Одним из предположений при моделировании является то, что закон распространения трещины является законом Париса с поправкой Элбера (ссылки [5], [6]), представленным в виде следующего уравнения:
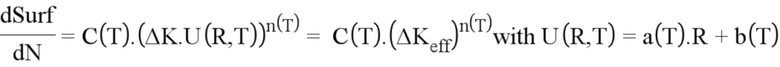
где C(T) и n(T) - коэффициенты Париса, а a(T) и b(T) - параметры закона закрытия трещины Элбера, ΔK - размах коэффициента КИН, который позволяет обойтись без нагрузочного отношения (то есть отношения R=Kmin/Kmax), и ΔKeff - эффективное значение коэффициента КИН, которая учитывает эффект закрытия трещины. Связь между ΔK и ΔKeff установлена Элбером.
Теперь приращение dSurf треснутой поверхности за цикл связано с эффективным значением ΔKeff коэффициента интенсивности напряжений.
Существует связь между K (или, соответственно, ΔKeff) и степенью восстановления энергии G (или, соответственно, эффективным значением ∆Geff указанной степени), которую выражают при помощи следующих отношений:
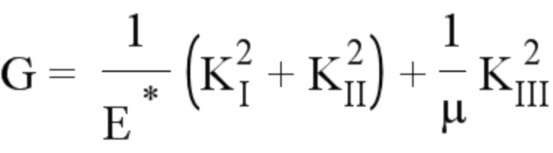

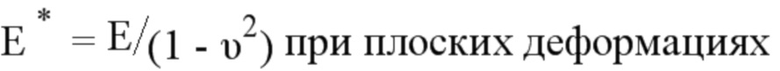
где Е является модулем Юнга, Е* является эквивалентным модулем Юнга, μ является модулем сдвига, υ является коэффициентом Пуассона.
Коэффициент КИН известен в каждой точке фронта трещины и для каждого шага распространения из цифрового моделирования на этапе Е1 и получен на этапе Е2.
Заменяя в предыдущих соотношениях значения на размах значений, получают по определению соотношение между степенью восстановления энергии и эффективным значением коэффициента интенсивности напряжений (s является криволинейной абсциссой вдоль фронта трещины):
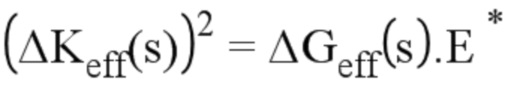
Энергию, рассеиваемую в ходе процесса трещинообразования, получают при помощи следующего соотношения (сохраняя предположение бесконечно малой трансформации, то есть рассматривая только один цикл нагружения):

Значение dSurf определено при помощи данных, относящихся к треснутой поверхности, вычисленных при цифровом моделировании на этапе Е1 и полученных на этапе Е2.
Принимая за аксиому эквивалентность проблемы трехмерного трещинообразования и проблемы плоского трещинообразования с прямым фронтом, можно уравнять рассеиваемые энергии и длины фронта трещины. Следовательно, можно записать:
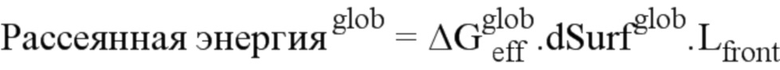
Обозначение “glob” значит, что данные относятся к моделированию при плоском трещинообразовании с прямым фронтом.
Плоское трещинообразование с прямым фронтом тоже происходит в соответствии с законом Париса. Следовательно, получаем
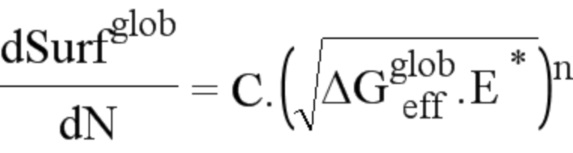
Если уравнять обе рассеянные энергии и переписать уравнение, получим следующее соотношение
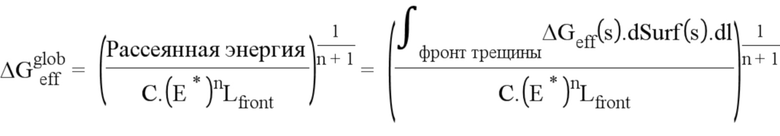
Однако dSurfglob/dN = dSurfglob (так как в данном случае dN = 1, поскольку мы рассматриваем только один цикл) является однородным по длине трещины. Следовательно, его интегрирование в течение времени между первым циклом и последним циклом позволяет получить эквивалентную длину трещины dSurfglob, обозначаемую как длина а, с точки зрения термодинамики. При этом получаем длину, которая имеет физический смысл.
Установленное выше соотношение между 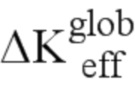 и
и 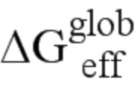 позволяет ввести эффективное значение коэффициента КИН в предыдущее уравнение.
позволяет ввести эффективное значение коэффициента КИН в предыдущее уравнение.
Таким образом, получаем соотношение, связывающее эффективное значение общего эквивалентного коэффициента КИН при моделировании плоской трещины с прямым фронтом с длиной трещины dSurfglob, то есть с длиной а. Эти данные в дальнейшем можно интерполировать.
Эта физическая конструкция является достоверной при любом обобщении. Однако она требует знания всей информации по проблеме для каждого цикла нагружения, что предполагает большие затраты с точки зрения времени вычисления и объема памяти для сохранения всех результатов (необходимо моделировать по меньшей мере около тысячи циклов). Вычисления при помощи конечных элементов часто осуществляют с фиксированным максимальным шагом распространения вдоль фронта трещины или производят заранее на заданном числе циклов (например, 10, 100 или 1000). Это вынуждает снизить степень дискретизации, чтобы сократить время вычисления.
Следовательно, закон распространения можно заменить на:
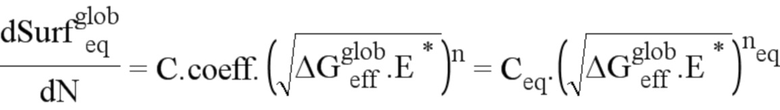
где 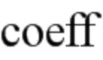 является коэффициентом, позволяющим предварительно интегрировать несколько циклов.
является коэффициентом, позволяющим предварительно интегрировать несколько циклов.
Это равнозначно замене коэффициентов закона Париса С и n на коэффициенты 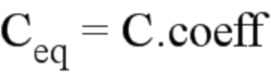 и
и  .
.
Следовательно, 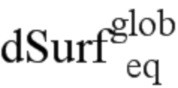 и
и 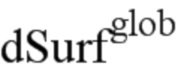 связаны следующим образом:
связаны следующим образом:
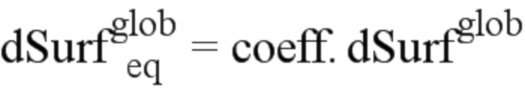
Кроме того, член 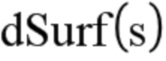 заменен поверхностью
заменен поверхностью 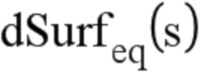 , которая является приращением между двумя шагами моделированного распространения (то есть не является бесконечно малой).
, которая является приращением между двумя шагами моделированного распространения (то есть не является бесконечно малой).
Подводя итог, можно сказать, что предыдущее рассуждение можно с приближением применить, производя вышеуказанные замены, и эквивалентную длину всегда можно выводить одинаково.
Таким образом, на этапе Е3 на основании множества первых и вторых наборов данных, полученных на этапе Е2, то есть данных КИН вдоль разных моделированных фронтов трещин с разными шагами и данных, относящихся к треснутым поверхностям, и с учетом вышесказанного можно определить общее эффективное значение 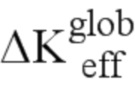 коэффициента КИН и соответствующую длину а плоской трещины с прямым фронтом. Это определение выполняют с помощью блока 12 обработки данных.
коэффициента КИН и соответствующую длину а плоской трещины с прямым фронтом. Это определение выполняют с помощью блока 12 обработки данных.
Для данного фронта трещины моделированные данные коэффициента КИН позволяют узнать K (первый набор данных) и при помощи предыдущих уравнений позволяют вычислить 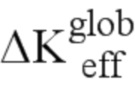 , а данные треснутой поверхности
, а данные треснутой поверхности 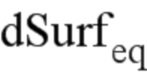 (второй набор данных) позволяют вычислить длину а. С учетом множества данных, соответствующих каждому фронту, получают множество пар (а,
(второй набор данных) позволяют вычислить длину а. С учетом множества данных, соответствующих каждому фронту, получают множество пар (а, 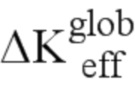 ).
).
Полученную эквивалентность можно также применить для плоской трещины с прямым фронтом. Нижеследующее соотношение показывает, что система остается инвариантной:
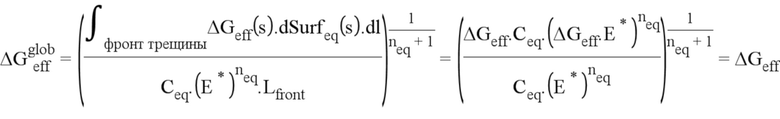
Отсюда вытекает, что треснутые поверхности являются одинаковыми, то есть конечная система соответствует первоначальной задаче. Это доказывает достоверность метода, основанного на термодинамическом анализе проблемы.
На фиг. 5, на плоскости показаны пары (а, 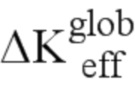 ). Обозначения F1, F2, F3, F4 приведены со ссылкой на фиг. 1 и указывают, какому фронту первоначальной трещины соответствуют точки графика. Речь идет об упрощении записи.
). Обозначения F1, F2, F3, F4 приведены со ссылкой на фиг. 1 и указывают, какому фронту первоначальной трещины соответствуют точки графика. Речь идет об упрощении записи.
Можно напомнить, что целью является обеспечение возможности определения КИН для состояний трещины, которые не были моделированы цифровым методом, то есть для состояний, которые проявляются строго между двумя последовательными шагами.
Для этого на этапе Е4 осуществляют интерполяцию значений 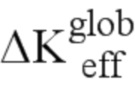 в зависимости от длины а. Интерполяцию осуществляют при помощи вычислительных средств 14 блока 12 обработки данных.
в зависимости от длины а. Интерполяцию осуществляют при помощи вычислительных средств 14 блока 12 обработки данных.
Интерполяцию можно производить с применением нескольких методов. Предпочтение отдается интерполяциям, которые не создают дополнительных данных для задачи или при которых добавляется лишь минимальная информация. Для этого применяют кусочно-линейную интерполяцию IL или интерполяцию с минимизацией энергии кривизны IMC. Можно также осуществлять оба вида интерполяции, учитывая, что они могут иметь разное применение.
На фиг. 6 показаны эти два вида интерполяции.
Интерполяцию с минимизацией энергии кривизны можно рассматривать как метод, основанный на физических рассуждениях, характерных для проблемы трещинообразования. Действительно, в научно-технической литературе по этому поводу указано, что, если трещина распространяется без разветвления, то изменение коэффициента интенсивности напряжений при расширении трещины можно представить в виде бесконечно дифференцируемой функции. Это значит, что имеет смысл вычислять кривизну такой функции.
Кроме того, минимизация энергии кривизны происходит в нескольких физических ситуациях, например, в физике мыльных пузырей или, в целом, в физике мембран.
На фиг. 7 показана линейная интерполяция между тремя точками. Этот пример показывает, что аппроксимацию интерполяции можно улучшать при помощи полиномов. Аппроксимация будет тем лучше, чем выше степень полинома. Можно также показать, что максимальное отклонение между линейной интерполяцией и полиномиальной интерполяцией стремится к нулю, когда степень полинома стремится к бесконечности. Таким образом, линейную интерполяцию можно рассматривать как переход к пределу на бесконечности, который можно применять для бесконечно дифференцируемой функции.
Этот подход придает также «физический» характер как кусочно-линейной интерполяции, так и интерполяции, основанной на минимизации энергии кривизны.
Осуществление интерполяции состоит в дополнении недостающей информации при помощи принципа, который должен как минимум соблюдать «физику» рассматриваемой задачи, то есть не вводить элементы, которые нарушали бы некоторые фундаментальные уравнения, которым подчиняется задача.
Именно по этой причине интерполяция с минимизацией энергии кривизны является «физическим» методом, так как она не противоречит теории механики разрыва. При первом рассмотрении метод кусочно-линейной интерполяции не является физическим, но его можно рассматривать как переход к границе метода общей полиномиальной интерполяции, который в широком смысле позволяет сделать метод кусочно-линейной интерполяции тоже почти «физическим».
С другой точки зрения, метод линейной интерполяции можно рассматривать как метод минимизации расстояния между точками. Этот подход позволяет отнести его к категории оптимальных методов. Линейная интерполяция минимизирует расстояние, тогда как другая минимизирует энергию кривизны под напряжениями положений связываемых точек. Минимизацию расстояний можно рассматривать как средство связывания точек без введения дополнительных данных в первоначальную задачу, и это дает в результате непрерывное поле. В случае второго метода вводят по меньшей мере одну дополнительную информацию, которая свидетельствует о том, что поле является равномерным. В этом случае минимизация энергии кривизны является оптимальным методом в том смысле, что вводимую информацию минимизируют, тогда как метод линейной интерполяции является оптимальным, в том смысле что минимизируют чисто математические данные.
Наконец, на этапе Е5 после этапа интерполяции интерполированные данные сохраняют, чтобы иметь к ним доступ для другого применения. Обычно сохранение производят в памяти 16. Как правило, говорят о «формуляре». Формуляр представляет собой таблицу, в которой приведены коэффициенты интенсивности напряжений в зависимости от длины трещины.
Следовательно, на этапе Е4 интерполяции создают файл в текстовом формате или в виде таблицы, содержащей формуляр, то есть объединяющий преобразованные данные и интерполированные преобразованные данные. На этапе Е5 этот файл сохраняют в памяти.
Действительно, как было указано выше, к получению формуляра обычно прибегают для вычисления срока службы детали. Следовательно, далее со ссылками на фиг.4 следует описание способа 200 определения срока службы анализируемой детали 20.
На этапе E’1 блок 12 обработки получает формуляр, вычисленный на этапе Е4 и/или сохраненный на этапе Е5 предыдущего способа. Этот этап получения может просто состоять в получении доступа к памяти 16.
На этапе Е’2 осуществляют способ вычисления срока службы детали при распространении усталостной трещины. Такой способ описан в документе [7].
Достаточно использовать существующее правило и заменить формуляр КИН формуляром, предложенным согласно настоящему изобретению, чтобы определить срок службы при распространении трещины.
Этот способ 200 можно осуществлять при помощи другой системы, отличной от описанной выше.
Уточнение погрешности
При наличии всех данных, относящихся к решаемой задаче, результат интерполяции будет всегда одним и тем же, независимо от используемого метода интерполяции, и будет соблюдать все «физические» условия задачи. Как правило, в интервалах I1 на фиг. 6 интерполяция воспринимается интуитивно как качественная; в интервалах I2 она воспринимается интуитивно как менее качественная.
Так, можно отметить отклонения между двумя оптимальными интерполяциями, называемыми «физическими или математическими», которые являются средством, позволяющим определить недостаток информации, которая была бы полезной для улучшения интерполяции или степени надежности при интерполяции.
Это рассуждение приводит к необходимости этапа проверки релевантности, показанного на фиг. 6.
На двух взаимозаменяемых подэтапах Е41 и Е42 интерполяции производят кусочно-линейную интерполяцию и интерполяцию по энергии кривизны.
Следует отметить, что строго между двумя значениями длины, соответствующими двум последовательным моделированным шагам, существуют разности δ значения 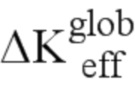 между двумя интерполяциями.
между двумя интерполяциями.
На подэтапе Е43 вычисляют по меньшей мере одну из разностей δ, которую на подэтапе Е44 сравнивают с заранее определенным пороговым значением VSP.
Заранее определенный порог VSP выбирают в зависимости от требуемого качества интерполяции.
Можно также сравнить значение этих разностей для каждой зоны между двумя последовательными шагами или сравнить среднее значение или максимальное значение и т.д. В целом речь может идти о величине δr, характеризующей разность. Эта величина δr показывает, что существует отклонение, которое можно определить количественно при помощи указанных выше функций.
Наконец, осуществляют подэтап Е45 сравнения между характеристической величиной δr и порогом VSP.
Если характеристическая величина δr меньше порога VSP, можно считать, что обе интерполяции являются качественными и что данные, если они были моделированы, являются близкими к двум значениям интерполяции.
Если характеристическая величина δr превышает порог VSP, то можно считать, что существует слишком большая погрешность в интерполяции и что желательно и даже необходимо получить новые моделированные значения. Для этого генерируют команду для вычисления, - на основании цифрового моделирования анализируемой детали 20, как правило, с применением метода конечных элементов (или расширенного метода конечных элементов), - по меньшей мере одного значения коэффициента интенсивности напряжений КИН и положения фронта трещины между двумя последовательными шагами. Иначе говоря, блок 12 обработки выдает команду для осуществления части этапа Е1 с меньшим шагом по меньшей мере для одного моделирования.
Таким образом, говорят о более точной дискретизации по длине трещины.
Например, можно принять заранее определенное пороговое значение VSP за 2%. Критерий зависит от технических требований.
Например, можно решить, что δr=δ и что, при δr/max (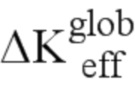 среди линейной интерполяции и интерполяции по кривизне) > 2% для данного значения длины а, создается команда на повторное вычисление моделирования.
среди линейной интерполяции и интерполяции по кривизне) > 2% для данного значения длины а, создается команда на повторное вычисление моделирования.
Наконец этап Е5 сохранения может включать в себя сохранение двух интерполяций и величин, характеризующих разности δr и/или разности δ.
Приложение 1: пример интерполяции с минимизацией энергии кривизны
Интерполяция посредством минимизации энергии кривизны дает достоверные физические предсказания только в случае плоской трещины с прямым фронтом, показанной на фиг. 8, где σ обозначает напряжение, и а обозначает длину трещины. Однако описанный выше способ позволяет рассматривать с точки зрения термодинамики любую трехмерную трещину как трещину, отвечающую этим свойствам.
Для осуществления этой интерполяции необходимо определить энергию кривизны.
Определяют функцию f следующим образом (х является «виртуальной» длиной трещины, которую до этого называли а):
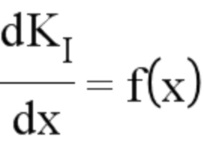
Необходимость введения «виртуальных» длин трещины детально пояснена в приложении 2.
Функцию f можно записать как ссылочную кусочно-линейную комбинацию представленных ниже полиномиальных функций (степени 5, чтобы обеспечивать равномерность С2 во всем диапазоне изменения «виртуальной» длины трещины, и речь идет об обобщении классических конечных элементов):
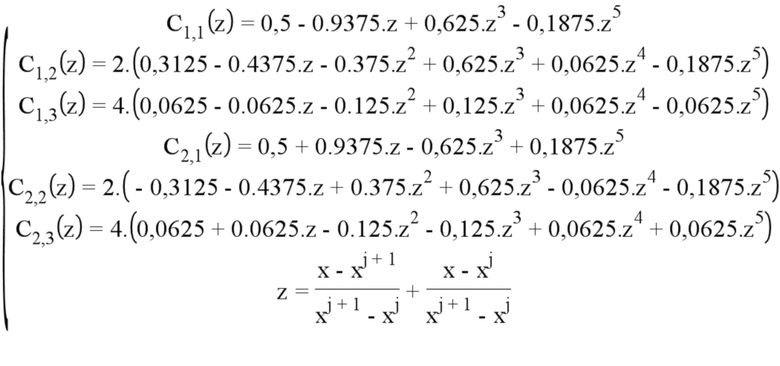
Первый индекс указывает на номер узла, в котором было определено узловое значение.
Второй индекс указывает на характер узлового значения:
1. Узловое значение коэффициента интенсивности напряжений (КИН)
2. Узловое значение производной относительно переменной z коэффициента КИН
3. Узловое значение второй производной относительно переменной z коэффициента КИН.
Связанный с этими функциями трехмерный элемент определен таким образом, чтобы первый узел находился на z = -1 и чтобы второй узел находился на z = 1.
Криволинейная абсцисса, соответствующая кривой, показывающей изменение коэффициента интенсивности напряжений в зависимости от «виртуальной» длины трещины, выражена как:
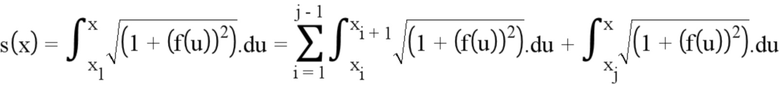
При этом:
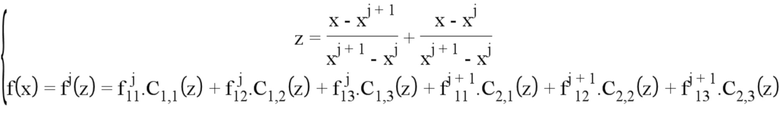
Следует отметить, что степени свободы 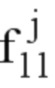 и
и  известны. Оптимизация будет касаться других степеней свободы.
известны. Оптимизация будет касаться других степеней свободы.
Отсюда получаем (Lx является длиной виртуального элемента):
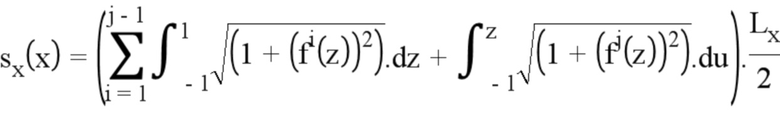
Унитарный касательный вектор получаем следующим образом:

На фиг. 9а-9с показаны значения функций форм С11, С12, С113, С21, С22 и С23 и их производной и второй производной. Следует отметить, что эти кривые отвечают своим специфическим условиям (0 или 1) на уровне узлов.
Теперь можно вычислить унитарный вектор, касательный к кривой К1. Приведенные выше формулы дают следующий результат:
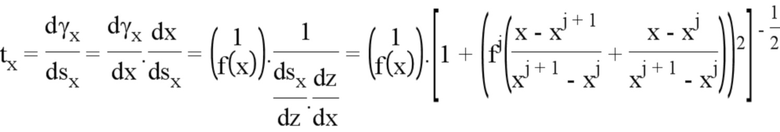
Остается лишь вычислить кривизну. Для этого вычисляют производную tx относительно криволинейной абсциссы:
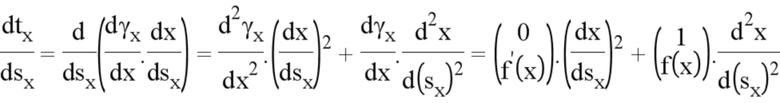
Для определения членов, производных по отношению к криволинейной абсциссе, применяют следующие дифференциальные формулы перехода от криволинейной координаты к виртуальной координате:
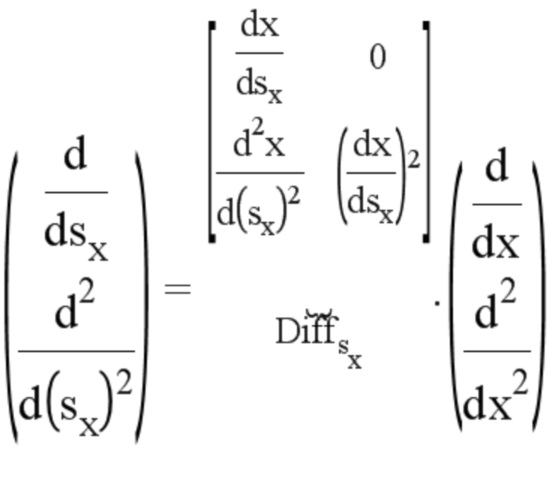
Это матричное уравнение является обратимым, что позволяет получить:
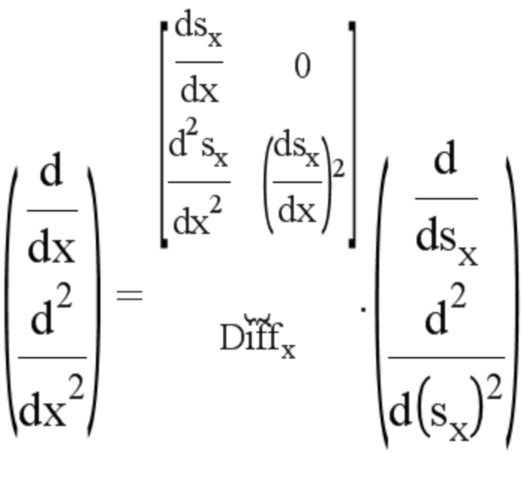
Можно отметить, что 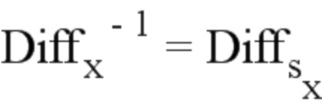 , что позволяет легко определить
, что позволяет легко определить 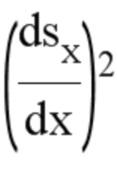 и
и  . В конечном итоге получаем:
. В конечном итоге получаем:
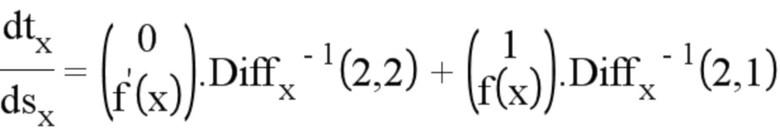
где:
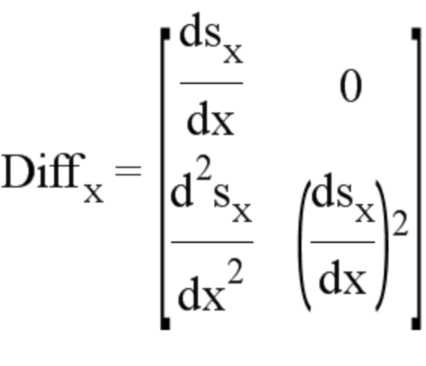
Отсюда автоматически вытекает кривизна:
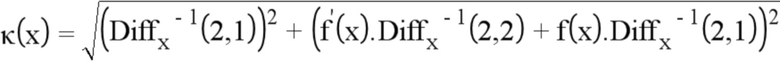
Далее следует уточнить матрицу 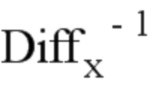 . Для этого применяют следующую классическую формулу инверсии матрицы 2×2:
. Для этого применяют следующую классическую формулу инверсии матрицы 2×2:

Таким образом:
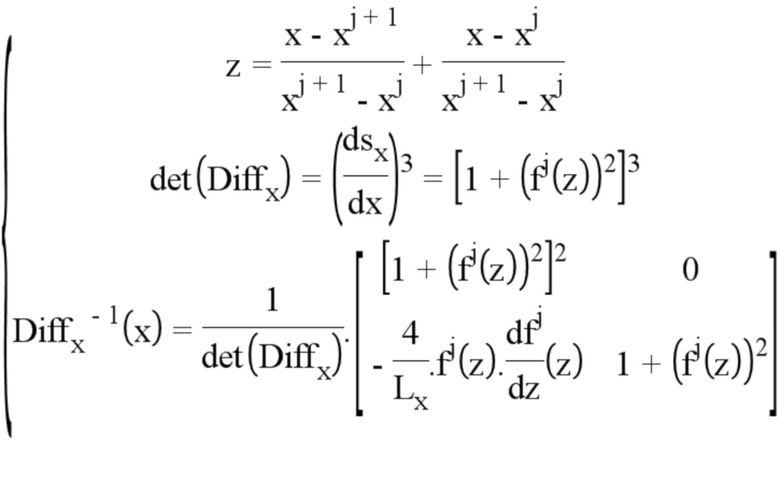
Минимизации подлежит следующий функционал (если сетка состоит из n-1 элементов):
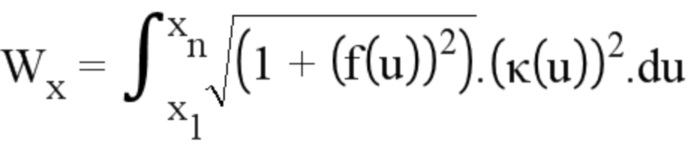
При этом предпочтительно применяют алгоритм Ньютона для определения параметров 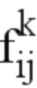 , минимизирующих этот функционал. Таким образом, необходимо знать вектор-градиенты и матрицы Гессе (относительно неизвестных переменных) величин, участвующих в задаче оптимизации.
, минимизирующих этот функционал. Таким образом, необходимо знать вектор-градиенты и матрицы Гессе (относительно неизвестных переменных) величин, участвующих в задаче оптимизации.

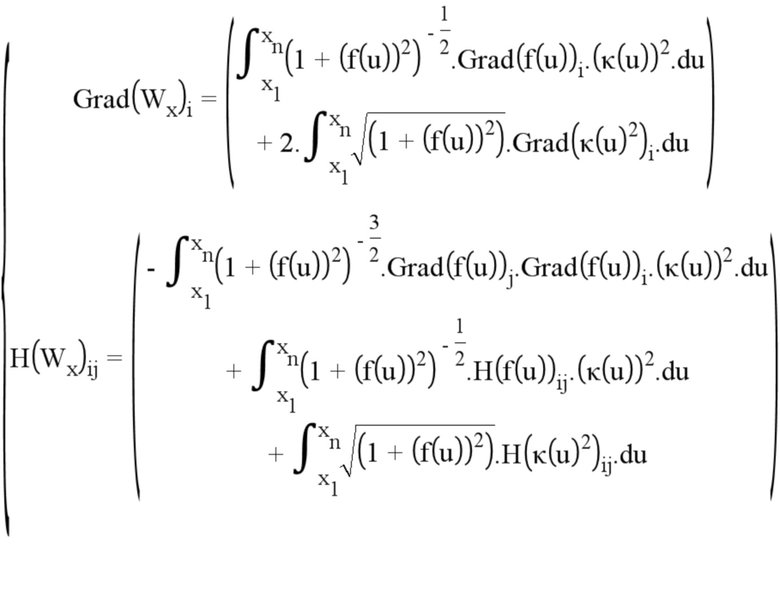
Этот алгоритм может применяться блоком 12 обработки.
Приложение 2: Метод переменных метрик
На фиг. 10а показаны точки фронта на разных шагах распространения. Следует отметить, что расстояние между одними и теми же точками фронта не является постоянным между двумя шагами, и это значит, что масштаб длины, соответствующий каждому элементу, является разным. В этом случае говорят о разных метриках.
Присутствие элементов с разными метриками (то есть прерывистыми в точке пересечения) и применение перехода равномерности С2 между элементами приводит к цифровой нестабильности.
Согласно другой точке зрения, элементы участвуют в функционале по-разному (учитывая их разные размеры), но все они переносят одинаковое количество информации. Независимо от точки зрения, это может привести к появлению цифровой погрешности, которую следует подвергнуть обработке.
Для решения этой проблемы достаточно использовать виртуальное пространство отображения, в котором все элементы интерполяции имеют одинаковые размеры. Например, если дискретными длинами трещины являются 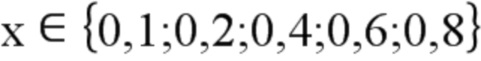 , то следует использовать
, то следует использовать 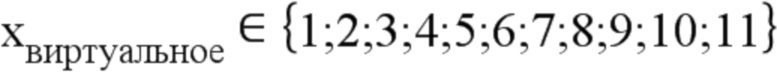 .
.
Чтобы перейти от виртуального отображения к реальному отображению, используют биекцию между двумя отметками (см. фиг. 10b).
Используют те же функции интерполяции, что и до этого. Соответствие между двумя пространствами отображения получают, задавая для каждого узла степени свободы 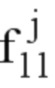 и
и  . Затем, чтобы получить метрику, которая изменяется «плавно» между каждым элементом, осуществляют описанный выше способ. Это позволяет получить сглаженное соответствие между двумя пространствами отображения, как показано на фиг.10с.
. Затем, чтобы получить метрику, которая изменяется «плавно» между каждым элементом, осуществляют описанный выше способ. Это позволяет получить сглаженное соответствие между двумя пространствами отображения, как показано на фиг.10с.
Ссылки
[1] Bueckner HGZ (1970), “A novel principle for the computation of stress intensity factors”, Angew, Math. Mech., Vol. 50, p. 529-546.
[2] Rice J.R. (1972), “Some remarks on elastic crack–tip stress fields”, Int. J. Solids and Structures, 8, 751-758.
[3] Rice J.R. (1989), “Weight function theory for three–dimensional elastic crack analysis”, Fracture Mechanics: Perspectives and Directions (Twentieth Symposium), ASTM STP 1020, R.P. Wei and R.P. Gangloff, Eds., American Society for Testing and Materials, Philadelphia, pp. 29-57.
[4] V. Lazarus (1997), “Some three-dimensional problems of the mechanics of brittle fracture”, Thesis, University of Paris 6.
[5] W. Elber. “The significance of fatigue crack closure”. ASTM STP, 486: 230-242, 1971.
[6] PC. Paris, F. Erdogan, 1963, “A critical analysis of crack propagation laws”. J Basic Eng 85, p/p 528-534.
[7] “NASGRO – Fracture Mechanics and Fatigue Crack Growth Analysis Software - Reference Manual”, Version 6.2, 2011.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ СРОКА СЛУЖБЫ ТРУБОПРОВОДА | 2014 |
|
RU2571018C2 |
| СПОСОБ УПРАВЛЕНИЯ ТРЕЩИНООБРАЗОВАНИЕМ В МАТЕРИАЛЕ И СООТВЕТСТВУЮЩЕЕ УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2016 |
|
RU2682583C1 |
| Устройство и способ прогнозирования и оптимизации срока службы газовой турбины | 2012 |
|
RU2617720C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СРОКА СЛУЖБЫ ТРУБОПРОВОДА | 2013 |
|
RU2518787C1 |
| МЕТОД ХАРАКТЕРИЗАЦИИ СОПРОТИВЛЕНИЯ УСТАЛОСТНЫМ НАПРЯЖЕНИЯМ ДЕТАЛИ, НАЧИНАЯ С ЕЕ ПРОФИЛЯ ПОВЕРХНОСТИ | 2007 |
|
RU2467306C2 |
| Способ оценки способности материала к торможению усталостного разрушения | 1987 |
|
SU1455276A1 |
| Способ оценки остаточного ресурса рабочего колеса гидротурбины на запроектных сроках эксплуатации | 2019 |
|
RU2721514C1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ ОЦЕНКИ ВЕЛИЧИН ДЕФЕКТОВ ПОСРЕДСТВОМ SAFT (СПОСОБА ФОКУСИРОВКИ СИНТЕЗИРОВАННОЙ АПЕРТУРЫ) | 2014 |
|
RU2615208C1 |
| ПРОДЛЕНИЕ СРОКА СЛУЖБЫ ДИСКА СИЛОВОЙ ТУРБИНЫ, ПОДВЕРЖЕННОГО КОРРОЗИОННОМУ ПОВРЕЖДЕНИЮ ПРИ ЭКСПЛУАТАЦИИ (ВАРИАНТЫ) | 2018 |
|
RU2737127C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК ТРЕЩИНЫ ГИДРОРАЗРЫВА ПЛАСТА | 2014 |
|
RU2550770C1 |

Изобретение относится к анализу распространения трещин в механических деталях. Сущность: предварительно получают цифровую модель поверхности детали, имеющей трещину и подвергаемой при эксплуатации циклическим нагрузкам. Выполняют оценку коэффициента интенсивности напряжений в детали на основе указанной цифровой модели детали, в рамках моделирования распространения усталостной трещины, при этом выполняют следующие этапы: - (Е2): из цифровой модели анализируемой детали (20) получают множество смоделированных значений в разных точках анализируемой детали (20), при этом указанное множество смоделированных значений включает в себя, для разных смоделированных шагов распространения трехмерной трещины, которая обнаруживается на указанной цифровой модели детали, совокупность смоделированных значений коэффициента интенсивности напряжений в соответствующих точках, положение этих точек и данные, относящиеся к треснутой поверхности указанной трещины, - (Е3): для каждого шага распространения и для указанной совокупности смоделированных значений для соответствующего шага определяют преобразованное эффективное значение общего эквивалентного коэффициента интенсивности напряжений, соответствующее эффективному значению коэффициента интенсивности напряжений плоской трещины с прямым фронтом, и определяют преобразованную длину рассматриваемой эквивалентной трещины, при этом указанные преобразованные значения определяют посредством уравнивания энергии, рассеиваемой в трехмерной трещине указанной цифровой модели, и энергии, рассеиваемой в трещине стандартной модели плоской трещины с прямым фронтом, при этом сами значения энергии определяют в соответствии с коэффициентами интенсивности напряжений, - (Е4): интерполируют преобразованные эффективные значения общего эквивалентного коэффициента интенсивности напряжений между двумя последовательными преобразованными длинами трещины; и - (Е5): сохраняют в памяти полученные интерполированные преобразованные эффективные значения общего эквивалентного коэффициента интенсивности напряжений вместе с соответствующими длинами трещины; и оценивают срок службы детали с использованием указанных сохраненных интерполированных преобразованных эффективных значений общего эквивалентного коэффициента интенсивности напряжений с соответствующими длинами трещины. Система для оценки срока службы детали содержит блок (12) обработки данных, содержащий средства (14) вычисления и память (16), при этом указанный блок обработки данных выполнен с возможностью осуществления способа оценки срока службы имеющей трещину детали, подвергаемой при эксплуатации циклическим нагрузкам и для которой имеется цифровая модель поверхности детали. Технический результат: возможность достоверно оценивать срок службы. 2 н. и 6 з.п. ф-лы, 10 ил.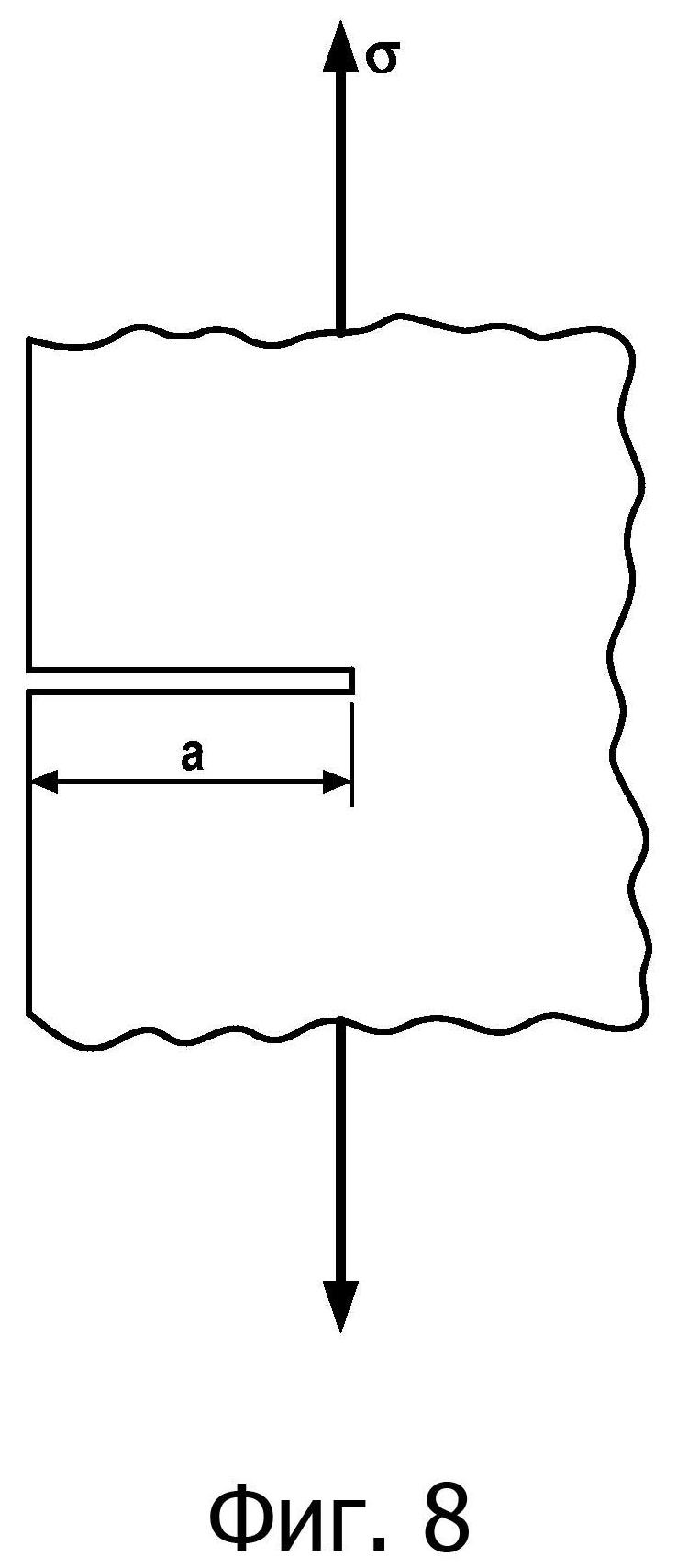
1. Компьютерно-реализуемый способ оценки срока службы имеющей трещину детали (20), подвергаемой при эксплуатации циклическим нагрузкам, для которой предварительно получена цифровая модель поверхности детали, характеризующийся тем, что
выполняют оценку коэффициента интенсивности напряжений в детали на основе указанной цифровой модели детали, в рамках моделирования распространения усталостной трещины, при этом выполняют следующие этапы:
- (Е2): из цифровой модели анализируемой детали (20) получают множество смоделированных значений в разных точках анализируемой детали (20), при этом указанное множество смоделированных значений включает в себя, для разных смоделированных шагов распространения трехмерной трещины, которая обнаруживается на указанной цифровой модели детали, совокупность смоделированных значений коэффициента интенсивности напряжений в соответствующих точках, положение этих точек и данные, относящиеся к треснутой поверхности указанной трещины;
- (Е3): для каждого шага распространения и для указанной совокупности смоделированных значений для соответствующего шага определяют преобразованное эффективное значение общего эквивалентного коэффициента интенсивности напряжений, соответствующее эффективному значению коэффициента интенсивности напряжений плоской трещины с прямым фронтом, и определяют преобразованную длину рассматриваемой эквивалентной трещины, при этом указанные преобразованные значения определяют посредством уравнивания энергии, рассеиваемой в трехмерной трещине указанной цифровой модели, и энергии, рассеиваемой в трещине стандартной модели плоской трещины с прямым фронтом, при этом сами значения энергии определяют в соответствии с коэффициентами интенсивности напряжений;
- (Е4): интерполируют преобразованные эффективные значения общего эквивалентного коэффициента интенсивности напряжений между двумя последовательными преобразованными длинами трещины; и
- (Е5): сохраняют в памяти полученные интерполированные преобразованные эффективные значения общего эквивалентного коэффициента интенсивности напряжений вместе с соответствующими длинами трещины; и
оценивают срок службы детали с использованием указанных сохраненных интерполированных преобразованных эффективных значений общего эквивалентного коэффициента интенсивности напряжений с соответствующими длинами трещины.
2. Способ оценки по п. 1, в котором на этапе (Е4) интерполяции применяют кусочно-линейную интерполяцию.
3. Способ оценки по п. 1, в котором на этапе (Е4) интерполяции применяют интерполяцию посредством минимизации энергии кривизны.
4. Способ оценки по п. 1, в котором этап (Е4) интерполяции включает в себя следующие подэтапы:
- (Е41) интерполяция с применением линейной интерполяции,
- (Е42) интерполяция с применением интерполяции посредством минимизации энергии кривизны, при этом оба вида интерполяции являются взаимозаменяемыми,
- (Е43) вычисление по меньшей мере одной величины, характеризующей разность эффективных значений общего эквивалентного коэффициента интенсивности напряжений между двумя интерполяциями, при этом указанную разность вычисляют строго между двумя значениями длины трещины, соответствующими двум последовательным шагам,
- (Е44) сравнение указанной величины, характеризующей разность, с заранее определенным порогом,
- (Е45) если величина, характеризующая разность, превышает указанный порог, генерируют команду на вычисление, на основании цифровой модели анализируемой детали (20), значений коэффициента интенсивности напряжений и значений положения трещины между двумя последовательными шагами.
5. Способ оценки по любому из пп. 1-4, в котором перед этапом получения (Е2) выполняют этап (Е1) вычисления с применением моделирования методом конечных элементов на последовательных шагах изменения трещины в анализируемой детали (20), при этом указанное моделирование осуществляет блок (12) обработки данных.
6. Способ оценки по любому из пп. 1-5, в котором указанные цифровые данные, выбранные на этапе (Е2) получения данных, получают посредством моделирования методом конечных элементов или расширенным методом конечных элементов.
7. Способ оценки по любому из пп. 1-6, в котором для этапа (Е3) определения:
первый набор данных позволяет определить эффективное значение степени восстановления энергии ΔG посредством следующих соотношений и их эквивалентности в отношении амплитуды:
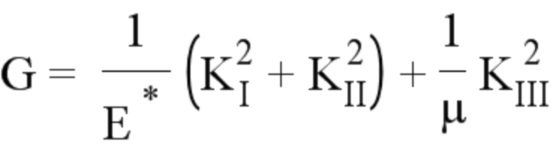
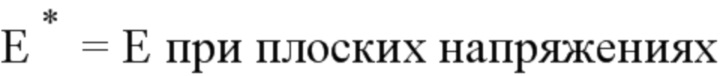
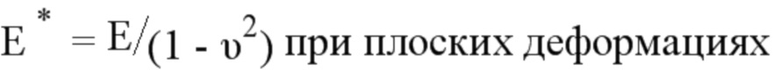
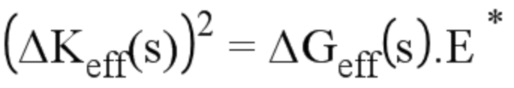 ,
,
где KI, KII и KIII - соответственно коэффициенты интенсивности напряжений КИН, соответствующие модам открытия трещины, плоского сдвига и антиплоского сдвига, 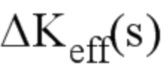 - эффективное значение коэффициента интенсивности напряжений,
- эффективное значение коэффициента интенсивности напряжений, 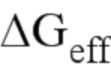 - эффективное значение степени восстановления энергии, s - криволинейная абсцисса вдоль фронта трещины, E - модуль Юнга, μ - модуль сдвига, E* - эквивалентный модуль Юнга, ν - коэффициент Пуассона,
- эффективное значение степени восстановления энергии, s - криволинейная абсцисса вдоль фронта трещины, E - модуль Юнга, μ - модуль сдвига, E* - эквивалентный модуль Юнга, ν - коэффициент Пуассона,
второй набор данных позволяет определить приращение dSurf треснутой поверхности,
причем указанные параметры позволяют получить значение рассеянной энергии:
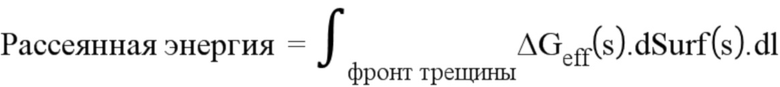
указанную рассеянную энергию уравнивают с рассеянной энергией трещины стандартной модели плоской трещины с прямым фронтом, которая имеет следующее выражение:
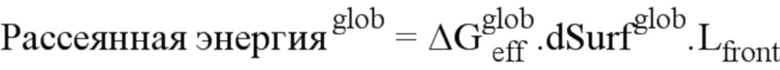
где обозначение glob относится к этой стандартной модели, а 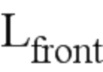 является длиной фронта трещины,
является длиной фронта трещины,
при этом благодаря моделированию с использованием закона Париса с параметрами закрытия трещины Элбера, устанавливают связь между dSurfglob и 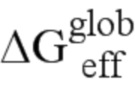
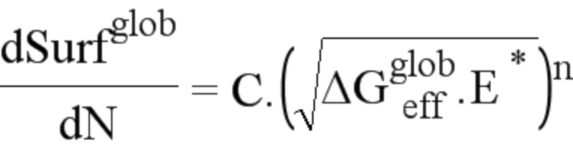 ,
,
где С и n - коэффициенты Париса,
при этом, уравнивая две указанные рассеянные энергии, получают:

и с помощью соотношений между  Geff и
Geff и  Keff определяют
Keff определяют 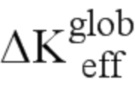 и определяют Surfglob, то есть указанную преобразованную длину эквивалентной трещины,
и определяют Surfglob, то есть указанную преобразованную длину эквивалентной трещины,
при этом указанный первый набор данных содержит значения коэффициента интенсивности напряжений в соответствующих точках на фронте трещины и их соответствующее положение, а указанный второй набор данных содержит данные, относящиеся к указанной треснутой поверхности.
8. Система для оценки срока службы детали, содержащая блок (12) обработки данных, содержащий средства (14) вычисления и память (16), при этом указанный блок обработки данных выполнен с возможностью осуществления способа оценки срока службы имеющей трещину детали, подвергаемой при эксплуатации циклическим нагрузкам и для которой имеется цифровая модель поверхности детали, по любому из пп. 1-7.
| Способ определения критического коэффициента интенсивности напряжения бетона после воздействия на него высоких температур | 2016 |
|
RU2621623C1 |
| МЕТОД ХАРАКТЕРИЗАЦИИ СОПРОТИВЛЕНИЯ УСТАЛОСТНЫМ НАПРЯЖЕНИЯМ ДЕТАЛИ, НАЧИНАЯ С ЕЕ ПРОФИЛЯ ПОВЕРХНОСТИ | 2007 |
|
RU2467306C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПОКАЗАТЕЛЕЙ БЕЗОТКАЗНОСТИ ИЗДЕЛИЯ ПО РЕЗУЛЬТАТАМ НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ | 2005 |
|
RU2301992C2 |
| CN 102279222 B, 15.05.2013. | |||
Авторы
Даты
2021-05-25—Публикация
2017-06-20—Подача