Изобретение относится к радиотехнике и может быть использовано в радиолокации для формирования фазокодоманипулированных (ФКМ) зондирующих сигналов, а также в системах связи.
Известны два способа формирования ансамбля (матрицы) D-кода. В первом способе [1, стр. 258] для построения матрицы D-кода размера N×N, где N=2k, k∈N, N - множество натуральных чисел, используется рекуррентное правило построения кода. То есть для построения D-кода порядка к необходимо предварительно построить коды меньшего порядка.
Во втором способе [2] для построения матрицы D-кода размера N×N, N=2k, используется трудоемкая процедура нахождения промежуточных векторов длины N через операции поэлементного умножения и сложения векторов.
Оба рассмотренных способа используются только для построения двоичных D-кодов длины N=pk, где р=2.
Наиболее близким к заявленному изобретению (прототипом) следует считать один из способов, изложенных в [3], где также используются два рассмотренных способа, но для построения р-ичных D-кодов длины N=pk, где р≥2, p - простое число.
Способ-прототип описывается следующим набором математических выражений:
 ,
,
j=1, 2, … k.
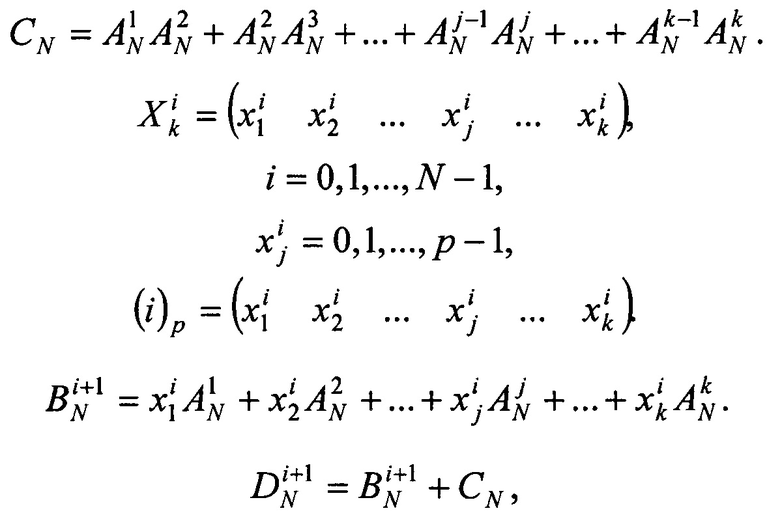
где (a)р - представление числа а в p-ичной системе счисления.
В данных математических выражениях все операции умножения и сложения векторов производятся поэлементно по модулю р.
Из анализа данного способа следует, что для получения любого элемента матрицы D-кода (элемента i+1-ой строки 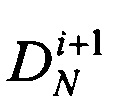 матрицы) следует предварительно вычислить вектора
матрицы) следует предварительно вычислить вектора  Кроме того, данный способ позволяет сформировать только один ансамбль D-кода порядка k (построить одну матрицу D-кода размера N×N, N=pk, р - простое число).
Кроме того, данный способ позволяет сформировать только один ансамбль D-кода порядка k (построить одну матрицу D-кода размера N×N, N=pk, р - простое число).
Целью изобретения является разработка способа (правила) формирования p-ичного D-кода порядка k, позволяющего построить множество из γ=2k-2 ансамблей D-кода порядка k (матриц D-кода размера N×N, N=pk, р - простое число, k≥2 - целое число).
На чертеже приведена структурная схема устройства, реализующего предлагаемый способ формирования множества ансамблей p-ичного D-кода порядка k.
Устройство, реализующее заявленный способ формирования множества ансамблей D-кода порядка k состоит из трех основных частей (фиг.): блок 1 формирования первой строки матрицы D-кода, блок 2 формирования матрицы системы функций Виленкина-Крестенсона (ВК) - Кронекера [4] и сумматор по модулю р 8, имеющий два входа и один выход, являющийся выходом всего устройства.
Значение элемента матрицы D-кода порядка k из x+1-ой строки и у+1-го столбца (см на чертеже) определяется согласно выражению:
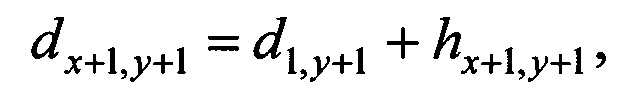
где dl,y+1 - значение элемента матрицы D-кода из первой строки и у+1-го столбца (на выходе сумматора 6);
hx+1,у+1 - значение элемента матрицы ВК-Кронекера из х+1-ой строки и у+1-го столбца (на выходе сумматора 7).
Блок 2 формирования матрицы ВК-Кронекера состоит (фиг.): регистр 3 на k ячеек памяти, имеющий один вход и k выходов, k умножителей 4 с двумя входами и одним выходом каждый и сумматор по модулю р 7, имеющий k входов и один выход.
Согласно чертежу i-ый выход регистра 3 блока 2 формирования матрицы ВК-Кронекера при i=1, 2, …, k, k≥2 соединен с одним из входов i-го умножителя 4, второй вход которого соединен с i-ым выходом регистра 3 блока 1 формирования первой строки матрицы D-кода. Выход i-го умножителя 4 соединен с соответствующим входом сумматор по модулю р 7.
Тогда значение элемента матрицы ВК-Кронекера из x+1-ой строки и y+1-го столбца определяется согласно следующему выражению [4, стр. 62]:

где i=1, 2, k, k≥2 - номер умножителя 4 из блока 2 формирования матрицы ВК-Кронекера (фиг.), совпадающий с номером выхода регистра 3 блока 2 формирования матрицы ВК-Кронекера и с номером входа сумматора по модулю р 7;
 - номер строки в p-ичной системе счисления (вектор
- номер строки в p-ичной системе счисления (вектор  на фиг.);
на фиг.);
 - номер столбца в p-ичной системе счисления (вектор
- номер столбца в p-ичной системе счисления (вектор  на фиг.);
на фиг.);
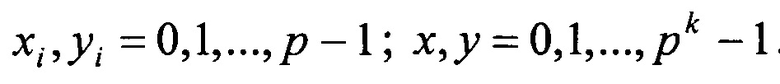 .
.
Т.о. блок 2 формирования матрицы ВК-Кронекера по записанным в регистры 3 номерам строки и столбца вычисляет значение элемента матрицы ВК-Кронекера.
Блок 1 формирования первой строки матрицы D-кода состоит (фиг.): регистр 3 на k ячеек памяти, имеющий один вход и k выходов, k-1 умножителей 4 с двумя входами и одним выходом каждый, k-2 электронных ключа 5 (при k=2 в схеме электронный ключ 5 отсутствует, т.к. со входами первого умножителя 4 непосредственно соединены первый и второй выходы регистра 3), имеющих до k-1 сигнальных входов, один сигнальный выход и один управляющий вход каждый, и сумматор по модулю р 6, имеющий k-1 входов и один выход.
Согласно фиг. i-ый выход регистра 3 блока 1 формирования первой строки матрицы D-кода при i=2, 3, …, k, k≥2 соединен с одним из входов i-1-го умножителя 4, второй вход которого соединен с выходом i-2-го электронного ключа 5, имеющего i-1 сигнальных входов, соединенных с соответствующими выходами регистра 3 (при i=2 в схеме на чертеже электронный ключ 5 отсутствует, т.к. со входами первого умножителя 4 непосредственно соединены первый и второй выходы регистра 3). Каждый электронный ключ 5 соединяет один из своих входов с соответствующим входом умножителя 4. Выход i-1-го умножителя 4 при i=2, 3, …, k, k≥2 соединен с соответствующим входом сумматор по модулю р 6.
Тогда значение элемента матрицы D-кода из первой строки и у+1-го столбца определяется согласно следующему выражению:
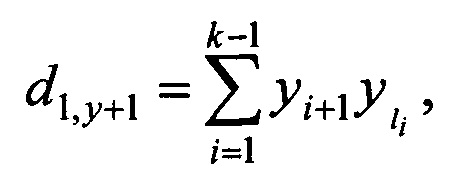
где i=1, 2, k-1, k≥2 - номер умножителя 4 из блока 1 формирования первой строки матрицы D-кода, один из входов которого соединен с i+1-ым выходом регистра 3 блока 1 формирования первой строки матрицы D-кода, а второй вход соединен с выходом i - 1-го электронного ключа 5;
li=1, 2, …, i - номер выхода регистра 3 блока 1 формирования первой строки матрицы D-кода, который i - 1-ым электронным ключом 5 соединяется с соответствующим входом i-го умножителя 4.
При этом для всех электронных ключей 5 блока 1 формирования первой строки матрицы D-кода должно выполняться условие:

Т.о. значение элемента матрицы D-кода порядка k из х+1-ой строки и у+1-го столбца определяется согласно выражению:

(здесь операция сложения выполняется по модулю р).
При этом число ансамблей (различных матриц) D-кода порядка к будет равно
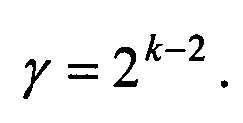
Рассмотрим пример формирования троичного D-кода порядка k=3 с длиной кодовых слов N=33=27, позволяющего заявленным способом построить γ=23-2=2 ансамбля D-кода.
Сформируем первые строки двух различных матриц (ансамблей) D-кода порядка k=3. Остальные строки матрицы D-кода получаются из первой строки поэлементным сложением по модулю р с соответствующими строками матрицы ВК-Кронекера.
В этом случае из общих выражений получаем:
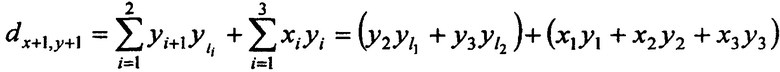 ;
;
(x)3=(x3 x2 x1); x1,x2,x3=0,1,2; х=0, 1, …, 26;
(y)3=(y3 y2 y1); y1,y2,y3=0,1,2; y=0, 1, ..., 26;
i=1, 2;
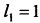 ;
;
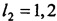 .
.
Откуда для двух ансамблей получаем:
d1,y+1=y2y1+y3y1 и
d1,y+1=y2y1+y3y2
(при х=0 (x)3=(0 0 0)).
При y=0, 1, …, 26 для первого ансамбля получим следующую первую строку D-кода:
(0 0 0 0 1 2 0 2 1 0 1 2 0 2 1 0 0 0 0 2 1 0 0 0 0 1 2).
Для второго ансамбля первая строка D-кода имеет следующий вид:
(0 0 0 0 1 2 0 2 1 0 0 0 1 2 0 2 1 0 0 0 0 2 0 1 1 0 2).
Литература
1. Варакин Л.Е. Теория сложных сигналов. М.: Сов. радио, 1970, 376 с.
2. Велти. Четверичные коды для импульсного радиолокатора. // Зарубежная радиотехника. 1961, №4, с. 3-19.
3. Ипанов Р.Н. Полифазные когерентные дополнительные сигналы. // Журнал радиоэлектроники: электронный журнал. 2017, №1. URL: http://jre.cplire.ru/jre/jan17/14/text.pdf.
4. Трахтман A.M., Трахтман В.А. Основы теории дискретных сигналов на конечных интервалах, М.: Сов. радио, 1975, 208 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство цифровой обработки полифазных дополнительных фазокодоманипулированных сигналов | 2017 |
|
RU2647632C1 |
| УСТРОЙСТВО ЦИФРОВОЙ ОБРАБОТКИ ПОЛИФАЗНЫХ ОРТОГОНАЛЬНЫХ ФАЗОКОДОМАНИПУЛИРОВАННЫХ СИГНАЛОВ | 2006 |
|
RU2346324C2 |
| ПЕРЕДАТЧИК С КОДОВЫМ РАЗДЕЛЕНИЕМ КАНАЛОВ С ВЫСОКОЙ СТРУКТУРНОЙ СКРЫТНОСТЬЮ ПЕРЕДАВАЕМЫХ СИГНАЛОВ | 2011 |
|
RU2494550C2 |
| Устройство для формирования многопозиционно-кодированных последовательностей | 1986 |
|
SU1336249A1 |
| Генератор периодических идеальных троичных последовательностей | 2017 |
|
RU2665290C1 |
| Устройство для операций над матрицами | 1990 |
|
SU1735868A1 |
| Устройство для реализации быстрых преобразований в базисах дискретных ортогональных функций | 1985 |
|
SU1292005A1 |
| Устройство для умножения | 1988 |
|
SU1578711A1 |
| Устройство для треугольного разложения ленточных матриц | 1988 |
|
SU1587540A1 |
| СИСТЕМА ДЛЯ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ С ИСПРАВЛЕНИЕМ ОШИБОК | 1991 |
|
RU2007042C1 |

Изобретение относится к области вычислительной техники. Техническим результатом является обеспечение возможности формирования множества ансамблей D-кода порядка k. Раскрыто устройство для формирования 2k-2 матриц p-ичного D-кода размером N×N, где N=pk, р - простое число, k≥2 - целое число, при этом вводом в устройство являются параметры х, у, где х, у=0, 1, …, pk-1, и параметры li, где i=1, 2, …, k-1, при этом li может принимать значения 1, 2, …, i и lk-1≠lk-2≠…≠l2, и на выходе устройства обеспечивается элемент dx+1,y+1 матрицы D-кода для номера строки х+1 и номера столбца у+1 матрицы. 1 ил.
Устройство для формирования 2k-2 матриц p-ичного D-кода размером N×N, где N=pk, р - простое число, k≥2 - целое число, при этом вводом в устройство являются параметры х, у, где х, у=0, 1, …, pk-1, и параметры li, где i=1, 2, …, k-1, при этом li может принимать значения 1, 2, …, i и lk-1≠lk-2≠…≠l2, и на выходе устройства обеспечивается элемент dx+1,y+1 матрицы D-кода для номера строки х+1 и номера столбца у+1 матрицы, при этом устройство содержит первый блок, второй блок и выходной сумматор по модулю р, при этом выходной сумматор по модулю р имеет первый вход, второй вход и один выход, при этом первый блок содержит регистр, имеющий один вход и k выходов, i=1, 2, …, k; k-1 умножителей, i=1, 2, …, k-1, при этом каждый из умножителей имеет первый вход, второй вход и один выход; k-2 электронных ключа, i=1, 2, …, k-2, при этом i-ый электронный ключ имеет один управляющий вход, i+1 сигнальных входов, j=1, 2, …, i+1, и один сигнальный выход; и сумматор по модулю р, имеющий k-1 входов, i=1, 2, …, k-1, и один выход; при этом второй блок содержит регистр, имеющий один вход и k выходов, i=1, 2, …, k; k умножителей, i=1, 2, …, k, при этом каждый из умножителей имеет первый вход, второй вход и один выход; и сумматор по модулю р, имеющий k входов, i=1, 2, …, k, и один выход; при этом на вход регистра первого блока обеспечивается параметр у и i-ый выход регистра первого блока соответствует коэффициенту yi разложения числа у в p-ичной системе счисления: (у)р=(yk yk-1 … yi … y1); при этом на вход регистра второго блока обеспечивается параметр х и i-ый выход регистра второго блока соответствует коэффициенту xi разложения числа х в p-ичной системе счисления: (х)р=(xk xk-1 … xi … х1); при этом на управляющий вход i-го электронного ключа первого блока обеспечивается значение параметра и на сигнальном выходе получается значение, поступившее на li+1-ый сигнальный вход; при этом j-ый сигнальный вход, j=1, 2, …, i+1, i-ого электронного ключа соединен с j-ым выходом регистра первого блока, а сигнальный выход i-ого электронного ключа соединен со вторым входом (i+1)-ого умножителя первого блока; при этом второй вход 1-ого умножителя первого блока соединен с 1-ым выходом регистра первого блока; при этом первый вход i-ого умножителя первого блока соединен с (i+1)-ым выходом регистра первого блока, а выход i-ого умножителя первого блока соединен с i-ым входом сумматора по модулю р первого блока; при этом первый вход i-ого умножителя второго блока соединен с i-ым выходом регистра первого блока, второй вход i-ого умножителя второго блока соединен с i-ым выходом регистра второго блока, а выход i-ого умножителя второго блока соединен с i-ым входом сумматора по модулю р второго блока; при этом выход сумматора по модулю р первого блока соединен с первым входом выходного сумматора по модулю р, выход сумматора по модулю р второго блока соединен со вторым входом выходного сумматора по модулю р, и выход выходного сумматора по модулю р является выходом всего устройства и обеспечивается элемент dx+1,у+1.
| СИСТЕМА ПЕРЕДАЧИ ЧЕТВЕРИЧНО-КОДИРОВАННЫХ РАДИОСИГНАЛОВ | 2001 |
|
RU2188516C1 |
| СИСТЕМА ПЕРЕДАЧИ ЧЕТВЕРИЧНО-КОДИРОВАННЫХ РАДИОСИГНАЛОВ | 2004 |
|
RU2258313C1 |
| Генератор последовательностей кодов | 1989 |
|
SU1675873A1 |
| Пресс для выдавливания из деревянных дисков заготовок для ниточных катушек | 1923 |
|
SU2007A1 |
Авторы
Даты
2018-10-25—Публикация
2017-09-22—Подача