Область техники
Изобретение относится к способам исследования образцов материалов при помощи их цифровых трехмерных моделей, в частности к изучению изменений, происходящих в результате некоторого воздействия на образец.
Предшествующий уровень техники
Изучение образцов материалов, например горных пород, может потребовать наблюдения структурных изменений при различных типах воздействия на образец. Типичными воздействиями являются: многофазная фильтрация газа, жидкости и твердого вещества через образец, химическое воздействие, механическое воздействие (деформация), нагрев, охлаждение, диффузия и т.п. Воздействие обычно тем или иным образом изменяет либо структуру самого образца, либо распределение веществ в объеме его пор.
Примером воздействия может также являться транспортировка или хранение образца, так как в ходе этих процессов образец тоже может претерпевать изменения.
Традиционно величина изменений, произошедших в образцах, характеризуется с помощью величин изменения различных объемных характеристик (физические размеры, массу, плотность, пористость, и т.д.). Широко известно множество различных методов определения указанных свойств. Например, пористость может быть измерена с помощью измерения зависимости давления от расхода газа в процессе насыщения образца, с помощью взвешивания насыщенного жидкостью образца или при помощи петрографического анализа шлифов (US 4562726, US 2840717). Очевидно, что для оценки величины изменений в образце необходимо применять эти методы дважды - до и после воздействия на образец.
Изменение смачиваемости образца ввиду изменения физических свойств поверхности пор может быть измерено с помощью метода Амотта (D. Tiab and Е.С. Donaldson, "Petrophysics: Theory and Practice of Measuring Reservoir Rock and Fluid Transport Properties", Gulf Professional Publishing, 2nd Edition, 371-373 (2004)). Сущность метода заключается в капиллярном вытеснении воды из полностью водонасыщенного образца жидкой углеводородной смесью (керосином) с последующим вытеснением из образца углеводородной смеси водой. Основным недостатком этого метода является низкая чувствительность вблизи нейтральных значений смачиваемости и высокая погрешность измерений в случае использования образцов малого размера, когда результаты измерения объемных характеристик становятся сопоставимы с погрешностью методов измерения.
Кроме того, упомянутые и подобные им методы имеют и другие недостатки:
- Отсутствие пространственного разрешения
- Невозможность определения непосредственной причины произошедших изменений
- Низкая чувствительность в случае малых изменений в образце - погрешность измерения может оказаться больше искомой разницы между измеряемыми величинами.
- Повреждение образца в процессе проведения измерений, что может затруднить обнаружение изменений от исследуемого воздействия.
Раскрытие изобретения
Предлагаемый способ оценки структурных изменений в образце в результате воздействия обеспечивает:
- Неразрушающий характер измерений
- Наличие пространственного разрешения
- Возможность определения непосредственной причины изменения структуры и свойств образца
- Высокую чувствительность в случае малых изменений в образце (т.е. даже если существенные изменения коснулись лишь небольшой доли образца).
В соответствии с предлагаемым способом сканируют, по меньшей мере, один образец материала и получают первое изображение каждого образца. Осуществляют воздействие на каждый образец, сканируют каждый образец после воздействия и получают второе изображение каждого образца.
Для каждого образца осуществляют совмещение первого и второго изображений в полном разрешении, используя по меньшей мере один фрагмент первого изображения и один фрагмент второго изображения, которые соответствуют одной и той же области образца.
После этого анализируют совмещенные изображения и производят оценку изменений в каждом образце, произошедших в результате воздействия на образец.
Предварительно может быть произведено пространственное совмещение первого и второго изображений каждого образца в грубом разрешении.
Круг возможных воздействий на образец достаточно широк и может включать, например, термические, химические или механические воздействия. Воздействие может также представлять собой транспортировку образца или его хранение. Например, когда на образец воздействует окружающая среда или в образце протекают некоторые внутренние процессы, изменяющие его.
Сканирование образца может быть осуществлено, например, посредством рентгеновской компьютерной томографии, нейтронной/позитронной томографии, позитрон-эмиссионной томографии, ядерно-магнитно-резонансной томографии, электронной микроскопии, лазерной флуоресцентной микроскопии, оптической микроскопии, конфокальной микроскопии, рамановской микроскопии.
Сканирования до и после воздействия может быть осуществлено разными методами.
Полученные изображения могут быть одномерными, двухмерными или трехмерными. Кроме того, каждая точка изображения (пиксел, воксел) может являться как одним числом, так и целым набором чисел.
Предварительно может быть произведена обработка, по меньшей мере, одного из двух полученных изображений образца для устранения искажений заранее известного характера.
Предварительная обработка изображений может включать, например, исправление масштаба изображений, геометрическую коррекцию, исправление цветовой палитры изображения.
В соответствии с одним из вариантов осуществления изобретения задают начальное приближение для совмещения полученных изображений.
Важной частью изобретения является анализ совмещенных изображений, который может включать, например, построение двухмерных гистограмм, анализ глубины повреждений, анализ зависимости количества повреждений от размера зерна.
При необходимости из совмещенных изображений может быть построено разностное изображение.
Каждый образец может быть подвергнут разным воздействиям (отличающимися как количественно, так и качественно) с последующим определением воздействия, вызвавшего изменения заданного типа и степени.
Существует возможность изучить эволюцию изменений в структуре образца при многократном одинаковом воздействии, а также при последовательности разных воздействий.
Краткое описание чертежей
Изобретение поясняется чертежами. На фиг. 1 представлена блок-схема одного из алгоритмов совмещения изображений образца. На фиг. 2 представлена блок-схема алгоритма грубого совмещения изображений образца. На фиг. 3 представлена блок-схема алгоритма лоскутного совмещения изображений образца. На фиг. 4 приведены примеры разностных изображений. На фиг. 5 приведен пример вычисления двухмерной гистограммы. На фиг. 6, 7 и 8 приведены примеры двухмерных гистограмм для различных пар изображений. На фиг. 9,а показан двухмерный срез микротомографического изображения песчаника в исходном состоянии. На фиг. 9,б - двухмерный срез микротомографического изображения песчаника после хранения (изображение совмещено с изображением, показанным на фиг. 9,а), а на фиг. 9,в показано их разностное изображение. На фиг. 10,а приведено изображение глинистого песчаника в исходном состоянии. На фиг. 10,б приведено изображение глинистого песчаника после заморозки, а на фиг. 10,в - разностное изображение.
Подробное описание изобретения
Предлагаемый способ реализуется следующим образом. По меньшей мере один образец материала подвергают какому-либо воздействию. Примерами воздействия являются: многофазная фильтрация флюидов/газа через образец, химическое воздействие, механическое воздействие, нагрев, охлаждение, диффузия и т.п. Воздействием может также являться транспортировка или хранение образца.
До и после воздействия осуществляют сканирование образца исследуемого материала. На сегодняшний день существует множество методик получения трехмерных изображений: конфокальная микроскопия, ультразвуковая томография, однофотонная эмиссионная компьютерная томография, магниторезонансная томография, позитрон-эмиссионная томография, рентгеновская томография, нейтронная томография и другие. Так же существует еще большее число методов получения двухмерных изображений образца: сканирующая электронная микроскопия, оптическая микроскопия, флуоресцентная микроскопия (в частности, - лазерная флуоресцентная микроскопия, рентгенофлуоресцентный анализ), акустическая микроскопия и другие. Очевидно, любое двухмерное изображение может считаться частным случаем изображения трехмерного. Результатом некоторых типов исследований, таких как зондовая микроскопия, профилирование температуропроводности обычно являются профили какой-либо характеристики - «одномерные изображения».
Таким образом, получаемые изображения могут быть одномерными, двухмерными или трехмерными. Кроме того, каждая точка изображения (пиксел, воксел) может являться как одним числом (например, на томограмме - коэффициент ослабления рентгеновского излучения в данной точке образца), так и целым набором чисел. Так при рентгеновском микроанализе поверхности образца на электронном микроскопе можно получить изображение, в каждой точке которого регистрируется дискретизированный спектр возбуждаемого электронным пучком рентгеновского излучения, испускаемого с поверхности образца, в некотором диапазоне энергий.
Следует отметить, что сканирование до и после воздействия в принципе может быть осуществлено разными методами. Например, и рентгеновская, и нейтронная томографии позволяют восстанавливать трехмерную внутреннюю структуру образца горной породы посредством различных физических величин. При этом на обоих изображениях могут быть выделены пустотные пространства образца до и после воздействия, совмещение которых позволит проанализировать произошедшие изменения в образце.
Для простоты изложения и одномерные, и двухмерные изображения далее по тексту считаются частным случаем трехмерных изображений.
Здесь и далее под трехмерным изображением будем понимать трехмерный массив, хранящийся в памяти компьютера. Этот массив можно также считать дискретной функцией I:Ω→ζ, где Ω - область определения дискретной функции, а ζ - область значений функции I. Область определения Ω дискретной функции I является пространством координат изображения. Например, точка A=[x, y, z], где x, y, z являются пространственными координатами точки (воксела) на изображении I (по определению), принадлежит Ω, что обычно обозначается как A∈Ω, при этом I(A)∈ζ.
В некоторых случаях полученное изображение может содержать какие-либо заранее известные искажения. Например, два изображения могут иметь незначительно отличающиеся пространства цветов, или, например, два реконструированных трехмерных рентгеновских изображения могут иметь несколько различный физический размер воксела. Во многих случаях изображения могут иметь заранее известный тип геометрического искажения. В случае наличия априорной информации об искажениях иногда возможна предварительная коррекция изображения с целью упрощения дальнейшего процесса совмещения. С другой стороны, этот шаг не является обязательным в случае, если характер искажений может быть учтен в самой процедуре совмещения.
В упомянутом примере, когда два изображения имеют различный размер воксела, возможны два варианта:
- Коррекция размера воксела перед процедурой совмещения и последующее совмещение без необходимости масштабирования изображения в процессе совмещения
- Не корректировать размер воксела, позволив алгоритму совмещения найти правильный масштаб (при этом пользователь может ограничить область поиска правильного коэффициента масштабирования)
Далее производят совмещение полученных изображений. Задача совмещения изображений в простейшем случае состоит в следующем. Даны два изображения, на которых представлен один и тот же объект, расположенный различным образом. Требуется найти такое пространственное преобразование для одного изображения, при котором объект, изображенный на нем, совпадет с объектом (самим собой), представленном на другом изображении.
Одним из частых способов упрощения данной задачи является использование существующих или искусственно внесенных в образец объектов-маркеров, легко выделяемых на совмещаемых изображениях. К таким маркерам могут, например, относиться характерные сколы, трещины, механические метки, контрастные (для используемого метода сканирования) частицы. В общем случае исследуемый образец может не содержать естественных маркеров. Введение же искусственных маркеров может быть нежелательным в виду дополнительного воздействия, разрушающего и/или модифицирующего структуру образца, которое никак не связано с основным исследуемым видом воздействия. Таким образом, подобный подход к упрощению задачи совмещения изображений имеет ограниченную область применения. Описываемое изобретение лишено данного недостатка.
В данном тексте мы ограничиваемся рассмотрением преимущественно преобразований подобия. Преобразование подобия - это преобразование евклидова пространства, при котором для любых двух точек A, B и их образов A', B' имеет место соотношение |A'B'|=k|AB|, где k - положительное число, называемое коэффициентом подобия. Данное преобразование позволяет осуществлять перемещение, поворот и масштабирование объекта. Его можно задать следующим набором параметров: x, y, z, ϕ, θ, ψ, s. Здесь параметры x, y, z связаны со смещением вдоль соответствующих пространственных осей, а ϕ, θ, ψ - с вращением вокруг осей x, y, z соответственно, s является «коэффициентом масштабирования».
Такое приближение оказывается вполне достаточным в большинстве встречающихся на практике случаев
На фиг. 1 в виде блок-схемы изображены основные этапы процесса совмещения изображений I1 и I2 в соответствии с одним из вариантов осуществления. На предварительном этапе (1) для сокращения требуемого количества вычислений может быть задано начальное приближение. На следующем этапе (2) при необходимости вычислительный алгоритм производит грубое совмещение изображений в низком качестве. На этапе (3) алгоритм производит «точную подстройку» параметров преобразования по фрагментам изображений в полном разрешении - так называемое лоскутное совмещение. В итоге по известным параметрам преобразования при необходимости может быть создано полное разностное изображение.
Далее эти этапы будут рассмотрены более подробно.
Основные процедуры описанного способа (получение изображения, выполнение алгоритма совмещения, а нередко и само осуществление воздействия на образец) реализуются с использованием электронных вычислительных систем. Эта система может быть единственной для всех упомянутых процедур. Однако, как правило, используются различные вычислительные машины для каждой из задач. Общие требования ко всем этим вычислительным системам состоят в наличии:
- процессора для выполнения необходимых команд и вычислений;
- памяти для хранения временной и постоянной информации (объемом достаточным для работы с получаемыми изображениями);
- устройств ввода и вывода для управления и контроля выполняемых процедур;
- а также возможности передачи информации через сеть или съемные носители.
В простейшем случае реализации изобретения такой вычислительной системой может быть персональный компьютер.
Современные коммерчески доступные рентгеновские сканеры могут достигать пространственного разрешения до 0.1 мкм/воксел при разрешении по цвету (коэффициенту поглощения используемых рентгеновских лучей) в 16 бит, при этом в результате реконструкции получается трехмерное изображение размером 4000×4000×4000 вокселов. Естественным образом высокое качество и разрешение получаемого изображения приводит к его большому размеру. Например, для описанных выше параметров, несжатое изображение будет занимать 40003×2=128 ГБ (здесь считается, что 1 ГБ=1000 МБ). Изображения подобного размера в настоящее время не могут быть обработаны за разумное время «прямолинейными» алгоритмами на современных персональных компьютерах.
Как правило, основанный на площадях алгоритм совмещения изображений (Image registration methods: a survey. Barbara Zitova'*, Jan Flusser, Image and Vision Computing 21 (2003) 977-1000) содержит два основных этапа: грубое предварительное совмещение изображений в низком качестве и совмещение изображений в полном качестве.
Во многих случаях первый этап вводится с целью ускорения процесса вычислений путем уменьшения требуемого количества итераций, использующих изображение в полном качестве. Однако даже с учетом этой оптимизации максимально достижимая производительность алгоритма окажется неудовлетворительной, особенно в случае, если суммарный размер изображений окажется больше имеющегося количества оперативной памяти вычислительной станции, что приведет к большому объему операций чтения/записи на более медленные носители информации.
На предварительном этапе предлагаемого способа с целью минимизации времени вычислений пользователь может самостоятельно выбрать набор соответствующих точек на совмещаемых изображениях. Таким образом, может быть задано начальное приближение для параметров совмещения. Несмотря на то, что начальное приближение зависит от оператора, конечный результат совмещения фактически не зависит от оператора, так как в процессе вычислений алгоритм сойдется к единственному верному преобразованию, независимо от начального приближения.
Пользователь может задавать точки при помощи имеющегося в его распоряжении графического интерфейса путем указания «похожих» на его взгляд точек на срезах изображений «до воздействия» и «после воздействия». То есть пользователь выбирает для каждого изображения «схожие» срезы, имеющие какую-либо общую особенность, затем пользователь выделяет упомянутую особенность на каждом из изображений, что приводит к созданию пары точек {Ai, Bi}. Пользователь может добавить любое количество пар точек. Для оценки начального приближения требуется, как минимум, 3 пары точек.
Параметры ([xm, ym, zm, ϕm, θm, ψm, sm]) преобразования подобия Tm, соответствующего выбранным парам точек, могут быть оценены по трем парам точек, например, с помощью метода Хорна (см., например, Berthold K.P. Horn "Closed-form solution of absolute orientation using unit quaternions", Journal of the Optical Society of America A, Vol. 4, page 629, April 1987). В случае если масштаб изображений известен достаточно точно, данным методом достаточно оценивать только параметры [xm, ym, zm, ϕm, θm, ψm].
Кроме того, можно оценить точность начального приближения, с целью определения «гиперпрямоугольника области поиска». Областью поиска решения задачи принято называть множество значений искомых переменных задачи, в которых будет произведен поиск ее решения. Так, задача по совмещению двух трехмерных изображений путем преобразования подобия в общем случае сводится к поиску семи значений параметров (переменных) [x, y, z, ϕ, θ, ψ, s] с соответствующей областью поиска: [R, R, R, [-180°;180°], [-90°;90°], [-180°;180°], s≠0], где R - множество действительных чисел. Как правило, в каждом конкретном случае поиск решения в такой бесконечной области не требуется. Часто область поиска искомого преобразования можно представить как гиперпрямоугольник, стороны которого параллельны координатным осям пространства искомых переменных. Диагональ гиперпрямоугольника [σx, σy, σz, σϕ, σθ, σψ, σs] будем называть «шириной области поиска», а центр области поиска совпадает с начальной оценкой [xm, ym, zm, ϕm, θm, ψm, sm] параметров преобразования.
Ширину области поиска при этом можно оценить через расстояние между точками, выбранными пользователем на первом изображении (Ai) и предсказываемыми преобразованием (Tm) положениями образов соответствующих точек (Bi):

где под |A| понимается модуль вектора A (евклидово расстояние от начала координат [0,0,0]). Соответственно, ширину области поиска можно оценить следующим образом:
σx=σ
σy=σ
σz=σ
σϕ=σ/Sx
σθ=σ/Sy
σψ=σ/Sz
σs=σ/min(Sx, Sy, Sz)
где Sx - наибольший из размеров вдоль оси x 1-го и 2-го трехмерных изображений.
В большинстве случаев пользователь может указать 3 пары точек достаточно быстро. Это, с одной стороны, позволяет экономить машинное время, а с другой (что, даже более важно) делает всю процедуру совмещения значительно более надежной.
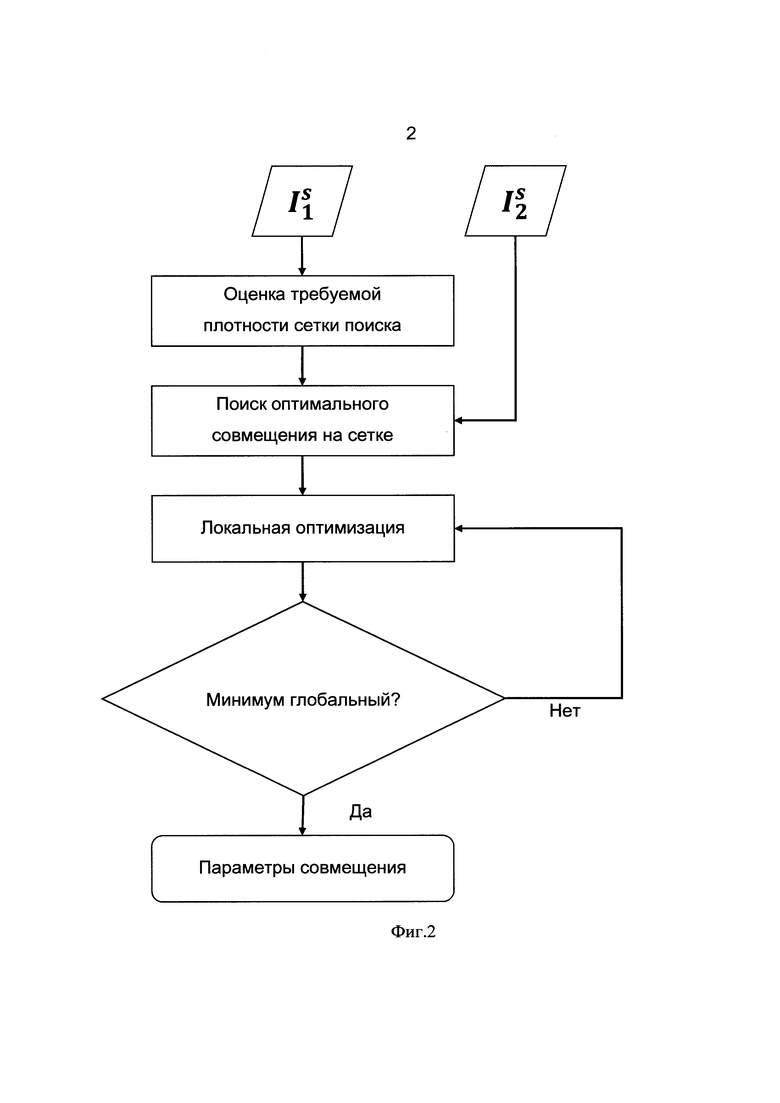
Следующий этап совмещения изображений - этап грубого совмещения - состоит из нескольких частей, что схематично изображено на фиг. 2. Основной задачей данного этапа является получения совмещения с точностью, достаточной для дальнейшего «лоскутного совмещения». Это позволяет использовать изображения с пониженным разрешением (имеющие более низкое пространственное разрешение и/или более грубо дискретизованное пространство цветов). Использование изображений с пониженным разрешением значительно повышает скорость вычислений.
Этап грубого совмещения изображений начинается с предварительного поиска по сетке. Поиск по сетке - широко известный прием во многих задачах оптимизации, позволяющий найти приблизительное положение глобального минимума, а также максимума или значения, удовлетворяющего какому-либо другому критерию (не ограничивая общности, далее рассматривается задача поиска минимума). В рассматриваемой задаче осуществляется минимизация функционала подобия изображений Q(Ti), который является мерой похожести (меньшее значение соответствует большему сходству) первого изображения и второго, подверженного преобразованию подобия Ti с параметрами [xi, yi, zi, ϕi, θi, ψi, si]. В простейшем случае совмещения двух изображений, имеющих одинаковое пространство цвета, полученных на одном устройстве и сохранивших между собой какие-либо общие структурные особенности, достаточным является использование простейшего L2-подобного функционала:

где:
Q - функционал подобия;
n - число пар пикселей в сравниваемых изображениях;
I 1 - первое трехмерное изображение;
I 2 - второе трехмерное изображение;
B - точка из множества Ω2.
A=T(B) - точка из множества Ω1, соответствующая точке B, согласно преобразованию T(B).
Простейшим методом поиска минимума функции является прямое вычисление ее значений в конечном наборе точек внутри области поиска. Удобно сформировать набор таких точек (например, в случае гиперпрямоугольной области поиска) равномерно по каждой из переменных. В результате получают сетку точек, на которой проводится поиск решения. Размер шага (шагов по каждой из переменной) сетки, или обратная величина шага - плотность сетки, существенным образом влияют на корректность найденного решения. Достаточной можно считать такую плотность сетки, при которой функция ведет себя монотонно между узлами сетки поиска. С другой стороны - увеличение плотности сетки ведет к быстрому росту требуемого на вычисления времени. Выбор оптимальной плотности сетки остается одной из основных сложностей, связанных с поиском по сетке.
В данном способе используется алгоритм, позволяющий автоматически оценить оптимальную для каждого конкретного совмещения плотность сетки. Обычно для быстрой оценки максимально возможного шага сетки (MAX_ST) достаточно проанализировать зависимость функционала подобия от параметров преобразования [x, y, z, ϕ, θ, ψ, s], взяв в качестве второго изображения (подвергающегося преобразованию) полную копию первого. Для этого вычисляется несколько точек зависимости функционала подобия от малых значений параметров преобразования [x, y, z, ϕ, θ, ψ, s].
Для каждого из 7 параметров преобразования выбирают минимальный значимый шаг сетки по этому параметру - ST и максимально возможный шаг сетки по этому параметру - MAX. Для каждого значения этого параметра от 0 до MAX с шагом ST преобразовывают изображение в соответствии с текущим значением оцениваемого параметра и вычисляют функционал подобия Q между исходным и преобразованным изображениями. По вычисленной зависимости определяют MAX_ST - значение оцениваемого параметра, ниже которого функционал подобия Q монотонно убывает. Выбранные таким образом шаги сетки по каждому из параметров обеспечивают монотонность изменения функционала подобия при совмещении исходного первого изображения со вторым, полученным после воздействия.
Поиск оптимального совмещения на заданной сетке представляет собой вычисление функционала подобия во всех узлах сетки, то есть для каждого из имеющихся в сетке наборов параметров преобразования или, другими словами, для всех имеющихся в гиперпрямоугольной области поиска значений параметров с соответствующим шагом MAX_ST по каждому из параметров. В качестве оптимального набора параметров преобразования выбирается тот, который соответствует минимальному значению функционала подобия.
Далее, в окрестности найденного на сетке решения производится поиск ближайшего локального минимума функционала подобия. В процедуре локальной оптимизации можно использовать фактически любой известный алгоритм оптимизации, или использовать несколько различных алгоритмов, выбирая затем лучший из полученных ими результатов. Например, ограниченный симплексный поиск оказывается достаточно быстрым и робастным в данном случае.
К сожалению, алгоритмы локального поиска нередко приводят к нахождению не глобального, а локального минимума. С целью проверки глобальности найденного минимума в описываемом алгоритме присутствует дополнительный шаг. После завершения процедуры локального поиска запускается еще одна аналогичная процедура, однако на этот раз начальной точкой выбирается точка, отстоящая на некоторое расстояние от найденного на предыдущем шаге минимума. В случае если найденный минимум является глобальным - второй поиск должен сойтись к тому же значению (с учетом задаваемой пользователем невязки), что и первый, в противном случае процедура поиска запускается еще раз. В случае если число повторных поисков превысит заданный порог, алгоритм уведомит пользователя об ошибке совмещения, таким образом, предлагая проверить и/или изменить параметры совмещения. Данная процедура основана на предположении о том, что область монотонности функционала подобия в случае глобального минимума больше, чем в случае ложного «локального» минимума. Такое предположение в большинстве случаев верно для встречающихся на практике трехмерных изображений.
После выполнения грубого совмещения изображений осталось лишь уточнить решение, вернувшись к полному (исходному) пространственному разрешению, то есть размеру пиксела (воксела). Однако, если размер полного изображения достаточно велик (как в случае современных микротомограмм), то даже одна итерация прямого локального совмещения полноразмерных изображений может занять значительное время. Прямой подбор параметров преобразования с использованием полных изображений является весьма неэффективным в данном случае, так как требует либо одновременного нахождения совмещаемых изображений в оперативной памяти, либо приводит к необходимости многократного чтения изображения с устройства хранения данных. Таким образом, метод прямого совмещения теряет свою эффективность по мере роста размеров изображения. Описываемый далее алгоритм позволяет совмещать большие трехмерные изображения без необходимости выполнять прямое сравнение полных изображений.
Блок-схема завершающего этапа совмещения изображений - лоскутного совмещения - представлена на фиг. 3, где I1 и I2 - совмещаемые изображения; 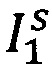 и
и  - фрагменты, вырезанные из соответствующих совмещаемых изображений.
- фрагменты, вырезанные из соответствующих совмещаемых изображений.
Общая сложность вычислений будет значительно меньше, если полное преобразование будет вычислено по нескольким независимо совмещенным фрагментам исходного изображения - «лоскутам» 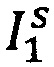 и
и  . Возможность совмещать малые части целых изображений появляется лишь благодаря предварительному грубому совмещению, после которого лоскуты, выделенные по одинаковым координатам для обоих изображений, приближенно будут соответствовать одной области образца. Каждая пара лоскутов совмещается полностью аналогично процедуре грубого совмещения.
. Возможность совмещать малые части целых изображений появляется лишь благодаря предварительному грубому совмещению, после которого лоскуты, выделенные по одинаковым координатам для обоих изображений, приближенно будут соответствовать одной области образца. Каждая пара лоскутов совмещается полностью аналогично процедуре грубого совмещения.
Упомянутые лоскуты могут быть выбраны как автоматически, так и вручную оператором. В качестве подобного лоскута может выступать любая, ограниченная часть изображения. Может быть использовано любое количество «лоскутов», в частности, можно полностью покрыть ими исходное изображение. Лоскуты могут также пространственно накладываться друг на друга. Процессы совмещения пар лоскутов совершенно независимы, что позволяет добиться высокого параллелизма вычислений. Целесообразным представляется формирование набора «лоскутов» в зависимости от типов образца и воздействия, а также цели исследования. Ниже рассмотрено несколько наиболее характерных случаев.
Если образец представляет собой твердое тело, лоскутное совмещение может быть использовано с целью ускорения процесса вычислений. Оно достигается за счет того, что оказывается достаточным совместить лишь несколько «лоскутов». В частности, могут быть использованы лоскуты, со следующими центрами (x, y, z):
1) (minx, cy, cz)
2) (maxx, cy, cz)
3) (cx, miny, cz)
4) (cx, maxy, cz)
5) (cx, cy, minz)
6) (cx, cy, maxz)
где minDIM и maxDIM соответствуют границам образца вдоль оси DIM. Эти значения выбираются автоматически, таким образом, чтобы лоскут соответствовал границе образца, а не пустому пространству возле него. DIM - одна из пространственных осей: x, y или z, a cDIM=(minDIM+maxDIM)/2 - центр образца вдоль оси DIM.
Такой выбор лоскутов позволяет добиться высокой точности совмещения благодаря расстоянию между лоскутами, близкому к максимально возможному. При этом вычислительная сложность остается сравнительно невысокой.
После совмещения всех запланированных лоскутов можно с высокой точностью оценить параметры преобразования подобия для всего образца, по парам точек, как описано выше, используя в качестве пар точек вершины лоскутов.
В случае если в процессе нахождения параметров пространственного преобразования для всего образца, в ходе этапа лоскутного совмещения в приближении твердого тела (то есть без деформаций) алгоритм получил неприемлемо большую величину ошибки, это может означать, что образец деформировался в процессе воздействия. Если подобная возможность разрешена оператором, алгоритм может автоматически перейти к использованию большего числа «лоскутов», с целью оценки и учета деформации образца.
Оценить трехмерное поле деформаций по совмещенным лоскутам можно, например, с помощью векторов смещений, описывающих смещение вершин «лоскутов» относительно глобального оптимального преобразования для совмещения изображений (в приближении твердого тела). Лоскутное совмещение деформированных образцов так же позволяет значительно повысить качество разностного изображения, которое, в этом случае может быть получено за счет «склейки» локально совмещенных лоскутов.
В некоторых случаях, одна часть образца повреждена значительно сильнее другой, и ее использование в процессе совмещения оказывается затруднительно. Большой относительный объем поврежденной части может привести к недостаточному качеству совмещения в случае прямого поиска оптимального преобразования по всему изображению. В описываемом алгоритме, пользователь может самостоятельно выбрать область, которая будет участвовать в процессе совмещения. Это может быть сделано как на грубом, так и на лоскутном этапе независимо. При этом разностное изображение будет построено для полного исходного изображения. Данная область так же может быть выбрана автоматически, как внутренняя часть образца, на некотором расстоянии от его границ.
При необходимости после того, как были вычислены параметры преобразования, совмещающего изображения до и после воздействия, можно построить разностное изображение, иллюстрирующее изменения, произошедшие в результате воздействия в структуре образца.
Обычно под разностным изображением понимают некую функцию от обоих совмещенных изображений, то есть:
 .
.
В качестве простейшего примера подобной функции можно предложить модуль разности Id(B)=|I1(T(B))-I2(B)|.
В случае приближения твердого тела, T(B) является преобразованием подобия. В случае деформируемого образца T(B) соответствует преобразованию подобия с последующей деформацией.
На фиг. 4 приведены два простых примера функции  . В случае сместившегося на некоторое расстояние круга, на разностном изображении проявляются две полярные области. В общем случае, анализ такого разностного изображения может дать информацию об изменениях в образце, включая миграцию частиц в поровом пространстве, появление/закупоривание пор и трещин различного масштаба, разрушение частиц породы и уплотнение или разрыхление вещества.
. В случае сместившегося на некоторое расстояние круга, на разностном изображении проявляются две полярные области. В общем случае, анализ такого разностного изображения может дать информацию об изменениях в образце, включая миграцию частиц в поровом пространстве, появление/закупоривание пор и трещин различного масштаба, разрушение частиц породы и уплотнение или разрыхление вещества.
Для оценки структурных изменений, произошедших в образце в результате воздействия, осуществляют анализ совмещенных изображений.
С целью количественной оценки и визуального анализа количества изменений, произошедших в структуре образца, могут быть вычислены различные статистические функции. Одной из практически полезных характеристик произошедших изменений является зависимость количества изменений от размера зерна.
Для многих типов пород исходное трехмерное изображение может быть кластеризовано. В простейшем случае для этого может быть использован алгоритм, основанный на методе водораздела (Serge Beucher and Christian  . Use of watersheds in contour detection. In International workshop on image processing: Real-time edge and motion detection. Rennes, France, 17-21 September 1979). На следующем этапе для каждого кластера вычисляется его размер (в вокселах) и среднее значение принадлежащих ему вокселов на разностном изображении. В случае если несколько кластеров имеют одинаковый размер, значения для них усредняются.
. Use of watersheds in contour detection. In International workshop on image processing: Real-time edge and motion detection. Rennes, France, 17-21 September 1979). На следующем этапе для каждого кластера вычисляется его размер (в вокселах) и среднее значение принадлежащих ему вокселов на разностном изображении. В случае если несколько кластеров имеют одинаковый размер, значения для них усредняются.
Другой полезной на практике характеристикой является корреляция между значениями цвета соответствующих пикселей первого и второго совмещенных изображений. Наиболее удобно представить эту корреляцию в виде двухмерной гистограммы. Здесь под двухмерной гистограммой H для изображений I1, I2 мы понимаем двухмерный массив, ячейка (c1, c2) которого хранит число вокселов первого изображения имеющих цвет c1, при том, что соответствующий пиксел второго изображения имеет цвет c2:

где:
I 1 - табличная дискретная функция, описывающая первое трехмерное изображение;
I 2 - табличная дискретная функция, описывающая второе трехмерное изображение;
 - арифметическая сумма по всем точкам изображения;
- арифметическая сумма по всем точкам изображения;
 - двухмерная гистограмма;
- двухмерная гистограмма;
c 1 - значение цвета, принадлежащее пространству цвета изображения I1;
c 2 - значение цвета, принадлежащее пространству цвета изображения I2;
"==" - оператор сравнения, равный 1, если оба операнда равны, и 0, если операнды не равны;
"&&" - оператор «и», равный 1, если оба операнда равны 1, и 0, если хотя бы один из операндов не равен 1.
На фиг. 5,а изображен пример вычисления двухмерной гистограммы по паре изображений с размером 2×2 пиксела. На первом изображении все четыре пиксела имеют разные значения от 1 до 4, в то время как на втором - все значения равны 1. Таким образом, в анализируемой паре изображений присутствуют следующие пары значений соответственных пикселов: (1;1), (2;1), (3;1) и (4;1). Каждая пара встречается лишь один раз, поэтому двухмерная гистограмма равна 1 в точках (1;1), (2;1), (3;1), (4;1) и равна 0 в остальных точках. Симметричная ситуация наблюдается в случае, представленном на фиг. 5,б.
Для вычисления двухмерной гистограммы изображения должны быть предварительно совмещены. Ясно, что в случае анализа двух идентичных изображений, значения соответствующих пикселей будут равны. Это приведет к тому, что двухмерная гистограмма будет равна 0 везде кроме диагональных элементов. Массив только диагональных элементов в этом случае будет эквивалентен стандартной одномерной гистограмме изображения.
При анализе же двух корректно совмещенных реальных изображений одного и того же образца без каких-либо структурных изменений гистограмма не будет диагональной из-за наличия экспериментальной погрешности. Тем не менее, значения в соответственных пикселах будут отличаться друг от друга лишь в пределах экспериментальной ошибки. По этой причине, двухмерная гистограмма будет симметрична относительно своей диагонали, имея на ней свои локальные максимумы. Пример двухмерной гистограммы реальной пары корректно совмещенных трехмерных изображений приведен на фиг. 6.
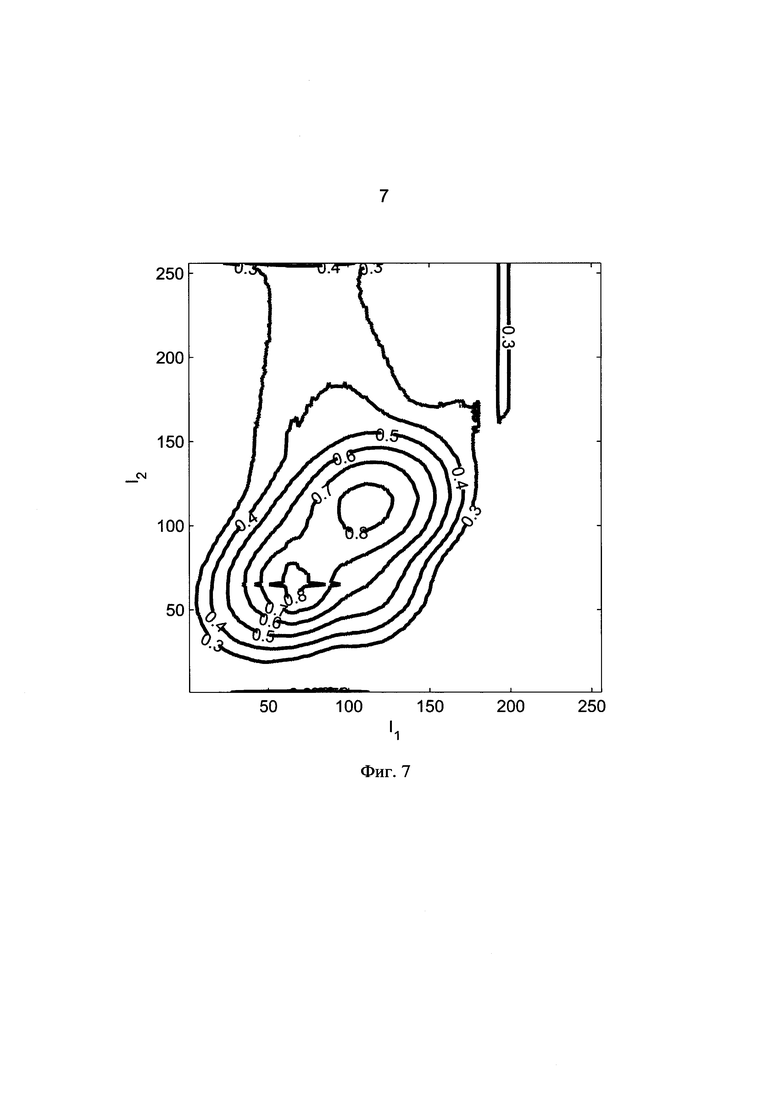
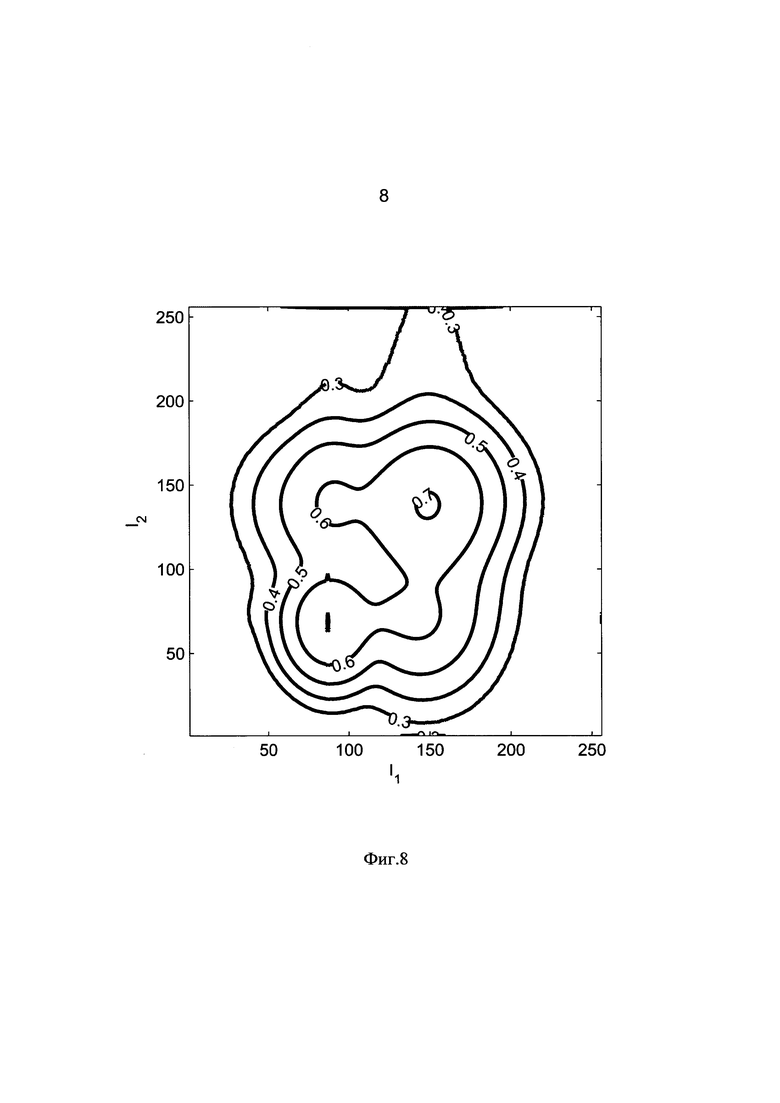
Наконец, в случае каких-либо изменений в образце, произошедших в период между первым и вторым сканированием, на двухмерной гистограмме будут возникать ненулевые области, смещенные в сторону от диагонали равных значений (фиг. 7). Следует отличать, случаи внутренних изменений в образце, от случаев некорректного совмещения изображений (или полного его отсутствия). На фиг. 8 приведен пример двухмерной гистограммы при некорректном совмещении двух изображений. Видно, что полученное распределение более-менее симметрично относительно диагонали равных значений, однако часть максимумов расположено в стороне от нее в отличие от фиг. 6.
Таким образом, двухмерная гистограмма может быть вычислена по совмещенным изображениям как с целью оценки типа и характера изменений произошедших в структуре породы, так и для проверки качества совмещения изображений.
Визуальный анализ двухмерных гистограмм оказывается полезен при изучении изменений в породе, произошедших, например, в результате химических реакций, когда отдельные вещества, включая минеральный скелет, могут частично растворяться, менять химический состав, изменяться в размерах. Применительно к рентгеновской томографии все эти изменения приводят к изменению коэффициента поглощения рентгеновского излучения, а, следовательно, могут быть отслежены на двухмерной гистограмме.
Во многих случаях, например, при изучении процессов, связанных с растворением минерала, оказывается полезным ввести характеристику, описывающую глубину повреждений. Соответствующие вычисления могут быть выполнены следующим образом. Осуществляют кластеризацию исходного изображения, как описано выше; вычисляют «преобразование расстояния» (данное преобразование сопоставляет каждому вокселу расстояние от него до ближайшего воксела, соответствующего «пустотному пространству» [http://en.wikipedia.org/w/index.php?title=Distance_transform&oldid=557170713]) и вычисляют двухмерную гистограмму для разностного изображения и преобразования расстояния.
Кроме того, полученный результат можно упростить до обычной, одномерной гистограммы, вычислив среднее значение разностного изображения для каждого значения преобразования расстояния.
Отдельно стоит отметить случай, когда каждому вокселу изображения можно поставить в соответствие определенный тип вещества. Например, в некоторых случаях тип минерала может быть непосредственно определен из значения коэффициента поглощения рентгеновского излучения в данной точке. Тогда оказывается возможным оценить количество и характер изменений для каждого типа вещества независимо.
В качестве примера описано применение способа для оценки сохранности образца породы.
Образец горной породы - песчаника - был отсканирован с помощью рентгеновского микротомографа дважды: в «начальном состоянии» и спустя год хранения в специфических, близких к комнатным, условиях. Затем полученные изображения были совмещены описанным выше способом. На фиг. 9,а показан двухмерный срез микротомографического изображения песчаника в исходном состоянии, на фиг. 9,б - после хранения (изображение совмещено с изображением, показанным на фиг. 9а). На фиг. 9,в показано разностное изображение D первого и второго изображений, яркость которого увеличена в 10 раз (D=10|I1-I2|). Измененным областям соответствуют яркие точки. В темных областях изменения отсутствуют. Из фигур видно, различия между первым и вторым изображениями фактически сводятся к некоррелированному шуму, что позволяет сделать вывод об отсутствии существенных изменений в поровом пространстве и/или структуре вещества в процессе хранения.
В качестве еще одного примера ниже описано применение способа для выбора наименее разрушающих методов заморозки образцов горной породы.
В процессе заморозки и последующего оттаивания образование льда из воды в поровом пространстве образца может приводить к различным разрушениям. Выбор наименее повреждающего метода для каждого типа породы - важная часть процесса хранения и транспортировки образцов, существенно влияющая на точность последующих лабораторных исследований. Были исследованы несколько типов заморозки (быстрая - путем помещения образца в жидкий азот, медленная - с постепенным понижением температуры и другие). Каждый тип заморозки был проверен на нескольких типах горных пород. После того, как изображения были совмещены, разностные изображения пород были изучены экспертом, который выбрал наименее повреждающий метод для каждого типа породы.
На фиг. 9,а приведено изображение глинистого песчаника в исходном состоянии, на фиг. 9,б приведено изображение глинистого песчаника после заморозки, а на фиг. 9,в - разностное изображение. Характерные типы изменений отмечены на фиг. 9: 1 - разделение зерна; 2 - разрушение зерна; 3 - миграция частиц; 4 - изменение характера контакта между зернами. Среднее расстояние, на которое перемещались отдельные частицы можно оценить как 2-3 их линейных размера. Появление ярких границ на разностном изображении связано с повреждением границ зерен вещества в процессе заморозки-оттаивания (фиг. 9,в).
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ФИЛЬТРАЦИОННЫХ СВОЙСТВ НЕОДНОРОДНЫХ ПОРИСТЫХ ОБРАЗЦОВ | 2021 |
|
RU2774959C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТРЕХМЕРНОГО ПРОСТРАНСТВЕННОГО РАСПРЕДЕЛЕНИЯ ПОРИСТОСТИ В ОБРАЗЦЕ НЕОДНОРОДНОЙ ПОРИСТОЙ СРЕДЫ | 2018 |
|
RU2783767C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕПЛОПРОВОДНОСТИ КЕРНА | 2009 |
|
RU2503956C1 |
| СПОСОБ ПОЛУЧЕНИЯ ТРЕХМЕРНОЙ МОДЕЛИ КЕРНА ГОРНЫХ ПОРОД ПО ДАННЫМ КОМПЬЮТЕРНОЙ ТОМОГРАФИИ ДЛЯ ОПРЕДЕЛЕНИЯ МЕЖЗЕРНОВОЙ ЭФФЕКТИВНОЙ ПОРИСТОСТИ | 2021 |
|
RU2777714C1 |
| СПОСОБ И СИСТЕМА ВЫРАВНИВАНИЯ ИЗОБРАЖЕНИЙ СЛОЁВ ОБРАЗЦА, ПОЛУЧЕННЫХ С ПОМОЩЬЮ РАСТРОВОГО ЭЛЕКТРОННОГО МИКРОСКОПА С ФОКУСИРОВАННЫМ ИОННЫМ ПУЧКОМ | 2020 |
|
RU2743231C1 |
| АНАЛИЗ ПЕТРОГРАФИЧЕСКИХ ИЗОБРАЖЕНИЙ ДЛЯ ОПРЕДЕЛЕНИЯ КАПИЛЛЯРНОГО ДАВЛЕНИЯ В ПОРИСТЫХ СРЕДАХ | 2012 |
|
RU2543698C1 |
| СПОСОБ ПРИГОТОВЛЕНИЯ МОДЕЛИ ПЛАСТОВОЙ ВОДЫ | 2022 |
|
RU2808505C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ РАВНОВЕСНОЙ СМАЧИВАЕМОСТИ ПОВЕРХНОСТИ РАЗДЕЛА ПУСТОТНОГО ПРОСТРАНСТВА И ТВЕРДОЙ ФАЗЫ ОБРАЗЦА ГОРНОЙ ПОРОДЫ | 2015 |
|
RU2670716C9 |
| КОЛИЧЕСТВЕННЫЙ АНАЛИЗ ПЕРФУЗИИ | 2010 |
|
RU2541175C2 |
| СПОСОБ И СИСТЕМА ДЛЯ ПРЕЦЕЗИОННОЙ АДДИТИВНОЙ ПЕЧАТИ ТРЕХМЕРНЫХ СТРУКТУР | 2022 |
|
RU2804779C1 |







Изобретение относится к способам исследования образцов материалов при помощи их цифровых трехмерных моделей. Для оценки структурных изменений в образце материала в результате воздействия на образец сканируют по меньшей мере один образец материала до и после воздействия и получают соответственно первое изображение и второе изображение каждого образца. Производят совмещение обоих изображений в полном разрешении, используя по меньшей мере один фрагмент первого изображения и один фрагмент второго изображения каждого образца, которые соответствуют одной и той же области образца. Анализируют совмещенные изображения и производят оценку изменений в каждом образце, произошедших в результате осуществленного воздействия. Технический результат – увеличение чувствительности в случае малых изменений в образце. 34 з.п. ф-лы, 10 ил.
1. Способ оценки структурных изменений в образце материала в результате воздействия на образец, в соответствии с которым:
- сканируют по меньшей мере один образец материала и получают первое изображение образца,
- осуществляют воздействие на каждый образец,
- сканируют каждый образец после воздействия и получают второе изображение каждого образца,
- для каждого образца производят предварительное совмещение первого и второго изображений в пониженном разрешении, и определяют области соответствия первого и второго изображений,
- для каждого образца из всей области соответствия первого и второго изображений выделяют по одинаковым координатам фрагменты первого и второго изображений, которые соответствуют одной и той же области образца,
- для каждого образца для каждой выбранной пары фрагментов первого и второго изображений производят автоматическое совмещение в полном разрешении и определяют параметры преобразования,
- для каждого образца по найденным для каждой пары фрагментов параметрам преобразования осуществляют совмещение первого и второго изображений целиком в полном разрешении,
- анализируют совмещенные изображения и производят оценку изменений в каждом образце, произошедших в результате осуществленного воздействия.
2. Способ по п. 1, в соответствии с которым предварительно задают начальное приближение для параметров совмещения.
3. Способ по п. 2, в соответствии с которым начальное приближение задают вручную и/или путем автоматического совмещения.
4. Способ по п. 1, в соответствии с которым область каждого образца, из которой выделяют совмещаемые фрагменты первого и второго изображений, является предварительно заданной.
5. Способ по п. 1, в соответствии с которым воздействие на образец представляет собой термическое воздействие.
6. Способ по п. 1, в соответствии с которым воздействие на образец представляет собой химическое воздействие.
7. Способ по п. 1, в соответствии с которым воздействие на образец представляет собой механическое воздействие.
8. Способ по п. 1, в соответствии с которым воздействие на образец представляет собой транспортировку образца.
9. Способ по п. 1, в соответствии с которым воздействие на образец представляет собой хранение образца.
10. Способ по п. 5, в соответствии с которым химическим воздействием является экстракция или очистка порового пространства.
11. Способ по п. 1, в соответствии с которым сканирование образца осуществляют посредством рентгеновской компьютерной томографии, нейтронной/позитронной томографии, позитрон-эмиссионной томографии, ядерно-магнитно-резонансной томографии.
12. Способ по п. 1, в соответствии с которым сканирование образца осуществляют посредством электронной микроскопии.
13. Способ по п. 1, в соответствии с которым сканирование образца осуществляют посредством лазерной флуоресцентной микроскопии.
14. Способ по п. 1, в соответствии с которым сканирование образца осуществляют посредством оптической микроскопии.
15. Способ по п. 1, в соответствии с которым сканирование образца осуществляют посредством конфокальной микроскопии.
16. Способ по п. 1, в соответствии с которым сканирование образца осуществляют посредством рамановской микроскопии.
17. Способ по п. 1, в соответствии с которым методы сканирования до и после воздействия отличны друг от друга.
18. Способ по п. 1, в соответствии с которым каждое полученное изображение образца является одномерным.
19. Способ по п. 1, в соответствии с которым каждое полученное изображение образца является двухмерным.
20. Способ по п. 1, в соответствии с которым каждое полученное изображение образца является трехмерным.
21. Способ по п. 1, в соответствии с которым размерность изображений, полученных до и после воздействия, отличны друг от друга.
22. Способ по п. 1, в соответствии с которым производят предварительную обработку по меньшей мере одного из двух полученных изображений образца для устранения искажений.
23. Способ по п. 22, в соответствии с которым в процессе предварительной обработки изображений исправляют масштаб изображений и/или выполняют геометрическую коррекцию.
24. Способ по п. 22, в соответствии с которым в процессе предварительной обработке изображений осуществляют исправление цветовой палитры изображения.
25. Способ по п. 1, в соответствии с которым анализ совмещенных изображений включает построение двухмерных гистограмм.
26. Способ по п. 1, в соответствии с которым анализ совмещенных изображений включает анализ глубины повреждений.
27. Способ по п. 1, в соответствии с которым анализ совмещенных изображений включает их кластеризацию и проведение усреднения анализируемой величины по кластерам со схожими параметрами.
28. Способ по п. 27, в соответствии с которым анализ совмещенных изображений включает анализ зависимости количества повреждений от размера зерна и особенностей структуры пустотного пространства.
29. Способ по п. 1, в соответствии с которым анализ совмещенных изображений включает анализ гистограммы повреждений отдельно для каждого типа вещества.
30. Способ по п. 1, в соответствии с которым из совмещенных изображений строят разностное изображение.
31. Способ по п. 1, в соответствии с которым образцы подвергают воздействиям разного типа и дополнительно определяют воздействия, вызывающие изменения заданного типа и степени.
32. Способ по п. 1, в соответствии с которым образцы подвергают многократному воздействию одного типа, вносящего изменения в структуру образца с каждым новым воздействием.
33. Способ по п. 1, в соответствии с которым каждая точка получаемых изображений содержит набор значений, характеризующих различные физические свойства образца.
34. Способ по п. 33, в соответствии с которым набором значений в каждой точке изображения является спектр поглощения или испускания электромагнитного излучения в некотором диапазоне длин волн или энергий.
35. Способ по п. 1, в соответствии с которым процедура совмещения использует преобразования подобия с последующей деформацией, что позволяет определить поле деформаций в образце.
| US 20110181701 A1, 28.07.2011 | |||
| СПОСОБ ПОЛУЧЕНИЯ ИЗОБРАЖЕНИЙ ВНУТРЕННЕЙ СТРУКТУРЫ ОБЪЕКТОВ | 2000 |
|
RU2184347C2 |
| Устройство для многорядной сплотки бревен | 1935 |
|
SU50066A1 |
| Способ измерения деформаций изделий | 1984 |
|
SU1245875A1 |
Авторы
Даты
2018-11-29—Публикация
2014-07-25—Подача