Изобретение относится к области технологий изучения свойств неоднородных пористых сред. Точнее, описываемый метод относится к методам получения изображений и анализа пористости образца неоднородной пористой среды.
Пористые среды играют важную роль в нашей жизни - их можно встретить практически всюду вокруг нас. Примером таких сред в нефтегазовой отрасли являются породы-коллектора, поровое пространство которых одновременно выполняет две важнейших функции - хранение и транспорт углеводородного вещества. Правильно продуманная пористая структура ткани делает современную одежду более эффективной при взаимодействии с влагой. Значение пористости и точная трехмерная геометрия порового пространства оказывает критическое влияние на итоговые характеристики строительных материалов (фундамент зданий, опоры мостов, и т.д.). Эти и многие другие примеры наглядно демонстрируют важность умения измерять и анализировать пористость образца, в том числе трехмерное пространственное распределение пористости внутри образца.
Существуют различные системы анализа пористых сред в зависимости от размера образца и масштаба пор. Например, в нефтегазовой отрасли, широко применяются каротажные измерения в скважинах для получения информации о пористости пласта. Тем не менее, такие данные не могут быть достоверно интерпретированы без определенной калибровки на лабораторные измерения. В лаборатории есть возможность проведения прямых измерений пористости при необходимых давлении и температуре в соответствующих установках (например, путем насыщения газом в газовом порозиметре) на образцах керна, отобранных на известной глубине. Эти и большинство других методов позволяют оценить лишь интегральное значение пористости.
Сегодня подходы к изучению свойств образца, основанные на анализе его изображений, становятся более распространенными и признанными в качестве альтернативы или дополнения к стандартным лабораторным методам. Так, трехмерные (далее 3D) цифровые модели пористых сред (например, пород-коллекторов) с последующим численным моделированием их физических свойств являются важными самодостаточными результатами, которые начинают играть значимую роль в современных промышленных технологиях (см. например, Е. Maire and P. J. Withers. Quantitative X-ray Tomography. International Materials Reviews. 2014; 59(1): 1-43).
Успех применения подобных технологий, включая упомянутую выше, существенно зависит от качества входных данных - цифровых моделей. Существующие решения для создания 3D цифровых моделей основаны на получении 3D изображений образца. Геометрическая точность получаемых 3D цифровых моделей ограничена пространственным разрешением используемого метода получения 3D изображения. Наиболее популярным методом для этих целей является рентгеновская микротомография, характерное разрешение которой в лучшем случае находится на уровне 1 мкм. В то же время, хорошо известно, что в зависимости от конкретного типа образца находящиеся внутри него поры могут иметь размеры от нанометров до миллиметров и больше. В результате, при построении 3D цифровой модели (например, керна) поровое пространство оказывается частично потерянным (неразрешенным).
Описываемое изобретение является способом получения 3D пространственного распределения пористости (или карты пористости, или пористой модели) внутри образца неоднородной пористой среды. Способ включает в себя получение 3D изображения микроструктуры образца с помощью метода получения 3D изображения микроструктуры образца и измерение общей пористости образца. Далее, определяются значения в вокселях (элементарных ячейках) 3D изображения микроструктуры, которые соответствуют полностью пустым (вся ячейка целиком является порой или ее частью) и полностью сплошным (внутри ячейки поры отсутствуют) областям. После этого 3D изображение микроструктуры нормируется с использованием определенных значений, соответствующих полностью пустым и сплошном вокселям. Наконец, 3D пространственное распределение пористости в образце определяется с помощью вычислительного устройства путем использования нормированного 3D изображения микроструктуры и измеренной общей пористости.
Изобретение поясняется чертежами:
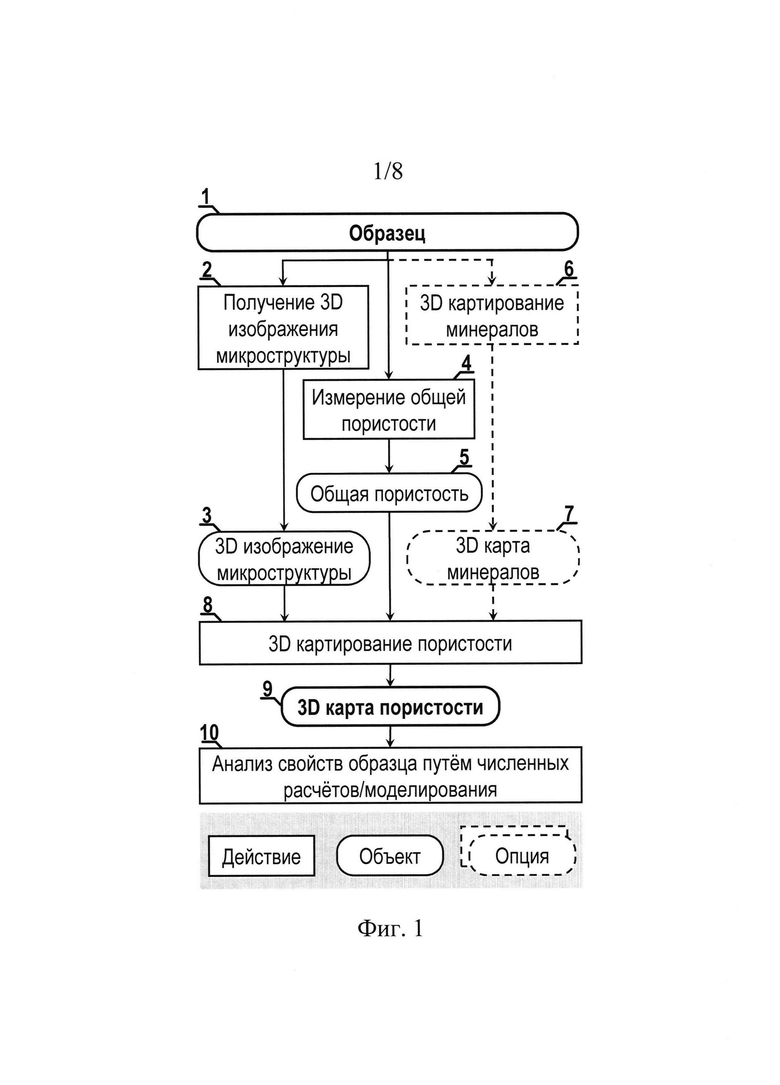
Фиг. 1 иллюстрирует блок-диаграмму способа, соответствующего одному из вариантов изобретения;
на Фиг. 2 показан пример двумерного (2D) слоя полученного 3D изображения микроструктуры (методом рентгеновской микротомографии) пористого образца (карбонатная порода);
Фиг. 3а-е демонстрируют проблему ограниченного пространственного разрешения метода получения 3D изображения микроструктуры: на Фиг. 3а показана некоторая искусственная «истинная» мономинеральная структура без частично пустых/сплошных вокселей; на Фиг. 3б - синтетическое изображение микроструктуры искусственной структуры, показанной на Фиг. 3а, с недостаточным пространственным разрешением; Фиг. 3в соответствует Фиг. 3б с добавленным шумом; Фиг. 3г - гистограмма Фиг. 3а; Фиг. 3д - гистограмма Фиг. 3б; Фиг. 3е - гистограмма Фиг. 3в;
Фиг. 4а-е демонстрируют особый шаг обработки для случая полиминеральных образцов: на Фиг. 4а показана некоторая искусственная «истинная» полиминеральная структура без частично пустых/сплошных вокселей, состоящая из двух видов минералов; на Фиг. 4б показано синтетическое зашумленное изображение микроструктуры с недостаточным пространственным разрешением; Фиг. 4в демонстрирует результат обработки изображения, показанного на Фиг. 4б; Фиг. 4г - гистограмма Фиг. 4а; Фиг. 4д - гистограмма Фиг. 4б; Фиг. 4е - гистограмма Фиг. 4г;
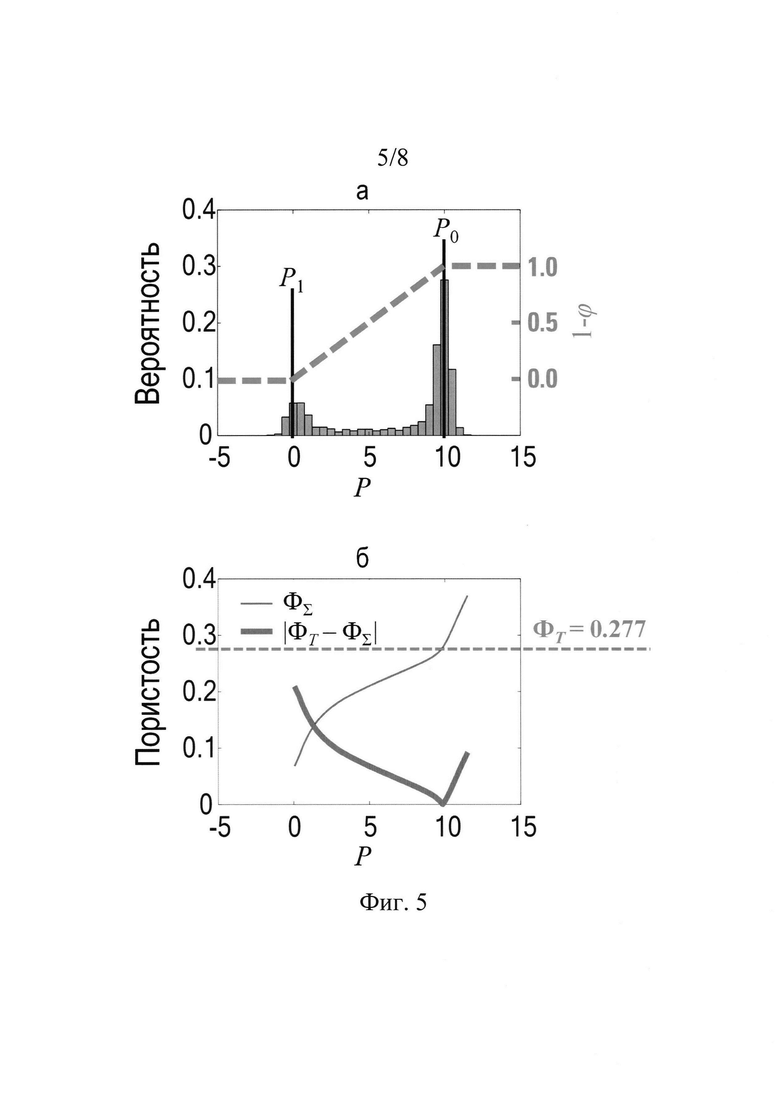
Фиг. 5а, б разъясняет процесс итогового создания пространственного 3D распределения пористости (3D карты пористости); Фиг. 5а - гистограмма изображения, соответствующего условию линейной зависимости между значениями в его вокселях и локальными плотностями образца в соответствующих вокселям элементарных объемах образца, значения P1 и Р0 являются средними значениями в вокселях для целиком пустых и сплошных вокселей соответственно; Фиг. 5б иллюстрирует, как строится итоговое пространственное 3D распределение пористости путем определения оптимальных Р1 или Р0 для соблюдения критерия равенства общей ФТ и суммарной цифровой Ф∑ пористостей образца.
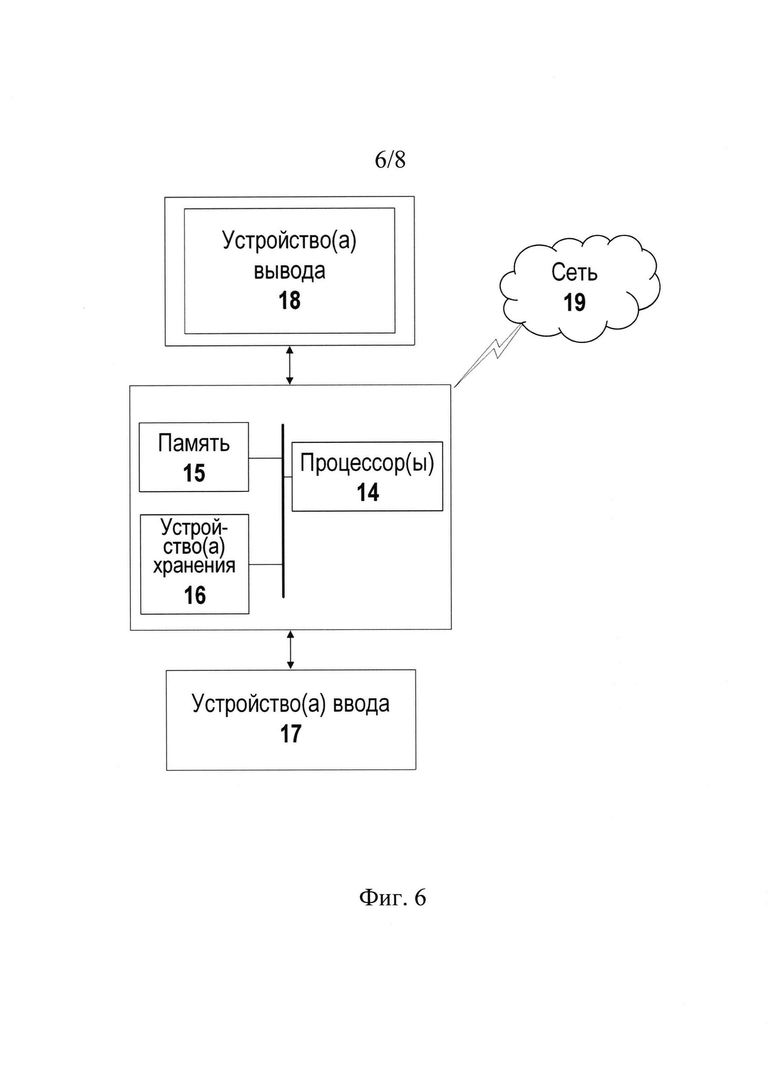
На Фиг. 6 схематически изображена вычислительная система В соответствии с одним из вариантов изобретения;
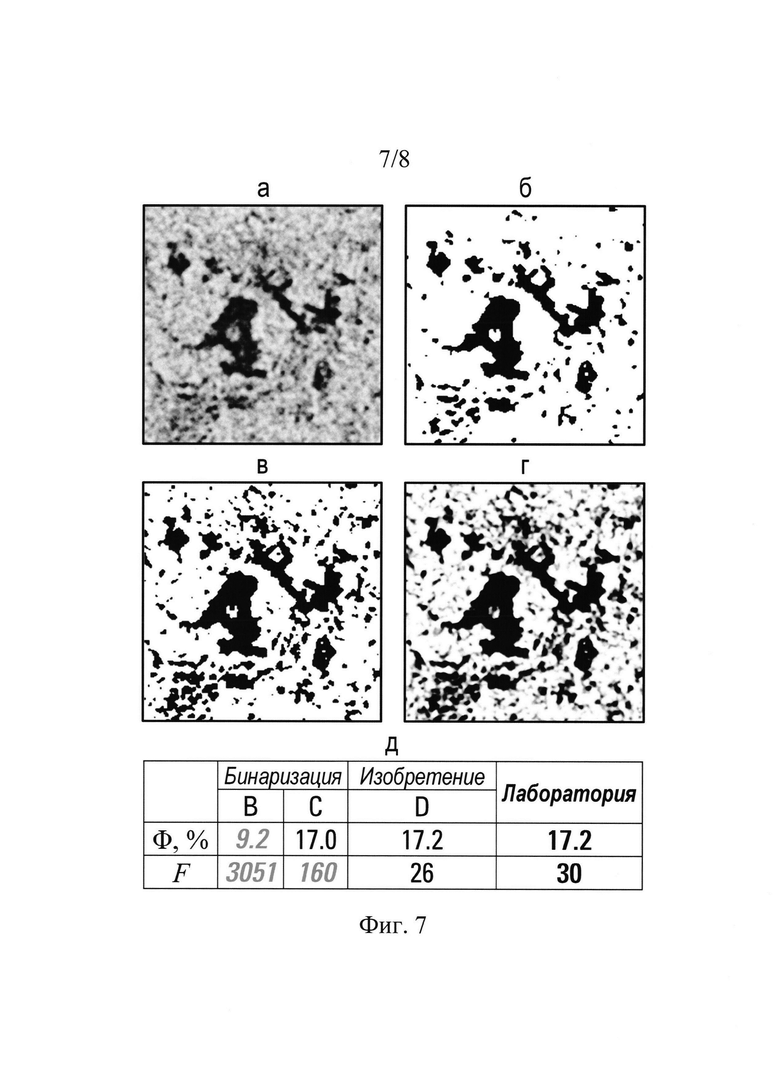
На Фиг. 7а-е продемонстрирован пример использования изобретения для построения 3D пористой модели образца карбоната и последующего определения параметра пористости F (через расчет электрического сопротивления): на Фиг. 7а показана часть двумерного слоя 3D изображения микроструктуры (получено методом рентгеновской микротомографии) образца карбоната; Фиг. 7б соответствует 3D цифровой модели, полученной методом автоматической бинаризации 3D изображения микроструктуры; Фиг. 7в соответствует 3D цифровой модели, полученной путем ручной бинаризации 3D изображения микроструктуры до соблюдения критерия равенства общей ФТ и суммарной цифровой Ф∑ пористостей образца; на Фиг. 7г показано полученное с помощью описываемого способа 3D пространственное распределение пористости; на Фиг. 7д показаны значения пористости и параметра пористости, численно определенные для построенных пространственных 3D распределений пористости (Фиг. 7б-г), а также приведены экспериментально измеренные значения.
Фиг. 8а-в иллюстрирует эффект сохранения связанности между порами в случае применения описываемого способа, в отличие от традиционного подхода: на Фиг. 8а изображен малый двумерный участок исходного 3D изображения микроструктуры; Фиг. 8б демонстрирует результат традиционной пороговой бинаризации; на Фиг. 8в показан соответствующий участок 3D пространственного распределения пористости, построенного описываемым способом.
Описываемое изобретение нацелено на существенное уменьшение негативных эффектов, связанных с неразрешенной пористостью. Это, в свою очередь, снижает вероятность ошибок в последующих технологических процессах, основанных на 3D распределении пористости в образце. Изобретение расширяет область применимости методов получения 3D изображений, включая, но не ограничиваясь, метод рентгеновской (микро)томографии. Более того, во многих задачах повышение пространственного разрешения может быть слишком дорогим решением и, как следствие, менее выгодным по сравнению с предлагаемым способом.
Фиг. 1 иллюстрирует блок-диаграмму способа, соответствующего одному из вариантов изобретения.
Блок 1 соответствует некоторому образцу неоднородного вещества. Например, это может быть образец керна, состоящий из различных минералов, который был извлечен из прискважной области, или образец строительного материала, такого как бетон.
Блок 2 соответствует получению исходного 3D изображения микроструктуры (соответствует Блоку 3) образца с помощью метода получения 3D изображений микроструктуры. Изображение микроструктуры (Блок 3) - это изображение, которое явно или неявно отражает внутреннюю геометрию и минеральную неоднородность в образце с ограничениями, обусловленными конечными пространственным разрешением и чувствительностью к минеральному составу.
С точки зрения цифрового представления, 3D изображение - это 3D массив скалярных или векторных величин. Каждый элемент этого массива соответствует точке на изображении (пикселю для 2D изображения и вокселю для 3D изображения). Существует множество методов и соответствующих приборов, позволяющих получать 3D изображение микроструктуры. Среди них рентгеновская микро- и нанотомография, рентгенофлюоресцентная томография, нейтронная (микро)томография, 3D ФИП-РЭМ (растровая электронная микроскопия с фокусированным ионным пучком (3D FIB-SEM)) и др., а также соответствующие им хорошо известные устройства.
Важным требованием к методу получения 3D изображения является следующее: значения в вокселях должны взаимнооднозначным образом зависеть от массовой плотности (следовательно, и пористости) для химически однородного вещества. В этом случае, значения в вокселях могут быть пересчитаны в линейно зависимые от плотности химически однородного вещества. Рентгеновская микротомография является хорошим примером метода, удовлетворяющего поставленное требование (NIST: X-Ray Mass Attenuation Coefficients - Section 2 - http://physics.nist.gov/PhysRerData/XrayMassCoef/chap2.html). Пример микротомографического изображения карбонатного образца представлен на Фиг. 2, где оттенки серого от черного до белого соответствуют локальным коэффициентам поглощения μ от низких до высоких значений, которые линейно зависят от плотности для каждого конкретного химически однородного вещества.
Следует отметить, что в общем случае каждое оборудование для получения изображений имеет некоторую аппаратную функцию соответствия между числовым значением в точке на изображении (т.е. в пикселе/вокселе в случае 2D/3D изображения) и значением некоторой реальной физической величины (например, локальным поглощением излучения) в соответствующей точке или области образца. Как правило, данная функция более-менее известна или может быть легко оценена и, как следствие, изображение может быть преобразовано так, что числовые значения в точках на изображении линейно зависят от значений реальной физической величины в соответствующих точках образца.
С учетом вышесказанного, здесь и далее будем называть 3D изображением микроструктуры такое изображение, значения в котором уже линейным образом зависят от плотности в вокселе. Причем увеличение плотности соответствует увеличению значения в изображении.
Следующим шагом является лабораторное измерение общей пористости образца (Блок 4 на Фиг. 1). Пористость образца неоднородного вещества может быть измерена любым из многочисленных и проверенных методов измерения пористости. В соответствии с одним из вариантов осуществления изобретения таким методом может быть газовая порометрия. Считается, что таким способом можно определить общую пористость ФТ образца (Блок 5 на Фиг. 1) в отличие от анализа 3D изображения микроструктуры, при котором часть порового объема «теряется» по причине ограниченного пространственного разрешения.
В случае работы с образцами керна значение пористости может быть измерено прямыми методами. Например, с помощью газа (по закону Бойля) или путем насыщения жидкостью (пластовой водой, нефтью, керосином и др.), т.е. путем заполнения флюидом порового пространства образца и измерения количества зашедшего флюида с помощью взвешивания. В соответствии с еще одним из вариантов осуществления изобретения, пористость может быть измерена методом ртутной порометрии. В некоторых случаях, информация о пористости может быть получена из каротажных данных.
В случае многокомпонентного (многофазного, т.е. химически неоднородного) образца (например, полиминеральная горная порода, многослойная структура) рекомендуется проводить дополнительную процедуру 3D картирования химически однородных компонент. Например, в случае полиминерального образца горной породы требуется 3D картирование минералов (Блок 6 на Фиг. 1). Здесь и далее будем называть минералом любое конкретное химически однородное вещество в образце (углерод, золото, конкретный сплав металла и т.д.) или конкретный тип минерала (кварц, кальцит, пирит и т.д.), или конкретную смесь минералов (например, смесь 30% полевого шпата и 70% кварца), или конкретную смесь химических веществ (например, различные слои в многослойной оболочке образца). Для простоты восприятия на протяжении всего описания изобретения любые из вышеназванных категорий веществ будут именоваться общим словом «минерал». Образцы, состав которых содержит более одного минерала (с только что введенной трактовкой термина «минерал»), будут называться полиминеральными на протяжении всего описания изобретения. Здесь и далее, 3D карта минералов - это изображение, в котором каждая точка проинтерпретирована как конкретный минерал. Таким образом, выполнения Блока 6 (на Фиг. 1) приводит к получению 3D карты минералов (Блок 7 на Фиг. 1), которая, в общем случае, соответствует 3D распределению химически однородных компонент в образце.
В соответствии с одним из вариантов осуществления изобретения, 3D картирование минералов (Блок 6 на Фиг. 1) может быть выполнено с помощью синхротронной микротомографии в монохроматическом пучке (F. Fusseis, X. Xiao, С.Schrank and F. De Carlo, "A brief guide to synchrotron radiation-based microtomography in (structural) geology and rock mechanics," Journal of Structural Geology, vol. 65, pp. 1-16, 2014). Способность разрешить различные минералы может быть дополнительно усилена путем сканирования образца несколько раз на разных энергиях излучения (длинах волн) рентгеновского пучка - мультиэнергетическая (микро)томография. В соответствии с другим вариантом изобретения, ФИП-РЭМ метод может быть использован. Он позволяет последовательно стравливать и сканировать поверхность образца слой за слоем. Таким образом можно получить 3D изображение малого приповерхностного объема с разрешением ~10 нм и полем зрения ~10 мкм. Регистрация обратно-рассеянных электронов и энерго-дисперсионная спектроскопия могут обеспечить идентификацию минералов для полученного 3D изображения. В соответствии с иными вариантами изобретения, прочие методы получения 3D изображений, чувствительные к химическому и минеральному составу могут быть использованы. Например, 3D рентгенофлюоресцентная микротомография, 3D конфокальная рамановская спектроскопия, 3D рентгеновская топо-томография.
В соответствии с другим вариантом изобретения, современные непрямые методы могут быть использованы. Например, восстанавливаемые значения на изображениях 3D рентгеновской микротомографии (микроКТ) могут быть увязаны с различными плотностями и химическими составами, включая минеральный состав (WO 2013058672). Такая процедура может быть улучшена путем сопоставления значений на 3D микроКТ изображении с пространственно совмещенным 2D распределением минералов, полученным с помощью электронной микроскопии и энерго-дисперсионной спектроскопии (US 20150104078 A1). Еще более аккуратный с научной точки зрения подход состоит в выделении (вычислении) различных локальных особенностей в точках на 3D микроКТ изображении до совмещения с 2D распределением минералов (I. Varfolomeev, I. Yakimchuk and В. Sharchilev, "Segmentation of 3D image of a rock sample supervised by 2D mineralogical image," // 2015 3rd IAPR Asian Conference on Pattern Recognition (ACPR), Kuala Lumpur, 2015, pp.346-350. doi: 10.1109/ACPR).
Далее выполняется 3D картирование пористости (Блок 8 на Фиг. 1) - особое преобразование 3D изображения микроструктуры. В результате получаем 3D пространственное распределение пористости или 3D карту пористости (Блок 9 на Фиг. 1), т.е. 3D изображение ϕ(x,y,z), содержащее в каждом своем вокселе значение доли пористого объема в объеме, соответствующем данному вокселю (внутренняя пористость вокселя). Значение "1" приписывается полностью пустому вокселю, а полностью сплошной воксель описывается значением "0". В отличие от классической бинаризации 3D изображения микроструктуры в описываемом подходе в карте/распределении пористости ϕ(x,y,z) существуют воксели с промежуточными значениями между "0" и "1". Такие значения<р описывают внутреннюю пористость частично пустых/сплошных вокселей.
Сделаем важное замечание, полностью пустой воксель соответствует отсутствию минеральной (твердой) фазы в соответствующем объеме образца, при этом, однако, данный объем не обязан быть совершенно пустым в физическом смысле (вакуум). Обычно этот объем заполнен воздухом, водой, нефтью или какими-либо другими жидкостями или газами. Несмотря на это, здесь и далее такие воксели будут называться целиком пустыми со значением внутренней пористости ϕ=1.
3D пространственное распределение пористости получается за счет учета лабораторно измеренной общей пористости (Блок 5 на Фиг. 1) и 3D карты минералов (Блок 7 на Фиг. 1) в ходе сегментации. Учет 3D карты минералов актуален в случае многокомпонентного (полиминерального) образца. Общая идея процедуры основана на следующих предположениях:
а) Большинство вокселей 3D изображения микроструктуры являются внутренне мономинеральными, т.е. могут содержать внутри себя пустоты и какой-либо один тип минерала. При этом в разных вокселях могут содержаться минералы разного типа.
б) В соответствии с (а) и вышеуказанным требованием к методу получения изображения микроструктуры значения в таких вокселях 3D изображения микроструктуры практически линейно убывают с увеличением внутренней пористости независимо для каждого типа минерала.
Таким образом, в случае мономинерального образца идеальное 3D изображение микроструктуры (на изображении нет шумов и прочих артефактов; пример на Фиг. 3б) должно содержать значения в вокселях в диапазоне от I1 до I0 (Фиг. 3д - гистограмма изображения на Фиг. 3б), где I1 соответствует целиком пустым вокселям (внутренняя пористость ϕ=1), а I0 - целиком сплошным вокселям (внутренняя пористость ϕ=0). Истинная структура (без частично пустых/сплошных вокселей), соответствующая этому изображению, показана на Фиг. 3а, где темно-серые круглые поры расположены внутри светло-серой минеральной матрице. «Истинное» изображение содержит лишь два значения I1 и I0 (Фиг. 3г - гистограмма изображения на Фиг. 3а). Реальные изображения всегда подвержены шумам и другим артефактам (Фиг. 3в). В связи с этим, на 3D изображении микроструктуры встречаются значения как ниже I1, так и выше I0 (Фиг. 3е - гистограмма изображения Фиг. 3в). В одном из вариантов изобретения, значения I0 (и I1) могут быть определены вручную путем усреднения группы вокселей, принадлежащих внутренней области разрешенной целиком пустой поры (или целиком сплошного минерального зерна). В другом варианте изобретения, вместо средней величины может быть взята статистическая мода (наиболее частое значение).
Следовательно, В соответствии с выше сделанными предположениями в случае мономинерального образца значения на изображении в диапазоне от I1 до I× могут быть легко пересчитаны в значения внутренней пористости.
В случае полиминерального образца такой подход корректен только для набора мономинеральных вокселей для каждого типа минерала независимо. Более точно, значение h во всех целиком пустых вокселях одинаково (с точностью до шума на изображении) для любого типа минерала М, но значение I0(M) зависит от типа минерала М. Другими словами, если образец является доломитом с включениями ангидрита (для простоты рассматриваются лишь два минерала), то все воксели могут быть классифицированы как «пористый доломит» и «пористый ангидрит». Значения I0(М) могут быть определены тем же способом, что и в мономинеральном случае. Данная процедура проиллюстрирована на Фиг. 4. Фиг. 4а демонстрирует искусственную структуру без частично пустых/сплошных вокселей и с двумя типами минералов - ангидрит в верхней половине изображения и доломит в нижней. На Фиг. 4г показана гистограмма Фиг. 4а. Как видно из гистограммы, на изображении Фиг. 4а существуют лишь три значения: I1 (соответствует целиком пустым вокселям), I0A (соответствует вокселям, целиком состоящим из сплошного доломита) и I0B (соответствует вокселям, целиком состоящим из сплошного ангидрита). Реальное шумное изображение с ограниченным разрешением показано на Фиг. 4б. Ему соответствует гистограмма (Фиг. 4д).
Для применения в таком случае способа В соответствии с описываемым изобретением необходима дополнительная процедура обработки 3D изображения, в результате которой значения на изображении станут линейно зависеть от внутренних плотностей в вокселях. В соответствии с одним из вариантов изобретения преобразование полиминерального изображения к псевдо-мономинеральному (т.е. такому, которое в дальнейшем может быть корректно обработано по мономинеральному сценарию) каждый не целиком пустой воксель изображения пересчитывается следующим образом:
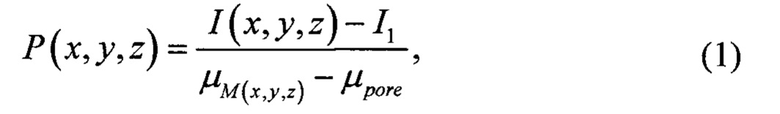
где P9x,y,z) - значение в вокселе (x,,y,z) после преобразования 3D изображения микроструктуры I(x,y,z), M(x,y,z) - это 3D карта минералов, полученная в ходе 3D картирования минералов, μpore - оценочное значение физической величины, соответствующей целиком пустым вокселям и выбранному методу получения изображения, μM(x,y,z) - аналогичное значение, соответствующее целиком сплошным вокселям минерального типа М. Метод получения этих оценочных значений строго зависит от метода получения 3D изображения микроструктуры.
В соответствии с одним из вариантов осуществления изобретения для 3D изображений рентгеновской микротомографии такие значения могут быть вычислены теоретически (NIST: X-Ray Mass Attenuation Coefficients - Section 2 -http://physics.nist.gov/PhysRefData/XrayMassCoef/chap2.html). В соответствии с другим вариантом изобретения, получение 3D изображения микроструктуры эталонов для минералов (газов, жидкостей) является более универсальным решением для любого метода получения изображения микроструктуры. В соответствии с еще одним вариантом осуществления изобретения определение значения моды в некоторой окрестности каждого вокселя (х, у, z) может быть использовано в качестве μM(x,у,z). Окрестность должна быть достаточно большой для обеспечения доминирования целиком сплошных вокселей в ней.
Обработка 3D изображения микроструктуры дает 3D изображение P(x,y,z) со значениями линейно зависимыми от внутренних пористостей - меньшие значения Р {х, у, z) соответствуют большим значениям внутренней пористости в вокселе (x,y,z) и наоборот. Аналогично значениям I0 и I1, будем называть Р0 и Р1 значения P(x,y,z) которые отвечают полностью сплошным и полностью пустым вокселям соответственно. В соответствии с (1), значение P1 равно 0, а 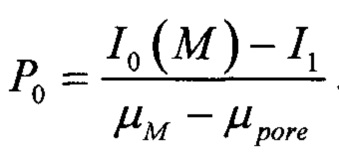 . При условии корректного получения 3D изображения микроструктуры и правильной оценки значений μpore и μM(х,у,z) значение Р0 окажется единым (в пределах шума на изображении) для каждого типа минерала.
. При условии корректного получения 3D изображения микроструктуры и правильной оценки значений μpore и μM(х,у,z) значение Р0 окажется единым (в пределах шума на изображении) для каждого типа минерала.
Результат описанного преобразования (1) продемонстрирован (Фиг. 4в) на примере искусственного полиминерального изображения (Фиг. 4б). Преобразованное изображение имеет значения в диапазоне от P1 до Р0 (Фиг. 4е - гистограмма изображения на Фиг. 4в), которые линейно зависят от внутренних пористостей в вокселях, аналогично случаю мономинерального образца.
Для удобства, оба случая (моно- и полиминеральный образец) в дальнейшем будут описаны в единых обозначениях. Пусть P(x,y,z)=1(x,y,z) в мономинеральном случае, тогда Р0 и P1 будут равны I0 и I1. Тем самым, все дальнейшие рассуждения и утверждения будут справедливыми для обоих моно- и полиминерального случаев.
Завершая и подытоживая описание обозначений I0 и I1, I0(M), P(x,y,z), Р0 и P1, можно утверждать следующее: для дальнейшего построения пространственного 3D распределения пористости после получения 3D изображения микроструктуры и измерения общей пористости образца необходимо определить значения на 3D изображении микроструктуры, которые соответствуют целиком пустым и целиком сплошным вокселям для каждого типа минерала в образце, т.е. I1 и I0 (или I0(М) в случае полиминерального образца).
В общем случае (моно- и полиминеральный образец) следующим необходимым шагом является нормировка 3D изображения микроструктуры с использованием найденных значений, которые соответствуют целиком пустым и целиком сплошным вокселям, т.е. I1 и I0 (или I0(M) в случае полиминерального образца). Процедура нормировки состоит в расчете P(x,y,z). Как говорилось выше, для мономинерального образца P(x,y,z)=1(x,y,z), а для полиминерального образца нормализация происходит согласно (1).
Наконец, используя нормированное 3D изображения микроструктуры P(x,y,z) и измеренную общую пористость, с помощью вычислительного устройства строится 3D пространственное распределение пористости образца. Далее эта процедура описана подробнее.
Все воксели со значениями ниже Р1 считаются целиком пустыми. Они формируют объем пространственно разрешенной пористости VRP.С учетом вышесказанного, как правило, объем VRP меньше реально измеренного общего объема VT пор в образце. Разница между этими величинами VNP=(VT - VRP) соответствует множеству (микро)пористых областей, пространственно неразрешенных с помощью использованного метода получения 3D изображений микроструктуры. Все воксели со значениями выше Р0 считаются целиком сплошными. Они соответствуют пространственно разрешенному объему сплошной минеральной матрицы VRS. Аналогично, VNS - это объем сплошной минеральной матрицы, пространственно неразрешенный с помощью использованного метода получения 3D изображений микроструктуры. Сумма значений VRS, VRP, VNS и VNP соответствует объему исследуемого образца V∑. Для удобства здесь и далее все объемы будут измеряться в вокселях. Таким образом, VRS соответствует числу полностью сплошных вокселей (ϕ=0), VRP - числу полностью пустых вокселей (ϕ=1), a VN=VNS+VNP соответствует числу вокселей, которые частично пустые/сплошные.
Наконец, для определения 3D распределения внутренних пористостей ϕ{x,y,z) необходимо найти связь между значениями P(x,y,z) и пористостями. В соответствии с одним из вариантов осуществления изобретения это можно сделать согласно ранее найденным значениям Р0 и P1, используя следующее правило:
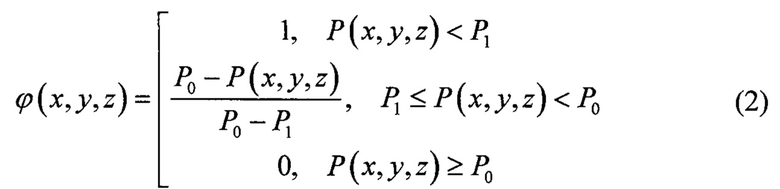
Пунктирная линия на Фиг. 5а иллюстрирует поведение ϕ(P(x,y,z)). Эта линия отображена поверх гистограммы изображения Фиг. 4в.
После преобразования 3D изображения микроструктуры согласно (2) общая пористость по изображению 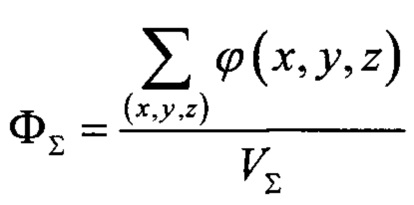 может отличаться от экспериментально измеренной общей пористости ФТ. В тех случаях, когда есть уверенность в том, что обе величины должны быть равными (близкими), предлагается следующий вариант осуществления изобретения: значение Р0 может быть найдено из условия равенства обоих значений пористости (экспериментальной общей пористости ФТ и вычисленной по изображению Ф∑). Такой подход имеет смысл, если определение значения Р0 по изображению затруднено, например, все воксели частично пористые. Данная процедура может быть осуществлена различными способами. В одном из вариантов осуществления изобретения значение Р0 итерационным образом (Фиг. 5б). Последовательное увеличение величины Р0 от известного значения P1 до больших значений ведет к монотонному увеличению величины Ф∑ от
может отличаться от экспериментально измеренной общей пористости ФТ. В тех случаях, когда есть уверенность в том, что обе величины должны быть равными (близкими), предлагается следующий вариант осуществления изобретения: значение Р0 может быть найдено из условия равенства обоих значений пористости (экспериментальной общей пористости ФТ и вычисленной по изображению Ф∑). Такой подход имеет смысл, если определение значения Р0 по изображению затруднено, например, все воксели частично пористые. Данная процедура может быть осуществлена различными способами. В одном из вариантов осуществления изобретения значение Р0 итерационным образом (Фиг. 5б). Последовательное увеличение величины Р0 от известного значения P1 до больших значений ведет к монотонному увеличению величины Ф∑ от 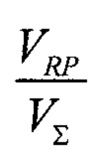 до 1 (при Р0→+∞). При корректных измерении общей пористости и получении 3D изображения микроструктуры общая пористость ФТ удовлетворяет условию:
до 1 (при Р0→+∞). При корректных измерении общей пористости и получении 3D изображения микроструктуры общая пористость ФТ удовлетворяет условию: 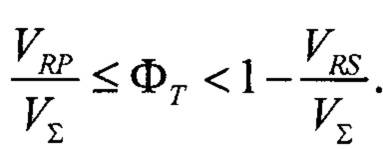 Таким образом, условие Ф∑=ФТ может быть итеративно достигнуто с приемлемой точностью. В соответствии с другим вариантом осуществления изобретения, более аккуратный альтернативный способ (https://en.wikipedia.org/w/index.php?title=Root-finding_algorithm&oldid=696250166) для определения оптимального Р0 и, следовательно, 3D распределения внутренних пористостей в вокселях ϕ{x,y,z).
Таким образом, условие Ф∑=ФТ может быть итеративно достигнуто с приемлемой точностью. В соответствии с другим вариантом осуществления изобретения, более аккуратный альтернативный способ (https://en.wikipedia.org/w/index.php?title=Root-finding_algorithm&oldid=696250166) для определения оптимального Р0 и, следовательно, 3D распределения внутренних пористостей в вокселях ϕ{x,y,z).
Отметим, что в случае отсутствия целиком пустых и/или сплошных вокселей в полученном 3D изображении микроструктуры искомые значения I0 и/или I1, P1 и/или Р0 будут находиться вне диапазона наблюдаемых на изображении значений, при этом VRP=0 и/или VRS=0, соответственно. Таким образом, значение I0 не может быть найдено по изображению, и процедура (1) не может быть выполнена. Хотя такая ситуация маловероятна, она все равно может быть успешно учтена в рамках описываемого способа, если хотя бы одно из значений I1, {I0(М)} может быть найдено по изображению.
В таком особом случае, для осуществления изобретения в мономинеральном случае (процедура (1) не выполнена) описанное выше решение работает без каких-либо изменений, если значение I1 (и, следовательно, P1) может быть определено по изображению (т.е. полностью пустые воксели могут быть найдены на изображении). Тогда значение Р0 может быть определено В соответствии с вышесказанным. Если только I0 (и, следовательно, Р0) может быть определено по изображению (т.е. полностью сплошные воксели могут быть найдены на изображении), процедура немного изменяется. Аналогично описанным выше вариантам осуществления изобретения, вместо значения Р0 значение P1 может быть найдено из условия равенства экспериментальной общей пористости ФТ и полученной по изображению общей пористости Ф∑. Данная процедура также может быть осуществлена разными способами. В соответствии с одним из вариантов изобретения, прямой итерационный способ может быть использован. Уменьшая значение P1 от Р0 до меньших значений, значение Ф∑ будет монотонно убывать от 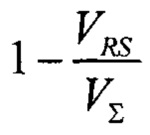 до 0. А т.к.
до 0. А т.к. 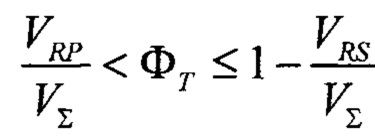 , условие Ф∑=ФТ может быть итеративно достигнуто с приемлемой точностью. В
, условие Ф∑=ФТ может быть итеративно достигнуто с приемлемой точностью. В
соответствие с другими вариантами осуществления изобретения, альтернативные более сложные подходы могут также быть использованы для определения оптимального значения P1 и, следовательно, 3D распределения внутренних пористостей в вокселях ϕ(x,y,z).
Для осуществления изобретения в полиминеральном случае, если I1 (и, следовательно P1) может быть определено по изображению (т.е. полностью пустые воксели могут быть найдены на изображении), то исходное решение остается применимым без каких-либо изменений. Процедуры (1) и (2) с определением Р0 из условия равенства экспериментальной общей пористости ФТ и вычисленной по изображению Ф∑ остаются такими же. В других вариантах осуществления изобретения, когда I1 (и, следовательно, Р1) не может быть определено прямо по изображению (все воксели частично сплошные, целиком пустых вокселей нет), но по крайней мере одно из значений {I0(М)} может быть получено - Iref, процедуры (1) и (2) должны быть заменены более общей задачей оптимизации:
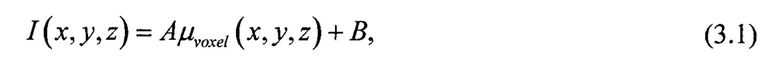

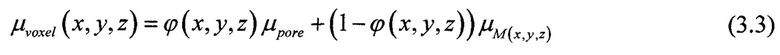
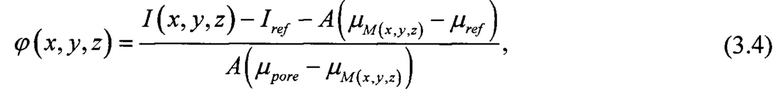

Равенство (3.1) отражает факт линейной зависимости значений на изображении I{x,y,z) от эффективного значения физической величины μvoxel(x,y,z), получаемого выбранным методом получения изображения; (3.2) - равенство (3.1), записанное для целиком сплошных вокселей некоторого типа минерала, для которого удалось получить значение I0 по изображению. Выражение (3.3) определяет эффективное значение физической величины μvoxel (x,y,z) при известном значении физической величины для вещества, заполняющего поровое пространство (μpore), сплошное пространство (μM(х,у,z) и внутреннюю пористость ϕ{x,y,z) в этом вокселе (x,y,z). (3.4) - это выражение для 3D распределения внутренних пористостей с неизвестным коэффициентом наклона А зависимости (3.1). Оптимизационная задача (3.5) состоит в определении значения.4, которое обеспечивает равенство экспериментальной общей пористости ФТ и общей пористости по изображению 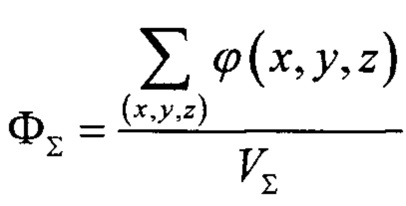 .
.
В действительности, равенство (3.5) является уравнением относительно неизвестного значения А с большим количеством членов (для каждого вокселя) аналогично (3.4). Такое уравнение легко может быть решено любым из хорошо известных способов, включая уже упомянутый итерационный подход.
В соответствии с одним из вариантов изобретения проблема отсутствия полностью пустых и/или сплошных вокселей на изображении образца может быть решена путем искусственного добавления полностью пустого и/или сплошного объекта в область изображения с последующим применением вариантов осуществления изобретения для более простого случая существования на изображении полностью пустых и/или сплошных вокселей. Кроме того, такое решение является единственным вариантом осуществления изобретения при невозможности определить хоть какое-либо из значений I1, {I0(М)} по изображению.
Полученное 3D распределение внутренних пористостей в вокселях ϕ(x,y,z) является 3D цифровой моделью образца с откартированной пористостью на каждый воксель или 3D картой пористости, т.е. искомым 3D пространственным распределением пористости в образце.
В соответствии с одним из вариантов осуществления изобретения построение итогового 3D пространственного распределения пористости в образце включает в себя дополнительную пост-обработку. Например, на практике, прямое 3D картирование пористости (В соответствии с данным выше описанием) может приводить к образованию частично сплошных вокселей (ϕ<1), окруженных целиком пустыми вокселями (ϕ=1), что противоречит реальной физике. Возможно и обратное, когда частично пустые воксели окружены полностью сплошными вокселями и, тем самым, не оказывают никакого влияния на исследуемый процесс, например, течение флюидов или движение электрических зарядов. В соответствии с одним из вариантов осуществления изобретения такие изолированные частично сплошные воксели внутри полностью пустого пространства (или наоборот) могут быть заменены окружающим типом вокселей (пустыми или сплошными).
В соответствии с одним из вариантов осуществления изобретения все необходимые вычисления и обработка изображений, необходимые для построения 3D пространственного распределения пористости в образце выполняются в режиме параллельных вычислений.
В результате 3D карта пористости (3D пространственное распределение пористости в образце) построено (Блок 9 на Фиг. 1). В соответствии с одним из вариантов осуществления изобретения эта карта может представлять собой 3D массив внутренних пористостей в каждом вокселе. Такой 3D массив данных может храниться одним файлом или набором двумерных слоев.
Полученное 3D пространственное распределение пористости в образце характеризует его с точки зрения структурных особенностей. Кроме того, такое распределение может быть использовано как цифровая модель неоднородной среды для численных расчетов различных физических явлений: течение газов и жидкостей, электромагнитные эффекты, механическая прочность и т.д.
Система для создания 3D пространственного распределения пористости в образце неоднородной среды включает в себя устройство получения изображений, настроенное на получение исходного 3D изображения микроструктуры образца. Это устройство выбирается из целой группы приборов, позволяющих выполнять сканирования методами рентгеновской микро- (нано-) томографии, рентгенофлюоресцентной микротомографии, нейтронной томографии, 3D ФИП-РЭМ и др.
Описываемый в рамках изобретения способ требует использования вычислительного устройства совместно с устройством получения изображений. Это вычислительное устройство может включать в себя программное обеспечение, аппаратные комплектующие, их программные прошивки, а также любую их комбинацию. Различные компоненты вычислительного устройства описаны ниже и проиллюстрированы на Фиг. 6.
Как показано на Фиг. 6, вычислительное устройство может быть практически любого типа, независимо от используемой платформы. Например, вычислительное устройство может быть одним или несколькими мобильными устройствами (например, портативным компьютером, смартфоном, умными часами, персональным цифровым помощником, планшетным компьютером или другим мобильным устройством), настольными компьютерами, серверами, блейд-модулями в серверном шасси или любым другим типом вычислительного устройства или устройств, который включает в себя, по меньшей мере, минимальную вычислительную мощность, память и устройство(а) ввода и вывода для выполнения одного или нескольких вариантов осуществления изобретения. Например, как показано на Фиг. 6, вычислительное устройство может включать в себя один или несколько компьютерных процессоров 14, связанную память 15 (например, оперативную память (RAM), кэш-память, флэш-память и т.д.), одно или несколько запоминающих устройств 16 (например, жесткий диск, оптический привод, такой как привод компакт-дисков (CD) или универсальный цифровой диск (DVD), флеш-накопитель и т.д.), а также множество других элементов и функций. Компьютерный процессор(ы) 14 может быть интегральной схемой для обработки инструкций. Например, компьютерный процессор(ы) может быть одним или несколькими ядрами или микроядрами процессора. Вычислительное устройство также может включать в себя одно или несколько устройств 17 ввода, таких как сенсорный экран, клавиатура, мышь, микрофон, сенсорная панель, электронное перо или любое другое устройство ввода. Кроме того, вычислительное устройство может включать в себя одно или несколько устройств вывода 18, таких как экран (например, жидкокристаллический дисплей (LCD), плазменный дисплей, монитор с электронно-лучевой трубкой (ЭЛТ), дисплей с электронными чернилами, проектор или другое устройство отображения), принтер, внешнее хранилище или любое другое устройство вывода. Одно или несколько устройств вывода могут быть такими же или отличаться от устройства ввода. Вычислительное устройство может быть подключено к сети 19 (например, к локальной сети (LAN), глобальной сети (WAN), такой как Интернет, мобильная сеть или любой другой тип сети) через соединение сетевого интерфейса. Устройство(а) ввода 17 и вывода 18 может быть локально или удаленно (например, через сеть 19) подключено к компьютерному процессору(ам) 14, памяти 15 и запоминающему устройству(ам) 16. Существует множество различных типов вычислительных устройств, и вышеупомянутые устройства ввода и вывода могут иметь другие формы. Программные инструкции в форме машиночитаемого программного кода для выполнения одного или нескольких вариантов осуществления изобретения могут храниться полностью или частично, временно или постоянно на энергонезависимом машиночитаемом носителе, таком как CD, DVD, запоминающее устройство, дискета, лента, флэш-память, физическая память или любой другой машиночитаемый носитель. В частности, программные инструкции могут соответствовать машиночитаемому программному коду, который при исполнении процессором(ами) конфигурируется для выполнения одного или нескольких вариантов осуществления способа.
Кроме того, один или несколько элементов вышеупомянутого вычислительного устройства могут быть расположены в удаленном месте и подключены к другим элементам по сети (19). Варианты осуществления изобретения могут быть реализованы в распределенной системе, имеющей несколько узлов, где каждая часть варианта осуществления изобретения может быть расположена на другом узле в распределенной системе. В одном или нескольких вариантах осуществления изобретения узел соответствует отдельному вычислительному устройству. В качестве альтернативы, узел может соответствовать процессору компьютера с соответствующей физической памятью или процессору компьютера или микроядру процессора компьютера с общей памятью и/или ресурсами.
Пример осуществления изобретения
Фрагмент 2D слоя исходного 3D изображения микроструктуры (рентгеновская микротомография) карбонатного образца представлена на Фиг. 7а. Согласно лабораторным измерениям общей пористости ФТ=17.2%. Стандартных подход бинаризации изображения дает лишь 9.2% пористости по изображению (Фиг. 7б). Для достижения экспериментально измеренной общей пористости необходимо неестественно завысить порог бинаризации (Фиг. 7в).
Применяя описанное изобретение с определением значения Р1 по изображению и численно найденного оптимального значения Р0, 3D пространственное распределение пористости в образце было получено (Фиг. 7д).
Важность описанного способа становится понятной при рассмотрении задачи определения электрического поля и электропроводности (или фактора пористости F) для образца горной породы (насыщенного пластовой водой) путем численного моделирования.
Для такого расчета необходимы:
(a). Пересчет построенного 3D пространственного распределения пористости в образце в пространственное 3D распределение локальных удельных электропроводностей σ(х,у,z) - проводимость каждого вокселя.
(b). Определение распределения электрического поля при заданных граничных условиях.
(c). Вычисление эффективных характеристик проводимости всей цифровой модели.
Шаг (а) может быть выполнен по следующему плану:
- удельная проводимость целиком сплошных вокселей σ(x,y,z)=σ(Мх,у,z);
- удельная проводимость целиком пустых вокселй σ(х, у, z)=σbrine;
удельная проводимость частично пустых/сплошных вокселей может быть задана так:
σ(x,y,z)=σM(x,y,z)+(σbrine-σM(x,y,z))ϕ(x,y,z).
Здесь M(x,y,z) является типом минерала в ячейке с координатами (x,y,z), σ(Мх,у,z) - соответствующая этому минералу удельная электропроводность,σbrine - удельная электропроводность пластовой воды. В приведенном примере, речь идет об образце доломита с включениями ангидрита, и следующие значения использовались:
σvbine=2.5 См/м, σdelomite=0.3×10-4 См/м, σanhydrite=10-9 См/м.
Численное моделирование электрического поля может быть выполнено путем итеративного решения уравнения Лапласа для значения электрического потенциала с использованием полученного распределения удельной электропроводности с заданными граничными условиями (Patankar S.V, "Numerical Heat transfer and fluid flow", 1980, pp. 59-66). Граничные условия могут быть заданы таким образом, чтобы наилучшим образом соответствовать рассматриваемой физической задаче.
Например, для кубической модели следующие граничные условия могут быть использованы:
- постоянная разность электрического потенциала устанавливается на гранях,
- перпендикулярных направлению электрического поля;
- нулевая нормальная составляющая потенциала на других гранях.
Иные численные подходы также возможны, например, основанные на инверсии матрицы законов Кирхгоффа для электрической цепи.
Используя электрический потенциал и распределения электропроводности в среде, В соответствии с законом Ома могут быть получены распределения электрических токов. Эффективная проводимость, фактор пористости и другие характеристики проводимости могут быть определены как усреднение распределения токов проводимости для заданной приложенной разнице электрических потенциалов. (https://en.wikipedia.org/w/index.php?title=Archie%27s_law&oldid=692860188).
В результате Фиг. 7д, для традиционного подхода к бинаризации (колонка В) численно полученный фактор пористости был в ~100 раз выше (Fb=3051), чем должен был быть для такой породы (Fexperiment=30, известно из независимых исследований). Для цифровой модели, построенной с завышенным порогом (колонка С), фактор пористости все равно выше в ~5 раз (Fc=160). В отличие от этих подходов, рассматриваемый способ (колонка D) обеспечивает хорошее соответствие между численными (Fd=26) и экспериментально полученными факторами пористости (Fexperiment=30). Одной из основных причин этого является сохранение связанности порового пространства внутри образца. Фиг. 8 демонстрирует это: малый 2D фрагмент оригинального 3D изображения микроструктуры показан на Фиг. 8а, результат традиционной пороговой бинаризации - Фиг. 8б и соответствующая часть 3D пространственного распределения пористости в образце - Фиг. 8в.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ РАВНОВЕСНОЙ СМАЧИВАЕМОСТИ ПОВЕРХНОСТИ РАЗДЕЛА ПУСТОТНОГО ПРОСТРАНСТВА И ТВЕРДОЙ ФАЗЫ ОБРАЗЦА ГОРНОЙ ПОРОДЫ | 2015 |
|
RU2670716C9 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ФИЛЬТРАЦИОННЫХ СВОЙСТВ НЕОДНОРОДНЫХ ПОРИСТЫХ ОБРАЗЦОВ | 2021 |
|
RU2774959C1 |
| СПОСОБ ИЗГОТОВЛЕНИЯ ТРЕХМЕРНЫХ ОПТИЧЕСКИХ МИКРОСТРУКТУР С ГРАДИЕНТОМ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ С ИСПОЛЬЗОВАНИЕМ ДВУХФОТОННОЙ ЛИТОГРАФИИ | 2023 |
|
RU2826645C1 |
| СПОСОБ ОЦЕНКИ СТРУКТУРНЫХ ИЗМЕНЕНИЙ ОБРАЗЦА МАТЕРИАЛА В РЕЗУЛЬТАТЕ ВОЗДЕЙСТВИЯ НА ОБРАЗЕЦ | 2014 |
|
RU2673774C2 |
| СПОСОБ И СИСТЕМА ДЛЯ ПРЕЦЕЗИОННОЙ АДДИТИВНОЙ ПЕЧАТИ ТРЕХМЕРНЫХ СТРУКТУР | 2022 |
|
RU2804779C1 |
| Способ определения коэффициента вытеснения нефти в масштабе пор на основе 4D-микротомографии и устройство для его реализации | 2021 |
|
RU2777702C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПОРИСТОСТИ ОБРАЗЦА ПОРОДЫ | 2012 |
|
RU2580174C1 |
| СПОСОБ И СИСТЕМА ДЛЯ ПРЕЦИЗИОННОЙ АДДИТИВНОЙ ПЕЧАТИ ТРЕХМЕРНЫХ СТРУКТУР (ВАРИАНТЫ) | 2021 |
|
RU2796486C1 |
| Способ оценки изменения характеристик пустотного пространства керновой или насыпной модели пласта при проведении физико-химического моделирования паротепловой обработки | 2023 |
|
RU2810640C1 |
| ЭФФЕКТИВНЫЙ СПОСОБ ВЫБОРА РЕПРЕЗЕНТАТИВНОГО ЭЛЕМЕНТАРНОГО ОБЪЕМА НА ЦИФРОВЫХ ПРЕДСТАВЛЕНИЯХ ПОРИСТЫХ СРЕД | 2013 |
|
RU2586397C2 |




Изобретение относится к области технологий изучения свойств неоднородных пористых сред, а именно к методам получения изображений и анализа пористости образца неоднородной пористой среды. Заявлен способ определения трехмерного пространственного распределения пористости в образце неоднородной среды, в соответствии с которым: получают 3D изображение микроструктуры образца с помощью метода получения 3D изображений микроструктуры, измеряют общую пористость образца, получают 3D карту минералов, входящих в состав образца, представляющую собой изображение микроструктуры образца, в котором каждая точка проинтерпретирована как конкретный минерал. Затем, используя полученные 3D изображение микроструктуры и 3D карту минералов, определяют значения физических величин, которые соответствуют полностью пустым вокселям, что соответствует отсутствию минеральной фазы в соответствующем объеме образца, и полностью сплошным вокселям, что соответствует отсутствию пор внутри ячейки каждого минерала, осуществляют нормировку полученного 3D изображения микроструктуры с использованием найденных для каждого минерала физических значений, соответствующих полностью пустым и полностью сплошным вокселям, получая нормированное 3D изображение, используя измеренную общую пористость, определяют значения, которые соответствуют на нормированном 3D изображении микроструктуры полностью пустым и полностью сплошным вокселям, таким образом, чтобы пористость, получающаяся в результате, соответствовала измеренной, тем самым определяя зависимость величины внутренней пористости в вокселе от значения величины на нормированном 3D изображении, и, используя нормированное 3D изображение микроструктуры и полученную зависимость величины внутренней пористости в вокселе от значения величины на нормированном 3D изображении, создают с помощью вычислительного устройства трехмерное пространственное распределение пористости в образце, учитывающее внутреннюю пористость вокселей. Технический результат - уменьшение негативных эффектов, связанных с неразрешенной пористостью, что в свою очередь снижает вероятность ошибок в последующих технологических процессах, основанных на 3D распределении пористости в образце, а также расширение области применения. 29 з.п. ф-лы, 8 ил.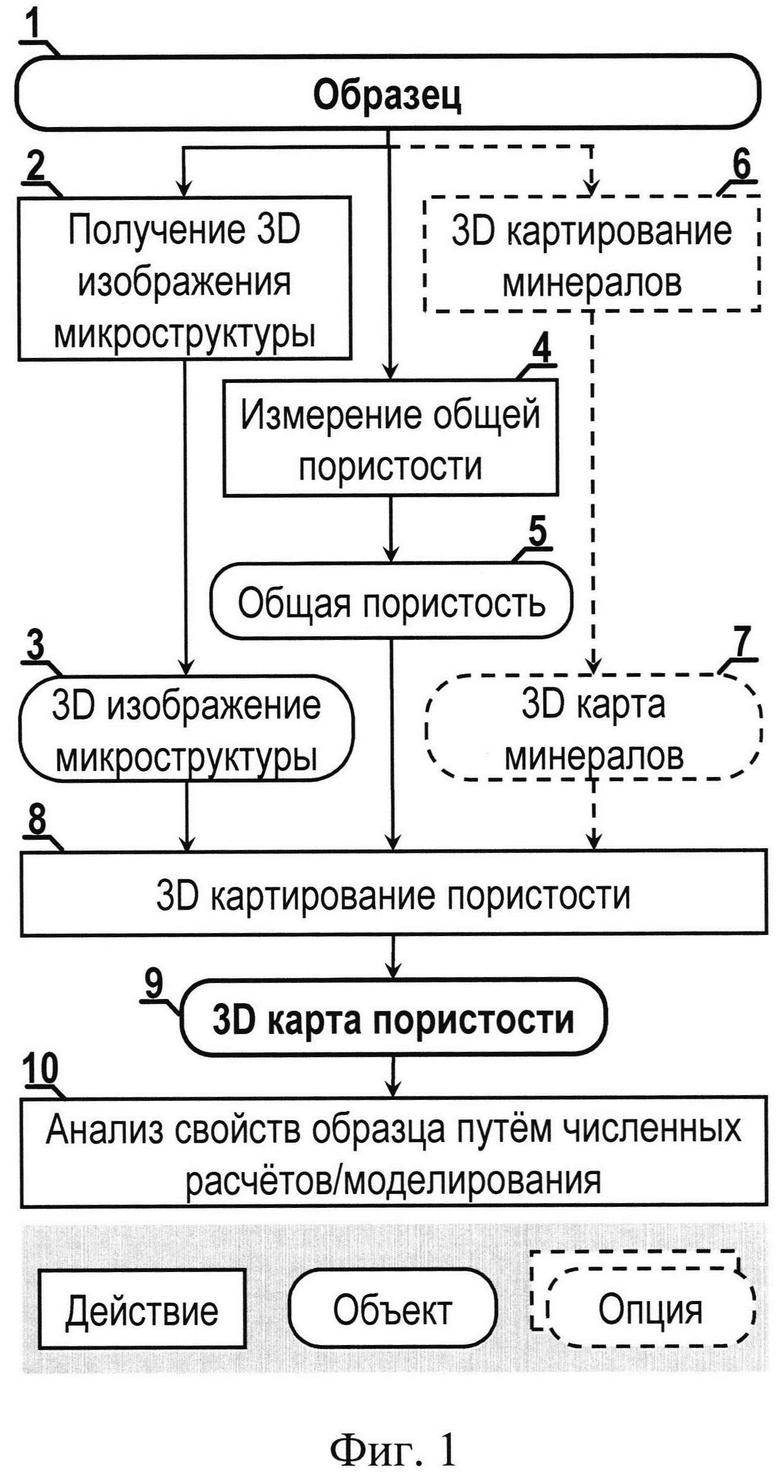
1. Способ определения трехмерного пространственного распределения пористости в образце неоднородной среды, в соответствии с которым:
- получают 3D изображение микроструктуры образца с помощью метода получения 3D изображений микроструктуры,
- измеряют общую пористость образца,
- получают 3D карту минералов, входящих в состав образца, представляющую собой изображение микроструктуры образца, в котором каждая точка проинтерпретирована как конкретный минерал,
- используя полученные 3D изображение микроструктуры и 3D карту минералов, определяют значения физических величин, которые соответствуют полностью пустым вокселям, что соответствует отсутствию минеральной фазы в соответствующем объеме образца, и полностью сплошным вокселям, что соответствует отсутствию пор внутри ячейки каждого минерала,
- осуществляют нормировку полученного 3D изображения микроструктуры с использованием найденных для каждого минерала физических значений, соответствующих полностью пустым и полностью сплошным вокселям, получая нормированное 3D изображение,
- используя измеренную общую пористость, определяют значения, которые соответствуют на нормированном 3D изображении микроструктуры полностью пустым и полностью сплошным вокселям, таким образом, чтобы пористость получающаяся в результате соответствовала измеренной, тем самым определяя зависимость величины внутренней пористости в вокселе от значения величины на нормированном 3D изображении
- используя нормированное 3D изображение микроструктуры и полученную зависимость величины внутренней пористости в вокселе от значения величины на нормированном 3D изображении, создают с помощью вычислительного устройства трехмерное пространственное распределение пористости в образце, учитывающее внутреннюю пористость вокселей.
2. Способ по п. 1, в соответствии с которым образцом неоднородной среды является образец кернового материала.
3. Способ по п. 1, в соответствии с которым методом получения 3D изображений микроструктуры является рентгеновская микро- и нанокомпьютерная томография.
4. Способ по п. 1, в соответствии с которым методом получения 3D изображений микроструктуры является нейтронная микротомография.
5. Способ по п. 1, в соответствии с которым получаемое 3D изображение микроструктуры является векторным.
6. Способ по п. 5, в соответствии с которым получаемое векторное 3D изображение микроструктуры является результатом мультиэнергетической рентгеновской микро- и нанокомпьютерной томографии.
7. Способ по п. 6, в соответствии с которым получаемое векторное 3D изображение микроструктуры является результатом двуэнергетической рентгеновской микро- и нанокомпьютерной томографии.
8. Способ по п. 5, в соответствии с которым получаемое векторное 3D изображение микроструктуры является результатом рентгенофлюоресцентной микротомографии.
9. Способ по п. 1, в соответствии с которым получаемое 3D изображение микроструктуры является результатом 3D ФИП-РЭМ сканирования.
10. Способ по п. 1, в соответствии с которым измерение общей пористости осуществляют с помощью газового порозиметра.
11. Способ по п. 1, в соответствии с которым измерение общей пористости осуществляют с помощью метода насыщения и взвешивания.
12. Способ по п. 1, в соответствии с которым измерение общей пористости осуществляют с помощью метода ртутной порометрии.
13. Способ по п. 1, в соответствии с которым в случае, если образец состоит только из одного минерала, 3D карта минералов представляет собой изображение микроструктуры образца, в котором каждая точка проинтерпретирована как данный минерал.
14. Способ по п. 1, в соответствии с которым 3D карту минералов получают с помощью синхротронной монохроматической рентгеновской микро- и нанотомографии.
15. Способ по п. 1, в соответствии с которым 3D карту минералов, входящих в состав образца, получают с помощью 3D ФИП-РЭМ с энергодисперсионной спектроскопией.
16. Способ по п. 1, в соответствии с которым 3D карту минералов, входящих в состав образца, получают с помощью комбинации 3D рентгеновской микротомографии и 2D растровой электронной микроскопии с энергодисперсионной спектроскопией.
17. Способ по п. 1, в соответствии с которым значения физических величин, которые соответствуют полностью пустым вокселям, что соответствует отсутствию минеральной фазы в соответствующем объеме образца, и полностью сплошным вокселям, что соответствует отсутствию пор внутри ячейки каждого минерала, определяют автоматически вычислительным устройством.
18. Способ по п. 1, в соответствии с которым значения физических величин, которые соответствуют полностью пустым вокселям, что соответствует отсутствию минеральной фазы в соответствующем объеме образца, и полностью сплошным вокселям, что соответствует отсутствию пор внутри ячейки каждого минерала, определяются оператором вручную.
19. Способ по п. 18, в соответствии с которым значения физических величин, которые соответствуют полностью пустым вокселям, что соответствует отсутствию минеральной фазы в соответствующем объеме образца, и полностью сплошным вокселям, что соответствует отсутствию пор внутри ячейки каждого минерала, определяют путем усреднения по выбранной оператором группе близлежащих вокселей на полученном изображении.
20. Способ по п. 18, в соответствии с которым значения физических величин, которые соответствуют полностью пустым вокселям, что соответствует отсутствию минеральной фазы в соответствующем объеме образца, и полностью сплошным вокселям, что соответствует отсутствию пор внутри ячейки каждого минерала, определяют путем нахождения статистической моды по выбранной оператором группе близлежащих вокселей.
21. Способ по п. 1, в соответствии с которым значения, которые соответствуют на полученном нормированном 3D изображении микроструктуры полностью пустым и полностью сплошным вокселям, определяют автоматически вычислительным устройством из условия равенства значений экспериментально измеренной общей пористости и общей пористости трехмерного пространственного распределения пористости в образце.
22. Способ по п. 21, в соответствии с которым автоматическое определение значений, которые соответствуют на полученном нормированном 3D изображении микроструктуры полностью пустым и полностью сплошным вокселям, состоит в итеративном подборе до нахождения значения, удовлетворяющего условию равенства пористостей.
23. Способ по п. 1, в соответствии с которым значения физических величин, которые соответствуют полностью пустым вокселям, что соответствует отсутствию минеральной фазы в соответствующем объеме образца, и полностью сплошным вокселям, что соответствует отсутствию пор внутри ячейки каждого минерала, оценивают теоретически.
24. Способ по п. 1, в соответствии с которым значения физических величин, которые соответствуют полностью пустым вокселям, что соответствует отсутствию минеральной фазы в соответствующем объеме образца, и полностью сплошным вокселям, что соответствует отсутствию пор внутри ячейки каждого минерала, определяют напрямую на эталонных минеральных образцах.
25. Способ по п. 1, в соответствии с которым в случае отсутствия полностью пустых и/или сплошных вокселей на полученном 3D изображении микроструктуры образца целиком пустые и целиком сплошные объекты (так называемые эталоны) искусственно добавляют при получении 3D изображения для последующего определения значений физических величин, которые соответствуют полностью пустым вокселям, что соответствует отсутствию минеральной фазы в соответствующем объеме образца, и полностью сплошным вокселям, что соответствует отсутствию пор внутри ячейки каждого минерала.
26. Способ по п. 1, в соответствии с которым найденные значения физических величин, которые соответствуют полностью пустым вокселям, что соответствует отсутствию минеральной фазы в соответствующем объеме образца, и полностью сплошным вокселям, что соответствует отсутствию пор внутри ячейки каждого минерала, и значения, которые соответствуют на полученном нормированном 3D изображении микроструктуры полностью пустым и полностью сплошным вокселям, используют для создания трехмерного пространственного распределения пористости в образце или похожих образцах, отсканированных в аналогичных условиях.
27. Способ по п. 1, в соответствии с которым создание трехмерного пространственного распределения пористости в образце включает дополнительную пост-обработку.
28. Способ по п. 27, в соответствии с которым в рамках постобработки частично сплошные воксели, окруженные целиком пустыми вокселями, заменяют на целиком пустые воксели.
29. Способ по п. 27, в соответствии с которым в рамках постобработки частично пустые воксели, окруженные целиком сплошными вокселями, заменяют на целиком сплошные воксели.
30. Способ по п. 1, в соответствии с которым созданное трехмерное пространственное распределение пористости в образце используют для выполнения численных расчетов различных физических процессов и явлений в неоднородной среде.
| US 20110004447 A1, 06.01.2011 | |||
| US 20170192118 A1, 06.07.2017 | |||
| WO 2013106508 A1, 18.07.2013 | |||
| FR 2988306 B1, 18.07.2014 | |||
| US 8908925 B2, 09.12.2014 | |||
| US 8938045 B2, 20.01.2015. |
Авторы
Даты
2022-11-17—Публикация
2018-02-02—Подача