Область техники, к которой относится изобретение
Настоящее изобретение относится к системе и способу для моделирования и калибровки устройства формирования изображения, которые компенсируют недостатки прямоугольности оси линии взгляда в плоскости изображения устройства формирования изображения.
Уровень техники
Калибровка цифровых камер и других устройств формирования изображения направлена на формирование математической модели, как такое изображение "отпечатывается" через объектив на поверхности устройства формирования изображения. В процедуре вначале используется изображение из цели калибровки с точно известным допуском, и выделяют целевые элементы из изображения. В конечном итоге математическая модель сопоставляет информацию изображения с реальной трехмерной (3D) целевой информацией. После калибровки устройство формирования изображения затем можно использовать для отображения объектов реального мира, используя коэффициент масштабирования, фокусное расстояние 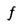 . При работе с камерами и объективами массового производства, необходимо выполнять калибровку камеры для компенсации допусков фокусного расстояния объектива, где такой допуск может достигать 10%.
. При работе с камерами и объективами массового производства, необходимо выполнять калибровку камеры для компенсации допусков фокусного расстояния объектива, где такой допуск может достигать 10%.
Кроме того, когда модель точно известна, ее затем можно использовать для воссоздания идеального изображения камеры, также называемого изображением точечной диафрагмы, необходимого для практически каждой профессиональной, автоматизированной системы формирования изображения. Благодаря программной коррекции изображения, можно компенсировать ошибки изображения, вводимые неидеальной природой объектива, деформации изображения типа "рыбий глаз", называемые геометрическими искажениями, и разделение света на цвета радуги в оптических элементах объектива, называемое хроматическими искажениями. Несколько устройств формирования изображения проявляют смещение от прямоугольности линии взгляда в отношении плоскости изображения. Для правильного измерения искажения изображения необходимо компенсировать неперпендикулярность плоскости изображения в отношении линии взгляда объектива. В известных технологиях калибровки с этой целью используют предположение наклонной оси. Однако, как оказалось, такое предположение смещает каждый параметр камеры в модели, вызывая систематические ошибки измерений. В результате, смещение типа искажений масштаба - размера вводится в изображение, которое каждый другой параметр камеры стремится компенсировать, также смещая эти параметры камеры. При 3D сканировании или телеметрии это переходит в смещение геометрии и местоположения 3D объектов при реконструкции из пары одновременно получаемых изображений камеры.
Поэтому, необходимо улучшить существующие технологии калибровки и моделирования для устройств формирования изображения.
Раскрытие изобретения
Предложенная технология калибровки и моделирования вводит точную коррекцию перспективы для учета допусков при сборке в устройстве формирования изображения или системе камера/объектив, что приводит к тому, что оптическая ось объектива становится неперпендикулярной плоскости изображения.
Точное знание узла плоскости камеры и объектива устраняет систематическое смещение в системах телеметрии при 3D сканировании, используя цифровую камеру или стереопару камер, что приводит к точному измерению фокусного расстояния (масштаба изображения), размещает положение истинного центра изображения на плоскости камеры и повышает точность при искажении измерений, вводимых кривизной изображения (геометрические искажения) и разделением света на цвета радуги в оптических элементах объектива (хроматическое искажение).
Точное знание узла плоскости камеры и объектива повышает эффективность расчетов и точность при устранении геометрических и хроматических искажений объектива.
Устранение искажения объектива повышает степень сжатия изображений без добавления каких-либо потерь.
В соответствии с первым широким аспектом, описан способ, воплощенный в компьютере, для моделирования устройства формирования изображения для использования при калибровке и коррекции изображений, способ, содержащий определяют первую 3D ортогональную систему координат, имеющую начало координат, расположенное в точке фокусирования устройства формирования изображения, первая ось первой системы координат продолжается вдоль направления линии взгляда устройства формирования изображения; определяют вторую 3D ортогональную систему координат, имеющую начало координат, расположенное на единичном расстоянии от точки фокусирования, первая ось второй системы координат, продолжающаяся вдоль направления линии взгляда, вторая и третья ось второй системы координат расположены, по существу, параллельно второй и третьей осям первой системы координат, соответственно, вторая и третья оси второй системы координат, таким образом, определяют истинный квадрат плоскости масштабирования с линией взгляда; определения третьей 3D системы координат, имеющей начало координат, расположенное на фокусном расстоянии от точки фокусирования, первая ось третьей системы координат, продолжающаяся вдоль направления линии взгляда, вторая и третья оси третьей системы координат, соответственно, наклонены под первым и вторым углом относительно ориентации второй и третьей оси второй системы координат, вторая и третья оси третьей системы координат, таким образом, определяют неперпендикулярность плоскости изображения относительно линии взгляда; принимают набор 3D координат, ассоциированных с точкой 3D объекта реального мира, снятой устройством формирования изображения; вычисляют проекцию точки на истинную плоскость масштабирования, получая, таким образом, первый набор плоских координат, и на плоскость изображения, получая, таким образом, второй набор плоских координат; и выводят второй набор плоских координат, обозначающих местоположения точки изображения, соответствующего точке 3D объекта.
В некоторых вариантах осуществления вторая система координат определена таким образом, что плоскость истинной шкалы устанавливает вход для системы линз устройства формирования изображения, и проекция в плоскости истинной шкалы выражает выход из внешней модели устройства формирования изображения, и третья система координат определена таким образом, что плоскость изображения устанавливает выход из системы линз, и проекцию на плоскость изображения, выраженную и выводимую внутренней моделью устройства формирования изображения.
В некоторых вариантах осуществления принятый набор 3D координат представляет собой [x y z 1]T, и проекция точки 3D объекта на плоскость истинной шкалы рассчитывается следующим образом:
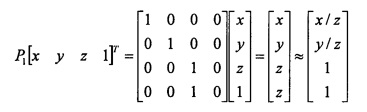 ,
,
где ≈ представляет собой оператор эквивалентной шкалы, и P1 определяет операцию проецирования в плоскости истинной шкалы в отношении первой системы координат.
В некоторых вариантах осуществления проекция точки 3D объекта на плоскость изображения рассчитывается следующим образом:
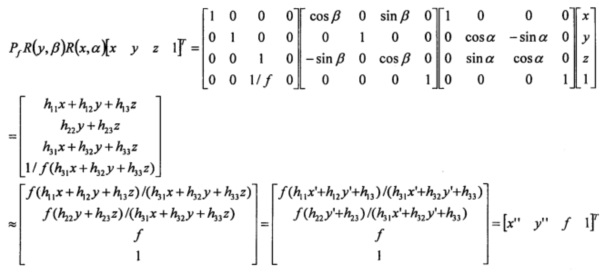
где 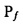 определяет операцию проецирования на плоскость изображения,
определяет операцию проецирования на плоскость изображения, 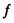 представляет собой фокусное расстояние, α представляет собой первый угол, β представляет собой второй угол, R (x, α) представляет собой матрицу вращения α относительно оси x плоскости изображения, ось x определена, как, по существу, параллельная второй оси первой системы координат перед выполнением вращения α, R (y, β) представляет собой матрицу вращения β относительно оси y плоскости изображения, ось y определена, как, по существу, параллельная третьей оси первой системы координат перед выполнением вращения β, вращение α рассчитывают в самом правом положении таким образом, что вращение β выполняется относительно оси x, поворачиваемой на угол α, и где
представляет собой фокусное расстояние, α представляет собой первый угол, β представляет собой второй угол, R (x, α) представляет собой матрицу вращения α относительно оси x плоскости изображения, ось x определена, как, по существу, параллельная второй оси первой системы координат перед выполнением вращения α, R (y, β) представляет собой матрицу вращения β относительно оси y плоскости изображения, ось y определена, как, по существу, параллельная третьей оси первой системы координат перед выполнением вращения β, вращение α рассчитывают в самом правом положении таким образом, что вращение β выполняется относительно оси x, поворачиваемой на угол α, и где
h11=cosβ,
h12=sinβsinα,
h13=sinβcosα,
h22=cosα,
h23=-sinα,
h31=-sinβ,
h32=cosβsinα, и
h33=cosβcosα.
В некоторых вариантах осуществления способ дополнительно содержит: определяют гомографию Н между плоскостью истинной шкалы и планом изображения следующим образом:
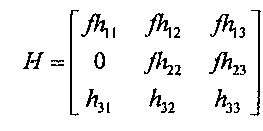 , где h31 и h32 представляют собой ненулевые элементы, применяющие коррекцию перспективы для масштабов x и y в плане изображения, и второй набор плоских координат (xʺ, yʺ) представляет собой гомографическое преобразование искаженного положения (x', y') для изображения точки на плоскости истинной шкалы, гомографическое преобразование выражается следующим образом:
, где h31 и h32 представляют собой ненулевые элементы, применяющие коррекцию перспективы для масштабов x и y в плане изображения, и второй набор плоских координат (xʺ, yʺ) представляет собой гомографическое преобразование искаженного положения (x', y') для изображения точки на плоскости истинной шкалы, гомографическое преобразование выражается следующим образом:
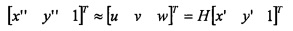 ,
,
где 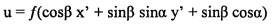 ,
,
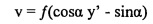 ,
,
w=-sinβx'+cosβsinαy'+cosβcosα,
xʺ=u/w+CX, и
yʺ=v/w+CY, где (CX, CY) представляет исходное положение третьей системы координат.
В некоторых вариантах осуществления гомография Н определена следующим образом:
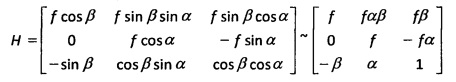
где аппроксимация cosθ~1 и sinθ~θ используется для малых углов α и β.
В некоторых вариантах осуществления способ дополнительно содержит: компенсируют искажение объектива устройства формирования изображения в плоскости истинной шкалы, компенсация содержит: применяют модели искажения объектива, определенные следующим образом:
r'=r+k1r3+k2r5+…,
где первый набор плоских координат содержит положение (x, y) без искажений для изображения точки в плоскости истинной шкалы, выраженной в радиальных координатах (r, θ), где r2=r2+y2 и tanθ=y/x, (x', y') представляет искаженное положение (x, y) на выходе объектива перед проекцией точки на плоскость изображения, r' представляет собой искаженное радиальное расстояние, рассчитанное на основе (x', y'), и k1 и k2 представляют собой параметры геометрических искажений объектива.
В соответствии со вторым широким аспектом, описана система для моделирования устройства формирования изображения для использования при калибровке и коррекции изображения, система, содержащая запоминающее устройство; процессор; и, по меньшей мере, одно приложение, сохраненное в запоминающем устройстве и исполняемое процессором для определения первой 3D ортогональной системы координат, имеющей начало координат, расположенное в точке фокусирования устройства формирования изображения, первая ось первой системы координат продолжается вдоль направления линии взгляда устройства формирования изображения; определения второй 3D ортогональную системы координат, имеющей место происхождения, расположенное на единичном расстоянии от точки фокусирования, первая ось второй системы координат, продолжающаяся вдоль направления линии обзора, вторая и третья оси второй системы координат, по существу, параллельны вторая и третья ось первой системы координат, соответственно, вторая и третья оси второй системы координат, таким образом, определяют истинный квадрат плоскости масштабирования с линией взгляда; определения третьей 3D системы координат, имеющей начало координат, расположенное на фокусном расстоянии от точки фокусирования, первая ось третьей системы координат, продолжающаяся вдоль направления линии взгляда, вторая и третья оси третьей системы координат, соответственно, наклонены под первым и вторым углом относительно ориентации второй и третьей оси второй системы координат, вторая и третья оси третьей системы координат, таким образом, определяют неперпендикулярность плоскости изображения относительно линии взгляда; принимают набор 3D координат, ассоциированных с точкой 3D объекта реального мира, снятой устройством формирования изображения; вычисляют проекцию точки на истинную плоскость масштабирования, получая, таким образом, первый набор плоских координат, и на плоскость изображения, получая, таким образом, второй набор плоских координат; и выводят второй набор плоских координат, обозначающих местоположения точки изображения, соответствующего точке 3D объекта.
В некоторых вариантах осуществления, по меньшей мере, одно приложение может быть выполнено, используя процессор для определения второй системы координат таким образом, что плоскость истинного масштаба устанавливает вход в систему объектива устройства формирования изображения, и проекция в плоскости истинного масштаба выражает выход внешней модели устройства формирования изображения и определяет третью систему координат таким образом, что плоскость формирования изображения устанавливает выход для системы объектива, и проекция для плоскости формирования изображения выражает выход внутренней модели устройства формирования изображения.
В некоторых вариантах осуществления, по меньшей мере, одно приложение может быть выполнено с помощью процессора для приема набора 3D координат, как [x y z 1]T и расчета проекции точки 3D объекта на плоскость истинного масштаба следующим образом:
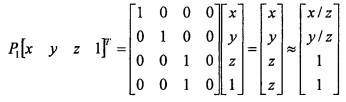 ,
,
где ≈ представляет собой оператор эквивалента шкалы, и P1 определяет операцию проекции на плоскость истинной шкалы в отношении первой системы координат.
В некоторых вариантах осуществления, по меньшей мере, одно приложение может быть выполнено процессором для расчета проекции точки 3D объекта на плоскость формирования изображения следующим образом:
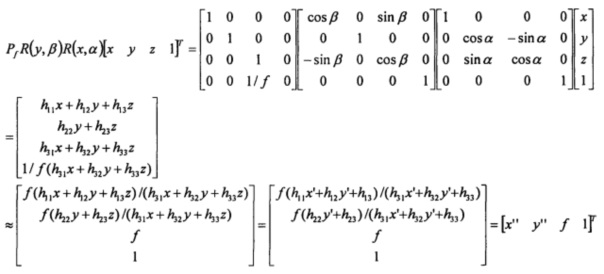
где 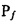 определяет операцию проецирования на плоскость изображения,
определяет операцию проецирования на плоскость изображения, 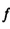 представляет собой фокусное расстояние, α представляет собой первый угол, β представляет собой второй угол, R (x, α) представляет собой матрицу вращения α относительно оси x плоскости изображения, ось x определена, как, по существу, параллельная второй оси первой системы координат перед выполнением вращения α, R (y, β) представляет собой матрицу вращения β относительно оси y плоскости изображения, ось y определена, как, по существу, параллельная третьей оси первой системы координат перед выполнением вращения β, вращение α рассчитывают в самом правом положении таким образом, что вращение β выполняется относительно оси x, поворачиваемой на угол α, и где
представляет собой фокусное расстояние, α представляет собой первый угол, β представляет собой второй угол, R (x, α) представляет собой матрицу вращения α относительно оси x плоскости изображения, ось x определена, как, по существу, параллельная второй оси первой системы координат перед выполнением вращения α, R (y, β) представляет собой матрицу вращения β относительно оси y плоскости изображения, ось y определена, как, по существу, параллельная третьей оси первой системы координат перед выполнением вращения β, вращение α рассчитывают в самом правом положении таким образом, что вращение β выполняется относительно оси x, поворачиваемой на угол α, и где
h11=cosβ,
h12=sinβsinα,
h13=sinβcosα,
h22=cosα,
h23=-sinα,
h31=-sinβ,
h32=cosβsinα, и
h33=cosβcosα.
В некоторых вариантах осуществления, по меньшей мере, одно приложение исполняется процессором для определения гомографии Н между плоскостью истинной шкалы и плоскостью изображения следующим образом:
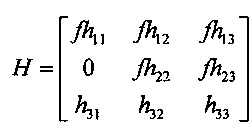 , где h31 ил h32 представляют собой ненулевые элементы, применяющие коррекцию перспективы для шкал x и y в плоскости изображения, и второй набор плоских координат (xʺ, yʺ) представляют собой гомографическое преобразование искаженного положения (x', y') изображения в точке плоскости истинной шкалы, гомографическое преобразование выражается следующим образом:
, где h31 ил h32 представляют собой ненулевые элементы, применяющие коррекцию перспективы для шкал x и y в плоскости изображения, и второй набор плоских координат (xʺ, yʺ) представляют собой гомографическое преобразование искаженного положения (x', y') изображения в точке плоскости истинной шкалы, гомографическое преобразование выражается следующим образом:
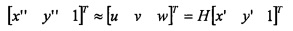 ,
,
где 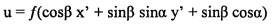 ,
,
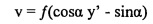 ,
,
w=-sinβx'+cosβsinαy'+cosβcosα,
xʺ=u/w+CX, и
yʺ=v/w+CY, где (CX, CY) представляет собой положение начала координат для третьей системы координат.
В некоторых вариантах осуществления, по меньшей мере, одно приложение исполняется процессором, для определения гомографии Н следующим образом:
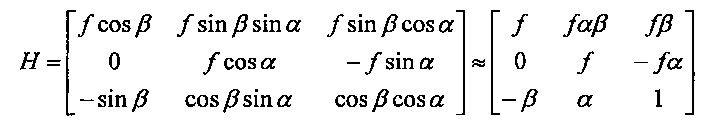
где аппроксимация cosθ~1 и sinθ~θ используется для малых углов α и β.
В некоторых вариантах осуществления, по меньшей мере, одно приложение может исполняться процессором для компенсации искажений объектива устройства формирования изображения в плоскости истинной шкалы, при этом компенсация содержит приложение модели искажений объектива, определенной следующим образом:
r'=r+k1r3+k2r5+…,
где первый набор плоских координат содержит неискаженное положение (x, y) изображения точки на плоскости истинной шкалы, которое выражено в радиальных координатах (r, θ), где r2=x2+y2 и tanθ=y/x, (x', y') представляет искаженное положение (x, y) на выходе объектива перед проекцией точки на плоскость изображения, r' представляет собой искаженное радиальное расстояние, рассчитанное на основе (x', y'), и k1 и k2 представляют собой параметры геометрического искажения объектива.
В некоторых вариантах осуществления устройство формирования изображения содержит одну из камеры с объективом с изменяемым масштабом изображения, устройства формирования изображения в близком инфракрасном свете, устройства формирования изображений в коротковолновом инфракрасном свете, устройства формирования изображений в длинноволновом инфракрасном свете, устройства радара, устройства детектирования и ранжирования света, формирователя изображения в виде телескопа с параболическим зеркалом, хирургической эндоскопической камеры, устройства сканирования для компьютерной томографии, устройства формирования изображения спутника, сонарного устройства и многоспектральной системы с множеством различных датчиков.
В соответствии с третьим широким аспектом описан считываемый компьютером носитель информации, на котором содержится программный код, исполняемый процессором для моделирования устройства формирования изображения, для использования при калибровке и коррекции изображения, программный код, исполняемый для определения первой 3D ортогональной системы координат, имеющей начало координат, расположенное в точке фокусирования устройства формирования изображения, первая ось первой системы координат, продолжающаяся вдоль направления линии обзора устройства формирования изображения; определения второй 3D ортогональной системы координат, имеющую начало координат, расположенное на единичном расстоянии от точки фокусирования, первая ось второй системы координат продолжается вдоль направления линии обзора, вторая и третья оси второй системы координат, по существу, параллельны второй и третьей осям первой системы координат, соответственно, вторая и третья оси второй системы координат, таким образом, определяют квадрат плоскости истинной шкалы с линией обзора; определения третьей 3D системы координат, имеющей начало координат, расположенное на фокусном расстоянии от точки фокусирования, первая ось третьей системы координат, продолжающаяся вдоль направления линии обзора, вторая и третья оси третьей системы координат, соответственно, наклонены на первый и второй углы относительно ориентации второй и третьей осей второй системы координат, вторая и третья оси третьей системы координат, таким образом, образуют не перпендикулярность плоскости изображения относительно линии обзора; приема набора 3D координат, ассоциированных с точкой 3D объекта реального мира, снятого устройством формирования изображения; расчета проекции точки на плоскость истинной шкалы, получая, таким образом, первый набор плоских координат, и на плоскость изображения, получая, таким образом, второй набор плоских координат; и выводят второй набор плоских координат, обозначающих местоположения точки изображения, соответствующей точке 3D объекта.
Краткое описание чертежей
Дополнительные свойства и преимущества настоящего изобретения будут понятны из следующего подробного описания изобретения, которое следует рассматривать в комбинации с приложенными чертежами, на которых:
на фиг. 1 показана схема, иллюстрирующая искажение объектива линзы;
на фиг. 2 показаны схематичные виды, иллюстрирующие бочкообразные искажения и подушкообразные геометрические искажения объектива;
на фиг. 3 показан вид в плане, иллюстрирующий размывание кромки, когда смешиваются два соседних цветных пикселя;
на фиг. 4 показана схема, иллюстрирующая параметры, которые определяют поведение комбинации камеры/объектива в идеальном представлении модели камеры, в которой предполагается, что плоскость изображения является квадратной по сравнению с линией обзора;
на фиг. 5 показана схема предположения наклона оси внутренней модели камеры, где компенсация наклоненной оси добавляется к идеальному представлению камеры на фиг. 4;
на фиг. 6 показана схема нового набора переменных для внутренней модели камеры, в соответствии с иллюстративным вариантом осуществления настоящего изобретения;
на фиг. 7 показана схема режима радиальных искажений, в соответствии с иллюстративным вариантом осуществления настоящего изобретения;
на фиг. 8а показана блок-схема последовательности операций способа для расчета местоположения точки изображения, в соответствии с иллюстративным вариантом осуществления настоящего изобретения;
на фиг. 8b показана блок-схема последовательности операций этапа по фиг. 8а проекции на плоскость  , используя внешнюю модель камеры;
, используя внешнюю модель камеры;
на фиг. 8с показана блок-схема последовательности операций этапа на фиг. 8а по применению модели искажения объектива;
на фиг. 8d показана блок-схема последовательности операций этапа на фиг. 8а проецирования наклонной плоскости 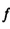 изображения, используя внутреннюю модель камеры;
изображения, используя внутреннюю модель камеры;
на фиг. 9а показана схема системы для расчета местоположения точки изображения, в соответствии с иллюстративным вариантом осуществления настоящего изобретения;
на фиг. 9b показана блок-схема, представляющая примерное приложение, работающее в процессоре по фиг. 9а;
на фиг. 10 показан искаженный вид фотографии цели калибровки;
на фиг. 11 показаны виды фотографий тестовой камеры с микрообъективом, с печатной платой;
на фиг. 12 показана комбинированная иллюстрация выделения цели;
на фиг. 13 показана схема стереопары, используемой для измерения объектов при 3D, в котором используются одновременно изображения двух камер;
на фиг. 14 показаны фотографии, иллюстрирующие коррекцию геометрических искажений, используя тестовую камеру;
на фиг. 15 показан график, иллюстрирующий хроматические искажения для объектива Cosmicar® С Mount 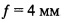 ;
;
на фиг. 16 показан график, иллюстрирующий хроматическое искажение красного цвета, радиальную коррекцию в зависимости от расстояния до центра изображения (пиксели);
на фиг. 17 показан график, иллюстрирующий хроматическое искажение синего цвета, радиальную коррекцию в зависимости от расстояния до центра изображения (пиксели); и
на фиг. 18 показана схематичная иллюстрация компоновки структуры Байера для цветовой камеры.
Следует отметить, что на приложенных чертежах, свойства обозначены одинаковыми номерами ссылочных позиций.
Краткое описание предпочтительных вариантов осуществления
1.1 Искажение объектива
Искажение объектива вводит наибольшую ошибку, которую можно найти при формировании цифровых изображений. Это представлено на фиг. 1 и 2. Как можно видеть на фиг. 1, эффект "рыбий глаз" называется геометрическим искажением и изгибает прямые линии. Цветное затенение на кромках изображения (называется здесь "Кромка, окрашенная в синий цвет" и "Кромка, окрашенная в красной цвет" на фиг. 1) называется хроматическими искажениями и вызвано расщеплением света в объективе устройства формирования изображения (не показано). Такие отклонения от поведения точечной диафрагмы увеличиваются с увеличение угла обзора объектива. Оба типа искажений должны быть моделированы и компенсированы для достижения субпиксельной точности, компенсация возможна только с использованием программного обеспечения, которое позволяет выйти за пределы возможностей аппаратных средств. Как можно видеть на фиг. 2, когда геометрическое искажение сжимает само изображение, оно называется бочкообразным искажением (см. фиг. 2 (а)); когда изображение расширяется, оно называется подушкообразным искажением (см. фиг. 2 (b)).
1.2 Размывание
Как показано на фиг. 3, размывание представляет собой промежуточный цвет пикселя, наблюдаемый, когда кромка проходит через заданный пиксель, и оба соседних цвета смешиваются. Цвет пикселя представляет собой средневзвешенное значение соседних значений цветов, по обе стороны от кромки, в отношении каждого из цветов на соответствующих поверхностях внутри пикселя.
Для изображений с малым разрешением размывание кромки (затенение на кромках объекта) образует интерференцию с искажениями объектива, геометрическими и хроматическими. При использовании цветных изображений из черно-белой цели, цветное затенение кромки вызвано хроматическими искажениями. Для черно-белой цели размывание кромки возникает в виде серых теней, как и при геометрических искажениях. Поэтому, желательно изолировать хроматические искажения объектива от размывания кромки или геометрических искажений, используя цвет на кромке.
1.3 Модель камеры
Моделирование камеры (или другого устройства формирования изображения) требует математической модели и процедуры калибровки для измерения параметров, которые определяют поведение определенной комбинации камера/объектив.
Следует понимать, что, хотя здесь делается ссылка на камеру, предложенная система и способ также применимы для других устройств формирования изображения. В частности, также могут применяться устройства, включающие в себя, но без ограничения этим, камеры с объективом с изменяемым масштабом изображения; устройства формирования изображения в близком инфракрасном свете (NIR), коротковолновом инфракрасном свете (SWIR) и длинноволновом инфракрасном свете (LWIR); и устройства радаров и детектирования света и устройства определения расстояния (LIDAR); устройства формирования изображения для телескопа с параболическим зеркалом; хирургические эндоскопические камеры; устройства сканирования компьютерной томографии (СТ); спутниковые устройства формирования изображения; сонарные устройства; и многоспектральные системы с множеством различных датчиков.
В соответствии с опубликованной литературой по данном предмету, идеальная модель камеры имеет три компонента, как показано на фиг. 4, а именно:
1 - Внешняя модель: Взаимосвязь между Координатами камеры в точке фокусирования О (точка в пространстве, где весь свет сходится в одну точку), и мировые координаты в мировой системе координат (XW YW ZW);
2 - Внутренняя модель: Система координаты в плоскости камеры (XC YC ZC), где ZC представляет собой оптическую ось объектива (то есть, линию обзора объектива); и
3 - Модель объектива: Формулы геометрических и хроматических искажений объектива.
Точка О фокусирования представляет собой местоположение в пространстве, где все изображения сходятся в одну точку; перед точкой О фокусирования находится плоскость изображения камеры (не показана). Оптическая ось ZC объектива пересекает плоскость изображения под двумя (2) прямыми углами (то есть, перпендикулярно ей), определяя место расположение от центра изображения (CX, Cy).
1.3.1 Внешняя модель камеры
Внешняя модель камеры точно представлена в литературе. Определяя два набора координат,
1 - Мировой (XW YW ZW) с началом координат, установленным в (0, 0, 0); и
2 - Камеры (XC YC ZC) в точке О фокусирования.
Как можно видеть на фиг. 4, на которой иллюстрируется идеальная модель камеры, набор координат камеры (XC YC ZC) начинается с оптической оси ZC объектива и точки О фокусирования, как в начале координат, XC выбирают так, чтобы она была совмещена с горизонтальной осью (не показана) плоскости изображения камеры. Геометрически, вертикальная ось YC должна завершать набор, используя правило правой руки. Внешняя модель записывается, как матрица [R3×3 T3×1] (дополнительно описана ниже) и представляет набор мировых координат (XW YW ZW) с началом координат, установленным в (0, 0, 0).
Внешняя модель камеры выражает вращение (κ ϕ Ω), и трансляции (TX Ty Tz), необходимые для выравнивания набора координат камеры (XC YC ZC) с мировым набором координат (XW YW ZW), и приводит точку О фокусирования в начало мировых координат (0, 0, 0). Внешняя модель камеры, поэтому, имеет шесть (6) степеней свободы, а именно, (κ ϕ Ω) углов вращения и трансляции (TX TY TZ).
1.3.2 Внутренняя модель камеры
Далее, обращаясь к фиг. 5, в дополнение к фиг. 4, будет описана внутренняя модель камеры предшествующего уровня техники, где выполняется компенсация неперпендикулярности. Если бы плоскость изображения представляла собой идеальный квадрат с оптической осью ZC объектива, то коэффициент шкалы между мировыми измерениями XW YW и измерениями камеры XC YC составлял бы 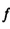 в обоих направлениях x и y. Для учета потерь перпендикулярности между оптической осью ZC объектива и плоскостью изображения, которая происходит из-за производственных ошибок, исследовательское сообщество ввело предположение наклонной оси, показанное на фиг. 5. В предположении наклонной оси, предполагается, что наклон оси плоскости изображения установлен так, что плоскость изображения можно рассматривать, как квадратную относительно оптической оси объектива.
в обоих направлениях x и y. Для учета потерь перпендикулярности между оптической осью ZC объектива и плоскостью изображения, которая происходит из-за производственных ошибок, исследовательское сообщество ввело предположение наклонной оси, показанное на фиг. 5. В предположении наклонной оси, предполагается, что наклон оси плоскости изображения установлен так, что плоскость изображения можно рассматривать, как квадратную относительно оптической оси объектива.
Существуют различные формулировки, в частности:
- Параметр a представляет собой шкалу горизонтального изображения, идеально выровненную с горизонтальной осью массива решетки пикселей камеры;
- Вертикальная шкала установлена в положение b, отличное от a;
- Шкала и ориентация вертикальной оси плоскости изображения наклонена на параметр s наклона относительно оси YC, где s представляет собой меру шкалы наклона относительно шкалы изображения.
Если бы центр изображения (CX, Cy) представлял собой точку, где оптическая ось ZC объектива пересекает плоскость изображения, вместе с координатами (CX, Cy), a, b и s представляли бы собой, в соответствии с уже опубликованной работой, использующей предположение наклонной оси, пять (5) параметров внутренней камеры. Модель внутренней камеры, поэтому, имеет пять (5) степеней свободы.
Массив решетки пикселей плоскости изображений проходит очень точную производственную обработку, при этом калибровка должна производить шкалу горизонтального изображения, равную шкале вертикального изображения, то есть 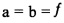 , без перекоса вертикальной оси, то есть, s=0. Однако широко распространенное предположение наклона оси вводит смещение перспективы, сдвиг всех других параметров камеры, что должно быть заменено полной 3D моделью перспективы плоскости изображения, которая удерживает геометрию плоскости изображения камеры. Поэтому, предложено ввести новый набор переменных для внутренней модели камеры, как показано на фиг. 6, в котором модель представлена в координатах камеры (начинающихся с фокальной точки О).
, без перекоса вертикальной оси, то есть, s=0. Однако широко распространенное предположение наклона оси вводит смещение перспективы, сдвиг всех других параметров камеры, что должно быть заменено полной 3D моделью перспективы плоскости изображения, которая удерживает геометрию плоскости изображения камеры. Поэтому, предложено ввести новый набор переменных для внутренней модели камеры, как показано на фиг. 6, в котором модель представлена в координатах камеры (начинающихся с фокальной точки О).
В предложенной модели центр (CX, Cy) изображения остается пересечением между оптической осью ZC объектива и камерой (то есть, плоскостью изображения). Рассматриваются две одновременные перспективы, независимые от шкалы, 3D объекта внешнего мира (его точка Р расположена где-то во внешней среде в заданных координатах относительно осей (XC YC ZC)).
В качестве иллюстрации, ввод системы объектива определен, как теоретическая плоскость при 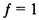 вдоль линии обзора оси ZC, теоретическая плоскость, представленная на фиг. 6 двумя осями, с единичным фокусным расстоянием при
вдоль линии обзора оси ZC, теоретическая плоскость, представленная на фиг. 6 двумя осями, с единичным фокусным расстоянием при 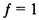 , и идеально квадратная (то есть, под прямым углом) относительно оптической оси ZC объектива. Первая плоскость представляет идеальную проекцию истинной шкалы 1:1 3D объекта на плоскость, имеющую бесконечные размеры в направлениях x и y.
, и идеально квадратная (то есть, под прямым углом) относительно оптической оси ZC объектива. Первая плоскость представляет идеальную проекцию истинной шкалы 1:1 3D объекта на плоскость, имеющую бесконечные размеры в направлениях x и y.
Проекция на 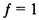 , поэтому, выражена матричным преобразованием [R3×3 T3×1]:
, поэтому, выражена матричным преобразованием [R3×3 T3×1]:

Используя однородные координаты, точка P=[X Y Z 1]T в 3D мировых координатах (X Y Z задана в отношении мировых координат (XW YW ZW), X' Y' Z' в отношении системы координат камеры (XC YC ZC)), проецируется следующим образом:
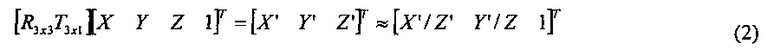
где третий компонент Z' получающегося в результате трехкомпонентного вектора масштабируют до единицы, таким образом, что [X' Y' Z']T представляет собой шкалу, эквивалентную для [X'/Z' Y'/Z' 1]T. 3D точка Р=(X, Y, Z) проецируется в двух измерениях, как (X'/Z', Y'/Z'). Символ ≈ в уравнении (2) представляет эквивалентный оператор шкалы в однородных координатах.
Элементы rij, i, j=1, 2, 3 в уравнении (1) представляют собой функции параметров модели, а именно, три (3) угла вращения (κ ϕ Ω), описанных выше, и (TX Ty, Tz), которые представляют собой положение мирового начала координат в отношении точки О фокусирования.
В дополнение к перспективе истинной шкалы 3D объекта внешнего мира вторая перспектива представляет собой саму плоскость изображения, то есть, выход системы объектива. Плоскость изображения представлена на фиг. 6 двумя осями, пересекающимися в точке (CX, Cy). Поскольку для плоскости камеры на фокусном расстоянии  наблюдается неперпендикулярность относительно оптической оси ZC объектива, требуется пять (5) параметров. Используя плоскость изображения в
наблюдается неперпендикулярность относительно оптической оси ZC объектива, требуется пять (5) параметров. Используя плоскость изображения в  , одинаковые ориентации горизонтальной и вертикальной осей определяют в наборе координат точки О фокусирования (то есть, в наборе координат (XC YC ZC)), при этом два угла α и β поворота относительно обеих осей x и Y используются для учета наклона плоскости камеры. В частности, как показано на фиг. 6, ось X плоскости изображения поворачивается на угол α, в то время как ось Y плоскости изображения поворачивается на угол β, таким образом, что плоскость изображения наклоняется на углы α и β относительно осей x и y, при этом оси x и Y плоскости изображения первоначально установлены параллельно XC и YC в начале координат О, то есть, перед любым поворотом. Другими словами, оси x и у иллюстративно установлены параллельно XC и YC в начале координат О и воспроизводятся на плоскости изображения перед применением любого поворота для наклона плоскости изображения. В результате, наклон плоскости изображения может быть выражен двумя (2) 3D поворотами в пространстве, а именно, поворотами вокруг оси YC на угол α и вторым поворотом вокруг оси XC на угол β. Ось X плоскости изображения, произвольно выбрана, как выровненная с направлением горизонтальной плоскости камеры, поэтому нет необходимости в угле поворота оси Z. Следует понимать, что в некоторых вариантах осуществления, например, в вариантах осуществления, где одновременно используются два устройства формирования изображения, совместно использующие одну и ту же линию визирования для захвата изображений объекта в мире, или в вариантах осуществления, где используются камеры с тремя CCD (с тремя отдельными приборами с зарядовой связью (CCD)), угол поворота оси Z может быть желательным. В дополнение к углам α и β поворота, три оставшиеся степени свободы для внутренней модели камеры затем представляют собой фокусное расстояние
, одинаковые ориентации горизонтальной и вертикальной осей определяют в наборе координат точки О фокусирования (то есть, в наборе координат (XC YC ZC)), при этом два угла α и β поворота относительно обеих осей x и Y используются для учета наклона плоскости камеры. В частности, как показано на фиг. 6, ось X плоскости изображения поворачивается на угол α, в то время как ось Y плоскости изображения поворачивается на угол β, таким образом, что плоскость изображения наклоняется на углы α и β относительно осей x и y, при этом оси x и Y плоскости изображения первоначально установлены параллельно XC и YC в начале координат О, то есть, перед любым поворотом. Другими словами, оси x и у иллюстративно установлены параллельно XC и YC в начале координат О и воспроизводятся на плоскости изображения перед применением любого поворота для наклона плоскости изображения. В результате, наклон плоскости изображения может быть выражен двумя (2) 3D поворотами в пространстве, а именно, поворотами вокруг оси YC на угол α и вторым поворотом вокруг оси XC на угол β. Ось X плоскости изображения, произвольно выбрана, как выровненная с направлением горизонтальной плоскости камеры, поэтому нет необходимости в угле поворота оси Z. Следует понимать, что в некоторых вариантах осуществления, например, в вариантах осуществления, где одновременно используются два устройства формирования изображения, совместно использующие одну и ту же линию визирования для захвата изображений объекта в мире, или в вариантах осуществления, где используются камеры с тремя CCD (с тремя отдельными приборами с зарядовой связью (CCD)), угол поворота оси Z может быть желательным. В дополнение к углам α и β поворота, три оставшиеся степени свободы для внутренней модели камеры затем представляют собой фокусное расстояние  (или шкалу изображения камеры) и координаты центра изображения (CX, Cy).
(или шкалу изображения камеры) и координаты центра изображения (CX, Cy).
Внутренняя матрица K, соответствующая широко распространенному предположению наклонной оси на фиг. 5, определяется в уравнении (3), представленном ниже.
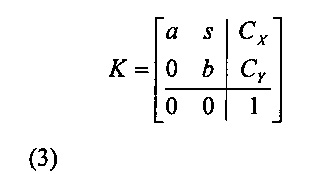
Верхняя левая часть матрицы размером 2×2 в уравнении (3) представляет оси x и y плоскости изображения с параметром s наклона, горизонтальной шкалой a и вертикальной шкалой b. Если их принять, как векторы столбцов, ось X плоскости изображения будет выровнена с горизонтальным направлением решетки массива пикселей плоскости камеры (не показана), с учетов значений 0 в положении (2,1) матрицы K. Ось у плоскости изображения наклонена на s в направлении x, как представлено на фиг. 5. Последний столбец представляет местоположение (CX, Cy) центра изображения.
Ошибка в предположении наклонной оси на фиг. 5 видна в нижней левой части матрицы размером 1×2. Два (2) члена нижней левой части 1×2 не должны быть равны нулю, когда оптическая ось объектива не перпендикулярна относительно плоскости камеры. Когда они не равны нулю, эти члены прикладывают коррекцию перспективы для шкал x и y в плоскости изображений, по мере движения в сторону из центра изображения.
Для расчета проецируемых осей x и y, так, чтобы они учитывали перспективу, поэтому, предложено начать с плоскости камеры изображения, которая является идеально квадратной, с оптической осью Zc объектива. Проецируемые оси x и Y камеры затем рассчитывают, как наклоненные, соответственно, на углы α и β, как описано выше, получая, таким образом, плоскость изображения, которая является неперпендикулярной относительно оптической оси Zc объектива. В предложенном способе модель внутренней камеры определена, как преобразование перспективы с пятью (5) степенями свободы, которое относится к проекции модели внешней камеры с истинной шкалой 1:1 для проекции плоскости изображения на фокусном расстоянии  на общей линии ZC обзора, и где плоскость изображения наклонена на углы α и β относительно осей x и y на плоскости изображения, причем оси x и Y приняты установленными параллельно XC и YC в начале координат О перед каким-либо вращением. На фиг. 6 показаны (CX, Cy) на линии обзора ZC. На фиг. 6, ZC принимают, как начало координат для всех плоскостей, пересекающихся с линией обзора. Первоначально предполагается (CX, Cy)=(0, 0), и, после проецирования, сдвиг начала координат применяют для смещения центра плоскости изображения из положения (0, 0) в (CX, Cy).
на общей линии ZC обзора, и где плоскость изображения наклонена на углы α и β относительно осей x и y на плоскости изображения, причем оси x и Y приняты установленными параллельно XC и YC в начале координат О перед каким-либо вращением. На фиг. 6 показаны (CX, Cy) на линии обзора ZC. На фиг. 6, ZC принимают, как начало координат для всех плоскостей, пересекающихся с линией обзора. Первоначально предполагается (CX, Cy)=(0, 0), и, после проецирования, сдвиг начала координат применяют для смещения центра плоскости изображения из положения (0, 0) в (CX, Cy).
В однородных координатах любая точка 3D в пространстве [x у z 1]T проецируется на плоскость истинной шкалы 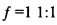 следующим образом:
следующим образом:
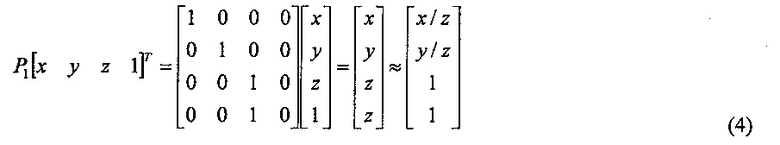
Последняя операция в уравнении (4) представляет собой изменение масштаба четвертой (4-ой) координаты на единицу. Третья координата показывает, что точка (x/z, y/z) лежит на плоскости в положении z=1.
Для плоскости изображения, наклоненной на углы α и β относительно осей x и y, соответственно, и фокусным расстоянием  , одна и та же точка также проецируется на наклоненную плоскость изображения следующим образом:
, одна и та же точка также проецируется на наклоненную плоскость изображения следующим образом:
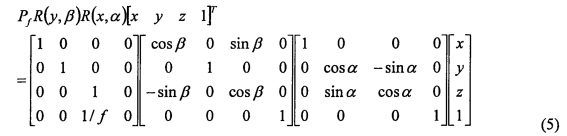
где 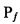 определяет операцию проекции, где элемент (4, 3) представляет собой
определяет операцию проекции, где элемент (4, 3) представляет собой 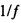 ,
,  представляет собой фокусное расстояние, R (y, β) представляет собой матрицу вращения β относительно оси Y, и R (x, α) представляет собой матрицу вращения α относительно оси X.
представляет собой фокусное расстояние, R (y, β) представляет собой матрицу вращения β относительно оси Y, и R (x, α) представляет собой матрицу вращения α относительно оси X.
Вращение α в уравнении (5) рассчитывают вправо, таким образом, что вращение β выполняется относительно оси Y плоскости изображения, с поворотом на угол α. Следует понимать, что вращение β может рассматриваться, как самая правая точка в уравнении (5), что означает, что вращение α может быть выполнено относительно оси X, повернутой на β. Однородные уравнения, считанные справа налево, и обращенным порядком умножения приводят к другим математическим формулам. Возможны несколько моделей.
Умножая матрицу в уравнении (5), получим:
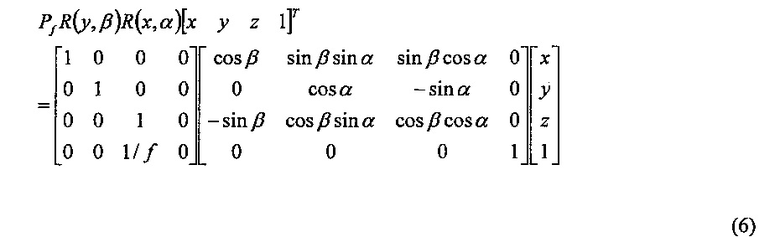
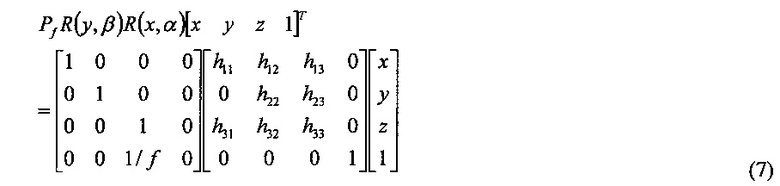
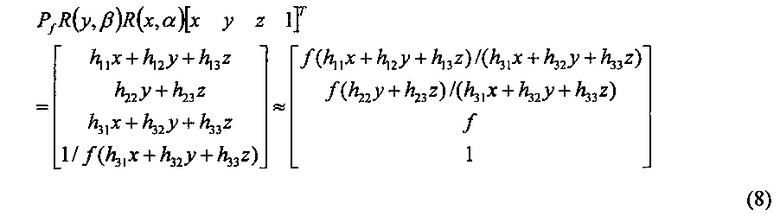
Последняя операция (уравнение (8)) снова представляет собой изменение шкалы четвертой (4-ой) координаты до единицы.
P1 [х у z 1]T и 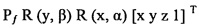 представляют собой две проекции одной и той же 3D точки [x у z 1]T и соотносятся посредством простого гомографического преобразования. При замене x'=x/z и y'=y/z и если отметить, что (x', y') представляет собой проекцию P1 [х у z 1]T, где отбросили компонент z (1, плоскость, расположенная в z=1), и единичный коэффициент шкалы,
представляют собой две проекции одной и той же 3D точки [x у z 1]T и соотносятся посредством простого гомографического преобразования. При замене x'=x/z и y'=y/z и если отметить, что (x', y') представляет собой проекцию P1 [х у z 1]T, где отбросили компонент z (1, плоскость, расположенная в z=1), и единичный коэффициент шкалы, 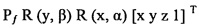 может быть записан следующим образом:
может быть записан следующим образом:
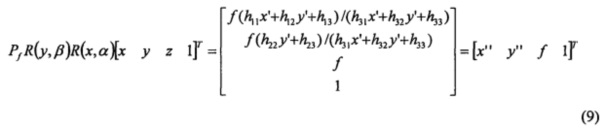
где h11=cosβ
h12=sinβsinα
h13=sinβcosα
h22=cosα
h23=-sinα
h31=-sinβ
h32=cosβsinα
h33=cosβcosα
Определение гомографии H между обеими плоскостями (при 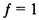 и
и  ) установлено следующим образом:
) установлено следующим образом:

Координаты наклонной плоскости изображения (xʺ, yʺ) представляют собой гомографическое преобразование (x', y') 1:1 проекции плоскости истинной шкалы, выраженной в 2D однородных координатах:
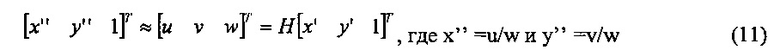
где символ ≈ представляет оператор эквивалентной шкалы в однородных координатах. Как ожидалось, элемент (2,1) в Н (уравнении (10)) равен 0, что означает, что ось x расположена параллельно горизонтальной решетке плоскости камеры. Элементы h31 и h32 перспективы в ряду 3 (см. уравнение (10)) формируют изменение шкалы перспективы плоскости при движении от центра изображения. Эти элементы исчезают, уменьшаясь до нуля, когда плоскость камеры является квадратной относительно оптической оси объектива, то есть, когда α=β=0.
Для не нулевых (CX, Cy), поскольку модель внутренней камеры должна обрабатываться в однородных координатах, повторное масштабирование перспективы требуется перед добавлением центра (CX, Cy) изображения. При двухэтапной обработке, предполагая отсутствие искажения объектива, между точкой (x', y') внешней модели в истинной шкалой 1:1 и в координатах плоскости (xʺ, yʺ) изображения получают:
Этап 1: [u v w]T=H [x' y' 1]T
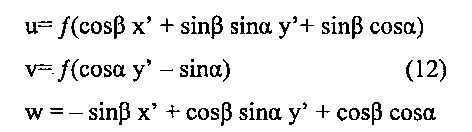
Этап 2: изменение масштаба для единице w=1 и трансляция по (CX, Cy) с учетом точки (xʺ, yʺ) изображения
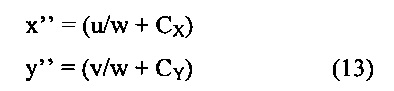
В случае отсутствия искажений объектива, калибровка, поэтому, представляет собой поиск наилучшего соответствия между двумя (2) проекциями. Каждая точка в пространстве отображается не две (2) независимые плоскости проекции, то есть, плоскость истинной шкалы и плоскость наклонного изображения. Как описано выше, плоскость 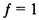 (то есть, истинная шкала) иллюстративно представляет собой идеальный квадрат с оптической осью объектива и имеет шесть (6) степеней свободы: (κ ϕ Ω) и (TX Ty Tz), в соответствии с нашей предложенной внешней моделью (то есть, взаимосвязь между координатами камеры и мировыми координатами). В положении
(то есть, истинная шкала) иллюстративно представляет собой идеальный квадрат с оптической осью объектива и имеет шесть (6) степеней свободы: (κ ϕ Ω) и (TX Ty Tz), в соответствии с нашей предложенной внешней моделью (то есть, взаимосвязь между координатами камеры и мировыми координатами). В положении  плоскость камеры (то есть, изображение) является инвариантом в отношении шкалы с плоскостью истинной шкалы: изображение в
плоскость камеры (то есть, изображение) является инвариантом в отношении шкалы с плоскостью истинной шкалы: изображение в  не может представлять собой чистое умножение шкалы изображения истинной шкалы
не может представлять собой чистое умножение шкалы изображения истинной шкалы 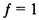 . В положении
. В положении  плоскость изображения имеет пять (5) степеней свободы: углы наклона плоскости α и β, центр изображения (CX, Cy) и фокусное расстояние
плоскость изображения имеет пять (5) степеней свободы: углы наклона плоскости α и β, центр изображения (CX, Cy) и фокусное расстояние  , учитывая внутреннюю модель.
, учитывая внутреннюю модель.
Точка на плоскости истинной шкалы 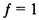 затем соответствует точке на плоскости наклонного изображения и всем соответствующим парам точек проекции при
затем соответствует точке на плоскости наклонного изображения и всем соответствующим парам точек проекции при 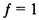 , и
, и  определяет линии, сходящиеся в точке О фокусирования (в отсутствие искажений объектива). Однако искажения объектива все еще возникают между двумя плоскостями, и его требуется учитывать в этой модели. Таким образом, если знать точную геометрию 3D объекта цели калибровки, калибровка представляет собой поиск 3D соответствия между парами координат, проецируемыми в двух плоскостях, компенсирующих искажение объектива.
определяет линии, сходящиеся в точке О фокусирования (в отсутствие искажений объектива). Однако искажения объектива все еще возникают между двумя плоскостями, и его требуется учитывать в этой модели. Таким образом, если знать точную геометрию 3D объекта цели калибровки, калибровка представляет собой поиск 3D соответствия между парами координат, проецируемыми в двух плоскостях, компенсирующих искажение объектива.
Альтернативные формулировки для внутренней модели камеры возможны, используя такой основной принцип, как описано выше, например, вращение относительно осей x и y на плоскости изображения, принятое параллельно XC и YC в начале О координат перед каким-либо вращением, может геометрически применяться в обратном порядке. Как описано выше, когда две плоскости изображений совместно используют одну и ту же линию обзора, вращение оси Z может быть добавлено к одной из них для выражения относительной несовмещенности между обоими изображениями на горизонтальной оси х.
1.3.3 Модель искажения объектива
После соответствующего учета углов наклона плоскости камеры α и β, изображение камеры может быть рассчитано на идеальном квадрате плоскости, с оптической осью Zc объектива, например, в плоскости при 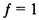 или в плоскости при
или в плоскости при  , скорректированном для прямоугольности с оптической осью Zc объектива, которая представляет собой линию обзора для всех рассматриваемых плоскостей, как описано выше. Хотя предложенная технология, описанная здесь, моделирует устройство формирования изображения (например, камеру), используя проекции на плоскость в
, скорректированном для прямоугольности с оптической осью Zc объектива, которая представляет собой линию обзора для всех рассматриваемых плоскостей, как описано выше. Хотя предложенная технология, описанная здесь, моделирует устройство формирования изображения (например, камеру), используя проекции на плоскость в 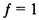 и плоскость в
и плоскость в  , следует понимать, что больше чем две плоскости проекции можно использовать для моделирования искажения объектива. Действительно, плоскость в
, следует понимать, что больше чем две плоскости проекции можно использовать для моделирования искажения объектива. Действительно, плоскость в 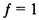 и в
и в  иллюстративно представляет минимальные требования, поскольку
иллюстративно представляет минимальные требования, поскольку 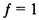 представляет собой проекцию во внешней модели, и
представляет собой проекцию во внешней модели, и  располагается в плоскости изображения. В некоторых вариантах осуществления одна или больше промежуточных плоскостей могут быть смоделированы между плоскостями при
располагается в плоскости изображения. В некоторых вариантах осуществления одна или больше промежуточных плоскостей могут быть смоделированы между плоскостями при 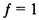 и плоскостью
и плоскостью  . Например, третья промежуточная плоскость может быть расположена на минимальном фокусном расстоянии
. Например, третья промежуточная плоскость может быть расположена на минимальном фокусном расстоянии 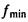 устройства формирования изображения, при этом первую гомографию рассчитывают между плоскостями при
устройства формирования изображения, при этом первую гомографию рассчитывают между плоскостями при 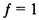 и
и 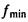 и вторую гомографию рассчитывают между плоскостями при
и вторую гомографию рассчитывают между плоскостями при 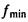 и
и  .
.
Для плоскости проекции под прямым углом с Zc модель искажения объектива может быть уменьшена до чисто радиальной функции, как геометрической, так и хроматической.
Были опубликованы множество моделей геометрических искажений объектива. Некоторые авторы заявляют точность 1/20 пикселя при удалении геометрических искажений объектива. В целом, их основной критерий состоит в большей или меньшей степени в одном и том же: линии, которые являются прямыми в действительности, должны выглядеть прямыми на изображении после устранения геометрических искажений. Очень небольшое количество авторов рассматривают хроматические искажения в своей модели объектива. Наиболее широко распространенная модель геометрических искажений объектива представляют собой модель Шона Беккера, которая может быть представлена следующим образом [3]:
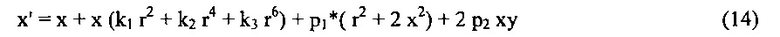
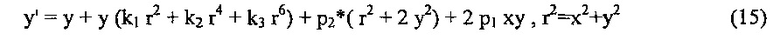
где (x', y') представляет новое местоположение точки (x, у), рассчитанной в отношении центра (CX, Cy) изображения, k1, k2 и k3 представляют собой три члена радиальных искажений, и p1, и р2 представляют собой два члена искажения децентровки. Калибровка отбирает цифровые значения для параметров k1, k2, k3, p1 и р2. Анализ изображений предоставляет (x' y'). Неискаженное положение (x y) находят, решая два уравнения, используя алгоритм поиска 2D.
Большинство моделей искажения объектива имело возможность выравнивания изогнутых линий. Ошибки моделирования проявлялись при восстановлении 3D положений из калиброванной стереопары. Прямые линии, выглядящие прямыми, представляют собой недостаточный критерий для гарантирования точной коррекции геометрических искажений. Неправильная перспектива приводила к ошибке измерений по изображению, и предположение названной оси на фиг. 5 создает систематическое смещение перспективы.
Предложенная модификация модели камеры повышала точность калибровки и снижала сложность модели геометрических искажений объектива. Были сохранены только параметры k1 и k2 модели геометрических искажений объектива Шона Беккера, и два уравнения Шона Беккера (14), (15) были уменьшены только до одного:
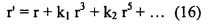 , (может быть расширено), найти r, зная r' из полностью радиальной модели смещения, которое могло быть расширено, используя нечетные члены в r, где г2=х2+у2. Как можно видеть на фиг. 7, модель полного радиального смещения может использоваться в случае, когда геометрические искажения могут быть смоделированы, как полностью радиальное смещение. Точка (x, у) изображения внешней модели (которая иллюстративно представляет измеряемое количество, например, в дюймах или миллиметрах, а не в пикселях) может быть выражена в радиальных координатах (r, θ), где r2=x2+y2 и tgθ=y/x, x и y, получают в отношении центра изображений.
, (может быть расширено), найти r, зная r' из полностью радиальной модели смещения, которое могло быть расширено, используя нечетные члены в r, где г2=х2+у2. Как можно видеть на фиг. 7, модель полного радиального смещения может использоваться в случае, когда геометрические искажения могут быть смоделированы, как полностью радиальное смещение. Точка (x, у) изображения внешней модели (которая иллюстративно представляет измеряемое количество, например, в дюймах или миллиметрах, а не в пикселях) может быть выражена в радиальных координатах (r, θ), где r2=x2+y2 и tgθ=y/x, x и y, получают в отношении центра изображений.
Даже из справочной таблицы (LUT), используя уравнение (16) уменьшается объем расчетов в соотношении 4:1, используется существенно меньше памяти, делая предложенную модель камеры более подходящей для расчетов в режиме реального времени. Даже с такой упрощенной моделью, исходят из цветной камеры CCD Структуры Байера 1/3 640×480 с микрообъективом 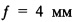 (угол обзора приблизительно 90°), фокусное расстояние
(угол обзора приблизительно 90°), фокусное расстояние  было получено с точностью 10-10 мм.
было получено с точностью 10-10 мм.
Как только истинный центр изображения становится известным, хроматические искажения могут быть смоделированы из одиночного центра изображений. Несколько формулировок возможны для хроматических искажений:
1 - Один центр из геометрической калибровки по зеленому каналу, используя отклонение синего и красного;
2 - Калибровка красного, зеленого и синего каналов независимо;
3 - Среднее значение красного, зеленого и синего каналов для геометрической калибровки, отклонение красного и синего для хроматического;
1.3.4 Общая модель камеры
Далее, на фиг. 8а, представлен способ 100 для вычислений, используя предложенную модель камеры, местоположения точки изображения, в соответствии с описанным выше. 3D точка в пространстве проходит через три преобразования для получения точки изображения, расположенной на плоскости изображения. Способ 100 иллюстративно содержит проекцию на плоскости 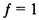 , используя предложенную внешняя модель камеры на этапе 102, применяя модель искажений объектива на этапе 104, и проецируя на плоскость наклонного изображения при
, используя предложенную внешняя модель камеры на этапе 102, применяя модель искажений объектива на этапе 104, и проецируя на плоскость наклонного изображения при  , используя модель внутренней камеры на этапе 106. После выполнения этапа 106 получают местоположение (xʺ, yʺ) точки изображения камеры, соответствующей 3D точке (X, Y, Z), снятой камерой.
, используя модель внутренней камеры на этапе 106. После выполнения этапа 106 получают местоположение (xʺ, yʺ) точки изображения камеры, соответствующей 3D точке (X, Y, Z), снятой камерой.
Далее на фиг. 8b, на этапе 102 иллюстративно вычисляют предложенное преобразование модели внешней камеры, и на этапе 106 получают координаты (X, Y, Z) 3D точки Р, выраженные в отношении мировой системы координат (XW YW ZW).
Как описано выше, с учетом положения 3D объекта, которому принадлежит точка Р, углов и положения, из которых камера видит объект, проекция 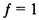 позволяет получить уникальное изображение в истинной шкале 1:1 объекта из его шести (6) степеней свободы: три (3) угла (κ ϕ Ω) и положение (TX Ty Tz), определяющее относительную ориентацию и положение между опорными системами окружающего мира и камерой (XW YW ZW) и (XC YC ZC). Используя параметры модели (κ ϕ Ω), (TX TY, TZ), на этапе 108, в однородных координатах, как описано выше, рассчитывают следующее:
позволяет получить уникальное изображение в истинной шкале 1:1 объекта из его шести (6) степеней свободы: три (3) угла (κ ϕ Ω) и положение (TX Ty Tz), определяющее относительную ориентацию и положение между опорными системами окружающего мира и камерой (XW YW ZW) и (XC YC ZC). Используя параметры модели (κ ϕ Ω), (TX TY, TZ), на этапе 108, в однородных координатах, как описано выше, рассчитывают следующее:
P=[X Y Z 1]T
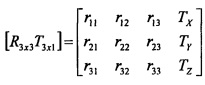 , rij, i, j=1…, 3
, rij, i, j=1…, 3
представляет собой функции целевых углов положения (κ ϕ Ω),
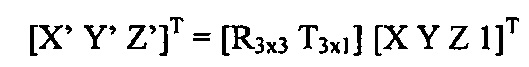
Масштабирование до единичного значения Z' позволяет получить точку (x, у) изображения внешней модели, где:
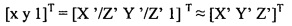 .
.
Точку изображения внешней модели заем выводят на этапе 110.
Далее, на фиг. 8с, представлено приложение модели искажений объектива на этапе 104, которое иллюстративно содержит прием точки (x, y) изображения внешней модели на этапе 112. Используя параметры модели, то есть, параметры геометрических искажений объектива k1 и k2 на этапе 114, иллюстративно выполняются вычисления r, r' и точки (x', y') изображения с искажениями. Следует понимать, что, в некоторых вариантах осуществления, например, в зависимости от эффекта "рыбий глаз" объектива устройства формирования изображения, параметры k1 и k2 могут быть расширены. Действительно, как описано выше, в его самой простой форме, геометрическое искажение может быть смоделировано, как полностью радиальное смещение. Точка (x, y) изображения внешней модели может быть выражена в радиальных координатах (r, θ), где r2=x2+y2 и tgθ=y/x, x и y выбирают в отношении центра (0, 0) изображения. Новое расстояние r' с искажениями, зная r, задают следующим образом:
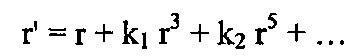 (может быть расширено),
(может быть расширено),
где k1 и k2 представляют собой параметры геометрических искажений объектива. Точка (x', y') искаженного изображения может быть рассчитана, зная θ или используя аналогичные свойства треугольника:
(x', y')=(r'cosθ, r'sinθ),
или (x', y')=(х r'/r, у r'/r)
Точку (x', y') искаженного изображения затем выводят на этапе 116.
В одном варианте осуществления искажение объектива моделируют в масштабе 1:1 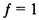 с центром изображения в (0, 0). Однако, как будет дополнительно описано ниже, следует понимать, что значение
с центром изображения в (0, 0). Однако, как будет дополнительно описано ниже, следует понимать, что значение  может быть разложено на множители из модели внутренней камеры, и искажения объектива могут обрабатываться в масштабе
может быть разложено на множители из модели внутренней камеры, и искажения объектива могут обрабатываться в масштабе  .
.
Далее, на фиг. 8d показано, что при получении 106 модель внутренней камеры иллюстративно содержит: принимают точку (x', y') искаженного изображения на этапе 118. Исходя из точки (x', y') искаженного изображения и из пяти степеней свободы модели внутренней камеры, а именно, α и β (углы наклона плоскости изображения), фокусного расстояния  и координат центра изображения (CX, Cy), следующее рассчитывают на этапе 120:
и координат центра изображения (CX, Cy), следующее рассчитывают на этапе 120:
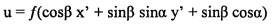 ,
,
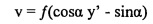 ,
,
w=-sinβx'+cosβsinαy'+cosβcosα,
xʺ=(u/w+CX)
yʺ=(v/w+CY)
где (xʺ, yʺ) представляет собой точку изображения на плоскости внутреннего изображения камере, которая может быть выведена на этапе 122.
Как описано выше, значение  может быть разложено на множители из модели внутренней камеры. Для формирования аппроксимации модели внутренней камеры, можно использовать для малых углов α и β аппроксимацию cos θ~1 и sin θ~θ. Следует понимать, что возможны другие последовательные аппроксимации sin и cos. Как можно видеть из уравнения (12), представленного ниже, при замене h33 становится единицей,
может быть разложено на множители из модели внутренней камеры. Для формирования аппроксимации модели внутренней камеры, можно использовать для малых углов α и β аппроксимацию cos θ~1 и sin θ~θ. Следует понимать, что возможны другие последовательные аппроксимации sin и cos. Как можно видеть из уравнения (12), представленного ниже, при замене h33 становится единицей, 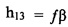 и
и 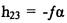 формируется коррекция центра изображения, h11 и h22 становятся
формируется коррекция центра изображения, h11 и h22 становятся  и задают идентичную шкалу в x и y,
и задают идентичную шкалу в x и y, 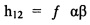 формирует эквивалентный наклон изображения, h31=-β, а также h32=α не могут стать равными нулю, как обозначено ранее. Они задают для изображения соответствующую коррекцию, которая отклоняется по координатам x и y от центра изображения, при повторном масштабировании на w'=1+yα-xβ, с x и y, измеренными в отношении центра изображения.
формирует эквивалентный наклон изображения, h31=-β, а также h32=α не могут стать равными нулю, как обозначено ранее. Они задают для изображения соответствующую коррекцию, которая отклоняется по координатам x и y от центра изображения, при повторном масштабировании на w'=1+yα-xβ, с x и y, измеренными в отношении центра изображения.

Также, как описано выше, искажение объектива может быть смоделировано в отношении шкалы  плоскости изображения. Для искажения объектива модели, в соответствии со шкалой плоскости изображения, воображаемая промежуточная плоскость проекции была добавлена к модели, расположенной в положении
плоскости изображения. Для искажения объектива модели, в соответствии со шкалой плоскости изображения, воображаемая промежуточная плоскость проекции была добавлена к модели, расположенной в положении  вдоль ZC, с центром (0, 0), и идеально перпендикулярно оптической оси ZC объектива.
вдоль ZC, с центром (0, 0), и идеально перпендикулярно оптической оси ZC объектива.

Преобразование представлено, используя чистую гомографию  масштабирования
масштабирования

Можно разложить  из Н в модели внутренней камеры. Можно применять масштабирование
из Н в модели внутренней камеры. Можно применять масштабирование  , в конце внешней модели, для расчета
, в конце внешней модели, для расчета 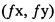 , использовать
, использовать 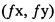 в модели искажения объектива и поэтому, устанавливать
в модели искажения объектива и поэтому, устанавливать 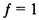 в модели внутренней камеры. Параметры искажения объектива будут затем рассчитаны, как в шкале
в модели внутренней камеры. Параметры искажения объектива будут затем рассчитаны, как в шкале  , как если бы плоскость изображения была скорректирована и наклонена назад под прямым углом с линией ZC обзора с центральным положением изображения (0, 0).
, как если бы плоскость изображения была скорректирована и наклонена назад под прямым углом с линией ZC обзора с центральным положением изображения (0, 0).
Требование моделирования искажения объектива состоит в том, чтобы рассчитать радиальное расстояние r для плоскости, идеально перпендикулярной линии обзора в отношении центра изображения. Это обеспечивает дополнительную свободу при моделировании фиксированного объектива, но при 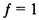 моделировании с истинной шкалой 1:1 искажений объектива представляет собой преимущество по сравнению с приложениями объектива с изменяемым масштабом изображения, что делает параметры искажения объектива независимыми от
моделировании с истинной шкалой 1:1 искажений объектива представляет собой преимущество по сравнению с приложениями объектива с изменяемым масштабом изображения, что делает параметры искажения объектива независимыми от  .
.
Рассмотрим теперь фиг. 9а, где представлена система 200 для моделирования и калибровки устройства формирования изображения. Система 200 содержит один или больше сервер (серверы) 202, доступ к которым может осуществляться через сеть 204. Например, может использоваться последовательность серверов, соответствующая вебсерверу, серверу приложений и серверу базы данных. Все эти серверы представлены сервером 202. Доступ к серверу 202 может быть получен пользователем, использующим одно из множества устройств 206, выполненных с возможностью передачи данных через сеть 204. Устройство 206 может содержать любое устройство, такое как персональный компьютер, планшетный компьютер, карманный персональный компьютер, смартфон и т.п., которое выполнено с возможностью связи через сеть 204, такую как Интернет, коммутируемая телефонная сеть общего пользования (PSTN), сотовая сеть или другие, известные для специалистов в данной области техники. Хотя сервер 202 представлен, как отдельное устройство и удаленное от устройств 206, следует понимать, что он может также быть интегрирован с устройствами 206, либо как загружаемое программное приложение, встроенное программное приложение или их комбинация. Следует также понимать, что несколько устройств, таких как 206, могут одновременно обращаться к серверу 202.
Данные формирования изображений могут быть получены устройством 207 формирования изображения, используемым для калибровки и коррекции изображения. Устройство 207 может быть отдельным от (как представлено) устройств 206 или может быть выполнено, как единое устройство вместе с ними. Данные формирования изображения могут содержать одно или больше изображений 3D объекта реального мира (не показан), такого как цель калибровки, как дополнительно будет описано ниже. Данные формирования изображения затем могут быть обработаны в сервере 202 для получения модели устройства 207 формирования изображения, с таким же подходом, как описано выше со ссылкой на фиг. 8а, фиг. 8b, фиг. 8с и фиг. 8d. Данные формирования изображения иллюстративно получают в режиме реального времени (например, с частотой 30 изображений в секунду) для объекта, такого как движущийся объект, движение которого в пространстве отслеживают. Сервер 202 может затем обрабатывать данные формирования изображения для определения точки изображения, ассоциированной с каждой точкой каждого полученного изображения. В качестве альтернативы, данные формирования изображения могут быть обработаны для определения точки изображения, ассоциированной с каждой из одной или больше точек, представляющих интерес в изображении.
Сервер 202 может содержать, помимо прочего, процессор 208, соединенный с запоминающим устройством 210 и имеющий множество приложений 212а … 212n, работающих в нем. Следует понимать, что, в то время как приложения 212а … 212n, представленные в нем, показаны и описаны, как отдельные объекты, они могут быть скомбинированы или разделены, используя различные подходы.
Одна или больше баз 214 данных могут быть непосредственно интегрированы в запоминающее устройство 210 или могут быть предусмотрены отдельно от нее и дистанционно от сервера 202 (как представлено). В случае удаленного доступа к базам 214 данных, доступ может происходить через любой тип сети 204, как обозначено выше. Различные базы 214 данных, описанные здесь, могут быть предусмотрены, как подборка данных или информация, организованная для быстрого поиска и представления компьютером. Базы 214 данных могут быть структурированы с тем, чтобы способствовать сохранению, возврату, модификации и удалению данных совместно с различными операциями обработки данных. Базы 214 данных могут состоять из файла или набора файлов, которые могут быть разбиты на записи, каждая из которых состоит из одного или больше полей. Информация о базе данных может быть получена через запросы, используя ключевые слова и команды сортировки для быстрого поиска, изменения компоновки, группирования и выбора поля. Базы 214 данных могут представлять собой любую организацию данных относительно носителя сохранения данных, такую как один или больше серверов.
В одном варианте осуществления базы 214 данных представляют собой защищенные веб-серверы и защищенный протокол транспортирования гипертекста, (HTTPS), позволяющий поддерживать защиту уровня транспортирования (TLS), которая представляет собой протокол, используемый для доступа к данным. Передача данных в и из серверов защищенной сети может обеспечиваться, используя протокол безопасных соединений (SSL). Проверка идентичности пользователя может выполняться, используя имена пользователей и пароли для всех пользователей. Различные уровни прав доступа могут быть предусмотрены для множества уровней пользователей.
В качестве альтернативы, могут использоваться любые известные протоколы передачи данных, которые обеспечивают возможность обмена информацией в устройстве, в пределах компьютерной сети. Примеры таких протоколов представляют собой следующие: IP (протокол Интернет), UDP (протокол пользовательских дейтаграмм), TCP (протокол управления передачей), DHCP (протокол динамического конфигурирования хост-устройства), HTTP (протокол передачи гипертекста), FTP (протокол передачи файлов), Telnet (протокол эмуляции терминала), SSH (сетевой протокол прикладного уровня).
Запоминающее устройство 210, доступ к которому может осуществлять процессор 208, может принимать и сохранять данные. Запоминающее устройство 210 может представлять собой основное запоминающее устройство, такое как высокоскоростное оперативное запоминающее устройство (RAM), или вспомогательный модуль накопителя, такой как жесткий диск, запоминающее устройство флэш или привод на магнитной ленте. Запоминающее устройство 210 может представлять собой любой другой тип памяти, такой как постоянное запоминающее устройство (ROM), стираемое программируемое постоянное запоминающее устройство (EPROM), или оптические накопители информации, такие как видеодиск и компактный диск.
Процессор 208 может осуществлять доступ к запоминающему устройству 210 для получения данных. Процессор 208 может представлять собой любое устройство, которое может выполнять операции с данными. Примеры представляют собой центральное процессорное устройство (CPU), буферный процессор, микропроцессор и сетевой процессор. Приложения 212а … 212n соединены с процессором 208 и выполнены с возможностью выполнения различных задач, как более подробно поясняется ниже. Выход может быть передан в устройства 206.
На фиг. 9b показана примерный вариант осуществления приложения 212а, работающего в процессоре 208. Приложение 212а может содержать приемный модуль 302, для приема данных формирования изображения из устройства 207 формирования изображения и получения из них координат точки 3D объекта реального мира, снятой устройством 207 формирования изображения, модуль 304 проекции внешней модели, обеспечивающий выполнение способа, представленного и описанного со ссылкой на фиг. 8b, модуль 306 компенсации искажения объектива, обеспечивающий выполнения способа, представленного и описанного со ссылкой на фиг. 8с, модуль 308 проекции внутренней модели, обеспечивающий выполнение способа, представленного и описанного со ссылкой на фиг. 8d, и модуль 310 вывода, предназначенный для вывода координат точки изображения камеры, рассчитанных модулем 308 определения внутренней модели.
2.0 Калибровка
Далее, со ссылкой на фиг. 10, фиг. 11 и фиг. 12, будут описаны модели калибровки для обработки формирования 3D-2D изображений. Из двух (2) калиброванных камер обратная операция стереопары от 2D до 3D используется для подтверждения точности модели.
2.1 Экспериментальная установка
Предложенная экспериментальная установка предназначена для использования в полевых условиях, даже при использовании с устройствами формирования изображений с низким разрешением, работающими в коротковолновом инфракрасном диапазоне (SWIR). На двух (2) 90° плоскостях из черного анодированного алюминия (не показан), сформированы две круглые решетки (не показаны) (например, выгравированы), которые изменяют свойства излучения поверхности в спектре SWIR и предоставляют черно-белую информацию для калибровки цветов, как представлено на фиг. 10.
В некоторых опубликованных подходах используется центральная часть изображения для исключения искажений и изоляции некоторых параметров камеры. К сожалению, это также формирует смещение оценки параметра. В предложенном подходе любой центр эллипса, взятый в любом месте в изображении, должен подходить к модели. Поэтому, предложенная модель является точной по всему изображению, даже для широкоугольного объектива.
После измерения центров эллипса на изображении, получают набор данных, который соотносит положения 3D цели в реальном мире с их соответствующими 2D местами расположения на изображении. Используя модель камеры для их корреляции, можно использовать алгоритм поиска Левенберга-Марквардта, для расчета параметров модели. Следует понимать, что можно применять другие алгоритмы, кроме алгоритма Левенберга-Марквардта. Например, можно использовать наискорейший спуск или алгоритмы Ньютона. Улучшения точности, достигаемые при использовании предложенной технологии, позволили использовать сумму наименьших квадратов критериев ошибки без смещения. Ошибка определена, как прогнозируемое целевое положение изображения из модели и набора 3D данных, минус соответствующее измерение реального изображения в 2D.
На цели калибровки использовали круги диаметром 1ʺ (2,54 см) с разносом между центрами 2ʺ (5,08 см). Использование кругов обеспечивает, что не будут детектированы какие-либо углы даже в изображении с высокой плотностью пикселей, см. фиг. 12.
Каждый круг задает локальную оценку поведения камеры без смещения или любой предпочтительной ориентации кромки. При этом больше внимания уделялось в точной установке центра эллипса, чем отношению сигнал-шум (S/N) при детектировании кромки. Потребовалась существенная работа для тестирования различных технологий, для моделирования эллипса и исключения оценки смещения центра. Поскольку изображение имело высокую плотность пикселей, площадь поверхности детектора кромки иллюстративно была ограничена до площади 3×3 пикселя.
Поскольку предполагается использовать предложенную технологию для камер с малым разрешением, в качестве иллюстрации была выбрана цветная камера Bayer Pattern Point Grey Research Firefly 640×480 с поставляемым вместе с нею микрообъективом 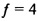 мм для тестирования, как показано на фиг. 11.
мм для тестирования, как показано на фиг. 11.
В конечном итоге был сделан вывод, что существующие в настоящее время технологии не позволяют решить проблему с бликами и отражением, поэтому, они не пригодны для калибровки в полевых условиях. В нескольких случаях определили от 1/4-1/2 пикселя смещения центра. Несмотря на то, что эти ошибки были малы, потребовался обширный математический анализ для их удаления из обработки восстановления формы; они невидимы для глаза человека.
Технологии определения градиента кромки, с другой стороны, проявились в смещении местоположения подпикселя, когда ориентация кромки не была выровнена с массивом пикселей горизонтальной или вертикальной решетки камеры. В конечном итоге, использовалась коррекция подпикселя для расширения подпикселя "без максимального подавления" Devernay [1]. В двухэтапном процессе этап 1 восстанавливал исходную оценку для точек кромки, добавляя компенсацию для смещения ориентации кромки. На этом исходном наборе рассчитывалась первая оценка геометрии эллипса. На этапе 2 использовалась подгонка исходного эллипса к оценке локальной кривизны и коррекция местоположения кромки.
2.2 Результат калибровки
Используя те же экспериментальные данные, оценку параметра сравнивали для двух (2) моделей камеры, как показано в таблице 1, представленной ниже.

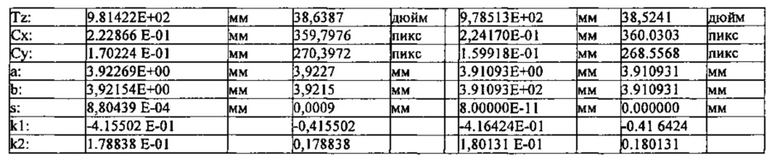
Представленный слева набор параметра камеры получают из самой точной опубликованной модели, тестированной по нашим собственным экспериментальным данным. Представленный справа набор был рассчитан из предложенной модели, где модель объектива использовалась, как чисто радиальное геометрическое искажение, и где для внутренней модели камеры использовали предложенное воплощение.
Первые шесть (6) строк в представленной выше таблице представляют параметры внешней камеры, три (3) угла и три (3) положения требуются для расчета [R3×3 T3×1]. Следующие пять (5) строк представляют собой параметры внутренней камеры; мы модифицировали наше представление параметра так, чтобы оно соответствовало обычно используемой модели по фиг. 5. Для наших степеней свободы использовали разные математические формулы. Затем остальные две (2) строки представляют основные параметры k1 и k2 геометрических искажений объектива. Эти две представлены в большинстве моделей и учитывают, в основном, геометрические искажения типа "рыбий глаз".
Из a, b и s, как описано здесь выше, можно учесть 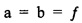 при s=0, как выражение прямоугольности пикселя камеры и ошибки по фокусному расстоянию
при s=0, как выражение прямоугольности пикселя камеры и ошибки по фокусному расстоянию  . Если пиксель является квадратным, шкала высоты должна быть равна шкале ширины, обе должны быть расположены точно под прямым углом, и
. Если пиксель является квадратным, шкала высоты должна быть равна шкале ширины, обе должны быть расположены точно под прямым углом, и 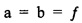 должно представлять шкалу изображений.
должно представлять шкалу изображений.
При переключении на предложенную модель, ошибка по  уменьшается с 10-3 мм до 10-10 мм. Первоначально, фокусное расстояние
уменьшается с 10-3 мм до 10-10 мм. Первоначально, фокусное расстояние  было неправильным на 0,03%. Хотя это кажется малым, смещение модели сдвинуло центр изображения (CX, Cy) на ближайшие два (2) пикселя в основном направлении Y. В то же время, произошел сдвиг всех внешних параметров. Все углы изменились, и расстояние TZ до объекта было с ошибкой на 0,3%: ошибка измерений расстояния усилилась в десять (10) раз относительно ошибки
было неправильным на 0,03%. Хотя это кажется малым, смещение модели сдвинуло центр изображения (CX, Cy) на ближайшие два (2) пикселя в основном направлении Y. В то же время, произошел сдвиг всех внешних параметров. Все углы изменились, и расстояние TZ до объекта было с ошибкой на 0,3%: ошибка измерений расстояния усилилась в десять (10) раз относительно ошибки  . Это представляет собой систематическую ошибку измерения расстояния: ошибка на 3 мм на расстоянии 1 м может привести к ошибке до 30 м на расстоянии 10 км. Процент ошибки по TX и Ty был еще хуже, что обозначает, что представленная слева модель стремилась сохранить расстояние вдоль оптической оси ZC объектива. Из калиброванной стереопары 3D восстановление показало ошибку, эквивалентную двум (2) пикселям на шкале изображения. Стерео 3D измерения дополнительно описаны ниже.
. Это представляет собой систематическую ошибку измерения расстояния: ошибка на 3 мм на расстоянии 1 м может привести к ошибке до 30 м на расстоянии 10 км. Процент ошибки по TX и Ty был еще хуже, что обозначает, что представленная слева модель стремилась сохранить расстояние вдоль оптической оси ZC объектива. Из калиброванной стереопары 3D восстановление показало ошибку, эквивалентную двум (2) пикселям на шкале изображения. Стерео 3D измерения дополнительно описаны ниже.
Рассматривая параметры искажения k1 и k2, (знак "минус" у k1 означает бочкообразное искажение), следует отметить, что оба они недооценены. Присутствует некоторая остаточная кривизна по мере движения от центра изображения. Она может быть меньше, чем пиксель, но кривизна может накапливаться при попытке склеивания изображений для формирования карты из множества изображений.
3.0 Влияние смещения на модель/калибровку
Основное влияние на смещение модели оказывается на 3D телеметрию из стереопары, как используется в приложениях 3D сканера. Такой же вывод справедлив для выделения 3D из движущейся камеры, поскольку в основном, обработка математической триангуляции является такой же.
3.1 Восстановление 3D из стереопары
Как упомянуто ранее, не учитываемая предложенная коррекция для модели камеры формирует систематическую ошибку при 3D триангуляции. На фиг. 13 показана стереопара, обычно используемая для измерительных объектов при 3D, используя два (2) одновременно снятых камерой изображения. Полное описание триангуляции представлено в [5].
О и О' представляют собой оптические центры для двух камер (не показаны), и обе оси объектива спроецированы под прямыми углами на плоскостях изображений в центрах изображений, соответственно 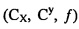 и
и 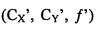 (не показаны для ясности), где (CX, CY) представляет собой начало координат для плоскости изображения, и
(не показаны для ясности), где (CX, CY) представляет собой начало координат для плоскости изображения, и  представляет собой расстояние между О и плоскостью изображения, как показано на фиг. 4. Аналогично,
представляет собой расстояние между О и плоскостью изображения, как показано на фиг. 4. Аналогично, 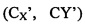 представляют собой начало координат для плоскости изображения, и
представляют собой начало координат для плоскости изображения, и 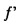 представляет собой расстояние между О' и плоскостью изображения.
представляет собой расстояние между О' и плоскостью изображения.
Обе камеры направлены на общую точку М объекта (не показана). Проекции М в обеих камерах представлены в виде изображений точек m и m'.
Для определения, где М находится в пространстве, вычерчены две линии, начинающиеся из О и О' через их соответствующие точки изображения камеры m и m'. М рассчитывают в точке пересечения обеих линий.
Точность 3D зависит от точного знания следующего:
1. Оптических центров О и О'
2. Фокусных расстояний  и
и 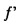
3. Центров изображений (CX, CY) и 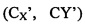
4. Ориентации осей ZC и 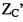 объектива
объектива
5. Точности точек изображений m и m'
6. Пересечения OM и O'M
Первые четыре (4) требования к точности 3D телеметрии определяются путем калибровки камеры, пятое - из выделения свойства изображения подпикселя. Последнее представляет собой само восстановление 3D триангуляции.
На первые четыре (4) зависимости от ошибки, описанные выше, а именно, оптические центры О и О', фокусные расстояния  и
и 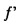 , точки изображения центров (CX, Cy) и
, точки изображения центров (CX, Cy) и 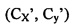 , и ориентация оси ZC и
, и ориентация оси ZC и 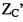 объектива, влияют раскрытые смещения модели камеры, описанные выше.
объектива, влияют раскрытые смещения модели камеры, описанные выше.
Хотя при предположении наклона оси образуется очень малая ошибка в фокусном расстоянии  , она генерирует большое смещение в центре изображения (CX, Cy) и точках О и О' фокусирования. Поскольку О и О' не находятся в нужном положении, триангуляция для определения М приводит к получению систематической 3D ошибки. Из предложенного примера калибровки ошибка в два (2) пикселя для оптических центров О и О' доминирует над любыми ошибками измерений в точках m и m' изображения, поскольку оказалось возможным довести их до точности
, она генерирует большое смещение в центре изображения (CX, Cy) и точках О и О' фокусирования. Поскольку О и О' не находятся в нужном положении, триангуляция для определения М приводит к получению систематической 3D ошибки. Из предложенного примера калибровки ошибка в два (2) пикселя для оптических центров О и О' доминирует над любыми ошибками измерений в точках m и m' изображения, поскольку оказалось возможным довести их до точности 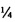 пикселя.
пикселя.
Выделение точки особых элементов (m и m') зависит от смещения ориентации кромки и смещения детектирования угла, которое требовалось устранить, используя калибровку.
И в конечном итоге, для триангуляции был восстановлен классический подход разложения одиночного значения (SVD) в отношении ее стабильности и скорости. При этом ничто никогда не гарантирует, что две линии пересекутся в пространстве. Поэтому, М определили, как точку в пространстве, где обе линии располагаются ближе всего друг к другу.
В ходе наших исследований выполнили измерения нескольких источников смещения, как влияющих на точность, при этом основным источником смещения оказалось смешение модели камеры. Источники смещения включают в себя следующие:
- Модель камеры/объектива (ошибка 2 пикселя для центра изображения (CX, CY))
- Смещение ориентации кромки подпикселя (смещение кромки на 1/4 пикселя)
- Смещение детектирования угла подпикселя (смещение угла на 1/4 пикселя)
- Неучтенные хроматические искажения (сдвиг кромки на 1/2 пикселя в зависимости от цвета)
- Некомпенсированное геометрическое искажение (с трудом детектируемая остаточная кривизна на 1/2 пикселя)
- Фильтрация изображения JPEG на уровне подпикселя (переменная с параметром качества JPEG)
Помимо смещения модели камеры, наибольшие источники смещения приводят к ошибкам выделения точки особого элемента. Устранение таких источников смещения привело к совокупному преимуществу. Достижение точности  до 10-10 мм даже в камере со структурой Байера и низким разрешением, использующей широкоугольный микрообъектив, путем простого изменения внутренней модели камеры представляет значительное улучшение, и поясняет, почему точная модель объектива с переменным масштабом изображения была невозможна до настоящего времени.
до 10-10 мм даже в камере со структурой Байера и низким разрешением, использующей широкоугольный микрообъектив, путем простого изменения внутренней модели камеры представляет значительное улучшение, и поясняет, почему точная модель объектива с переменным масштабом изображения была невозможна до настоящего времени.
3.2 Смещение модели: Общий обзор и объектив с переменным фокусным расстоянием
Как описано выше, каждый параметр объектива "загрязнен" смещением модели внутренней камеры, называемым предположением наклонной оси. Такое смещение может быть устранено путем изменения предположения наклона для точной модели перспективы плоскости изображения внутренней 3D камеры.
При 3D триангуляции, при использовании стереокамеры или движущейся камеры, влияние является таким, что, поскольку шкала изображения и центр изображения представлены неправильно, происходит сдвиг триангуляции.
Пример, представленный в таблице 1, также показывает, что параметры искажения объектива недооценены, со знаком "минус" у k1, что означает бочкообразное искажение. При склеивании множества изображений, для формирования карты, это приводит к накоплению кривизны от изображения к изображению.
Измерения расстояния и цели также смещаются и связаны с процентом ошибки для фокусного расстояния  , поскольку камера позволяет получить масштабированное измерение.
, поскольку камера позволяет получить масштабированное измерение.
Это также делает невозможным точное моделирование, используя камеру с объективом с изменяемым фокусным расстоянием. В объективе с изменяемым масштабом изображения точка О фокусирования движется вдоль оси ZC объектива. В результате калибровки определяют О по известному центру (CX, Cy) изображения, на расстоянии  под прямым углом с плоскостью изображения. Предложенный пример показывает систематическое смещение в этих параметрах. Еще хуже становится при учете отклонения механизмом объектива, поскольку это сдвигает ось ZC объектива.
под прямым углом с плоскостью изображения. Предложенный пример показывает систематическое смещение в этих параметрах. Еще хуже становится при учете отклонения механизмом объектива, поскольку это сдвигает ось ZC объектива.
Без предложенной модификации для модели камеры становится невозможным моделировать объектив с переменным масштабом изображения.
Моделирование камеры с объективом с переменным масштабом изображения требует построения диаграммы смещения в точке О фокусирования в пространстве.
Идеальный объектив с изменяемым масштабом изображения мог бы иметь точку О, движущуюся по прямой линии на оси ZC объектива, с плоскостью входа 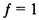 , движущейся вдоль нее. Как только возникают ошибки механической сборки, нарушается взаимосвязь для линейного смещения точки О. Единственный способ оценки механического качества объектива с переменным масштабом изображения, поэтому, зависит от точного знания центра изображения (CX, Cy) и
, движущейся вдоль нее. Как только возникают ошибки механической сборки, нарушается взаимосвязь для линейного смещения точки О. Единственный способ оценки механического качества объектива с переменным масштабом изображения, поэтому, зависит от точного знания центра изображения (CX, Cy) и  .
.
Поведение механического качества также представляет собой компромисс для объектива с переменным масштабом изображения: увеличение изображения для повышения добавленной точности, когда это требуется, за счет потери точности в отношении допусков сборки в механизме объектива.
3.3 Пример устранения геометрических искажений
Далее, на фиг. 14, показано использование ранее калиброванной тестируемой камеры, описанной выше, и по предложенному алгоритму, где геометрическое искажение объектива выражено, как уравнение (16), на фиг. 14 показано, как искажение объектива устраняют из изображения. Хроматическое искажение не видно на черно-белом изображении.
3.4 Хроматическое искажение
Ниже сделана ссылка на фиг. 15, на которой иллюстрируется хроматическое искажение для объектива 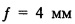 Cosmicar® С Mount, при разрешении 1024×768. Поскольку истинный центр (CX, Cy) изображения известен, можно моделировать хроматическое искажение. В большинстве изображений хроматическое искажение малозаметно, если только субъект не будет полностью черно-белым, и его изображение не будет снято с использованием цветной камерой. В ссылочном документе [2] представлена модель, где каждый канал цвета RGB моделируют независимо.
Cosmicar® С Mount, при разрешении 1024×768. Поскольку истинный центр (CX, Cy) изображения известен, можно моделировать хроматическое искажение. В большинстве изображений хроматическое искажение малозаметно, если только субъект не будет полностью черно-белым, и его изображение не будет снято с использованием цветной камерой. В ссылочном документе [2] представлена модель, где каждый канал цвета RGB моделируют независимо.
На фиг. 15 смещение цели хроматических искажений представлено с усилением в пятьдесят (50) раз. Целевые положения показаны для красного, зеленого и синего (RGB) цветных каналов камеры, и сгруппированы по кластерам из трех (3). Символ маркера в виде знака "х" или крестика обозначают выделение цели в синем, символ маркера в виде "+" или символ знака "плюс" обозначает выделение цели в красном, и символ маркера в виде точки или крапинки обозначает выделение цели в зеленом цвете. Расширение видимого спектра сдвигает целевые центры красного наружу и целевые центры синего внутрь относительно зеленого. График на фиг. 15 показывает практически радиальное поведение. Воображаемые линии, соединяющие центры красного, зеленого и синего до любого заданного целевого местоположения, проявляют тенденцию выравнивания и направлены в центр изображения, обозначенный символом маркера знака "плюс", который близок к координате пикселя (500, 400).
Далее на двух (2) графиках, показанных на фиг. 16 и фиг. 17, представлено, что как синие, так и красные хроматические искажения равны нулю в центре изображения, начиная из начала ординат (0,0), как и ожидалось. Как прогнозируется в соответствии с теоретическим поведением объектива, хроматическое искажение должно быть равно нулю в центре изображения.
Оба хроматических искажения синего и красного имеют свои пиковые значения на разных радиальных расстояниях от центра. Начиная от ±1/2 пикселя, хроматическое искажение можно моделировать и сводить до менее, чем 1/8 пикселя.
В радиальных координатах, снятых из центра изображения (CX, Cy), неучтенное хроматическое искажение создает ошибку ±1/2 пикселя в местоположении кромки с изменяющимся цветом объекта, или с изменяющимся спектром источника света. Это подчеркивает необходимость быть внимательным при выделении RGB из цветного изображения структуры Байера, поскольку, определение кромки смещается вместе с цветом.
3.5 Восстановление структуры Байера
Далее, со ссылкой на фиг. 18, цветные камеры со структурой Байера задают одиночный цветовой сигнал для каждого заданного пикселя, красного, зеленого или синего, как обозначено префиксом R, G или В в номере пикселя на фиг. 18. Потерянную информацию цвета интерполируют, используя информацию соседнего пикселя.
В наиболее точной схеме интерполяции структуры Байера используется определение кромки для восстановления потерянной информации RGB. При этом невозможно выполнить интерполяцию по кромке, поскольку требуется точное восстановление структуры Байера для исключения разрывов.
При двухэтапной обработке вначале рассчитывают потерянные значения пикселя G для пикселей В и R. Например, для красного пикселя R13, потерянное значение G13 рассчитывается следующим образом:

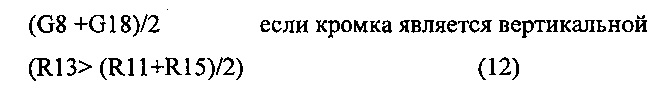
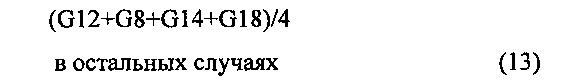
На этапе два рассчитывают потерянные значения В и R, используя известное значение G для определения кромки, предполагая, что кромки В и R находятся геометрически в тех же местах расположения плоскости, где и кромки G.
Поскольку объектив вводит хроматические искажения, восстановление структуры Байера требует адаптации для компенсации место кромки "сдвига цвета", как получилось при сканировании от В до G и до R пикселей.
3.6 Конструктивный компромисс оптической системы
Для целей наблюдения, 3D телеметрии и сканеров оказалось, что требуется исключить смещение калибровки камеры. Другие ключевые преимущества технологии включают в себя, но не ограничены этим:
1. Программный подход формирует открытую архитектуру интеграции;
2. Позволяет использовать широкоугольные объективы или объективы с уменьшенным размером;
3. Позволяет моделировать камеру с объективом с переменным масштабом изображения;
4. Повышается скорость расчетов алгоритмов коррекции геометрических и хроматических искажений изображения, и добавляется возможность сжатия изображений без потерь;
5. Устраняется ошибка восстановления структуры Байера, связанная с хроматическим искажением.
Следует отметить, что программное обеспечение представляет собой единственную стратегию для повышения точности за пределами возможностей аппаратных средств камеры.
Как необходимое условие, технология позволяет:
- Использовать широкоугольные объективы для увеличения угла обзора камеры без потери точности. Комбинация 1/3 CCD 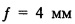 обеспечивает угол обзора 90 градусов.
обеспечивает угол обзора 90 градусов.
- Компенсировать низкое разрешение камеры путем добавления моделирования хроматического искажения и измерений кромки подпикселя по спектру.
- Миниатюризация: Мы достигли калибровки, используя микрообъектив и оценку фокусного расстояния с точностью до 10-10 мм, что приблизительно представляет собой размер молекулы водорода.
- Набор разнообразных датчиков между цветными синтетическими изображениями SWIR-Colour-synthetic images-Radar-LIDAR для достижения точного набора датчиков, при этом каждая шкала изображения и центра изображения должна быть известна, и искажения изображения должны быть устранены.
Сдвиг по фазе цифрового изображения может привести к морской болезни для наблюдателя - человека, что делает желательным упрощение предложенного устранения геометрических искажений 4:1. Остаточная 3D ошибка после смещения калибровки также приводит к дискомфорту человека, такому как головная боль или кибермания. Тестируемое усиление возможностей зрения для солдата позволило сделать вывод, что сдвиг по фазе формирования синтетического изображения на 1/4 секунды от реального может привести к морской болезни у наблюдателя - человека.
Поскольку решение воплощается в виде программных средств, оно становится независимым для разных платформ.
Для изображений с низким разрешением выделение кромки пикселя и составление графика помогают мозгу человека интерпретировать это изображение. Изображения SWIR с низким разрешением можно объединять с цветными изображениями с более высоким разрешением.
В области расширенной реальности сгенерированное компьютером изображение имеет идеальную перспективу и известное фокусное расстояние. Поскольку сгенерированное в компьютере изображение представляет собой изображение, полученное от идеального микроотверстия, сформированного из установленного значения для  , разумно скорректировать изображение камеры в отношении искажений и установить ее на том же масштабе изображения, что и синтетического изображения.
, разумно скорректировать изображение камеры в отношении искажений и установить ее на том же масштабе изображения, что и синтетического изображения.
При наблюдении с Земли и при спутниковом наблюдении, любая система объектива будет проявлять искажения на определенном уровне. Атмосфера Земли также добавляет искажения, которые могут быть скомпенсированы только, когда точно известно искажение объектива. Когда склеивают изображения, недостаточно компенсированные геометрические искажения будут накапливать кривизну, и смещенная перспектива, вызванная предположением наклонной оси будет формировать изменение формы: потеря прямоугольности, потеря вертикальности...
Выделение кромки подпикселя представляет собой гораздо более эффективное средство сжатия изображений. При коррекции изображения в отношении искажения объектива и путем модификации JPEG, также было продемонстрировано дополнительное 30%-ое сжатие изображений без потерь.
Предложенный подход является желательным для телеметрии с использованием объектива с изменяемым масштабом изображения, увеличения скорости и точности в приложениях с использованием широкоугольного объектива, и позволяет обеспечить миниатюризацию системы двумя способами. Во-первых, путем предоставления добавленной точности из систем с малым объективом, и во-вторых, в результате фильтрации через программное обеспечение обеспечивается возможность построения более простой оптики.
Это обеспечивает самый лучший компромисс в отношении точности, скорости, стоимости, габаритных размеров, веса, технического обслуживания и возможности обновления.
4.0 Выводы
Автоматизированная система является более точной, чем ее инструмент. Использование цифровых камер в качестве измерительных инструментов в интеллектуальных системах (IS) требует калибровки камеры.
Добавленная точность может быть достигнута только используя программное средство, поскольку коммерческий объектив может иметь 10% допуск для фокусного расстояния  , и программное обеспечение представляет собой единственный способ компенсации искажения объектива на уровне подпикселя.
, и программное обеспечение представляет собой единственный способ компенсации искажения объектива на уровне подпикселя.
Предположение наклонной оси создает основное смещение и должно быть заменено перспективной моделью плоскости изображения, которая поддерживает 3D геометрию плоскости изображения камеры: горизонтальные и вертикальные шкалы изображения равны и находятся под прямым углом. Предположение наклонной оси вводит смещение калибровки, проявляющееся при 3D триангуляции, поскольку центр изображения находится за пределами требуемого положения. В примере, описанном выше, смещение центра изображения на два (2) пикселя превышает любую другую ошибку при обработке триангуляции, поскольку свойства изображения могут быть выделены с точностью 1/4 пикселя.
Следует внимательно подходить к выделению свойств изображения для калибровки, поскольку может возникать несколько смещений подпикселя. Источники смещения подпикселя включают в себя, но не ограничены этим:
- Смещение местоположения - ориентации кромки подпикселя;
- Смещение детектирования угла подпикселя;
- Неучтенное хроматическое искажение;
- Недокомпенсированное геометрическое искажение;
- Фильтрация изображения JPEG на уровне подпикселя.
Перспективная модель для плоскости изображения внутренней камеры требуется для определения местоположения смещения в точке фокусирования объектива в объективе с изменяемым масштабом изображения. Подход, в соответствии с программной коррекцией повышает скорость и точность при применении широкоугольных объективов и позволяет обеспечить миниатюризацию системы двумя путями. Во-первых, путем предоставления дополнительной точности в системах малых объективов, и, во-вторых, фильтрация через программное обеспечение обеспечивает получение более простой оптики. Программная модель/калибровка представляет собой единственную технологию для улучшения характеристик камеры за пределами аппаратных ограничений.
Хотя они иллюстрируются в блок-схемах, как группы дискретных компонентов, связывающихся друг с другом через отдельные соединения передачи сигналов и данных, для специалистов в данной области техники будет понятно, что настоящие варианты осуществления представлены путем комбинирования аппаратных и программных компонентов с некоторыми компонентами, которые воплощаются заданной функцией или операцией аппаратной или программной системы, и множества из представленных путей передачи данных воплощаются при передаче данных в пределах компьютерного приложения или операционной системы. Представленная структура, таким образом, предоставляется для эффективности при описании настоящего варианта осуществления.
Следует отметить, что настоящее изобретение может выполняться, как способ, может быть воплощено в виде системы и/или считываемого в компьютере носителя информации. Варианты осуществления изобретения, описанные выше, предназначены для использования только в качестве примеров. Объем изобретения, поэтому, должен быть ограничен исключительно объемом приложенной формулы изобретения.
Список литературы
[1]  Devernay. A Non-Maxima Suppression Method for Edge Detection with Sub-Pixel Accuracy. INRIA: INSTITUT NATIONAL DE RECHERCHE EN INFORMATIQUE ET EN AUTOMATIQUE. Report N° 2724, November 1995, 20 pages.
Devernay. A Non-Maxima Suppression Method for Edge Detection with Sub-Pixel Accuracy. INRIA: INSTITUT NATIONAL DE RECHERCHE EN INFORMATIQUE ET EN AUTOMATIQUE. Report N° 2724, November 1995, 20 pages.
[2] Y.M. Harry Ng, C.P. Kwong. Correcting the Chromatic Aberration in Barrel Distortion of Endoscopic Images. Department of Automation and Computer Aided Engineering, Chinese University of Hong Kong. 6 pages
[3] Shawn Becker. Semiautomatic Camera Lens Calibration from Partially Known Structure. MIT: Massachusetts Institute of Technology.
http://alumni.media.mit.edu/~sbeck/results/Distortion/distortion.html © 1994, 1995
[4] Konstantinos G. Derpanis. The Harris Corner Detector. October 2004, 2 pages.
[5] L.H. Hartley, P. Sturm. Triangulation. Proc. of the ARPA Image Understanding Workshop 1994, Monterey, CA 1994, pp. 957-966.
| название | год | авторы | номер документа |
|---|---|---|---|
| Метод совместной калибровки лидара и камеры | 2021 |
|
RU2837595C2 |
| СПОСОБ КАЛИБРОВКИ ОПТИЧЕСКОЙ СИСТЕМЫ | 2008 |
|
RU2381474C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ РАССТОЯНИЯ ДО ОБЪЕКТА ПРИ ПОМОЩИ КАМЕРЫ (ВАРИАНТЫ) | 2014 |
|
RU2602729C2 |
| УПРАВЛЕНИЕ АВТОФОКУСИРОВКОЙ С ИСПОЛЬЗОВАНИЕМ СТАТИСТИЧЕСКИХ ДАННЫХ ИЗОБРАЖЕНИЯ НА ОСНОВАНИИ ПОКАЗАТЕЛЕЙ ГРУБОЙ И ТОЧНОЙ АВТОФОКУСИРОВКИ | 2011 |
|
RU2543974C2 |
| СИСТЕМА И СПОСОБ РЕКОНСТРУКЦИИ СВОЙСТВ ПОВЕРХНОСТИ И ОПРЕДЕЛЕНИЯ ПОЛОЖЕНИЯ ОЦИФРОВАННЫХ 3D ОБЪЕКТОВ | 2022 |
|
RU2806729C1 |
| СПОСОБ ПОСАДКИ БВС САМОЛЕТНОГО ТИПА НА ВЗЛЕТНО-ПОСАДОЧНУЮ ПОЛОСУ С ИСПОЛЬЗОВАНИЕМ ОПТИЧЕСКИХ ПРИБОРОВ РАЗЛИЧНОГО ДИАПАЗОНА | 2019 |
|
RU2724908C1 |
| Способ калибровки видеосистемы для контроля объектов на плоской площадке | 2016 |
|
RU2610137C1 |
| СПОСОБ И СИСТЕМА КАЛИБРОВКИ КАМЕРЫ | 2012 |
|
RU2601421C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ САМОЛЕТА-ЗАПРАВЩИКА И КОНУСА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2009 |
|
RU2402035C1 |
| СПОСОБ КОРРЕКЦИИ ХРОМАТИЧЕСКОЙ АБЕРРАЦИИ ОПТИЧЕСКОЙ ПОДСИСТЕМЫ СИСТЕМЫ ТЕХНИЧЕСКОГО ЗРЕНИЯ | 2007 |
|
RU2352988C1 |
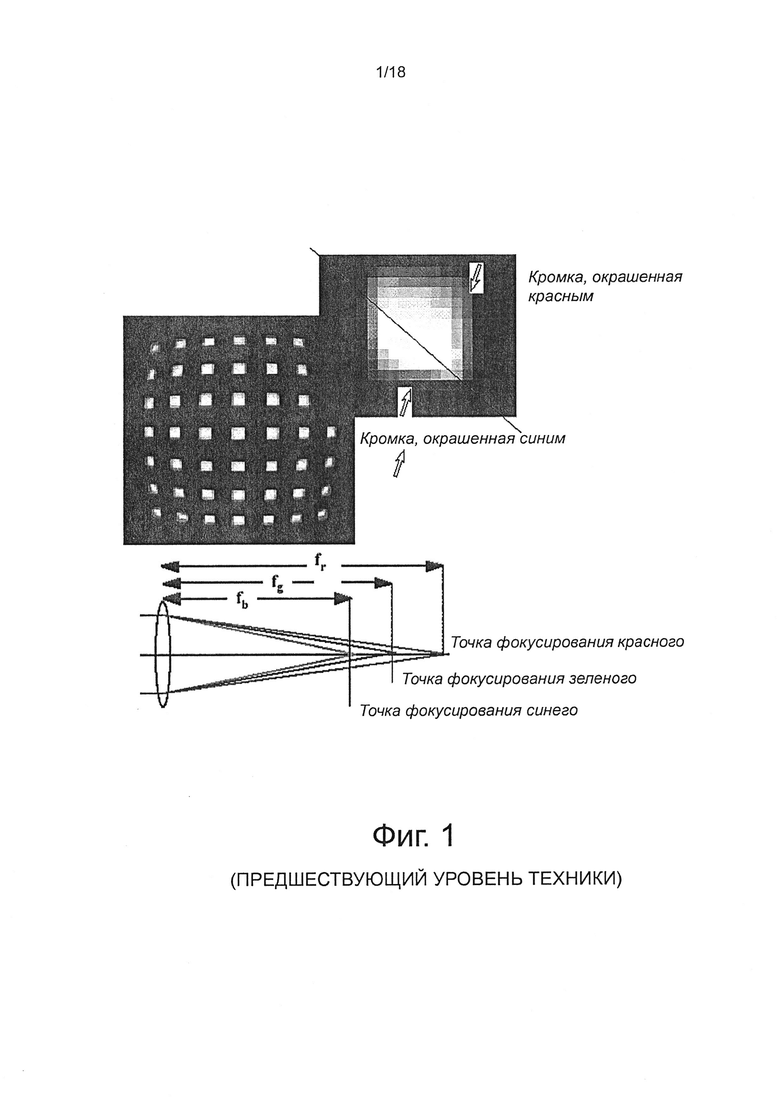
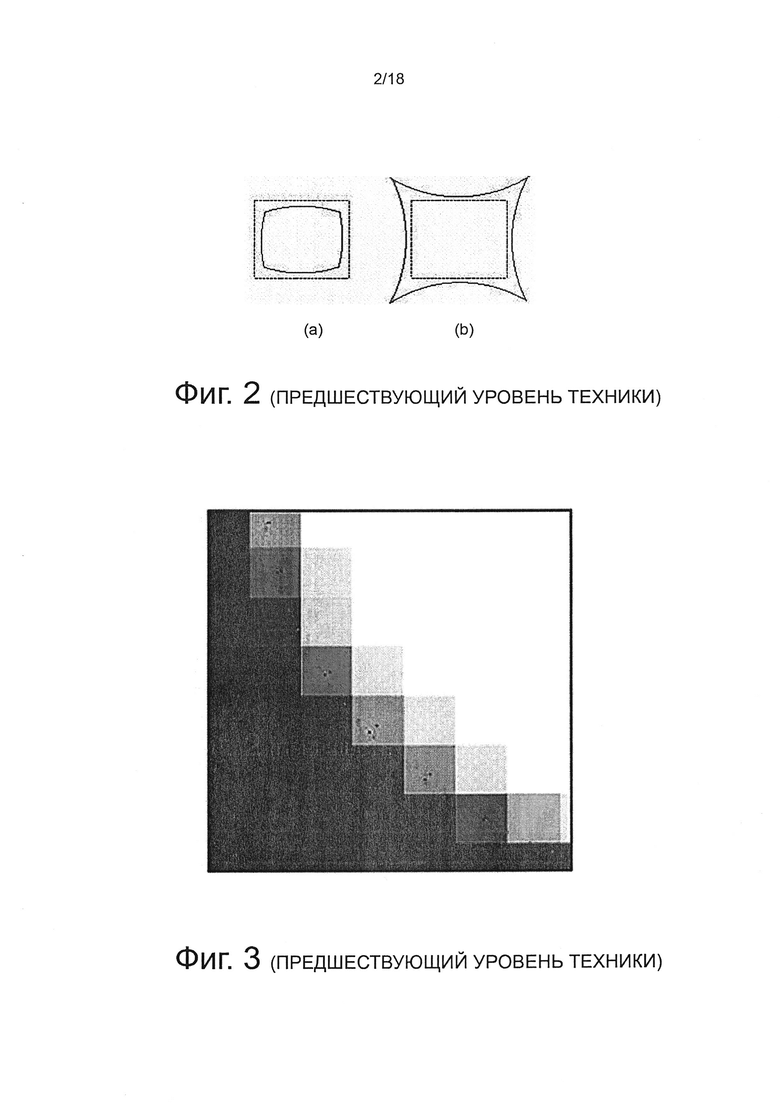
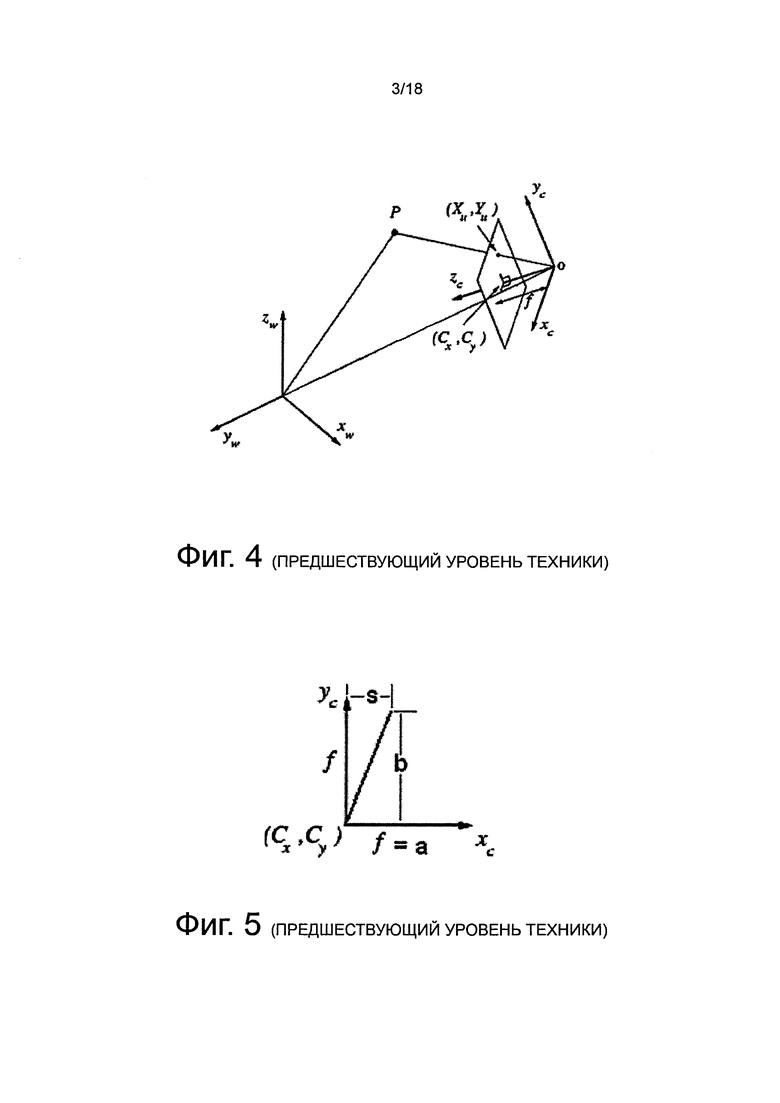
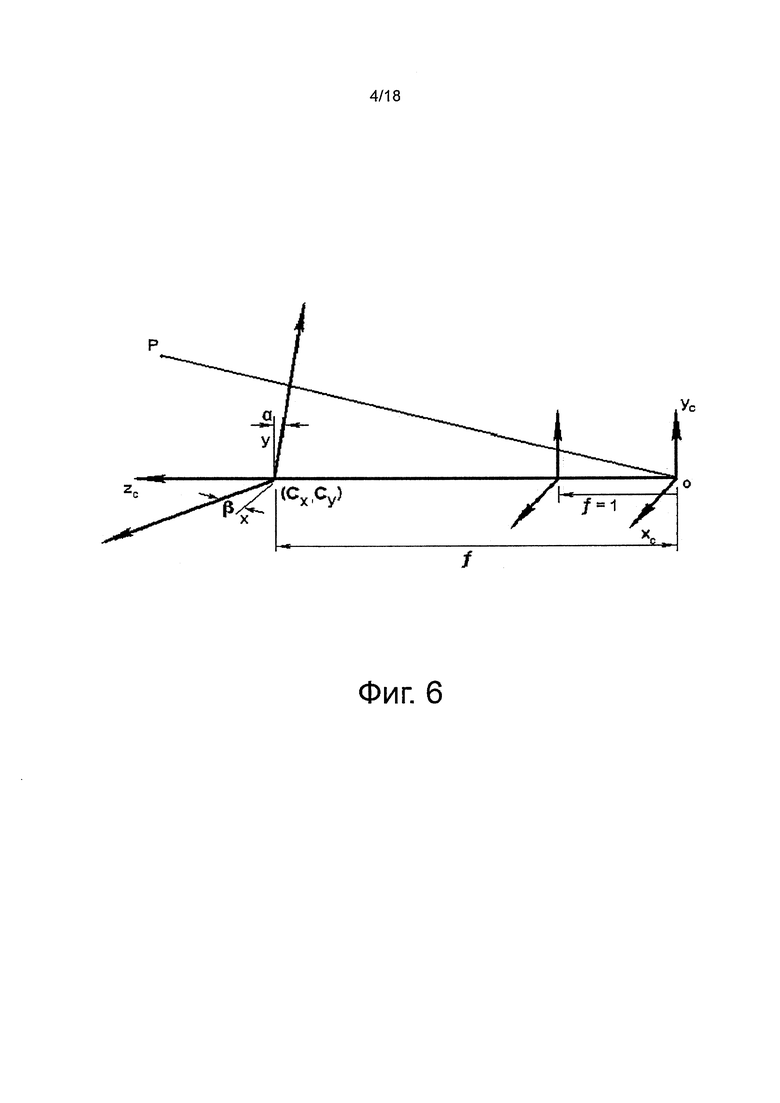
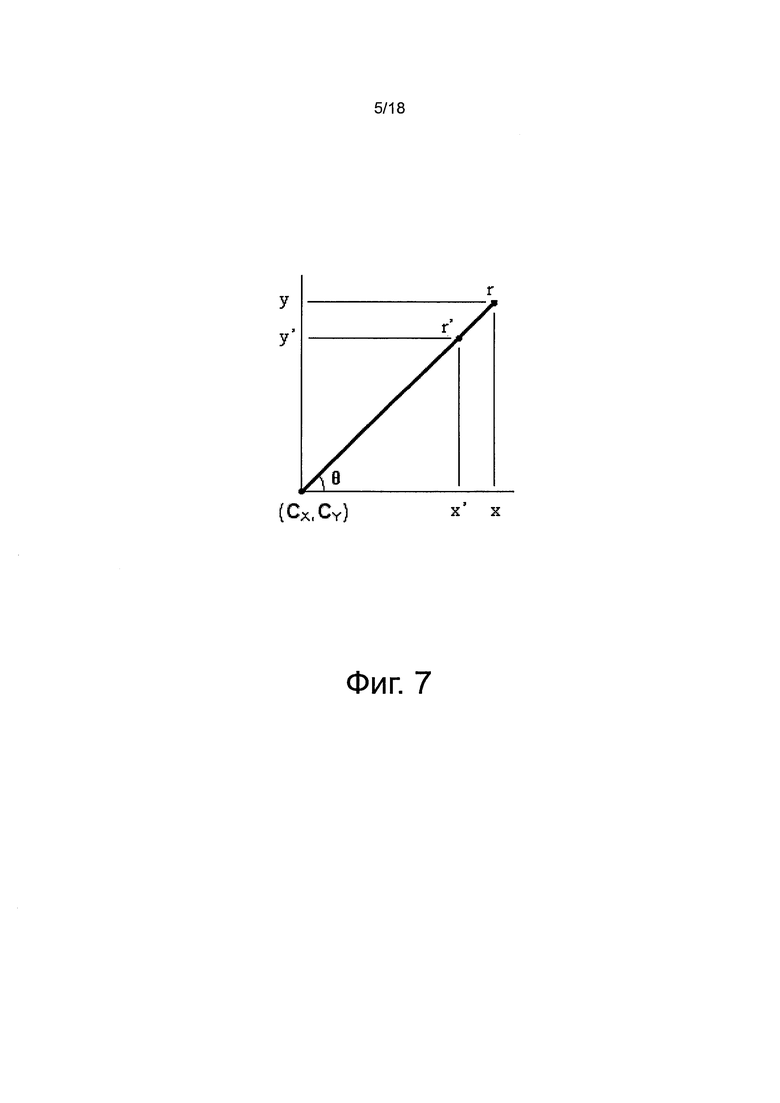
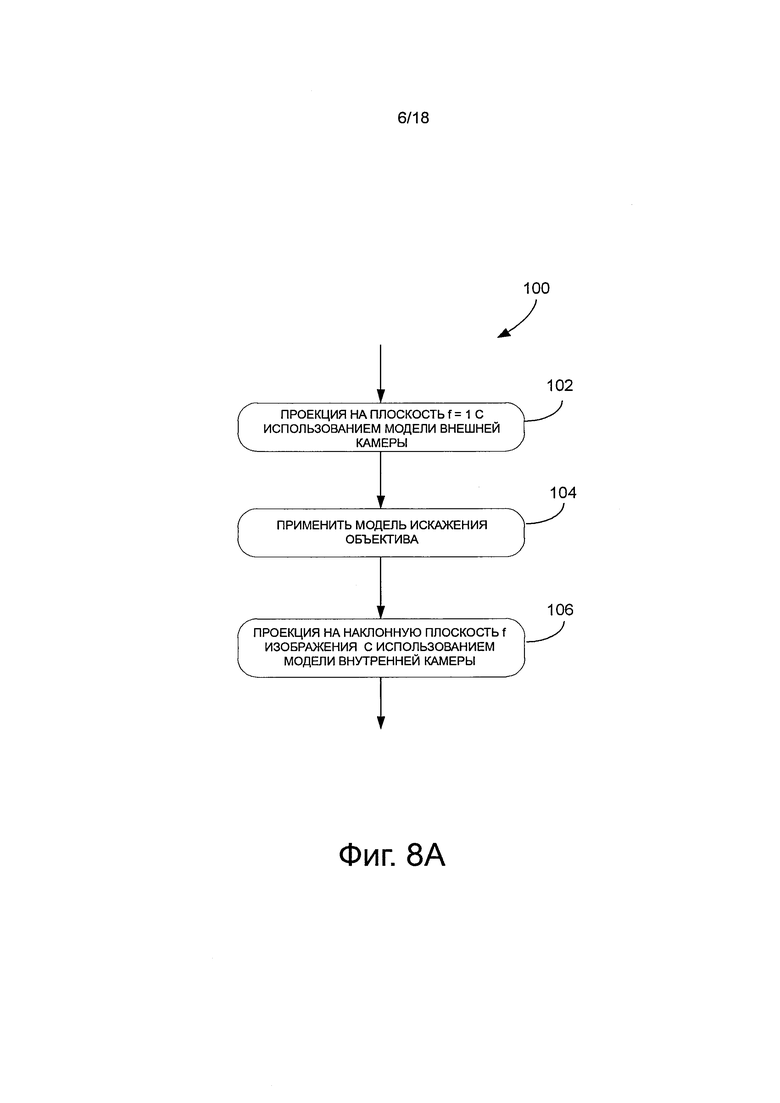
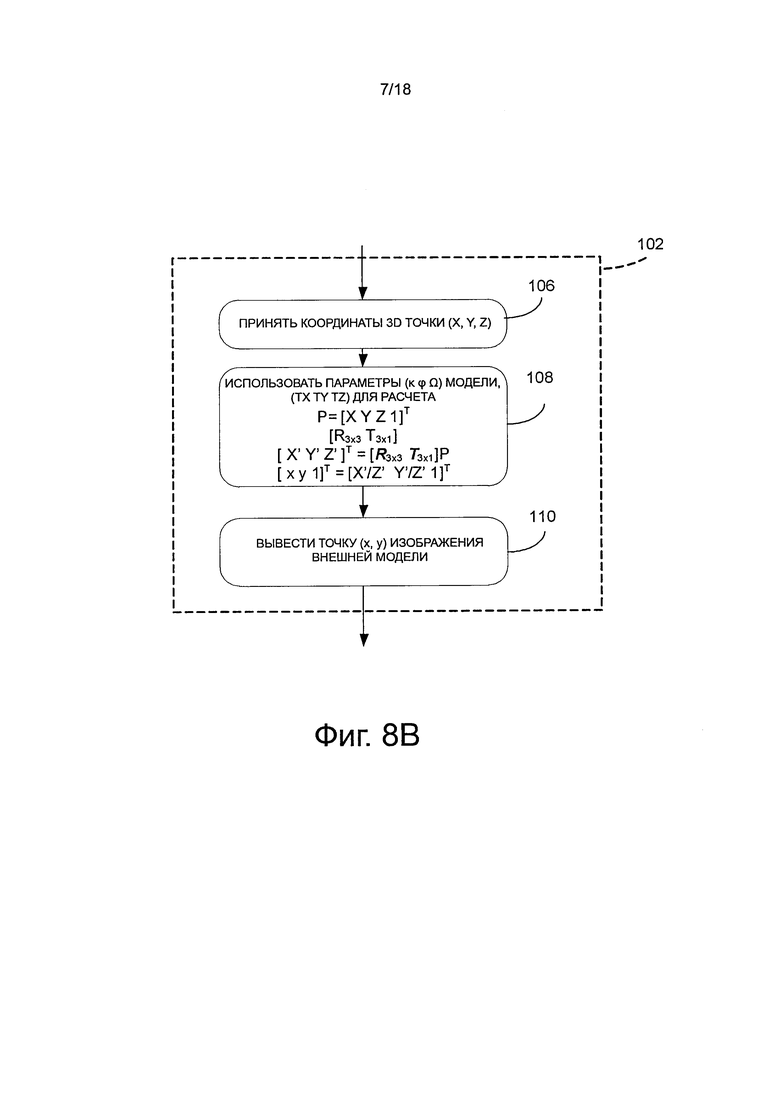
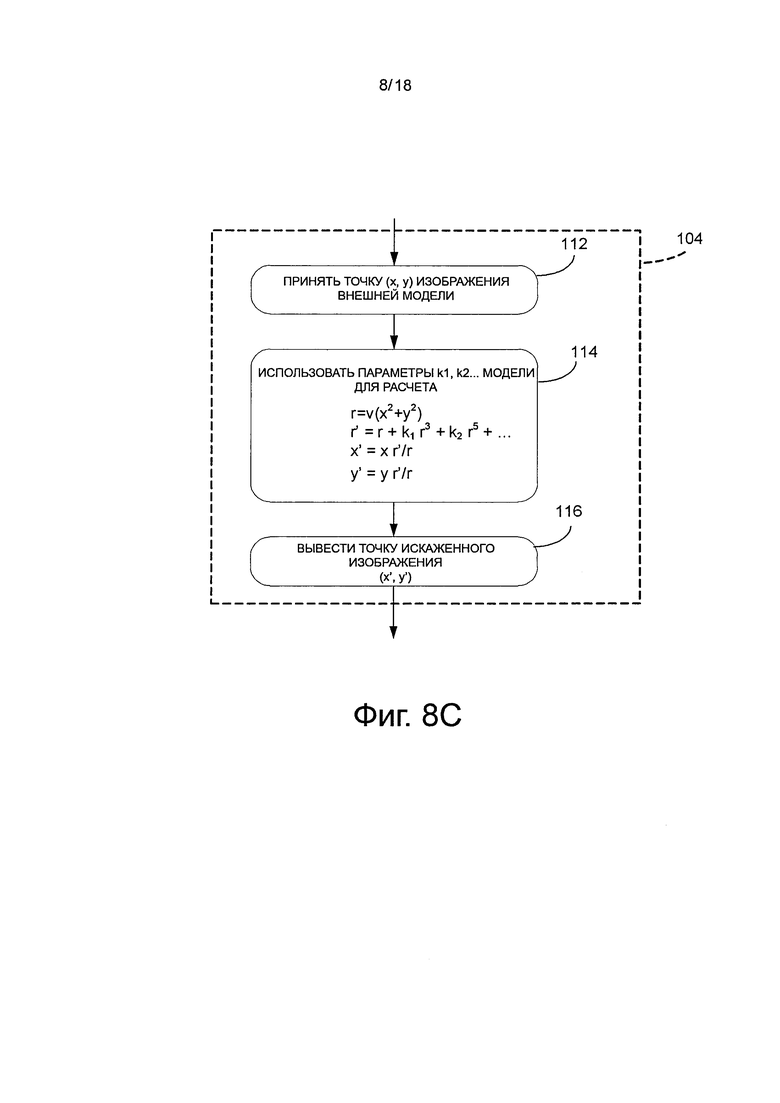
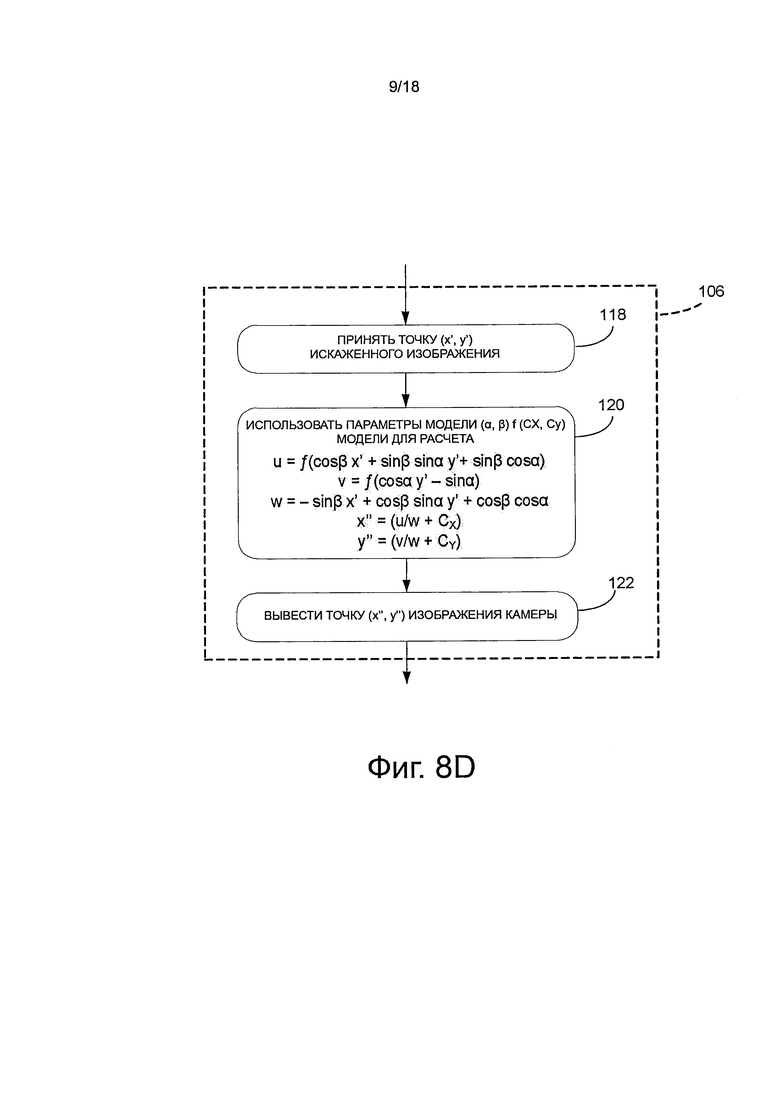
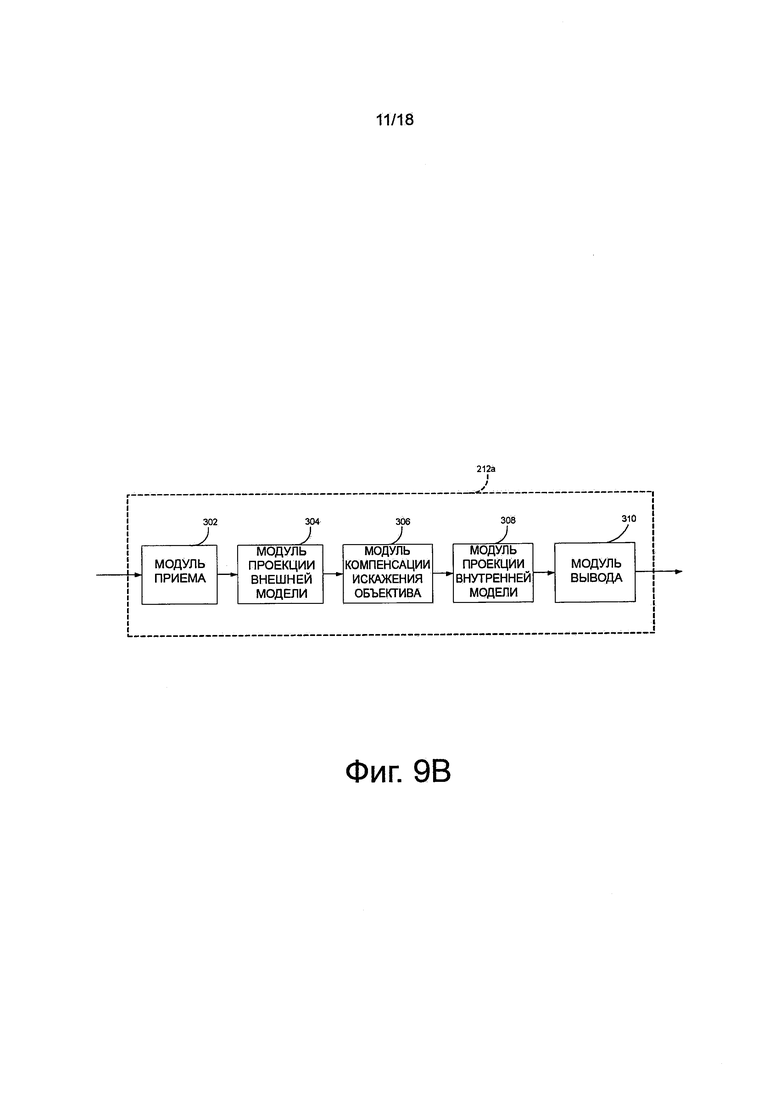

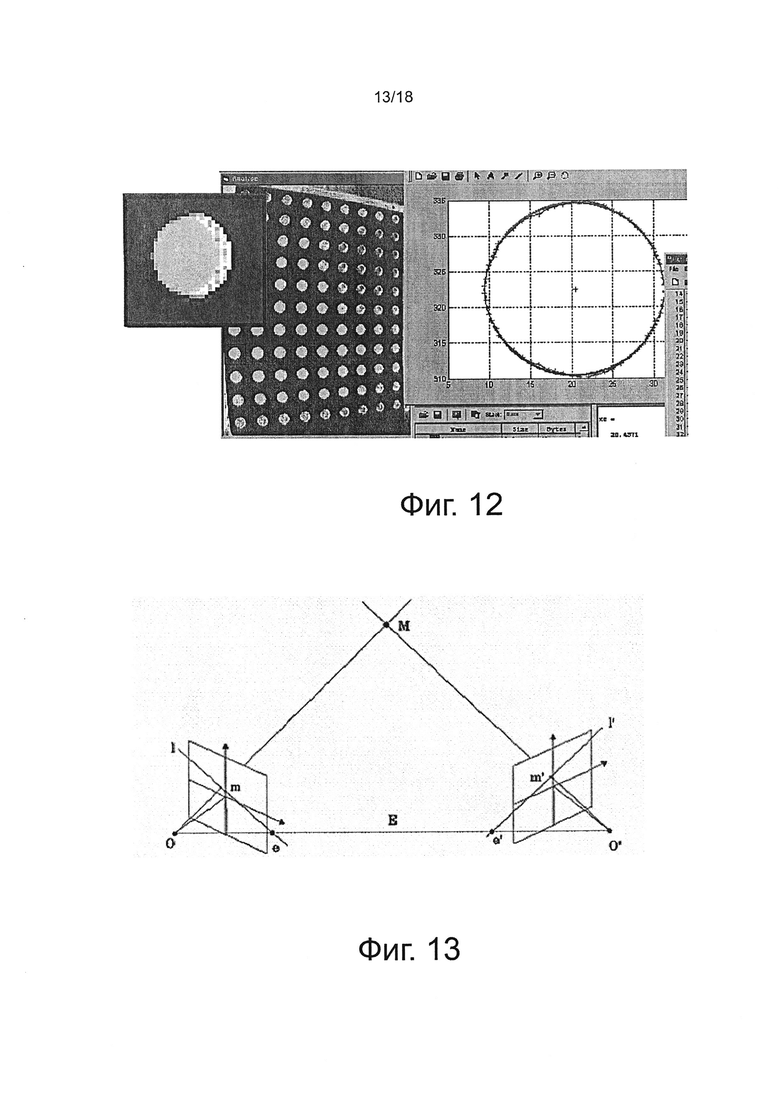

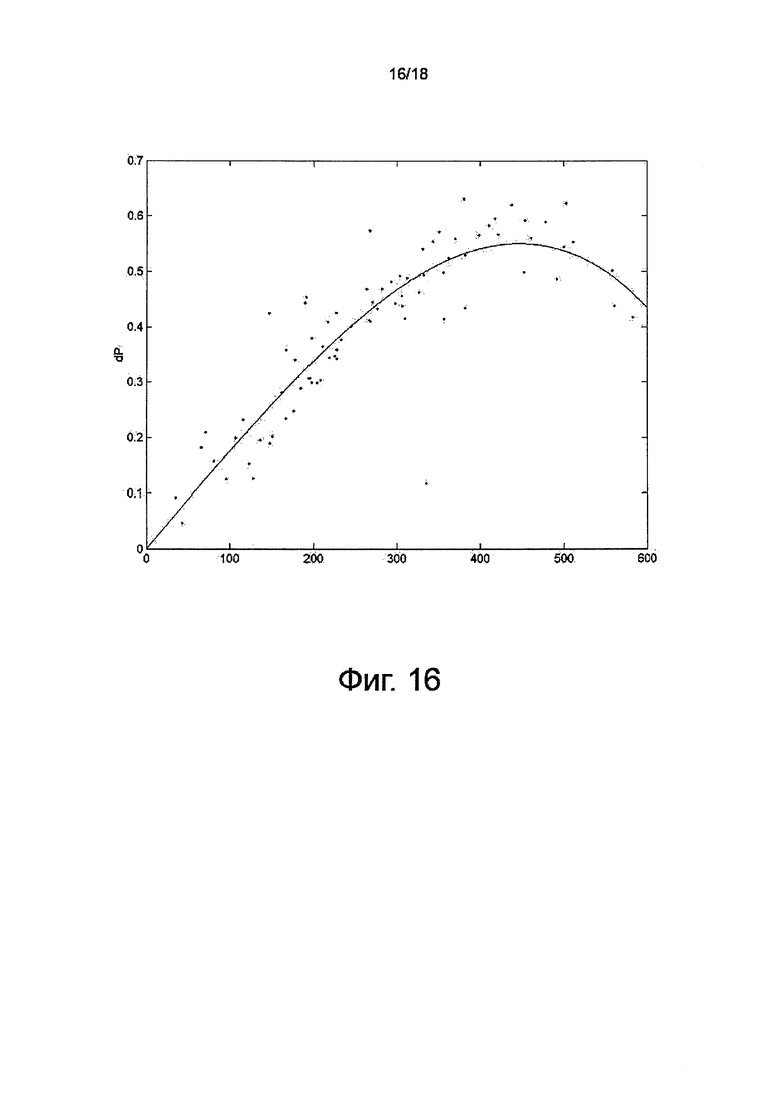
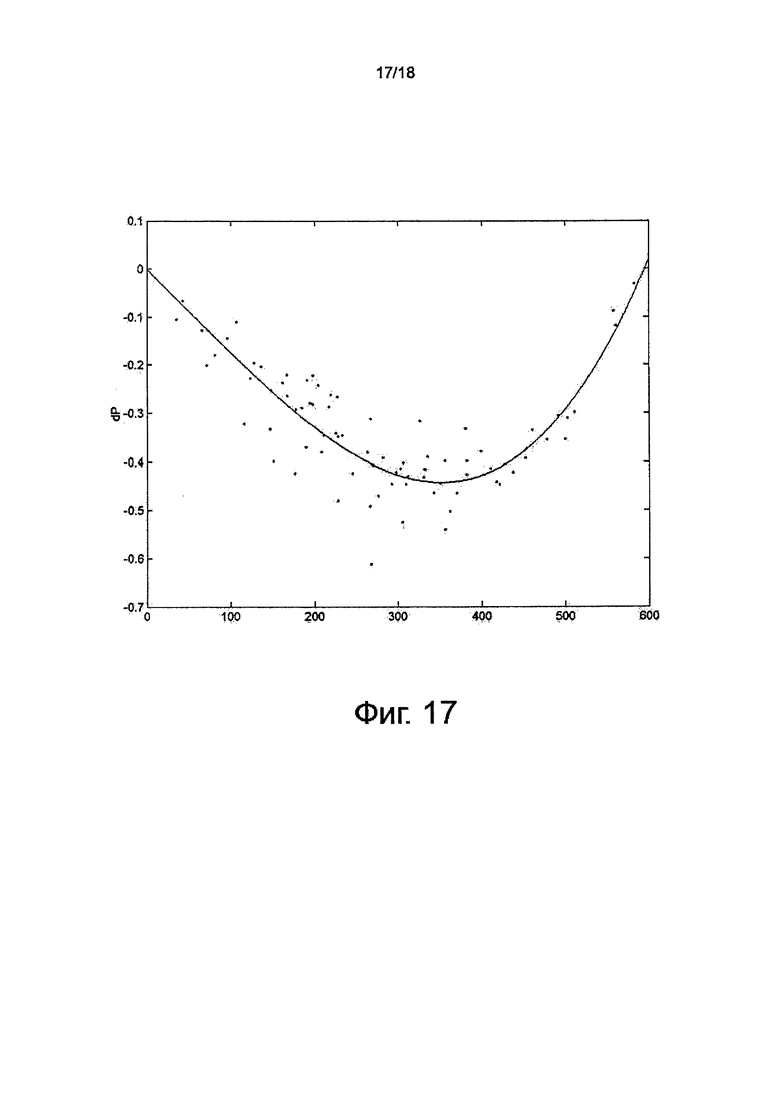

Изобретение относится к области моделирования и калибровки устройства формирования изображений. Технический результат – улучшение технологии моделирования для устройства формирования изображений. Способ моделирования устройства формирования изображения включает: определение первой трехмерной ортогональной системы координат, имеющей начало координат, расположенное в точке фокусирования устройства формирования изображения; определение второй трехмерной ортогональной системы координат, имеющей начало координат, расположенное на единичном расстоянии от точки фокусирования; определение третьей трехмерной системы координат, имеющей начало координат, расположенное на фокусном расстоянии от точки фокусирования; получение набора трехмерных координат, связанных с точкой реального трехмерного объекта, снятого устройством формирования изображения; вычисление проекции точки на плоскость истинного масштаба и на плоскость изображения; и вывод второго набора плоских координат, указывающих местоположение точки изображения, соответствующей точке трехмерного объекта. 3 н. и 13 з.п. ф-лы, 22 ил.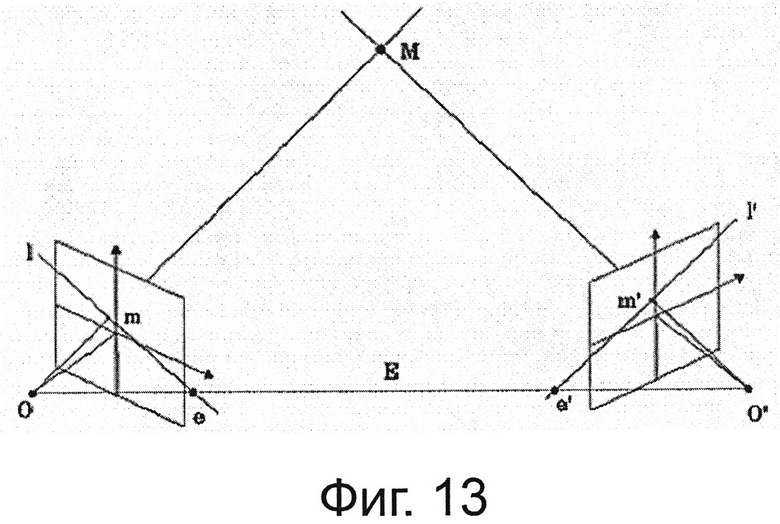
1. Реализуемый в компьютере способ моделирования устройства формирования изображения, содержащий этапы, на которых:
определяют первую трехмерную ортогональную систему координат, имеющую начало координат, расположенное в точке фокусирования устройства формирования изображения, причем первая ось первой системы координат проходит вдоль направления линии визирования устройства формирования изображения;
определяют вторую трехмерную ортогональную систему координат, имеющую начало координат, расположенное на единичном расстоянии от точки фокусирования, причем первая ось второй системы координат проходит вдоль направления линии визирования, вторая и третья оси второй системы координат по существу параллельны соответственно второй и третьей осям первой системы координат, тем самым вторая и третья оси второй системы координат задают плоскость истинного масштаба, перпендикулярную линии визирования;
определяют третью трехмерную систему координат, имеющую начало координат, расположенное на фокусном расстоянии от точки фокусирования, причем первая ось третьей системы координат проходит вдоль направления линии визирования, а вторая и третья оси третьей системы координат наклонены соответственно под первым и вторым углами относительно ориентации второй и третьей осей второй системы координат, тем самым вторая и третья оси третьей системы координат задают неперпендикулярность плоскости изображения относительно линии визирования;
принимают набор трехмерных координат, связанных с точкой реального трехмерного объекта, снятого устройством формирования изображения;
вычисляют проекцию точки на плоскость истинного масштаба, тем самым получая первый набор плоских координат, и на плоскость изображения, тем самым получая второй набор плоских координат; и
выводят второй набор плоских координат, указывающих местоположение точки изображения, соответствующей точке трехмерного объекта.
2. Способ по п. 1, в котором вторая система координат задана так, что плоскость истинного масштаба устанавливает вход в систему объектива устройства формирования изображения, а проекция на плоскость истинного масштаба выражает выход из внешней модели устройства формирования изображения, а третья система координат задана так, что плоскость изображения устанавливает выход для системы объектива, а проекция на плоскость изображения выражает выход из внутренней модели устройства формирования изображения.
3. Способ по п. 1, в котором принятый набор трехмерных координат представляет собой [x y z 1]T, и проекция точки трехмерного объекта на плоскость истинного масштаба рассчитывается по формуле:
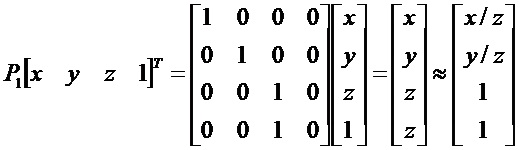 ,
,
где знак  представляет собой эквивалентный оператор масштабирования, а P1 задает операцию проецирования на плоскость истинного масштаба относительно первой системы координат.
представляет собой эквивалентный оператор масштабирования, а P1 задает операцию проецирования на плоскость истинного масштаба относительно первой системы координат.
4. Способ по п. 3, в котором проекция точки трехмерного объекта на плоскость изображения рассчитывается по формуле:

где Pƒ задает операцию проецирования на плоскость изображения, ƒ - фокусное расстояние, α - первый угол, β - второй угол, R (x, α) - матрица поворота на угол α относительно оси x плоскости изображения, причем ось x задана по существу параллельной второй оси второй системы координат перед выполнением поворота на угол α, R (y, β) - матрица поворота на угол β относительно оси y плоскости изображения, причем ось y задана по существу параллельной третьей оси второй системы координат перед выполнением поворота на угол β, поворот на угол α рассчитывают в самом правом положении, так что поворот на угол β выполняют относительно оси x, повернутой на угол α, и где
h11 = cosβ,
h12 = sinβ sinα,
h13 = sinβ cosα,
h22 = cosα,
h23 = -sinα,
h31 = -sinβ,
h32 = cosβ sinα, и
h33 = cosβ cosα.
5. Способ по п. 4, дополнительно содержащий этап, на котором определяют гомографию H между плоскостью истинного масштаба и плоскостью изображения по формуле:
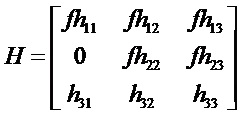 , где h31 и h32 - ненулевые элементы, применяющие коррекцию перспективы для масштабов x и y в плоскости изображения, и второй набор плоских координат (x'', y'') представляет собой гомографическое преобразование искаженного положения (x', y') изображения точки на плоскости истинного масштаба, причем гомографическое преобразование выражается следующей формулой:
, где h31 и h32 - ненулевые элементы, применяющие коррекцию перспективы для масштабов x и y в плоскости изображения, и второй набор плоских координат (x'', y'') представляет собой гомографическое преобразование искаженного положения (x', y') изображения точки на плоскости истинного масштаба, причем гомографическое преобразование выражается следующей формулой:
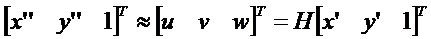 ,
,
где u = ƒ(cosβ x' + sinβ sinα y' + sinβ cosα),
v = ƒ(cosα y' - sinα),
w = -sinβ x' + cosβ sinα y' + cosβ cosα,
x'' = u/w + CX, и
y'' = v/w + CY, где (CX ,CY) представляет положение начала третьей системы координат.
6. Способ по п. 5, в котором гомография H определена формулой:
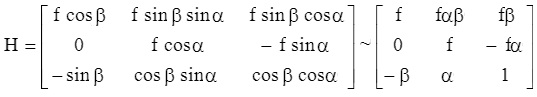
где аппроксимация cosθ~1 и sinθ~θ используется для малых углов α и β.
7. Способ по п. 1, дополнительно содержащий этап, на котором компенсируют искажение объектива устройства формирования изображения в плоскости истинного масштаба, причем компенсация содержит этап, на котором: применяют модель искажения объектива, задаваемую формулой:
r' = r + k1 r3 + k2 r5 + …,
где первый набор плоских координат содержит положение (x, y) без искажений для изображения точки на плоскости истинного масштаба, выраженной в полярных координатах (r, θ), где r2=x2+y2 и tgθ = y/x, (x', y') представляет искаженное положение (x, y) на выходе объектива перед проекцией точки на плоскость изображения, r' представляет собой искаженное радиальное расстояние, рассчитанное на основе (x', y'), а k1 и k2 представляют собой параметры геометрических искажений объектива.
8. Система для моделирования устройства формирования изображения, содержащая:
запоминающее устройство;
процессор; и
по меньшей мере одно приложение, хранящееся в запоминающем устройстве и исполняемое процессором для
определения первой трехмерной ортогональной системы координат, имеющей начало координат, расположенное в точке фокусирования устройства формирования изображения, причем первая ось первой системы координат проходит вдоль направления линии визирования устройства формирования изображения;
определения второй трехмерной ортогональной системы координат, имеющей начало координат, расположенное на единичном расстоянии от точки фокусирования, причем первая ось второй системы координат проходит вдоль направления линии визирования, вторая и третья оси второй системы координат по существу параллельны соответственно второй и третьей осям первой системы координат, тем самым вторая и третья оси второй системы координат задают плоскость истинного масштаба, перпендикулярную линии визирования;
определения третьей трехмерной системы координат, имеющей начало координат, расположенное на фокусном расстоянии от точки фокусирования, причем первая ось третьей системы координат проходит вдоль направления линии визирования, вторая и третья оси третьей системы координат наклонены соответственно под первым и вторым углами относительно ориентации второй и третьей осей второй системы координат, тем самым вторая и третья оси третьей системы координат задают неперпендикулярность плоскости изображения относительно линии визирования;
приема набора трехмерных координат, связанных с точкой реального трехмерного объекта, снятого устройством формирования изображения;
вычисления проекции точки на плоскость истинного масштаба, тем самым получая первый набор плоских координат, и на плоскость изображения, тем самым получая второй набор плоских координат; и
вывода второго набора плоских координат, указывающих местоположение точки изображения, соответствующее точке трехмерного объекта.
9. Система по п. 8, в которой указанное по меньшей мере одно приложение выполнено с возможностью выполнения процессором для определения второй системы координат так, что плоскость истинного масштаба устанавливает вход в систему объектива устройства формирования изображения, а проекция на плоскость истинного масштаба выражает выход из внешней модели устройства формирования изображения, и определения третьей системы координат так, что плоскость изображения устанавливает выход для системы объектива, а проекция на плоскость изображения выражает выход из внутренней модели устройства формирования изображения.
10. Система по п. 8, в которой указанное по меньшей мере одно приложение выполнено с возможностью выполнения процессором для приема набора трехмерных координат в виде [x y z 1]T и расчета проекции точки трехмерного объекта на плоскость истинного масштаба по формуле:
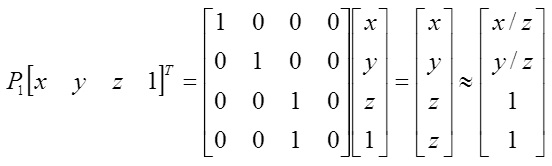 ,
,
где 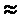 представляет собой эквивалентный оператор масштабирования, и P1 задает операцию проецирования на плоскость истинного масштаба относительно первой системы координат.
представляет собой эквивалентный оператор масштабирования, и P1 задает операцию проецирования на плоскость истинного масштаба относительно первой системы координат.
11. Система по п. 10, в которой указанное по меньшей мере одно приложение выполнено с возможностью выполнения процессором для расчета проекции точки трехмерного объекта на плоскость формирования изображения по формуле:

где Pƒ определяет операцию проецирования на плоскость изображения, ƒ - фокусное расстояние, α - первый угол, β - второй угол, R (x, α) - матрица поворота на угол α относительно оси x плоскости изображения, причем ось x определена как по существу параллельная второй оси второй системы координат перед выполнением поворота на угол α, R (y, β) - матрица поворота на угол β относительно оси y плоскости изображения, причем ось y определена как по существу параллельная третьей оси второй системы координат перед выполнением поворота на угол β, поворот на угол α рассчитан в крайнем правом положении, так что поворот на угол β выполняется относительно оси x, повернутой на угол α, и где
h11 = cosβ,
h12 = sinβ sinα,
h13 = sinβ cosα,
h22 = cosα,
h23 = -sinα,
h31 = -sinβ,
h32 = cosβ sinα, и
h33 = cosβ cosα.
12. Система по п. 11, в которой указанное по меньшей мере одно приложение выполнено с возможностью выполнения процессором для определения гомографии H между плоскостью истинного масштаба и плоскостью изображения по формуле:
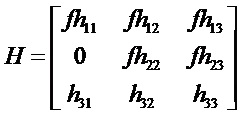 , где h31 и h32 представляют собой ненулевые элементы, применяющие коррекцию перспективы для масштабов x и y в плоскости изображения, а второй набор плоских координат (x'', y'') представляют собой гомографическое преобразование искаженного положения (x', y') изображения точки на плоскости истинного масштаба, причем гомографическое преобразование выражено следующей формулой:
, где h31 и h32 представляют собой ненулевые элементы, применяющие коррекцию перспективы для масштабов x и y в плоскости изображения, а второй набор плоских координат (x'', y'') представляют собой гомографическое преобразование искаженного положения (x', y') изображения точки на плоскости истинного масштаба, причем гомографическое преобразование выражено следующей формулой:
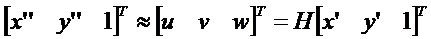 ,
,
где u = ƒ(cosβ x' + sinβ sinα y' + sinβ cosα),
v = ƒ(cosα y' - sinα),
w = -sinβ x' + cosβ sinα y' + cosβ cosα,
x'' = u/w + CX, и
y'' = v/w + CY, где (CX ,CY) - положение начала координат для третьей системы координат.
13. Система по п. 12, в которой указанное по меньшей мере одно приложение исполняется процессором для определения гомографии H по формуле:
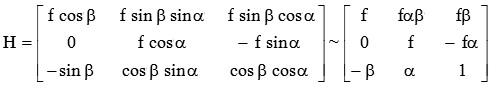
где аппроксимация cosθ~1 и sinθ~θ используется для малых углов α и β.
14. Система по п. 12, в которой указанное по меньшей мере одно приложение выполнено с возможностью выполнения процессором для компенсации искажений объектива устройства формирования изображения в плоскости истинного масштаба, при этом компенсация содержит применение модели искажений объектива, определяемой формулой:
r' = r + k1 r3 + k2 r5 + …,
где первый набор плоских координат содержит неискаженное положение (x, y) изображения точки на плоскости истинного масштаба, которое выражено в полярных координатах (r, θ), где r2=x2+y2, и tgθ = y/x, (x', y') - искаженное положение (x, y) на выходе объектива перед проекцией точки на плоскость изображения, r' - искаженное радиальное расстояние, рассчитанное на основе (x', y'), а k1 и k2 - параметры геометрического искажения объектива.
15. Система по п. 8, в которой устройство формирования изображения содержит одно устройство из камеры с объективом с переменным фокусным расстоянием, устройства формирования изображения в близком инфракрасном свете, устройства формирования изображения в коротковолновом инфракрасном свете, устройства формирования изображения в длинноволновом инфракрасном свете, радарного устройства, устройства детектирования и ранжирования света, формирователя изображения в виде телескопа с параболическим зеркалом, хирургической эндоскопической камеры, устройства сканирования для компьютерной томографии, спутникового устройства формирования изображения, сонарного устройства и многоспектральной системы с множеством различных датчиков.
16. Считываемый компьютером носитель информации, на котором содержится программный код, исполняемый процессором, для моделирования устройства формирования изображения, причем программный код исполняется для:
определения первой трехмерной ортогональной системы координат, имеющей начало координат, расположенное в точке фокусирования устройства формирования изображения, причем первая ось первой системы координат проходит вдоль направления линии визирования устройства формирования изображения;
определения второй трехмерной ортогональной системы координат, имеющей начало координат, расположенное на единичном расстоянии от точки фокусирования, причем первая ось второй системы координат проходит вдоль направления линии визирования, а вторая и третья оси второй системы координат по существу параллельны соответственно второй и третьей осям первой системы координат, тем самым вторая и третья оси второй системы координат задают плоскость истинного масштаба, перпендикулярную линии визирования;
определения третьей трехмерной системы координат, имеющей начало координат, расположенное на фокусном расстоянии от точки фокусирования, причем первая ось третьей системы координат проходит вдоль направления линии визирования, вторая и третья оси третьей системы координат наклонены соответственно на первый и второй углы относительно ориентации второй и третьей осей второй системы координат, тем самым вторая и третья оси третьей системы координат задают неперпендикулярность плоскости изображения относительно линии визирования;
приема набора трехмерных координат, связанных с точкой реального трехмерного объекта, снятого устройством формирования изображения;
вычисления проекции точки на плоскость истинного масштаба, тем самым получая первый набор плоских координат, и на плоскость изображения, тем самым получая второй набор плоских координат; и
вывода второго набора плоских координат, указывающих местоположение точки изображения, соответствующей точке трехмерного объекта.
| Многоступенчатая активно-реактивная турбина | 1924 |
|
SU2013A1 |
| Изложница с суживающимся книзу сечением и с вертикально перемещающимся днищем | 1924 |
|
SU2012A1 |
| Станок для изготовления деревянных ниточных катушек из цилиндрических, снабженных осевым отверстием, заготовок | 1923 |
|
SU2008A1 |
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
| УСТРОЙСТВО КАЛИБРОВКИ ОПТИКОЭЛЕКТРОННОЙ СИСТЕМЫ | 2001 |
|
RU2199150C2 |
Авторы
Даты
2019-01-17—Публикация
2014-07-02—Подача