Изобретение относится к исследованию дисперсных характеристик аэрозолей различной природы, и может быть использовано в метеорологии, в нанопроизводстве, для контроля нанобезопасности на рабочих местах, для определения ингаляционной дозы при применении аэрозольных форм доставки лекарственных средств и в других сферах человеческой деятельности.
В последние десятилетия в различных областях науки, технике и других видов деятельности значительно возросла потребность в измерении спектров размеров аэрозольных частиц. К таким областям относятся контроль качества окружающего воздуха [1-4], аэрозольные формы доставки лекарственных средств [5, 6], нанотехнологии [7], контроль содержания аэрозольных частиц в воздухе рабочих помещений [8-10] и др.
Аэрозольные измерения можно разделить на две категории. Первая категория предполагает отбор образцов с последующим лабораторным анализом (оптическая, силовая, электронная микроскопия [11-13], импакторы [11, 14, 15] и др.). Методы второй категории позволяют получить результаты практически в реальном времени (светорассеяние, аэродинамические спектрометры, методы, основанные на диффузионной сепарации и измерении подвижности в электрическом поле [16, 17]).
Среди методов второй категории получили большое распространение анализаторы дифференциальной подвижности [18]. Слабыми сторонами данной методики являются сложность использования в полевых измерениях, высокая цена и необходимость в электрической зарядке частиц. Другим хорошо известным методом измерения спектра размеров аэрозольных частиц, свободным от вышеперечисленных недостатков, является сепарация с помощью диффузионной батареи (ДБ). Диффузионные батареи имеют простую конструкцию и хорошо подходят для использования в полевых измерениях [19], в лабораторных экспериментах [20-22] и для контроля уровня аэрозольной загрязненности на рабочих местах [23, 24]. В данном методе используется зависимость коэффициента осаждения в секциях диффузионной батареи от размера частиц. Чаще всего диффузионные батареи выполнены в виде последовательных секций, заполненных набором капилляров (параллельных аэрозольному протоку) или набором плоских сеток (перпендикулярных потоку). По мере движения аэрозольного потока через батарею, частицы осаждаются на внутренней поверхности капилляров или на поверхности волокон, из которых состоят сетки.
После опубликования работ [25, 26] диффузионные батареи сетчатого типа стали наиболее популярны. Батареи этого типа просты в изготовлении и компактны. Сетки в случае необходимости легко заменяемы. Число сеток в секции прогрессивно нарастает с увеличением последовательного номера i секции. В ходе работы батареи измеряется счетная концентрация Сi частиц ниже по потоку после каждой секции. Эти концентрации дают вероятность gi прохождения частиц через последовательности секций ("проскоки"), где gi есть отношение счетной концентрации Сi к концентрации С0 на входе в диффузионную батарею. Полученные проскоки, в свою очередь, позволяют рассчитать спектр частиц по размерам. Однако функции осаждения частиц в секциях имеют плавную зависимость от размера, т.е. области размеров, в которых происходит осаждение частиц в разных секциях, перекрываются друг с другом. Поэтому, в принципе, бесконечное количество функций распределения частиц по размерам может удовлетворять одному и тому же набору проскоков. Тем не менее, при правильной обработке данных экспериментальных измерений диффузионной батареи можно рассчитать функцию ƒ(D) распределения частиц по диаметрам D близкую к реальному спектру размеров. Заметим, что далее в данном решении будет рассматриваться функция распределения по диаметрам, нормированная на единицу.
Для того чтобы извлечь спектр размеров, необходимо применить математическую процедуру, называемую инверсия. Для этого необходимо решить интегральные уравнения Фредгольма первого рода, которые в идеальном случае выражаются в виде

где Ki(D) есть ядро диффузионной батареи, т.е. функция, описывающая долю частиц, прошедших через первые i секций, для монодисперсного аэрозоля с диаметром частиц D; а и b - пределы диапазона размеров. Однако экспериментальное измерение проводится с некоторой погрешностью, поэтому уравнение (1) выполняется лишь в пределах экспериментальной точности:

где εi - экспериментальные ошибки. Уравнения (2) представляет собой, так называемую некорректную обратную задачу, которая не может быть решена без привлечения дополнительной информации. Как правило, такие обратные задачи решаются численно. Существуют различные численные подходы для решения уравнения (2), такие как линейные и нелинейные итерационные методы [27-29], метод регуляризации Тихонова [30, 31], метод наименьших квадратов [32], метод максимального ожидания [33], матричный факторный анализ [34], метод максимальной энтропии [35-37] и др. Основными недостатками численных методов являются сложность алгоритма и большие вычислительные затраты.
Наиболее близким к заявленному изобретению, является прибор для измерения спектра аэрозольных частиц и способ измерения спектра размеров аэрозольных частиц, разработанный в Институте химической кинетики и горения СО РАН [38, 39, 41]. Основными элементами этого прибора являются диффузионная батарея, конденсационный укрупнитель частиц до оптически регистрируемого размера, оптический счетчик частиц и блок связи с персональным компьютером для управления и обработки данных. При использовании прибора-прототипа восстановление спектра размеров из экспериментально измеренных проскоков диффузионной батареи осуществляется с помощью численного решения обратной задачи.
К недостаткам метода восстановления спектра, используемого в приборе-прототипе, следует отнести численное решение обратной задачи, т.е. системы интегральных уравнений Фредгольма первого рода (уравнение (2)). Проблема заключается в том, что данная задача является некорректной, что, в частности, проявляется в том, что одному набору проскоков соответствует бесконечное множество решений. Кроме того, малые погрешности измерений могут приводить к огромным ошибкам в решении. Для того, чтобы решить данные проблемы, приходится накладывать ограничения на решение, и, что более важно, применять процедуру выбора конечного решения из большого количества математически возможных решений. В результате, процедура восстановления спектра становится ресурсозатратной, и зачастую получаются недостоверные решения.
Задачей предлагаемого изобретения является повышение точности измерения спектров размеров аэрозольных частиц и упрощение метода расчета. Данное повышение точности достигается реализованной конструкцией диффузионной батареи, позволяющей осуществить такой способ измерения, при котором измеряются спектры размеров фракций аэрозольных частиц, осевших в отдельных секциях, за исключением последней, при прохождении через них аэрозольного потока, а также частиц прошедших через все секции, за исключением последней. При этом, общий спектр исходных частиц является суммой спектров фракций.
Техническим результатом данного изобретения является упрощение процедуры измерения функции распределения частиц по размерам и получение более достоверных спектров размеров частиц, по сравнению с ранее использовавшимися способами.
Технический результат достигается предложенным устройством для измерения спектра размеров частиц, включающего диффузионную батарею с несколькими секциями в которых установлены сетки перпендикулярно потоку. Согласно изобретению, сетки в секциях диффузионной батареи распределены так, что количество сеток в каждой секции, за исключением первой, равно суммарному числу сеток во всех предыдущих секциях, расположенных выше по потоку. Другими словами, распределение сеток в секциях выбрано таким образом, чтобы средний диаметр Di фракции частиц, осевших в i-й секции ДБ можно было математически выразить с помощью экспериментально измеренных проскоков по формуле:
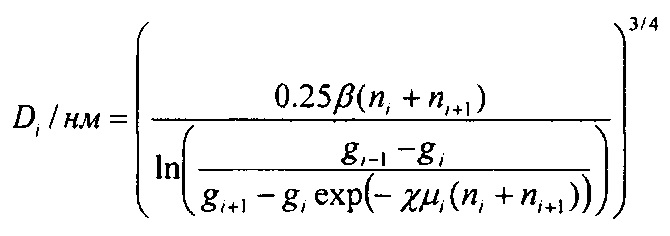
где i - последовательный номер секции, ni и ni+1 - количества сеток в секциях с номерами i и i+1, соответственно, gi - доля частиц, прошедших через i-ю секцию без осаждения, μi - эффективность осаждения на одиночном волокне в пакете, содержащем ni+ni+1, сеток, для частиц, содержащихся в потоке после i-й секции, 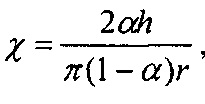 h - толщина сетки, r - радиус волокна сетки, α - отношение объема, занимаемого волокнами, к полному объему сетки,
h - толщина сетки, r - радиус волокна сетки, α - отношение объема, занимаемого волокнами, к полному объему сетки, 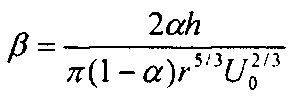 , U0 - линейная скорость аэрозольного потока.
, U0 - линейная скорость аэрозольного потока.
Технический результат достигается также за счет того, что устанавливается однозначное соответствие между измеренными проскоками и спектрами фракций, что приводит к устойчивости решения, т.е. случайные экспериментальные погрешности измерения диффузионной батареи не приводят к существенному разбросу восстановленного спектра размеров, поскольку экспериментальные проскоки ДБ однозначно определяют среднюю эффективность осаждения на отдельных волокнах сетки для фракций частиц по формуле
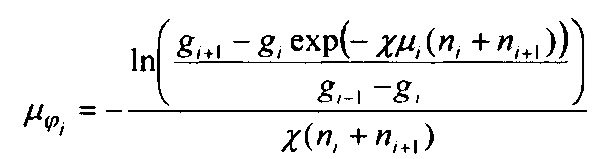
где i - последовательный номер секции ДБ или фракции частиц, 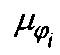 - эффективность осаждения частиц i-й фракции на отдельном волокне i-й секции, ni, и ni+1 - количества сеток в секциях с номерами i и i+1, соответственно, gi - доля частиц, прошедших через i-ю секцию, μi - эффективность осаждения на одиночном волокне в пакете, содержащем ni +ni+1 сеток, для частиц, содержащихся в потоке после i-й секции,
- эффективность осаждения частиц i-й фракции на отдельном волокне i-й секции, ni, и ni+1 - количества сеток в секциях с номерами i и i+1, соответственно, gi - доля частиц, прошедших через i-ю секцию, μi - эффективность осаждения на одиночном волокне в пакете, содержащем ni +ni+1 сеток, для частиц, содержащихся в потоке после i-й секции, 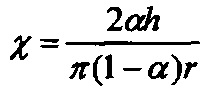 , h - толщина сетки, r - радиус волокна сетки, α - отношение объема, занимаемого волокнами, к полному объему сетки,
, h - толщина сетки, r - радиус волокна сетки, α - отношение объема, занимаемого волокнами, к полному объему сетки, 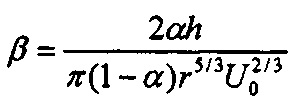 , U0 - линейная скорость аэрозольного потока; далее из величины
, U0 - линейная скорость аэрозольного потока; далее из величины 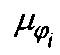 однозначно определяют средний диаметр Di частиц i-й фракции по формулам веерной модели фильтров Кирша-Стечкиной-Фукса, долю hi частиц i-й фракции определяют по формуле hi=gi-gi+1, спектр частиц i-й фракции аппроксимируют любой функцией мономодального распределения, включая логнормальное распределение, Гауссово распределение, причем Di и hi являются параметрами мономодального распределения, далее спектр исходного аэрозоля определяется как сумма спектров фракций.
однозначно определяют средний диаметр Di частиц i-й фракции по формулам веерной модели фильтров Кирша-Стечкиной-Фукса, долю hi частиц i-й фракции определяют по формуле hi=gi-gi+1, спектр частиц i-й фракции аппроксимируют любой функцией мономодального распределения, включая логнормальное распределение, Гауссово распределение, причем Di и hi являются параметрами мономодального распределения, далее спектр исходного аэрозоля определяется как сумма спектров фракций.
Предлагаемое изобретение иллюстрируется чертежами, на которых изображены:
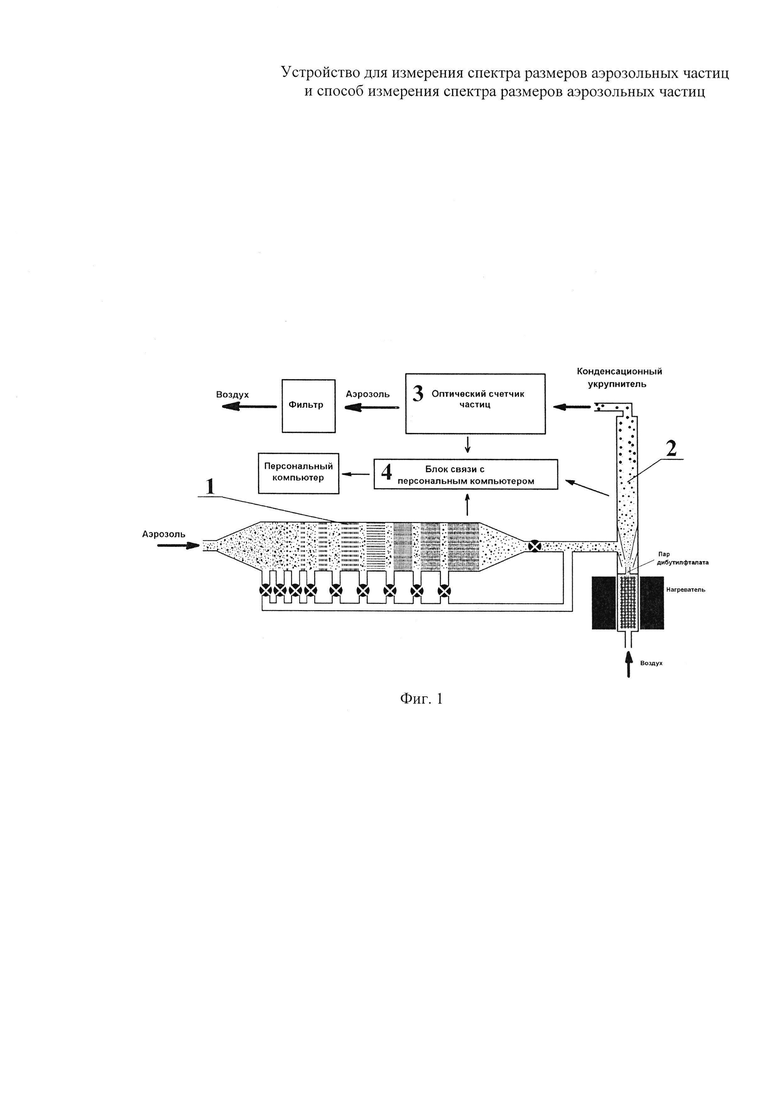
на фиг. 1 - блок-схема прибора для измерения спектра размеров частиц: 1 - сетчатая диффузионная батарея, 2 - конденсационный укрупнитель частиц до оптически регистрируемого размера, 3 - оптический счетчик частиц, 4 - блок связи с персональным компьютером;
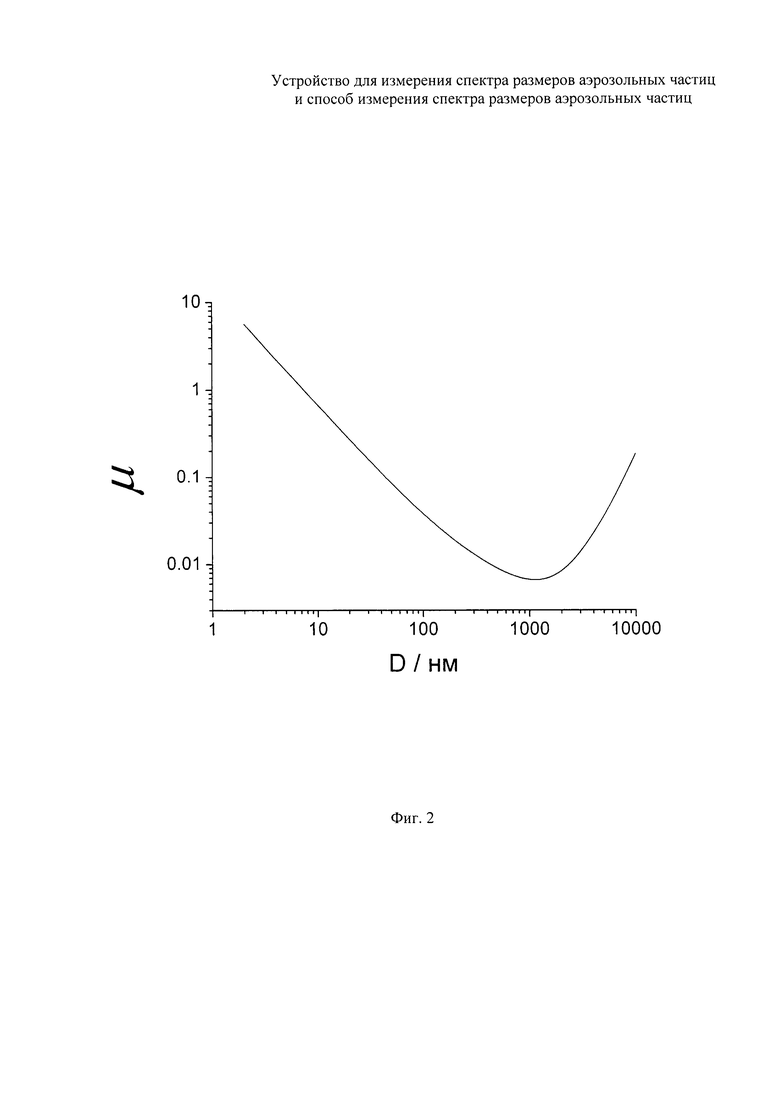
на фиг. 2 - эффективность осаждения аэрозольных частиц на одиночном волокне в зависимости от диаметра частиц;
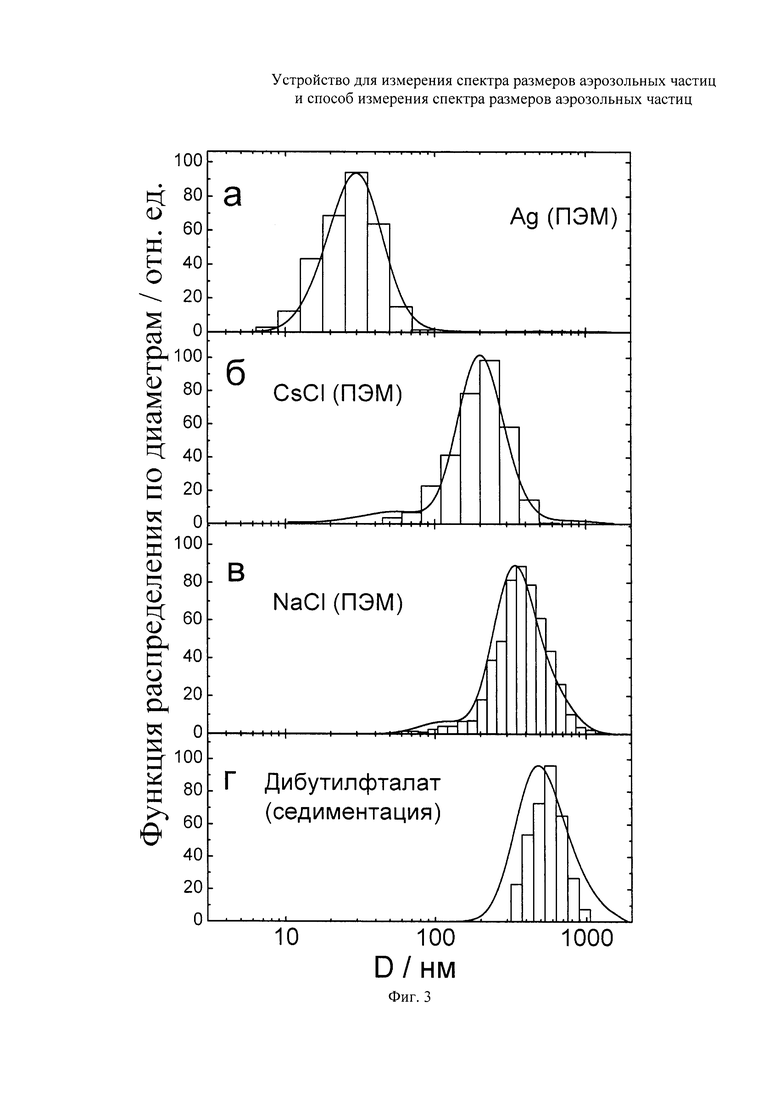
на фиг. 3 - сравнение функций распределения частиц по диаметрам, измеренных с помощью диффузионной батареи (сплошные линии) со спектрами размеров, измеренных с помощью просвечивающей электронной микроскопии (а, б, в) и седиментации в гравитационном поле (г) (гистограммы).
Суть изобретения сводится к следующему. Основными элементами устройства (фиг. 1) для измерения спектра размеров аэрозольных частиц являются сетчатая диффузионная батарея 1, конденсационный укрупнитель частиц до оптически регистрируемого размера 2, оптический счетчик частиц 3 и блок связи с персональным компьютером 4 для управления и обработки данных. Диффузионная батарея состоит из последовательных секций, заполненных сетками, поглощающими аэрозольные частицы по механизму диффузии, захвату, инерции и др. Сетки установлены перпендикулярно аэрозольному потоку. Отличительными признаками устройства является то, что число сеток в каждой секции равно суммарному числу сеток в предыдущих секциях, расположенных выше по потоку. В данном изобретении в качестве примера рассматривается сетчатая батарея из девяти цилиндрических секций, число сеток в которых возрастает с номером секции следующим образом: 2, 2, 4, 8, 16, 32, 64, 128, 256. Внутренний диаметр канала секций составляет 50 мм. Использовались капроновые плетеные сетки с диаметром волокна 50 мкм, шагом 172 мкм, отношение объема, занимаемого волокнами, к полному объему сетки α=0.231. Объемная скорость аэрозольного потока через батарею составляла 1 л/мин. Счетная концентрация аэрозоля Сi измеренная после i-й секции зависит от общего числа N1,i=n1+n2+…+ni, сеток, через которые прошел аэрозольный поток, где n1, …, ni числа сеток в секциях 1, …, i, соответственно. Для аэрозоля, все частицы которого имеют один и тот же диаметр D доля частиц, прошедших через последовательность секций 1, …, i, составляет [25, 26, 41-46]

где μ - эффективность осаждения частиц на отдельном волокне, расположенным перпендикулярно аэрозольному потоку, 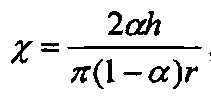 , h - толщина сетки, r - радиус волокна сетки. Батарея, рассматриваемая в данном изобретении, предназначена для работы в нанометровом и субмикронном диапазонах. Для частиц в этой области размеров, осаждение на волокна в основном определяется тремя механизмами - диффузией, захватом и инерцией. Зависимость эффективности осаждения на одиночном волокне от диаметра частицы можно рассчитать в рамках теории веерных фильтров Кирша, Стечкиной и Фукса [42-45]. На фиг. 2 для монодисперсных частиц приведена эта зависимость для параметров батареи, рассмотренной в данном изобретении. Видно, что функция μ(D) имеет минимум при D≈1100 нм, что означает, что однозначное соответствие между диаметром и эффективностью осаждения имеет место при размерах частиц D<1100 нм. Другими словами, данная диффузионная батарея имеет динамический диапазон размеров 3<D<1100 нм (при размерах меньших 3 нм эффективность укрупнения частиц в конденсационном укрупнителе становится существенно меньше единицы).
, h - толщина сетки, r - радиус волокна сетки. Батарея, рассматриваемая в данном изобретении, предназначена для работы в нанометровом и субмикронном диапазонах. Для частиц в этой области размеров, осаждение на волокна в основном определяется тремя механизмами - диффузией, захватом и инерцией. Зависимость эффективности осаждения на одиночном волокне от диаметра частицы можно рассчитать в рамках теории веерных фильтров Кирша, Стечкиной и Фукса [42-45]. На фиг. 2 для монодисперсных частиц приведена эта зависимость для параметров батареи, рассмотренной в данном изобретении. Видно, что функция μ(D) имеет минимум при D≈1100 нм, что означает, что однозначное соответствие между диаметром и эффективностью осаждения имеет место при размерах частиц D<1100 нм. Другими словами, данная диффузионная батарея имеет динамический диапазон размеров 3<D<1100 нм (при размерах меньших 3 нм эффективность укрупнения частиц в конденсационном укрупнителе становится существенно меньше единицы).
Для того, чтобы получить аналитические выражения для расчета спектра размеров ƒ(D) исходных аэрозольных частиц его можно представить в виде

где m - число секций ДБ, ϕ1(D), ϕ2(D), …, ϕm-1(D) - спектры размеров фракций частиц, осевших соответственно в секциях 1, 2, …, m-1 при прохождении через них аэрозольного потока, a ϕm(D) - спектр последней фракции, т.е. частиц, вышедших из секции m-1. Величины h1, h2, …, hm-1 представляют собой доли частиц осажденных в секциях 1, 2, …, m-1, соответственно, и hm - доля частиц, вышедших из секции m-1. Данные величины связаны с проскоками следующим образом h1=1-g1, h2=g1-g2, h3=g2-g3, …, hm-1=gm-2-gm-1, hm=gm-1. Таким образом, найдя функции ϕi(D), мы получим общий спектр размеров.
Число сеток в секции монотонно увеличивается с ростом номера секции. Поэтому при прохождении аэрозольного потока через батарею в начальных секциях осаждаются преимущественно частицы малого размера, в последующих секциях оседают все более крупные частицы. Поэтому средний диаметр частиц, описываемых функциями ϕi(D), монотонно возрастает с увеличением номера i. Для того, чтобы найти решение ƒ(D) в виде (4) мы аппроксимируем каждую функцию ϕi(D) логнормальным распределением
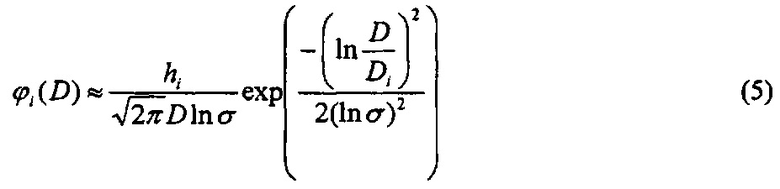
где Di - средний геометрический диаметр и σ - стандартное геометрическое отклонение. В нашем случае удобно рассматривать функции ϕi с величиной σ=1.35. Данное значение стандартного геометрического отклонения приводит к тому, что, с одной стороны, функции ϕi(D) достаточно узкие и их суперпозиция позволяет описать любую реальную функцию распределения любого аэрозоля естественного или антропогенного происхождения, а с другой стороны, функции ϕi(D) достаточно широкие для того, чтобы получить гладкий конечный спектр для ограниченного числа секций диффузионной батареи. Таким образом, для того, чтобы найти решение ƒ(D) нужно только найти средние диаметры Di для фракций частиц, отсекаемых секциями диффузионной батареи. Аппроксимация исходной функции распределения частиц по размеру суммой логнормальных функций (уравнение (5)) является простым и ресурсонезатратным способом определения спектра размеров частиц. Полученный спектр хорошо воспроизводит структуру исходного распределения и позволяет точно определить средний размер частиц. Средние диаметры Di можно найти из проскоков, измеренных с помощью диффузионной батареи.
Способ определения средних диаметров Di осуществляется следующим образом. Эффективность осаждения μ на одиночном волокне связана с диаметром частиц аналитическими формулами в рамках теории веерных фильтров Кирша, Стечкиной, Фукса [42-45] (см. также фиг. 2), следовательно, величина μ может рассматриваться как мера размера частиц. Будет удобным для фракции частиц, осевших в i-й секции ДБ, ввести среднюю эффективность 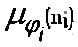 осаждения на одиночном волокне. Для частиц, выходящих из j-й секции, мы также можем ввести среднюю эффективность μj(N) осаждения на одиночном волокне в пакете из N сеток. Так, например, величина μk-1(nk) является средней эффективностью осаждения на одиночном волокне в k-й секции, заполненной nk сетками, для аэрозоля, вышедшего из секции k-1 (или для входного аэрозоля в случае k=1). Как видно из уравнения (3), эту величину можно выразить следующим образом
осаждения на одиночном волокне. Для частиц, выходящих из j-й секции, мы также можем ввести среднюю эффективность μj(N) осаждения на одиночном волокне в пакете из N сеток. Так, например, величина μk-1(nk) является средней эффективностью осаждения на одиночном волокне в k-й секции, заполненной nk сетками, для аэрозоля, вышедшего из секции k-1 (или для входного аэрозоля в случае k=1). Как видно из уравнения (3), эту величину можно выразить следующим образом
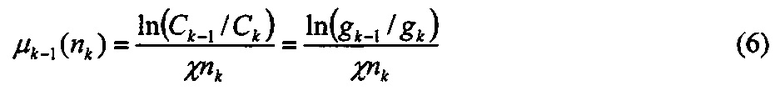
Для последовательности секций 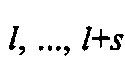 с общим числом сеток
с общим числом сеток 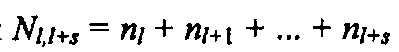 средняя эффективность осаждения на волокне для частиц, прошедших через предыдущие
средняя эффективность осаждения на волокне для частиц, прошедших через предыдущие 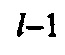 секций запишется в виде
секций запишется в виде
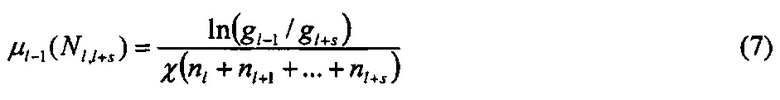
Определим теперь средний диаметр D1 для первой фракции, т.е. для частиц осевших в первой секции. Все частицы, составляющие исходный спектр могут быть разбиты на две группы: первая группа - прошедшие через первую секцию частицы, доля которых составляет g1, и вторая группа - осажденные на сетках первой секции частицы, доля которых

Эти две группы можно рассматривать как два независимых ансамбля частиц, каждый из которых описывается своей функцией распределения по размерам. Если мы выделим из всего исходного аэрозоля только первую группу частиц и пропустим их через первую секцию батареи, то доля этих частиц, прошедших через первую секцию составит величину g1exp(-χμ1(n1)n1). Если же мы выделим только вторую группу, то доля этих частиц, прошедших через первую секцию составит 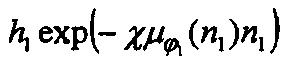 . Поэтому суммарно мы можем записать:
. Поэтому суммарно мы можем записать:
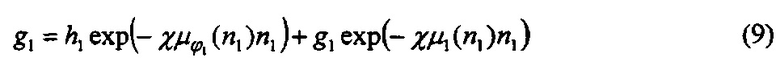
В нашем случае n1=n2=2, поэтому μ1(n1)=μ1(n2). Тогда, как следует из уравнения (6)
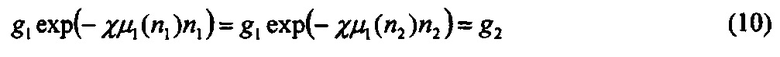
и мы получаем из уравнений (8-10)

Средняя эффективность осаждения на волокне 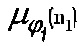 связана с эквивалентным диаметром частиц через уравнения теории веерных фильтров Кирша, Стечкиной, Фукса [42-45] (фиг. 2). Данный эквивалентный диаметр примерно равен искомому среднему геометрическому диаметру D1. Таким образом, подставляя
связана с эквивалентным диаметром частиц через уравнения теории веерных фильтров Кирша, Стечкиной, Фукса [42-45] (фиг. 2). Данный эквивалентный диаметр примерно равен искомому среднему геометрическому диаметру D1. Таким образом, подставляя 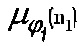 из уравнения (11) в уравнения теории веерных фильтров и решая их численно, или графически, подставляя значения
из уравнения (11) в уравнения теории веерных фильтров и решая их численно, или графически, подставляя значения 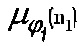 вместо μ на фиг. 2, получаем D1.
вместо μ на фиг. 2, получаем D1.
В общем случае, для 1<i<m-1 для аэрозоля, проходящего через две смежные секции i и i+1 можно записать выражение, аналогичное уравнению (9):
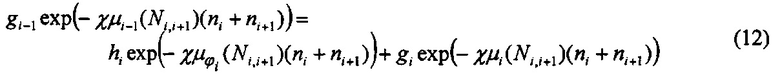
Как следует из уравнения (3),
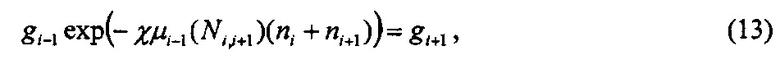
и мы получаем из уравнений (12, 13)
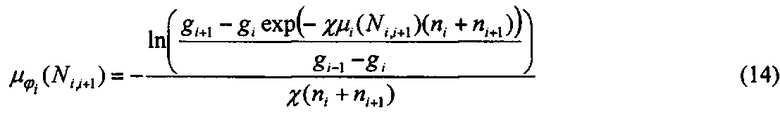
Величину μi(Ni,i+1) в правой части уравнения (14) нельзя напрямую определить из измеренных проскоков диффузионной батареи. Однако учитывая тот факт, что μi(N) является монотонной функцией N, можно найти приблизительное значение μi(Ni,i+1) c помощью простой интерполяции. Другими словами, для аэрозоля, выходящего из i-й секции, эквивалентная эффективность μi(Ni,i+1) осаждения на одиночном волокне в пакете, содержащем ni+ni+1 сеток, можно оценить, как среднее арифметическое эффективностей осаждения на волокне в пакетах из ni+1 и (ni+1 + ni+2) сеток. Тогда для 1<i<m-2 имеем:
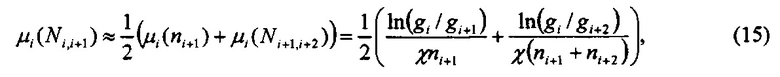
Для i=m-1 с хорошей точностью можно считать, что
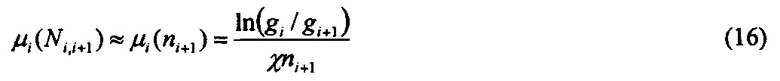
Подставляя уравнения (15, 16) в (14), и, далее, используя однозначное соответствие между эффективностью осаждения на волокне и диаметром частиц (фиг. 2) получаем из величины 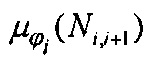 (уравнение (14)) в рамках теории веерных фильтров средний диаметр Di.
(уравнение (14)) в рамках теории веерных фильтров средний диаметр Di.
Для i=m величина 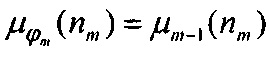 определяется выражением
определяется выражением

что позволяет получить Dm. Таким образом, зная средние диаметры Di, получаем функцию распределения по диаметрам ƒ(D) с помощью уравнений (4) и (5).
Для частиц диаметром D<200 нм осаждение на сетки обусловлено только диффузионным механизмом. Для диффузии в воздухе при температуре 293 K и атмосферном давлении средние диаметры Di можно рассчитать из экспериментальных проскоков диффузионной батареи по формулам:
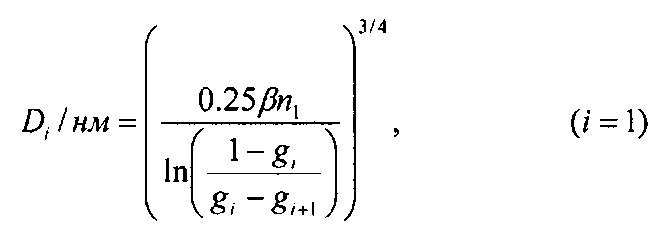
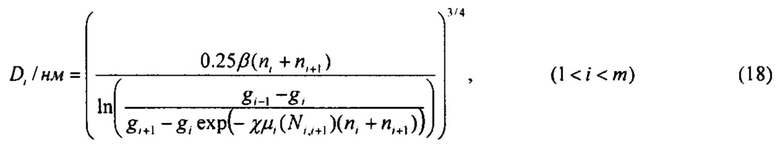
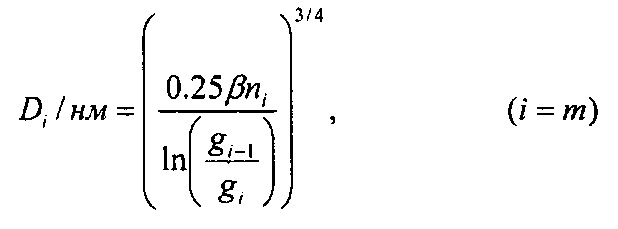
где 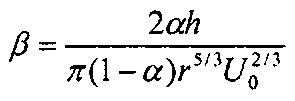 и μi(Ni,i+1) рассчитывается по формулам (15, 16).
и μi(Ni,i+1) рассчитывается по формулам (15, 16).
Для демонстрации точности формул (11, 14, 17) было проведено сравнение функции распределения по диаметрам, измеренной с помощью диффузионной батареи со спектрами размеров, измеренными другими физическими методами. Генерация аэрозоля для измерений осуществлялась с помощью термоконденсационного генератора. Суть термоконденсационного метода заключалась в нагреве исходной субстанции (материнской фазы) в потоке фильтрованного воздуха. В результате поток насыщался паром материнского вещества. Далее поток с насыщенным паром подавался в зону охлаждения, где пар становился пересыщенным. В результате осуществлялось аэрозолеобразование за счет гомогенной нуклеации. Анализ размеров частиц для сравнения с измерениями диффузионной батареи осуществлялся с помощью просвечивающего электронного микроскопа (ПЭМ) JEM-100SX или метода седиментации в гравитационном поле [47, 48].
На фиг. 3 проведено сравнение спектров размеров частиц Ag, CsCl, NaCl и дибутилфталата, полученных с помощью диффузионной батареи (сплошная линия) и методами ПЭМ/седиментации (гистограммы). Средние арифметические диаметры, полученные различными методами, приведены в таблице 1.
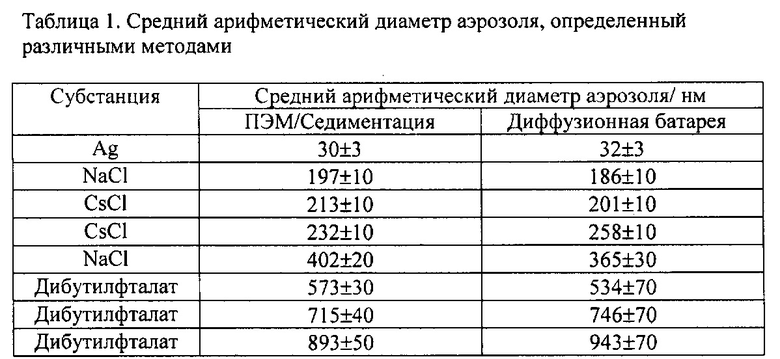
Как видно из таблицы средние диаметры, полученные с помощью диффузионной батареи в пределах экспериментальной погрешности совпадают с величинами, полученными другими физическими методами, что подтверждает справедливость разработанного метода определения спектра размеров с помощью измерения спектра фракций.
Источники информации:
1. Межгосударственный стандарт. Охрана природы. Атмосфера. Правила контроля качества воздуха населенных пунктов, ГОСТ 17.2.3.01-86, Москва, Стандартинформ, 2005.
2. Handbook of Air Pollution Analysis, Edited by Roy M. Harrison and Roger Perry, CHAPMAN and HALL, New York, 1986.
3. S. Manzoor and U. Kulshrestha, Atmospheric Aerosols: Air Quality and Climate Change Perspectives, Current World Environment, 2015, 10(3), 738-746
4. S. Fuzzi, U. Baltensperger, K. Carslaw, S. Decesari, H. Denier van der Gon, M.C. Facchini, D. Fowler, I. Koren, B. Langford, U. Lohmann, E. Nemitz, S. Pandis, I. Riipinen, Y. Rudich, M. Schaap, J.G. Slowik, D.V. Spracklen, E. Vignati, M. Wild, M. Williams, and S. Gilardoni, Particulate matter, air quality and climate: lessons learned and future needs, Atmos. Chem. Phys., 2015, 15, 8217-8299.
5. Controlled Pulmonary Drug Delivery, H. D.C. Smyth and A.J. Hickey (Editors), Springer, New York, 2011.
6. Pulmonary Drug Delivery. Advances and Challenges, A. Nokhodchi and G.P. Martin (Editors), Wiley, London, 2015.
7. G. Biskos, V. Vons, C. U. Y. and A. Schmidt-Ott, Generation and Sizing of Particles for Aerosol-Based Nanotechnology, KONA Powder and Particle Journal, 2008, No. 28, 13-35.
8. J.C. Volkwein, A.D. Maynard, M. Harper, Workplace aerosol measurement, in book: AEROSOL MEASUREMENT. Principles, Techniques, and Applications, P. Kulkarni, P.A. Baron, K. Willeke (Editors), Willey, New Jersey, 2011, 571-590.
9. ГН 2.2.5.1313-03 "Предельно допустимые концентрации (ПДК) вредных веществ в воздухе рабочей зоны".
10. ГН 1.2.2633-10 "Гигиенические нормативы содержания приоритетных наноматериалов в объектах окружающей среды".
11. S.S. Amaral, J.A. de Carvalho, М. А. М. Costa, С. Pinheiro, An Overview of Particulate Matter Measurement Instruments, Atmosphere 2015, 6, 1327-1345.
12. W.C. Hinds, Aerosol Technology: Properties, Behavior, and Measurement of Airborne Particles, John Wiley & Sons, New-York, 1999.
13. J.A. Last, P. Russell, P.F. Nealey, and C.J. Murphy, The Applications of Atomic Force Microscopy to Vision Science, Investigative Ophthalmology & Visual Science, 2010, 51, 6083-6094.
14. J.P. Mitchell, and M.W. Nagel, Cascade Impactors for the Size Characterization of Aerosols from Medical Inhalers: Their Uses and Limitations, Journal of Aerosol Medicine, 2003, 16, 341-377
15. J.S. Kang, K.S. Lee, K.H. Lee, H.J. Sung & S.S. Kim, Characterization of a Microscale Cascade Impactor, Aerosol Science and Technology, 2012, 46: 966-972.
16. Aerosol Measurement. Principles, Techniques, and Applications, P. Kulkarni, P.A. Baron, K. Willeke (Editors), Willey, New Jersey, 2011.
17. P.H. McMurry, A review of atmospheric aerosol measurements, Atmospheric Environment, 2000, 34 1959-1999.
18. P. Intra and N. Tippayawong, An overview of differential mobility analyzers for size classification of nanometer-sized aerosol particles, Songklanakarin J. Sci. Technol., 2008, 30 (2), 243-256.
19. S. Dubtsov, T. Ovchinnikova, S. Valiulin, X. Chen, H.E. Manninen, P.P. Aalto, T. Petaja, Laboratory verification of Aerosol Diffusion Spectrometer and the application to ambient measurements of new particle formation, Journal of Aerosol Science, 2017,105, 10-23.
20. A.A. Onischuk, S.V. Vosel, О.V. Borovkova, A.M. Baklanov, V.V. Karasev, and S. di Stasio, Experimental study of homogeneous nucleation from the bismuth supersaturated vapor: Evaluation of the surface tension of critical nucleus, The Journal of Chemical Physics 2012, 136, 224506 (1-18)
21. A.A. Onischuk, S.V. Valiulin, S.V. Vosel, V.V. Karasev, V.D. Zelik, A.M. Baklanov, Surface tension of sulfur nanoparticles as determined from homogeneous nucleation experiments, Journal of Aerosol Science 2016, 97 1-21.
22. A.A. Onischuk, T.G. Tolstikova, S.V.  , A.M. Baklanov, S.V. Valiulin, M.V. Khvostov, I.V. Sorokina, G.G. Dultseva, N.A. Zhukova Ibuprofen, indomethacin and diclofenac sodium nanoaerosol: Generation, inhalation delivery and biological effects in mice and rats, Journal of Aerosol Science 2016, 100 164-177.
, A.M. Baklanov, S.V. Valiulin, M.V. Khvostov, I.V. Sorokina, G.G. Dultseva, N.A. Zhukova Ibuprofen, indomethacin and diclofenac sodium nanoaerosol: Generation, inhalation delivery and biological effects in mice and rats, Journal of Aerosol Science 2016, 100 164-177.
23. D.J.H. Vosburgh, T. Klein, M. Sheehan, T.R. Anthony and Т. M. Peters, Design and Evaluation of a Personal Diffusion Battery, 2013, 47:4, 435-443
24. B. Gorbunov, N.D. Priest, R.B. Muir, P.R. Jackson and H. Gnewuch, A Novel Size-Selective Airborne Particle Size Fractionating Instrument for Health Risk Evaluation, Ann. Occup. Hyg., 2009, 53(3) 225-237.
25. S. Cheng and H.C. Yeh, Theory of a screen-type diffusion battery, J. Aerosol Sci. 1980, 11, 313-320.
26. Y.S. Cheng, H.C. Yeh, K.J. Brinsko, Use of Wire Screens as a Fan Model Filter, Aerosol Science and Technology, 1985, 4:2, 165-174.
27. S. Twomey, Comparison of Constrained Linear Inversion and an Iterative Nonlinear Algorithm Applied to the Indirect Estimation of Particle Size Distributions, Journal of Computational Physics 1975, 18, 188-200.
28. F. Ferri, A. Bassini, and E. Paganini, Modified version of the Chahine algorithm to invert spectral extinction data for particle sizing, APPLIED OPTICS, 1995, 34, No. 25, 5829-5839.
29. A. Reineking and J. Porstendorfer, High-volume screen diffusion batteries and α-spectroscopy for measurement of the radon daughter activity size distributions in the environment, J. Aerosol Sci., 1986, 17, 873-879.
30 Y.S. Bashurova, V. Dreiling, Т.V. Hodger, R. Jaenicke, K.P. Koutsenogii, P.K. Koutsenogii, M. Kraemer, V.I. Makarov, V.A. Obolkin, Y.L. Potjomkin and A.Y. Pusep, Measurements of Atmospheric Condensation Nuclei Size Distributions in Siberia. J. Aerosol Sci., 1992, 23, 191-199.
31 Y. Wang and Ch. Yangm, Regularizing active set method for retrieval of the atmospheric aerosol particle size distribution function, J. Opt. Soc. Am. A, 2008, 25, 348-356.
32. A. Voutilainen, V. Kolehmainen, F. Stratmann, and J.P. Kaipio, Computational Methods for the Estimation of the Aerosol Size Distributions, in Book: Mathematical Modeling. Problems, Methods, Applications, Edited by L.A. Uvarova and A.V. Latyshev, Springer Science+Business Media, Lle, 2001, New York, Page 219-230.
33. E.F. Maher, N.M. Laird, EM Algorithm Reconstruction Of Particle Size Distributions From Diffusion Battery Data, J. Aerosol Sci., 1985, Vol. 16, No. 6, pp. 557-570.
34. P. Paatero, U. Tapper, P. Aalto and M. Kulmala, Matrix Factorization Methods for Analysing Diffusion Battery Data, J. Aerosol Sci., 1991, Vol. 22, Suppl. 1. pp. S273-S276.
35. S. Eremenko and A. Ankilov, Conversion of the diffusion battery data to particle size distribution: Multiple Solutions Averaging algorithm (MSA), J. Aerosol Sci., (1995) Vol. 26. Suppl 1, 749-750.
36. Y. Gulak, E. Jayjock, F. Muzzio, A. Bauer & P. McGlynn, Inversion of Andersen Cascade Impactor Data using the Maximum Entropy Method, Aerosol Science and Technology, 2010, 44:1,29-37.
37. E. Yee, On the interpretation of diffusion battery data, J. Aerosol Sci., 1989, 20, 797-811.
38. Ankilov, A., Baklanov, A., Colhoun, M., Enderle, K.-H., Gras, J., Junlanov, Yu, Kaller, D., Lindner, A., Lushnikov, A., Mavliev, R., McGovern, F., Mirme, A.,  , Т.C, Podzimek, J., Preining, O., Reischl, G.P., Rudolf, R., Sem, G.J., Szymanski, W. W., Tamm, E., Vrtala, A.E., Wagner, P.E., Winklmayr, W., & Zagaynov, V. (2002). Intercomparison of number concentration measurements by various aerosol particle counters. Atmospheric Research, 62, 177-207.
, Т.C, Podzimek, J., Preining, O., Reischl, G.P., Rudolf, R., Sem, G.J., Szymanski, W. W., Tamm, E., Vrtala, A.E., Wagner, P.E., Winklmayr, W., & Zagaynov, V. (2002). Intercomparison of number concentration measurements by various aerosol particle counters. Atmospheric Research, 62, 177-207.
39. Ankilov, A., Baklanov, A., Mavliev, R., & Eremenko, S. (1991). Comparison of the Novosibirsk automated diffusion battery with the Vienna electro mobility spectrometer. Journal of Aerosol Science, 22, S325-S328.
40. V.S. Bashurova, K.P. Koutsenogii, A.Y. Pusep, N.V. Shokhirev (1991) Determination of atmospheric aerosol size distribution functions from screen diffusion battery data: mathematical aspects. J. Aerosol Sci. 22, 373-388.
41. Y.S. Cheng, J.A. Keating and G.M. Kanapilly, Theory and calibration of a screen-type diffusion battery, J Aerosol Sci., 1980, 11, 549-556.
42. Kirsch, A.A., Stechkina, I.B., & Fuchs, N.A. (1975). Studies on fibrous aerosol filters-experimental determination of fibrous filters efficiency in the range of maximum particle penetration. Colloid J. USSR, 1969, 31(2), 227-232.
43. Stechkina I.В., Kirsch A.A., Fuchs N.A., Studies on fibrous aerosol filters-IV Calculation of aerosol deposition in model filters in the range of maximum penetration, Ann. Occup. Hyg., 1969, 12, 1-8.
44. Kirsch, A.A., Stechkina, I.B. Inertial deposition of aerosol particles in model filters at low Reynolds numbers, Journal of Aerosol Science, 1977, 8, 301-307.
45. A.A. Kirsch & P.V. Chechuev, Diffusion Deposition of Aerosol in Fibrous Filters at Intermediate Peclet Numbers, Aerosol Science and Technology, 1985, 4:1, 11-16.
46. V.A. Kirsh D.A. Pripachkin, A.K. Budyka, Inertial deposition of aerosol particles from laminar flows in fibrous filters, Colloid Journal, 2010, 72(2), 211-215.
47. P.C. Reist, Aerosol science and technology, (McGraw-Hill Inc., USA, 1993).
48. Аэрозоли-пыли, дымы и туманы, Ред. П.Л. Фукс, Химия, Ленинград, 1972.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ИЗМЕРЕНИЯ СПЕКТРА РАЗМЕРОВ ЯДЕР КОНДЕНСАЦИИ АЭРОЗОЛЬНЫХ ЧАСТИЦ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2006 |
|
RU2340885C2 |
| Способ измерения спектра гидрофобных аэрозольных частиц и устройство для его осуществления | 1987 |
|
SU1603244A1 |
| Способ измерения среднего размера аэрозольных частиц и устройство для его осуществления | 1980 |
|
SU879405A1 |
| Устройство для измерения среднего размера аэрозольных частиц | 1985 |
|
SU1312449A2 |
| Способ измерения среднего размера аэрозольных частиц | 1979 |
|
SU894480A1 |
| Аэрозольный принтер с зарядкой и электростатической фокусировкой оптимизированных частиц | 2024 |
|
RU2840133C1 |
| Способ измерения концентрации и спектра размеров аэрозольных частиц | 1983 |
|
SU1173883A1 |
| Способ измерения среднего размера аэрозольных частиц | 1983 |
|
SU1100538A1 |
| УСТРОЙСТВО КОНТРОЛЯ ЗАРЯДА БИОЛОГИЧЕСКИ АКТИВНЫХ НАНОАЭРОЗОЛЕЙ | 2017 |
|
RU2656762C1 |
| Устройство для измерения среднего размера дисперсных частиц в аэрозолях | 1983 |
|
SU1111073A1 |
Изобретение относится к исследованию дисперсных характеристик аэрозолей различной природы и может быть использовано в метеорологии, в нанопроизводстве, для контроля нанобезопасности на рабочих местах, для определения ингаляционной дозы при применении аэрозольных форм доставки лекарственных средств. Заявлено устройство измерения спектра размеров аэрозольных частиц, которое включает диффузионную батарею, состоящую из ряда последовательных секций, заполненных сетками, состоящими, например, из металлических или полимерных волокон, на которые осаждаются аэрозольные частицы при прохождении аэрозольного потока через батарею, конденсационный укрупнитель частиц, оптический счетчик частиц и персональный компьютер для управления устройством в целом, накапливания и обработки полученных данных. Согласно изобретению количество установленных сеток в каждой секции диффузионной батареи, за исключением первой, равно суммарному числу сеток во всех предыдущих секциях, расположенных выше по потоку, что позволяет осуществить расчет среднего диаметра частиц, осажденных в каждой секции батареи, по приведенной в описании математической формуле. Способ измерения спектра размеров аэрозольных частиц реализован путем последовательного пропускания аэрозольного потока через секции диффузионной батареи, заполненные сетками, затем через конденсационный укрупнитель частиц, измерения аэрозольной концентрации оптическим счетчиком и компьютерной обработки данных. Согласно способу, используя измеренные вероятности прохождения частиц через секции батареи, определяют среднюю эффективность осаждения на отдельных волокнах сетки для фракций частиц, то есть для частиц, осевших в секциях диффузионной батареи, по приведенной в описании формуле. Далее из величины эффективности осаждения определяют средний диаметр частиц каждой фракции по формулам веерной модели фильтров Кирша-Стечкиной-Фукса, спектр частиц каждой фракции аппроксимируют любой функцией мономодального распределения, включая логнормальное распределение, Гауссово распределение, далее спектр исходного аэрозоля определяется как сумма спектров фракций. Технический результат - упрощение процесса измерения спектра размеров аэрозольных частиц и повышение точности, 2 н.п. ф-лы, 3 ил., 1 табл.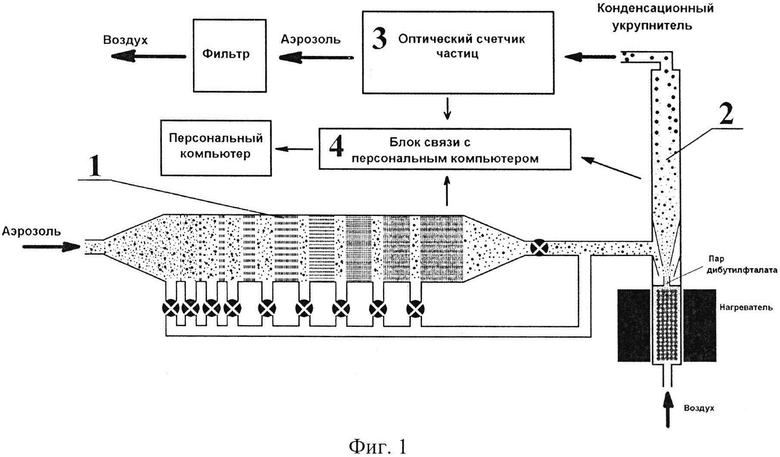
1. Устройство измерения спектра размеров аэрозольных частиц, включающее диффузионную батарею (ДБ), состоящую из ряда последовательных секций, заполненных сетками, состоящими, например, из металлических или полимерных волокон, на которые осаждаются аэрозольные частицы при прохождении аэрозольного потока через батарею, конденсационный укрупнитель частиц, оптический счетчик частиц и персональный компьютер для управления устройством в целом, накапливания и обработки полученных данных, отличающееся тем, что количество установленных сеток в каждой секции диффузионной батареи, за исключением первой, равно суммарному числу сеток во всех предыдущих секциях, расположенных выше по потоку, что позволяет осуществить расчет среднего диаметра частиц Di, осажденных в i-й секции ДБ, по математической формуле
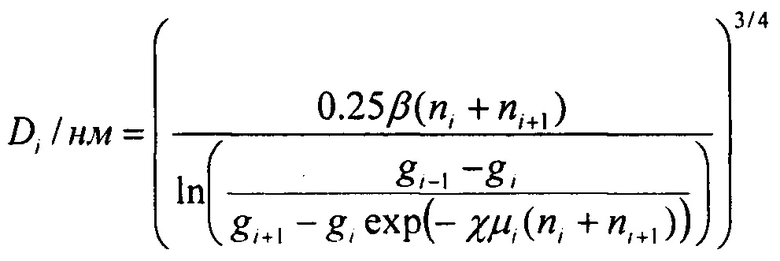 ,
,
где i - последовательный номер секции, ni и ni+1 - количества сеток в секциях с номерами i и i+1 соответственно, gi - доля частиц, прошедших через i-ю секцию без осаждения, μi - эффективность осаждения на одиночном волокне в пакете, содержащем ni+ni+1 сеток, для частиц, содержащихся в потоке после i-й секции, 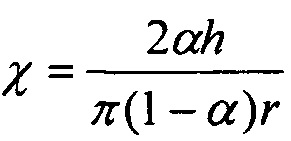 , h - толщина сетки, r - радиус волокна сетки, α - отношение объема, занимаемого волокнами, к полному объему сетки,
, h - толщина сетки, r - радиус волокна сетки, α - отношение объема, занимаемого волокнами, к полному объему сетки, 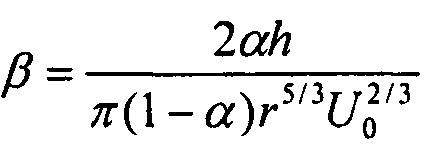 , U0 - линейная скорость аэрозольного потока.
, U0 - линейная скорость аэрозольного потока.
2. Способ измерения спектра размеров аэрозольных частиц путем последовательного пропускания аэрозольного потока через секции диффузионной батареи (ДБ), заполненные сетками, затем через конденсационный укрупнитель частиц, измерения аэрозольной концентрации оптическим счетчиком и компьютерной обработки данных, отличающийся тем, что определяют эффективность осаждения на отдельных волокнах сетки для фракций частиц, то есть для частиц, осевших в секциях диффузионной батареи, по формуле
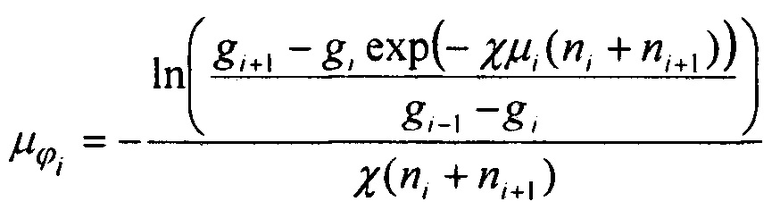
где i - последовательный номер секции ДБ или фракции частиц, 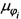 - эффективность осаждения i-й фракции на отдельном волокне i-й секции, ni и ni+1 - количества сеток в секциях с номерами i и i+1 соответственно, gi - доля частиц, прошедших через i-ю секцию, μi - эффективность осаждения на одиночном волокне в пакете, содержащем ni+ni+1 сеток, для частиц, содержащихся в потоке после i-й секции,
- эффективность осаждения i-й фракции на отдельном волокне i-й секции, ni и ni+1 - количества сеток в секциях с номерами i и i+1 соответственно, gi - доля частиц, прошедших через i-ю секцию, μi - эффективность осаждения на одиночном волокне в пакете, содержащем ni+ni+1 сеток, для частиц, содержащихся в потоке после i-й секции, 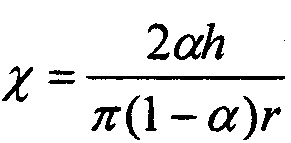 , h - толщина сетки, r - радиус волокна сетки, α - отношение объема, занимаемого волокнами, к полному объему сетки,
, h - толщина сетки, r - радиус волокна сетки, α - отношение объема, занимаемого волокнами, к полному объему сетки, 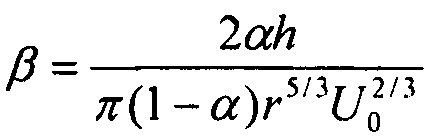 , U0 - линейная скорость аэрозольного потока, далее из величины
, U0 - линейная скорость аэрозольного потока, далее из величины 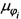 определяют средний диаметр Di частиц i-й фракции по формулам веерной модели фильтров Кирша-Стечкиной-Фукса, долю hi частиц i-й фракции определяют по формуле hi=gi-gi+1, спектр частиц i-й фракции аппроксимируют любой функцией мономодального распределения, включая логнормальное распределение, Гауссово распределение, причем Di и hi являются параметрами мономодального распределения, далее спектр исходного аэрозоля определяется как сумма спектров фракций.
определяют средний диаметр Di частиц i-й фракции по формулам веерной модели фильтров Кирша-Стечкиной-Фукса, долю hi частиц i-й фракции определяют по формуле hi=gi-gi+1, спектр частиц i-й фракции аппроксимируют любой функцией мономодального распределения, включая логнормальное распределение, Гауссово распределение, причем Di и hi являются параметрами мономодального распределения, далее спектр исходного аэрозоля определяется как сумма спектров фракций.
| СПОСОБ ИЗМЕРЕНИЯ СПЕКТРА РАЗМЕРОВ ЯДЕР КОНДЕНСАЦИИ АЭРОЗОЛЬНЫХ ЧАСТИЦ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2006 |
|
RU2340885C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СПЕКТРА РАЗМЕРОВ ВЗВЕШЕННЫХ НАНОЧАСТИЦ | 2014 |
|
RU2558281C1 |
| Топка с несколькими решетками для твердого топлива | 1918 |
|
SU8A1 |
| Определение размеров наночастиц методом диффузионной спектрометрии | |||
| Очаг для массовой варки пищи, выпечки хлеба и кипячения воды | 1921 |
|
SU4A1 |
| Романов П | |||
| С., Пантелова Х.М, "Возможности применения диффузионной аэрозольной спектрометрии для определения среднего размера частиц нанодисперсных порошков", Территория науки, номер 2, 2016, С.47-52 | |||
| US 4463595 A, 07.08.1984 | |||
| УСТРОЙСТВО ОПРЕДЕЛЕНИЯ СПЕКТРА РАЗМЕРОВ ВЗВЕШЕННЫХ НАНОЧАСТИЦ | 2014 |
|
RU2555353C1 |
Авторы
Даты
2019-02-25—Публикация
2017-07-07—Подача