Способ диагностики недвоичных блоковых кодов относится к технике связи и может быть использован для определения неизвестной структуры кодера недвоичных блоковых систематических кодов, включая коды Рида-Соломона, и несистематических кодов на основе анализа принимаемой кодовой последовательности.
Известны различные способы блокового кодирования и декодирования, используемые для исправления возникающих при передаче ошибок, и описанные, например, в книгах: Ипатов В.П., Орлов В.К., Самойлов И.М. Системы мобильной связи - М.: Горячая линия-Телеком, 2003; Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение - М: Техносфера, 2006; Скляр Б. Цифровая связь. Теоретические основы и практическое применение - М: Изд. дом «Вильяме», 2003.
В них описываются операции получения кодового блока из входной информационной последовательности символов путем осуществления операций свертки определенного количества информационных символов с полиномиальными генераторами (порождающими полиномами) и последовательной передачи подобных кодовых блоков. При этом для реализации несистематического кода группа последовательно идущих исходных информационных символов умножается на порождающий полином, представленный в виде вектора с двоичными элементами. Для реализации систематического кода исходная группа информационных символов сдвигается на определенное количество двоичных разрядов. Далее результат сдвига делится на порождающий полином и частное от деления складывается по модулю 2 со сдвинутой группой символов. После приема последовательность раскодируется одними из возможных методов, при декодировании весь принятый кодовый блок делится на порождающий полином, и результат деления используется для локализации и исправления ошибок.
Недостатком описанного способа является необходимость знания на приемной стороне правильного вида используемого порождающего полинома. Если он неизвестен, например, утерян или поврежден, то декодирование с исправлением ошибок невозможно и исправляющая способность кода не может быть реализована. Это приводит к снижению помехоустойчивости передачи информации.
Наиболее близким к заявляемому является способ по патенту РФ №2631142 на «Способ диагностики циклических кодов» по заявке №2016107245, приоритет от 29.02.2016, зарегистрирован в государственном реестре изобретений 19.09.2017, МПК H04L 17/00, авторы Корнеева Н.Н., Полушин П.А., Никитин О.Р.
Способ-прототип предназначен для диагностики двоичных блоковых кодов. В способе-прототипе производится запоминание принятых N кодовых блоков, далее извлечение пар кодовых блоков, попарное сравнение и сложение блоков, запоминание вида полиномов и выбор максимального числа результатов, при этом операция попарного сравнения и сложения блоков состоит из последовательных операций сравнения полиномов, поразрядного сдвига полинома, сравнения результата со сдвинутым полиномом и поразрядного сложения по модулю 2.
С помощью операций способа определяется общий полином для каждой пары анализируемых кодовых блоков и запоминается его вид. После рассмотрения всех кодовых блоков в качестве результата диагностики выбирается полином, запомненный в памяти максимальное число раз.
Основным недостатком прототипа является то, что в недвоичных кодах каждый символ представлен не единственным битом, а нескольким битами (m битами), и описывается не двоичным числом, а специальными коэффициентами - объектами конечной алгебры полей Галуа (см., например, упомянутые книги Б. Скляра или Р. Морелоса-Сарагосы). К этим коэффициентам неприменимы правила обычной двоичной Булевой алгебры, а операции сложения, умножения и т.д., хотя и базируются на логической обработке групп двоичных бит, составляющих каждый символ, но должны выполняться на основе специальных правил, вырабатываемых с использованием т.наз. примитивных полиномов. Таким образом, все операции прототипа, выполняемые на основе Булевой алгебры, непригодны для обработки недвоичных символов.
Кроме этого, когда для операции попарного сложения по модулю 2 выровнены старшие степени двоичных полиномов, то в способе-прототипе всегда старшие члены полиномов вычитаются и пропадают, и максимальная степень полиномов уменьшается. В случае недвоичных полиномов коэффициенты при старшем полиноме могут иметь не два допустимых значения (0 и 1), а гораздо больше возможных значений. Поэтому в общем случае непосредственное вычитание полиномов не может уменьшить максимальной степени полинома, и принцип, реализуемый в способе-прототипе, для недвоичных кодов реализован быть не может.
Требуемый уровень помехоустойчивости передачи информации с использованием исправляющих способностей декодеров в отсутствие информации о кодере не обеспечивается, поскольку работоспособность декодеров нарушается.
Задачей предлагаемого способа диагностики недвоичных блоковых кодов является определение структуры используемого недвоичного кодера на основе анализа принимаемых кодовых блоков для обеспечения работоспособности декодеров и повышения помехоустойчивости передачи информации.
Поставленная задача решается тем, что в способ диагностики недвоичных блоковых кодов, включающий в себя запоминание N кодовых блоков, извлечение пар блоков, попарное сравнение и сложение блоков, поразрядный сдвиг полинома, запоминание вида полинома и выбор максимального числа результатов, вводят сравнение степеней полиномов, деление на коэффициенты при старшей степени полинома, определение равенства полиномов и сложение полиномов в поле Галуа, при этом сначала запоминают N кодовых блоков, затем извлекают пары кодовых блоков, после этого кодовые блоки попарно сравнивают и складывают, далее запоминают вид полученных в результате сравнения и сложения полиномов, после чего выбирают максимальное число полученных одинаковых результатов сравнения и сложения, причем при попарном сравнении и сложении кодовых блоков сравнивают максимальные степени членов выбранных полиномов, описывающих сравниваемые кодовые блоки, затем поразрядно сдвигают меньший полином, после чего делят все коэффициенты каждого полинома на коэффициент при его члене максимальной степени, далее сравнивают больший полином со сдвинутым меньшим полиномом, в случае их равенства вид меньшего полинома до сдвига запоминают, в случае их неравенства складывают в поле Галуа коэффициенты при членах с одинаковыми степенями полиномов и возвращаются к сравнению меньшего полинома и полученного результата сложения в поле Галуа.
На чертежах представлены: на фиг. 1 - схематическая последовательность операций заявляемого способа; на фиг. 2 - пример структурной схемы устройства для реализации предлагаемого способа; на фиг. 3 - пример реализации регистров для запоминания символов кодового слова.
На фиг. 1 обозначены: 1 - запоминание N кодовых блоков; 2 - извлечение пар блоков; 3 - запоминание вида полиномов; 4 - выбор максимального числа результатов; 5 - сравнение степеней полиномов; 6 - поразрядный сдвиг полинома; 7 - деление на коэффициенты при старшей степени полинома; 8 - определение равенства полиномов; 9 - сложение полиномов в поле Галуа; 10 - попарное сложение и сравнение блоков.
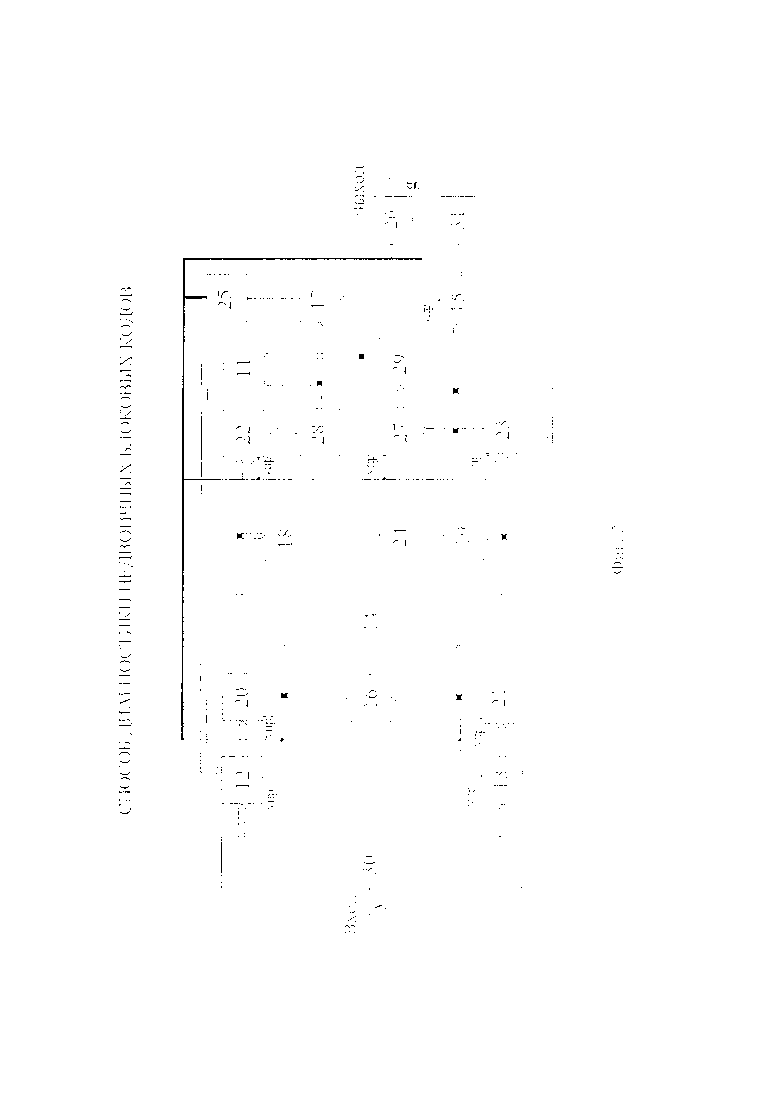
На фиг. 2 представлены: блок сложения в поле Галуа 11; первый 12, второй 13, третий 14 и четвертый 15 коммутаторы; первый 16 и второй 17 блоки сравнения; первый 18 и второй 19 определители максимальной степени полинома; первый 20, второй 21, третий 22 и четвертый 23 регистры; вычитатель 24; блок управления 25; блок выделения максимальной суммы 26; сдвиговый регистр 27, первый 28 и второй 29 делители; первый 30 и второй 31 блоки памяти.
На фиг. 3 представлены: регистр 32 для запоминания символов кодового слова; двоичные ячейки 33 для запоминания битов, составляющих символы кодового слова.
Операции предлагаемого способа осуществляются следующим образом. Во время операции 1 производится запоминание N пришедших кодовых блоков. При этом имеется возможность далее извлекать из памяти любые из запомненных кодовых блоков. Далее попарно сравниваются различные два кодовых блока из запомненных. При количестве N блоков возможны N(N-1)/2 различных сочетаний пар разных блоков. Эти блоки извлекаются из памяти попарно операцией 2 (последовательность извлечения значения не играет) и далее обрабатываются общей операцией 10 попарного сравнения и сложения блоков.
Операция 10 попарного сложения и сравнения блоков состоит из нескольких операций. Как известно, каждый кодовый блок представляет собой последовательность из n символов, каждый символ состоит из m двоичных бит, где m - выбранное при кодировании целое число. Кодовый блок может быть описан в виде некоторого полинома, 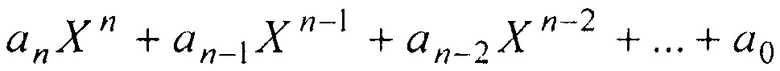 , где через X обозначается сдвиг по времени на длительность одного символа, через X2 сдвиг по времени на длительность двух символов, через X3 - трех символов, и т.д., при этом максимальная степень полинома на единицу меньше количества двоичных разрядов кодового блока. Коэффициенты ai при членах полинома различных степеней являются элементами поля Галуа, и действия над ними подчиняются правилам конечной алгебры (см., например, упомянутые книги Б. Скляра или Р. Морелоса-Сарагосы).
, где через X обозначается сдвиг по времени на длительность одного символа, через X2 сдвиг по времени на длительность двух символов, через X3 - трех символов, и т.д., при этом максимальная степень полинома на единицу меньше количества двоичных разрядов кодового блока. Коэффициенты ai при членах полинома различных степеней являются элементами поля Галуа, и действия над ними подчиняются правилам конечной алгебры (см., например, упомянутые книги Б. Скляра или Р. Морелоса-Сарагосы).
В операции 5 сравнения полиномов сравниваются максимальные степени при старших членах полиномов, описывающих два выбранных кодовых блока. При этом определяется, какой из них больше другого (максимальная степень которого блока больше) и на сколько разрядов. Сравниваемые два кодовых слова y1 и y2 можно описать в виде полиномов:

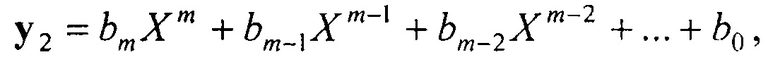
где n и m - номера максимальных разрядов в первом и втором сравниваемых кодовых словах, содержащих единицу в двоичной записи кодового слова, считая от первого разряда; X обозначает задержку на один такт (на длительность одного символа); коэффициенты ai и bi являются элементами поля Галуа и могут принимать значения в интервале от нуля до 2m-1.
Операцией 5 определяются степени n и m. Пусть больше окажется первый полином y1. В операции 6 поразрядного сдвига меньшего полинома производится сдвиг полинома y2 вверх на определенное количество разрядов. Количество разрядов, на которое производится сдвиг, равно разности их максимальных степеней, т.е. равно n-m. В результате сдвига получается полином Xn-m y2. Таким образом, если m>m, то такой сдвиг производится, если n=m, (хотя при этом полиномы различаются), то они не сдвигаются. После такого сдвига второй полином приобретает вид 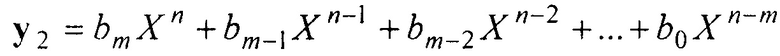 .
.
В операции 7 все коэффициенты при членах обоих полиномов меньших степеней делятся на коэффициенты при их старших степенях, т.е. у полинома y1 на an, у полинома y2 на bm. После этого старшие члены обоих полиномов становятся одинаковыми и равными Xn.
В следующей операции 8 определяется, не стали ли полиномы полностью равны после предыдущей операции 7. Если эти полиномы становятся точно равны между собой (равны все коэффициенты при членах всех степеней), т.е. одинаковы, то цикл обработки данной пары кодовых блоков прекращается, и на операцию 3 подается меньший полином до его сдвига. Если они остаются не равными один другому, то операцией 9 производится поразрядное сложение полиномов в поле Галуа по правилам конечной алгебры (сложение коэффициентов при членах с одинаковыми степенями). Согласно правилам конечной алгебры сложение полиномов равнозначно вычитанию коэффициентов при членах одинаковых степеней. Таким образом, после операции 9 старшие члены обоих полиномов исчезают, и результат сложения всегда имеет меньшую степень, чем складываемые полиномы.
После этого обработка возвращается к операции 5, где уже сравниваются другие полиномы. Один из них полином - результат произведенного операцией 9 сложения в поле Галуа (вычитания старших членов полиномов). Другой сравниваемый полином - меньший полином до его сдвига. Далее вновь повторяются описанные последующие операции. Таким образом, для выбранной пары исходных кодовых блоков в общем случае неоднократно повторяются операции 5-6-7-8-9. Вид анализируемых полиномов при каждом повторении изменяется. При каждом повторении обязательно уменьшаются сами полиномы, уменьшается и степень максимального полинома. Это происходит до тех пор, пока операция 8 не зафиксирует равенство анализируемых полиномов. После этого полученный до сдвига вид меньшего полинома запоминается операцией 3, и операция 10 в целом переходит к анализу следующей пары кодовых блоков.
После каждого завершения в целом операции 10 (попарное сравнение и сложение блоков) в операции 3 (запоминание вида полиномов) производится запоминание результата операции 10. Если уже ранее при предыдущих выполнениях операции 10 был запомнен такой же результат (такой же полином), относящийся к другой паре сравниваемых кодовых блоков, то этот факт запоминается и увеличивает сумму, накопленную предыдущими результатами, относящимися к полиному этого полученного вида. Количество поступивших результатов каждого вида подсчитывается.
Операции 10 попарного сравнения и сложений блоков осуществляется над всеми различающимися N блоками, которые запомнены в операции 1.
Число таких попарных обработок равно N(N-1)/2. Когда все эти попарные обработки завершены, то в результате выполнения операции 3 запомненными оказываются все обнаруженные виды общих полиномов у всех сочетаний полиномов в парах. После завершения всех N(N-1)/2 сравнений операция 4 выбора максимального числа результатов определяет наиболее часто запомненные результаты, т.е. полиномов какого вида больше запомнено. (Если, например, каждый факт запоминания, производится в форме прибавления единицы к уже имеющейся сумме в ячейке памяти, относящейся к полиному данного вида, то фактически, эта операция определяет, какому полиному из запомненных процедурой 3, соответствует наибольшая запомненная в памяти сумма.) Этот полином представляет собой набор коэффициентов при членах полинома различных степеней, определяющий тот порождающий полином, который используется в передатчике для кодирования анализируемого сигнала. Он выводится далее, как конечный результат процедуры диагностики.
Блоки устройства на фиг. 2., как примера реализации предлагаемого способа, работают следующим образом. На первый блок памяти 30 поступают принятые кодовые блоки в форме последовательностей символов. В нем запоминается N различных кодовых блоков. (Последовательность запомненных блоков значения не имеет, это могут быть либо подряд следующие блоки, либо расположенные другим образом.)
Из этого блока памяти извлекаются пары различных блоков, один из этих блоков подается на вход первого коммутатора 12, другой блок подается на вход второго коммутатора 13. Последовательность извлечения из памяти пар блоков значения не имеет, текущие номера извлекаемых блоков задаются блоком управления 25. В блоке памяти 30 занесено N кодовых блоков, значит, осуществляя N(N-1)/2 циклов, имеется возможность анализировать N(N-1)/2 различных пар блоков. В каждом цикле производится одинаковый набор действий.
Цикл анализа очередной пары кодовых блоков состоит в следующем. В самом начале цикла первый 12 и второй 13 коммутаторы подключают первый и второй многоканальные выходы первого блока памяти 30 на многоканальные параллельные входы, соответственно, первого 20 и второго 21 регистров, где анализируемая в данный момент пара кодовых блоков записывается в форме последовательности символов, каждый из которых состоит из т бит.
В первом блоке сравнения 16 сравнивается степени при старшем члене полинома каждого кодового блока (старшие степени) записанных в первом 20 и втором 21 регистрах. Выходной сигнал этого первого блока сравнения управляет третьим коммутатором 14.
Если старшие степени полиномов кодовых блоков, записанные в регистрах 20 и 21, не равны между собой, то первый блок сравнения 16 с помощью третьего коммутатора 14 подает кодовый блок с большей старшей степенью ко входу первого определителя максимальной степени 18 и к параллельному входу третьего регистра 22, а кодовый блок с меньшей старшей степенью подается коммутатором 14 ко входу второго определителя максимальной степени 19 и к параллельному входу четвертого регистра 23. Поступившие на регистры сигналы записываются в эти регистры. Полином, записанный в четвертом регистре 23, также перезаписывается в сдвиговый регистр 27.
Если же окажется, что старшие степени записанных в регистрах 20 и 21 полиномов равны между собой, то с помощью третьего коммутатора 14 на вход первого определителя максимальной степени полинома 18 подается сигнал с выхода первого регистра 20, а на вход второго определителя максимальной степени полинома 19 подается сигнал с выхода второго регистра 21.
В определителях максимальной степени 18 и 19 определяются порядки полиномов, т.е. максимальные степени у X.
Далее в вычитателе 24 находится арифметическая разность их порядков (разность максимальных степеней полиномов), и на основе выходного сигнала вычитателя в сдвиговом регистре 27 производится сдвиг всего записанного в четвертом регистре 23 полинома в сторону увеличения степени на полученную величину этой арифметической разности. Таким образом, после этого сдвига, порядки (максимальные степени) полиномов, записанных в третьем регистре 22 и в сдвиговом регистре 27 становятся одинаковыми.
Далее в первом 28 делителе производится деление всех коэффициентов при членах первого полинома на коэффициент при старшей степени этого полинома, и во втором 29 делителе производится деление всех коэффициентов при членах второго полинома на коэффициент при старшей степени этого полинома. Эти полиномы подаются на второй блок сравнения 17 и на блок 11, где производится сложение коэффициентов при одинаковых степенях полиномов в поле Галуа по правилам конечной алгебры.
Во втором блоке сравнения 17 сравниваются полиномы, записанные в регистрах 22 и 28. Если они полностью равны между собой (т.е. одинаковы), то второй блок сравнения сообщает об этом блоку управления 25. После чего данный цикл заканчивается, блок управления открывает четвертый коммутатор 15 и сигнал с выхода четвертого регистра 23 подается на второй блок памяти 31. В этом втором блоке памяти каждому возможному виду полиномов соответствует своя ячейка памяти. Первоначально до начала процедуры диагностики все ячейки содержат нули. Когда в очередном цикле определен очередной полином, то в ячейку, ему соответствующую, прибавляется единица к той сумме, которая там уже была записана ранее.
Если второй блок сравнения 17 не зафиксировал равенства полиномов в третьем и четвертом регистрах, результат сложения в блоке 11 подается на другой вход первого коммутатора 12, а на другой вход второго коммутатора 13 подается полином, записанный в четвертом регистре 23. После этого на выходы обоих коммутаторов подключаются не сигналы с первого блока памяти 30, а вновь поступившие сигналы с их других входов. После этого вся последовательность действий повторяется. Работа коммутаторов, регистров и блоков памяти управляется блоком управления 25.
Когда перебраны все N(N-1)/2 сочетаний рассматриваемых кодовых блоков, во втором блоке памяти 31 в различные ячейки оказывается записанными разное количество единиц. После этого блок выделения максимальной суммы 26 определяет, в какой ячейке записано максимальное число. Полином, соответствующий этой ячейке, подается на выход, как конечный результат всей процедуры диагностики.
Регистр 32 на фиг. 3 состоит из n групп, в которых находятся последовательно расположенные m ячеек 33 для запоминания m бит, составляющих символ кодового слова. Регистры 20-23 допускают параллельный ввод и вывод информации по группам. Сдвиговый регистр 27 осуществляет сдвиг содержимого ячеек группами по m бит.
Рассмотрим операции предлагаемого способа подробнее. Как известно, (см. указанные выше книги) при несистематическом кодировании каждое i-тый кодовый блок может быть описан в виде произведения двух полиномов: yi(X)=mi(X)g(X), где g(X) - порождающий полином (полиномиальный генератор) используемого кодера, общий для всех кодовых слов; mi(Х) - часть i-го кодового слова, содержащая передаваемую в нем информацию. То есть, все кодовые блоки имеют как минимум один общий полином g(X). Максимальная степень полинома g(X) равна b. Степень полинома mj(X) зависит от передаваемой в данном блоке информации и может достигать максимальной величины, равной k.
При систематическом кодировании кодовый блок в кодере формируется по-другому. Для этого исходный двоичный информационный полином mi(Х) первоначально домножается на Xb, что соответствует сдвигу на b разрядов в сторону увеличения. В результате получается полином mi(Х)Xb с максимальной степенью, в общем случае равной n=k+b. Далее он делится на полиномиальный генератор g(X). Максимальная степень образующегося остатка ri(Х) равна b, т.е. равна количеству нулей в записи mi(X)Xb, начиная с первого разряда. После этого остаток ri(Х) складывается с полиномом, образуя передаваемый по каналу передачи кодовый блок yi(Х)=mi(Х)Xb+ri(Х). Таким образом, и в этом случае кодовый блок кратен полиному g(X), т.е. полиномиальный генератор является одним из множителей полинома yi(Х), и можно записать yi(X)=Mi(X)g(X). Именно этот факт используется в приемнике для вычисления синдромов ошибок и их исправления.
Если попарно сравнивать различные кодовые блоки, то хотя наборы множителей, на которые разлагаются их полиномы, и будут различаться, но множитель g(X) будет присутствовать во всех кодовых блоках. Естественно, иногда могут появляться одинаковые множители и в информационной части Mi(Х) разных кодовых слов.
Обозначим одинаковые множители в информационной части двух сравниваемых кодовых блоков через MC(Х), а различающиеся части через Md1(Х) и Md2(X). В другой паре кодовых слов часть MC(Х) будет в общем случае отличаться от общей части в первой паре, в третьей паре отличаться от первых двух, и т.д. Таким образом, если сравнивать достаточно большое количество пар, то, несмотря на то, что в каждой паре по отдельности кроме полинома g(X) могут быть общими и другие полиномы-множители, но во всей совокупности анализируемых кодовых блоков общим множителем будет только искомый порождающий полиномиальный генератор g(X).
В соответствии с этим операции на фиг. 1 производят следующие действия. В операции 1 запоминается N поступивших на приемник кодовых блоков. Количество N должно быть достаточно большим, например, значительно большим, чем общее число n символов в кодовом блоке.
Поскольку информационные части разных блоков в подавляющем большинстве случаев различаются, то и появление одинаковых множителей в информационной части также маловероятно, гораздо вероятнее, что общая часть будет состоять только из полиномиального генератора. Большое количество N необходимо, чтобы вероятность появления при анализе именно искомого порождающего полинома была значительно больше, чем других результатов анализа. При дальнейшем увеличении N эта вероятность увеличивается, что дает возможность уменьшить ошибку диагностики до требуемых уровней.
Появление ошибочных символов при передаче по каналу связи лишь приводит к появлению других результатов анализа и запоминанию других видов полиномов. Это негативное явление может быть ослаблено до приемлемого уровня увеличением N. Таким образом, операция 1 обеспечивает запоминание N кодовых слов и попарную их передачу для последующей обработки. Количество пар различающихся кодовых блоков при этом равно N(N-1)/2.
Операция 10 в целом производит сравнение и сложение подаваемых на нее кодовых блоков. Она состоит из нескольких последовательных операций. В операции 5 производится сравнение полиномов двух анализируемых кодовых блоков, и определяются максимальные степени полиномов обоих блоков. Пусть полином одного из кодовых блоков имеет вид  , а второй полином равен
, а второй полином равен 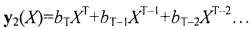 , где aS÷a0 и bS÷b0 - некоторые коэффициенты при членах полиномов, являющиеся элементами поля Галуа. Операцией 5 сравниваются величины старших степеней S и Т.
, где aS÷a0 и bS÷b0 - некоторые коэффициенты при членах полиномов, являющиеся элементами поля Галуа. Операцией 5 сравниваются величины старших степеней S и Т.
Предположим, оказалось, что S>T, т.е. полином y1 длиннее, чем полином y2. Тогда следующей операцией 6 поразрядного сдвига меньшего полинома производится домножение второго полинома на XS-T, т.е сдвиг в большую сторону на S-T степеней всех его членов. Если же второй полином больше первого, то тогда первый полином домножается на необходимую разностную величину, т.е. степени всех его членов увеличиваются на соответствующее разностное число. В том случае, если максимальные степени обоих полиномов равны, (т.е. S=T), то в операции 6 никакого сдвига степеней не производится. Таким образом, после операции 6 максимальные степени обоих полиномов станут совпадать.
Следующей операцией 7 производится деление всех коэффициентов первого полинома на величину aS и деление всех коэффициентов второго полинома на величину bT. Предположим, что S>T, т.е. старшая степень второго полинома была меньше. Тогда полиномы после деления приобретают вид: 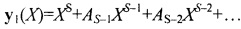 ,
, 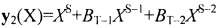 , где AS-1=aS-1/aS, AS-2=aS-2/AS, …, BS-1=bS-1/bS, BS-2=bS-2/bS и т.д. Коэффициенты при членах старших степеней становятся одинаковыми и равными единице.
, где AS-1=aS-1/aS, AS-2=aS-2/AS, …, BS-1=bS-1/bS, BS-2=bS-2/bS и т.д. Коэффициенты при членах старших степеней становятся одинаковыми и равными единице.
Далее в операции 8 определения равенства полиномов проверяется, не стали ли полностью равны y1(Х) и y2(Х), т.е. сравнивается величина большего полинома и результата сдвига меньшего полинома. Если в результате сдвига меньший полином становится полностью равным большему полиному, то общая операция 10 попарного сравнения и сложения блоков прекращается. Вид меньшего полинома передается к операции 3 и запоминается.
Если же сравниваемые полиномы не равны между собой, то далее производится операция 9. В ней выполняется в соответствие с правилами конечной алгебры сложение в поле Галуа коэффициентов при членах одинаковых степеней обоих полиномов. Операция сложения эквивалентна операции вычитания, и поскольку их члены максимальных степеней стали одинаковыми, то после осуществления этой операции максимальная степень разности уменьшается на единицу. Естественно, изменяются и значения коэффициентов при членах других степеней. После этого вновь осуществляется операция 5 сравнения полиномов, но уже с двумя другими полиномами, из которых один равен упомянутому полиному меньшей старшей степени до его поразрядного сдвига, а другой - результату сложения в поле Галуа операции 9. После нее вновь выполняются описанные операции, пока операцией 8 не будет установлено равенство обрабатываемых полиномов.
Когда процедура, производимая общей операцией 10 сравнения и сложения полиномов, заканчивается, это приводит к тому, что в результате остаются общие для обоих анализируемых в ней кодовых блоков полиномы. Действительно, пусть сравниваемые кодовые блоки описываются полиномами: y1(Х)=Md1(Х)MC(Х)g(Х) и y2(X)=Md2(X)MC(X)g(X).
Как указывалось известно, сложение и вычитание в поле Галуа являются эквивалентными операциями, т.к. приводят к одинаковым результатам. Поэтому разностный полином y3=y1-y2=(Md1+Md2)MCg=(Md1-Md2)MCg=M3MCg, будет содержать те же совпадающие общие множители, что и исходные полиномы до сложения, а изменяются только различающиеся в y1 и y2 части полиномов.
Поскольку перед сложением (вычитанием) старшая степень меньшего полинома был временно приравнена к старшей большего, то после этой операции старшая степень результата сложения всегда уменьшается на единицу по сравнению с порядком максимального из анализируемых полиномов. Если после нее результат оказывается не равен меньшему из текущих полиномов, то вновь повторяется выравнивание старших степеней двух анализируемых полиномов и их вычитание. Порядок различающейся части (М3) вновь уменьшается на единицу, и т.д. Таким образом, после проведения определенного числа повторяющихся операций 5-9 полином М3 становится равным единице. Число повторяющихся операций определяется конкретным видом полиномов Md1 и Md2 и равно порядку максимального их них.
Продемонстрируем данную процедуру определения одинаковых делителей у пары кодовых блоков на конкретном примере. Как известно, коэффициенты в поле Галуа могут быть пронумерованы по-разному. В указанных выше книгах применяется нумерация в форме степеней базового элемента а. Для удобства конкретных вычислений также применяется нумерация в форме индексов при базовом элементе а, например, в вычислительной среде Matlab (где а0=0, а1=1).
Пусть в рассмотренном примере конкретном примере применения предложенного способа длина кодовых блоков составляет n=7, символы содержат три бита (m=3), количество элементов поля Галуа равно восьми (а0÷a7). Общий полином (полиномиальный генератор) образован многочленом g(X)=a1X+a6. При этом исходные выражения для первого и второго в паре выбранных кодовых блоков пусть имеют вид, соответственно:
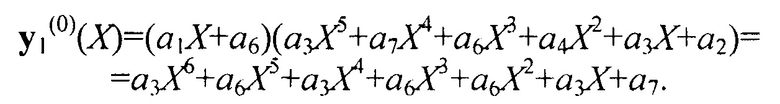
и
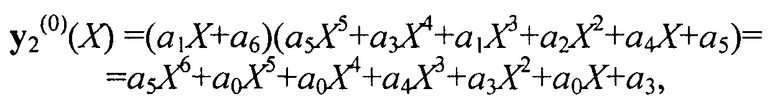
где 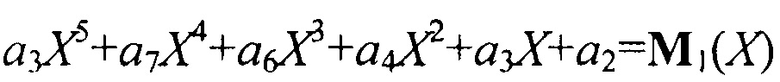 и
и 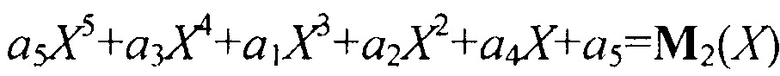 - информационные (различающиеся) части первого и второго кодовых слов.
- информационные (различающиеся) части первого и второго кодовых слов.
Старшие степени полиномов пока одинаковы и операциии 5 и 6 оставляют их без изменений. В операции 7 нормируются оба кодовых блока таким образом, чтобы коэффициент при старшей степени стал равным единице, т.е. делятся все коэффициенты первого полинома на а3 и второго полинома на а5. Тогда (с учетом того, что а1=1):
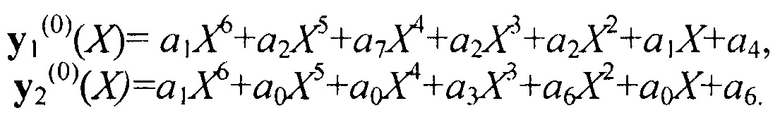
Полиномы в текущем состоянии не равны один другому, поэтому операция 8 оставляет из без изменений.
С помощью операции 9 находим разностное выражение:
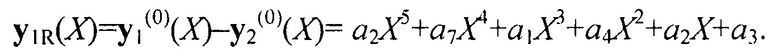
После нормировки (деления на коэффициент а2) оно станет равным:
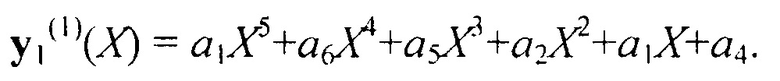
В результате операций данного шага исчез член полинома первого кодового блока со старшей степенью, равной шести, количество членов в полиноме уменьшилось на один. После этого повторяется последовательность аналогичных операций, в результате уменьшается полином второго кодового блока. Для этого временно умножим полином y1(1)(Х) на I и вычтем из полинома y2(0)(Х):
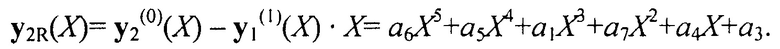
После нормировки:
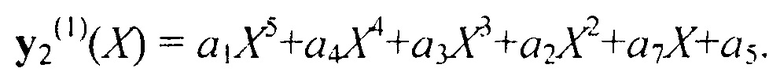
Теперь и во втором кодовом блоке исчез член полинома со старшей степенью, равной шести, количество членов в полиноме также уменьшилось на один. Далее с полученными полиномами и проделываем аналогичные операции, в результате чего получаем еще более укороченные полиномы вида (без нормировки по коэффициенту при старшей степени):
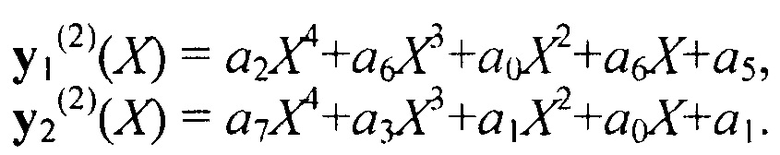
После нормировки:

Старшая степень вновь уменьшилась на единицу, уменьшилось и количество членов в полиномах. Продолжая аналогичные действия, получаем:
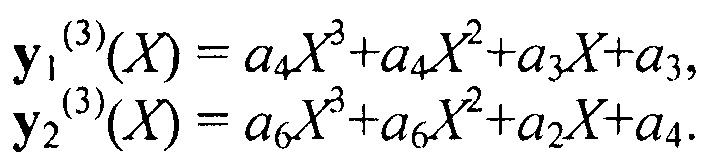
После нормировки:
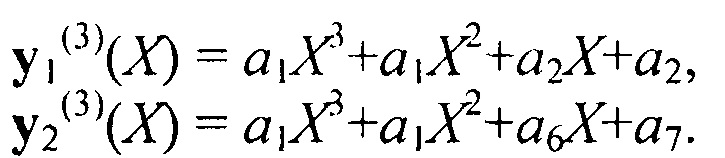
После их вычитания степень полинома уменьшилась сразу на две единицы (что обусловлено получившимся сочетанием коэффициентов), т.е.: 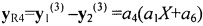 . После нормировки
. После нормировки 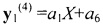 .
.
В результате для формирования второго полинома при вычитании yR4 его нужно домножать не на X, а на X2, т.е.:
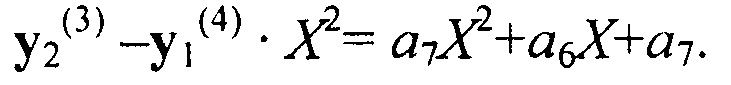
После нормировки:
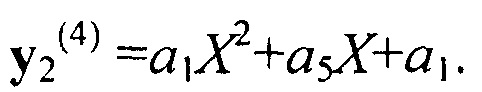
Далее получаем разность (повторно умножая полином 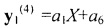 , но теперь на величину X):
, но теперь на величину X): 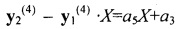 . Проводя нормировку, получаем выражение
. Проводя нормировку, получаем выражение 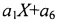 . Операцией 8 определяется, что полиномы стали равны. Полином стал равным оставшемуся первому полиному
. Операцией 8 определяется, что полиномы стали равны. Полином стал равным оставшемуся первому полиному 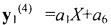 , т.е. выражение для общего полинома g(X) выводится к операции 3 и запоминается.
, т.е. выражение для общего полинома g(X) выводится к операции 3 и запоминается.
После анализа всех отобранных пар блоков операцией 4 выводится тот полином, который был заполнен наибольшее число раз. Поскольку полиномиальный генератор присутствует во всех кодовых блоках, то он будет встречаться максимальное число раз и выведется, как результат диагностической процедуры. Информационные части разных блоков различаются, и появление одинаковых множителей в информационной части маловероятно, гораздо вероятнее, что общая часть будет состоять только из порождающего полинома.
Вероятность появления в каждом цикле анализа только порождающего полинома g(X) гораздо выше, и именно он будет определен максимальное число раз, а все другие результаты, появляющиеся случайно, будут зафиксированы меньшее число раз. Поэтому операция 4 определит именно полином g(X), являющийся искомым результатом диагностики. Для каждой пары кодовых слов производится постепенное циклическое уменьшение порядка соответствующих полиномов до тех пор, пока в паре не останутся только общий полином для каждой пары. Если максимальная степень различающихся частей равна k, то в общем случае общий полином будет получен максимум за к повторений описанного набора операций.
Таким образом, заявляемый способ позволяет определять структуру используемого кодера без предварительной информации о ней и обеспечивать эффективную работу декодера по исправлению ошибок, тем самым повышая помехоустойчивость передачи информации.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ диагностики циклических кодов | 2016 |
|
RU2631142C2 |
| Способ диагностики сверточных кодов | 2015 |
|
RU2616180C1 |
| ПАРАЛЛЕЛЬНЫЙ РЕКОНФИГУРИРУЕМЫЙ КОДЕР БЧХ КОДОВ | 2015 |
|
RU2591474C1 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ ФУНКЦИОНАЛЬНЫХ ЗАВИСИМОСТЕЙ | 2015 |
|
RU2602989C2 |
| УСТРОЙСТВО для КОДИРОВАНИЯ двоичных ЦИКЛИЧЕСКИХ кодов | 1972 |
|
SU335691A1 |
| Устройство для формирования элементов расширенных полей Галуа GF ( @ ) и кодовых последовательностей на их основе | 1987 |
|
SU1441413A1 |
| РЕКОНФИГУРИРУЕМЫЙ КОДЕР БЧХ КОДОВ | 2015 |
|
RU2601827C1 |
| СПОСОБ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ (ВАРИАНТЫ) | 2015 |
|
RU2598781C1 |
| Устройство для кодирования | 1986 |
|
SU1390801A1 |
| СПОСОБ РАСКРЫТИЯ СТРУКТУРЫ НЕЛИНЕЙНЫХ РЕКУРРЕНТНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ В ВИДЕ КОДОВ КВАДРАТИЧНЫХ ВЫЧЕТОВ, СУЩЕСТВУЮЩИХ В ПРОСТЫХ ПОЛЯХ ГАЛУА GF(p), И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2017 |
|
RU2661542C1 |


Изобретение относится к технике связи и может быть использовано для определения неизвестной структуры кодера недвоичных блоковых систематических кодов и несистематических кодов на основе анализа принимаемой кодовой последовательности. Техническим результатом является повышение помехоустойчивости передачи информации. Способ содержит этапы: запоминают N кодовых блоков, извлекают пары кодовых блоков, которые попарно сравнивают и складывают, при этом сравнивают максимальные степени членов выбранных полиномов, описывающих сравниваемые кодовые блоки, поразрядно сдвигают меньший полином, делят все коэффициенты каждого полинома на коэффициент при его члене максимальной степени, сравнивают больший полином со сдвинутым меньшим полиномом, в случае их равенства вид меньшего полинома до сдвига запоминают, в случае их неравенства складывают в поле Галуа коэффициенты при членах с одинаковыми степенями полиномов и возвращаются к сравнению меньшего полинома и полученного результата сложения в поле Галуа, запоминают вид полученных полиномов, выбирают максимальное число полученных одинаковых результатов сравнения и сложения. 3 ил.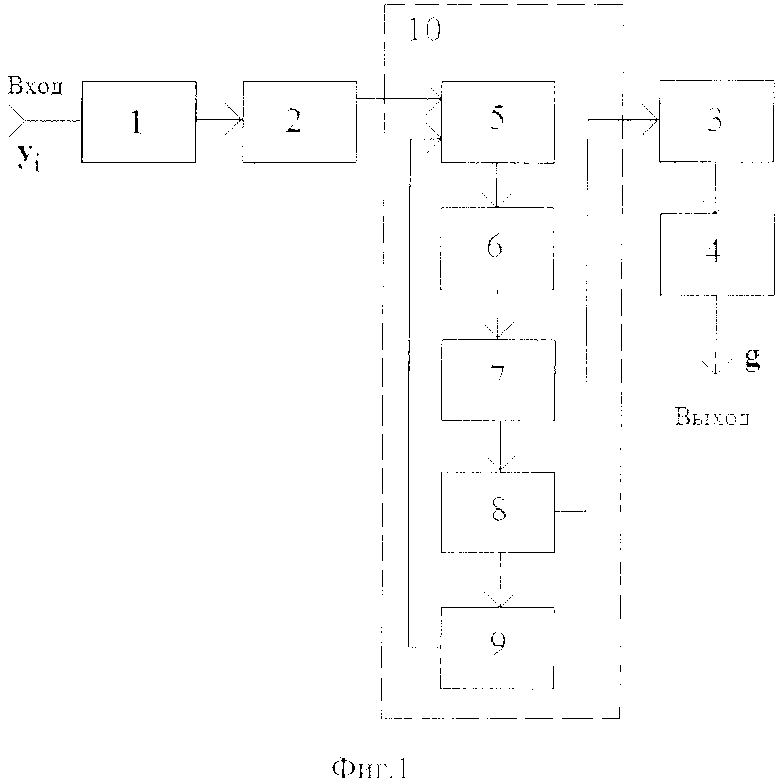
Способ диагностики недвоичных блоковых кодов, включающий в себя запоминание N кодовых блоков, извлечение пар блоков, попарное сравнение и сложение блоков, поразрядный сдвиг полинома, запоминание вида полинома и выбор максимального числа результатов, отличающийся тем, что в него вводят сравнение степеней полиномов, деление на коэффициенты при старшей степени полинома, определение равенства полиномов и сложение полиномов в поле Галуа, при этом сначала запоминают N кодовых блоков, затем извлекают пары кодовых блоков, после этого кодовые блоки попарно сравнивают и складывают, далее запоминают вид полученных в результате сравнения и сложения полиномов, после чего выбирают максимальное число полученных одинаковых результатов сравнения и сложения, причем при попарном сравнении и сложении кодовых блоков сравнивают максимальные степени членов выбранных полиномов, описывающих сравниваемые кодовые блоки, затем поразрядно сдвигают меньший полином, после чего делят все коэффициенты каждого полинома на коэффициент при его члене максимальной степени, далее сравнивают больший полином со сдвинутым меньшим полиномом, в случае их равенства вид меньшего полинома до сдвига запоминают, в случае их неравенства складывают в поле Галуа коэффициенты при членах с одинаковыми степенями полиномов и возвращаются к сравнению меньшего полинома и полученного результата сложения в поле Галуа.
| Способ диагностики циклических кодов | 2016 |
|
RU2631142C2 |
| Способ диагностики сверточных кодов | 2015 |
|
RU2616180C1 |
| JP 2009171540 A, 30.07.2009 | |||
| Автомобиль-сани, движущиеся на полозьях посредством устанавливающихся по высоте колес с шинами | 1924 |
|
SU2017A1 |
| Способ получения цианистых соединений | 1924 |
|
SU2018A1 |
Авторы
Даты
2019-07-01—Публикация
2018-07-02—Подача