Способ диагностики сверточных кодов относится к технике связи и может быть использован для определения неизвестной структуры сверточного кодера со скоростью кодирования, равной 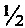 , и кодовым ограничением, равным K, на основе анализа принимаемой кодовой последовательности.
, и кодовым ограничением, равным K, на основе анализа принимаемой кодовой последовательности.
Известны различные способы сверточного кодирования и декодирования, описанные, например, в книгах: Ипатов В.П., Орлов В.К., Самойлов И.М. Системы мобильной связи. - М.: Горячая линия-Телеком, 2003; Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. - М.: Техносфера, 2006. В них описываются операции получения кодированного сигнала из входной информационной последовательности символов путем осуществления операций свертки определенного количества информационных символов с полиномиальными генераторами (порождающими полиномами) и последовательной передачи кодовых символов, полученных с помощью каждого генератора. После приема последовательность раскодируется одними из возможных методов. Однако для успешного раскодирования любым из методов должны быть известны используемые порождающие полиномы, без чего раскодирование невозможно.
Наиболее близким к заявляемому является способ, описанный в кн.: Скляр Б. Цифровая связь. Теоретические основы и практическое применение. - М.: Изд. дом «Вильяме», 2003. Для кодовой скорости, равной 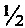 (с приходом каждого нового информационного символа вырабатываются два кодовых символа), для получения этих двух кодовых символов используется K запомненных предыдущих последовательных информационных символов. Их значения поразрядно складываются по модулю 2, причем в этом сложении участвуют только те из запомненных символов, которые соответствуют единицам в порождающем полиноме. При этом параллельно используется два различных порождающих полинома, определяющих структуру сверточного кодера и свойства кода. Два полученных кодовых символа передаются последовательно по линии передачи. После этого запоминается следующий информационный символ, а символ, запомненный раньше всех, из памяти удаляется. (Т.е. вся совокупность запомненных К информационных символов сдвигается на один символ). После этого все операции вновь повторяются, вырабатывая два новых кодовых символа.
(с приходом каждого нового информационного символа вырабатываются два кодовых символа), для получения этих двух кодовых символов используется K запомненных предыдущих последовательных информационных символов. Их значения поразрядно складываются по модулю 2, причем в этом сложении участвуют только те из запомненных символов, которые соответствуют единицам в порождающем полиноме. При этом параллельно используется два различных порождающих полинома, определяющих структуру сверточного кодера и свойства кода. Два полученных кодовых символа передаются последовательно по линии передачи. После этого запоминается следующий информационный символ, а символ, запомненный раньше всех, из памяти удаляется. (Т.е. вся совокупность запомненных К информационных символов сдвигается на один символ). После этого все операции вновь повторяются, вырабатывая два новых кодовых символа.
При декодировании определяются пары кодовых символов, соответствующие одному информационному символу и направляются на декодер. При декодировании чаще всего используется процедура Витерби, при которой различным вариантам возможных информационных последовательностей ставятся в соответствие различные пути по кодовой решетке. При этом на основе известных порождающих полиномов (известной структуры кода) задаются сочетания пары кодовых символов для всех вариантов переходов и определяются метрики переходов, т.е. расстояния (либо по Хеммингу, либо по Эвклиду) от значений пары принятых символов до всех вариантов соответствующих значений пар переходов. Метрики накапливаются, меньшие их величины отбрасываются. Кодирование дает возможность исправлять определенное количество ошибок, возникающих при передаче по каналу связи.
Недостатком описанного способа является необходимость знания используемой структуры кода, т.е. вида используемых порождающих полиномов. Если они неизвестны, то правильное раскодирование невозможно и исправляющая способность кода не может быть реализована. Это приводит к снижению помехоустойчивости передачи информации.
Задачей предлагаемого способа диагностики сверточных кодов является определение структуры используемого кодера для обеспечения работоспособности декодеров и повышения помехоустойчивости передачи информации.
Поставленная задача решается тем, что в способ диагностики сверточных кодов, включающий в себя определение пар символов, соответствующих одному информационному символу, запоминание K подряд идущих символов, соответствующих первой кодовой последовательности, запоминание K подряд идущих символов, соответствующих второй кодовой последовательности, первое сложение по модулю 2 и второе сложение по модулю 2, вводят разделение на две кодовые последовательности, ввод первого полинома, ввод второго полинома, сравнение, генерацию 22K-1 двоичных чисел, добавление в память результата сравнения по адресу, вывод адреса с максимальной суммой и управление циклами работы, причем определение пар кодовых символов, соответствующих одному информационному символу и разделение на две кодовые последовательности производят последовательно, затем параллельно осуществляют запоминание K подряд идущих символов первой кодовой последовательности и запоминание K подряд идущих символов второй кодовой последовательности, после этого управляют осуществлением циклов работы, при этом в каждом цикле генерируют последовательно возрастающие 22K-1 двоичных чисел, в соответствие каждым из них вводят первый полином в первое суммирование по модулю 2 и вводят второй полином во второе суммирование по модулю 2, производят сравнение результатов обоих суммирований по модулю 2 и добавление результата сравнения в память по адресу, определяемому текущим значением двоичного числа, после осуществления количества циклов, много большего K, выводят адрес, по которому накоплено максимальное число.
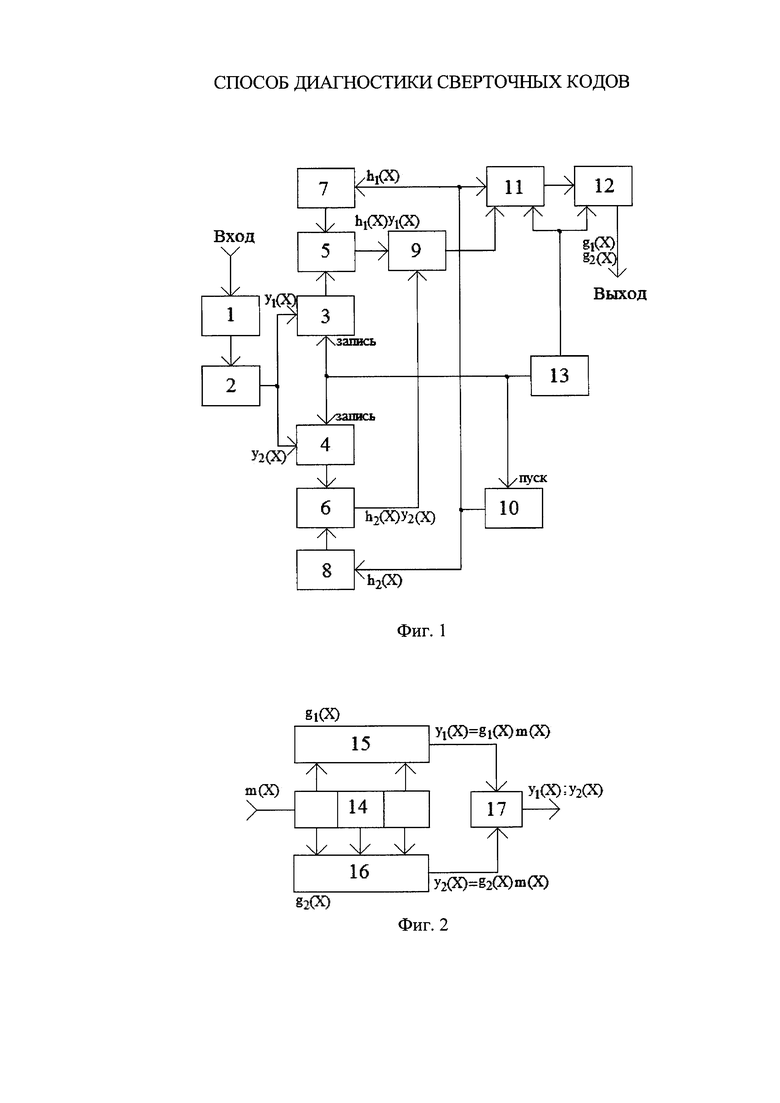
На чертежах представлены: на фиг. 1 - схематическая последовательность операций предлагаемого способа; на фиг. 2 - простейшая структурная схема примера реализации сверточного кодера со скоростью кодирования 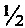 , на фиг. 3 - структурная схема устройства для реализации предлагаемого способа.
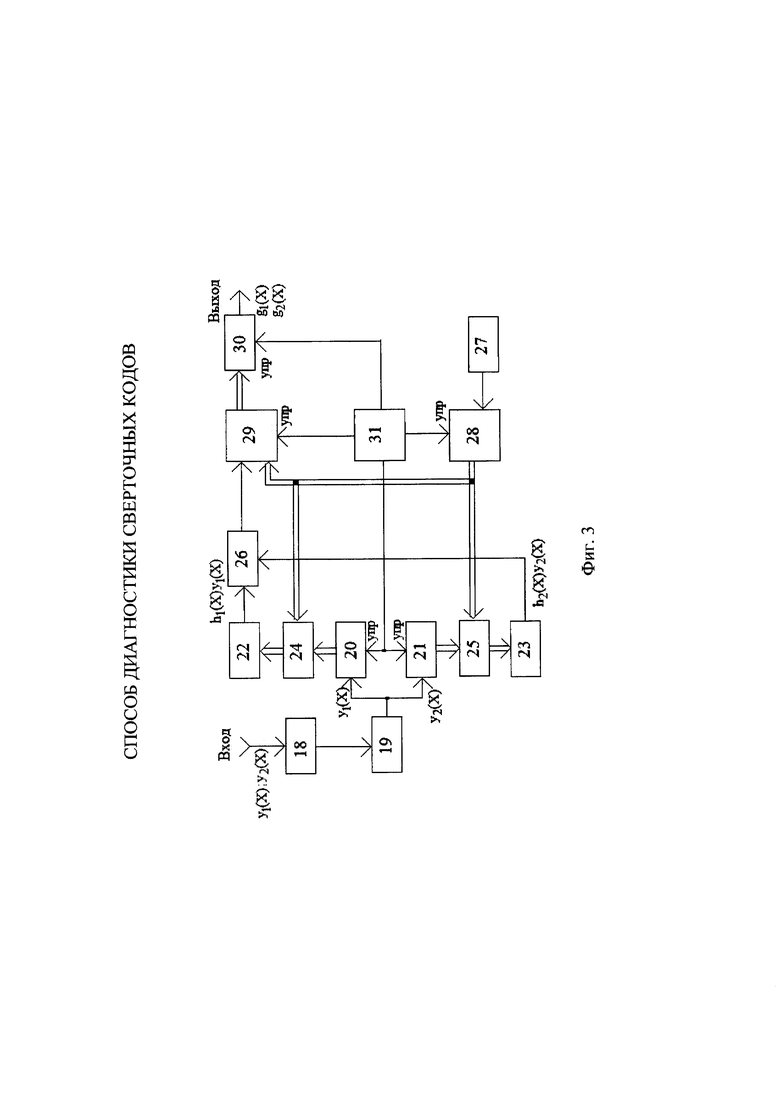
, на фиг. 3 - структурная схема устройства для реализации предлагаемого способа.
На фиг. 1 обозначены операции: определение пар кодовых символов, соответствующих одному информационному символу 1; разделение на две кодовые последовательности 2; запоминание K подряд идущих символов первой кодовой последовательности 3; запоминание K подряд идущих символов второй кодовой последовательности 4; первое 5 сложение по модулю два; второе 6 сложение по модулю два; ввод первого полинома 7; ввод второго полинома 7; сравнение 9; генерация 22K-1 двоичных чисел 10; добавление 11 в память результата сравнения по адресу; вывод адреса с максимальной суммой 12; управление циклами работы 13.
На фиг. 2 обозначены: регистр 14; первый 15 и второй 16 сумматоры; переключатель 17.
На фиг. 3 обозначены: блок выделения 18; коммутатор 19; первый 20 и второй 21 сдвиговые регистры; первый 22 и второй 23 сумматоры по модулю 2; первый 24 и второй 25 блоки ключей; схема сравнения 26; тактовый генератор 27; двоичный счетчик 28; блок памяти 29; блок определения адреса 30 и блок управления 31.
Операции предлагаемого способа осуществляются следующим образом. Операция 1 определения пар кодовых символов, соответствующих одному информационному символу производится аналогично этой операции в указанном прототипе и практически функционирующей на его основе декодирующей аппаратуре. В передатчике при кодовой скорости R=1/2 при поступлении в кодер каждого информационного символа в канал связи выдается подряд два кодовых символа, полученных с помощью одного, а потом другого полиномиального генератора. В декодере приемника для нормального функционирования алгоритма Витерби в принятой непрерывной кодовой последовательности выделяются пары символов полученные из одного и того же информационного символа, обычно для этого используются специальные маркеры, указывающие, который символ - первый в паре, который - второй.
В операции 2 разделения на две кодовые последовательности отдельно формируется последовательность первых кодовых символов в каждой паре (первая кодовая последовательность), и отдельно - последовательность вторых в паре кодовых символов (вторая кодовая последовательность).
Весь процесс диагностики сверточных кодов состоит из N одинаковых циклов, причем N>>K. Для начала процесса диагностики и его завершения с выводом результатов, а также для начала каждого цикла и генерации двоичных чисел, производится операция 13 управления циклами работы. В начале каждого цикла первоначально производятся однотипные операции 3 и 4 запоминания значений K подряд идущих символов, соответственно, первой и второй кодовых последовательностей. После этого запоминания производятся операция 5 сложения по модулю 2 запомненных символов первой кодовой последовательности в соответствии с порождающим полиномом h1(X) и одновременно операция 6 сложения по модулю 2 запомненных символов второй кодовой последовательности в соответствии с порождающим полиномом h2(X).
После этого производится операция 9 сравнения результатов обеих операций сложения по модулю 2.
Операция 10 генерации двоичных чисел производится в каждом цикле работы после завершения операций 3 и 4 запоминания символов кодовых последовательностей. В ней генерируются 22K-1 последовательно возрастающих чисел в двоичном коде, начиная с единицы. Каждое число состоит из 2K разрядов, каждое последующее число больше текущего на единицу. На основе первых K разрядов (с первого до K-го) операцией 7 вводится в первое 5 сложение по модулю 2 первый порождающий полином h1(X). На основе следующих K разрядов (с K+1 до 2K-го) операцией 8 вводится во второе 6 сложение по модулю 2 второй порождающий полином h2(X).
С помощью операции 13 управления циклами работы перед началом самого первого цикла память обнуляется. По результатам сравнения 9 в операции 11 арифметически добавляется в память результат сравнения к запомненной там ранее сумме. Добавление производится по адресу, равному текущему значению двоичного числа, выработанному операцией 10 генерации двоичных чисел. По завершении всех N циклов работы с помощью операции 12 вывода адреса с максимальной суммой определяется адрес ячейки памяти, в котором накопилась число максимальной величины. Этот адрес состоит из 2K двоичных разрядов. Первые K разрядов представляют собой искомую структуру одного порождающего полинома, другие K разрядов представляют собой искомую структуру второго порождающего полинома. Эти результаты используются как выходной результат работы способа диагностики структуры кодера.
Блоки на фиг. 2 работают следующим образом. Регистр 14 осуществляет запись трех последовательных символов информационной последовательности. Первый сумматор 15 определяет сумму по модулю 2 содержимого первой и третьей ячеек регистра 14. Второй сумматор определяет сумму по модулю 2 содержимого всех трех ячеек регистра 14. Переключатель 17 поочередно подключает к своему выходу выходные сигналы первого сумматора 15, потом второго сумматора 16. С приходом на вход регистра следующего информационного символа он записывается в первую ячейку регистра, содержимое первой и второй ячеек сдвигается вправо, содержимое третьей ячейки удаляется.
Блоки на фиг. 3 работают следующим образом. На вход блока выделения 18 поступает общий кодированный сигнал, представляющий собой поочередное чередование символов первой y1(X) и второй y2(X) кодовых последовательностей. В нем определяются пары символов этих последовательностей, соответствующие передаче одного и того же информационного символа. Далее коммутатор 19 направляет символы первой кодовой последовательности на вход первого сдвигового регистра 20, а символы второй кодовой последовательности на вход второго сдвигового регистра 21. Оба регистра имеют K разрядов (K двоичных ячеек памяти). Первый блок ключей 24 представляет собой набор K однотипных ключей, соединяющих параллельные выходы первого сдвигового регистра 20 с одноименными входами первого 22 сумматора по модулю 2.
Второй блок ключей 25 также представляет собой набор K однотипных ключей, соединяющих параллельные выходы второго сдвигового регистра 21 с одноименными входами второго 22 сумматора по модулю 2. Ключи открываются сигналами с двоичного счетчика 28. При подаче единицы на управляющий вход каждого ключа он соединяет выход одной из ячеек сдвигового регистра с соответствующим входом сумматора по модулю 2. Если на управляющий вход ключа поступает ноль, то на его выходе также появляется ноль.
При работе в каждый момент времени некоторые из ключей закрыты, а другие открыты. Таким образом, реализуется определенная структура полиномов h1(X) и h2(X), изменяемая в зависимости от сигналов двоичного счетчика 28. При этом на выходе первого сумматора по модулю 2 образуется сигнал h1(X)y1(X), на выходе второго сумматора по модулю 2 образуется сигнал h2(X)y2(X).
Эти сигналы подаются на схему сравнения 26. Если оба ее входных сигнала одновременно равны единице или одновременно равны нулю, то схема сравнения вырабатывает на своем выходе единицу. Если на ее входы поступают разные сигналы, то она вырабатывает на своем выходе ноль. (Это соответствует логической функции  , где x1 и x2 - входные сигналы схемы сравнения, x3 - ее выходной сигнал.)
, где x1 и x2 - входные сигналы схемы сравнения, x3 - ее выходной сигнал.)
Тактовый генератор 27 работает постоянно и вырабатывает последовательность импульсов. Блок управления 31 управляет организацией N циклов работы. В начале каждого цикла работы по его управляющему сигналу в сдвиговые регистры 20 и 21 заносится по K символов, а в двоичном счетчике 28 устанавливается первое значение двоичного числа. (В первом разряде - единица, во всех остальных разрядах – нули.) После этого двоичный счетчик начинает считать импульсы тактового генератора и на его выходе последовательно возрастают числа в двоичном коде. Каждый цикл заканчивается, когда двоичный счетчик досчитает до 22K-1. После этого начинается следующий цикл и все повторяется вновь.
Первые K разрядов выходного сигнала двоичного счетчика (двоичного числа) подключены к управляющим входам ключей блока 24, вторые K разрядов выходного сигнала двоичного счетчика подключены к управляющим входам ключей блока 25.
Кроме этого выходной сигнал двоичного счетчика подключен к адресному входу блока памяти. Блок памяти содержит 22K-1 ячеек. В самом начале работы перед первым циклом все ячейки обнуляются. В каждом цикле изменяющееся двоичное число с двоичного счетчика последовательно перебирает адреса всех ячеек памяти. На сигнальный вход блока памяти при этом поступают сигналы с выхода схемы сравнения. Каждый сигнал схемы сравнения арифметически складывается при этом с содержимым той ячейки, адрес которой определяется текущей величиной двоичного числа с двоичного счетчика.
После завершения N циклов работы (N>>K) процесс накопления останавливается блоком управления. После этого блок 30 определения адреса определяет адрес той ячейки блока памяти, в которой накоплена максимальная сумма. Две части этого двоичного адреса описывают искомую структуру порождающих полиномов g1(X) и g2(X) и по сигналу блока управления подаются на выход устройства.
Для пояснения принципа обработки сигналов в соответствии с предлагаемым способом первоначально рассмотрим работу простейшего сверточного кодера (фиг. 2).
Как известно (см., например, упомянутую книгу Б.Скляра), последовательность передаваемых информационных символов m0, m1, m2, m3, …, mi, … можно представить как вектор m либо как полином m(Х)=m0+m1X+m2X2+m3X3+…+miXi+…, где символы mi принимают значения, равные либо 1, либо 0, в зависимости от передаваемой информации; X - оператор, описывающий задержку по времени на интервал T длительности одного символа (X2 означает задержку по времени на 2T, X3 означает задержку на 3T, и т.д.).
Сверточный кодер для скорости R=1/2 можно представить в виде набора из двух полиномиальных генераторов, реализующих свертку входной последовательности m(X) с порождающими полиномами g1(X) и g2(X). Вид этих порождающих полиномов и определяет структуру кодера и формируемого сверточного кода. Каждый полином обычно имеет порядок, равный K, и описывает связь ячеек регистра сдвига, куда заносятся K последовательных символов входной последовательности с сумматором по модулю 2. Коэффициенты возле каждого слагаемого полинома равны либо 1, либо 0, в зависимости от того, имеется ли связь между соответствующей ячейкой регистра сдвига или сумматора по модулю 2.
Для иллюстрации на фиг. 2 приведен пример структурной схемы сверточного кодера с кодовым ограничением K=3. На вход сдвигового регистра 14 подается последовательность m(X) информационных символов. Он выполняет функцию запоминания трех подряд идущих символов. На входы первого 15 сумматора по модулю 2 поступают сигналы с первой и третьей ячейки регистра, на входы второго 16 сумматора по модулю 2 поступают сигналы со всех ячеек регистра. Полином, описывающий первый сумматор: g1(X)=1+X2, полином, описывающий второй сумматор: g2(X)=1+X+X2. На выходе первого сумматора образуется первая кодовая последовательность y1(X)=g1(X)m(X), на выходе второго сумматора образуется вторая кодовая последовательность y2(X)=g2(X)m(X). (При нахождении результатов произведения этих многочленов необходимо учитывать, что сложение одинаковых степеней производится по модулю 2). На выходе кодера с помощью переключателя 17 в канал передачи производится последовательная передача символов первой и второй кодовых последовательностей, образуя общую кодовую последовательность.
Работа предлагаемого способа основана на том, что, несмотря на то, что символы кодовых последовательностей y1(X) и y2(X), относящиеся к одному информационному символу, не совпадают, но между ними, тем не менее, существуют скрытые связи, т.к. они образованы постоянным методом из одной и той же исходной последовательности m(X). Поэтому, можно эти две кодовые последовательности вновь закодировать сверточным кодированием с помощью некоторых новых полиномов и независимо менять вид этих полиномов, перебирая все возможные комбинации. Если сравнивать получающиеся такие новые «дважды закодированные» последовательности, то только в том случае, если новые полиномы совпадут со старыми, то все символы этих двух новых последовательностей будут совпадать. При всех других видах новых полиномов совпадение символов двух новых последовательностей будет случайным с вероятностью, близкой к 0,5. Таким образом, постоянное совпадение символов новых последовательностей укажет на искомый вид полиномов.
Рассмотрим операции способа подробнее. С помощью операции 1 из принятой общей кодовой последовательности выделяются первая y1(X) и вторая y2(X) кодовые последовательности и их символы с помощью операций 3 и 4 запоминаются. (В каждом цикле из каждой последовательности запоминается по K подряд идущих символов.) После запоминания над ними вновь производится сверточное кодирование, но уже с использованием других порождающих полиномов, соответственно, h1(X) и h2(X). В результате получаются символы, определяемые функциями: z1(X)=h1(X)g1(X)m(X) и z2(X)=h2(X)g2(X)m(X) и в операции 9 сравниваются значения этих символов.
Полиномы h1(X) и h2(X) можно записать: h1(Х)=а0+a1X+a2X2+…+aK-1 XK-1 и h2(X)=b0+b1X+b2X2+…+bK-1 XK-1, где коэффициенты ai и bi могут принимать значения 0 или 1, и наборы значений этих коэффициентов определяют «индивидуальную» структуру каждого полинома.
Каждый полином h1(X) и h2(X) в общем случае имеет K таких коэффициентов, значит возможны всего 2K различных вариантов структуры каждого полинома. В каждом цикле операцией 10 генерируются последовательные 2K-разрядные двоичные числа. Первые K разрядов каждого из этих числе с помощью операции 7 используются как коэффициенты полинома h1(x), другие K разрядов этих чисел с помощью операции 8 используются как коэффициенты полинома h2(X). Поскольку для каждого цикла генерируется 22K-1=(2K)2-1 вариантов двоичных чисел, то в течение каждого цикла будут получены все возможные сочетания видов обоих полиномов кроме «бессмысленного» сочетания, когда оба полинома одновременно равны нулю.
Одно из перебираемых сочетаний, которое будет в некоторый момент сгенерировано, сформирует полиномы: h2(X)=g1(X) и h1(X)=g2(X). При этом результат первой 5 операции сложения по модулю 2 будет описываться выражением z1(X)=h1(X)y1(X)=g2(X)g1(X)m(X), а результат второй 6 операции сложения по модулю 2 будет описываться выражением z2(X)=h2(X)y2(X)=g1(X)g2(X)m(X). Поскольку g1(X)g2(X)=g2(X)g1(X), то независимо от значения символов последовательности m(X) будет выполняться равенство z1(X)=z2(X). То есть именно при таком значении сгенерированного двоичного числа значения символов после обеих операций сложения по модулю 2 всегда будут совпадать.
При любых других значениях сгенерированных операцией 10 двоичных чисел совпадение будет случайным, а поскольку исходные информационные символы последовательности m(X) независимы и равновероятны, то и свернутые с полиномами различающегося вида тоже будут давать равновероятный результат, либо равный 1, либо равный 0.
Эти результаты операцией 11 арифметически добавляются в память по соответствующим адресам, определяемым генерируемыми двоичными числами. Таким образом, после завершения всего цикла только в одну ячейку памяти, соответствующую «правильным» полиномам (т.е., h2(X)=g1(X) и h1(X)=g2(X)), будет всегда добавляться единица, а во все другие ячейки памяти - равновероятно либо единица, либо ноль.
В каждом следующем цикле запоминаются другие K подряд идущих символов обеих кодовых последовательностей, значения которых не связаны со значениями символов, запомненных в предыдущем цикле. Таким образом, после осуществления N циклов (N>>K) все значения величин, накопленные операцией 11, будут примерно равны 0,5N для всех вариантов полиномов h1(X) и h2(X) и только для варианта h2(X)=g1(X) и h1(X)=g2(X) в ячейке с соответствующим номером будет значение, близкое к N.
После завершения N циклов операция 12 выводит двоичный номер этой ячейки на выход. Первая половина разрядов этого двоичного номера определит искомые коэффициенты при одном из искомых полиномов g1(X) и g2(X), вторая половина разрядов этого двоичного номера - при другом из этих искомых полиномов. Таким образом, будет диагностирован используемый сверточный код.
Предлагаемый способ будет устойчиво работать даже при плохих условиях распространения сигналов и больших шумах. Предположим, из-за больших шумов в принимаемой последовательности возникает много ошибок, что ведет к заметной величине вероятности ошибки, например, она равна РОШ=10-1. Это приведет лишь к тому, что в ячейке с «правильным» адресом по завершении всех циклов будет накоплена величина, равная (1-PОШ)N=0,9N, что также значительно больше величины 0,5N, накопленной в других ячейках, и позволяет легко определить номер нужной ячейки.
Поясним принцип работы устройства для реализации предлагаемого метода, пример которого приведен на фиг. 3.
В каждом цикле работы K символов первой и второй кодовых последовательностей вновь подвергаются сверточному кодированию со всеми возможными вариантами порождающих полиномов. По каждому варианту схемой сравнения 26 проверяется совпадение результатов кодирования с помощью операции 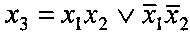 , где x1 и x2 - входные сигналы схемы сравнения, x3 - ее выходной сигнал. Результат этой операции арифметически складывается в блоке памяти 29 с содержимым той ячейки, адрес которой в данный момент выработал двоичный счетчик.
, где x1 и x2 - входные сигналы схемы сравнения, x3 - ее выходной сигнал. Результат этой операции арифметически складывается в блоке памяти 29 с содержимым той ячейки, адрес которой в данный момент выработал двоичный счетчик.
Фактически, производится запоминание коэффициентов a0÷aK-1 и b0÷bK-1 для обоих полиномов. Поскольку значения коэффициентов принимают единичные или нулевые значения, то их совокупность может служить двоичным адресом, в который заносится результат сравнения.
В каждом цикле в сдвиговые регистры заносятся новые отрезки кодовых последовательностей, в результате во все ячейки блока памяти 29 в каждом цикле прибавляются с равной вероятностью единичные и нулевые значения, кроме ячейки, номер которой определяет структуру искомых полиномов g1(X) и g2(X), куда практически всегда прибавляется единичное значение. В результате после осуществления достаточно большого количества циклов в этой ячейке накапливается сумма, в два раза большая, чем во всех остальных ячейках. Определением ее двоичного адреса завершается диагностика применяемого в системе связи сверточного кода.
Таким образом, использование предлагаемого способа позволяет определить неизвестную структуру используемого кодера для обеспечения работоспособности декодеров и повышения помехоустойчивости передачи информации.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ диагностики циклических кодов | 2016 |
|
RU2631142C2 |
| Способ диагностики недвоичных блоковых кодов | 2018 |
|
RU2693190C1 |
| СПОСОБ ПЕРЕДАЧИ ГОЛОСОВЫХ ДАННЫХ В ЦИФРОВОЙ СИСТЕМЕ РАДИОСВЯЗИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2005 |
|
RU2301492C2 |
| УСТРОЙСТВО И СПОСОБ ВЫРАБОТКИ И РАСПРЕДЕЛЕНИЯ ЗАКОДИРОВАННЫХ СИМВОЛОВ В СИСТЕМЕ СВЯЗИ МНОЖЕСТВЕННОГО ДОСТУПА С КОДОВЫМ РАСПРЕДЕЛЕНИЕМ КАНАЛОВ | 1999 |
|
RU2197786C2 |
| СВЕРТОЧНЫЕ КОДЫ С ЗАДАВАЕМОЙ КОНЦЕВОЙ КОМБИНАЦИЕЙ БИТОВ, ПРЯМОЙ СВЯЗЬЮ И ОПТИМАЛЬНЫМ СПЕКТРОМ РАССТОЯНИЙ | 2008 |
|
RU2466497C2 |
| Пороговый декодер сверточного кода | 1985 |
|
SU1252944A1 |
| ПАРАЛЛЕЛЬНЫЙ КОДЕР БЧХ С РЕКОНФИГУРИРУЕМОЙ КОРРЕКТИРУЮЩЕЙ СПОСОБНОСТЬЮ | 2021 |
|
RU2777527C1 |
| ПАРАЛЛЕЛЬНЫЙ РЕКОНФИГУРИРУЕМЫЙ КОДЕР БЧХ КОДОВ | 2015 |
|
RU2591474C1 |
| ВЫСОКОСКОРОСТНОЙ МОДУЛЬ СЛОЖЕНИЯ (СРАВНЕНИЯ) ВЫБОРА ДЛЯ ДЕКОДЕРА ВИТЕРБИ | 2000 |
|
RU2246751C2 |
| СПОСОБ СИНДРОМНОГО ДЕКОДИРОВАНИЯ ДЛЯ СВЕРТОЧНЫХ КОДОВ | 2004 |
|
RU2282307C2 |
Изобретение относится к технике связи и может быть использовано для определения неизвестной структуры сверточного кодера со скоростью кодирования, равной  , и кодовым ограничением, равным K, на основе анализа принимаемой кодовой последовательности. Технический результат – определение структуры используемого кодера для обеспечения работоспособности декодеров и повышение помехоустойчивости передачи информации. При осуществлении декодирования сверточных кодов необходимо знание структуры используемого кодера и сверточного кода, так как при отсутствии этой информации невозможно производить исправление ошибок. В данном способе повторно кодируют составляющие принимаемой общей кодовой последовательности с различными порождающими полиномами, перебирая их структуру, сравнивают результаты повторного кодирования. Поскольку символы исходной кодовой последовательности взаимно независимы, то результаты сравнения для всех сочетаний вида полиномов будут также случайны, кроме искомого вида полиномов. Для него они всегда будут совпадать. После накопления достаточно большого количества результатов сравнения преобладающая накопленная сумма укажет диагностируемую структуру порождающих полиномов и диагностируемую структуру кода. 3 ил.
, и кодовым ограничением, равным K, на основе анализа принимаемой кодовой последовательности. Технический результат – определение структуры используемого кодера для обеспечения работоспособности декодеров и повышение помехоустойчивости передачи информации. При осуществлении декодирования сверточных кодов необходимо знание структуры используемого кодера и сверточного кода, так как при отсутствии этой информации невозможно производить исправление ошибок. В данном способе повторно кодируют составляющие принимаемой общей кодовой последовательности с различными порождающими полиномами, перебирая их структуру, сравнивают результаты повторного кодирования. Поскольку символы исходной кодовой последовательности взаимно независимы, то результаты сравнения для всех сочетаний вида полиномов будут также случайны, кроме искомого вида полиномов. Для него они всегда будут совпадать. После накопления достаточно большого количества результатов сравнения преобладающая накопленная сумма укажет диагностируемую структуру порождающих полиномов и диагностируемую структуру кода. 3 ил.
Способ диагностики сверточных кодов, включающий в себя определение пар символов, соответствующих одному информационному символу, запоминание К подряд идущих символов, соответствующих первой кодовой последовательности, запоминание К подряд идущих символов, соответствующих второй кодовой последовательности, первое сложение по модулю 2 и второе сложение по модулю 2, отличающийся тем, что в него вводят разделение на две кодовые последовательности, ввод первого полинома, ввод второго полинома, сравнение, генерацию 22К-1 двоичных чисел, добавление в память результата сравнения по адресу, вывод адреса с максимальной суммой и управление циклами работы, причем определение пар кодовых символов, соответствующих одному информационному символу, и разделение на две кодовые последовательности производят последовательно, затем параллельно осуществляют запоминание К подряд идущих символов первой кодовой последовательности и запоминание К подряд идущих символов второй кодовой последовательности, после этого управляют осуществлением циклов работы, при этом в каждом цикле генерируют последовательно возрастающие 22К-1 двоичных чисел, в соответствие каждым из них вводят первый полином в первое суммирование по модулю 2 и вводят второй полином во второе суммирование по модулю 2, производят сравнение результатов обоих суммирований по модулю 2 и добавление результата сравнения в память по адресу, определяемому текущим значением двоичного числа, после осуществления количества циклов, много большего К, выводят адрес, по которому накоплено максимальное число.
| СКЛЯР Б., Цифровая связь | |||
| Теоретические основы и практическое применение.,Москва, изд | |||
| дом "Вильямс", 2003, стр.406-415 | |||
| СПОСОБ КОДИРОВАНИЯ, СПОСОБ ДЕКОДИРОВАНИЯ, КОДЕР И ДЕКОДЕР | 2010 |
|
RU2532702C2 |
| МНОГОСКОРОСТНОЙ ПОСЛЕДОВАТЕЛЬНЫЙ ДЕКОДЕР ВИТЕРБИ ДЛЯ ИСПОЛЬЗОВАНИЯ В СИСТЕМЕ МНОГОСТАНЦИОННОГО ДОСТУПА С КОДОВЫМ РАЗДЕЛЕНИЕМ | 1994 |
|
RU2222110C2 |
| СВЕРТОЧНЫЕ КОДЫ С ЗАДАВАЕМОЙ КОНЦЕВОЙ КОМБИНАЦИЕЙ БИТОВ, ПРЯМОЙ СВЯЗЬЮ И ОПТИМАЛЬНЫМ СПЕКТРОМ РАССТОЯНИЙ | 2008 |
|
RU2466497C2 |
| US 7673213 B2, 02.03.2010 | |||
| US 6167552 A1, 26.12.2000 | |||
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
| Способ обработки целлюлозных материалов, с целью тонкого измельчения или переведения в коллоидальный раствор | 1923 |
|
SU2005A1 |
Авторы
Даты
2017-04-12—Публикация
2015-11-30—Подача