Изобретение относится к области разработки способов и устройств для лабораторных исследований физических процессов, в частности для исследования закономерностей движения твердых частиц в жидкости.
Процесс движения частиц в поле силы тяжести имеет важное практическое значение в задачах экологии (очистка водоемов от примесей), в угольной промышленности (гидроподавление пыли в угольных шахтах), при ликвидации последствий катастрофических явлений техногенного или природного характера (извержение вулканов, промышленные взрывы и т.п.), в теплоэнергетике (сжигание водоугольных суспензий), в процессах химической технологии (осадительные колонны) и в целом ряде других отраслей техники и технологии [1].
Одной из основных характеристик, определяющих закономерности движения частиц в двухфазном потоке, является входящий в уравнение движения коэффициент сопротивления среды движению частиц Сх [2]. Обработка многочисленных опытных данных по коэффициенту сопротивления твердой сферы представлена в виде так называемой стандартной кривой сопротивления - зависимости Сх от числа Рейнольдса [2].
Стандартная кривая сопротивления и подавляющее большинство зависимостей для Сх, приведенных в литературе для усложненных условий обтекания частиц (обзорные публикации [3, 4]), получены в изотермических условиях (равенство температур частиц и несущей среды).
В ряде технических систем и технологических процессов движение частиц в несущей среде происходит в неизотермических условиях. При этом температура частиц может быть существенно выше или ниже температуры среды (плазмохимический синтез керамических порошков, тушение пожаров с применением авиации, процессы нагрева или охлаждения частиц в аппаратах химической технологии и т.п. [5, 6]). В этих условиях использование стандартной кривой сопротивления приводит к существенным погрешностям при расчете скорости движения частиц. Это связано с изменением физических свойств (в первую очередь вязкости) среды в пограничном слое вблизи частицы, входящих в число Рейнольдса.
Известен способ определения зависимости коэффициента сопротивления сферических частиц в неизотермических условиях от разности температур ΔT частицы и среды [7]. Этот способ основан на аппроксимации зависимости Cx(ΔT), полученной при численном решении задачи обтекания сферы. Показано, что уточнение зависимости Cx(ΔT) реализуется при расчете чисел Рейнольдса для параметров обтекающей среды при «пленочной» температуре 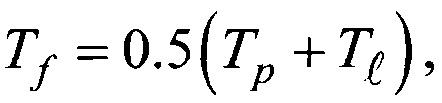 где Тр и
где Тр и 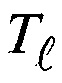 - температура частицы и среды соответственно. Недостатком данного способа является необходимость оценки его адекватности путем сравнения с экспериментальными данными, которые в литературе отсутствуют.
- температура частицы и среды соответственно. Недостатком данного способа является необходимость оценки его адекватности путем сравнения с экспериментальными данными, которые в литературе отсутствуют.
Известен способ оценки зависимости Cx(ΔT) путем измерения скорости свободно падающих горящих капель пентана, гептана и бензола в холодной атмосфере [8]. Недостатком данного способа является влияние вдува продуктов испарения капель и изменение размера капель за счет горения в процессе осаждения на коэффициент сопротивления.
Наиболее близким по технической сущности к заявляемому изобретению является способ, основанный на введении в кювету с вязкой жидкостью твердых сферических частиц и измерение скорости их гравитационного осаждения в стационарном режиме с последующим расчетом коэффициента сопротивления из уравнения движения частицы [9]. Указанный способ применим только для изотермических режимов осаждения частиц.
Техническим результатом настоящего изобретения является разработка способа определения коэффициента сопротивления твердых сферических частиц при их гравитационном осаждении в вязкой жидкости в неизотермических условиях.
Технический результат достигается тем, что разработан способ определения коэффициента сопротивления твердых сферических частиц в неизотермических условиях, включающий введение частиц в кювету с вязкой жидкостью, выполненную в виде правильной призмы с прозрачными стенками, и измерение скорости их гравитационного осаждения в жидкости. В кювету вводят с нулевой начальной скоростью одновременно две частицы одинакового диаметра, выполненные из одного материала. Одну из частиц предварительно перед введением в жидкость нагревают (или охлаждают) до температуры, отличающейся от температуры другой (эталонной) частицы, равной температуре жидкости, не менее, чем на±20 К. Скорость осаждения каждой из частиц измеряют времяпролетным методом с помощью видеосъемки процесса осаждения через прозрачные стенки кюветы. Время предварительного нагрева (или охлаждения) одной из частиц, расстояние, на котором измеряют скорость осаждения частиц в жидкости и коэффициент сопротивления нагретой (или охлажденной) частицы определяют из соотношений:



где

t1 - время предварительного нагрева (или охлаждения) одной из частиц, с;
Dp - диаметр частицы, м;
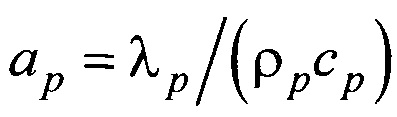 - коэффициент температуропроводности материала частиц, м2/с;
- коэффициент температуропроводности материала частиц, м2/с;
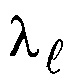 - коэффициент теплопроводности жидкости, Вт/(м⋅К);
- коэффициент теплопроводности жидкости, Вт/(м⋅К);
ρр - плотность материала частиц, кг/м3;
ср - удельная теплоемкость материала частиц, Дж/(кг⋅К);
х1 - расстояние, на котором измеряют скорость осаждения частиц в жидкости, м;
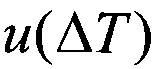 - скорость осаждения нагретой (или охлажденной) частицы, м/с;
- скорость осаждения нагретой (или охлажденной) частицы, м/с;
ΔT=(Т-To) - величина нагрева (или охлаждения) частицы, К;
Т - температура нагретой (или охлажденной) частицы, К;
To - температура эталонной частицы, К;
Cx(ΔT) - коэффициент сопротивления нагретой (или охлажденной) частицы;
Схо - коэффициент сопротивления эталонной частицы;
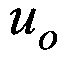 - скорость осаждения эталонной частицы, м/с;
- скорость осаждения эталонной частицы, м/с;
g - ускорение свободного падения, м/с2;
 - плотность жидкости, кг/м3.
- плотность жидкости, кг/м3.
Положительный эффект изобретения обусловлен следующими факторами.
1. Одновременное введение двух частиц одинакового диаметра, выполненных из одного материала, обеспечивает идентичность теплофизических характеристик частиц - эталонной и нагретой (или охлажденной).
2. Введение частиц с нулевой начальной скоростью позволяет строго оценить длину участка установления стационарного режима осаждения.
3. Предварительный нагрев (или охлаждение) одной из частиц перед введением в жидкость снижает погрешность определения температуры частицы за счет ее охлаждения (или нагрева) в воздухе.
4. Нагрев (или охлаждение) одной из частиц до температуры, отличающейся от температуры эталонной частицы, равной температуре жидкости не менее, чем на ±20 К обеспечивает изменение вязкости в пограничном слое жидкости, достаточное для получения разной скорости осаждения эталонной и нагретой (или охлажденной) частицы.
5. Равенство температур эталонной частицы и жидкости позволяет реализовать изотермический режим осаждения и определить опорное значение коэффициента сопротивления Схо при 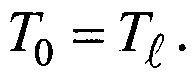
6. Время t1 предварительного нагрева (или охлаждения) частицы определяется из условия [10]:

При значении числа Фурье Fo=1 частица полностью прогревается (или охлаждается) до равномерной по всему объему температуры. Из (5) следует формула (1) для определения времени нагрева (охлаждения):
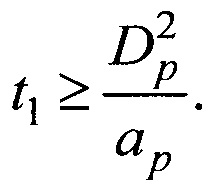
7. Изменение температуры нагретой (или охлажденной) частицы во времени T(t) при ее движении в жидкости, температура которой 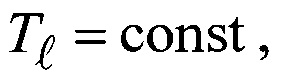 определяется в соответствии с законом Ньютона уравнением теплового баланса [10]:
определяется в соответствии с законом Ньютона уравнением теплового баланса [10]:
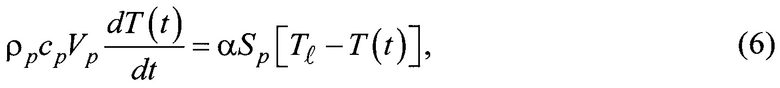
где Vp - объем частицы, м3;
T(t) - изменение температуры нагретой (или охлажденной) частицы во времени, К;
t - время, с;
α - коэффициент теплоотдачи, Вт/(м⋅К);
Sp - площадь поверхности частицы, м2.
Интеграл уравнения (6) имеет вид
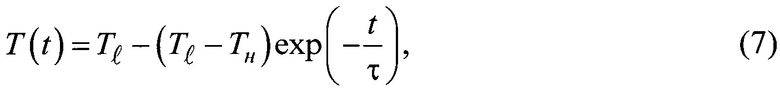
где Тн - начальная температура нагретой (или охлажденной) частицы, К;
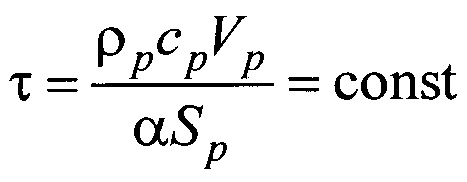 - постоянная времени, с.
- постоянная времени, с.
Для сферической частицы диаметром Dp 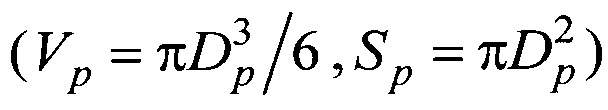 постоянная времени равна:
постоянная времени равна:

Преобразуем уравнение (7) к виду:

где 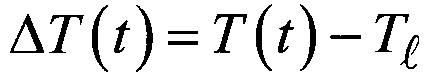 - текущая разность температур частицы и жидкости в процессе охлаждения;
- текущая разность температур частицы и жидкости в процессе охлаждения;
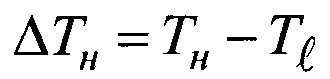 - начальная разность температур частицы и жидкости.
- начальная разность температур частицы и жидкости.
Значения 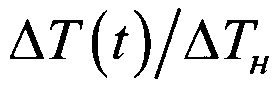 для разных моментов времени t/τ, рассчитанные по уравнению (9), приведены в таблице 1.
для разных моментов времени t/τ, рассчитанные по уравнению (9), приведены в таблице 1.
Таблица 1 - Значения 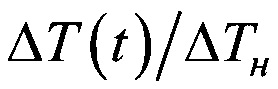 для разных моментов времени t/τ
для разных моментов времени t/τ

Из приведенных в таблице 1 данных следует, что изменение температуры нагретой (или охлажденной) частицы за счет конвективного теплообмена с жидкостью не более, чем на 5%, происходит за промежуток времени
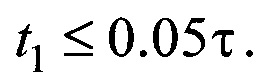
Расстояние, пройденное частицей за время t1 от момента начала осаждения, определяется формулой

Величина коэффициента теплоотдачи α определяется через число Нуссельта [10]
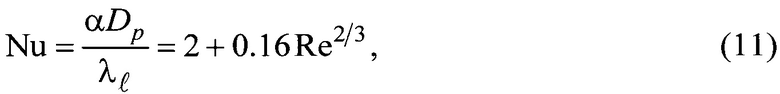
где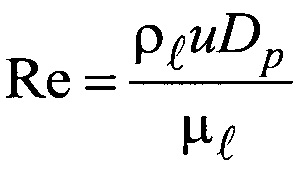 - число Рейнольдса;
- число Рейнольдса;
 - скорость осаждения частицы, м/с;
- скорость осаждения частицы, м/с;
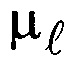 - коэффициент динамической вязкости жидкости, Па⋅с.
- коэффициент динамической вязкости жидкости, Па⋅с.
При осаждении частиц в стоксовском режиме (Re<1) из (11) следует приближенная оценка

При этом с учетом (11, 12) формула (8) для постоянной времени примет вид
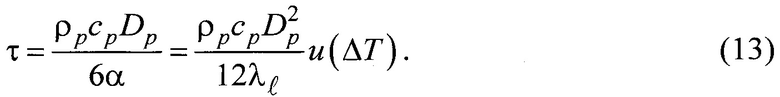
Подставляя (13) в формулу (10), получим соотношение (2) для расстояния х1, на котором можно пренебречь изменением температуры частицы (с погрешностью 5%)
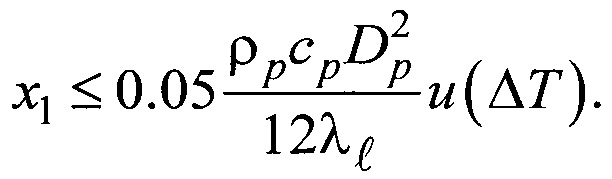
8. Уравнение гравитационного осаждения твердой частицы в жидкости имеет вид [9]:
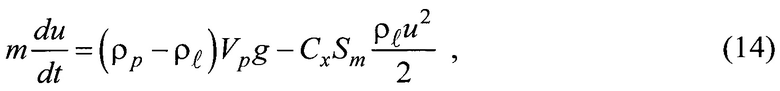
где m - масса частицы, кг;
Sm - площадь миделева сечения частицы, м2;
Сх - коэффициент сопротивления.
При стационарном режиме осаждения 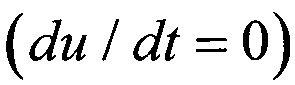 из уравнения (14) следует формула для определения коэффициента сопротивления сферической частицы:
из уравнения (14) следует формула для определения коэффициента сопротивления сферической частицы:

При нагреве (или охлаждении) частицы скорость ее гравитационного осаждения изменяется за счет нагрева (или охлаждения) прилегающего к частице пограничного слоя жидкости. При нагреве пограничного слоя вязкость жидкости уменьшается, что приводит к снижению коэффициента сопротивления и увеличению скорости осаждения частицы. При охлаждении пограничного слоя наблюдается снижение скорости осаждения частицы.
В таблице 2 приведены значения коэффициента динамической вязкости 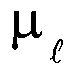 и плотности типичной вязкой жидкости - глицерина
и плотности типичной вязкой жидкости - глицерина 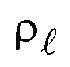 в зависимости от температуры [11].
в зависимости от температуры [11].
Таблица 2 - Значения плотности глицерина и его динамической вязкости в интервале температур (20÷200)°С

Из приведенных данных следует, что изменение плотности жидкости с увеличением температуры намного меньше изменения коэффициента динамической вязкости 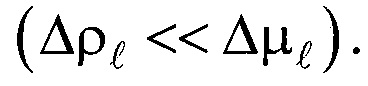 Предполагая
Предполагая 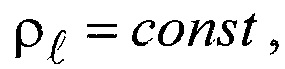 формулу (15) можно записать для эталонной и нагретой (или охлажденной) частиц в виде:
формулу (15) можно записать для эталонной и нагретой (или охлажденной) частиц в виде:


где 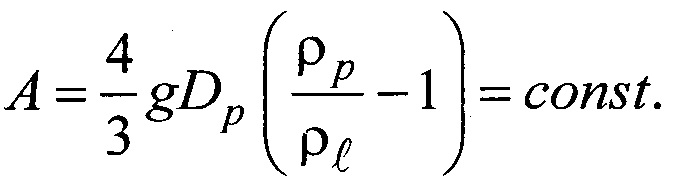
При этом из (16), (17) следует соотношение (3) для определения коэффициента сопротивления нагретой (или охлажденной) частицы:
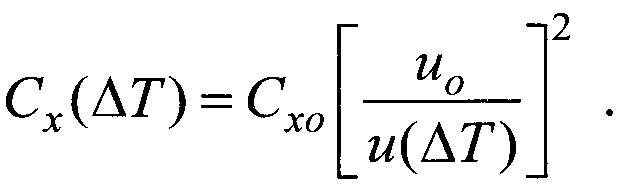
Соотношение для Схо (4) получается из формулы (16) при подстановке в нее выражения для А=const.
Пример реализации
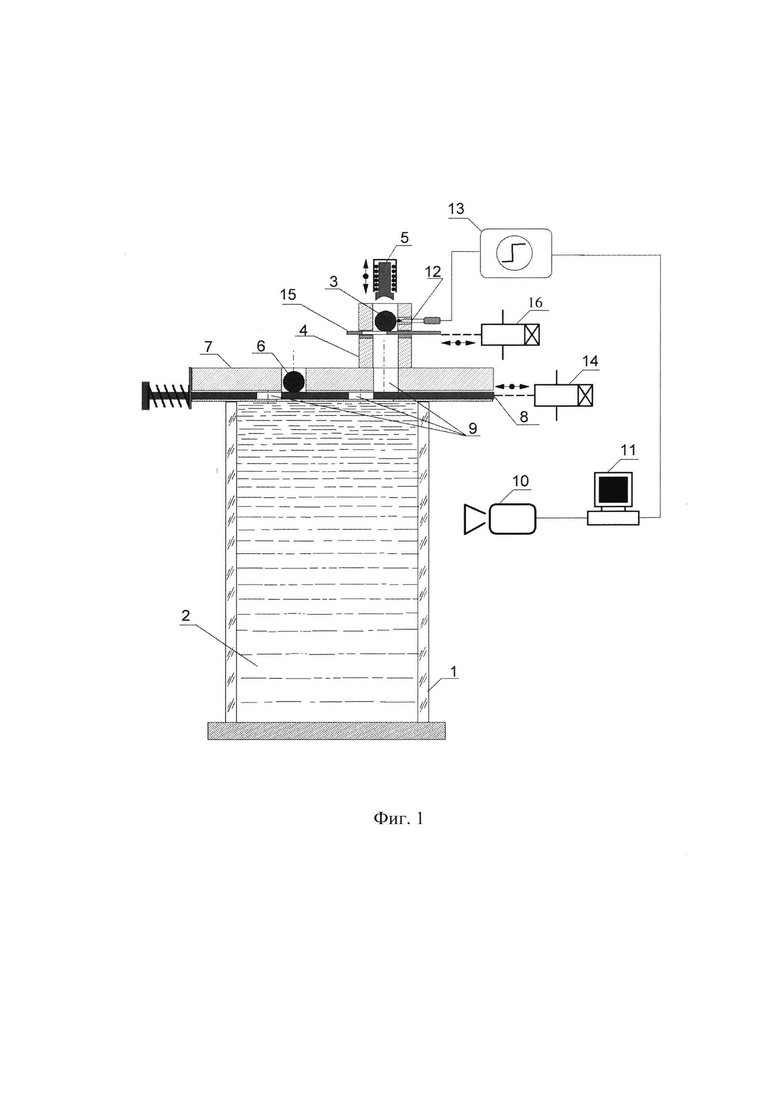
Сущность заявленного изобретения поясняется схемой, приведенной на Фиг. 1. Установка для реализации способа состоит из призматической кюветы 1 с вязкой жидкостью 2, устройства нагрева частицы, устройства ввода эталонной и нагретой частиц в жидкость и системы визуализации процесса осаждения частиц.
Кювета 1 выполнена из оптического стекла в виде правильной призмы размером 30×30×90 см. Устройство нагрева частицы 3 состоит из цилиндрического контейнера 4 со спиралью накаливания 5. Устройство ввода эталонной 6 и нагретой 3 частиц состоит из неподвижной 7 и подвижной 8 пластин, в которых выполнены совмещенные круглые отверстия 9. Визуализацию процесса осаждения частиц в жидкости проводили скоростной цифровой видеокамерой 10 типа Citius С100 с темпом съемки (50÷200) кадров в секунду. Обработка видеорядов проводилась с использованием компьютера 11.
Устройство для реализации способа определения коэффициента сопротивления твердых сферических частиц в неизотермических условиях работает следующим образом. Предварительно нагревали одну из частиц 3 в контейнере 4 до заданной температуры, которую измеряли термопарой 12, соединенной через усилитель 13 с осциллографом 11. После нагрева частицы 3 ее вводили в отверстие 9 неподвижной пластины 7 за счет свободного падения при удалении стопора 15 электромагнитным приводом 16.
Затем подвижную пластину 8 с помощью электромагнитного привода 14 смещали в горизонтальном направлении до совмещения отверстий 9 в подвижной 8 и неподвижной 7 пластинах. При этом эталонная 6 и нагретая 3 частицы осаждались в вязкой жидкости 2 с нулевой начальной скоростью.
Полученные с видеокамеры 10 данные обрабатывались на компьютере 11 с целью определения скорости осаждения каждой из частиц времяпролетным методом.
Эффективность заявленного способа подтверждена проведением серии экспериментов, по исследованию влияния температуры нагретой частицы на коэффициент сопротивления при малых числах Рейнольдса.
В экспериментах использовались стальные шарики диаметром 3.0, 8.87 и 17.47 мм. В качестве вязкой жидкости использовалось силиконовое масло ПМС-10000. Измеренная методом взвешивания на аналитических весах плотность материала частиц составляла 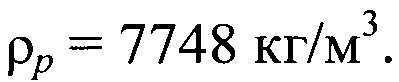 Плотность жидкости, измеренная ареометром при температуре эксперимента
Плотность жидкости, измеренная ареометром при температуре эксперимента 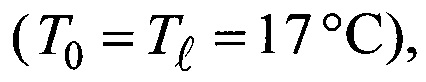 составляла
составляла 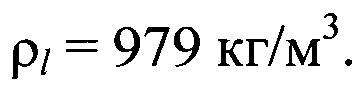 Значение коэффициента динамической вязкости жидкости, измеренного по стационарной скорости осаждения шарика диаметром Dp=3 мм
Значение коэффициента динамической вязкости жидкости, измеренного по стационарной скорости осаждения шарика диаметром Dp=3 мм 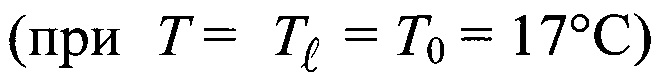 в стоксовском режиме [9], составляла
в стоксовском режиме [9], составляла 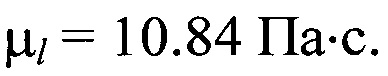
Значение времени предварительного нагрева частиц t1 и расстояния х1 на котором измеряли скорость осаждения частиц в жидкости, рассчитывались по соотношениям (1), (2). При этом использовались табличные значения теплофизических характеристик стали:
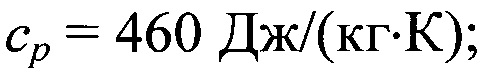
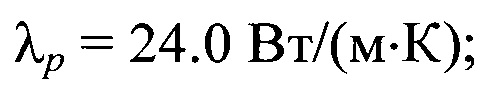
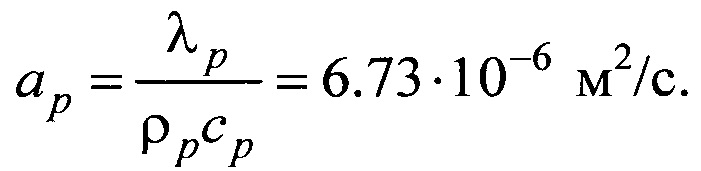
Рассчитанные значения t1, x1 приведены в таблице 3.
Таблица 3 - Рассчитанные значения t1, х1
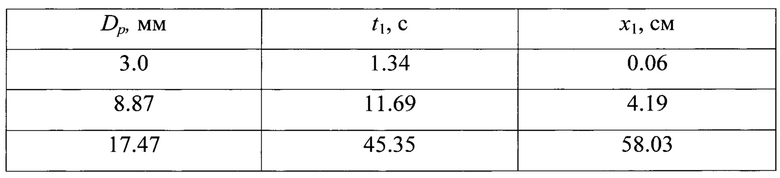
С учетом неидеальности теплового контакта шарика с устройством его нагрева значения времени нагрева были увеличены в несколько раз в соответствие с неравенством (1).
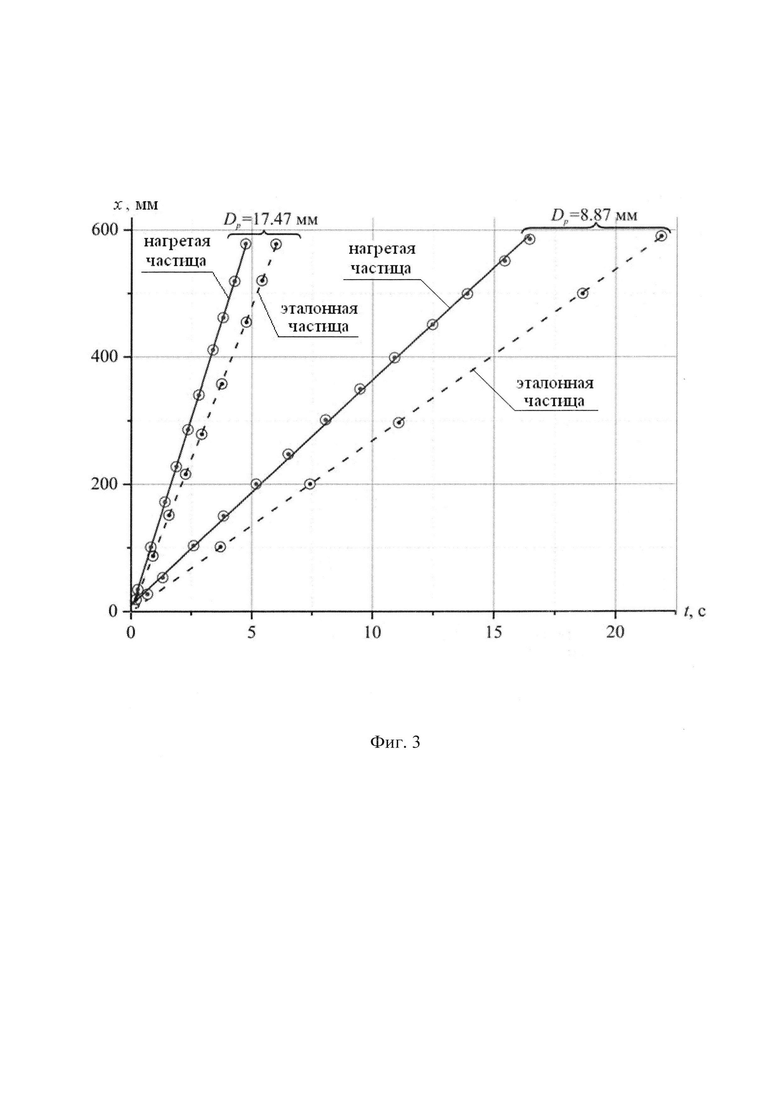
Видеоряд процесса осаждения нагретого и эталонного шариков диаметром Dp=17.47 мм приведен на Фиг. 2. Из приведенных видеокадров видно, что скорость осаждения нагретого шарика 6 существенно превышает скорость осаждения эталонного шарика 3. Графики зависимости пройденного нагретыми до 300°С и эталонными частицами (Dp=8.87 мм, Dp=17.47 мм) расстояния х от времени t приведены на Фиг. 3. Из графиков следует, что скорости частицы соответствуют стационарному режиму осаждения.
Измеренные значения скорости осаждения эталонного шарика, осредненные по 5 дублирующим опытам, рассчитанные значения числа Рейнольдса и коэффициента сопротивления Схо приведены в таблице 4.
Таблица 4 - Характеристики осаждения частиц в изотермических условиях 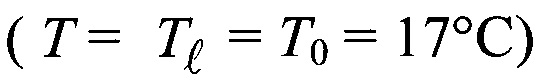
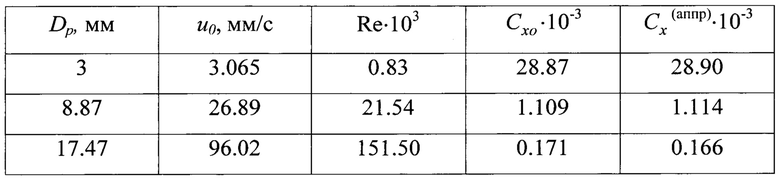
Здесь же приведены значения коэффициента сопротивления 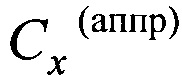 , рассчитанные по аппроксимационной зависимости [9]:
, рассчитанные по аппроксимационной зависимости [9]:

где 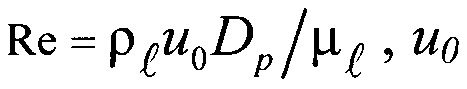 - измеренное значение скорости осаждения частиц.
- измеренное значение скорости осаждения частиц.
Из результатов, приведенных в таблице 3, следует, что в изотермических условиях измеренные значения коэффициента сопротивления Схо соответствуют зависимости (18). Расхождение составляет 0.1% (для Dp=3 мм), 0.4% (для Dp=8.87 мм), 2.9% (для Dp=17.47 мм). Увеличение расхождения для более крупных частиц связано, по-видимому, с погрешностью аппроксимационной зависимости (18).
Измеренные значения скорости осаждения 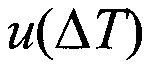 и рассчитанные значения коэффициента сопротивления для нагретых частиц (при
и рассчитанные значения коэффициента сопротивления для нагретых частиц (при 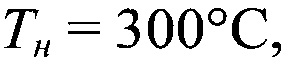
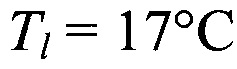 ) приведены в таблице 5.
) приведены в таблице 5.
Таблица 5 - Характеристики осаждения частиц в неизотермических условиях 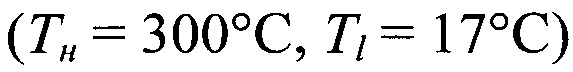

Здесь же приведены значения относительного снижения коэффициента сопротивления частиц при их нагреве до 300°С, рассчитанные по формуле
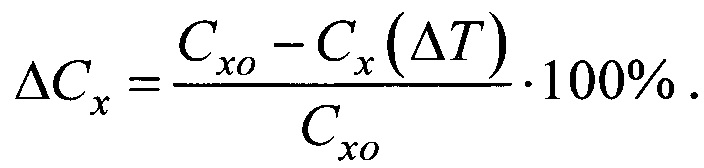
Из результатов, приведенных в таблице 3, следует, что при нагреве шариков диаметром Dp=8.87 мм и Dp=17.47 мм относительное снижение коэффициента сопротивления одинаково и составляет 38%.
Таким образом, из приведенного примера следует, что заявляемый способ обеспечивает достижение технического результата изобретения - возможность определения коэффициента сопротивления твердых сферических частиц при их гравитационном осаждении в вязкой жидкости в неизотермических условиях.
ЛИТЕРАТУРА
1. Романков П.Г., Курочкина М.И. Гидромеханические процессы химической технологии. - Л.: Химия, 1982. - 288 с.
2. Нигматулин Р.И. Динамика многофазных сред. Ч. 1. - М: Наука, 1987. - 464 с.
3. Шрайбер А.А. Многофазные полидисперсные течения с переменным фракционным составом дискретных включений // Итоги науки и техники: Комплексные и специальные разделы механики. - М.: ВИНИТИ, 1988. - С. 3-80.
4. Келбалиев Г.И. Коэффициенты сопротивления твердых частиц, капель и пузырей различной формы // Теоретические основы химической технологии. - 2011. - Т. 45, №3. - С. 264-283.
5. Гуляев И.П., Солоненко О.П. Моделирование поведения полых частиц ZrO2 в плазменной струе с учетом их термического расширения // Теплофизика и аэромеханика. - 2013. - Т. 20, №6. - С. 789-802.
6. Асовский В.П. Особенности тушения лесных пожаров вертолетами с использованием подвесных водосливных устройств // Научный вестник МГТУ ГА: Аэромеханика и прочность. - 2009. - №138. - С. 142-149.
7. Pfender Е., Lee Y.C. Particle dynamics and particle heat and mass transfer in thermal plasmas. Part 1. The motion of a single particle without thermal effects // Plasma chemistry and plasma processing. - 1985. - V. 5, No. 3. - P. 211-237.
8. Eisenklam P., Arunachalam S.A. The drag resistance of burning drops // Combustion and flame. - 1966. - Vol. 10, No. 2. - P. 171-181.
9. Архипов В.А., Усанина А.С. Гравитационное осаждение совокупности твердых сферических частиц в режиме частично продуваемого облака // Инженерно-физический журнал. - 2017. - Т. 90, №5. - С. 1-8.
10. Лыков А.В. Теория теплопроводности. - М: Высшая школа, 1967. - 599 с.
11. Справочник химика. Основные свойства неорганических и органических соединений. Т. 2. - Л.: Химия, 1971. - 1168 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ исследования осаждения сферического облака полидисперсных твердых частиц в вязкой жидкости | 2018 |
|
RU2703935C1 |
| Способ определения коэффициента сопротивления сферической частицы при вдуве газа с ее поверхности | 2018 |
|
RU2700728C1 |
| Установка для исследования осаждения совокупности твердых частиц в жидкости | 2015 |
|
RU2617167C1 |
| Способ исследования осаждения сферического облака твердых частиц в жидкости | 2016 |
|
RU2620761C1 |
| СПОСОБ ИССЛЕДОВАНИЯ ПРОЦЕССА ГРАВИТАЦИОННОГО ОСАЖДЕНИЯ СОВОКУПНОСТИ ТВЕРДЫХ ЧАСТИЦ В ЖИДКОСТИ | 2015 |
|
RU2610607C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СМАЧИВАЕМОСТИ МЕЛКОДИСПЕРСНЫХ ПОРОШКОВ | 2013 |
|
RU2522805C1 |
| СПОСОБ ИЗМЕРЕНИЯ ТЕМПЕРАТУРОПРОВОДНОСТИ ПСЕВДООЖИЖЕННОГО СЛОЯ В НАПРАВЛЕНИИ, ПРОДОЛЬНОМ ПОТОКУ ОЖИЖАЮЩЕГО ГАЗА | 2020 |
|
RU2748141C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕПЛОПРОВОДНОСТИ ТВЕРДЫХ ТЕЛ | 2016 |
|
RU2625599C9 |
| СПОСОБ РАСПОЗНАВАНИЯ ГАЗООБРАЗНЫХ ВЕЩЕСТВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2002 |
|
RU2209425C1 |
| Способ определения геометрии трещин ГРП с учетом разделения и взаимодействия потоков жидкости ГРП между трещинами | 2022 |
|
RU2786303C1 |

Изобретение относится к области разработки способов и устройств для лабораторных исследований физических процессов, в частности для исследования закономерностей движения твердых частиц в жидкости. Способ включает введение частиц в кювету с вязкой жидкостью, выполненную в виде правильной призмы с прозрачными стенками, и измерение скорости их гравитационного осаждения в жидкости. В кювету вводят с нулевой начальной скоростью одновременно две частицы одинакового диаметра, выполненные из одного материала. Одну из частиц непосредственно перед введением в жидкость нагревают или охлаждают до температуры, отличающейся от температуры другой эталонной частицы, равной температуре жидкости, не менее чем на ±20 К. Скорость осаждения каждой из частиц измеряют времяпролетным методом с помощью видеосъемки процесса осаждения через прозрачные стенки кюветы. Время предварительного нагрева или охлаждения одной из частиц, расстояние, на котором измеряют скорость осаждения частиц в жидкости и коэффициент сопротивления нагретой или охлажденной частицы, определяются по заданным алгебраическим соотношениям. Технический результат – повышение достоверности получаемых результатов. 3 ил., 5 табл.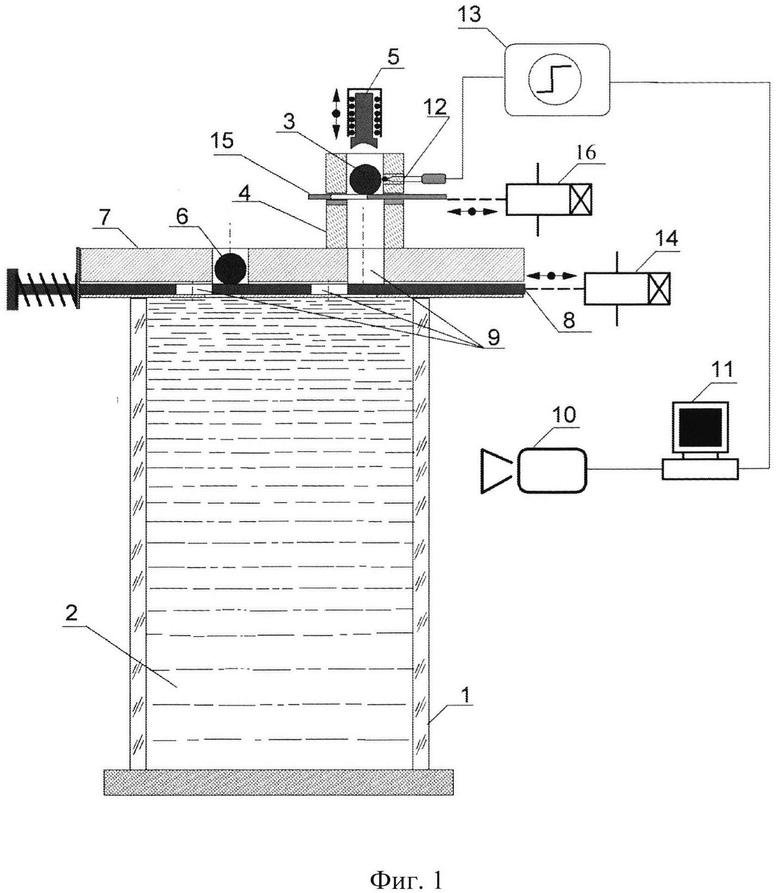
Способ определения коэффициента сопротивления твердых сферических частиц в неизотермических условиях, включающий введение частиц в кювету с вязкой жидкостью, выполненную в виде правильной призмы с прозрачными стенками, и измерение скорости их гравитационного осаждения в жидкости, отличающийся тем, что в кювету вводят с нулевой начальной скоростью одновременно две частицы одинакового диаметра, выполненные из одного материала, причем одну из частиц предварительно перед введением в жидкость нагревают или охлаждают до температуры, отличающейся от температуры другой эталонной частицы, равной температуре жидкости, не менее чем на ±20 К, а скорость осаждения каждой из частиц измеряют времяпролетным методом с помощью видеосъемки процесса осаждения через прозрачные стенки кюветы, при этом время предварительного нагрева или охлаждения одной из частиц, расстояние, на котором измеряют скорость осаждения частиц в жидкости и коэффициент сопротивления нагретой или охлажденной частицы, определяют из соотношений
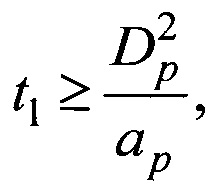
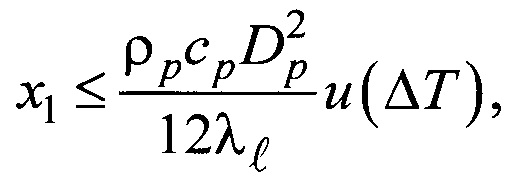
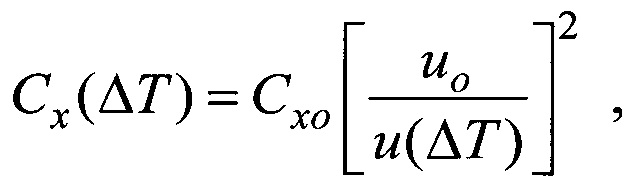
где
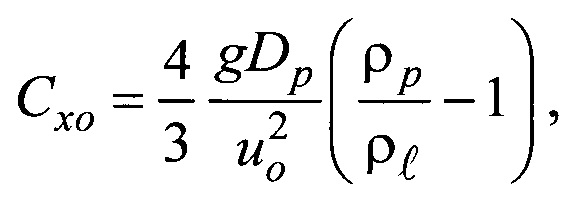
t1 - время предварительного нагрева или охлаждения одной из частиц, с;
Dp - диаметр частицы, м;
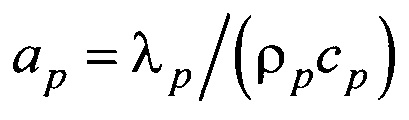 - коэффициент температуропроводности материала частиц, м2/с;
- коэффициент температуропроводности материала частиц, м2/с;
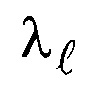 - коэффициент теплопроводности жидкости, Вт/(м⋅К);
- коэффициент теплопроводности жидкости, Вт/(м⋅К);
ρр - плотность материала частиц, кг/м3;
ср - удельная теплоемкость материала частиц, Дж/(кг⋅К);
x1 - расстояние, на котором измеряют скорость осаждения частиц в жидкости, м;
u(ΔТ) - скорость осаждения нагретой или охлажденной частицы, м/с;
ΔT=(Т-To) - величина нагрева или охлаждения частицы, К;
Т - температура нагретой или охлажденной частицы, К;
To - температура эталонной частицы, К;
Cx(ΔT) - коэффициент сопротивления нагретой или охлажденной частицы;
Cxo - коэффициент сопротивления эталонной частицы;
uo - скорость осаждения эталонной частицы, м/с;
g - ускорение свободного падения, м/с2;
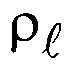 - плотность жидкости, кг/м3.
- плотность жидкости, кг/м3.
| Архипов Β.Α., Усанина А.С., "Гравитационное осаждение совокупности твердых сферических частиц в режиме частично продуваемого облака", Инженерно-физический журнал, 2017, Т | |||
| Пожарный двухцилиндровый насос | 0 |
|
SU90A1 |
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| МАЛАЙ Н.В., ГЛУШАК А.В., "О некоторых особенностях движения нагретых сферических частиц в вязких неизотермических газообразных средах", Научные ведомости Белгородского государственного университета | |||
| Серия: Математика | |||
| Физика, 2009, НОМЕР 5 (60), с.92-98 | |||
| CN 103323377 A, 25.09.2013 | |||
| Способ седиментационного анализа тонкодисперсных материалов | 1990 |
|
SU1814050A1 |
| СПОСОБ АНАЛИЗА АЭРОЗОЛЕЙ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1983 |
|
SU1662226A3 |
Авторы
Даты
2019-07-16—Публикация
2018-10-25—Подача