Изобретение относится к технике связи и может использоваться при проектировании новых и модернизации существующих систем передачи дискретной информации. Заявленный способ может быть применен для декодирования помехоустойчивых систематических блоковых кодов, обеспечивая снижение уровня сложности реализации декодера и повышение достоверность восстановления информации.
Заявленное техническое решение расширяет арсенал применения помехоустойчивых блоковых кодов за счет повышения кратности исправляемых кодом стираний с существенным уменьшением требуемого объема памяти когнитивной карты декодера и снижением сложности реализации вычислительного процесса в процедуре поиска порождающих матриц эквивалентных кодов.
Известен способ мягкого когнитивного декодирования систематических блоковых кодов (см. патент РФ 2644507), в котором реализуется функция обучения декодера и запоминания в его когнитивной карте комбинаций перестановок мягких решений символов для принятых кодовых векторов. С каждой перестановкой единственным образом связывается образец вычисленной эталонной матрицы эквивалентного кода. В последующем в ходе работы при повторении известных декодеру перестановок в нем используются готовые решения без выполнения сложной процедуры матричных вычислений определителя, матрицы миноров и обратной матрицы и определения на этой основе порождающей матрицы соответствующего перестановке эквивалентного кода. Индивидуальные номера в когнитивной карте декодера для их быстрого поиска фиксируются в лексикографической последовательности. Эти номера являются ключами, для извлечения из базы данных декодера соответствующей матрицы эквивалентного кода, что является несомненным достоинством способа. К недостаткам этого способа следует отнести необходимость удерживать в памяти декодера большое число эталонных матриц, соответствующих допустимым для данного кода перестановкам упорядоченных номеров мягких решений символов
Указанный способ реализует устройство (см. патент РФ 2644507), в котором режим обучения декодера осуществляется предварительно за счет использования вычислительных возможностей внешних устройств. С их помощью когнитивная карта декодера может быть заполнена эталонными образцами порождающих матриц эквивалентных кодов до момента оперативной работы декодера. Под оперативной работой понимается процедура непосредственного применения декодера для защиты обрабатываемых данных от ошибок, передаваемых по каналам связи не свободных от влияния деструктивных факторов. Устройство сохраняет положительные свойства описанного выше способа, однако и не устраняет его недостатки.
В случае иного порядка номеров символов кодовой комбинации, зависящий от ранжированных мягких решений символов этой комбинации и отличающегося от лексикографического образца в когнитивной карте, для получения порождающей матрицы эквивалентного кода в систематической форме декодер использует систему быстрых матричных преобразований эталонной матрицы по правилам (см. Гладких А.А., Ал Тамими Т.Ф.Х. Структура быстрых матричных преобразований в процедуре формирования эквивалентных избыточных кодов // Радиотехника. №6, 2017, С. 41-44 и Гладких А.А. Перестановочное декодирование как инструмент повышения энергетической эффективности систем обмена данными // Электросвязь. №8 2017, С. 52 -56).
Наиболее близким по технической сущности к заявленному способу является способ, представленный патентом РФ 2644507. Способ мягкого когнитивного декодирования систематических блоковых кодов, заключающиеся в том, что нумераторы символов принятой кодовой комбинации V исходного систематического (n, k) - кода вместе со своими символами по основному алгоритму упорядочиваются по убыванию их мягких решений и на основании выполненных перестановок формируется вектор V', который совместно с вектором V образуют двудольный граф для формирования матрицы перестановок Р, умножение на которую нумераторов столбцов порождающей матрицы G исходного кода приводит к их перестановке, а вместе с закрепленными за ними столбцами из матрицы G обеспечивает образование новой переставленной матрицы G', при этом взаимоувязанные группы значений нумераторов первых k столбцов Fk и группы значений нумераторов оставшихся (n-k) столбцов R(n-k), распределенных случайно в зависимости от показателей мягких решений символов, временно ранжируется по возрастанию значений этих решений в канонические последовательности нумераторов Fran и Rran, после чего последовательность Fran лексикографически сравнивается с предварительно вычисленными в каноническом формате и внесенными в когнитивную карту декодера всевозможными перестановками из k нумераторов, характеризующих линейно зависимые перестановки и в случае отрицательного исхода этой проверки с использованием той же последовательности Fran переходит к лексикографическому поиску соответствующего образца перестановки в множестве канонических образцов линейно независимых перестановок когнитивной карты декодера, при этом отыскивается образец в точности совпадающий по следованию нумераторов из последовательности Fran, после чего из базы данных положительных решений извлекается готовый образец проверочной части H's порождающей матрицы G's эквивалентного кода, при этом в матрице H's строки оказываются пронумерованными в соответствии с каноническим следованием нумераторов из Fran, а столбцы нумеруются в соответствии с каноническим следованием нумераторов Rran, после чего строки матрицы H's переставляются в строгом соответствии с последовательностью Fk, образуя промежуточную матрицу Н'р1, в которой затем переставляются столбцы в строгом с соответствии с R(n-k) и после добавления к полученной таким образом матрице Н'р2 единичной матрицы слева получают порождающую матрицу эквивалентного кода G's в систематической форме, при этом первые k наиболее надежных элементов вектора V' путем умножения на G's образуют вектор эквивалентного кода Vэкв, который при поэлементном сложении по модулю два с вектором V' формирует переставленный вектор ошибок Е' и после умножения вектора E' на PT формируется истинный вектор ошибок Е, действовавший в канале связи на вектор V, при этом в случае отрицательного результата проверки линейной независимости строк матрицы G' осуществляется замена k-того столбца этой матрицы на (k+1)-й столбец и в случае необходимости на последующие столбцы до выполнения условия линейной независимости k первых столбцов матрицы G' и при выполнении этого условия адекватно меняются местами элементы в V' и столбцы Р.
Достоинством данного способа декодирования является возможность исправлять число ошибок, кратность которых превосходит число ошибок, определяемых метрикой Хэмминга. Кроме того, нет необходимости при декодировании каждого принятого кодового вектора раз за разом осуществлять емкие в вычислительном отношении матричные процедуры поиска определителя переставленной матрицы G', поиска матрицы миноров, вычисления обратной матрицы и поиска по результатам этих вычислений собственно порождающей матрицы G's эквивалентного кода в систематической форме.
Недостаток прототипа заключается в необходимости создания двух элементов памяти декодера. Во-первых, лексикографически организованной памяти когнитивной карты декодера (сравнительно небольшого объема), в которой хранятся образцы перестановок в каноническом формате и, во-вторых, памяти для хранения проверочных частей порождающих матриц эквивалентных кодов, соответствующих каноническим образцам, хранящимся в когнитивной карте декодера. Даже для сравнительно небольших длин избыточных кодов объем этой памяти в зависимости от числа информационных разрядов становится неоправданно велик.
Задачей изобретения является разработка способа декодирования кодовых комбинаций любых блоковых кодов, обеспечивающего получение технического результата, заключающегося в повышении скорости декодирования и достоверности принимаемой информации при исправлении ошибок, а также резкого снижения объемов памяти необходимых для хранения проверочных частей систематических порождающих матриц эквивалентных кодов.
Технический результат достигается тем, что нумераторы символов принятой кодовой комбинации V исходного систематического (n,k) - кода вместе со своими символами по основному алгоритму упорядочиваются по убыванию их мягких решений и на основании выполненных перестановок формируется вектор V', который совместно с вектором V образуют двудольный граф для формирования матрицы перестановок Р, умножение на которую нумераторов столбцов порождающей матрицы G исходного кода, приводит к их перестановке, а вместе с закрепленными за ними столбцами из матрицы G обеспечивает образование новой переставленной матрицы G', при этом взаимоувязанные группы значений нумераторов первых k столбцов Fk и группы значений нумераторов оставшихся (n-k) столбцов R(n-k), распределенных случайно в зависимости от показателей мягких решений символов, временно ранжируется по возрастанию значений этих решений в канонические последовательности нумераторов Fran и Rran, после чего последовательность Fran лексикографически сравнивается с предварительно вычисленными в каноническом формате и внесенными в когнитивную карту декодера всевозможными перестановками из k нумераторов, характеризующих линейно зависимые перестановки и в случае отрицательного исхода этой проверки с использованием той же последовательности Fran переходит к лексикографическому поиску соответствующего образца перестановки в множестве канонических образцов линейно независимых перестановок когнитивной карты декодера, при этом отыскивается образец в точности совпадающий по следованию нумераторов из последовательности Fran, после чего из базы данных положительных решений извлекается готовый образец проверочной части H's порождающей матрицы G's эквивалентного кода, при этом в матрице H's строки оказываются пронумерованными в соответствии с каноническим следованием нумераторов из Fran, а столбцы нумеруются в соответствии с каноническим следованием нумераторов Rran, после чего строки матрицы H's перемещаются в строгом соответствии с последовательностью Fk, образуя промежуточную матрицу Н'р1, в которой затем перемещаются столбцы в строгом с соответствии с R(n-k) и после добавления к полученной таким образом матрице Н'р2 единичной матрицы слева получают порождающую матрицу эквивалентного кода G's в систематической форме, при этом первые k наиболее надежных элементов вектора V' путем умножения на G's образуют вектор эквивалентного кода Vэкв, который при поэлементном сложении по модулю два с вектором V' формирует переставленный вектор ошибок Е' и после умножения вектора Е' на PT формируется вектор ошибок Е, действовавший в канале связи на вектор V, при этом в случае отрицательного результата проверки линейной независимости строк матрицы G' осуществляется замена k-того столбца этой матрицы на (k+1)-й столбец и в случае необходимости на последующие столбцы до выполнения условия линейной независимости k первых столбцов матрицы G' и при выполнении этого условия адекватно меняются местами элементы в V' и столбцы Р, отличающиеся тем, что все образцы перестановок когнитивной карты Fran разбиваются на 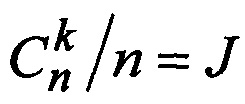 циклические группы, в основе каждой из которых стоит формирующая комбинация нумераторов Zj, при этом из-за циклических сдвигов часть образцов может утратить свою каноническую форму и принять вид Fcyc и Rcyc, однако все циклические сдвиги образцов из циклической группы Zj представляются единственной систематической порождающей матрицей G'sj, а когнитивная карта декодера для каждой пары значений Fran и Rran дополняется номером j, указывающим на принадлежность конкретной комбинации из Fran и Rran к G'sj, в случаях, кода Fran≠Fcyc и Rran≠Rcyc в когнитивную карту декодера вносятся значения Fcyc и Rcyc для образования шаблона перевода Fcyc в Fran и Rcyc в Rran за счет целенаправленного перемещения их строк и столбцов, после чего выполняются действия по основному алгоритму.
циклические группы, в основе каждой из которых стоит формирующая комбинация нумераторов Zj, при этом из-за циклических сдвигов часть образцов может утратить свою каноническую форму и принять вид Fcyc и Rcyc, однако все циклические сдвиги образцов из циклической группы Zj представляются единственной систематической порождающей матрицей G'sj, а когнитивная карта декодера для каждой пары значений Fran и Rran дополняется номером j, указывающим на принадлежность конкретной комбинации из Fran и Rran к G'sj, в случаях, кода Fran≠Fcyc и Rran≠Rcyc в когнитивную карту декодера вносятся значения Fcyc и Rcyc для образования шаблона перевода Fcyc в Fran и Rcyc в Rran за счет целенаправленного перемещения их строк и столбцов, после чего выполняются действия по основному алгоритму.
Способ применим к любому систематическому блоковому коду, рассматривается на примере группового кода (7,4) и осуществляется следующим образом. Пусть порождающая матрица G исходного кода имеет вид
Нумераторы столбцов 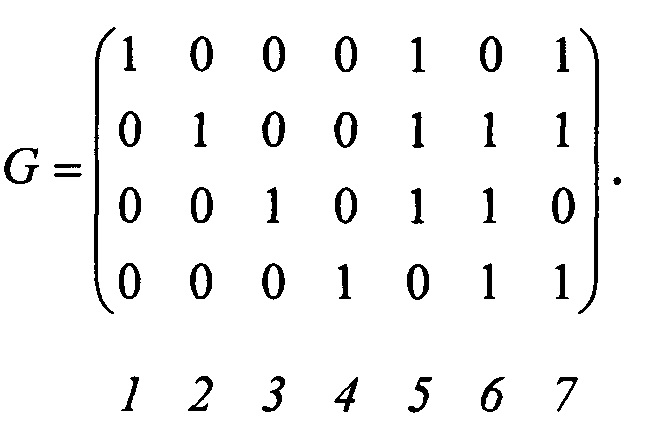
Нумерация столбцов матрицы осуществляется слева направо с использованием нумераторов столбцов, при этом за каждым нумератором постоянно закрепляется конкретный столбец матрицы G. В ходе декодирования возможно образование 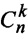 перестановок, относящихся к группе нумераторов Fk, которые для кода (7,4) представлены в таблице 1.
перестановок, относящихся к группе нумераторов Fk, которые для кода (7,4) представлены в таблице 1.
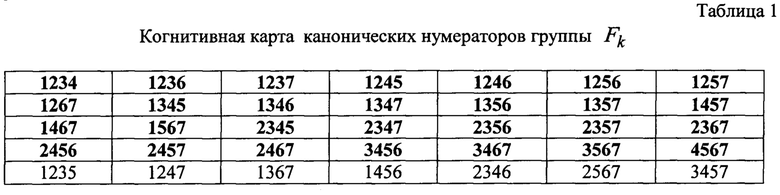
В таблице 1 в первых четырех строках выделены нумераторы линейно независимых перестановок, последняя строка таблицы 1 соответствует линейно зависимым перестановкам, которые не позволяют получить эквивалентный код. Для быстрого поиска произвольной перестановки столбцов матрицы G нумераторы в когнитивной карте декодера имеют лексикографическое распределение. Каждому нумератору из числа линейно независимых перестановок соответствует порождающая матрица эквивалентного кода, проверочная часть которой хранится в отдельной базе данных декодера и даже для сравнительно небольших длин кодовых комбинаций требует значительных объемов памяти. Анализ содержания таблицы 1 показывает, что все нумераторы для Fcyc и Rcyc имеют циклическую структуру, которая показана в таблице 2.
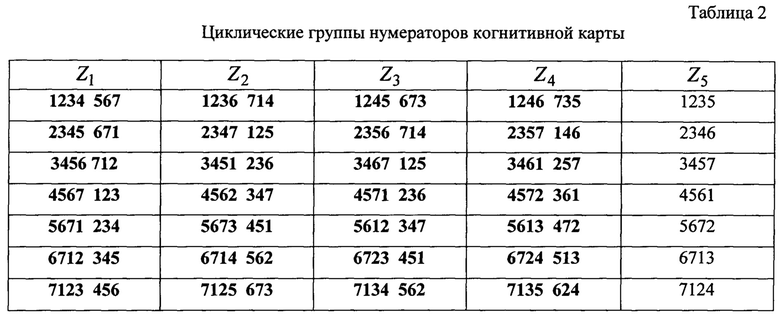
Формирующие комбинации нумераторов циклических групп Zj показаны в первой строке таблицы 2, а проверочные части порождающих матриц для этих групп имеют вид
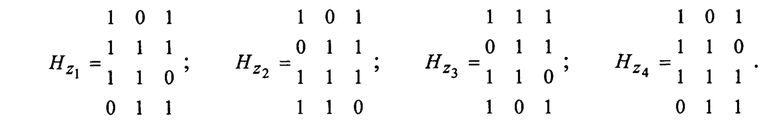
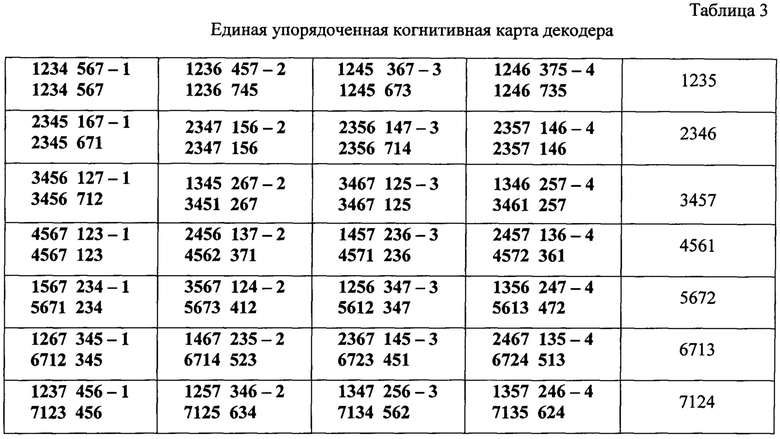
Таким образом, объем памяти необходимой для хранения в базе данных проверочных частей порождающих матриц эквивалентных кодов в систематической форме уменьшается в k раз. Для осуществления эффективного поиска порождающей матрицы эквивалентного кода необходимо объединение данных из таблиц 1 и 2 в рамках единой упорядоченной когнитивной карты, формат которой представлен в таблице 3. На базе этой карты декодер может реализовать унифицированный алгоритм обработки данных, используя сокращенное число порождающих матриц, но для быстрого поиска требуемого элемента когнитивной карты целесообразно использовать единую лексикографически упорядоченную когнитивную карту декодера, представленную в таблице 4.
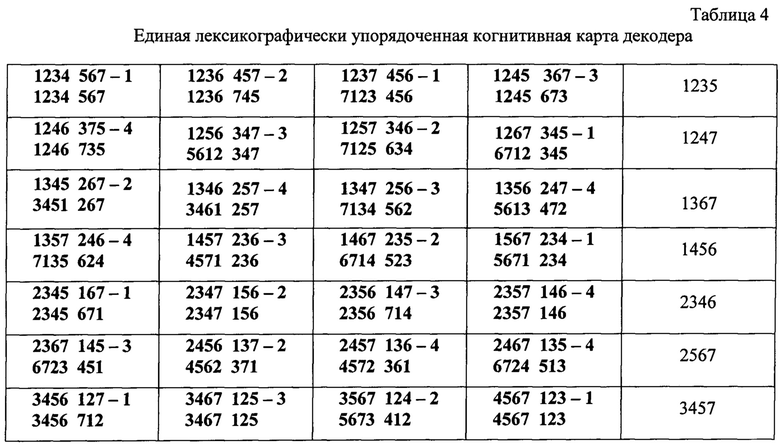
Пусть принят вектор V, для которого в результате преобразования в вектор V' нумераторы значений надежных и ненадежных символов приняли вид Fk=7415 и R(n-k)=623. Отсюда Fran=1457 и значения нумераторов надежных символов приняли лексикографически упорядоченную конфигурацию вида 1457. Проверка принадлежности полученной конфигурации Fran к категории линейно зависимых дает отрицательный результат, следовательно, декодер осуществляет лексикографический поиск значения Fran=1457 в группе линейно независимых перестановок, получая значение когнитивной карты в виде шаблона:
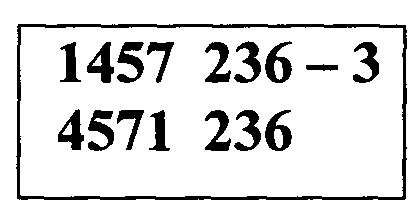
из которого следует, что образцом дальнейших матричных преобразований является матрица с номером 3. Извлекая эту матрицу из базы данных, декодер выполняет над ней в соответствии с шаблоном обычные перестановки строк и столбцов, как показано ниже.

Последовательность дальнейших преобразований в соответствии верхней строкой шаблона имеет вид:
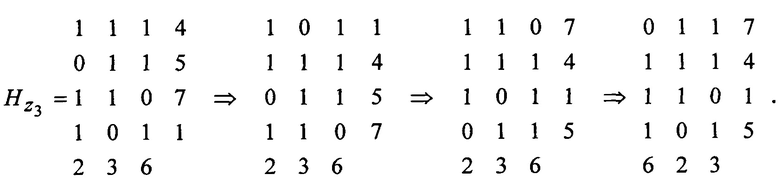
Подстановка единичной матрицы слева обеспечивает получение требуемой матрицы эквивалентного кода G's.
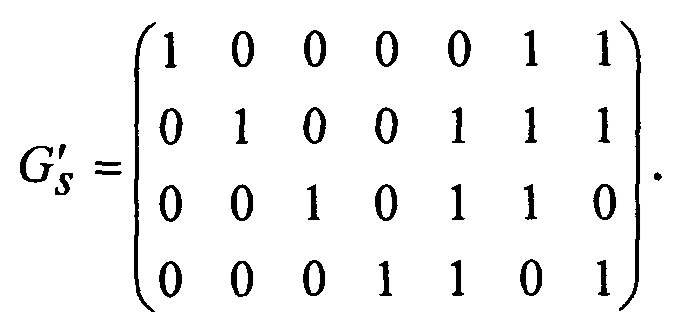
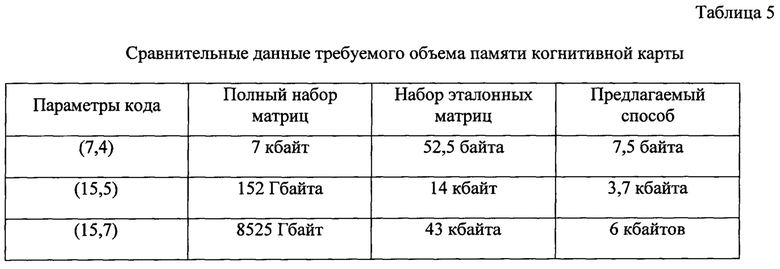
Матричные преобразования классического типа приводят к аналогичному результату, но требуют значительных вычислительных затрат. Сравнительные характеристики требуемых объемов памяти когнитивной карты декодера при различных подходах к ее организации для некоторых двоичных кодов приведены в таблице 5. Учитывая свойства групповых кодов, рассматриваемых над двоичными полями Галуа заданной степени расширения становится очевидным преимущество предлагаемого способа, поскольку нет необходимости выполнять арифметические действия над элементами матриц с соблюдением соответствующих правил сложение и умножения обрабатываемых матриц.
| название | год | авторы | номер документа |
|---|---|---|---|
| ПЕРЕСТАНОВОЧНЫЙ ДЕКОДЕР С СИСТЕМОЙ БЫСТРЫХ МАТРИЧНЫХ ПРЕОБРАЗОВАНИЙ | 2019 |
|
RU2718224C1 |
| Перестановочный декодер с альтернативными решениями | 2024 |
|
RU2826701C1 |
| Генератор комбинаций двоичного эквивалентного кода | 2019 |
|
RU2743854C1 |
| СПОСОБ МЯГКОГО ДЕКОДИРОВАНИЯ СИСТЕМАТИЧЕСКИХ БЛОКОВЫХ КОДОВ | 2010 |
|
RU2444127C1 |
| СПОСОБ МЯГКОГО КОГНИТИВНОГО ДЕКОДИРОВАНИЯ СИСТЕМАТИЧЕСКИХ БЛОКОВЫХ КОДОВ | 2016 |
|
RU2646372C1 |
| СПОСОБ МЯГКОГО ДЕКОДИРОВАНИЯ БЛОКОВЫХ КОДОВ | 2015 |
|
RU2580797C1 |
| ПЕРЕСТАНОВОЧНЫЙ ДЕКОДЕР С ПАМЯТЬЮ | 2017 |
|
RU2672300C2 |
| ПЕРЕСТАНОВОЧНЫЙ ДЕКОДЕР С ОБРАТНОЙ СВЯЗЬЮ | 2018 |
|
RU2704722C2 |
| Перестановочный декодер с режимом обучения | 2017 |
|
RU2644507C1 |
| ДЕКОДЕР С УПОРЯДОЧЕННОЙ СТАТИСТИКОЙ СИМВОЛОВ | 2012 |
|
RU2490804C1 |
Изобретение относится к технике связи и может использоваться при проектировании новых и модернизации существующих систем передачи дискретной информации. Технический результат заключается в возможности сократить объем памяти для хранения порождающих матриц эквивалентных кодов. Способ перестановочного декодирования блоковых кодов на базе упорядоченной когнитивной карты заключается в том, что нумераторы символов принятой кодовой комбинации V исходного систематического блокового кода вместе со своими символами по основному алгоритму упорядочиваются по убыванию их мягких решений. Все мягкие решения делятся на две группы. В первую группу входят наиболее надежные оценки, и именно по ним определяют структуру порождающей матрицы эквивалентного кода. Поскольку перестановки надежных символов могут повторяться при обработке последующих комбинаций, то они запоминаются декодером вместе с соответствующими им результатами их обработки и заносятся в когнитивную карту декодера. Получив конкретный образец перестановки, декодер лексикографически находит этот образец в когнитивной карте и извлекает из базы данных готовый образец порождающей матрицы эквивалентного кода, после чего работа декодера выполняется по основному алгоритму. Поскольку все допустимые перестановки в групповых кодах подчиняются циклическим сдвигам, то для каждой такой группы перестановок вырабатывается образец порождающей матрицы, а все допустимые перестановки в лексикографическом списке сопровождаются дополнительно номером циклической группы, к которой относится конкретная перестановка. 5 табл.
Способ перестановочного декодирования блоковых кодов на базе упорядоченной когнитивной карты, заключающийся в том, что нумераторы символов принятой кодовой комбинации V исходного систематического (n,k)-кода вместе со своими символами по основному алгоритму упорядочиваются по убыванию их мягких решений и на основании выполненных перестановок формируется вектор V', который совместно с вектором V образуют двудольный граф для формирования матрицы перестановок Р, умножение на которую нумераторов столбцов порождающей матрицы G исходного кода приводит к их перестановке, а вместе с закрепленными за ними столбцами из матрицы G обеспечивает образование новой переставленной матрицы G', при этом взаимоувязанные группы значений нумераторов первых k столбцов Fk и группы значений нумераторов оставшихся (n-k) столбцов R(n-k), распределенных случайно в зависимости от показателей мягких решений символов, временно ранжируется по возрастанию значений этих решений в канонические последовательности нумераторов Fran и Rran, после чего последовательность Fran лексикографически сравнивается с предварительно вычисленными в каноническом формате и внесенными в когнитивную карту декодера всевозможными перестановками из k нумераторов, характеризующих линейно зависимые перестановки, и в случае отрицательного исхода этой проверки с использованием той же последовательности Fran переходит к лексикографическому поиску соответствующего образца перестановки в множестве канонических образцов линейно независимых перестановок когнитивной карты декодера, при этом отыскивается образец, в точности совпадающий по следованию нумераторов из последовательности Fran, после чего из базы данных положительных решений извлекается готовый образец проверочной части 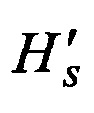 порождающей матрицы
порождающей матрицы 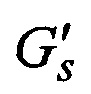 эквивалентного кода, при этом в матрице
эквивалентного кода, при этом в матрице 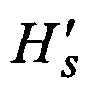 строки оказываются пронумерованными в соответствии с каноническим следованием нумераторов из Fran, а столбцы нумеруются в соответствии с каноническим следованием нумераторов Rran, после чего строки матрицы
строки оказываются пронумерованными в соответствии с каноническим следованием нумераторов из Fran, а столбцы нумеруются в соответствии с каноническим следованием нумераторов Rran, после чего строки матрицы 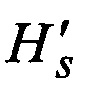 перемещаются в строгом соответствии с последовательностью Fk, образуя промежуточную матрицу
перемещаются в строгом соответствии с последовательностью Fk, образуя промежуточную матрицу 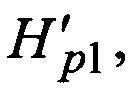 в которой затем перемещаются столбцы в строгом с соответствии с R(n-k), и после добавления к полученной таким образом матрице
в которой затем перемещаются столбцы в строгом с соответствии с R(n-k), и после добавления к полученной таким образом матрице 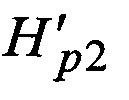 единичной матрицы слева получают порождающую матрицу эквивалентного кода
единичной матрицы слева получают порождающую матрицу эквивалентного кода 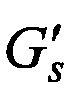 в систематической форме, при этом первые k наиболее надежных элементов вектора V' путем умножения на
в систематической форме, при этом первые k наиболее надежных элементов вектора V' путем умножения на 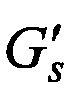 образуют вектор эквивалентного кода Vэкв, который при поэлементном сложении по модулю два с вектором V' формирует переставленный вектор ошибок Е', и после умножения вектора E' на PT формируется вектор ошибок Е, действовавший в канале связи на вектор V, при этом в случае отрицательного результата проверки линейной независимости строк матрицы G' осуществляется замена k-го столбца этой матрицы на (k+1)-й столбец и в случае необходимости на последующие столбцы до выполнения условия линейной независимости k первых столбцов матрицы G' и при выполнении этого условия адекватно меняются местами элементы в V' и столбцы Р, отличающийся тем, что все образцы перестановок когнитивной карты Fran разбиваются на
образуют вектор эквивалентного кода Vэкв, который при поэлементном сложении по модулю два с вектором V' формирует переставленный вектор ошибок Е', и после умножения вектора E' на PT формируется вектор ошибок Е, действовавший в канале связи на вектор V, при этом в случае отрицательного результата проверки линейной независимости строк матрицы G' осуществляется замена k-го столбца этой матрицы на (k+1)-й столбец и в случае необходимости на последующие столбцы до выполнения условия линейной независимости k первых столбцов матрицы G' и при выполнении этого условия адекватно меняются местами элементы в V' и столбцы Р, отличающийся тем, что все образцы перестановок когнитивной карты Fran разбиваются на 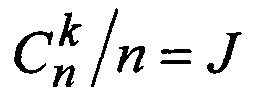 циклические группы, в основе каждой из которых стоит формирующая комбинация нумераторов Zj, при этом из-за циклических сдвигов часть образцов может утратить свою каноническую форму и принять вид Fcyc и Rcyc, однако все циклические сдвиги образцов из циклической группы Zj представляются единственной систематической порождающей матрицей
циклические группы, в основе каждой из которых стоит формирующая комбинация нумераторов Zj, при этом из-за циклических сдвигов часть образцов может утратить свою каноническую форму и принять вид Fcyc и Rcyc, однако все циклические сдвиги образцов из циклической группы Zj представляются единственной систематической порождающей матрицей 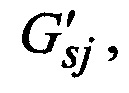 а когнитивная карта декодера для каждой пары значений Fran и Rran дополняется номером j, указывающим на принадлежность конкретной комбинации из Fran и Rran к
а когнитивная карта декодера для каждой пары значений Fran и Rran дополняется номером j, указывающим на принадлежность конкретной комбинации из Fran и Rran к 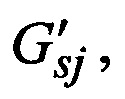 а в случаях, кода Fran≠Fcyc и Rran≠Rcyc, в когнитивную карту декодера вносятся значения Fcyc и Rcyc для образования шаблона перевода Fcyc в Fran и в Rran за счет целенаправленного перемещения их строк и столбцов, после чего выполняются действия по основному алгоритму.
а в случаях, кода Fran≠Fcyc и Rran≠Rcyc, в когнитивную карту декодера вносятся значения Fcyc и Rcyc для образования шаблона перевода Fcyc в Fran и в Rran за счет целенаправленного перемещения их строк и столбцов, после чего выполняются действия по основному алгоритму.
| СПОСОБ МЯГКОГО КОГНИТИВНОГО ДЕКОДИРОВАНИЯ СИСТЕМАТИЧЕСКИХ БЛОКОВЫХ КОДОВ | 2016 |
|
RU2646372C1 |
| Перестановочный декодер с режимом обучения | 2017 |
|
RU2644507C1 |
| СПОСОБ МЯГКОГО ДЕКОДИРОВАНИЯ БЛОКОВЫХ КОДОВ | 2015 |
|
RU2580797C1 |
| Колосоуборка | 1923 |
|
SU2009A1 |
| Способ и приспособление для нагревания хлебопекарных камер | 1923 |
|
SU2003A1 |
Авторы
Даты
2019-08-19—Публикация
2018-07-11—Подача