Изобретение относится к области космонавтики, а именно к технике выполнения траекторных измерений и определения параметров орбиты искусственного спутника Земли (ИСЗ), и может быть использовано на наземных и бортовых комплексах управления полетом ИСЗ для точного определения текущих параметров движения ИСЗ.
Известен способ определения координат навигационных ИСЗ [1], заключающийся в том, что:
выбирают группу из четырех навигационных ИСЗ, находящихся в зоне прямой видимости, состоящей из первой пары навигационных ИСЗ, находящихся на одной орбите, и второй пары навигационных ИСЗ, находящихся на другой орбите;
одновременно измеряют линейные межспутниковые расстояния между всеми четырьмя навигационными ИСЗ группы;
передают измеренные значения линейных расстояний от каждого ИСЗ группы к каждому;
вычисляют на каждом навигационном ИСЗ сферические расстояния между ним и координаты точки пересечения орбит выбранных навигационных ИСЗ;
определяют значения координат навигационных ИСЗ на основе значений сферических расстояний между ними и координат точки пересечения орбит.
К недостаткам способа определения координат навигационных ИСЗ [1] относят:
длительное время определения координат навигационных ИСЗ, связанное с необходимостью циркуляции информации между соседними ИСЗ;
высокую стоимость устройства, реализующего способ, обусловленную необходимостью размещения на борту навигационных ИСЗ дополнительных передатчиков, приемников, а также аппаратуры обработки информации.
Известен способ определения параметров орбиты геостационарного ИСЗ [2], заключающийся в том, что:
размещают приемо-излучающую наземную радиотехническую станцию (НРТС) на позиции с известными координатами с известными координатами;
выбирают начальные (априорные) значения параметров орбиты геостационарного ИСЗ;
измеряют наклонную дальность от НРТС до геостационарного ИСЗ;
многократно, в течении мерного интервала, составляющего не менее двух суток, измеряют наклонную дальность от НРТС до геостационарного ИСЗ с интервалом 2…3 часа;
делят полученную совокупность измерений на две части: обучаемую и контрольную;
делят определяемые параметры орбиты ИСЗ на две группы: внутриплоскостные и внеплоскостные;
производят серию оценок внутриплоскостных параметров орбиты ИСЗ при различных фиксированных значениях внеплоскостных параметров;
выбирают параметры орбиты геостационарного ИСЗ на основе серии произведенных оценок.
Недостатком способа определения параметров орбиты геостационарного ИСЗ [2] является большая продолжительность мерного интервала проведения измерений дальностей, которая должна составлять не менее двух последовательных суток.
Из известных способов наиболее близким аналогом (прототипом) предлагаемого способа по технической сущности является способ определения параметров орбиты искусственного спутника Земли [3]. Для реализации данного способа последовательно выполняют следующие этапы:
излучают тестовые радиосигналы НРТС на средней частоте ƒ0 и N ИОРС на средних частотах ƒn в момент времени t0;
принимают тестовые радиосигналов после их ретрансляции ИЗС с помощью НРТС в моменты времени  на средних частотах
на средних частотах  соответственно;
соответственно;
измеряют наклонные дальности от ИСЗ до НРСТ RSK и до каждой из N ИОРС 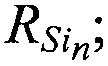
вычисляют координаты ИСЗ x0, у0, z0 по известным координатам НРСТ, известным координатам N ИОРС и измеренным наклонным дальностям RSK, и 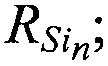 ;
;
вычисляют ортогональные составляющие вектора скорости ИСЗ 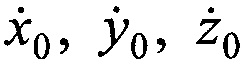 по известным координатам НРСТ, известным координатам N ИОРС, вычисленным координатам ИСЗ х0, уо, z0, запомненным номиналам средних частот переданных ƒ0, ƒn и принятых
по известным координатам НРСТ, известным координатам N ИОРС, вычисленным координатам ИСЗ х0, уо, z0, запомненным номиналам средних частот переданных ƒ0, ƒn и принятых 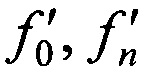 тестовых радиосигналов, предварительно заданной частоте сдвига ƒG рабочей частоты ИСЗ;
тестовых радиосигналов, предварительно заданной частоте сдвига ƒG рабочей частоты ИСЗ;
в качестве параметров орбиты ИСЗ принимают совокупность координат ИСЗ x0, у0, z0 и ортогональных составляющих вектора его скорости 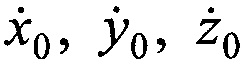 в момент времени t0.
в момент времени t0.
Недостатками способа прототипа [3] являются:
относительно-невысокая точность определения параметров орбиты ИСЗ, обусловленная ограничениями, накладываемыми на время излучения и на ширину спектра тестовых радиосигналов;
ограниченная область применения способа, вызванная необходимостью прямой ретрансляции (без обработки на борту ИСЗ) тестовых радиосигналов указанным ИСЗ.
Целью изобретения является разработка способа, обеспечивающего повышение точности определения параметров орбиты ИСЗ и обеспечивающего более широкую областью применения.
Поставленная цель достигается тем, что в известном способе определения параметров орбиты ИСЗ включающим размещение НРТС на позиции с известными координатами xK, yK, zK, выбор начальных значений параметров орбиты ИСЗ, прием в НРТС радиосигналов от ИСЗ, измерение с помощью аппаратуры НРТС временных задержек и частотных сдвигов радиосигналов, принятых от ИСЗ в момент времени t0, вычисление координат ИСЗ x0, у0, z0 по известным координатам НРСТ и значениям временных задержек радиосигналов, вычисление ортогональных составляющих вектора скорости ИСЗ 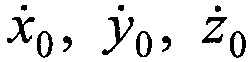 по известным координатам НРСТ, вычисленным координатам ИСЗ и частотным сдвигам радиосигналов, принятие в качестве параметров орбиты ИСЗ совокупности координат ИСЗ x0, у0, z0 и ортогональных составляющих вектора его скорости
по известным координатам НРСТ, вычисленным координатам ИСЗ и частотным сдвигам радиосигналов, принятие в качестве параметров орбиты ИСЗ совокупности координат ИСЗ x0, у0, z0 и ортогональных составляющих вектора его скорости  в момент времени t0, дополнительно устанавливают на земной поверхности М≥3 ПОРС на позициях с известными координатами x1m, y1m, z1m, где m=1…М - номер ПОРС.
в момент времени t0, дополнительно устанавливают на земной поверхности М≥3 ПОРС на позициях с известными координатами x1m, y1m, z1m, где m=1…М - номер ПОРС.
Далее принимают от ИСЗ и записывают с помощью аппаратуры НРТС и М ПОРС радиосигналы совместно с метками времени. Передают на НРСТ записанные копии радиосигналов ИСЗ совместно с метками времени от М ПОРС. Выбирают радиосигнал, принятый от ИСЗ и записанный с помощью аппаратуры НРТС совместно с метками времени в качестве опорного. Формируют М отличающихся друг от друга пар радиосигналов, принятых от ИСЗ, одним из элементов в каждой из пар выбирают опорный радиосигнал. Для каждой сформированной пары радиосигналов измеряют с помощью корреляционной обработки значения взаимной временной задержки Δtm и частотного сдвига Δƒm. Рассчитывают М разностей дальностей ΔRm на основе временных задержек Δtm. Рассчитывают М разностей радиальных скоростей ΔRm на основе частотных сдвигов Δƒm. Вычисляют координаты ИСЗ х0, у0, z0 по известным координатам НРСТ и М ПОРС, рассчитанным разностям дальностей ARm. Вычисляют ортогональные составляющие вектора скорости ИСЗ  по известным координатам НРСТ и М ПОРС, вычисленным координатам ИСЗ х0, у0, z0, рассчитанным разностям радиальных скоростей ΔRm. В качестве параметров орбиты ИСЗ принимают совокупность координат ИСЗ х0, у0, z0 и ортогональных составляющих вектора его скорости
по известным координатам НРСТ и М ПОРС, вычисленным координатам ИСЗ х0, у0, z0, рассчитанным разностям радиальных скоростей ΔRm. В качестве параметров орбиты ИСЗ принимают совокупность координат ИСЗ х0, у0, z0 и ортогональных составляющих вектора его скорости  в момент времени t0.
в момент времени t0.
Благодаря перечисленной новой совокупности существенных признаков, за счет использования НРТС, размещенной на позиции с известными координатами, работающей в режиме приема и М≥3 ПОРС на позициях с известными координатами достигается цель изобретения: повышение точности определения параметров орбиты ИСЗ с одновременным расширением области применения способа.
Заявленный способ поясняется чертежами, на которых показаны: на фиг. 1 - система трех возмущающих тел: Земли, Солнца и Луны, на фиг. 2 - схема алгоритма прогноза координат ИСЗ, на фиг. 3 - структурная схема подсистемы определения координат ИСЗ, на фиг. 4 - схема алгоритма расчета координат ИСЗ, на фиг. 5 - структурная схема подсистемы определения ортогональных составляющих вектора скорости ИСЗ.
Теория полета ИСЗ, или, как ее еще называют, астродинамика, небесная механика, космическая баллистика, основана на законах И. Кеплера и законе всемирного тяготения И. Ньютона.
В первом приближении движение ИСЗ представляется как невозмущенное - такое движение, которое происходило бы только под влиянием силы притяжения Земли по закону Ньютона, т.е. точно соответствует задаче двух тел (Земля - ИСЗ) в небесной механике. Это движение называется движением по Кеплеровой орбите, так как подчиняется трем законам Кеплера [4].
Достоинством Кеплеровой орбиты является простота вычисления координат и вектора скорости ИСЗ в прогнозируемый момент времени. Это предопределило широкое использование элементов Кеплеровой орбиты. В настоящем изобретении элементы Кеплеровой орбиты ИСЗ выступают в качестве априорных данных об ИСЗ. С помощью этих элементов ориентируют приемные антенны НРСТ и М ПОРС на ИСЗ, Кроме того элементы Кеплеровой орбиты ИСЗ служат для устранения двузначности определения координат ИСЗ.
Недостатком Кеплеровой орбиты является относительно низкая точность определения координат и вектора скорости ИСЗ, которая недостаточна для выполнения ряда прикладных задач, например, для корректировки движения ИСЗ.
Более точно движение ИСЗ описывается с помощью возмущенной орбиты [4, 5], которая задается:
каноническими параметрами ИСЗ, включающими координаты ИСЗ х0, у0, z0 и ортогональные составляющие вектора его скорости 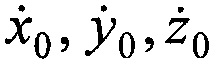 в начальный момент времени t0,
в начальный момент времени t0,
факторами, приводящими к отклонениям ИСЗ от идеальной (Кеплеровой) орбиты и называемыми возмущающими факторами.
Например, для геостационарного ИСЗ достаточно учитывать только три фактора, приводящих к отклонениям ИСЗ от идеальной (Кеплеровой) орбиты, - влияние Солнца, Луны и нецентральности гравитационного поля Земли. Схема трех возмущающих тел: Земли Sз, Солнца Sc и Луны Sл отображена на фиг. 1. Точками S0 (х0, у0, z0) и Sпр (хпр, упр, zпр) показаны координаты, а стрелками  - векторы скоростей ИСЗ в начальный момент времени t0 и в прогнозируемый момент времени tnp соответственно в геоцентрической декартовой системе координат OзXYZ.
- векторы скоростей ИСЗ в начальный момент времени t0 и в прогнозируемый момент времени tnp соответственно в геоцентрической декартовой системе координат OзXYZ.
Алгоритм прогноза координат геостационарного ИСЗ описан в приложении А, при этом процедуры расчета координат Солнца и Луны вынесены в приложение Б.
Прогноз канонических параметров ИСЗ 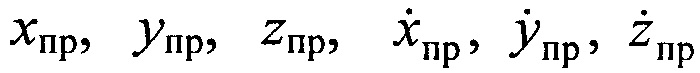 в нужный (прогнозируемый) момент времени tnp осуществляют на основе исходных данных
в нужный (прогнозируемый) момент времени tnp осуществляют на основе исходных данных 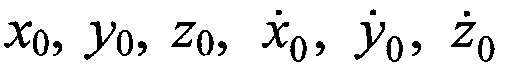 в момент t0 и рассчитанных силовых функций (ускорений) U1, U2, U3, действующих на ИСЗ со стороны Земли, Солнца и Луны соответственно на основе решения системы дифференциальных уравнений (А.2).
в момент t0 и рассчитанных силовых функций (ускорений) U1, U2, U3, действующих на ИСЗ со стороны Земли, Солнца и Луны соответственно на основе решения системы дифференциальных уравнений (А.2).
Прогноз координат других (не геостационарных) ИСЗ проводят на основе алгоритма аналогичного рассмотренному, с той лишь разницей, что учитывают больше факторов, приводящих к отклонениям ИСЗ от идеальной (Кеплеровой) орбиты. В качестве таких факторов, например, для ИСЗ на низких орбитах выступают: влияние сопротивления атмосферы Земли, светового давления, притяжения планет.
Система определения канонических параметров ИСЗ S0 содержит одну НРТС K и М≥3 ПОРС Im, m=1…М (см. фиг. 3) на позициях с известными координатами, принимающие радиосигналы ИСЗ [6].
Для обеспечения синхронности работы приемников НРТС и М ПОРС используют метки времени высокостабильного генератора частот.
Для определения координат ИСЗ х0, у0, z0 в момент времени to используют временные задержки радиосигналов, принятых НРТС и М ПОРС Δtm. Для получения таких задержек предварительно принимают от ИСЗ и записывают с помощью аппаратуры НРТС и М ПОРС радиосигналы совместно с метками времени. Передают по каналам радиосвязи на НРСТ записанные копии радиосигналов ИСЗ совместно с метками времени от М ПОРС.
Выбирают радиосигнал, принятый от ИСЗ и записанный с помощью аппаратуры НРТС совместно с метками времени в качестве опорного. Формируют М отличающихся друг от друга пар радиосигналов, принятых от ИСЗ, одним из элементов в каждой из пар выбирают опорный радиосигнал. Для каждой сформированной пары радиосигналов измеряют с помощью корреляционной обработки значения взаимной временной задержки Δtm и частотного сдвига Δƒm [7].
На основе полученных задержек во времени Δtm рассчитывают М разностей дальностей ΔRm от НРТС и m-й ПОРС до ИСЗ:

где c=3×108 м/с - скорость света в вакууме.
Полученные разности дальностей ΔRm являются координатно-информативными параметрами ИСЗ, а поверхностями положения ИСЗ будут двуполостными гиперболоидами вращения с фокусами, совпадающими с известными координатами НРТС и соответствующей ПОРС.
Координаты точки пересечения полученных гиперболоидов вращения соответствуют искомым координатам ИСЗ х0, у0, z0 в момент времени t0.
Для одномоментного определения координат ИСЗ необходимо наличие трех гиперболоидов вращения а, следовательно, трех ПОРС I1, I2 и I3. Дальнейшее увеличение количества ПОРС будет приводить к повышению точности определения координат ИСЗ и сопутствующим увеличением суммарной стоимости устройства, реализующего способ. Двузначность определения координат ИСЗ, обусловленная тем, что три гиперболоида вращения пересекаются в двух точках, устраняется априорными данными о координатах ИСЗ, в качестве которых выступают известные элементы Кеплеровой орбиты ИСЗ.
Для определения координат ИСЗ возможно использование и двух, и одной ПОРС.Однако, в таком случае время, необходимое для определения координат ИСЗ будет значительно возрастать.
В качестве примера в приложении В представлена аналитическая интерпретация алгоритма построения трех поверхностей положения в виде гиперболоидов вращения, а также нахождения точки пересечения таких поверхностей. В качестве выходных результатов представленного алгоритма выступают координат ИСЗ х0, у0, z0 в момент времени t0.
Для определения ортогональных составляющих вектора скорости ИСЗ 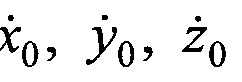 в момент времени t0 используют частотные сдвиги радиосигналов приятых НРТС и М ПОРС от ИСЗ Δƒm. Для частотного сдвига Δƒm рассчитывают разность радиальных скоростей
в момент времени t0 используют частотные сдвиги радиосигналов приятых НРТС и М ПОРС от ИСЗ Δƒm. Для частотного сдвига Δƒm рассчитывают разность радиальных скоростей  .
.
Для одномоментного и однозначного определения ортогональных составляющих вектора скорости ИСЗ необходимо использование трех разностей радиальных скоростей  а следовательно, трех ПОРС. Дальнейшее увеличение количества ПОРС будет приводить к повышению точности определения ортогональных составляющих вектора скорости ИСЗ, но с сопутствующим увеличением суммарной стоимости устройства, реализующего способ.
а следовательно, трех ПОРС. Дальнейшее увеличение количества ПОРС будет приводить к повышению точности определения ортогональных составляющих вектора скорости ИСЗ, но с сопутствующим увеличением суммарной стоимости устройства, реализующего способ.
Для определения ортогональных составляющих вектора скорости ИСЗ возможно использование и двух, и одной ПОРС. Однако, в таком случае время, необходимое для определения ортогональных составляющих вектора скорости ИСЗ неизбежно будет существенно возрастать.
В качестве примера в приложении Г представлена аналитическая интерпретация алгоритма определения ортогональных составляющих вектора скорости ИСЗ на основе разностей радиальных скоростей  для частного случая, когда M=3.
для частного случая, когда M=3.
Окончательно, в качестве параметров орбиты ИСЗ принимают координаты ИСЗ х0, у0, z0 и ортогональные составляющие вектора его скорости  в момент времени t0.
в момент времени t0.
Имитационное моделирование [8, 9] заявленного способа показывает возможность повышения точности определения параметров орбиты ИСЗ по сравнению со способом прототипом на 30…60% (в зависимости от ширины полосы частотного спектра и времени записи принимаемых радиосигналов НРСТ и М ПОРС от ИСЗ). Указанное повышение точности объясняется отсутствием ограничений на время излучения и на ширину спектра тестовых радиосигналов, присутствовавших в способе прототипе.
Кроме того, реализация заявленного способа, как следует из описания, возможна в отношении любого ИСЗ, осуществляющего излучение радиосигналов. При этом не требуется, чтобы ИСЗ осуществлял ретрансляцию тестовых радиосигналов, что существенно расширяет область применения заявленного способа.
Источники информации
1. Каменский В.В., Кучеренко П.А., Соколов С.В., Акперов А.И., Крамаров C.O., Лукасевич В.И. Способ определения координат навигационных спутников Патент на изобретение №2615634, опубл. 06.04.2017 Бюл. №10.
2. Урличич Ю.М., Балуевский Ю.Н., Ганженко В.П., Ежов С.А., Жодзишский А.И., Измайлов Ю.Д., Круглов А.В., Махненко Ю.Ю., Поповкин В.А. Способ определения параметров орбиты геостационарного спутника Патент RU №2313104, опубл. 20.12.2007 Бюл. №8.
3. Балабанов В.В., Беспалов В.Л., Кельян А.Х., Пономарев А.А., Севидов В.В., Чемаров А.О. Способ определения параметров орбиты искусственного спутника Земли. Патент на изобретение №2652603, опубл. 27.04.2018 Бюл. №12.
4. Машбиц Л.М. Компьютерная картография и зоны спутниковой связи, - 2-е изд., перераб и доп. - М.: Горячая линия - Телеком, 2009. - 236 с.
5. Волков Р.В., Малышев С.Р., Симонов А.Н., Севидов В.В. Определение канонических параметров спутников-ретрансляторов по радиосигналам опорных реперных станций // Труды Военно-космической академии им. А.Ф. Можайского. 2016. Вып. 655. С. 88-92.
6. Богдановский С.В., Волков Р.В., Севидов В.В., Теслевич С.Ф. Модель поверхности Земли при определении местоположения земной станции по сигналам спутников-ретрансляторов // Наукоемкие технологии. 2016. №12. С. 44-50.
7. Волков Р.В., Саяпин В.Н., Севидов В.В. Модель измерения временной задержки и частотного сдвига радиосигнала, принятого от спутника-ретранслятора при определении местоположения земной станции // T-Comm: Телекоммуникации и транспорт. 2016. Том 10. №9. С. 14-18.
8. Волков Р.В., Саяпин В.Н., Севидов В.В. Модель движения искусственного спутника Земли // Программы для ЭВМ. Базы данных. Топологии интегральных микросхем. 2016. №2. С. 112.
9. Севидов В.В. Определение координат и параметров движения источника радиоизлучения на основе разностно-временных и разностно-доплеровских измерений // Программы для ЭВМ. Базы данных. Топологии интегральных микросхем. 2015. №11. С. 2.
Приложение А
Алгоритм прогноза координат геостационарного искусственного спутника Земли
Схема алгоритма прогноза координат геостационарного ИСЗ представлена на фиг. 2, которая включает следующие этапы:
На этапе 1 вводят исходные данные, которыми являются канонические параметры ИСЗ 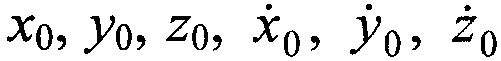 в момент времени t0, время прогноза tnp, время шага tш, начальное значение счетчика h=0.
в момент времени t0, время прогноза tnp, время шага tш, начальное значение счетчика h=0.
На этапе 2 рассчитывают количество шагов алгоритма в соответствии с выражением
Nш≈tnp/tш
при этом Nш округляют до ближайшего целого числа.
На этапе 3 значение счетчика h увеличивают на единицу.
На этапе 4 рассчитывают текущее значение времени по формуле
th=t0+tшh
На этапах 5 и 6 рассчитывают координаты Солнца хс, ус, zc и Луны хл, ул, zл для текущего момента времени. Алгоритмы таких расчетов исследованы в астродинамике [4], они представлены в приложении Б.
На этапе 7 рассчитывают силовые функции (ускорения) U0, U1, U2, обусловленные влиянием на ИСЗ в текущий момент времени Земли, Солнца и Луны соответственно.
На этапе 8 с учетом данных, полученных на этапах 4-7, рассчитывают текущие координаты ИСЗ.
Далее этапы 3-8 алгоритма повторяют до выполнения условия h>Nш (этап 9). В качестве выходных результатов алгоритма выступают канонические параметры ИСЗ  в момент времени Гпр (этап 10).
в момент времени Гпр (этап 10).
Общее уравнение движения ИСЗ в гравитационном поле Земли, образуемом действием центрального тела (Земли) и других небесных тел (Солнца, Луны, планет и др.), в векторной форме записывает как

где Г - радиус-вектор ИСЗ; Ψсум - геометрическая сумма сил, действующих на ИСЗ.
С учетом того, что на ИСЗ действуют только три небесных тела (Земля, Солнце и Луна), а также того, что масса ИСЗ пренебрежимо мала по сравнению с массой любого из указанных тел, компоненты выражения (А. 1) можно представить в инерциальной геоцентрической ДСК OзXYZ:

где Ψk - силовая функция, действующая на ИСЗ со стороны k-го тела; Uxk, Uyk, Uzk - компоненты ускорения, сообщаемые ИСЗ k-м небесным телом, k=1…3 (k=1 - Земля, k=2 - Солнце, k=3 - Луна).
Система нелинейных дифференциальных уравнений (А.2) преобразуется в систему из шести уравнений первого порядка:
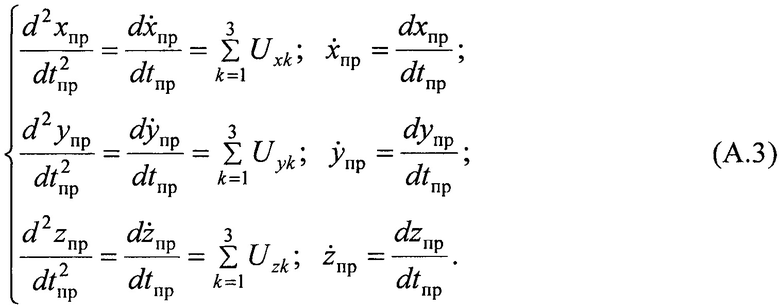
Для численного решения системы уравнений (А.3) необходимо задать шесть начальных условий и выразить в явном виде компоненты векторов ускорения Uxk, Uyk, Uzk. В качестве начальных условий выступают канонические параметры ИСЗ 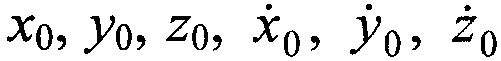 для момента времени t0, рассчитанные на основе измерений временных задержек и частотных сдвигов радиосигналов ПОРС.
для момента времени t0, рассчитанные на основе измерений временных задержек и частотных сдвигов радиосигналов ПОРС.
Силовая функция Земли в настоящее время хорошо изучена [4]. Компоненты вектора ускорения применительно к модели Земли, учитывающие полярное сжатие, можно представить в следующем виде:

где gl=398,602×1012 м3/с2; g2=66043,987×106 м2; g3=-1,492×1015 м3; g4=-2,193×1021 м4; хпр, упр, znp - прогнозируемые координаты ИСЗ в геоцентрической системе координат;  - расстояние между центрами масс ИСЗ и Земли.
- расстояние между центрами масс ИСЗ и Земли.
Для определения возмущающих влияний Солнца и Луны пользуются общей формулой силовой функции небесного тела [4]:
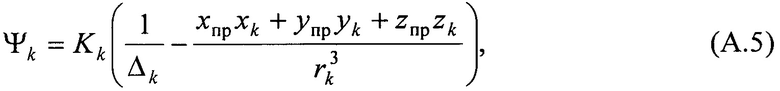
где Kk - гравитационный параметр (для Солнца=13,2318×1019 м3/с2, для Луны K3=4891,0532×109 м3/с2), равный произведению гравитационной постоянной на массу возмущающего тела; 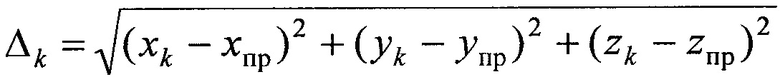 - расстояние между центрами масс ИСЗ и возмущающего тела; xk, yk, zk - координаты центра масс возмущающего тела;
- расстояние между центрами масс ИСЗ и возмущающего тела; xk, yk, zk - координаты центра масс возмущающего тела; 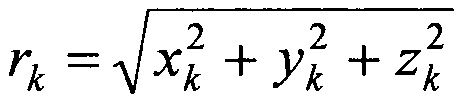 - расстояние между центрами масс Земли и возмущающего тела.
- расстояние между центрами масс Земли и возмущающего тела.
Возмущающие ускорения согласно системе уравнений (А.2) определяются как частные производные (А.5) по координатам ИСЗ:
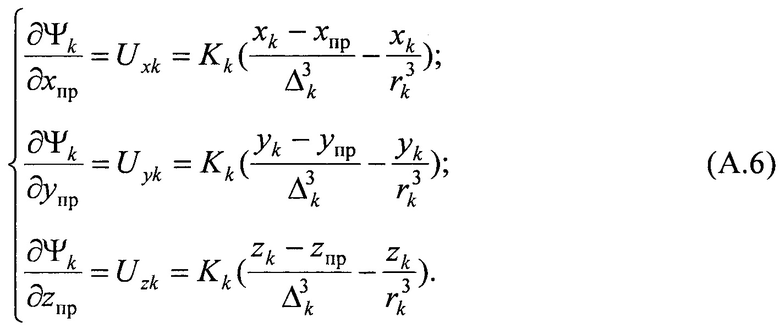
Решая систему дифференциальных уравнений (А.3) одним из известных численных методов (метод Рунге-Кутта, метод Адамса и др.), с учетом выражений (А.4) и (А.6), при предварительном определении координат Солнца и Луны в соответствии с выражениями (Б.1) и (Б.7), получают канонические параметры ИСЗ  в момент времени tnp.
в момент времени tnp.
Приложение Б
Расчет координат Солнца и Луны
Расчет координат Солнца и Луны производят на основе алгоритмов, хорошо известных в астрономии. Исходными данными являются декретное время и декретная добавка, а выходными результатами - декартовы координаты указанных небесных тел.
Текущие координаты Солнца рассчитывают в соответствии с алгоритмом:
На этапе 1 рассчитывают Юлианские даты начала года JD0 и заданного момента времени JD:
JD0=2440000+0,5+gг.M;

где gг.M - табличное значение для текущих «г» и «м» [4]; «г» - год; «м» -месяц;  - год, часы, минуты, секунды местного декретного времени; tд - декретная добавка (например, для Москвы tд=3 ч).
- год, часы, минуты, секунды местного декретного времени; tд - декретная добавка (например, для Москвы tд=3 ч).
Юлианская дата представляет собой текущее время, исчисляемое в днях (сутках с десятичными долями), отсчитываемых от полудня 1 января 4713 года до н.э.
На этапе 2 определяют прямое восхождение для среднего Солнца αсс, которое согласно С. Ньюкому равно:
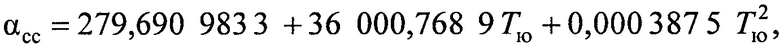
где Тю - эпоха в Юлианских столетиях от среднего гринвичского полудня (всемирного времени) 1 января 1900 года, которую определяют как
Тю={JD-2 415 020)/365 25.
На этапе 3 рассчитывают уравнения времени ηс и прямого восхождения истинного Солнца αс в соответствии с выражениями
αс=1,925sin(αсс+78)-2,375 sin(2αсс);
αс=αсс+ηс.
На этапе 4 вычисляют склонение Солнца:
δс=arctg(sinαсtgεэкл),
где εэкл=23,4371722 - угол наклонения плоскости эклиптики к плоскости Экватора, рассчитанный для k=2016 по формуле
εэкл=23,4457889-(k-1950)×1,31×10-4.
На этапе 5 определяют истинную аномалию Θс и расстояние от Земли до Солнца rс:
Θс=2π(JD0-JD)/365,25636;
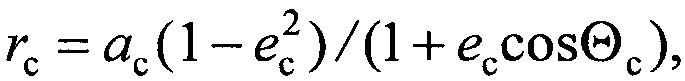
где aс=149597870 км - большая полуось орбиты Земли; ес=0,0167 - эксцентриситет орбиты Земли.
На этапе 6 рассчитывают линейные координаты Солнца в инерциальной геоцентрической системе координат:

Рассчитанные линейные координаты Солнца по формуле (Б.1) в инерциальной геоцентрической системе координат позволят вычислить силовую функцию - ускорение U2, придаваемое Солнцем искусственному спутнику земли в момент времени t0.
Луна является спутником Земли, и в отношении нее справедливо все то, что касается движения спутников вообще. Однако вопрос о ее движении рассматривается особо, так как Луна - самое близкое к Земле небесное тело, движущееся непосредственно вокруг Земли, и ее движение изучается весьма детально. При этом отклонения Луны от эллиптического движения, т.е. возмущения, велики, они гораздо больше, чем возмущения планет.
Видимое движение Луны изучается с древних времен. Луна перемещается по небу, как и Солнце, все время с запада на восток и описывает за один месяц большой круг. За сутки перемещение Луны составляет около 12…13°.
При детальном рассмотрении обнаруживаются весьма сложные особенности движения Луны. Отклонения от равномерного перемещения обусловлены, во-первых, тем, что Луна движется не по окружности, а в первом приближении по эллипсу с эксцентриситетом, равным ел=0,005, а во-вторых, возмущениями от Солнца и от сжатия Земли.
В теории движения Луны выводятся формулы непосредственно для геоцентрической эклиптической долготы λл, широты βл и расстояния rзл от Луны до Земли. В упрощенном виде (если ограничиться наибольшими членами) эти формулы записывают следующим образом:



где Lл - осредненная (т.е. освобожденная от периодических возмущений) средняя долгота Луны в орбите;  - осредненная средняя аномалия Луны; Dn - разность средних долгот Луны и Солнца;
- осредненная средняя аномалия Луны; Dn - разность средних долгот Луны и Солнца; 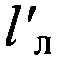 - осредненная средняя аномалия Земли, увеличенная на 180°; Fл - средняя долгота Луны, отсчитываемая от восходящего узла орбиты.
- осредненная средняя аномалия Земли, увеличенная на 180°; Fл - средняя долгота Луны, отсчитываемая от восходящего узла орбиты.
В формулах (Б.2) и (Б.З) отброшены по сравнению с точными (содержащими каждая по нескольку сотен членов) членами, которые имеют коэффициенты менее 100'' (0,028°), а в формуле (Б.4) отброшены члены с коэффициентами меньше 0,0003.
Углы 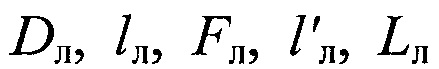 называются основными аргументами в теории движения Луны. Они выведены по многолетним наблюдениям в сочетании с теорией и определяются как
называются основными аргументами в теории движения Луны. Они выведены по многолетним наблюдениям в сочетании с теорией и определяются как

В основе преобразований эклиптических координат в экваториальные лежит сферический треугольник Леонардо-Эйлера PмSлPэ. Вершинами этого треугольника являются полюс Мира Рм, полюс эклиптики Рэ и небесное тело, в данном случае Луна Sл.
В соответствии с теоремой косинусов сферической тригонометрии справедливы соотношения, связывающие геоцентрические эклиптические координаты Луны λл, βл с геоцентрическими экваториальными координатами Луны - прямым восхождением αл и склонением δл:
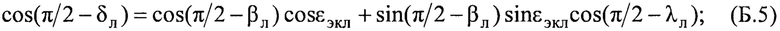

После преобразования выражений (Б.5) и (Б.6) получают формулы для расчета прямого восхождения ал и склонения Луны δл:
δл=arcsin(sinβлCosεэкл+cosβлSinεэклsinλл);
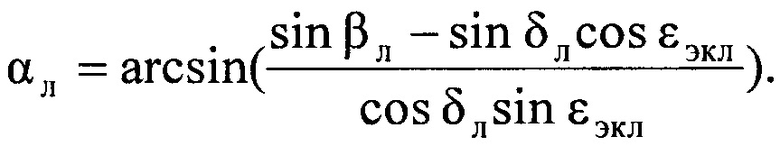
Линейные координаты Луны хл, ул, zл в инерциальной геоцентрической системе координат вычисляют по формулам

Рассчитанные по формулам (Б. 7) линейные координаты Луны в инерциальной геоцентрической системе позволят вычислить силовую функцию - ускорение U3, придаваемое Луной искусственному спутнику Земли в момент времени t0.
Приложение В
Алгоритм построения трех поверхностей положения ИСЗ и нахождение точки пересечения этих поверхностей
Для расчета координат ИСЗ на основе построения трех поверхностей положения ИСЗ разработан алгоритм, схема которого представлена на фиг. 4.
Указанный алгоритм основан на том, что каждой из временных задержек Δtm соответствует своя разность дальностей ΔRm, рассчитываемая по формуле (1). В свою очередь, каждой разности дальностей ΔRm ставят в соответствие поверхность положения - двуполостный гиперболоид вращения с фокусами, совпадающими с известными координатами НРТС и соответствующей ПОРС.
Координаты точки пересечения трех гиперболоидов вращения соответствуют искомым координатам ИСЗ х0, у0, z0 в момент времени t0.
На этапе 1 производят ввод исходных данных, в качестве которых выступают координаты НРТС хK, уK, zK; координаты трех ПОРС  временные задержки между принятым НРТС и принятыми каждой из ПОРС радиосигналами Δt1, Δt2, и Δt3; порог точности δ0 расчета координат ИСЗ.
временные задержки между принятым НРТС и принятыми каждой из ПОРС радиосигналами Δt1, Δt2, и Δt3; порог точности δ0 расчета координат ИСЗ.
На этапе 2 рассчитывают координатно-информативные параметры -разности расстояния ΔR1, ΔR2 и ΔR3 по формуле (1).
На этапе 3 выбирают, на основе элементов Кеплеровой орбиты ИСЗ, координаты опорной точки х'0, у'0, z'0.
На этапе 4 рассчитывают разности расстояний ΔR1, ΔR2 и ΔR3, при условии равенства координат ИСЗ координатам опорной точки х'0, y'0, z'0 по формулам
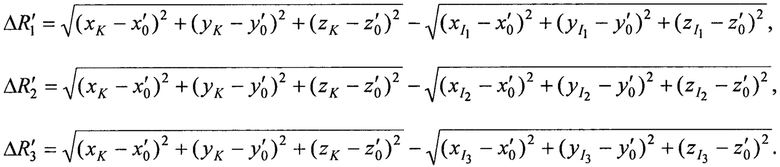
На этапе 5 рассчитывают невязки n1, n2 и n3 как разницы между определенными на этапе 4 разностей расстояний ΔR'1, ΔR'2 и ΔR'3 и координатно-информативными параметрами ΔR1, ΔR2 и ΔR3 определенными на этапе 2 соответственно
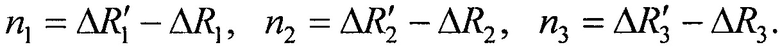
На этапе 6 формируют систему линейных уравнений при разложении в ряд Тейлора функций ΔR1, ΔR2 и ΔR3, с точностью до первых членов, где в качестве переменных выступают поправки к координатам Δх0, Δу0, Δz0:

где частные производные, в свою очередь, рассчитываются согласно выражениям

где -  - расстояния от НРТС и соответствующей ПОРС до опорной точке, которые в свою очередь равны
- расстояния от НРТС и соответствующей ПОРС до опорной точке, которые в свою очередь равны

Решая систему линейных уравнений (В.1) одним из известных методов, получают поправки к координатам ИСЗ Δх0, Δу0, Δz0.
На этапе 7 рассчитывают координаты новой опорной точки 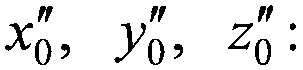
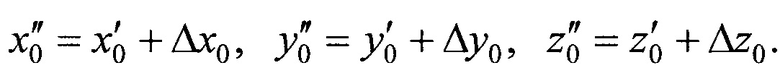
Этапы 4-7 в совокупности составляют первую итерацию. Далее итерации повторяют, используя каждый раз новую опорную точку, полученную на предыдущей итерации. Количество необходимых итераций зависит требуемой точности определения координат ИСЗ. С точностью определения координат ИСЗ напрямую связан шаг итерации dш.
На этапе 8 определяют шаг итерации dш как расстояние между текущей и предыдущей опорными точками:
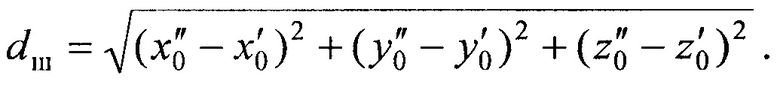
На этапе 8 сравнивают dm с порогом δ0, задаваемом на этапе 1.
Необходимое число итераций, как правило, составляет 2…4. В качестве координат ИСЗ х0, уо и z0 выбирают значения координат опорной точки на последней итерации, вывод которых осуществляют на этапе 10.
В общем случае, когда количество ПОРС М≥4, алгоритм определения координат ИСЗ остается прежним, с той лишь разницей, что система уравнений (В.1) будет содержать более трех уравнений. Тогда такую систему уравнений решают, например, методом наименьших квадратов.
Приложение Г
Алгоритм определения ортогональных составляющих вектора скорости искусственного спутника Земли
Для одномоментного определения ортогональных составляющих вектора скорости ИСЗ 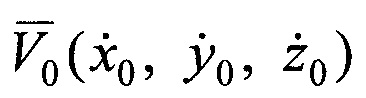 возможно использование НРТС и минимум трех ПОРС, обозначенных на фиг. 5, - K и Im соответственно, где для рассматриваемого частного случая m=1…3. Введены следующие обозначения: ΘK - угол между вектором
возможно использование НРТС и минимум трех ПОРС, обозначенных на фиг. 5, - K и Im соответственно, где для рассматриваемого частного случая m=1…3. Введены следующие обозначения: ΘK - угол между вектором  и направлением на НРТС;
и направлением на НРТС;  - углы между вектором
- углы между вектором  и направлениями на m-ю ПОРС;
и направлениями на m-ю ПОРС; 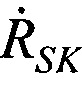 - радиальная скорость ИСЗ относительно НРТС;
- радиальная скорость ИСЗ относительно НРТС; 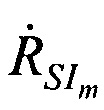 - радиальные скорости ИСЗ относительно т-й ПОРС.
- радиальные скорости ИСЗ относительно т-й ПОРС.
Предполагается, что координаты ПОРС  - известны, а координаты ИСЗ х0, уо, z0 - рассчитаны в соответствии с алгоритмом, представленном в приложении В.
- известны, а координаты ИСЗ х0, уо, z0 - рассчитаны в соответствии с алгоритмом, представленном в приложении В.
Соотношения средней частоты ƒs радиосигнала, излученного ИСЗ, а также средних частот ƒ0, ƒm того же радиосигнала принимаемого в НРТС и трех ПОРС, имеют вид:


где 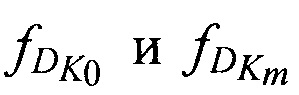 - доплеровские сдвиги частот на выходе ИСЗ за счет его сближения (удаления) с (от) НРТС и каждой из трех ПОРС.
- доплеровские сдвиги частот на выходе ИСЗ за счет его сближения (удаления) с (от) НРТС и каждой из трех ПОРС.
За счет корреляционной обработки записанных с метками времени в НРТС и трех ПОРС радиосигналов возможно получение частотных сдвигов, равных:

Влияние других эффектов на изменение частотных сдвигов, например гравитационный и релятивистский эффекты в рамках рассматриваемой задачи, пренебрежимо мало и поэтому не учитывают.
Доплеровские сдвиги частот  на выходе ИСЗ рассчитывают следующим образом:
на выходе ИСЗ рассчитывают следующим образом:
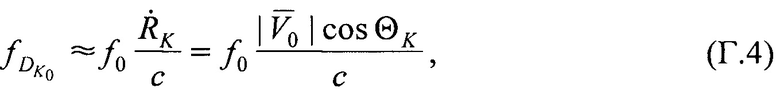
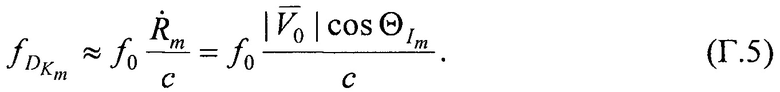
Из (Г.3), с учетом (Г.4) и (Г.5) следует:

где 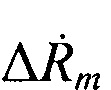 - разно.сти радиальных скоростей ИСЗ относительно m-й ПОРС и НРТС.
- разно.сти радиальных скоростей ИСЗ относительно m-й ПОРС и НРТС.
Из (Г.6) следует, что разности радиальных скоростей ИСЗ относительно m-й ПОРС и НРТС 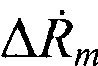 возможно рассчитать на основе измеренных частотных сдвигов Δƒm:
возможно рассчитать на основе измеренных частотных сдвигов Δƒm:

Согласно теореме о скалярном произведении векторов справедливо:
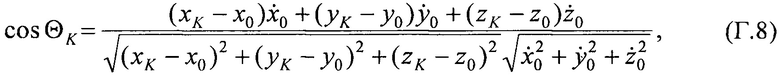
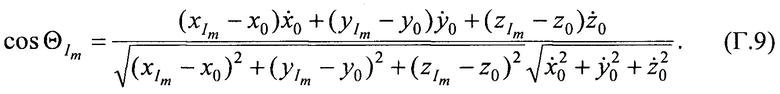
Модуль вектора скорости ИСЗ равен:

а расстояния от НРТС и m-х ПОРС до ИСЗ 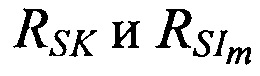 рассчитывают как
рассчитывают как


Из (Г.4) и (Г.5) с учетом (Г.6), (Г.8), (Г.9), (Г.10), (Г.11), (Г.12) получают систему линейных уравнений:


где коэффициенты при переменных 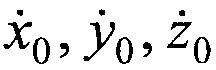 и свободные члены равны:
и свободные члены равны:
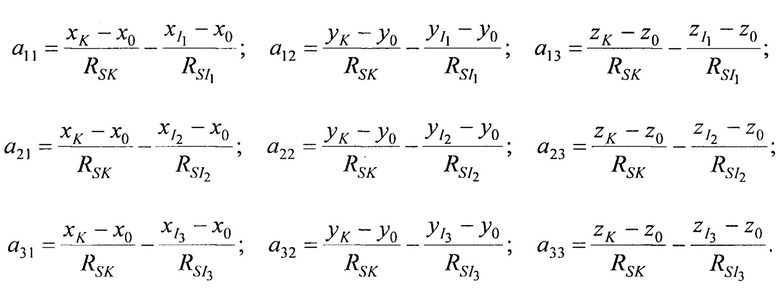
Система из трех линейных уравнений с тремя неизвестными (Г.12) решают одним из известных методов, например, методом Крамера. Результатом решения системы уравнений (Г.12) выступают ортогональные составляющие вектора скорости ИСЗ 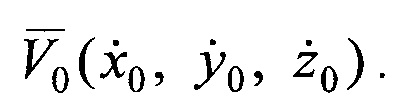
В общем случае, когда количество ПОРС М≥4, алгоритм определения ортогональных составляющих вектора скорости ИСЗ остается прежним, с той лишь разницей, что система уравнений (Г.12) будет содержать более трех уравнений. Тогда такую систему уравнений решают, например, методом наименьших квадратов.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ОРБИТЫ ИСКУССТВЕННОГО СПУТНИКА ЗЕМЛИ С ИСПОЛЬЗОВАНИЕМ ПРИЕМО-ПЕРЕДАЮЩИХ ОПОРНЫХ РЕПЕРНЫХ СТАНЦИЙ | 2018 |
|
RU2708883C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ОРБИТЫ ИСКУССТВЕННОГО СПУТНИКА ЗЕМЛИ | 2017 |
|
RU2652603C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОРТОГОНАЛЬНЫХ СОСТАВЛЯЮЩИХ ВЕКТОРОВ СКОРОСТЕЙ И СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ДВУХ КОСМИЧЕСКИХ АППАРАТОВ С ИСПОЛЬЗОВАНИЕМ ЗЕМНЫХ СТАНЦИЙ | 2020 |
|
RU2749878C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОРТОГОНАЛЬНЫХ СОСТАВЛЯЮЩИХ ВЕКТОРА СКОРОСТИ И СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ КОСМИЧЕСКОГО АППАРАТА С ИСПОЛЬЗОВАНИЕМ ЗЕМНЫХ СТАНЦИЙ | 2020 |
|
RU2750228C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОРТОГОНАЛЬНЫХ СОСТАВЛЯЮЩИХ ВЕКТОРА СКОРОСТИ И СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ КОСМИЧЕСКОГО АППАРАТА С ИСПОЛЬЗОВАНИЕМ ЗЕМНЫХ СТАНЦИЙ | 2020 |
|
RU2750753C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОРТОГОНАЛЬНЫХ СОСТАВЛЯЮЩИХ ВЕКТОРОВ СКОРОСТЕЙ И СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ДВУХ КОСМИЧЕСКИХ АППАРАТОВ С ИСПОЛЬЗОВАНИЕМ ЗЕМНЫХ СТАНЦИЙ | 2020 |
|
RU2750983C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОРТОГОНАЛЬНЫХ СОСТАВЛЯЮЩИХ ВЕКТОРОВ СКОРОСТИ ДВУХ КОСМИЧЕСКИХ АППАРАТОВ С ИСПОЛЬЗОВАНИЕМ ЗЕМНЫХ СТАНЦИЙ И ИЗЛУЧАЮЩЕЙ ОПОРНОЙ РЕПЕРНОЙ СТАНЦИИ | 2022 |
|
RU2791153C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ КОСМИЧЕСКОГО АППАРАТА С ИСПОЛЬЗОВАНИЕМ ЗЕМНЫХ СТАНЦИЙ И ИЗЛУЧАЮЩЕЙ ОПОРНОЙ РЕПЕРНОЙ СТАНЦИИ | 2023 |
|
RU2805667C1 |
| Способ определения координат космического аппарата с использованием земных станций и излучающей опорной реперной станции | 2023 |
|
RU2803662C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ДВУХ КОСМИЧЕСКИХ АППАРАТОВ С ИСПОЛЬЗОВАНИЕМ ЗЕМНЫХ СТАНЦИЙ И ИЗЛУЧАЮЩЕЙ ОПОРНОЙ РЕПЕРНОЙ СТАНЦИИ | 2022 |
|
RU2787890C1 |



Изобретение относится к области космонавтики, а именно к технике выполнения траекторных измерений и определения параметров орбиты искусственного спутника Земли (ИСЗ), и может быть использовано на наземных и бортовых комплексах управления полетом ИСЗ для точного определения текущих параметров движения ИСЗ. Технический результат изобретения - повышение точности определения параметров орбиты ИСЗ, обеспечение более широкой области применения за счет использования наземной радиотехнической станции (НРТС), размещенной на позиции с известными координатами, работающей в режиме приема и М≥3 приемных опорных реперных станции (ПОРС) на позициях с известными координатами. Способ основан на приеме и записи радиосигналов НРТС и МПОРС от ИСЗ совместно с метками времени. С помощью корреляционной обработки измеряют значения взаимных временных задержек и частотных сдвигов. Вычисляют координаты ИСЗ по известным координатам НРСТ и М ПОРС, а также рассчитанным разностям дальностей ΔRm, где m - номер ПОРС. Вычисляют ортогональные составляющие вектора скорости ИСЗ по известным координатам НРСТ и М ПОРС, вычисленным координатам ИСЗ, рассчитанным разностям радиальных скоростей и предварительно заданной частоте сдвига рабочей частоты ИСЗ. В качестве параметров орбиты ИСЗ принимают совокупность координат ИСЗ и ортогональных составляющих вектора его скорости в момент времени t0. 5 ил., 4 прил.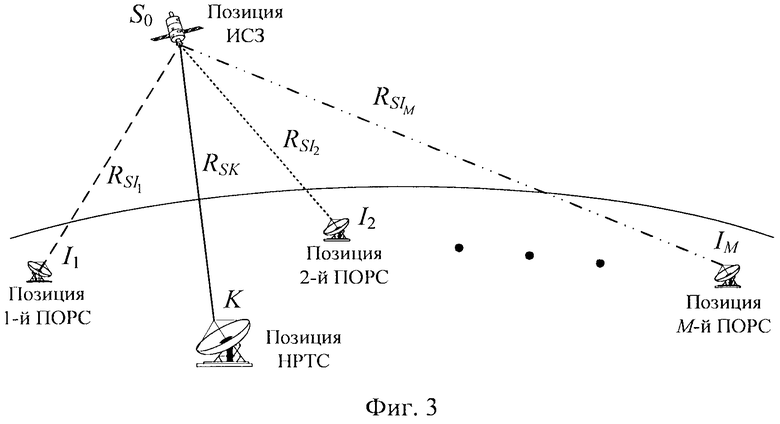
Способ определения параметров орбиты искусственного спутника Земли (ИСЗ) с использованием приемных опорных реперных станций (ПОРС), заключающийся в том, что размещают наземную радиотехническую станцию (НРТС) на позиции с известными координатами xK, yK, zK, выбирают начальные значения параметров орбиты ИСЗ, принимают в НРТС радиосигналы от ИСЗ, измеряют с помощью аппаратуры НРТС временные задержки и частотные сдвиги радиосигналов, принятых от ИСЗ в момент времени t0, вычисляют координаты ИСЗ x0, y0, z0 по известным координатам НРСТ и значениям временных задержек радиосигналов, вычисляют ортогональные составляющие вектора скорости ИСЗ  по известным координатам НРСТ, вычисленным координатам ИСЗ и частотным сдвигам радиосигналов, а в качестве параметров орбиты ИСЗ принимают совокупность координат ИСЗ x0, y0, z0 и ортогональных составляющих вектора его скорости
по известным координатам НРСТ, вычисленным координатам ИСЗ и частотным сдвигам радиосигналов, а в качестве параметров орбиты ИСЗ принимают совокупность координат ИСЗ x0, y0, z0 и ортогональных составляющих вектора его скорости 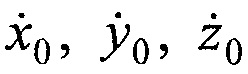 в момент времени t0, отличающийся тем, что предварительно устанавливают на земной поверхности М≥3 ПОРС на позициях с известными координатами xIm, yIm, zIm, где m=1…М - номер ПОРС, принимают от ИСЗ и записывают с помощью аппаратуры НРТС и М ПОРС радиосигналы совместно с метками времени, передают на НРСТ записанные копии радиосигналов ИСЗ совместно с метками времени от М ПОРС, выбирают радиосигнал, принятый от ИСЗ и записанный с помощью аппаратуры НРТС совместно с метками времени в качестве опорного, формируют М отличающихся друг от друга пар радиосигналов, принятых от ИСЗ, одним из элементов в каждой из пар выбирают опорный радиосигнал, для каждой сформированной пары радиосигналов измеряют с помощью корреляционной обработки значения взаимной временной задержки Δtm и частотного сдвига Δƒm, рассчитывают М разностей дальностей ΔRm на основе временных задержек Δtm, рассчитывают М разностей радиальных скоростей
в момент времени t0, отличающийся тем, что предварительно устанавливают на земной поверхности М≥3 ПОРС на позициях с известными координатами xIm, yIm, zIm, где m=1…М - номер ПОРС, принимают от ИСЗ и записывают с помощью аппаратуры НРТС и М ПОРС радиосигналы совместно с метками времени, передают на НРСТ записанные копии радиосигналов ИСЗ совместно с метками времени от М ПОРС, выбирают радиосигнал, принятый от ИСЗ и записанный с помощью аппаратуры НРТС совместно с метками времени в качестве опорного, формируют М отличающихся друг от друга пар радиосигналов, принятых от ИСЗ, одним из элементов в каждой из пар выбирают опорный радиосигнал, для каждой сформированной пары радиосигналов измеряют с помощью корреляционной обработки значения взаимной временной задержки Δtm и частотного сдвига Δƒm, рассчитывают М разностей дальностей ΔRm на основе временных задержек Δtm, рассчитывают М разностей радиальных скоростей  на основе частотных сдвигов Δƒm, вычисляют координаты ИСЗ x0, y0, z0 по известным координатам НРСТ и М ПОРС, рассчитанным разностям дальностей ΔRm, вычисляют ортогональные составляющие вектора скорости ИСЗ
на основе частотных сдвигов Δƒm, вычисляют координаты ИСЗ x0, y0, z0 по известным координатам НРСТ и М ПОРС, рассчитанным разностям дальностей ΔRm, вычисляют ортогональные составляющие вектора скорости ИСЗ 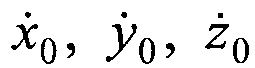 по известным координатам НРСТ и М ПОРС, вычисленным координатам ИСЗ x0, y0, z0, рассчитанным разностям радиальных скоростей
по известным координатам НРСТ и М ПОРС, вычисленным координатам ИСЗ x0, y0, z0, рассчитанным разностям радиальных скоростей  а в качестве параметров орбиты ИСЗ принимают совокупность координат ИСЗ x0, y0, z0 и ортогональных составляющих вектора его скорости
а в качестве параметров орбиты ИСЗ принимают совокупность координат ИСЗ x0, y0, z0 и ортогональных составляющих вектора его скорости 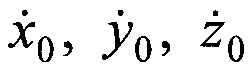 в момент времени t0.
в момент времени t0.
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ОРБИТЫ ИСКУССТВЕННОГО СПУТНИКА ЗЕМЛИ | 2017 |
|
RU2652603C1 |
| СИСТЕМА ОЦЕНИВАНИЯ ТОЧНОСТИ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ ИСЗ | 2009 |
|
RU2391265C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ ИСКУССТВЕННОГО СПУТНИКА ЗЕМЛИ ПО ИЗМЕРЕНИЯМ ТЕКУЩИХ НАВИГАЦИОННЫХ ПАРАМЕТРОВ НА КОРОТКОМ МЕРНОМ ИНТЕРВАЛЕ | 2011 |
|
RU2498219C2 |
| СИСТЕМА ОРИЕНТАЦИИ НАВИГАЦИОННОГО СПУТНИКА | 2012 |
|
RU2535979C2 |
| WO 2004011955 A2, 05.02.2004 | |||
| US 6417798 B1, 09.07.2002 | |||
| US 8965395 B2, 24.02.2015. | |||
Авторы
Даты
2019-10-04—Публикация
2018-07-25—Подача