Изобретение относится к области электрорадиотехники и связи, и может быть использовано в системах передачи данных, использующих многочастотные сигналы с ортогональным частотным разделением каналов с двухпозиционной относительной фазовой модуляцией, для оценки параметров канала связи.
Для обеспечения стабильной работы системы передачи данных необходимо осуществлять контроль качества используемого канала связи. Критерием качества канала в цифровых системах связи является вероятность ошибки на бит, которая однозначно связана с параметрами модели замираний. Поэтому актуальной является задача определения параметров модели замираний огибающей сигнала по закону Накагами по результатам анализа информационного многочастотного сигнала.
Наиболее близким к заявленному техническому решению является способ, описанный в [патент РФ на изобретение №2608363], который принят за прототип. Оценка параметров формируется с помощью анализа амплитуд полезного сигнала и шума, а также только шума на заданных поднесущих частотах внутри выделенной полосы.
Известный способ определения параметров распределения Накагами работает следующим образом.
Способ оценки параметров модели замираний огибающей сигнала по закону Накагами по информационному многочастотному сигналу, заключающийся в том, что на приемной стороне оцифровывают принимаемый сигнал в аналогово-цифровом преобразователе, затем передают оцифрованный сигнал с выхода аналогово-цифрового преобразователя одновременно на вход первого блока вычисления амплитуды и на вход второго блока вычисления амплитуды, при этом, в первом блоке вычисления амплитуды определяют значение амплитуды смеси принимаемого сигнала и шума на всех n частотах, используемых для передачи информационного сигнала, на длительности элементарной посылки, а c n выходов первого блока вычисления амплитуды на первые входы n соответствующих делителей передают вычисленные значения амплитуд, также, во втором блоке вычисления амплитуды определяют значение амплитуды шума на n частотах, неиспользуемых для передачи информационного сигнала, на длительности элементарной посылки, а с n выходов второго блока вычисления амплитуды передают вычисленные значения амплитуд на вторые входы n соответствующих делителей, в каждом делителе осуществляют деление значения амплитуды шума на частоте, неиспользуемой для передачи информационного сигнала, полученное по второму входу на значение амплитуды смеси сигнала и шума на частоте, используемой для передачи информационного сигнала полученное по первому входу, а результат деления передают с выхода каждого из n делителей на n соответствующих входов блока накопления, в котором накапливают выборку полученных n значений на длительности интервала анализа, равной М посылкам, получая, таким образом, выборку размером n×М значений, а с выхода блока накопления передают накопленный массив значений на вход блока вычисления параметров распределения, в котором методом наискорейшего спуска, определяют параметры модели замирания огибающей сигнала по закону Накагами m и 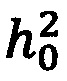 , являющиеся координатами максимума функции правдоподобия
, являющиеся координатами максимума функции правдоподобия 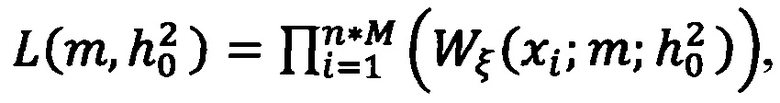 где x1 - это i-е значение выборки, а
где x1 - это i-е значение выборки, а 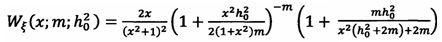 - плотность распределения вероятности измеряемой случайной величины.
- плотность распределения вероятности измеряемой случайной величины.
Недостатком прототипа является то, что его можно применять только в том случае, если в принимаемом информационном многочастотном сигнале для передачи данных используются не все поднесущие частоты внутри выделенной полосы, таким образом, снижается скорость передачи данных.
Целью изобретения является получение оценки параметров модели замираний радиоканала по закону Накагами путем анализа принимаемого информационного многочастотного сигнала.
Поставленная цель достигается тем, что способ оценки параметров модели замираний огибающей сигнала по закону Накагами по многочастотному сигналу состоит в том, что на приемной стороне оцифровывают принимаемый сигнал в аналогово-цифровом преобразователе, затем передают оцифрованный сигнал с выхода аналогово-цифрового преобразователя на вход блока вычисления преобразования Фурье, в котором вычисляют преобразование Фурье на длительности текущей элементарной посылки и результат в виде массива комплексных чисел, соответствующих используемым частотам, передают одновременно на вход линии задержки, на первый вход первого сумматора и на первый вход второго сумматора, затем в линии задержки задерживают поступивший массив на время, равное длительности элементарной посылки и далее с выхода передают его одновременно на второй вход первого сумматора со знаком минус и на второй вход второго сумматора, а в первом сумматоре осуществляют поэлементное сложение поступивших массивов, один из которых поступил со знаком минус, а во втором сумматоре также осуществляют поэлементное сложение поступивших массивов, далее с выхода первого сумматора передают массив комплексных чисел на вход первого блока вычисления модуля, а с выхода второго сумматора передают массив комплексных чисел на вход второго блока вычисления модуля, а в первом блоке вычисления модуля вычисляют поэлементно модуль поступившего массива, и передают результат в виде массива вещественных чисел на первый вход делителя, а во втором блоке вычисления модуля вычисляют поэлементно модуль поступившего массива, и передают результат в виде массива вещественных чисел на второй вход делителя, затем в делителе производят поэлементное деление массива, полученного по первому входу на массив, полученный по второму входу и результат деления в виде массива передают на вход блока накопления, и в блоке накопления производят накопление М последних полученных массивов, где М - заранее заданное число, а с выхода блока накопления передают накопленные массивы значений на вход блока вычисления параметров распределения, в котором, методом наискорейшего спуска, определяют параметры модели замираний огибающей сигнала по закону Накагами m и 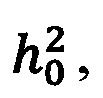 являющиеся координатами максимума функции правдоподобия
являющиеся координатами максимума функции правдоподобия 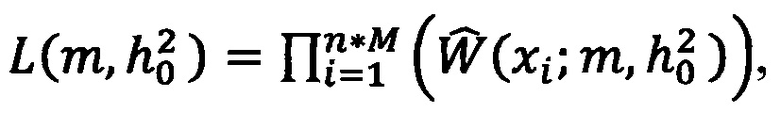 где xi - это i-е значение выборки,
где xi - это i-е значение выборки, 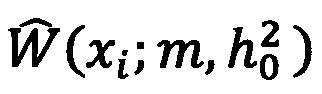 - плотность распределения вероятности измеряемой случайной величины, при этом,
- плотность распределения вероятности измеряемой случайной величины, при этом, 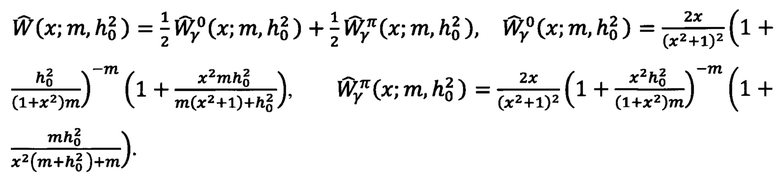
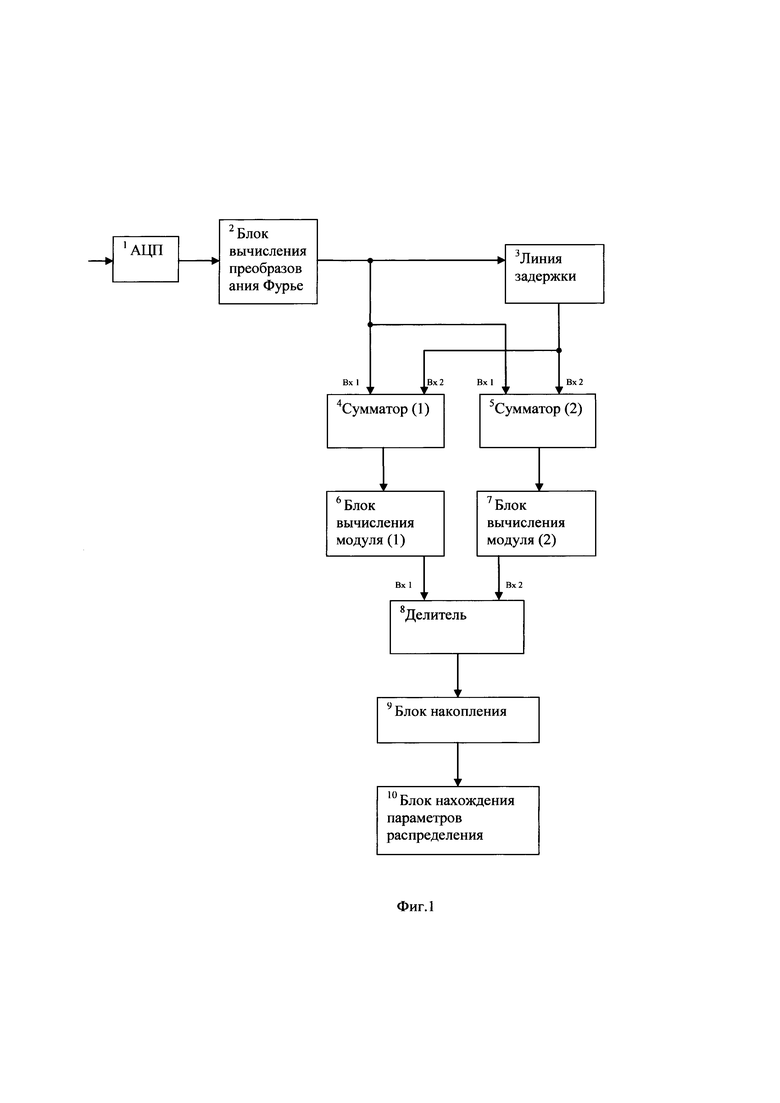
Структурная схема предложенного способа приведена на фиг. 1.
Способ основан на следующих предположениях.
В общем случае для определения плотности распределения огибающей сигнала в канале с замираниями, когда доступными для измерения являются только значения огибающей смеси сигнал + шум можно использовать подход, заключающийся в том, чтобы по плотности распределения огибающей смеси сигнал + шум определить параметры распределения Накагами. При этом, восстановить истинную плотность распределения огибающей можно, используя выборочную плотность распределения огибающей смеси сигнал + шум, получаемую посредством измерений на приемной стороне.
В данном подходе следует учитывать техническую проблему, связанную с тем, что на приемной стороне чаще всего сигнал перед обработкой проходит через устройство автоматической регулировки усиления (АРУ). Поскольку коэффициент усиления АРУ неизвестен и динамически меняется в процессе измерений, статистические характеристики выборочной плотности распределения амплитуды сигнала значительно меняются и, применение указанных выше способов напрямую, дает неадекватные оценки.
Избавиться от указанной трудности при приеме сигнала с использованием АРУ, можно, если для оценки параметров модели канала использовать выборку случайных величин, инвариантную к значению коэффициента усиления АРУ.
Предположим, что в принимаемом OFDM сигнале используется двухпозиционная относительная фазовая модуляция, а замирания сигнала являются медленными, то есть такие, что на соседних посылках амплитуда практически одинакова.
Тогда, амплитуда суммы спектральных составляющих сигнала на соседних посылках, в зависимости от разницы фаз, может принимать значения либо удвоенной помехи, либо удвоенного сигнала плюс удвоенной помехи. Так получается потому, что спектральные составляющие в векторном виде будут либо направлены в одну сторону, любо противоположно направлены. Аналогичным образом можно вычислить амплитуду разности сигналов на этих же соседних посылках. Таким образом, при демодуляции сигналов такими действиями всегда можно получить две случайные (СВ) α и β, одна из которых (α) будет соответствовать огибающей удвоенной помехи, а другая (β) - огибающей удвоенного сигнала плюс удвоенная помеха. При этом, какая из них будет соответствовать сложению, а какая вычитанию, в условиях априорной неопределенности принимаемых данных, указать невозможно. В условиях канала с постоянными параметрами СВ α и β являются независимыми и имеют плотности распределения Релея и Райса соответственно:
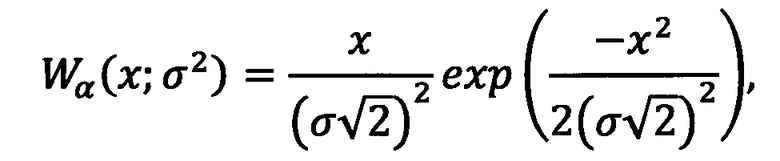
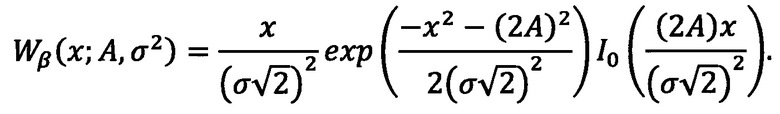
Теперь рассмотрим СВ, равную отношению огибающих суммы и разности сигналов:
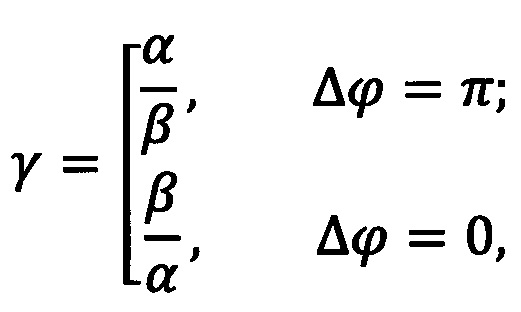
где Δϕ - разница фаз между соседними посылками.
Как видно, γ в зависимости от разницы фаз, может иметь либо одну, либо другую плотность распределения.
В случае, когда Δϕ=0 функция распределения СВ γ удается найти в замкнутом виде:
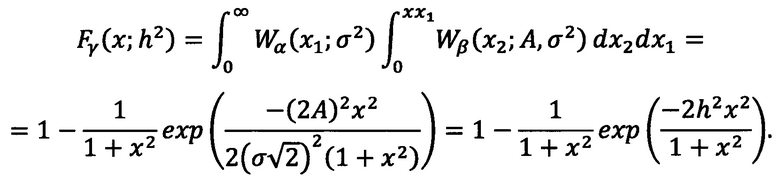
Тогда плотность распределения СВ γ находим, дифференцируя функцию распределения:
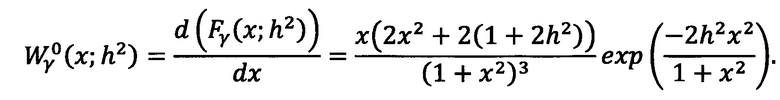
Плотность распределения СВ γ, когда Δϕ=π имеет вид:
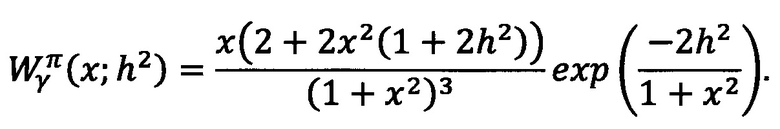
Таким образом, величина γ является случайной, которая может иметь одну из двух возможных плотностей вероятностей. При этом неизвестно, к какой именно плотности будет относиться полученная величина.
Далее предлагается рассматривать всю выборку величины γ целиком, то есть смесь выборок двух разных величин. Тогда, при условии, что передаваемые данные случайны и равновероятны (количество «0» и «1» примерно равно), можно представить плотность распределения СВ γ в виде следующей смеси двух плотностей:
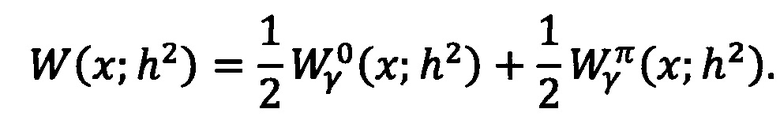
Тогда в случае наличия замираний по закону Накагами плотности будут иметь вид:
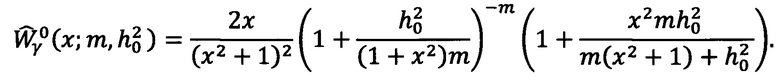
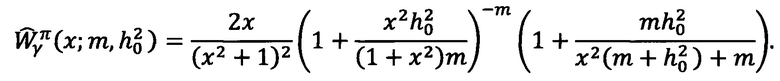
Соответствующая смесь плотностей будет иметь вид:
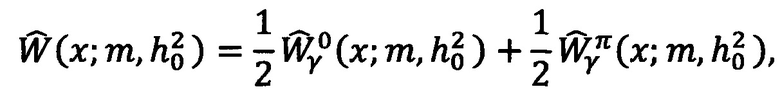
Таким образом, для модели закона замираний Накагами и для указанного вида OFDM сигнала, удается получить в замкнутом виде выражение для плотности распределения измеряемой СВ γ. Сформировав выборку СВ, и имея аналитическое выражение для ее плотности распределения, можно воспользоваться методом максимального правдоподобия, как одним из методов оценки неизвестных параметров распределений. Неизвестными параметрами для случая, когда огибающая распределена по закону Накагами, будут среднее ОСП 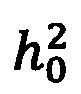 и глубина замираний m.
и глубина замираний m.
Тогда функция правдоподобия L, определяется выражением:
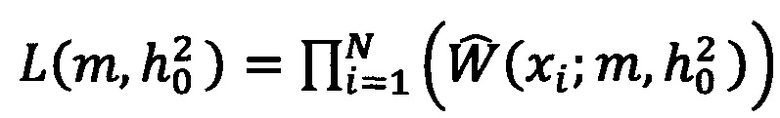 - для распределения Накагами,
- для распределения Накагами,
где xi - i-тое значение измеренной СВ γ;
N - объем выборки.
В этом случае координаты максимума функции правдоподобия 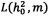 являются оценками искомых величин
являются оценками искомых величин 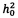 и m. При этом максимум можно найти любым численным методом, например, методом наискорейшего спуска [Н.С. Бахвалов. Численные методы - М.: Наука, 1973. - 632 с.].
и m. При этом максимум можно найти любым численным методом, например, методом наискорейшего спуска [Н.С. Бахвалов. Численные методы - М.: Наука, 1973. - 632 с.].
Способ работает следующим образом.
На приемной стороне оцифровывают принимаемый сигнал в аналогово-цифровом преобразователе 1, затем передают оцифрованный сигнал с выхода аналогово-цифрового преобразователя 1 на вход блока вычисления преобразования Фурье 2, в котором вычисляют преобразование Фурье на длительности текущей элементарной посылки и результат в виде массива комплексных чисел, соответствующих используемым частотам, передают одновременно на вход линии задержки 3, на первый вход первого сумматора 4 и на первый вход второго сумматора 5. Затем в линии задержки 3 задерживают поступивший массив на время, равное длительности элементарной посылки и далее с выхода передают его одновременно на второй вход первого сумматора 4 со знаком минус и на второй вход второго сумматора 5. В первом сумматоре 4 осуществляют поэлементное сложение поступивших массивов, один из которых поступил со знаком минус. Во втором сумматоре 5 также осуществляют поэлементное сложение поступивших массивов. Далее с выхода первого сумматора 4 передают массив комплексных чисел на вход первого блока вычисления модуля 6, а с выхода второго сумматора 5 передают массив комплексных чисел на вход второго блока вычисления модуля 7. В первом блоке вычисления модуля 6 вычисляют поэлементно модуль поступившего массива, и передают результат в виде массива вещественных чисел на первый вход делителя 8. Во втором блоке вычисления модуля 7 вычисляют поэлементно модуль поступившего массива, и передают результат в виде массива вещественных чисел на второй вход делителя 8. В делителе 8 производят поэлементное деление массива, полученного по первому входу на массив, полученный по второму входу и результат деления в виде массива чисел передают на вход блока накопления 9. В блоке накопления 9 производят накопление М последних полученных массивов, где М - заранее заданное число. С выхода блока накопления 9 передают накопленные массивы значений на вход блока вычисления параметров распределения 10, в котором, методом наискорейшего спуска, определяют параметры модели замираний огибающей сигнала по закону Накагами m и 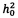 , являющиеся координатами максимума функции правдоподобия
, являющиеся координатами максимума функции правдоподобия 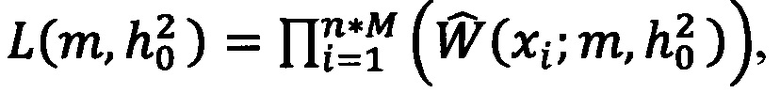 где xi - это i-е значение выборки,
где xi - это i-е значение выборки, 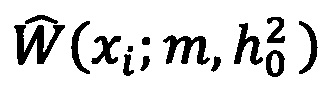 - плотность распределения вероятности измеряемой случайной величины, при этом,
- плотность распределения вероятности измеряемой случайной величины, при этом, 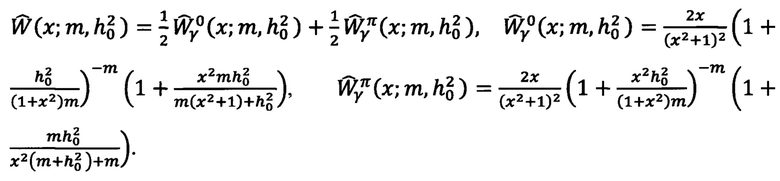
Предлагаемый способ может быть использован для систем связи, использующих многочастотные сигналы с ортогональным частотным разделением каналов связи. Предлагаемое устройство по сравнению с прототипом обладает следующим преимуществом: обеспечивает получение оценки параметров модели замираний огибающей сигнала по закону Накагами по информационному многочастотному сигналу, в случае, если в принимаемом информационном многочастотном сигнале для передачи данных используются все поднесущие частоты внутри выделенной полосы, таким образом, не снижает скорость передачи данных.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОЦЕНКИ ПАРАМЕТРОВ МОДЕЛИ ЗАМИРАНИЯ ОГИБАЮЩЕЙ СИГНАЛА ПО ЗАКОНУ НАКАГАМИ ПО ИНФОРМАЦИОННОМУ МНОГОЧАСТОТНОМУ СИГНАЛУ | 2015 |
|
RU2608363C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ МОДЕЛИ ЗАМИРАНИЯ РАДИОКАНАЛА ПО ЗАКОНУ РАЙСА ПО ИНФОРМАЦИОННОМУ МНОГОЧАСТОТНОМУ СИГНАЛУ | 2014 |
|
RU2559734C1 |
| СПОСОБ ОЦЕНИВАНИЯ ОТНОШЕНИЯ СИГНАЛ/ШУМ ПРИ ИСПОЛЬЗОВАНИИ СИГНАЛОВ С ФАЗОВОЙ МОДУЛЯЦИЕЙ | 2012 |
|
RU2548032C2 |
| Цифровой измеритель параметров случайных процессов с распределением Накагами | 2020 |
|
RU2742695C1 |
| Система автоматического управления декаметровой радиосвязью | 2022 |
|
RU2800643C1 |
| СПОСОБ ОЦЕНИВАНИЯ ОТНОШЕНИЯ СИГНАЛ/ПОМЕХА НА ДЛИТЕЛЬНОСТИ ОТРЕЗКА ГАРМОНИЧЕСКОГО КОЛЕБАНИЯ | 2012 |
|
RU2502077C1 |
| СПОСОБ УМЕНЬШЕНИЯ ПИК-ФАКТОРА МНОГОЧАСТОТНОГО СИГНАЛА С ОТНОСИТЕЛЬНОЙ ФАЗОВОЙ МОДУЛЯЦИЕЙ | 2018 |
|
RU2707271C1 |
| Устройство для определения оптимальных рабочих частот | 1980 |
|
SU926779A2 |
| Устройство поэлементной синхронизации | 1985 |
|
SU1319301A1 |
| СПОСОБ ИНДЕНТИФИКАЦИИ ТОНАЛЬНЫХ СИГНАЛОВ В СЕТЯХ СВЯЗИ И ЦИФРОВОЕ УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2004 |
|
RU2291405C2 |
Изобретение относится к области электрорадиотехники и связи и может быть использовано в системах передачи данных, использующих многочастотные сигналы с ортогональным частотным разделением каналов, для оценки параметров канала связи. Техническим результатом заявленного изобретения является обеспечение получения оценки параметров модели замираний огибающей сигнала по закону Накагами по информационному многочастотному сигналу в случае, если в принимаемом информационном многочастотном сигнале для передачи данных используются все поднесущие частоты внутри выделенной полосы. Таким образом, не снижается скорость передачи данных. В способе осуществляется измерение значений амплитуды смеси сигнала и шума на всех частотах, используемых для передачи информационного сигнала с предварительным сложением и вычитанием двух соседних посылок, и используется аналитическое выражение для плотности случайной величины, равной отношению измеренных величин. 1 ил.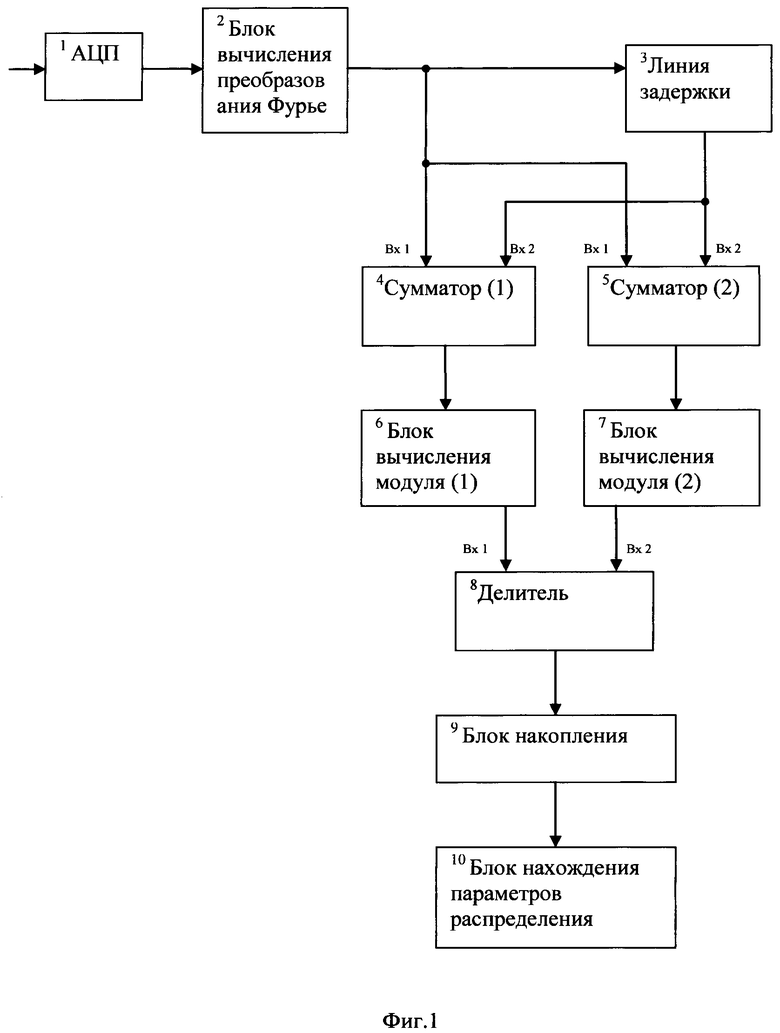
Способ оценки параметров модели замираний огибающей сигнала по закону Накагами по многочастотному сигналу, заключающийся в том, что на приемной стороне оцифровывают принимаемый сигнал в аналогово-цифровом преобразователе, отличающийся тем, что затем передают оцифрованный сигнал с выхода аналогово-цифрового преобразователя на вход блока вычисления преобразования Фурье, в котором вычисляют преобразование Фурье на длительности текущей элементарной посылки, и результат в виде массива комплексных чисел, соответствующих используемым частотам, передают одновременно на вход линии задержки, на первый вход первого сумматора и на первый вход второго сумматора, затем в линии задержки задерживают поступивший массив на время, равное длительности элементарной посылки, и далее с выхода передают его одновременно на второй вход первого сумматора со знаком минус и на второй вход второго сумматора, а в первом сумматоре осуществляют поэлементное сложение поступивших массивов, один из которых поступил со знаком минус, а во втором сумматоре также осуществляют поэлементное сложение поступивших массивов, далее с выхода первого сумматора передают массив комплексных чисел на вход первого блока вычисления модуля, а с выхода второго сумматора передают массив комплексных чисел на вход второго блока вычисления модуля, а в первом блоке вычисления модуля вычисляют поэлементно модуль поступившего массива и передают результат в виде массива вещественных чисел на первый вход делителя, а во втором блоке вычисления модуля вычисляют поэлементно модуль поступившего массива и передают результат в виде массива вещественных чисел на второй вход делителя, затем в делителе производят поэлементное деление массива, полученного по первому входу на массив, полученный по второму входу, и результат деления в виде массива передают на вход блока накопления и в блоке накопления производят накопление М последних полученных массивов, где М - заранее заданное число, а с выхода блока накопления передают накопленные массивы значений на вход блока вычисления параметров распределения, в котором, методом наискорейшего спуска, определяют параметры модели замираний огибающей сигнала по закону Накагами m и 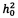 , являющиеся координатами максимума функции правдоподобия
, являющиеся координатами максимума функции правдоподобия 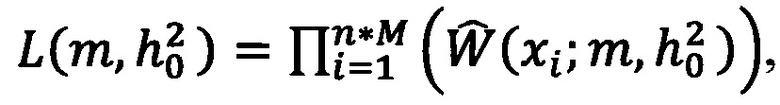 где xi - это i-е значение выборки,
где xi - это i-е значение выборки, 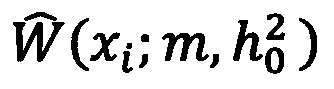 - плотность распределения вероятности измеряемой случайной величины, при этом
- плотность распределения вероятности измеряемой случайной величины, при этом 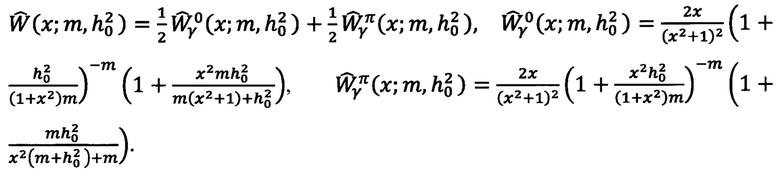
| СПОСОБ ОЦЕНКИ ПАРАМЕТРОВ МОДЕЛИ ЗАМИРАНИЯ ОГИБАЮЩЕЙ СИГНАЛА ПО ЗАКОНУ НАКАГАМИ ПО ИНФОРМАЦИОННОМУ МНОГОЧАСТОТНОМУ СИГНАЛУ | 2015 |
|
RU2608363C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ МОДЕЛИ ЗАМИРАНИЯ РАДИОКАНАЛА ПО ЗАКОНУ РАЙСА ПО ИНФОРМАЦИОННОМУ МНОГОЧАСТОТНОМУ СИГНАЛУ | 2014 |
|
RU2559734C1 |
| Способ приготовления мыла | 1923 |
|
SU2004A1 |
| Е.В.Чучин | |||
| Система моделей качества передачи цифровых сигналов по радиоканалам с замираниями Накагами | |||
| Auditorium: Электронный научный журнал Курского Государственного Университета | |||
| Способ защиты переносных электрических установок от опасностей, связанных с заземлением одной из фаз | 1924 |
|
SU2014A1 |
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Разборный с внутренней печью кипятильник | 1922 |
|
SU9A1 |
Авторы
Даты
2019-11-21—Публикация
2019-02-05—Подача