Изобретение относится к областям радиотехники и измерительной техники и может быть использовано в устройствах измерения параметров случайных сигналов с распределением вероятностей Накагами для оценки характеристик канала связи при наличии замираний и управления системой передачи информации.
Замирания сигнала в радиоканале описываются различными законами распределения вероятностей [1]. При этом наиболее универсальной моделью является распределение Накагами. Оценки его параметров m (характеристики глубины замираний сигнала) и Ω (характеристики средней мощности сигнала) используются, например, в системах передачи данных с многочастотными сигналами и ортогональным частотным разделением каналов в режиме частотной адаптации для повышения помехоустойчивости приема.
Известно аналоговое устройство для оценки параметра m случайного процесса с распределением Накагами [2], работа которого основана на логарифмическом преобразовании сигнала и приближенном решении уравнения с дзета-функцией Римана для нахождения параметра m распределения Накагами. Его недостатком является приближенность аналоговых математических преобразований и измерение только одного параметра.
Известны [3, 4] способы оценки параметров модели замираний радиоканала по закону Накагами в многочастотных системах связи с ортогональным частотным разделением каналов, в которых определяются амплитуды откликов каналов при наличии и отсутствии сигнала, на основе которых оцениваются значения m и отношения сигнал/шум  , соответствующие максимуму функции правдоподобия, либо эти оценки формируются по результатам комплексного спектрального анализа информационных сигналов. Общим недостатком этих способов является сложность технической реализации, особенно в режиме реального времени.
, соответствующие максимуму функции правдоподобия, либо эти оценки формируются по результатам комплексного спектрального анализа информационных сигналов. Общим недостатком этих способов является сложность технической реализации, особенно в режиме реального времени.
Близким к предлагаемому техническому решению является алгоритм оценки параметров m и Ω распределения Накагами по коррелированной выборке [5]. Его недостатком является высокая сложность полной вычислительной процедуры. Для ее упрощения предлагается использовать метод моментов второго и четвертого порядков.
Наиболее близким по технической сущности к предлагаемому цифровому устройству является цифровой измеритель статистических характеристик случайных сигналов [6], содержащий аналого-цифровой преобразователь, регистр, цифровой фильтр, канал формирования среднего значения, первый и второй квадратичные преобразователи, канал формирования среднего квадрата, вычитатель и генератор тактовых импульсов. Его недостатком является невозможность измерения параметров распределения вероятностей Накагами.
Задачей предлагаемого технического решения является обеспечение непрерывного цифрового измерения параметров m и Ω распределения вероятностей Накагами с высокой точностью при минимальном числе необходимых арифметических операций.
Поставленная задача решается тем, что цифровой измеритель параметров случайных процессов с распределением Накагами, содержащий каскадно соединенные аналого-цифровой преобразователь (АЦП), первый регистр (РГ1) и первый квадратичный преобразователь (КП1), первый (КФС1) и второй (КФС2) каналы формирования среднего значения, каждый из которых состоит из n (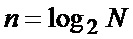 , N – объем выборки, по которой проводится усреднение отсчетов) каскадно соединенных накопителей отсчетов НО1–НО
, N – объем выборки, по которой проводится усреднение отсчетов) каскадно соединенных накопителей отсчетов НО1–НО , вход НО1 КФС1 является входом КФС1, а выход его НО
, вход НО1 КФС1 является входом КФС1, а выход его НО – выходом КФС1, вход НО1 КФС2 является входом КФС2, а выход его НО
– выходом КФС1, вход НО1 КФС2 является входом КФС2, а выход его НО – выходом КФС2, каждый НО состоит из сумматора (СУМ) и регистра сдвига многоразрядных кодов (МР), первый вход СУМ и вход МР соединены параллельно и образуют вход НО, а выход МР соединен со вторым входом СУМ, выход СУМ является выходом НО, выход КП1 соединен с входом КФС1, второй квадратичный преобразователь (КП2), вход которого соединен с выходом КФС1, а выход – с первым входом вычитателя (ВЫЧ), второй вход которого подключен к выходу КФС2, и генератор тактовых импульсов (ГТИ), дополнительно содержит третий квадратичный преобразователь (КП3), вход которого подключен к выходу КП1, а выход – к входу КФС2, второй регистр (РГ2), вход которого подключен к выходу КФС1, а на его выходе формируется двоичный код параметра Ω, цифровой делитель (ЦД), вход делимого которого соединен с выходом КП2, а вход делителя – с выходом вычитателя ВЫЧ, третий регистр (РГ3), вход которого подключен к выходу ЦД, а на его выходе формируется двоичный код параметра m, выход ГТИ подключен к тактовым входам АЦП, РГ1, НО1–НО
– выходом КФС2, каждый НО состоит из сумматора (СУМ) и регистра сдвига многоразрядных кодов (МР), первый вход СУМ и вход МР соединены параллельно и образуют вход НО, а выход МР соединен со вторым входом СУМ, выход СУМ является выходом НО, выход КП1 соединен с входом КФС1, второй квадратичный преобразователь (КП2), вход которого соединен с выходом КФС1, а выход – с первым входом вычитателя (ВЫЧ), второй вход которого подключен к выходу КФС2, и генератор тактовых импульсов (ГТИ), дополнительно содержит третий квадратичный преобразователь (КП3), вход которого подключен к выходу КП1, а выход – к входу КФС2, второй регистр (РГ2), вход которого подключен к выходу КФС1, а на его выходе формируется двоичный код параметра Ω, цифровой делитель (ЦД), вход делимого которого соединен с выходом КП2, а вход делителя – с выходом вычитателя ВЫЧ, третий регистр (РГ3), вход которого подключен к выходу ЦД, а на его выходе формируется двоичный код параметра m, выход ГТИ подключен к тактовым входам АЦП, РГ1, НО1–НО , входящих в КФС1 и КФС2, РГ2 и РГ3.
, входящих в КФС1 и КФС2, РГ2 и РГ3.
Предлагаемое техническое решение поясняется чертежами.
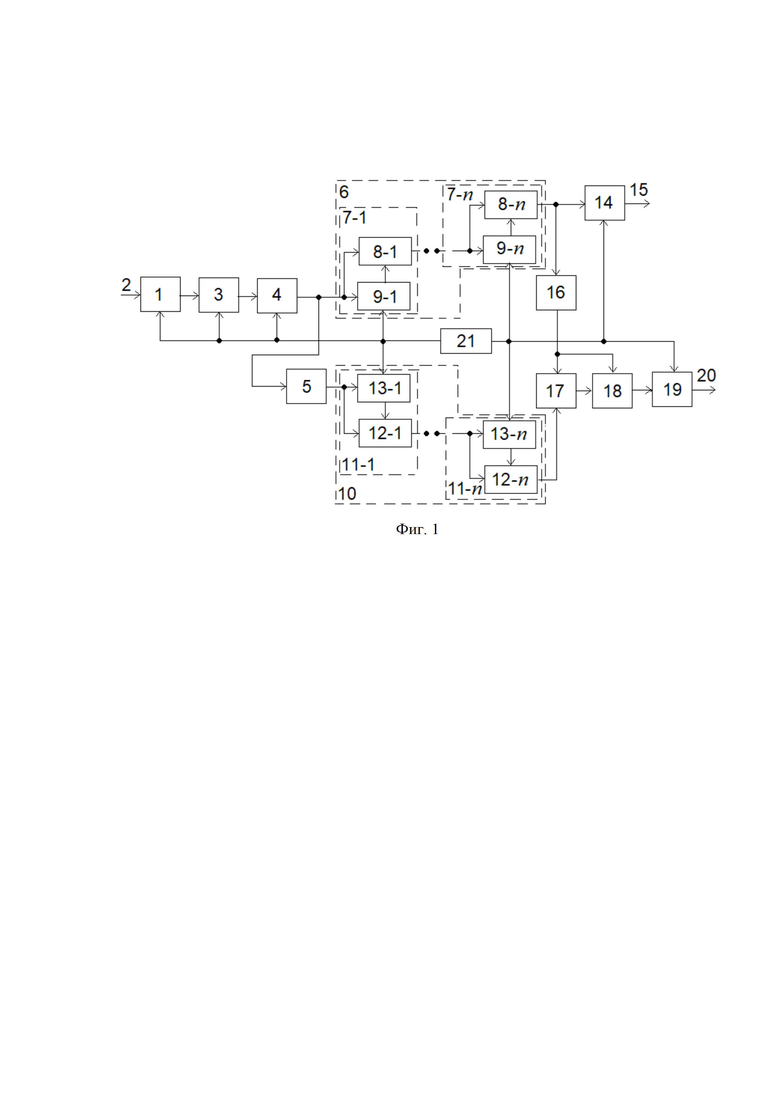
На фиг. 1 представлена структурная схема предлагаемого устройства, на фиг. 2 – временные диаграммы случайного сигнала с распределением Накагами, на фиг. 3 – результаты моделирования измерителя параметров некоррелированного сигнала, на фиг. 4 – результаты моделирования измерителя параметров коррелированного сигнала, а на фиг. 5 – оценки погрешностей измерений.
Устройство содержит АЦП 1, на вход которого поступает принимаемый сигнал 2. Выход АЦП 1 соединен с входом РГ1 3, выход которого соединен с входом первого квадратичного преобразователя КП1 4. Выход КП1 4 подключен к входу первого КФС1 6 и к входу КП3 5, выход которого соединен с входом второго КФС2 10. Каждый канал формирования среднего КФС1 6 (КФС2 10) состоит из 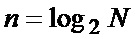 каскадно соединенных накопителей отсчетов НО1 7-1 ÷ НО
каскадно соединенных накопителей отсчетов НО1 7-1 ÷ НО 7-n (НО1 11-1 ÷ НОn 11-n), каждый из НО1 7-1 ÷ НОn 7-n (НО1 11-1 ÷ НОn 11-n) состоит из регистра сдвига многоразрядных кодов и сумматора. Блоки 7-1 ÷ 7-n (11-1 ÷ 11-n) накопления отсчетов содержат сумматоры 8-1 ÷ 8-n (12-1 ÷ 12-n) и регистры 9-1 ÷ 9-n (13-1 ÷ 13-n) сдвига многоразрядных кодов соответственно. В каждом НО первый вход сумматора 8 (12) соединен с первым входом регистра 9 (13) и является входом НО 7 (11). Второй вход сумматора 8 (12) соединен с выходом регистра сдвига 9 (13), выход сумматора 8 (12) является выходом НО 7 (11), а тактовый вход регистра 9 (13) является управляющим входом НО 7 (11). Вход НО 7-1 (11-1) является входом КФС1 6 (КФС2 10), а выход НО 7-n (11-n) соответственно выходом КФС1 6 (КФС2 10). Выход КФС1 6 соединен с входами регистра РГ2 14, на выходе которого формируется двоичный код 15 параметра Ω, и КП2 16, выход которого подключен к первому входу вычитателя ВЫЧ 17. Второй вход вычитателя ВЫЧ 17 подключен к выходу КФС2 10, а выход ВЫЧ 17 – к входу цифрового делителя ЦД 18, вход делимого которого соединен с выходом КП2 16. Выход ЦД 18 подключен к входу РГ3 19, на выходе которого формируется двоичный код 20 параметра m. На управляющие входы АЦП, РГ1, НО1–НОn, входящих в КФС1 и КФС2, РГ2 и РГ3 подаются сигналы от генератора тактовых импульсов ГТИ 21.
7-n (НО1 11-1 ÷ НОn 11-n), каждый из НО1 7-1 ÷ НОn 7-n (НО1 11-1 ÷ НОn 11-n) состоит из регистра сдвига многоразрядных кодов и сумматора. Блоки 7-1 ÷ 7-n (11-1 ÷ 11-n) накопления отсчетов содержат сумматоры 8-1 ÷ 8-n (12-1 ÷ 12-n) и регистры 9-1 ÷ 9-n (13-1 ÷ 13-n) сдвига многоразрядных кодов соответственно. В каждом НО первый вход сумматора 8 (12) соединен с первым входом регистра 9 (13) и является входом НО 7 (11). Второй вход сумматора 8 (12) соединен с выходом регистра сдвига 9 (13), выход сумматора 8 (12) является выходом НО 7 (11), а тактовый вход регистра 9 (13) является управляющим входом НО 7 (11). Вход НО 7-1 (11-1) является входом КФС1 6 (КФС2 10), а выход НО 7-n (11-n) соответственно выходом КФС1 6 (КФС2 10). Выход КФС1 6 соединен с входами регистра РГ2 14, на выходе которого формируется двоичный код 15 параметра Ω, и КП2 16, выход которого подключен к первому входу вычитателя ВЫЧ 17. Второй вход вычитателя ВЫЧ 17 подключен к выходу КФС2 10, а выход ВЫЧ 17 – к входу цифрового делителя ЦД 18, вход делимого которого соединен с выходом КП2 16. Выход ЦД 18 подключен к входу РГ3 19, на выходе которого формируется двоичный код 20 параметра m. На управляющие входы АЦП, РГ1, НО1–НОn, входящих в КФС1 и КФС2, РГ2 и РГ3 подаются сигналы от генератора тактовых импульсов ГТИ 21.
Устройство работает следующим образом.
Входной случайный сигнал 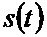 2, описывающийся распределением Накагами с двумерной плотностью вероятности [5]
2, описывающийся распределением Накагами с двумерной плотностью вероятности [5]
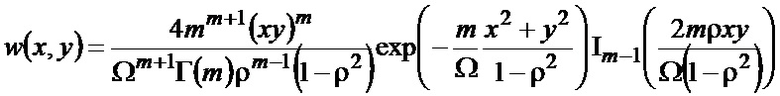 ,
,  ,
, 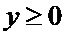 ,
,
поступает на вход аналого-цифрового преобразователя (АЦП) 1. Здесь 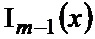 – модифицированная функция Бесселя
– модифицированная функция Бесселя  -го порядка,
-го порядка,  – гамма-функция, ρ – параметр корреляции, Ω, m – параметры, характеризующие среднюю мощность флуктуаций уровня сигнала и глубину его замираний соответственно.
– гамма-функция, ρ – параметр корреляции, Ω, m – параметры, характеризующие среднюю мощность флуктуаций уровня сигнала и глубину его замираний соответственно.
АЦП 1 в моменты времени 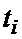 , определяемые ГТИ 21 (i – порядковый номер), формирует отсчеты
, определяемые ГТИ 21 (i – порядковый номер), формирует отсчеты 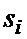 входного сигнала. На фиг. 2а и 2б показаны примеры реализаций случайного процесса с распределением Накагами для шестиразрядного АЦП (значения сигнала
входного сигнала. На фиг. 2а и 2б показаны примеры реализаций случайного процесса с распределением Накагами для шестиразрядного АЦП (значения сигнала 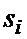 квантуются в диапазоне от 0 до 63) при
квантуются в диапазоне от 0 до 63) при 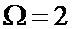 ,
,  (замирания глубже релеевских) и
(замирания глубже релеевских) и 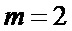 (замирания слабее релеевских) соответственно.
(замирания слабее релеевских) соответственно.
В текущий момент времени 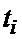 (
( ) обрабатывается выборка отсчетов
) обрабатывается выборка отсчетов 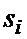 ,
,  , …,
, …,  объемом
объемом 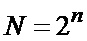 (n – целое число), по которой в каналах формирования среднего КФС1 и КФС2 определяются оценки
(n – целое число), по которой в каналах формирования среднего КФС1 и КФС2 определяются оценки 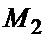 и
и 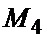 моментов второго и четвертого порядков:
моментов второго и четвертого порядков:
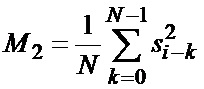 ,
,  .(1)
.(1)
Далее согласно [5, 6] на основе (1) формируются оценки параметров Ω и m распределения Накагами:
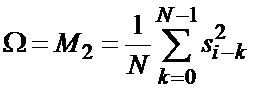 ,
, 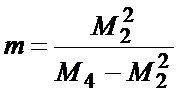 .(2)
.(2)
Для формирования оценок (1), (2) отсчеты 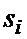 с выхода АЦП 1 запоминаются в РГ1 3 и их квадраты накапливаются в КФС1, а четвертые степени в КФС2. В момент времени
с выхода АЦП 1 запоминаются в РГ1 3 и их квадраты накапливаются в КФС1, а четвертые степени в КФС2. В момент времени 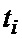 квадрат отсчета
квадрат отсчета 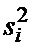 подается в КФС1 6 на вход первого НО 7-1. В сумматоре 8-1 он складывается с предшествующим значением
подается в КФС1 6 на вход первого НО 7-1. В сумматоре 8-1 он складывается с предшествующим значением 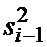 из регистра 9-1 емкостью в одну ячейку памяти, которое было записано в него на предшествующем шаге, и на выходе сумматора 8-1 формируется сумма отсчетов
из регистра 9-1 емкостью в одну ячейку памяти, которое было записано в него на предшествующем шаге, и на выходе сумматора 8-1 формируется сумма отсчетов  , после чего новое значение
, после чего новое значение  записывается в регистр 9-1. Полученная сумма подается во второй НО 7-2, в сумматоре 8-2 которого она складывается со значением
записывается в регистр 9-1. Полученная сумма подается во второй НО 7-2, в сумматоре 8-2 которого она складывается со значением 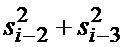 на выходе регистра сдвига 9-2 на две ячейки памяти. После этого содержимое регистра сдвигается, и в освободившуюся ячейку записывается новое значение
на выходе регистра сдвига 9-2 на две ячейки памяти. После этого содержимое регистра сдвигается, и в освободившуюся ячейку записывается новое значение 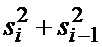 . Таким образом, на выходе сумматора 8-2 получим сумму четырех отсчетов
. Таким образом, на выходе сумматора 8-2 получим сумму четырех отсчетов  . Далее вычисления проводятся аналогично, и на вход последнего НО 7-n подается сумма
. Далее вычисления проводятся аналогично, и на вход последнего НО 7-n подается сумма
 ,(3)
,(3)
которая складывается в сумматоре 8-n с суммой
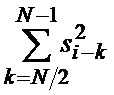 ,
,
ранее записанной в регистре сдвига 9-n на  ячеек. В результате на выходе сумматора 8-n формируется искомая сумма
ячеек. В результате на выходе сумматора 8-n формируется искомая сумма
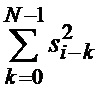 ,(4)
,(4)
после чего содержимое регистра 9-n сдвигается и в освободившуюся ячейку записывается величина (3).
Нетрудно видеть, что для вычисления полной суммы (4) требуется 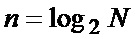 блоков НО. Например, при
блоков НО. Например, при  отсчета имеем
отсчета имеем 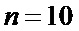 . Полученное на выходе КФС1 6 число пропорционально второму моменту
. Полученное на выходе КФС1 6 число пропорционально второму моменту 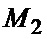 (1) входного сигнала. Операция его деления на
(1) входного сигнала. Операция его деления на 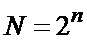 , как требуется согласно (1), выполняется отбрасыванием n младших двоичных разрядов.
, как требуется согласно (1), выполняется отбрасыванием n младших двоичных разрядов.
Блок КФС2 10 функционирует аналогично за исключением того, что накапливаются четвертые степени отсчетов 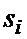 . Тогда на выходе КФС2 генерируется сумма
. Тогда на выходе КФС2 генерируется сумма
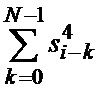 .(5)
.(5)
Для получения момента 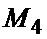 согласно (1) необходимо разделить результат (5) на N, что достигается отбрасыванием n младших разрядов двоичного кода.
согласно (1) необходимо разделить результат (5) на N, что достигается отбрасыванием n младших разрядов двоичного кода.
Число (4) на выходе КФС1 6 после отбрасывания n младших двоичных разрядов является измеренным значением 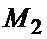 , которое записывается в регистр РГ2 14 и передается на его выход. Таким образом, выходной сигнал 15 регистра РГ2 является оценкой (2) параметра Ω. С выхода КФС1 6 значение
, которое записывается в регистр РГ2 14 и передается на его выход. Таким образом, выходной сигнал 15 регистра РГ2 является оценкой (2) параметра Ω. С выхода КФС1 6 значение 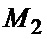 подается на вход КП2 16, с выхода которого величина
подается на вход КП2 16, с выхода которого величина 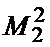 поступает в вычитатель ВЫЧ 17, на второй вход которого с выхода КФС2 10 после отбрасывания n младших двоичных разрядов подается значение
поступает в вычитатель ВЫЧ 17, на второй вход которого с выхода КФС2 10 после отбрасывания n младших двоичных разрядов подается значение 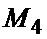 , а на выходе ВЫЧ 17 формируется величина
, а на выходе ВЫЧ 17 формируется величина  , поступающая на вход ЦД 18. Выходной код делителя 18 записывается в регистр РГ3 19, и на его выходе 20 формируется оценка (2) параметра m.
, поступающая на вход ЦД 18. Выходной код делителя 18 записывается в регистр РГ3 19, и на его выходе 20 формируется оценка (2) параметра m.
Согласно описанной процедуре обработки в предлагаемом устройстве на один отсчет сигнала необходимо выполнить всего 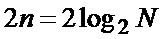 операций сложения, одну операцию вычитания, три квадратичных преобразования (умножения) и одну операцию деления целых чисел. При этом необходимо запоминать всего 2N многоразрядных двоичных кодов. Таким образом, обеспечивается минимальное количество арифметических операций на отсчет сигнала и, следовательно, высокая скорость обработки при минимальных аппаратных затратах. Технически устройство наиболее целесообразно реализовать на базе программируемых логических интегральных схем (ПЛИС). Современные ПЛИС средней сложности, например фирмы Xilinx серии Spartan-6 или отечественная интегральная схема 5576ХС4Т позволяют реализовать предлагаемое устройство при
операций сложения, одну операцию вычитания, три квадратичных преобразования (умножения) и одну операцию деления целых чисел. При этом необходимо запоминать всего 2N многоразрядных двоичных кодов. Таким образом, обеспечивается минимальное количество арифметических операций на отсчет сигнала и, следовательно, высокая скорость обработки при минимальных аппаратных затратах. Технически устройство наиболее целесообразно реализовать на базе программируемых логических интегральных схем (ПЛИС). Современные ПЛИС средней сложности, например фирмы Xilinx серии Spartan-6 или отечественная интегральная схема 5576ХС4Т позволяют реализовать предлагаемое устройство при 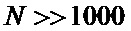 с рабочими частотами до 50-100 МГц.
с рабочими частотами до 50-100 МГц.
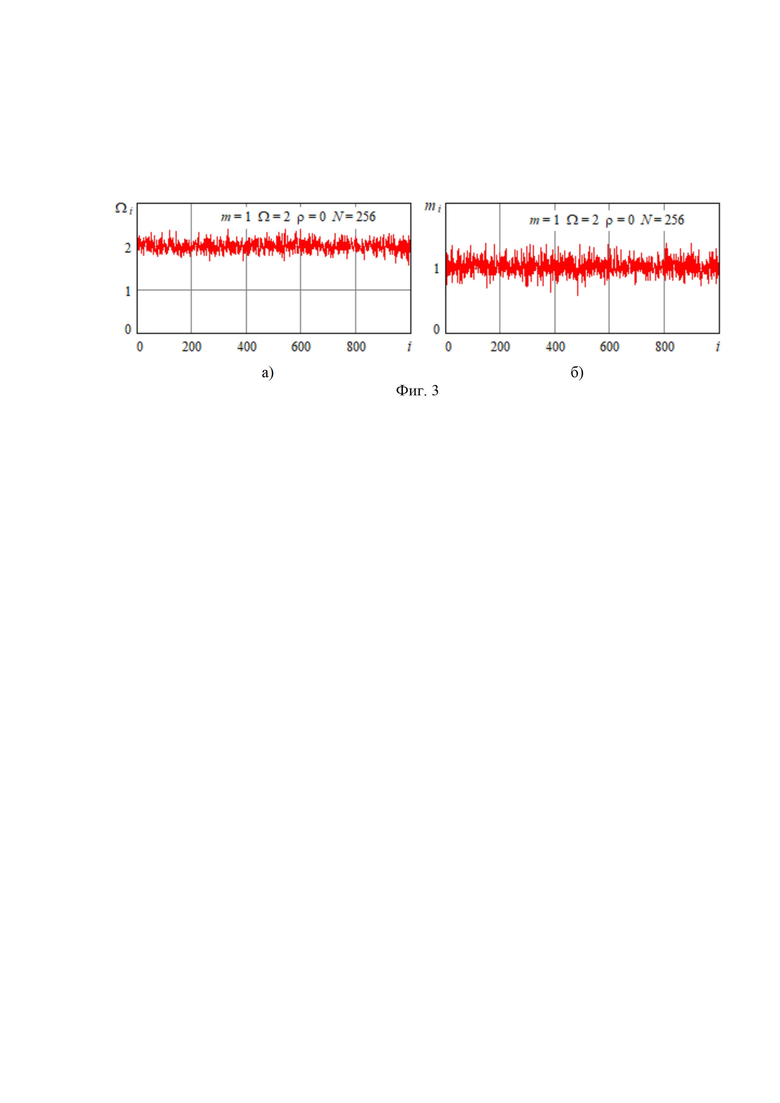
На фиг. 3 показаны полученные в результате статистического имитационного моделирования зависимости оценок параметров Ω и m случайного процесса с распределением Накагами от номера i текущего отсчета при 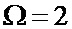 ,
, 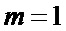 (релеевские замирания),
(релеевские замирания), 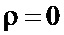 и небольшом объеме выборки
и небольшом объеме выборки 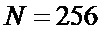 (
( ). Погрешность измерения δ оценивается отношением среднеквадратического отклонения оценки к ее абсолютному значению. Для реализаций оценок, представленных на фиг. 3а и 3б, эти погрешности составляют 6% и 12%. На фиг. 4 приведены аналогичные зависимости при обработке коррелированного входного сигнала с параметром корреляции
). Погрешность измерения δ оценивается отношением среднеквадратического отклонения оценки к ее абсолютному значению. Для реализаций оценок, представленных на фиг. 3а и 3б, эти погрешности составляют 6% и 12%. На фиг. 4 приведены аналогичные зависимости при обработке коррелированного входного сигнала с параметром корреляции 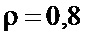 . В этом случае погрешности измерения параметров Ω и m возрастают до 15% и 17 % соответственно.
. В этом случае погрешности измерения параметров Ω и m возрастают до 15% и 17 % соответственно.
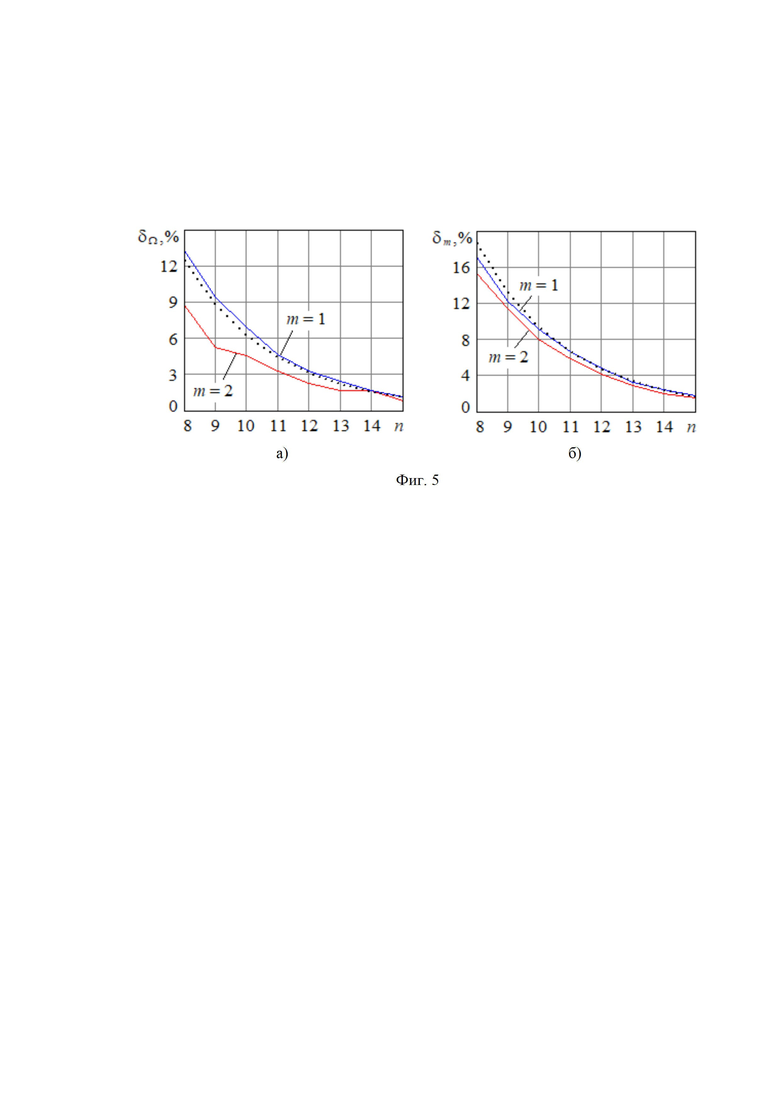
Погрешность статистических измерений определяется, прежде всего, объемом  выборки отсчетов, по которым проводится усреднение. На фиг. 5а и фиг. 5б показаны зависимости погрешностей измерения
выборки отсчетов, по которым проводится усреднение. На фиг. 5а и фиг. 5б показаны зависимости погрешностей измерения 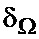 и
и 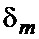 (в процентах) от
(в процентах) от 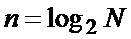 для
для  и
и  соответственно. Нетрудно видеть, что с ростом n погрешность измерения уменьшается и становится приемлемой при
соответственно. Нетрудно видеть, что с ростом n погрешность измерения уменьшается и становится приемлемой при  , то есть при объеме выборки
, то есть при объеме выборки 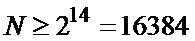 .
.
Согласно [7, 8] погрешность оценок обратно пропорциональна 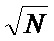 . На фиг. 5а точечной линией показана зависимость
. На фиг. 5а точечной линией показана зависимость 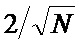 , а на фиг. 5б –
, а на фиг. 5б – 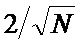 в процентах. Из фиг. 5 следует, что указанные теоретические зависимости хорошо согласуются с результатами моделирования в широком диапазоне значений объема выборки обрабатываемых отсчетов. Отметим также, что в устройстве управления системой радиосвязи по замирающим каналам требования к точности оценок параметров Ω и m существенно ниже, чем в измерительной аппаратуре.
в процентах. Из фиг. 5 следует, что указанные теоретические зависимости хорошо согласуются с результатами моделирования в широком диапазоне значений объема выборки обрабатываемых отсчетов. Отметим также, что в устройстве управления системой радиосвязи по замирающим каналам требования к точности оценок параметров Ω и m существенно ниже, чем в измерительной аппаратуре.
Частота квантования АЦП от ГТИ должна выбираться в соответствии с теоремой Котельникова, то есть примерно соответствовать удвоенной верхней граничной частоте спектра входного сигнала.
Литература
1. РЕКОМЕНДАЦИЯ МСЭ-R P.1057-3. Распределения вероятностей, касающихся моделирования распространения радиоволн (1994-2001-2007-2013). – 2013. – 21 с.
2. Иванкин П.А., Лебединский Е.В., Черненко В.Б. Устройство для оценки параметра m случайного процесса с распределением Накагами // Авторское свидетельство SU 481907, МПК G06F7/00 от 25.08.75 (Бюл. № 31).
3. Егоров В.В., Катанович А.А., Лобов С.А., Маслаков М.Л., Мингалев А.Н., Смаль М.С., Тимофеев А.Е. Способ оценки параметров модели замирания огибающей сигнала по закону Накагами по информационному многочастотному сигналу // Патент № 2608363 С1, МПК H04B17/391 от 18.01.2017 (Бюл. № 2); заявка № 2015129277 от 16.07.2015.
4. Егоров В.В., Лобов С.А., Маслаков М.Л., Мингалев А.Н., Смаль М.С., Тимофеев А.Е. Способ оценки параметров модели замираний радиоканала по закону Накагами по многочастотному сигналу // Патент № 2706939 С1, МПК H04L1/00, H04B17/309 от 21.11.2019 (Бюл. № 33); заявка № 2019103159 от 05.02.2019.
5. Парфенов В.И. Оценка параметров распределения Накагами по коррелированной выборке // Вестник Воронежского государственного университета. Серия: Физика. Математика. – 2004. – №1. – С. 39-44.
6. Чернояров О.В., Макаров А.А., Глушков А.Н., Литвиненко В.П., Литвиненко Ю.В., Матвеев Б.В. Цифровой измеритель статистических характеристик случайных сигналов // Патент № 2662412 C1, МПК G06F17/18, G01R19/25, G01R19/255, G01R19/02, H03K25/00 от 25.07.2018 (Бюл. № 21); заявка № 2017141798 от 30.11.2017.
7. Кендалл М., Стюарт А. Статистические выводы и связи. – М.: Наука, 1973. – 900 с.
8. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. – М.: Наука, 1970. – 720 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| Цифровой некогерентный демодулятор сигналов с амплитудно-фазовой манипуляцией | 2021 |
|
RU2766429C1 |
| Цифровой измеритель коэффициента корреляции случайного сигнала | 2020 |
|
RU2747725C1 |
| Цифровой обнаружитель фазоманипулированных сигналов | 2015 |
|
RU2634382C2 |
| ЦИФРОВОЙ ОБНАРУЖИТЕЛЬ ФАЗОМАНИПУЛИРОВАННЫХ СИГНАЛОВ | 2018 |
|
RU2693930C1 |
| ЦИФРОВОЙ ИЗМЕРИТЕЛЬ СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ СИГНАЛОВ | 2017 |
|
RU2662412C1 |
| Цифровой измеритель отношения сигнал/шум сигналов с фазовой манипуляцией | 2023 |
|
RU2799234C1 |
| ЦИФРОВОЙ ДЕМОДУЛЯТОР СИГНАЛОВ С ОТНОСИТЕЛЬНОЙ ФАЗОВОЙ МАНИПУЛЯЦИЕЙ | 2011 |
|
RU2505922C2 |
| ЦИФРОВОЙ ДЕМОДУЛЯТОР ДВОИЧНЫХ СИГНАЛОВ С ОТНОСИТЕЛЬНОЙ ФАЗОВОЙ МАНИПУЛЯЦИЕЙ ВТОРОГО ПОРЯДКА | 2018 |
|
RU2690959C1 |
| ЦИФРОВОЙ ДЕМОДУЛЯТОР СИГНАЛОВ С АМПЛИТУДНО-ФАЗОВОЙ МАНИПУЛЯЦИЕЙ | 2022 |
|
RU2786159C1 |
| ЦИФРОВОЙ ОБНАРУЖИТЕЛЬ УЗКОПОЛОСНЫХ СИГНАЛОВ | 2003 |
|
RU2257671C1 |


Изобретение относится к областям радиотехники и измерительной техники и может быть использовано в устройствах измерения параметров случайных сигналов с распределением вероятностей Накагами для оценки характеристик канала связи при наличии замираний и управления системой передачи информации. Достижимый технический результат – обеспечение непрерывного цифрового измерения параметров m и Ω распределения вероятностей Накагами с высокой точностью при минимальном числе необходимых арифметических операций. Цифровой измеритель параметров случайных процессов с распределением Накагами содержит аналого-цифровой преобразователь, первый, второй и третий регистры, первый, второй и третий квадратичные преобразователи, первый и второй каналы формирования среднего значения, каждый из которых состоит из  накопителей отсчетов, каждый из которых состоит из сумматора и регистра сдвига многоразрядных кодов, вычитатель, генератор тактовых импульсов и цифровой делитель. 5 ил.
накопителей отсчетов, каждый из которых состоит из сумматора и регистра сдвига многоразрядных кодов, вычитатель, генератор тактовых импульсов и цифровой делитель. 5 ил.
Цифровой измеритель параметров случайных процессов с распределением Накагами, содержащий каскадно соединенные аналого-цифровой преобразователь (АЦП), первый регистр (РГ1) и первый квадратичный преобразователь (КП1), первый (КФС1) и второй (КФС2) каналы формирования среднего значения, каждый из которых состоит из n (n = log2N, N – объем выборки, по которой проводится усреднение отсчетов) каскадно соединенных накопителей отсчетов НО1–НОn, вход НО1 КФС1 является входом КФС1, а выход его НОn – выходом КФС1, вход НО1 КФС2 является входом КФС2, а выход его НОn – выходом КФС2, каждый НО состоит из сумматора (СУМ) и регистра сдвига многоразрядных кодов (МР), первый вход СУМ и вход МР соединены параллельно и образуют вход НО, а выход МР соединен со вторым входом СУМ, выход СУМ является выходом НО, выход КП1 соединен с входом КФС1, второй квадратичный преобразователь (КП2), вход которого соединен с выходом КФС1, а выход – с первым входом вычитателя (ВЫЧ), второй вход которого подключен к выходу КФС2, и генератор тактовых импульсов (ГТИ), дополнительно содержит третий квадратичный преобразователь (КП3), вход которого подключен к выходу КП1, а выход – к входу КФС2, второй регистр (РГ2), вход которого подключен к выходу КФС1, а на его выходе формируется двоичный код параметра Ω, цифровой делитель (ЦД), вход делимого которого соединен с выходом КП2, а вход делителя – с выходом вычитателя ВЫЧ, третий регистр (РГ3), вход которого подключен к выходу ЦД, а на его выходе формируется двоичный код параметра m, выход ГТИ подключен к тактовым входам АЦП, РГ1, НО1–НОn, входящих в КФС1 и КФС2, РГ2 и РГ3.
| СПОСОБ ОЦЕНКИ ПАРАМЕТРОВ МОДЕЛИ ЗАМИРАНИЙ РАДИОКАНАЛА ПО ЗАКОНУ НАКАГАМИ ПО МНОГОЧАСТОТНОМУ СИГНАЛУ | 2019 |
|
RU2706939C1 |
| Цифровой измеритель действующего значения сигнала | 2018 |
|
RU2685062C1 |
| ЦИФРОВОЙ ИЗМЕРИТЕЛЬ СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ СИГНАЛОВ | 2017 |
|
RU2662412C1 |
| СПОСОБ ОЦЕНКИ ПАРАМЕТРОВ МОДЕЛИ ЗАМИРАНИЯ ОГИБАЮЩЕЙ СИГНАЛА ПО ЗАКОНУ НАКАГАМИ ПО ИНФОРМАЦИОННОМУ МНОГОЧАСТОТНОМУ СИГНАЛУ | 2015 |
|
RU2608363C1 |
| CN 102466750 B, 20.05.2015 | |||
| US 7046963 B2, 16.05.2006. | |||
Авторы
Даты
2021-02-09—Публикация
2020-07-17—Подача