Предлагаемое решение относится к методам измерения динамических механических параметров материалов.
Известно множество способов измерения динамического модуля упругости и коэффициента механических потерь материалов [1-8]. Часть этих методов вошло в международные и национальные стандарты РФ [1-7]. В [1] приведен сравнительный анализ методов измерения и указано, что наилучшим образом типичные условия применения материала воспроизводят испытания со сжатием образца, изготовленного из исследуемого материала [1, п. B3f]. Такие испытания отражают многие типичные условия нагружения при реальном использовании материала [1, п. В2b]. Но нужно учитывать, что испытания на сжатие требуют более высоких уровней вынуждающей силы. Для создания значительных амплитуд деформации сдвига и сжатия, а также для создания условий предварительного нагружения требуется испытательное оборудование, способное развивать значительную силу [1, п. B2d]. В связи с этим многие из рассматриваемых в стандарте методов находят очень ограниченное применение, и, чтобы снизить энергопотребление, габаритные размеры и массу испытательного оборудования «Измерение модуля Юнга рекомендуется проводить с возбуждением резонансных колебаний» [1, п. В3а]. Таким образом, резонансные способы измерения динамических механических параметров материалов являются предпочтительными.
Известен резонансный способ определения динамических характеристик низкомодульных материалов [8]. В этом способе образец материала располагают между подложкой из высокодобротного материала и неподвижной поверхностью. В подложке возбуждают изгибные колебания и по массогабаритным параметрам образца материала и амплитудно-частотным характеристикам подложки вычисляют динамический модуль упругости и коэффициент механических потерь. Недостатком способа является неравномерность нагружения (деформации) исследуемого материала, приводящая к погрешностям измерения динамических параметров. Известно, что динамические параметры материала зависят от частоты колебаний, температуры, статической нагрузки, величины деформации (возникающих напряжений). Учитывая, что деформация материала неравномерная, то не известно, какой именно деформации соответствуют параметры материалов, полученные с использованием рассматриваемого метода.
Наиболее близким к предлагаемому является резонансный способ измерения динамического модуля упругости и коэффициента механических потерь [2]. Суть метода состоит в установке образца, изготовленного из исследуемого материала, между вибрирующим основанием, у которого имеется возможность плавного изменения частоты колебаний, и инерционным элементом (фиг. 1). При этом получается колебательная система, состоящая из образца материала и инерционного элемента. Образец материала создает упругие свойства колебательной системы за счет модуля продольной упругости материала, формы и размеров образца материала. Инерционный элемент задает инерционные свойства колебательной системы (массу). Изменяя частоту основания, измеряют амплитудно-частотную характеристику полученной системы и по массогабаритным размерам образца материала, массе инерционного элемента, собственной частоте колебаний инерционного элемента рассчитывают динамический модуль упругости материала. Коэффициент механических потерь находят по ширине резонансной кривой на уровне 0,707 и собственной частоте колебаний колебательной системы.
Одним из недостатков этого способа является наличие статической деформации образца материала за счет силы тяжести инерционного элемента. При исследовании низкомодульных материалов такая деформация является значительной, часто недопустимой.
Другим недостатком известного способа является сложность измерения параметров высокодемпфированных материалов. При использовании образца из высокодемпфированного материала резонанс становится невыраженным, и измерить собственную частоту и ширину резонансной кривой не удается.
Третьим недостатком способа является возможность измерения динамических параметров низкомодульных материалов только в низкочастотной области. Как известно собственная частота ω0 упруго-инерционной системы с одной степенью свободы рассчитывается по формуле
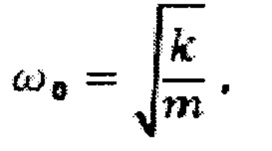
где k - жесткость упругого элемента; m - масса инерционного элемента.
При малой жесткости k получается малая частота резонансных колебаний системы.
Для устранения указанных недостатков предлагается дополнительно устанавливать высокодобротные упругие элементы (пружины) между инерционным элементом и вибрирующим основанием, измерять собственную частоту колебаний и ширину резонансной кривой упругоинерционной системы с пружинами без образца материала и с образцом из исследуемого материала. Динамический модуль упругости в паскалях рассчитывают по формуле

где m - масса инерционного элемента, кг;
m0 - масса образца материала, которая добавляется к массе инерционного элемента с коэффициентом 1/3 в соответствии с [9, с. 191], кг;
m1 - масса пружин, кг;
h, А - высота и площадь поперечного сечения образца материала, соответственно, м;
f1 - собственная частота колебаний инерционного элемента на пружинах без образца из исследуемого материала, Гц;
f∑ - собственная частота колебаний инерционного элемента на пружинах с установленным образцом из исследуемого материала, Гц.
Коэффициент механических потерь материала находят по формуле

где η∑=Δf∑/f∑ - коэффициент механических потерь оснастки с исследуемым материалом;
η1=Δf1/f1 - коэффициент механических потерь оснастки без исследуемого материала;
k1=4π2*f12*m - жесткость пружин, Н/м;
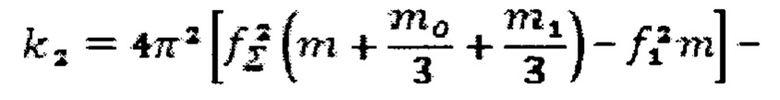 жесткость образца материала, Н/м.
жесткость образца материала, Н/м.
В случае необходимости испытаний материалов со статической деформацией при установке пружин обеспечивают необходимую статическую деформацию образца из исследуемого материала путем закрепления инерционного элемента на пружинах таким образом, чтобы при установке образца материала между инерционным элементом и вибрирующим основанием обеспечивалась требуемая статическая деформация образца.
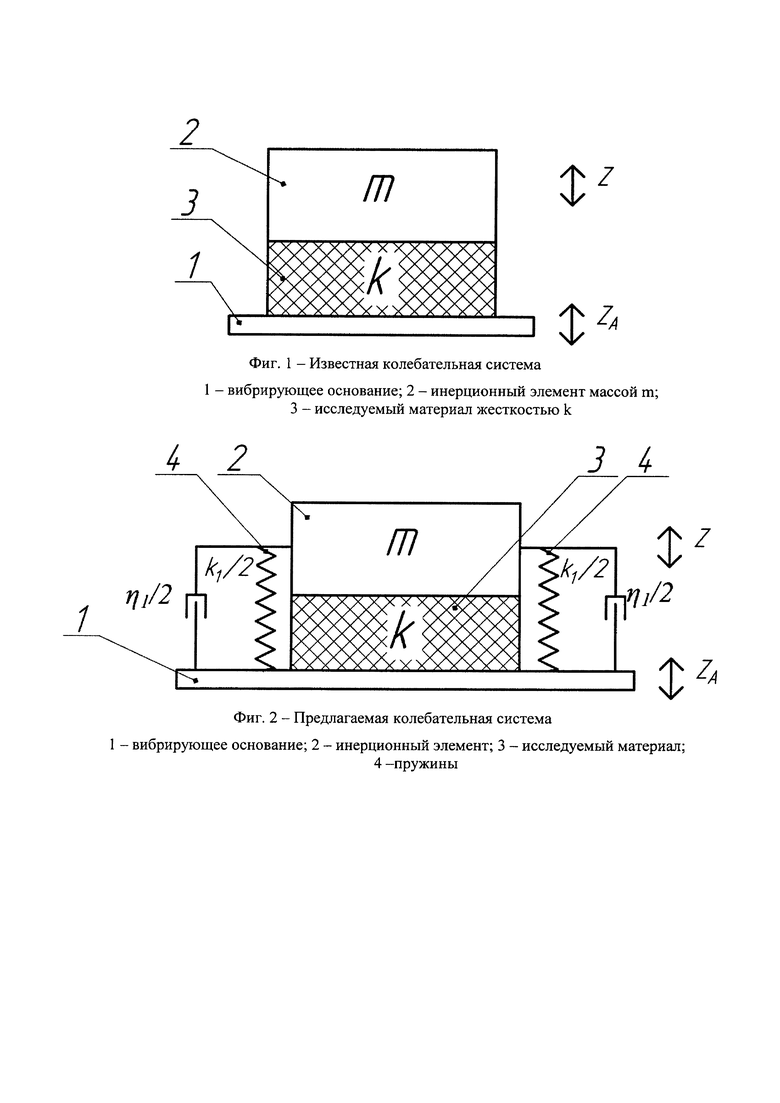
На фиг. 1 показана колебательная система, с помощью которой измеряют динамические параметры в известном способе. На основание 1 приклеивается образец материала 2, выполненный в форме прямоугольного параллелепипеда, либо цилиндра, а на образец материала приклеивается инерционный элемент 3.
На фиг. 2 показана колебательная система, с помощью которой измеряют динамические параметры в предлагаемом способе. В предлагаемой системе дополнительно устанавливаются упругие элементы 4 (пружины), повышающие жесткость и резонансную частоту колебательной системы. Кроме этого, пружины создают дополнительные силы, удерживающие инерционный элемент 2 на необходимом удалении от основания 1. Выбирая пружины определенной длины или изменяя уровень крепления инерционного элемента на пружинах можно получать различные статические деформации исследуемого материала.
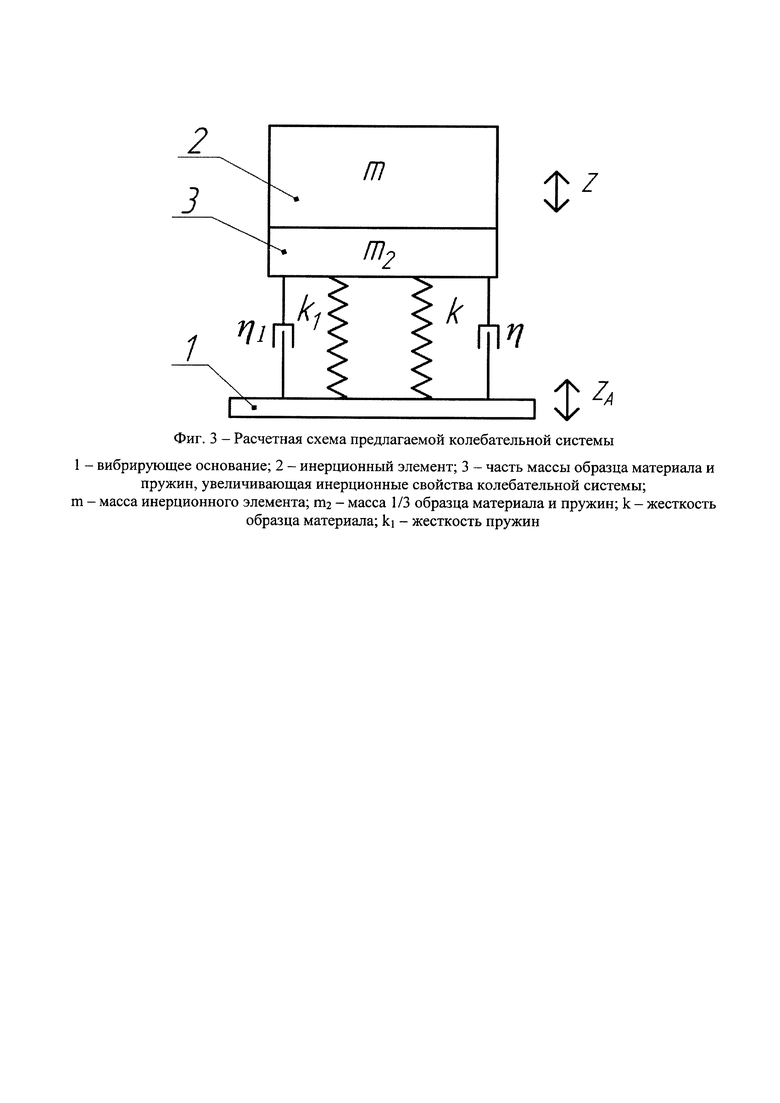
На фиг. 3 показана расчетная схема колебательной системы, реализующей предлагаемый способ. Грузом массой m2 обозначена суммарная масса 1/3 части образца материала и 1/3 части пружин. Известно [9], что масса упругих элементов увеличивает инерционные свойства колебательной системы с весовым коэффициентом 1/3. Если масса образца материала и пружин много меньше массы инерционного элемента 2, то составляющей m2 можно пренебречь.
Предложение может быть реализовано следующим образом:
1) Для испытаний низкомодульных материалов изготавливается технологическая оснастка, включающая плоское основание высокой жесткости, прямоугольный параллелепипед либо цилиндр из материала большой объемной плотности и жесткости (металл, камень), выполняющий роль инерционного элемента, и пружины.
2) Измеряется масса инерционного элемента m и пружин m1. Инерционный элемент боковой поверхностью закрепляется на пружинах.
3) У полученной колебательной системы измеряется резонансная частота f1 и ширина резонансной кривой на уровне 0.707 Δf1. Находится коэффициент механических потерь оснастки без исследуемого материала по формуле η1=Δf1/f1 и жесткость пружин по формуле k1=4π2*f12*(m+m1/3).
4) Измеряется расстояние между инерционным элементом и основанием.
5) Изготавливаются образец материала в форме инерционного элемента (прямоугольного параллелепипеда либо цилиндра), с размерами основания равными размерам основания инерционного элемента, но своей высотой h. При этом, если нам не нужна статическая деформация материала, то высота h берется равной расстоянию, полученному в п. 4. При требуемой статической деформации растяжения материала высоту образца уменьшают, а при требуемой статической деформации сжатия - увеличивают.
6) Измеряют массу образца материала то-
7) Вклеивают образец материала между инерционным элементом и основанием.
8) У полученной колебательной системы измеряется резонансная частота f∑ и ширина резонансной кривой на уровне 0,707 Δf∑ оснастки с образцом исследуемого материала.
9) Находится коэффициент механических потерь оснастки с исследуемым материалом по формуле η∑=Δf∑/f∑. По формуле (1) вычисляется модуль упругости материала. Жесткость образца материала находится по формуле
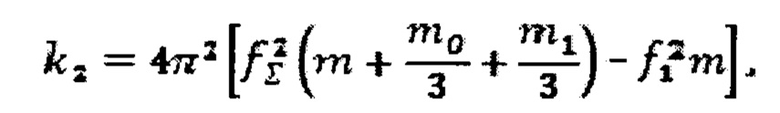
и по формуле (2) рассчитывается коэффициент механических потерь материала.
Выбирая пружины различной жесткости, инерционные элементы различной массы и размеров, образцы материалов различных высот получаем различные значения резонансных частот. Если в оснастке предусмотреть возможность крепления инерционных элементов на различном расстоянии от основания, то дополнительно получаем различные статические деформации исследуемого материала.
Список использованных источников
1) ГОСТ Р ИСО 18437-1-2014 НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ Вибрация и удар ОПРЕДЕЛЕНИЕ ДИНАМИЧЕСКИХ МЕХАНИЧЕСКИХ СВОЙСТВ ВЯЗКОУПРУГИХ МАТЕРИАЛОВ Часть 1. Общие принципы.
2) ГОСТ Р ИСО 18437-2-2014 НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ Вибрация и удар ОПРЕДЕЛЕНИЕ ДИНАМИЧЕСКИХ МЕХАНИЧЕСКИХ СВОЙСТВ ВЯЗКОУПРУГИХ МАТЕРИАЛОВ Часть 2. Резонансный метод
3) ГОСТ Р 56801-2015 (ИСО 6721-1:2011) Пластмассы. Определение механических свойств при динамическом нагружении. Часть 1. Общие принципы
4) ГОСТ Р 56802-2015 Пластмассы. Определение механических свойств при динамическом нагружении. Часть 7. Крутильные колебания. Нерезонансный метод
5) ГОСТ Р 56803-2015 (ИСО 6721-3:1994) Пластмассы. Определение механических свойств при динамическом нагружении. Часть 3. Колебания изгиба. Метод резонансной кривой
6) ГОСТ Р 56804-2015 (ИСО 6721-4:2008) Пластмассы. Определение механических свойств при динамическом нагружении. Часть 4. Колебания при растяжении. Нерезонансный метод
7) ГОСТ Р 56805-2015 (ИСО 14125:1998) Композиты полимерные. Методы определения механических характеристик при изгибе
8) А.с. №1539578. Долгов Г.Ф., Евграфов В.В., Талицкий Е.Н. Резонансный способ определения динамических характеристик низкомодульных материалов.
9) Работнов Ю.Н. Механика деформируемого твердого тела. - Учеб. пособие для вузов. - 2-е изд., испр. - М.: Наука. Гл. ред. физ.-мат.лит., 1988. - 712 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для измерения горизонтальных ускорений | 2021 |
|
RU2838579C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДЕФОРМАЦИОННЫХ ПОКАЗАТЕЛЕЙ ПОЛИМЕРНЫХ МАТЕРИАЛОВ | 2005 |
|
RU2300751C1 |
| Резонансный способ определения динамических характеристик низкомодульных материалов | 1987 |
|
SU1539578A1 |
| Способ определения комплексного модуля Юнга мягких вязкоупругих материалов | 1985 |
|
SU1350546A1 |
| СПОСОБ ИЗМЕРЕНИЯ МЕХАНИЧЕСКИХ СВОЙСТВ ПОЛИМЕРОВ В ПРОЦЕССЕ ОТВЕРЖДЕНИЯ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2005 |
|
RU2307337C2 |
| СЛОИСТАЯ ВИБРОШУМОДЕМПФИРОВАННАЯ ПАНЕЛЬ КАБИНЫ ВОДИТЕЛЯ И/ИЛИ ПАССАЖИРСКОГО ПОМЕЩЕНИЯ КУЗОВА ТРАНСПОРТНОГО СРЕДСТВА | 2010 |
|
RU2449904C1 |
| СПОСОБ МОДЕЛИРОВАНИЯ ПАРАМЕТРИЧЕСКИХ КОЛЕБАНИЙ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ (ВАРИАНТЫ) | 2020 |
|
RU2748870C1 |
| Динамический наноиндентор | 2019 |
|
RU2721020C1 |
| Датчик крутильных колебаний | 2016 |
|
RU2615915C1 |
| АКУСТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ОБРАЗЦА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1992 |
|
RU2044298C1 |
Изобретение относится к измерительной технике и может быть использовано для измерения динамического модуля упругости и коэффициента механических потерь полимера. Технический эффект заключается в расширении частотного диапазона измерений, обеспечении необходимой статической деформации материала и измерении параметров высокодемпфированных материалов, достигается за счёт того, что дополнительно устанавливают высокодобротные упругие элементы (пружины) между инерционным элементом и вибрирующим основанием, измеряют собственную частоту колебаний и ширину резонансной кривой упругоинерционной системы с пружинами без образца материала и с образцом из исследуемого материала и рассчитывают динамический модуль упругости материала. 1 з.п. ф-лы, 3 ил.
1. Резонансный способ измерения динамических механических параметров низкомодульных вибропоглощающих материалов, заключающийся в формировании колебательной системы путем установки образца с известной массой и размерами из исследуемого материала между вибрирующим основанием и инерционным элементом с известной массой, измерении собственной частоты колебаний и ширины резонансной кривой колебательной системы и расчете модуля упругости и коэффициента механических потерь исследуемого материала, отличающийся тем, что дополнительно устанавливают пружины между вибрирующим основанием и инерционным элементом, определяют собственную частоту колебаний и ширину резонансной кривой на уровне 0,707 полученной колебательной системы с образцом из исследуемого материала и без образца из исследуемого материала, динамический модуль упругости материала рассчитывают по формуле
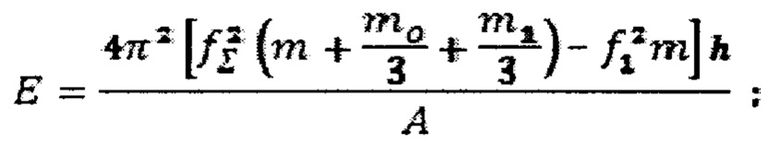
коэффициент механических потерь материала рассчитывают по формуле
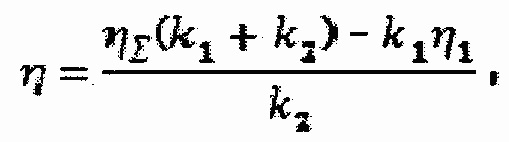
где m - масса инерционного элемента;
m0 - масса образца материала, которая добавляется к массе инерционного элемента с коэффициентом 1/3;
m1 - масса пружин;
h, А - высота и площадь поперечного сечения образца материала соответственно;
f1 - собственная частота колебаний инерционного элемента на пружинах без образца из исследуемого материала;
f∑ - собственная частота колебаний инерционного элемента на пружинах с установленным образцом из исследуемого материала;
η∑=Δf∑/f∑ - коэффициент механических потерь оснастки с исследуемым материалом;
η1=Δf1/f1 - коэффициент механических потерь оснастки без исследуемого материала;
k1=4π2*f12*m - жесткость пружин;
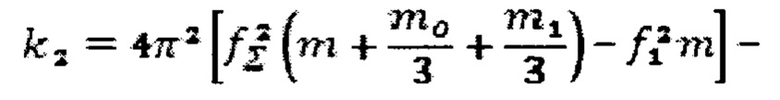 жесткость образца материала.
жесткость образца материала.
2. Способ по п. 1, отличающийся тем, что при установке пружин обеспечивают необходимую статическую деформацию образца из исследуемого материала путем закрепления инерционного элемента на пружинах на требуемом расстоянии от вибрирующего основания.
| Установка для определения динамических характеристик низкомодульных полимерных материалов | 2016 |
|
RU2628737C1 |
| Резонансный способ определения динамических характеристик низкомодульных материалов | 1987 |
|
SU1539578A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРИВЕДЕННЫХ ПАРАМЕТРОВ МЕХАНИЧЕСКОЙ СИСТЕМЫ | 1991 |
|
RU2006717C1 |
| Детектор частотно-модулированных колебаний | 1941 |
|
SU61875A1 |
| US 7966134 B2, 21.06.2011. | |||
Авторы
Даты
2020-05-29—Публикация
2019-08-12—Подача