Изобретение относится к области классического экспериментального модального анализа конструкций. Примером свободной конструкции является летательный аппарат, характеристики собственных тонов колебаний которого используют при решении задач прочности, устойчивости и управляемости авиационной и космической техники.
Известен метод экспериментального определения характеристик собственных тонов колебаний: собственных частот и форм, обобщенных масс и обобщенных декрементов колебаний методом фазового резонанса. Для реализации метода на исследуемую конструкцию устанавливают датчики вибраций (перемещений, скоростей, ускорений). Возбуждение колебаний конструкции производится с помощью нескольких независимых источников вибраций. Выделяют собственные тона конструкции в заданном диапазоне частот воспроизведением режимов фазового резонанса путем использования многоканальной системы возбуждения и измерения колебаний. Определяют собственные частоты и формы колебаний тонов по частотам фазовых резонансов и конфигурациям вынужденных колебаний на этих частотах. (Хейлен Вард, Ламменс Стефан, Сас Пол. Модальный анализ: теория и испытания. - М.: ООО «Новатест», 2010. - 319 с.).
Обобщенные характеристики собственных тонов колебаний определяются различными способами.
Известен способ определения обобщенных масс и декрементов колебаний по изменению частоты фазового резонанса (реализация режимов «фиктивного» фазового резонанса) после введения квадратурной составляющей возбуждения. (Васильев К.И., Смыслов В.И., Ульянов В.И. Экспериментальное исследование упругих колебаний летательных аппаратов с помощью многоканального оборудования АВДИ-1Н // Тр. ЦАГИ им. Н.Е. Жуковского. - 1975. - Вып. 1634. - С. 1-36.).
Известен энергетический метод определения обобщенной массы и обобщенного декремента колебаний, заключающийся в приравнивании работы сил неупругого сопротивления работе сил возбуждения за период колебаний. При этом работа сил демпфирования записывается для конкретной модели рассеяния энергии и выражается через декремент колебаний и обобщенную массу. Определяя декремент известными методами, можно вычислить обобщенную массу. И наоборот, если известна обобщенная масса, то энергетический метод служит для определения декремента колебаний. (Clerc D. Methode de recherche des modes propres par calcul de l'excitation harmonique optimum d'apres les res les resultats bruts d'essais de vibrations // Note technique: ONERA. - 1967. - №119. - 57 p.).
Известен способ определения обобщенных масс методом механической догрузки. Метод предполагает оценивать обобщенную массу тона по изменению его собственной частоты в результате установки на объекте дополнительных масс (Микишев Г.Н., Рабинович Б.И. Динамика тонкостенных конструкций с отсеками, содержащими жидкость. - М.: Машиностроение, 1971. - 564 с.).
Известен способ определения обобщенных характеристик собственных тонов колебаний методом выделения аппроксимирующей окружности. В его основе лежит тот факт, что частотная характеристика системы с одной степенью свободы описывает окружность в диаграмме Найквиста. Для реализации этого метода выделяется совокупность точек частотной характеристики вблизи частоты фазового резонанса, через которые проводится аппроксимирующая окружность. После этого находится собственная частота тона как точка с максимальной скоростью изменения угла между экспериментальными значениями частотной характеристики. Параметры окружности являются также исходными данными для определения коэффициента демпфирования. (Хейлен Вард, Ламменс Стефан, Сас Пол. Модальный анализ: теория и испытания. - М.: ООО «Новатест», 2010. - 319 с.).
Известен способ определения модальных характеристик конструкций, основанный на соотношениях между собственными и вынужденными монофазными колебаниями. (Бернс В.А., Жуков Е.П., Маленкова В.В. Способ определения параметров собственных тонов колебаний конструкций в резонансных испытаниях: пат. на изобретение №2658125).
Недостатками всех представленных аналогов являются:
- использование допущения о том, что система упругого вывешивания конструкции не оказывает влияния на характеристики собственных тонов колебаний свободной конструкции;
- отсутствие требований к механическим характеристикам системы упругого вывешивания конструкции.
Известны способы и стенды определения собственных частот и обобщенных масс колеблющихся конструкций, которые отличаются от описанных выше тем, что позволяют определять массы испытываемого объекта без ошибок, вносимых испытательным оборудованием. (Патенты RU 2499239, RU 2489696, RU 2485468). Но при этом недостатки самого метода определения обобщенных характеристик не устраняются.
Известен способ определения параметров собственных тонов колебаний свободного летательного аппарата по результатам наземных модальных испытаний из условия, что система упругого вывешивания не должна оказывать заранее оговоренного влияния на собственные тона упругих колебаний конструкции. Считается, что частота колебаний летательного аппарата как твердого тела на подвеске должна в 4-6 раз быть ниже собственной частоты первого упругого тона. (О современных методиках наземных испытаний самолетов в аэроупругости / Карклэ П.Г., Малютин В.А., Мамедов О.С., Поповский В.Н., Смотров А.В., Смыслов В.И. // Уч. записки ЦАГИ им. Н.Е. Жуковского, 2012, вып. 2708. - 34 с.
Данный способ экспериментального определения параметров собственных тонов колебаний свободной конструкций выбран за прототип.
Недостатком способа является отсутствие оценок погрешностей определения модальных характеристик свободной конструкции в зависимости от жесткости системы упругого вывешивания.
Задачей (техническим результатом) является исключение влияния жесткости системы упругого вывешивания на погрешности определения собственных частот и форм колебаний свободной конструкции по результатам наземных модальных испытаний.
Поставленная задача решается тем, что строят расчетной динамической модель свободной конструкции, проводят наземные модальные испытания конструкции, зафиксированной системой упругого вывешивания, корректируют расчетную модель по результатам испытаний, определяют собственные частоты и формы колебаний свободной конструкции по скорректированной расчетной модели, при этом производится освобождение модели от закреплений при условии, что известны масса и массовые моменты инерции свободной конструкции.
Изобретение относится к области классического экспериментального модального анализа конструкций. Способ определения собственных частот и форм колебаний свободной конструкции по результатам испытаний этой конструкции с наложенными связями осуществляется следующим образом. На этапе проектирования конструкции разрабатывается ее расчетная модель как свободной динамической системы. Затем эта модель корректируется по результатам наземных модальных испытаний конструкции, помещенной в специальную систему упругого вывешивания. Скорректированная по результатам испытаний закрепленная модель описывается матрицами жесткости K и масс М, имеет n степеней свободы и N узлов. Система уравнений собственных колебаний этой модели имеет следующий вид:

Предлагается освободить модель от закреплений при условии, что известны инерционные характеристики свободной конструкции, а именно: масса и массовые моменты инерции. Для этой цели модель «устанавливается» на виртуальную платформу, к которой она прикреплена зафиксированными системой вывешивания узлами. Платформа может перемещаться и поворачиваться как жесткое целое. Положение платформы в глобальной неподвижной системе координат определяется координатами некоторой точки С - вектором 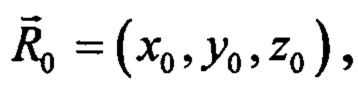 а ориентация в пространстве задается вектором конечного поворота
а ориентация в пространстве задается вектором конечного поворота 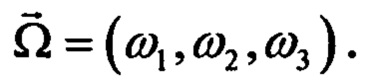 Виртуальная платформа в общем случае находится на упругом основании, заданном тремя линейными и тремя крутильными жесткостями.
Виртуальная платформа в общем случае находится на упругом основании, заданном тремя линейными и тремя крутильными жесткостями.
При движении платформы на закрепленную модель действуют дополнительные силы инерции, обусловленные ускорением каждой точки за счет перемещения и поворота платформы, поэтому уравнение движения (1) перепишется в следующем виде:

где 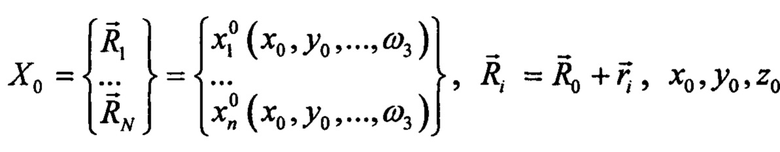 - линейные перемещения платформы, ω1, ω2, ω3 - компоненты вектора конечного поворота
- линейные перемещения платформы, ω1, ω2, ω3 - компоненты вектора конечного поворота 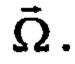 Каждый узел модели до деформирования имеет координаты
Каждый узел модели до деформирования имеет координаты 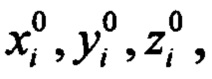 i=1, 2, …, N в своей системе координат, которая необязательно совпадает с системой координат, выбранной выше, тогда точка С в этой системе имеет координаты x0, y0, z0. Так как рассматриваются малые перемещения, то зависимость
i=1, 2, …, N в своей системе координат, которая необязательно совпадает с системой координат, выбранной выше, тогда точка С в этой системе имеет координаты x0, y0, z0. Так как рассматриваются малые перемещения, то зависимость  - линейная относительно компонент вектора конечного поворота:
- линейная относительно компонент вектора конечного поворота:
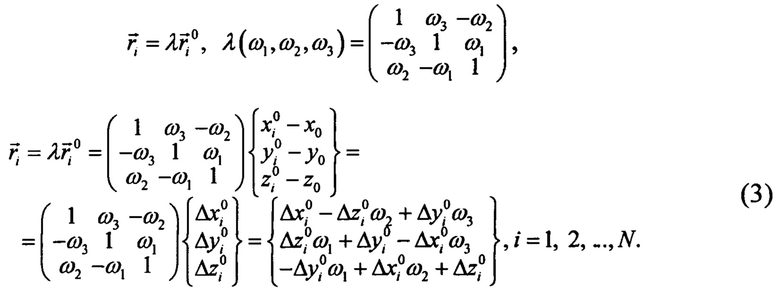
Каждый узел описывается тремя линейными и тремя угловыми степенями свободы, тогда выражение (2) с учетом (3) перепишется в следующем виде:

Раскрывая скобки в (4), получим:
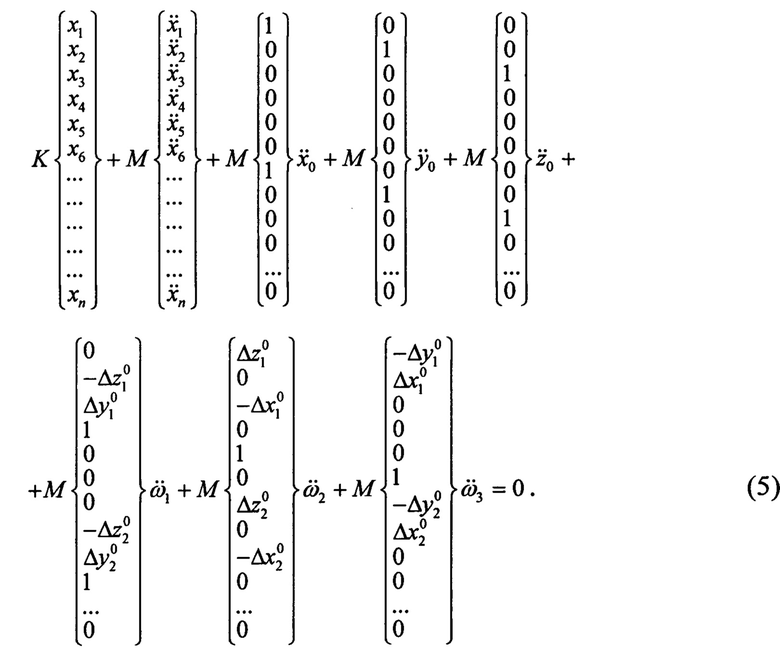
Перепишем уравнение (5) в матричном виде:

где 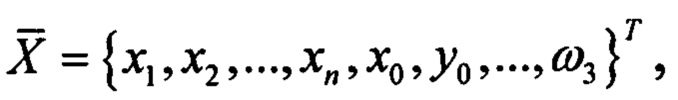
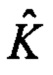 - матрица жесткости K, дополненная шестью нулевыми столбцами, чтобы соответствовать
- матрица жесткости K, дополненная шестью нулевыми столбцами, чтобы соответствовать 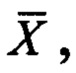 а матрица
а матрица 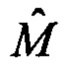 определяется так:
определяется так:
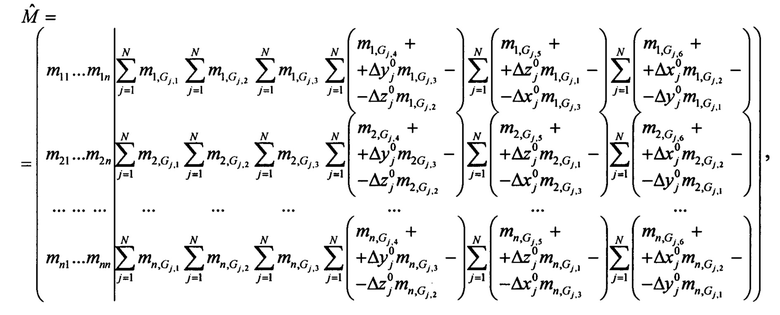
где матрица Gj,i - содержит порядковый номер уравнения, соответствующего i-ой степени свободы j-го узла.
Составим уравнения движения платформы. Пусть с1,2,3, к1,2,3 - линейные и угловые жесткости крепления платформы. Если платформа свободна, эти жесткости равны нулю. Пусть m0 - общая масса платформы и модели (масса свободной конструкции), a J1,2,3 - соответствующие массовые моменты инерции. Тогда можно записать 6 уравнений движения платформы:

где
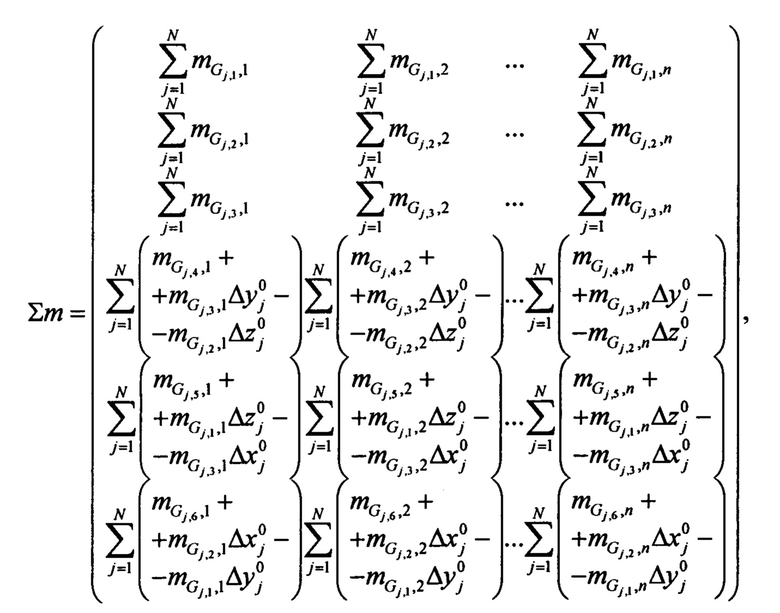
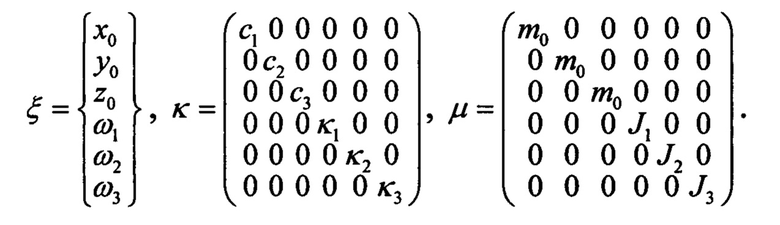
Уравнения (6) и (7) образуют новую систему уравнений движения с симметричными матрицами размером (n+6):
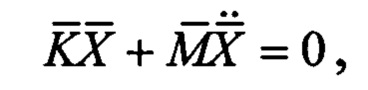
или
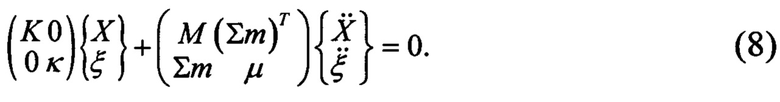
Система (8) описывает собственные колебания модели вместе с платформой. Если модель получена путем закрепления свободной модели, то жесткости крепления платформы равны нулю, а собственные частоты, найденные из (8), близки к частотам колебаний свободной модели. При этом формы собственных колебаний также близки к формам колебаний свободной модели.
Переведем (8) в глобальную систему координат. Согласно (3) можно записать следующее:
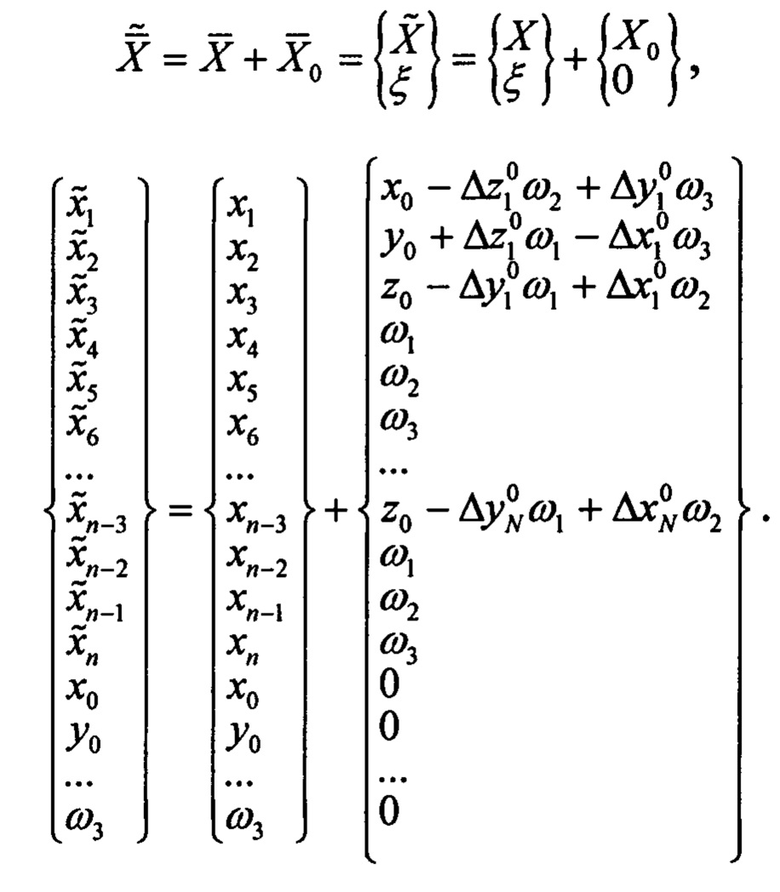
Выразим локальные координаты 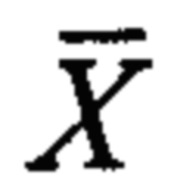 :
:
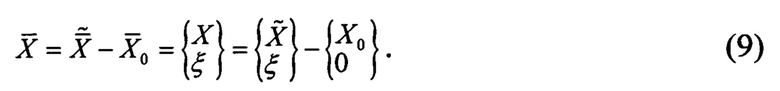
Подставим (9) в (8):
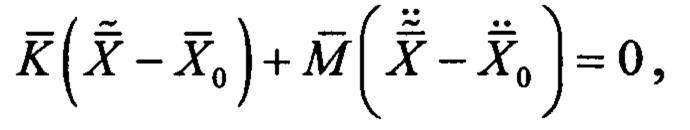
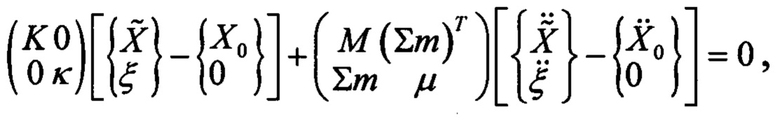
так как 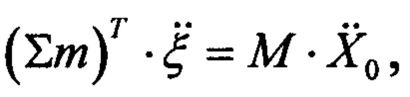
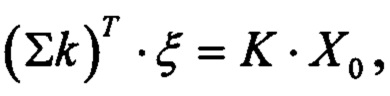 тогда
тогда
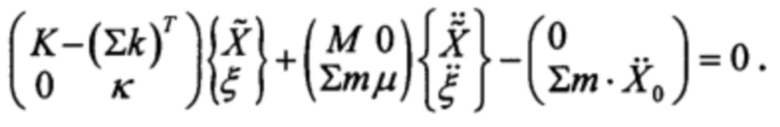
Введем обозначение: 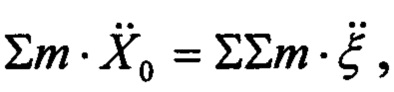 тогда последняя система уравнений перепишется следующим образом:
тогда последняя система уравнений перепишется следующим образом:
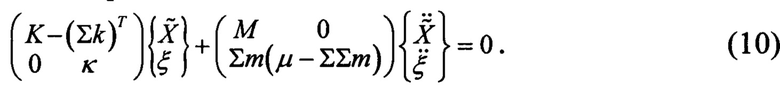
Для приведения системы (10) к симметричному виду, воспользуемся линейными комбинациями первых n строк (10) в соответствии с матрицей Gj,i:
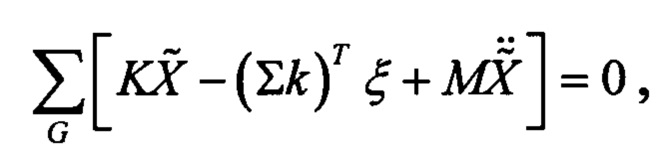
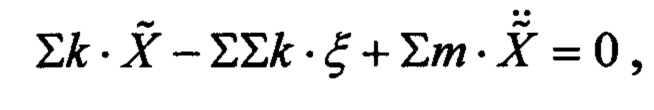
тогда, с учетом (10), получим итоговую систему уравнений:
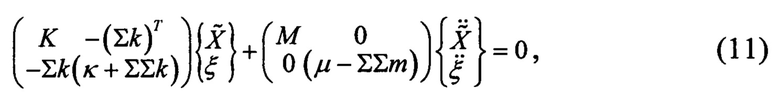 Получим выражение для ΣΣm аналогично (5):
Получим выражение для ΣΣm аналогично (5):
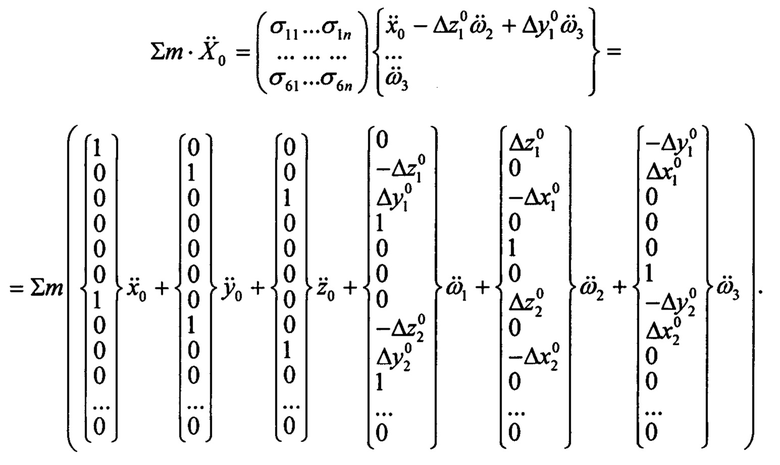
Итак:
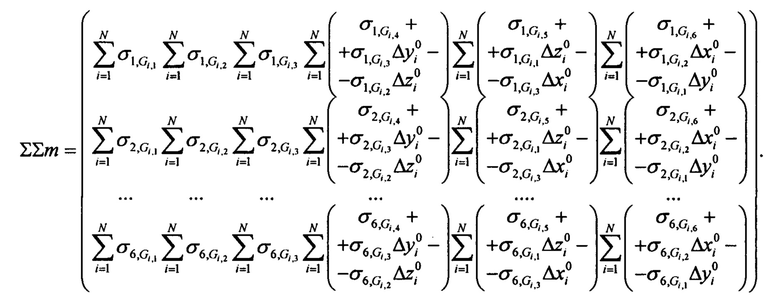
Аналогично можно получить выражения для ΣΣk.
Необходимо отметить, что точка С не обязательно должна располагаться в центре масс, она может находиться в любом месте конструкции. Пусть точка С находится на расстоянии, ΔX, ΔY, ΔZ от центра тяжести, тогда матрица μ может быть вычислена следующим образом:
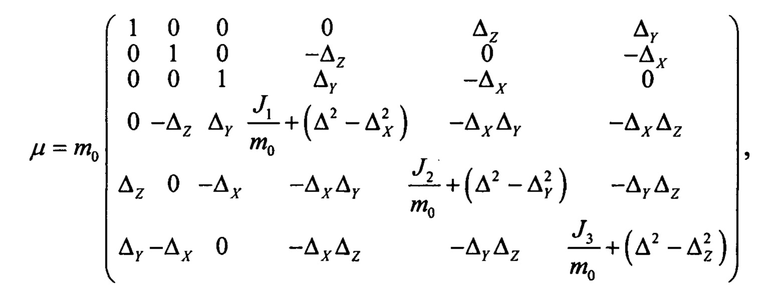
где 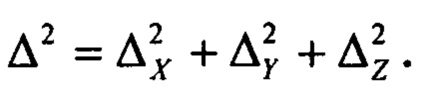
Пример освобождения расчетной модели.
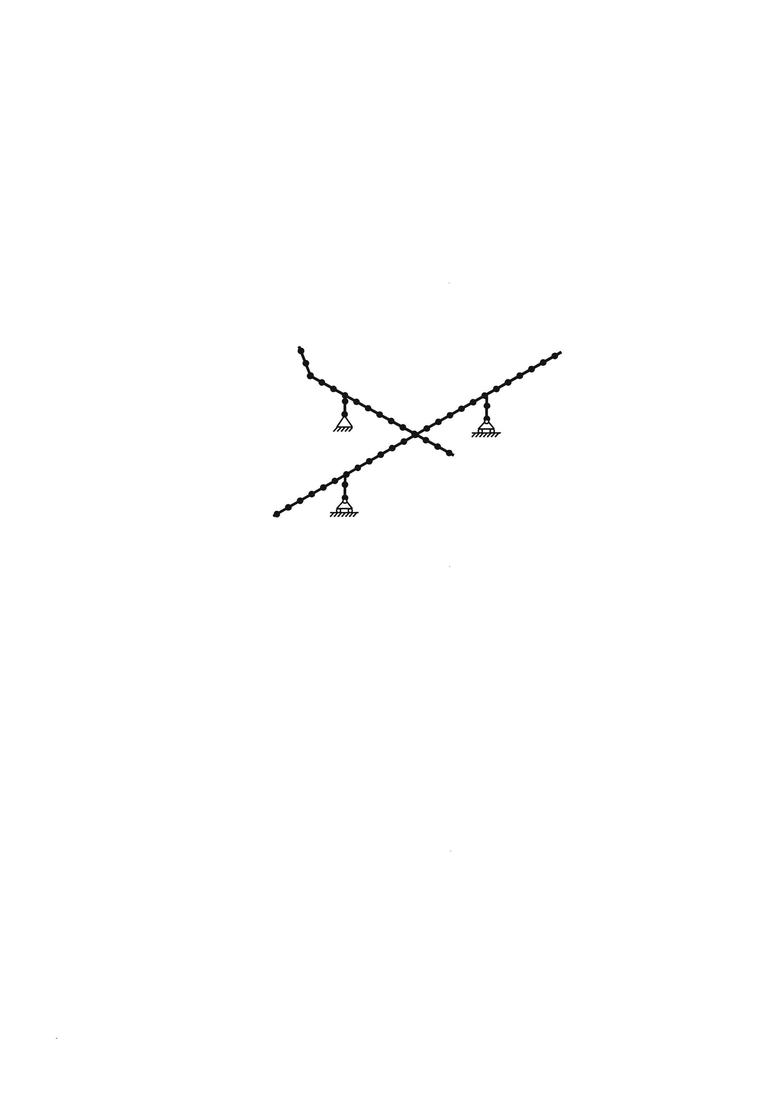
На чертеже представлена условная балочная модель самолета, стоящего на трех стойках шасси.
Балки, имитирующие шасси, закреплены следующим образом: для задней опоры запрещены перемещения в трех направлениях и по углу рыскания самолета, а для двух передних - только перемещения по вертикали.
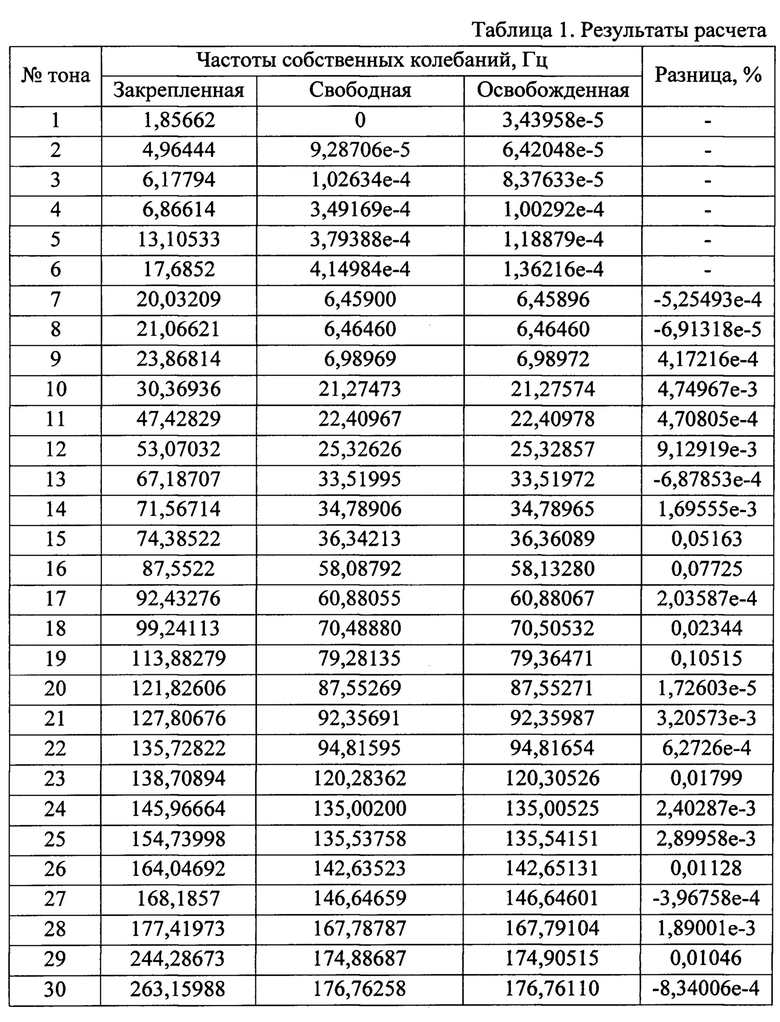
В таблице 1 приведены первые 30 частот собственных колебаний закрепленной модели, свободной модели и модели, освобожденной от закреплений по предлагаемому способу. В последней колонке показана разница в процентах между частотами свободной и освобожденной модели. Из представленных результатов следует, что частоты практически совпали между собой. Анализ форм колебаний освобожденной модели показал, что они также близки к формам колебаний свободной модели.
Техническим результатом является исключение влияния жесткости системы упругого вывешивания на погрешности определения собственных частот и форм колебаний свободной конструкции по результатам наземных модальных испытаний.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения параметров собственных тонов колебаний конструкций в резонансных испытаниях | 2017 |
|
RU2658125C1 |
| Способ определения обобщенных параметров колебаний конструкций по частотным характеристикам | 2020 |
|
RU2758152C1 |
| Способ оценки влияния воздушной среды на демпфирование колебаний конструкций | 2019 |
|
RU2737031C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭЛЕМЕНТОВ КОНСТРУКЦИИ ЛЕТАТЕЛЬНОГО АППАРАТА | 2014 |
|
RU2568959C1 |
| Способ определения парциальных частот управляемой поверхности летательного аппарата и устройство для его осуществления | 2019 |
|
RU2715369C1 |
| Способ испытаний систем и приборов космического назначения в условиях имитации невесомости | 2023 |
|
RU2823384C1 |
| Способ исключения резонансных режимов в фрикционных дисках гидромеханической трансмиссии транспортной машины | 2019 |
|
RU2728584C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СОБСТВЕННЫХ ЧАСТОТ И ОБОБЩЕННЫХ МАСС КОЛЕБЛЮЩИХСЯ КОНСТРУКЦИЙ | 2012 |
|
RU2489696C1 |
| Устройство для гашения колебаний упругой конструкции | 1988 |
|
SU1580318A1 |
| Измеритель частоты собственного тона колебаний конструкции и способ мониторинга изменения жесткости конструкции летательного аппарата при эксплуатации | 2020 |
|
RU2736346C1 |
Изобретение относится к области классического экспериментального модального анализа конструкций. При реализации способа строят расчетную динамическую модель свободной конструкции, которую корректируют по результатам наземных модальных испытаний. На время испытаний объект исследований фиксируют специальной системой упругого вывешивания, характеристики которой вводят в расчетную модель наложением внешних связей. В испытаниях выделяют собственные тона конструкции в заданном диапазоне частот методом фазового резонанса. По частотам фазовых резонансов определяют собственные частоты колебаний тонов, которые используют для прямой коррекции матриц жесткости и/или масс расчетной модели. Затем расчетную модель освобождают от внешних связей: закрепленную модель «устанавливают» на подвижную платформу, которая имеет инерционные характеристики исходной свободной конструкции. Систему уравнений движения закрепленной модели дополняют уравнениями движения платформы. Полученные уравнения не нарушают симметрию матриц жесткости и масс. Частоты и формы собственных колебаний освобожденной модели близки к соответствующим частотам и формам свободной модели. Технический результат заключается в исключении влияния жесткости системы упругого вывешивания на погрешности определения собственных частот и форм колебаний свободной конструкции по результатам наземных модальных испытаний. 1 ил. 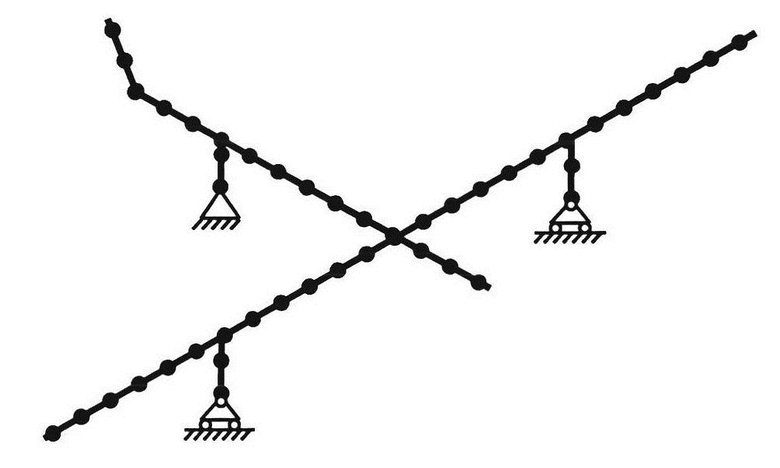
Способ определения собственных частот и форм колебаний свободной конструкции по результатам испытаний этой конструкции с наложенными связями, заключающийся в построении расчетной динамической модели свободной конструкции, проведении наземных модальных испытаний конструкции, зафиксированной системой упругого вывешивания, коррекции расчетной модели по результатам испытаний, определении собственных частот и форм колебаний свободной конструкции по скорректированной расчетной модели, отличающийся тем, что производится освобождение модели от закреплений при условии, что известны масса и массовые моменты инерции свободной конструкции.
| О современных методиках наземных испытаний самолетов в аэроупругости / Карклэ П.Г., Малютин В.А., Мамедов О.С., Поповский В.Н., Смотров А.В., Смыслов В.И | |||
| // Уч | |||
| записки ЦАГИ им | |||
| Н.Е | |||
| Жуковского, 2012, вып | |||
| Электрический максимальный прерыватель для ограничения силы тока в цепи потребления электрической энергии | 1924 |
|
SU2708A1 |
| Нивелир для отсчетов без перемещения наблюдателя при нивелировании из средины | 1921 |
|
SU34A1 |
| Способ определения параметров собственных тонов колебаний конструкций в резонансных испытаниях | 2017 |
|
RU2658125C1 |
| СПОСОБ ЭКСПЕРИМЕНТАЛЬНОГО ОПРЕДЕЛЕНИЯ ЧАСТОТ СОБСТВЕННЫХ КОЛЕБАНИЙ И ОБОБЩЕННОЙ МАССЫ ИСПЫТЫВАЕМОГО ОБЪЕКТА | 2012 |
|
RU2499239C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СОБСТВЕННЫХ ЧАСТОТ И ОБОБЩЕННЫХ МАСС КОЛЕБЛЮЩИХСЯ КОНСТРУКЦИЙ | 2012 |
|
RU2489696C1 |
| Способ обезвешивания и возбуждения колебаний при модальных испытаниях и устройство для его осуществления | 2017 |
|
RU2677942C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭЛЕМЕНТОВ КОНСТРУКЦИИ ЛЕТАТЕЛЬНОГО АППАРАТА | 2014 |
|
RU2568959C1 |
Авторы
Даты
2020-07-29—Публикация
2019-06-19—Подача