Изобретение относится к способам имитации невесомости при наземных испытаниях космической техники. Изобретение направлено на решение задачи имитации невесомости в сочетании с факторами микрогравитации, возникающими в космическом полете: вибрацией корпуса космического аппарата, сил и моментов от систем управления и от внешних возмущений.
Уровень техники
Из всего перечня условий космического полета невесомость является наиболее сложным для имитации. Тем не менее, как для подготовки космонавтов, так и для отработки различных механизмов, которые должны нормально работать в условиях космического полета, важны испытания в невесомости. К наиболее критичным операциям, требующим такого рода испытаний, относятся стыковка, работа манипуляторов на борту космического корабля, внекорабельная деятельность (выход в космос), раскрытие антенн или солнечных батарей (и других крупногабаритных конструкций).
Требования снижения массы приводят к тому, что большинство механизмов, предназначенных для работы на орбите, не способны в наземных условиях поднять свой вес или выдержать собственный вес без подпорок. Для их испытаний широко применяются тросовые системы разгружения (KR 101129345 B1, WO 2016142724 A1, CN 108674698 B, CN 107741334 A и др.). Эти системы обладают двумя недостатками: во-первых, тросы должны располагаться вертикально, что исключает свободу движений обезвешенной конструкции (элементы конструкции не должны пересекать трос), во-вторых даже трос, установленный на каретку, движется с некоторым трением, и при перемещении системы будет создавать силу тяги, направленную против движения обезвешенного компонента. Последнее обстоятельство не позволяет получить с помощью тросовых систем адекватную оценку демпфирующих свойств конструкции в невесомости, и всегда дает заниженный результат относительно инерционных нагрузок, возникающих при движении. В результате испытания не могут надежно гарантировать прочность изделия, и для оценки этой прочности приходится задаваться коэффициентом запаса, полученным расчетным путем, что снижает точность испытаний.
Кроме тросовых, используются системы с другими видами подвесов:
- аэродинамическим (WO 2021071604 A2, CN 114261543 В),
- магнитным (ЕР 0421029 В1),
- гидростатическим (RU 174475 U1).
Недостатком аэродинамического и магнитного методов является ограничение по массе испытуемого объекта и его габаритам: с учетом современного уровня техники испытание в таких подвесах систем с массой более 100 кг нецелесообразно ввиду стоимости испытательной установки: дешевле обойдутся испытания с пуском на орбиту или в салоне свободно падающего самолета. Также эти методы подходят только для испытаний компактных объектов, и не позволяют испытывать развертываемые конструкции размером в несколько десятков метров.
Недостатком гидростатического метода является необходимость использования воды. Во-первых, это не всегда допустимо с точки зрения испытуемого устройства, так как погружение в воду может негативно сказаться на его работе. Во-вторых, вода оказывает существенное сопротивление перемещению, даже большее, чем в случае с тросовыми системами.
Всех перечисленных недостатков лишен метод, основанный на применении кинематически полных или избыточных манипуляторов, оснащенных шестистепенным датчиком силы и момента, реализованный в решении CN 108394572 В (Метод моделирования ремонта космического аппарата на орбите, МПК B64G 7/00), и принимаемый в качестве прототипа.
В данном методе обезвешивание производится за счет закрепления испытуемого прибора (или, в частности, космонавта) на манипуляторе, который поддерживает такую траекторию конечного звена, которую бы описывал испытуемый объект, если бы на него действовали все силы, кроме силы тяготения Земли. Высокая точность следования промышленных манипуляторов (порядка 60 мкм, манипуляторы семейства KUKA Quantech) совместно с высокой чувствительностью датчика сил и моментов (порядка 0,025%, датчик FTE-Omega-160-IP65 SI 1000-120) обеспечивает точную компенсацию действия силы тяготения, а кинематическая свобода манипулятора обеспечивает произвольное положение испытуемой сборки или космонавта относительно других объектов, расположенных на испытательном стенде.
Основным недостатком прототипа является невозможность учета факторов, нарушающих условия микрогравитации: вибрации и управляющие моменты, созданные системами управления движением космического аппарата и другими приборами на его борту (например, вентиляторами), действие внешних моментов, в особенности приливного.
Также, прототип рассчитан на испытания достаточно компактных и прочных устройств, которые как минимум способны выдержать собственный вес. Таким образом, испытания, включающие в себя раскрытие крупногабаритных солнечных панелей, ферм и другого подобного оборудования, на прототипе невозможны, как невозможна и имитация воздействия таких конструкций на движение испытуемой сборки или космонавта.
Решение, выбранное в качестве прототипа заявляемого изобретения, характеризуется следующими общими с ним признаками:
- использование манипулятора для компенсации веса испытуемой сборки или космонавта;
- определение усилий, созданных рукой космонавта (или испытуемой сборкой) с помощью датчика сил и моментов или иным способом;
- реализация податливого движения обезвешивающего манипулятора в соответствии с величиной этих усилий.
Раскрытие сущности изобретения
Целью настоящего изобретения является расширение возможностей способа, приведенного в раскрытии прототипа, на той же или аналогичной элементной базе, таким образом, чтобы учесть:
- силовые возмущения от устройств на борту космического аппарата,
- внешние силовые воздействия на космический аппарат, характерные для орбитального полета,
- взаимодействие космического аппарата с упругими протяженными элементами конструкции (солнечные батареи, фермы, антенны), которые невозможно испытывать в наземных условиях ввиду их малой прочности и жесткости.
Также, в качестве дополнительного результата, возникающего из реализации предложенного способа, можно отметить возможность имитации дополнительной присоединенной массы, то есть увеличения инерции испытуемой сборки или космонавта. Это позволяет проводить только частичные испытания подсистемы, или же испытания с частично укомплектованным скафандром космонавта, и получать результаты, релевантные для полномасштабной системы.
Предлагаемый способ заключается в следующем:
1) определяют собственные частоты каждого из присоединенных к космическому аппарату упругих элементов (антенны, солнечные батареи, фермы и т.п.), а также матрицы парциальных динамических связей для этих элементов и матрицы жесткости и масс для использования в модели суперэлемента согласно методу динамической редукции Крейга-Бамптона. Соответствующие измерения могут проводиться как на реальных объектах, с использованием данных виброиспытаний, так и с помощью математических имитационных моделей, известным в литературе способом,
2) рассчитывают внешние силы и моменты, действующие на космический аппарат, исходя из данных о нем: масса, момент инерции, положение центра масс, низкополигональная модель для расчета давления света и остаточной атмосферы, собственный магнитный момент, параметры орбиты, начальные условия (аргумент широты космического аппарата, ориентация и угловая скорость),
3) рассчитывают силы и моменты, вызванные колебаниями присоединенных упругих элементов космического аппарата, на основании данных п. 1 способа, используя сумму внешних сил и моментов и сил и моментов управления как возбуждение модели,
4) используя известные уравнения динамики и кинематики для космического аппарата, определяют параметры его линейного и углового движений, имитируют работу необходимых измерительных приборов в составе космического аппарата, опрашивают имеющиеся в составе стенда реальные приборы из состава космического аппарата, корректируют их показания, внося поправки на гравитацию Земли и суточное вращение, на основе полученных данных формируют аргументы управления движением КА, имитируя работу контура управления,
5) коррекцию на суточное вращение Земли применяются только в том случае, если в составе фактически испытываемых приборов имеются датчики угловой скорости. В этом случае рассчитывают проекции угловой скорости вращения Земли в системе координат, связанной с конечным звеном манипулятора, на основании данных о положении этого звена и ориентации манипулятора в географической системе координат. Точно таким же образом вычисляют поправки к линейному ускорению, в том случае, если для его измерений используют реальные акселерометры,
6) рассчитанные аргументы управления передаются для исполнения в математическую модель органов управления космического аппарата или же на реальные приборы (прибор), испытываемые на стенде, с целью создания управляющих сил и моментов,
7) определяют сумму всех рассчитанных сил и моментов, а на основании показаний датчика сил и моментов на манипуляторе определяют вес испытываемой сборки и момент от его приложения к конечному звену манипулятора,
8) движение конечного звена задают таким, каким оно было бы, если бы на испытуемую сборку не действовал фактический вес и момент от его приложения, но действовали рассчитанные в п. 7 способа силы и моменты.
Краткое описание чертежей
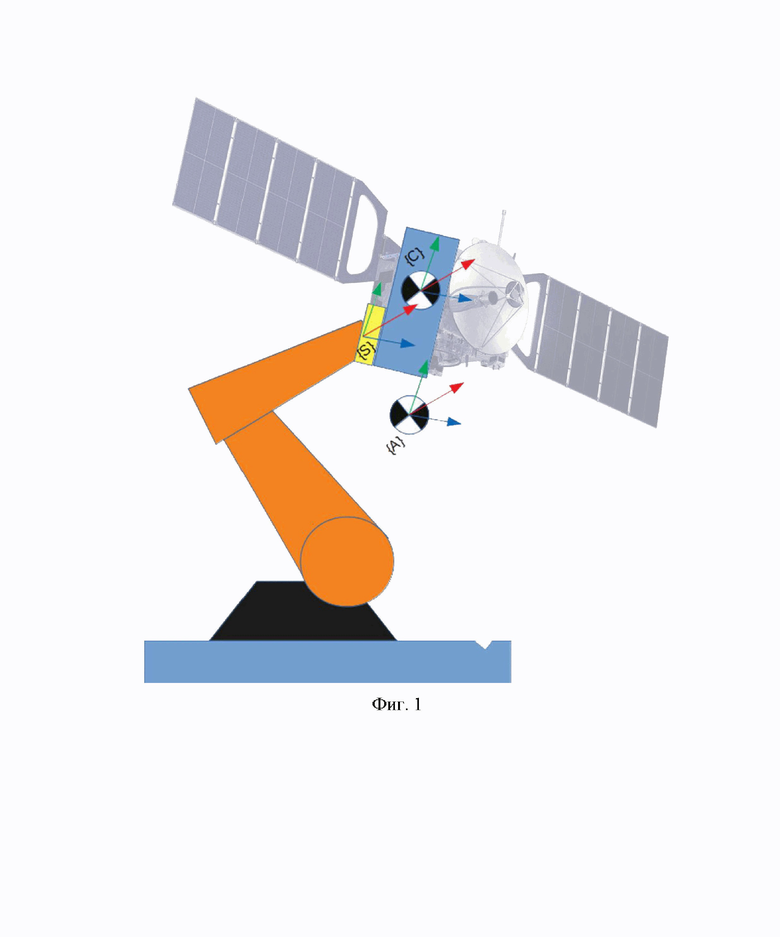
Сущность изобретения поясняется следующими рисунками и чертежами. На фиг. 1 показан общий вид системы, реализующей предлагаемый способ. На фиг. 2 показана условная схема реализации способа с перечислением соответствующих уравнений.
Осуществление изобретения
Внешние силовые воздействия на космические аппараты хорошо изучены, и не зависят от особенностей взаимодействия систем космического аппарата. Общее уравнение динамики вращательного движения космического аппарата дается формулой (1)
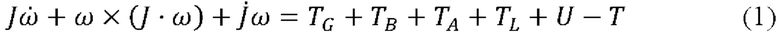
где J - тензор инерции тела (космического аппарата), ω - его угловая скорость в собственной системе коордиант, TG - гравитационный приливный момент, TB - механический магнитный момент, TA - аэродинамический момент, TL - момент светового давления, U - управление, Т - момент реакции от упругих тел. Задачей манипулятора является имитация движения тела (космического аппарата) в соответствии с (1), при условии, что управление U измеряют датчиком сил и моментов, а все прочие моменты вычисляют исходя из модельной обстановки. Кинематическое уравнение вращательного движения тела в кватернионной форме (2):
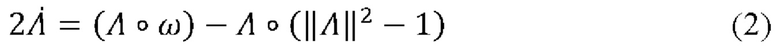
где Λ - кватернион ориентации тела. Второй член в правой части предназначен для автоматической коррекции нормы кватерниона на случай ошибок при численном решении уравнения.
Моменты, входящие в выражение (1), хорошо известны, и могут быть определены по формулам



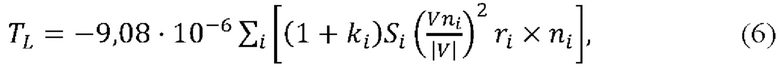
где U - модуль ускорения свободного падения в месте расположения центра масс космического аппарата, u - направляющий вектор этого ускорения, L - вектор магнитного момента КА, В - вектор напряженности магнитного поля Земли, ρ - плотность остаточной атмосферы, зависящая от высоты полета, V - скорость полета космического аппарата, Si - площадь элементарной площадки поверхности космического аппарата, ni - нормаль к этой площадке, ri - радиус-вектор элементарной площадки относительно центра масс КА, ki - альбедо площадки.
Уравнение движения упругих присоединенных элементов в редуцированной форме записываются в виде (7)
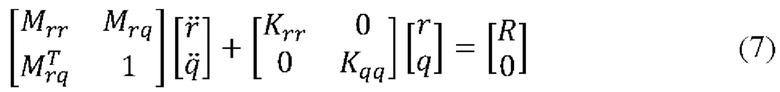
где М - матрицы масс, К - матрицы жесткости, r - вектор перемещений в декартовой системе координат или индекс, относящийся к этой системе, q - вектор обобщенных координат колебаний или индекс, относящийся к модальному подпространству, R - вектор усилия в декартовой системе координат (сила и момент реакции). Вектор r содержит по 6 компонент (три трансляционные и три вращательные) для каждого интерфейсного узла.
Раскрывая уравнение (7), можно получить систему уравнений для расчета сил и моментов, действующих на космический аппарат со стороны присоединенных к нему упругих элементов:


где F - равнодействующая силы реакции, Т - равнодействующая момента реакции, v - линейная скорость центра тяжести всей модели, ω - угловая скорость всей модели.
При необходимости, демпфирование может быть учтено приближением по Рэлею, с модификацией уравнения (9):
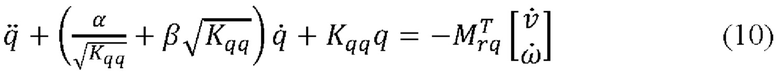
где α - коэффициент массового демпфирования (обусловлен силами трения между частями конструкции), β - коэффициент структурного демпфирования (обусловлен материалом).
Коэффициенты демпфирования по Рэлею рассчитывают по зависимости демпфирующего отношения ξ от частоты возбуждения ω, исходя как минимум из двух испытаний:

Уравнение движения центра масс записывается в виде второго закона Ньютона:

где Fout - сумма всех сил, действующих на космический аппарат в орбитальном движении (гравитация, торможение светом и остаточной атмосферой), х - радиус-вектор центра масс космического аппарата, m - масса космического аппарата.
Формулы 1-12 подразумевают, что для расчетов будут использованы фактические значения, соответствующие космическому аппарату или другому объекту, движение которого воспроизводится обезвешивающим манипулятором. Например, если производится испытание робота, перемещающегося по космическому аппарату, причем робот испытывается натурно, а космический аппарат симулируется, то все физические характеристики в формулах 1-12 должны относиться к космическому аппарату в его полном составе. Если в испытаниях помимо робота задействован фрагмент космического аппарата, то характеристики в формулах 1-12 должны быть определены для космического аппарата за исключением из него этого фрагмента.
Рассмотрим закрепленную на конечном звене робота испытуемую сборку массы mm и момента инерции Jm. Введем систему координат, связанную с конечным звеном как {S}, и систему координат центра масс испытуемой сборки {С}. На испытуемую сборку действуют следующие силы и моменты:
- момент веса tg=0∈R3;
- сила реакции датчика, в том числе с учетом веса Fs∈R3;
- силы/моменты актуаторов τа∈R3 (управляющие моменты), размещенных на испытуемой сборке.
В собственной системе координат {С}, связанной с центром масс испытуемой сборки, уравнения движения этой сборки примут вид (13)

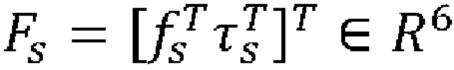 - вектор силы и момента, измеренный датчиком,
- вектор силы и момента, измеренный датчиком,
ωm - угловая скорость испытуемой сборки,
W=[-[cgm×]I3] - матрица преобразования момента из {S} в {С}, где
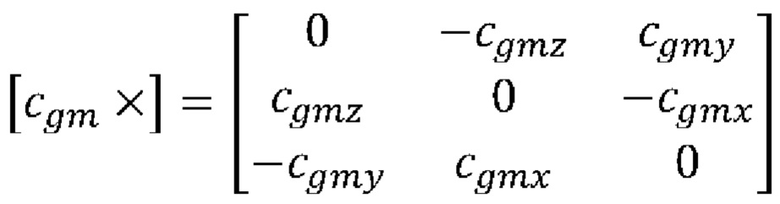 - матрица векторного произведения,
- матрица векторного произведения,
cgm=[cgmx, cgmy, cgmz]T - положение центра масс испытуемой сборки относительно {S}.
Система управления активного обезвешивания должна при одинаковых начальных угловых скоростях испытуемой сборки и имитируемого тела ωm=ω и одинаковых управляющих воздействиях τа=U развивать одинаковые ускорения  Данное условие обеспечивает подобие движения.
Данное условие обеспечивает подобие движения.
Вычитая (13) из (1) получим (12)
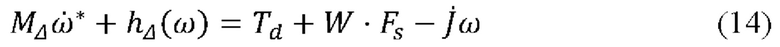
МΔ=(J-Jm), hΔ=ω×((J-Jm)⋅ω)
где Td=TG+ТВ+ТА+TL - Т - суммарный возмущающий момент. Формула преобразования мгновенных ускорений {С} в обобщенные координаты манипулятора имеет вид

где Yω(q)∈R3×6 - часть якобиана манипулятора (относительно центра масс муляжа), отвечающая за ващение; 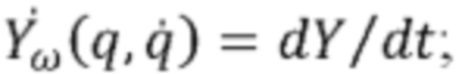 q - обобщенные координаты степеней свободы манипулятора.
q - обобщенные координаты степеней свободы манипулятора.
Откуда получают требуемые ускорения движения манипулятора
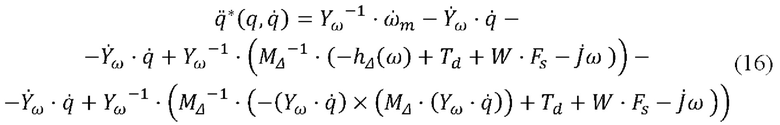
Реализовать соответствующее движение может либо кинематически полный, либо кинематически избыточный манипулятор. Под кинематической полнотой понимается возможность определить однозначное соответствие между углами поворота шарниров манипулятора и совокупностью линейного и углового положения конечного звена (радиус-вектор и параметры углового движения, например углы Эйлера или параметры Кейли-Клейна) в некоторой области, называемой сервисной зоной манипулятора. Под кинематической избыточностью понимается возможная многозначность упомянутого соотношения, то есть одному положению конечного звена может соответствовать несколько различных сочетаний углов поворота шарниров.
Можно отметить, что в формуле (14) используется разность между инерцией симулируемого тела (космического аппарата) и инерцией испытуемой сборки. Если эта разность оказывается отрицательной, то есть испытуемая сборка имеет инерцию больше, нежели симулируемое тело, обратная связь, обусловленная датчиком сил и моментов, оказывается положительной, и работа системы невозможна. Из этих же соображений можно утверждать, что чем больше разница (положительная) между инерцией имитируемого тела и инерцией испытуемой сборки, тем точнее будет подобие движения.
| название | год | авторы | номер документа |
|---|---|---|---|
| ДИНАМИЧЕСКИЙ ТРЕНАЖЕР | 2006 |
|
RU2326447C1 |
| ФУНКЦИОНАЛЬНО-МОДЕЛИРУЮЩИЙ СТЕНД ДЛЯ СОЗДАНИЯ УСЛОВИЙ ИНТЕРАКТИВНОГО БЕЗОПОРНОГО ПРОСТРАНСТВА И ПОНИЖЕННОЙ ГРАВИТАЦИИ | 2012 |
|
RU2518478C2 |
| ТРЕНАЖЕР ПИЛОТИРУЕМОГО КОСМИЧЕСКОГО КОРАБЛЯ | 2008 |
|
RU2367027C1 |
| МНОГОФУНКЦИОНАЛЬНЫЙ УЧЕБНО-ТРЕНИРОВОЧНЫЙ КОМПЛЕКС ДЛЯ ПОДГОТОВКИ КОСМОНАВТОВ (АСТРОНАВТОВ) К ВНЕКОРАБЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ (ВАРИАНТЫ) | 2013 |
|
RU2524503C1 |
| ТРЕНАЖЕР ВНЕКОРАБЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ КОСМОНАВТОВ | 2012 |
|
RU2506648C1 |
| УЧЕБНЫЙ ТРЕНАЖЕРНО-МОДЕЛИРУЮЩИЙ КОМПЛЕКС ДЛЯ ПОДГОТОВКИ КОСМОНАВТОВ К ВНУТРИКОРАБЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ | 2020 |
|
RU2738489C1 |
| ИСПЫТАТЕЛЬНЫЙ СТЕНД ДЛЯ РАСКРЫТИЯ БАТАРЕИ СОЛНЕЧНОЙ | 2010 |
|
RU2468969C2 |
| СПОСОБ МОНИТОРИНГА ВОЗДЕЙСТВИЯ НЕВЕСОМОСТИ НА ДВИГАТЕЛЬНУЮ АКТИВНОСТЬ НАХОДЯЩЕГОСЯ НА БОРТУ КОСМИЧЕСКОГО АППАРАТА ОПЕРАТОРА | 2021 |
|
RU2777476C1 |
| ТРЕНАЖЕРНЫЙ КОМПЛЕКС ОРБИТАЛЬНОГО УЗЛОВОГО МОДУЛЯ РОССИЙСКОГО СЕГМЕНТА МЕЖДУНАРОДНОЙ КОСМИЧЕСКОЙ СТАНЦИИ | 2012 |
|
RU2506647C1 |
| Способ моделирования пониженной гравитации и устройство для его осуществления | 2022 |
|
RU2802135C1 |

Изобретение относится к способам имитации невесомости при наземных испытаниях космической техники. Способ реализуется за счет использования кинематически полного или кинематически избыточного манипулятора, способного к измерению вектора силы и вектора момента, действующих на его конечное звено, например, за счет установки на конечном звене датчика силы и момента, и установленного на подвижном или неподвижном основании. Способ подразумевает создание манипулятором такого движения, которое реализовалось бы для испытуемой сборки под действием всех сил и моментов, действующих на нее в условиях космического полета, с учетом отсутствия веса сборки и связанного с ним момента. При этом часть сил и моментов могут возникать при испытаниях непосредственно в результате работы испытуемой сборки, а часть - имитироваться манипулятором с учетом особенностей космического полета. Достигается возможность имитации дополнительной массы в процессе испытаний систем и приборов космического назначения и учета воздействий от нее на испытуемую систему. 1 з.п. ф-лы, 2 ил.
1. Способ испытаний систем и приборов космического назначения в условиях имитации невесомости, заключающийся в том, что испытуемую сборку устанавливают на манипулятор и производят измерения силы и момента реакции от испытуемой сборки, возникающие в месте этого крепления в результате действия веса испытуемой сборки и ее собственных движений, а на основании этих измерений манипулятор, перемещаясь в податливом режиме, реализует траекторию, которая соответствует движению испытуемой сборки под действием суммы измеренных ранее сил и моментов за вычетом силы и момента веса, отличающийся тем, что
– определяют собственные частоты каждого из присоединенных к космическому аппарату упругих элементов, а также матрицы парциальных динамических связей для этих элементов и матрицы жесткости и масс как на реальных объектах, так и с помощью математических имитационных моделей,
– рассчитывают внешние силы и моменты, действующие на космический аппарат, исходя из данных о нем: масса, момент инерции, положение центра масс, низкополигональная модель для расчета давления света и остаточной атмосферы, собственный магнитный момент, параметры орбиты, начальные условия – аргумент широты космического аппарата, ориентация и угловая скорость,
– рассчитывают силы и моменты, вызванные колебаниями присоединенных упругих элементов космического аппарата, используя сумму внешних сил и моментов и сил, и моментов управления как возбуждение модели,
– определяют параметры линейного и углового движений космического аппарата, имитируют работу необходимых измерительных приборов в составе космического аппарата, опрашивают имеющиеся в составе стенда реальные приборы из состава космического аппарата, корректируют их показания, внося поправки на гравитацию Земли и суточное вращение, на основе полученных данных формируют аргументы управления движением КА, имитируя работу контура управления,
– если в составе фактически испытываемых приборов имеются датчики угловой скорости, рассчитывают проекции угловой скорости вращения Земли в системе координат, связанной с конечным звеном манипулятора, на основании данных о положении этого звена и ориентации манипулятора в географической системе координат, далее таким же образом вычисляют поправки к линейному ускорению, в случае если для его измерений используют реальные акселерометры,
– рассчитанные аргументы управления передаются для исполнения в математическую модель органов управления космического аппарата или же на реальные приборы, испытываемые на стенде, с целью создания управляющих сил и моментов,
– определяют сумму всех рассчитанных сил и моментов, а на основании показаний датчика сил и моментов на манипуляторе определяют вес испытываемой сборки и момент от его приложения к конечному звену манипулятора,
– движение конечного звена задают таким, каким оно было бы, если бы на испытуемую сборку не действовал фактический вес и момент от его приложения, но действовали рассчитанные выше силы и моменты.
2. Способ испытаний систем и приборов космического назначения по п.1, отличающийся тем, что в случае если в состав реальных объектов входят датчики угловой скорости и/или линейного ускорения и для расчета управляющих воздействий имитируемых тел используют их реальные показания, то перед этим расчетом показания датчиков корректируют на величину вектора угловой скорости суточного вращения Земли и величину вектора местного ускорения свободного падения соответственно, рассчитанных в подвижной системе координат, связанной с соответствующим датчиком.
| СПОСОБ ИМИТАЦИИ ПОНИЖЕННОЙ ГРАВИТАЦИИ | 2010 |
|
RU2410299C1 |
| CN 108394572 B, 26.02.2019 | |||
| МНОГОФУНКЦИОНАЛЬНЫЙ УЧЕБНО-ТРЕНИРОВОЧНЫЙ КОМПЛЕКС ДЛЯ ПОДГОТОВКИ КОСМОНАВТОВ (АСТРОНАВТОВ) К ВНЕКОРАБЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ (ВАРИАНТЫ) | 2013 |
|
RU2524503C1 |
| ФУНКЦИОНАЛЬНО-МОДЕЛИРУЮЩИЙ СТЕНД ДЛЯ СОЗДАНИЯ УСЛОВИЙ ИНТЕРАКТИВНОГО БЕЗОПОРНОГО ПРОСТРАНСТВА И ПОНИЖЕННОЙ ГРАВИТАЦИИ | 2012 |
|
RU2518478C2 |
| СТЕНД ДЛЯ ИСПЫТАНИЙ УСТРОЙСТВ ОТДЕЛЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ | 2012 |
|
RU2489331C1 |
Авторы
Даты
2024-07-22—Публикация
2023-12-15—Подача