Изобретение относится к области помехоустойчивого кодирования и может быть использовано для декодирования кода Рида-Соломона с коррекцией многократных ошибок.
Одним из основных направлений повышения помехоустойчивости передачи сообщений в каналах связи различного качества, в том числе низкого качества, является применение помехоустойчивого кодирования. Коды Рида-Соломона являются одними из лучших недвоичных кодов с точки зрения помехоустойчивости. Однако, сложность декодирования этого кода даже с коррекцией ошибок только в пределах минимального кодового расстояния довольно высокая, что вызывает затруднения при его практической реализации. В настоящее время известны различные способы декодирования кода Рида-Соломона. Одним из первых известных способов декодирования кода Рида-Соломона был способ Питерсона-Горенстейна-Цирлера, исправляющий ошибки за четыре этапа: вычисление синдрома, вычисление многочлена локаторов ошибок, определение корней многочлена локаторов и, наконец, вычисление значений ошибок. В дальнейшем был предложен более простой способ на основе спектрального подхода, в котором первый этап декодирования выполнялся как дискретное преобразование кодового вектора из временной области в частотную область. Применение быстрых преобразований Фурье ускорило декодирование в несколько или даже в большее число раз. При этом два последних этапа способа Питерсона-Горенстейна-Цирлера были исключены, а для определения спектра ошибок выполнялось рекуррентное продолжение синдрома на основе ключевого уравнения. Наиболее простой способ декодирования был предложен Гао. Способ включает три этапа: вычисление синдрома, вычисление многочлена локаторов ошибок и восстановление информации. Сложность этого способа соизмерима со сложностью лучших способов декодирования кода Рида-Соломона.
Известен способ декодирования кода Рида-Соломона, заключающийся в том, что на первом этапе декодирования вычисляют синдром помехоустойчивого кода, затем на втором этапе определяют многочлен локаторов ошибок, далее на третьем этапе декодирования вычисляют локаторы ошибок и, наконец, на четвертом этапе определяют значения ошибок (Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. Пер. с англ. - М.: Мир, 1976. - 594 с.).
Недостатком этого способа является чрезмерно большая сложность, поскольку вычисление локаторов ошибок на третьем этапе требует решения алгебраического уравнения, степень которого равна числу ошибок в коде, а для определения значений ошибок на четвертом этапе требуется решение системы алгебраических уравнений.
Известен также способ декодирования кода Рида-Соломона, заключающийся в том, что на первом этапе декодирования вычисляют синдром помехоустойчивого кода на основе дискретного преобразования Фурье, на втором этапе определяют многочлен локаторов ошибок и, наконец, на последнем третьем этапе вычисляют продолжение спектра ошибок, используя ключевое уравнение для компонент синдрома. (Блейхут Р. Теория и практика кодов, контролирующих ошибки. Пер. с англ. - М.: Мир, 1986. - 448 с.).
Недостатком этого способа также является большая сложность, поскольку вычисление многочлена локаторов ошибок на втором этапе требует выполнения большого числа арифметических операций.
Наиболее близким к предлагаемому способу является способ (прототип) декодирования кода Рида-Соломона, заключающийся в том, что на первом этапе декодирования вычисляют синдром помехоустойчивого кода, затем на втором этапе определяют многочлены локаторов и значений ошибок и, наконец, на третьем этапе вычисляют продолжение спектра ошибок путем деления многочлена локаторов ошибок на многочлен значений ошибок. (Федоренко С.В. Простой алгоритм декодирования алгебраических кодов. // Информационно-управляющие системы. - 2008. - №3(34). - с. 23-27.)
Недостатком этого способа также является большая сложность, поскольку требуется выполнение трех этапов декодирования, в каждом из которых необходимо вычисление большого числа операций.
Целью изобретения является снижение сложности декодирования за счет того, что декодирование включает только два этапа: вычисление синдрома помехоустойчивого кода и определение продолжения спектра ошибок. В отличие от известных способов, вычисления многочлена локаторов ошибок не требуется, а для продолжения спектра ошибок используют одни и те же достаточно простые рекуррентные соотношения, для реализации которых можно применять однотипные комбинационные схемы вычислений.
Для достижения цели предложен способ декодирования кода Рида-Соломона, заключающийся в том, что на первом этапе декодирования вычисляют синдром помехоустойчивого кода, а затем определяют продолжение спектра ошибок. Новым является то, что продолжение спектра ошибок определяют на основе рекуррентных соотношений между ганкелевскими определителями различных порядков, составленными из компонент синдрома. Причем ганкелевскими определителями различных порядков заполняют С-таблицу. При этом для начального заполнения С-таблицы первую строку заполняют последовательностью единиц 1,1,1,1,1,…, вторую строку заполняют последовательностью известных компонент синдрома кода s0,s1,s2,… и первый столбец заполняют последовательностью 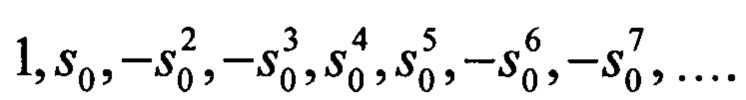 Причем при заполнении оставшихся клеток С-таблицы используют трехчленные рекуррентные соотношения между ганкелевскими определителями различных порядков. При этом заполнение оставшихся клеток С-таблицы выполняют сначала сверху вниз, а затем слева направо. Причем, если синдром содержит нулевые компоненты, то С-таблица будет содержать нулевые квадратные блоки, стороны которых равны длине последовательности подряд идущих нулевых компонент синдрома. При этом С-таблица будет содержать бесконечный блок нулей, правый верхний угол которого имеет координаты в С-таблице, равные (t, t+1), где t - число ошибок в коде.
Причем при заполнении оставшихся клеток С-таблицы используют трехчленные рекуррентные соотношения между ганкелевскими определителями различных порядков. При этом заполнение оставшихся клеток С-таблицы выполняют сначала сверху вниз, а затем слева направо. Причем, если синдром содержит нулевые компоненты, то С-таблица будет содержать нулевые квадратные блоки, стороны которых равны длине последовательности подряд идущих нулевых компонент синдрома. При этом С-таблица будет содержать бесконечный блок нулей, правый верхний угол которого имеет координаты в С-таблице, равные (t, t+1), где t - число ошибок в коде.
Рассмотрим осуществление предлагаемого способа декодирования кода Рида-Соломона.
Код Рида-Соломона (n,k,d), задаваемый над полем Галуа GF(pm), имеет блоковую длину n=pm-1, информационную длину k<n и минимальное кодовое расстояние d=n-k+1. Число корректируемых ошибок в пределах минимального кодового расстояния 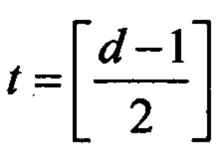 , где [х] - целая часть х.
, где [х] - целая часть х.
Сначала опишем кодирование кода Рида-Соломона. Исходную информацию mi ∈ GF(pm), i=0..k-1 зададим в виде вектора
М=(m0,m1,…,mk-1).
При спектральном подходе символы кода получают умножением дополненного нулями до длины n транспонированного информационного вектора на матрицу Вандермонда, задающего дискретное преобразование Фурье информационного вектора из временной области в частотную область
C=W×MT,
где матрица Вандермонда
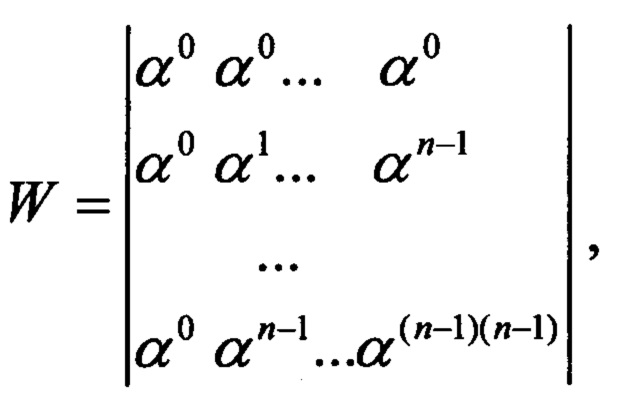
α - примитивный элемент поля.
На приемной стороне символы кода С=(c0,c1,…,cn-1), часть из которых может быть искажена, представляются в виде
ri=ci+ei, i=0..n-1,
где ei - ошибки символов.
Первый этап декодирования заключается в вычислении синдрома кода. Для этого строим интерполяционный вектор Т длины n. При спектральном подходе интерполяционный вектор получают умножением принятого кодового вектора на обратную матрицу Вандермонда, задающего обратное дискретное преобразование из частотной области во временную область
T=W-1×rT,
где обратная матрица Вандермонда
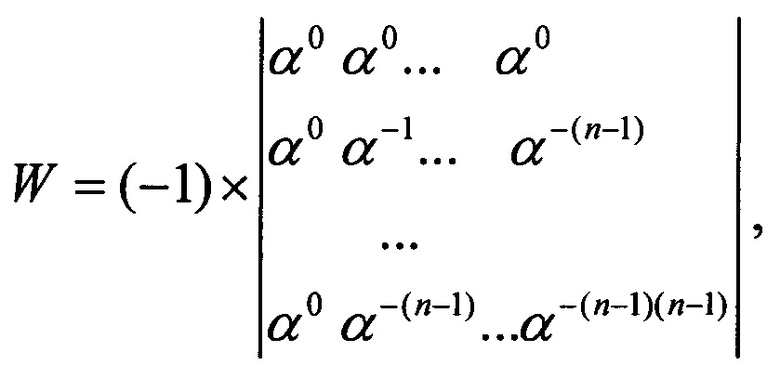
По определению интерполяционный вектор для неискаженных символов кода ci, i=0...n-1 равен информационному вектору М, а для ошибок ei, i=0…n-1 есть вектор спектра ошибок, который обозначим Е. Интерполяция является линейной операцией и поэтому справедливо уравнение

Вектор М имеет k информационных компонент, поэтому старшие n-k компонент вектора Т зависят только от ошибок ei, i=0…n-1 и называют вектором синдрома
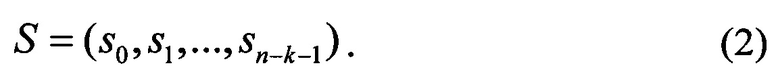
Для компонент синдрома справедливо соотношение, которое называют ключевым уравнением (Блейхут Р. Теория и практика кодов, контролирующих ошибки. Пер. с англ. - М.: Мир, 1986. - 448 с.). При t ошибках ключевое уравнение запишется
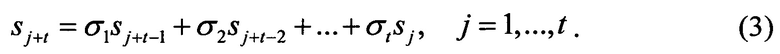
Компоненты синдрома являются известными компонентами спектра ошибок Е. Уравнение (3) для j=t+1…n позволяет продолжить вектор S и получить неизвестные компоненты спектра ошибок Е. Тогда, из (1) исходный информационный вектор восстанавливается по формуле

Систему линейных уравнений (3) можно записать в векторно-матричном виде
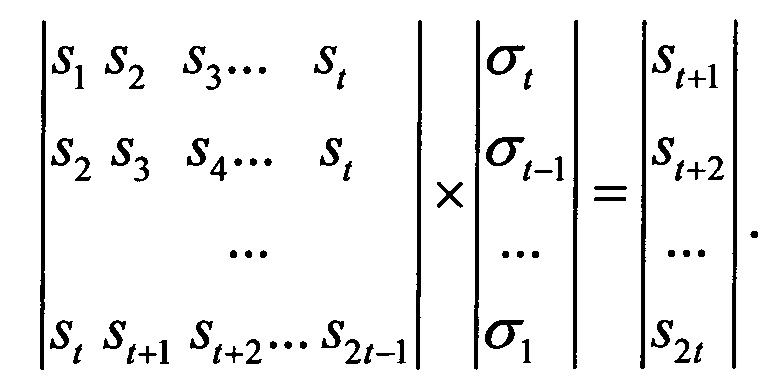
Сопоставим квадратным блокам матрицы этой системы уравнений определители Ганкеля (Бейкер Дж., мл., Грейвс-Моррис П. Аппроксимация Паде. Пер. с англ. - М., Мир, 1986. - 502 с.)
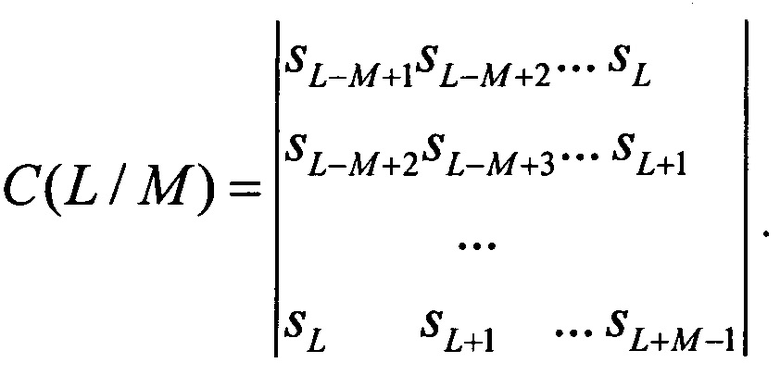
Из множества значений C(L/М), L,M=0,1,2… составим С-таблицу
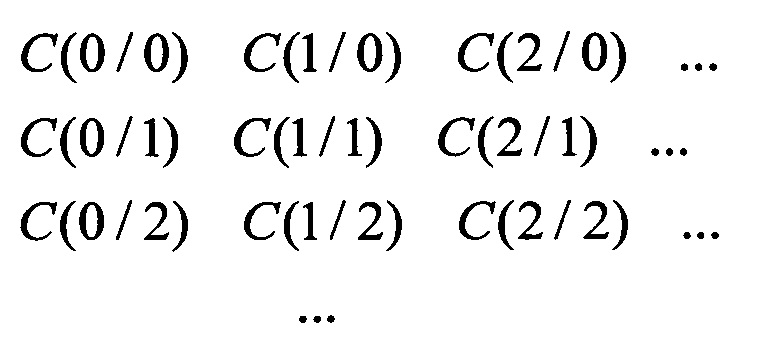
По определению начальные условия будут:
- первая строка таблицы C(L/0)=1;
- вторая строка C(L/1)=sL;
- первый столбец С(0/М)=(-1)M(M-1)/2⋅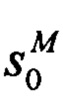 , т.е. будет последовательностью символов
, т.е. будет последовательностью символов 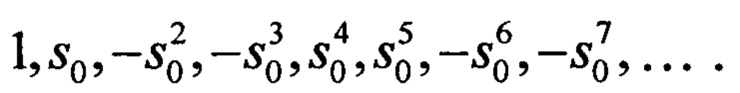
При заполнении таблицы оставшиеся элементы таблицы можно вычислить, используя рекуррентное тождество
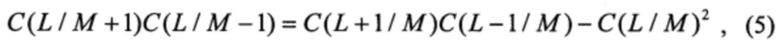
которое называют еще звездным равенством. Равенство (6) является частным случаем теоремы Сильвестра. Оно показывает, как связаны соседние элементы С-таблицы.
Из (6) можно выразить один из определителей
C(L+1/M),C(L-1/M),C(L/М+1),C(L/М+1),C(L/М),
через остальные определители. Это позволяет заполнять С-таблицу в различных направлениях: сверху вниз, слева направо и т.д.
В С-таблице нулевые элементы образуют квадратные блоки, которые окружены со всех сторон ненулевыми элементами. В С-таблице будут бесконечные нулевые блоки, поскольку степенной ряд из компонентов синдрома соответствует разложению рациональной функции.
Последние замечания позволяют заполнять С-таблицу, даже если вычисления (5) приводят к делению на ноль. Достаточно определить нули только в одной строке или столбце таблицы, чтобы заполнить квадратные нулевые блоки. При t ошибках верхний правый угол бесконечного нулевого блока будет иметь координаты (t+1,t). При наличии нулевых блоков таблицу заполняют при движении сверху вниз или слева направо вдоль сторон этого блока. При этом деление на ноль исключается, а будет использоваться умножение на ноль, при котором одно из слагаемых в равенстве (5) обнуляется.
Перечислим последовательность шагов заполнения С-таблицы.
Шаг 1. Начальное заполнение первого столбца и первой строки таблицы, а также частичное заполнение второй строки таблицы компонентами синдрома.
Шаг 2. Начальное заполнение нулевых квадратных блоков и определение местоположения бесконечного нулевого блока.
Шаг 3. Заполнение таблицы сверху вниз
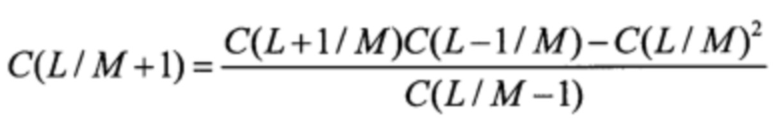
Шаг 4. Заполнение таблицы слева направо
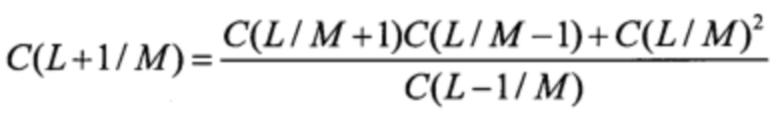
Вторая строка С-таблицы представляет собой компоненты синдрома, поэтому при продолжении этой строки таблицы С(L/1)=sL, L=0..n-1 получают спектр ошибок, который затем используют для восстановления информации по формуле (4).
Наибольшее число операций требуется при заполнении С-таблицы. При коррекции t ошибок для заполнения С-таблицы необходимо выполнить M(t)=2⋅(t+(t+1)+…+2+1)=O(t2) операций. Таким образом, сложность декодирования запишется O(n2). Однако, при заполнении С-таблицы используются довольно простые вычисления по формуле (5), которые могут быть реализованы на комбинационных схемах за один такт рабочей частоты. При этом исключен этап вычисления многочлена локаторов ошибок, который используется в известных способах декодирования кода Рида-Соломона.
В качестве примера рассмотрим декодирование кода Рида-Соломона (6,2), определенного над полем Галуа GF(7). Примитивный элемент поля будет α=3. Матрица Вандермонда и ее обратная матрица будут
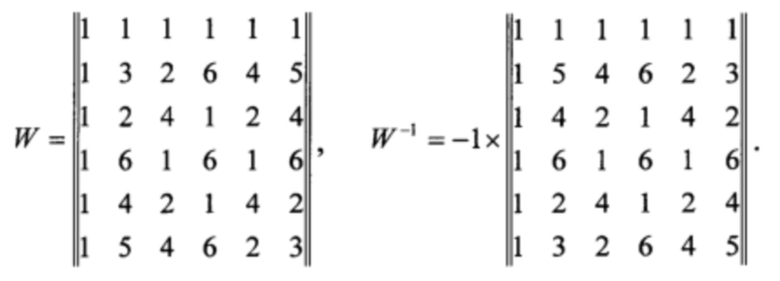
Пусть задана исходная информация из двух символов поля (5,2). Кодирование заключается в умножении дополненного нулями транспонированного информационного вектора М=(5,2,0,0,0,0) на матрицу Вандермонда. Получим кодовый вектор
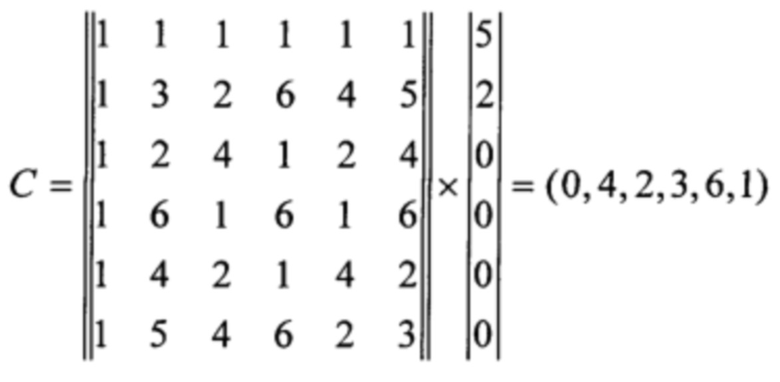
Предположим, что при передаче кодового слова произошло две ошибки е=(0,0,1,0,1,0), тогда принятое кодовое слово
r=С+е=(0,4,3,3,0,1).
Интерполяционный вектор Т вычисляют умножением транспонированного принятого кодового слова на обратную матрицу Вандермонда

Последние четыре компоненты вектора Т составляют синдром ошибок, а первые две компоненты равны неизвестной сумме информационных символов и спектра ошибок. Сначала заполним клетки С-таблицы начальными значениями. Первая строка таблицы содержит последовательность единиц 1,1,1,1,1,…. Первый столбец таблицы содержит последовательность 1,1,-1,-1,1,1,-1,-1,…. Первые 4 ячейки второй строки таблицы заполняются известными компонентами синдрома 1,1,5,1. Верхний левый угол бесконечного блока нулей будет иметь координаты (3,2). Начальное заполнение представлено в табл. 1.
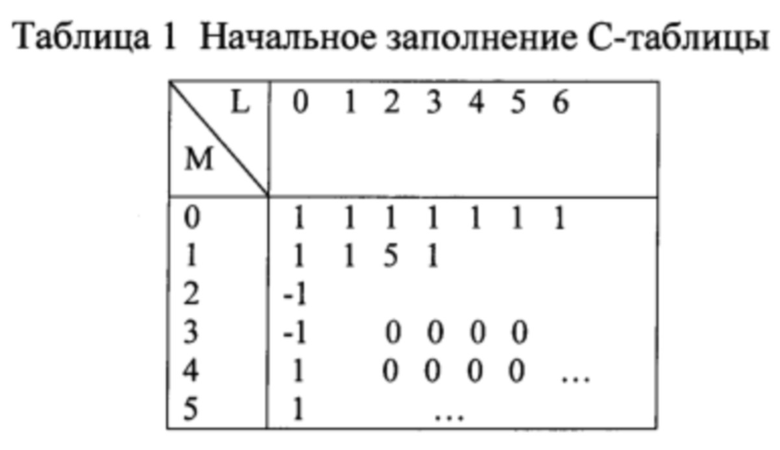
Теперь, используя соотношение (5), заполняем остальные клетки С-таблицы, двигаясь сначала сверху вниз по столбцу 1
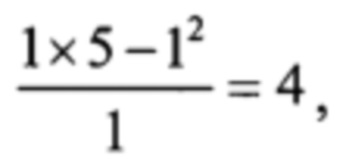
а затем по столбцу 2 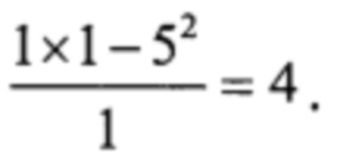
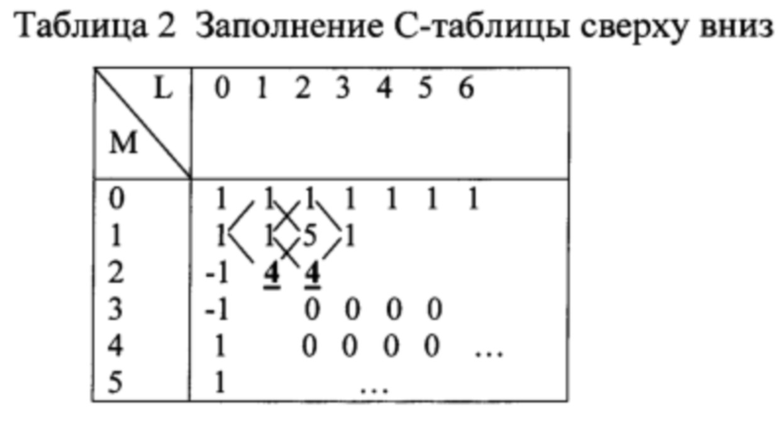
Далее заполняем С-таблицу, двигаясь слева направо по строке 2
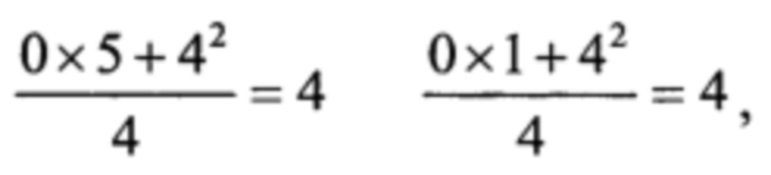
а затем по строке 1
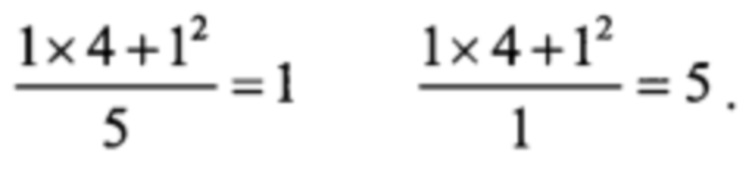
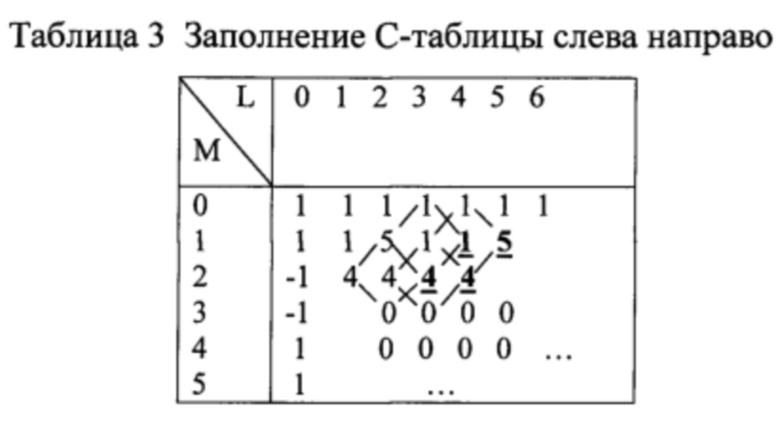
Отсюда из строки 1 спектр ошибок будет Е=(1,1,5,1,1,5).
Восстановленная информация согласно (4) будет
М=Т-Е=(3,3,1,5,1,1) - (5,1,1,5,1,1)=(5,2,0,0,0,0),
что соответствует исходной информации М=(5,2).
В данном примере в С-таблице имеется бесконечный нулевой блок. Заполнение ячеек С-таблицы вдоль верхней стороны нулевого блока выполняется при движении вдоль стороны блока слева направо. Вычисления в направлении слева направо вдоль стороны нулевого блока исключает деление на 0, а используется только умножение на 0.
Упрощение декодирования кода Рида-Соломона в предлагаемом способе достигается за счет исключения этапа вычисления многочлена локаторов ошибок. После определения синдрома ошибок сразу вычисляют продолжение спектра ошибок путем заполнения С-таблицы с использованием простых трехчленных рекуррентных соотношений между ганкелевскими определителями различного порядка.
Достигаемым техническим результатом способа декодирования кода Рида-Соломона является уменьшение сложности реализации.
| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для вычисления синдромов кода Рида-Соломона | 1990 |
|
SU1751860A1 |
| СПОСОБ ПЕРЕДАЧИ И ПРИЕМА СООБЩЕНИЙ В СИСТЕМЕ СВЯЗИ | 2008 |
|
RU2369023C1 |
| УСТРОЙСТВО КОДИРОВАНИЯ-ДЕКОДИРОВАНИЯ ИНФОРМАЦИИ | 1994 |
|
RU2115231C1 |
| СПОСОБ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ | 2005 |
|
RU2295198C1 |
| Устройство кодирования и вычисления синдромов помехоустойчивых кодов для коррекции ошибок во внешней памяти ЭВМ | 1989 |
|
SU1656689A1 |
| Устройство для декодирования составного корректирующего кода | 1983 |
|
SU1229969A1 |
| СПОСОБ ДЕКОДИРОВАНИЯ ЦИКЛИЧЕСКОГО ПОМЕХОУСТОЙЧИВОГО КОДА | 2002 |
|
RU2231216C2 |
| Устройство декодирования произведений кодов Рида-Соломона | 2017 |
|
RU2677372C1 |
| СПОСОБ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ | 2007 |
|
RU2359414C1 |
| УСТРОЙСТВО ДЕКОДИРОВАНИЯ КОДОВ РИДА-СОЛОМОНА | 2010 |
|
RU2441318C1 |
Изобретение относится к области помехоустойчивого кодирования и может быть использовано для декодирования кода Рида-Соломона с коррекцией многократных ошибок. Технический результат - исключение вычисления многочлена локаторов ошибок и уменьшение сложности реализации способа. Для этого на первом этапе декодирования вычисляют синдром помехоустойчивого кода, а затем на основе рекуррентных соотношений между ганкелевскими определителями различных порядков определяют продолжение спектра ошибок для продолжения спектра ошибок ганкелевскими определителями различных порядков заполняют С-таблицу и если синдром содержит нулевые компоненты, то С-таблица будет содержать нулевые квадратные блоки, стороны каждого блока равны длине последовательности подряд идущих нулевых компонент синдрома. 6 з.п. ф-лы.
1. Способ декодирования кода Рида-Соломона, заключающийся в том, что сначала на первом этапе декодирования вычисляют синдром помехоустойчивого кода, а затем определяют продолжение спектра ошибок, отличающийся тем, что продолжение спектра ошибок определяют на основе рекуррентных соотношений между ганкелевскими определителями различных порядков, составленными из компонент синдрома.
2. Способ по п. 1, отличающийся тем, что для продолжения спектра ошибок ганкелевскими определителями различных порядков заполняют С-таблицу.
3. Способ по п. 2, отличающийся тем, что при начальном заполнении С-таблицы первую строку заполняют последовательностью единиц 1,1,1,1,1,…, вторую строку заполняют последовательностью известных компонент синдрома кода s0,s1,s2,…, первый столбец заполняют последовательностью 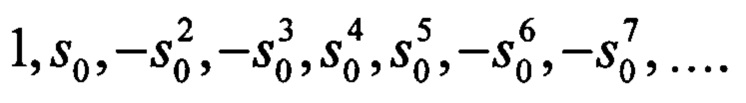 , где s0 есть первая известная компонента синдрома кода.
, где s0 есть первая известная компонента синдрома кода.
4. Способ по п. 2, отличающийся тем, что при заполнении оставшихся клеток С-таблицы используют трехчленные рекуррентные соотношения между ганкелевскими определителями различных порядков.
5. Способ по п. 2, отличающийся тем, что заполнение оставшихся клеток С-таблицы выполняют сначала сверху вниз, а затем слева направо.
6. Способ по п. 2, отличающийся тем, что если синдром содержит нулевые компоненты, то С-таблица будет содержать нулевые квадратные блоки, стороны каждого блока равны длине последовательности подряд идущих нулевых компонент синдрома.
7. Способ по п. 2, отличающийся тем, что С-таблица будет содержать бесконечный блок нулей, правый верхний угол которого имеет координаты на плоскости (t, t+1), где t - число ошибок в коде.
| US 2003028842 A1 - 2003-02-06 | |||
| СТРУКТУРА ГЕТЕРОПЕРЕХОДНОГО ФОТОЭЛЕКТРИЧЕСКОГО ПРЕОБРАЗОВАТЕЛЯ С ПРОТИВОЭПИТАКСИАЛЬНЫМ ПОДСЛОЕМ | 2017 |
|
RU2675069C1 |
| FERDAOUSS MATTOUSSI et al | |||
| Complexity Comparison of the Use of Vandermonde versus Hankel Matrices to Build Systematic MDS Reed-Solomon Codes, 2012 IEEE 13th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), June 2012 | |||
| ФЕДОРЕНКО С.В | |||
| Простой алгоритм | |||
Авторы
Даты
2020-09-04—Публикация
2019-12-05—Подача