Изобретение относится к электросвязи и может быть использовано для цикловой синхронизации при приеме передач, использующих блочные турбокоды (ТКБ) [Pyndiah R.M. Near-Optimum Decoding of Product Codes: Block Turbo Codes. - IEEE Transactions on Communications, Vol.46, №8, August 1998, p.1003] длины N=(n1+1)(n2+1), в которых компонентными кодами являются двоичные циклические коды примитивных длин n1 и n2 [Блейхут Р. Теория и практика кодов, контролирующих ошибки: Пер. с англ. / Под ред. К.Ш.Зигангирова. - М.: Мир, 1986, с.122] с порождающими многочленами, имеющими общий делитель, расширенные за счет добавления проверки на четность [Мак-Вильямс Ф.Дж., Слоэн Н.Дж.А. Теория кодов, исправляющих ошибки: Пер с англ. - М.: Связь, 1979, с.37], в условиях параметрической неопределенности структуры кодера.
Известен способ кодовой цикловой синхронизации при передаче информации помехоустойчивыми блоковыми кодами (фазирование по словам), основанный на методе последовательных сдвигов, заключающийся в том, что принимаемая дискретная последовательность символов поступает на вход приемника дискретной информации, после чего производится анализ его состояния. При этом различают два состояния: синхронное, при котором точно известна информация о начале кодовых комбинаций, и асинхронное, - когда информация о начале кодовых комбинаций в принимаемой последовательности неизвестна. В качестве признака синхронного состояния используется равенство нулю синдрома. В случае принятия решения об асинхронном состоянии осуществляется сдвиг на один символ по принимаемой последовательности в одну и ту же сторону. Сдвиги производятся до тех пор, пока не будут обнаруживаться только кодовые комбинации. В этом случае принимается решение о наличии синхронного состояния и процесс вхождения в синхронизм заканчивается. [Лосев В.В., Бродская Е.Б., Коржик В.И. Поиск и декодирование сложных дискретных сигналов / Под ред. В.И.Коржика. - М.: Радио и связь, 1988, с 132-134].
Однако этот способ невозможно использовать в условиях параметрической неопределенности структуры кодера помехоустойчивого кода, поскольку вычисление синдрома требует знания проверочной матрицы кода или порождающего полинома [Кларк Дж., мл., Кейн Дж. Кодирование с исправлением ошибок в системах цифровой связи: Пер. с англ. - М.: Радио и связь, 1986, с 81; Блейхут Р. Теория и практика кодов, контролирующих ошибки: Пер. с англ. / Под ред. К.Ш.Зигангирова. - М.: Мир, 1986, с 119].
Наиболее близким к предлагаемому способу является способ кодовой цикловой синхронизации кодов Рида-Соломона, заключающийся в том, что принимаемая дискретная последовательность символов поступает на вход приемника дискретной информации, после чего производится анализ его состояния. При этом различают два состояния: синхронное, при котором точно известна информация о начале кодовых слов, и асинхронное, - когда информация о начале кодовых слов в принимаемой последовательности неизвестна. Анализ состояния приемника основан на расчете дискретного преобразования Фурье Галуа (ДПФГ) принимаемой дискретной последовательности на длине кодового слова. По определению коды Рида-Соломона обладают примитивной длиной qm-1 [Блейхут Р. Теория и практика кодов, контролирующих ошибки: Пер. с англ. / Под ред. К.Ш.Зигангирова. - М.: Мир, 1986, с 201], что позволяет произвести ДПФГ в поле GF(qm), где m - степень расширения поля. В качестве признака синхронного состояния используется превышение числа нулевых компонентов в спектрах над пороговым значением. [Зайцев И.Е. Формирование признаков для фазирования кодов Рида-Соломона в условиях параметрической неопределенности структуры кодера. - Известия вузов. Приборостроение. 1998. Т.41, №8, с.16]. В случае принятия решения об асинхронном состоянии осуществляется сдвиг на один символ по принимаемой последовательности в одну и ту же сторону. Сдвиги производятся до установления синхронного состояния. Принят за прототип.
Однако ТКБ длины N не обладают свойством примитивной длины, что не позволяет использовать расчет ДПФГ принимаемой дискретной последовательности на длине кодового слова применительно к ТКБ длины N [Блейхут Р. Теория и практика кодов, контролирующих ошибки: Пер. с англ. / Под ред. К.Ш.Зигангирова. - М.: Мир, 1986, с 240].
Таким образом, недостатком прототипа (способа кодовой цикловой синхронизации на основе признака синхронного состояния приемника дискретной информации по превышению числа нулевых спектральных составляющих над пороговым значением) является то, что он применим только к коду Рида-Соломона.
Технический результат - увеличение количества синхронизируемых кодов по отношению к прототипу в условиях параметрической неопределенности (известна только длина кодового слова N) и расширение арсенала средств аналогичного назначения.
Для достижения указанного технического результата в способе кодовой цикловой синхронизации входную дискретную последовательность символов кодовых слов ТКБ принимают с использованием приемника дискретной информации, после чего производят анализ его состояния. При этом различают два состояния: синхронное, при котором точно известна информация о начале кодовых слов, и асинхронное, когда информация о начале кодовых слов в принимаемой последовательности неизвестна. Анализ состояния приемника производят по признаку синхронного состояния путем выделения из принятой дискретной последовательности фрагмента длины N-1 и расчета ДПФГ данного фрагмента. Признаком синхронного состояния приемника дискретной информации является равенство нулю, по меньшей мере, одного спектрального компонента в спектре выделенного фрагмента. После выявления данного признака дополнительно производят проверку истинности установления синхронного состояния по наличию признака истинности фазирования. Для этого выделяют не менее четырех фрагментов длины N-1, последовательно расположенных за фрагментом, выбранным на этапе определения синхронного состояния, при этом начало очередного фрагмента отделено от окончания предшествующего фрагмента на один символ последовательности, выполняют ДПФГ дополнительно выделенных фрагментов и определяют наличие признака истинности фазирования. В качестве признака истинности фазирования используют непустое пересечение множеств номеров нулевых компонентов в полученных спектрах.
В результате имитационного моделирования работы данного способа на ЭВМ для кодовой синхронизации ТКБ длины N установлено, что при анализе состояния приемника необходимо производить выделение и ДПФГ не менее пяти фрагментов длины N-1.
При отсутствии синхронизации (асинхронном состоянии приемника) до ее установления производят поиск синхронного состояния. Для этого производят последовательный сдвиг по принимаемой последовательности на один символ в одну и ту же сторону с последующим выделением нового фрагмента, его ДПФГ и определением наличия синхронного состояния приемника по признаку синхронного состояния, а также проверкой истинности синхронного состояния по признаку истинности фазирования в случае выявления признака синхронного состояния. При отсутствии признака истинности фазирования поиск синхронного состояния возобновляют с момента выявления признака синхронного состояния.
Общим с прототипом является то, что с использованием приемника дискретной информации принимают входную дискретную последовательность, представляющую собой последовательно передаваемые символы кодовых слов, выделяют фрагмент дискретной последовательности, выполняют его ДПФГ и определяют наличие синхронного состояния приемника дискретной информации по признаку синхронного состояния. При отсутствии синхронизации до ее установления производят поиск синхронного состояния путем последовательного сдвига по принимаемой последовательности на один символ в одну и ту же сторону с последующим выделением нового фрагмента, его ДПФГ и определением наличия синхронного состояния приемника по признаку синхронного состояния.
Отличием от прототипа является то, что выделяют фрагмент дискретной последовательности длиной меньше длины кодового слова на один символ. В качестве признака синхронного состояния приемника дискретной информации используют равенство нулю, по меньшей мере, одного спектрального компонента в спектре выделенного фрагмента. После выявления данного признака дополнительно производят проверку истинности установления синхронного состояния по наличию признака истинности фазирования. Для этого выделяют не менее четырех фрагментов той же длины, последовательно расположенных за фрагментом, выбранным на этапе определения синхронного состояния, при этом начало очередного фрагмента отделено от окончания предшествующего фрагмента на один символ последовательности, выполняют ДПФГ дополнительно выделенных фрагментов и определяют наличие признака истинности фазирования. В качестве признака истинности фазирования используют непустое пересечение множеств номеров нулевых компонентов в полученных спектрах. В случае отсутствия признака истинности фазирования поиск синхронного состояния возобновляют с момента выявления признака синхронного состояния.
Благодаря новой совокупности существенных признаков технический результат проявляется в возможности кодовой цикловой синхронизации всех ТКБ длины N, в качестве компонентных кодов в которых используются двоичные циклические коды примитивных длин с порождающими многочленами, имеющими общий делитель, расширенные за счет добавления проверки на четность.
Известно, что ТКБ являются кодами произведений [Мак-Вильямс Ф.Дж., Слоэн Н.Дж.А. Теория кодов, исправляющих ошибки: Пер с англ. - М.: Связь, 1979, с.548], которые задаются порождающей матрицей, представляющей собой прямое произведение порождающих матриц исходных кодов:

где G - порождающая матрица компонентного циклического кода [Мак-Вильямс Ф.Дж., Слоэн Н.Дж.А. Теория кодов, исправляющих ошибки: Пер с англ. - М.: Связь, 1979, с.548].
Известно, что порождающая матрица исходного циклического кода с порождающим многочленом g(x) имеет вид

где n и r - длина кодового слова и длина проверочной части кодового слова исходного циклического кода соответственно [Мак-Вильямс Ф.Дж., Слоэн Н.Дж.А. Теория кодов, исправляющих ошибки: Пер с англ. - М.: Связь, 1979, с.191], а порождающая матрица кода с проверкой на четность имеет вид

[Зюко А.Г., Кловский Д.Д., Назаров М.В., Финк Л.М. Теория передачи сигналов: Учебник для вузов. - 2-е изд., перераб. и доп. - М.: Радио и связь, 1986, с.147]. Тогда порождающая матрица расширенного циклического кода имеет вид
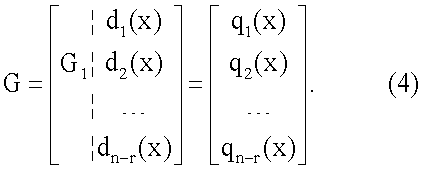
Рассмотрим случай, когда исходные циклические коды одинаковые, т.е. g1(x)=g2(x)=g(x) и n1=n2=n. В результате прямого произведения порождающих матриц расширенных циклических кодов (4) порождающая матрица ТКБ имеет вид

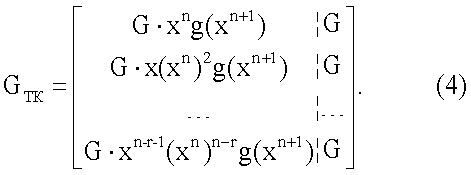
Длина ТКБ с порождающей матрицей (4) равна N.
Рассмотрим структуру кодового слова ТКБ, полученного удалением символа проверки на четность. В данном случае длина ТКБ становится равной N-1. Этому действию соответствует удаление крайнего правого столбца из порождающей матрицы (4), что приводит к порождающей матрице вида
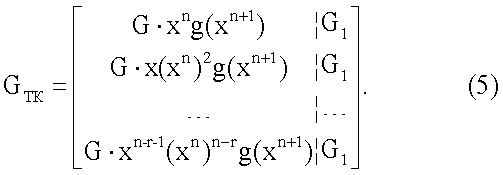
Заменив в (5) G1 и G согласно (2) и (3) соответственно, получим

Объединив правую и левую части строк порождающей матрицы (6), получим
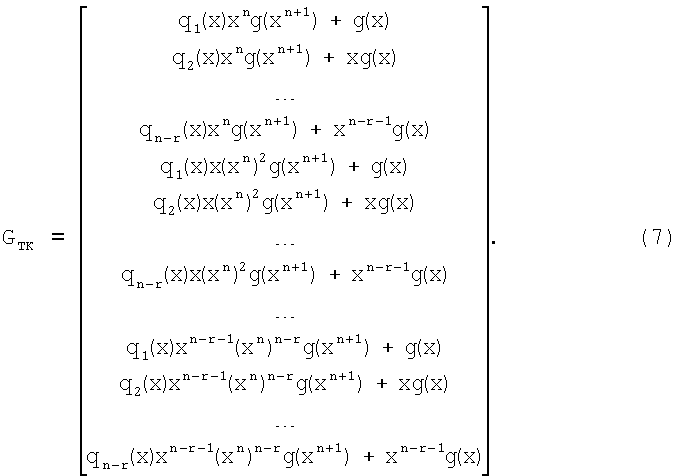
Вынесем общий сомножитель в каждой строке порождающей матрицы (7) за скобки. В данном случае общий сомножитель представляет собой порождающий многочлен исходного циклического кода g(x). Порождающая матрица ТКБ имеет вид

В случае, когда порождающие многочлены исходных циклических кодов g1(x) и g2(x) имеют различные длины, т.е. n1≠n2, и общие делители, за скобки выносится наибольший общий делитель (НОД) g(x). Тогда порождающая матрица ТКБ имеет вид
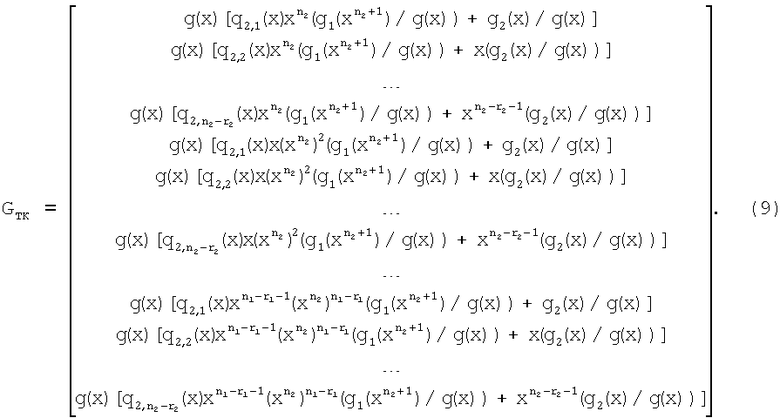
В результате анализа порождающих матриц ТКБ (8) и (9) установлено, что строки порождающей матрицы в качестве сомножителя содержат порождающий многочлен исходного нерасширенного циклического кода или содержат НОД порождающих многочленов исходных нерасширенных циклических кодов, и, кроме того, строки порождающей матрицы содержат множители задержки, а это значит, что ТКБ на длине фрагмента N-1, полученного удалением из каждого кодового слова символа проверки на четность, является циклическим кодом.
Так как компонентными кодами ТКБ являются двоичные циклические коды примитивных длин n1=2m1-1 и n2=2m2-1, и в результате расширения за счет добавления проверки на четность их длины равны n1+1=(2m1-1)+1=2m1 и n2+1=(2m2-1)+1=2m2, то длина ТКБ равна N=(n1+1)(n2+1)=2m12m2=2m1+m2=2m'. В результате удаления одного символа
проверки на четность длина фрагмента ТКБ равна N-1=2m'-1 и она является примитивной, что позволяет провести ДПФГ фрагментов принимаемой дискретной последовательности ТКБ длины N-1.
Известно, что разрешенными являются все кодовые слова циклического кода, у которых все спектральные компоненты, принадлежащие заданному множеству проверочных частот, равны нулю [Блейхут Р. Теория и практика кодов, контролирующих ошибки: Пер. с англ. / Под ред. К.Ш.Зигангирова. - М.: Мир, 1986, с 248]. Таким образом, если приемник находится в синхронном состоянии, то в спектрах всех принимаемых кодовых слов при отсутствии ошибок будут содержаться нулевые спектральные составляющие с одинаковыми номерами, то есть можно найти множество нулевых компонентов, содержащееся в каждом множестве компонентов спектров всех принимаемых слов. При наличии параметрической неопределенности относительно структуры кодера, за исключением длины кодового слова, множество проверочных частот неизвестно. В прототипе, в свойствах 1-3, [Зайцев И.Е. Формирование признаков для фазирования кодов Рида-Соломона в условиях параметрической неопределенности структуры кодера - Известия вузов. Приборостроение. 1998. Т.41, №8, с.14-16], показано, что количество нулевых компонентов в спектрах разрешенных кодовых слов кода Рида-Соломона не зависит от выбора порождающего полинома кода определенной степени, примитивного элемента и неприводимого многочлена, по которому построено поле. Поэтому в прототипе превышение числа нулевых компонентов над пороговым значением служит признаком синхронного состояния приемника дискретной информации.
Однако в результате имитационного моделирования работы данного способа на ЭВМ для кодовой синхронизации ТКБ длины N установлено, что использование расчета ДПФГ принимаемой дискретной последовательности на длине кодового слова не приводит к установлению синхронного состояния, так как длина ТКБ N не является примитивной. Это не позволяет использовать данный способ применительно к ТКБ длины N. Поэтому, для расширения класса синхронизируемых кодов предлагается использовать другие признаки. В качестве признака синхронного состояния предлагается использовать наличие в спектре выделенного из принимаемой последовательности фрагмента длиной меньше длины кодового слова на один символ, по меньшей мере, одного нулевого спектрального компонента, что позволит синхронизировать приемник дискретной информации по словам ТКБ. Так как номера нулевых спектральных компонентов в спектрах (полученных с учетом особенностей, обусловленных параметрической неопределенностью структуры кодера) всех разрешенных кодовых слов одинаковы, то признаком истинности фазирования может служить непустое пересечение множеств номеров нулевых спектральных компонентов в спектрах нескольких последовательно расположенных друг за другом фрагментов кодовых слов, при этом начало очередного фрагмента отделено от окончания предшествующего фрагмента на один символ последовательности. В результате имитационного моделирования на ЭВМ для кодовой синхронизации ТКБ длины N установлено, что при анализе состояния приемника необходимо производить выделение и ДПФГ не менее пяти фрагментов.
Проведенный анализ уровня существующей техники позволил установить, что аналоги, характеризующиеся совокупностью признаков, которые тождественны всем признакам заявленного технического решения, отсутствуют, что указывает на соответствие заявленного способа условию патентоспособности "новизна". Результаты поиска известных решений в данной и смежной областях техники с целью выявления признаков, совпадающих с отличными от прототипа признаками заявленного объекта показали, что они не следуют явным образом из уровня техники. Из уровня техники также не выявлена известность влияния предусматриваемых существенными признаками заявленного изобретения преобразований на достижение указанного технического результата. Следовательно, заявленное изобретение соответствует условию патентоспособности "изобретательский уровень".
Заявленный способ поясняется иллюстрацией, на которой изображена структурная схема способа кодовой цикловой синхронизации ТКБ.
Способ кодовой цикловой синхронизации ТКБ длины N в условиях параметрической неопределенности (известна длина кодового слова N) осуществляются следующим образом:
Этап 1. Дискретную последовательность символов кодовых слов ТКБ принимают с использованием приемника дискретной информации.
Данный этап может быть реализован с помощью специализированных средств цифровой обработки сигналов или программно на ЭВМ.
Далее производят анализ состояния приемника дискретной информации (этапы 2, 3, 4, 6, 7, 8).
Этап 2. Выделяют из принятой дискретной последовательности фрагмент длиной
N-1:

Этап 3. Рассчитывают ДПФГ выделенного фрагмента:
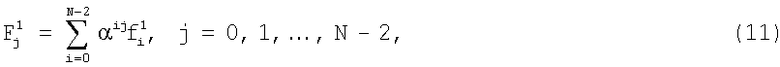
где F1 j - j-й спектральный компонент в спектре 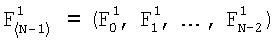 фрагмента
фрагмента 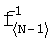 ;
;
α - элемент порядка N-1 над полем GF(2m);
i - время;
j - частота.
При этом элементы двоичного кодового слова преобразуют в элементы расширенного поля следующим образом: 0→α-∞, 1→α0.
Этап 4. Определяют наличие синхронного состояния приемника дискретной информации по признаку синхронного состояния. В качестве признака используют равенство нулю, по меньшей мере, одного спектрального компонента в спектре выделенного фрагмента:

Этап 5. Если F1 j≠0, j=0, 1, …, N-2, или признак истинности фазирования не выявлен (переход с этапа 8), то осуществляют сдвиг на один символ по принимаемой последовательности и заново анализируют состояние приемника (возвращаются на этап 2).
При наличии признака синхронного состояния осуществляют проверку истинности синхронного состояния приемника дискретной информации (этапы 6, 7, 8).
Этап 6. Выделяют не менее четырех фрагментов длины N-1, последовательно расположенных за фрагментом, выбранным на этапе 2, при этом начало очередного фрагмента отделено от окончания предшествующего фрагмента на один символ последовательности,
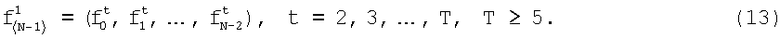
Этап 7. Выполняют дискретное преобразование Фурье Галуа дополнительно выделенных фрагментов:
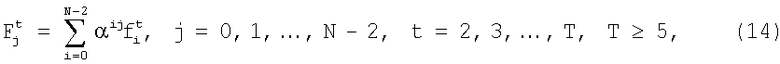
где Fj t - j-е спектральные компоненты в спектрах 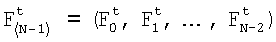 фрагментов
фрагментов 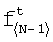 ;
;
α - элемент порядка N-1 над полем GF(2m);
i - время;
j - частота.
Этап 8. Проверяют истинность синхронного состояния приемника дискретной информации по признаку истинности фазирования. Для этого рассчитывают пересечение множеств нулевых компонентов всех полученных спектров:
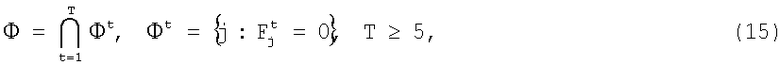
где Фt - множество номеров нулевых компонентов в спектре t-го фрагмента.
В качестве признака истинности фазирования используют непустое пересечение множеств номеров нулевых компонентов в полученных спектрах, т.е. если

где 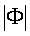 - мощность множества Ф,
- мощность множества Ф,
то считают, что приемник синхронизирован с началом кодовой комбинации, в противном случае процедуру поиска синхронного состояния возобновляют с момента выявления признака синхронного состояния (переходят на этап 5).
Этапы 2-8 могут быть реализованы с помощью специализированных вычислителей или программно на ЭВМ.
Для исследования возможности осуществления предложенного способа на ПЭВМ проведено имитационное моделирование его работы. Программа написана на языке Delphi 7.0.
Результаты решения контрольного примера с помощью имитационной модели выглядят следующим образом. Например, приемник дискретной информации принимает двоичную дискретную последовательность ТКБ, длина кодового слова которого N=64 символа и в качестве компонентных кодов в кодере которого используется семиэлементный расширенный (n+1=8) двоичный (q=2) циклический код:
{1011000101100011010011100100111010011100011000111001110010110001001011011000101111101000110001010100111010100110011000110000000001001110110100100110001100000000111111111011000110011100001011010100111010100110011101001001110010011100010011100111010010100110101001101000101101001110100010110110001101001110101001100110001100111010100010}. Найдем синхронное состояние приемника.
Для анализа состояния приемника, используя априорные данных о длине кодового слова N, построим поле Галуа, в котором будем выполнять ДПФГ. Укороченная на один символ длина кодового слова двоичного турбокода связана с размерностью и основанием поля (основание поля совпадает с основанием кода, так как кодовые слова принадлежат полю GF(q), а их спектры являются векторами над GF(qm)) выражением N-1=qm-1 [Блейхут Р. Теория и практика кодов, контролирующих ошибки: Пер. с англ. / Под ред. К.Ш.Зигангирова. - М.: Мир, 1986, с 122, 248]. Отсюда получим степень расширения m поля GF(qm):
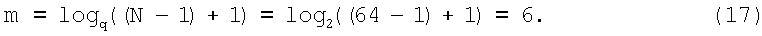
В качестве неприводимого многочлена шестой степени выберем многочлен f(x)=x6+x+1. Элементы расширенного поля Галуа GF(26) по выбранному полиному приведены в таблице 1.
Выражение (2) может быть записано в матричном виде:

где 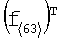 - транспонированный вектор
- транспонированный вектор 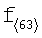 , W - квадратная матрица размерности
, W - квадратная матрица размерности
N-1 вида:

где j=0,1,…,N-2 - номер весовой функции (строки);
i=0,1,…,N-2 - номер элемента весовой функции (столбца).
Согласно выражению (10) проведем расчет спектра фрагмента 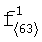 :
:
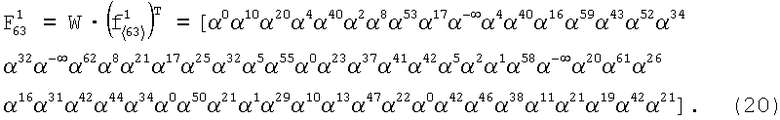
Выявлен признак синхронного состояния, так как

Выделим из дискретной последовательности 4 дополнительных фрагмента длиной 63 символа, при этом начало очередного фрагмента отделено от окончания предшествующего фрагмента на один символ последовательности:

Согласно выражению (18) проведем расчет спектров этих фрагментов:

В результате вычислений получены множества номеров нулевых компонентов всех спектров:
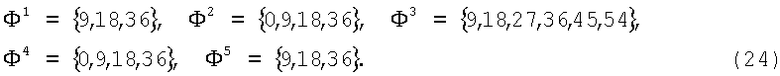
Результатом пересечения этих множеств является непустое множество Ф={9,18,36}. Так как 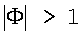 , то приемник дискретной информации находится в синхронном состоянии.
, то приемник дискретной информации находится в синхронном состоянии.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ | 2006 |
|
RU2319308C1 |
| СПОСОБ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ | 2011 |
|
RU2455773C1 |
| СПОСОБ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ ТУРБОКОДОВ | 2014 |
|
RU2566945C1 |
| СПОСОБ ДЕКОДИРОВАНИЯ ЦИКЛИЧЕСКОГО ПОМЕХОУСТОЙЧИВОГО КОДА | 2006 |
|
RU2309537C1 |
| СПОСОБ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ БЛОКОВЫХ НИЗКОПЛОТНОСТНЫХ КОДОВ | 2024 |
|
RU2827582C1 |
| СПОСОБ УСТОЙЧИВОЙ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ ПРИ ПРИМЕНЕНИИ ЖЕСТКИХ И МЯГКИХ РЕШЕНИЙ И МОДУЛЯЦИИ ПО ТИПУ СТЫКА С1-ФЛ | 2023 |
|
RU2812964C1 |
| Способ устойчивой кодовой цикловой синхронизации при применении жестких решений | 2022 |
|
RU2784953C1 |
| Способ устойчивой кодовой цикловой синхронизации при применении жестких и мягких решений | 2022 |
|
RU2797444C1 |
| Способ кодовой цикловой синхронизации для каскадного кода при применении жестких решений | 2016 |
|
RU2633148C2 |
| СПОСОБ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ | 2005 |
|
RU2295198C1 |
Изобретение относится к электросвязи и применимо для синхронизации сообщения, передаваемого последовательностью слов блочного турбокода, в котором компонентными кодами являются двоичные циклические коды примитивных длин с порождающими многочленами, имеющими общий делитель, расширенные за счет добавления проверки на четность, в условиях параметрической неопределенности, выраженной в отсутствии каких-либо данных о структуре кодера, за исключением длины кодового слова. Сущность способа кодовой цикловой синхронизации заключается в том, что дискретную последовательность символов кодовых слов принимают с использованием приемника дискретной информации. Из принимаемой дискретной последовательности выделяют фрагмент длиной меньше длины кодового слова на один символ, выполняют дискретное преобразования Фурье Галуа (ДПФГ) этого фрагмента и определяют синхронное состояние приемника дискретной информации по наличию признака синхронного состояния. Признаком синхронного состояния приемника дискретной информации является равенство нулю, по меньшей мере, одного спектрального компонента в спектре выделенного фрагмента. При отсутствии синхронизации до ее установления производят поиск синхронного состояния путем последовательного сдвига по принимаемой последовательности на один символ в одну и ту же сторону с последующим выделением нового фрагмента, его ДПФГ и определением наличия синхронного состояния приемника по признаку синхронного состояния. После выявления признака синхронного состояния дополнительно производят проверку истинности установления синхронного состояния по наличию признака истинности фазирования. Для этого выделяют не менее четырех фрагментов той же длины, последовательно расположенных за фрагментом, выбранным на этапе определения синхронного состояния, при этом начало очередного фрагмента отделено от окончания предшествующего фрагмента на один символ последовательности, выполняют ДПФГ дополнительно выделенных фрагментов и определяют наличие признака истинности фазирования. Признаком истинности фазирования является непустое пересечение множеств номеров нулевых компонентов в полученных спектрах. В случае отсутствия признака истинности фазирования поиск синхронного состояния возобновляют с момента выявления признака синхронного состояния. Достигаемым техническим результатом способа кодовой цикловой синхронизации является увеличение количества синхронизируемых кодов в условиях параметрической неопределенности, выраженной в отсутствие каких-либо данных о структуре кодера, за исключением длины кодового слова. Технический результат - увеличение количества синхронизируемых кодов в условиях параметрической неопределенности. 1 табл., 1 ил.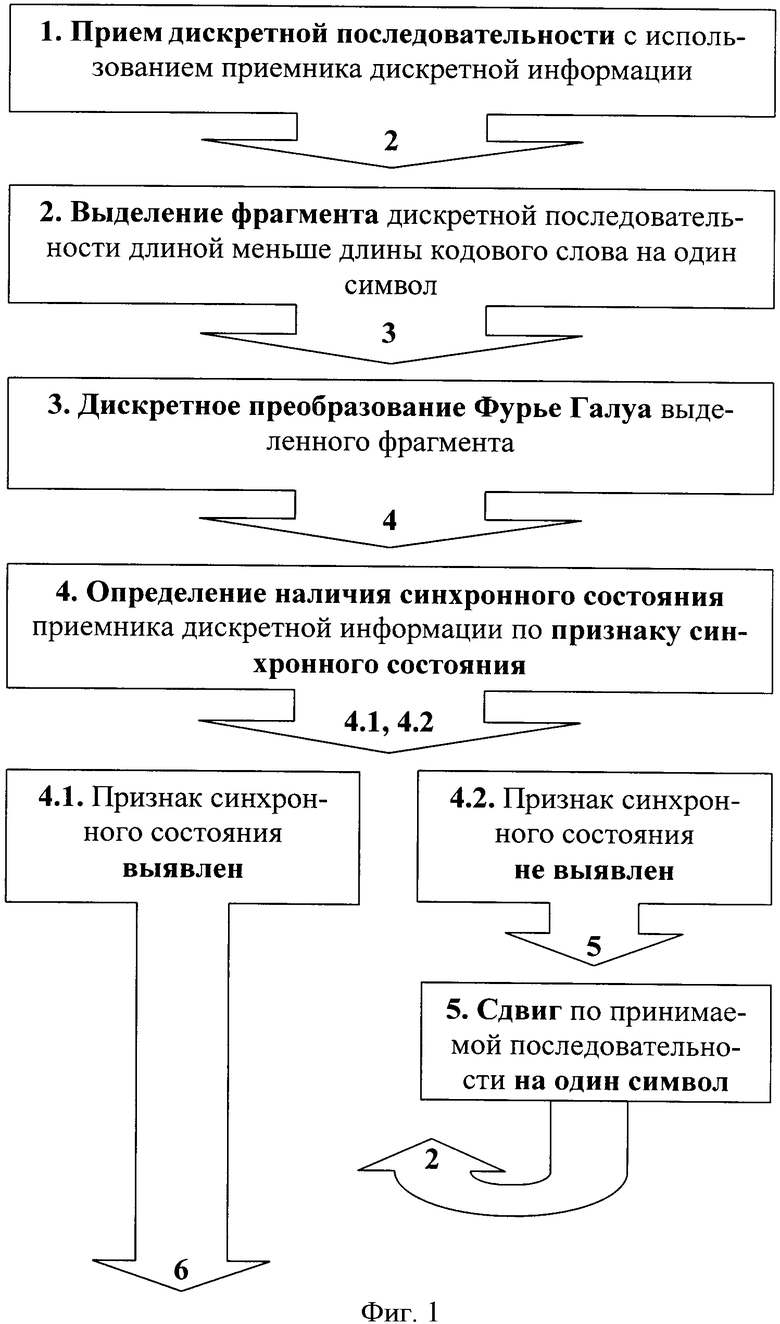
Способ кодовой цикловой синхронизации, заключающийся в том, что с использованием приемника дискретной информации принимают входную дискретную последовательность, представляющую собой последовательно передаваемые символы кодовых слов, выделяют фрагмент дискретной последовательности, выполняют его дискретное преобразование Фурье Галуа и определяют наличие синхронного состояния приемника дискретной информации по признаку синхронного состояния, а при отсутствии синхронизации до ее установления производят поиск синхронного состояния путем последовательного сдвига по принимаемой последовательности на один символ в одну и ту же сторону с последующим выделением нового фрагмента, его дискретным преобразованием Фурье Галуа и определением наличия синхронного состояния приемника по признаку синхронного состояния, отличающийся тем, что выделяют фрагмент дискретной последовательности длиной меньше длины кодового слова на один символ, в качестве признака синхронного состояния приемника дискретной информации используют равенство нулю, по меньшей мере, одного спектрального компонента в спектре выделенного фрагмента, после выявления данного признака дополнительно производят проверку истинности установления синхронного состояния по наличию признака истинности фазирования, для чего выделяют не менее четырех фрагментов той же длины, последовательно расположенных за фрагментом, выбранным на этапе определения синхронного состояния, при этом начало очередного фрагмента отделено от окончания предшествующего фрагмента на один символ последовательности, выполняют дискретное преобразование Фурье Галуа дополнительно выделенных фрагментов и определяют наличие признака истинности фазирования, в качестве которого используют непустое пересечение множеств номеров нулевых компонентов в полученных спектрах, а в случае отсутствия признака истинности фазирования поиск синхронного состояния возобновляют с момента выявления признака синхронного состояния.
| БЛЕЙХУТ Р | |||
| Теория и практика кодов, контролирующих ошибки: Пер | |||
| с англ | |||
| / Под ред | |||
| К.Ш.Зигангирова.- М.: Мир, 1986, с.202 | |||
| УСТРОЙСТВО КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ | 2005 |
|
RU2302701C1 |
| СПОСОБ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ | 2005 |
|
RU2295198C1 |
| СПОСОБ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ | 2001 |
|
RU2214689C2 |
| US 5969631 А, 1999.10.19 | |||
| Устройство для крепления ножа землеройной машины | 1977 |
|
SU735717A1 |
Авторы
Даты
2009-06-20—Публикация
2007-10-30—Подача