Область техники, к которой относится изобретение
Изобретение относится к области передачи информации и может быть использовано при передаче сообщений в широкополосных системах радиосвязи с кодовым разделением каналов.
Уровень техники
Известен способ многостанционного доступа с кодовым разделением каналов в системах передачи данных (см. Громаков Ю.А. Стандарты и системы подвижной радиосвязи. - М.: АОЗТ «Эко-трендз КО», 1996), суть которого заключается в расширении спектра частот на основе использования 64 видов последовательностей, сформированных по закону функций Уолша. Базовая станция может передавать информацию по 64 каналам одновременно. В каждом канале при передаче информации используется одна из 64 последовательностей Уолша. При изменении бита информационного сообщения фаза используемой последовательности Уолша изменяется на 180 градусов. Поскольку применяемые последовательности взаимно ортогональны, то взаимные помехи между каналами передачи базовой станции отсутствуют.
Информационные сигналы передаются на фоне специального синхронизирующего сигнала, структура которого формируется по закону случайных последовательностей максимальной длины. Синхронизирующий сигнал служит для введения передатчика базовой станции и приемника абонентской станции в цикловую фазу, а его манипуляция на этапе вхождения в связь обеспечивает передачу служебной информации.
Недостатком этого способа является то, что сигналы Уолша имеют регулярную структуру, которая заранее известна и поэтому широкополосная система радиосвязи с кодовым разделением каналов, построенная на основе этого способа, будет обладать низкой структурной скрытностью.
Известен генератор функций Попенко-Турко (см. патент СССР №1753464 А1, кл. G06F 1/02 от 07.08.1992), позволяющий генерировать дискретные ортогональные базисные функции, содержащий матрицу вычислителей, группу блоков деления, группы блоков элементов «И», матрицу операционных блоков, элементы задержки, блок синхронизации, регистр сдвига, блоки памяти и кольцевой регистр сдвига.
Недостатком этого генератора является отсутствие возможности генерирования хаотических ансамблей ортогональных сигналов (собственных векторов) различной структуры.
Наиболее близким по технической сущности к предлагаемому способу является способ, используемый в системе передачи данных с кодовым разделением каналов (см. патент Российской Федерации №2234191, кл. Н04В 7/216, H04L 9/26 от 24.07.2001), который включает операцию одновременной передачи сложных широкополосных сигналов на основе нелинейных последовательностей де Брейна со сменой формы последовательности в процессе передачи сообщения от одного информационного символа к другому.
Последовательности де Брейна так же как и словари Уолша обладают свойством ортогональности в точке, а большое разнообразие словарей де Брейна и наличие нелинейных операций в алгоритме формирования данного класса последовательностей позволяет использовать их в системах с многостанционным доступом для кодового уплотнения канала передачи.
Отличительным признаком этого способа является применение в каналах передачи сообщений, сменяемых от одного информационного символа к другому, ортогональных кодовых словарей де Брейна, каждое кодовое слово которых может быть построено путем суммирования по модулю два сигналов, снимаемых с разрядов регистра сдвига с нелинейными обратными связями по одному, по два и так далее до m включительно, где m - число разрядов регистра сдвига, функция обратных связей, которого задается соотношением:
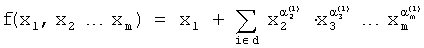 ,
,
где 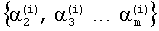 - разрешенный набор двоичных чисел, определяющий порядок подключения прямых и инверсных выходов элементов памяти регистра сдвига;
- разрешенный набор двоичных чисел, определяющий порядок подключения прямых и инверсных выходов элементов памяти регистра сдвига;
d - число разрешенных двоичных наборов, необходимых для генерирования максимального периода последовательности L, равного 2m;
Несмотря на то, что количество ортогональных сигналов, формируемых на основе кодовых словарей де Брейна, больше числа ортогональных сигналов Уолша размерности N, однако их количество является конечным для любой размерности N, что позволяет сделать вывод об их низкой структурной скрытности.
Целью изобретения является. разработка способа и устройства, позволяющего повысить структурную скрытность системы передачи информации с кодовым разделением каналов.
Раскрытие изобретения
Задачей предлагаемого изобретения является повышение уровня структурной скрытности широкополосных систем радиосвязи с кодовым разделением каналов.
Технический результат
Технический результат, который может быть достигнут с помощью предлагаемого изобретения, заключается в том, что для передачи сообщений, сменяемых от одного информационного символа к другому, предлагается использовать сформированные стохастическим образом ортогональные системы сигналов, описываемые собственными векторами диагональных положительно определенных симметрических матриц размерностью N. При этом используется свойство ортогональности собственных векторов, заключающееся в том, что собственные векторы, соответствующие различным собственным значениям нормального оператора, попарно ортогональны (см. Г.Корн, Т.Корн. Справочник по математике (для научных работников и инженеров). - М.: Издательство «Наука», 1974. - С.436).
Известно, что всякий ненулевой вектор х называется собственным вектором матрицы λ, если найдется такое число λ, что будет выполняться равенство:

Это число λ называется собственным значением матрицы А, соответствующим собственному вектору х.
Если в пространстве выбран определенный базис, то уравнение (1) для собственных векторов и собственных значений линейного преобразования можно записать в матричной форме:
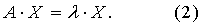
Всякий ненулевой столбец Х, для которого выполняется равенство (2), называется собственным вектором матрицы А, соответствующим собственному значению λ.
Собственный вектор матрицы А - это столбец вида (3), составленный из координат собственного вектора 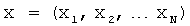 линейного преобразования
линейного преобразования 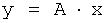 в выбранном базисе.
в выбранном базисе.
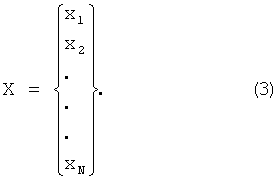
Собственные векторы вещественной диагональной симметрической матрицы, отвечающие различным собственным значениям, ортогональны, т.е. их скалярное произведение равно нулю (см. Клиот-Дашинский М.И.Алгебра матриц и векторов. 3-е изд., стер., / - СПб.: Издательство «Лань», 2001. - 160 с. - (Учебники для вузов. Специальная литература)).
Из всего выше сказанного следует, что для любой вещественной диагональной симметрической матрицы А соотношение (4) существует набор собственных значений 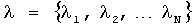 и каждому собственному значению соответствует собственный вектор X, который попарно ортогонален с любым из векторв ансамбля.
и каждому собственному значению соответствует собственный вектор X, который попарно ортогонален с любым из векторв ансамбля.
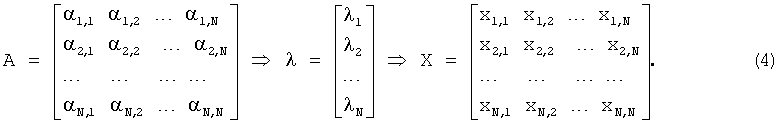
При этом расширение информационной последовательности происходит таким образом, что если информационный бит равен единице, то используется ортогональный сигнал инверсной структуры, а если информационный бит равен нулю, то используется ортогональный сигнал прямой структуры (см. Столингс В. Беспроводные линии связи и сети.: Пер. с англ. - М.: Издательский дом «Вильямс», 2003. - С.213).
Нелинейность формируемых структур сигналов достигается за счет того, что на каждом такте передачи информации расширяющая последовательность в виде одного из сигналов ортогональной системы сигналов, описываемых собственными векторами диагональных положительно определенных симметрических матриц, формируется путем стохастического задания набора диагональных коэффициентов, положительно определенной симметрической матрицы А (вида 4), генератором случайных положительных чисел.
Для достижения названного технического результата в передающую аппаратуру базовой станции наиболее близкого технического решения (см. патент Российской Федерации №2234191, кл. Н04В 7/216, H04L 9/26 от 24.07.2001), состоящую из N, равное 2m-1 каналов, каждый из которых содержит блок цифровой информации, подключенный к первому входу модулятора каждого из каналов, а вторые m входов подключены к выходу генератора де Брейна, причем выходы каждого канала подключены к объединителю блока формирования группового сигнала, выход которого подключен к первому входу модулятора, второй вход которого соединен с выходом генератора псевдослучайного сигнала синхронизации, а выход является выходом блока формирования группового сигнала, который через блок фазовой модуляции и усилитель мощности подключен к передающей антенне, причем первый вход генератора псевдослучайного сигнала синхронизации блока формирования группового сигнала одновременно соединен с первым выходом блока служебной информации, с первым входом генератора де Брейна и первым входом блока перестройки структуры сигнала, а второй вход генератора псевдослучайного сигнала синхронизации одновременно соединен с выходом генератора тактовых импульсов и четвертым входом блока перестройки структуры сигнала, при этом второй выход блока служебной информации одновременно подключен ко второму входу генератора де Брейна и второму входу блока перестройки структуры сигнала, а третий выход блока служебной информации параллельно подключен к входу блока цифровой информации и третьему входу блока перестройки структуры сигнала, первый выход которого подключен к третьему входу генератора де Брейна, второй к четвертому входу генератора де Брейна, третий к пятому входу генератора де Брейна, а четвертые d(m-1) входов подключены к шестым соответствующим входам генератора де Брейна, дополнительно введены блок формирования хаотических ансамблей ортогональных сигналов, содержащий матрицу вычислителей, блоки деления, блоки элемента «И» и блок синхронизации, причем с 1-го по N-й выходы блока генерации сигналов управления итерационным процессом, происходящим в блоке формирования хаотических ансамблей ортогональных сигналов, соединены со вторыми входами с 1-го по N-й вычислитель первой строки матрицы, второй вход вычислителя i-й (i=1, N-1, где N - порядок квадратной симметрической матрицы коэффициентов) строки матрицы соединен с вторым информационным входом соответствующего вычислителя 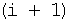 -й строки матрицы, выход вычислителя i-го столбца матрицы соединен с информационным входом соответствующего вычислителя
-й строки матрицы, выход вычислителя i-го столбца матрицы соединен с информационным входом соответствующего вычислителя 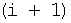 -го столбца матрицы, третьи информационные входы вычислителей первого столбца матрицы соединены с входом логического нуля блока формирования хаотических ансамблей ортогональных сигналов, регистр сдвига, первый и второй блоки памяти, матрицу операционных блоков, кольцевой регистр сдвига, причем выход вычислителя
-го столбца матрицы, третьи информационные входы вычислителей первого столбца матрицы соединены с входом логического нуля блока формирования хаотических ансамблей ортогональных сигналов, регистр сдвига, первый и второй блоки памяти, матрицу операционных блоков, кольцевой регистр сдвига, причем выход вычислителя 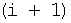 -й строки
-й строки 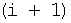 -го столбца матрицы соединен с первыми входами делителя блоков деления, вход делимого j-го блока деления
-го столбца матрицы соединен с первыми входами делителя блоков деления, вход делимого j-го блока деления 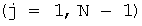 соединен с вторым входом вычислителя j-й строки (N-i+1)-го столбца матрицы, выход j-го блока деления соединен с первым входом j-го блока элементов «И», вторые входы блоков элементов «И» соединены с выходом i-го разряда регистра сдвига, выходы блока синхронизации соединены соответственно с тактовыми входами операционных блоков матрицы, с тактовым входом элемента задержки, с входом разрешения сдвига регистра сдвига, с входами разрешения записи первого блока памяти, с входами разрешения записи второго блока памяти, с тактовыми входами первого и второго блоков памяти, с входами разрешения считывания первого и второго блоков памяти и входом разрешения сдвига кольцевого регистра сдвига, вторые выходы вычислителей последней строки матрицы соединены с 1-го по N-й информационный вход второго блока памяти, первый информационный вход операционного блока i-й строки первого столбца матрицы соединен с i-м выходом второго блока памяти, первые выходы операционных блоков i-й строки S-x(S=i, N-1) столбцов матрицы соединены с (N-i+1)-м информационным входом второго блока памяти, первый информационный вход операционного блока k-й (k=1, N-2) строки М-го (М=2, N-1) столбца матрицы соединен с первым выходом операционного блока (k+1)-й строки (M-1)-го столбца матрицы, первый информационный вход операционного блока (Р-2)-й строки М-го столбца матрицы подключен к выходу элемента задержки, информационный вход которого подключен к второму выходу операционного блока
соединен с вторым входом вычислителя j-й строки (N-i+1)-го столбца матрицы, выход j-го блока деления соединен с первым входом j-го блока элементов «И», вторые входы блоков элементов «И» соединены с выходом i-го разряда регистра сдвига, выходы блока синхронизации соединены соответственно с тактовыми входами операционных блоков матрицы, с тактовым входом элемента задержки, с входом разрешения сдвига регистра сдвига, с входами разрешения записи первого блока памяти, с входами разрешения записи второго блока памяти, с тактовыми входами первого и второго блоков памяти, с входами разрешения считывания первого и второго блоков памяти и входом разрешения сдвига кольцевого регистра сдвига, вторые выходы вычислителей последней строки матрицы соединены с 1-го по N-й информационный вход второго блока памяти, первый информационный вход операционного блока i-й строки первого столбца матрицы соединен с i-м выходом второго блока памяти, первые выходы операционных блоков i-й строки S-x(S=i, N-1) столбцов матрицы соединены с (N-i+1)-м информационным входом второго блока памяти, первый информационный вход операционного блока k-й (k=1, N-2) строки М-го (М=2, N-1) столбца матрицы соединен с первым выходом операционного блока (k+1)-й строки (M-1)-го столбца матрицы, первый информационный вход операционного блока (Р-2)-й строки М-го столбца матрицы подключен к выходу элемента задержки, информационный вход которого подключен к второму выходу операционного блока  -й строки
-й строки  -го столбца матрицы, второй информационный вход операционного блока М-й строки i-го столбца матрицы подключен к второму выходу операционного блока (М-1)-й строки i-го столбца матрицы, входы значения компонент исходной матрицы блока формирования хаотических ансамблей ортогональных сигналов соединены с информационными входами первого блока памяти, выходы которого соединены с третьими информационными входами вычислителей соответствующих строк матрицы, k-й выход второго блока памяти соединен с k-м дополнительным информационным входом первого блока памяти, выходы разрядов кольцевого регистра сдвига соединены с соответствующими входами разрешения считывания второго блока памяти, выходы которого являются выходами блока формирования ансамблей хаотических ортогональных сигналов, генератор случайных положительных чисел (ГСПЧ), вход которого соединен с выходом блока синхронизации, а информационные с 1-го по N-й выходы ГСПЧ являются информационными с 1-го по N-й входами второго запоминающего устройства, элемент «И», а также запоминающие устройства каждого из каналов, на первый вход которых подается информационная последовательность, а на второй управляющий сигнал с элемента «И». Причем в каждом канале передающей аппаратуры исключен блок перестройки структуры сигнала, генератор де Брейна, блок служебной информации и соответствующие связи этих устройств; приемную аппаратуру абонентской станции, содержащую блок высокочастотной селекции, вход которого соединен с приемной антенной, а выход одновременно подключен к первому входу блока обнаружения сигнала синхронизации и первому входу блока корреляционной обработки, выход которого через блок выделения информации подключен к блоку получения информации, причем первый выход блока обнаружения сигнала синхронизации через блок поиска и первый вход генератора копии сигнала синхронизации подключен ко второму входу блока обнаружения сигнала синхронизации, выход которого подключен ко входу блока выделения служебной информации, первый выход блока выделения служебной информации одновременно подключен к первым входам блока перестройки структуры сигнала и генератору копии сигнала де Брейна, второй выход блока выделения служебной информации параллельно подключен ко вторым входам генератора копии сигнала де Брейна и блока перестройки структуры сигнала, а третий выход к третьему входу блока перестройки структуры сигнала, четвертый вход которого одновременно соединен с выходом генератора тактовых импульсов, со вторым входом генератора копии сигнала синхронизации и вторым входом блока выделения информации, при этом первый, второй и третий выходы блока перестройки структуры сигнала подключены соответственно к третьему, четвертому и пятому входам генератора копии сигнала де Брейна, а четвертые d(m-1) выходы к шестым входам генератора копии сигнала де Брейна, выход которого подключен ко второму входу блока корреляционной обработки, дополнительно введены блок формирования хаотических ансамблей ортогональных сигналов, содержащий матрицу вычислителей, блоки деления, блоки элементов «И» и блок синхронизации, причем с 1-го по N-й выходы блока генерации копий сигналов управления итерационным процессом, происходящим в блоке формирования копий хаотических ансамблей ортогональных сигналов, соединены со вторыми входами с 1-го по N-й вычислитель первой строки матрицы, второй вход вычислителя i-й строки матрицы соединен с вторым информационным входом вычислителя (i+1)-й строки матрицы, выход вычислителя г-го столбца матрицы соединен с вторым информационным входом вычислителя (i+1)-го столбца матрицы, третьи информационные входы вычислителей первого столбца матрицы соединены с входом логического нуля блока формирования копий ансамблей хаотических ортогональных сигналов, регистр сдвига, первый и второй блоки памяти, матрицу операционных блоков, элемент задержки и кольцевой регистр сдвига, причем выход вычислителя (i+1)-й строки (i+1)-го столбца матрицы соединен с первыми входами делителя блоков деления, вход делимого j-го блока деления (j=1, N-1) соединен с вторым входом вычислителя j-й строки (N-i+1)-го столбца матрицы, выход j-го блока деления соединен с первым входом j-го блока элементов «И», вторые входы блоков элементов «И» соединены с выходом i-го разряда регистра сдвига, выходы блока синхронизации соединены соответственно с тактовыми входами операционных блоков матрицы, с тактовым входом элемента задержки, с входом разрешения сдвига регистра сдвига, с входами разрешения записи первого блока памяти, с входами разрешения записи второго блока памяти, с тактовыми входами первого и второго блоков памяти, с входами разрешения считывания первого и второго блоков памяти и входом разрешения сдвига кольцевого регистра сдвига, выходы j-x блоков элементов «И» с первой по (N-1) соединены с первым информационным входом вычислителя (j+1)-й строки j-го столбца матрицы, вторые выходы вычислителей последней строки матрицы соединены с информационными входами второго блока памяти, первый информационный вход операционного блока i-й строки первого столбца матрицы соединен с i-м выходом второго блока памяти, первые выходы операционных блоков i-й строки S-x(S=i, N-1) столбцов матрицы соединены с (N-i+1)-м информационным входом группы второго блока памяти, первый информационный вход операционного блока k-й (k=1, N-2) строки М-го (М=2, N-1) столбца матрицы соединен с первым выходом операционного блока (k+1)-й строки (М-1)-го столбца матрицы, первый информационный вход операционного блока (N-2)-й строки М-го столбца матрицы подключен к выходу элемента задержки, информационный вход которого подключен к второму выходу операционного блока (N-1)-й строки (M-1)-го столбца матрицы, второй информационный вход операционного блока М-й строки i-го столбца матрицы подключен к второму выходу операционного блока (М-1)-й строки i-го столбца матрицы, входы значения компонент исходной матрицы блока формирования копий хаотических ансамблей ортогональных сигналов соединены с информационными с 1-го по N-й входами первого блока памяти, выходы которого соединены с первыми информационными входами с 1-го по N-й вычислитель соответствующей строки матрицы, выходы с 1-го по N-й разрядов кольцевого регистра сдвига соединены с 1-го по N-й входами разрешения считывания второго блока памяти, генератор случайных положительных чисел (ГСПЧ), управляющий вход которого соединен с выходом блока синхронизации, а информационные с 1-го по N-й выходы являются информационными с 1-го по N-й входами запоминающего устройства, элемент «И», а также запоминающее устройство каждого из каналов, на первый вход которого подается управляющий сигнал, а на второй - копии ансамблей ортогональных сигналов. Причем в каждом канале приемной аппаратуры исключен блок перестройки структуры сигнала, блок выделения служебной информации, генератор копии сигнала де Брейна и соответствующие связи этих устройств.
-го столбца матрицы, второй информационный вход операционного блока М-й строки i-го столбца матрицы подключен к второму выходу операционного блока (М-1)-й строки i-го столбца матрицы, входы значения компонент исходной матрицы блока формирования хаотических ансамблей ортогональных сигналов соединены с информационными входами первого блока памяти, выходы которого соединены с третьими информационными входами вычислителей соответствующих строк матрицы, k-й выход второго блока памяти соединен с k-м дополнительным информационным входом первого блока памяти, выходы разрядов кольцевого регистра сдвига соединены с соответствующими входами разрешения считывания второго блока памяти, выходы которого являются выходами блока формирования ансамблей хаотических ортогональных сигналов, генератор случайных положительных чисел (ГСПЧ), вход которого соединен с выходом блока синхронизации, а информационные с 1-го по N-й выходы ГСПЧ являются информационными с 1-го по N-й входами второго запоминающего устройства, элемент «И», а также запоминающие устройства каждого из каналов, на первый вход которых подается информационная последовательность, а на второй управляющий сигнал с элемента «И». Причем в каждом канале передающей аппаратуры исключен блок перестройки структуры сигнала, генератор де Брейна, блок служебной информации и соответствующие связи этих устройств; приемную аппаратуру абонентской станции, содержащую блок высокочастотной селекции, вход которого соединен с приемной антенной, а выход одновременно подключен к первому входу блока обнаружения сигнала синхронизации и первому входу блока корреляционной обработки, выход которого через блок выделения информации подключен к блоку получения информации, причем первый выход блока обнаружения сигнала синхронизации через блок поиска и первый вход генератора копии сигнала синхронизации подключен ко второму входу блока обнаружения сигнала синхронизации, выход которого подключен ко входу блока выделения служебной информации, первый выход блока выделения служебной информации одновременно подключен к первым входам блока перестройки структуры сигнала и генератору копии сигнала де Брейна, второй выход блока выделения служебной информации параллельно подключен ко вторым входам генератора копии сигнала де Брейна и блока перестройки структуры сигнала, а третий выход к третьему входу блока перестройки структуры сигнала, четвертый вход которого одновременно соединен с выходом генератора тактовых импульсов, со вторым входом генератора копии сигнала синхронизации и вторым входом блока выделения информации, при этом первый, второй и третий выходы блока перестройки структуры сигнала подключены соответственно к третьему, четвертому и пятому входам генератора копии сигнала де Брейна, а четвертые d(m-1) выходы к шестым входам генератора копии сигнала де Брейна, выход которого подключен ко второму входу блока корреляционной обработки, дополнительно введены блок формирования хаотических ансамблей ортогональных сигналов, содержащий матрицу вычислителей, блоки деления, блоки элементов «И» и блок синхронизации, причем с 1-го по N-й выходы блока генерации копий сигналов управления итерационным процессом, происходящим в блоке формирования копий хаотических ансамблей ортогональных сигналов, соединены со вторыми входами с 1-го по N-й вычислитель первой строки матрицы, второй вход вычислителя i-й строки матрицы соединен с вторым информационным входом вычислителя (i+1)-й строки матрицы, выход вычислителя г-го столбца матрицы соединен с вторым информационным входом вычислителя (i+1)-го столбца матрицы, третьи информационные входы вычислителей первого столбца матрицы соединены с входом логического нуля блока формирования копий ансамблей хаотических ортогональных сигналов, регистр сдвига, первый и второй блоки памяти, матрицу операционных блоков, элемент задержки и кольцевой регистр сдвига, причем выход вычислителя (i+1)-й строки (i+1)-го столбца матрицы соединен с первыми входами делителя блоков деления, вход делимого j-го блока деления (j=1, N-1) соединен с вторым входом вычислителя j-й строки (N-i+1)-го столбца матрицы, выход j-го блока деления соединен с первым входом j-го блока элементов «И», вторые входы блоков элементов «И» соединены с выходом i-го разряда регистра сдвига, выходы блока синхронизации соединены соответственно с тактовыми входами операционных блоков матрицы, с тактовым входом элемента задержки, с входом разрешения сдвига регистра сдвига, с входами разрешения записи первого блока памяти, с входами разрешения записи второго блока памяти, с тактовыми входами первого и второго блоков памяти, с входами разрешения считывания первого и второго блоков памяти и входом разрешения сдвига кольцевого регистра сдвига, выходы j-x блоков элементов «И» с первой по (N-1) соединены с первым информационным входом вычислителя (j+1)-й строки j-го столбца матрицы, вторые выходы вычислителей последней строки матрицы соединены с информационными входами второго блока памяти, первый информационный вход операционного блока i-й строки первого столбца матрицы соединен с i-м выходом второго блока памяти, первые выходы операционных блоков i-й строки S-x(S=i, N-1) столбцов матрицы соединены с (N-i+1)-м информационным входом группы второго блока памяти, первый информационный вход операционного блока k-й (k=1, N-2) строки М-го (М=2, N-1) столбца матрицы соединен с первым выходом операционного блока (k+1)-й строки (М-1)-го столбца матрицы, первый информационный вход операционного блока (N-2)-й строки М-го столбца матрицы подключен к выходу элемента задержки, информационный вход которого подключен к второму выходу операционного блока (N-1)-й строки (M-1)-го столбца матрицы, второй информационный вход операционного блока М-й строки i-го столбца матрицы подключен к второму выходу операционного блока (М-1)-й строки i-го столбца матрицы, входы значения компонент исходной матрицы блока формирования копий хаотических ансамблей ортогональных сигналов соединены с информационными с 1-го по N-й входами первого блока памяти, выходы которого соединены с первыми информационными входами с 1-го по N-й вычислитель соответствующей строки матрицы, выходы с 1-го по N-й разрядов кольцевого регистра сдвига соединены с 1-го по N-й входами разрешения считывания второго блока памяти, генератор случайных положительных чисел (ГСПЧ), управляющий вход которого соединен с выходом блока синхронизации, а информационные с 1-го по N-й выходы являются информационными с 1-го по N-й входами запоминающего устройства, элемент «И», а также запоминающее устройство каждого из каналов, на первый вход которого подается управляющий сигнал, а на второй - копии ансамблей ортогональных сигналов. Причем в каждом канале приемной аппаратуры исключен блок перестройки структуры сигнала, блок выделения служебной информации, генератор копии сигнала де Брейна и соответствующие связи этих устройств.
Краткое описание чертежей
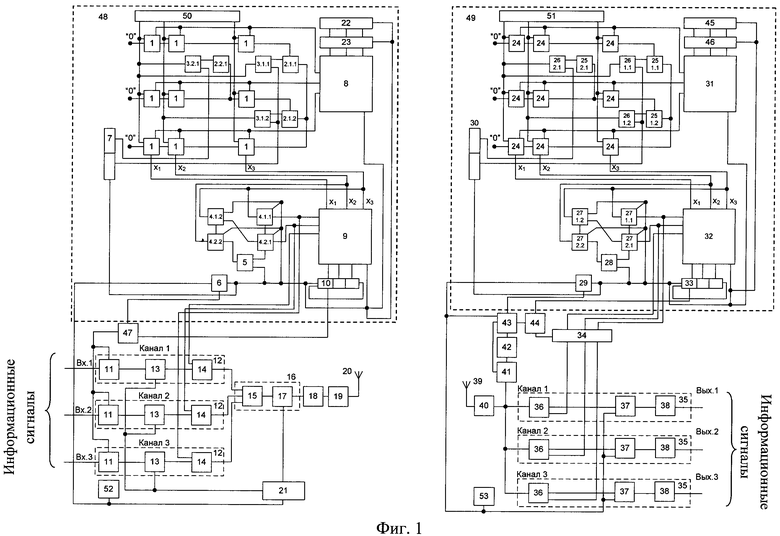
На фиг.1 показана структурная схема приемопередающей аппаратуры устройства передачи информации на основе хаотически формируемых ансамблей дискретных многоуровневых ортогональных сигналов.
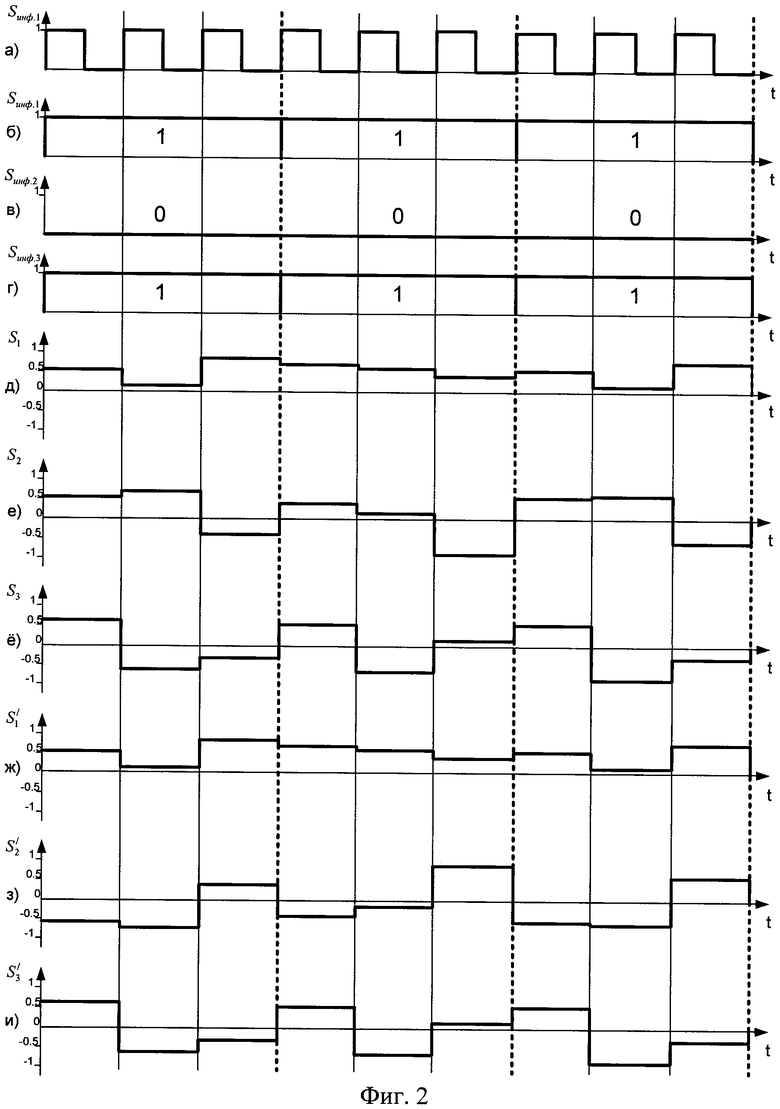
На фиг.2 показаны временные диаграммы принципа функционирования устройства передачи информации на основе хаотически формируемых ансамблей дискретных многоуровневых ортогональных сигналов, где: а) сигналы тактового генератора, б) сигнал, поступающий в первый канал связи Sинф.1(t), в) сигнал, поступающий во второй канал связи Sинф.2(t), г) сигнал, поступающий в третий канал связи Sинф.3(t), д) ортогональный хаотический сигнал, поступающий в первый канал связи S1(t), е) ортогональный хаотический сигнал, поступающий во второй канал связи S2(t), ё) ортогональный хаотический сигнал, поступающий в третий канал связи S3(t), ж) промодулированный информационный сигнал 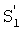 на выходе первого канала, з) промодулированный информационный сигнал
на выходе первого канала, з) промодулированный информационный сигнал 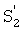 на выходе второго канала, и) промодулированный информационный сигнал
на выходе второго канала, и) промодулированный информационный сигнал 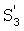 на выходе третьего канала.
на выходе третьего канала.
На фиг.3 представлен сравнительный анализ количества ансамблей ортогональных сигналов, формируемых устройством передачи информации на основе хаотически формируемых ансамблей дискретных многоуровневых ортогональных сигналов и прототипом.
Осуществление изобретения
Предлагаемый способ осуществляется в следующей последовательности: сначала с помощью вспомогательного синхронизирующего сложного сигнала передающая аппаратура базовой станции и приемная аппаратура каждой из 2m-1 абонентских станций вводится в цикловую фазу. Затем, посредством манипуляции вспомогательного сигнала синхронизации на каждый канал передается служебная информация (единый начальный блок для всех абонентских станций). После выполнения указанной процедуры начинается одновременная передача всем абонентам цифровой информации, при этом каждому биту информации фиксированного канала ставится в соответствие сложный сигнал, структура которого зависит от значений коэффициентов диагональной положительно определенной симметрической матрицы, которые формируются генератором случайных положительных чисел, причем расширение информационной последовательности происходит в случае, если информационный бит равен единице за счет использования ортогонального сигнала инверсной структуры, в случае если информационный бит равен нулю за счет использования ортогонального сигнала прямой структуры (см. Столингс В. Беспроводные линии связи и сети.: Пер. с англ. - М.: Издательский дом «Вильямс», 2003. - С.213).
После передачи очередного информационного бита на передающей и приемной стороне производится синхронная смена коэффициентов диагональной положительно определенной симметрической матрицы, поступающих от идентичных ГСПЧ в приемной и передающей стороне, на основе которых происходит расчет сформированных стохастическим образом ортогональных систем сигналов, описываемых собственными векторами диагональных положительно определенных симметрических матриц. При этом сигнал, используемый на приемной стороне для корреляционной обработки, будет иметь структуру, совпадающую с сигналом, излучаемым передатчиком, и, следовательно, может быть использован для обработки информационного потока, адресованного получателю цифровой информации.
Устройство содержит в передающей аппаратуре (фиг.1) N=2m-1 каналов 12, каждый из которых состоит из запоминающего устройства 11, второй вход которого связан с первым выходом блока элемента «И» 47, второй выход которого подключен к управляющему входу блока синхронизации 6, причем вход блока элемента «И» 47 связан с управляющим выходом старшего разряда кольцевого регистра сдвига 10, вход которого связан с блоком синхронизации 6, выход которого подключен к входу регистра сдвига 7, выходы которого, в свою очередь, связаны с вторыми входами блоков элемента «И» 3, а выходы блока памяти 8 являются первыми входами вычислителей 1, причем на второй вход N-го (N - размерность матрицы коэффициентов) вычислителя подается сигнал с N-го выхода блока генерации сигналов управления итерационным процессом 50, а третьи входы вычислителей 1 первого столбца матрицы соединены с входом логического нуля блока формирования хаотических ансамблей ортогональных сигналов, с выходов вычислителей 1 сигналы поступают на первый и второй входы блоков деления 2 и через первые входы блоков элемента «И» 3 поступают на вторые входы первого и второго столбцов матрицы вычислителей 1, вторые выходы вычислителей 1.3.1, 1.3.2, 1.3.3 подключены к информационным с 1-го по N-й вход блока памяти 9, информационные с 1-го по (N-1)-й выходы которого связаны с первыми входами операционных блоков 4 первого столбца, причем выход операционного блока 4 первого столбца и первой строки подключен к N-му входу блока памяти 9, а выходы операционных блоков 4 первого столбца i-й (i=2, N-1) строки подключены к первым входам операционных блоков 4 j-го (j=2, N-1) столбца i-й (i=1, N-1) строки, при этом операционные блоки каждого из столбцов соединены между собой, вторые входы операционных блоков 4 связаны с выходом блока синхронизации 6, причем второй выход операционного блока 4 (N-1)-й строки первого столбца связан со вторым входом элемента задержки 5, первый вход которого связан с выходом блока синхронизации 6, а выход подключен к первому операционному блоку 4 (N-1)-й строки (N-1)-го столбца, при этом информационные выходы операционных блоков 4 j-го (j=N-l) столбца i-й (i=1, N-1) строки подключены к информационным с 2-го по N-й входам блока памяти 9, при этом синхроимпульсы с блока синхронизации 6 одновременно поступают на вход кольцевого регистра сдвига 10, управляющие входы блоков памяти 8 и 9, управляющий вход генератора случайных положительных чисел 22 и запоминающее устройство 23, информационные входы которого с 1-го по N-й подключены к информационным с 1-го по N-й выходам генератора случайных положительных чисел 22, а информационные с 1-го по N-й выходы подключены к информационным входам блока памяти 8, первый управляющий выход кольцевого регистра сдвига 10 подключен к входу блока элемента «И» 47, а вторые с 1-го по N-й выходы связаны с 1-го по N-й управляющий вход блока памяти 9, причем выход запоминающего устройства 11 подключен к первому входу блока цифровой информации 13, второй вход которого связан с вторым выходом генератора сигналов синхронизации 21, выход блока цифровой информации 13 подключен к первому входу модулятора 14 каждого из каналов передачи 12, а второй вход модулятора 14 связан с информационными выходами блока памяти 9, выход каждого N-го модулятора 14 является выходом каждого N-го канала 12, который через объединитель входов 15 блока формирования группового сигнала 16 подключен к первому входу модулятора 17 блока формирования группового сигнала 16, второй вход которого соединен с первым выходом генератора сигналов синхронизации 21, а выход является выходом блока формирования группового сигнала 16, который через блок фазовой модуляции 18 и усилитель мощности 19 подключен к передающей антенне 20, причем вход генератора сигналов синхронизации 21 подключен к выходу генератора тактовых импульсов 52, который параллельно подключен к тактовому входу блока синхронизации 6; приемную аппаратуру (фиг.1), содержащую блок высокочастотной селекции 40, вход которого соединен с приемной антенной 39, а выход подключен к первому входу блока обнаружения сигнала синхронизации 41 и вторым входам блока корреляционной обработки 36 каждого из 2m-1 каналов 35, причем выход блока корреляционной обработки 36 подключен к первому входу блока выделения информации 37, второй вход которого связан с выходом генератора тактовых импульсов 53, причем выход блока обнаружения сигнала синхронизации 41 через блок поиска 42 соединен с входом генератора копий сигналов синхронизации 43, первый выход которого подключен к второму входу блока обнаружения сигнала синхронизации 41, второй - к управляющему входу блока синхронизации 29, выход которого связан с управляющим входом регистра сдвига 30, выходы которого являются вторыми входами соответствующих блоков элементов «И» 26, а третий выход генератора копий сигналов синхронизации 43 соединен с первым управляющим входом блока элемента «И» 44, выход которого подключен к управляющему входу запоминающего устройства 34, информационные с 1-го по N-й входы которого подключены к информационным с 1-го по N-й выходам блока памяти 32, причем выход блока синхронизации 29 подключен к управляющему входу блока памяти 31, информационные с 1-го по N-й выходы которого являются первыми входами вычислителей 24, причем на второй вход каждого N-го (N - размерность матрицы коэффициентов) вычислителя 24 подается сигнал с N-го выхода блока генерации сигналов управления итерационным процессом 51, который полностью идентичен сигналу, вырабатываемому блоком генерации сигналов управления итерационным процессом 50 на передающей стороне, а третьи входы вычислителей 24 первого столбца матрицы соединены с входом логического нуля блока формирования копий хаотических ансамблей ортогональных сигналов, причем с выходов вычислителей 24 сигналы поступают на первый и второй входы блоков деления 25 и через первые входы блоков элемента «И» 26 поступают на вторые входы первого и второго столбцов матрицы вычислителей 24, вторые выходы вычислителей 24.3.1, 24.3.2, 24.3.3 подключены к информационным с 1-го по N-й вход блока памяти 32, информационные с 1-го по (N-1)-й выходы которого связаны с первыми входами операционных блоков 27 первого столбца, причем выход операционного блока 27 первого столбца и первой строки подключен к N-му входу блока памяти 32, а выходы операционных блоков 27 первого столбца j-й (i=2, N-1) строки подключены к первым входам операционных блоков 27 j-го (j=2, N-1) столбца i-й (i=1, N-1) строки, при этом операционные блоки каждого из столбцов соединены между собой, вторые входы операционных блоков 27 связаны с выходом блока синхронизации 29, причем второй выход операционного блока 27 (N-1)-й строки первого столбца связан со вторым входом элемента задержки 28, первый вход которого связан с выходом блока синхронизации 29, а выход подключен к первому операционному блоку 27 (N-1)-й строки (N-1)-го столбца, при этом информационные выходы операционных блоков 27 j-го (j=N-1) столбца i-й (i=1, N-1) строки подключены к информационным с 2-го по N-й входам блока памяти 32, при этом синхроимпульсы с блока синхронизации 29 одновременно поступают на вход кольцевого регистра сдвига 33, на управляющий вход блока памяти 31 и 32, управляющий вход генератора случайных положительных чисел 45 и запоминающее устройство 46, информационные входы которого с 1-го по N-й подключены к информационным с 1-го по N-й выходам генератора случайных положительных чисел 45, а информационные выходы с 1-го по N-й подключены к информационным с 1-го по N-й входам блока памяти 31, при этом управляющий выход кольцевого регистра сдвига 33 подключен к второму входу блока элемента «И» 44, выход которого связан с управляющим входом запоминающего устройства 34, N-й выход которого подключен к второму входу N-го блока корреляционной обработки 36 каждого из каналов 35, вторые управляющие выходы кольцевого регистра 33 с 1-го по N-й связаны с 1-го по N-й управляющий вход блока памяти 32, причем выход каждого из блоков корреляционной обработки 36 подключен к первому входу блока выделения информации 37, второй вход которого подключен к выходу генератора тактовых импульсов 53, который параллельно подключен к тактовому входу блока синхронизации 29 и тактовому входу генератора копий сигналов синхронизации 43, при этом выход блока выделения информации 37 связан с входом блока приема информации 38.
Устройство работает следующим образом. Информационные сигналы поступают в запоминающее устройство 11 каждого из каналов передачи 12 и хранятся в нем до момента получения управляющего сигнала с блока элемента «И» 47, свидетельствующего о завершении этапа формирования стохастическим образом ортогональной системы сигналов, описываемых собственными векторами диагональных положительно определенных симметрических матриц размерностью N в блоке формирования хаотических ансамблей ортогональных сигналов 48. Затем информационный бит каждого из каналов 12 через блок цифровой информации 13 подается в модулятор 14, где он модулируется расширяющей последовательностью, поступающей с блока памяти 9 блока формирования хаотических ансамблей ортогональных сигналов 48. Сигналы, снимаемые с выхода модулятора 14 каждого канала, одновременно подаются в сумматор 15 блока формирования группового сигнала 16, где после их объединения и наложения в модуляторе 17 сигнала синхронизации, поступающего с выхода генератора сигналов синхронизации 21, происходит формирование группового сигнала, спектр которого после переноса в область несущей частоты в блоке фазовой модуляции 18 и усилителе мощности 19 через антенну 20 излучается в эфир. На приемной стороне поступающий сигнал принимается антенной 39 и подвергается предварительной обработке в блоке высокочастотной селекции 40. С выхода этого блока сигнал одновременно подается в блок обнаружения сигнала синхронизации 41 и блоки корреляционной обработки 36 каждого канала 35. При этом блок обнаружения сигнала синхронизации 41 совместно с блоком поиска 42 вводят в синхронизм генератор копии сигналов синхронизации 43. После чего с генератора копий сигналов синхронизации 43 подается управляющий сигнал на блок синхронизации 29 блока формирования копий ансамблей хаотических ортогональных сигналов 49, свидетельствующий о начале формирования копий хаотических ансамблей ортогональных сигналов блоком формирования копий хаотических ансамблей ортогональных сигналов 49. Подача управляющего сигнала на блок элемента «И» 44 с кольцевого регистра сдвига 33 блока формирования копий хаотических ансамблей ортогональных сигналов 49 говорит о завершении этапа формирования ортогональных кодовых последовательностей и записи их в запоминающее устройство 34. После чего под воздействием управляющего сигнала с блока элемента «И» 44 копии хаотических ансамблей ортогональных сигналов подаются с запоминающего устройства 34 на блоки корреляционной обработки 36 каждого из каналов связи 35 и, пройдя через первый вход блока выделения информации 37, на второй вход которого подается копия сигнала синхронизации с генератора копий сигналов синхронизации 43, направляются на вход блока приема информации 38.
При этом на передающей стороне блок формирования хаотических ансамблей ортогональных сигналов 48 функционирует следующим образом: при отсутствии на входе элемента «И» 47 информационного сигнала с кольцевого регистра сдвига 10, активируется работа блока синхронизации 6 блока формирования хаотических ансамблей ортогональных сигналов 48, с выхода которого подается управляющий сигнал на управляющий вход генератора случайных положительных чисел 22 и запоминающее устройство 23, в результате чего происходит генерация и запись случайных коэффициентов матрицы А в блок памяти 8, после этого начинается вычисление 1-го собственного значения и соответствующего ему собственного вектора, которое осуществляется в течение времени нахождения «1» в 1-м разряде регистра сдвига 7, поэтому период поступления тактовых импульсов на тактовый вход регистра сдвига 7 равен времени сходимости итерационного процесса и вычисления оставшейся части компонент собственного вектора.
В течение первого периода работы «1» с выхода первого разряда регистра сдвига 7 поступает на вторые входы блоков элементов «И» 3.1.1 и 3.1.2. На второй вход блока элемента «И» 3.2.1 поступает «0» с выхода второго разряда первого регистра сдвига 7, в результате на выходе блока 3.2.1 формируется «0».
С поступлением последовательности синхроимпульсов с блока синхронизации 6 коэффициенты, находящиеся в первом блоке памяти 8, последовательно поступают на первые входы вычислителей 1 и запоминаются в них. Вычислители так же выполняют функцию накопления каждый раз в случае подачи на их вход нового слагаемого.
На вторые входы вычислителей 1, кроме последнего, подаются произвольные сигналы  с блока генерации сигналов управления итерационным процессом 50.
с блока генерации сигналов управления итерационным процессом 50.
На вторых входах вычислителей 1 последнего столбца присутствует сигнал «1».
Следовательно, для реализации итерационной процедуры отыскания собственного числа λ1 матрицы А в качестве начального приближения выбирается вектор 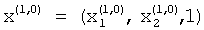 .
.
На выходе последнего вычислителя 1 последней строки матрицы при этом образуется сигнал:

который является первым приближением собственного числа λ1.
На выходе последнего вычислителя 11-й строки (i=1…n-1) образуется сигнал
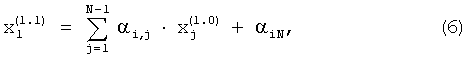
где i=1,2…n-1.
Этот сигнал является i-м компонентом первого ненормированного приближения первого собственного вектора матрицы коэффициентов А:
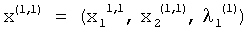 .
.
Нормирование первого приближения первого вектора осуществляется путем деления всех его компонентов на величину последнего компонента 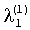 . Так как в результате нормирования последняя компонента равна 1, то ее деление не производится и «1» поступает на вторые входы последнего столбца матрицы вычислителей 1. Нормирование остальных компонент осуществляется при помощи блоков 2.1.1 и 2.1.2 путем деления компонент на величину последней компоненты
. Так как в результате нормирования последняя компонента равна 1, то ее деление не производится и «1» поступает на вторые входы последнего столбца матрицы вычислителей 1. Нормирование остальных компонент осуществляется при помощи блоков 2.1.1 и 2.1.2 путем деления компонент на величину последней компоненты 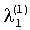 . Сигнал с выхода блока 2.1.1 деления через первый вход блока 3.1.1 поступает на вторые входы вычислителей 1.2.1 и 1.3.1, т.е. вычислителей 1 первого столбца матрицы. Сигнал с выхода блока деления 2.1.2 через первый вход блока 3.1.2 поступает на второй вход вычислителя 1.3.2, т.е. вычислителя 1 второго столбца матрицы.
. Сигнал с выхода блока 2.1.1 деления через первый вход блока 3.1.1 поступает на вторые входы вычислителей 1.2.1 и 1.3.1, т.е. вычислителей 1 первого столбца матрицы. Сигнал с выхода блока деления 2.1.2 через первый вход блока 3.1.2 поступает на второй вход вычислителя 1.3.2, т.е. вычислителя 1 второго столбца матрицы.
Таким образом, в соответствии с соотношением:
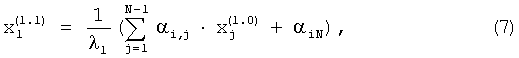
где i=1,2...,N-1 после окончания первой итерации на вторых выходах вычислителей 1.3.1, 1.3.2, 1.3.3 присутствуют сигналы, соответствующие компонентам первого нормированного приближения первого собственного вектора:
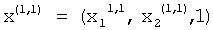 .
.
Затем итерационный процесс повторяется и после окончания второй итерации на вторых выходах вычислителей 1.3.1, 1.3.2, 1.3.3 присутствуют сигналы, соответствующие компонентам второго нормированного приближения первого собственного вектора:
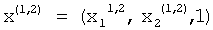
Повторение итераций будет осуществляться до полной сходимости итерационного процесса. В результате на 'вторых выходах вычислителей 1.3.1, 1.3.2, 1.3.3 присутствуют сигналы, соответствующие компонентам нормированного первого собственного вектора:
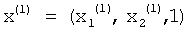 ,
,
а на выходе вычислителя 1.3.3 присутствует сигнал, соответствующий собственному значению 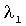 .
.
Таким образом, для матрицы А система уравнений, решаемая методом итерации, в соответствии с соотношениями (5) и (7) следующая:

После реализации сходимости итерационного процесса на вторых выходах вычислителей 1.3.1, 1.3.2, 1.3.3 будут получены значения компонент первого собственного вектора, а на выходе вычислителя 1.3.3 будет получено первое собственное значение.
По окончании времени, необходимого для реализации сходимости итерационного процесса, по средствам тактовых импульсов, подаваемых с блока синхронизации 6 во второй блок памяти 9, записываются компоненты первого собственного вектора. В следующий момент времени на тактовый вход регистра сдвига 7 поступает тактовый импульс, под воздействием которого «1» из первого разряда регистра сдвига 7 сдвигается во второй разряд.
Таким образом, «1» с выхода второго разряда регистра сдвига 7 поступает на второй вход второго сомножителя блока умножения 3.2.1. На вторые входы вторых сомножителей блоков умножения 3.1.1 и 3.1.2 поступает «0» с выхода первого разряда регистра сдвига 7, в результате на выходах блоков 3.1.1 и 3.1.2 формируется «0».
Для определения второго собственного значения и компонент 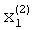 ,
, 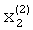 второго собственного вектора необходимо методом итерации решить систему уравнений
второго собственного вектора необходимо методом итерации решить систему уравнений
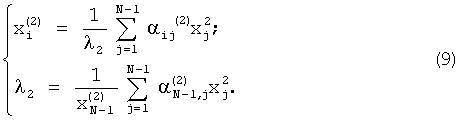
Для матрицы А вторая система уравнений, решаемая методом итерации, определяется из условия ортогональности векторов 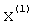 и
и 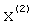 . Полученную систему уравнений необходимо решить методом итерации, но для этого нужно предварительно сформировать коэффициенты
. Полученную систему уравнений необходимо решить методом итерации, но для этого нужно предварительно сформировать коэффициенты 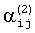 . Для этого используются коэффициенты
. Для этого используются коэффициенты 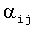 , записанные в блоке памяти 8.
, записанные в блоке памяти 8.
После подачи на входы вторых вычислителей 1.1.1 и 1.2.1 произвольного сигнала 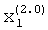 , а на входы вторых вычислителей 1.1.2 и 1.2.2 сигнала «1» начнется реализация итерационного процесса. После достижения сходимости итерационного процесса на выходе делителя 2.2.1, а соответственно на выходе вычислителя 1.2.1 будет получено значение
, а на входы вторых вычислителей 1.1.2 и 1.2.2 сигнала «1» начнется реализация итерационного процесса. После достижения сходимости итерационного процесса на выходе делителя 2.2.1, а соответственно на выходе вычислителя 1.2.1 будет получено значение 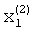 , на выходе вычислителя 1.2.2 будет присутствовать сигнал
, на выходе вычислителя 1.2.2 будет присутствовать сигнал 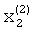 , а также значение
, а также значение 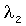 .
.
По окончании времени, необходимого для реализации сходимости итерационного процесса за счет поступления синхроимпульсов, компоненты 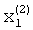 и
и 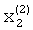 второго собственного вектора окажутся записанными в элементах памяти блока памяти 9.
второго собственного вектора окажутся записанными в элементах памяти блока памяти 9.
Компонента 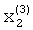 определяется за счет решения уравнения с одним неизвестным с использованием известного устройства для операций над матрицами, способного решать уравнения или системы из n уравнений с n неизвестными по методу Гаусса-Жордана. В его состав входят операционные блоки 4.1.1,4.1.2,4.1.3,4.1.4, элемент задержки 5. В нем выполняется обработка матрицы размерности N×M (N=1,2), которая представляет собой матрицу коэффициентов при неизвестных системы линейных уравнений, к которой справа дописана матрица размерности N×1 свободных членов.
определяется за счет решения уравнения с одним неизвестным с использованием известного устройства для операций над матрицами, способного решать уравнения или системы из n уравнений с n неизвестными по методу Гаусса-Жордана. В его состав входят операционные блоки 4.1.1,4.1.2,4.1.3,4.1.4, элемент задержки 5. В нем выполняется обработка матрицы размерности N×M (N=1,2), которая представляет собой матрицу коэффициентов при неизвестных системы линейных уравнений, к которой справа дописана матрица размерности N×1 свободных членов.
Таким образом, например, для решения системы из двух линейных уравнений на входы устройства будет поступать матрица В вида:
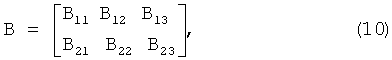
где B11 В12 В21 В22 - коэффициенты при неизвестных, а В13 В23 - свободные члены.
Элементы матрицы В поступают на первые входы операционных блоков 4 построчно со сдвигом на один такт под воздействием синхроимпульсов с выходов блока 6 синхронизации, подаваемых на вторые входы операционных блоков 4, т.е. первая строка поступает на первый вход операционного блока 4.1.1, начиная с первого такта, вторая строка поступает на первый вход операционного блока 4.2.1, начиная с второго такта, и т.д. На выходах операционных блоков 4.i.j(i=1…n, j=n) получается семейство решений системы линейных уравнений.
Таким образом, решения системы из двух уравнений получаются на выходах операционных блоков 4.1.2 и 4.2.2. Решение уравнения с одним неизвестным - на выходе операционного блока 4.1.1.
Следовательно, при вычислении значения 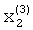 будет задействован только операционный блок 4.1.1. Коэффициент при неизвестном и свободный член будут вычислены блоком памяти 9.
будет задействован только операционный блок 4.1.1. Коэффициент при неизвестном и свободный член будут вычислены блоком памяти 9.
Значение 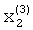 с выхода операционного блока 4.1.1 поступает на информационный вход блока памяти 9 и с поступлением синхроимпульса оказывается записанным в элементе блока памяти 9.
с выхода операционного блока 4.1.1 поступает на информационный вход блока памяти 9 и с поступлением синхроимпульса оказывается записанным в элементе блока памяти 9.
Таким образом, в блок памяти 9 будут записаны компоненты второго собственного вектора матрицы А.
По окончании времени, необходимого для вычисления компонент второго собственного вектора, на тактовый вход регистра сдвига 7 поступает тактовый импульс, в результате чего второй разряд регистра сдвига 7 обнуляется. Так как на второй вход второго сомножителя блока 3.2.1 поступает «0» с выхода второго разряда регистра 7, то на выходе блока 3.2.1 формируется «0».
Вычисление компонент третьего собственного вектора производится следующим образом. На вторые входы вычислителей 1.1.1, 1.2.1, 1.3.1 подается сигнал «1». С выхода блока 1.3.1 значение  поступает на информационный вход блока памяти 9.
поступает на информационный вход блока памяти 9.
После этого осуществляется вычисление компонент 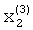 и
и 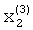 .
.
Так как значение 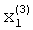 вычислено и записано в элементе памяти, то полученная система линейных уравнений легко решается методом Гаусса-Жордана.
вычислено и записано в элементе памяти, то полученная система линейных уравнений легко решается методом Гаусса-Жордана.
В соответствии с алгоритмом работы операционных блоков 4 на выходах блоков 4.1.2 и 4.2.2 будут сформированы соответственно значения 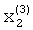 и
и 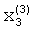 поступающие на входы блока памяти 9.
поступающие на входы блока памяти 9.
Таким образом, в элементах блока памяти 9 будут записаны компоненты третьего собственного вектора матрицы А. На этом процесс вычисления компонент собственных векторов матрицы А заканчивается. Значения компонент собственных векторов хранятся в блоке памяти 9.
Синхроимпульсы с блока синхронизации 6 одновременно поступают на тактовый вход кольцевого регистра сдвига 10, управляющий вход генератора случайных положительных чисел 22, где происходит случайное формирование коэффициентов матрицы А и подача их на информационные входы запоминающего устройства 23, которое под воздействием управляющего сигнала, подаваемого на его второй вход, записывает сформированные коэффициенты в блок памяти 8.
В кольцевом регистре сдвига 10 перед началом работы записывается код вида «10…0», причем «1» в первом разряде кольцевого регистра сдвига 10. Поскольку на тактовый вход кольцевого регистра сдвига 10 поступает периодическая последовательность импульсов, то «1», перемещаясь из разряда в разряд кольцевого регистра сдвига 10, управляет формированием дискретных базисных функций на выходах блока памяти 9. При этом считывание производится по столбцам.
Вместе с подачей синхроимпульса на кольцевой регистр сдвига 10 на элемент «И» 47 подается информационный сигнал «1», в результате чего на выходе элемента 47 формируется управляющий сигнал.
Аналогичным образом функционирует блок формирования копий хаотических ансамблей ортогональных сигналов 49 на приемной стороне, который запускается генератором копии сигналов синхронизации 43.
Пример конкретного осуществления способа передачи информации в системах с кодовым разделением каналов
В качестве примера рассмотрим тот случай, когда для передачи последовательности информационных бит используются 3 канала связи, в которых бит информации модулируется хаотической расширяющей последовательностью (N=3 выбрана для упрощения расчетов). Допустим, что на входы запоминающих устройств 11 каждого из каналов передачи 12 подается информационная последовательность «1 0 1» и в блок памяти 8 заранее введена случайная последовательность коэффициентов матрицы А размерностью 3×3, вырабатываемая генератором случайных чисел 22:
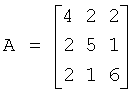 .
.
В регистре 7 сдвига записан код вида «100», причем "1" записана в первом разряде регистра 7 сдвига.
Последовательности информационных бит, представленные на фиг.2 б, в, г, побитно поступают на первые входы запоминающих устройств 11 соответствующих каналов передачи 12. Далее биты записываются в запоминающие устройства 11 каждого из каналов 12 передачи и ожидают управляющего сигнала с блока элемента «И» 47 для дальнейшей передачи их в блок цифровой информации 13 и модуляции расширяющей последовательностью в модуляторе 14. Отсутствие сигнала с блока элемента «И» 47 свидетельствует о начале формирования стохастическим образом ортогональных систем сигналов, описываемых собственными векторами диагональных положительно определенных симметрических матриц, в результате чего начинает функционировать блок синхронизации 6, с выхода которого подается управляющий сигнал на управляющий вход генератора случайных положительных чисел 22 и запоминающее устройство 23, в результате чего происходит генерация и запись случайных коэффициентов матрицы А в блок памяти 8, после этого начинается вычисление 1-го собственного значения и соответствующего ему собственного вектора (первой расширяющей последовательности), которое осуществляться в течение времени нахождения «1» в 1-м разряде регистра 7 сдвига, поэтому период поступления тактовых импульсов на тактовый вход регистра 7 сдвига равен времени сходимости итерационного процесса и вычисления оставшейся части компонент собственного вектора.
В течение первого периода работы «1» с выхода первого разряда регистра 7 сдвига поступает на вторые входы блоков элементов «И» 3.1.1 и 3.1.2. На второй вход блока элемента «И» 3.2.1 поступает «0» с выхода второго разряда первого регистра 7 сдвига, в результате на выходе блока 3.2.1 формируется «0».
С поступлением последовательности синхроимпульсов коэффициенты, находящиеся в первом блоке памяти 8, последовательно поступают на первые входы вычислителей 1 и запоминаются в них. Причем вычислитель осуществляет так же функцию накопления каждый раз при подаче на его вход нового слагаемого.
На вторые входы вычислителей 1, кроме последнего, подаются произвольные сигналы 
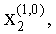
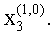 На вторых входах вычислителей 1 последнего столбца присутствует сигнал «1».
На вторых входах вычислителей 1 последнего столбца присутствует сигнал «1».
Следовательно, для реализации итерационной процедуры отыскания собственного числа λ1 матрицы А в качестве начального приближения выбирается вектор 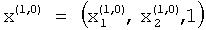 .
.
На втором выходе последнего вычислителя 1 последней строки матрицы при этом образуется сигнал в соответствии с соотношением (5), который является первым приближением собственного числа λ1.
На выходе последнего вычислителя 1 1-й строки (i=1…n-1) образуется сигнал, формируемый на основе соотношения (6). Этот сигнал является i-м компонентом первого ненормированного приближения первого собственного вектора матрицы коэффициентов А 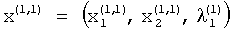 .
.
Нормирование первого приближения первого вектора осуществляется путем деления всех его компонентов на величину последнего компонента 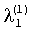 . Так как в результате нормирования последняя компонента равна «1», то ее деление не производится и «1» поступает на вторые входы последнего столбца матрицы вычислителей 1. Нормирование остальных компонент осуществляется при помощи блоков 2.1.1 и 2.1.2 путем деления компонент на величину последней компоненты
. Так как в результате нормирования последняя компонента равна «1», то ее деление не производится и «1» поступает на вторые входы последнего столбца матрицы вычислителей 1. Нормирование остальных компонент осуществляется при помощи блоков 2.1.1 и 2.1.2 путем деления компонент на величину последней компоненты 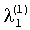 . Сигнал с выхода блока 2.1.1 деления через блок 3.1.1 поступает на вторые входы вычислителей 1.2.1 и 1.3.1, т.е. вычислителей 1 первого столбца матрицы. Сигнал с выхода блока 2.1.2 деления через блок 3.1.2 поступает на второй вычислителя 1.3.2, т.е. вычислителя 1 второго столбца матрицы.
. Сигнал с выхода блока 2.1.1 деления через блок 3.1.1 поступает на вторые входы вычислителей 1.2.1 и 1.3.1, т.е. вычислителей 1 первого столбца матрицы. Сигнал с выхода блока 2.1.2 деления через блок 3.1.2 поступает на второй вычислителя 1.3.2, т.е. вычислителя 1 второго столбца матрицы.
Таким образом, в соответствии с соотношением (7) после окончания первой итерации на выходах вычислителей 1.3.1, 1.3.2, 1.3.3 присутствуют сигналы, соответствующие компонентам первого нормированного приближения первого собственного вектора 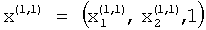 .
.
Затем итерационный процесс повторяется и после окончания второй итерации на вторых выходах вычислителей 1.3.1,1.3.2,1.3.3 присутствуют сигналы, соответствующие компонентам второго нормированного приближения первого собственного вектора 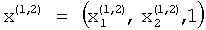 .
.
Повторение итераций будет осуществляться до полной сходимости итерационного процесса. В результате на вторых выходах вычислителей 1.3.1, 1.3.2, 1.3.3 присутствуют сигналы, соответствующие компонентам нормированного первого собственного вектора 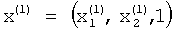 , а на втором выходе вычислителя 1.3.3 присутствует сигнал, соответствующий собственному значению λ1.
, а на втором выходе вычислителя 1.3.3 присутствует сигнал, соответствующий собственному значению λ1.
Таким образом, для матрицы А система уравнений, решаемая методом итерации, представлена в соотношении (8).
После реализации сходимости итерационного процесса на вторых выходах вычислителей 1.3.1, 1.3.2, 1.3.3 будут получены значения компонент первого собственного вектора 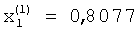 ,
,  ,
, 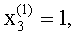 а на втором выходе вычислителя 1.3.3 будет получено первое собственное значение λ1=0,8077.
а на втором выходе вычислителя 1.3.3 будет получено первое собственное значение λ1=0,8077.
По окончании времени, необходимого для реализации сходимости итерационного процесса, по средствам тактового импульса во второй блок памяти 9 записываются компоненты первого собственного вектора, который представлен на фиг.2, д. В следующий момент времени на тактовый вход регистра 7 сдвига поступает тактовый импульс, под воздействием которого «1» из первого разряда регистра 7 сдвига сдвигается во второй разряд.
Таким образом, «1» с выхода второго разряда регистра 7 сдвига поступает на вход второго сомножителя блока 3.2.1 умножения. На входы вторых сомножителей блоков 3.1.1 и 3.1.2 умножения поступает «0» с выхода первого разряда регистра 7 сдвига, в результате на выходах блоков 3.1.1 и 3.1.2 формируется «0».
Для определения второго собственного значения и компонент 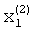 ,
, 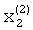 второго собственного вектора необходимо методом итерации решить систему уравнений в соотношении (9).
второго собственного вектора необходимо методом итерации решить систему уравнений в соотношении (9).
Для матрицы А вторая система уравнений, решаемая методом итерации, определяется из условия ортогональности векторов 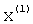 и
и 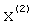 . Так как
. Так как
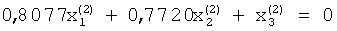 ,
,
То
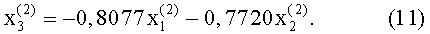
Подставляя это выражение в систему вида
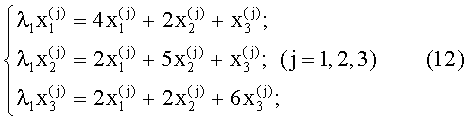
и полагая 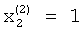 , получим
, получим

Систему (13) необходимо решить методом итерации, но для этого нужно предварительно сформировать коэффициенты 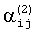 с использованием соотношения (9). Для этого используются коэффициенты
с использованием соотношения (9). Для этого используются коэффициенты 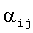 , записанные в блоке 8 памяти.
, записанные в блоке 8 памяти.
После подачи на входы вторых вычислителей 1.1.1 и 1.2.1 произвольного сигнала 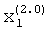 , а на входы вторых вычислителей 1.1.2 и 1.2.2 сигнала «1» начнется реализация итерационного процесса. После достижения сходимости итерационного процесса на выходе делителя 2.2.1, а соответственно на выходе вычислителя 1.2.1 будет получено значение
, а на входы вторых вычислителей 1.1.2 и 1.2.2 сигнала «1» начнется реализация итерационного процесса. После достижения сходимости итерационного процесса на выходе делителя 2.2.1, а соответственно на выходе вычислителя 1.2.1 будет получено значение 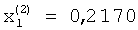 , на выходе вычислителя 1.2.2 будет присутствовать сигнал
, на выходе вычислителя 1.2.2 будет присутствовать сигнал 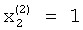 , а также второе собственное значение
, а также второе собственное значение 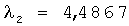 .
.
По окончании времени, необходимого для реализации сходимости итерационного процесса за счет поступления синхроимпульсов, компоненты 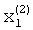 и
и  второго собственного вектора окажутся записанными в элементах памяти блока памяти 9.
второго собственного вектора окажутся записанными в элементах памяти блока памяти 9.
Компонента  определяется из соотношения (12), т.е. уравнения с одним неизвестным с использованием известного устройства для операций над матрицами, способного решать уравнения с одним неизвестным или системы из n уравнений с n неизвестными по методу Гаусса-Жордана. В его состав входят операционные блоки 4.1.1, 4.1.2, 4.1.3, 4.1.4, элемент 5 задержки, блок 6 синхронизации. В нем выполняется обработка матрицы размерности N×M (N=1,2), которая представляет собой матрицу коэффициентов при неизвестных системы линейных уравнений, к которой справа дописана матрица размерности N×1 свободных членов.
определяется из соотношения (12), т.е. уравнения с одним неизвестным с использованием известного устройства для операций над матрицами, способного решать уравнения с одним неизвестным или системы из n уравнений с n неизвестными по методу Гаусса-Жордана. В его состав входят операционные блоки 4.1.1, 4.1.2, 4.1.3, 4.1.4, элемент 5 задержки, блок 6 синхронизации. В нем выполняется обработка матрицы размерности N×M (N=1,2), которая представляет собой матрицу коэффициентов при неизвестных системы линейных уравнений, к которой справа дописана матрица размерности N×1 свободных членов.
Таким образом, например, для решения системы из двух линейных уравнений на входы устройства будет поступать матрица В, соотношение (10).
Элементы матрицы В поступают на входы операционных блоков 4 построчно со сдвигом на один такт под воздействием синхроимпульсов с выходов блока 6 синхронизации, т.е. первая строка поступает на первый вход операционного блока 4.1.1, начиная с первого такта, вторая строка поступает на первый вход операционного блока 4.2.1, начиная с второго такта, и т.д. На выходах операционных блоков 4.i.j (i=1…n, j=n) получается семейство решений системы линейных уравнений.
Таким образом, решения системы из двух уравнений получаются на выходах операционных блоков 4.1.2 и 4.2.2. Решение уравнения с одним неизвестным - на выходе операционного блока 4.1.1.
Следовательно, при вычислении значения 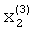 будет задействован только операционный блок 4.1.1. Коэффициент при неизвестном и свободный член будут вычислены блоком 9 памяти.
будет задействован только операционный блок 4.1.1. Коэффициент при неизвестном и свободный член будут вычислены блоком 9 памяти.
Значение 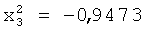 с выхода операционного блока 4.1.1 поступает на информационный вход блока 9 памяти и с поступлением синхроимпульса оказывается записанным в блоке памяти 9.
с выхода операционного блока 4.1.1 поступает на информационный вход блока 9 памяти и с поступлением синхроимпульса оказывается записанным в блоке памяти 9.
Таким образом, в блок памяти 9 будут записаны компоненты второго собственного вектора матрицы А: 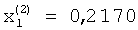 ;
; 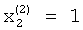 ;
; 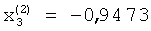 , который представлен на фиг.2, е.
, который представлен на фиг.2, е.
По окончании времени, необходимого для вычисления компонент второго собственного вектора на тактовый вход регистра 7 сдвига поступает тактовый импульс, в результате чего второй разряд регистра 7 сдвига обнуляется. Так как на вход второго сомножителя блока 3.2.1 поступает «0» с выхода второго разряда регистра 7, то на выходе блока 3.2.1 формируется «0».
Вычисление компонент третьего собственного вектора производится следующим образом. На вторые входы вычислителей 1.1.1, 1.2.1, 1.3.1 подается сигнал «1». С выхода блока 1.3.1 значение 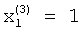 поступает на информационный вход блока 9 памяти. С поступлением синхроимпульса на вход блока 9 памяти значение
поступает на информационный вход блока 9 памяти. С поступлением синхроимпульса на вход блока 9 памяти значение 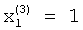 записывается в элемент памяти.
записывается в элемент памяти.
После этого осуществляется вычисление компонент 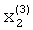 и
и  с использованием соотношений ортогональности:
с использованием соотношений ортогональности:
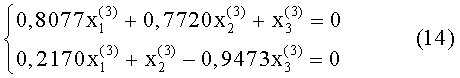
Так как значение 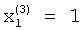 вычислено и записано в элементе памяти, то систему уравнений (14) можно представить в виде:
вычислено и записано в элементе памяти, то систему уравнений (14) можно представить в виде:
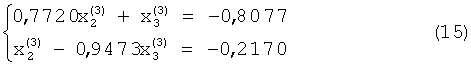
Эта система линейных уравнений легко решается методом Гаусса-Жордана. Поскольку коэффициенты 'при неизвестных и свободные члены записаны в блоке 9 памяти, то уравнение (15) решается следующим образом.
При поступлении синхроимпульса значение 0,7720 считывается и поступает на вход операционного блока 4.1.1.
При поступлении синхроимпульса значение «1» считывается и поступает на вход операционного блока 4.2.1.
Аналогичным образом считываются все оставшиеся значения.
В соответствии с алгоритмом работы операционных блоков 4 на выходах блоков 4.1.2 и 4.2.2 будут сформированы соответственно значения 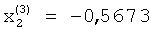 ;
; 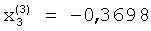 , поступающие на входы блока 9 памяти.
, поступающие на входы блока 9 памяти.
Таким образом, в элементах блока памяти 9 будут записаны компоненты третьего собственного вектора матрицы А: 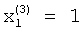 ;
; 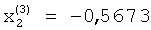 ;
; 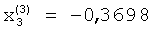 , которые представлены на фиг.2, е. На этом процесс вычисления компонент собственных векторов матрицы А заканчивается. Значения компонент собственных векторов хранятся в блоке 9 памяти.
, которые представлены на фиг.2, е. На этом процесс вычисления компонент собственных векторов матрицы А заканчивается. Значения компонент собственных векторов хранятся в блоке 9 памяти.
После того как расширяющие последовательности сформированы, с блока 6 синхронизации поступают тактовые импульсы на вход регистра 10 сдвига и как следствие на второй управляющий вход блока элемента «И» 47. После чего происходит модуляция информационных бит расширяющей последовательностью в модуляторе 14 каждого из каналов передачи 12. Причем расширение информационной последовательности происходит в случае, если информационный бит равен единице за счет использования ортогонального сигнала инверсной структуры, в случае, если информационный бит, равен нулю - за счет использования ортогонального сигнала прямой структуры (см. Столингс В. Беспроводные линии связи и сети.: Пер. с англ. - М.: Издательский дом «Вильямс», 2003. - С.213).
Затем в блоке формирования группового сигнала происходит объединение всех промодулированных сигналов и через блок фазовой модуляции 18 и усилитель мощности 19 излучаются через передающую антенну 20 в эфир.
Одновременно с процессом модуляции происходит формирование новых коэффициентов диагональной симметрической матрицы А в генераторе случайных положительных чисел 22 и запись их в блок памяти 8 через запоминающее устройство 23.
На приемной стороне происходит обратная процедура.
Использование в качестве коэффициентов диагональной положительно определенной симметрической матрицы случайных чисел позволяет повысить количество возможных кодовых последовательностей, используемых для передачи последовательности информационного сообщения.
Для подтверждения того, что предлагаемая система передачи информации обладает повышенной структурной скрытностью по сравнению с прототипом, произведем расчет количества всех возможных ансамблей ортогональных сигналов, формируемых данными системами. Поэтому нами будет рассмотрена матрица А следующей структуры:
 .
.
где α1,1, α2,2, α3,3…αN,N - коэффициента главной диагонали;
(α1,2, а2,1),(α1,3, α3,1)…(αN-1,N,αN,N-1) - симметричные элементы верхней и нижней диагонали.
Для расчета количества ансамблей сигналов в предлагаемом устройстве использовалась формула для неупорядоченных сочетаний с повторением элементов (см. Волковец А.И. Теория вероятности и математическая статистика: Практикум для студ. всех спец. БГУИР дневной формы обучения / А.И.Волковец, А.Б.Гуринович. - Мн.: БГУИР, 2003. С.5):

где n - диапазон возможных значений диагональных коэффициентов матрицы A;
k - количество элементов диагональной симметрической матрицы размерностью N, находящихся ниже или выше главной диагонали.
Формула для расчета k:
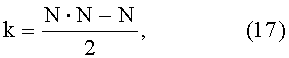
где N- размерность матрицы А.
Для расчета количества кодовых словарей де Брейна, используемых в прототипе, в качестве расширяющих последовательностей использовалась формула (см. патент Российской Федерации №2234191, кл. Н04В 7/216, H04L 9/26 24.07.2001):

где bi - число элементов в i-м цикле подстановки V10, содержащей два и более элементов;
m - число элементов памяти регистра сдвига;
d - общее число циклов подстановки V10 с двумя и более элементами.
Результаты расчетов, которые представлены на фиг.3, показывают, что с увеличением элементов n, используемых для вычисления хаотических ансамблей ортогональных многоуровневых сигналов, увеличивается количество М возможных структур данных сигналов по сравнению с количеством сигналов Q, формируемых на основе кодовых словарей де Брейна.
В соответствии с предложенным способом при передаче каждого бита должен использоваться новый хаотический ансамбль ортогональных многоуровневых сигналов, поэтому если обеспечить смену хаотических ансамблей ортогональных многоуровневых сигналов с периодом, равным Т0, где T0=1/R - временной интервал использования хаотического ансамбля ортогональных многоуровневых сигналов, равный длительности бита информации, a R - скорость передачи бита информации, то период повторения хаотического ансамбля ортогональных многоуровневых сигналов будет определяться соотношением:

В соответствии с соотношением (19), когда скорость передачи данных R равна 1МБит/с, размерность N матрицы А равна 256 и диапазон возможных значений n равен 10, то период повторения одного хаотического ансамбля ортогональных многоуровневых сигналов составит 3,54·1022 лет.
Это говорит о том, что при передаче одинаковых последовательностей бит генерируемые расширяющие последовательности не будут повторяться в течение длительного времени.
В соответствии с соотношениями (16) и (17) расчет количества ансамблей сигналов, которое можно сформировать на основе диагональной симметрической матрицы А размерностью N=4×4, проводится следующим образом:
 .
.
где α1,1, α2,2, α3,3, α4,4 - коэффициенты главной диагонали матрицы А;
α1,2, α1,3, α1,4, α2,3, α2,4, α3,4 - коэффициенты матрицы A, находящиеся над главной диагональю;
α2,1, α3,1, α3,2, α4,1, α4,2, α4,3 - коэффициенты матрицы А, находящиеся под главной диагональю;
Допустим, что диапазон n возможных значений диагональных коэффициентов матрицы А равен 5 (n=5).
1. Рассчитывается количество элементов диагональной симметрической матрицы А, находящихся ниже или выше главной диагонали, в соответствии с соотношением (17):
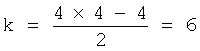 .
.
2. Рассчитывается количество ансамблей дискретных многоуровневых ортогональных сигналов в соответствии с соотношением (16):
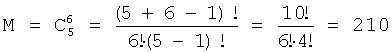
3. Рассчитаем в соответствии с соотношением (19) период повторения одного хаотического ансамбля ортогональных многоуровневых сигналов для диагональной симметрической матрицы А при скорости передачи равной R=1000 кБит/с:
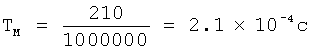 .
.
Для наглядности на фиг.2 один и тот же сигнал был повторен 3 раза, при этом, как можно увидеть на фиг.2 ж, з, и, ни одна из расширяющих последовательностей не повторилась.
| название | год | авторы | номер документа |
|---|---|---|---|
| СИСТЕМА ПЕРЕДАЧИ ИНФОРМАЦИИ С ПРИМЕНЕНИЕМ СТОХАСТИЧЕСКИХ ОРТОГОНАЛЬНЫХ КОДОВ | 2021 |
|
RU2780418C1 |
| СИСТЕМА НЕПРЕРЫВНОЙ ПЕРЕДАЧИ ИНФОРМАЦИИ АНСАМБЛЯМИ СТОХАСТИЧЕСКИХ ОРТОГОНАЛЬНЫХ КОДОВ | 2022 |
|
RU2801172C1 |
| УСТРОЙСТВО ФОРМИРОВАНИЯ СТОХАСТИЧЕСКИХ ОРТОГОНАЛЬНЫХ КОДОВ | 2021 |
|
RU2773107C1 |
| ГЕНЕРАТОР СТОХАСТИЧЕСКИХ ОРТОГОНАЛЬНЫХ КОДОВ | 2016 |
|
RU2615322C1 |
| Генератор функций Попенко-Турко | 1990 |
|
SU1753464A1 |
| Устройство для операций над матрицами | 1989 |
|
SU1777153A1 |
| СИСТЕМА ДЛЯ СЖАТИЯ ДВУХМЕРНОГО МАССИВА ИНФОРМАЦИИ | 1993 |
|
RU2046398C1 |
| Устройство для разложения цифровых сигналов по Уолшо-подобным базисам | 1983 |
|
SU1108461A1 |
| Процессор для преобразования цифровых сигналов по Хааро-подобным базисам | 1984 |
|
SU1168966A1 |
| Процессор для преобразования цифровых сигналов по Хааро-подобным базисам | 1987 |
|
SU1418745A1 |

Изобретение относится к области передачи информации и может быть использовано при передаче сообщений в широкополосных системах радиосвязи с кодовым разделением каналов. Технический результат заключается в повышении структурной скрытности системы передачи информации с кодовым разделением каналов за счет использования ансамблей ортогональных сигналов, хаотически формируемых на основе собственных векторов диагональной положительно определенной симметрической матрицы размерностью N. Указанный технический результат достигается тем, что для передачи сообщений, сменяемых от одного информационного символа к другому, применяют ортогональные кодовые комбинации, в качестве которых используют ансамбли дискретных ортогональных сигналов, формируемые путем расчета собственных чисел и собственных векторов диагональной положительно определенной симметрической матрицы, диагональными коэффициентами которой являются хаотически формируемые числовые последовательности. 3 ил.
Способ передачи информации в системах с кодовым разделением каналов заключается в том, что для передачи сообщений, сменяемых от одного информационного символа к другому, применяют ортогональные кодовые комбинации, отличающийся тем, что в качестве ортогональных кодовых комбинаций используют ансамбли дискретных ортогональных сигналов, формируемые путем расчета собственных чисел и собственных векторов диагональной положительно определенной симметрической матрицы, диагональными коэффициентами которой являются хаотически формируемые числовые последовательности.
| WO 2005071864 А2, 04.08.2005 | |||
| СПОСОБ ПЕРЕДАЧИ ИНФОРМАЦИИ В СИСТЕМАХ С КОДОВЫМ РАЗДЕЛЕНИЕМ КАНАЛОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2001 |
|
RU2234191C2 |
| RU 2008131106 A, 10.02.2010 | |||
| US 7551698 B2, 23.06.2009 | |||
| Манипулятор для доения коров | 1982 |
|
SU1034665A1 |
| EP 0491668 А2, 24.06.1992. | |||
Авторы
Даты
2011-09-10—Публикация
2010-02-24—Подача