Изобретение относится к области радиотехники и предназначено для передачи дискретных сообщений по каналам связи с переменными параметрами.
Достигаемый технический результат – повышение помехоустойчивости передачи дискретных сообщений по каналам связи с переменными параметрами. Особенностью предлагаемого способа квадратурной амплитудно-фазовой модуляции (КАФМ) является то, что, в отличие от обычной квадратурной амплитудной модуляции (КАМ), передача сообщения при КАФМ производится для всех вершин сигнального созвездия с одинаковой максимально возможной амплитудой и с индивидуальной относительной манипуляцией амплитуд и фаз квадратур несущего колебания, а на приемном конце радиолинии по внесенным на передающей стороне радиолинии признакам, заключающимся во внутриимпульсной фазовой манипуляции квадратур несущего колебания взаимно ортогональными бинарными последовательностями, определяются конкретные значения вершин сигнального созвездия и в зависимости либо от конкретной значения этих вершин, либо от сочетания двух вершин из общего их числа, с учетом отношения амплитуд и разности начальных фаз квадратур несущего колебания, выносится решение о конкретной совокупности принимаемых элементарных символов в передаваемой кодовой комбинации. В заявляемом изобретении КАФМ в отличие от обычного способа КАМ информация в сигнальном созвездии о передаваемом фрагменте кодовой комбинации содержится не в абсолютных значениях координат вершин сигнального созвездия, соответствующих конкретным значениям фаз и амплитуд вектора сигнала, а в разности начальных фаз и в относительных значениях амплитуд квадратур очередного передаваемого радиоимпульса. При этом относительные значения амплитуд и разность начальных фаз квадратур радиоимпульса определяются с предельно высокой точностью благодаря тому, что, в отличие, например, от относительной фазовой манипуляции, обе квадратуры радиоимпульса испытывают абсолютно одинаковые искажения в среде распространения, поскольку условия прохождения по каналу связи у обеих квадратур радиоимпульса совершенно не отличаются друг от друга.
Изобретение относится к области радиотехники и предназначено для передачи дискретных сообщений по каналам связи с переменными параметрами. Достигаемый технический результат – повышение помехоустойчивости передачи дискретных сообщений по каналам связи с переменными параметрами.
Особенностью предлагаемого метода КАФМ является то, что информация в сигнальные созвездия о передаваемых фрагментах кодовых комбинаций закладывается не в абсолютные значения координат вершин сигнального созвездия, а в относительные значения амплитуд квадратур радиоимпульса и в разность их начальных фаз. А сами созвездия делятся на отдельные группы, которые отличаются друг от друга тем, что имеют характерную для каждой группы дополнительную внутриимпульсную фазовую манипуляцию квадратур несущего колебания взаимно ортогональными на интервале времени, равном длительности одиночного радиоимпульса, бинарными последовательностями.
За аналог изобретения принят метод двойной относительной фазовой манипуляции (ДОФМ) [Петрович Н.Т. Передача дискретной информации в каналах с фазовой манипуляцией. Москва, Сов. радио, 1965. Стр. 32-37], при котором квадратуры несущего колебания играют разные роли: первый информационный символ передается изменением фазы одной квадратуры радиоимпульса на 0° или 180°, а второй информационный символ передается изменением фазы второй квадратуры радиоимпульса на 0° или 180° относительно фаз соответствующих квадратур предшествующего радиоимпульса в зависимости от того, какие значения имеют очередные передаваемые элементы кодовой комбинации («1» или «0»). Недостатком прототипа является то, что одним очередным радиоимпульсом возможно передавать всего лишь два значения символов кодовой комбинации. А увеличение кратности фазовой манипуляции снижает помехоустойчивость модема. Вторым недостатком ДОФМ является необходимость сравнения фаз двух соседствующих по времени элементарных посылок, что ограничивает возможность использования модемов ДОФМ в каналах связи с быстро изменяющимися параметрами и исключает возможность поэлементной передачи дискретных сообщений в режиме ППРЧ, поскольку требует одновременного присутствия на одной и той же частоте, как минимум, двух соседних элементарных посылок передаваемого сообщения.
Известен способ фазо-кодовой внутриимпульсной манипуляции, который используется в радиолокации для повышения помехоустойчивости приема отраженных от объектов радиоимпульсов [Бакут П.А. и др. Вопросы статистической теории радиолокации. Том II. М.:- Советское радио. 1964. Стр. 494]. Этот способ внутриимпульсной фазо-кодовой манипуляции используется в заявляемом изобретении для фазовой манипуляции взаимно ортогональными бинарными последовательностями каждой из квадратур отдельных радиоимпульсов, что дает возможность разделять эти квадратуры на приемной стороне радиолинии и позволяет выносить решения о принимаемых элементах сообщения в соответствии с конкретным сочетанием двух взаимно ортогональных бинарных последовательностей, манипулирующих фазы квадратур радиоимпульсов, оценивая отношение амплитуд и определяя разность фаз квадратур радиоимпульсов после их деманипуляции на приемной стороне радиолинии.
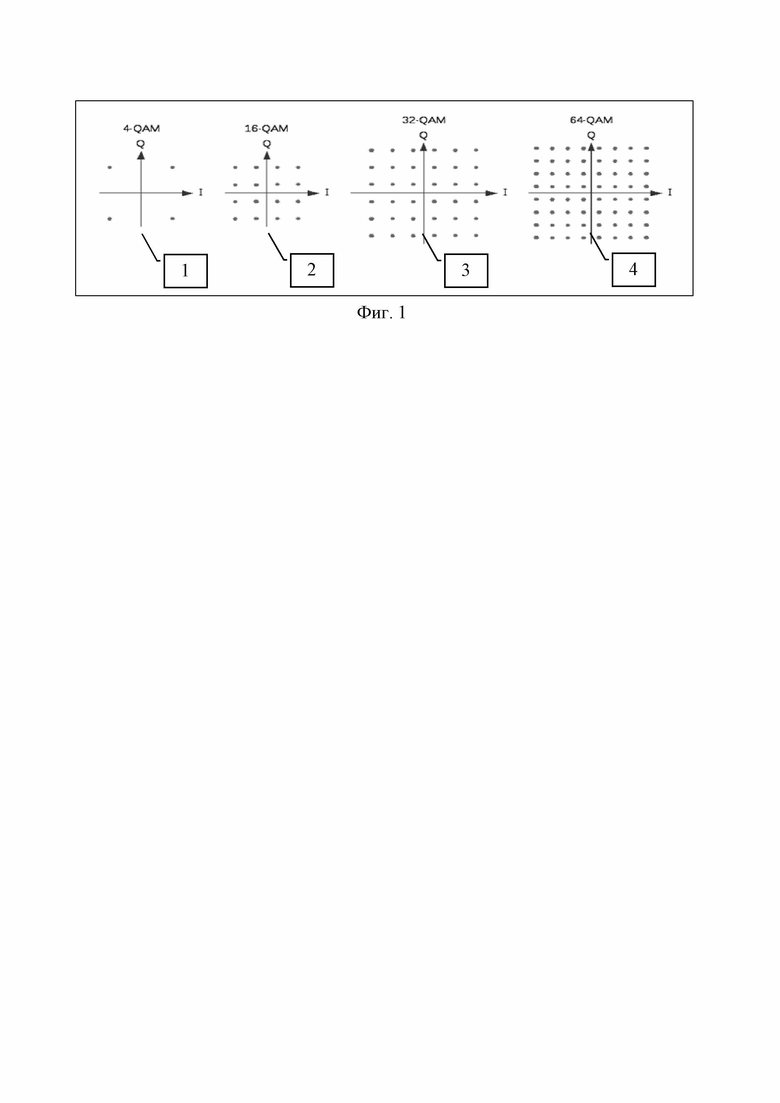
В качестве прототипа предлагаемого метода принят обычный метод квадратурной амплитудной модуляции (КАМ) [Бернард Скляр. Цифровая связь. – М: Изд. дом «Вильямс», 2003. Стр. 585], который значением амплитуд квадратур каждого отдельного радиоимпульса способен передавать сразу большое количество элементарных символов, как показано на фиг. 1.
На фиг. 1 обозначено:
1 – сигнальное созвездие с четырьмя вершинами (одним очередным радиоимпульсом передается два элемента, аналогично ДОФМ);
2 – сигнальное созвездие с шестнадцатью вершинами (одним очередным радиоимпульсом передается четыре элемента);
3 – сигнальное созвездие с тридцатью двумя вершинами (одним очередным радиоимпульсом передается шесть элементов);
4 – сигнальное созвездие с шестьюдесятью четырьмя вершинами (одним очередным радиоимпульсом передается восемь элементов).
Если количество вершин в сигнальном созвездии m=2Z, то количество элементов в кодовой комбинации, которое может быть передано одним радиоимпульсом равно Z=log2m.
Если у сигнального созвездия две вершины, то с помощью одного радиоимпульса можно передавать только значение одной элементарной посылки кодовой комбинации (Z=1), как это делается при однократной фазовой модуляции. Если у сигнального созвездия четыре вершины ((1) на фиг. 1), то с помощью одного радиоимпульса можно передавать значения двух элементарных посылок кодовой комбинации, как это делается при двукратной фазовой модуляции. При восьми, шестнадцати ((2) на фиг. 1), тридцати двух ((3) на фиг. 1), шестидесяти четырех ((4) на фиг. 1) и большем числе вершин в сигнальном созвездии одним радиоимпульсом передается, соответственно, 3, 4, 5, 6 и большее число элементарных посылок в кодовых комбинациях.
Однако недостатком КАМ является то, что при приеме одиночного радиоимпульса из-за отсутствия данных о начальных фазах квадратур этого радиоимпульса и конкретном значении их амплитуд невозможно принять решение о значении принимаемого фрагмента дискретного сообщения, соответствующего этому радиоимпульсу, что не позволяет использовать КАМ при поэлементной передаче сообщений в режиме ППРЧ. Для определения конкретного значения амплитуд квадратур, которые соответствуют координатам вершин сигнального созвездия КАМ, требуется специальная преамбула, предшествующая принимаемому сообщению и занимающая достаточно продолжительное время. Это является серьезным недостатком прототипа заявляемого способа модуляции. Вторым серьезным недостатком прототипа является также то, что при достаточно большом числе вершин созвездия (16 и более) передающее устройство теряет около 6 дБ излучаемой мощности по той причине, что амплитуда сигнала при передаче сообщения все время изменяется от максимального до минимального уровня, что снижает коэффициент полезного действия радиопередатчика.
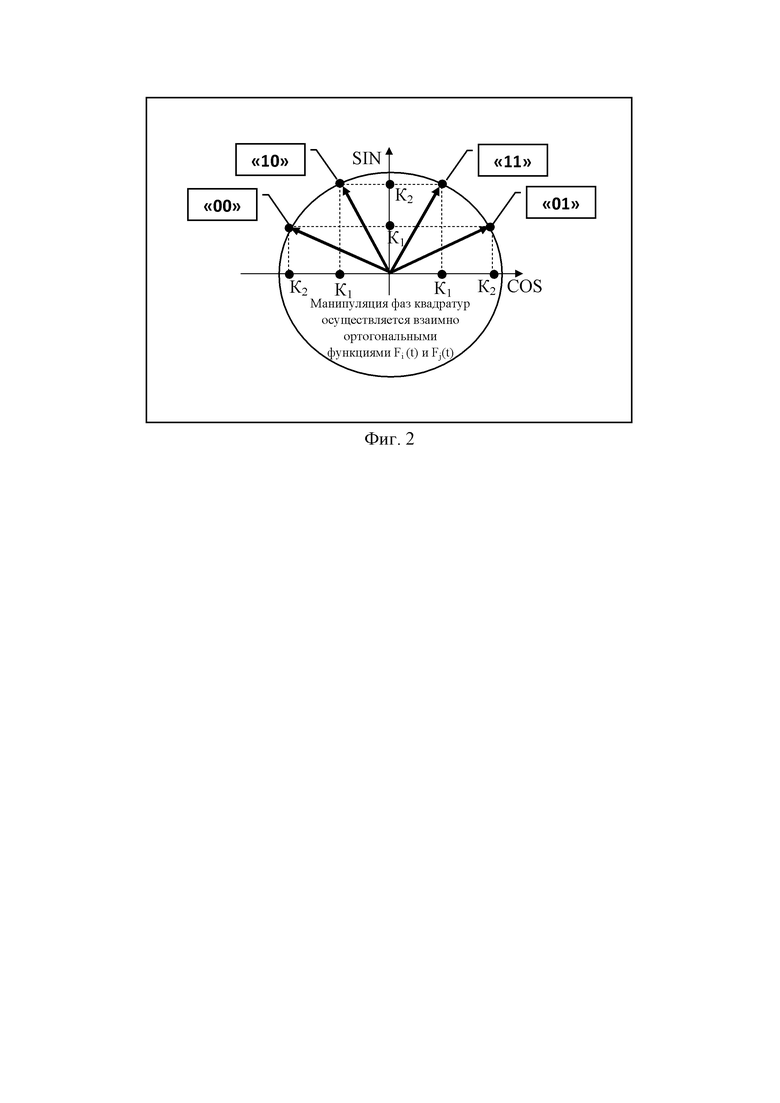
Заявляемый способ квадратурной амплитудно-фазовой модуляции имеет преимущество как перед аналогом, так и перед прототипом, позволяя передавать достаточно большое число элементов кодовой комбинации одним отдельно взятым радиоимпульсом без каких-либо дополнительных преамбул, что дает возможность использовать данный метод для передачи достаточно большого количества элементов в кодовой комбинации одиночным радиоимпульсом в режиме ППРЧ. Передача всех радиоимпульсов при КАФМ в отличие от КАМ производится с одинаковой максимально возможной амплитудой, что гарантирует 100% использование мощности передатчика и обеспечивает максимально возможную помехоустойчивость приема сообщений. В заявляемом способе КАФМ производится внутриимпульсная манипуляция начальных фаз квадратур радиоимпульса разными взаимно ортогональными бинарными последовательностями. От количества используемых для манипуляции взаимно ортогональных бинарных последовательностей зависит число вершин в сигнальном созвездии. Если синусоидальная квадратура несущего колебания манипулируется взаимно ортогональными бинарными последовательностями в количестве M, а косинусоидальная квадратура несущего колебания манипулируется такого же рода бинарными последовательностями в количестве N, то этим количеством бинарных последовательностей можно организовать количество вершин сигнального созвездия m=(N·M). Таким количеством вершин сигнального созвездия можно передавать одновременно Zm бит информации, где Zm целое число выражения log2m. При манипуляции двух квадратур несущего колебания учитываются как отношение амплитуд квадратур радиоимпульса при определении, например, значения первого элемента в кодовой комбинации, так и относительные значения начальных фаз квадратур радиоимпульса при определении, соответственно, значения второго элемента в кодовой комбинации. Если, например, синусоидальная квадратура радиоимпульса больше косинусоидальной, то также как и на фиг. 2, передается значение символа «1», а в противном случае передается значение символа «0» (первые символы кодовых комбинаций на фиг. 2). Количество уровней амплитуд квадратур может быть и более двух, что хотя и позволяет увеличить пропускную способность канала связи, но приводит к снижению помехоустойчивости КАФМ модема. При начальной фазе косинусоидальной квадратуры 0°, как и на фиг. 2, производится передача второй элементарной посылки «1», а при начальной фазе 180°, соответственно, передача второй элементарной посылки «0». Манипуляция квадратур радиоимпульса по амплитуде и по начальной фазе, как показано на фиг. 2, дает возможность передавать, как минимум, значения двух элементарных посылок кодовой комбинации.
Наиболее рациональный метод манипуляции, который обеспечивает максимальную помехоустойчивость реализуется в том случае, когда на интервале времени, в течение которого фаза несущего колебания остается постоянной, укладывается целое число периодов несущего колебания.
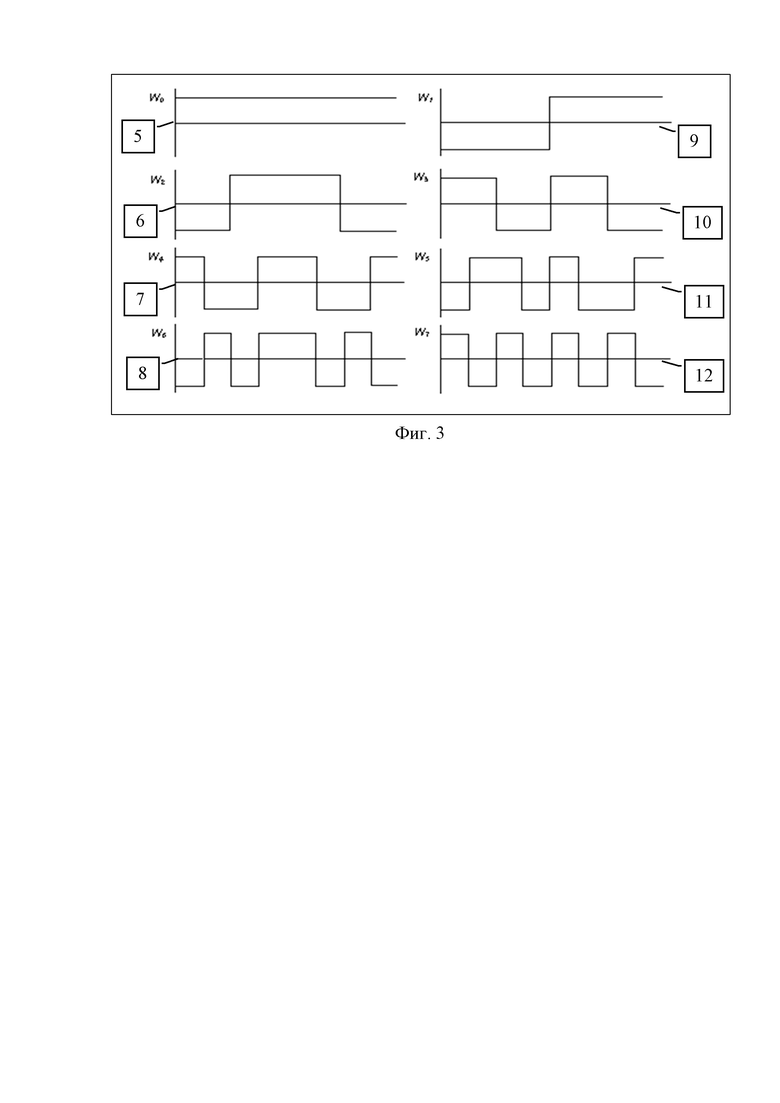
В качестве взаимно ортогональных бинарных последовательностей могут быть использованы функции Уолша [Радиотехнические цепи и сигналы. Под ред. К.А. Самойло. М.: Радио и связь. 1982. Стр. 79-82, табл. 2-4]. На фиг. 3 изображены графики функций Уолша от нулевого до седьмого порядка.
На фиг. 3 обозначено:
5 – функция Уолша 0-го порядка W0(t);
6 – функция Уолша 1-го порядка W1(t);
7 - функция Уолша 2-го порядка W2(t);
8 - функция Уолша 3-го порядка W3(t);
9 - функция Уолша 4-го порядка W4(t);
10 - функция Уолша 5-го порядка W5(t);
11 - функция Уолша 6-го порядка W6(t);
12 - функция Уолша 7-го порядка W7(t).
В таблице 1 приведен вариант значений параметров квадратур радиоимпульса и порядков функций Уолша для случая передачи одним радиоимпульсом пятиэлементной кодовой комбинации.
Таблица 1
Комбинация
Как видно из таблицы 1, значение 1-го элемента кодовой комбинации обусловлено отношением значений амплитуд квадратур несущего колебания. Отношение (синусоидальная квадратура)/(косинусоидальная квадратура) > 1 соответствует значению первого элемента кодовой комбинации «1». Случай отношения (синусоидальная квадратура)/(косинусоидальная квадратура) < 1 соответствует значению первого элемента кодовой комбинации «0». Значение второго элемента обусловлено разностью начальных фаз квадратур радиоимпульса. Значение второго элемента кодовой комбинации «1» соответствует разности начальных фаз квадратур несущего колебания равной 0°. Значение второго элемента кодовой комбинации «0» соответствует разности начальных фаз квадратур несущего колебания равной 180°. Остальные три элемента пятиэлементной кодовой комбинации обусловлены типами двух взаимно ортогональных бинарных последовательностей (в нашем случае - функций Уолша двух разных порядков из общего числа шести), которые манипулируют фазы квадратур радиоимпульса. В этом случае нулевой и первый порядки функций Уолша используются для манипуляции синусоидальной квадратуры несущего колебания, а функции Уолша со второго по пятый порядок используются для манипуляции косинусоидальной квадратуры несущего колебания.
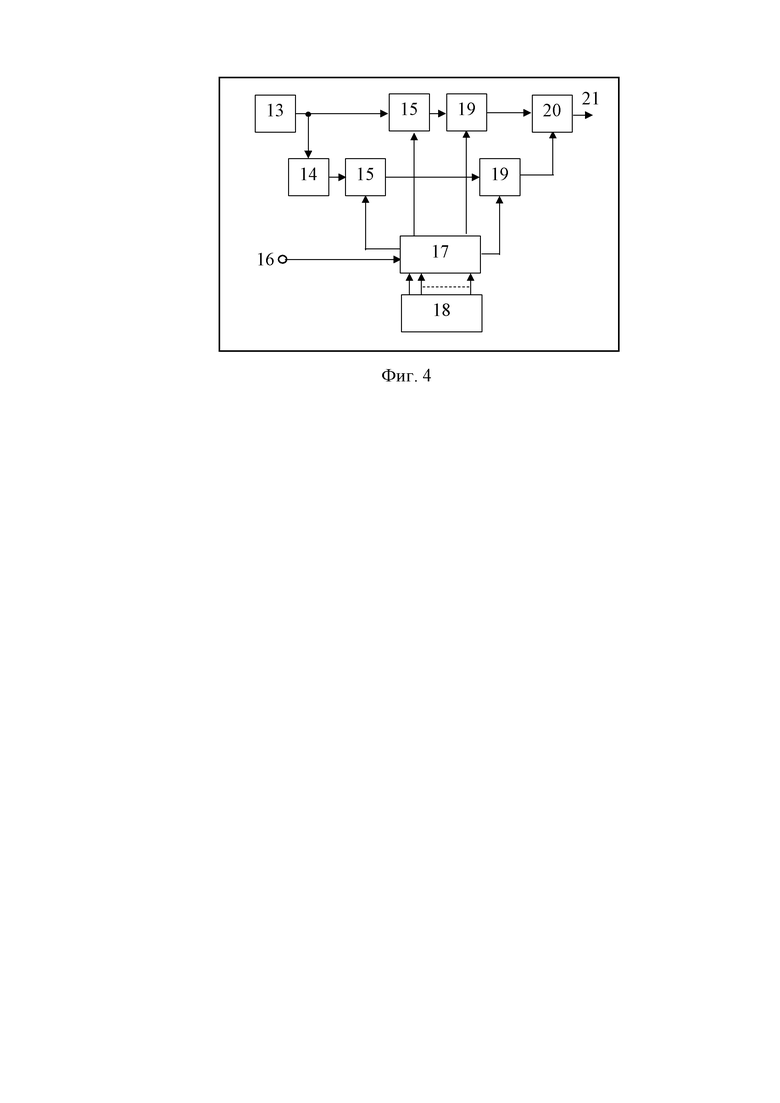
На фиг. 4 приведена блок-схема манипулятора сигнала с КАФМ на передающей стороне радиолинии.
На фиг. 4 обозначено:
13 – генератор гармонического колебания;
14 – фазовращатель на 90°;
15 – манипуляторы амплитуд квадратур несущего колебания;
16 – вход манипулятора КАФМ для передаваемой Z-значной кодовой комбинации;
17 – формирователь функций, манипулирующих амплитуды и фазы квадратур несущего колебания;
18 – генератор функций Уолша;
19 – манипуляторы фаз квадратур несущего колебания функциями Уолша;
20 – сумматор;
21 – выход манипулятора КАФМ (ко входу передатчика).
Генератор (13) выдает гармоническое колебание 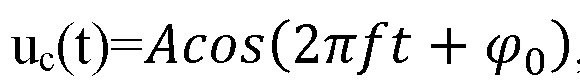 являющееся косинусоидальной квадратурой несущего колебания, которое подается на фазовращатель (14), создающий синусоидальную квадратуру несущего колебания
являющееся косинусоидальной квадратурой несущего колебания, которое подается на фазовращатель (14), создающий синусоидальную квадратуру несущего колебания 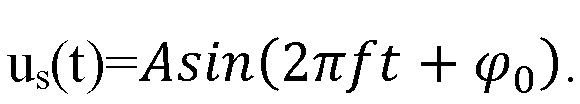 Манипуляторы амплитуд (15) манипулируют амплитуды квадратур колебания, которые соответствуют определенным символам. Если с помощью амплитудной манипуляции квадратур радиоимпульса передается только один элемент (например, первый) передаваемой Z-значной кодовой комбинации, поступающей на вход модулятора (16), то на выходе амплитудных манипуляторов (15) в соответствии с командой, подаваемой от формирователя манипулирующих сигналов (17) в момент передачи этой кодовой комбинации имеют место колебания:
Манипуляторы амплитуд (15) манипулируют амплитуды квадратур колебания, которые соответствуют определенным символам. Если с помощью амплитудной манипуляции квадратур радиоимпульса передается только один элемент (например, первый) передаваемой Z-значной кодовой комбинации, поступающей на вход модулятора (16), то на выходе амплитудных манипуляторов (15) в соответствии с командой, подаваемой от формирователя манипулирующих сигналов (17) в момент передачи этой кодовой комбинации имеют место колебания:
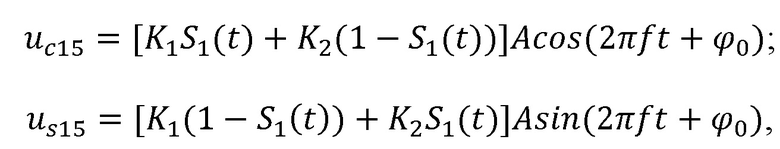
где S1(t) – значение первого символа в передаваемой кодовой комбинации («1» или «0»).
После амплитудных манипуляторов (15) колебания подаются на входы манипуляторов фазы (19). Фазовые манипуляторы (19) изменяют фазы квадратур передаваемого радиоимпульса в соответствии с подаваемыми на вторые входы этих манипуляторов взаимно ортогональными бинарными последовательностями, которыми, например, являются функции Уолша, которые взаимно ортогональны на интервале времени равном длительности радиоимпульса. При этом синусоидальная квадратура радиоимпульса манипулируется одной М-совокупностью функций Уолша, а косинусоидальная квадратура радиоимпульса манипулируется другой N-совокупностью функций Уолша. Определение пары функций Уолша, манипулирующих параметры двух квадратур несущего колебания, производится формирователем сигналов (17). Эти функции выбираются из подаваемых на вход формирователя сигналов (17) общего их числа R=N+M от генератора функций Уолша (18) в зависимости от конкретного вида очередного фрагмента Zm передаваемой кодовой комбинации. Например, пусть передается одной парой функций Уолша три символа. В таблице 1 приведен вариант кодирования трехзначных последовательностей (трех последних элементов 5-значной кодовой комбинации) парой функций Уолша соответствующих порядков (M=2, N=4).
Если для передачи манипуляцией фазы косинусоидальной квадратуры несущего колебания на манипулятор поступает символ «1», то начальная фаза косинусоидальной квадратуры несущего колебания не изменяется. При передаче символа «0» начальная фаза косинусоидальной квадратуры несущего колебания изменяется на 180°. Для этого на манипулятор фазы косинусоидальной квадратуры манипулирующая фазу функция (в нашем конкретном примере функция Уолша) подается инвертированной, т.е. со знаком «минус».
Записать итоговое аналитическое выражение для несущего колебания u(t) на выходе КАФМ модулятора (21) в случае передачи фрагмента кодовой комбинации посредством амплитудной и фазовой манипуляции квадратур радиоимпульса функциями Уолша Wr(t) можно в следующем виде:
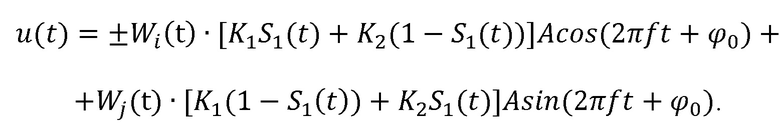
Конкретные значения функций Уолша Wi(t) и Wj(t), манипулирующих фазы квадратур несущего колебания, определяются формирователем функций (17) в соответствии с конкретно реализованными значениями фрагментов передаваемых кодовых комбинаций, поступающими на вход модулятора (16), которые обусловливают сочетание этих функций для придания параметрам радиоимпульса необходимых значений.
Итак, в рассмотренном примере первый элемент кодовой комбинации передается посредством манипуляции амплитуд квадратур радиоимпульса (если передается символ «1», то амплитуде синусоидальной квадратуры радиоимпульса придается значение большее по сравнению с амплитудой косинусоидальной квадратуры этого радиоимпульса, а если передается символ «0», то, наоборот, амплитуде синусоидальной квадратуры радиоимпульса придается значение меньшее по сравнению с амплитудой косинусоидальной квадратуры этого радиоимпульса). Второй элемент кодовой комбинации передается значением фазы косинусоидальной квадратуры радиоимпульса (если передается символ «1», то фаза косинусоидальной квадратуры должна быть равна 0°, а если передается символ «0», то фаза косинусоидальной квадратуры должна быть равна 180°). Значения остальных символов фрагмента кодовой комбинации передаются одним радиоимпульсом посредством сочетания пар взаимно ортогональных бинарных последовательностей, манипулирующих фазы квадратур несущего колебания, например, функций Уолша в соответствии с таблицей 1.
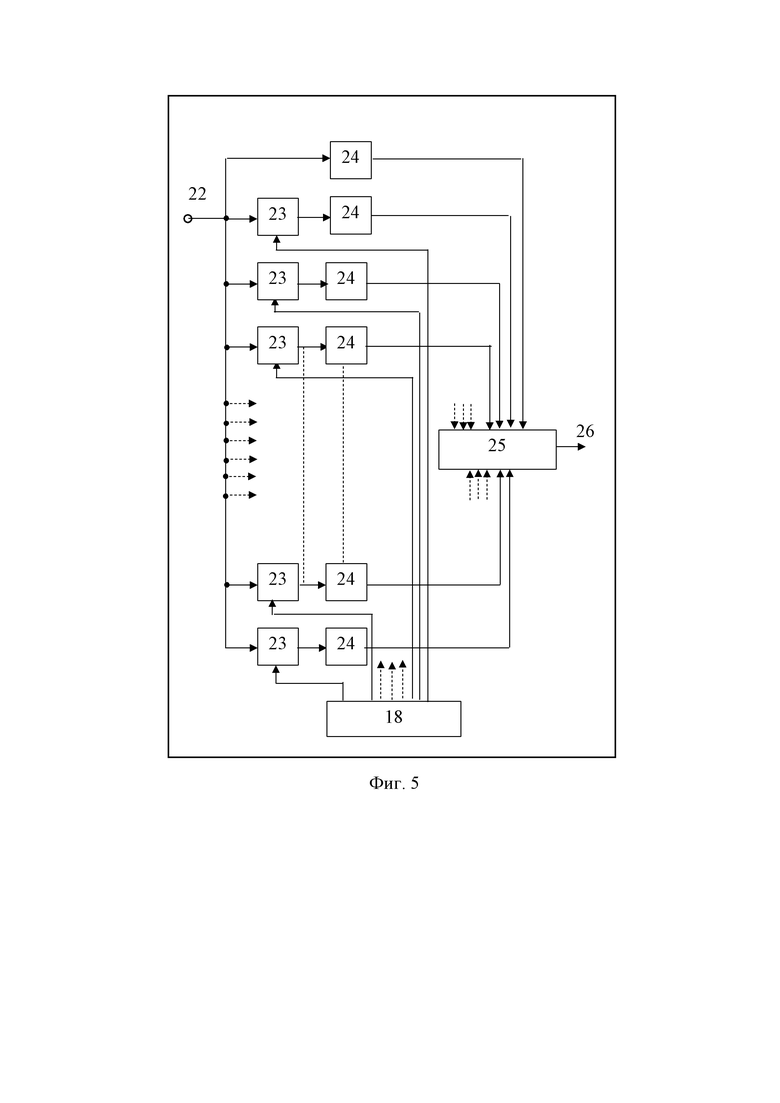
На фиг. 5 приведена блок-схема КАФМ демодулятора на приемной стороне радиолинии.
На фиг. 5 обозначено:
22 – вход демодулятора;
23 – деманипуляторы фазы сигнала функциями Уолша;
24 – узкополосные фильтры;
25 – устройство цифровой обработки принятых сигналов;
26 – выход демодулятора.
Если бы в точке приема сигнала помехи отсутствовали, то сигнал uпр(t) на входе демодулятора (22) отличался бы от сигнала на выходе модулятора передатчика только уровнем амплитуды и начальной фазой, обусловленной временем распространения сигнала в радиолинии:
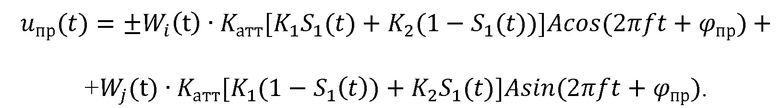
На входе демодулятора стоят деманипуляторы (23), после которых имеет место напряжение u23(t):
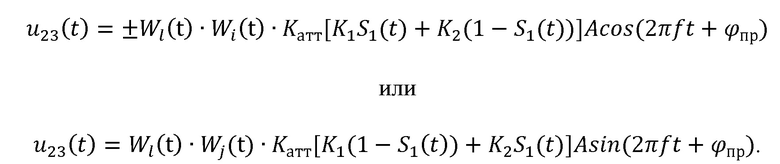
Известно, что произведение функций Уолша является новой функцией Уолша [Радиотехнические цепи и сигналы. Под ред. К.А. Самойло. М.: Радио и связь. 1982. Стр. 81]. При этом, если порядки перемножаемых функций Уолша одинаковые, то результатом перемножения является функция Уолша нулевого порядка, т.е. значение функции на интервале длительности радиоимпульса равно единице. Поэтому после деманипуляторов (23), если перемножаются функции разных порядков, имеют место колебания, манипулированные по фазе функциями Уолша:
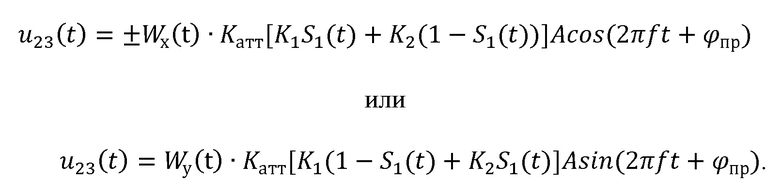
Если же порядки функций Уолша совпадают, то тогда на выходе деманипуляторов (23) имеют место гармонические колебания:
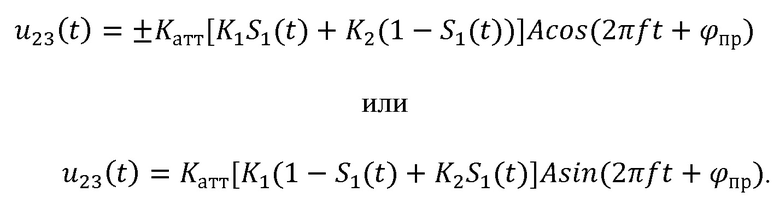
Поскольку при фазовой манипуляции гармонических колебаний функциями Уолша порядком не равным нулю, в случае, когда на отрезках времени с начальными фазами равными 0° и 180° укладывается одинаковое число периодов, которые, соответственно, имеют одинаковое число отрицательных и положительных периодов, то на выходе узкополосных фильтров (24) при окончании каждого принимаемого радиоимпульса уровень высокочастотного колебания будет равен нулю. Если же фаза радиоимпульса в течение всего времени его приема остается постоянной, то на выходе соответствующего узкополосного фильтра к моменту окончания этого радиоимпульса накапливается уровень его амплитуды пропорциональный амплитуде соответствующей квадратуры принимаемого радиоимпульса. У квадратур радиоимпульса на выходах узкополосных фильтров устройство цифровой обработки сигнала определяет амплитуды и начальные фазы. При этом известны конкретные узкополосные фильтры, которые соответствуют как синусоидальной квадратуре, так и косинусоидальной квадратуре принимаемого радиоимпульса. Если амплитуда синусоидальной квадратуры радиоимпульса больше амплитуды косинусоидальной квадратуры радиоимпульса, то о соответствующем принимаемом элементе выносится решение «1». В противном случае об этом элементе выносится решение «0». Если начальная фаза косинусоидальной квадратуры радиоимпульса равна 0° (разность начальной фазы между синусоидальной и косинусоидальной квадратурами радиоимпульса равна 0°), то о принимаемом соответствующем элементе выносится решение «1». В противном случае (разность начальной фазы между синусоидальной и косинусоидальной квадратурами радиоимпульса равна 180°) об этом элементе выносится решение «0». Решения о значении остальных элементов зависят от того, на выходе каких конкретных узкополосных фильтров амплитуды квадратур отличаются от нуля. Количество элементов в фрагменте кодовой комбинации зависит от количества различных пар используемых взаимно ортогональных бинарных последовательностей, манипулирующих по фазе квадратуры передаваемого радиоимпульса. Если из общего числа бинарных последовательностей R=M+N число бинарных последовательностей, манипулирующих синусоидальную квадратуру радиоимпульса, равно M, а число бинарных последовательностей, манипулирующих косинусоидальную квадратуру радиоимпульса, равно N, то общее число элементов Zm в фрагменте кодовой комбинации, которая передается бинарными последовательностями, манипулирующими квадратуры радиоимпульса будет равно целому числу выражения log2(M·N). Например, если M=2, а N=4, как в таблице 1, то в этом случае Z6=3. И тогда общее число элементов Z в кодовой комбинации за счет манипуляции квадратур радиоимпульса по амплитуде, начальной фазе одной из квадратур на 180°и фазовой манипуляции обеих квадратур радиоимпульса взаимно ортогональными бинарными последовательностями будет равно Z=5. Решения о значениях элементов в принимаемой кодовой комбинации выносятся устройством цифровой обработки (25) и выдаются им на выход демодулятора (26).
Если использовать 16 функций Уолша, то за счет манипуляции фаз квадратур радиоимпульса только этими функциями, можно передавать одним радиоимпульсом 6 элементарных символов (64 вершины в сигнальном созвездии (8х8)), при использовании 24 функции Уолша, можно передавать, соответственно, 7 элементарных символов (128 вершин в сигнальном созвездии (16x8)), а при 32-х функциях Уолша одним радиоимпульсом можно передать целую 8-элементную кодовую комбинацию, которой обычно кодируются отдельные знаки алфавита кода (256 вершин в сигнальном созвездии (16х16)). То есть, если использовать 32 функции Уолша, то одним радиоимпульсом возможно передавать один 8-элементный знак кодового алфавита даже без дополнительной манипуляции квадратур радиоимпульса по амплитуде и начальной фазе.
Необходимо заметить, что увеличение порядка функций Уолша приводит к соответствующему расширению спектра передаваемого сигнала, но это не снижает помехоустойчивости при приеме сообщения, так как на приемной стороне решение принимается после деманипуляции сигнала, которая уменьшает спектр сигнала и возвращает ему значение, которое соответствует скорости манипуляции, обусловленной длительностью радиоимпульса без манипуляции взаимно ортогональными бинарными последовательностями типа функций Уолша.
Положительным фактором при использовании КАФМ является также то, что спектральная плотность сосредоточенной по спектру помехи, попавшей на частоту принимаемого сигнала, снижается при деманипуляции принимаемого радиоимпульса бинарными взаимно ортогональными последовательностями и в результате повышается отношение сигнал/помеха и снижается вероятность ошибки при наличии такого рода сосредоточенных по спектру помех.
Заявляемый способ квадратурной амплитудно-фазовой модуляции в отличие от прототипа, обеспечивает передачу радиоимпульсов все время с постоянным максимально возможным уровнем, т.е., в отличие от прототипа, передатчик все время излучает сигнал с максимально допустимой для этого передатчика мощностью.
Подводя итог всему вышеизложенному, можно описать весь алгоритм функционирования квадратурного амплитудно-фазового модема как на передающем, так и на приемном концах радиолинии.
На передающей стороне радиолинии модулятор КАФМ при передаче кодовой комбинации, содержащей Z символов, функционирует следующим образом:
1. Из общего числа символов кодовой комбинации берется, например, первый символ, который изменением амплитуд квадратур передаваемого радиоимпульса кодируется так, что при передаче «1» синусоидальная квадратура имеет амплитуду больше половины амплитуды радиоимпульса, а косинусоидальная квадратура имеет амплитуду меньше половины амплитуды радиоимпульса, а при передаче «0» наоборот, синусоидальная квадратура имеет амплитуду меньше половины амплитуды радиоимпульса, а косинусоидальная квадратура имеет амплитуду больше половины амплитуды радиоимпульса.
2. Далее, изменяется начальная фаза одной из квадратур радиоимпульса, например, начальной фазе косинусоидальной квадратуры радиоимпульса придается значение равное 0°, если следующим элементом является «1» или придается значение 180°, если следующим элементом является «0». Это осуществляется выбором знака («плюс» или «минус») манипулирующей косинусоидальную квадратуру бинарной последовательности типа функции Уолша.
3. И, наконец, остаток фрагмента кодовой комбинации, содержащей (Z-2) элементов передается совокупностью двух (по числу квадратур) взаимно ортогональных на интервале передачи радиоимпульса бинарных последовательностей, например, функций Уолша, каждая из которых манипулирует соответствующую квадратуру несущего колебания по фазе. Если синусоидальную квадратуру несущего колебания манипулировать М взаимно ортогональными бинарными последовательностями а косинусоидальную квадратуру несущего колебания манипулировать N взаимно ортогональными бинарными последовательностями, то для передачи (Z-2) элементов требуется общее число этих функций равное M·N=2(Z-2) и в этом случае возможно передавать Z элементов кодовой комбинации (Z=log2(N·M)+2).
На приемной стороне канала связи при приеме кодовой комбинации, содержащей Z символов, демодулятор КАФМ функционирует следующим образом:
1. С помощью деманипуляторов фазы, включенных на входе приемного устройства в количестве равном числу взаимно ортогональных бинарных последовательностей, используемых для внутриимпульсной фазовой манипуляции квадратур несущего колебания на передающей стороне радиолинии, и управляемых на приемной стороне радиолинии такого же рода взаимно ортогональными бинарными последовательностями, производится свертка квадратур несущего колебания, т. е. квадратуры несущего колебания на интервале принимаемого фрагмента кодовой комбинации на выходе деманипуляторов приобретают на интервале времени равной длительности радиоимпульса вид гармонического колебания, если деманипуляция фазы осуществляется той же функцией, какой производилась манипуляция этих квадратур несущего колебания на передающем конце радиолинии.
2. Все сигналы после деманипуляции подаются на узкополосные фильтры, и на выходе двух фильтров (по числу квадратур радиоимпульса), из общего числа m появляются гармонические колебания только в том случае, если имеет место свертка несущего колебания на выходе соответствующего деманипулятора. Таким образом, количество Zm элементарных посылок, которое возможно передать с помощью внутриимпульсной фазовой модуляции квадратур взаимно ортогональными бинарными последовательностями равно целой части выражения log2m, где m=M·N (M - число взаимно ортогональных функций, манипулирующих фазу синусоидальной квадратуры радиоимпульса, N - число взаимно ортогональных функций, манипулирующих фазу косинусоидальной квадратуры радиоимпульса).
3. У полученных сверток квадратур определяются амплитуды. Если амплитуда синусоидальной квадратуры оказывается больше амплитуды косинусоидальной квадратуры, то соответствующему элементу присваивается значение «1». Если амплитуда синусоидальной квадратуры оказывается меньше амплитуды косинусоидальной квадратуры. то соответствующему элементу присваивается значение «0».
4. У полученных сверток квадратур радиоимпульса определяются начальные фазы. Если разность начальных фаз у квадратур радиоимпульса равна 0°, то соответствующему элементу присваивается значение «1». Если разность начальных фаз у квадратур радиоимпульса равна 180°, то соответствующему элементу присваивается значение «0».
5. Остальным элементам передаваемого фрагмента кодовой комбинации присваиваются значения, которые соответствуют конкретным фильтрам (а следовательно, и взаимно ортогональным бинарным последовательностям типа функций Уолша, манипулирующим квадратуры радиоимпульсов), на выходе которых амплитуды сверток квадратур принимаемого радиоимпульса отличны от нуля.
В итоге общее число элементов Z в принимаемой кодовой комбинации равно Z=Zm+2.
Ниже в таблице 2 приведены данные по количеству элементов Z кодовой комбинации, которое может быть передано с помощью фазовой манипуляции квадратур радиоимпульса взаимно ортогональными бинарными последовательностями типа функций Уолша (M взаимно ортогональных бинарных последовательностей для фазовой манипуляции синусоидальной квадратуры радиоимпульса и N взаимно ортогональных бинарных последовательностей для фазовой манипуляции косинусоидальной квадратуры радиоимпульса). В таблице учтено то, что два элемента кодовой комбинации передаются амплитудной манипуляцией двух квадратур и манипуляцией начальной фазы одной из квадратур радиоимпульса.
Таблица 2
В таблице 3 приведены данные по минимальному количеству взаимно ортогональных функций, которое необходимо для передачи Z элементов кодовой комбинации.
Таблица 3
Имеется возможность дополнительного увеличения пропускной способности канала связи с КАФМ за счет того, что взаимно ортогональные бинарные последовательности, манипулирующие по фазе квадратуры радиоимпульса не закреплять за квадратурами этого радиоимпульса, а группы вершин сигнального созвездия обозначать соответствующими сочетаниями двух взаимно ортогональных бинарных последовательностей. При этом наиболее низким порядком такого рода последовательности манипулировать по фазе всегда одну и ту же квадратуру радиоимпульса (либо синусоидальную, либо косинусоидальную), а другим, более высоким порядком манипулировать вторую квадратуру радиоимпульса (соответственно, либо косинусоидальную, либо синусоидальную).
В таблице 4 приведено число сочетаний по два (по числу квадратур радиоимпульса), равное числу m вершин сигнального созвездия, в зависимости от общего числа R используемых взаимно ортогональных бинарных последовательностей и соответствующее количество элементов кодовой комбинации Z, которое может быть передано таким количеством вершин сигнального созвездия.
Таблица 4
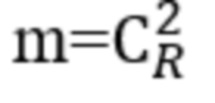
Из таблицы 4 видно, что, как правило, если учитывать, что количество вершин m должно быть равно 2Zm, иногда остаются неиспользованными достаточно большое количество команд. Например, если взять Zm=3, то 23=8 и в данном случае m=10 и при передаче трехзначных кодовых комбинаций не используются 2 вершины сигнального созвездия. Однако эти вершины сигнального созвездия могут быть использованы в радиолинии для передачи служебных команд.
В таблице 5 аналогично таблице 1 приведены варианты параметров модуляции квадратур радиоимпульса для пятиэлементных кодовых комбинаций при использовании пяти функций Уолша.
Из таблицы 5 следует, что при 5-элементной кодовой комбинации для внутриимпульсной фазовой манипуляции взаимно ортогональными бинарными последовательностями требуется пять такого рода бинарных последовательностей, в то время, как в предыдущем случае в соответствии с таблицей 1 требовалось 6 бинарных последовательностей. Но при этом согласно таблице 5 имеется 8 дополнительных команд, которые могут быть использованы, например, для адаптации радиолинии к условиям связи.
Блок-схемы модулятора и демодулятора для последнего варианта модема КАФМ не изменяются, а алгоритмы функционирования модема изменяются по сравнению с предыдущим вариантом только в программе в части определения пар взаимно ортогональных бинарных последовательностей блоками (17) и (25) на фиг. 4 и 5, которые соответствуют передаваемому фрагменту кодовой комбинации.
Заявляемый способ квадратурной амплитудно-фазовой модуляции в отличие от аналога позволяет одним радиоимпульсом без каких-либо предварительно передаваемых преамбул передавать во много раз больше двух число Z=Zm+2 элементарных посылок в кодовой комбинации, что дает возможность с помощью заявляемого способа квадратурной амплитудно-фазовой модуляции передавать дискретные сообщения в режиме ППРЧ, излучая на каждой частоте один единственный радиоимпульс.
Заявляемый способ квадратурной амплитудно-фазовой модуляции в отличие от прототипа имеет более высокую помехоустойчивость, поскольку передача радиоимпульсов все время производится с максимально возможной амплитудой.
Таблица 5
комбинация
Изобретение относится к области радиотехники и предназначено для передачи дискретных сообщений в каналах связи с переменными параметрами. Достигаемый технический результат – повышение помехоустойчивости передачи дискретных сообщений в каналах связи с переменными параметрами. Передача сообщения при квадратурной амплитудно-фазовой модуляции (КАФМ) производится для всех вершин сигнального созвездия с одинаковой максимально возможной амплитудой и с индивидуальной манипуляцией амплитуд и фаз квадратур несущего колебания, а на приемном конце радиолинии по внесенным на передающей стороне радиолинии признакам, заключающимся в фазовой манипуляции квадратур несущего колебания взаимно ортогональными бинарными последовательностями, определяются отдельные группы вершин сигнального созвездия и в зависимости от той или другой конкретной группы вершин сигнального созвездия с учетом отношения амплитуд и разности начальных фаз квадратур несущего колебания в каждой группе сигнального созвездия выносится решение о конкретной совокупности принимаемых элементарных символов в передаваемой кодовой комбинации. 2 н. и 3 з.п. ф-лы, 5 табл., 5 ил.
1. Способ квадратурной амплитудно-фазовой модуляции с раздельной амплитудной и фазовой манипуляцией квадратур несущего колебания, отличающийся тем, что внутриимпульсная манипуляция квадратур несущего колебания по фазе производится на длительности одного радиоимпульса индивидуально и одновременно двумя разными взаимно ортогональными бинарными последовательностями в количестве M для манипуляции синусоидальной квадратуры и в количестве N для манипуляции косинусоидальной квадратуры, выбор которых из общего их количества (М+N) обусловлен конкретным видом передаваемого фрагмента кодовой комбинации, при этом количество элементов в передаваемом фрагменте этой кодовой комбинации за счет манипуляции по фазе квадратур несущего колебания взаимно ортогональными бинарными последовательностями равно целому числу от выражения log2(M·N).
2. Способ квадратурной амплитудно-фазовой модуляции с раздельной амплитудной и фазовой манипуляцией квадратур несущего колебания взаимно ортогональными бинарными последовательностями по п. 1, отличающийся тем, что одна из квадратур помимо внутриимпульсной манипуляции взаимно ортогональными бинарными последовательностями манипулируется по фазе на 180°, что позволяет дополнительно увеличить на единицу количество знаков в передаваемой одним радиоимпульсом кодовой комбинации.
3. Способ квадратурной амплитудно-фазовой модуляции с раздельной амплитудной и фазовой манипуляцией квадратур несущего колебания взаимно ортогональными бинарными последовательностями по п. 1, отличающийся тем, что квадратуры радиоимпульса манипулируются по амплитуде таким образом, что для отдельных фрагментов передаваемой кодовой комбинации, содержащей некоторое количество определенных элементов, формируются определенные отношения амплитуд синусоидальной и косинусоидальной квадратур.
4. Способ квадратурной амплитудно-фазовой модуляции с раздельной амплитудной и фазовой манипуляцией квадратур несущего колебания взаимно ортогональными бинарными последовательностями, отличающийся тем, что модуляция квадратур несущего колебания производится на длительности одного радиоимпульса одновременно двумя разными взаимно ортогональными бинарными последовательностями, выбор которых из общего их числа R обусловлен конкретным видом передаваемого фрагмента кодовой комбинации, что позволяет передавать количество различных фрагментов кодовых комбинаций m, равное числу сочетаний по 2 из общего числа К различных взаимно ортогональных бинарных последовательностей 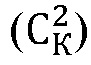 , при этом количество знаков ZM в передаваемом фрагменте кодовой комбинации за счет манипуляции по фазе квадратур сигнала бинарными взаимно ортогональными бинарными последовательностями равно целому числу значения выражения
, при этом количество знаков ZM в передаваемом фрагменте кодовой комбинации за счет манипуляции по фазе квадратур сигнала бинарными взаимно ортогональными бинарными последовательностями равно целому числу значения выражения 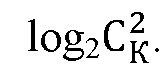
5. Способ квадратурной амплитудно-фазовой модуляции с раздельной амплитудной и фазовой манипуляцией квадратур несущего колебания взаимно ортогональными бинарными последовательностями по п. 4, отличающийся тем, что число образованных за счет раздельной амплитудной и фазовой манипуляции квадратур несущего колебания взаимно ортогональными бинарными последовательностями вершин сигнальных созвездий, превышающее число вершин сигнальных созвездий, необходимое для передачи кодовых комбинаций заданной значности, используется для передачи различного рода команд управления приемо-передающей аппаратурой канала связи.
| УСТРОЙСТВО ФОРМИРОВАНИЯ СИГНАЛОВ КВАДРАТУРНОЙ АМПЛИТУДНОЙ МАНИПУЛЯЦИИ | 2014 |
|
RU2568315C1 |
| СПОСОБ И СИСТЕМА ДЛЯ ФОРМИРОВАНИЯ ВОСЬМИТОЧЕЧНОЙ СИГНАЛЬНО-КОДОВОЙ КОНСТРУКЦИИ | 2016 |
|
RU2614585C1 |
| СПОСОБ ФОРМИРОВАНИЯ АМПЛИТУДНО-ФАЗОМАНИПУЛИРОВАННОГО СИГНАЛА | 2013 |
|
RU2537042C1 |
| СПОСОБ И УСТРОЙСТВО ФОРМИРОВАНИЯ СИГНАЛОВ КВАДРАТУРНОЙ АМПЛИТУДНОЙ МАНИПУЛЯЦИИ | 2012 |
|
RU2486681C1 |
| Генератор квадратурных гармони-чЕСКиХ КОлЕбАНий | 1979 |
|
SU798890A1 |
| US 4646326 A1, 24.02.1987. | |||
Авторы
Даты
2020-12-08—Публикация
2020-07-10—Подача