Изобретение относится к области радиотехники и предназначено для передачи дискретных сообщений по каналам связи с быстро меняющимися параметрами, например, по каналам связи с псевдослучайной перестройкой рабочей частоты.
Достигаемый технический результат – максимально возможное повышение помехоустойчивости передачи дискретных сообщений по каналам связи с переменными параметрами. Особенностью предлагаемого способа квадратурной внутриимпульсной фазовой модуляции (КВИФМ) является то, что, в отличие квадратурной амплитудно-фазовой модуляции (КАФМ), принятой за прототип, передача сообщения при КВИФМ за счет амплитудной модуляции не производится, а производится исключительно только по фазе, и на приемном конце радиолинии по внесенным на передающей стороне радиолинии признакам, заключающимся во внутриимпульсной фазовой манипуляции квадратур несущего колебания взаимно ортогональными бинарными последовательностями, по максимальным значениям сигналов и разности фаз квадратур определяются конкретные значения двух вершин сигнального созвездия из общего их числа, которые обусловливают конкретное решение о принимаемой кодовой комбинации. В заявляемом изобретении КВИФМ, в отличие от способа КАФМ,в котором относительной фазовой манипуляцией квадратур передается один конкретный символ кодовой комбинации, относительная фазовая манипуляция квадратур используется для указания одного из двух семейств в общемсигнальном созвездии, которому принадлежит передаваемая кодовая комбинация. На приемной стороне канала связи квадратуры сигнала принимаются индивидуально, с помощью фазовращателейликвидируется разность фаз между ними и осуществляется их взаимно корреляционный прием, который позволяет однозначно идентифицировать принимаемую кодовую комбинацию.
Изобретение относится к области радиотехники и предназначено для передачи дискретных сообщений по каналам связи с быстро меняющимися параметрами, например, по каналам связи с псевдослучайной перестройкой рабочей частоты (ППРЧ). Особенностью предлагаемого метода КВИФМ является то, что информация о передаваемых кодовых комбинацияхсодержитсякак вмодулирующих квадратуры сигнала взаимно ортогональных бинарных последовательностях, так и в их начальных фазах. Сигнальные созвездия делятся на две отдельные группы, которые отличаются друг от друга тем, что для их формирования используются как не инвертированные, так и инвертированные взаимно ортогональные бинарные последовательности.
За аналог изобретения принятметод квадратурной амплитудной модуляции (КАМ) [Бернард Скляр. Цифровая связь. –М: Изд. дом «Вильямс», 2003. Стр. 585], при котором значением амплитуд квадратур каждого отдельного радиоимпульсавозможно передавать сразу большое количество элементарных символов. Недостатком КАМ является то, что во времяпередачи сигнала уровень радиоимпульсов постоянно меняется в широких пределах, что приводит к большим энергетическим потерям равным порядка 6 дБ. Кроме того, в модеме с КАМ при увеличении пропускной способности канала связи за счет увеличения значности сигнального созвездия векторное расстояние между вершинами уменьшается и в результате этого увеличивается вероятность ошибки при приеме кодовой комбинации. Еще одним недостатком КАМ является то, что одиночным импульсом невозможно передавать очередную кодовую комбинацию так как для ее декодирования необходимо знать начальные фазы квадратур, информация о которых закладывается в преамбуле передаваемого методами КАМ сообщении. В связи с этим модемы с КАМ не могут быть использованы в каналах связи с быстро меняющимися параметрами, например, в каналах связи с ППРЧ.
Другого рода аналогом заявляемого метода являетсяметод двойной относительной фазовой манипуляции (ДОФМ) [Петрович Н.Т. Передача дискретной информации в каналах с фазовой манипуляцией. Москва, Сов.радио, 1965. Стр. 106-109], при котором квадратуры несущего колебания играют разные роли: первый информационный символ передается изменением фазы одной квадратуры радиоимпульса на 0° или 180°, а второй информационный символ передается изменением фазы второй квадратуры радиоимпульса на 0° или 180° относительно фаз соответствующих квадратур предшествующего радиоимпульса в зависимости от того, какие значения имеют очередные передаваемые элементы кодовой комбинации («1» или «0»).Одним из вариантов детектирования сигналов с ДОФМ является метод сравнения фаз, в котором используется автокорреляционный способ детектирования сигналов с перемножением текущего сигнала и задержанного на время длительности элементарной посылки [Петрович Н.Т. Передача дискретной информации в каналах с фазовой манипуляцией. Москва, Сов.радио, 1965. Рис. 2.14].Недостатком этого аналога является то, что одним очередным радиоимпульсом возможно передавать всего лишь два значения символов кодовой комбинации. А увеличение кратности фазовой манипуляции снижает помехоустойчивость модема. Вторым недостатком ДОФМ является необходимость сравнения фаз двух соседствующих по времени элементарных посылок, что ограничивает возможность использования модемов ДОФМ в каналах связи с быстро изменяющимися параметрами и исключает возможность поэлементной передачи дискретных сообщений в режиме ППРЧ, поскольку требует одновременного присутствия на одной и той же частоте, как минимум, двух соседних по времени элементарных посылок передаваемого сообщения.
Известен способ фазо-кодовой внутриимпульсной манипуляции, который используется в радиолокации для повышения помехоустойчивости приема отраженных от объектов радиоимпульсов [Бакут П.А. и др. Вопросы статистической теории радиолокации. Том II. М.:- Советское радио. 1964. Стр. 494].Этот способ внутриимпульсной фазо-кодовой манипуляции используется в заявляемом изобретении для фазовой манипуляции взаимно ортогональными бинарными последовательностями отдельно каждой из квадратур передаваемого в соответствующий момент времени радиоимпульса, что дает возможность разделять эти квадратуры на приемной стороне радиолинии и позволяет выносить решения о принимаемых элементах сообщения в соответствии с конкретным сочетанием двух взаимно ортогональных бинарных последовательностей, манипулирующих фазы квадратур радиоимпульсова также разностиначальных фаз квадратур радиоимпульсов после их деманипуляциии ликвидации разности фаз между ними на приемной стороне канала связи.
Известен метод приема маломощных сигналов методом взаимной корреляции [Кулакова В. И. Обнаружение слабых сигналов методом взаимной корреляции с компенсацией фазовых нестабильностей при радиоконтроле частотного ресурса спутниковых систем связи // Системы управления, связи и безопасности. 2020. № 1.С. 33-48]. В этом аналоге маломощные сигналы обнаруживаются посредством перемножения двух сигналов, принятых от разных спутников, с последующим усреднением во времени результата перемножения (взаимно корреляционный прием сигналов). Этот метод детектирования используется в заявляемом изобретении для получения информации о номере сигнального созвездия и вынесении решения о принимаемой кодовой комбинации.
В качестве прототипа заявляемого метода принят СПОСОБ КВАДРАТУРНОЙ АМПЛИТУДНО-ФАЗОВОЙ МОДУЛЯЦИИ (КАФМ) (патент № 2738091, публ. 08.12.2020 г.). Способ КАФМ относительно высоко помехоустойчив по сравнению с КАМ благодаря тому, что в отличие от КАМ, все передаваемые одиночные радиоимпульсы имеют одинаковую максимально возможную амплитуду. Однако, в случае манипуляции амплитуды для повышения пропускной способности канала связи помехоустойчивость модема с КАФМ существенно снижается. Поэтому в заявляемом способе КВИФМ манипуляция амплитуды не используется. Кроме того, в указанном способе КАФМ на передающей стороне канала связи разность фаз между квадратурами используется для передачи одного бита из общего их числа в кодовой комбинации, что снижает информационную эффективность модема по сравнению с заявляемым вариантом. На приемной стороне канала связи при использовании КАФМ не производится взаимно-корреляционное детектирование квадратур радиоимпульса, в результате чего модем с КАФМ (прототип) в значительной степени энергетически проигрывает вновь заявляемому модему с КВИФМ.
Заявляемый способ квадратурной внутриимпульсной фазовой модуляции имеет преимущество перед аналогами, так как позволяет передавать достаточно большое число элементов кодовой комбинации с высокой помехоустойчивостью одним отдельно взятым радиоимпульсом без каких-либо дополнительных преамбул, что дает возможность использовать данный метод для передачи достаточно большого количества элементов в кодовой комбинации одиночным радиоимпульсом в режиме ППРЧ. Метод КВИФМ имеет преимущество перед прототипом, обеспечивая значительный энергетический выигрыш относительно егоза счет взаимно корреляционного детектирования квадратур в демодуляторе принимаемого сигнала. В заявляемом способе КВИФМ, как ив прототипе КАФМ, на передающем конце канала связи производится внутриимпульсная манипуляция начальных фаз квадратур радиоимпульса разными взаимно ортогональными бинарными последовательностями. От количества используемых для манипуляции взаимно ортогональных бинарных последовательностей зависит число вершин в сигнальном созвездии. Если синусоидальная квадратура несущего колебания манипулируется взаимно ортогональными бинарными последовательностями в количестве M а косинусоидальная квадратура несущего колебания манипулируется такого же рода бинарными последовательностями в количестве N, то этим количеством бинарных последовательностей можно передавать z кодовых комбинаций:z=N·M. В случае дополнительного использования относительной манипуляции квадратур сигнала по фазе на 180° для передачи такого же количества z кодовых комбинаций количество M (или N) взаимно ортогональных бинарных последовательностей может быть уменьшено в 2 раза, что дает возможность уменьшить, соответственно, полосу частот, занимаемую спектром передаваемого сигнала с внутриимпульсной модуляцией.
При количестве вершин z сигнального созвездия можно одним радиоимпульсом передавать одновременно Rz бит информации, где Rz целое число выражения log2z: Rz=ent[log2z].
Наиболее рациональный метод манипуляции, который обеспечивает максимальную помехоустойчивость реализуется в том случае, когда на интервале времени, в течение которого фаза несущего колебания остается постоянной, укладывается целое число периодов несущего колебания.
Далее, для примера, в качестве взаимно ортогональных бинарных последовательностей используются функции Уолша [Радиотехнические цепи и сигналы. Под ред. К,А, Самойло. М.: Радио и связь. 1982. Стр. 79-82, табл. 2-4.].
В таблице 1 приведен вариант используемых порядков функций Уолша Wm и Wn для случая передачи одним радиоимпульсом семиэлементной кодовой комбинации (десятичных чисел от 0 до 127).
Таблица 1
В таблице 2 приведены значения порядков функций Уолша еще для 128 чисел (от 128 до255), передаваемых за счет смены знака 8 функций Уолша (от 16 до 23) на обратный, то есть за счет инверсии функций Уолша, обеспечивающих изменение знака соответствующей квадратуры сигнала на 180°.
Таблица 2
Таким образом, для передачи одним радиоимпульсом сообщения объемом один байт достаточно 24-х функций Уолша.
Если, например, передается число 53, то для внутриимпульсной манипуляции используются функции Уолша W5 и W19:

где u1c – косинусоидальная квадратура радиоимпульса, а u1s – синусоидальная квадратура радиоимпульса. В этом случае передается сигнал:
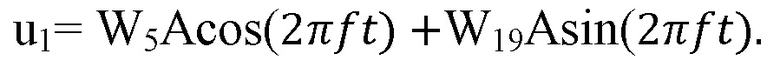
Если же, например, передается число 181, то для внутриимпульсной манипуляции используются функции Уолша W5 и -W19:
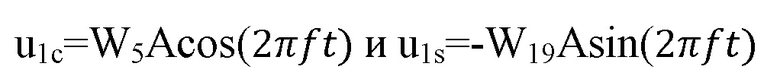
где u1c – косинусоидальная квадратура радиоимпульса, а u1s – синусоидальная квадратура радиоимпульса. В этом случае передается сигнал:
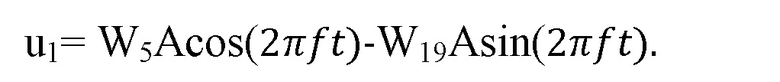
Разница при передаче числа 181 и числа 53 будет только в знаке функции Уолша, то есть только в начальной фазесинусоидальной квадратуры.
Алгоритм определения порядка m функции Уолшадля десятичного числа N, соответствующего передаваемому байту,описывается выражением:
m = (NMOD (128)) MOD (16).
А алгоритм определения порядка n функции Уолша для десятичного числа N (с учетом знака ±), соответствующего передаваемому байту, описывается, соответственно, выражением:
n = (ent[((NMOD (128)) / 16)] + 16) (1 - (1 - (127.5 - N) / ABS(127.5 - N))).
Необходимо заметить, что увеличение порядка функций Уолша приводит к соответствующему расширению спектра передаваемого сигнала, но это не снижает помехоустойчивость при приеме сообщения, так как на приемной стороне решение принимается после деманипуляции сигнала, которая уменьшает спектр сигнала и возвращает ему значение, которое соответствует скорости манипуляции, обусловленной длительностью радиоимпульса без манипуляции взаимно ортогональными бинарными последовательностями типа функций Уолша.
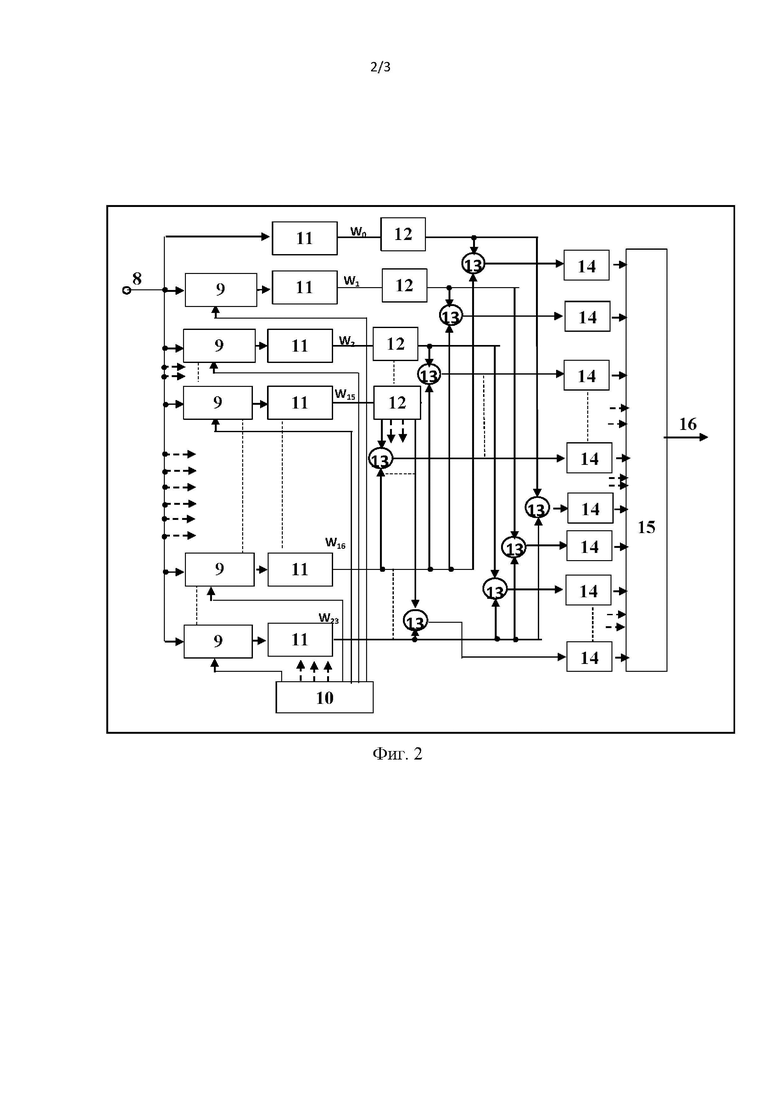
На фиг. 1 изображена блок-схема модулятора с КВИФМ.
На фиг. 1 обозначено:
1 – вход модулятора для передаваемых кодовых комбинаций;
2 – генератор несущего колебания;
3 – фазовращатель несущего колебания на 90°;
4 – манипуляторы фаз квадратур несущего колебания взаимно ортогональными бинарными последовательностями;
5 – генератор взаимно ортогональных бинарных последовательностей;
6 – сумматор квадратур несущего колебания;
7 – выход манипулятора (на вход передатчика).
Генератор (2) формирует гармоническое колебание 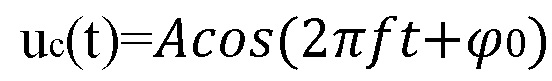 , являющееся косинусоидальной квадратурой несущего колебания, которое подается на фазовращатель (3), создающий синусоидальную квадратуру несущего колебания
, являющееся косинусоидальной квадратурой несущего колебания, которое подается на фазовращатель (3), создающий синусоидальную квадратуру несущего колебания  . Манипуляторы фаз (4) манипулируют фазы квадратур колебания согласно взаимно ортогональным бинарным последовательностям, поступающим от генератора этих последовательностей (5). Форма взаимно ортогональных бинарных последовательностей обусловлена кодовой комбинацией, поступающей на вход модулятора (1). Манипулированные по фазе квадратуры суммируются на сумматоре (6) и поступают на выход модулятора (7).
. Манипуляторы фаз (4) манипулируют фазы квадратур колебания согласно взаимно ортогональным бинарным последовательностям, поступающим от генератора этих последовательностей (5). Форма взаимно ортогональных бинарных последовательностей обусловлена кодовой комбинацией, поступающей на вход модулятора (1). Манипулированные по фазе квадратуры суммируются на сумматоре (6) и поступают на выход модулятора (7).
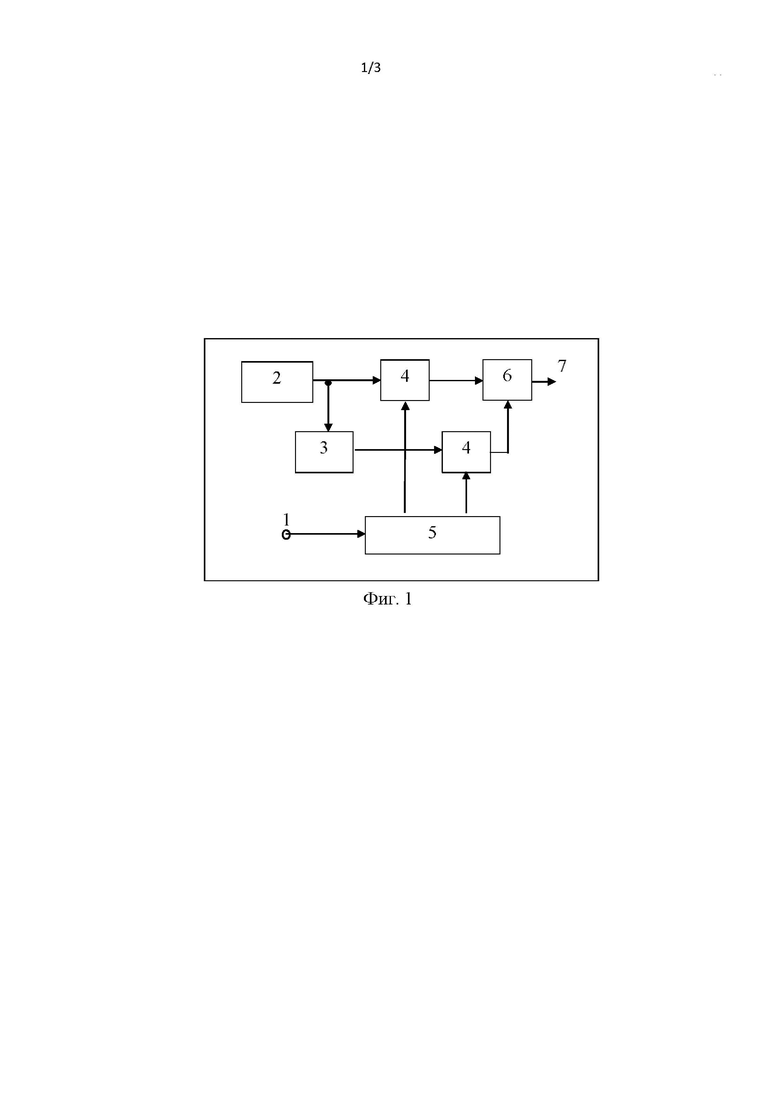
На фиг. 2 приведена блок-схема демодулятора сигналов с КВИФМ на приемной стороне радиолинии.
На фиг. 2 обозначено:
8 – вход демодулятора;
9 – деманипулятры фазы принимаемого сигнала взаимно ортогональными бинарными последовательностями (в рассматриваемом примере - функциями Уолша);
10 – генератор взаимно ортогональных бинарных последовательностей (в рассматриваемом примере - функций Уолша);
11 – узкополосные фильтры, рассчитанные на прием сигналов длительностью равной длительности принимаемого радиоимпульса;
12 – фазовращатели гармонических колебаний на 900;
13 – перемножители сигналов;
14 – интеграторы (коммутируемы фильтры нижних частот);
15 – решающее устройство;
16 – выход демодулятора.
Если бы в точке приема сигнала помехи отсутствовали, то сигнал uпр(t) на входе демодулятора (8) отличался бы от сигнала на выходе модулятора передатчика только уровнем амплитуды и начальной фазой, обусловленной временем распространения сигнала в радиолинии:
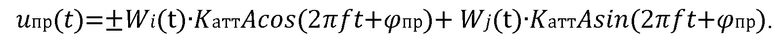
На входе демодулятора стоят деманипуляторы (9), на второй вход которых подаются взаимноортогональныебнарные последовательности (в рассматриваемом примере – функции Уолша Wl),и после которых имеет место напряжение u2(t):

Известно, что произведение функций Уолша является новой функцией Уолша [Радиотехнические цепи и сигналы. Под ред. К,А, Самойло. М.: Радио и связь. 1982. Стр. 81]. При этом, если порядки перемножаемых функций Уолша одинаковые, то результатом перемножения является функция Уолша нулевого порядка, имеющей значение на интервале длительности радиоимпульса равное единице. Поэтому после деманипуляторов (9), если перемножаются функции разных порядков имеют место колебания, манипулированные по фазе функциями Уолша:
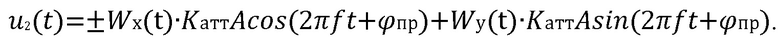
Если же порядки функций Уолша совпадают, то тогда на выходе деманипуляторов (9) имеют место колебания:
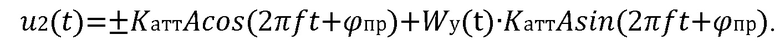
или
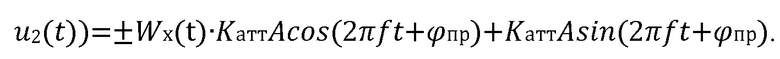
Поскольку при фазовой манипуляции гармонических колебаний функциями Уолша порядком не равным нулю, в случае, когда на отрезках времени с начальными фазами равными 0° и 180° укладывается одинаковое число периодов, одна половина из которых имеет фазу равную нулю, а вторая половина имеет противоположную фазу, то на выходе узкополосных фильтров (11) при окончании каждого принимаемого радиоимпульса уровень высокочастотного колебания будет равен нулю. Если же фаза радиоимпульса в течение всего времени его приема остается постоянной, то на выходе соответствующего узкополосного фильтра к моменту окончания этого радиоимпульса накапливается уровень его амплитуды пропорциональный амплитуде соответствующей квадратуры принимаемого радиоимпульса.
Если перемножаются функций Уолша разных порядковWl и Wi (Wl≠Wi), то, благодаря их взаимной ортогональности, на выходах соответствующих узкополосных фильтров(11) напряжения будут равны нулю. Если же перемножаются функции Уолша одинакового порядка (Wl=Wi), то на выходах двух соответствующих узкополосных фильтров (11) напряжения будут равны, соответственно
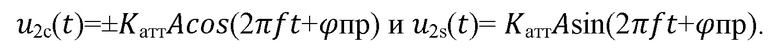
У сигналов на выходах фильтров, соответствующих косинусоидальным (или синусоидальным) квадратурам с помощью фазовращателей (12) изменяют фазу на 900, что позволяет для вышеприведенного примера у синусоидальной икосинусоидальной квадратур при приеме чисел от 0 до 127 получать одинаковые начальные фазы, а при приеме чисел от 128 до 255 фазы сигналов, поступающих с выхода узкополосных фильтров (11), получать с противоположными начальными фазами. Сигналы с выходов фазовращателей (12) и с выхода фильтров, на выходе которых фазовращатели отсутствуют попарно перемножаются на перемножителях (13) и интегрируются с помощью коммутируемых фильтров нижних частот (интеграторов) (14) [Финк Л.М. Теория передачи дискретных сообщений. М.: Сов.радио. 1970. Стр. 153-154]. Выход каждого интегратора (14) соответствует одному из 128 чисел. Но если в результате перемножения сигналов на выходе интегратора имеет место положительное напряжение, то принимаемому числу присваивается значение, например, в пределах от 0 до 127, а если на выходе соответствующего интегратора имеет место отрицательное напряжение, то принимаемому числу присваивается значение из другой половины передаваемого массива чисел в пределах от 128 до 255, в зависимости от конкретного интегратора, на выходе которого имеет место напряжение, отличное от нуля. Решение о конкретном значении принимаемого числа выносит решающее устройство (15).После принятия решения это число поступает на выход демодулятора (16).
Таким образом, решающее устройство (15) по максимальному значению модуля напряжения на выходе интегратора (14) определяет номера двух узкополосных фильтров (11), на выходах которых имеются напряжения с наибольшими амплитудами. Одновременно решающим устройством (15) определяется и знак напряжения на выходе интегратора (14) с наибольшим значением модуля этого напряжения. Согласно определенным номерам фильтров (11) и знаку напряжения на выходе интегратора (14), имеющего наибольший модуль напряжения на своем выходе, выносится решение о принимаемом числе (в нашем примере передачи одним радиоимпульсом одного байта информации из общего массива чисел 256).
Заявляемый способ квадратурной внутриимпульсной фазовой модуляции в отличие от прототипа, имеет более высокую помехоустойчивость за счет того, что разность фаз между квадратурами сигнала на приемном конце канала связи ликвидируется с помощью фазовращателей и осуществляется их взаимно корреляционное детектирование, обеспечивающее максимально возможную помехоустойчивость приема сообщения.
На фиг. 3 приведены кривые помехоустойчивости для передачи одного байта сообщения для различных видов модуляции.
На фиг. 3 обозначено:
17 – кривая помехоустойчивости передачи одного байта сообщения методом квадратурной амплитудной модуляции (КАМ) (аналог);
18 – кривая помехоустойчивости передачи одного байта сообщения методом простой амплитудной модуляции (АМ);
19 – кривая помехоустойчивости передачи одного байта сообщения методом частотной модуляции (ЧМ);
20 – кривая помехоустойчивости передачи одного байта сообщения методом относительной фазовой модуляции (ДОФМ) (аналог);
21 – кривая помехоустойчивости передачи одного байта сообщения методом относительной фазовой модуляции (ОФМ);
22 – кривая помехоустойчивости передачи одного байта сообщения методом квадратурной амплитудно-фазовой модуляции (КАФМ) (прототип);
23 – кривая помехоустойчивости передачи одного байта сообщения методом квадратурной внутриимпульсной фазовой модуляции (КВИФМ) (заявляемый метод);
Кривая (17) получена методом экстраполяции из кривых помехоустойчивостиКАМ, приведенных в [Бернард Скляр. Цифровая связь. –М: Изд. дом «Вильямс», 2003. Стр. 256. Рис. 435].
Кривая (18) для АМ рассчитана по формуле, описывающей вероятность ошибочного приема передаваемой в одних и тех же условиях 8-элементной кодовой комбинации:
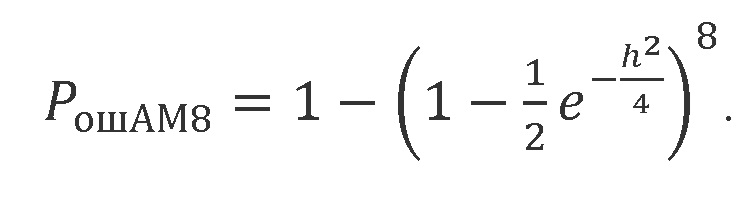
Кривые (19) и (20) соответственно для ЧМ и ДОФМ рассчитаны аналогичным образом по формуле, описывающей вероятность ошибочного приема передаваемой в одних и тех же условиях 8-элементной кодовой комбинации:

Степень 9 в последней формуле для ДОФМ в отличие от степени 8 в предыдущих двух формулах для АМ и ЧМ взята в предположении.что передача сообщения производится в канале связи с ППРЧ и в случае ДОФМ для передачи каждого байта требуется не 8 бит а 9 бит (один первый бит - «опорный»).
Кривая (21) для ОФМ рассчитана аналогичным образом по формуле, описывающей вероятность ошибочного приема байта, передаваемого методом ОФМ:
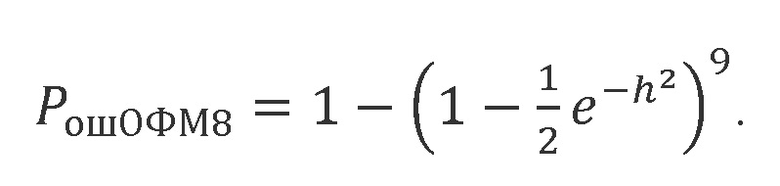
Кривая (22) для модема с КВИФМ,в котором не производится когерентное сложение квадратур принимаемого радиоимпульса,(для прототипа) рассчитывалась по формуле:
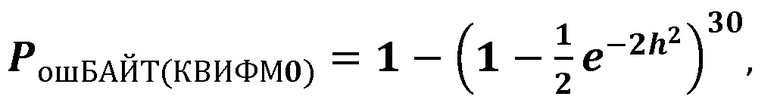
в которойучитывается как факт равномерного распределения мощности радиоимпульса между его квадратурами, так и факт увеличения мощности передачи одного байта по сравнению с мощностью передачи одного бита сообщения. Степень 30 обусловлена числом сравнения уровней сигналов в демодуляторе при определении номеров функций Уолша для первой и второйих половины.
Кривая (23) для заявляемого модулятора с КВИФМ, у которого на приемной стороне радиолинии производится когерентное сложение квадратур радиоимпульса, с учетом получаемого энергетического выигрыша рассчитывалась по формуле:
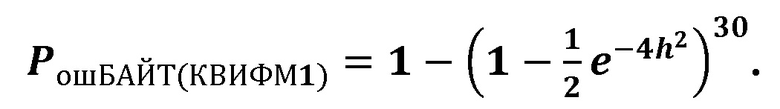
Подводя итог всему вышеизложенному, можно описать алгоритм функционирования сигнала с квадратурной внутриимпульсной фазовой модуляцией на передающем конце радиолинии, например, при передаче очередного байта сообщения следующим образом:
1. Поступающий для передачи байт сообщения соответствует числу N (одному из 256 чисел).
1.1. Определяется порядок функции Уолша m для соответствующего столбца кодовой матрицы (см. таблицу 1 и таблицу 2)по алгоритму:
m= (NMOD (128)) MOD (16).
1.2. Определяется порядок функции Уолша n и ее знак для соответствующей строки кодовой матрицы (см. таблицу 1 и таблицу 2)по алгоритму:
n = (ent[((N MOD (128)) / 16)] + 16) (1 - (1 - (127.5 - N) / ABS(127.5 - N)))
2. Формируется гармоническое колебание uс(t) на заданной частоте f, которое имеет какую-то начальную фазу φ0.
3. С помощью фазовращателя формируется второе гармоническое колебание us(t) на этой же частоте, которое имеет начальную фазу (φ0-π/2).
4. Гармоническое колебание uc(t) манипулируется по фазе на 180° функциями Уолша Wm:Uc(t)=Wm*uc(t).
5. Гармоническое колебание us(t) манипулируется по фазе на 180° функциями Уолша Wn:Us(t)=Wn*us(t).
6. Полученные таким образом колебания Uc(t) и Us(t) суммируются и подаются на вход возбудителя передатчика для преобразования по частоте, усиления по мощности и излучения в эфир.
На приемном конце канала связи осуществляется следующий алгоритм демодуляции и декодирования:
1. Принимаемый сигнал деманипулируется по фазе на приемном конце канала связи параллельно всеми функциями Уолша порядка m и n, генерируемым и синхронно с функциями Уолша на передающем конце канала связи.
2. Деманипулированные по фазе колебания с выхода деманипуляторов подаются на входы узкополосных фильтров.
3. На выходах тех двух фильтров, которые соответствуют порядкам функций Уолша, используемых для передачи принимаемого байта появляются гармонические колебания. На выходах всех остальных фильтров реакция на принимаемый сигнал будет равна нулю так как манипулирующие квадратуры функции Уолша являются взаимно ортогональными функциями.
4. Сигналы с выходов фильтров, которые соответствуют функциям Уолша для столбцов кодовой матрицы (или для строк этой матрицы) поступают на входы фазовращателей на 900, что позволяет получить разность фаз между квадратурами равную или 0°, или 180°.
5. Сигналы с выходов всех фазовращателей и всех узкополосных фильтров, не имеющих на своих выходах фазовращателей, попарно перемножаются. Число перемножителей равно половине количества принимаемых кодовых комбинаций (при передаче байтов это число равно 128).
6. Результаты перемножения сигналов интегрируются.
7. Решающее устройство определяет тот интегратор, на выходе которого имеет место напряжение с наибольшим уровнем. При этом, если напряжение на выходе интегратора имеет положительное значение, то в этом случае принимаемому числу присваивается соответствующее значение из первой половины возможных значений, а если это напряжение имеет отрицательное значение, топринимаемому числу присваивается соответствующее значение из второй половины возможных значений.
Заявляемый способ квадратурной внутриимпульсной фазовой модуляции в отличие от прототипа имеет более высокую помехоустойчивость, за счет того, чтона приемной стороне производится нивелирование разности фаз между квадратурами принимаемого сигнала, и осуществляется их взаимнокорреляционное детектирование, которое позволяет обеспечить максимально возможную помехоустойчивость принимаемого сигнала.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ КВАДРАТУРНОЙ АМПЛИТУДНО-ФАЗОВОЙ МОДУЛЯЦИИ | 2020 |
|
RU2738091C1 |
| СПОСОБ ДВОЙНОЙ ОТНОСИТЕЛЬНОЙ ФАЗОВОЙ МОДУЛЯЦИИ | 2023 |
|
RU2804056C1 |
| СПОСОБ ФОРМИРОВАНИЯ ШУМОПОДОБНЫХ РАДИОИМПУЛЬСОВ ДЛЯ ПЕРЕДАЧИ БИНАРНЫХ СИМВОЛОВ ИНФОРМАЦИИ СЛОЖНЫМИ СИГНАЛАМИ | 2003 |
|
RU2231924C1 |
| СПОСОБ ПОВЫШЕНИЯ ПРОПУСКНОЙ СПОСОБНОСТИ И ОЦЕНКИ КАЧЕСТВА КОРОТКОВОЛНОВЫХ КАНАЛОВ СВЯЗИ С ЧАСТОТНОЙ МАНИПУЛЯЦИЕЙ ПРИ ИХ АДАПТАЦИИ К УСЛОВИЯМ СВЯЗИ | 2020 |
|
RU2746495C1 |
| СПОСОБ ФОРМИРОВАНИЯ ПОМЕХОУСТОЙЧИВЫХ СИГНАЛОВ | 2009 |
|
RU2412551C2 |
| СПОСОБ ПЕРЕДАЧИ ДВОИЧНОЙ ИНФОРМАЦИИ СЛОЖНЫМИ СИГНАЛАМИ С ВНУТРИИМПУЛЬСНОЙ МИНИМАЛЬНОЙ ЧАСТОТНОЙ МАНИПУЛЯЦИЕЙ | 2008 |
|
RU2358404C1 |
| Способ передачи информации с помощью широкополосных сигналов | 2018 |
|
RU2713384C1 |
| Способ передачи дискретной информации с помощью широкополосных сигналов | 2022 |
|
RU2816580C1 |
| УСТРОЙСТВО МНОГОКАНАЛЬНОЙ РАДИОСВЯЗИ | 2023 |
|
RU2809552C1 |
| СПОСОБ ДЕМОДУЛЯЦИИ РАДИОСИГНАЛОВ С ФАЗОРАЗНОСТНОЙ МОДУЛЯЦИЕЙ | 2011 |
|
RU2469488C1 |

Изобретение относится к области радиотехники. Технический результат – повышение помехоустойчивости. Для этого предложен способ квадратурной внутриимпульсной фазовой модуляции, особенностью которого является то, что передача сообщения за счет амплитудной модуляции не производится, а производится исключительно только по фазе, и на приемном конце радиолинии по внесенным на передающей стороне радиолинии признакам, заключающимся во внутриимпульсной фазовой манипуляции квадратур несущего колебания взаимно ортогональными бинарными последовательностями, по максимальным значениям сигналов и разности фаз квадратур определяются конкретные значения двух вершин сигнального созвездия из общего их числа, которые обусловливают конкретное решение о принимаемой кодовой комбинации. В данном способе относительная фазовая манипуляция квадратур используется для указания одного из двух семейств в общем сигнальном созвездии, которому принадлежит передаваемая кодовая комбинация. На приемной стороне канала связи квадратуры сигнала принимаются индивидуально, с помощью фазовращателей ликвидируется разность фаз между ними и осуществляется их взаимно корреляционный прием. 3 ил., 2 табл.
Способ квадратурной внутриимпульсной фазовой модуляции с раздельной манипуляцией фаз квадратур несущего колебания взаимно ортогональными бинарными последовательностями, отличающийся тем, что в модеме весь массив передаваемых кодовых комбинаций делится на две равные по количеству кодовых комбинаций группы и для каждой из этих групп производится манипуляция фазы одной из квадратур взаимно ортогональными бинарными последовательностями, соответственно, в одном случае без инверсии, а в другом случае с инверсией, а в демодуляторе после внутриимпульсной деманипуляции квадратур сигнала с помощью фазовращателей ликвидируется разность фаз между ними и производится их взаимно корреляционное детектирование и вынесение решения о принимаемой кодовой комбинации с учетом идентифицированной пары взаимно ортогональных бинарных последовательностей и разности фаз между квадратурами.
| СПОСОБ КВАДРАТУРНОЙ АМПЛИТУДНО-ФАЗОВОЙ МОДУЛЯЦИИ | 2020 |
|
RU2738091C1 |
| УСТРОЙСТВО ФОРМИРОВАНИЯ СИГНАЛОВ КВАДРАТУРНОЙ АМПЛИТУДНОЙ МАНИПУЛЯЦИИ | 2014 |
|
RU2568315C1 |
| US 4646326 A1, 24.02.1987 | |||
| СХЕМА МОДУЛЯЦИИ НА НЕСКОЛЬКИХ НЕСУЩИХ, А ТАКЖЕ ПЕРЕДАЮЩЕЕ УСТРОЙСТВО И ПРИЕМНОЕ УСТРОЙСТВО, ИСПОЛЬЗУЮЩИЕ УКАЗАННУЮ СХЕМУ | 2006 |
|
RU2454808C2 |
Авторы
Даты
2022-02-07—Публикация
2021-05-26—Подача