Изобретение относится к способам определения остаточных напряжений и может быть использовано для определения распределения остаточных напряжений по сечению стенки трубы.
Известны экспериментальные способы определения остаточных напряжений в трубах (Соколов И.А., Уральский В.И. Остаточные напряжения и качество металлопродукции М.: Металлургия, 1981 г. с. 96), в которых предлагается фиксировать упругие деформации образцов при разрушающем либо частично разрушающем внешним воздействии на них и последующем расчете остаточных напряжений на основе проведенных измерений.
Известен способ Закса (Соколов И.А., Уральский В.И. Остаточные напряжения и качество металлопродукции М.: Металлургия, 1981 г. с. 96), который используется преимущественно для экспериментального определения остаточных напряжений в прутках и толстостенных трубах, предполагает определение распределения остаточных осевых, тангенциальных и радиальных напряжений по стенке трубы по результатам анализа ее деформации после послойной обточки с наружной поверхности. У метода есть существенные недостатки: невозможно определить напряжения по всей толщине сечения, так как, начиная с некоторого момента, стенка становится слишком тонкой для токарной обточки, в связи с этим деформации в этой области определяют экстраполяцией, что вносит погрешности; необходима корректировка деформационной кривой, построенной по экспериментальным данным; необходимы высокоточные средства измерения весьма малых деформаций изделия при последовательных удалениях слоев металла; возможны значительные погрешности при замерах на начальной стадии расточки; необходимо применение длинных образцов для исключения влияния концов, что в свою очередь требует специальных приспособлений для расточки и центровки изделия.
Известен способ «разрезных колец» для определения остаточных напряжений в тонких дисках и кольцах и доработан для определения остаточных напряжений в трубах (Биргер И.А. Остаточные напряжения. М.: Машгиз, 1963. 232 с.). Метод предполагает вырезку кольца из трубы, разрезке вдоль образующей и последующее измерение изменения диаметра в результате разрезки. После изменения диаметра кольца, как и во всех подобных способах, осуществляется переход от измеренных деформаций к напряжениям на основе законов теории упругости. Недостатком способа следует считать не учет дополнительных тангенциальных напряжений, возникающих при вырезке кольца, при разрезке кольца вдоль образующей.
Известен способ Давиденкова (Соколов И.А., Уральский В.И. Остаточные напряжения и качество металлопродукции М.: Металлургия, 1981 г. с. 96), в котором для определения тангенциальных остаточных напряжений образец трубы сначала разрезается по образующей с замером изменения диаметра, затем подвергается растворению в кислоте последовательными слоями небольшой толщины, при этом каждый раз измеряется изменение диаметра. Недостатком способа можно считать необходимость отрезки образка от трубы и разрезки его по образующей, что приводит к серьезному нарушению геометрии образца и как следствие меняет распределение остаточных напряжений в нем по сравнению с исходной трубой. При реализации способа возникают проблемы удаления слоев без нарушения геометрии трубы, что является источником дополнительных ошибок в определении остаточных тангенциальных напряжений даже в тонком поверхностном слое.
Известен способ Андерсена и Фальмана для определения остаточных напряжений в трубах (Остаточные напряжения: сборник статей / под ред. В.Р. Осгуда. М.: Иностранная литература, 1957. 395 с.), в котором авторы для определения тангенциальных остаточных напряжений применяют отрезку кольца от трубы и разрезку его по образующей с дальнейшим измерением изменения диаметра, а для определения осевых остаточных напряжений из трубы вырезается полоска, параллельная оси трубы, и замеряется возникший прогиб. Способ реализован для определения нормальных и касательных остаточных напряжений с использованием постепенного снятия слоев металла с вырезанного из трубы кольца и полоски (патент RU 2121666, МПК G01L1/06, 1996 г.). Недостатком этого способа является необходимость многократного снятия слоев металла с образца.
Известен способ определения остаточных напряжений в осесимметричных трубных изделиях после пластического деформирования, в котором известным экспериментальным способом определяют тангенциальное остаточное напряжение в поверхностном слое трубного изделия, по значению которого определяют распределение остаточных напряжений по поперечному сечению стенки трубы исходя из:
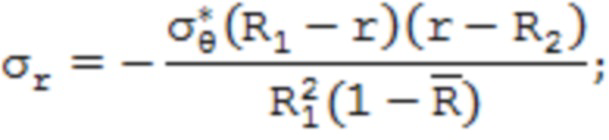
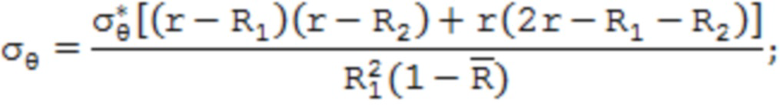
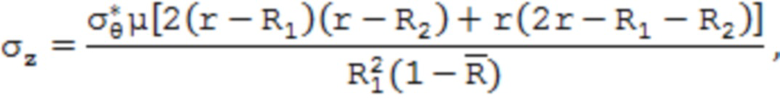
где уr, уи, уz – соответственно радиальные, тангенциальные и осевые остаточные напряжения; 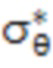 – значение тангенциального остаточного напряжения в поверхностном слое трубного изделия; R1 и R2 – соответственно внешний и внутренний радиусы трубы;
– значение тангенциального остаточного напряжения в поверхностном слое трубного изделия; R1 и R2 – соответственно внешний и внутренний радиусы трубы; 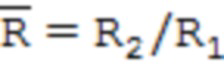 – безразмерный параметр, характеризующий относительную толщину стенки трубы;
– безразмерный параметр, характеризующий относительную толщину стенки трубы; 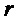
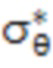 , например способом «разрезных колец», что приводит к снижению точности и достоверности способа. Кроме того способ не предполагает определение остаточного напряжения на внутренней поверхности трубы.
, например способом «разрезных колец», что приводит к снижению точности и достоверности способа. Кроме того способ не предполагает определение остаточного напряжения на внутренней поверхности трубы.
Проблема повышения точности и расширения возможностей методов определения остаточных напряжений решена в предлагаемом способе определения распределения остаточных напряжений по сечению стенки трубы, характеризующимся тем, что слой металла стравливают:
- с наружной поверхности образца трубы, вращая его в процессе травления, после чего фиксируют абсолютное изменение длины образца трубы относительно начальных размеров, определяют усредненное по толщине стравленного слоя осевое остаточное напряжение исходя из 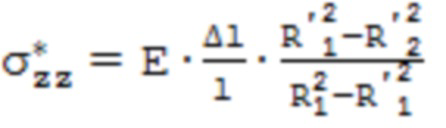 , где l – исходная длина образца трубы, E – модуль упругости материала трубы, и затем определяют распределение компонентов тензора остаточных напряжений по поперечному сечению стенки трубы из выражений:
, где l – исходная длина образца трубы, E – модуль упругости материала трубы, и затем определяют распределение компонентов тензора остаточных напряжений по поперечному сечению стенки трубы из выражений:
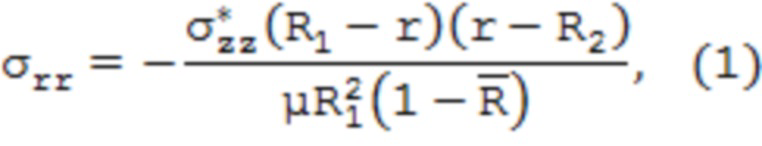
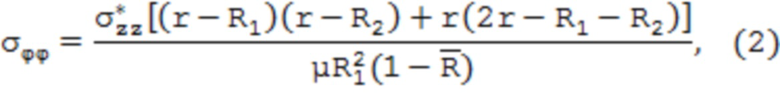
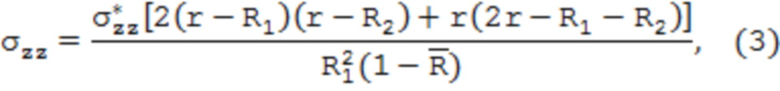
где уrr, уцц, уzz – соответственно радиальные, тангенциальные и осевые остаточные напряжения; R1 и R2 – соответственно внешний и внутренний радиусы трубы; 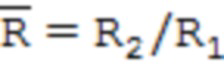 – безразмерный параметр, характеризующий относительную толщину стенки трубы;
– безразмерный параметр, характеризующий относительную толщину стенки трубы; 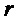
- с внутренней поверхности образца трубы, вращая его в процессе травления, после чего фиксируют абсолютное изменение длины образца трубы относительно начальных размеров, определяют усредненное по толщине стравленного слоя осевое остаточное напряжение исходя из  , где l – исходная длина образца трубы, E – модуль упругости материала трубы, и затем определяют распределение компонентов тензора остаточных напряжений по поперечному сечению стенки трубы из выражений:
, где l – исходная длина образца трубы, E – модуль упругости материала трубы, и затем определяют распределение компонентов тензора остаточных напряжений по поперечному сечению стенки трубы из выражений:
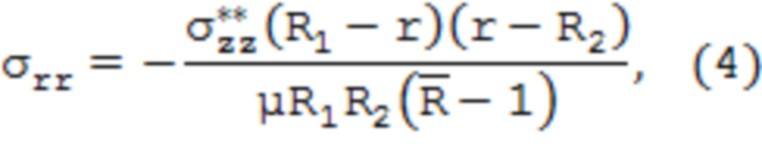
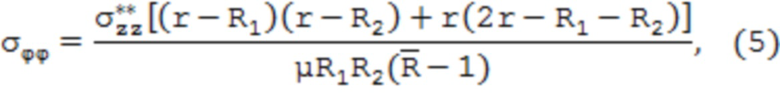
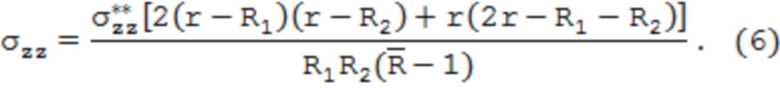
где уrr, уцц, уzz – соответственно радиальные, тангенциальные и осевые остаточные напряжения; 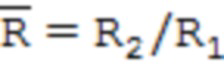 – безразмерный параметр, характеризующий относительную толщину стенки трубы;
– безразмерный параметр, характеризующий относительную толщину стенки трубы; 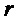
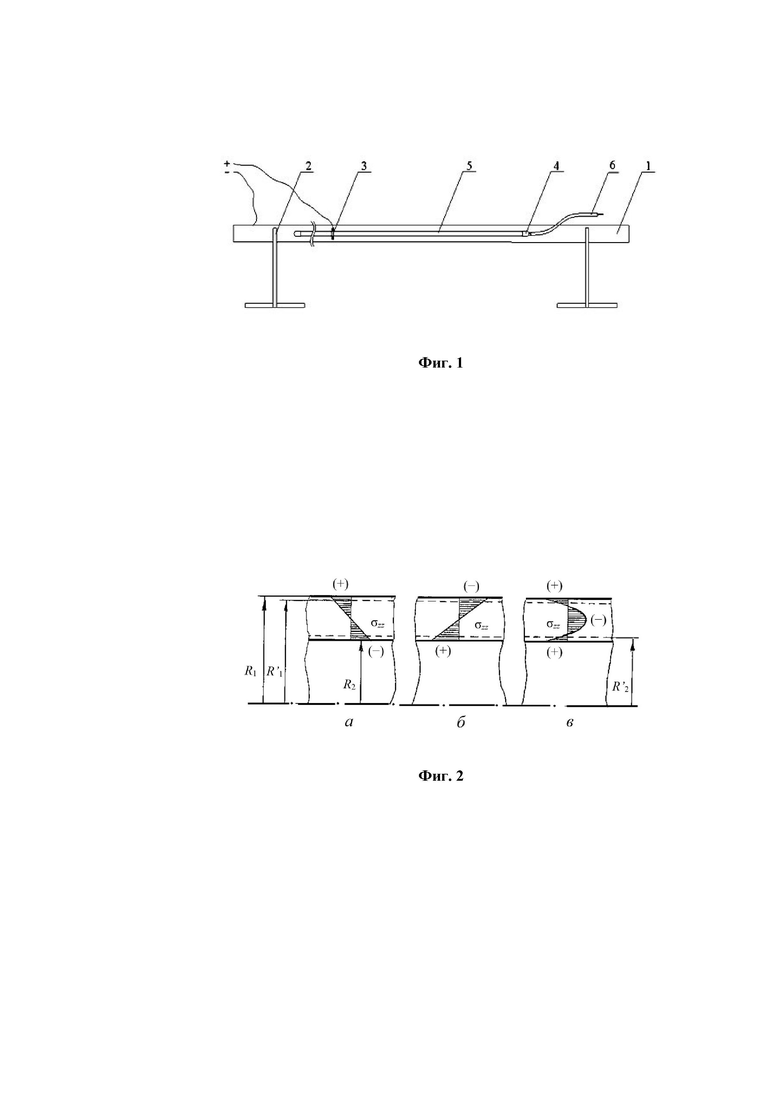
Предлагаемый способ может быть осуществлен следующим образом. Образец трубы подвергают травлению с наружной либо с внутренней поверхности на специальной установке, приведенной на фиг. 1. Измеренный образец 5 с предварительно заглушенными торцами с помощью полипропиленовых пробок и закрепленным подшипником 3 устанавливается в захватах 4, на гибких валах 6. После этого к подшипнику и ванне 1 подключаются контакты источника тока, и вся подвижная конструкция опускается в ванну 1, установленную на опорах 2 и заполненную электролитом. Включается привод вращения образца, замыкается электрическая цепь, и начинается процесс травления. После расчетного времени и снятия слоя нужной толщины измеряется диаметр образца и его длина.
На фиг. 2 изображены эпюры возможных вариантов распределения осевых остаточных напряжений в стенке трубы, где а – эпюра, в которой на наружной поверхности трубы присутствуют растягивающие напряжения, а на внутренней – сжимающие; б – эпюра, в которой на наружной поверхности трубы присутствуют сжимающие напряжения, а на внутренней – растягивающие; в – эпюра, в которой на обеих поверхностях присутствуют растягивающие напряжения.
Если стравливается наружный поверхностный слой трубы и радиус ее меняется с R1 до R'1, то происходит некоторая разгрузка трубы по остаточным напряжениям и длина образца трубы изменяется на величину Δl. При этом положительное значение Δl соответствует удлинению образца и наличию в поверхностном слое положительных (растягивающих) напряжений 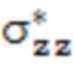 . Если значение Δl отрицательно, то образец укорачивается, что означает наличие в поверхностном слое отрицательных (сжимающих) напряжений
. Если значение Δl отрицательно, то образец укорачивается, что означает наличие в поверхностном слое отрицательных (сжимающих) напряжений 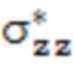 , которые после замера радиуса R'1 и длины образца l + Δl после завершения травления могут быть определены по формуле
, которые после замера радиуса R'1 и длины образца l + Δl после завершения травления могут быть определены по формуле
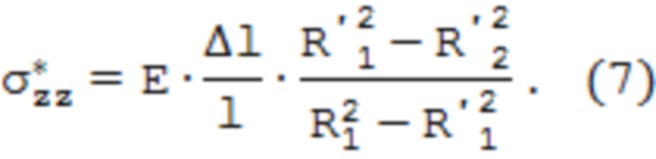
При стравливании слоя металла с внутренней поверхности внутренний радиус увеличивается с R2 до R'2. Образец трубы также изменяет длину на Δl, и величина остаточного осевого напряжения во внутреннем поверхностном слое определяется по формуле
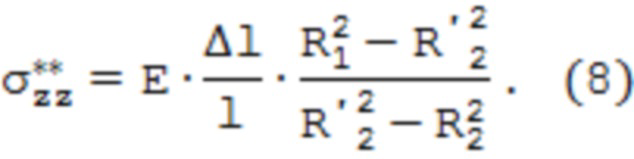
Найденные значения 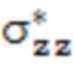 или
или 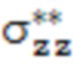 являются усредненными в объеме стравливаемого слоя. После определения осевого остаточного напряжения в поверхностном слое трубы возможно определить распределение остаточных напряжений по стенке, используя предлагаемую в способе методику.
являются усредненными в объеме стравливаемого слоя. После определения осевого остаточного напряжения в поверхностном слое трубы возможно определить распределение остаточных напряжений по стенке, используя предлагаемую в способе методику.
Если на поверхностях трубы присутствуют однозначные остаточные напряжения растяжения или сжатия, приходится использовать определенные гипотезы распределения напряжений по стенке трубы, в частности гипотезу параболического распределения. На фиг. 3 схематично показана эпюра распределения осевых остаточных напряжений, имеющая место при использовании гипотезы параболического распределения остаточных напряжений по сечению стенки трубы. Для определения распределения остаточных напряжений в стенке трубы в этом случае напряжения 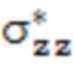 и
и 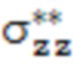 определяются описанным способом стравливания, а
определяются описанным способом стравливания, а 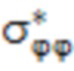 и
и 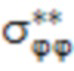 при r = R1 и r = R2 соответственно, по формулам
при r = R1 и r = R2 соответственно, по формулам
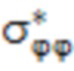 =
= 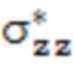 /м , (9)
/м , (9)
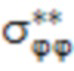 =
= 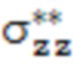 /м . (10)
/м . (10)
Распределения напряжений по толщине стенки трубы в соответствии с гипотезой параболического распределения представляются уравнениями
σzz = azr2 – bzr – cz , (11)
σϕϕ = aϕr2 – bϕr – cϕ , (12)
коэффициенты аппроксимации которых находятся из системы уравнений
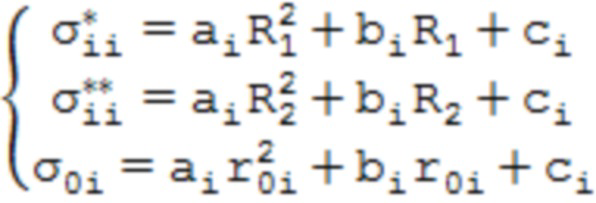 , (13)
, (13)
где i – индекс, принимающий значение z или φ в зависимости от направления действия напряжений.
Координаты r0i, σ0i, определяют положение вершины параболы и определяются при расчете эпюр σzz(r) и σϕϕ(r) из условий равновесия остаточных напряжений в объёме трубы. Коэффициенты аппроксимации с точностью до неизвестных координат вершины параболы находятся из выражений:
 ; (14)
; (14)
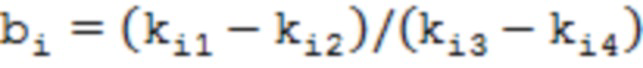 ; (15)
; (15)
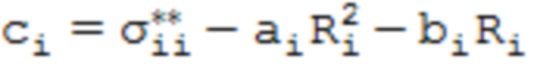 , (16)
, (16)
где 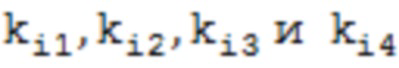 – корни уравнений, определяемые по формулам
– корни уравнений, определяемые по формулам
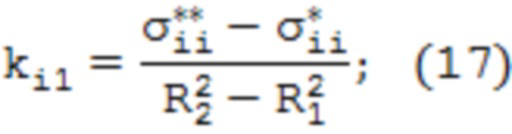
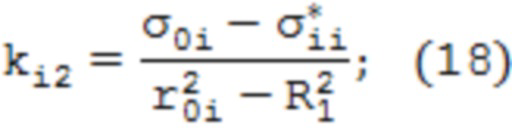
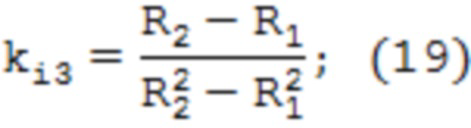
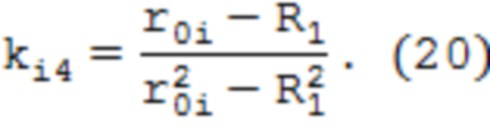
На значения координаты r0i накладывается условие dσii/dr = 0, из которого следует, что a0i = – bi/2ai.
Уравнение равновесия напряжений σzz в поперечном сечении трубы, составленное в соответствии с обозначениями на фиг. 3, имеет вид:
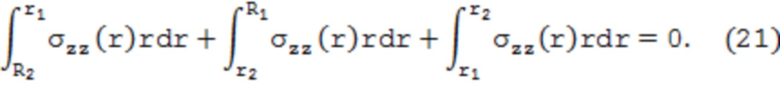
После интегрирования уравнение равновесия, представленное в форме
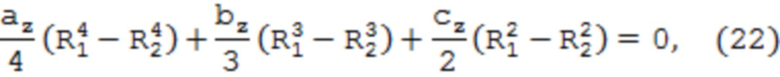
позволяет найти σ0z последовательными приближениями по r0z . При этом в качестве первого приближения принято значение
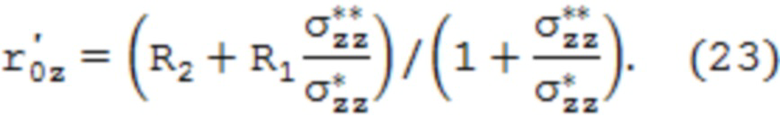
Распределение тангенциальных напряжений σϕϕ(r) строится аналогичным образом при удовлетворении уравнению равновесия моментов окружных сил относительно оси трубы и имеет вид:
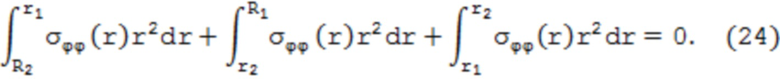
Координаты вершины параболы (σ0ϕ, r0ϕ) находятся аналогичной процедурой из уравнения:
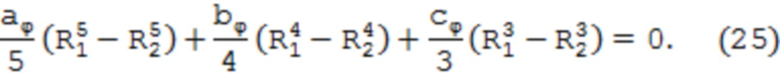
Первое приближение по r0ϕ определено выражением
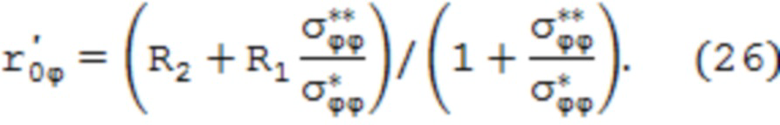
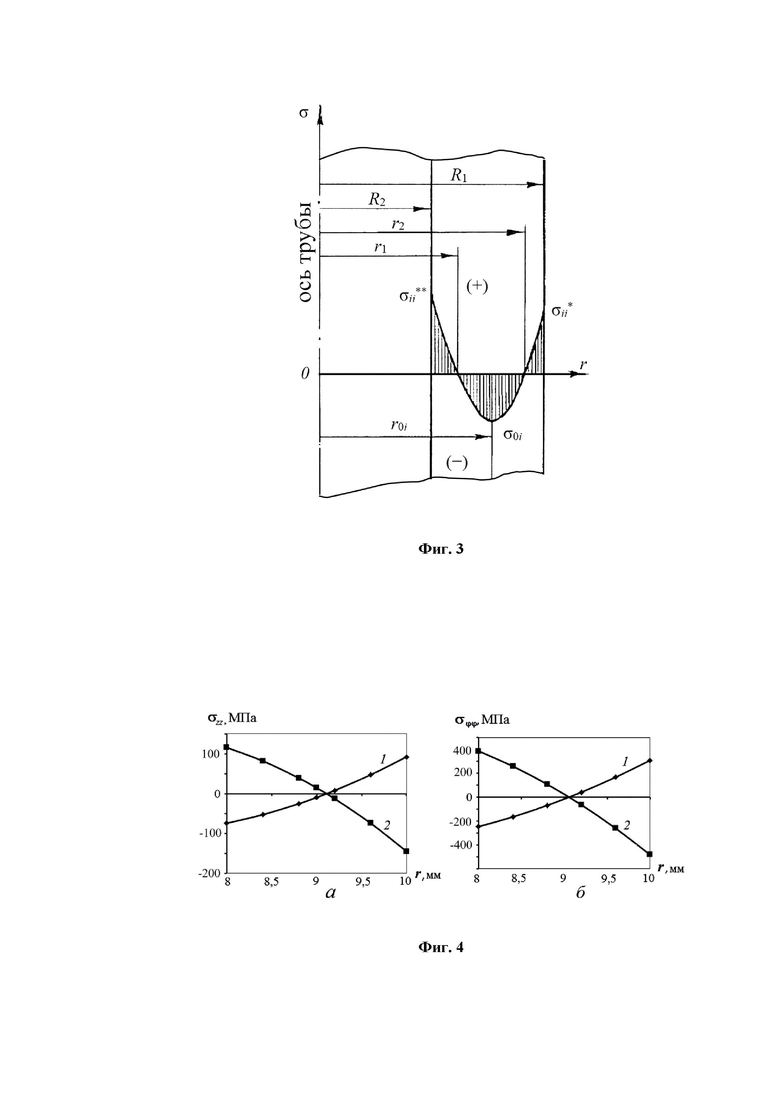
Предлагаемый способ иллюстрируется следующим примером конкретного исполнения. Труба диаметром 20 мм с толщиной стенки 2 мм из стали 08Х18Н10Т подвергнута травлению с наружной поверхности. Базовая длина, на которой осуществлено снятие слоя толщиной Δr = 0,2 мм, составляла l = 1100 мм. Коэффициент Пуассона стали 08Х18Н10Т принят равным 0,3. Модуль упругости стали 08Х18Н10Т принят равным 194000 МПа. После травления и охлаждения образец трубы удлинился на величину Δl = 0,12 мм, что свидетельствует о растягивающих осевых остаточных напряжениях в удаленном слое. Это усредненное в стравливаемом слое напряжение, рассчитанное по формуле (7), условно принимается за поверхностное: 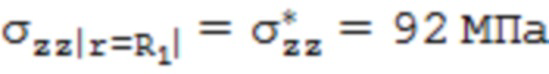 . Тогда
. Тогда 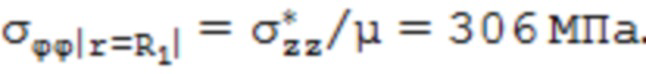 Распределение σzz и σϕϕ по толщине стенки трубы, рассчитанные по предлагаемой в патенте методике показаны на фиг. 4 (кривые 1).
Распределение σzz и σϕϕ по толщине стенки трубы, рассчитанные по предлагаемой в патенте методике показаны на фиг. 4 (кривые 1).
У второго образца трубы удален слой металла Δr = 0,2 мм с внутренней поверхности. При этом удлинение составило Δl = 0,135 мм, что в соответствии с формулой (8) свидетельствует о растягивающих осевых напряжениях 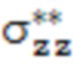 = 118 МПа. Тогда
= 118 МПа. Тогда 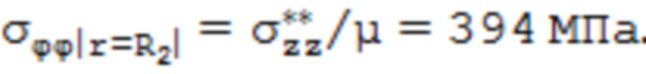 На фиг. 4 показаны распределения напряжений σzz и σϕϕ по толщине стенки трубы при растягивающих осевых напряжениях на внутренней поверхности (кривые 2). Полученные распределения напряжений удовлетворяют условиям равновесия продольных сил для σzz(r) и крутящих моментов для σϕϕ(r).
На фиг. 4 показаны распределения напряжений σzz и σϕϕ по толщине стенки трубы при растягивающих осевых напряжениях на внутренней поверхности (кривые 2). Полученные распределения напряжений удовлетворяют условиям равновесия продольных сил для σzz(r) и крутящих моментов для σϕϕ(r).
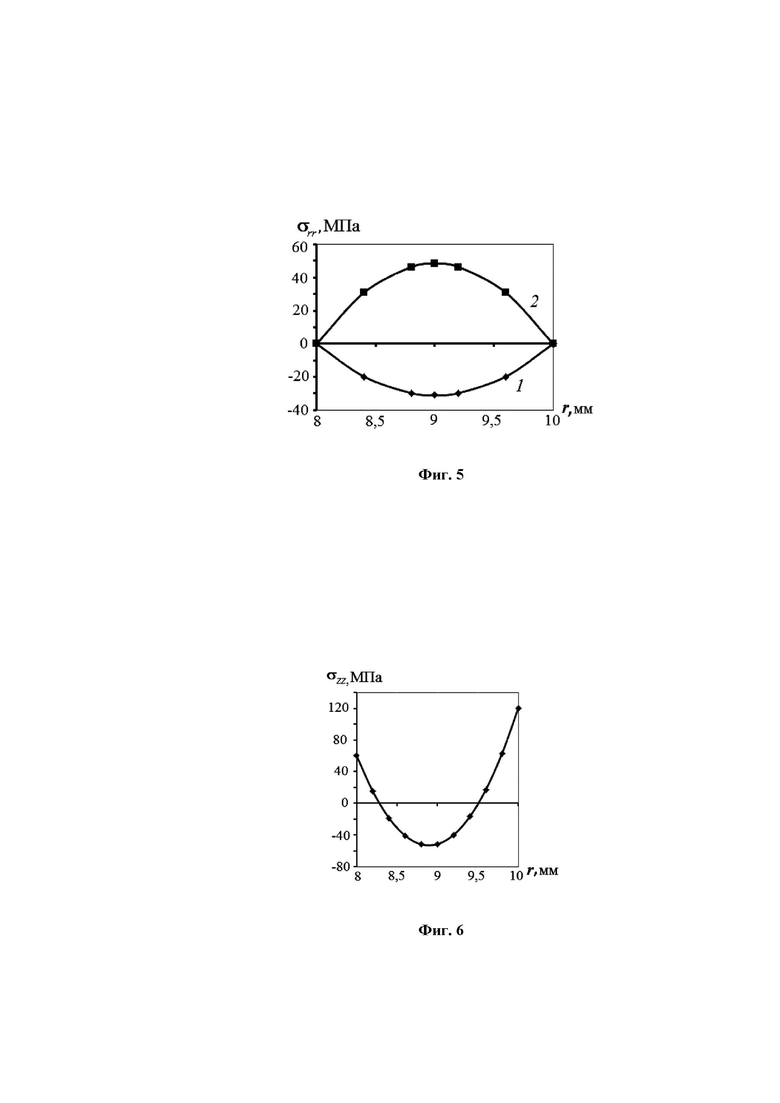
Распределения напряжений σrr по толщине стенки трубы построены с использованием экспериментально полученных значений 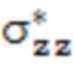 и
и 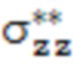 и представлены на фиг. 5, где отрицательные радиальные напряжения соответствуют случаю стравливания слоя Δr с наружной поверхности (фиг. 4, кривая 1), а положительные – стравливанию внутреннего слоя (фиг. 4, кривая 2). В обоих случаях значения
и представлены на фиг. 5, где отрицательные радиальные напряжения соответствуют случаю стравливания слоя Δr с наружной поверхности (фиг. 4, кривая 1), а положительные – стравливанию внутреннего слоя (фиг. 4, кривая 2). В обоих случаях значения 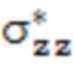 и
и 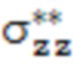 положительны, а значения σrr(r) меняют знак на противоположный. При r = R1 и r =R2 значение σrr = 0.
положительны, а значения σrr(r) меняют знак на противоположный. При r = R1 и r =R2 значение σrr = 0.
Для примера построения эпюры распределения остаточных напряжений по сечению трубы в соответствии с гипотезой параболического распределения труба диаметром 20 мм с толщиной стенки 2 мм из стали 08Х18Н10Т подвергнута травлению с наружной и внутренней поверхностей: на наружной поверхности осевые остаточные напряжения, рассчитанные по формуле (7) составили 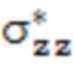 = 120 МПа, на внутренней поверхности осевые остаточные напряжения, рассчитанные по формуле (8) составили
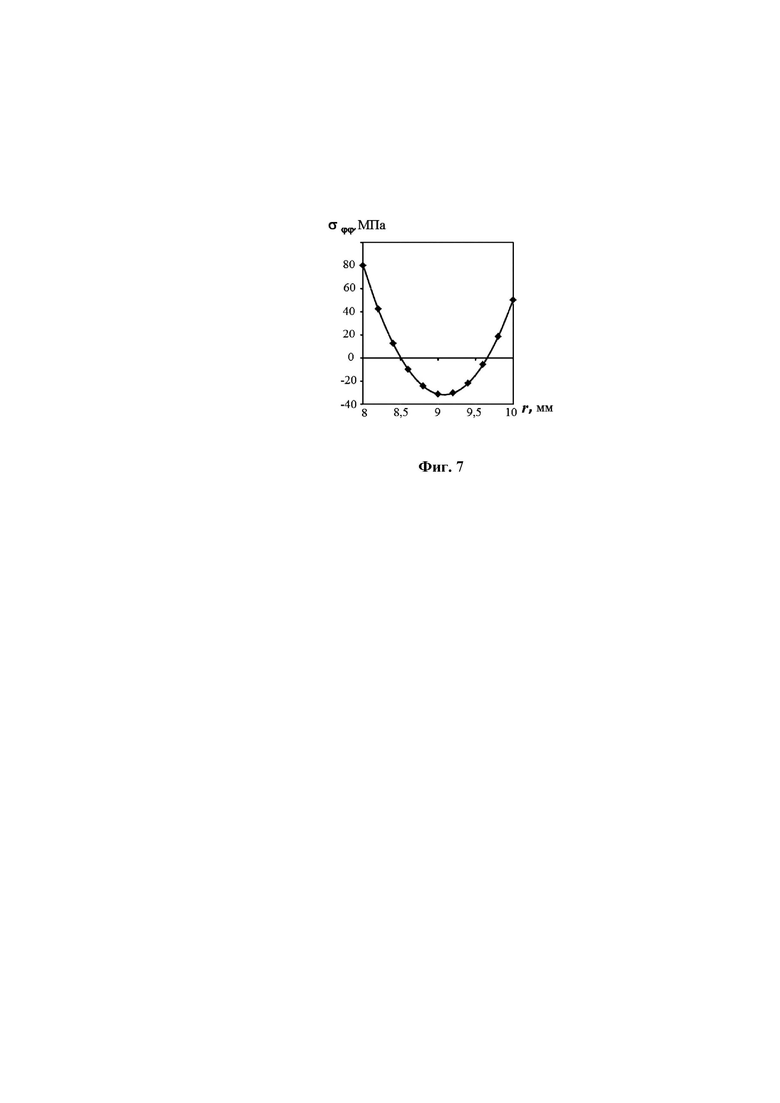
= 120 МПа, на внутренней поверхности осевые остаточные напряжения, рассчитанные по формуле (8) составили 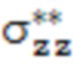 = 60 МПа. В соответствии с предложенной в способе методикой равновесие продольных сил относительно оси трубы достигается при σ0z = – 50,17 МПа, а эпюра напряжений описывается уравнением: σzz = 138,5r2 – 2464r + 10903. При этом r0z = 8,89 мм, r1 = 8,29 мм, r2 = 9,49 мм. Распределение σzz(r) для рассмотренного случая графически представлено на фиг. 6.
= 60 МПа. В соответствии с предложенной в способе методикой равновесие продольных сил относительно оси трубы достигается при σ0z = – 50,17 МПа, а эпюра напряжений описывается уравнением: σzz = 138,5r2 – 2464r + 10903. При этом r0z = 8,89 мм, r1 = 8,29 мм, r2 = 9,49 мм. Распределение σzz(r) для рассмотренного случая графически представлено на фиг. 6.
Распределение тангенциальных напряжений σϕϕ(r) рассчитанное по предлагаемой в способе методике приведено на фиг. 7. Сходимость при рассмотрении баланса моментов окружных сил относительно оси достигнута при r0ϕ = 9,145 мм и σ0ϕ = 51,8 МПа, при этом за исходные экспериментально полученные значения поверхностных тангенциальных напряжений приняты следующие, рассчитанные по формулам (9) и (10) 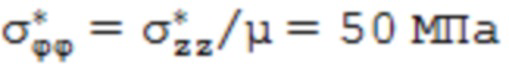 ,
, 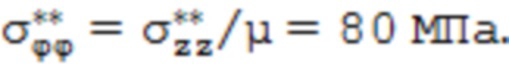
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ | 2008 |
|
RU2366912C1 |
| Способ определения остаточных напряжений в кольцевых деталях | 1989 |
|
SU1654646A2 |
| Способ (варианты) и система (варианты) определения траектории бурения скважины | 2019 |
|
RU2728039C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ | 1997 |
|
RU2125252C1 |
| Способ определения остаточных напряжений в прокате из алюминиевых сплавов | 2023 |
|
RU2804605C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ В ПРУТКОВЫХ И ПРОВОЛОЧНЫХ ИЗДЕЛИЯХ | 2009 |
|
RU2415390C1 |
| УЛЬТРАЗВУКОВОЙ СПОСОБ ОПРЕДЕЛЕНИЯ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ В СВАРНЫХ СОЕДИНЕНИЯХ ТРУБОПРОВОДОВ | 2014 |
|
RU2598980C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ | 2007 |
|
RU2354952C1 |
| Способ определения остаточных напряжений в кольцевых деталях | 1981 |
|
SU996855A1 |
| ОБРАЗЕЦ ДЛЯ ИСПЫТАНИЯ МЕТАЛЛА ТРУБ ПРИ ДВУХОСНОМ НАПРЯЖЕННОМ СОСТОЯНИИ | 1992 |
|
RU2073842C1 |
Изобретение относится к способам определения остаточных напряжений и может быть использовано для определения распределения остаточных напряжений по сечению стенки трубы. Способ включает определение осевого остаточного напряжения в поверхностном слое на наружной поверхности образца трубы методом травления и последующее определение распределения осевых, тангенциальных и радиальных остаточных напряжений по сечению стенки трубы. Способ включает определение осевого остаточного напряжения в поверхностном слое на внутренней поверхности образца трубы методом травления и последующее определение распределения осевых, тангенциальных и радиальных остаточных напряжений по сечению стенки трубы. Способом можно определять распределение остаточных напряжений по сечению стенки трубы в случае действия на обеих поверхностях трубы остаточных напряжений одинакового знака с применением гипотезы параболического распределения. Технический результат заключается в повышении точности и расширении возможностей методов определения остаточных напряжений. 2 н.п. ф-лы, 7 ил. 
1. Способ определения распределения остаточных напряжений по сечению стенки трубы, характеризующийся тем, что слой металла стравливают с наружной поверхности образца трубы, вращая его в процессе травления, после чего фиксируют абсолютное изменение длины образца трубы относительно начальных размеров, определяют усредненное по толщине стравленного слоя осевое остаточное напряжение исходя из 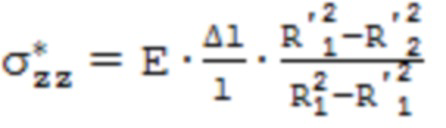 , где l – исходная длина образца трубы, E – модуль упругости материала трубы, и затем определяют распределение компонентов тензора остаточных напряжений по поперечному сечению стенки трубы из выражений:
, где l – исходная длина образца трубы, E – модуль упругости материала трубы, и затем определяют распределение компонентов тензора остаточных напряжений по поперечному сечению стенки трубы из выражений:
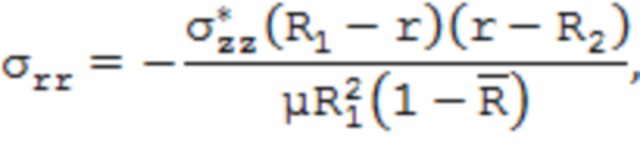
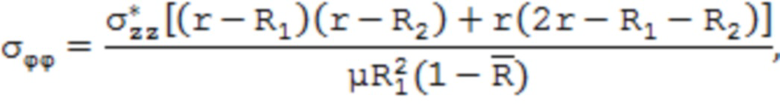
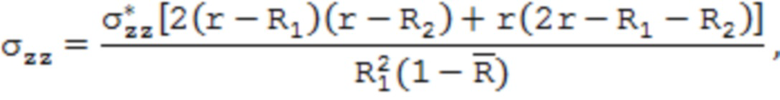
где σrr, σφφ, σzz – соответственно радиальные, тангенциальные и осевые остаточные напряжения; R1 и R2 – соответственно внешний и внутренний радиусы трубы; 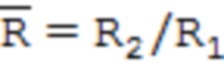 – безразмерный параметр, характеризующий относительную толщину стенки трубы;
– безразмерный параметр, характеризующий относительную толщину стенки трубы; 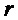 – радиальная координата слоя; μ – коэффициент Пуассона материала трубы.
– радиальная координата слоя; μ – коэффициент Пуассона материала трубы.
2. Способ определения распределения остаточных напряжений по сечению стенки трубы, характеризующийся тем, что слой металла стравливают с внутренней поверхности образца трубы, вращая его в процессе травления, после чего фиксируют абсолютное изменение длины образца трубы относительно начальных размеров, определяют усредненное по толщине стравленного слоя осевое остаточное напряжение исходя из  , где l – исходная длина образца трубы, E – модуль упругости материала трубы, и затем определяют распределение компонентов тензора остаточных напряжений по поперечному сечению стенки трубы из выражений:
, где l – исходная длина образца трубы, E – модуль упругости материала трубы, и затем определяют распределение компонентов тензора остаточных напряжений по поперечному сечению стенки трубы из выражений:
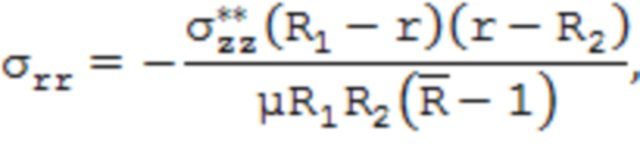
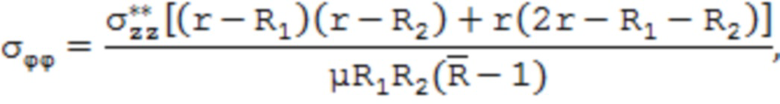
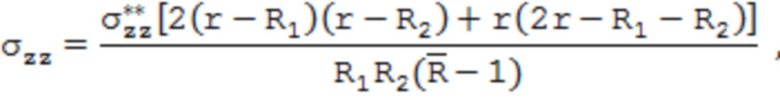
где σrr, σφφ, σzz – соответственно радиальные, тангенциальные и осевые остаточные напряжения; 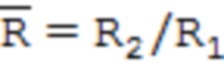 – безразмерный параметр, характеризующий относительную толщину стенки трубы;
– безразмерный параметр, характеризующий относительную толщину стенки трубы; 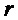 – радиальная координата слоя; μ – коэффициент Пуассона материала трубы.
– радиальная координата слоя; μ – коэффициент Пуассона материала трубы.
| СПОСОБ ОПРЕДЕЛЕНИЯ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ | 2008 |
|
RU2366912C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ | 1996 |
|
RU2121666C1 |
| Устройство для измерения остаточных напряжений плоских и кольцевых образцов | 1981 |
|
SU974107A1 |
| Соколов И.А., Уральский В.И | |||
| Остаточные напряжения и качество металлопродукции М.: Металлургия, 1981 г., с.96. | |||
Авторы
Даты
2020-12-21—Публикация
2019-07-05—Подача