Изобретение относится к области теплофизических измерений и предназначено для измерения теплопроводностей разнородных твердых тел, значения которых априорно неизвестны. Заявляемый способ ориентирован на метрологию и может быть использован в качестве теоретической основы для современного эталона единицы теплопроводности.
Известен способ измерения теплопроводности, который заключается в регистрации перепада температуры и тепловых потоков через испытуемые образцы, а также в регистрации электрического сигнала, пропорционального разности тепловых потоков через образцы (авт. свид. СССР №1337749, МПК G01N 25/18, опубл. 15.09.1987, БИ №34).
Известен способ измерения теплопроводности, согласно которому монотонно изменяют температуру поверхности плоского образца, тепловым воздействием на его противоположную поверхность задают плотность теплового потока через образец, измеряют перепад температуры по образцу посредством контактных термопреобразователей, при двух заданных плотностях теплового потока повторяют те же операции с контрольным образцом из высокотеплопроводного материала, по полученным данным рассчитывают контактное термическое сопротивление и характеристику неидентичности контактных термопреобразователей, а искомую теплопроводность находят расчетным путем с учетом полученных данных (авт. свид. СССР №1561025, МПК G01N 25/18, опубл. 30.04.1990, БИ №16).
Известен способ определения теплопроводности материалов (патент на изобретение РФ №2478940, МПК G01N 25/18, опубл. 10.04.2013, БИ №10). В данном способе исследуемый плоский образец известной толщины через источник теплоты с заданной плотностью теплового потока приводят в тепловой контакт по плоскости с плоским эталонным образцом. При заданной температуре термостатируют внешние плоскости исследуемого и эталонного образцов с теплоизолированными боковыми поверхностями и измеряют температуру в плоскости контакта. При этом эталонный образец формируют из двух идентичных пакетов, содержащих уложенные одна на другую параллельно плоскости теплового контакта плоские пластины, толщина которых определяется допускаемым для исследуемого образца давлением. Причем один из пакетов предварительно устанавливают вместо исследуемого образца, определяют среднее тепловое сопротивление обоих пакетов и используют его двойное значение при определении теплопроводности исследуемого образца.
Наиболее близким к предлагаемому способу по технической сущности является способ (прототип) определения теплопроводности материалов (патент на изобретение РФ №2276781, МПК G01N 25/00, опубл. 20.05.2006, БИ №14). Согласно данному способу, исследуемый плоский образец известной толщины через источник теплоты заданной удельной мощности приводят в тепловой контакт по плоскости с эталонным образцом, имеющим меньшее термическое сопротивление, чем исследуемый, и предварительно установленный в нем дополнительный источник теплоты. Внешние плоскости исследуемого и эталонного образцов с теплоизолированными боковыми поверхностями термостатируют при заданной температуре и измеряют температуру в плоскости контакта. Вместо исследуемого образца устанавливают дополнительный эталонный образец, идентичный основному, определяют эффективное термическое сопротивление эталонных образцов в зависимости от удельной мощности дополнительных источников теплоты в тех же температурных условиях, при которых требуется определить теплопроводность исследуемого образца. Затем вновь устанавливают исследуемый образец и подбирают такую удельную мощность дополнительного источника теплоты, при которой эффективное термическое сопротивление эталонного образца в пределах погрешности совпадает с термическим сопротивлением исследуемого образца, и расчетным путем определяют его теплопроводность.
Один из главных недостатков способов-аналогов и способа-прототипа заключается в том, что способы не являются абсолютными - для их осуществления требуется эталонный образец, по теплопроводности которого находят теплопроводность исследуемого образца. Это увеличивает погрешность измерений. Другой недостаток заключается в том, что при измерении перечисленными способами теплопроводность исследуемого образца она не должна существенно отличаться от теплопроводности эталонного образца. Таким образом, способы не обеспечивают возможность измерения теплопроводности образцов с сильно отличающимися теплопроводностями. В качестве доказательного примера можно привести государственный эталон единицы теплопроводности ГЭТ 59-2007, который основан на способе-прототипе и который воспроизводит единицу теплопроводности в диапазонах 0,1-5; 5-20 Вт/(м⋅К), при этом расширенная относительная неопределенность измерений находится в диапазоне 0,8-2%.
Цель изобретения - повышение точности измерения теплопроводности твердых тел с одновременным расширением динамического диапазона и номенклатуры исследуемых материалов.
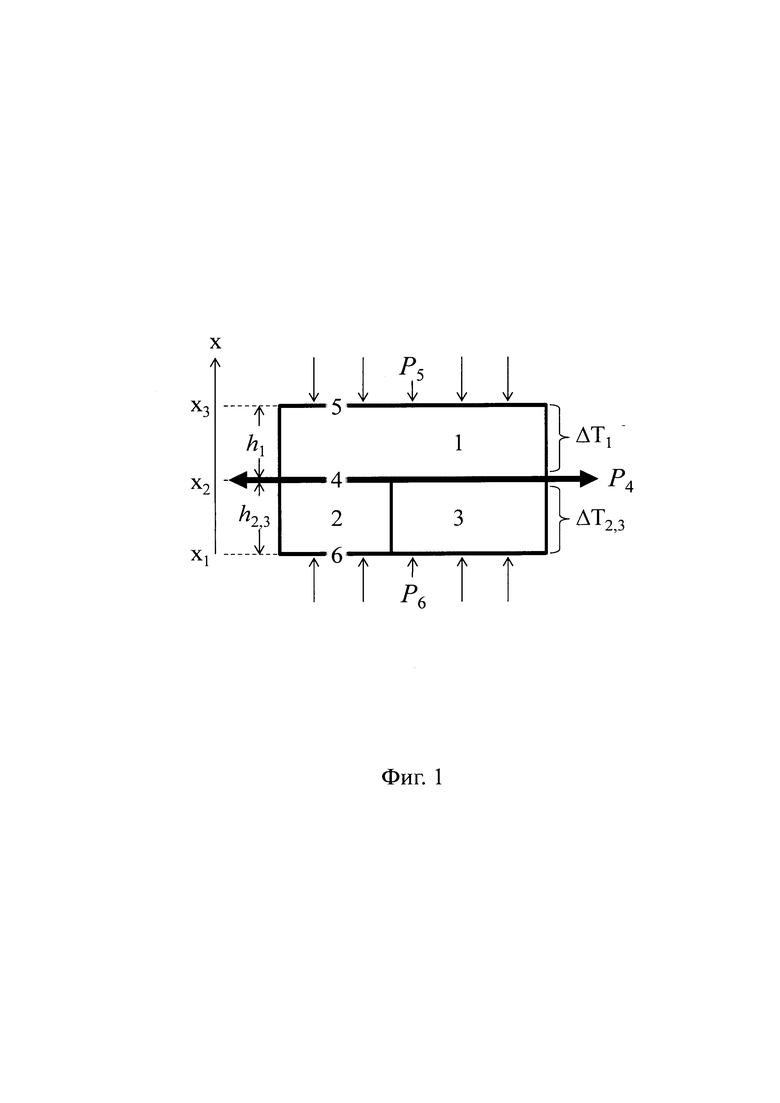
Указанная цель достигается тем, что формируют измерительную ячейку, для чего образуют систему тел из трех образцов, внутри образованной системы тел размещают равномерно распределенный по плоскости поперечного сечения образцов внутренний сток теплоты, а на ее двух противоположных наружных плоскостях размещают однонаправленные и равномерно распределенные по плоскости поперечного сечения образцов внешние источники теплоты, задают мощность внутреннего стока и стабилизируют ее во времени, регулируют мощности внешних источников теплоты до достижения равенства стационарных перепадов температуры на образцах, находящихся по разные стороны внутреннего стока теплоты, измеряют достигнутые мощности и стационарные равные перепады температуры, затем уравнивают мощности внешних источников и измеряют достигнутые стационарные перепады температуры на образцах, находящихся по разные стороны от внутреннего стока теплоты, после чего по измеренным данным расчетным путем находят искомые теплопроводности каждого образца, при этом в сформированной измерительной ячейке по одну сторону внутреннего стока теплоты располагают наибольший образец с более высокой теплопроводностью и с наибольшим поперечным сечением, а по его другую сторону располагают два разнородных образца, сумма поперечных сечений которых равна поперечному сечению наибольшего образца, а периметр их общего поперечного сечения совпадает с периметром поперечного сечения наибольшего образца, причем материал одного из двух разнородных образцов идентичен материалу наибольшего образца, соотношение поперечных сечений двух разнородных образцов, а также соотношение их толщины с толщиной наибольшего образца задают предварительно, которое получают расчетным путем, исходя из требования обеспечить достаточную для точного измерения разность мощностей внешних источников теплоты и соизмеримость перепадов температуры по обе стороны внутреннего стока теплоты, а для расчета искомых теплопроводностей используют следующую систему уравнений:
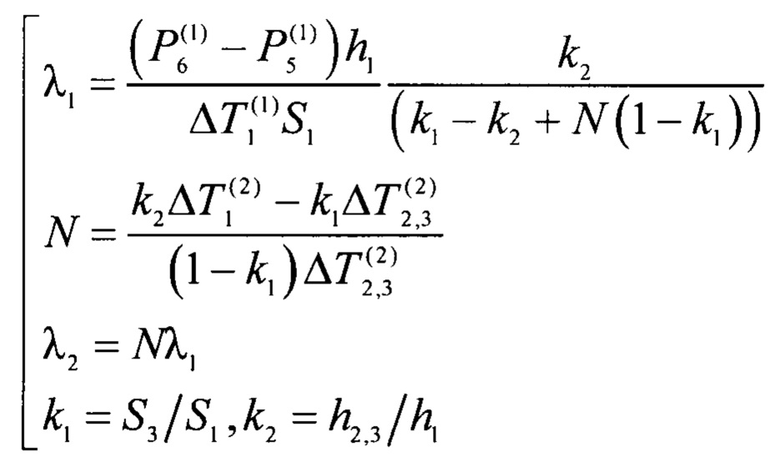
где
λ1 - теплопроводность наибольшего образца с более высокой теплопроводностью и идентичного ему по материалу образца из двух разнородных образцов,
λ2 - теплопроводность образца с меньшей теплопроводностью,
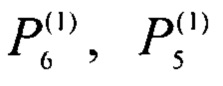 - измеренные мощности внешних источников, соответствующие стационарным равным перепадам температуры,
- измеренные мощности внешних источников, соответствующие стационарным равным перепадам температуры,
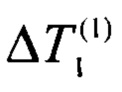 - измеренные стационарные равные перепады температуры,
- измеренные стационарные равные перепады температуры,
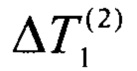 - измеренный перепад температуры на наибольшем образце с более высокой теплопроводностью, достигнутый при равенстве мощностей внешних источников теплоты,
- измеренный перепад температуры на наибольшем образце с более высокой теплопроводностью, достигнутый при равенстве мощностей внешних источников теплоты,
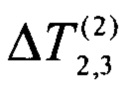 - измеренный перепад температуры на двух разнородных образцах,
- измеренный перепад температуры на двух разнородных образцах,
достигнутый при равенстве мощностей внешних источников теплоты,
h1 - толщина наибольшего образца,
h2,3 - толщина каждого из разнородных образцов,
S1, S3 - площадь поперечного сечения наибольшего образца и образца,
идентичного по материалу наибольшему образцу, соответственно.
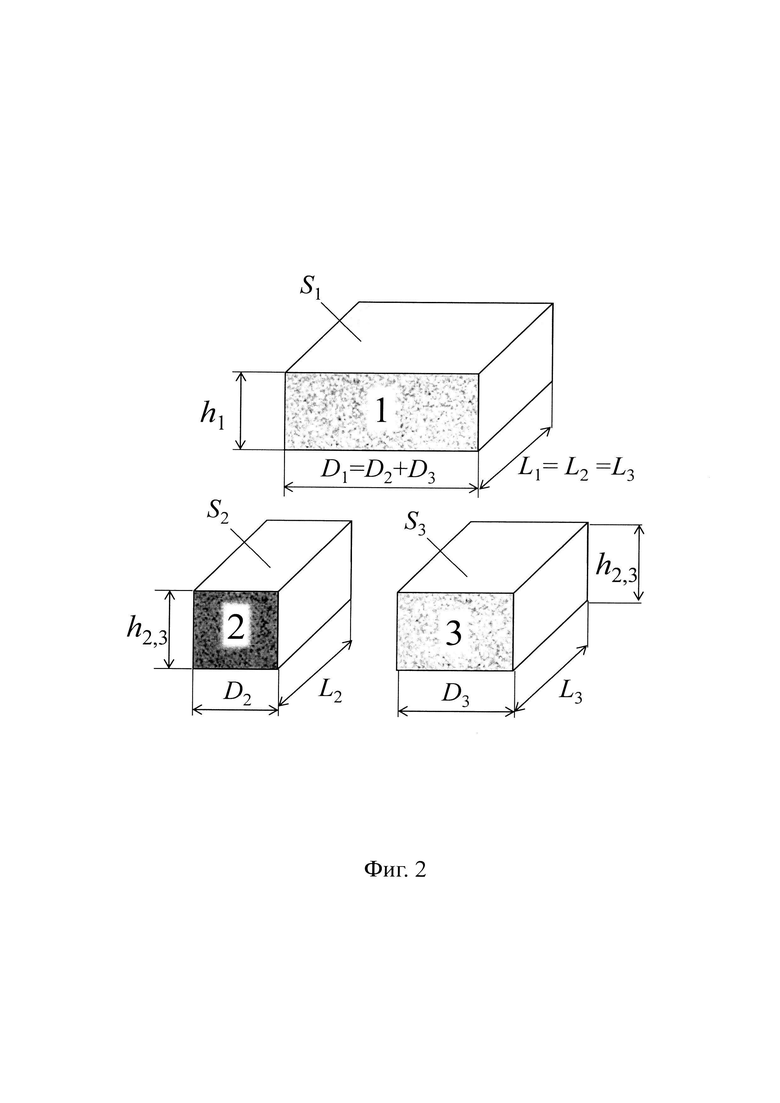
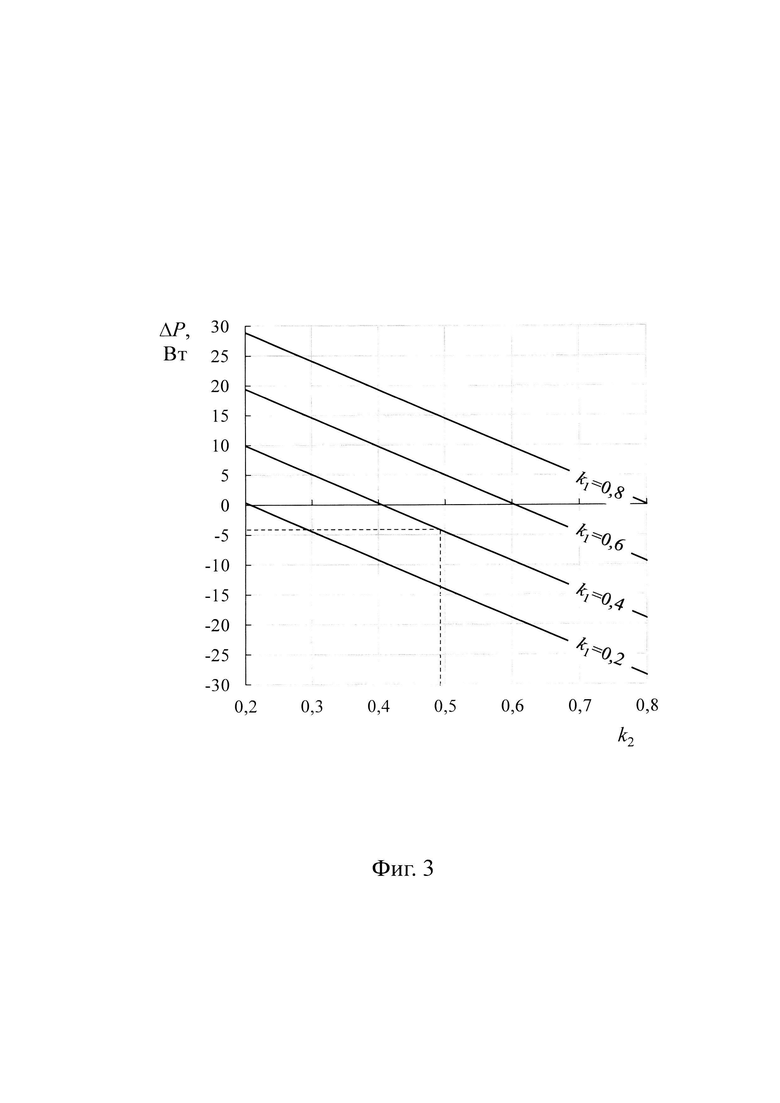
Сущность способа поясняется фиг. 1, 2, 3. На фиг. 1 представлена схема измерительной ячейки, с помощью которой осуществляют измерение теплопроводностей двух разнородных твердых материалов. Измерительная ячейка состоит из трех образцов 1, 2, 3, из которых образцы 1, 3 выполнены из идентичного твердого материала и имеют теплопроводность λ1, причем более высокую или намного более высокую, чем теплопроводность λ2 образца 2, выполненного из иного твердого материала, чем образцы 1, 3. Образец 1 обладает наибольшим поперечным сечением, чем другие образцы 2, 3, сумма площадей поперечных сечений которых равна площади поперечного сечения образца 1, а общий поперечный периметр образцов 2, 3 совпадает с поперечным периметром образца 1. Кроме того, измерительная ячейка содержит равномерно распределенный по плоскости поперечного сечения образцов внутренний сток теплоты 4, который установлен между образцом 1 и образцами 2, 3; она также содержит однонаправленные и равномерно распределенные по плоскости поперечного сечения образцов внешние источники теплоты 5, 6, которые установлены на внешних плоскостях образца 1 и образцов 2, 3, соответственно. На фиг. 2 представлен внешний вид образцов 1, 2, 3, выполненных в форме параллелепипеда. На фиг. 3 представлены примеры зависимостей разности ΔР измеряемых мощностей внешних источников 5, 6 от соотношения толщин образцов 2, 3 и образца 1 при различных соотношениях поперечных сечений образцов 2, 3. Указанные зависимости используют для предварительного нахождения оптимального соотношения габаритных размеров образцов 1, 2, 3.
Заявляемый способ относится к стационарным способам измерения теплопроводности, в отличие от способов-аналогов и прототипа является абсолютным способом и не требует наличия эталонного образца, теплопроводность которого заранее и точно известна. Это сразу существенно повышает точность способа.
В теоретическую основу заявляемого способа положена краевая задача теплопроводности, соответствующая теплообмену 2-х соприкасающихся тел по закону теплопроводности Фурье с граничными условиями 4-го рода для случая одномерного стационарного распределения температуры в данных телах. Данная краевая задача в общем виде математически записывается в виде:
- уравнения теплопроводности для каждого из тел:
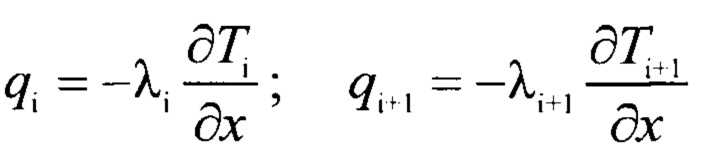
- граничные условия 4-го рода:
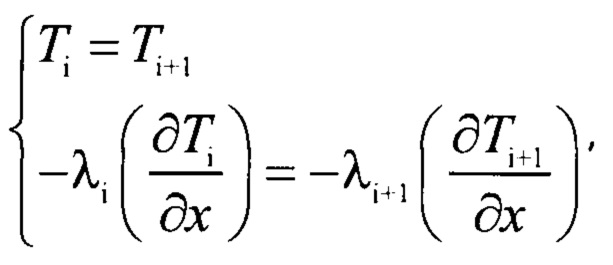
где
λi, λi+1 - теплопроводности соприкасающихся тел,
Ti, Ti+1 - температуры соприкасающихся тел,
qi, qi+1 - стационарный тепловой поток в каждом из соприкасающихся тел.
Согласно общей формулировке, краевая задача для измерительной ячейки, тепловая модель которой представлена на фиг. 1, математически записывается в виде:
- уравнения теплопроводности, выраженные через тепловые проводимости образца 1 и образцов 2, 3, имеют вид:

- граничные условия 4-го рода:
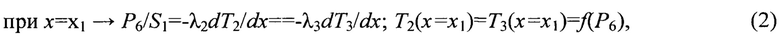
при 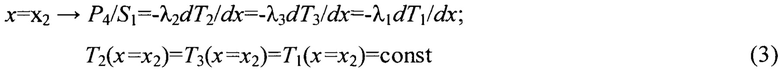
при 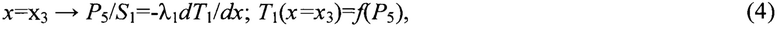
где
P5, Р6 - мощности внешних источников теплоты 5, 6, соответственно,
Р4 - мощность внутреннего стока теплоты 4,
σ1=λ1S1/h1 - тепловая проводимость образца 1,
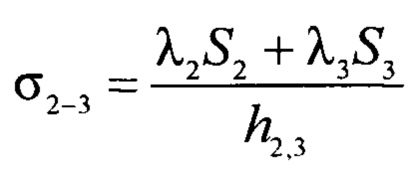 - эффективная тепловая проводимость системы тел образец 2 - образец 3,
- эффективная тепловая проводимость системы тел образец 2 - образец 3,
λι, λ2, λ3 - теплопроводности образцов 1, 2, 3, соответственно, при этом λ1=λ3>λ2,
S1, S2, S3 - площади поперечного сечения образцов 1, 2, 3, соответственно, при этом принимают, что S3=k1S1, S2=(1-k1)S1, где k1 - постоянный коэффициент, причем S1=S2+S3,
h2,3, h1 - толщины образцов 2, 3 и 1, соответственно, при этом принимают, что
h2,3=k2h1, где k2 - постоянный коэффициент,
T - температура,
x - текущая координата в направлении, нормальном к поперечному сечению образцов.
Для расчета эффективной тепловой проводимости σ2-3 системы тел образец 2 - образец 3 используют т.н. электротепловую аналогию - метод расчета тепловых систем, сводящийся к расчету эквивалентных линейных электрических схем (Фокин В.М., Бойков Г.П., Видин Ю.В. Основы технической теплофизики - М.: Машиностроение-1. 2004. - 172 с.). Согласно электротепловой аналогии эффективная тепловая проводимость двух параллельно расположенных участков тепловой цепи (образцов 2, 3) равна сумме тепловых проводимостей каждого участка. При этом тепловая проводимость каждого участка тепловой цепи прямо пропорциональна его теплопроводности и площади его поперечного сечения и обратно пропорциональна длине данного участка тепловой цепи (толщине h2,3 образцов 2, 3). Исходя из этого, получают приведенное выше соотношение для эффективной тепловой проводимости σ2-3 системы тел образец 2 - образец 3.
Габаритные размеры образцов 1, 2, 3 выбирают предварительно, исходя из двух одновременных требований, которые заключаются в том, что:
- измеряемая разность мощностей внешних источников теплоты 5, 6, при которой достигается равенство стационарных перепадов температуры, должна быть достаточной для ее точного измерения,
- стационарный перепад температуры в системе тел образец 2 - образец 3, достигаемый при равенстве мощностей внешних источников теплоты, должен быть соизмерим с заданным стационарным перепадом температуры на образце 1.
Для этого используют предварительно получаемые расчетные зависимости разности мощностей внешних источников 5, 6 от соотношения толщин образцов 2, 3 и образца 1 для различного соотношения площадей поперечного сечения образцов 2, 3. Как получить указанные зависимости и определить наиболее оптимальные размеры образцов 1, 2, 3 - показано ниже в примере осуществления способа.
Способ осуществляют на основе уравнений (1)-(4) и выполняют его в два этапа.
На первом этапе выполняют компарирование образцов 2, 3 и образца 1 по мощности соответствующих им внешних источников теплоты 6, 5. Для этого при заданной неизменной и стабилизированной во времени мощности Р4 внутреннего стока теплоты 4 путем регулирования мощностей внешних источников теплоты 6, 5 достигают заданного равенства стационарных перепадов температуры 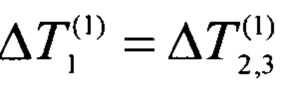 на образце 1 и в системе тел образец 2 - образец 3. По достижении равенства перепадов измеряют стационарный перепад температуры
на образце 1 и в системе тел образец 2 - образец 3. По достижении равенства перепадов измеряют стационарный перепад температуры 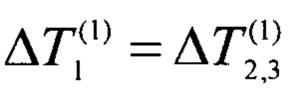 и мощности внешних источников теплоты
и мощности внешних источников теплоты 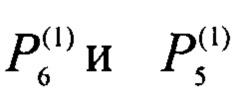 . Далее находят разность указанных мощностей, которая, согласно системе уравнений (1), связана с искомыми теплопроводностями следующим соотношением:
. Далее находят разность указанных мощностей, которая, согласно системе уравнений (1), связана с искомыми теплопроводностями следующим соотношением:
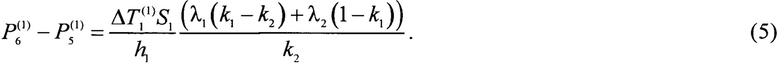
На втором этапе выполняют компарирование образцов 2, 3 и образца 1 по стационарным перепадам температуры на них. Для этого при заданной неизменной и стабилизированной мощности Р4 внутреннего стока теплоты 4, которая использовалась на первом этапе, задают равные мощности внешних источников теплоты, причем делают их равными мощности 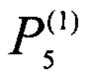 внешнего источника 5, который соприкасается с более теплопроводным наибольшим образцом, т.е. с образцом 1. Таким образом, получают равенство мощностей
внешнего источника 5, который соприкасается с более теплопроводным наибольшим образцом, т.е. с образцом 1. Таким образом, получают равенство мощностей 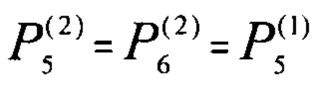 . Измеряют достигнутый стационарный перепад температуры
. Измеряют достигнутый стационарный перепад температуры 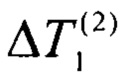 на образце 1 и стационарный перепад температуры
на образце 1 и стационарный перепад температуры 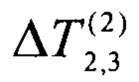 в системе тел образец 2 - образец 3. Из системы уравнений (1) выражают разность мощностей внешних источников теплоты 6, 5 и приравнивают ее нулю (так как мощности одинаковые), в результате чего получают уравнение для расчета отношения теплопроводностей λ2/λ1:
в системе тел образец 2 - образец 3. Из системы уравнений (1) выражают разность мощностей внешних источников теплоты 6, 5 и приравнивают ее нулю (так как мощности одинаковые), в результате чего получают уравнение для расчета отношения теплопроводностей λ2/λ1:

Затем совместно решают уравнения (5), (6) относительно теплопроводности λ1 образца 1, в результате получают систему уравнений измерения для заявленного способа:
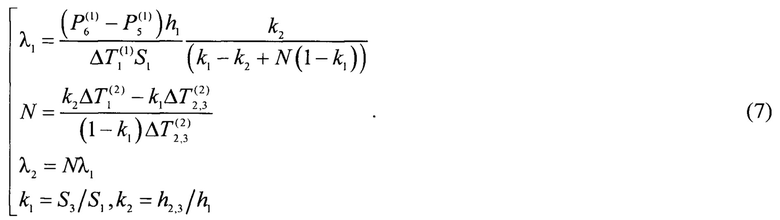
Пример осуществления способа. Пусть, например, требуется измерить априори неизвестные теплопроводности образцов из стали - образцы 1, 3 с теплопроводностью λ1 и образца из оргстекла - образец 2 с теплопроводностью λ2. Ожидаемо, что значения указанных теплопроводностей существенно различаются: теплопроводность стали намного выше теплопроводности оргстекла λ1>λ2. Формируют измерительную ячейку по схеме, как это показано на фиг. 1. При этом, предварительно определяют оптимальные размеры образцов 1, 2, 3, для чего выполняют расчет зависимостей разности электрических мощностей 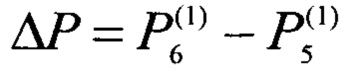 от коэффициента k2=h2,3/h1 в диапазоне 0<k2<1,0 при нескольких разных фиксированных значениях k1=S3/S1, взятого из диапазона 0<k1<1. Вид таких зависимостей для рассматриваемого примера представлен на фиг. 3. Для расчета указанной зависимости используют соотношение (5), в котором используют ожидаемые значения теплопроводностей λ1 и λ2. При этом, например, задают исходные расчетные данные:
от коэффициента k2=h2,3/h1 в диапазоне 0<k2<1,0 при нескольких разных фиксированных значениях k1=S3/S1, взятого из диапазона 0<k1<1. Вид таких зависимостей для рассматриваемого примера представлен на фиг. 3. Для расчета указанной зависимости используют соотношение (5), в котором используют ожидаемые значения теплопроводностей λ1 и λ2. При этом, например, задают исходные расчетные данные:
- принимают размеры образца 1: h1=20 мм, D1=40 мм, L1=40 мм, площадь поперечного сечения S1=D1L1=0,04⋅0,04=1,6⋅10-3 м2,
- стационарный перепад температуры на 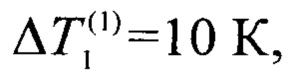
- ожидаемое значение теплопроводности образцов 1, 3 - λ1≈30 Вт/(м⋅К),
- ожидаемое значение теплопроводности образца 2 - λ2≈0,3 Вт/(м⋅К),
- ожидаемое отношение теплопроводностей N=λ2/λ1≈0,01.
В результате расчета по соотношению (5) получают набор зависимостей, которые показаны на фиг. 3. Из указанных зависимостей выбирают такое значение k2, при котором разность мощностей ΔР будет достаточной для ее точного измерения, и при этом одновременно стационарный перепад температуры в системе тел образец 2 - образец 3, достигаемый на втором этапе измерения, будет соизмерим с заданным стационарным перепадом температуры на образце 1.
Например, из полученной зависимости на фиг. 3 выбирают значение коэффициента k2, равное k2=0,5, а значение коэффициента к1, равное k1=0,4. Выбранным значениям коэффициентов соответствует разность мощностей ΔР внешних источников теплоты, приблизительно равная ΔP≈-4,8 Вт, что вполне достаточно для ее точного измерения. Для получения расчетного соотношения для ожидаемого значения перепада температуры 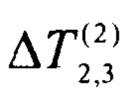 используют уравнение из (7):
используют уравнение из (7):

в котором принимают равенство перепадов температур 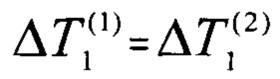 (в рассматриваемом примере
(в рассматриваемом примере 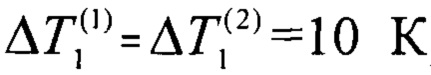 ). С учетом принятого, из (8) получают соотношение для оценки ожидаемого перепада температуры
). С учетом принятого, из (8) получают соотношение для оценки ожидаемого перепада температуры 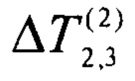 :
:
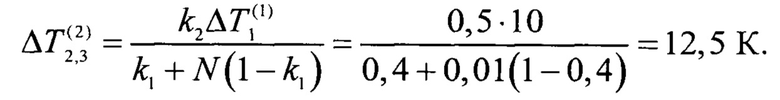
Полученное значение стационарного перепада температуры 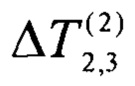 близко к стационарному перепаду температуры
близко к стационарному перепаду температуры 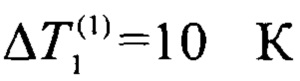 на образце 1, что соответствует сформулированному выше требованию.
на образце 1, что соответствует сформулированному выше требованию.
Исходя из полученных значений коэффициентов k1 и k2 с учетом соотношений (7) задают размеры образцов 2, 3:
- образец 2: h2,3=k2h1=10 мм, D2=24 мм, L2=40 мм, площадь поперечного сечения S2=(1-k1)S2=D2L2=0,024⋅0,04=9,6⋅10-4 м2.
- образец 3: h2,3=k2h1=10 мм, D3=16 мм, L3=40 мм, площадь поперечного сечения S3=k1S2=D3L3=0,016⋅0,04=6,4⋅10-4 м2.
Согласно заданным размерам изготавливают образцы 1, 2, 3 и собирают измерительную ячейку, как показано на фиг. 1. Затем, согласно первому этапу, выполняют компарирование образцов 2, 3 и образца 1 по мощности соответствующих им внешних источников теплоты 6, 5. В результате получают значения мощностей внешних источников теплоты, например, равные 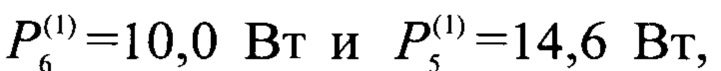 при которых достигаются одинаковые стационарные перепады температуры
при которых достигаются одинаковые стационарные перепады температуры 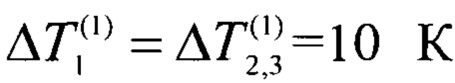 . Затем, согласно второму этапу, выполняют компарирование образцов 2, 3 и образца 1 по их стационарным перепадам температуры. В результате получают значения достигнутых стационарных перепадов температуры, например,
. Затем, согласно второму этапу, выполняют компарирование образцов 2, 3 и образца 1 по их стационарным перепадам температуры. В результате получают значения достигнутых стационарных перепадов температуры, например, 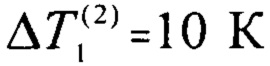 и
и 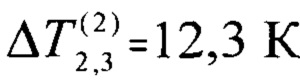 , которые соответствуют равенству мощностей
, которые соответствуют равенству мощностей 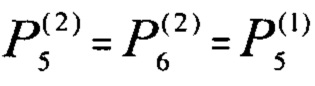 .
.
Далее выполняют расчет искомых теплопроводностей, для чего используют систему уравнений (7), получают:
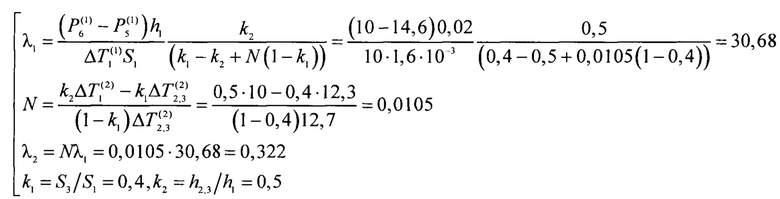
Таким образом, согласно способу найдены следующие значения теплопроводностей: теплопроводность стали - λ1=30,68 Вт/(м⋅К), теплопроводность оргстекла - λ2=0,322 Вт/(м⋅К).
Оценка погрешности заявленного способа. Относительную погрешность измерения теплопроводности δλ, номинально обеспечиваемую заявленным способом, в общем виде оценивают по соотношению:
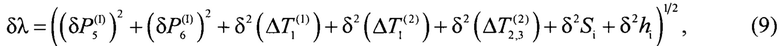
где
δ - символ, означающий относительную погрешность измерения физической величины.
Основной вклад в погрешность измерений вносит погрешность измерения перепада температуры на образцах, остальными составляющими погрешности (погрешностью измерения электрической мощности и размеров образцов) можно пренебречь, так как их относительная неопределенность измерения в настоящее время составляет:
δh≈dS≈δP≈5⋅10-5=0,005%.
Поэтому соотношение (8) правомерно преобразуют к упрощенному виду:
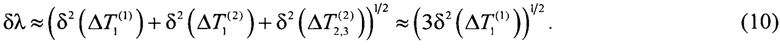
В идеальном случае погрешность измерения перепада температуры определяется относительной погрешностью номинальных статических характеристик используемых контактных термопреобразователей. Так, например, для платиновых термометров сопротивления 1-го разряда расширенная неопределенность при температуре 0°С составляет Δ1=0,002 К. Для примера зададим значения измеряемых стационарных перепадов температуры 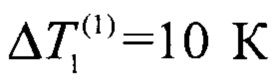 . Допустим, что каждый из перепадов температуры измеряется с помощью 2-х термометров сопротивления, с учетом этого, соотношение (10) трансформируется к виду:
. Допустим, что каждый из перепадов температуры измеряется с помощью 2-х термометров сопротивления, с учетом этого, соотношение (10) трансформируется к виду:

Для принятых исходных данных: Δ1=0,002 К, 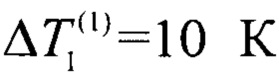 , согласно (11), получаем δλ≈4,9⋅10-4=0,049%.
, согласно (11), получаем δλ≈4,9⋅10-4=0,049%.
При конкретной реализации заявленного способа фактическая погрешность будет всегда несколько выше приведенной оценки и в каждом конкретном случае должна определяться индивидуально.
Заявляемый способ является более универсальным, абсолютным способом, не требует наличия эталонного образца и в отличие от всех известных способов позволяет измерять теплопроводности, различающиеся в 100 и более раз. Данное преимущество обеспечивается за счет использования трех образцов и возможности варьирования соотношением их габаритных размеров. Кроме того, способ позволяет одновременно измерять априори неизвестные теплопроводности сразу двух разнородных твердых материалов, при этом обеспечивает высокую точность измерений, характеризуемую относительной неопределенностью порядка 0,05%.
| название | год | авторы | номер документа |
|---|---|---|---|
| АБСОЛЮТНЫЙ СПОСОБ ДИФФЕРЕНЦИАЛЬНО-СКАНИРУЮЩЕЙ ТЕПЛОВОЙ КОНДУКТОМЕТРИИ | 2020 |
|
RU2755090C1 |
| СПОСОБ СОВОКУПНОГО ИЗМЕРЕНИЯ ТЕПЛОПРОВОДНОСТИ РАЗНОРОДНЫХ ТВЕРДЫХ МАТЕРИАЛОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2020 |
|
RU2752398C1 |
| СПОСОБ ИЗМЕРЕНИЯ ТЕПЛОПРОВОДНОСТИ | 2020 |
|
RU2755330C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕПЛОПРОВОДНОСТИ ТВЕРДОГО ТЕЛА ЦИЛИНДРИЧЕСКОЙ ФОРМЫ ПРИ СТАЦИОНАРНОМ ТЕПЛОВОМ РЕЖИМЕ | 2013 |
|
RU2551663C2 |
| СПОСОБ КОМПЛЕКСНОГО ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК МАТЕРИАЛОВ | 2009 |
|
RU2387981C1 |
| СПОСОБ КОМПЛЕКСНОГО ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК ТВЕРДЫХ И ДИСПЕРСНЫХ МАТЕРИАЛОВ | 1999 |
|
RU2178166C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕПЛОПРОВОДНОСТИ МАТЕРИАЛОВ | 2004 |
|
RU2276781C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕПЛОПРОВОДНОСТИ МАТЕРИАЛОВ | 2007 |
|
RU2343466C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ ТВЕРДЫХ ТЕЛ С ВЫСОКОЙ ТЕПЛОПРОВОДНОСТЬЮ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2024 |
|
RU2828623C1 |
| СПОСОБ ИЗМЕРЕНИЯ ОТНОСИТЕЛЬНОЙ ТЕПЛОПРОВОДНОСТИ ПРИ ВНЕШНЕМ ВОЗДЕЙСТВИИ | 2014 |
|
RU2569933C1 |
Изобретение относится к области теплофизических измерений и предназначено для измерения теплопроводностей разнородных твердых тел, значения которых априорно неизвестны. Заявляемый способ ориентирован на метрологию и может быть использован в качестве теоретической основы для современного эталона единицы теплопроводности. Согласно заявленному решению формируют измерительную ячейку, для чего образуют систему тел из трех образцов. Внутри образованной системы тел размещают равномерно распределенный по плоскости поперечного сечения образцов внутренний сток теплоты, а на ее двух противоположных наружных плоскостях размещают однонаправленные и равномерно распределенные по плоскости поперечного сечения образцов внешние источники теплоты. Задают мощность внутреннего стока и стабилизируют ее во времени, регулируют мощности внешних источников теплоты до достижения равенства стационарных перепадов температуры на образцах, находящихся по разные стороны внутреннего стока теплоты. Измеряют достигнутые мощности и стационарные равные перепады температуры, затем уравнивают мощности внешних источников и измеряют достигнутые стационарные перепады температуры на образцах, находящихся по разные стороны от внутреннего стока теплоты. После чего по измеренным данным расчетным путем находят искомые теплопроводности. Технический результат - повышение точности измерения теплопроводности твердых тел с одновременным расширением динамического диапазона и номенклатуры исследуемых материалов. 3 ил.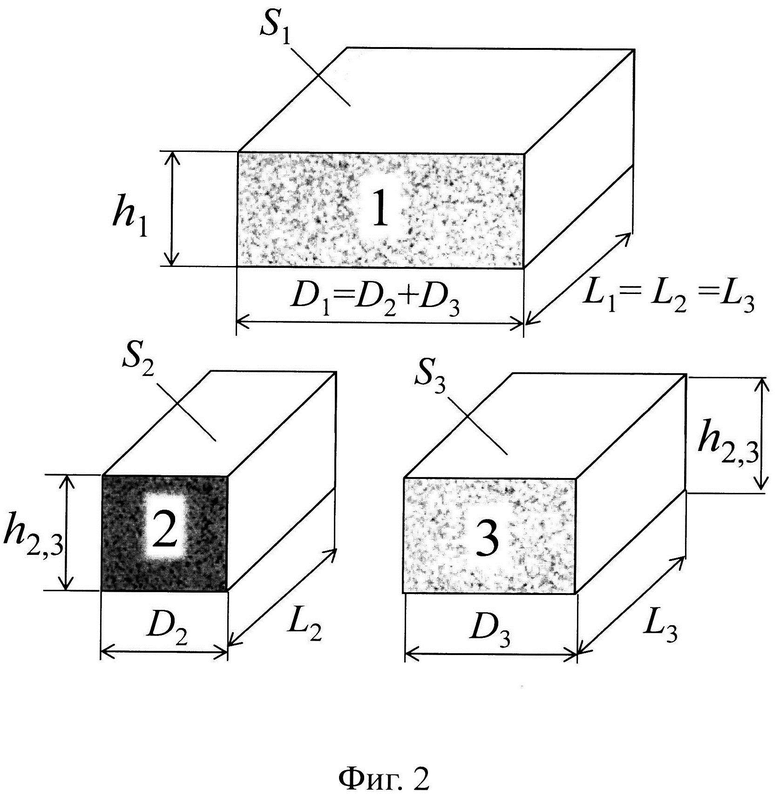
Абсолютный способ дифференциально-сканирующей кондуктометрии разнородных твердых материалов, заключающийся в том, что формируют измерительную ячейку, для чего образуют систему тел из трех образцов, внутри образованной системы тел размещают равномерно распределенный по плоскости поперечного сечения образцов внутренний сток теплоты, а на ее двух противоположных наружных плоскостях размещают однонаправленные и равномерно распределенные по плоскости поперечного сечения образцов внешние источники теплоты, задают мощность внутреннего стока и стабилизируют ее во времени, регулируют мощности внешних источников теплоты до достижения равенства стационарных перепадов температуры на образцах, находящихся по разные стороны внутреннего стока теплоты, измеряют достигнутые мощности и стационарные равные перепады температуры, затем уравнивают мощности внешних источников и измеряют достигнутые стационарные перепады температуры на образцах, находящихся по разные стороны от внутреннего стока теплоты, после чего по измеренным данным расчетным путем находят искомые теплопроводности каждого образца, при этом в сформированной измерительной ячейке по одну сторону внутреннего стока теплоты располагают наибольший образец с более высокой теплопроводностью и с наибольшим поперечным сечением, а по его другую сторону располагают два разнородных образца, сумма поперечных сечений которых равна поперечному сечению наибольшего образца, а периметр их общего поперечного сечения совпадает с периметром поперечного сечения наибольшего образца, причем материал одного из двух разнородных образцов идентичен материалу наибольшего образца, соотношение поперечных сечений двух разнородных образцов, а также соотношение их толщины с толщиной наибольшего образца задают предварительно, которое получают расчетным путем, исходя из требования обеспечить достаточную для точного измерения разность мощностей внешних источников теплоты и соизмеримость перепадов температуры по обе стороны внутреннего стока теплоты, а для расчета искомых теплопроводностей используют следующую систему уравнений:
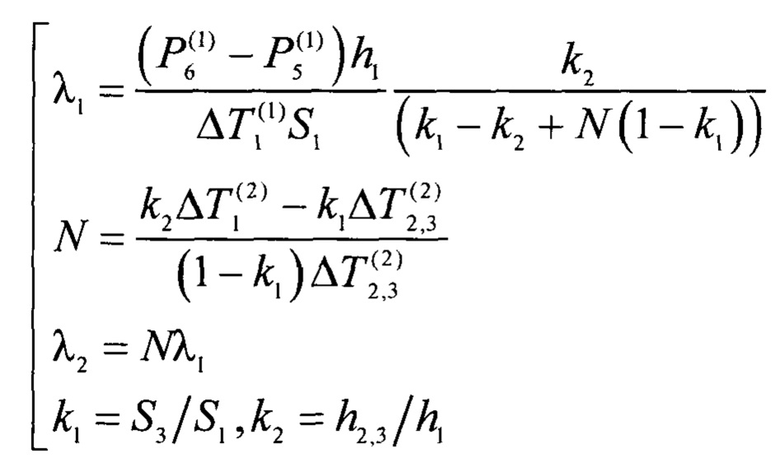 ,
,
где
λ1 - теплопроводность наибольшего образца с более высокой теплопроводностью и идентичного ему по материалу образца из двух разнородных образцов,
λ2 - теплопроводность образца с меньшей теплопроводностью,
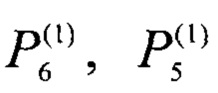 - измеренные мощности внешних источников, соответствующие стационарным равным перепадам температуры,
- измеренные мощности внешних источников, соответствующие стационарным равным перепадам температуры,
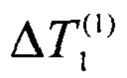 - измеренные стационарные равные перепады температуры,
- измеренные стационарные равные перепады температуры,
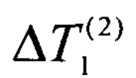 - измеренный перепад температуры на наибольшем образце с более высокой теплопроводностью, достигнутый при равенстве мощностей внешних источников теплоты,
- измеренный перепад температуры на наибольшем образце с более высокой теплопроводностью, достигнутый при равенстве мощностей внешних источников теплоты,
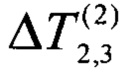 - измеренный перепад температуры на двух разнородных образцах, достигнутый при равенстве мощностей внешних источников теплоты,
- измеренный перепад температуры на двух разнородных образцах, достигнутый при равенстве мощностей внешних источников теплоты,
h1 - толщина наибольшего образца,
h2,3 - толщина каждого из разнородных образцов,
S1, S3 - площадь поперечного сечения наибольшего образца и образца, идентичного по материалу наибольшему образцу, соответственно.
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕПЛОПРОВОДНОСТИ МАТЕРИАЛОВ | 2004 |
|
RU2276781C1 |
| Способ измерения коэффициента теплопроводности | 1983 |
|
SU1165958A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕПЛОПРОВОДНОСТИ МАТЕРИАЛОВ | 2007 |
|
RU2343466C1 |
| Способ измерения коэффициента теплопроводности теплоизолирующего материала | 2019 |
|
RU2731840C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕПЛОПРОВОДНОСТИ МАТЕРИАЛОВ | 2011 |
|
RU2478940C1 |
| Способ измерения теплопроводности | 1988 |
|
SU1561025A1 |
| EP 459036 A1, 04.12.1991 | |||
| DE 10206045 A1, 11.09.2003. | |||
Авторы
Даты
2021-06-16—Публикация
2020-11-23—Подача