Изобретение относится к тепловым испытаниям, а именно, к определению теплопроводности и объемной теплоемкости материалов.
Известен способ комплексного определения теплофизических характеристик материалов, заключающийся в том, что измеряют толщину исследуемого образца и приводят его в тепловой контакт по плоскости с эталонным образцом, термостатируют исследуемый и эталонный образцы при начальной заданной температуре, затем подводят непрерывно теплоту к плоскости сечения внутри эталонного образца, расположенной на заданном расстоянии и параллельно плоскости контакта, при этом температуры на внешних поверхностях исследуемого и эталонного образцов поддерживают равными заданной начальной температуре термостатирования, регистрируют удельную мощность источника теплоты и измеряют с постоянным шагом во времени температуру эталонного образца в заданном сечении, на каждом шаге определяют величину динамического параметра, представляющего собой отношение температуры в заданном сечении эталонного образца на шаге измерения, номер которого на постоянное целое число меньше номера последнего шага измерения, к температуре в этом же сечении эталонного образца на последнем шаге измерения, сравнивают величину динамического параметра с заданным максимальным значением, испытания заканчивают при превышении максимального значения динамического параметра, задают максимальное значение динамического параметра в диапазоне 0,2…0,8, и определяют искомые теплофизические характеристики по формулам. (Патент РФ №2027172, МПК6 G01N 25/18, 1995).
Недостатком способа является большая длительность экспериментального определения теплофизических характеристик, обусловленная необходимостью предварительного термостатирования образцов, а также возможность определения теплофизических характеристик только тех материалов, которые имеют значения теплофизических свойств, близкие со свойствами эталонного образца.
Наиболее близким техническим решением является способ комплексного определения теплофизических характеристик материалов, заключающийся в том, что измеряют толщину исследуемого образца, подводят теплоту к образцам, поддерживают температуру на внешних поверхностях образцов равной заданной температуре, регистрируют удельную мощность источника теплоты, измеряют с постоянным шагом во времени температуру в течение всего эксперимента, определяют на каждом шаге величину динамического параметра и сравнивают с максимальным значением, лежащим в заданном диапазоне, определяют искомые теплофизические характеристики по формулам, в качестве второго образца используют образец, идентичный первому образцу, эти образцы с двух сторон приводят в тепловой контакт с объемным источником теплоты, эксперимент проводят в два этапа, причем на первом этапе подводят постоянную мощность к объемному источнику теплоты, на каждом шаге во времени регистрируют среднеинтегральную температуру объемного источника теплоты и вычисляют величину динамического параметра как отношение разности скоростей изменения измеряемой среднеинтегральной температуры на первом и текущем шаге к скорости изменения среднеинтегральной температуры на первом шаге, заканчивают проведение первого этапа эксперимента при превышении заданного максимального значения динамического параметра, а на следующем шаге во времени начинают проведение второго этапа эксперимента, а именно прекращают подвод мощности к объемному источнику теплоты, на каждом шаге второго этапа вычисляют безразмерную температуру и число Фурье, проведение второго этапа эксперимента прекращают на том шаге, на котором значение безразмерной температуры становится меньше заданного значения, причем, по зарегистрированным на первом этапе эксперимента данным, вычисляют искомую теплопроводность, а по зарегистрированным на втором этапе эксперимента данным определяют искомую температуропроводность. (Патент РФ №2243543, МПК7 G01N 25/18. Способ комплексного определения теплофизических характеристик материалов / Мищенко С.В., Пономарев С.В., Трофимов А.В., Балабанов П.В., Пономарева Е.С. Опубл. 27.12.2004. Бюл. №36). Принято за прототип.
Недостатками известного способа являются большая длительность измерений, обусловленная необходимостью проведения двух этапов эксперимента, а также возможность измерения теплофизических свойств с заданной точностью только в тех диапазонах по теплопроводности и температуропроводности для которых определены предельные значения динамических параметров.
Такие признаки прототипа, как измерение толщины исследуемого образца, использование второго образца, идентичного первому образцу, приведение образцов с двух сторон в тепловой контакт с объемным источником теплоты, подведение теплоты к образцам, регистрация удельной мощности источника теплоты, измерение с постоянным шагом во времени температуры в течение всего эксперимента, определение искомых теплофизических характеристик по формулам, совпадают с существенными признаками заявляемого изобретения.
Технической задачей является сокращение длительности эксперимента и повышение точности определения теплофизических характеристик.
Данная техническая задача решается тем, что в способе комплексного определения теплофизических характеристик материалов, заключающемся в том, что измеряют толщину исследуемого образца, в качестве второго образца используют образец, идентичный первому образцу, эти образцы с двух сторон приводят в тепловой контакт с объемным источником теплоты, подводят теплоту к образцам, регистрируют удельную мощность источника теплоты, измеряют с постоянным шагом во времени температуру в течение всего эксперимента, определяют искомые теплофизические характеристики по формулам, дополнительно внешние поверхности исследуемых образцов приводят в тепловой контакт с эталонными образцами, внешние поверхности эталонных образцов приводят в тепловой контакт с плоскими нагревателями, подводят постоянную мощность к нагревателям и регистрируют перепад температур на поверхностях эталонных образцов в плоскости контакта эталонного образца с плоским нагревателем и в плоскости контакта эталонного образца с исследуемым образцом, вычисляют тепловые потоки через первый 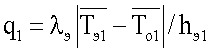 и второй
и второй 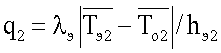 исследуемые образцы, вычисляют число Фурье
исследуемые образцы, вычисляют число Фурье 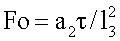 и безразмерную среднеинтегральную температуру объемного источника теплоты
и безразмерную среднеинтегральную температуру объемного источника теплоты 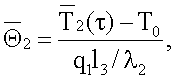 по экспериментальным данным вычисляют константу А как тангенс угла наклона прямолинейного участка графика функции
по экспериментальным данным вычисляют константу А как тангенс угла наклона прямолинейного участка графика функции 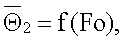 искомую объемную теплоемкость ср вычисляют по формуле
искомую объемную теплоемкость ср вычисляют по формуле
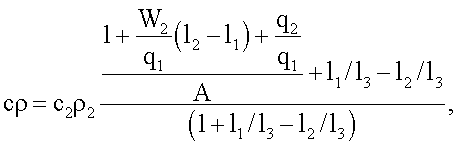
где λ2, λэ - соответственно теплопроводность материала объемного
источника теплоты и эталонного образца, Вт/(мК),
с2ρ2 - объемная теплоемкость материала объемного источника теплоты, Дж/(м3К),
а2 - температуропроводность материала объемного источника теплоты, м2/с,
W2 - удельная мощность объемного источника теплоты, Вт/м3,
q1, q2 - соответственно удельные тепловые потоки через первый и второй исследуемые образцы, Вт/м2,
l1, l2, l3 - координаты, определяемые через толщины первого исследуемого образца, объемного источника теплоты, второго исследуемого образца, м,
Т0 - начальная температура исследуемых образцов, К,
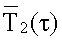 - среднеинтегральная температура объемного источника теплоты, К,
- среднеинтегральная температура объемного источника теплоты, К,
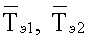 - соответственно среднеинтегральные температуры, измеренные на поверхностях первого и второго эталонных образцов в плоскости контакта соответствующего эталонного образца с соответствующим плоским нагревателем, К,
- соответственно среднеинтегральные температуры, измеренные на поверхностях первого и второго эталонных образцов в плоскости контакта соответствующего эталонного образца с соответствующим плоским нагревателем, К,
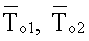 - соответственно среднеинтегральные температуры, измеренные на поверхностях первого и второго эталонных образцов в плоскости контакта соответствующего эталонного образца с соответствующим исследуемым образцом, К,
- соответственно среднеинтегральные температуры, измеренные на поверхностях первого и второго эталонных образцов в плоскости контакта соответствующего эталонного образца с соответствующим исследуемым образцом, К,
hэ1,hэ2 - соответственно толщина первого и второго эталонного образца, м,
τ - время, отсчитываемое с момента начала эксперимента, с, а искомую теплопроводность X определяют по формуле
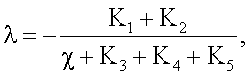
где K1, K2, K3, K4, K5 χ - множители, определяемые по формулам
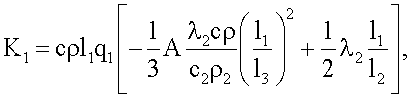
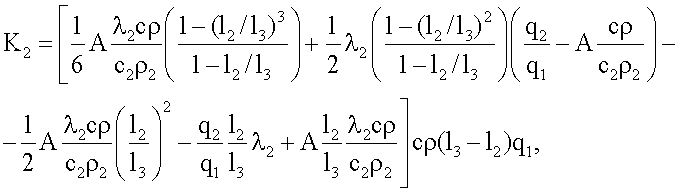
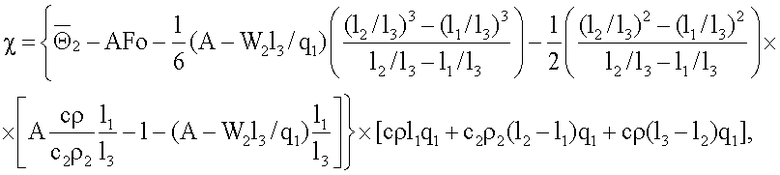
K3=Π2Π6,
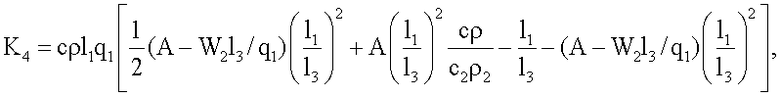
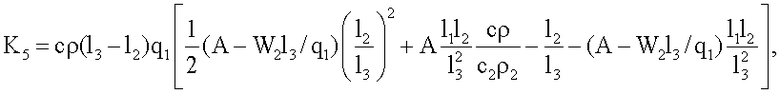
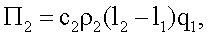
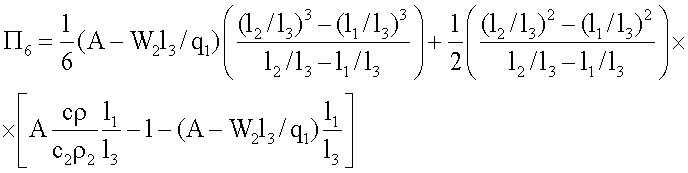
В прототипе для измерения теплофизических свойств проводится два этапа эксперимента, причем на первом этапе эксперимента контролируют динамический параметр с целью не дожидаться фактического наступления стационарного теплового режима. Это позволяет сократить первую стадию эксперимента, но и повышает погрешность измерения теплопроводности, так как вместо стационарной среднеинтегральной температуры в расчетах используют величину, отличающуюся от фактической стационарной среднеинтегральной температуры. В отличие от прототипа предложенный способ определения теплофизических характеристик осуществляется на стадии регулярного теплового режима второго рода в один этап, что обусловливает не только сокращение длительности эксперимента, но и повышение точности измерения за счет уменьшения погрешности измерения среднеинтегральной температуры.
Искомые теплофизические характеристики определяются по точным формулам без использования в расчетах численных методов, что также повышает точность их определения.
В конструкции измерительного устройства не используются жидкостные термостаты, что удешевляет его изготовление и эксплуатацию.
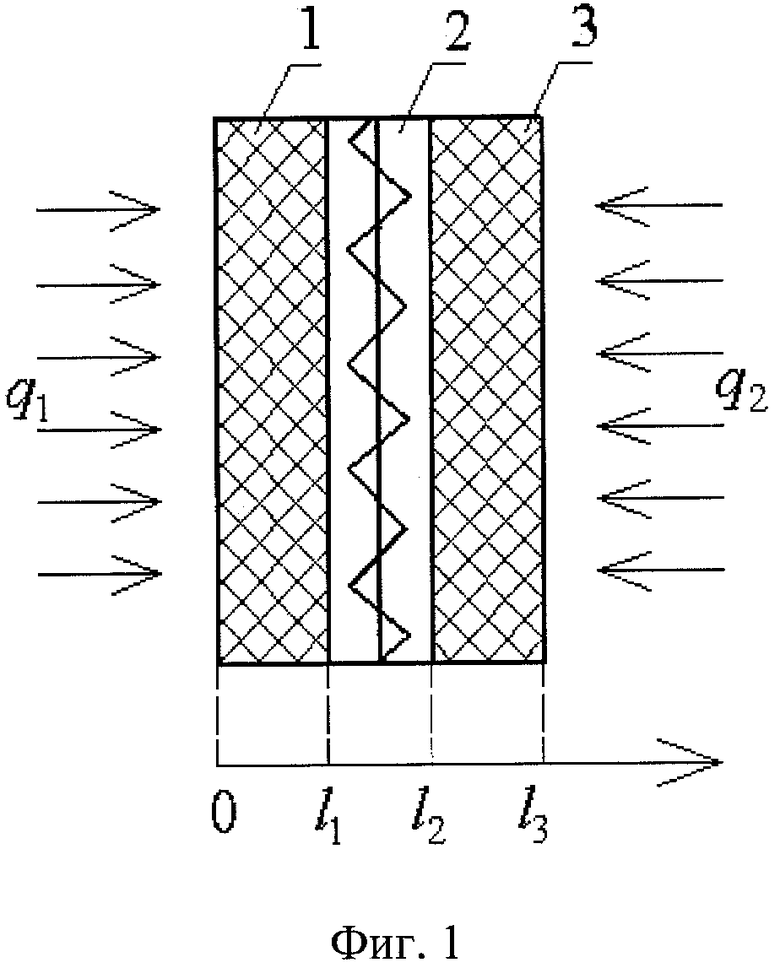
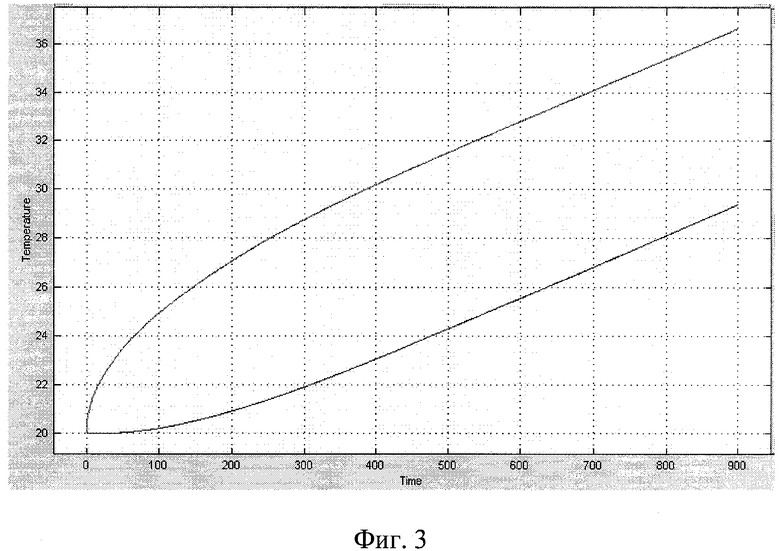
На фиг.1 приведена физическая модель измерительной ячейки, реализующей предлагаемый способ. На фиг.2 изображена схема конструкции измерительной ячейки. На фиг.3 изображены графики изменения среднеинтегральной температуры объемного источника теплоты по показаниям термометра ТС3 и среднеинтегральной температуры на поверхности исследуемого образца по показаниям термометра ТС 1.
Физическая модель измерительной ячейки (фиг.1) представляет собой плоскую трехслойную систему. Слои 1 и 3 системы образованы идентичными по свойствам и размерам исследуемыми образцами, между которыми расположен слой 2, состоящий из нагревателя и термометра сопротивления, выполненных из манганиновой и медной проволок, навитых по спирали Архимеда. Такая конструкция слоя 2 позволяет сделать допущение о том, что мощность, выделяемая на нагревателе, будет равномерно распределена по всему объему слоя, а термометр сопротивления, выполненный из медной проволоки, позволяет измерять среднеинтегральную температуру второго слоя. На внешних поверхностях исследуемых образцов заданы тепловые потоки q1 и q2.
Математическая модель, описывающая температурное поле в измерительном устройстве, была сформулирована при следующих допущениях: 1) теплоперенос излучением в исследуемых образцах отсутствует; 2) температурное поле внутри системы считается одномерным; 3) термические сопротивления на границах контакта слоев отсутствуют; 4) на внешних границах исследуемых образцов заданы постоянные тепловые потоки; 5) в ходе эксперимента температура слоев системы изменяется незначительно, поэтому теплофизические свойства слоев постоянны. С учетом допущений, математическая модель получена в виде системы дифференциальных уравнений теплопроводности
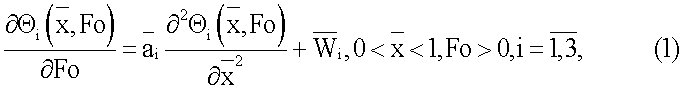
с начальными условиями 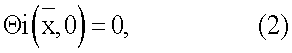
и граничными условиями
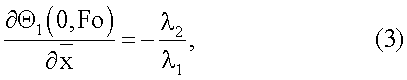
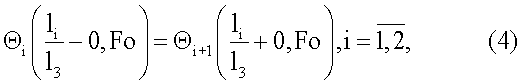
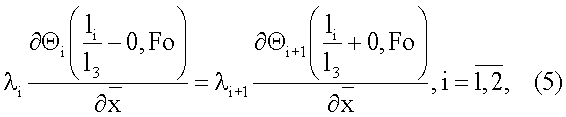
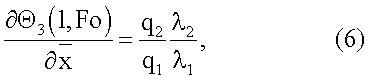
где 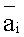 - безразмерная температуропроводность i-го слоя, определяемая из выражения
- безразмерная температуропроводность i-го слоя, определяемая из выражения 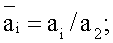 λi - теплопроводность;
λi - теплопроводность; 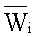 - безразмерная объемная мощность внутренних источников теплоты, определяемая из выражения
- безразмерная объемная мощность внутренних источников теплоты, определяемая из выражения 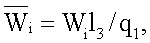 причем объемная мощность внутренних источников теплоты первого и третьего слоев равны W1=W3=0, а объемная мощность внутренних источников теплоты второго слоя определяется как отношение мощности Р нагревателя и объема V2 второго слоя, т.е W2=P/V2;
причем объемная мощность внутренних источников теплоты первого и третьего слоев равны W1=W3=0, а объемная мощность внутренних источников теплоты второго слоя определяется как отношение мощности Р нагревателя и объема V2 второго слоя, т.е W2=P/V2; 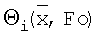 - безразмерная температура, определяемая из выражения
- безразмерная температура, определяемая из выражения
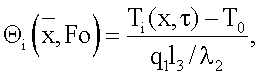
где Тi(x,τ) - температурное поле i-го слоя; Т0 - начальная температура;
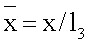 - безразмерная пространственная координата;
- безразмерная пространственная координата; 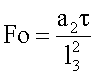 - число Фурье, x,τ - пространственная координата и время.
- число Фурье, x,τ - пространственная координата и время.
Из теории теплопроводности известно, что поле температур 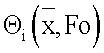 будет автомодельным относительно координаты Fo. Решение задачи (1)-(6) имеет следующий вид
будет автомодельным относительно координаты Fo. Решение задачи (1)-(6) имеет следующий вид
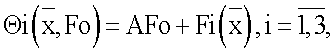
где А - постоянный коэффициент; F^x) - функция, определяемая по следующими выражениями
где А - постоянный коэффициент; 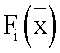 - функция, определяемая по следующими выражениями
- функция, определяемая по следующими выражениями
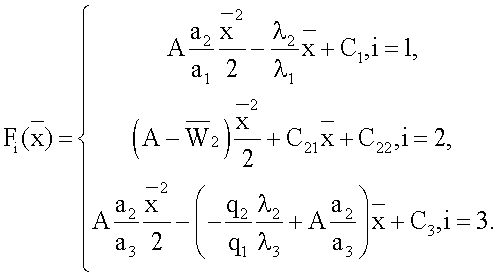
Константы А, C1, С21, С22, С3 определяются из четырех уравнений, составляющих граничные условия (3)-(6), а также из уравнения теплового баланса записанного для многослойной системы в виде
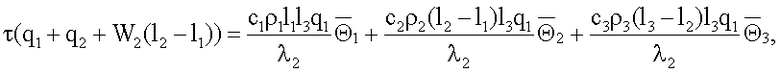
где 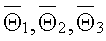 - безразмерные средиеинтегральные температуры 1-3 слоев системы, определяемые по формулам
- безразмерные средиеинтегральные температуры 1-3 слоев системы, определяемые по формулам
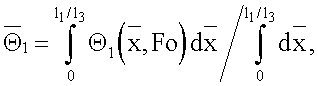
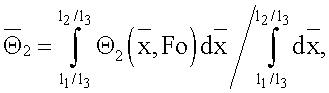
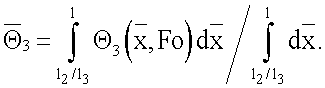
С учетом приведенных выше уравнений и граничных условий (3)-(6) получены следующие выражения для расчета констант А, С1, С21, С22, С3
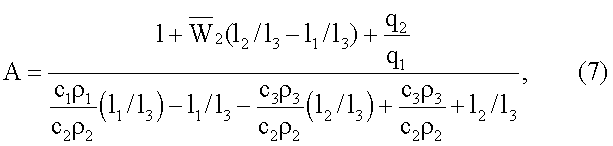
C1=Π8+C22,
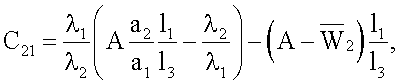
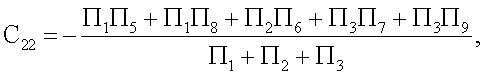
C3=Π9+C22,
где
Π1=c1ρ1l1q1,
Π2=c2ρ2(l2-l1)q1,
Π3=c3ρ3(l3-l2)q1,
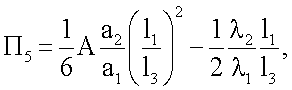
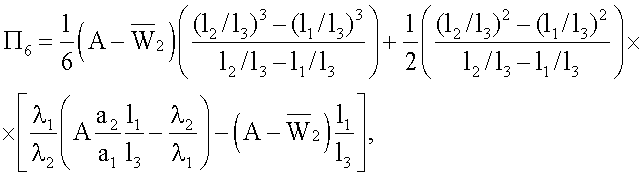
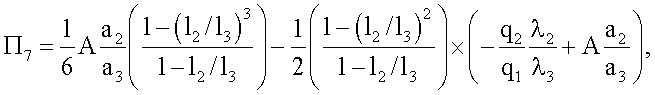
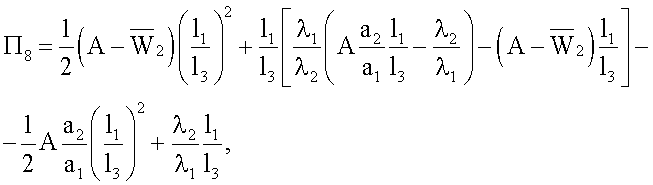
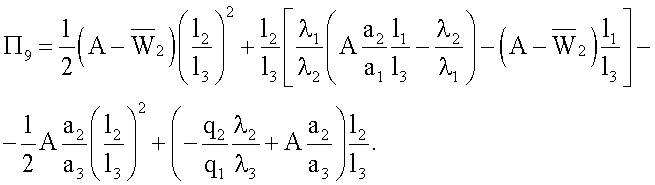
Учитывая, что теплофизические свойства первого и третьего слоев системы равны, обозначим с1ρ1=с3ρ3=сρ и из (7) получим выражение для расчета объемной теплоемкости исследуемых образцов
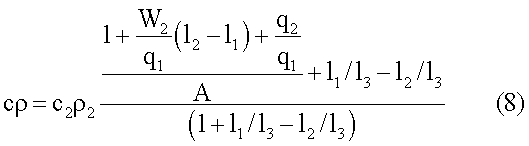
Расчетная формула для вычисления теплопроводности получена следующим образом. С учетом равенства теплопроводностей первого и третьего слоев обозначим λ1=λ3=λ. Из выражения для безразмерной среднеинтегральной температуры второго слоя
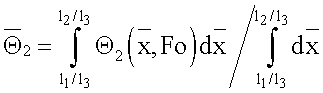
выразим λ с учетом известных выражений для констант С21, С22 и безразмерной температуры 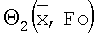 . Получим следующую расчетную формулу
. Получим следующую расчетную формулу
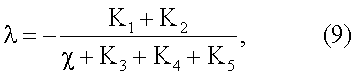
где 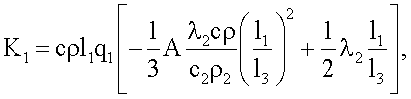
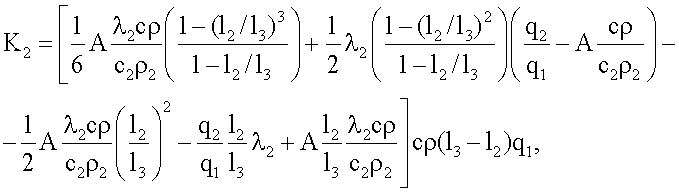
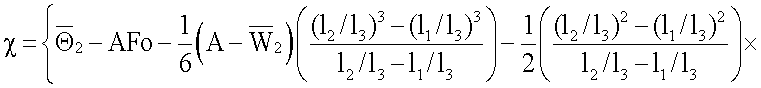
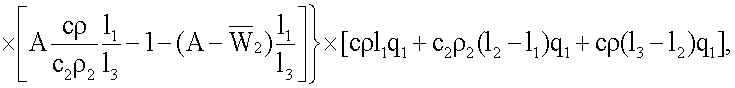
K3=Π2Π6,
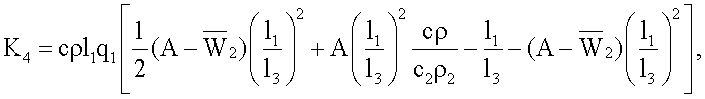
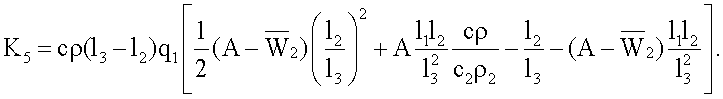
Измерительная ячейка (фиг.2) для реализации предлагаемого способа состоит из трех частей: верхней, нижней и центральной части.
Нижняя и верхняя части измерительной ячейки полностью идентичны, поэтому приведем описание конструктивных особенностей только нижней части. На верхнюю поверхность пластины 7 из полиметилметакрилата в форме круга по спирали Архимеда приклеивается медная проволока, выполняющая функцию термометра сопротивления ТС1. Такая конструкция термометра сопротивления позволит в эксперименте измерить среднеинтегральную температуру 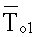 на верхней поверхности пластины 7 в плоскости ее контакта с исследуемым образцом. На нижнюю поверхность пластины 7 по спирали Архимеда наклеивают медную (термометр сопротивления ТС2) и манганиновую (нагреватель Н2) проволоки. Термометром сопротивления ТС2 в эксперименте измеряют среднеинтегральную температуру
на верхней поверхности пластины 7 в плоскости ее контакта с исследуемым образцом. На нижнюю поверхность пластины 7 по спирали Архимеда наклеивают медную (термометр сопротивления ТС2) и манганиновую (нагреватель Н2) проволоки. Термометром сопротивления ТС2 в эксперименте измеряют среднеинтегральную температуру 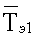 на нижней поверхности пластины 7. Применение в конструкции измерительной ячейки пластины из полиметилметакрилата дает возможность вычислить величину удельного теплового потока q1, воздействующего на поверхность исследуемого образца, по формуле
на нижней поверхности пластины 7. Применение в конструкции измерительной ячейки пластины из полиметилметакрилата дает возможность вычислить величину удельного теплового потока q1, воздействующего на поверхность исследуемого образца, по формуле
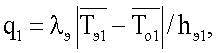
где λэ - теплопроводность полиметилметакрилата (эталонного образца), hэl - толщина пластины 7.
Поверхность термометра ТС 1, непосредственно контактирующая с исследуемым образцом, защищена от загрязнения тонкой металлической оболочкой. На нижнюю поверхность термометра сопротивления ТС2 и нагревателя Н2 приклеивается пластина 8, идентичная пластине 7. На нижнюю поверхность 8 наносится слой теплоизоляции 9. В деталях 7, 8, 9 предусмотрено наличие канала 10, предназначенного для вывода концов термометров сопротивления ТС 1, ТС2 и нагревателя Н2 наружу и подключения их к контактам разъема 11. Нижняя часть измерительной ячейки установлена на подставку 12.
Центральная часть измерительной ячейки выполнена из двух тонких латунных пластин 4, между которыми располагаются, навитые по спирали Архимеда, медная (термометр сопротивления ТС3) и манганиновая (нагреватель Н3) проволоки. Пластины 4 размещены между кольцами 5 из теплоизоляционного материала и закреплены между собой болтами 6. Концы медной и манганиновой проволок подключаются к контактам разъема 13.
Нагревателем Н5, расположенным в верхней части измерительной ячейки, задают удельный тепловой поток q2 через второй (верхний) исследуемый образец. Величину удельного теплового потока вычисляют по формуле
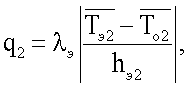
где λэ - теплопроводность полиметилметакрилата, hэ2 - толщина пластины 7, расположенной в верхней части измерительной ячейки,
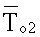 - среднеинтегральная температура по показаниям термометра ТС4,
- среднеинтегральная температура по показаниям термометра ТС4,
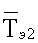 - среднеинтегральная температура по показаниям термометра ТС5.
- среднеинтегральная температура по показаниям термометра ТС5.
Измерительную ячейку помещают в вакуум-камеру 14.
Способ комплексного определения теплофизических характеристик реализуется следующим образом. На верхнюю поверхность термометра ТС1 (фиг.2) нижней части измерительной ячейки помещают первый исследуемый образец. Сверху помещают центральную часть измерительной ячейки. На верхнюю пластину 4 центральной части устанавливают второй исследуемый образец, идентичный первому образцу. Сверху на второй образец устанавливают верхнюю часть измерительной ячейки. Измерительную ячейку помещают в вакуум-камеру 14, герметично закрывают и откачивают из нее воздух до достижения небольшого вакуума. Дождавшись постоянства во времени показаний термометров сопротивления ТС1, ТС2, ТС3, ТС4, ТС5 подводят постоянное напряжение U1 к нагревателям Н2 и Н5 измерительной ячейки и постоянное напряжение U2 к нагревателю Н3. В результате в слое 2 (фиг.1) начинают действовать внутренние источники теплоты с объемной плотностью 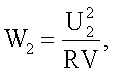 где R - сопротивление нагревателя Н3, V=S(l2-l1) - объем второго слоя, S - площадь второго слоя, l2-l1 - толщина второго слоя.
где R - сопротивление нагревателя Н3, V=S(l2-l1) - объем второго слоя, S - площадь второго слоя, l2-l1 - толщина второго слоя.
Одновременно на поверхность исследуемых образцов будут воздействовать тепловые потоки q1 и q2 (фиг.1). Термометрами сопротивления ТС4 и ТС5 (фиг.2) контролируют перепад температур 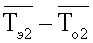 на поверхностях верхнего эталонного образца 7. Аналогично, термометрами сопротивления ТС2 и ТС 1 (фиг.2) контролируют перепад температур
на поверхностях верхнего эталонного образца 7. Аналогично, термометрами сопротивления ТС2 и ТС 1 (фиг.2) контролируют перепад температур 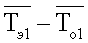 на поверхностях нижнего эталонного образца 7. По измеренным перепадам температур вычисляют удельные тепловые потоки
на поверхностях нижнего эталонного образца 7. По измеренным перепадам температур вычисляют удельные тепловые потоки 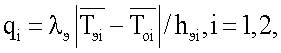 где hэi - толщина эталонного образца 7.
где hэi - толщина эталонного образца 7.
На каждом шаге во времени τ термометром сопротивления ТС3 измеряют среднеинтегральную температуру 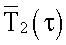 второго слоя. Вычисляют безразмерную среднеинтегральную температуру второго слоя
второго слоя. Вычисляют безразмерную среднеинтегральную температуру второго слоя 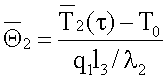 и число Фурье
и число Фурье 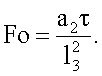 Определяют время наступления регулярного теплового режима второго рода. После наступления регулярного теплового режима термометром ТС3 регистрируют два показания
Определяют время наступления регулярного теплового режима второго рода. После наступления регулярного теплового режима термометром ТС3 регистрируют два показания 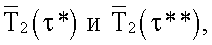 где τ**>τ*, вычисляют безразмерную среднеинтегральную температуру по зарегистрированным данным
где τ**>τ*, вычисляют безразмерную среднеинтегральную температуру по зарегистрированным данным 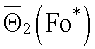 и
и 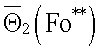 и вычисляют А по формуле
и вычисляют А по формуле 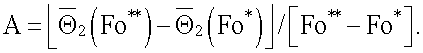 Искомую объемную теплоемкость вычисляют по формуле (8), а теплопроводность - по формуле (9).
Искомую объемную теплоемкость вычисляют по формуле (8), а теплопроводность - по формуле (9).
Рассмотрим конкретный пример реализации предложенного способа.
Для измерения теплофизических характеристик изготовлены по два образца из органического стекла толщиной 8 мм. Теплофизические свойства исследуемых образцов: λ-=0,195 Вт/(мК), сρ=1839622 Дж/(м3К). Толщина слоя 2 (фиг.1) измерительной ячейки составила 4 мм, причем пластина 4 выполнена из латуни, толщиной 1,5 мм, нагреватель Н3 и термометр ТС3 выполнены из манганиновой и медной проволок, толщиной 0,15 и 0,3 мм соответственно. Начальная температура исследуемых образцов была 20°С. В течение эксперимента напряжение к нагревателю НЗ не подводилось, а к нагревателям Н2 и Н5 подводилось напряжение 20 В. В этом случае перепад температур на эталонных образцах 7 из полиметилметакрилата при их толщине 1 мм составил порядка 1,4°С, а удельная мощность тепловых потоков q1 и q2 составила порядка 270 Вт/м2. Из показаний термометров ТС1 (верхняя кривая на фиг.3) и ТС3 (нижняя кривая на фиг.3) видно, что регулярный режим второго рода наступает при τ>400 с (кривые имеют линейный участок). Регистрируют два показания термометра 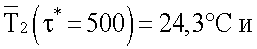
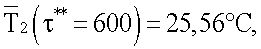 вычисляют безразмерную среднеинтегральную температуру по зарегистрированным данным
вычисляют безразмерную среднеинтегральную температуру по зарегистрированным данным 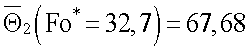
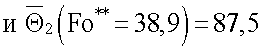 и вычисляют А по формуле
и вычисляют А по формуле 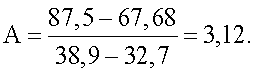 Подставив полученное значение для А в формулу (8) вычисляют объемную теплоемкость исследуемых образцов
Подставив полученное значение для А в формулу (8) вычисляют объемную теплоемкость исследуемых образцов
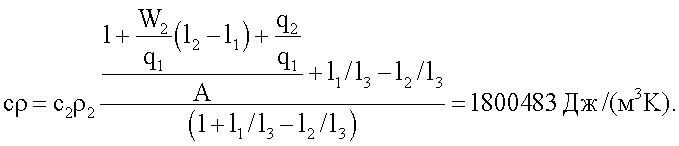
В расчетах использовались следующие данные: с2=378 Дж/(кг °С), р2=8600 кг/м3, W2=0, q1=q2=270 Вт/м2, l1=0,008 мм, l2=0,012 мм, l3=0,02 мм.
Для вычисления искомой теплопроводности вначале вычисляют значения множителей, входящих в состав формулы (9)
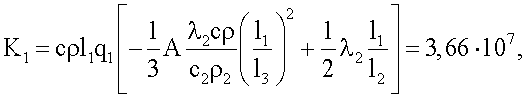
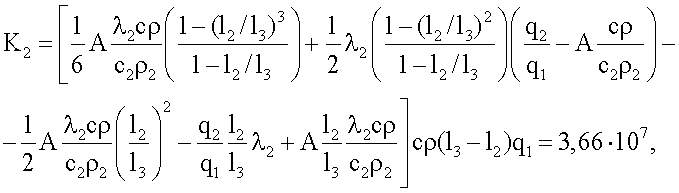
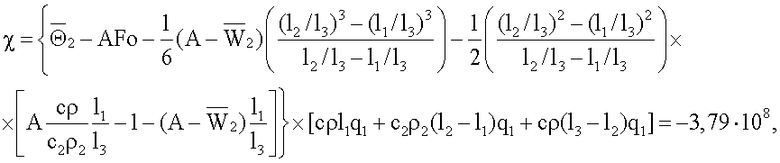
K3=Π2Π6=-1,38·106,
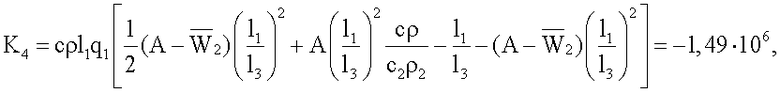
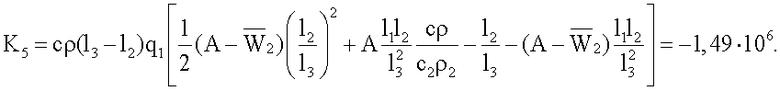
Значение теплопроводности, вычисленное по формуле (9), составило λ=0,190 Вт/(мК).
Как видно из фиг.3, длительность эксперимента по измерению теплофизических свойств образцов из полиметилметакрилата толщиной 8 мм составила не более 600 с, тогда как при использовании метода и устройства, взятого за прототип, для измерения идентичных образцов длительность эксперимента составила 27 мин (1-й этап эксперимента) и 24 мин (второй этап эксперимента). Таким образом, применение разработанного метода и устройства позволило сократить длительность эксперимента примерно в 6 раз.
В предложенном методе не требуется контролировать значения динамического параметра, что позволяет более точно определять среднеинтегральную температуру объемного источника теплоты, а как следствие повысить точность определения теплофизических характеристик.
При обработке экспериментальных данных используются простые расчетные формулы, исключающие необходимость применения численных методов, что также приводит к повышению точности определения теплофизических свойств по сравнению с прототипом.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ УДЕЛЬНОЙ ТЕПЛОЕМКОСТИ МАТЕРИАЛОВ | 2013 |
|
RU2523090C1 |
| СПОСОБ КОМПЛЕКСНОГО ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК МАТЕРИАЛОВ | 2003 |
|
RU2243543C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УДЕЛЬНОЙ ТЕПЛОЕМКОСТИ СЫПУЧИХ МАТЕРИАЛОВ | 2015 |
|
RU2613591C1 |
| СПОСОБ ИЗМЕРЕНИЯ ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ АНИЗОТРОПНЫХ МАТЕРИАЛОВ МЕТОДОМ ЛИНЕЙНОГО ИМПУЛЬСНОГО ИСТОЧНИКА ТЕПЛОТЫ | 2015 |
|
RU2613194C1 |
| СПОСОБ КОМПЛЕКСНОГО ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК МАТЕРИАЛОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1991 |
|
RU2027172C1 |
| СПОСОБ КОМПЛЕКСНОГО ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК МАТЕРИАЛОВ | 2010 |
|
RU2439543C1 |
| Способ определения температуропроводности и коэффициента теплопроводности | 2022 |
|
RU2785084C1 |
| СПОСОБ КОМПЛЕКСНОГО ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК ТВЕРДЫХ И ДИСПЕРСНЫХ МАТЕРИАЛОВ | 1999 |
|
RU2178166C2 |
| СПОСОБ КОМПЛЕКСНОГО ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ МАТЕРИАЛОВ | 1991 |
|
RU2018117C1 |
| СПОСОБ ИЗМЕРЕНИЯ ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ ТЕПЛОИЗОЛЯЦИОННЫХ МАТЕРИАЛОВ МЕТОДОМ ПЛОСКОГО ИМПУЛЬСНОГО ИСТОЧНИКА ТЕПЛОТЫ | 2015 |
|
RU2601234C1 |
Изобретение относится к тепловым испытаниям. В способе в качестве второго образца используют образец, идентичный первому образцу, эти образцы с двух сторон приводят в тепловой контакт с объемным источником теплоты. Внешние поверхности исследуемых образцов приводят в тепловой контакт с эталонными образцами, внешние поверхности эталонных образцов приводят в тепловой контакт с плоскими нагревателями. Измеряют тепловые потоки через первый и второй исследуемые образцы, вычисляют число Фурье и безразмерную среднеинтегральную температуру объемного источника теплоты, по экспериментальным данным вычисляют тангенс угла наклона прямолинейного участка графика зависимости безразмерной среднеинтегральной температуры объемного источника теплоты от числа Фурье. По зарегистрированным в ходе эксперимента данным вычисляют искомую объемную теплоемкость и теплопроводность. Технический результат - сокращение длительности эксперимента и повышение точности определения теплофизических характеристик. 3 ил.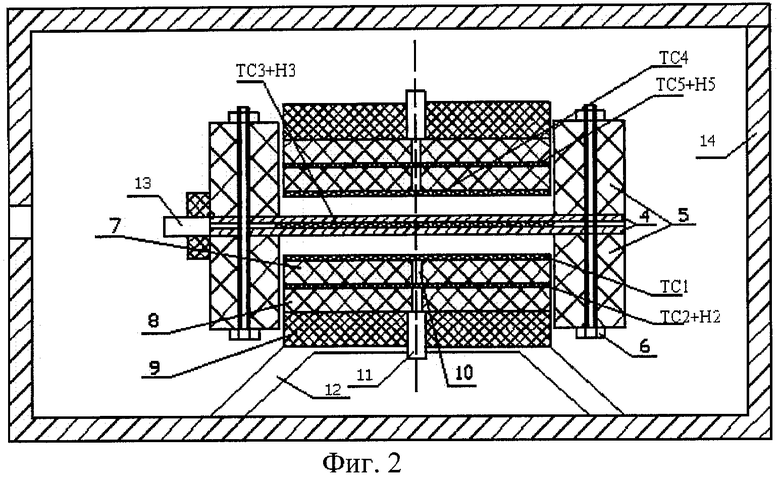
Способ комплексного определения теплофизических характеристик материалов, заключающийся в том, что измеряют толщину исследуемого образца, в качестве второго образца используют образец, идентичный первому образцу, эти образцы с двух сторон приводят в тепловой контакт с объемным источником теплоты, подводят теплоту к образцам, регистрируют удельную мощность источника теплоты, измеряют с постоянным шагом во времени температуру в течение всего эксперимента, определяют искомые теплофизические характеристики по формулам, отличающийся тем, что внешние поверхности исследуемых образцов приводят в тепловой контакт с эталонными образцами, внешние поверхности эталонных образцов приводят в тепловой контакт с плоскими нагревателями, подводят постоянную мощность к нагревателям и регистрируют перепад температур на поверхностях эталонных образцов в плоскости контакта эталонного образца с плоским нагревателем и в плоскости контакта эталонного образца с исследуемым образцом, вычисляют тепловые потоки через первый 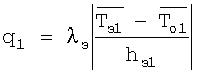 и второй
и второй 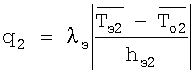
исследуемые образцы, вычисляют число Фурье 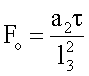
и безразмерную среднеинтегральную температуру объемного источника теплоты 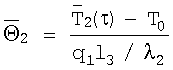 , по экспериментальным данным вычисляют константу А как тангенс угла наклона прямолинейного участка графика функции
, по экспериментальным данным вычисляют константу А как тангенс угла наклона прямолинейного участка графика функции 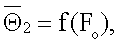 искомую объемную теплоемкость сρ вычисляют по формуле
искомую объемную теплоемкость сρ вычисляют по формуле
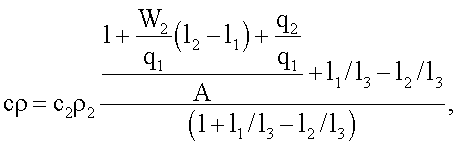
где λ2, λэ - соответственно теплопроводность материала объемного источника теплоты и эталонного образца, Вт/(мК);
с2ρ2 - объемная теплоемкость материала объемного источника теплоты, Дж/(м3К);
а2 - температуропроводность материала объемного источника теплоты, м2/c;
W2 - удельная мощность объемного источника теплоты, Вт/м3;
q1, q2 - соответственно удельные тепловые потоки через первый и второй исследуемые образцы, Вт/м2;
l1, l2, l3 - координаты, определяемые через толщины первого исследуемого образца, объемного источника теплоты, второго исследуемого образца, м;
Т0 - начальная температура исследуемых образцов, К;
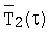 - среднеинтегральная температура объемного источника теплоты, К;
- среднеинтегральная температура объемного источника теплоты, К;
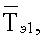
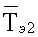 - соответственно среднеинтегральные температуры, измеренные на поверхностях первого и второго эталонных образцов в плоскости контакта соответствующего эталонного образца с соответствующим плоским нагревателем, К;
- соответственно среднеинтегральные температуры, измеренные на поверхностях первого и второго эталонных образцов в плоскости контакта соответствующего эталонного образца с соответствующим плоским нагревателем, К;
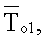
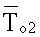 - соответственно среднеинтегральные температуры, измеренные на поверхностях первого и второго эталонных образцов в плоскости контакта соответствующего эталонного образца с соответствующим исследуемым образцом, К;
- соответственно среднеинтегральные температуры, измеренные на поверхностях первого и второго эталонных образцов в плоскости контакта соответствующего эталонного образца с соответствующим исследуемым образцом, К;
hэ1, hэ2 - соответственно толщина первого и второго эталонных образцов, м;
τ - время, отсчитываемое с момента начала эксперимента, с;
а искомую теплопроводность λ определяют по формуле
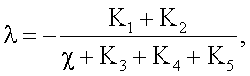
где K1, K2, K3, K4, K5, χ - множители, определяемые по формулам
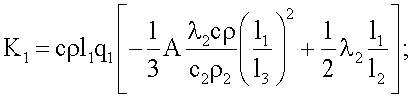
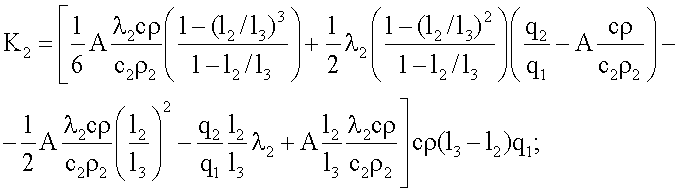
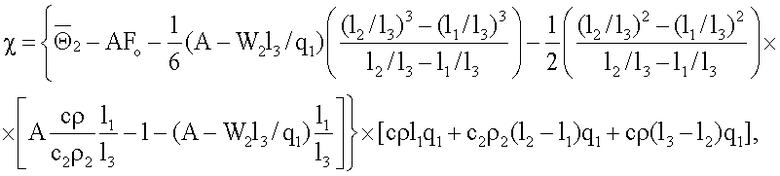
K3=Π2Π6;
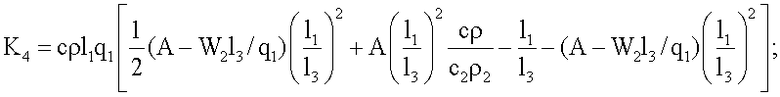
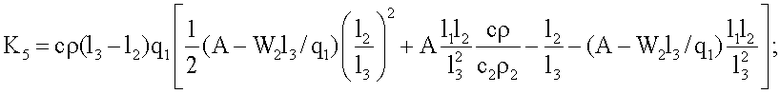
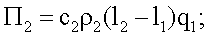
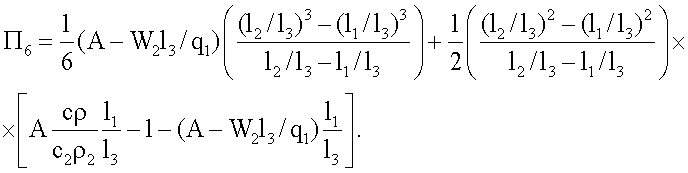
| СПОСОБ КОМПЛЕКСНОГО ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК МАТЕРИАЛОВ | 2003 |
|
RU2243543C1 |
| СПОСОБ КОМПЛЕКСНОГО ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК МАТЕРИАЛОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1991 |
|
RU2027172C1 |
| СПОСОБ ИЗМЕРЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК (ВАРИАНТЫ) И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ (ВАРИАНТЫ) | 2005 |
|
RU2326370C2 |
| Способ определения теплофизических характеристик плоских образцов материалов и устройство для его осуществления | 1983 |
|
SU1165957A1 |
Авторы
Даты
2010-04-27—Публикация
2009-03-11—Подача