Изобретение относится к области оптики и может быть использовано для характеристики качества оптических систем или оптических элементов при их изготовлении и эксплуатации.
В настоящее время существуют различные методы измерений волновых аберраций оптических систем, в том числе измерений распределения волновых аберраций w(x,y) по поперечному сечению пучка на выходе оптической системы. Особенности схемного и конструктивного решения оптической системы, связанные с ее назначением и условиями применения, а также свойства материалов оптических элементов системы могут значительно усложнять задачу определения w(x,y), особенно в случае применения методов, использующих распределение интенсивности в поперечном сечении прошедшего систему пучка. Связано это с тем, что оптическая система способна вносить в проходящий через нее световой пучок наряду с аберрационными, еще и амплитудные искажения.
Подобные оптические системы достаточно распространены. Формирование пучка с неоднородным распределением интенсивности на выходе оптической системы может происходить и в светосильных, и во внеосевых, и в работающих в наклонных пучках оптических системах. На появление неоднородностей влияет различие углов падения центральных и краевых лучей светового пучка на преломляющие и отражающие поверхности элементов оптической системы, а также поглощение излучения материалами линз, входящих в систему, особенно с большой разницей толщин от центра к краю линз.
В тех случаях, когда на пути распространения светового пучка за оптической системой формируется неоднородное распределение интенсивности по сечению пучка, являющееся следствием суперпозиции аберрационных и амплитудных искажений, определение волновых аберраций w(x,y) из данных по распределению интенсивности в поперечном сечении прошедшего систему пучка неизбежно приводит к значениям, которые отличаются от действительных. Под действительными значениями здесь и далее мы подразумеваем те значения волновых аберраций, которые вносит оптическая система в проходящий через нее световой пучок.
Известен способ определения волновых аберраций оптической системы [Патент РФ №2680657, МПК G01M 11/02, дата приор. 10.04.2018 г., опубл.25.02.2019 г., Бюлл.№6], принятый за прототип. При осуществлении способа направляют некогерентный гомоцентрический световой пучок с длиной волны X на оптическую систему. Определяют положение плоскости Пмакс, в которой пиковая интенсивность светового пучка в распределении интенсивности светового пучка имеет максимальное значение Iмакс. Измеряют расстояние Lмакс от плоскости Пмакс до плоскости П, перпендикулярной оси светового пучка и соприкасающейся с последней поверхностью оптической системы. Определяют контур изофоты в распределении интенсивности светового пучка в плоскости Пмакс по уровню 0,2 Iмакс и расстояние ρ максимального удаления точки Омакс с пиковой интенсивностью Iмакс от контура изофоты. Регистрируют распределение интенсивности 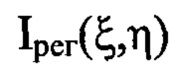 светового пучка в координатах
светового пучка в координатах 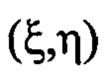 плоскости Прег, положение которой выбирают на удалении
плоскости Прег, положение которой выбирают на удалении 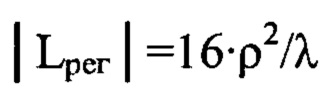 от плоскости Пмакс. Волновые аберрации w(x,y) определяют из уравнения, связывающего w(x,y) в координатах (х,у) плоскости П, с распределением интенсивности светового пучка в плоскости Прег:
от плоскости Пмакс. Волновые аберрации w(x,y) определяют из уравнения, связывающего w(x,y) в координатах (х,у) плоскости П, с распределением интенсивности светового пучка в плоскости Прег:
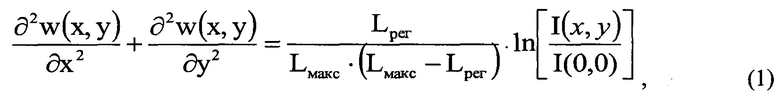
при этом используют распределение интенсивности светового пучка I(х,у), выраженное в координатах плоскости П путем замены переменных в распределении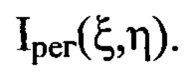 Значения w(x,y) находят путем численного решения уравнения (1).
Значения w(x,y) находят путем численного решения уравнения (1).
К причинам, препятствующим достижению указанного ниже результата при использовании известного способа, принятого за прототип, относятся следующие.
В способе прототипе уравнение (1) устанавливает в приближении геометрической оптики связь между волновыми аберрации w(x,y) на выходе оптической системы, т.е. в плоскости П, с распределением интенсивности по сечению пучка в плоскости Прег. Однако, как указывалось выше, существуют оптические системы, которые вносят в проходящий световой пучок, помимо аберрационных, еще и амплитудные искажения, т.е. сразу на выходе формируют неоднородное распределение интенсивности по сечению пучка. Так, амплитудные искажения с параболическим профилем по сечению пучка и перепадом от центра к краю вплоть до нескольких десятков процентов на выходе объектива могут проявляться в светосильных системах, а поперечные градиенты интенсивности - во внеосевых. Эти искажения распределения интенсивности накладываются в плоскости регистрации на те, которые имеют аберрационную природу, в результате определяемые значения волновых аберраций существенно отличаются от действительных значений, и использование способа не обеспечивает получение достоверных значений волновых аберраций.
Сущность изобретения заключается в следующем.
Задачей изобретения является определение волновых аберраций оптической системы, формирующей на выходе неоднородное распределение интенсивности пучка, с высокой точностью и достоверностью, без ужесточения требований к реализации способа и усложнения обработки результатов измерений.
Технический результат, который может быть достигнут при осуществлении заявленного способа, заключается в определении волновых аберраций оптической системы, формирующей на выходе неоднородное распределение интенсивности пучка, с высокой точностью и достоверностью, без ужесточения требований к реализации способа и усложнения обработки результатов измерений.
Указанный технический результат при осуществлении изобретения достигается тем, что в способе определения волновых аберраций оптической системы, включающем направление некогерентного гомоцентрического светового пучка с длиной волны X на оптическую систему, измерение распределений интенсивности светового пучка в плоскостях, перпендикулярных оси светового пучка, прошедшего оптическую систему и сфокусированного в пространстве изображений, определение положения плоскости Пмакс, перпендикулярной оси светового пучка в пространстве изображений, в которой пиковая интенсивность светового пучка в распределении интенсивности светового пучка имеет максимальное значение Iмакс среди экспериментально зарегистрированных пиковых интенсивностей в распределениях интенсивностей светового пучка в плоскостях, перпендикулярных оси светового пучка, определение контура изофоты в распределении интенсивности светового пучка в плоскости Пмакс по уровню 0,2⋅Iмакс и расстояние ρ максимального удаления точки Омакс с пиковой интенсивностью Iмакс от контура изофоты, измерение расстояния Lмакс по оси пучка от плоскости Пмакс до плоскости П, перпендикулярной оси светового пучка и соприкасающейся с последней поверхностью оптической системы, с учетом правила знаков, измерение распределения интенсивности I1рег(ξ1,η1) светового пучка в координатах (ξ1,η1) плоскости П1рег, перпендикулярной оси светового пучка в пространстве изображений, которая удалена от плоскости Пмакс на расстояние L1рег по оси пучка, при этом начало координат в плоскостях П, П1рег, Пмакс лежит на оси светового пучка, определение волновых аберраций оптической системы w1(x,y) в координатах (х,у) плоскости П из уравнения
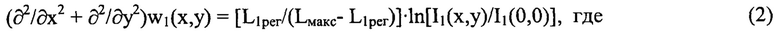
- I1(x,y) - распределение интенсивности светового пучка, выраженное в координатах плоскости П, полученное путем замены переменных в распределении интенсивности I1рег(ξ1,η1) по формулам ξ1=x⋅(L1рег/Lмакс) и η1=y⋅(L1рег/Lмакс);
- I1(0,0) - значение функции I1(x,y) на оси пучка,
путем численного решения его вариационным методом при свободных граничных условиях, аппроксимируя w1(x,y) степенным полиномом, удовлетворяющим условию w1(0,0)=0 на оси пучка, в соответствии с заявляемым техническим решением положение плоскости П] рег выбирают между плоскостью П и плоскостью Прег, перпендикулярной оси светового пучка в пространстве изображений и удаленной от плоскости Пмакс на расстояние Lper=-16⋅ρ2/λ с учетом правила знаков, дополнительно измеряют распределение интенсивности L2рег(ξ2,η2) светового пучка в координатах (ξ2,η2) плоскости П2рег, перпендикулярной оси светового пучка, положение которой выбирают в пространстве изображений за плоскостью Пмакс по ходу пучка из условия L2рег=-L1рег⋅[Lмакс/(Lмакс-2L1рег)], где L2рег - расстояние по оси пучка от плоскости Пмакс до плоскости П2рег, при этом начало координат в плоскости П2рег лежит на оси светового пучка, определяют волновые аберрации оптической системы w2(x,y) в координатах (х,у) плоскости П из уравнения
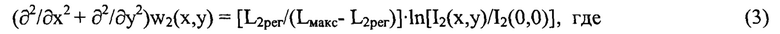
- I2(х,у) - распределение интенсивности светового пучка, выраженное в координатах плоскости П, полученное путем замены переменных в распределении интенсивности I2рег(ξ2,η2) по формулам ξ2=x⋅(L2рег/Lмакс) и η2=y⋅(L2рег/Lмакс);
- I2(0,0) - значение функции I2(х,у) на оси пучка,
путем численного решения его вариационным методом при свободных граничных условиях, аппроксимируя w2(х,у) степенным полиномом, удовлетворяющим условию w2(0,0)=0 на оси пучка, значения волновых аберраций w(x,y) оптической системы находят из соотношения w(x,y)=[w1(x,y)+w2(x,y)]/2, считая значения волновых аберраций w1(x,y) и w2(х,у) оценочными.
Совокупность вышеизложенных признаков изобретения связана причинно-следственной связью с техническим результатом изобретения.
Уравнение (1) связывает волновые аберрации w(x,y) в плоскости П, перпендикулярной оси светового пучка и соприкасающейся с последней поверхностью оптической системы, с распределением интенсивности светового пучка в плоскости регистрации (Прег в способе прототипе). При этом предполагается, что условия геометрооптического приближения в плоскости регистрации выдерживаются и пучок имеет равномерное распределение интенсивности на выходе оптической системы в плоскости П.
Если же световой пучок в этой плоскости имеет неравномерное распределение интенсивности, порожденное свойствами оптической системы, то наличие амплитудных искажений неизбежно приводит к отклонениям от точного результата в сторону больших или, наоборот, меньших значений в зависимости от положения плоскости регистрации. Выбор положения плоскости регистрации крайне важен при проведении экспериментов по определению волновых аберраций. В самом деле, профиль распределения интенсивности на выходе оптической системы в отсутствие аберраций, обусловленный лишь амплитудными искажениями, сохраняется в поперечных сечениях светового пучка по пути его распространения (если пренебречь влиянием дифракции). Классический тому пример - распространение сфокусированного гауссовского пучка: в отсутствие аберраций во всех его поперечных сечениях как до, так и за плоскостью фокусировки сохраняется гауссовский профиль. Однако если оптическая система вносит аберрационные искажения в распределение интенсивности светового пучка, то степень неоднородности регистрируемого распределения интенсивности будет изменяться на дистанции распространения светового пучка.
Как было обнаружено в наших экспериментах, выраженные в координатах (х,у) плоскости П аберрационные искажения распределения интенсивности в сечении пучка, зарегистрированные в плоскости регистрации, расположенной в пространстве между плоскостью П и Пмакс, имеют профиль, обратный по знаку к выраженному в тех же координатах профилю распределения интенсивности, которое зарегистрировано в плоскости регистрации, расположенной за плоскостью Пмакс. Например, если под влиянием сферической аберрации в плоскости регистрации перед Пмакс распределение интенсивности приобретает параболический профиль с максимумом в приосевой области, то в плоскости регистрации, расположенной за Пмакс, также формируется параболический профиль, но с минимумом на оси пучка. Поэтому в тех участках пути распространения светового пучка, где амплитудные и аберрационные искажения распределения интенсивности имеют сходный профиль, они накладываются друг на друга и усиливают степень неоднородности суммарного распределения интенсивности. И, наоборот, в тех участках пути, где профили амплитудных и аберрационных искажений распределения интенсивности противоположны по отношению друг к другу, степень неоднородности распределения понижается. В обоих случаях это влияет на достоверность определения значений волновых аберраций и приводит к получению значений, отличающихся от действительных: в первом случае - в сторону увеличения значений волновых аберраций, во втором - в сторону уменьшения значений.
В заявляемом способе регистрация распределений интенсивности светового пучка осуществляется в двух плоскостях П1рег и П2рег, расположенных перед и за плоскостью Пмакс по ходу пучка, соответственно. Расстояния удаления плоскостей регистрации от плоскости Пмакс обозначим как L1рег и L2рег, соответственно.
В способе прототипе было получено предельное расстояние удаления плоскости регистрации изображения от плоскости Пмакс для аберрированного пучка, равное 16ρ2/λ по обе стороны от Пмакс, определяющее зону пространства, вне которой еще можно рассматривать распространение пучка в геометрооптическом приближении.
Положение плоскости Прег мы выбираем на расстоянии Lрег=-16⋅ρ2/λ от плоскости Пмакс с учетом правила знаков. Тогда с учетом упомянутых выше ограничений положение плоскости П1рег можно выбирать перед плоскостью Пмакс в промежутке между плоскостями П и Прег. Определяя положение плоскости П1рег в экспериментах с реальными оптическими системами, следует руководствоваться следующим. С одной стороны, условия геометрооптического приближения выполняются тем лучше и, следовательно, тем меньше проявляются погрешности расчета, связанные с дифракцией, чем более удалены положения плоскостей регистрации от плоскости Пмакс. С другой стороны, уменьшается амплитуда неоднородности распределения интенсивности аберрационного происхождения и, соответственно, ее относительный вклад в сравнении с амплитудными искажениями распределения и случайными флуктуациями интенсивности.
Как показали наши эксперименты и последующий анализ, выбранное положение плоскости П1рег задает положение второй плоскости регистрации П2рег. Было обнаружено, что оптимальное для точного определения волновых аберраций расстояние L2рег нужно выбирать из условия:
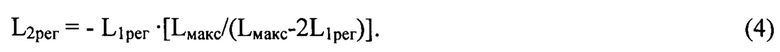
Уравнения (2) и (3) связывают волновые аберрации искаженного пучка в координатах (х,у) плоскости П с распределениями интенсивности светового пучка в плоскостях П1рег и П2рег. Используя эти уравнения, можно определить значения волновых аберраций w1(x,y) и w2(x,y) в плоскости П по распределениям интенсивности светового пучка в плоскостях П1рег и П2рег, соответственно. С учетом того, что значения функций w1(x,y) и w2(x,y) получены с отличиями от действительных в сторону их увеличения или уменьшения, мы будем считать их оценочными значениями волновых аберраций оптической системы.
В заявляемом способе значения волновых аберраций w(x,y) оптической системы находят из соотношения w(x,y)=[w1(x,y)+w2(x,y)]/2. При арифметическом усреднении функций w1(x,y) и w2(x,y), предполагающем их сложение, отличия от действительных значений будут взаимно скомпенсированы. Функция волновых аберраций w(x,y) имеет такую же, как w1(x,y) и w2(х,у), структуру в виде линейной комбинации базовых функций, описывающих отдельные виды аберраций.
Таким образом, регистрация распределений интенсивности светового пучка в двух плоскостях, расположенных по разные стороны от Пмакс на определенном удалении, определение по ним значений волновых аберраций, рассматриваемых нами как оценочные, последующее арифметическое усреднение полученных значений позволяет экспериментально отделить вклад присутствующих в них амплитудных искажений и получить действительные значения волновых аберраций с высокой точностью, не уступающей точности определения w(x,y) с равномерным распределением интенсивности на выходе оптической системы. Как будет показано ниже, проведенные нами эксперименты подтвердили высокую степень точности и достоверности определяемых значений волновых аберраций. Способ осуществляется без ужесточения требований к его реализации и усложнения обработки результатов измерений.
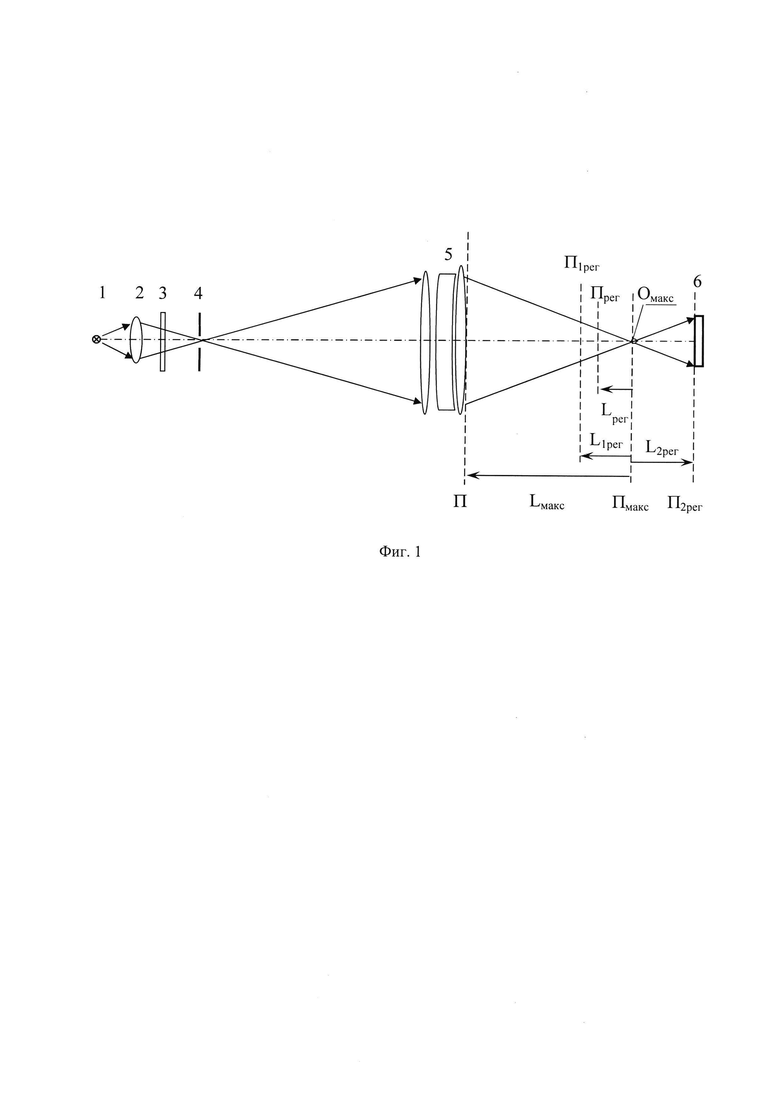
На фиг. 1 приведена оптическая схема установки для измерения волновых аберраций линзового объектива, где 1 - некогерентный источник света (лампа накаливания); 2 - конденсор; 3 - узкополосный светофильтр; 4 - микродиафрагма; 5 - многокомпонентный линзовый объектив; 6 - ПЗС-матрица, регистрирующая распределение интенсивности в поперечном сечении светового пучка. Плоскость П - плоскость, в системе координат которой определяют волновые аберрации, соприкасается с последней поверхностью линзового объектива 5, плоскость П1рег - плоскость, в которой регистрируют распределение интенсивности I1рег(ξ1,η1), плоскость Пмакс - плоскость, в которой пиковая интенсивность светового пучка достигает максимального значения Iмакс среди экспериментально зарегистрированных пиковых интенсивностей в распределениях интенсивностей светового пучка в плоскостях, перпендикулярных оси светового пучка, Омакс - точка пиковой интенсивности Iмакс в плоскости Пмакс, П2рег - плоскость, в которой регистрируют распределение интенсивности L2рег(ξ2,η2). Плоскость Прег удалена от плоскости Пмакс на расстояние Lрег=-16⋅ρ2/λ с учетом правила знаков, где ρ - расстояние максимального удаления точки Омакс от изофоты распределения интенсивности в плоскости Пмакс на уровне 0,2⋅Iмакс. Плоскости П1рег, П2рег, Прег и Пмакс перпендикулярны оси светового пучка, начало координат в плоскостях П, П1рег, П2рег, Прег и Пмакс лежит на оси светового пучка. L1рег, L2рег и Lмакс - расстояния от плоскости Пмакс до плоскостей П1рег, П2рег и П, соответственно, по оси пучка с учетом правила знаков.
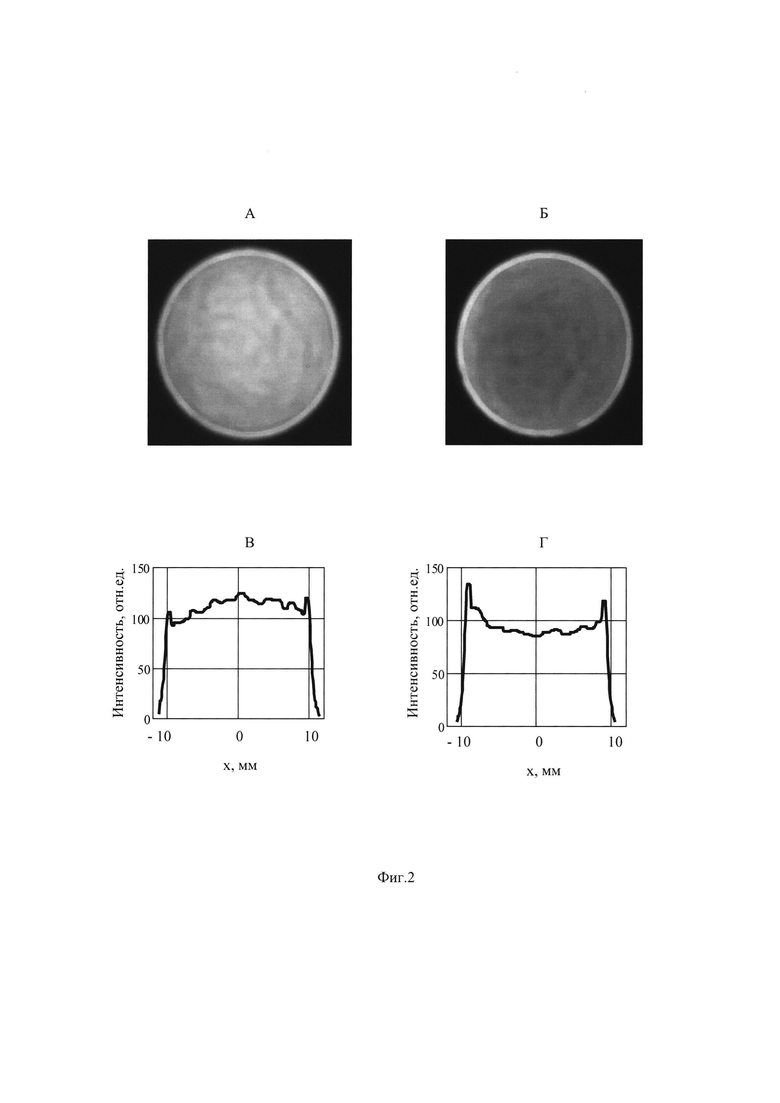
На фиг. 2, А и Б, представлены экспериментально зарегистрированные изображения поперечного сечения пучка в плоскостях П1рег и П2рег, отстоящих от плоскости Пмакс на расстояния L1рег=-20 мм и L2рег=25 мм, соответственно.
На фиг. 2, В и Г, представлены приведенные к координатам в плоскости П экспериментальные распределения интенсивности светового пучка вдоль горизонтального диаметра в плоскостях П1рет и П2рет, отстоящих от плоскости Пмакс на расстояния L1рег=-20 мм и L2рег=25 мм, соответственно.
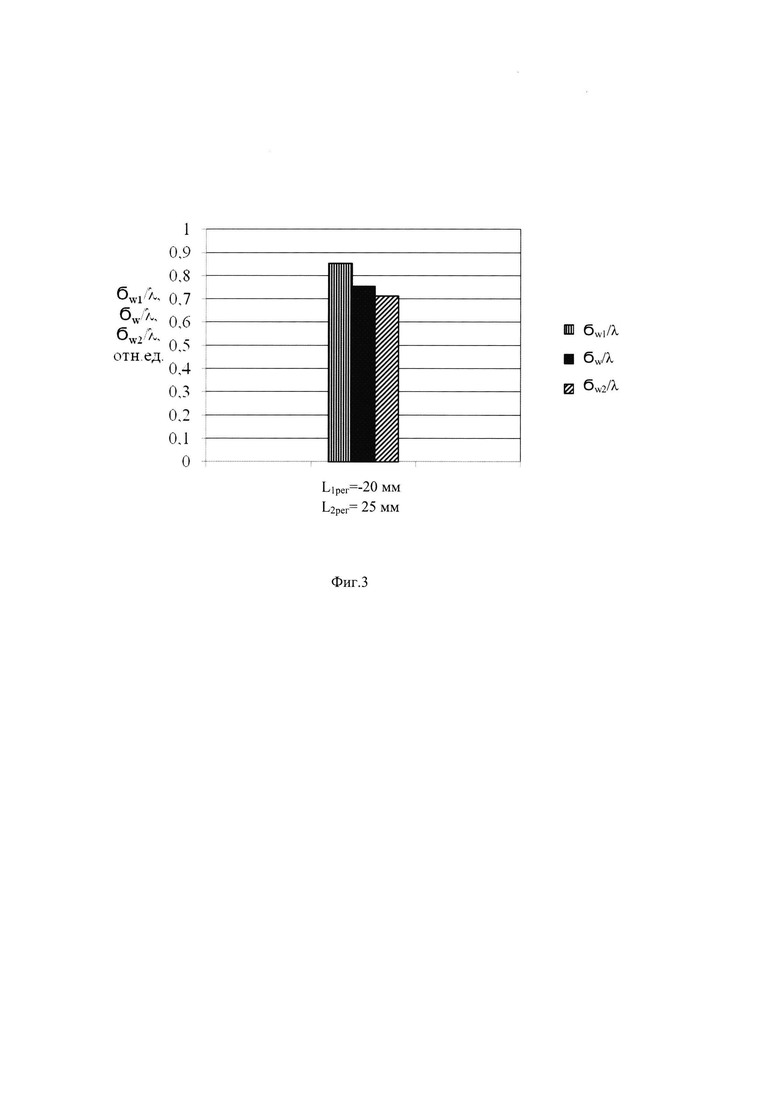
На фиг. 3 представлены в виде гистограммы нормированные на длину волны среднеквадратические значения волновых аберраций σw1/λ, σw2/λ и σw/λ на выходе оптической системы, соответствующие эксперименту по определению волновых аберраций w1(x,y), w2(x,y) и w(x,y). На горизонтальной оси гистограммы приведены соответствующие эксперименту значения L1рег=-20 мм и L2рег=25 мм. По вертикальной оси гистограммы высота левого столбца представляет величину σw1/λ, - нормированное среднеквадратическое значение волновых аберраций w1(x,y), вычисленных по распределению пучка в плоскости П1рег. Высота правого столбца представляет величину σw2/λ, - нормированное среднеквадратическое значение волновых аберраций w2(x,y), вычисленных по распределению пучка в плоскости П2рег. Высота среднего столбца σw/λ гистограммы соответствует нормированному среднеквадратическому значению волновых аберраций w(x,y).
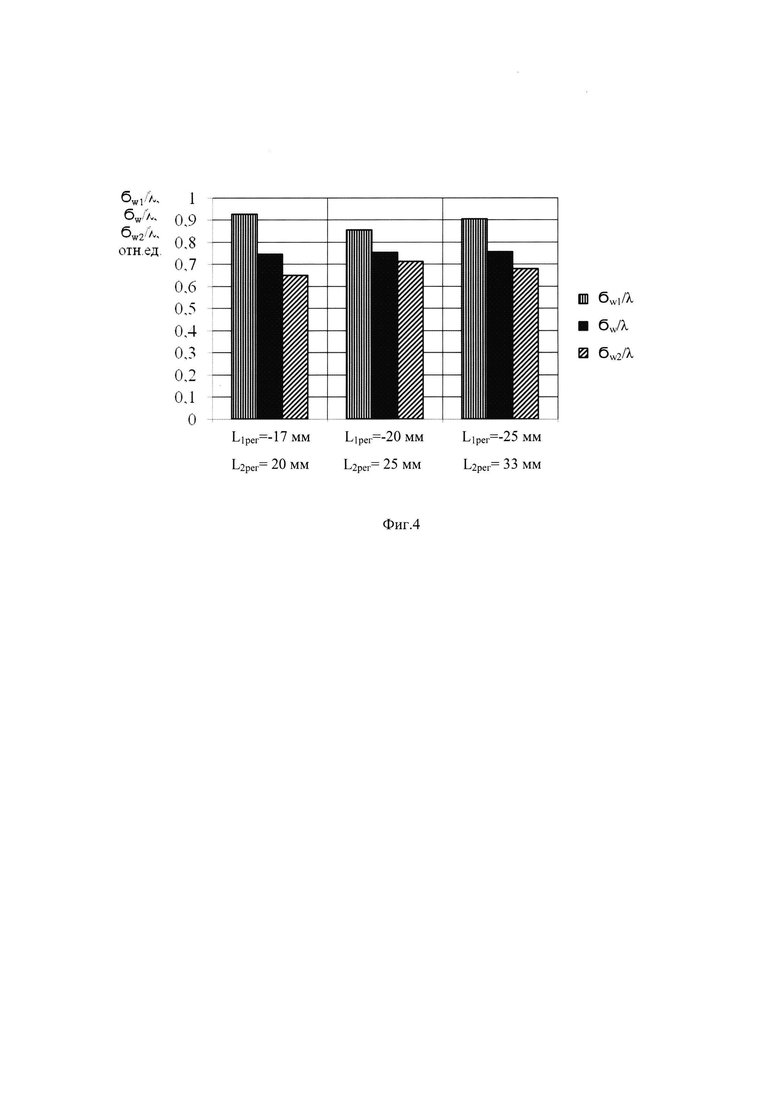
На фиг. 4 представлены в виде трех гистограмм нормированные на длину волны среднеквадратические значения волновых аберраций σw1/λ, σw2/λ и σw/λ на выходе оптической системы, соответствующие трем проведенным экспериментам. В каждом из экспериментов определялись волновые аберрации w1(x,y), w2(x,y) и w (х,у). Эксперименты отличались выбором положения плоскостей П1рег и П2рег. На горизонтальной оси каждой гистограммы приведены соответствующие эксперименту значения L1рег и L2рег. По вертикальной оси каждой гистограммы высота левого столбца представляет величину σw1/λ - нормированное среднеквадратическое значение волновых аберраций w1(x,y), вычисленных по распределению пучка в плоскости П1рег. Высота правого столбца представляет величину σw2/λ - нормированное среднеквадратическое значение волновых аберраций w2(x,y), вычисленных по распределению пучка в плоскости П2рег. Высота среднего столбца σw/λ каждой гистограммы соответствует нормированному среднеквадратическому значению волновых аберраций w(x,y), рассчитанных для соответствующего эксперимента.
Заявленный способ был экспериментально осуществлен для измерения волновых аберраций многокомпонентного линзового объектива. Для этого была создана экспериментальная установка.
Пример конкретного выполнения способа.
Излучение от лампы накаливания 1 проецируется конденсором 2 на отверстие микродифрагмы 4 диаметром 50 мкм через узкополосный светофильтр 3 с максимумом пропускания на длине волны 0,55 мкм (фиг. 1). За отверстием микродиафрагмы, имитирующей точечный источник излучения, формируется сферический пучок с однородным распределением интенсивности в пределах входной апертуры исследуемого объектива. Такой пучок можно считать гомоцентрическим. Микродиафрагма 4 была установлена на расстоянии 870 мм от первой оптической поверхности объектива 5 со смещением в горизонтальном направлении относительно центра поля зрения объектива. В такой геометрии эксперимента прошедший оптическую систему световой пучок приобретает волновые аберрации в основном типа комы и сферической. Диаметр пучка на выходе оптической системы составлял 20 мм.
ПЗС-матрицу 6 автоколлимационным методом выставляют ортогонально оси светового пучка, прошедшего объектив 5. Затем определяют местоположение плоскости Пмакс на оси пучка путем перемещения ПЗС-матрицы вдоль каустики светового пучка, сравнения пиковых значений в распределении интенсивности в разных позициях по ходу пучка и фиксации положения ПЗС-матрицы, в котором пиковая интенсивность излучения имеет максимальное значение Iмакс. ПЗС-матрицу при этом ориентируют ортогонально оси пучка. Используя систему отсчета, задаваемую системой координат в плоскости Пмакс, в которой начало координат лежит на оси светового пучка, а положительное направление оси аппликат совпадает с направлением распространения светового пучка, измеряют расстояние Lмакс от плоскости Пмакс до плоскости П, перпендикулярной оси светового пучка и соприкасающейся с последней поверхностью объектива 5. В нашем эксперименте Lмакс=-200 мм.
В плоскости Пмакс регистрируют распределение интенсивности в поперечном сечении пучка. Программными средствами из комплекта технического обеспечения ПЗС-матрицы определяют контур изофоты на уровне сигнала 0,2 от пикового значения Iмакс и находят расстояние ρ максимального удаления точки Омакс пиковой интенсивности Iмакс от этой границы. Определяют положение плоскости Прег, перпендикулярной оси светового пучка и удаленной от плоскости Пмакс на расстояние Lрег=-16⋅ρ2/λ с учетом правила знаков. Выбирают расположение плоскости П1рег в пространстве между плоскостями П и Прег, этому положению будет соответствовать расстояние L1рег, определяющее удаление плоскости П1per от плоскости Пмакс. В нашем эксперименте ρ=23 мкм, Lрег=-15 мм, L1рег=-20 мм. В плоскости П1per регистрируют ПЗС-матрицей распределение интенсивности I1рег(ξ1,η1) светового пучка. Зарегистрированное изображение поперечного сечения пучка в этой плоскости представлено на фиг. 2,А. Полученное распределение затем преобразуют путем замены координат по формулам ξ1=x⋅(L1рег/Lмакс) и η1=y⋅(L1рег/Lмакс) в распределение интенсивности I1(x,y) в координатах плоскости П. На фиг. 2,В представлено приведенное к координатам плоскости П распределение интенсивности светового пучка вдоль горизонтального диаметра I1(x,0).
Определяют волновые аберрации оптической системы w1(x,y) в плоскости П из уравнения (2), в котором I1(0,0) - значение функции I1(x,y) на оси пучка, путем численного решения уравнения вариационным методом при свободных граничных условиях. При этом для аппроксимации волновых аберраций в качестве базовых функций 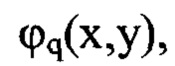 составляющих сумму w1(x,y), выбирают степенные полиномы 3-й и 4-й степени. Каждая из базовых функций
составляющих сумму w1(x,y), выбирают степенные полиномы 3-й и 4-й степени. Каждая из базовых функций 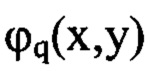 отвечает определенному типу волновых аберраций и удовлетворяет условию
отвечает определенному типу волновых аберраций и удовлетворяет условию 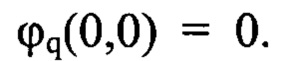 Так, волновым аберрациям третьего порядка типа комы будут отвечать функции вида
Так, волновым аберрациям третьего порядка типа комы будут отвечать функции вида 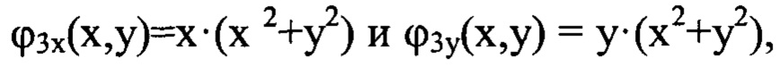 а сферической аберрации - функция вида
а сферической аберрации - функция вида 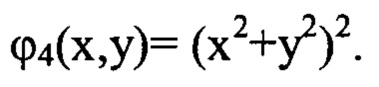
Значения аберрационных коэффициентов Aq являются решением системы линейных уравнений [Л.В.Канторович, В.И. Крылов. Приближенные методы высшего анализа. М.-Л.: Гос. Изд-во физ.-мат.лит.1962. - 708 с.]:

где коэффициенты 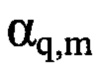 вычисляют по формуле:
вычисляют по формуле:
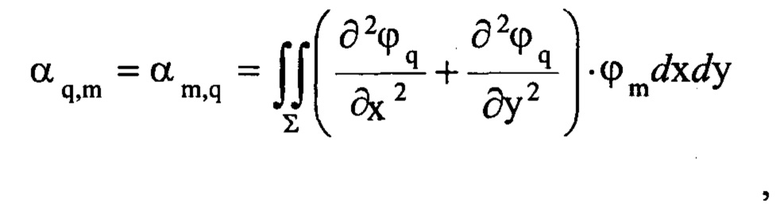
коэффициенты βm вычисляют по формуле:
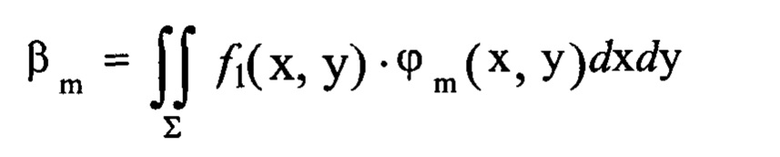
Здесь 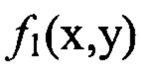 - это правая часть уравнения (2), т.е.
- это правая часть уравнения (2), т.е. 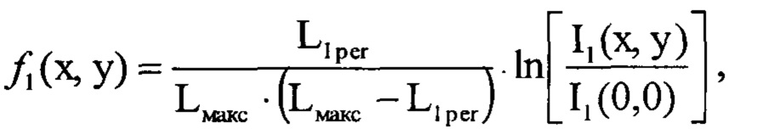
область интегрирования ∑ - есть поперечное сечение пучка за исключением узкой краевой зоны поперечного сечения, где распределение интенсивности несколько возмущено дифракцией пучка на апертурной диафрагме оптической системы.
С учетом дискретного характера экспериментальных данных и замены координат (х,у) на дискретные переменные по формулам 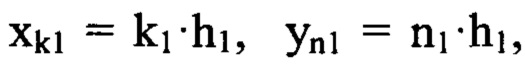 базовые функции
базовые функции 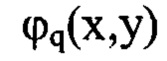 преобразуют к виду:
преобразуют к виду:
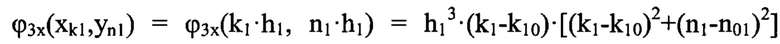 - нечетная функция от координаты хк описывает кому 3-го порядка,
- нечетная функция от координаты хк описывает кому 3-го порядка,
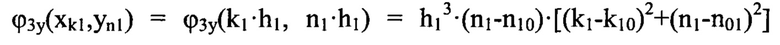 - нечетная функция от координаты ук описывает кому 3-го порядка,
- нечетная функция от координаты ук описывает кому 3-го порядка,
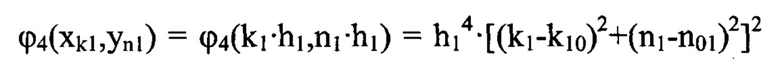 - четная функция от координат xk1 и yn1 описывают сферическую аберрацию 3-го порядка.
- четная функция от координат xk1 и yn1 описывают сферическую аберрацию 3-го порядка.
Здесь 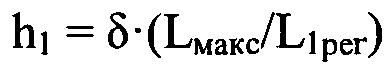 - шаг координатной сетки в плоскости П;
- шаг координатной сетки в плоскости П;
δ - размер пиксела ПЗС-матрицы;
k1=0,…kj и ni=0, …Ni - индексы нумерации пикселей ПЗС-матрицы;
k10 и n10 - индексы оси пучка (или центра поперечного сечения пучка) в кадре.
Аппроксимирующая волновые аберрации в целом функция w1(x,y), выраженная в дискретных координатах, имеет вид:
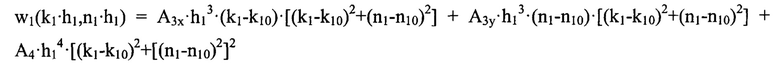
Используя указанные базовые функции и выраженное в дискретных координатах распределение интенсивности по сечению пучка I1(xk,yn), находят коэффициенты αq,m и βm системы уравнений (5), заменяя операцию интегрирования суммированием по индексам пикселей ПЗС-матрицы. Решая алгебраическую систему уравнений (5), вычисляют искомые аберрационные коэффициенты А3х, А3у и А4. В проведенном эксперименте были получены следующие значения аберрационных коэффициентов: А3х=-8,42⋅10-7 мм-2, А3у=1,48⋅10-7 мм-2 и A4=8,06⋅10-8 мм-3.
Поскольку на длине шага координатной сетки изменения величины волновой аберрации очень малы, то можно пренебречь дискретностью координат и рассматривать волновые аберрации для каждого эксперимента как непрерывные функции координат х и y.
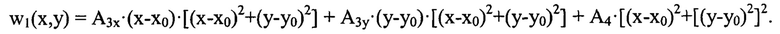
На следующем этапе измеряют распределение интенсивности I2рег(ξ2,η2) светового пучка в координатах (ξ2,η2) плоскости П2рег, положение которой задают в пространстве изображений за плоскостью Пмакс по ходу пучка из условия L2рег=-L1рег⋅[Lмакс/(Lмакс-2L1рег)], где L2рег - расстояние по оси пучка от плоскости Пмакс до плоскости П2рег. Выбранному значению L1рег=-20 мм отвечает значение L2рег=25 мм. На фиг. 2, Б представлено зарегистрированное изображение поперечного сечения пучка в плоскости П2рег. Распределение I2рег(ξ2,η2) преобразуют путем замены координат по формулам ξ2=x⋅(L2рег/Lмакс) и η2=y⋅(L2рег/Lмакс) в распределение интенсивности I2(х,у) в координатах плоскости П. На фиг. 2,Г представлено приведенное к координатам плоскости П распределение интенсивности светового пучка вдоль горизонтального диаметра I2(х,0).
Из сравнения распределений интенсивности I1(x,0) и I2(х,0), представленных на фиг. 2,В и Г, отчетливо видно, что под влиянием сферической аберрации в плоскости регистрации П1рег распределение интенсивности приобретает параболический профиль с максимумом в приосевой области, а в плоскости П2рег - параболический профиль с минимумом на оси пучка.
Измеренные распределения интенсивности используют для определения волновых аберраций оптической системы w2(x,y) в координатах (х,у) плоскости П из уравнения (3), в котором I2(0,0) - значение функции I2(х,у) на оси пучка, путем численного решения уравнения (3) вариационным методом при свободных граничных условиях. При этом для аппроксимации волновых аберраций w2(x,y) выбирают те же степенные полиномы 3-й и 4-й степени, что были использованы при аппроксимации волновых аберраций w1(x,y), но с заменой координат (х,у) на дискретные переменные по формулам 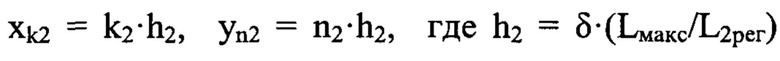 - шаг координатной сетки в плоскости П,
- шаг координатной сетки в плоскости П,
k2=0,…k2 и n2=0,…N2 - индексы нумерации пикселей ПЗС-матрицы;
k20 и n20 - индексы оси пучка (или центра поперечного сечения пучка) в кадре.
В этом случае аппроксимирующая волновые аберрации функция w2(x,y), выраженная в дискретных координатах, имеет вид:
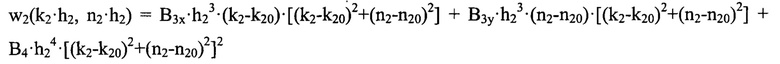
Искомые аберрационные коэффициенты В3х, В3у, В4 также находят описанным выше методом, аналогично вычислению аберрационных коэффициентов А3х, А3у и А4. В проведенном эксперименте были получены следующие значения аберрационных коэффициентов: В3х=-2,11⋅10-7 мм-2, В3у=4,23⋅10-7 мм-2 и В4=7,94⋅10-8 мм-3.
Пренебрегая, как и выше, дискретностью координат, полученные волновые аберрации будем рассматривать как непрерывные функции координат х и у: 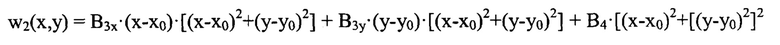
Как уже указывалось выше, значения волновых аберраций w1(x,y) и w2(x,y) считают оценочными. На последнем этапе определяют волновые аберрации w(x,y) путем арифметического усреднения найденных функций волновых аберраций: w(x,y)=[w1(x,y)+w2(x,y)]/2. В силу линейности операции арифметического усреднения, w(x,y) также имеет вид суммы базовых функций, характеризующих отдельные типы аберраций. Аберрационные коэффициенты для определения волновых аберраций w(x,y), рассчитанные по формулам 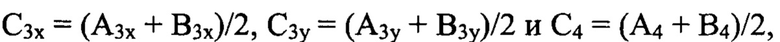 имеют значения
имеют значения 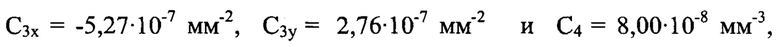 а искомые волновые аберрации представлены выражением:
а искомые волновые аберрации представлены выражением:
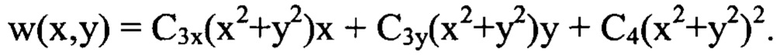
Волновые аберрации, включающие в себя несколько аберрационных компонент, обычно количественно характеризуют среднеквадратическим значением, вычисляемым по формуле:
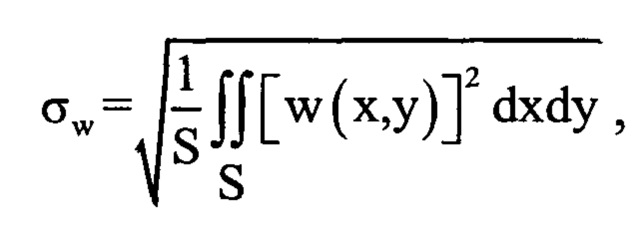
где S - площадь поперечного сечения светового пучка на выходе оптической системы.
На фиг. 3 представлены в виде гистограммы нормированные на длину волны среднеквадратические значения волновых аберраций 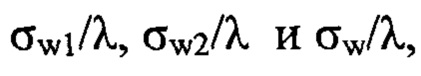 соответствующие эксперименту, в котором значения L1рег=-20 мм и L2рег=25 мм. По вертикальной оси гистограммы высота левого столбца представляет величину
соответствующие эксперименту, в котором значения L1рег=-20 мм и L2рег=25 мм. По вертикальной оси гистограммы высота левого столбца представляет величину 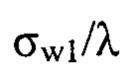 - нормированное среднеквадратическое значение волновых аберраций w1(x,y), вычисленных по распределению пучка в плоскости П1рег. Высота правого столбца представляет величину
- нормированное среднеквадратическое значение волновых аберраций w1(x,y), вычисленных по распределению пучка в плоскости П1рег. Высота правого столбца представляет величину 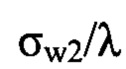 - нормированное среднеквадратическое значение волновых аберраций w2(x,y), вычисленных по распределению пучка в плоскости П2рег. Высота среднего столбца
- нормированное среднеквадратическое значение волновых аберраций w2(x,y), вычисленных по распределению пучка в плоскости П2рег. Высота среднего столбца 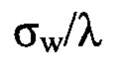 гистограммы соответствует нормированному среднеквадратическому значению волновых аберраций w(x,y). Видно, что значение
гистограммы соответствует нормированному среднеквадратическому значению волновых аберраций w(x,y). Видно, что значение 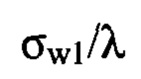 заметно отличается от значения
заметно отличается от значения 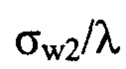 (на десятые доли λ), что говорит о присутствии амплитудных искажений пучка оптической системой в эксперименте. При этом, как и следовало ожидать, отклонение значений
(на десятые доли λ), что говорит о присутствии амплитудных искажений пучка оптической системой в эксперименте. При этом, как и следовало ожидать, отклонение значений 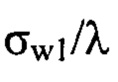 и
и 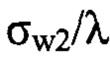 от значения
от значения 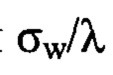 имеет разный знак.
имеет разный знак.
Таким образом, осуществление операций способа позволило устранить влияние амплитудных искажений и получить действительные значения волновых аберраций.
Для подтверждения высокой точности и достоверности полученного результата были проведены дополнительные эксперименты. В них положение плоскости П1рег выбиралось на пути распространения светового пучка как до, так и после положения, соответствующего описанному выше основному эксперименту, значения L1рег составляли, соответственно, L1рег=17 мм для первого дополнительного эксперимента и L1рег=-25 мм для второго дополнительного эксперимента.
Аналогичным образом, как и в описанном выше основном эксперименте, были получены значения аберрационных коэффициентов А3х, А3у и А4 для двух дополнительных экспериментов. Эти значения приведены в Табл.1 (для наглядности вместе со значениями, соответствующими значению L1рег=-20 мм).
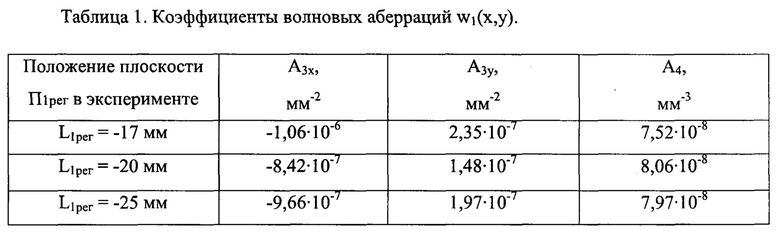
Выбранному значению L1рег=-17 мм в первом дополнительном эксперименте отвечает значение L2рег=20 мм, значению L1рег=-25 мм во втором дополнительном эксперименте - значение L2рег=33 мм.
Далее аналогичным образом, как и в описанном выше основном эксперименте, были получены значения аберрационных коэффициентов В3х, В3у, В4 для двух дополнительных экспериментов. Эти значения приведены в Табл.2 (для наглядности вместе со значениями, соответствующими значению L2рег=25 мм).

Аналогичным образом, как и в описанном выше основном эксперименте, были получены значения аберрационных коэффициентов С3х, С3у и С4 для двух дополнительных экспериментов. Эти значения приведены в Табл. 3 (для наглядности вместе со значениями, полученными в основном эксперименте).
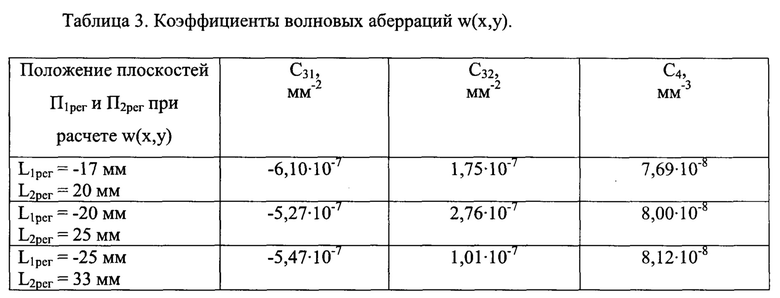
На фиг. 4 представлены в виде трех гистограмм нормированные на длину волны среднеквадратические значения волновых аберраций σw1, σw2 и σw, полученные в основном и двух дополнительных экспериментах для трех положений плоскостей П1рег и П2рег. Их числовые значения приведены в таблице 4.
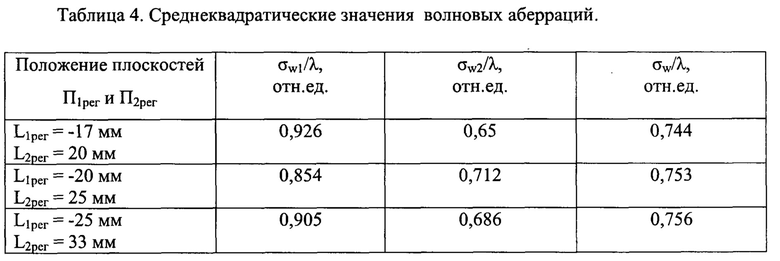
Из фиг. 4 и таблицы 4 видно, что значения σw1 и σw2 в каждом из выбранных положений П1рег и П2рег сильно отличаются - их разница составляет ~0.2λ÷0.3λ, причем во всех случаях σw1/λ > σw2/λ. Такое различие свидетельствует о том, что световой пучок на выходе оптической системы имеет неоднородное по сечению распределение интенсивности. Сравнение значений σw1 для трех разных положений П1рег и П2рег показывает, что они также отличаются. То же можно сказать и о значениях σw2. В противоположность этому разброс значений σw/λ вычисленных для каждого из трех положений П1рег и П2рег, незначителен и не превышает величины λ/50.
Поскольку в каждом из трех проведенных экспериментов реализуется своя независимая суперпозиция вкладов амплитудных и аберрационных искажений в неоднородности распределения интенсивности пучка и, в то же время, результаты всех трех измерений волновых аберраций, оцениваемые среднеквадратическим значением, оказываются чрезвычайно близки, то это говорит о высокой степени их точности и достоверности.
Отметим также, что при определении волновых аберраций заявленным способом остаются неизменными приемы настройки схемы измерений и используемая аппаратура регистрации изображений светового пучка, применяются те же самые математические методы и алгоритмы обработки изображений, что и при реализации способа-прототипа. Поэтому можно утверждать, что по сравнению с прототипом ужесточения требований к реализации заявленного способа и усложнения обработки результатов измерений не происходит.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ВОЛНОВЫХ АБЕРРАЦИЙ ОПТИЧЕСКОЙ СИСТЕМЫ | 2018 |
|
RU2680657C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДЕФОРМАЦИЙ ВОЛНОВОГО ФРОНТА СВЕТОВОГО ПУЧКА, ВЫЗВАННЫХ ВОЛНИСТОСТЬЮ ПОВЕРХНОСТЕЙ ОПТИЧЕСКОЙ СИСТЕМЫ | 2018 |
|
RU2680615C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕЛКОМАСШТАБНЫХ ДЕФОРМАЦИЙ ВОЛНОВОГО ФРОНТА СВЕТОВОГО ПУЧКА | 2024 |
|
RU2830845C1 |
| Способ определения положения фокальной плоскости объектива | 1988 |
|
SU1571459A1 |
| СПОСОБ АТТЕСТАЦИИ ТЕЛЕСКОПА | 1987 |
|
RU2036491C1 |
| СПОСОБ АТТЕСТАЦИИ ТЕЛЕСКОПА | 1988 |
|
RU2036492C1 |
| УСТРОЙСТВО И СПОСОБ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЯ С ОБЕСПЕЧЕНИЕМ УВЕЛИЧЕННОЙ ГЛУБИНЫ ИЗОБРАЖАЕМОГО ПРОСТРАНСТВА (ВАРИАНТЫ) | 2021 |
|
RU2782980C1 |
| ИНТЕРФЕРОМЕТРИЧЕСКИЙ СПОСОБ ЮСТИРОВКИ ДВУХЗЕРКАЛЬНОГО ОБЪЕКТИВА С АСФЕРИЧЕСКИМИ ЭЛЕМЕНТАМИ | 2014 |
|
RU2561018C1 |
| УСТРОЙСТВО ДЛЯ ФОРМИРОВАНИЯ ЛАЗЕРНОГО ПУЧКА | 1994 |
|
RU2083039C1 |
| Способ контроля качества объективов | 2017 |
|
RU2662492C1 |
Изобретение относится к области оптического приборостроения и касается способа определения волновых аберраций оптической системы. При осуществлении способа направляют световой пучок с длиной волны λ на оптическую систему и измеряют распределение интенсивности светового пучка в различных плоскостях в пространстве изображений. Определяют положение плоскости Пмакс, в которой пиковая интенсивность имеет максимальное значение Iмакс, и определяют контур изофоты в распределении интенсивности светового пучка в плоскости Пмакс по уровню 0,2⋅Iмакс и расстояние ρ максимального удаления точки с интенсивностью Iмакс от контура изофоты. Измеряют расстояние Lмакс от плоскости Пмакс до плоскости П, соприкасающейся с последней поверхностью оптической системы. Далее измеряют распределение интенсивности светового пучка в координатах двух плоскостей П1рег и П2рег, расположенных от плоскости П на расстояниях, определяемых в зависимости от величин λ, ρ и Lмакс. По полученным данным определяют волновые аберрации оптической системы w1(x,y) и w2(x,y) в координатах плоскости П. Значения волновых аберраций w(x,y) оптической системы определяют как w(x,y)=[w1(x,y)+w2(x,y)]/2. Технический результат заключается в повышении точности и достоверности определения волновых аберраций. 4 ил., 4 табл.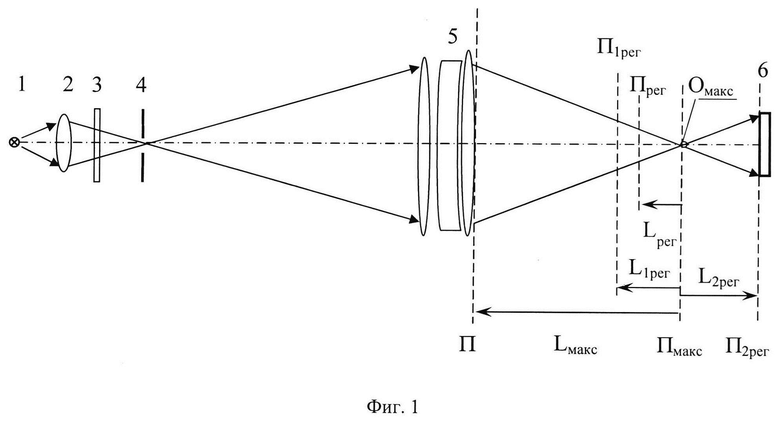
Способ определения волновых аберраций оптической системы, включающий направление некогерентного гомоцентрического светового пучка с длиной волны λ на оптическую систему, измерение распределений интенсивности светового пучка в плоскостях, перпендикулярных оси светового пучка, прошедшего оптическую систему и сфокусированного в пространстве изображений, определение положения плоскости Пмакс, перпендикулярной оси светового пучка в пространстве изображений, в которой пиковая интенсивность светового пучка в распределении интенсивности светового пучка имеет максимальное значение Iмакс среди экспериментально зарегистрированных пиковых интенсивностей в распределениях интенсивностей светового пучка в плоскостях, перпендикулярных оси светового пучка, определение контура изофоты в распределении интенсивности светового пучка в плоскости Пмакс по уровню 0,2⋅Iмакс и расстояния ρ максимального удаления точки Омакс с пиковой интенсивностью Iмакс от контура изофоты, измерение расстояния Lмакс по оси пучка от плоскости Пмакс до плоскости П, перпендикулярной оси светового пучка и соприкасающейся с последней поверхностью оптической системы, с учетом правила знаков, измерение распределения интенсивности I1рег(ξ1,η1) светового пучка в координатах (ξ1,η1) плоскости П1рег, перпендикулярной оси светового пучка в пространстве изображений, которая удалена от плоскости Пмакс на расстояние L1рег по оси пучка, при этом начало координат в плоскостях П, П1рег, Пмакс лежит на оси светового пучка, определение волновых аберраций оптической системы w1(x,y) в координатах (х,у) плоскости П из уравнения
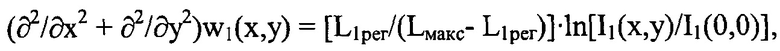
где I1(x,y) - распределение интенсивности светового пучка, выраженное в координатах плоскости П, полученное путем замены переменных в распределении интенсивности I1рег(ξ1,η1) по формулам ξ1=x⋅(L1рег/Lмакс) и η1=y⋅(L1рег/Lмакс);
I1(0,0) - значение функции I1(x,y) на оси пучка,
путем численного решения его вариационным методом при свободных граничных условиях, аппроксимируя w1(x,y) степенным полиномом, удовлетворяющим условию w1(0,0)=0 на оси пучка, отличающийся тем, что положение плоскости П1рег выбирают между плоскостью П и плоскостью Прег, перпендикулярной оси светового пучка в пространстве изображений и удаленной от плоскости Пмакс на расстояние Lper=-16⋅ρ2/λ с учетом правила знаков, дополнительно измеряют распределение интенсивности L2рег(ξ2,η2) светового пучка в координатах (ξ2,η2) плоскости П2рег, перпендикулярной оси светового пучка, положение которой выбирают в пространстве изображений за плоскостью Пмакс по ходу пучка из условия L2рег=-L1рег⋅[Lмакс/(Lмакс-2L1рег)], где L2рег - расстояние по оси пучка от плоскости Пмакс до плоскости П2рег, при этом начало координат в плоскости П2рег лежит на оси светового пучка, определяют волновые аберрации оптической системы w2(x,y) в координатах (х,у) плоскости П из уравнения
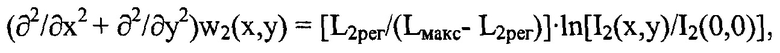
где I2(х,у) - распределение интенсивности светового пучка, выраженное в координатах плоскости П, полученное путем замены переменных в распределении интенсивности I2рег(ξ2,η2) по формулам ξ2=x⋅(L2рег/Lмакс) и η2=y⋅(L2рег/Lмакс);
I2(0,0) - значение функции I2(х,у) на оси пучка,
путем численного решения его вариационным методом при свободных граничных условиях, аппроксимируя w2(x,y) степенным полиномом, удовлетворяющим условию w2(0,0)=0 на оси пучка, значения волновых аберраций w(x,y) оптической системы находят из соотношения w(x,y)=[w1(x,y)+w2(x,y)]/2, считая значения волновых аберраций w1(x,y) и w2(x,y) оценочными.
| В | |||
| С | |||
| Сиразетдинов и др | |||
| "Метод определения волновых аберраций оптической системы по распределению интенсивности фокусируемого пучка", ОПТИЧЕСКИЙ ЖУРНАЛ, т | |||
| Пюпитр для работы на пишущих машинах | 1922 |
|
SU86A1 |
| Кипятильник для воды | 1921 |
|
SU5A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ВОЛНОВЫХ АБЕРРАЦИЙ ОПТИЧЕСКОЙ СИСТЕМЫ | 2018 |
|
RU2680657C1 |
| US 2002122162 A1, 05.09.2002 | |||
| JP 2004014764 A, 15.01.2004. | |||
Авторы
Даты
2021-08-18—Публикация
2020-11-10—Подача