Область техники, к которой относится изобретение
Изобретение относится к области оптики и может быть использовано для характеристики световых пучков, формируемых оптическими элементами и системами. Деформации волнового фронта таких пучков определяются качеством изготовления оптических элементов и систем. Изобретение может найти свое применение при контроле качества оптических систем или оптических элементов в процессе их изготовления.
При полировке больших поверхностей оптических элементов, например, асферических или плоских, обычно используется доводочный инструмент малых размеров. В результате на оптической поверхности остаются следы обработки в виде мелкомасштабных неоднородностей профиля поверхности, которые порождают мелкомасштабные деформации волнового фронта светового пучка, прошедшего оптический элемент.
Под мелкомасштабными деформациями поверхности оптического элемента подразумеваются деформации поверхности, период которых τ меньше или равен 1/5 длины радиуса оптического элемента, взятой в качестве базовой длины [Проектирование оптических систем. Под ред. Р. Шеннона, Дж. Вайнта. М.: Изд-во Мир. 1983. - 432 с.] Аналогичным образом можно характеризовать мелкомасштабные деформации волнового фронта светового пучка, порожденные мелкомасштабными деформациями поверхностей оптических элементов, рассматривая в качестве базовой длины радиус светового пучка.
Уровень техники
Пространственный спектр мелкомасштабных деформаций или, другими словами, разброс пространственных периодов мелкомасштабных деформаций волнового фронта светового пучка может захватывать достаточно широкий диапазон. Это присуще оптическим системам, содержащим элементы, обработанные доводочными инструментами, разными по размеру, шагу и характеру перемещения. Так, например, для дисковых активных элементов и оптики лазерных систем на стекле, создаваемых для решения задач управляемого термоядерного синтеза [J.H. Campbell, R.A. Howley- Fedder, C.J. Stolz et al. Proceedings of SPIE, v.5341, 2004, p. 84-101], диапазоны пространственных частот, в которых требуется осуществление контроля мелкомасштабных деформаций поверхности, задаются достаточно широкими - диапазон 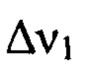 в границах 0,03÷0,4 мм-1, а диапазон
в границах 0,03÷0,4 мм-1, а диапазон 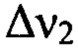 в границах 0,4÷8 мм-1. Эти два диапазона рассматривают раздельно как из-за разных значений допуска на среднеквадратическое отклонение профиля поверхности - 1,8 нм
в границах 0,4÷8 мм-1. Эти два диапазона рассматривают раздельно как из-за разных значений допуска на среднеквадратическое отклонение профиля поверхности - 1,8 нм 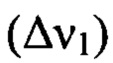 и 1,1 нм
и 1,1 нм 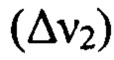 , так и вследствие различия аппаратуры, применяемой для измерений деформаций волнового фронта. При превышении допусков на среднеквадратическое отклонение профиля поверхности в мощном усилительном канале лазера мелкомасштабные возмущения волнового фронта провоцируют развитие самофокусировки излучения, приводящей к катастрофическому разрушению активной среды лазера. Видно, что граничные значения
, так и вследствие различия аппаратуры, применяемой для измерений деформаций волнового фронта. При превышении допусков на среднеквадратическое отклонение профиля поверхности в мощном усилительном канале лазера мелкомасштабные возмущения волнового фронта провоцируют развитие самофокусировки излучения, приводящей к катастрофическому разрушению активной среды лазера. Видно, что граничные значения 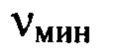 и
и 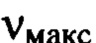 для каждого диапазона пространственных частот мелкомасштабных деформаций отличаются на порядок, а границы совокупного диапазона
для каждого диапазона пространственных частот мелкомасштабных деформаций отличаются на порядок, а границы совокупного диапазона 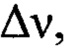 объединяющего
объединяющего 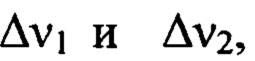 - на два порядка. При этом измерение мелкомасштабных деформаций волнового фронта должно выполняться с точностью до долей нанометра во всем спектральном диапазоне пространственных частот.
- на два порядка. При этом измерение мелкомасштабных деформаций волнового фронта должно выполняться с точностью до долей нанометра во всем спектральном диапазоне пространственных частот.
Известен способ определения волнистых деформаций волнового фронта по сечению светового пучка, реализованный в схеме высокоточного интерферометра типа Intellium Н2000 (производитель фирма ESDI, США) [Н.В. Барышников, Я.В. Гладышева, Д.Г. Денисов, И.В. Животовский, В.Е. Патрикеев, И.Н. Судариков. Вестник МГТУ им. Н.Э. Баумана. Сер. «Приборостроение», 2012, с. 4-16]. При реализации способа формируют два наклоненных под небольшим углом друг к другу когерентных гомоцентрических лазерных пучка с ортогональными поляризациями. Оба пучка пропускают через коллимирующую систему, включающую пространственный фильтр, затем пучки направляют на эталонный оптический элемент и на установленную за ним контролируемую оптическую систему. Лазерные пучки частично отражаются от рабочей поверхности эталона и от поверхности контролируемой оптической системы и после прохождения пространственного фильтра поступают в трехканальное поляризационное устройство фазового сдвига с ПЗС-матрицами на выходе каналов. Это устройство синхронно формирует и регистрирует три интерференционные картины, отличающиеся величиной фазового сдвига опорной волны относительно искаженной. Далее для определения искомых деформаций волнового фронта численным методом используют математическое соотношение, связывающее разность фаз искаженной и опорной волн в каждой точке поперечного сечения светового поля с алгебраической комбинацией значений интенсивности, зарегистрированных в той же точке в каждой из трех интерферограмм.
К причинам, препятствующим достижению указанного ниже технического результата при использовании известного способа, относятся сложность реализации, высокая трудоемкость, ограничение точности определения деформаций волнового фронта точностью изготовления эталона интерферометра. Реализация способа требует применения прецизионно изготовленного трехканального поляризационного светоделителя, а также высококогерентного лазерного источника поляризованного излучения. Используемая оптическая схема отличается высокими требованиями к точности юстировки ее элементов и высокой чувствительностью результатов к воздействию шумовых, фазовых и когерентных помех, присущих интерферометрам. Когерентные шумы и помехи ограничивают пространственные частоты измеряемых деформаций волнового фронта диапазоном Δv1, в котором, собственно, и используется указанный интерферометр. Обеспечиваемая точность измерений в лучшем случае определяется качеством эталона, т.е., как правило, на уровне λ/20÷λ/50.
Для выполнения измерений в диапазоне пространственных частот Δv2 применяют способ, реализуемый в схеме измерений с помощью микроинтерферометра типа Nanocam Dynamic Profiler, построенного по схеме микроинтерферометра Линника [Н.В. Барышников, Я.В. Гладышева, Д.Г. Денисов, И.В. Животовский, В.Е. Патрикеев, И.Н. Судариков. Вестник МГТУ им. Н.Э. Баумана. Сер. «Приборостроение», 2012, с. 4-16].
К причинам, препятствующим достижению указанного ниже технического результата при использовании известного способа, относятся следующие. Регистрируемая интерференционная картина, несущая информацию о профиле поверхности, подвержена искажениям, обусловленным когерентными шумами и помехами, шумами фотоприемника. Кроме того, поскольку поле зрения составляет единицы миллиметров и менее, то для контроля крупногабаритных оптических деталей необходимо осуществлять сканирование поверхности, выдерживая с высокой точностью геометрию и траекторию зондирования поверхности объектным пучком интерферометра, и выполнять затем совместную обработку данных, зарегистрированных на разных участках для определения вносимых поверхностью деформаций в волновой фронт пучка. Эти особенности данного способа снижают точность контроля поверхности элементов в производственных условиях, точное измерение искажения профиля поверхности и волнового фронта пучка с пространственным периодом, превышающим величину линейного поля зрения микроинтерферометра, практически невозможно осуществить.
Таким образом, отличие пространственных частот мелкомасштабных деформаций более чем на порядок усложняет задачу определения мелкомасштабных деформаций волнового фронта с высокой точностью в широком диапазоне пространственных частот.
Наиболее близким способом того же назначения к заявленному изобретению по совокупности признаков является способ определения мелкомасштабных деформаций волнового фронта светового пучка [Патент РФ №2680615, дата приор. 10.04.2018, опубл. 25.02.2019, Бюл.№6], принятый за прототип. Понятие деформаций волнового фронта светового пучка, вызванных волнистостью поверхностей оптической системы, вводимое в способе-прототипе, эквивалентно используемому нами определению мелкомасштабных деформаций.
При осуществлении способа направляют некогерентный гомоцентрический световой пучок с длиной волны X на оптическую систему. Определяют положение плоскости Пмакс, перпендикулярной оси светового пучка в пространстве изображений, для которой пиковая интенсивность светового пучка в пределах фигуры рассеяния светового пучка имеет максимальное значение 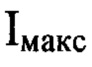 среди экспериментально зарегистрированных пиковых интенсивностей в изображениях поперечных сечений светового пучка, перпендикулярных оси светового пучка. Измеряют расстояние
среди экспериментально зарегистрированных пиковых интенсивностей в изображениях поперечных сечений светового пучка, перпендикулярных оси светового пучка. Измеряют расстояние 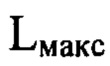 по оси пучка от плоскости
по оси пучка от плоскости 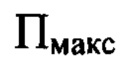 до последней по ходу пучка поверхности оптической системы с учетом правила знаков, измеряют диаметр пучка D в плоскости П, перпендикулярной оси светового пучка в пространстве изображений и соприкасающейся с последней поверхностью оптической системы, выбирают положение плоскости
до последней по ходу пучка поверхности оптической системы с учетом правила знаков, измеряют диаметр пучка D в плоскости П, перпендикулярной оси светового пучка в пространстве изображений и соприкасающейся с последней поверхностью оптической системы, выбирают положение плоскости 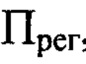 , перпендикулярной оси светового пучка в пространстве изображений и удаленной по оси пучка от плоскости
, перпендикулярной оси светового пучка в пространстве изображений и удаленной по оси пучка от плоскости 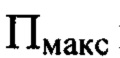 на расстояние
на расстояние 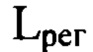 с учетом правила знаков, регистрируют распределение интенсивности
с учетом правила знаков, регистрируют распределение интенсивности 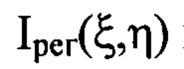 светового пучка в координатах
светового пучка в координатах 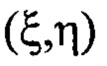 плоскости
плоскости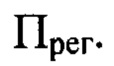
Задают математическое выражение для определения деформаций волнового фронта светового пучка w(x,y) в виде уравнения, связывающего w(x,y) в координатах (х,у) плоскости П, с распределением интенсивности светового пучка в плоскости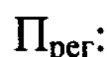
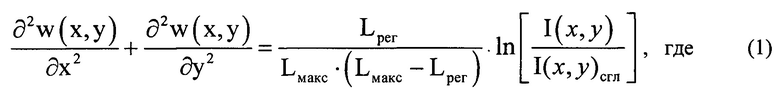
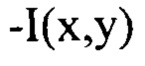 - распределение интенсивности светового пучка, выраженное в координатах плоскости П, полученное путем замены переменных в распределении интенсивности
- распределение интенсивности светового пучка, выраженное в координатах плоскости П, полученное путем замены переменных в распределении интенсивности 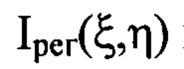 по формулам
по формулам 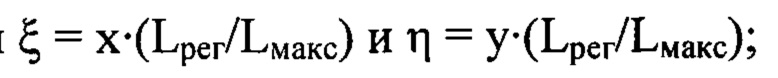
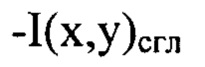 - сглаженное с использованием метода наименьших квадратов распределение интенсивности светового пучка I(х,у);
- сглаженное с использованием метода наименьших квадратов распределение интенсивности светового пучка I(х,у);
значения w(x,y) определяют путем численного решения уравнения (1) вариационным методом при свободных граничных условиях, аппроксимируя w(x,y) тригонометрическим полиномом, состоящим из суммы членов двумерного ряда Фурье с порядковыми номерами гармоник 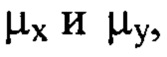 пробегающими диапазон от 1 до
пробегающими диапазон от 1 до 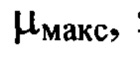 за исключением тех членов ряда, для которых оба порядковых номера
за исключением тех членов ряда, для которых оба порядковых номера 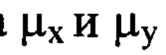 имеют значения, меньшие 10.
имеют значения, меньшие 10.
В способе-прототипе определенным образом находят расстояние 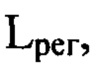 зависящее от значения
зависящее от значения 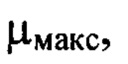 и, соответственно, определяют положение плоскости
и, соответственно, определяют положение плоскости 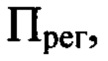 являющееся оптимальным для регистрации гармоник деформаций волнового фронта с
являющееся оптимальным для регистрации гармоник деформаций волнового фронта с 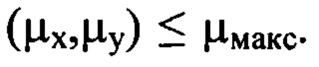 Значение
Значение 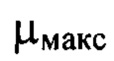 определяет номер наивысшей наблюдаемой на фоне шума гармоники. Его значение зависит от случайной реализации частотных компонент шума в структуре конкретного анализируемого изображения поперечного сечения пучка.
определяет номер наивысшей наблюдаемой на фоне шума гармоники. Его значение зависит от случайной реализации частотных компонент шума в структуре конкретного анализируемого изображения поперечного сечения пучка.
К причинам, препятствующим достижению указанного ниже результата при использовании известного способа, принятого за прототип, относятся следующие.
Уравнение (1) связывает оператор Лапласа 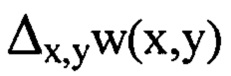 в координатах (х,у) плоскости П с функцией флуктуаций уровня интенсивности
в координатах (х,у) плоскости П с функцией флуктуаций уровня интенсивности 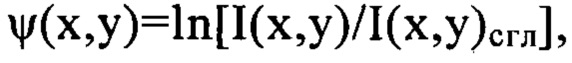 полученной из зарегистрированного изображения поперечного сечения светового пучка в плоскости Прег, приведенной затем к координатам плоскости П. Принимая во внимание двукратное дифференцирование, выполняемое оператором Лапласа над суммой членов двумерного ряда Фурье, аппроксимирующего функцию w(x,y), можно заключить, что амплитуды соответствующих членов ряда, на которые может быть разложена функция флуктуаций уровня интенсивности светового пучка, пропорциональны квадрату значений пространственных частот гармоник, содержащихся в членах ряда, аппроксимирующего функцию w(x,y). Отсюда следует, что члены ряда, содержащие гармоники с большей пространственной частотой, будут вносить больший вклад в значение функции флуктуаций уровня интенсивности
полученной из зарегистрированного изображения поперечного сечения светового пучка в плоскости Прег, приведенной затем к координатам плоскости П. Принимая во внимание двукратное дифференцирование, выполняемое оператором Лапласа над суммой членов двумерного ряда Фурье, аппроксимирующего функцию w(x,y), можно заключить, что амплитуды соответствующих членов ряда, на которые может быть разложена функция флуктуаций уровня интенсивности светового пучка, пропорциональны квадрату значений пространственных частот гармоник, содержащихся в членах ряда, аппроксимирующего функцию w(x,y). Отсюда следует, что члены ряда, содержащие гармоники с большей пространственной частотой, будут вносить больший вклад в значение функции флуктуаций уровня интенсивности 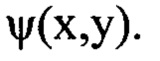 К примеру, при 5-кратном превышении максимальной пространственной частоты
К примеру, при 5-кратном превышении максимальной пространственной частоты 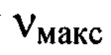 по сравнению с минимальной частотой
по сравнению с минимальной частотой 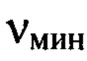 в спектре функции флуктуаций уровня интенсивности гармоника с минимальной частотой проявится с амплитудой в 25 раз меньшей, чем амплитуда гармоники с максимальной частотой. Вследствие этого с большой вероятностью амплитуды членов двумерного ряда Фурье, содержащих гармоники, близкие к минимальной границе частот, в спектре функции флуктуаций уровня интенсивности ψ(х,у) будут найдены с существенной ошибкой или вовсе подавлены шумом фотоприемника. Использование способа не будет гарантировать получение достоверных значений искомых деформаций волнового фронта во всем диапазоне частот. Таким образом, возможности способа прототипа ограничены и не обеспечивают высокоточные измерения мелкомасштабных деформаций волнового фронта светового пучка, охватывающих широкий диапазон пространственных частот.
в спектре функции флуктуаций уровня интенсивности гармоника с минимальной частотой проявится с амплитудой в 25 раз меньшей, чем амплитуда гармоники с максимальной частотой. Вследствие этого с большой вероятностью амплитуды членов двумерного ряда Фурье, содержащих гармоники, близкие к минимальной границе частот, в спектре функции флуктуаций уровня интенсивности ψ(х,у) будут найдены с существенной ошибкой или вовсе подавлены шумом фотоприемника. Использование способа не будет гарантировать получение достоверных значений искомых деформаций волнового фронта во всем диапазоне частот. Таким образом, возможности способа прототипа ограничены и не обеспечивают высокоточные измерения мелкомасштабных деформаций волнового фронта светового пучка, охватывающих широкий диапазон пространственных частот.
Под широким диапазоном пространственных частот мы подразумеваем такой диапазон пространственных частот от 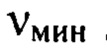 до
до 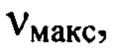 при котором
при котором 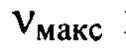 в несколько раз, возможно на порядок и более превышает
в несколько раз, возможно на порядок и более превышает 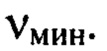
Раскрытие сущности изобретения
Сущность изобретения заключается в следующем.
Технической проблемой, которую решает изобретение, является определение мелкомасштабных деформаций волнового фронта светового пучка в широком диапазоне пространственных частот с высокой точностью и достоверностью.
Технический результат, который может быть достигнут при осуществлении заявленного способа, заключается в определении мелкомасштабных деформаций волнового фронта светового пучка в широком диапазоне пространственных частот с высокой точностью и достоверностью.
Указанный технический результат при осуществлении изобретения достигается тем, что в способе определения мелкомасштабных деформаций волнового фронта светового пучка w(x,y), включающем направление некогерентного гомоцентрического светового пучка с длиной волны λ на оптическую систему, определение положения плоскости 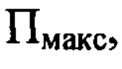 перпендикулярной оси светового пучка в пространстве изображений, для которой пиковая интенсивность светового пучка в пределах фигуры рассеяния светового пучка имеет максимальное значение
перпендикулярной оси светового пучка в пространстве изображений, для которой пиковая интенсивность светового пучка в пределах фигуры рассеяния светового пучка имеет максимальное значение 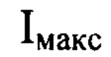 среди экспериментально зарегистрированных пиковых интенсивностей в изображениях поперечных сечений светового пучка, перпендикулярных оси светового пучка, измерение расстояния
среди экспериментально зарегистрированных пиковых интенсивностей в изображениях поперечных сечений светового пучка, перпендикулярных оси светового пучка, измерение расстояния 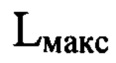 по оси пучка от плоскости
по оси пучка от плоскости 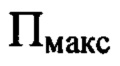 до последней по ходу пучка поверхности оптической системы с учетом правила знаков, измерение диаметра пучка D в плоскости П, перпендикулярной оси светового пучка в пространстве изображений и соприкасающейся с последней поверхностью оптической системы, регистрацию распределения интенсивности
до последней по ходу пучка поверхности оптической системы с учетом правила знаков, измерение диаметра пучка D в плоскости П, перпендикулярной оси светового пучка в пространстве изображений и соприкасающейся с последней поверхностью оптической системы, регистрацию распределения интенсивности 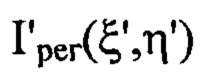 светового пучка в координатах
светового пучка в координатах 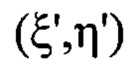 плоскости
плоскости 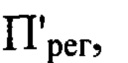 перпендикулярной оси светового пучка в пространстве изображений и удаленной по оси пучка от плоскости Пмакс на расстояние
перпендикулярной оси светового пучка в пространстве изображений и удаленной по оси пучка от плоскости Пмакс на расстояние 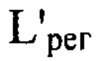 с учетом правила знаков, определение значения
с учетом правила знаков, определение значения 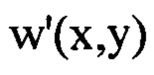 путем численного решения уравнения:
путем численного решения уравнения:
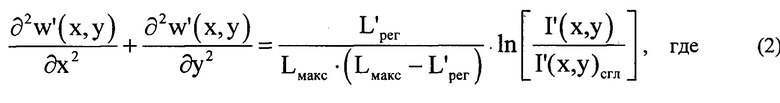
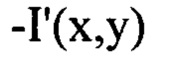 - распределение интенсивности светового пучка, выраженное в координатах плоскости П, полученное путем замены переменных в распределении интенсивности
- распределение интенсивности светового пучка, выраженное в координатах плоскости П, полученное путем замены переменных в распределении интенсивности 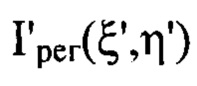 по формулам
по формулам 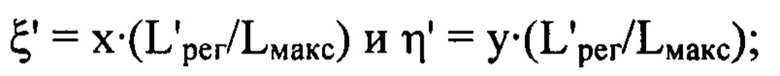
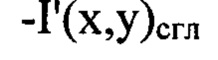 - сглаженное с использованием метода наименьших квадратов распределение интенсивности светового пучка
- сглаженное с использованием метода наименьших квадратов распределение интенсивности светового пучка 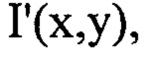
вариационным методом при свободных граничных условиях, аппроксимируя 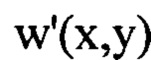 тригонометрическим полиномом, состоящим из суммы членов двумерного ряда Фурье с порядковыми номерами гармоник
тригонометрическим полиномом, состоящим из суммы членов двумерного ряда Фурье с порядковыми номерами гармоник 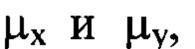 пробегающими диапазон от 1 до
пробегающими диапазон от 1 до 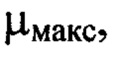 за исключением тех членов ряда, для которых оба порядковых номера
за исключением тех членов ряда, для которых оба порядковых номера 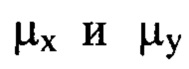 имеют значения, меньшие 10, в соответствии с заявляемым техническим решением задаваемый диапазон пространственных частот от
имеют значения, меньшие 10, в соответствии с заявляемым техническим решением задаваемый диапазон пространственных частот от 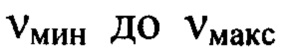 разбивают на m последовательных интервалов пространственных частот
разбивают на m последовательных интервалов пространственных частот 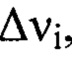 где
где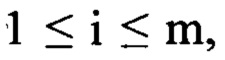 так, что верхняя vi и нижняя vi-1 границы каждого i-ro интервала удовлетворяют соотношению
так, что верхняя vi и нижняя vi-1 границы каждого i-ro интервала удовлетворяют соотношению

где 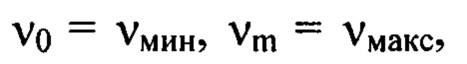 при этом μ1=Vj -D, а
при этом μ1=Vj -D, а 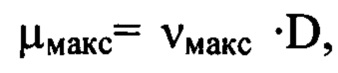 если порядковые номера гармоник
если порядковые номера гармоник 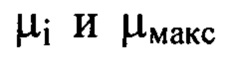 получаются нецелыми числами, то выбирают значение ближайшего меньшего целого числа, расстояние
получаются нецелыми числами, то выбирают значение ближайшего меньшего целого числа, расстояние 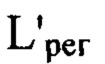 определяют для каждого интервала пространственных частот
определяют для каждого интервала пространственных частот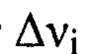 из соотношения
из соотношения
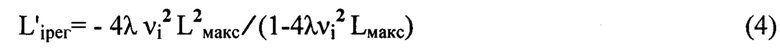
с учетом правила знаков и получают таким образом набор значений 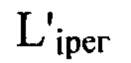 удаления плоскостей
удаления плоскостей 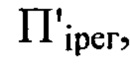 перпендикулярных оси светового пучка в пространстве изображений, от плоскости
перпендикулярных оси светового пучка в пространстве изображений, от плоскости 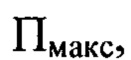 регистрацию распределения интенсивности
регистрацию распределения интенсивности 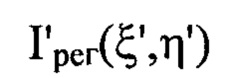 светового пучка осуществляют в координатах
светового пучка осуществляют в координатах 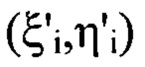 каждой из плоскостей
каждой из плоскостей 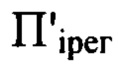 и получают таким образом набор значений
и получают таким образом набор значений 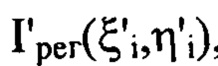 , значение
, значение 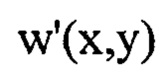 определяют для каждого интервала пространственных частот
определяют для каждого интервала пространственных частот 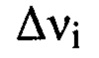 путем численного решения уравнения (2), в котором величины
путем численного решения уравнения (2), в котором величины 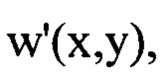
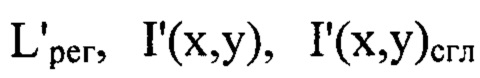 заменяют на
заменяют на 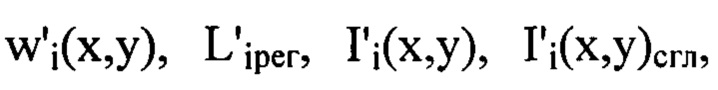 соответственно, считая, что
соответственно, считая, что 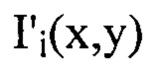 - распределения интенсивностей светового пучка, выраженные в координатах плоскости П, полученные путем замены переменных в распределениях интенсивностей
- распределения интенсивностей светового пучка, выраженные в координатах плоскости П, полученные путем замены переменных в распределениях интенсивностей 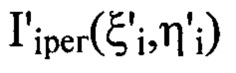 по формулам
по формулам 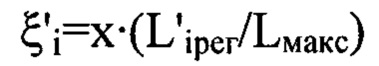 и
и 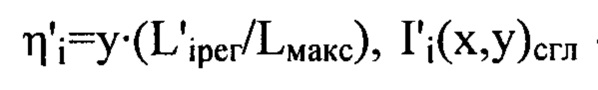 - сглаженные с использованием метода наименьших квадратов распределения интенсивностей светового пучка
- сглаженные с использованием метода наименьших квадратов распределения интенсивностей светового пучка 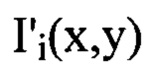 , и получают таким образом набор значений
, и получают таким образом набор значений 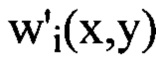 , выбирают из
, выбирают из 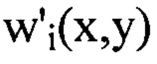 члены ряда Фурье, содержащие гармоники, удовлетворяющие условиям, когда хотя бы один порядковый номер гармоники
члены ряда Фурье, содержащие гармоники, удовлетворяющие условиям, когда хотя бы один порядковый номер гармоники 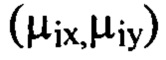 превышает значение
превышает значение 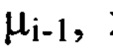 и оба порядковых номера гармоник
и оба порядковых номера гармоник 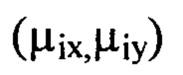 не превышают значение
не превышают значение 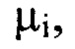 из суммы выбранных членов ряда Фурье составляют компоненту
из суммы выбранных членов ряда Фурье составляют компоненту 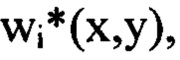 определяющую деформации волнового фронта светового пучка в интервале пространственных частот
определяющую деформации волнового фронта светового пучка в интервале пространственных частот 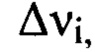 мелкомасштабные деформации волнового фронта
мелкомасштабные деформации волнового фронта 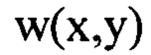 в диапазоне пространственных частот от
в диапазоне пространственных частот от 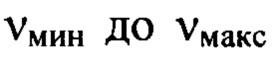 определяют путем суммирования всех найденных компонент
определяют путем суммирования всех найденных компонент 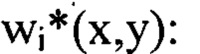
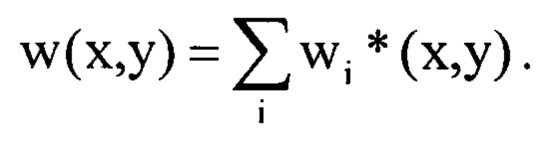
Совокупность вышеизложенных признаков изобретения связана причинно-следственной связью с техническим результатом изобретения.
Как указывалось выше, из уравнения (2) для определения 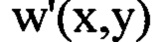 в общем случае следует, что амплитуды членов двумерного ряда Фурье, в который может быть разложена функция флуктуаций уровня интенсивности светового пучка
в общем случае следует, что амплитуды членов двумерного ряда Фурье, в который может быть разложена функция флуктуаций уровня интенсивности светового пучка 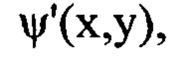 пропорциональны квадрату значений пространственных частот гармоник, содержащихся в членах ряда Фурье, аппроксимирующего функцию 1
пропорциональны квадрату значений пространственных частот гармоник, содержащихся в членах ряда Фурье, аппроксимирующего функцию 1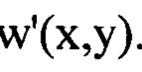 Вследствие этого, содержащиеся в функции
Вследствие этого, содержащиеся в функции 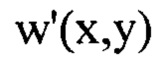 гармоники с большей пространственной частотой будут вносить больший вклад в значения функции флуктуаций уровня интенсивности
гармоники с большей пространственной частотой будут вносить больший вклад в значения функции флуктуаций уровня интенсивности 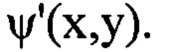 С уменьшением частоты содержащихся в функции
С уменьшением частоты содержащихся в функции 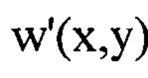 гармоник от значений
гармоник от значений 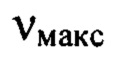 до
до 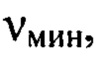 амплитуда соответствующих гармоник в пространственном спектре функции флуктуаций уровня интенсивности
амплитуда соответствующих гармоник в пространственном спектре функции флуктуаций уровня интенсивности 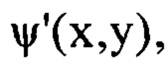 порождаемых мелкомасштабными деформациями волнового фронта, снижается в
порождаемых мелкомасштабными деформациями волнового фронта, снижается в 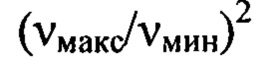 раз. Соответственно, снижается относительный вклад низкочастотных гармоник в структуру изображения пучка по сравнению с шумом. Если диапазон от
раз. Соответственно, снижается относительный вклад низкочастотных гармоник в структуру изображения пучка по сравнению с шумом. Если диапазон от 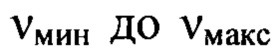 широкий, то с большой вероятностью амплитуды гармоник на минимальных частотах диапазона в пространственном спектре функции флуктуаций уровня интенсивности
широкий, то с большой вероятностью амплитуды гармоник на минимальных частотах диапазона в пространственном спектре функции флуктуаций уровня интенсивности 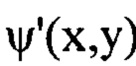 будут заметно искажены шумом.
будут заметно искажены шумом.
В проведенных нами экспериментах, в том числе имитационных, было обнаружено, что случайный шум в изображении не снижает точность измерения амплитуды мелкомасштабных деформаций волнового фронта, если соотношение между минимальной и максимальной частотами деформаций, присутствующих в спектре пространственных частот изображения таково, что максимальная частота не более, чем в 2,5 раза превышает минимальную частоту. Поэтому, если диапазон пространственных частот широкий, и 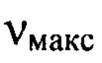 в несколько раз, а возможно на порядок и более превышает
в несколько раз, а возможно на порядок и более превышает 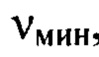 , то его необходимо разбить на m последовательных интервалов пространственных частот
, то его необходимо разбить на m последовательных интервалов пространственных частот 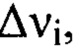 где 1≤i≤m, так, что верхняя vi и нижняя
где 1≤i≤m, так, что верхняя vi и нижняя 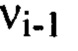 границы каждого i-го интервала удовлетворяют соотношению (3).
границы каждого i-го интервала удовлетворяют соотношению (3).
Далее для каждого интервала пространственных частот 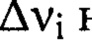 необходимо выбрать свое положение плоскости регистрации изображения
необходимо выбрать свое положение плоскости регистрации изображения 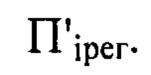 При значительном удалении плоскости
При значительном удалении плоскости 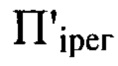 от плоскости П, вследствие волновой природы света каждому лучу, приходящему в плоскость регистрации изображения .
от плоскости П, вследствие волновой природы света каждому лучу, приходящему в плоскость регистрации изображения .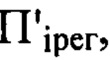 отвечает некоторый участок волнового фронта - зона Френеля, определяемая диаметром зоны Френеля
отвечает некоторый участок волнового фронта - зона Френеля, определяемая диаметром зоны Френеля 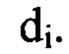 Выбор положения плоскости
Выбор положения плоскости 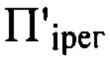 необходимо осуществлять так, чтобы в указанной плоскости период наиболее высокочастотных деформаций
необходимо осуществлять так, чтобы в указанной плоскости период наиболее высокочастотных деформаций 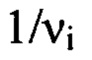 волнового фронта был равен или превышал диаметр зоны Френеля di. В противном случае действие высокочастотных деформаций будет усредняться, а порожденные ими флуктуации интенсивности в плоскости
волнового фронта был равен или превышал диаметр зоны Френеля di. В противном случае действие высокочастотных деформаций будет усредняться, а порожденные ими флуктуации интенсивности в плоскости 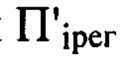 будут сглаживаться.
будут сглаживаться.
Для определения расстояний 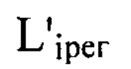 удаления плоскостей
удаления плоскостей 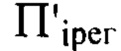 по оси пучка от плоскости
по оси пучка от плоскости 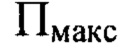 нами было получено соотношение (4), где
нами было получено соотношение (4), где 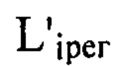 определяют с учетом правила знаков. После определения положения плоскостей
определяют с учетом правила знаков. После определения положения плоскостей 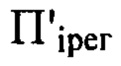 для каждого интервала частот регистрируют в них изображения поперечного сечения светового пучка.
для каждого интервала частот регистрируют в них изображения поперечного сечения светового пучка.
Путем численного решения уравнения (2) определяют 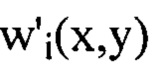 для каждого интервала пространственных частот
для каждого интервала пространственных частот 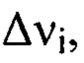 заменяя величины
заменяя величины 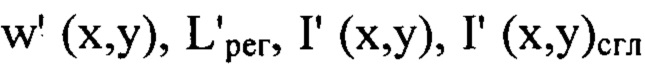 на
на 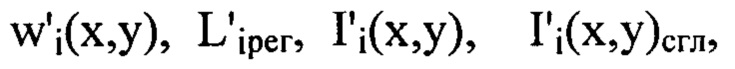 соответственно, при этом
соответственно, при этом 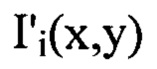 - распределение интенсивности светового пучка, выраженное в координатах плоскости П, полученное путем замены переменных в распределении интенсивности
- распределение интенсивности светового пучка, выраженное в координатах плоскости П, полученное путем замены переменных в распределении интенсивности 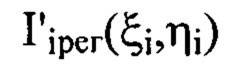 по формулам
по формулам 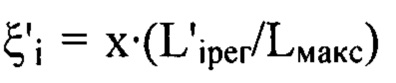 и
и 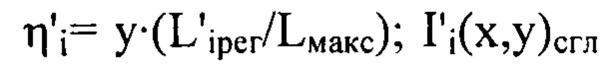 - сглаженное с использованием метода наименьших квадратов распределение интенсивности светового пучка
- сглаженное с использованием метода наименьших квадратов распределение интенсивности светового пучка 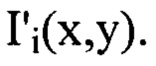
В полученном наборе значений 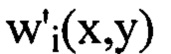 каждая из величин
каждая из величин 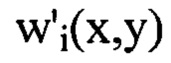 аппроксимирована тригонометрическим полиномом, состоящим из суммы членов двумерного ряда Фурье, содержащих гармоники с порядковыми номерами
аппроксимирована тригонометрическим полиномом, состоящим из суммы членов двумерного ряда Фурье, содержащих гармоники с порядковыми номерами 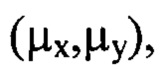 пробегающими диапазон от 1 до
пробегающими диапазон от 1 до 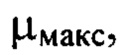 за исключением тех членов ряда, для которых оба порядковых номера
за исключением тех членов ряда, для которых оба порядковых номера 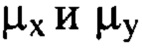 имеют значения, меньшие 10.
имеют значения, меньшие 10.
Для того чтобы перейти от 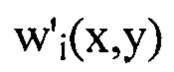 к компоненте
к компоненте 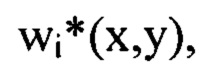 отвечающей мелкомасштабным деформациям волнового фронта в интервале пространственных частот
отвечающей мелкомасштабным деформациям волнового фронта в интервале пространственных частот 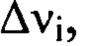 осуществляют следующие действия. Выбирают из
осуществляют следующие действия. Выбирают из 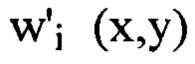 члены ряда Фурье, содержащие гармоники, хотя бы один порядковый номер которых
члены ряда Фурье, содержащие гармоники, хотя бы один порядковый номер которых 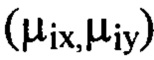 превышает значение
превышает значение 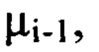 соответствующее пространственной частоте
соответствующее пространственной частоте 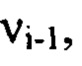 и оба порядковых номера которых
и оба порядковых номера которых 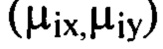 " не превышают значение соответствующее пространственной частоте vi. Из суммы выбранных членов ряда Фурье составляют компоненту
" не превышают значение соответствующее пространственной частоте vi. Из суммы выбранных членов ряда Фурье составляют компоненту 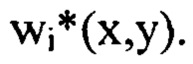
Мелкомасштабные деформации волнового фронта 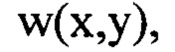 содержащие пространственные гармоники в широком диапазоне пространственных частот от
содержащие пространственные гармоники в широком диапазоне пространственных частот от 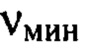 до
до 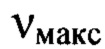 определяют как
определяют как 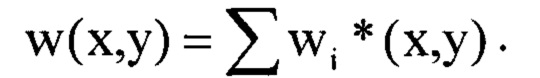
Таким образом, выполнение всей совокупности операций способа с соблюдением вводимых условий их осуществления позволяет устранить источники ошибок определения мелкомасштабных деформаций волнового фронта в широком диапазоне пространственных частот, обусловленные влиянием на результат как дифракционных эффектов, так и усилением относительного вклада шума в структуру изображения в области низких частот.
Краткое описание чертежей
На фиг. 1 представлена оптическая схема для реализации описанного способа измерений мелкомасштабных деформаций волнового фронта светового пучка, где 1 - некогерентный источник света (лампа накаливания); 2 - конденсор; 3 - узкополосный светофильтр; 4 - микродиафрагма; 5 - оптическая система, фокусирующая и искажающая пучок, 6 - проекционный объектив; 7 - ПЗС-матрица, регистрирующая распределение интенсивности в поперечном сечении светового пучка. Плоскость П - плоскость, в системе координат которой определяют деформации волнового фронта, соприкасается с последней поверхностью оптической системы 5, плоскость 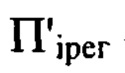 - плоскость, в которой регистрируют распределение интенсивности
- плоскость, в которой регистрируют распределение интенсивности 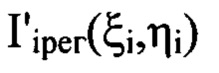 в интервале пространственных частот
в интервале пространственных частот 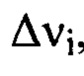 , где 1≤i≤m, плоскость
, где 1≤i≤m, плоскость 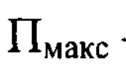 - плоскость, в которой пиковая интенсивность светового пучка достигает максимального значения среди экспериментально зарегистрированных пиковых интенсивностей в распределениях интенсивностей светового пучка в плоскостях, перпендикулярных оси светового пучка. Плоскости П,
- плоскость, в которой пиковая интенсивность светового пучка достигает максимального значения среди экспериментально зарегистрированных пиковых интенсивностей в распределениях интенсивностей светового пучка в плоскостях, перпендикулярных оси светового пучка. Плоскости П, 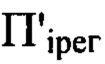 и
и 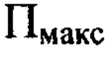 перпендикулярны оси светового пучка, начало координат в плоскостях П,
перпендикулярны оси светового пучка, начало координат в плоскостях П, 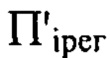 и
и 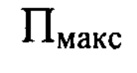 лежит на оси светового пучка.
лежит на оси светового пучка. 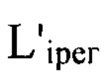 и
и 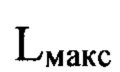 - расстояния от плоскости
- расстояния от плоскости 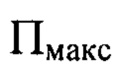 до плоскостей
до плоскостей 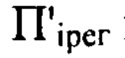 и П, соответственно, по оси пучка с учетом правила знаков.
и П, соответственно, по оси пучка с учетом правила знаков.
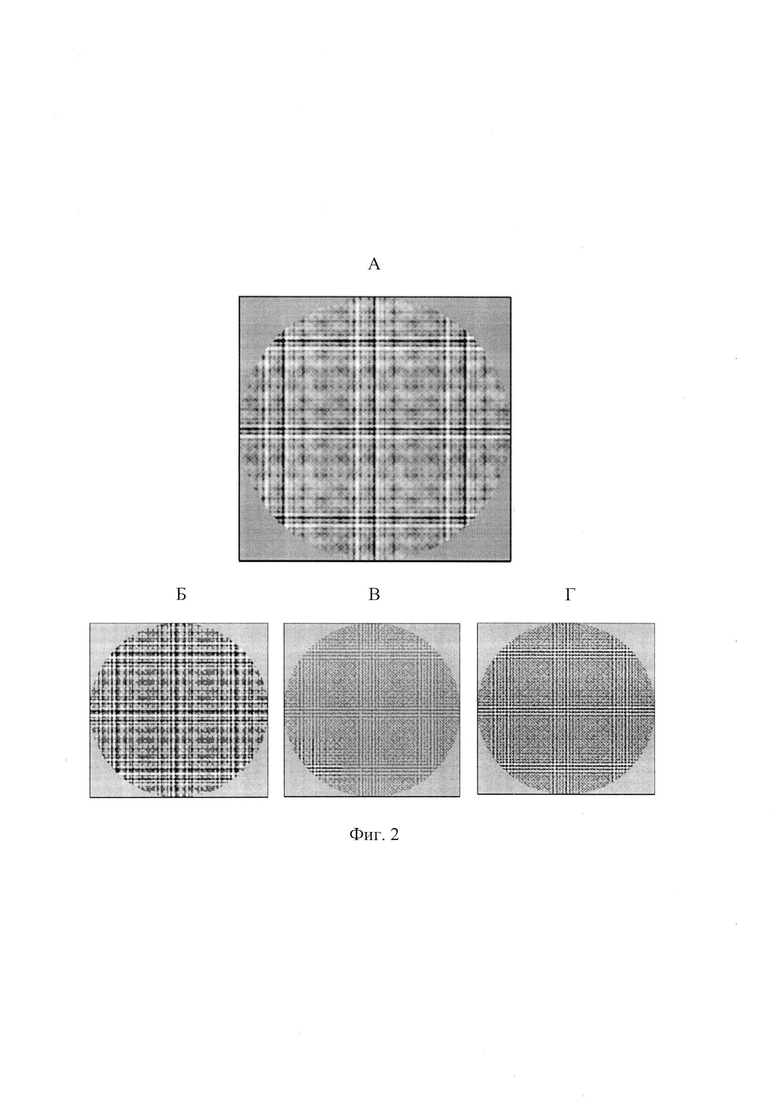
На фиг. 2, А представлены в виде полутонового изображения исходные мелкомасштабные деформации волнового фронта 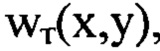 имитирующие искажения сферического волнового фронта светового пучка, внесенные оптической системой. На фиг. 2, Б; 2, В и 2, Г в виде полутонового изображения показаны функции флуктуаций уровня интенсивности
имитирующие искажения сферического волнового фронта светового пучка, внесенные оптической системой. На фиг. 2, Б; 2, В и 2, Г в виде полутонового изображения показаны функции флуктуаций уровня интенсивности 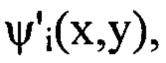 отвечающие изображениям сечения пучка на дистанциях регистрации:
отвечающие изображениям сечения пучка на дистанциях регистрации: 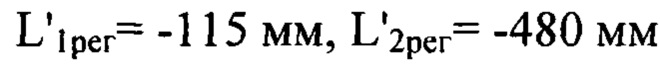 и
и 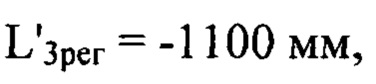 соответственно.
соответственно.
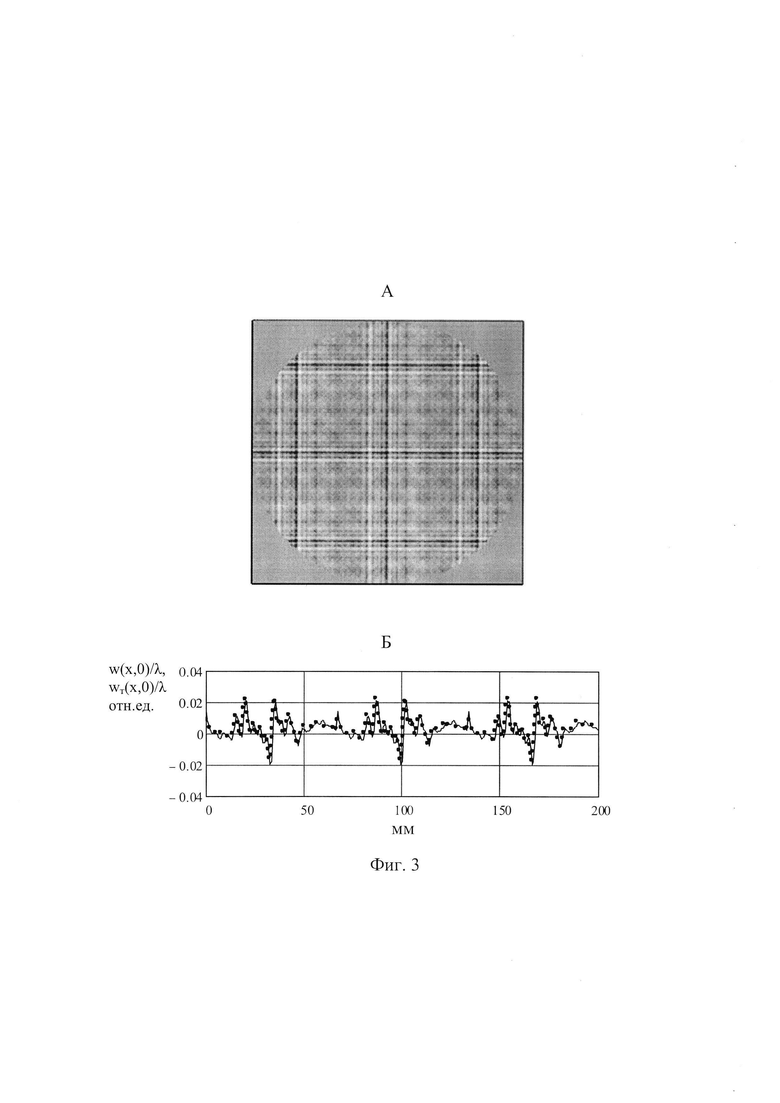
На фиг. 3, А показаны в виде полутонового изображения деформации волнового фронта w(x,y), найденные предложенным способом по трем изображениям пучка, зарегистрированным на дистанциях регистрации: 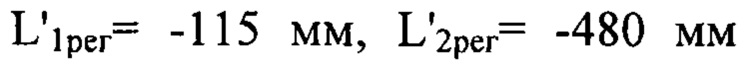 и
и 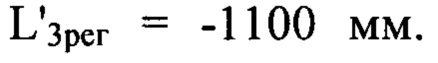 На фиг. 3, Б показаны для сравнения нормированный профиль найденных деформаций волнового фронта w(x,0)/λ, (сплошная кривая) и нормированный профиль исходных деформаций волнового фронта
На фиг. 3, Б показаны для сравнения нормированный профиль найденных деформаций волнового фронта w(x,0)/λ, (сплошная кривая) и нормированный профиль исходных деформаций волнового фронта 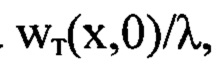 показанный точками.
показанный точками.
Осуществление изобретения.
Реализация способа осуществляется по оптической схеме, представленной на Фиг. 1. Некогерентный гомоцентрический световой пучок с длиной волны λ направляют на оптическую систему 5. Определяют положение плоскости 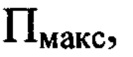 измеряют расстояние
измеряют расстояние 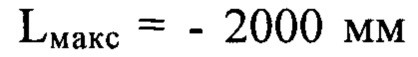 по оси пучка с учетом правила знаков и поперечный размер пучка D=200 мм в плоскости П, соприкасающейся с последней поверхностью оптической системы. Мелкомасштабные деформации волнового фронта светового пучка на выходе оптической системы (5) изначально задают как
по оси пучка с учетом правила знаков и поперечный размер пучка D=200 мм в плоскости П, соприкасающейся с последней поверхностью оптической системы. Мелкомасштабные деформации волнового фронта светового пучка на выходе оптической системы (5) изначально задают как 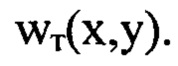 Исходные значения
Исходные значения 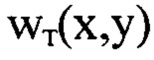 сформированы добавлением фазовых искажений в комплексную амплитуду поля сферической световой волны на выходе оптической системы (5) в широком диапазоне пространственных частот от
сформированы добавлением фазовых искажений в комплексную амплитуду поля сферической световой волны на выходе оптической системы (5) в широком диапазоне пространственных частот от 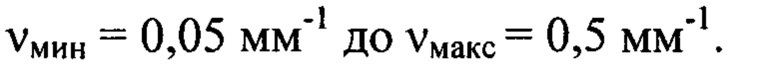
Определение деформаций волнового фронта при реализации предложенного способа производилось в соответствии с описанным выше разделением диапазона пространственных частот на несколько интервалов. С учетом требования (3) разделение диапазона было осуществлено на 3 частотных интервала и рассчитаны соответствующие дистанции регистрации с учетом правила знаков. Они имели значения 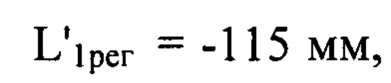
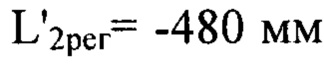 и
и 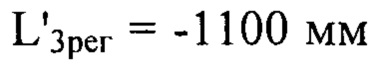 при
при 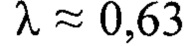 мкм и определяли положения плоскостей регистрации
мкм и определяли положения плоскостей регистрации 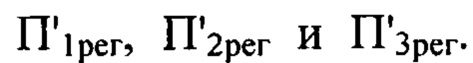 Далее методом расчета дифракционного интеграла Френеля были вычислены распределения амплитуд поля и интенсивности в каждой из плоскостей
Далее методом расчета дифракционного интеграла Френеля были вычислены распределения амплитуд поля и интенсивности в каждой из плоскостей 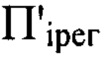 и получены 3 изображения поперечного сечения светового пучка в плоскостях регистрации
и получены 3 изображения поперечного сечения светового пучка в плоскостях регистрации 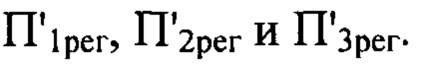
Значения 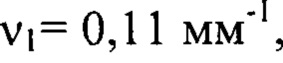
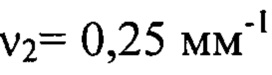 и
и 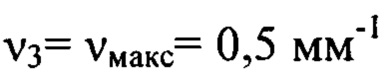 отвечали номерам гармоник
отвечали номерам гармоник 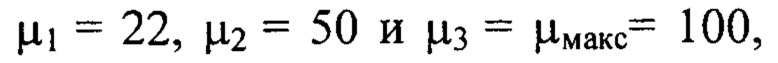 соответственно. Таким образом, изображение пучка в плоскости
соответственно. Таким образом, изображение пучка в плоскости 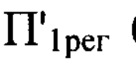 было использовано для определения деформаций волнового фронта в диапазоне пространственных частот от
было использовано для определения деформаций волнового фронта в диапазоне пространственных частот от 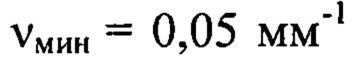 до
до 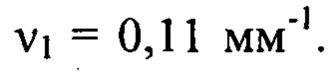 Изображение пучка в плоскости
Изображение пучка в плоскости 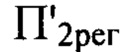 было использовано для определения деформаций в диапазоне пространственных частот от
было использовано для определения деформаций в диапазоне пространственных частот от 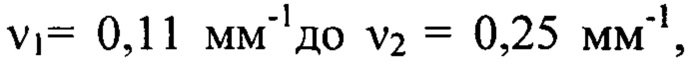 а изображение в плоскости
а изображение в плоскости 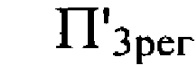 было использовано для определения деформаций в диапазоне пространственных частот от
было использовано для определения деформаций в диапазоне пространственных частот от 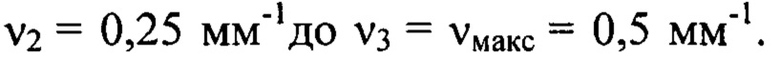 При этом соотношения границ частотных интервалов составляют
При этом соотношения границ частотных интервалов составляют 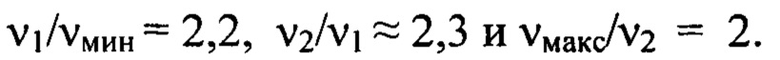
Значения 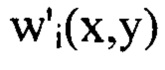 определяют, аппроксимируя приближенное решение уравнения (2)
определяют, аппроксимируя приближенное решение уравнения (2) 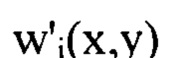 тригонометрическим полиномом в виде отрезка двумерного ряда Фурье, члены которого содержат гармоники с порядковыми номерами
тригонометрическим полиномом в виде отрезка двумерного ряда Фурье, члены которого содержат гармоники с порядковыми номерами 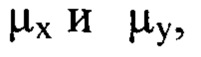 пробегающими диапазон от 1 до
пробегающими диапазон от 1 до 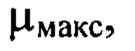 за исключением тех членов ряда, для которых оба порядковых номера
за исключением тех членов ряда, для которых оба порядковых номера 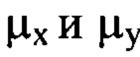 имеют значения, меньшие 10:
имеют значения, меньшие 10:
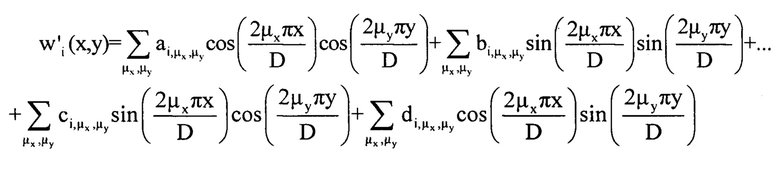
Значения коэффициентов в разложении по тригонометрическим функциям определяют из условия минимума функционала, отвечающего уравнению (2) [Л.В. Канторович, В.И. Крылов. Приближенные методы высшего анализа. М.-Л.: Гос. Изд-во физ.-мат .лит. 1962. - 708 с.], откуда следует:
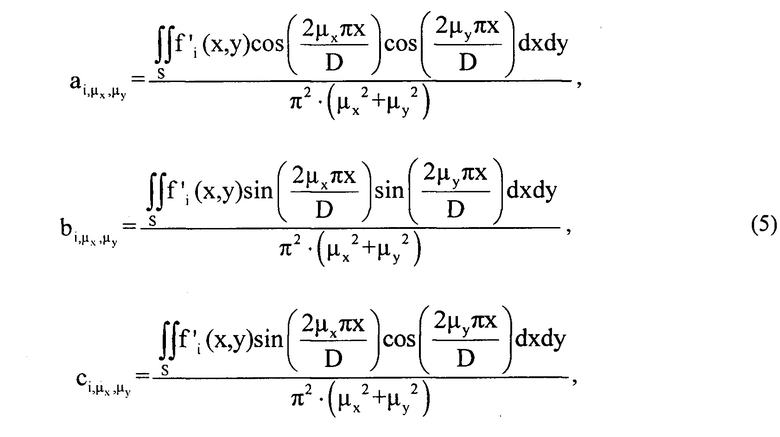
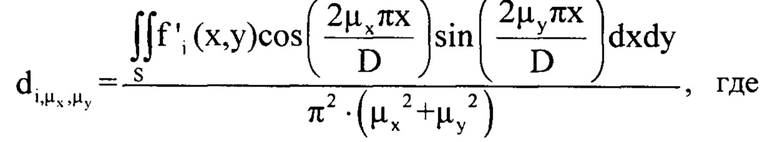
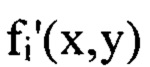 - это правая часть уравнения (2), т.е
- это правая часть уравнения (2), т.е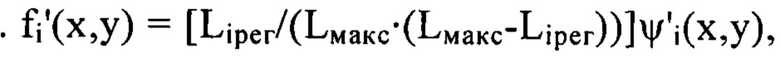 где
где 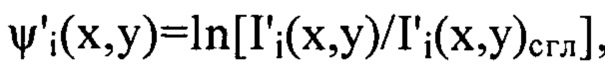 , область интегрирования S - есть поперечное сечение пучка в плоскости П. При расчете коэффициентов в силу дискретного характера координат точек в зарегистрированных ПЗС-матрицей изображениях пучка интегрирование по его сечению в приведенных соотношениях заменяют суммированием по пикселям изображения.
, область интегрирования S - есть поперечное сечение пучка в плоскости П. При расчете коэффициентов в силу дискретного характера координат точек в зарегистрированных ПЗС-матрицей изображениях пучка интегрирование по его сечению в приведенных соотношениях заменяют суммированием по пикселям изображения.
Далее из полученного ряда Фурье 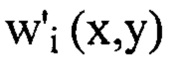 выбирают члены, содержащие гармоники, хотя бы один порядковый номер которых
выбирают члены, содержащие гармоники, хотя бы один порядковый номер которых 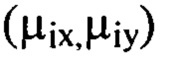 превышает значение
превышает значение 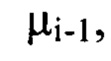 соответствующее пространственной частоте
соответствующее пространственной частоте 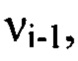 и оба порядковых номера которых
и оба порядковых номера которых 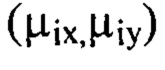 не превышают значение соответствующее пространственной частоте vi. Из суммы выбранных членов ряда Фурье составляют компоненту
не превышают значение соответствующее пространственной частоте vi. Из суммы выбранных членов ряда Фурье составляют компоненту 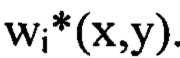 Так, в состав компоненты
Так, в состав компоненты 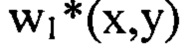 будут входить члены ряда Фурье, содержащие гармоники в диапазоне частот от
будут входить члены ряда Фурье, содержащие гармоники в диапазоне частот от 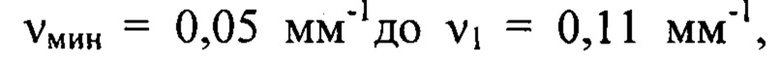 т.е. гармоники с номерами от
т.е. гармоники с номерами от 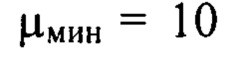 до
до 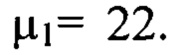 В состав компоненты
В состав компоненты 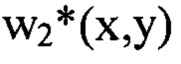 будут входить члены ряда Фурье, содержащие гармоники в диапазоне частот от
будут входить члены ряда Фурье, содержащие гармоники в диапазоне частот от 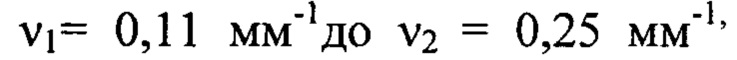 т.е. гармоники с номерами от
т.е. гармоники с номерами от 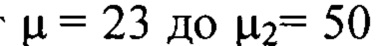 . В состав компоненты
. В состав компоненты 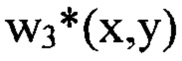 будут входить члены ряда Фурье, содержащие гармоники в диапазоне частот от
будут входить члены ряда Фурье, содержащие гармоники в диапазоне частот от 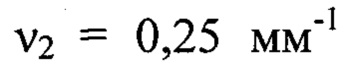 до
до 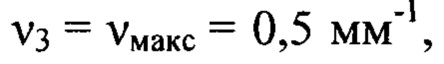 т.е. гармоники с номерами от
т.е. гармоники с номерами от 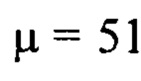 до
до 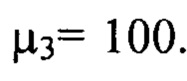 Мелкомасштабные деформации волнового фронта w(x,y) во всем заданном диапазоне пространственных частот от
Мелкомасштабные деформации волнового фронта w(x,y) во всем заданном диапазоне пространственных частот от 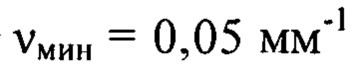 до
до 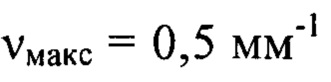 определяют путем суммирования найденных компонент
определяют путем суммирования найденных компонент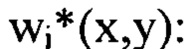
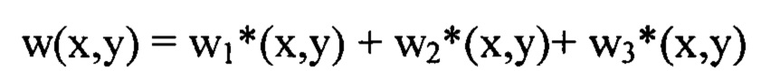
На фиг. 2, А представлены в виде полутонового изображения исходные мелкомасштабные деформации волнового фронта 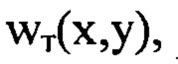 имитирующие искажения сферического волнового фронта светового пучка, внесенные оптической системой. На фиг. 2, Б; 2, В и 2, Г в виде полутонового изображения показаны функции флуктуаций уровня интенсивности
имитирующие искажения сферического волнового фронта светового пучка, внесенные оптической системой. На фиг. 2, Б; 2, В и 2, Г в виде полутонового изображения показаны функции флуктуаций уровня интенсивности 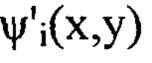 в плоскостях
в плоскостях 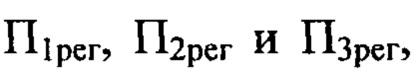 отвечающих дистанциям регистрации:
отвечающих дистанциям регистрации: 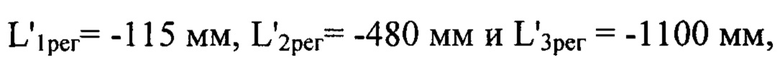 соответственно. Плоскость
соответственно. Плоскость 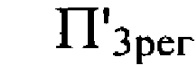 отвечает наименьшей длине пути, пройденного пучком за плоскостью П. Изображение в этой плоскости хорошо воспроизводит мелкомасштабную структуру флуктуаций уровня интенсивности, обусловленных деформациями волнового фронта пучка. Напротив, в плоскости
отвечает наименьшей длине пути, пройденного пучком за плоскостью П. Изображение в этой плоскости хорошо воспроизводит мелкомасштабную структуру флуктуаций уровня интенсивности, обусловленных деформациями волнового фронта пучка. Напротив, в плоскости 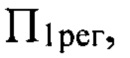 наиболее удаленной от плоскости П, мелкие детали изображения заметно сглажены. В этом изображении лучше проявились более крупные по поперечному размеру неоднородности интенсивности. Эти особенности зарегистрированных изображений поперечного сечения пучка и есть следствие проявления описанных выше эффектов, снижающих точность измерений мелкомасштабных деформаций волнового фронта.
наиболее удаленной от плоскости П, мелкие детали изображения заметно сглажены. В этом изображении лучше проявились более крупные по поперечному размеру неоднородности интенсивности. Эти особенности зарегистрированных изображений поперечного сечения пучка и есть следствие проявления описанных выше эффектов, снижающих точность измерений мелкомасштабных деформаций волнового фронта.
На фиг. 3, А показаны в виде полутонового изображения найденные предложенным методом мелкомасштабные деформации волнового фронта w(x,y) светового пучка. Сравнение этого изображения с представленным на фиг. 2, А 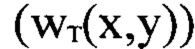 показывает хорошее соответствие общей структуры деформаций. На фиг. 3Б показаны для сравнения нормированный профиль найденных деформаций волнового фронта
показывает хорошее соответствие общей структуры деформаций. На фиг. 3Б показаны для сравнения нормированный профиль найденных деформаций волнового фронта 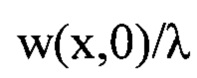 (сплошная кривая) и нормированный профиль исходных деформаций волнового фронта
(сплошная кривая) и нормированный профиль исходных деформаций волнового фронта 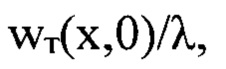 показанный точками. Видно хорошее сходство кривых вплоть до мелких деталей. Оценка среднеквадратических значений амплитуды исходных и найденных деформаций волнового фронта светового пучка показала хорошее совпадение:
показанный точками. Видно хорошее сходство кривых вплоть до мелких деталей. Оценка среднеквадратических значений амплитуды исходных и найденных деформаций волнового фронта светового пучка показала хорошее совпадение: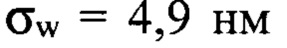 и 4,7 нм, соответственно.
и 4,7 нм, соответственно.
Таким образом, предложенный способ позволяет осуществить определение мелкомасштабных деформаций волнового фронта светового пучка, охватывающих широкий спектр пространственных частот, с высокой точностью без заметного усложнения измерительных процедур.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ДЕФОРМАЦИЙ ВОЛНОВОГО ФРОНТА СВЕТОВОГО ПУЧКА, ВЫЗВАННЫХ ВОЛНИСТОСТЬЮ ПОВЕРХНОСТЕЙ ОПТИЧЕСКОЙ СИСТЕМЫ | 2018 |
|
RU2680615C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ВОЛНОВЫХ АБЕРРАЦИЙ ОПТИЧЕСКОЙ СИСТЕМЫ | 2018 |
|
RU2680657C1 |
| Способ измерения статистических характеристик поля флуктуации плотности и устройство для его реализации | 1990 |
|
SU1831710A3 |
| СПОСОБ КОМПЕНСАЦИИ ФАЗОВЫХ ИСКАЖЕНИЙ ВОЛНОВОГО ФРОНТА НА ОСНОВЕ СВЕТОВОГО ПОЛЯ | 2022 |
|
RU2808933C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ВЫСОТНОГО ПРОФИЛЯ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ ВОЗДУХА ОБЪЕМНОЙ ОБЛАСТИ ПРОСТРАНСТВА НА ОСНОВЕ АНАЛИЗА СВЕТОВОГО ПОЛЯ | 2020 |
|
RU2773390C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ВОЛНОВЫХ АБЕРРАЦИЙ ОПТИЧЕСКОЙ СИСТЕМЫ | 2020 |
|
RU2753627C1 |
| Способ и устройство для Фурье-анализа жидких светопропускающих сред | 2021 |
|
RU2770415C1 |
| Способ определения частоты и амплитуды модуляции фазы волнового фронта, создаваемого колебаниями мембраны клетки | 2020 |
|
RU2743973C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА НЕЛИНЕЙНОСТИ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ ОПТИЧЕСКИХ СРЕД | 2003 |
|
RU2253102C1 |
| СПОСОБ АНАЛИЗА ВОЛНОВЫХ ФРОНТОВ СВЕТОВОГО ПОЛЯ | 1992 |
|
RU2051397C1 |
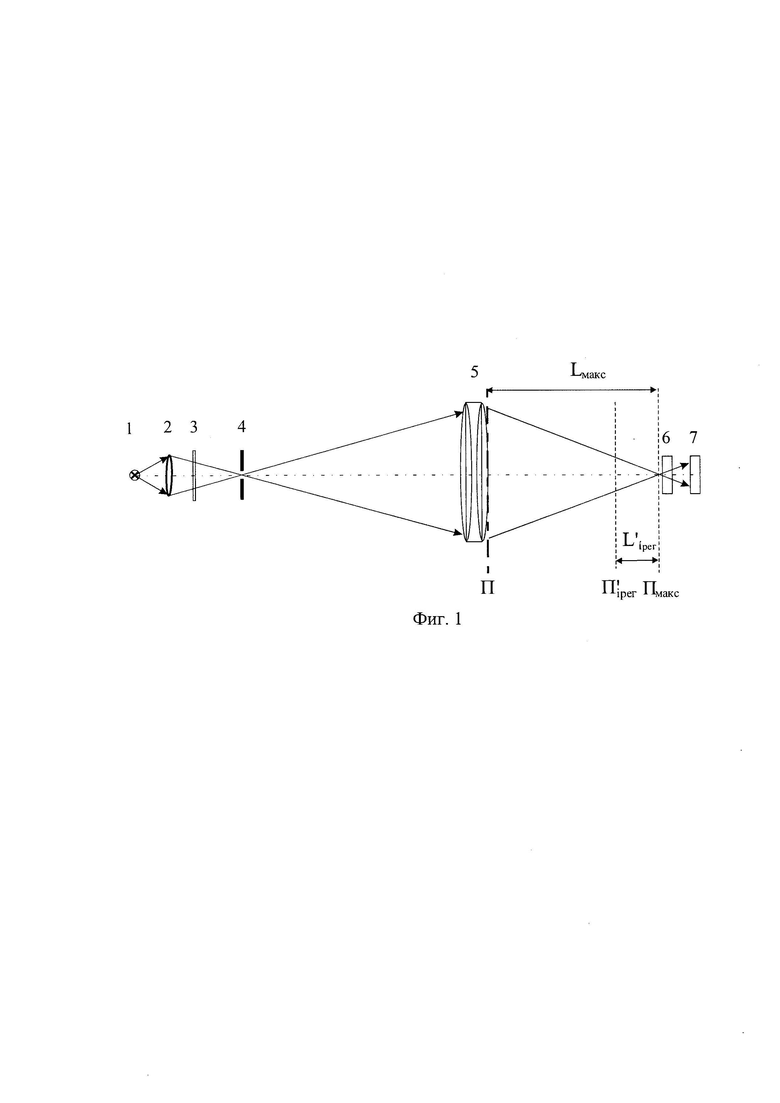
Изобретение относится к области оптики, к контролю качества оптических систем или элементов. При осуществлении способа направляют световой пучок с длиной волны λ на оптическую систему и определяют положение плоскости Пмакс, для которой пиковая интенсивность светового пучка имеет максимальное значение Iмакс. Измеряют расстояние Lмакс от плоскости Пмакс до плоскости П, соприкасающейся с последней поверхностью оптической системы, и диаметр пучка D в плоскости П. Измеряют распределения интенсивности светового пучка в координатах плоскостей, удаленных на расстояние от плоскости Пмакс, которое определяют для каждого интервала пространственных частот Δvi, полученного в результате разбиения диапазона от vмин до vмакс на m последовательных интервалов пространственных частот Δvi. Определяют значение 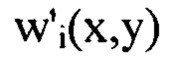 для каждого интервала Δvi путем численного решения уравнения. Выбирая из
для каждого интервала Δvi путем численного решения уравнения. Выбирая из 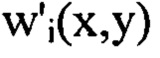 члены ряда Фурье, содержащие гармоники, удовлетворяющие условиям, когда один порядковый номер гармоники
члены ряда Фурье, содержащие гармоники, удовлетворяющие условиям, когда один порядковый номер гармоники 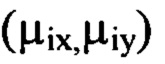 превышает значение μi-1 и оба
превышает значение μi-1 и оба 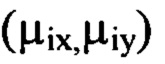 не превышают значение μi, из суммы выбранных членов ряда Фурье составляют компоненту
не превышают значение μi, из суммы выбранных членов ряда Фурье составляют компоненту 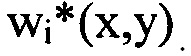 Деформации волнового фронта w(x,y) определяют, суммируя все компоненты. Технический результат - повышение точности и достоверности. 3 ил.
Деформации волнового фронта w(x,y) определяют, суммируя все компоненты. Технический результат - повышение точности и достоверности. 3 ил.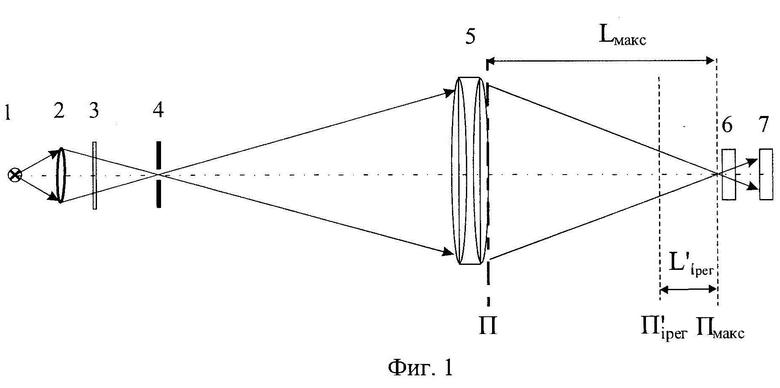
Способ определения мелкомасштабных деформаций волнового фронта светового пучка 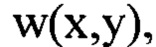 включающий направление некогерентного гомоцентрического светового пучка с длиной волны λ на оптическую систему, определение положения плоскости Пмакс, перпендикулярной оси светового пучка в пространстве изображений, для которой пиковая интенсивность светового пучка в пределах фигуры рассеяния светового пучка имеет максимальное значение Iмакс среди экспериментально зарегистрированных пиковых интенсивностей в изображениях поперечных сечений светового пучка, перпендикулярных оси светового пучка, измерение расстояния Lмакс по оси пучка от плоскости Пмакс до последней по ходу пучка поверхности оптической системы с учетом правила знаков, измерение диаметра пучка D в плоскости П, перпендикулярной оси светового пучка в пространстве изображений и соприкасающейся с последней поверхностью оптической системы, регистрацию распределения интенсивности
включающий направление некогерентного гомоцентрического светового пучка с длиной волны λ на оптическую систему, определение положения плоскости Пмакс, перпендикулярной оси светового пучка в пространстве изображений, для которой пиковая интенсивность светового пучка в пределах фигуры рассеяния светового пучка имеет максимальное значение Iмакс среди экспериментально зарегистрированных пиковых интенсивностей в изображениях поперечных сечений светового пучка, перпендикулярных оси светового пучка, измерение расстояния Lмакс по оси пучка от плоскости Пмакс до последней по ходу пучка поверхности оптической системы с учетом правила знаков, измерение диаметра пучка D в плоскости П, перпендикулярной оси светового пучка в пространстве изображений и соприкасающейся с последней поверхностью оптической системы, регистрацию распределения интенсивности 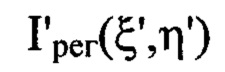 светового пучка в координатах
светового пучка в координатах 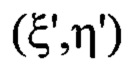 плоскости
плоскости 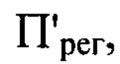 перпендикулярной оси светового пучка в пространстве изображений и удаленной по оси пучка от плоскости
перпендикулярной оси светового пучка в пространстве изображений и удаленной по оси пучка от плоскости 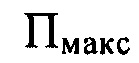 на расстояние
на расстояние 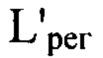 с учетом правила знаков, определение значения
с учетом правила знаков, определение значения 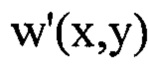 путем численного решения уравнения
путем численного решения уравнения
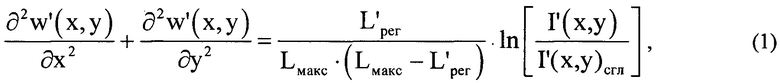
где 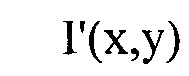 - распределение интенсивности светового пучка, выраженное в координатах плоскости П, полученное путем замены переменных в распределении интенсивности
- распределение интенсивности светового пучка, выраженное в координатах плоскости П, полученное путем замены переменных в распределении интенсивности 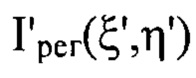 по формулам
по формулам 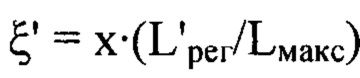 и
и 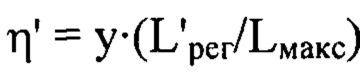 ;
;
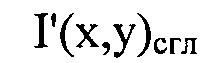 - сглаженное с использованием метода наименьших квадратов распределение интенсивности светового пучка
- сглаженное с использованием метода наименьших квадратов распределение интенсивности светового пучка 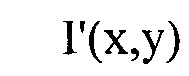 ,
,
вариационным методом при свободных граничных условиях, аппроксимируя 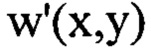 тригонометрическим полиномом, состоящим из суммы членов двумерного ряда Фурье с порядковыми номерами гармоник
тригонометрическим полиномом, состоящим из суммы членов двумерного ряда Фурье с порядковыми номерами гармоник 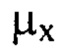 и
и 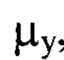 , пробегающими диапазон от 1 до
, пробегающими диапазон от 1 до 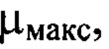 за исключением тех членов ряда, для которых оба порядковых номера
за исключением тех членов ряда, для которых оба порядковых номера 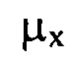 и
и 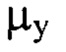 имеют значения, меньшие 10, отличающийся тем, что задаваемый диапазон пространственных частот от
имеют значения, меньшие 10, отличающийся тем, что задаваемый диапазон пространственных частот от 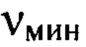 до
до 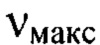 разбивают на m последовательных интервалов пространственных частот
разбивают на m последовательных интервалов пространственных частот 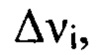 где
где 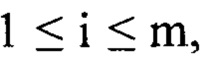 так, что верхняя vi и нижняя
так, что верхняя vi и нижняя 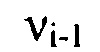 границы каждого i-го интервала удовлетворяют соотношению
границы каждого i-го интервала удовлетворяют соотношению
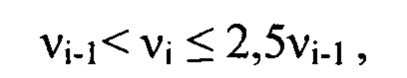
где 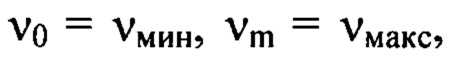 при этом
при этом 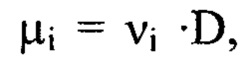 а
а 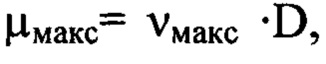 если порядковые номера гармоник
если порядковые номера гармоник 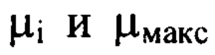 получаются нецелыми числами, то выбирают значение ближайшего меньшего целого числа, расстояние
получаются нецелыми числами, то выбирают значение ближайшего меньшего целого числа, расстояние 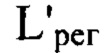 определяют для каждого интервала пространственных частот
определяют для каждого интервала пространственных частот 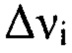 из соотношения
из соотношения
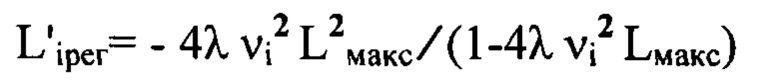
с учетом правила знаков и получают таким образом набор значений 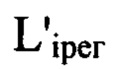 удаления плоскостей
удаления плоскостей 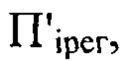 перпендикулярных оси светового пучка в пространстве изображений, от плоскости
перпендикулярных оси светового пучка в пространстве изображений, от плоскости 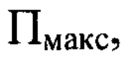 регистрацию распределения интенсивности
регистрацию распределения интенсивности 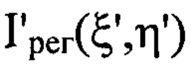 светового пучка осуществляют в координатах
светового пучка осуществляют в координатах 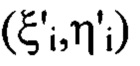 каждой из плоскостей
каждой из плоскостей 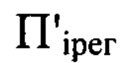 и получают таким образом набор значений
и получают таким образом набор значений 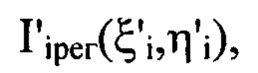 значение
значение 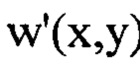 определяют для каждого интервала пространственных частот
определяют для каждого интервала пространственных частот 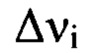 путем численного решения уравнения (1), в котором величины
путем численного решения уравнения (1), в котором величины 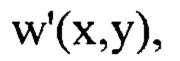
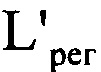 ,
, 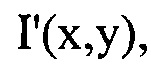
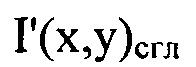 заменяют на
заменяют на 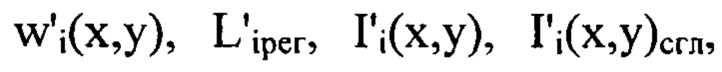 соответственно, считая, что
соответственно, считая, что 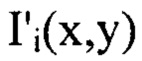 - распределения интенсивностей светового пучка, выраженные в координатах плоскости П, полученные путем замены переменных в распределениях интенсивностей
- распределения интенсивностей светового пучка, выраженные в координатах плоскости П, полученные путем замены переменных в распределениях интенсивностей 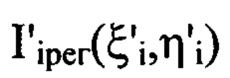 по формулам
по формулам 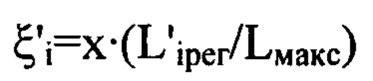 и
и 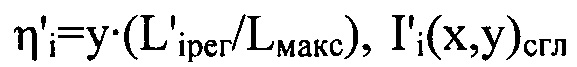 - сглаженные с использованием метода наименьших квадратов распределения интенсивностей светового пучка
- сглаженные с использованием метода наименьших квадратов распределения интенсивностей светового пучка 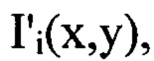 и получают таким образом набор значений
и получают таким образом набор значений 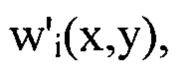 выбирают из
выбирают из 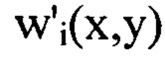 члены ряда Фурье, содержащие гармоники, удовлетворяющие условиям, когда хотя бы один порядковый номер гармоники
члены ряда Фурье, содержащие гармоники, удовлетворяющие условиям, когда хотя бы один порядковый номер гармоники 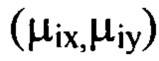 превышает значение
превышает значение 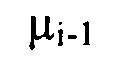 и оба порядковых номера гармоник
и оба порядковых номера гармоник 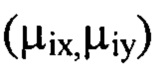 не превышают значение
не превышают значение 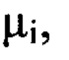 из суммы выбранных членов ряда Фурье составляют компоненту
из суммы выбранных членов ряда Фурье составляют компоненту 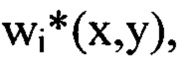 определяющую деформации волнового фронта светового пучка в интервале пространственных частот
определяющую деформации волнового фронта светового пучка в интервале пространственных частот 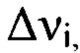 мелкомасштабные деформации волнового фронта
мелкомасштабные деформации волнового фронта 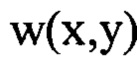 в диапазоне пространственных частот от
в диапазоне пространственных частот от 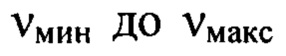 определяют путем суммирования всех найденных компонент
определяют путем суммирования всех найденных компонент 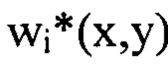
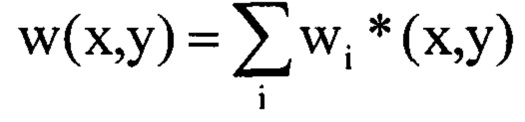 .
.
| СПОСОБ ОПРЕДЕЛЕНИЯ ДЕФОРМАЦИЙ ВОЛНОВОГО ФРОНТА СВЕТОВОГО ПУЧКА, ВЫЗВАННЫХ ВОЛНИСТОСТЬЮ ПОВЕРХНОСТЕЙ ОПТИЧЕСКОЙ СИСТЕМЫ | 2018 |
|
RU2680615C1 |
| СПОСОБ КОМПЕНСАЦИИ ФАЗОВЫХ ИСКАЖЕНИЙ ВОЛНОВОГО ФРОНТА НА ОСНОВЕ СВЕТОВОГО ПОЛЯ | 2022 |
|
RU2808933C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ВОЛНОВЫХ АБЕРРАЦИЙ ОПТИЧЕСКОЙ СИСТЕМЫ | 2020 |
|
RU2753627C1 |
| СПОСОБ АНАЛИЗА ВОЛНОВОГО ФРОНТА СВЕТОВОГО ПОЛЯ | 2010 |
|
RU2430389C1 |
| CN 102865931 B, 04.06.2014 | |||
| US 6496253 B1, 17.12.2002. | |||
Авторы
Даты
2024-11-26—Публикация
2024-05-02—Подача