Изобретение относится к области оптики и может быть использовано для характеристики качества оптических систем или оптических элементов при их изготовлении и эксплуатации.
Реальные оптические системы всегда вносят те или иные искажения в проходящие через них световые пучки. Поэтому точечный предмет может изображаться оптической системой в виде некоторого размытого пятна, прямая линия - в виде кривой и т.д. С точки зрения волновой теории света форма волнового фронта светового пучка в пространстве изображений будет отличаться от формы волнового фронта того же пучка в пространстве предметов, вследствие искажений, вносимых оптической системой. Для характеристики величины искажений волнового фронта используют понятие волновых аберраций, которые определяют отступлениями волновой поверхности в пространстве изображений от идеальной сферической поверхности (поверхности сравнения) [М.М. Русинов. Техническая Оптика, Л.: Изд-во Машиностроение. 1979. - 488 с.].
В настоящее время существуют различные методы измерений волновых аберраций оптических систем, в том числе измерений распределения волновых аберраций w(x, y) по поперечному сечению пучка на выходе оптической системы. Среди них наибольшее распространение получили интерференционные методы, основанные на обработке результатов смешения опорного и искаженного когерентных лазерных пучков, и методы, построенные на анализе искажений некогерентных световых пучков, прошедших оптическую систему. Последние методы при этом выгодно отличаются гораздо меньшей чувствительностью к влиянию помех на точность и надежность получаемых результатов. К таким помехам относятся вибрации, атмосферная турбулентность, зернистость изображений (спекл-структура), присущая лазерным пучкам.
Известен способ измерения волновых аберраций оптических систем - метод Гартмана, изложенный в работе [Э.А. Витриченко. Методы исследования астрономической оптики. М.: Изд-во Наука. 1980. - 152 с.]. Суть способа заключается в разбиении растром из отверстий в непрозрачном экране направляемого в оптическую систему пучка некогерентного света с плоским или сферическим волновым фронтом на множество отдельных пучков, регистрации следов этих суб-пучков в плоскости в пространстве изображений, определении отступлений волнового фронта прошедшего систему излучения от идеальной формы, т.е. волновых аберраций системы. Прошедший оптическую систему и определенное расстояние в пространстве изображений массив суб-пучков регистрируют фотоприемным устройством. При отсутствии волновых аберраций оптической системы центры изображений суб-пучков должны воспроизвести сетку, отвечающую конфигурации растра. В этой ситуации считают, что каждый из центров изображений суб-пучков находится в «нулевой» позиции. При наличии волновых аберраций каждый из центров изображений суб-пучков будет смещен относительно «нулевой» позиции пропорционально усредненному наклону волнового фронта соответствующего суб-пучка. Согласно способу, определяют координаты центров суб-пучков и величину уклонения каждого из центров от «нулевого» положения. Полученные данные подвергают математической обработке по тому или иному алгоритму с целью реконструкции отступлений поверхности волнового фронта w(x, y) от идеальной формы поверхности (поверхности сравнения) по апертуре оптической системы.
К причинам, препятствующим достижению указанного ниже результата при использовании известного способа, относятся следующие.
Получаемые в способе данные о волновой поверхности излучения на выходе оптической системы носят выборочный характер. Выборочность получаемых данных согласно теореме Котельникова-Шеннона не позволяет восстанавливать деформации волновой поверхности с поперечным размером меньшим двух интервалов между элементами растра. В то же время, расстояние между элементами (или шаг) растра не может быть меньше диаметра суб-пучка, а диаметр суб-пучка, в свою очередь, не может быть выбран произвольно малым вследствие дифракционного расплывания изображения суб-пучка в плоскости регистрации. Отсюда возникают ограничения на точность и достоверность результатов определения волновых аберраций. Также измерения координат центров изображений суб-пучков существенно зависят от соотношения яркость/фон (точнее, сигнал/шум, где шум включает в себя и постороннюю фоновую засветку, и собственные шумы фотоприемного устройства) в изображении суб-пучков. В методе Гартмана лишь малая доля источника излучения через отверстия в экране попадает в оптическую систему, что многократно снижает яркость получаемых изображений. Возникающие вследствие этого ошибки измерений, также как и погрешности центровки элементов оптической схемы, снижают точность определения волновых аберраций. Кроме того, возникает усложнение, вызванное тем, что требуемый для измерений шаг растра зависит от аберрационных свойств оптической системы, т.е. растр необходимо изготавливать, предварительно оценив характер аберраций оптической системы, что не всегда можно реализовать, особенно при отсутствии предварительных сведений о схемных решениях оптической системы.
Наиболее близким способом того же назначения к заявленному изобретению по совокупности признаков является способ определения волновых аберраций оптической системы, изложенный в [Claude Roddier,  Roddier, J. Optical Society of America / 1993, Vol. 10, No. 11, pp. 2277-2287.], принятый за прототип. Способ включает направление некогерентного светового пучка с плоским волновым фронтом на оптическую систему, измерение распределений интенсивности светового пучка в двух плоскостях, перпендикулярных направлению распространения светового пучка в пространстве изображений. Расположение плоскостей выбирают перед и за фокальной плоскостью оптической системы на одном и том же расстоянии от последней. Положение фокальной плоскости на оптической оси системы задают, исходя из заранее известных расчетных характеристик оптической системы или на основе паспортных данных системы, полученных от изготовителя. Определяют в виде дифференциального уравнения математическое соотношение, связывающее волновые аберрации светового пучка в плоскости, проходящей через центр зрачка оптической системы (главного зеркала телескопа) перпендикулярной распространению светового пучка, с измеренными распределениями интенсивности в двух упомянутых плоскостях. Путем решения численным методом полученного уравнения при граничных условиях Неймана производят первичную оценку волновых аберраций светового пучка и затем методом многократных итераций осуществляют их уточнение. Полученные в численном виде значения волновых аберраций аппроксимируют функцией, представленной суммой полиномов Цернике, которую определяют методом наименьших квадратов. Отдельные составляющие аберраций оптической системы определяют как коэффициенты при полиномах Цернике.
Roddier, J. Optical Society of America / 1993, Vol. 10, No. 11, pp. 2277-2287.], принятый за прототип. Способ включает направление некогерентного светового пучка с плоским волновым фронтом на оптическую систему, измерение распределений интенсивности светового пучка в двух плоскостях, перпендикулярных направлению распространения светового пучка в пространстве изображений. Расположение плоскостей выбирают перед и за фокальной плоскостью оптической системы на одном и том же расстоянии от последней. Положение фокальной плоскости на оптической оси системы задают, исходя из заранее известных расчетных характеристик оптической системы или на основе паспортных данных системы, полученных от изготовителя. Определяют в виде дифференциального уравнения математическое соотношение, связывающее волновые аберрации светового пучка в плоскости, проходящей через центр зрачка оптической системы (главного зеркала телескопа) перпендикулярной распространению светового пучка, с измеренными распределениями интенсивности в двух упомянутых плоскостях. Путем решения численным методом полученного уравнения при граничных условиях Неймана производят первичную оценку волновых аберраций светового пучка и затем методом многократных итераций осуществляют их уточнение. Полученные в численном виде значения волновых аберраций аппроксимируют функцией, представленной суммой полиномов Цернике, которую определяют методом наименьших квадратов. Отдельные составляющие аберраций оптической системы определяют как коэффициенты при полиномах Цернике.
К причинам, препятствующим достижению указанного ниже результата при использовании известного способа, принятого за прототип, относятся следующие.
Необходимая для решения используемого в способе-прототипе уравнения информация, позволяющая определить волновые аберрации w(x, y), содержится в так называемой сигнальной части уравнения (по терминологии авторов способа-прототипа), представляющей собой отношение, содержащее в числителе разность поэлементно вычтенных распределений интенсивности в изображениях поперечного сечения пучка, а в знаменателе сумму поэлементно сложенных тех же распределений, экспериментально зарегистрированных в двух плоскостях, при этом одно из распределений должно быть предварительно инвертировано по поперечным координатам. Для точного выполнения математического соотношения необходимо соблюсти условие, чтобы каждый элемент одного изображения и соответствующий ему элемент другого изображения отвечали также соответственно одной и той же точке поперечного сечения светового пучка, в которой определяется w(x, y). В то же время, если эти изображения поперечных сечений пучка не идентичны по размеру, форме или положению в кадре, то теряется требуемое соответствие элементов двух изображений одной и той точке (x, y) поперечного сечения пучка, в плоскости, в которой определяют волновые аберрации. Другими словами, оказывается невозможным осуществить точное наложение одного изображения на другое и, как следствие, при выполнении операций сложения или вычитания в результирующем цифровом изображении будут наблюдаться порожденные этим обстоятельством искажения.
Возможные экспериментальные различия настроек используемых для измерения распределений интенсивностей фотоприемников, а также неточности взаимной центрировки изображений, также вносят вклад в искажения результирующего изображения, который при таком виде сигнальной части уравнения может быть значительным. При отсутствии сведений о схемном решении оптической системы невозможно точное задание фокальной плоскости оптической системы, от которой ведут отсчет расстояний до плоскостей регистрации распределений интенсивности.
Указанные факторы заметно усложняют применяемые процедуры обработки изображений и ограничивают точность вычисления волновых аберраций.
Для устранения искажений и повышения точности вычислений авторы прототипа применяют дополнительные трудоемкие процедуры математической обработки изображений с целью их исправления. Для этого из анализа первично полученных изображений поперечных сечений пучка оценивают волновые аберрации, вычисляют вносимые ими геометрические искажения и корректируют изображения. На основе откорректированных первичных экспериментальных данных авторы определяют сигнальную часть уравнения и находят его решение. Это решение авторы способа-прототипа рассматривают лишь в качестве первого приближения к окончательному результату, поскольку его точность оказывается неудовлетворительной. На следующих этапах, также с использованием последовательно вносимых поправок в первично зарегистрированные распределения интенсивностей, заново, раз за разом, решают уравнение и вычисляют компоненты волновых аберраций. Понятно, что с увеличением искажений, вносимых оптической системой, число итерационных процедур, требуемых для вычисления волновой аберрации будет нарастать.
По сведениям авторов способа-прототипа при измерении и обработке распределений интенсивности реальных изображений светового пучка в астрономическом телескопе им удалось достичь относительной точности вычисления волновых аберраций на уровне 10% при абсолютном значении погрешности определения волновой аберрации типа комы 50 нм, что отвечает величине ~ λ/15 для λ=0.7 мкм. При этом, по факту, выполнялось порядка семи итераций.
Еще одной причиной, препятствующей достижению указанного ниже технического результата, является использование авторами способа-прототипа математического выражения, полученного в простейшем приближении из так называемого транспортного уравнения для плоских световых волн путем замены в нем производной от интенсивности по продольной координате на конечную разность интенсивностей, отнесенную к введенной авторами эффективной дистанции распространения светового пучка в пространстве за оптической системой, вносящей искажения в пучок. Такая замена, как известно, справедлива лишь при небольших значениях приращений переменных. Из этого следует, что измерения нужно проводить в условиях небольших изменений интенсивности, обусловленных аберрациями, что уменьшает точность измерений и существенно повышает требования к условиям проведения эксперимента в части подавления световых помех и учета шумов ПЗС-матрицы.
Сущность изобретения заключается в следующем.
Задачей изобретения является определение волновых аберраций оптической системы с высокой точностью, упрощением требований к реализации операций способа, меньшей трудоемкостью и сложностью обработки результатов измерений.
Технический результат, который может быть достигнут при осуществлении заявленного способа, заключается в определении волновых аберраций оптической системы с высокой точностью, упрощении требований к реализации операций способа, уменьшении трудоемкости и сложности обработки результатов измерений. Способ применим к определению аберраций оптических систем при отсутствии предварительных сведений об их схемном решении.
Указанный технический результат при осуществлении изобретения достигается тем, что в способе определения волновых аберраций оптической системы, включающем направление некогерентного гомоцентрического светового пучка с длиной волны λ на оптическую систему, измерение распределений интенсивности светового пучка в плоскостях, перпендикулярных оси светового пучка, прошедшего оптическую систему и сфокусированного в пространстве изображений, получение математического выражения для определения волновых аберраций, определение волновых аберраций оптической системы путем решения численным методом полученного математического выражения, в соответствии с заявляемым техническим решением определяют положение плоскости Пмакс, перпендикулярной оси светового пучка в пространстве изображений, в которой пиковая интенсивность светового пучка в распределении интенсивности светового пучка имеет максимальное значение Iмакс среди экспериментально зарегистрированных пиковых интенсивностей в распределениях интенсивностей светового пучка в плоскостях, перпендикулярных оси светового пучка, определяют контур изофоты в распределении интенсивности светового пучка в плоскости Пмакс по уровню 0,2⋅Iмакс и расстояние ρ максимального удаления точки Омакс с пиковой интенсивностью Iмакс от контура изофоты, измеряют расстояние Lмакс по оси пучка от плоскости Пмакс до плоскости П, перпендикулярной оси светового пучка и соприкасающейся с последней поверхностью оптической системы, с учетом правила знаков, измеряют распределение интенсивности Iрег(ξ, η) светового пучка в координатах (ξ, η) плоскости Прег, перпендикулярной оси светового пучка в пространстве изображений, которую выбирают так, что выполняется условие |Lрег|=16⋅ρ2/λ, где Lрег - расстояние по оси пучка от плоскости Пмакс до плоскости Прег с учетом правила знаков, при этом начало координат в плоскостях П, Прег, Пмакс лежит на оси светового пучка, математическое выражение для определения волновых аберраций представляют в виде уравнения, связывающего волновые аберрации w(x, y) в координатах (x, y) плоскости П, с распределением интенсивности светового пучка в плоскости Прег:
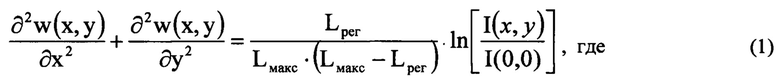
- I(x, y) - распределение интенсивности светового пучка, выраженное в координатах плоскости П, полученное путем замены переменных в распределении интенсивности Iрег(ξ, η) по формулам ξ=x⋅(Lрег/Lмакс) и η=y⋅(Lрег/Lмакс);
- I(0, 0) - значение функции I(x, y) на оси пучка;
значения w(x, y) находят путем численного решения уравнения (1) вариационным методом при свободных граничных условиях, аппроксимируя w(x, y) степенным полиномом, удовлетворяющим условию w(0, 0)=0 на оси пучка.
Совокупность вышеизложенных признаков изобретения связана причинно-следственной связью с техническим результатом изобретения.
Как уже отмечалось, гомоцентрический в пространстве предметов пучок после прохождения оптической системы приобретает в ней искажения, нарушающие сферичность его волнового фронта, т.е. волновые аберрации. Эти приобретенные волновые аберрации по мере распространения пучка в пространстве изображений трансформируются в искажения распределения интенсивности по поперечному сечению пучка. С использованием волнового уравнения, описывающего распространение сфокусированного светового пучка в приближении геометрической оптики, нами было получено уравнение (1), связывающее волновые аберрации w(x, y) искаженного пучка в плоскости П, соприкасающейся с последней поверхностью оптической системы, с распределением интенсивности светового пучка в плоскости, перпендикулярной оси светового пучка в пространстве изображений, Прег, положение которой выбирают определенным образом.
Выбор положения плоскости Прег в пространстве изображений существенно влияет на точность решения поставленной задачи. Чем дальше от плоскости П плоскость Прег, в которой осуществляются измерения распределения интенсивности искаженного светового пучка, тем сильнее выражены неоднородности распределения интенсивности, и тем точнее их можно измерить на фоне шумов. В то же время по мере удаления светового пучка от оптической системы в проявлениях неоднородностей распределения интенсивности в поперечном сечении пучка начинает сказываться волновая природа светового поля из-за нарушений условий геометрооптического приближения. Вследствие этого на волновой поверхности пучка на выходе оптической системы каждому лучу следует адресовать не просто точку исхода, а некоторый окружающий точку участок волновой поверхности, так называемую зону Френеля, размер которой растет по мере удаления от оптической системы. Геометрооптическое приближение остается справедливым, если зоны Френеля лучей, входящих в световой пучок, не перекрываются на поверхности волнового фронта [Ю.А. Кравцов, Ю.И. Орлов. Успехи физических наук, т. 132, №3, с. 475-496.]. Введем пространственную частоту γ распределения точек исхода лучей, определяющих положение центров зон Френеля. Тогда величина 2γ в соответствии с теоремой Котельникова-Шеннона (теоремой отсчетов) будет определять высокочастотную границу пространственного спектра деформаций волновой поверхности, которые могут быть восстановлены без искажений по выборке точек на волновой поверхности.
Нами было показано, что при облучении оптической системы гомоцентрическим пучком значение частоты 2γ, характеризующей верхнюю границу спектра пространственных частот деформаций волновой поверхности пучка, прошедшего оптическую систему, можно оценить по величине введенного нами параметра ρ. Для определения этого параметра устанавливают положение плоскости Пмакс, перпендикулярной оси светового пучка в пространстве изображений, в которой пиковое значение интенсивности в распределении интенсивности светового пучка достигает максимального значения Iмакс среди экспериментально зарегистрированных пиковых интенсивностей в распределениях интенсивностей светового пучка в плоскостях, перпендикулярных оси светового пучка. Далее определяют контур изофоты в распределении интенсивности светового пучка в плоскости Пмакс по уровню 0,2⋅Iмакс. Под изофотой мы подразумеваем кривую, соединяющую точки равной интенсивности в распределении интенсивности светового пучка. Расстояние максимального удаления точки Омакс в плоскости Пмакс с пиковой интенсивностью Iмакс от изофоты определяет параметр ρ, связанный, как нами было установлено, с 2γ следующим соотношением 2γ=2ρ/(λ⋅|Lмакс|), где Lмакс - расстояние по оси пучка от плоскости Пмакс до плоскости П, перпендикулярной оси светового пучка и соприкасающейся с последней поверхностью оптической системы, с учетом правила знаков.
Далее было получено соотношение для определения положения плоскости Прег. В соответствии с введенным нами условием плоскость Прег должна отстоять от плоскости Пмакс на расстояние |Lрег|=16⋅ρ2/λ, либо по ходу пучка, либо в обратном направлении. Соотношение получено нами при условии |Lмакс|>>|Lрег|, как правило выполняемом на практике.
Измерение расстояний Lмакс и Lрег от плоскости Пмакс до плоскостей П и Прег, соответственно, осуществляют, используя систему отсчета, задаваемую системой координат в плоскости Пмакс, в которой начало координат лежит на оси светового пучка, а положительное направление оси аппликат совпадает с направлением распространения светового пучка.
Мы соотносим точку пересечения оси светового пучка и плоскости Пмакс в пространстве изображений с центром кривизны сферы сравнения на оси светового пучка. Относительно этой сферы сравнения и вычисляются волновые аберрации. При указанном в заявляемом техническом решении выборе положения плоскостей Пмакс и Прег волновые аберрации, т.е. отступления волновой поверхности пучка от сферы сравнения, будут минимизированы на максимально возможной (или близкой к этому) части поперечного сечения пучка в плоскости П.
Определив положение плоскости Прег, регистрируют распределение интенсивности Iрег(ξ, η) светового пучка в координатах (ξ, η) плоскости Прег. Начало координат в плоскостях П и Прег лежит на оси светового пучка. Выбор положения плоскости Прег от плоскости Пмакс либо по ходу пучка, либо в обратном направлении при условии |Lмакс|>>|Lрег| равнозначен и зависит лишь от конструктивных особенностей конкретных схем измерения распределения интенсивности светового пучка.
Как указывалось выше, нами было получено уравнение (1), связывающее волновые аберрации w(x, y) искаженного пучка в координатах (x, y) плоскости П с распределением интенсивности светового пучка в плоскости Прег. Вычисление волновых аберраций w(x, y) осуществляют вариационным методом, основанном на поиске минимума функционала, отвечающего уравнению вида (1). Варианты этого метода (метод Галеркина или метод Ритца) позволяют найти с высокой точностью устойчивые решения уравнений такого типа [Л.В. Канторович, В.И. Крылов. Приближенные методы высшего анализа. М. - Л.: Гос. Изд-во физ.-мат. лит. 1962. - 708 с.].
Согласно этому методу решение ищут в виде суммы функций 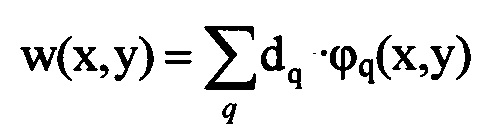 с неопределенными коэффициентами dq, численные значения которых, дающие решение, определяются из условия минимума функционала. Находят минимум при свободных граничных условиях [Л.В. Канторович, В.И. Крылов. Приближенные методы высшего анализа. М.-Л.: Гос. Изд-во физ.-мат. лит. 1962. - 708 с.], но при заданных значениях w(0, 0)=0 на оси пучка. Последнее условие необходимо выполнить, чтобы получить решение, удовлетворяющее принятым в оптике условиям отсчета волновых аберраций от сферы сравнения, при которых в точке поверхности, лежащей на оси пучка, аберрации равны нулю.
с неопределенными коэффициентами dq, численные значения которых, дающие решение, определяются из условия минимума функционала. Находят минимум при свободных граничных условиях [Л.В. Канторович, В.И. Крылов. Приближенные методы высшего анализа. М.-Л.: Гос. Изд-во физ.-мат. лит. 1962. - 708 с.], но при заданных значениях w(0, 0)=0 на оси пучка. Последнее условие необходимо выполнить, чтобы получить решение, удовлетворяющее принятым в оптике условиям отсчета волновых аберраций от сферы сравнения, при которых в точке поверхности, лежащей на оси пучка, аберрации равны нулю.
Составляющие сумму w(x, y) функции ϕq(x, y) выбирают в виде степенных полиномов. Каждая из функций ϕq(x, y) отвечает определенному типу волновых аберраций и удовлетворяет условию ϕq(0, 0)=0. Например, волновым аберрациям типа комы будут отвечать функции вида ϕ31(x, y)=x⋅(x2+y2) и ϕ32(x, y)=y⋅(x2+y2), а сферическим аберрациям - функции вида ϕ4(x, y)=(x2+y2)2, ϕ6(x, y)=(x2+y2)4 и т.д.
Значения аберрационных коэффициентов dq являются решением системы линейных уравнений [Л.В. Канторович, В.И. Крылов. Приближенные методы высшего анализа. М.-Л.: Гос. Изд-во физ.-мат. лит. 1962. - 708 с.]:

где коэффициенты αq,m вычисляют по формуле:
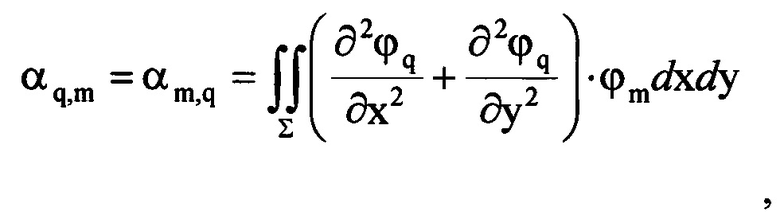
коэффициенты βm вычисляют по формуле:
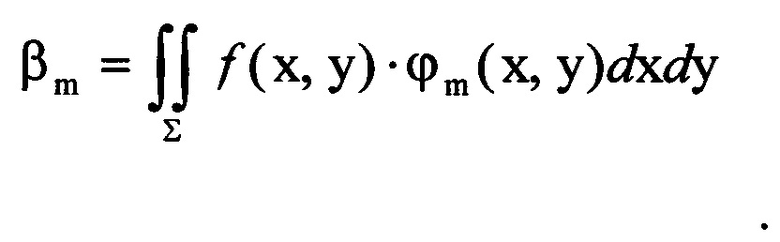
Здесь ƒ(x, y) - это правая часть уравнения (1), т.е. 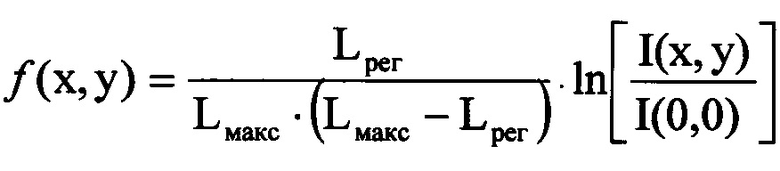 , область интегрирования Σ - есть поперечное сечение пучка за исключением узкой краевой зоны поперечного сечения, где распределение интенсивности возмущено дифракцией пучка на апертурной диафрагме оптической системы.
, область интегрирования Σ - есть поперечное сечение пучка за исключением узкой краевой зоны поперечного сечения, где распределение интенсивности возмущено дифракцией пучка на апертурной диафрагме оптической системы.
Как видно, заявляемый способ достаточно прост в реализации. Подходы к определению требуемых для выполнения способа параметров Iмакс и ρ известны и могут быть реализованы с применением как цифровых ПЗС-камер, так и аналоговых фотоприемников на основе светочувствительных материалов с последующим фотометрированием зарегистрированных распределений интенсивности пучка.
Для реализации способа световой пучок, прошедший оптическую систему, должен быть сфокусирован в пространстве изображений. Если оптическая система не фокусирует сама световой пучок в пространстве изображений, осуществляют его фокусировку с помощью безаберрационных оптических элементов. Подходы к решению этой задачи известны [Э.А. Витриченко. Методы исследования астрономической оптики. М.: Изд-во Наука. 1980. - 152 с.]. Уточним здесь также, что понятие прохождения светового пучка через оптическую систему подразумевает как случаи непосредственного прохождения пучка через оптическую систему, так и случаи отражения светового пучка от нее.
Уравнение (1) для определения волновых аберраций оптической системы включает минимальное число параметров, измеряемых экспериментально. Из процедуры обработки данных исключены трудоемкие, многократно повторяемые операции исправления и подгонки двух изображений сечений пучка, требуемых при реализации способа-прототипа. Используемое для расчетов в заявляемом способе уравнение (1) в правой части содержит логарифм от нормированных значений зарегистрированного распределения интенсивности в плоскости Прег, а не приближенное значение производной от интенсивности по продольной координате, как в способе-прототипе. В результате снимаются ограничения на проведение измерений в условиях небольших превышений изменения интенсивности по отношению к шумам матрицы и световым помехам. Допустимые изменения интенсивности, обусловленные аберрациями, могут быть достаточно велики, их уровень может достигать нескольких десятков процентов (вплоть до 40-50%) от уровня интенсивности на оси пучка, что было подтверждено результатами математического моделирования.
Способ применим к оптическим системам, о схемных решениях которых нет предварительных сведений. При реализации операций способа нет необходимости знания номинального фокусного расстояния оптической системы, точного положения точки фокуса на оптической оси, положения входного или выходного зрачков системы.
Совокупное действие всех признаков изобретения позволяет определить волновые аберрации оптических систем с высокой точностью при существенном упрощении требований к реализации операций способа, меньшей трудоемкости и сложности обработки результатов измерений.
В результате применения способа волновые аберрации определяют в виде распределения значений волновых аберраций w(x, y) в координатах (x, y) поперечного сечения светового пучка. Исходя из этого, полученные результаты могут быть представлены различным образом. В числовом виде значения w(x, y) образуют трехмерный массив числовых данных, который позволяет производить расчетную оценку качества изображения, создаваемого оптической системой. На основе этого массива также можно создать несколько вариантов графического представления полученных значений w(x, y). К наиболее наглядным относятся распределения волновых аберраций вдоль диаметров поперечного сечения светового пучка на выходе оптической системы (плоскость П), ориентированных вдоль координатных осей. Можно также представить волновые аберрации в виде объемного графика или в виде системы изолиний с заданным шагом между уровнями отступлений волновой поверхности от сферы сравнения. Численное решение используемого в предложенном способе уравнения позволяет представлять значения w(x, y) в виде суммы составляющих функций ϕq(x, y) с определенными аберрационными коэффициентами dq. Каждая из составляющих функций ϕq(x, y) отвечает определенному типу волновых аберраций, характеризующих качество оптической системы, а величины аберрационных коэффициентов позволяют оценить вклад отдельных видов волновых аберраций (комы, сферической аберрации) в общую сумму.
На фиг. 1 приведена оптическая схема установки для измерения волновых аберраций линзового объектива, где 1 - некогерентный источник света (лампа накаливания); 2 - конденсор; 3 - узкополосный светофильтр; 4 - микродиафрагма; 5 - линзовый объектив; 6 - ПЗС-матрица, регистрирующая распределение интенсивности в поперечном сечении светового пучка. Плоскость П - плоскость, в системе координат которой определяют волновые аберрации, перпендикулярна оси светового пучка и соприкасается с последней поверхностью линзового объектива 5, плоскость Прег - плоскость, в которой регистрируют распределение интенсивности Iрег(ξ, η), плоскость Пмакс - плоскость, в которой пиковая интенсивность светового пучка достигает максимального значения Iмакс среди экспериментально зарегистрированных пиковых интенсивностей в распределениях интенсивностей светового пучка в плоскостях, перпендикулярных оси светового пучка, Омакс - точка пиковой интенсивности Iмакс в плоскости Пмакс. Плоскости Прег и Пмакс перпендикулярны оси светового пучка, Lрег и Lмакс - расстояния от плоскости Пмакс до плоскостей Прег и П, соответственно, по оси пучка с учетом правила знаков. Начало координат в плоскостях П, Прег и Пмакс лежит на оси светового пучка.
На фиг. 2. представлено распределение интенсивности светового пучка в плоскости Пмакс, ограниченное изофотой интенсивности по уровню 0,2⋅Iмакс (сплошная линия), а также показано расстояние ρ максимального удаления точки Омакс пиковой интенсивности Iмакс от этой границы. Штриховой линией показана изофота на уровне 0,4⋅Iмакс, штрих-пунктирной - на уровне 0,8⋅Iмакс.
На фиг. 3А и 3Б штриховой линией показаны графики распределения интенсивности I(x, y) по поперечному сечению пучка в относительных единицах, приведенного к координатам в плоскости П из распределения интенсивности Iрег(ξ, η), зарегистрированного в плоскости Прег: на фиг. 3А - вдоль горизонтального диаметра изображения пучка - по оси ОХ, на фиг. 3Б - вдоль вертикального диаметра - по оси OY.
На фиг. 3А и 3Б сплошной линией показаны графики распределения интенсивности I(x, y)расч, полученные в результате математического моделирования, при котором распределение I(x, y)расч рассчитывалось с использованием уравнения (1), исходя из экспериментально найденных графиков распределения значений волновых аберраций, представленных на фиг. 4А и 4Б, соответственно. Рассчитанные распределения не включают краевую зону изображения пучка, несколько искаженную дифракционными явлениями и исключенную из расчетов.
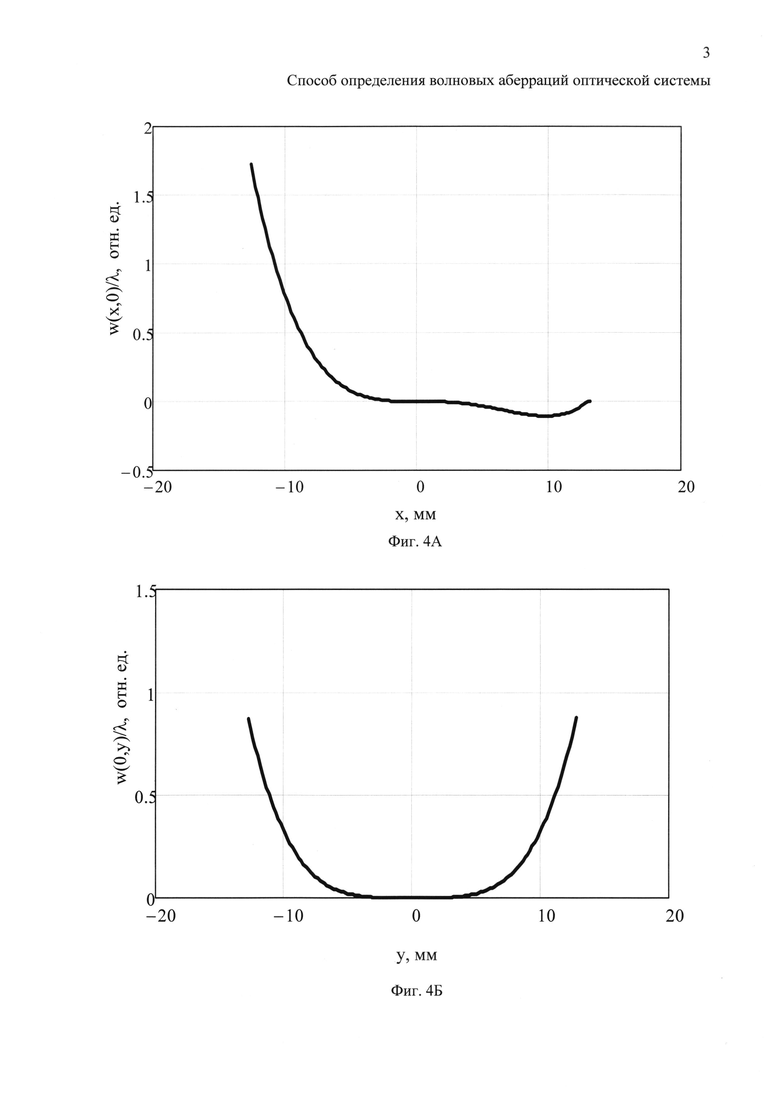
На фиг. 4А и 4Б приведены графики зависимости от координат в плоскости П экспериментально найденных волновых аберраций линзового объектива, нормированных на длину волны светового пучка. На фиг. 4А представлено распределение волновых аберраций вдоль горизонтального диаметра - по оси ОХ, на фиг. 4Б - вдоль вертикального диаметра изображения - по оси OY.
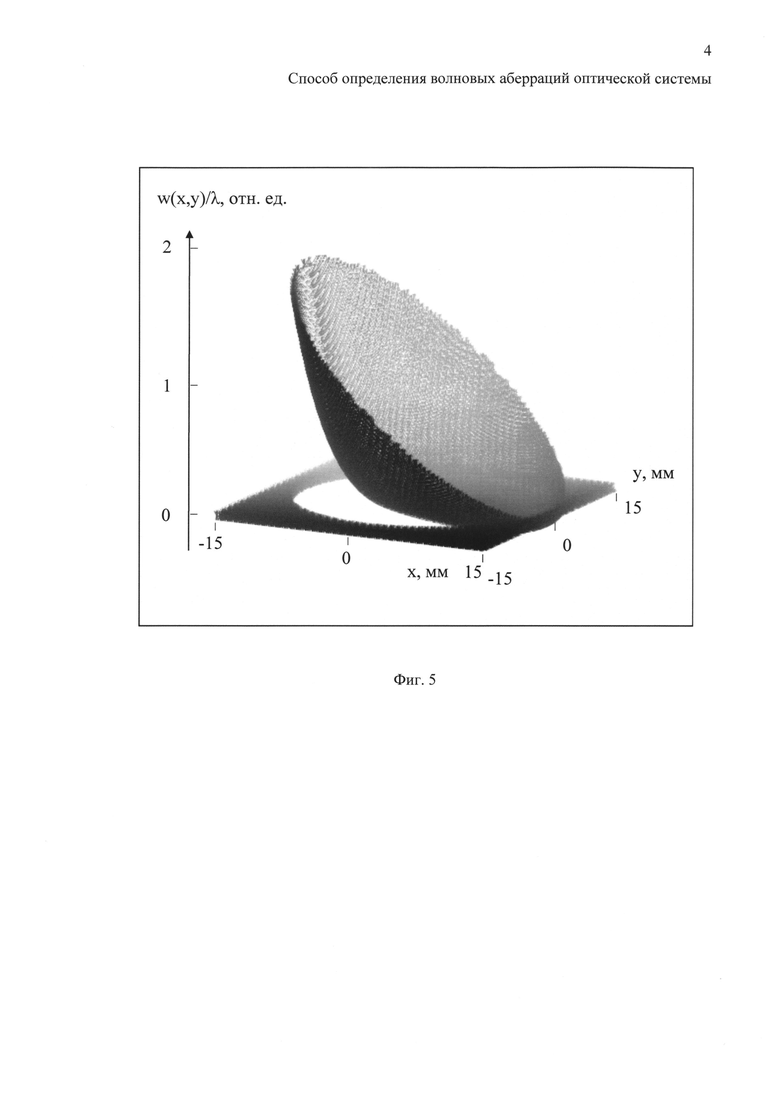
На фиг. 5 показаны в виде трехмерного распределения нормированные на длину волны светового пучка волновые аберрации w(x, y)/λ, оптической системы в системе координат плоскости П, полученные в результате применения способа.
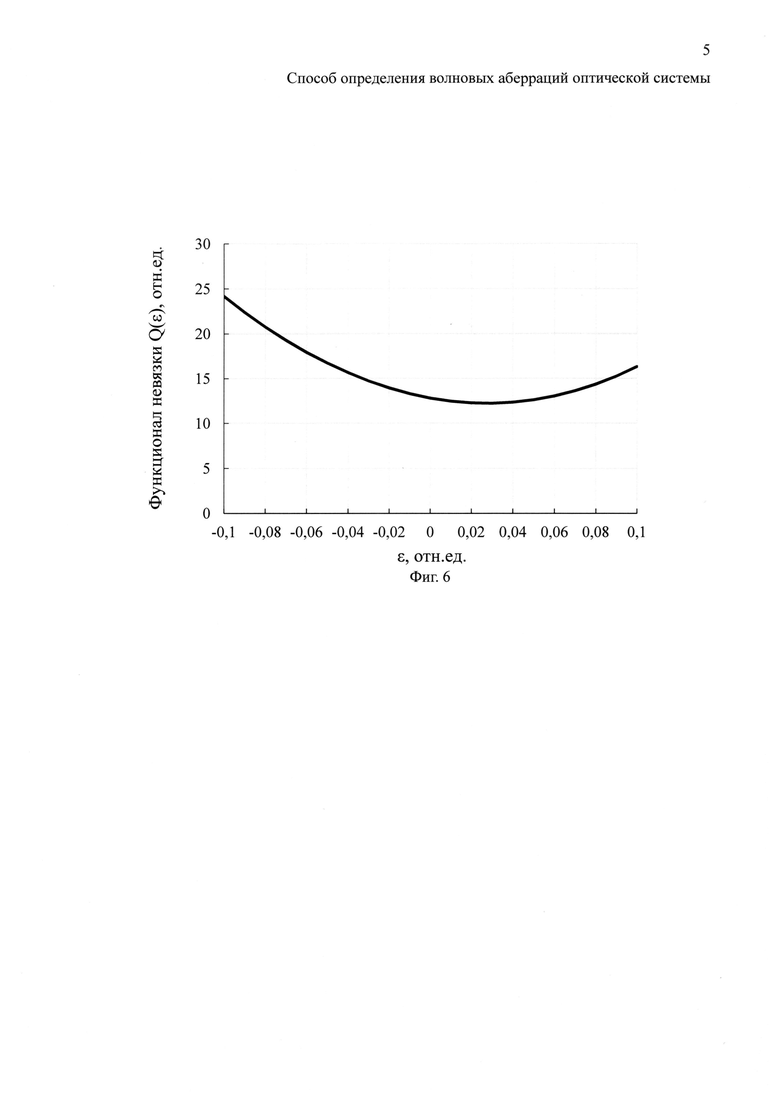
На фиг. 6 показана зависимость величины функционала невязки Q(ε) от величины ε, где ε - относительная величина отклонения распределения волновых аберраций δw(x, y) от распределения w(x, y), полученного в результате применения способа.
Заявленный способ был экспериментально осуществлен для измерения волновых аберраций многокомпонентного фотографического линзового объектива. Для этого была создана экспериментальная установка.
Пример конкретного выполнения способа.
Излучение от лампы накаливания 1 проецируется конденсором 2 на отверстие микродифрагмы 4 диаметром 25 мкм через узкополосный светофильтр 3 с максимумом пропускания на длине волны 0,6 мкм (фиг. 1). За отверстием микродиафрагмы, имитирующей точечный источник излучения, формируется сферический пучок с однородным распределением интенсивности, который можно считать гомоцентрическим. Микродиафрагма 4 была установлена на расстоянии 790 мм от первой оптической поверхности объектива 5 со смещением в горизонтальном направлении на 20 мм относительно центра поля зрения объектива. Выбор такой геометрии эксперимента был продиктован необходимостью внести искажения в пучок типа комы и сферической аберрации с целью демонстрации предложенного способа определения аберраций.
ПЗС-матрицу 6 автоколлимационным методом выставляют ортогонально оси светового пучка, прошедшего объектив 5. Затем определяют местоположение плоскости Пмакс на оси пучка путем перемещения ПЗС-матрицы вдоль каустики светового пучка, сравнения пиковых значений интенсивности в разных позициях по ходу пучка при помощи стандартных программных средств из комплекта технического обеспечения цифровой ПЗС-матрицы и фиксации положения ПЗС-матрицы, в котором пиковая интенсивность излучения имеет максимальное значение Iмакс. В найденном положении, т.е. в плоскости Пмакс, ПЗС-матрицу, в случае необходимости, дополнительно центрируют относительно оси пучка и регистрируют распределение интенсивности в поперечном сечении пучка. Программными средствами из комплекта технического обеспечения ПЗС-матрицы определяют контур изофоты на уровне сигнала 0,2 от пикового значения Iмакс и находят расстояние ρ максимального удаления точки Омакс пиковой интенсивности Iмакс от этой границы, как показано на Фиг. 2. Зная параметр ρ и учитывая ограничение |Lрег|=16⋅ρ2/λ, определяют расстояние Lрег от плоскости Пмакс по ходу пучка или в обратном направлении, нами было выбрано направление по ходу пучка. В нашем эксперименте ρ=23 мкм, Lрег=15 мм. Определив положение плоскости Прег, устанавливают в этом положении ПЗС-матрицу для регистрации распределения интенсивности Iрег(ξ, η) светового пучка. Используя систему отсчета, задаваемую системой координат в плоскости Пмакс, в которой начало координат лежит на оси светового пучка, а положительное направление оси аппликат совпадает с направлением распространения светового пучка, измеряют расстояние Lмакс от плоскости Пмакс до плоскости П, перпендикулярной оси светового пучка и соприкасающейся с последней поверхностью объектива 5. В нашем эксперименте Lмакс=-320 мм. Уточним здесь, что, согласно правилу знаков, принятому в оптике, расстояние между плоскостями Пмакс и П, Пмакс и Прег считают положительным, если отсчет ведется от плоскости Пмакс по ходу пучка, и отрицательным при отсчете в обратном направлении.
Преобразуют распределение интенсивности Iрег(ξ, η), зарегистрированное в плоскости Прег, в распределение I(x, y) в координатах плоскости П путем замены координат в распределении Iрег(ξ, η) по формулам ξ=x⋅(Lрег/Lмакс) и η=y⋅(Lрег/Lмакс).
На фиг. 3А и 3Б штриховой линией показаны графики распределения интенсивности I(x, y) по поперечному сечению пучка в относительных единицах, приведенного к координатам в плоскости П: на фиг. 3А - вдоль горизонтального диаметра изображения пучка - по оси ОХ, на фиг. 3Б - вдоль вертикального диаметра - по оси OY.
Для вычисления волновых аберраций были выбраны базовые степенные функции 3-й, 4-й и 6-степеней, которые, с учетом дискретного характера экспериментальных данных и замены координат (x, y) на дискретные переменные по формулам хk=k⋅h, yn=n⋅h, имеют вид:
ϕ3(xk, yn)=ϕ3(k⋅h, n⋅h)=h3⋅(k-k0)⋅[(k-k0)2+[(n-n0)2] - нечетная функция от координаты xk описывает кому 3-го порядка,
ϕ4(xk, yn)=ϕ4(k⋅n, n⋅h)=h4⋅[(k-k0)2+[(n-n0)2]2 и ϕ6(хk, yk)=ϕ6(k⋅h, n⋅h)=h6⋅[(k-k0)2+[(n-n0)2]4 - четные функции от координат xk и yn описывают сферическую аберрацию 3-го и 5-го порядков.
Здесь h=h1⋅(|Lмакс|/|Lрег|) - шаг координатной сетки в плоскости П;
h1 - размер пиксела ПЗС-матрицы;
k=0, … K и n=0, … N - индексы нумерации пикселей ПЗС-матрицы;
k0 и n0 - индексы оси пучка (или центра поперечного сечения пучка) в кадре.
Используя эти функции и выраженное в дискретных координатах распределение интенсивности по сечению пучка Iрег(xk, yn), находят коэффициенты αq,m и βm системы уравнений (2), заменяя операцию интегрирования суммированием по индексам пикселей ПЗС-матрицы. Решая систему уравнений (2) стандартными методами, вычисляют искомые аберрационные коэффициенты dq. Вычисленные таким путем по экспериментальным данным значения аберрационных коэффициентов составили: d3=-2.57⋅10-7 мм-2, d4=-1.5⋅10-8 мм-3, d6=2.6⋅10-12 мм-5.
Полученное аналитическое выражение для найденных волновых аберраций в дискретных координатах w(xKk,yn) имеет следующий вид:
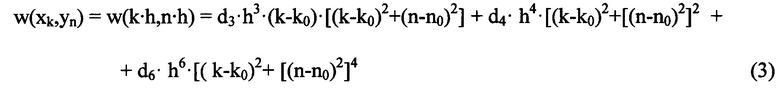
Поскольку на длине шага координатной сетки изменения величины волновой аберрации очень малы, то можно пренебречь дискретностью координат и при анализе рассматривать полученные распределения как непрерывные функции координат x и y.
На фиг. 4А и 4Б приведены графики зависимости от координат в плоскости П экспериментально найденных волновых аберраций линзового объектива w(x, y)/λ, нормированных на длину волны, как это принято в оптике. На фиг. 4А представлено распределение волновых аберраций вдоль горизонтального диаметра - по оси ОХ, на фиг. 4Б - вдоль вертикального диаметра изображения - по оси OY. График на фиг. 4А демонстрирует зависимость, характерную для совместного проявления искажений типа комы и сферической аберрации, которая описывается сочетанием всех трех функций, а на графике фиг. 4Б ход кривой симметричен относительно центра, что характерно для сферической аберрации. Такая картина в целом отвечает условиям эксперимента, поскольку точечный источник излучения, т.е. микродиафрагма, смещен именно по горизонтальной оси ОХ относительно центра поля зрения объектива, что и является причиной проявления полевой аберрации типа комы.
Проверка правильности решения уравнения (1) выбранным численным методом была выполнена следующим образом. Вычисляют левую часть уравнения (1), т.е. 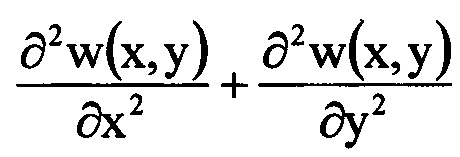 , подставляя в нее полученное аналитическое выражение вида (3), представляющее собой найденное распределение w(x, y). Приравнивая полученный результат к правой части уравнения (1), расчетным образом определяют распределение значений функции I(x, y)расч в плоскости П:
, подставляя в нее полученное аналитическое выражение вида (3), представляющее собой найденное распределение w(x, y). Приравнивая полученный результат к правой части уравнения (1), расчетным образом определяют распределение значений функции I(x, y)расч в плоскости П:
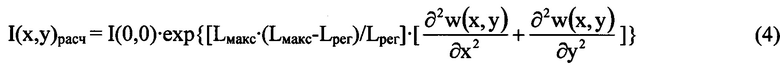
На фиг. 3А и Б сплошными линиями показаны результаты такого восстановления распределения интенсивности вдоль горизонтального и вертикального диаметров сечения пучка по осям ОХ и OY. Рассчитанные распределения не включают краевую зону изображения пучка, несколько искаженную дифракционными явлениями и исключенную из расчетов. Как указывалось выше, на фиг. 3А и 3Б штриховой линией показаны графики распределения интенсивности I(x, y) по поперечному сечению пучка в относительных единицах, приведенного к координатам в плоскости П из распределения интенсивности Iрег(ξ, η), зарегистрированного в плоскости Прег, вдоль горизонтального и вертикального диаметров сечения пучка по осям ОХ и OY. Если отвлечься от небольших местных возмущений интенсивности в экспериментальном распределении, то видно хорошее сходство зависимостей, показанных штриховой и сплошной линиями.
Оценка достигаемой точности определения волновых аберраций была выполнена путем анализа квадратичного функционала невязки, характеризующего различие экспериментально зарегистрированного и восстановленного распределений интенсивности, имеющего вид:
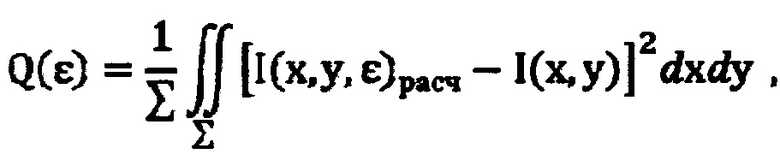 где
где
Σ - площадь поперечного сечения пучка в плоскости П за исключением узкой краевой зоны, возмущенной дифракцией;
ε=δw(x, y)/w(x, y) - относительная величина отклонения распределения волновых аберраций δw(x, y) от распределения w(x, y), полученного в результате применения способа;
I*(x, y, ε)расч - распределение интенсивности, рассчитанное по формуле (4) с заменой функции волновых аберраций w(x, y) на функцию w*(x, y, ε)=w(x, y)+δw(x, y)=(1+ε)w(x, y).
Ход зависимости функционала невязки Q(ε) показан на Фиг. 6. С учетом отмеченного сходства зависимостей I(x, y) и I(x, y)расч параметр ε варьируют в окрестности нулевого значения в пределах, охватывающих точку минимального значения невязки. График демонстрирует, что минимум невязки смещен относительно нулевого значения ε, при котором δw(x, y)=0, и достигается при значении εмин≈0.02 с неопределенностью ±0.01 с учетом слабого изменения величины Q(ε) вблизи минимума. Полученное ненулевое значение отклонения ε в совокупности с величиной неопределенности позволяют оценить погрешность определения значений волновых аберраций. Наибольшее значение волновой аберрации, полученной при реализации способа, составляет величину wмакс≈1.7λ. Погрешность определения наибольшего значения волновой аберрации составит δwмакс=(0.02+0.0l)⋅wмакс≈λ/20. Заметим, что полученная величина [Q(ε)]1/2 определяет среднеквадратичное значение отклонения распределения интенсивности, восстановленного расчетным путем, от экспериментально зарегистрированного. Степень расхождения распределений интенсивности можно оценить величиной отношения [Q(εмин)]1/2/I(0, 0)=0.03.
Таким образом, конкретный пример выполнения и оценки точности способа определения волновых аберраций подтверждают его основные достоинства: высокую точность получаемых результатов при существенном упрощении требований к реализации операций способа, меньшую трудоемкость и сложность обработки результатов измерений, а также расширение области применения на оптические системы, о схемных решениях которых нет предварительных сведений.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ДЕФОРМАЦИЙ ВОЛНОВОГО ФРОНТА СВЕТОВОГО ПУЧКА, ВЫЗВАННЫХ ВОЛНИСТОСТЬЮ ПОВЕРХНОСТЕЙ ОПТИЧЕСКОЙ СИСТЕМЫ | 2018 |
|
RU2680615C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ВОЛНОВЫХ АБЕРРАЦИЙ ОПТИЧЕСКОЙ СИСТЕМЫ | 2020 |
|
RU2753627C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕЛКОМАСШТАБНЫХ ДЕФОРМАЦИЙ ВОЛНОВОГО ФРОНТА СВЕТОВОГО ПУЧКА | 2024 |
|
RU2830845C1 |
| СПОСОБ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЯ С СУБДИФРАКЦИОННЫМ РАЗРЕШЕНИЕМ | 2013 |
|
RU2533502C1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ОПТИЧЕСКИХ АБЕРРАЦИЙ ГЛАЗА | 2012 |
|
RU2601853C2 |
| ИНТЕРФЕРЕНЦИОННЫЙ СПОСОБ ОПРЕДЕЛЕНИЯ ОПТИЧЕСКИХ ХАРАКТЕРИСТИК ОПТИЧЕСКИХ ЭЛЕМЕНТОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ (ВАРИАНТЫ) | 1993 |
|
RU2078307C1 |
| СПОСОБ И ОПТИЧЕСКАЯ СИСТЕМА ДЛЯ ПОЛУЧЕНИЯ ТОМОГРАФИЧЕСКОГО РАСПРЕДЕЛЕНИЯ ВОЛНОВЫХ ФРОНТОВ ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ | 2018 |
|
RU2733822C1 |
| УСТРОЙСТВО ВИДЕНИЯ ОБЪЕКТА | 2006 |
|
RU2329526C1 |
| Способ сужения диаграммы направленности лазерного пучка | 1987 |
|
SU1674050A1 |
| Устройство для контроля качества оптической системы | 1980 |
|
SU1087800A1 |
Изобретение относится к области оптики и касается способа определения волновых аберраций. При осуществлении способа направляют гомоцентрический световой пучок с длиной волны λ на оптическую систему. Определяют положение плоскости Пмакс, в которой пиковая интенсивность светового пучка в распределении интенсивности светового пучка имеет максимальное значение Iмакс. Измеряют расстояние Lмакс от плоскости Пмакс до плоскости П, соприкасающейся с последней поверхностью оптической системы. Определяют контур изофоты в распределении интенсивности в плоскости Пмакс по уровню 0,2⋅Iмакс и расстояние ρ максимального удаления точки с пиковой интенсивностью Iмакс от контура изофоты. Регистрируют распределение интенсивности Iрег(ξ, η) светового пучка в координатах (ξ, η) плоскости Прег, положение которой выбирают на удалении |Lрег|=16⋅ρ2/λ от плоскости Пмакс. Волновые аберрации w(x, y) определяют из уравнения, связывающего w(x, y) в координатах (x, y) плоскости П с распределением интенсивности светового пучка в плоскости Прег. Технический результат заключается в повышении точности, упрощении требований к реализации операций способа, уменьшении сложности обработки результатов измерений и обеспечении возможности применения способа к оптическим системам, о схемных решениях которых нет предварительных сведений. 8 ил.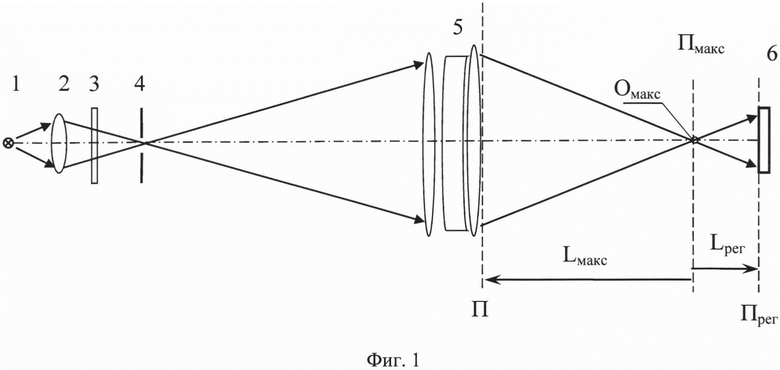
Способ определения волновых аберраций оптической системы, включающий направление некогерентного гомоцентрического светового пучка с длиной волны λ на оптическую систему, измерение распределений интенсивности светового пучка в плоскостях, перпендикулярных оси светового пучка, прошедшего оптическую систему и сфокусированного в пространстве изображений, получение математического выражения для определения волновых аберраций, определение волновых аберраций оптической системы путем решения численным методом полученного математического выражения, отличающийся тем, что определяют положение плоскости Пмакс, перпендикулярной оси светового пучка в пространстве изображений, в которой пиковая интенсивность светового пучка в распределении интенсивности светового пучка имеет максимальное значение Iмакс среди экспериментально зарегистрированных пиковых интенсивностей в распределениях интенсивностей светового пучка в плоскостях, перпендикулярных оси светового пучка, определяют контур изофоты в распределении интенсивности светового пучка в плоскости Пмакс по уровню 0,2⋅Iмакс и расстояние ρ максимального удаления точки Омакс с пиковой интенсивностью Iмакс от контура изофоты, измеряют расстояние Lмaкс по оси пучка от плоскости Пмакс до плоскости П, перпендикулярной оси светового пучка и соприкасающейся с последней поверхностью оптической системы, с учетом правила знаков, измеряют распределение интенсивности Iрег(ξ,η) светового пучка в координатах (ξ,η) плоскости Прег, перпендикулярной оси светового пучка в пространстве изображений, которую выбирают так, что выполняется условие |Lрег|=16⋅ρ2/λ, где Lрег - расстояние по оси пучка от плоскости Пмакс до плоскости Прег с учетом правила знаков, при этом начало координат в плоскостях П, Прег, Пмакс лежит на оси светового пучка, математическое выражение для определения волновых аберраций представляют в виде уравнения, связывающего волновые аберрации w(x,y) в координатах (х,у) плоскости П, с распределением интенсивности светового пучка в плоскости Прег
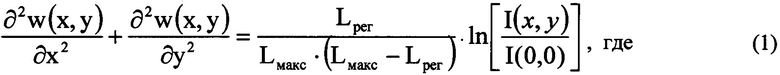
- I(х,у) - распределение интенсивности светового пучка, выраженное в координатах плоскости П, полученное путем замены переменных в распределении интенсивности Iрег(ξ,η) по формулам ξ=х⋅(Lрег/Lмакс) и η=y⋅(Lрег/Lмакс);
- I(0,0) - значение функции I(х,у) на оси пучка;
значения w(x,y) находят путем численного решения уравнения (1) вариационным методом при свободных граничных условиях, аппроксимируя w(x,y) степенным полиномом, удовлетворяющим условию w(0,0)=0 на оси пучка.
| Claude Roddier, Fransois Roddier "Wave-front reconstruction from defocused images and the testing of ground-based optical telescopes", JOURNAL OF THE OPTICAL SOCIETY OF AMERICA A, т | |||
| Печь-кухня, могущая работать, как самостоятельно, так и в комбинации с разного рода нагревательными приборами | 1921 |
|
SU10A1 |
| Самолетная самоустанавливающаяся лыжа | 1917 |
|
SU2277A1 |
| US 4641962 A1, 10.02.1987 | |||
| WO 2004052189 A1, 24.06.2004 | |||
| Способ контроля качества оптических систем | 1984 |
|
SU1223033A1 |
Авторы
Даты
2019-02-25—Публикация
2018-04-10—Подача