Изобретение относится к вычислительной технике и может быть использовано для нахождения остатка по модулю и неполного частного в цифровых вычислительных устройствах, в криптографических приложениях, а также в устройствах цифровой обработки сигналов и в системах управления.
Известно устройство для формирования остатка по произвольному модулю от числа, содержащее регистры, элементы ИЛИ, вычислитель, схемы сравнения, мультиплексор, элемент задержки, сумматор, группу блоков элементов «И» и блок постоянной памяти со связями (см. АС СССР №1633495, кл. H 03 M 7/18, 1991). Недостатком известного устройства является низкая надежность, так как для его реализации требуется большой объем оборудования.
Известен комбинационный рекуррентный формирователь остатков, содержащий комбинационный формирователь частичных остатков, блок ключей и блок сумматоров по модулю (см. патент РФ №2029435, кл. 6 H 03 M 7/18, 20.02.1995, бюл. №5). Недостатком данного устройства являются его ограниченные функциональные возможности, а именно отсутствие возможности формирования неполного частного.
Известно вычислительное устройство, содержащее сумматоры и мультиплексоры (см. патент РФ № 2348965, МПК G06F 7/72 (2006.01), H03M 7/18 (2006.01), 10.03.2009. Бюл. № 7). Недостатком данного вычислительного устройства является большой объем оборудования.
Наиболее близким по технической сущности к заявляемому изобретению является вычислительное устройство, содержащее сумматоры и мультиплексоры (см. патент РФ № 2717915, МПК G06F 7/72 (2006.01), H03M 7/18 (2006.01), 26.03.2020. Бюл. № 9). Недостатком данного вычислительного устройства является низкое быстродействие.
Техническим результатом изобретения является повышение быстродействия устройства, а именно увеличение скорости вычисления остатка по модулю и неполного частного.
Для достижения технического результата в вычислительное устройство, содержащее (n/2-1) сумматоров, (n/2-1) мультиплексоров, где n-разрядность входного числа, 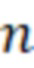 – четное и больше 2, образующих (n/2-1) ступеней преобразования, вход подачи двоичного кода числа, выход двоичного кода неполного частного, выход двоичного кода остатка от числа дополнительно введены на каждой ступени преобразования три схемы сравнения, трехвходовый элемент ИЛИ и двухвходовый элемент И, на первые информационные входы первых схем сравнения всех ступеней преобразования подается двоичный код модуля, на первые информационные входы вторых схем сравнения всех ступеней преобразования подается двоичный код удвоенного модуля, на первые информационные входы третьих схем сравнения всех ступеней преобразования подается двоичный код утроенного модуля, выходы первой, второй и третьей схем сравнения соединены соответственно с первым, вторым и третьим управляющими входами мультиплексора и с первым, вторым и третьим входами трехвходового элемента ИЛИ соответствующих ступеней преобразования, выход трехвходового элемента ИЛИ каждой ступени преобразования соединен с первым входом двухвходового элемента И соответствующей ступени преобразования, на второй вход двухвходового элемента И всех ступеней преобразования подается логическая единица, выход двухвходовых элементов И всех ступеней преобразования соединен со входом переноса сумматоров соответствующей ступени преобразования, на первый, второй и третий информационные входы мультиплексоров всех ступеней преобразования подаются соответственно инверсные двоичные коды модуля, удвоенного модуля и утроенного модуля, первые информационные выходы мультиплексоров всех ступеней преобразования соединены с первыми информационными входами сумматоров соответствующих ступеней преобразования, j-е разряды вторых информационных входов сумматоров и вторых информационных входов схем сравнения i-й ступени преобразования, где j=(0;1), соединены с (n-2i-j-1)-ми разрядами двоичного кода входного числа соответственно, второй и третий разряды вторых информационных входов сумматора и вторых информационных входов схем сравнения первой ступени преобразования соединены с (n-2)-м и (n-1)-м разрядами двоичного кода входного числа соответственно, информационные выходы сумматоров i-й ступени преобразования, где i=1,.., n/2-2, соединены со сдвигом на два разряда в сторону старших со вторыми информационными входами сумматоров и вторыми информационными входами схем сравнения (i+1)-й ступени преобразования, информационный выход сумматора (n/2-1)-й ступени преобразования является выходом двоичного кода остатка, вторые информационные выходы мультиплексоров являются выходом двоичного кода неполного частного, причем мультиплексор каждой ступени преобразования содержит два инвертора, трехвходовый элемент И, двухвходовый элемент И, три ключа, блок элементов ИЛИ и два элемента ИЛИ, причем первый вход трехвходового элемента И является первым управляющим входом мультиплексора, первый вход двухвходового элемента И является вторым управляющим входом мультиплексора и соединен со входом первого инвертора, выход которого соединен со вторым входом трехвходового элемента И, управляющий вход третьего ключа является третьим управляющим входом мультиплексора и соединен со входом второго инвертора и со вторыми входами первого и второго элементов ИЛИ, выходы которых являются вторым информационным выходом мультиплексора, выход второго инвертора соединен с третьим входом трехвходового элемента И и со вторым входом двухвходового элемента И, выход которого соединен с управляющим входом второго ключа и с первым входом второго элемента ИЛИ, выход трехвходового элемента И соединен с первым входом первого элемента ИЛИ и с управляющим входом первого ключа, информационные входы первого, второго и третьего ключей являются соответствующими информационными входами мультиплексора, а выходы соединены с соответствующими информационными входами блока элементов ИЛИ, выход которого является первым информационным выходом мультиплексора.
– четное и больше 2, образующих (n/2-1) ступеней преобразования, вход подачи двоичного кода числа, выход двоичного кода неполного частного, выход двоичного кода остатка от числа дополнительно введены на каждой ступени преобразования три схемы сравнения, трехвходовый элемент ИЛИ и двухвходовый элемент И, на первые информационные входы первых схем сравнения всех ступеней преобразования подается двоичный код модуля, на первые информационные входы вторых схем сравнения всех ступеней преобразования подается двоичный код удвоенного модуля, на первые информационные входы третьих схем сравнения всех ступеней преобразования подается двоичный код утроенного модуля, выходы первой, второй и третьей схем сравнения соединены соответственно с первым, вторым и третьим управляющими входами мультиплексора и с первым, вторым и третьим входами трехвходового элемента ИЛИ соответствующих ступеней преобразования, выход трехвходового элемента ИЛИ каждой ступени преобразования соединен с первым входом двухвходового элемента И соответствующей ступени преобразования, на второй вход двухвходового элемента И всех ступеней преобразования подается логическая единица, выход двухвходовых элементов И всех ступеней преобразования соединен со входом переноса сумматоров соответствующей ступени преобразования, на первый, второй и третий информационные входы мультиплексоров всех ступеней преобразования подаются соответственно инверсные двоичные коды модуля, удвоенного модуля и утроенного модуля, первые информационные выходы мультиплексоров всех ступеней преобразования соединены с первыми информационными входами сумматоров соответствующих ступеней преобразования, j-е разряды вторых информационных входов сумматоров и вторых информационных входов схем сравнения i-й ступени преобразования, где j=(0;1), соединены с (n-2i-j-1)-ми разрядами двоичного кода входного числа соответственно, второй и третий разряды вторых информационных входов сумматора и вторых информационных входов схем сравнения первой ступени преобразования соединены с (n-2)-м и (n-1)-м разрядами двоичного кода входного числа соответственно, информационные выходы сумматоров i-й ступени преобразования, где i=1,.., n/2-2, соединены со сдвигом на два разряда в сторону старших со вторыми информационными входами сумматоров и вторыми информационными входами схем сравнения (i+1)-й ступени преобразования, информационный выход сумматора (n/2-1)-й ступени преобразования является выходом двоичного кода остатка, вторые информационные выходы мультиплексоров являются выходом двоичного кода неполного частного, причем мультиплексор каждой ступени преобразования содержит два инвертора, трехвходовый элемент И, двухвходовый элемент И, три ключа, блок элементов ИЛИ и два элемента ИЛИ, причем первый вход трехвходового элемента И является первым управляющим входом мультиплексора, первый вход двухвходового элемента И является вторым управляющим входом мультиплексора и соединен со входом первого инвертора, выход которого соединен со вторым входом трехвходового элемента И, управляющий вход третьего ключа является третьим управляющим входом мультиплексора и соединен со входом второго инвертора и со вторыми входами первого и второго элементов ИЛИ, выходы которых являются вторым информационным выходом мультиплексора, выход второго инвертора соединен с третьим входом трехвходового элемента И и со вторым входом двухвходового элемента И, выход которого соединен с управляющим входом второго ключа и с первым входом второго элемента ИЛИ, выход трехвходового элемента И соединен с первым входом первого элемента ИЛИ и с управляющим входом первого ключа, информационные входы первого, второго и третьего ключей являются соответствующими информационными входами мультиплексора, а выходы соединены с соответствующими информационными входами блока элементов ИЛИ, выход которого является первым информационным выходом мультиплексора.
Сущность изобретения заключается в реализации следующего способа вычисления остатка R от числа A по модулю P. Пусть
A = Q·P +R, (1)
где A – целое положительное число, от которого необходимо вычислить остаток R;
P – целое положительное число, называемое модулем;
Q – целое положительное число, являющееся неполным частным от деления A на P;
R – целое положительное число, являющееся остатком от деления A на P.
Причем
A = an-1·2n-1+an-2·2n-2+ an-3·2n-3+an-4·2n-4+ . . . +a3·23+a2·22+a1·2+a0, (2)
P = pn-1·2n-1+pn-2·2n-2+ . . . +p1·21+p0, (3)
Q = qn-2·2n-2+ . . . +q1·21+q0, (4)
R = rn-2·2n-2+ . . . +r1·21+r0, (5)
где ai, 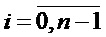
pi, 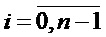
qi, 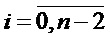
ri, 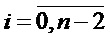
n – количество разрядов в представлении чисел, n – четное.
Задача состоит в том, чтобы по известным A и P отыскать остаток R и неполное частное Q. Остаток R является в терминах теории чисел вычетом числа A по модулю P, поэтому говорят, что A сравнимо с R по модулю P:
A ≡ R (mod P). (6)
Значение остатка R может быть вычислено следующим образом:
R ≡ A (mod P)= (an-1·2n-1+an-2·2n-2+ . . . +a1·2+a0)mod P. (7)
Перепишем выражение (2) в следующем виде, объединив по два соседних слагаемых:
A = (an-1·2n-1+an-2·2n-2)+ (an-3·2n-3+an-4·2n-4)+ . . . +(a3·23+a2·22)+(a1·2+a0), (8)
Из каждой суммы в скобках в выражении (8) вынесем 2i за скобки, где 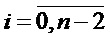
A = 2n-2(an-1·2+an-2)+2n-4(an-3·2+an-4)+ . . . +22(a3·2+a2)+(a1·2+a0), (9)
В выражении (9) перед каждой из n/2 образовавшихся сумм вида (ai+1·2+ai), получаем множитель 2i, где 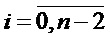
Далее вынесем в (9) наименьшую ненулевую степень 2 за скобки:
A = 22(2n-4(an-1·2+an-2)+ 2n-6 (an-3·2+an-4)+ . . . + (a3·2+a2))+(a1·2+a0), (10)
Выполняя последовательно преобразование (10) (n/2)-2 раз получим:
A = 22(22…(22(an-1·2+an-2)+(an-3·2+an-4))+ . . . + (a3·2+a2))+(a1·2+a0), (11)
где 22 встречается (n/2)-1 раз.
Тогда выражение (7) может быть представлено в следующем виде:
R = (22(22…(22(an-1·2+an-2)+(an-3·2+an-4))+ . . . + (a3·2+a2))+(a1·2+a0)) mod P. (12)
Из теории чисел известно, что операция приведения по модулю инвариантна к сложению и умножению, т. е. величина остатка не зависит от того, вычислен ли он от суммы (произведения) или от каждого слагаемого (сомножителя), а затем соответствующие частичные остатки просуммированы (перемножены) и от результата вычислен остаток по модулю.
Исходя из вышесказанного, выражение (12) может быть вычислено следующим образом.
Вначале на первой ступени преобразования вычисляют величину
t 1=(22(an-1·2+an-2)+(an-3·2+an-4)) mod P. (13)
На второй ступени преобразования вычисляют величину
t 2=(22·t1+(an-5·2+an-6)) mod P. (14)
На последней (n/2-1)-й ступени преобразования вычисляют величину
tn /2-1=(22·tn/2-2+(a1·2+a0)) mod P, (15)
которая и является искомым остатком R от числа A по модулю P.
Операция приведения по модулю P на каждой ступени преобразования выполняется исходя из следующих соображений.
По определению величина ti-1 лежит в диапазоне 0≤ti-1≤P-1, поэтому в соответствии с выражениями (13)-(15) величина
ti=22 ti-1 +(a n-2i-1·2+a n-2i-2), (16)
до приведения ее по модулю может принимать значения в диапазоне от 0 до 4P-1. Приведение по модулю величины ti осуществляется по следующим правилам
ti (mod P)=ti, если 0 ≤ ti < P, (17)
ti (mod P)=ti - P, если P≤ ti < 2P,
ti (mod P)=ti - 2P, если 2P ≤ ti < 3P,
ti (mod P)=ti - 3P, если 3P ≤ ti < 4P.
Разряды неполного частного Q на каждом этапе вычислений принимают значения в соответствии с таблицей 1.
Таблица 1.
Условия попадания значения ti в один из указанных в таблице 1 интервалов определяются значениями сигналов сравнения «больше или равно» на выходах сравнения схем сравнения в соответствии с таблицей 2.
Таблица 2.
Таким образом, если значение сигналов сравнения равно «1» на выходах сравнения всех трех схем сравнения, то ti (mod P)=ti - 3P, если значение сигналов сравнения равно «1» на выходах сравнения двух схем сравнения, то ti (mod P)=ti - 2P, если значение сигнала сравнения равно «1» на выходах сравнения одной схемы сравнения, то ti (mod P)=ti – P. Если значение сигналов сравнения равно «0» на выходах сравнения всех трех схем сравнения, то тогда ti (mod P)=ti, т.е. операция вычитания модуля P из величины ti не выполняется.
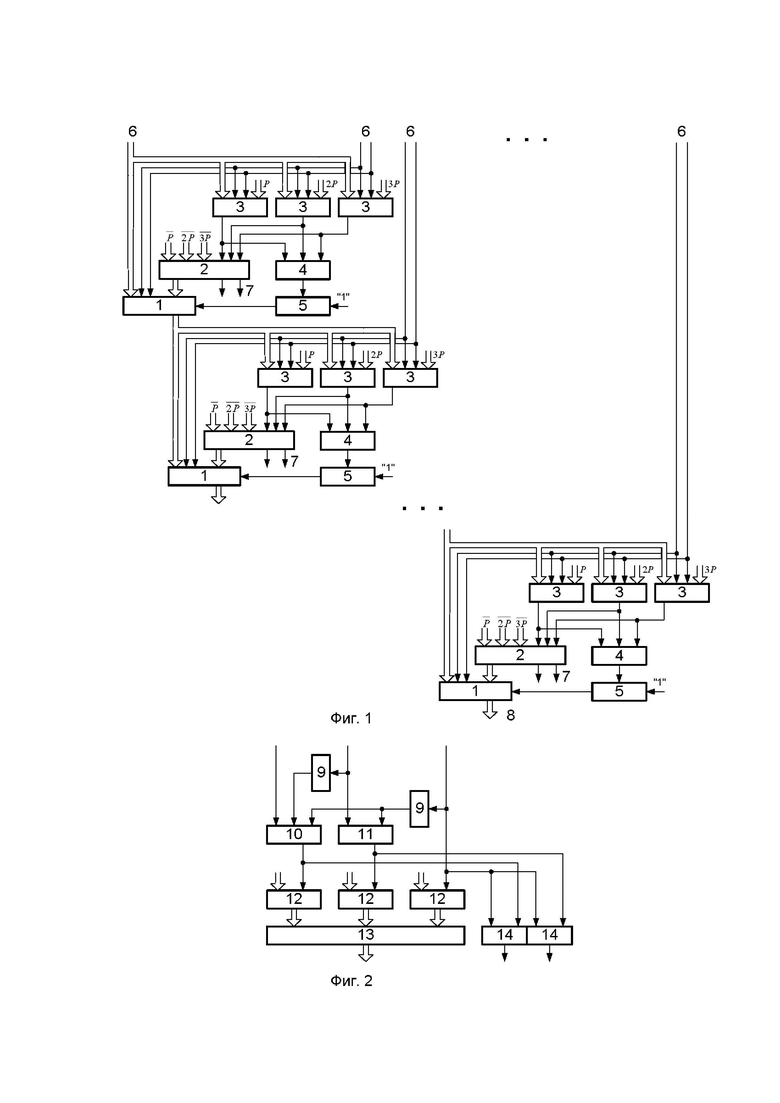
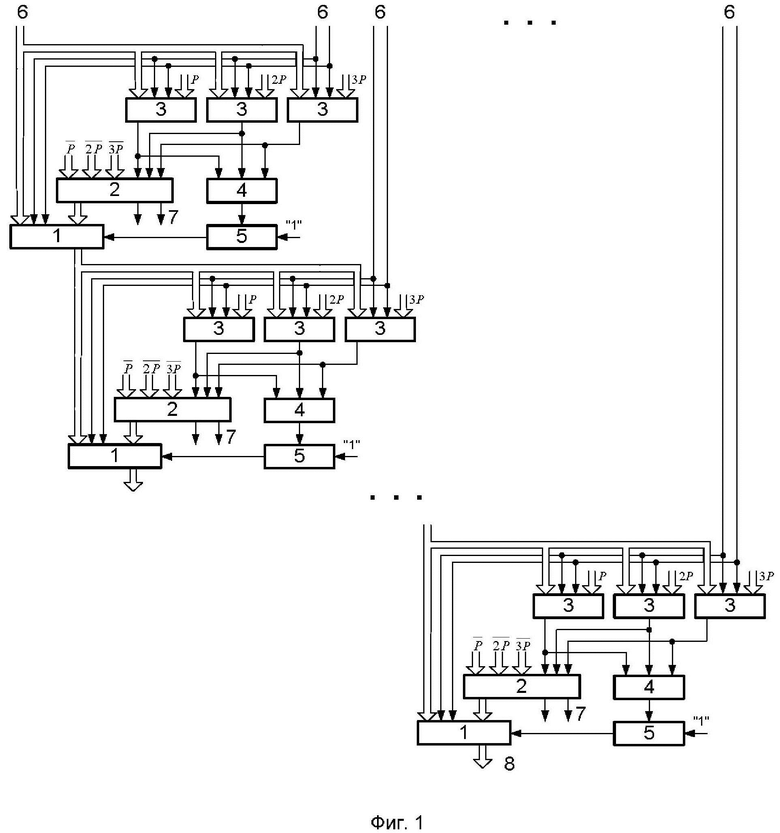
На фиг.1 представлена схема вычислительного устройства.
Вычислительное устройство содержит (n/2-1) ступеней преобразования, где n-разрядность входного числа, каждая из которых содержит сумматоры 1 и мультиплексоры 2, три схемы сравнения 3, трехвходовый элемент ИЛИ 4, двухвходовый элемент И 5, вход 6 подачи двоичного кода числа A, выход 7 двоичного кода неполного частного Q и выход 8 двоичного кода остатка R от числа A. На первые информационные входы первых схем сравнения 3 всех ступеней преобразования подается двоичный код модуля, на первые информационные входы вторых схем сравнения 3 всех ступеней преобразования подается двоичный код удвоенного модуля, на первые информационные входы третьих схем сравнения 3 всех ступеней преобразования подается двоичный код утроенного модуля. Выходы первой, второй и третьей схем сравнения 3 соединены соответственно с первым, вторым и третьим управляющими входами мультиплексора 2 и с первым, вторым и третьим входами трехвходового элемента ИЛИ 4 соответствующих ступеней преобразования. Выход элемента ИЛИ 4 каждой ступени преобразования соединен с первым входом двухвходового элемента И 5 соответствующей ступени преобразования. На второй вход двухвходового элемента И 5 всех ступеней преобразования подается логическая единица, выход двухвходовых элементов И 5 всех ступеней преобразования соединен со входом переноса сумматоров 1 соответствующей ступени преобразования. На первый, второй и третий информационные входы мультиплексоров 2 всех ступеней преобразования подаются соответственно инверсные двоичные коды модуля, удвоенного модуля и утроенного модуля. Первые информационные выходы мультиплексоров 2 всех ступеней преобразования соединены с первыми информационными входами сумматоров 1 соответствующих ступеней преобразования, j-е разряды вторых информационных входов сумматоров 1 и вторых информационных входов схем сравнения 3 i-й ступени преобразования, где j=(0;1), соединены с (n-2i-j-1)-ми разрядами двоичного кода 6 входного числа соответственно. Второй и третий разряды вторых информационных входов сумматора 1 и вторых информационных входов схем сравнения 3 первой ступени преобразования соединены с (n-2)-м и (n-1)-м разрядами двоичного кода 6 входного числа соответственно. Информационные выходы сумматоров 1 i-й ступени преобразования, где i=1,.., n/2-2, соединены со сдвигом на два разряда в сторону старших со вторыми информационными входами сумматоров 1 и вторыми информационными входами схем сравнения 3 (i+1)-й ступени преобразования. Информационный выход сумматора 1 (n/2-1)-й ступени преобразования является выходом 8 двоичного кода остатка. Вторые информационные выходы мультиплексоров 2 являются выходом 7 двоичного кода неполного частного.
На фиг.2 представлена схема мультиплексоров 2.
Мультиплексоры 2 содержат три инвертора 9, трехвходовый элемент И 10, двухвходовый элемент И 11, три ключа 12, блок элементов ИЛИ 13 и два элемента ИЛИ 14. Первый вход трехвходового элемента И 10 является первым управляющим входом мультиплексора 2. Первый вход двухвходового элемента И 11 является вторым управляющим входом мультиплексора 2 и соединен со входом первого инвертора 9, выход которого соединен со вторым входом трехвходового элемента И 10. Управляющий вход третьего ключа 12 является третьим управляющим входом мультиплексора 2 и соединен со входом второго инвертора 9 и со вторыми входами первого и второго элементов ИЛИ 14, выходы которых являются вторым информационным выходом мультиплексора 2. Выход второго инвертора 9 соединен с третьим входом трехвходового элемента И 10 и со вторым входом двухвходового элемента И 11, выход которого соединен с управляющим входом второго ключа 12 и с первым входом второго элемента ИЛИ 14. Выход трехвходового элемента И 10 соединен с первым входом первого элемента ИЛИ 14 и с управляющим входом первого ключа 12. Информационные входы первого, второго и третьего ключей 12 являются соответствующими информационными входами мультиплексора 2, а выходы соединены с соответствующими информационными входами блока элементов ИЛИ 13, выход которого является первым информационным выходом мультиплексора 2.
Вычислительное устройство работает следующим образом.
На вход 6 устройства подается двоичный код числа A от которого необходимо сформировать остаток R и неполное частное Q. Старшие разряды числа A подаются на вход первой ступени преобразования, а младшие – на вход последней.
На первые информационные входы первых схем сравнения 3 всех ступеней преобразования подается двоичный код модуля P, вторых схем сравнения 3 – удвоенный двоичный код модуля P, третьих схем сравнения 3 – утроенный двоичный код модуля P.
На первые информационные входы мультиплексоров 2 всех ступеней преобразования подается инверсный двоичный код модуля P, на вторые информационные входы – удвоенный инверсный двоичный код модуля P, а на третьи информационные входы – утроенный инверсный код модуля P.
На первой ступени преобразования осуществляется вычисление значения t1=(22(an-1·2+an-2)+(an-3·2+an-4)) mod P. Причем вычисление значения 22(an-1·2+an-2)+(an-3·2+an-4) осуществляется путем подачи соответствующих разрядов an-1…an-4 на соответствующие входы первой ступени преобразования. Для приведения этого значения по модулю P с помощью схем сравнения 3 осуществляют одновременное сравнение значений P, 2P и 3P с входным значением и в зависимости от того, в каком диапазоне находится входное значение, в соответствии с табл. 2 появляются сигналы на соответствующих выходах «больше или равно» схем сравнения 3, которые далее поступают на соответствующие управляющие входы мультиплексора 2.
Управляющие сигналы мультиплексора 2 (см. Фиг. 2) открывают один из ключей 12.
Если управляющий сигнал появляется на всех трех управляющих входах, то окажется открытым третий ключ 12. Управляющий сигнал с третьего управляющего входа откроет третий ключ 12 и через второй инвертор 9 в виде логического нуля поступит на третий вход трехвходового элемента И 10 и на второй вход двухвходового элемента И 11, запрещая прохождение управляющих сигналов с их первых входов на их выходы. В результате первый и второй ключи 12 окажутся закрытыми и на выход мультиплексора 2 поступит значение инверсного двоичного кода утроенного модуля P с его третьего информационного входа. В результаты на выходе сумматора 1 окажется величина 22(an-1·2+an-2)+(an-3·2+an-4) - 3P.
Если управляющий сигнал появляется на первом и втором управляющих входах мультиплексора 2, то аналогичным образом окажется открытым только второй ключ 12, а первый и третий ключи 12 окажутся закрытыми. В результате на выход мультиплексора 2 поступит значение инверсного двоичного кода удвоенного модуля P с его второго информационного входа. На выходе сумматора 1 окажется величина 22(an-1·2+an-2)+(an-3·2+an-4) - 2P.
Если управляющий сигнал появляется только на первом управляющем входе мультиплексора 2, то аналогичным образом окажется открытым только первый ключ 12, а второй и третий ключи 12 окажутся закрытыми. В результате на выход мультиплексора 2 поступит значение инверсного двоичного кода модуля P с его первого информационного входа. На выходе сумматора 1 окажется величина 22(an-1·2+an-2)+(an-3·2+an-4) - P.
Если же на управляющих входах мультиплексора 2 будут только нулевые сигналы, то все ключи 12 окажутся закрытыми и на выходе мультиплексора 2 образуется нулевое значение. В результате на выходе сумматора 1 окажется величина 22(an-1·2+an-2)+(an-3·2+an-4).
Сформированное на первой ступени преобразования значение t1=(22(an-1·2+an-2)+(an-3·2+an-4)) mod P поступает со сдвигом на два разряда в сторону старших (т.е. фактически осуществляя умножение на 22) на вход следующей ступени преобразования. На младшие два разряда подаются сигналы an-5, an-6 разрядов входного числа A.
На второй ступени преобразования осуществляются аналогичные вычисления. Аналогично происходит работа устройства и на остальных ступенях преобразования.
Так как на каждой ступени преобразования осуществляется обработка одновременно двух разрядов входного числа, то через (n/2-1) преобразований на выходе 8 устройства сформируется двоичный код остатка R от числа A по модулю P, а на выходе 7 устройства сформируется двоичный код неполного частного Q.
Рассмотрим работу вычислительного устройства на примере.
Пусть входное число A=21510=110101112, модуль P=610=000001102, разрядность n=8. Двоичные прямые и инверсные коды значений модуля P, 2P, 3P представлены в табл. 3.
Таблица 3.
Значения сигналов при работе устройства на входах и выходах сумматоров 1, мультиплексоров 2 и схем сравнения 3 представлены в табл. 4. Номер ступени преобразования приведен в первом столбце таблицы 4. «Схема сравнения 1», «Схема сравнения 2» и «Схема сравнения 3», соответственно обозначение первой, второй и третьей схем сравнения 3. «Мультиплексор инф» - обозначения информационных входов и выходов мультиплексоров 2, «Мультиплексор упр» - обозначения управляющих входов мультиплексоров 2. «Вход 1» и «Вход 2», соответственно первый и второй информационные входы сумматоров 1, мультиплексоров 2 и схем сравнения 3, а также первый и второй управляющий входы мультиплексоров 2. «Вход 3» - вход переноса сумматоров 1, а также третий информационный и третий управляющий вход мультиплексоров 2. «Выход 1» - информационные выходы сумматоров 1, мультиплексоров 2 и схем сравнения 3. «Выход 2» - второй информационный выход мультиплексоров 2.
Таблица 4.
В результате на информационных выходах сумматора 1 третьей ступени преобразования, являющихся выходом 8 двоичного кода остатка R от числа A устройства, образуется код числа 000001012=510, который и является вычисленным остатком R числа A=215 по модулю P=6, а на выходах 7 устройства образуется двоичный код 1000112=3510, который и является неполным частным Q. Непосредственной проверкой устанавливаем, что 215=35·6 + 5, что доказывает правильность функционирования устройства.
В устройстве прототипе вычисление остатка осуществляется за (n-1) последовательных шагов преобразования, а в предлагаемом устройстве за (n/2-1) шагов. В результате быстродействие предлагаемого технического решения по сравнению с устройством прототипом будет выше не менее чем в два раза.
| название | год | авторы | номер документа |
|---|---|---|---|
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 2020 |
|
RU2739338C1 |
| УМНОЖИТЕЛЬ ПО МОДУЛЮ | 2020 |
|
RU2751802C1 |
| УМНОЖИТЕЛЬ ПО МОДУЛЮ | 2024 |
|
RU2829089C1 |
| УМНОЖИТЕЛЬ ЧИСЕЛ ПО ПРОИЗВОЛЬНОМУ МОДУЛЮ | 2024 |
|
RU2839987C1 |
| АРИФМЕТИКО-ЛОГИЧЕСКОЕ УСТРОЙСТВО ДЛЯ СЛОЖЕНИЯ, ВЫЧИТАНИЯ И УМНОЖЕНИЯ ЧИСЕЛ ПО МОДУЛЮ | 2019 |
|
RU2711051C1 |
| АРИФМЕТИКО-ЛОГИЧЕСКОЕ УСТРОЙСТВО ДЛЯ ФОРМИРОВАНИЯ ОСТАТКА ПО ПРОИЗВОЛЬНОМУ МОДУЛЮ ОТ ЧИСЛА | 2018 |
|
RU2696223C1 |
| КОНВЕЙЕРНЫЙ ФОРМИРОВАТЕЛЬ ОСТАТКОВ ПО ПРОИЗВОЛЬНОМУ МОДУЛЮ | 2022 |
|
RU2791440C1 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 2023 |
|
RU2798746C1 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 2007 |
|
RU2356086C2 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 2022 |
|
RU2796555C1 |
Изобретение относится к области вычислительной техники. Техническим результатом изобретения является повышение быстродействия устройства вычисления остатка по модулю и неполного частного. Раскрыто вычислительное устройство для нахождения остатка по модулю и неполного частного, обеспечивающее вычисление остатка R от числа A по модулю P путем последовательного выполнения (n/2-1) операций, где n – количество разрядов входного числа A, в соответствии с выражением: R=(22(22…(22(an-1·2+an-2)+(an-3·2+an-4))+…+(a3·2+a2))+(a1·2+a0)) mod P, где ai, 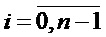
Вычислительное устройство для нахождения остатка по модулю и неполного частного, содержащее (n/2-1) сумматоров, (n/2-1) мультиплексоров, где n - разрядность входного числа, n – четное и больше 2, образующих (n/2-1) ступеней преобразования, вход подачи двоичного кода числа, выход двоичного кода неполного частного, выход двоичного кода остатка от числа, отличающееся тем, что в него дополнительно введены на каждой ступени преобразования три схемы сравнения, трехвходовый элемент ИЛИ и двухвходовый элемент И, на первые информационные входы первых схем сравнения всех ступеней преобразования подается двоичный код модуля, на первые информационные входы вторых схем сравнения всех ступеней преобразования подается двоичный код удвоенного модуля, на первые информационные входы третьих схем сравнения всех ступеней преобразования подается двоичный код утроенного модуля, выходы первой, второй и третьей схем сравнения соединены соответственно с первым, вторым и третьим управляющими входами мультиплексора и с первым, вторым и третьим входами трехвходового элемента ИЛИ соответствующих ступеней преобразования, выход трехвходового элемента ИЛИ каждой ступени преобразования соединен с первым входом двухвходового элемента И соответствующей ступени преобразования, на второй вход двухвходового элемента И всех ступеней преобразования подается логическая единица, выход двухвходовых элементов И всех ступеней преобразования соединен со входом переноса сумматоров соответствующей ступени преобразования, на первый, второй и третий информационные входы мультиплексоров всех ступеней преобразования подаются соответственно инверсные двоичные коды модуля, удвоенного модуля и утроенного модуля, первые информационные выходы мультиплексоров всех ступеней преобразования соединены с первыми информационными входами сумматоров соответствующих ступеней преобразования, j-е разряды вторых информационных входов сумматоров и вторых информационных входов схем сравнения i-й ступени преобразования, где j=(0; 1), соединены с (n-2i-j-1)-ми разрядами двоичного кода входного числа соответственно, второй и третий разряды вторых информационных входов сумматора и вторых информационных входов схем сравнения первой ступени преобразования соединены с (n-2)-м и (n-1)-м разрядами двоичного кода входного числа соответственно, информационные выходы сумматоров i-й ступени преобразования, где i=1, …, n/2-2, соединены со сдвигом на два разряда в сторону старших со вторыми информационными входами сумматоров и вторыми информационными входами схем сравнения (i+1)-й ступени преобразования, информационный выход сумматора (n/2-1)-й ступени преобразования является выходом двоичного кода остатка, вторые информационные выходы мультиплексоров являются выходом двоичного кода неполного частного, причем мультиплексор каждой ступени преобразования содержит два инвертора, трехвходовый элемент И, двухвходовый элемент И, три ключа, блок элементов ИЛИ и два элемента ИЛИ, причем первый вход трехвходового элемента И является первым управляющим входом мультиплексора, первый вход двухвходового элемента И является вторым управляющим входом мультиплексора и соединен со входом первого инвертора, выход которого соединен со вторым входом трехвходового элемента И, управляющий вход третьего ключа является третьим управляющим входом мультиплексора и соединен со входом второго инвертора и со вторыми входами первого и второго элементов ИЛИ, выходы которых являются вторым информационным выходом мультиплексора, выход второго инвертора соединен с третьим входом трехвходового элемента И и со вторым входом двухвходового элемента И, выход которого соединен с управляющим входом второго ключа и с первым входом второго элемента ИЛИ, выход трехвходового элемента И соединен с первым входом первого элемента ИЛИ и с управляющим входом первого ключа, информационные входы первого, второго и третьего ключей являются соответствующими информационными входами мультиплексора, а выходы соединены с соответствующими информационными входами блока элементов ИЛИ, выход которого является первым информационным выходом мультиплексора.
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 2019 |
|
RU2717915C1 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 2007 |
|
RU2348965C1 |
| US 4555769 A, 26.11.1985 | |||
| US 4949293 A, 14.08.1990. | |||
Авторы
Даты
2021-09-30—Публикация
2020-07-29—Подача