Изобретение относится к вычислительной технике и может быть использовано в цифровых вычислительных устройствах, а также в устройствах цифровой обработки сигналов и в системах управления.
Известно устройство для формирования остатка по произвольному модулю от числа, содержащее регистры, элементы ИЛИ, вычислитель, схемы сравнения, мультиплексор, элемент задержки, сумматор, группу блоков элементов «И» и блок постоянной памяти со связями (см. АС СССР №1633495, кл. H 03 M 7/18, 1991).
Недостатком известного устройства является низкая надежность, так как для его реализации требуется большой объем оборудования.
Известен комбинационный рекуррентный формирователь остатков, содержащий комбинационный формирователь частичных остатков, блок ключей и блок сумматоров по модулю (см. патент РФ №2029435, кл. 6 H 03 M 7/18, 20.02.1995, бюл. №5).
Недостатком данного устройства являются его ограниченные функциональные возможности, а именно отсутствие возможности формирования неполного частного.
Наиболее близким по технической сущности к заявляемому изобретению является вычислительное устройство, содержащее сумматоры и мультиплексоры (см. патент РФ № 2348965, МПК G06F 7/72 (2006.01), H03M 7/18 (2006.01), 10.03.2009. Бюл. № 7).
Недостатком данного вычислительного устройства является большой объем оборудования.
Техническим результатом изобретения является сокращение объема оборудования и как следствие уменьшения энергопотребления за счет исключения n сумматоров.
Для достижения технического результата в вычислительном устройстве, содержащем (n-1) сумматоров и (n-1) мультиплексоров, где n-разрядность входного числа, образующих (n-1) ступеней преобразования, причем i-я ступень преобразования, где i=2,.., n-1, соединена с (n-i-1)-м разрядом двоичного кода входного числа, а первая ступень преобразования соединена с (n-1)-м и (n-2)-м разрядами двоичного кода входного числа, на первые информационные входы сумматоров подается дополнительный двоичный код модуля, информационные выходы сумматора i-й ступени преобразования, где i=1,.., n-1, соединены с первыми информационными входами мультиплексора этой же ступени преобразования, а выходы переноса соединены с управляющими входами соответствующих мультиплексоров и являются информационными выходами двоичного кода неполного частного устройства, информационный выход мультиплексора (n-1)-й ступени преобразования является информационным выходом двоичного кода остатка устройства, информационные выходы мультиплексоров (1,.., n-2)-й ступеней преобразования соединены со сдвигом на один двоичный разряд в сторону старшего со вторыми информационными входами сумматоров (2,.., n-1)-й ступени преобразования соответственно, также информационные выходы мультиплексоров (1,.., n-2)-й ступени преобразования соединены со сдвигом на один двоичный разряд в сторону старшего со вторыми информационными входами мультиплексоров (2,.., n-1)-й ступени преобразования, i-й разряд двоичного кода входного числа, где i=0,.., n-2, соединен с младшим разрядом вторых информационных входов сумматоров и с младшим разрядом вторых информационных входов мультиплексоров (n-i-1)-й ступени преобразования, (n-1)-й разряд двоичного кода входного числа соединен со вторым разрядом второго информационного входа мультиплексора и со вторым разрядом второго информационного входа сумматора первой ступени преобразования.
Сущность изобретения заключается в реализации следующего способа формирования остатка по произвольному модулю.
Пусть требуется сформировать остаток R от числа A по модулю P и вычислить частное Q, то есть решить уравнение A=QP+R.
Число  может быть представлено в позиционной двоичной системе счисления в виде:
может быть представлено в позиционной двоичной системе счисления в виде:
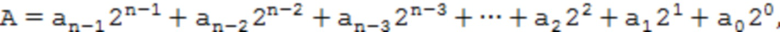
где ai, 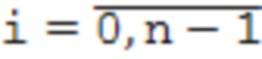 - коэффициенты, принимающие значения 0 или 1;
- коэффициенты, принимающие значения 0 или 1;
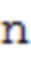 - количество разрядов в двоичном представлении числа
- количество разрядов в двоичном представлении числа  .
.
Это выражение может быть представлено в следующем виде:
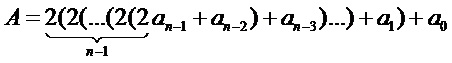 .
.
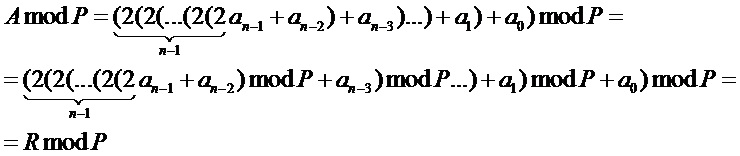 .
.
Из теории чисел известно, что операция приведения по модулю инвариантна к сложению и умножению, т. е. величина остатка не зависит от того, вычислен он от суммы (произведения) или от каждого слагаемого (сомножителя), а затем соответствующие частичные остатки просуммированы (перемножены) и от результата вычислен остаток по модулю.
В таком виде значительно облегчается задача нахождения остатка R от числа А.
При проведении вычислений по модулю P на первой ступени преобразования значение выражения (2an-1+an-2) сравнивается с модулем P, где n - количество разрядов числа A. Если значение (2an-1+an-2)≥P, то из числа (2an-1+an-2) вычитается значение модуля P, то есть
t1=(2an-1+an-2)-P. При этом формируется ненулевой старший (n-2)-й разряд неполного частного Q. Если (2an-1+an-2)<P, то число (2an-1+an-2) остается без изменений t1=(2an-1+an-2), а значение старшего (n-2)-го разряда неполного частного Q принимается равным нулю. Полученное на первой ступени преобразования значение t1 на второй ступени преобразования умножается на 2, складывается с an-3 и сравнивается со значением P. Если значение (2t1+an-3) ≥ P, то из (2t1+an-3) вычитается значение модуля P, то есть t2=(2t1+an-3)-P, при этом формируется ненулевой (n-3)-й разряд неполного частного Q. Если (2t1+an-3)<P, то число (2t1+an-3) остается без изменений t2=(2t1+an-3), а значение
(n-3)-го разряда неполного частного Q принимается равным нулю. Полученное в результате значение t2 на третьей ступени преобразования умножается на 2, складывается с an-4 и сравнивается со значением P и т.д. На (n-1)-й ступени преобразования число (2tn-2+a0) сравнивается с модулем P. Если значение (2tn-2+a0) ≥ P, то из (2tn-2+a0) вычитается значение числа P, то есть tn-1=(2tn-2+a0)-P, при этом формируется ненулевой младший разряд неполного частного Q. Если (2tn-2+a0) < P, то число (2tn-2+a0) остается без изменений tn-1=(2tn-2+a0), а значение младшего разряда неполного частного Q принимается равным нулю. Полученное в результате значение R=tn-1 является остатком от деления числа A на число P. Операция умножения на два во всех случаях осуществляется сдвигом всех разрядов множимого на один в сторону старших. Сравнения выполняются на каждой ступени преобразования с использованием сумматора и мультиплексора. Сумматор выполняет операцию вычисления выражения 2xi+a(n-i-1)-P, где xi – результаты вычислений на предыдущей ступени преобразования. Значение модуля P подается на информационный вход сумматора в дополнительном коде, что эквивалентно выполнению вычитания. Значение a(n-i-1) подается на самый младший разряд второго информационного входа сумматора, который в результате сдвига кода xi на один разряд в сторону старших оказывается свободен. Мультиплексор управляется сигналом переноса с сумматора, который при 2xi+a(n-i-1) ≥ P принимает значение «1», при 2xi+a(n-i-1) < P принимает значение «0».
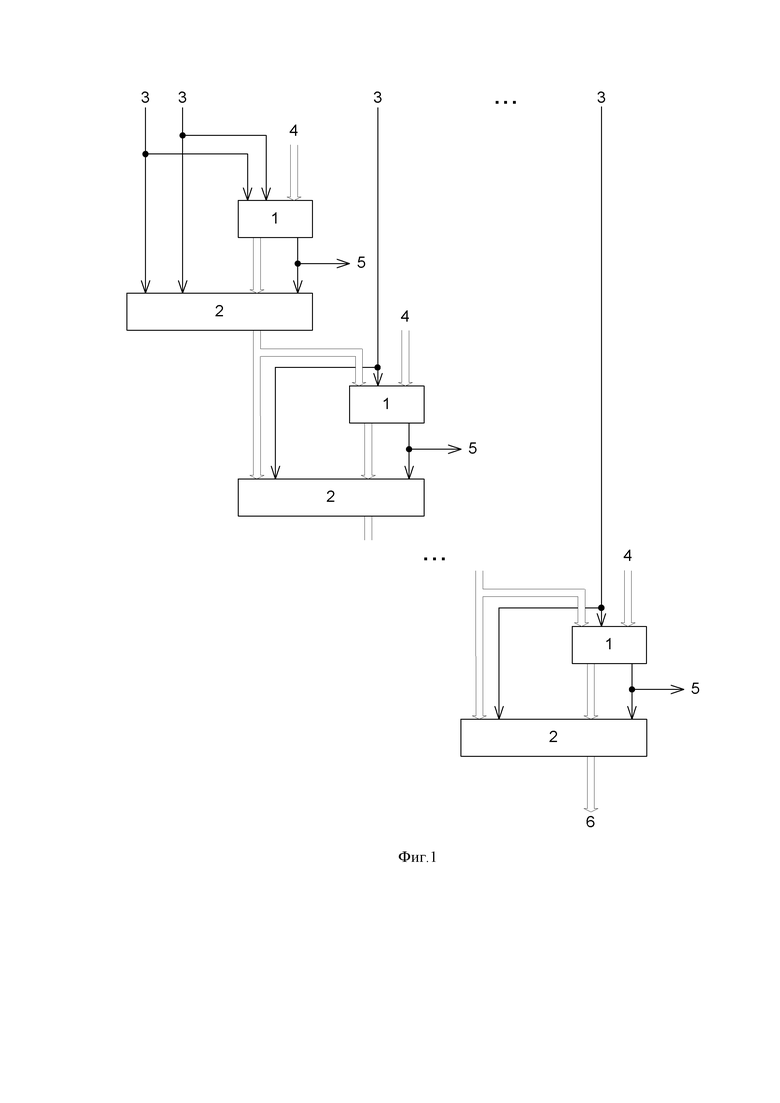
На фиг.1 представлена схема вычислительного устройства.
Вычислительное устройство содержит (n-1) сумматоров 1 и (n-1) мультиплексоров 2, где n-разрядность входного числа, образующих
(n-1) ступеней преобразования, причем i-я ступень преобразования, где i=1,.., n-2, соединена с (n-i-1)-м разрядом двоичного кода входного числа A, а первая ступень преобразования соединена с
(n-1)-м и (n-2)-м разрядами двоичного кода входного числа A, входы 3 устройства являются входами подачи двоичного кода числа A, входы 4 устройства являются входами подачи дополнительного двоичного кода модуля P, выходы 5 устройства являются выходами кода неполного частного Q, а выходы 6 устройства являются выходами кода остатка R, на первые информационные входы сумматоров 1 со входов 4 устройства подается дополнительный двоичный код модуля P, информационные выходы сумматора 1 i-й ступени преобразования, где i=1,.., n-1, соединены с первыми информационными входами мультиплексора 2 этой же ступени преобразования, а выходы переноса соединены с управляющими входами соответствующих мультиплексоров 2 и соединены с выходами 5 устройства двоичного кода неполного частного Q, информационный выход мультиплексора 2 (n-1)-й ступени преобразования соединен с выходом 6 устройства двоичного кода остатка R, информационные выходы мультиплексоров 2 (1,.., n-2)-й ступеней преобразования соединены со сдвигом на один двоичный разряд в сторону старшего со вторыми информационными входами сумматоров 1 (2,.., n-1)-й ступени преобразования соответственно, информационные выходы мультиплексоров 2 (1,.., n-2)-й ступени преобразования соединены со сдвигом на один двоичный разряд в сторону старшего со вторыми информационными входами мультиплексоров 2 (2,.., n-1)-й ступени преобразования, i-й разряд двоичного кода входного числа A, где i=0,.., n-2, соединен с младшим разрядом вторых информационных входов сумматоров 1 и с младшим разрядом вторых информационных входов мультиплексоров 2
(n-i-1)-й ступени преобразования, (n-1)-й разряд двоичного кода входного числа A соединен со вторым разрядом второго информационного входа мультиплексора 2 и со вторым разрядом второго информационного входа сумматора 1 первой ступени преобразования.
Вычислительное устройство работает следующим образом.
На первые информационные входы сумматоров 1 подается дополнительный код модуля P со входов 4 устройства. На вторые информационные входы сумматора 1 первой ступени преобразования подается код двух старших разрядов числа A an-1 и an-2, причем код разряда an-2 подается на младший разряд сумматора 1, а код разряда an-1 подается на второй разряд. Аналогичным образом подается код двух старших разрядов на второй информационный вход мультиплексора 2 первой ступени преобразования. Сумматор 1 первой ступени преобразования выполняет операцию (2an-1+an-2)-P. Если значение
(2an-1+an-2) окажется ≥P, то на выходе переноса сумматора 1 появится «1», которая подключит к выходу мультиплексора 2 первой ступени преобразования его первый информационный вход и на его выходе появится значение t1=(2an-1+an-2)-P. Если же значение (2an-1+an-2) окажется <P, то на выходе переноса сумматора 1 появится «0» и информационный выход мультиплексора 2 первой ступени преобразования окажется скоммутированным с его вторым информационным выходом. В результате на информационном выходе мультиплексора 2 первой ступени преобразования окажется число t1=(2an-1+an-2). Число t1 с информационного выхода мультиплексора 2 со сдвигом на один двоичный разряд в сторону старшего (что эквивалентно умножению на 2) поступит на вторые информационные входы сумматора 1 и мультиплексора 2 второй ступени преобразования. Значение an-3–го разряда входного числа A поступит на младшие разряды вторых информационных входов сумматора 1 и мультиплексора 2 второй ступени преобразования. В результате на вторых информационных входах сумматора 1 и мультиплексора 2 второй ступени преобразования образуется число (2t1+an-3), а на информационном выходе сумматора 1 второй ступени преобразования образуется число (2t1+an-3)-P, которое поступает на первый информационный вход мультиплексора 2 второй ступени преобразования. Если число (2t1+an-3) окажется ≥ P, то на выходе переноса сумматора 1 второй ступени преобразования появится «1», которая, поступая на управляющий вход мультиплексора 2 второй ступени преобразования подключит к его информационным выходам первые информационные входы. В результате на информационном выходе мультиплексора 2 появится число t2=(2t1+an-3)-P, в противном случае появится число t2=(2t1+an-3).
Аналогично происходит работа устройства и на остальных ступенях преобразования.
В результате после выполнения (n-1) таких преобразований на выходе 6 устройства окажется код остатка Q от числа A по модулю P, а на выходах 5 – код неполного частного Q.
Рассмотрим работу вычислительного устройства на примере.
Пусть входное число A=2710=110112, модуль P=510=001012, дополнительный код модуля Pд=110112, разрядность n=5. Сумматор 1 первой ступени преобразования формирует значение
(2a4+a3)-P =10+1+11011=11110. На его выходе переноса формируется сигнал «0», следовательно на информационном выходе мультиплексора 2 первой ступени преобразования появится число с его второго информационного входа t1=(2a4+a3)=10+1=11. Старший разряд неполного частного будет равен «0». На вторых информационных входах сумматора 1 и мультиплексора 2 второй ступени преобразования образуется число
(2t1+a2)=110+0=110. На информационном выходе сумматора 1 второй ступени преобразования образуется число (2t1+a2)-P=00110+0+11011=00001. На выходе переноса этого сумматора 1 образуется сигнал «1», который является следующим разрядом неполного частного и скоммутирует на информационные выходы мультиплексора 2 второй ступени преобразования сигнал с его первых информационных входов. В результате на информационных выходах мультиплексора 2 второй ступени преобразования окажется сигнал t2=(2t1+a2)-P=00001. На вторых информационных входах сумматора 1 и мультиплексора 2 третьей ступени преобразования образуется число (2t2+a1)=00010+1=00011. На информационном выходе сумматора 1 третьей ступени преобразования образуется число (2t2+a1)-P=00010+1+11011=11110. На его выходе переноса формируется сигнал «0», следовательно на информационном выходе мультиплексора 2 третьей ступени преобразования появится число с его второго информационного входа t3=(2t2+a1)= 00011. На вторых информационных входах сумматора 1 и мультиплексора 2 четвертой ступени преобразования образуется число (2t3+a0) = 00110+1 = 00111. На информационном выходе сумматора 1 четвертой ступени преобразования образуется число (2t3+a0)-P=00110+1+11011=00010. На выходе переноса этого сумматора 1 образуется сигнал «1», который является младшим разрядом неполного частного и скоммутирует на информационные выходы мультиплексора 2 четвертой ступени преобразования сигнал с его первых информационных входов. В результате на информационных выходах мультиплексора 2 четвертой ступени преобразования окажется код числа t4=(2t3+a0)-P=00110+1+11011=00010, который и является вычисленным остатком: 27=5·5+2. На выходах 5 устройства неполного частного образуется двоичный код неполного частного 01012=510.
| название | год | авторы | номер документа |
|---|---|---|---|
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 2007 |
|
RU2348965C1 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 2020 |
|
RU2756408C1 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 2020 |
|
RU2739338C1 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 2007 |
|
RU2356086C2 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 2022 |
|
RU2796555C1 |
| УМНОЖИТЕЛЬ ПО МОДУЛЮ | 2020 |
|
RU2751802C1 |
| УМНОЖИТЕЛЬ ПО МОДУЛЮ | 2024 |
|
RU2829089C1 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 2023 |
|
RU2798746C1 |
| Вычислительное устройство | 2017 |
|
RU2661797C1 |
| КОНВЕЙЕРНЫЙ ВЫЧИСЛИТЕЛЬ | 2023 |
|
RU2804380C1 |
Вычислительное устройство относится к вычислительной технике и может быть использовано в цифровых вычислительных устройствах, а также в устройствах цифровой обработки сигнала и в криптографических приложениях. Технический результат - сокращение объема оборудования и, как следствие, уменьшение энергопотребления за счет исключения n сумматоров. Устройство содержит сумматоры и мультиплексоры. Данное вычислительное устройство позволяет достичь результат путем последовательного выполнения (n-1) операций, где n – количество разрядов входного числа A. В ходе i-й операции значение (2ti+an-2-i) сравнивается с модулем P путем вычисления разности (2ti+an-2-i)-P, где i=1, …, (n-1), и формируется (n-i-1)-й разряд неполного частного Q. При выполнении (n-1)-й операции результатом вычисления числа A по модулю P будет являться значение разности, полученное на последнем (n-1)-м шаге. 1 ил.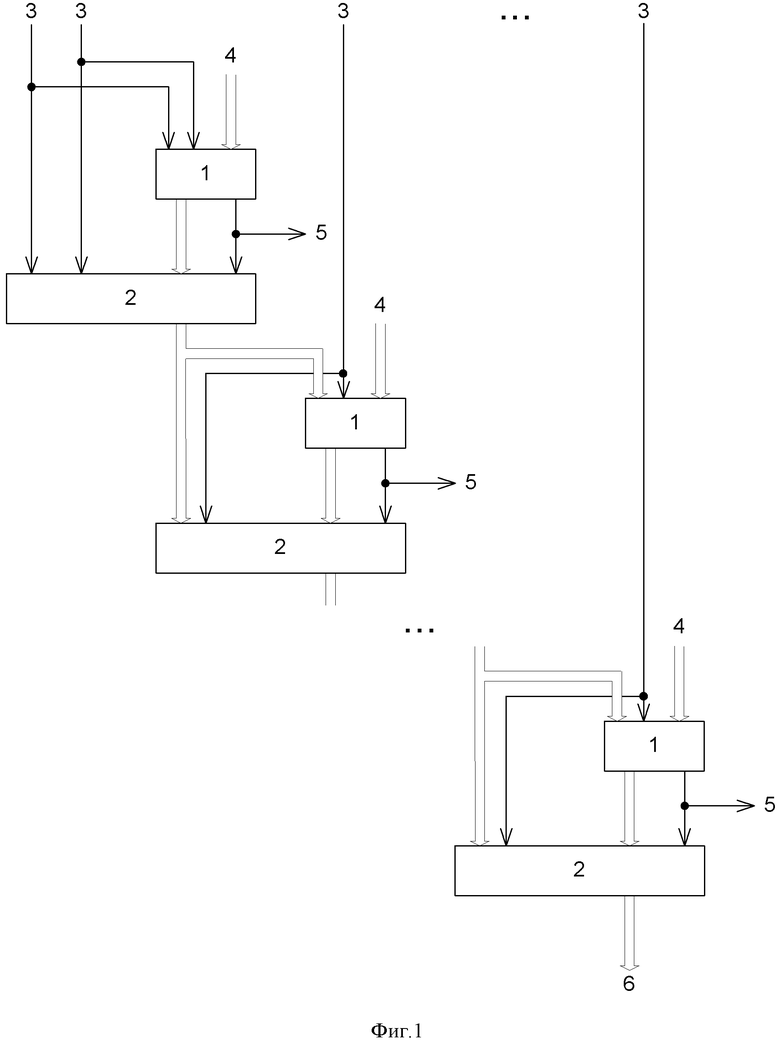
Вычислительное устройство, содержащее (n-1) сумматоров и (n-1) мультиплексоров, где n - разрядность входного числа, образующих (n-1) ступеней преобразования, причем i-я ступень преобразования, где i=2,.., n-1, соединена с (n-i-1)-м разрядом двоичного кода входного числа, а первая ступень преобразования соединена с (n-1)-м и (n-2)-м разрядами двоичного кода входного числа, на первые информационные входы сумматоров подается дополнительный двоичный код модуля, информационные выходы сумматора i-й ступени преобразования, где i=1,.., n-1, соединены с первыми информационными входами мультиплексора этой же ступени преобразования, а выходы переноса соединены с управляющими входами соответствующих мультиплексоров и являются информационными выходами двоичного кода неполного частного устройства, информационный выход мультиплексора (n-1)-й ступени преобразования является информационным выходом двоичного кода остатка устройства, информационные выходы мультиплексоров (1,.., n-2)-й ступеней преобразования соединены со сдвигом на один двоичный разряд в сторону старшего со вторыми информационными входами сумматоров (2,.., n-1)-й ступени преобразования соответственно, отличающееся тем, что информационные выходы мультиплексоров (1,.., n-2)-й ступени преобразования соединены со сдвигом на один двоичный разряд в сторону старшего со вторыми информационными входами мультиплексоров (2,.., n-1)-й ступени преобразования, i-й разряд двоичного кода входного числа, где i=0,.., n-2, соединен с младшим разрядом вторых информационных входов сумматоров и с младшим разрядом вторых информационных входов мультиплексоров (n-i-1)-й ступени преобразования, (n-1)-й разряд двоичного кода входного числа соединен со вторым разрядом второго информационного входа мультиплексора и со вторым разрядом второго информационного входа сумматора первой ступени преобразования.
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 2007 |
|
RU2348965C1 |
| КОМБИНАЦИОННЫЙ РЕКУРРЕНТНЫЙ ФОРМИРОВАТЕЛЬ ОСТАТКОВ | 1992 |
|
RU2029435C1 |
| Реле профильного разделения пиломатериала на сортаменты | 1960 |
|
SU131886A1 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 2007 |
|
RU2356086C2 |
| Вычислительное устройство | 1981 |
|
SU1018113A1 |
Авторы
Даты
2020-03-26—Публикация
2019-02-21—Подача