Область техники, к которой относится изобретение
Изобретение относится к вычислительной технике и может быть использовано в цифровых вычислительных устройствах, в криптографических приложениях, а также в устройствах цифровой обработки сигналов и в системах управления.
Уровень техники
Известен умножитель на два по модулю, содержащий сумматор и мультиплексор [1]. Устройство представляет собой решение в области умножения чисел на два по произвольному модулю. В его состав входят сумматор и мультиплексор, которые совместно обеспечивают повышенную эффективность и быстродействие процесса умножения. Недостатком данного устройства являются его ограниченные функциональные возможности, а именно отсутствие возможности умножения на число, отличное от двух.
Известно устройство для умножения чисел по произвольному модулю, содержащее сумматоры, мультиплексоры, ключи, блоки сдвига, инвертор и сумматор по модулю [2]. Устройство является эффективным решением для умножения чисел по произвольному модулю. Это устройство предлагает расширенные функциональные возможности, которые могут быть применены в цифровых вычислительных устройствах и системах для формирования элементов конечных полей. Недостатком данного устройства является низкое быстродействие, так как умножение осуществляется за (n−1) последовательных шагов преобразования, где n – разрядность устройства.
Наиболее близким по технической сущности к заявляемому изобретению является умножитель по модулю, содержащий ключи, сумматоры, мультиплексоры [3], выбранный в качестве прототипа. Умножитель по модулю позволяет умножать два числа по произвольному модулю за n/2 этапов преобразования, образующих ступени преобразования, где n – разрядность устройства, одновременно обрабатывая два разряда множимого. Однако на каждой ступени преобразования приведение результатов вычисления по произвольному модулю выполняется за два шага, вначале выполняется операция суммирования промежуточных вычислений, а затем осуществляется приведение полученного значения по модулю, что снижает быстродействие устройства.
Техническим результатом изобретения является повышение быстродействия.
Раскрытие сущности изобретения
Для достижения технического результата в умножитель по модулю, содержащий входы кодов множимого, входы кодов множителя, выходы кодов произведения, n/2 ступеней преобразования, где n-разрядность устройства, причем первая ступень преобразования содержит n/2 узлов, а (2…n/2)-е ступени преобразования содержат по одному узлу, каждый узел преобразования первой ступени преобразования содержит первый и второй ключи, двухвходовый сумматор и трехвходовый мультиплексор, а узлы преобразования (2…n/2)-й ступеней преобразования содержат двухвходовые сумматоры и пятивходовые мультиплексоры, информационные входы всех ключей первой ступени преобразования соединены со входами кода множителя, управляющие входы соединены с соответствующими разрядами кода множимого, информационные выходы первых ключей каждого узла первой ступени преобразования соединены с первыми информационными входами соответствующих двухвходовых сумматоров со сдвигом на один разряд в сторону старших, информационные выходы вторых ключей каждого узла первой ступени преобразования соединены со вторыми информационными входами соответствующих двухвходовых сумматоров, информационные выходы двухвходовых сумматоров соединены с первыми информационными входами соответствующих трехвходовых мультиплексоров, информационные выходы трехвходового мультиплексора первого узла первой ступени преобразования соединены со сдвигом на два разряда в сторону старших с первыми информационными входами двухвходового сумматора второй ступени преобразования, информационные выходы трехвходовых мультиплексоров j-го узла первой ступени преобразования, где j=2…n/2, соединены со вторыми информационными входами двухвходовых сумматоров j-й ступени преобразования, информационные выходы двухвходовых сумматоров j-й ступени преобразования соединены с первыми информационными входами соответствующих пятивходовых мультиплексоров, информационные выходы пятивходовых мультиплексоров j-й ступени преобразования, где j=2,…, n/2−1 соединены со сдвигом на два разряда в сторону старших с первыми информационными входами двухвходовых сумматоров (j+1)-й ступени преобразования, а n/2-й ступени преобразования являются выходами кодов произведения дополнительно введены на первой ступени преобразования в каждый узел первый и второй трехвходовые сумматоры, а на (2…n/2)-й ступени преобразования введены первый, второй, третий и четвертый трехвходовые сумматоры, причем первые информационные входы первых и вторых трехвходовых сумматоров первой ступени преобразования соединены с информационными выходами первых ключей соответствующего узла со сдвигом на один разряд в сторону старших, вторые информационные входы соединены с информационными выходами вторых ключей соответствующего узла, на третьи информационные входы первых трехвходовых сумматоров подается инверсный код модуля, а на третьи информационные входы вторых трехвходовых сумматоров подается инверсный код удвоенного модуля, информационные выходы первых трехвходовых сумматоров соединены со вторыми информационными входами соответствующих трехвходовых мультиплексоров, информационные выходы вторых трехвходовых сумматоров соединены с третьими информационными входами соответствующих трехвходовых мультиплексоров, выходы переноса первых трехвходовых сумматоров соединены с первыми управляющими входами соответствующих трехвходовых мультиплексоров, выходы переноса вторых трехвходовых сумматоров соединены со вторыми управляющими входами соответствующих трехвходовых мультиплексоров, первые информационные входы первых, вторых, третьих и четвертых трехвходовых сумматоров второй ступени преобразования соединены со сдвигом на два разряда в сторону старших с информационными выходами трехвходового мультиплексора первого узла первой ступени преобразования, вторые информационные входы первого, второго, третьего и четвертого трехвходовых сумматоров j-й ступени преобразования, где j=2…n/2, соединены с информационными выходами трехвходового мультиплексора j-го узла первой ступени преобразования, на третьи информационные входы первых, вторых, третьих и четвертых трехвходовых сумматоров j-й ступени преобразования, подаются соответственно инверсные коды модуля, инверсные коды удвоенного модуля, инверсные коды утроенного модуля и инверсные коды учетверенного модуля, на входы переноса всех трехвходовых сумматоров подается сигнал логической единицы, причем каждый трехвходовый сумматор содержит m полных одноразрядных сумматоров и (m+1)-разрядный сумматор, (1…m)-й разряды информационных выходов которого являются информационными выходами трехвходового сумматора, а (m+1)-й разряд является выходом переноса трехвходового сумматора, первые информационные входы полных одноразрядных сумматоров соединены с соответствующими разрядами первых информационных входов трехвходового сумматора, вторые информационные входы соединены с соответствующими разрядами вторых информационных входов трехвходового сумматора, третьи информационные входы соединены с соответствующими разрядами третьих информационных входов трехвходового сумматора, информационные выходы (1…m)-го полных одноразрядных сумматоров соединены с (1…m)-м разрядами первых информационных входов (m+1)-разрядного сумматора, а выходы переноса соединены с (2…m+1)-м разрядами вторых информационных входов (m+1)-разрядного сумматора, первый разряд которых соединен со входом переноса трехвходового сумматора, на (m+1)-й разряд первых информационных входов (m+1)-разрядного сумматора подается сигнал логического нуля.
Сущность изобретения заключается в реализации следующего способа вычисления произведения чисел A и B по модулю P. Пусть
(A·B) ≡ R (mod P), (1)
где A – неотрицательное целое число, являющееся множимым;
B – неотрицательное целое число, являющееся множителем, причем B<P;
P – неотрицательное целое число, называемое модулем;
R – неотрицательное целое число, являющееся остатком от произведения чисел A и B по модулю P, R <P.
При этом пусть
A = an−1·2n−1+an−2·2n−2+ an−3·2n−3+an−4·2n−4+ . . . +a3·23+a2·22+a1·2+a0, (2)
B = bm−1·2m−1+ . . . + b1·2+b0, (3)
P = pm−1·2m−1+ . . . +p1·21+p0, (4)
R = rm−1·2m−1+ . . . +r1·21+r0, (5)
где ai, 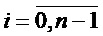 – коэффициенты, принимающие значение 0 или 1 в зависимости от значения числа A;
– коэффициенты, принимающие значение 0 или 1 в зависимости от значения числа A;
n – количество разрядов в представлении множимого, n – четное;
bi, 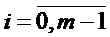 – коэффициенты, принимающие значение 0 или 1 в зависимости от значения числа B;
– коэффициенты, принимающие значение 0 или 1 в зависимости от значения числа B;
pi, 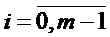 – коэффициенты, принимающие значение 0 или 1 в зависимости от значения модуля P;
– коэффициенты, принимающие значение 0 или 1 в зависимости от значения модуля P;
ri, 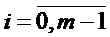 – коэффициенты, принимающие значение 0 или 1 в зависимости от значения остатка R;
– коэффициенты, принимающие значение 0 или 1 в зависимости от значения остатка R;
m – количество разрядов в представлении множителя B, модуля P и остатка R.
Представим произведение чисел A и B следующим образом:
A·B = (an−1·2n−1+an−2·2n−2+ an−3·2n−3+an−4·2n−4+ . . . +a3·23+a2·22+a1·2+a0)·B. (6)
Перепишем выражение (6) следующим образом:
A·B = (an−1·2n−1·B +an−2·2n−2·B + an−3·2n−3·B +an−4·2n−4·B + ...
... +a3·23·B +a2·22·B +a1·2·B +a0·B), (7)
Преобразуем выражение (7) в следующий вид, объединив по два соседних слагаемых:
A·B = (an−1·2n−1·B +an−2·2n−2·B)+ (an−3·2n−3·B +an−4·2n−4·B)+ . . .
. . . +(a3·23·B +a2·22·B)+(a1·2·B +a0·B), (8)
Из каждой суммы в скобках в выражении (8) вынесем 2i за скобки, где 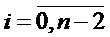 , принимает только четные значения:
, принимает только четные значения:
A·B = 2n−2(an−1·2·B +an−2·B)+2n−4(an−3·2·B +an−4·B)+ . . .
. . . +22(a3·2·B +a2·B)+(a1·2·B +a0·B), (9)
В выражении (9) перед каждой из n/2 образовавшихся сумм вида
(ai+1·2·B+ai·B), получаем множитель 2i, где 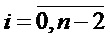 , принимает только четные значения.
, принимает только четные значения.
Далее вынесем в (9) наименьшую ненулевую степень 2 за скобки:
A·B = 22(2n−4(an−1·2·B +an−2·B)+ 2n−6 (an−3·2·B +an−4·B)+ . . .
. . . + (a3·2·B +a2·B))+(a1·2·B +a0·B), (10)
Выполняя последовательно преобразование (10) (n/2)-2 раз получим:
A·B = 22(22…(22(an-1·2·B +an-2·B)+(an-3·2·B +an-4·B))+ . . .
. . . + (a3·2·B +a2·B))+(a1·2·B +a0·B), (11)
где 22 встречается (n/2)−1 раз.
Тогда выражение (1) может быть представлено в следующем виде:
A·B ≡ (22(22…(22(an−1·2·B +an−2·B)+(an−3·2·B +an−4·B))+ . . .
. . . + (a3·2·B +a2·B))+(a1·2·B +a0·B)) mod P. (12)
Из теории чисел известно, что операция приведения по модулю инвариантна к сложению и умножению, т. е. величина остатка не зависит от того, вычислен ли он от суммы (произведения) или от каждого слагаемого (сомножителя), а затем соответствующие частичные остатки просуммированы (перемножены) и от результата вычислен остаток по модулю.
Исходя из вышесказанного, выражение (12) может быть вычислено следующим образом.
Вначале на первой ступени преобразования одновременно в (n/2) узлах вычисляют величины t1i, 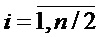 :
:
t 11=(an−1·2·B +an−2·B) mod P,
t12=(an−3·2·B +an−4·B) mod P, (13)
… ,
t1(n/2)=(a1·2·B +a0·B) mod P.
На второй ступени преобразования вычисляют величину
t 2=(22t11+t12) mod P. (14)
Аналогичным образом производят вычисления на последующих ступенях преобразования.
На последней (n/2)-й ступени преобразования вычисляют величину
tn /2=(22tn/2−1+t1(n/2)) mod P, (15)
которая и является искомым произведением чисел A и B по модулю P.
Операция приведения по модулю P на первой ступени преобразования во всех узлах выполняется исходя из следующих соображений.
По определению величина множителя B лежит в диапазоне 0≤ B ≤P-1. Поэтому значение любой величины t1i в (13) до приведения ее по модулю находится в диапазоне от 0 до 3P-3.
Приведение по модулю величины t1i, 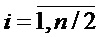 осуществляется по следующим правилам:
осуществляется по следующим правилам:
t 1 i (mod P)= t1i, если 0 ≤ t1i < P, (16)
t 1 i (mod P)= t1i − P, если P ≤ t1i < 2P,
t1i (mod P)= t1i − 2P, если 2P ≤ t1i ≤ (3P − 3),
Условия попадания значения t1i в один из указанных в (16) интервалов определяются значениями сигналов переноса на выходах переноса сумматоров, осуществляющих операцию вычитания (t1i − kP), где k=1, 2 в соответствии с таблицей 1.
Таблица 1.
Таким образом, если значение сигналов переноса равно «1» на выходах переноса двух сумматоров, то t1i (mod P)=t1i − 2P, если значение сигнала переноса равно «1» на выходах переноса одного сумматора, то t1i (mod P) = t1i – P. Если значение сигналов переноса равно «0» на выходах переноса двух сумматоров, то тогда ti (mod P)=ti, т.е. операция вычитания не выполняется.
Операция приведения по модулю P на второй и последующих ступенях преобразования выполняется следующим образом. Значение величин ti,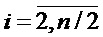 в (14), (15) до приведения по модулю находится в диапазоне от 0 до 5P-5.
в (14), (15) до приведения по модулю находится в диапазоне от 0 до 5P-5.
Приведение по модулю P величины ti, 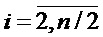 осуществляется по следующим правилам
осуществляется по следующим правилам
ti (mod P)=ti, если 0 ≤ ti < P, (17)
ti (mod P)=ti − P, если P≤ ti < 2P,
ti (mod P)=ti − 2P, если 2P ≤ ti < 3P,
ti (mod P)=ti − 3P, если 3P ≤ ti < 4P,
ti (mod P)=ti − 4P, если 4P ≤ ti ≤ (5P−5).
Условия попадания значения ti в один из указанных в (17) интервалов определяются значениями сигналов переноса на выходах переноса сумматоров, осуществляющих операцию вычитания (ti − kP), где k=1, 2, 3, 4 в соответствии с таблицей 2.
Таблица 2.
Таким образом, если значение сигналов переноса равно «1» на выходах переноса всех четырех сумматоров, то ti (mod P)=ti − 4P, если значение сигналов переноса равно «1» на выходах переноса трех сумматоров, то
ti (mod P)=ti − 3P, если значение сигналов переноса равно «1» на выходах переноса двух сумматоров, то ti (mod P)=ti − 2P, если значение сигнала переноса равно «1» на выходах переноса одного сумматора, то
ti (mod P)=ti − P. Если значение сигналов переноса равно «0» на выходах переноса всех четырех сумматоров, то тогда ti (mod P)=ti, т.е. операция вычитания не выполняется.
В устройстве прототипе на каждой ступени преобразования приведение результатов вычисления по произвольному модулю по выражениям (13)-(15) выполняется за два шага – вначале выполняется операция суммирования промежуточных вычислений, а затем осуществляется приведение полученного значения по модулю. В предлагаемом устройстве операция суммирования промежуточных вычислений и операция приведения по модулю выполняются одновременно.
Краткое описание чертежей
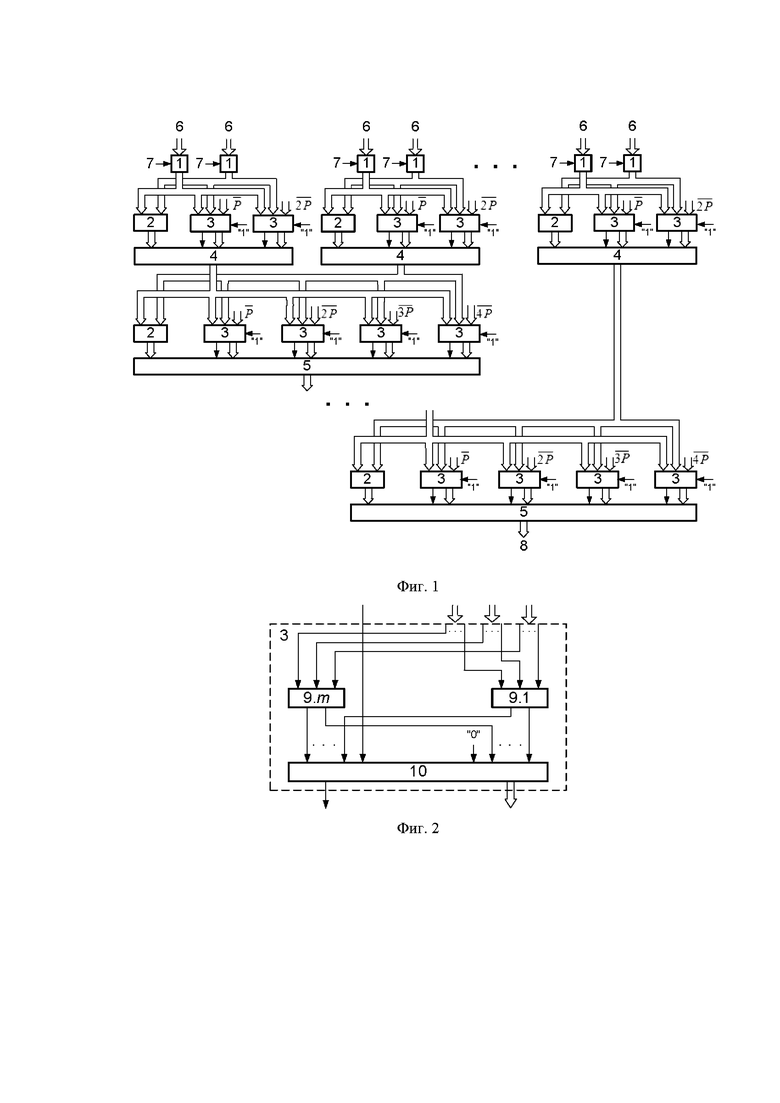
На фиг. 1 представлена схема умножителя по модулю.
Умножитель по модулю содержит входы кодов множимого 7, входы кодов множителя 6, выходы кодов произведения 8, n/2 ступеней преобразования, где n - разрядность кода множимого. Первая ступень преобразования содержит n/2 узлов включающих n ключей 1, n/2 сумматоров 2, n трехвходовых сумматоров 3 и n/2 трехвходовых мультиплексоров 4. Вторая и последующая ступени преобразования содержат каждая сумматор 2, четыре трехвходовых сумматора 3 и пятивходовый мультиплексор 5. Управляющие входы ключей 1 соединены с соответствующими разрядами входов кода множимого 7, а информационные входы соединены со входами кода множителя 6. Информационные выходы первого ключа 1 каждого узла первой ступени преобразования соединены со сдвигом на один разряд в сторону старших с первыми информационными входами сумматора 2, а также первого и второго трехвходовых сумматоров 3 этого же узла. Информационные выходы второго ключа 1 каждого узла первой ступени преобразования соединены со вторыми информационными входами сумматора 2 и первого и второго трехвходовых сумматоров 3. На третьи информационные входы первых трехвходовых сумматоров 3 подается инверсный код модуля, а на третьи информационные входы вторых трехвходовых сумматоров подается инверсный код удвоенного модуля. Информационные выходы сумматора 2 каждого узла первой ступени преобразования соединены с первыми информационными входами трехвходового мультиплексора 4. Информационные выходы первых трехвходовых сумматоров 3 соединены со вторыми информационными входами соответствующих трехвходовых мультиплексоров 4, информационные выходы вторых трехвходовых сумматоров 3 соединены с третьими информационными входами соответствующих трехвходовых мультиплексоров 4, выходы переноса первых трехвходовых сумматоров 3 соединены с первыми управляющими входами соответствующих трехвходовых мультиплексоров 4, выходы переноса вторых трехвходовых сумматоров 3 соединены со вторыми управляющими входами соответствующих трехвходовых мультиплексоров 4. Информационные выходы трехвходового мультиплексора 4 первого узла первой ступени преобразования соединены со сдвигом на два разряда в сторону старших с первыми информационными входами сумматора 2, первого, второго, третьего и четвертого трехвходовых сумматоров 3 второй ступени преобразования. Информационные выходы трехвходового мультиплексора 4 j-го узла первой ступени преобразования, где j=2, ..., n/2, соединены со вторыми информационными входами сумматора 2, первого, второго, третьего и четвертого трехвходовых сумматоров 3 j-й ступени преобразования. На третьи информационные входы первого, второго, третьего и четвертого трехвходовых сумматоров 3 j-й ступени преобразования, подаются соответственно инверсные коды модуля, инверсные коды удвоенного модуля, инверсные коды утроенного модуля и инверсные коды учетверенного модуля. На входы переноса трехвходовых сумматоров 3 всех ступеней преобразования подается сигнал логической единицы. Информационные выходы сумматора 2, первого, второго, третьего и четвертого трехвходовых сумматоров 3 j-й ступени преобразования, соединены соответственно с первым, вторым, третьим, четвертым и пятым информационными входами пятивходового мультиплексора 5 этой же ступени преобразования, а выходы переносов первого, второго, третьего и четвертого трехвходовых сумматоров 3 соединены соответственно с первым, вторым, третьим и четвертым управляющими входами пятивходового мультиплексора 5. Информационные выходы пятивходового мультиплексора 5 j-й ступени преобразования, где j=2, …, n/2-1, соединены со сдвигом на два разряда в сторону старших с первыми информационными входами сумматора 2, первого, второго, третьего и четвертого трехвходовых сумматоров 3 (j+1)-й ступени преобразования. Информационные выходы пятивходового мультиплексора 5 n/2-й ступени преобразования соединены с выходами кодов произведения 8 устройства.
На фиг. 2 представлена схема трехвходового сумматора.
Трехвходовый сумматор содержит m полных одноразрядных сумматоров 9.1÷9.m и (m+1)-разрядный сумматор 10, (1…m)-й разряды информационных выходов которого являются информационными выходами трехвходового сумматора 3, а (m+1)-й разряд является выходом переноса трехвходового сумматора 3. Первые, вторые и третьи информационные входы полных одноразрядных сумматоров 9.1÷9.m соединены с соответствующими разрядами первых, вторых и третьих информационных входов трехвходового сумматора 3. Информационные выходы полных одноразрядных сумматоров 9.1÷9.m соединены соответственно с (1…m)-м разрядами первых информационных входов (m+1)-разрядного сумматора 10, а выходы переноса соединены соответственно со (2…m+1)-м разрядами вторых информационных входов (m+1)-разрядного сумматора 10, первый разряд которых соединен со входом переноса трехвходового сумматора 3. На (m+1)-й разряд первых информационных входов (m+1)-разрядного сумматора 10 подается сигнал логического нуля.
Осуществление изобретения.
Умножитель по модулю работает следующим образом (см. Фиг. 1).
На вход 7 устройства подается n-разрядный двоичный код множимого A. На вход 6 устройства подается m-разрядный код множителя B. На третьи информационные входы первых и вторых трехвходовых сумматоров 3 первой ступени преобразования подается инверсный код модуля и соответственно инверсный код удвоенного модуля. На входы переноса первых и вторых трехвходовых сумматоров 3 всех узлов первой ступени преобразования подается логическая единица. На третьи информационные входы первых, вторых, третьих и четвертых трехвходовых сумматоров 3 второй и последующих ступеней преобразования подается соответственно инверсный код модуля, инверсный код удвоенного модуля, инверсный код утроенного модуля и инверсный код учетверенного модуля.
Вначале на первой ступени преобразования одновременно в (n/2) узлах вычисляют величины t1i, 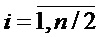 , где i – номер узла:
, где i – номер узла:
t 11=(an-1·2·B +an-2·B) mod P,
t12=(an-3·2·B +an-4·B) mod P,
… ,
t1(n/2)=(a1·2·B +a0·B) mod P.
Умножение разрядов множимого ai на множитель B осуществляется с помощью ключей 1. Умножение множителя B на 2 осуществляется путем сдвига разрядов на один в сторону старших с информационных выходов первых ключей 1 каждого узла при подключении к первым информационным входам сумматоров 2, первым информационным входам первых и вторых трехвходовых сумматоров 3 соответствующего узла. Параллельно сумматор 2, первый и второй трехвходовые сумматоры 3 каждого узла первой ступени преобразования осуществляют суммирование значений ai·2·B и ai-1·B, а первый и второй трехвходовые сумматоры 3 еще приводят получившиеся суммы по модулю путем одновременного вычитания из нее значений P и 2P и трехвходового мультиплексора 4 соответствующего узла, осуществляющего коммутацию на выходы, поступивших на его информационные входы значений сигналов переноса, в соответствии с таблицей 1.
В результате на выходах всех узлов первой ступени преобразования образуются значения t1i, 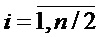 в соответствии с выражением (13).
в соответствии с выражением (13).
На второй ступени преобразования осуществляется вычисление значения t2=(22t11+t12) mod P, где t11 и t12 значения на выходах первого и второго узла первой ступени преобразования. Умножение значения t11 на 22 осуществляется сдвигом разрядов кода t11 на два в сторону старшего. Приведение по модулю P осуществляется аналогичным образом путем одновременного вычитания из суммы значений модуля, удвоенного модуля, утроенного модуля и учетверенного модуля и выбором окончательного значения с помощью пятивходового мультиплексора 4 в зависимости от управляющих сигналов, подаваемых на его вход в соответствии с таблицей 2. Операция вычитания осуществляется с помощью соответствующих трехвходовых сумматоров 3 на третьи информационные входы которых подается в инверсном виде код соответствующих значений модуля, а на вход переноса подается сигнал логической единицы, преобразуя инверсный код в дополнительный.
Трехвходовый мультиплексор 4 в зависимости от комбинаций сигналов на его управляющих входах, коммутирует на свой выход сигнал с одного из своих трех информационных входов. Пятивходовый мультиплексор 5 в зависимости от комбинаций сигналов на его управляющих входах, коммутирует на свой выход один из своих пяти информационных входов в соответствии с таблицей 2.
Трехвходовые сумматоры 3 (см. Фиг. 2) суммируют коды чисел, поступающие на их первые и вторые информационные входы и одновременно вычитают из этой суммы коды чисел, поступающие на их третьи информационные входы. Так как на входы переноса этих сумматоров подается сигнал логической единицы, а на третьи информационные входы поступают инверсные коды значений модуля (удвоенного модуля, утроенного модуля или учетверенного модуля), то в результате образуются соответствующие дополнительные коды, которые и приводят к реализации операции вычитания. На выходах каждого из m полных одноразрядных сумматоров 9.1÷9.m трехвходовых сумматоров 3 формируется сигнал частичной суммы и сигналы сквозного переноса трех чисел, поступающих на их входы. В результате на информационных выходах полных одноразрядных сумматоров 9.1÷9.m образуются поразрядные сигналы частичной суммы, а на выходах переноса образуются поразрядные сигналы сквозного переноса. Сигналы частичной суммы с информационных выходов полных одноразрядных сумматоров 9.1÷9.m поступают на (1, …, m)-й разряды первых информационных входов (m+1)-разрядного сумматора 10, на (m+1)-й разряд которого подается сигнал логического нуля. Сигналы с выходов переноса полных одноразрядных сумматоров 9.1÷9.m поступают на (2, …, (m+1))-й разряды вторых информационных входов (m+1)-разрядного сумматора 10, на первый разряд которого поступает сигнал логической единицы, преобразуя инверсный код модуля в дополнительный. В результате на (1, …, m)-ом разрядах информационных выходов (m+1)-разрядного сумматора 10 образуется значение суммы в соответствии с (13), (14) или (15), причем значение формируемое на (m+1)-м разряде информационных выходов (m+1)-разрядного сумматора 10 является сигналом переноса.
Аналогичные вычисления производятся и на последующих ступенях преобразования. В результате этих вычислений на выходе последней (n/2)-й ступени преобразования образуется значение произведения чисел A и B по модулю P.
Так как на каждой ступени преобразования осуществляется обработка одновременно двух разрядов множимого, то через (n/2) шагов преобразований на выходе кода произведения 8 устройства сформируется двоичный код произведения чисел A и B по модулю P. При этом приведение результатов вычисления по произвольному модулю на каждой ступени преобразования выполняется за один шаг, одновременно с операцией суммирования промежуточных вычислений, что повышает быстродействие устройства.
Источники информации
1. Умножитель на два по модулю. Патент РФ №2015537, МПК G06F 7/49 (1990.01), опубл. 30.06.1994.
2. Устройство для умножения чисел по произвольному модулю. Патент РФ №2316042, МПК G06F 7/523 (2006.01), G06F 7/72 (2006.01), опубл. 27.01.2008. Бюл. № 3.
3. Умножитель по модулю. Патент РФ №2751802, МПК G06F 7/72 (2006.01), G06F 7/523 (2006.01), опубл. 19.07.2021. Бюл. № 20.
| название | год | авторы | номер документа |
|---|---|---|---|
| УМНОЖИТЕЛЬ ПО МОДУЛЮ | 2020 |
|
RU2751802C1 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 2020 |
|
RU2739338C1 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 2020 |
|
RU2756408C1 |
| УМНОЖИТЕЛЬ ЧИСЕЛ ПО ПРОИЗВОЛЬНОМУ МОДУЛЮ | 2024 |
|
RU2839987C1 |
| КОНВЕЙЕРНЫЙ УМНОЖИТЕЛЬ ПО МОДУЛЯМ | 2024 |
|
RU2838847C1 |
| КОНВЕЙЕРНЫЙ ФОРМИРОВАТЕЛЬ ОСТАТКОВ ПО ПРОИЗВОЛЬНОМУ МОДУЛЮ | 2022 |
|
RU2791440C1 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 2022 |
|
RU2796555C1 |
| КОНВЕЙЕРНЫЙ УМНОЖИТЕЛЬ ПО МОДУЛЮ | 2023 |
|
RU2797164C1 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 2023 |
|
RU2798746C1 |
| Устройство для умножения чисел по произвольному модулю | 2020 |
|
RU2755734C1 |
Изобретение относится к вычислительной технике. Технический результат заключается в повышении быстродействия устройства. Технический результат достигается за счет того, что устройство содержит ключи, сумматоры, трехвходовые сумматоры, которые содержат одноразрядные полные сумматоры и (m+1)-разрядный сумматор, и пятивходовые мультиплексоры; при этом при вычислении произведения чисел по модулю P путем последовательного выполнения (n/2) операций, где n – количество разрядов входного числа A, приведение результатов вычисления по произвольному модулю на каждой ступени преобразования выполняется за один шаг, одновременно с операцией суммирования промежуточных вычислений. 2 ил.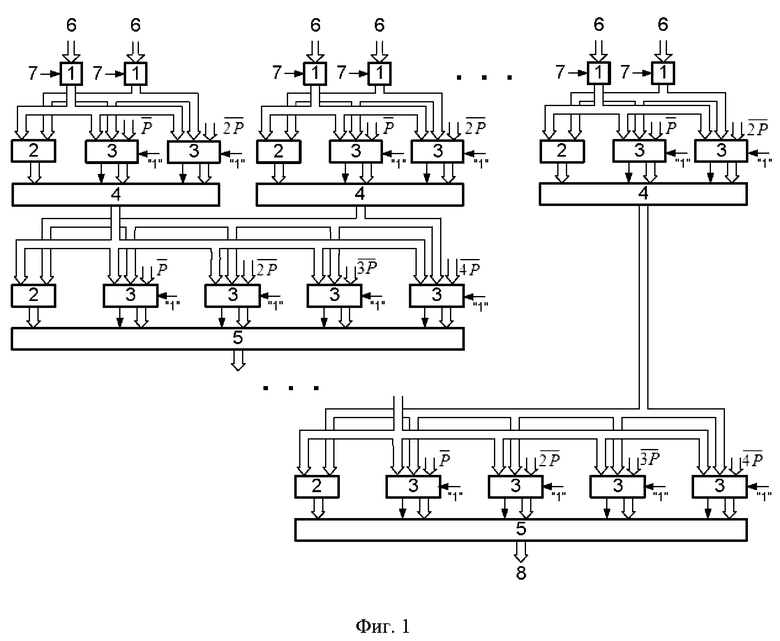
Умножитель по модулю, содержащий входы кодов множимого, входы кодов множителя, выходы кодов произведения, n/2 ступеней преобразования, где n - разрядность устройства, причем первая ступень преобразования содержит n/2 узлов, а (2…n/2)-е ступени преобразования содержат по одному узлу, каждый узел преобразования первой ступени преобразования содержит первый и второй ключи, двухвходовый сумматор и трехвходовый мультиплексор, а узлы преобразования (2…n/2)-й ступеней преобразования содержат двухвходовые сумматоры и пятивходовые мультиплексоры, информационные входы всех ключей первой ступени преобразования соединены со входами кода множителя, управляющие входы соединены с соответствующими разрядами кода множимого, информационные выходы первых ключей каждого узла первой ступени преобразования соединены с первыми информационными входами соответствующих двухвходовых сумматоров со сдвигом на один разряд в сторону старших, информационные выходы вторых ключей каждого узла первой ступени преобразования соединены со вторыми информационными входами соответствующих двухвходовых сумматоров, информационные выходы двухвходовых сумматоров соединены с первыми информационными входами соответствующих трехвходовых мультиплексоров, информационные выходы трехвходового мультиплексора первого узла первой ступени преобразования соединены со сдвигом на два разряда в сторону старших с первыми информационными входами двухвходового сумматора второй ступени преобразования, информационные выходы трехвходовых мультиплексоров j-го узла первой ступени преобразования, где j=2…n/2, соединены со вторыми информационными входами двухвходовых сумматоров j-й ступени преобразования, информационные выходы двухвходовых сумматоров j-й ступени преобразования соединены с первыми информационными входами соответствующих пятивходовых мультиплексоров, информационные выходы пятивходовых мультиплексоров j-й ступени преобразования, где j=2,…, n/2−1, соединены со сдвигом на два разряда в сторону старших с первыми информационными входами двухвходовых сумматоров (j+1)-й ступени преобразования, а n/2-й ступени преобразования являются выходами кодов произведения, отличающийся тем, что в него введены на первой ступени преобразования в каждый узел первый и второй трехвходовые сумматоры, а на (2…n/2)-й ступени преобразования введены первый, второй, третий и четвертый трехвходовые сумматоры, причем первые информационные входы первых и вторых трехвходовых сумматоров первой ступени преобразования соединены с информационными выходами первых ключей соответствующего узла со сдвигом на один разряд в сторону старших, вторые информационные входы соединены с информационными выходами вторых ключей соответствующего узла, на третьи информационные входы первых трехвходовых сумматоров подается инверсный код модуля, а на третьи информационные входы вторых трехвходовых сумматоров подается инверсный код удвоенного модуля, информационные выходы первых трехвходовых сумматоров соединены со вторыми информационными входами соответствующих трехвходовых мультиплексоров, информационные выходы вторых трехвходовых сумматоров соединены с третьими информационными входами соответствующих трехвходовых мультиплексоров, выходы переноса первых трехвходовых сумматоров соединены с первыми управляющими входами соответствующих трехвходовых мультиплексоров, выходы переноса вторых трехвходовых сумматоров соединены со вторыми управляющими входами соответствующих трехвходовых мультиплексоров, первые информационные входы первых, вторых, третьих и четвертых трехвходовых сумматоров второй ступени преобразования соединены со сдвигом на два разряда в сторону старших с информационными выходами трехвходового мультиплексора первого узла первой ступени преобразования, вторые информационные входы первого, второго, третьего и четвертого трехвходовых сумматоров j-й ступени преобразования, где j=2…n/2, соединены с информационными выходами трехвходового мультиплексора j-го узла первой ступени преобразования, на третьи информационные входы первых, вторых, третьих и четвертых трехвходовых сумматоров j-й ступени преобразования подаются соответственно инверсные коды модуля, инверсные коды удвоенного модуля, инверсные коды утроенного модуля и инверсные коды учетверенного модуля, на входы переноса всех трехвходовых сумматоров подается сигнал логической единицы, причем каждый трехвходовый сумматор содержит m полных одноразрядных сумматоров и (m+1)-разрядный сумматор, (1…m)-й разряды информационных выходов которого являются информационными выходами трехвходового сумматора, а (m+1)-й разряд является выходом переноса трехвходового сумматора, первые информационные входы полных одноразрядных сумматоров соединены с соответствующими разрядами первых информационных входов трехвходового сумматора, вторые информационные входы соединены с соответствующими разрядами вторых информационных входов трехвходового сумматора, третьи информационные входы соединены с соответствующими разрядами третьих информационных входов трехвходового сумматора, информационные выходы (1…m)-го полных одноразрядных сумматоров соединены с (1…m)-м разрядами первых информационных входов (m+1)-разрядного сумматора, а выходы переноса соединены с (2…m+1)-м разрядами вторых информационных входов (m+1)-разрядного сумматора, первый разряд которых соединен со входом переноса трехвходового сумматора, на (m+1)-й разряд первых информационных входов (m+1)-разрядного сумматора подается сигнал логического нуля.
| УСТРОЙСТВО ДЛЯ УМНОЖЕНИЯ ЧИСЛА ПО МОДУЛЮ НА КОНСТАНТУ | 2017 |
|
RU2653310C1 |
| Устройство вычисления модулярного произведения Монтгомери | 2017 |
|
RU2652450C1 |
| КОНВЕЙЕРНЫЙ УМНОЖИТЕЛЬ ПО МОДУЛЮ | 2023 |
|
RU2797164C1 |
| УМНОЖИТЕЛЬ ПО МОДУЛЮ | 2015 |
|
RU2589361C1 |
| US 20050033790 A1, 10.02.2005. | |||
Авторы
Даты
2024-10-23—Публикация
2024-06-04—Подача