Изобретение относится к способам определения прочности сложнонапряженных деталей, нагруженных системой сил, отдельные компоненты которых могут меняться несинхронно по отношению друг к другу, а количество циклов их нагружения не превышает предела квазистатической усталости.
Работоспособность детали при количестве циклов нагружения не более 103-104 определяется её статической прочностью [1]. Статическую прочность деталей из пластичных металлов обычно оценивают посредством коэффициента запаса по пределу текучести, а из хрупких металлов - по пределу прочности. Допустимые напряжения назначают с расчетом, чтобы до наступления текучести или разрушения был обеспечен определенный коэффициент запаса n статической прочности.
Наибольшие напряжения вне зон воздействия на деталь контактных сил обычно возникают на поверхности деталей. Это обусловлено тем, что в любом сечении детали по мере приближения к её поверхности напряжения от изгибающих и крутящих моментов достигают наибольших значений. Поэтому разрушение обычно начинается с поверхностного слоя, и статическую прочность детали вне зон воздействия на неё внешних контактных сил обычно можно оценить величиной напряжений на поверхности детали.
Вне зон воздействия контактных сил составляющая усилий, направленных перпендикулярно поверхности детали, отсутствует, поэтому напряженное состояние на каждом из участков поверхностного слоя такой детали носит плосконапряженный характер. При несинхронном изменении различных составляющих системы сил, действующих на деталь, отдельные компоненты тензоров плосконапряженного состояния на каждом из участков поверхностного слоя детали изменяются несинхронно по отношению друг к другу. При анализе статической прочности таких участков оценка степени опасности возникающих в них напряженных состояний должна быть выполнена с учетом различного сочетания компонентов тензоров их плосконапряженного состояния.
Известен способ графической записи изменения тензора двухосных напряжений в рассматриваемой точке поверхности детали [2]. В одном из вариантов указанного способа запись изменения тензора плосконапряженного состояния может быть представлена в виде кругов Мора, последовательно отображаемых вдоль оси Оσ в прямоугольной системе координат Оστ. Такая запись однозначно определяет характер изменения тензора напряжений в исследуемой зоне поверхности детали. Предложенный способ записи изменения двухосных напряжений может быть реализован путем обработки результатов расчета напряжений в детали при последовательно изменяемых схемах её нагружения или путем обработки показаний, экспериментально снимаемых в исследуемой зоне поверхности этой детали трехкомпонентной розеткой тензорезисторов . При этом круги Мора, отображающие тензоры напряжений, у которых напряжения растяжения-сжатия, действующие в плоскости поверхности детали параллельно начально выбранному на ней направлению, имеет алгебраически (с учетом знаков) более высокие значения по сравнению с напряжениями растяжения-сжатия, действующими в той же плоскости в перпендикулярном начально выбранному на поверхности детали направлении, изображают сплошными линиями, а круги, у которых напряжения растяжения-сжатия выше в направлении, перпендикулярном по отношении к начально выбранному, изображают пунктирными линиями.
К недостаткам указанного способа следует отнести то, что в нем не указано, как по характеру записи последовательного изменения тензора напряжений в исследуемой зоне поверхности детали определить статическую прочность детали в этой зоне.
Известны следующие способы определения статической прочности детали или её материала при сложном (двух- и трехосном) напряженном состоянии:
- способ с применением метода Мора;
- способы с использованием различных гипотез прочности [3, 4].
Более точную оценку статической прочности сложнонапряженной детали обеспечивает метод Мора [3, 4]. При его применении сначала при различных напряженных состояниях производят испытание материала детали. При этом в испытываемых образцах из материала детали создают определенные соотношения между действующими в них главными напряжениями σ1 и σ3. Далее, не меняя пропорции между указанными главными напряжениями, увеличивают их вплоть до появления текучести или разрушения образца. Зафиксированные при этом предельные величины главных напряжений σ1 и σ3 отображают в прямоугольной системе координат Оστ в виде круга Мора. Производя аналогичные операции при других, доступных для проведения испытаний пропорциях между σ1 и σ3, в прямоугольной системе координат Оστ выполняют построение серии кругов Мора, которые соответствуют исследуемым предельным напряженным состояниям при заданных соотношениях компонентов тензоров напряжений. На построенные таким способом круги Мора наносят огибающую их кривую, которая и определяет границу области предельных напряженных состояний (область статической прочности) рассматриваемого материала детали при различных сочетаниях σ1 и σ3.
После этого в той же прямоугольной системе координат Оστ строят круги Мора, которые при каждом из рассматриваемых вариантов нагружения исследуемой детали отображают возникающие в ней тензоры напряжений, действующие в плоскости главных напряжений σ1 и σ3. При этом если каждый из этих кругов находится внутри области допускаемых напряженных состояний, то статическая прочность детали в исследуемой зоне обеспечена.
К недостаткам метода следует отнести его чрезмерную сложность, связанную с тем, что взаимно перпендикулярные векторы напряжений σ1 и σ3 могут иметь самые различные направления в пространстве. Значения σ1 и σ3 в испытываемых образцах из материала детали и в исследуемой детали часто могут быть установлены расчетным путем, причем с неизбежными погрешностями расчета, а экспериментальным путем - лишь с использованием замораживаемых объемных поляризационных оптических моделей. Поэтому указанный классический метод Мора целесообразно применять для исследования статической прочности деталей в зоне воздействия на них контактных сил, где тензор максимальных напряжений имеет трехосный характер. При оценке статической прочности сложнонапряженный детали вне зон воздействия на неё контактных сил, как уже было отмечено, достаточно учесть наибольшие напряжения, которые возникают на её поверхности и носят плосконапряженный характер, поэтому проще поддаются расчетному и экспериментальному определению. К тому же в классическом методе Мора отсутствует учет влияния на статическую прочность второго главного напряжения σ2.
К недостаткам классического метода Мора также можно отнести построение границы области предельных напряженных состояний рассматриваемого материала (границы области статической прочности) в виде линии, огибающей окружности серии предельных кругов Мора. Если, например, выяснится, что потеря работоспособности материала детали при трехосном растяжении возникает при более низкой величине первого главного напряжения σ1, чем при его одноосном растяжении, то предельный круг Мора, соответствующий трехосному растяжению, окажется внутри круга Мора, соответствующего напряженному состоянию при одноосном растяжении. В этом случае построение области статической прочности в виде огибающей предельных кругов Мора будет невозможно.
Известны также способы определения статической прочности сложнонапряженной детали с использованием гипотез прочности, позволяющих привести сложное напряженное состояние материала к эквивалентному ему по разрушающей способности одноосному напряженному состоянию [3, 4]. Эти способы удобны тем, что расчет запаса статической прочности производится в виде отношения эквивалентных напряжений, действующих в исследуемой детали, к эквивалентным напряжениям предельного напряженного состояния её материала, которые выражены в виде чисел. Наиболее распространенными и часто применяемыми в настоящее время являются гипотезы наибольших касательных напряжений Треска - Сен-Венана и энергии изменения формы Хубера - Мизеса.
К недостаткам способов определения статической прочности по каждой из указанных гипотез следует отнести то, что при ряде напряженных состояний эти гипотезы не в полной мере отображают поведение реального материала. В частности, в указанных гипотезах не отражено, что предел текучести или разрушения реального материала при его растяжении и сжатии одинаковыми по модулю напряжениями часто не совпадают между собой. Помимо этого, расчет по различным гипотезам прочности дает неодинаковые между собой результаты, и каждая из этих гипотез больше подходит к какому-то одному типу материалов. В настоящее время не выполнено наглядного сравнения результатов, получаемых при разных видах напряженного состояния материала детали путем экспериментального определения статической прочности и по каждой из указанных гипотез прочности.
Техническим результатом изобретения является увеличение точности определения статической прочности деталей на участках их поверхности, расположенных вне зон воздействия контактных сил. Увеличение точности достигают за счет:
- определения запаса статической прочности n в исследуемой зоне поверхности детали путем выявления отношения максимально допустимых напряжений в материале детали к максимальным напряжениям, возникающим в указанной зоне детали при одинаковом соотношении всех компонентов тензоров сравниваемых между собой плосконапряженных состояний;
- определения по данным экспериментального исследования на образцах из материала детали точных величин компонентов тензоров плосконапряженного состояния, соответствующих пределу текучести или достижению предела статической прочности этого материала и построения в прямоугольной системе координат Оστ точной границы области предельных плосконапряженных состояний этого материала;
- выбора для расчета той из используемых гипотез прочности, согласно которой граница области предельных плосконапряженных состояний в наибольшей мере повторяет границу, полученную экспериментальным путем;
- учета не двух, а всех трех главных напряжений тензоров сравниваемых между собой напряженных состояний (одно из этих главных напряжений направлено перпендикулярно поверхности детали и равно нулю).
Технический результат по первому варианту достигается тем, что в способе определения статической прочности сложнонапряженной детали вне зон воздействия на неё контактных сил, включающем построение в прямоугольной системе координат Оστ графической записи малоцикловой смены тензоров двухосных напряжений в рассматриваемой точке поверхности детали в процессе её эксплуатации, выполняемой в виде серии кругов Мора, построенных на основе данных о двухосных напряжениях в этой точке в последовательно взятые моменты времени, с центрами кругов Мора, расположенными на оси Оσ, направление которой связано с выбранным направлением на поверхности исследуемой детали, также включающем построение в той же прямоугольной системе координат Оστ границы области предельных напряженных состояний материала детали, построенной путем обобщения отдельных экспериментальных данных, которые отображены в виде серии предельных кругов Мора, описывающих различные, доступные для получения при проведении испытаний, тензоры предельных напряженных состояний в образцах из материала детали, по данным экспериментального исследования, проводимого на образцах из материала детали, определяют точные величины различных сочетаний компонентов тензоров плосконапряженного состояния, при которых достигается предел текучести или предел статической прочности материала детали, указанные сочетания компонентов тензоров плосконапряженного состояния отображают в прямоугольной системе координат Оστ в виде серии предельных кругов Мора, затем путем проведения параллельно оси Оτ диаметров предельных кругов Мора и последующего построения линии, огибающей точки пересечения этих диаметров с окружностями, ограничивающими указанные предельные круги Мора, выполняют построение границы области предельных плосконапряженных состояний материала детали, при этом критерием обеспечения статической прочности исследуемой зоны детали является расположение точек пересечения диаметров, проведенных параллельно оси Оτ во всех кругах Мора, которые отображают отдельные плосконапряженные состояния, возникающие в исследуемой зоне поверхностного слоя детали, с окружностями, ограничивающими эти круги, внутри границ области предельных плосконапряженных состояний, дополнительно определяют уточненный запас статической прочности n в исследуемой зоне поверхности детали путем выявления отношения максимально допустимых касательных напряжений в материале детали, выявленных по данным экспериментального исследования, к максимальным касательным напряжениям, возникающим в исследуемой зоне детали при одинаковом соотношении всех компонентов тензоров сравниваемых между собой плосконапряженных состояний.
Технический результат по второму варианту достигается тем, что в способе определения статической прочности сложнонапряженной детали вне зон воздействия на неё контактных сил, включающем построение в прямоугольной системе координат Оστ графической записи малоцикловой смены тензоров двухосных напряжений в рассматриваемой точке поверхности детали в процессе её эксплуатации, выполняемой в виде серии кругов Мора, построенных на основе данных о двухосных напряжениях в этой точке в последовательно взятые моменты времени, с центрами кругов Мора, расположенными на оси Оσ, направление которой связано с выбранным направлением на поверхности исследуемой детали, также включающем построение в той же прямоугольной системе координат Оστ границы области предельных напряженных состояний материала детали, построенной путем обобщения отдельных экспериментальных данных, которые отображены в виде серии предельных кругов Мора, описывающих различные, доступные для получения при проведении испытаний, тензоры предельных напряженных состояний в образцах из материала детали, построение границы области предельных плосконапряженных состояний материала детали в прямоугольной системе координат Оστ выполняют путем построения по каждой из гипотез прочности при различных тензорах напряжений серии предельных кругов Мора, параллельно оси Оτ проводят диаметры указанных предельных кругов Мора и строят линию, огибающую точки пересечения этих диаметров с окружностями, ограничивающими указанные предельные круги Мора, выбирают ту границу области предельных плосконапряженных состояний, которая в наибольшей мере повторяет границу, построенную экспериментальным путем, при этом критерием обеспечения статической прочности исследуемой зоны детали является расположение точек пересечения диаметров, проведенных параллельно оси Оτ, во всех кругах Мора, отображающих отдельные плосконапряженные состояния, возникающие в исследуемой зоне поверхностного слоя детали, с окружностями, ограничивающими эти круги, внутри указанной границы области предельных плосконапряженных состояний, дополнительно определяют запас статической прочности n в исследуемой зоне поверхности детали путем выявления отношения максимально допустимых касательных напряжений в материале детали, полученных по формулам той гипотезы прочности, согласно которой построена граница области предельных плосконапряженных состояний, в наибольшей степени совпадающая с границей, построенной экспериментальным путем, к максимальным касательным напряжениям, возникающим в исследуемой зоне детали при одинаковом соотношении всех компонентов тензоров сравниваемых между собой плосконапряженных состояний.
Предложенные способы определения статической прочности сложнонапряженной детали поясняются фигурами.
На фиг. 1 показаны границы области предельных плосконапряженных состояний материала детали, построенные экспериментальным и расчетными способами, а также представлен пример определения запаса статической прочности при одном из тензоров плосконапряженного состояния на поверхности рассматриваемой детали.
На фиг. 2 представлено состояние предельного плосконапряженного сжатия поверхностного слоя детали.
На фиг. 3 - состояние предельного плосконапряженного растяжения - сжатия поверхностного слоя детали.
На фиг. 4 - состояние предельного плосконапряженного растяжения поверхностного слоя детали.
На фиг. 5 показано построение границы области предельных плосконапряженных состояний материала детали расчетным способом по гипотезе прочности наибольших касательных напряжений Треска - Сен-Венана.
На фиг. 6 показано построение границы области предельных плосконапряженных состояний материала детали расчетным способом по гипотезе прочности Хубера-Мизеса.
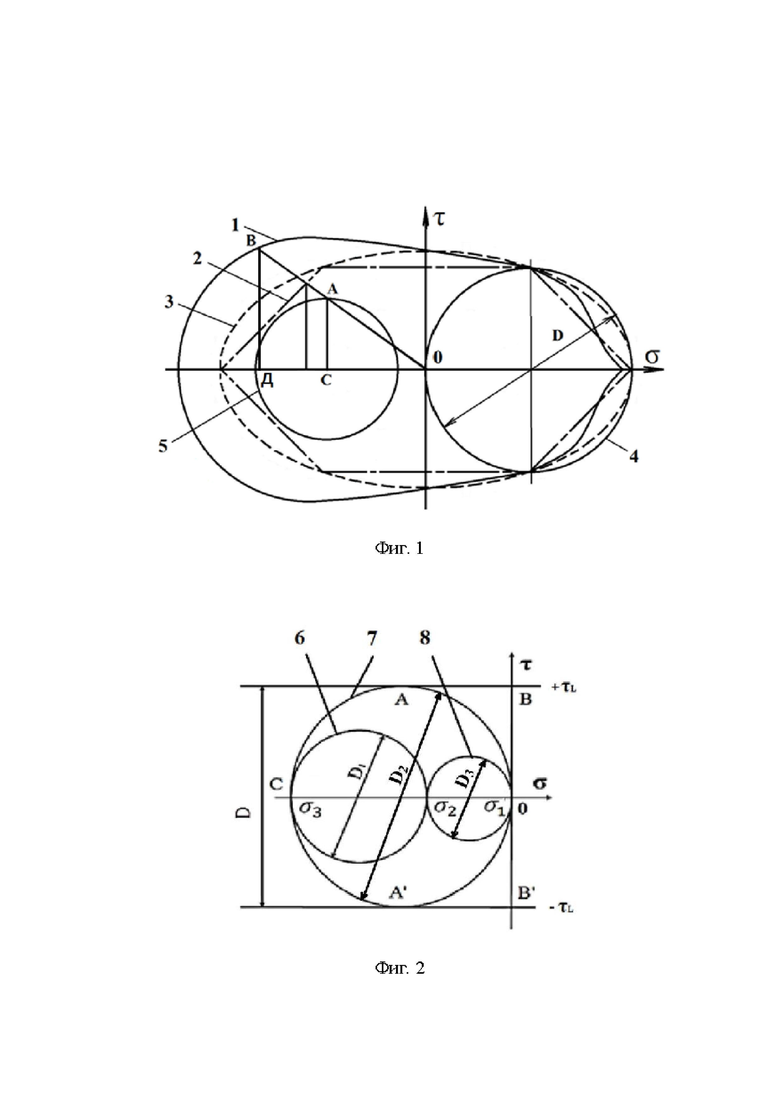
Линиями 1, 2, 3 на фиг. 1 представлены различные границы области предельных плосконапряженных состояний материала детали, определяющие статическую прочность поверхностного слоя этой детали в зонах, где на неё не действуют контактные силы. Границы представлены в прямоугольной системе координат Оστ, где σ и τ - соответственно, нормальное и касательное напряжения, действующие в рассматриваемой точке поверхностного слоя. Сплошной линией 1 обозначена граница области предельных плосконапряженных состояний, построенная на основе экспериментальных данных по исследованию испытываемых образцов, изготовленных из материала детали. Штрихпунктирной линией 2 обозначена граница области предельных плосконапряженных состояний, построенная по гипотезе наибольших касательных напряжений. Пунктирной линией 3 - граница области предельных плосконапряженных состояний материала детали, построенная по гипотезе прочности энергии формоизменения. Круг Мора 4 соответствует предельно допустимому одноосному растяжению исследуемого материала. Круг Мора 5 отображает один из тензоров напряжений, последовательно возникающих в рассматриваемой точке поверхности детали во время её эксплуатации.
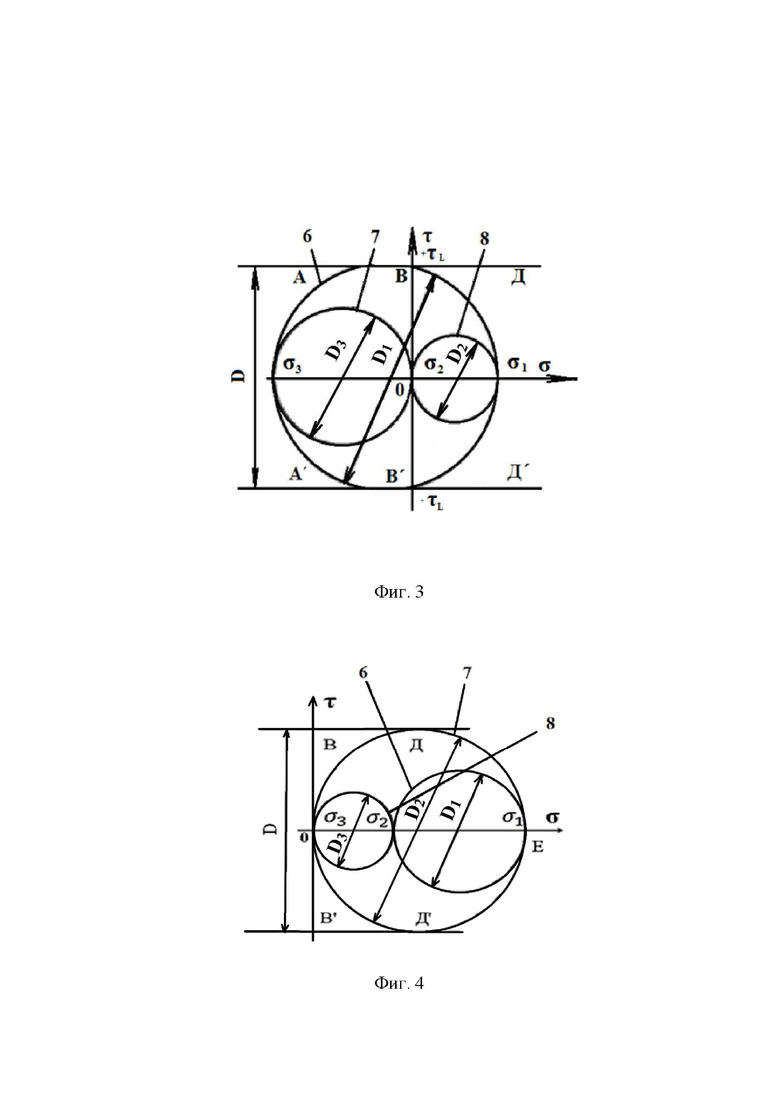
На фиг. 2-4 представлены три возможных варианта расположения трех кругов Мора, характеризующих в объемном представлении плоское напряженное состояние, которое возникает в трех главных площадках исследуемой точки, расположенной на поверхности детали вне зоны воздействия на неё внешних сил. При этом позицией 6 обозначен круг Мора, соответствующий тензору предельных напряжений, возникающих в исследуемой точке поверхности детали в той главной плоскости, которая расположена касательно к поверхности детали. Позициями 7 и 8 обозначены круги Мора, соответствующие тензорам предельных напряженных состояний, возникающих в исследуемой точке в двух других главных плоскостях, расположенных перпендикулярно по отношению к направлениям двух главных напряжений, действующих в плоскости, касательной к поверхности детали.
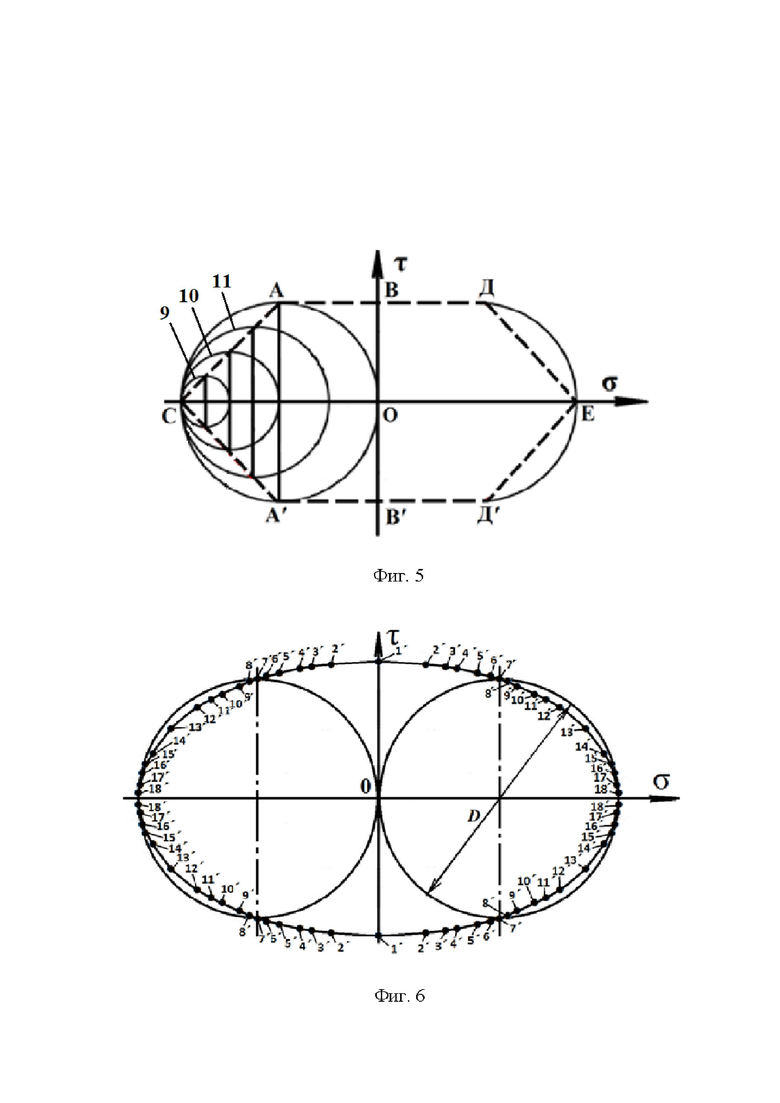
На фиг. 5 показано построение в системе координат Оστ границы АВДЕД'В'А'С области статической прочности поверхностного слоя материала детали по гипотезе прочности наибольших касательных напряжений. Позициями 9, 10, 11 обозначены отдельные круги Мора, соответствующие тензорам предельных плосконапряженных состояний, возникающим в главной плоскости, совпадающей с плоскостью, касательной к поверхности детали (кругам Мора 9, 10, 11 на фиг.5 соответствуют круги Мора 6 на фиг. 2-3).
На фиг. 6 показано построение в системе координат Оστ границы области статической прочности поверхностного слоя материала детали по гипотезе прочности энергии формоизменения. Позициями 1', 2', …, 18' отмечены отдельные точки этой границы, соответствующие тензорам предельных плосконапряженных состояний, возникающих в главной плоскости, которая совпадает с плоскостью, касательной к поверхности детали.
Способ определения статической прочности сложнонапряженной детали вне зон воздействия на нее контактных сил в рассматриваемой точке её поверхности осуществляют следующим образом.
Из материала детали изготавливают испытательные образцы, в поверхностном слое которых создают различные заданные пропорции между отдельными компонентами тензоров напряжений. Далее, плавно увеличивая прикладываемую к образцам нагрузку и сохраняя при этом заданную пропорцию между отдельными компонентами тензора напряжений, определяют величины напряжений, при которых происходит нарушение нормальных условий работы этих образцов по причине начала текучести или достижения предела статической прочности исследуемого материала.
Тензоры предельных плосконапряженных состояний, которые возникают в плоскости поверхности испытываемых образцов в период, предшествующий началу текучести или разрушения, изображают в системе прямоугольных координат Оστ в виде предельных кругов Мора. Далее, параллельно оси Оτ проводят диаметры этих кругов. Точки пересечения этих диаметров с окружностями, ограничивающими круги Мора, соответствуют величинам максимальных касательных напряжений при рассматриваемом сочетании компонентов тензоров плосконапряженного состояния. Проводят линию, огибающую эти точки, которая и представляет собой границу области предельно допустимых напряжений для данного материала, полученную на основе данных эксперимента. Возможный вид такой границы представлен на фиг. 1 сплошной линией 1.
Конфигурация построенной указанным образом границы отличается от той, которую обычно изображают при изложении обобщенной теории прочности Мора [3, 4]. Это связано с тем, что в классической обобщенной теории прочности Мора граница предельных напряженных состояний строится по напряжениям, действующим в плоскости наибольшего и наименьшего главных напряжений σ1 и σ3. При этом направление указанных главных напряжений в пространстве испытываемого образца во внимание не принимается. В классической теории прочности Мора величина второго главного напряжения σ2 в системе координат Оστ находится между величинами σ1 и σ3. Отрицательным значениям σ1 и σ3 соответствует состояние трехстороннего сжатия. При пропорциональном увеличении абсолютных значений трех близких по модулю сжимающих напряжений разрушить материал детали невозможно. Поэтому верхняя и нижняя ветви границы области предельно допустимых напряжений материала детали в классической обобщенной теории прочности Мора между собой не смыкаются.
На фиг. 1 левую часть границы области допускаемых плосконапряженных состояний определяет предельный круг Мора, который построен при одноосном или двухосном напряжении сжатия с главными напряжениями, действующими в плоскости поверхностного слоя материала детали, σ2 и σ3, (фиг. 2). Максимальное σ1 из трех главных напряжений в этом случае направлено перпендикулярно поверхности детали и равно нулю. Поэтому, если в исследуемой точке значение σ3 по модулю превысит допустимое значение, то превысит допустимое значение и величина |σ1 - σ3|, при этом условие прочности детали в исследуемой точке нарушится. В связи с этим на фиг. 1, левая часть границы 1 области допускаемых плосконапряженных состояний является замкнутой.
Конфигурация правой части границы 1 области предельных плосконапряженных состояний в материале детали, которая показана на фиг. 1, соответствует такому поведению материала, при котором в случае равномерного двухосного растяжения поверхностного слоя его разрушение происходит при меньшей величине первых двух главных напряжений, чем в случае предельного одноосного растяжения, отображенного на фиг. 1 кругом Мора 4. В таком случае построить границу области статической прочности в виде огибающей серии предельных кругов Мора, как это принято в классической обобщенной теории прочности Мора, невозможно. Поэтому границу 1 области предельных плосконапряженных состояний материала детали предлагается проводить в системе координат Оστ путем соединения между собой верхних, а затем нижних точек вертикально проведенных диаметров кругов Мора, которые в процессе экспериментальных исследований отображают предельные плосконапряженные состояния в этом материале.
При указанном построении границы 1 области предельных плосконапряженных состояний материала детали в плоскости её поверхностного слоя выполнен точный учет всех трех главных напряжений. (Одно из этих главных напряжений направлено перпендикулярно к поверхности детали и равно нулю). Учет всех трех главных напряжений повышает точность и достоверность рассматриваемого способа определения статической прочности детали по сравнению со способом, предложенным в классической теории прочности Мора, где влияние на статическую прочность второго главного напряжения не учитывают.
После построения по данным экспериментального исследования границы 1 области статической прочности (фиг.1) в той же системе координат Оστ строят круги Мора, которые в разные моменты времени отображают тензоры напряжений, возникающих в рассматриваемой точке поверхности детали во время её эксплуатации, например, круг Мора 5. Параллельно оси Оτ проводят радиусы или диаметры этих кругов. (В круге Мора 5 это радиус АС). Точки пересечения указанных радиусов или диаметров с окружностями, ограничивающими круги Мора (в круге Мора 5 это точка А), отображают максимальные касательные напряжения, последовательно возникающие в указанной зоне детали во время её эксплуатации. Критерием обеспечения статической прочности исследуемой зоны детали является расположение указанных точек внутри границы, построенной по данным экспериментального исследования.
Запас статической прочности n в исследуемой зоне поверхности детали при каждом из её плосконапряженных состояний определяют путем выявления отношения максимальных касательных напряжений, при которых возникает состояние текучести или достигается предел статической прочности материала детали, к максимальным касательным напряжениям, возникающим в указанной зоне детали во время её эксплуатации. При этом соотношение всех компонентов тензоров, сравниваемых между собой плосконапряженных состояний должно быть одинаковым. Для определения запаса статической прочности n в рассматриваемой точке поверхности детали при её плосконапряженном состоянии, определяемом кругом Мора 5, через точку О начала системы координат Оστ и точку А радиуса СА, проведенного параллельно оси Оτ, проводят прямую до её пересечения в точке В с границей 1 рассматриваемой области статической прочности, построенной по данным экспериментального исследования. Коэффициент запаса статической прочности определяется соотношением:
n = BД/АС = ОВ/ОА =ОД/ОС (1)
Выражение (1) составлено на основании того, что при увеличении пропорционально коэффициенту запаса статической прочности n всех компонентов рассматриваемого тензора плосконапряженного состояния, отображаемого кругом Мора 5, положение центра круга Мора 5 на оси Оσ и его диаметр увеличатся пропорционально коэффициенту запаса статической прочности n. При этом у круга Мора 5 верхняя точка А радиуса СА, проведенного параллельно оси Оτ, совпадет с точкой В (фиг. 1) и окажется на границе 1 области статической прочности.
Граница области предельных плосконапряженных состояний материала детали в прямоугольной системе координат Оστ может также быть построена по различным гипотезам прочности. На фиг. 1 позициями 2 и 3 обозначены границы, построенные, соответственно, по гипотезе наибольших касательных напряжений Треска - Сен-Венана и по гипотезе прочности энергии формоизменения Хубера-Мизеса.
Принцип построения границы по гипотезе наибольших касательных напряжений поясняется на фиг. 2-4. На каждой из этих фигур в системе прямоугольных координат Оστ показаны три круга Мора, отображающие полное плосконапряженное состояние в материале детали. Круг Мора 6 (фиг. 2-4) описывает плосконапряженное состояние в главной площадке, расположенной в плоскости, касательной к поверхности детали, а два других круга Мора 7 и 8 описывают напряженное состояние в главных площадках, расположенных в плоскостях перпендикулярных этой поверхности. Так как модуль главного напряжения, направленного перпендикулярно поверхности детали, равен нулю, то круги Мора 7 и 8 одной из своих точек касаются начала системы координат Оστ. Два главных напряжения, действующих в плоскости поверхности детали, могут иметь одинаковые знаки - двухосное сжатие (фиг. 2) или двухосное растяжение (фиг. 4) поверхностного слоя. Характер расположения трех кругов Мора при разных знаках главных напряжений, действующих в плоскости поверхности детали, представлен на фиг. 3.
Согласно гипотезе прочности наибольших касательных напряжений Треска - Сен-Венана, опасное напряженное состояние в рассматриваемой точке материала детали наступает, если наибольшее из трех максимальных касательных напряжений τmax, действующих в этой точке в главных площадках, достигает предельно допустимой величины τL. В свою очередь, эта предельно допустимая величина τL определяет эквивалентное напряжение σэкв.касат., по указанной гипотезе прочности [3, 4]. Таким образом, условие прочности соблюдено, если:

где τmax - наибольшее из трех максимальных касательных напряжений, действующих в главных площадках в рассматриваемой точке;
τL - предельно допустимая величина касательных напряжений;
σ1 - максимальное главное напряжение в рассматриваемой точке;
σ3 - минимальное главное напряжение в рассматриваемой точке;
σэкв.касат. - эквивалентное напряжение по гипотезе прочности наибольших касательных напряжений.
Согласно (2), чтобы соответствовать гипотезе прочности наибольших касательных напряжений Треска - Сен-Венана, диаметр D наибольшего из трех кругов Мора (фиг. 2-4), отображающего наибольшую разность главных напряжений σ1 - σ3 , не должен выходить за пределы области максимальных касательных напряжений ±τL. Исходя из этих условий, путем рассмотрения различных сочетаний двух главных напряжений, которые действуют в плоскости поверхности детали и участвуют в построении круга Мора 6 диаметром D1, можно в прямоугольной системе координат Оστ выполнить построение области предельных напряженных состояний в поверхностном слое детали, при которых полный тензор напряжений в исследуемой зоне её поверхности принимает предельно допустимые значения. При этом максимальные касательные напряжения τL могут быть достигнуты в плоскости, касательной к поверхностному слою детали (фиг. 3) или в одной из главных плоскостей, перпендикулярных её поверхностному слою (фиг. 2, 4).
Максимальные касательные напряжения τmax возникают в плоскости, касательной к поверхности детали, если в её поверхностном слое действуют напряжения двухосного растяжения-сжатия (фиг 3). В этом случае статическая прочность детали определяется главными напряжениями σ1 и σ3, действующими в плоскости её поверхности. Согласно принятому условию (2), касательные напряжения τmax не должны превышать максимальных допускаемых напряжений τL. В зависимости от соотношения между абсолютными значениями главных напряжений σ1 и σ3 круг Мора 6, отображающий тензор предельно допустимых напряжений в поверхностном слое материала детали, может перемещаться на фиг 3 влево или вправо, а граница области плоских предельных плосконапряженных состояний в поверхностном слое материала детали (граница области статической прочности) на фиг 3 при этом располагается в промежутке между прямыми АВД и А'В'Д'. При напряжениях двухосного растяжения-сжатия в поверхностном слое детали в случае, если (σ1 - σ3) > 2τL, плоскость наибольших касательных напряжений, по которой происходит пластический сдвиг материала, будет расположена перпендикулярно поверхности детали.
При различных плосконапряженных состояниях, соответствующих двухосному сжатию или двухосному растяжению поверхностного слоя детали (фиг. 2 и 4), максимальные касательные напряжения τmax в исследуемой точке поверхности детали действуют в главных площадках, перпендикулярных поверхностному слою. Предельно допустимые величины тензоров этих напряжений на фиг. 2 и 4 отображены кругами Мора 7. Как уже отмечено выше, тензоры напряжений, которые при этом возникают в плоскости поверхности детали, отображены кругами Мора 6. На фиг. 5 тензоры напряжений, которые в случае двухосного сжатия поверхностного слоя детали действуют в плоскости её поверхности и соответствуют появлению предельных тензоров напряжений в плоскостях, перпендикулярных поверхности детали, изображены кругами Мора 9, 10 и 11. Аналогичные круги могут быть изображены с правой стороны фигуры 5 в зоне двухосного растяжения поверхностного слоя. При напряжениях двухосного растяжения или двухосного сжатия в поверхностном слое детали в случае, если (σ1 - σ3) > 2τL, плоскость наибольших касательных напряжений, по которой происходит пластический сдвиг материала, будет расположена примерно под углом 45° к поверхности детали.
На фиг. 5 видно, что представлять границу области максимально допустимых напряжений в виде линии, огибающей окружности 9, 10 и 11 предельных кругов Мора, которые при двустороннем сжатии отображают тензоры предельных напряжений, действующих в поверхностном слое детали, невозможно. Это связано с тем, что в таком случае в системе координат Оστ области максимально допустимых напряжений, которые определяются одними кругами Мора, перекрываются областями, которые определяются другими кругами Мора (фиг. 5), в результате чего граница области статической прочности будет определена неоднозначно. Аналогичный вывод мог бы быть сделан при рассмотрении кругов Мора, соответствующих двухосному растяжению поверхностного слоя (на фиг. 5 не показаны).
В связи с изложенным границу области статической прочности в системе координат Оστ удобнее строить, не в виде огибающей кругов Мора, отображающих предельно допустимые напряжения в плоскости поверхности детали, а в виде огибающей верхней и нижней конечных точек диаметров этих кругов, проведенных параллельно оси Оτ, то есть по точкам, которые выражают величину максимальных и минимальных касательных напряжений, определяемых этими кругами. На фиг. 5 таким способом получены прямые СА и СА', а также ДЕ и ЕД'. Указанный способ построения можно распространить и на классическую теорию прочности Мора. При таком построении каждому кругу Мора, описывающему предельные напряженные состояния в плоскости поверхности детали, ставятся в соответствие две строго определённые точки границы области статической прочности. На фиг. 5 граница полученной таким способом области статической прочности представлена в виде шестиугольника САДЕД'А', изображенного пунктирной линией.
Не менее распространенной в настоящее время является гипотеза прочности Хубера-Мизеса, которая основана на принятом допущении о том, что опасное состояние материала возникает по причине превышения определенного порога предельно допустимой удельной энергии деформации, связанной с изменением формы элементарных объемов этого материала [3, 4]. Согласно данной гипотезе, сложное напряжённое состояние с главными напряжениями σ1, σ2 и σ3 однозначно эквивалентному ему по разрушающей способности одноосному напряжению σэкв энерг, которое может быть определено по формуле:
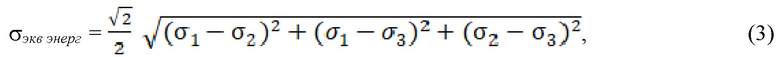
где σ1 - максимальное главное напряжение в рассматриваемой точке;
σ2 - второе главное напряжение в рассматриваемой точке;
σ3 - минимальное главное напряжение в рассматриваемой точке.
В любой из гипотез прочности различные многоосные напряженные состояния посредством определенных формул приводятся к эквивалентным им по разрушающей способности, но более доступным для проведения экспериментальных исследований. Обычно в качестве такого более доступного напряженного состояния выбирают одноосное растяжение исследуемого материала. Величина напряжений, при которых во время одноосного растяжения достигнута их предельно допустимая величина σпред, определяется экспериментально и не зависит от выбранной гипотезы прочности, поэтому круги Мора, соответствующие напряженному состоянию одноосного растяжения, в различных гипотезах прочности имеют одинаковый диаметр D круга Мора 4 (фиг. 1). Таким образом, при построении в системе координат Оστ границы области статической прочности поверхностного слоя материала по гипотезе энергии формоизменения Хубера-Мизеса круг Мора, соответствующий одноосному растяжению материала, на фиг. 6 совпадает с тем, что был выбран за основу при построении границы области статической прочности по гипотезе наибольших касательных напряжений Треска - Сен-Венана. Диаметр этого круга, проведенный параллельно оси Оτ, определяет также две точки области статической прочности, построенной на основе данных экспериментального исследования (фиг. 1 граница 1).
В случае одноосного растяжения материала 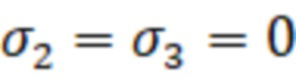 . При этом на фиг. 4 точка, соответствующая напряжению
. При этом на фиг. 4 точка, соответствующая напряжению 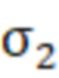 , переместится в начало координат, а диаметры кругов Мора 6 и 7, отображающих тензоры напряжений в двух главных плоскостях, проходящих через линию действия первого главного напряжения σ1, будут иметь одинаковый диаметр D, отображающий указанную величину напряжений растяжения σ1. Подставляя в формулу (3) указанные значения напряжений
, переместится в начало координат, а диаметры кругов Мора 6 и 7, отображающих тензоры напряжений в двух главных плоскостях, проходящих через линию действия первого главного напряжения σ1, будут иметь одинаковый диаметр D, отображающий указанную величину напряжений растяжения σ1. Подставляя в формулу (3) указанные значения напряжений 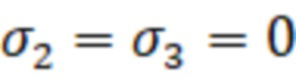 , получим, что в этом случае σэкв энерг=
, получим, что в этом случае σэкв энерг=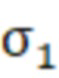 . В тоже время первое главное напряжение
. В тоже время первое главное напряжение 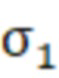 , является предельно допустимым напряжением:
, является предельно допустимым напряжением: 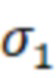 =σпред.
=σпред.
Как и в гипотезе наибольших касательных напряжений, в гипотезе энергии формоизменения принято, что предельные напряжения при одноосном растяжении и одноосном сжатии материала конструкции равны по модулю, поэтому круги Мора, соответствующие этим двум напряженным состояниям, на фиг. 1 и 6 имеют одинаковый диаметр D. Указанные круги Мора диаметром D определяют на фиг. 6 положения четырех точек границы области статической прочности - точек 7'.
Построение в системе координат Оστ всего контура границы области статической прочности поверхностного слоя материала детали по гипотезе энергии формоизменения выполняют по следующему алгоритму:
- разницы величин главных напряжений 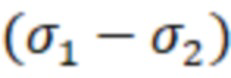 ,
,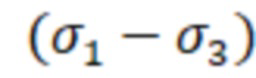 и
и 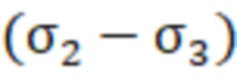 в формуле (3) заменяют диаметрами D1, D2 и D3 трех главных кругов Мора (фиг. 2 - 4), которые в системе координат Оστ в выбранном масштабе отображают плосконапряженное состояние в рассматриваемой точке детали в его трехмерном представлении. Если рассматривается предельно допустимое плосконапряженное состояние, то величину σэкв энерг заменяют диаметром D круга Мора, отображающего предельно допустимую величину напряжений в исследуемом материале при его одноосном растяжении (фиг.4), а диаметры D1, D2 и D3 определяют различные сочетания трех максимально допустимых главных напряжений, действующих в рассматриваемой точке детали. В результате указанных преобразований формула (3) может быть записана в виде:
в формуле (3) заменяют диаметрами D1, D2 и D3 трех главных кругов Мора (фиг. 2 - 4), которые в системе координат Оστ в выбранном масштабе отображают плосконапряженное состояние в рассматриваемой точке детали в его трехмерном представлении. Если рассматривается предельно допустимое плосконапряженное состояние, то величину σэкв энерг заменяют диаметром D круга Мора, отображающего предельно допустимую величину напряжений в исследуемом материале при его одноосном растяжении (фиг.4), а диаметры D1, D2 и D3 определяют различные сочетания трех максимально допустимых главных напряжений, действующих в рассматриваемой точке детали. В результате указанных преобразований формула (3) может быть записана в виде:

где D1 , D2 , D3 - диаметры трех кругов Мора, отображающих предельно допустимое плосконапряженное состояние в рассматриваемой точке детали;
D - диаметр круга Мора, отображающего предельно допустимую величину напряжений в исследуемом материале при его одноосном растяжении. В зависимости от расположения кругов Мора на фиг. 2 - 4 последовательность расположения слагаемых D1, D2 и D3 в формуле (4) может не соответствовать последовательности расположения слагаемых 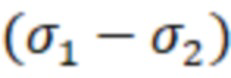 ,
,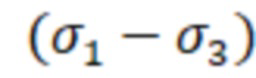 и
и 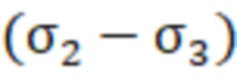 в формуле (3);
в формуле (3);
- в выбранном масштабе строят круг Мора диаметром D (фиг. 6), который отображает экспериментально найденную величину предельного плосконапряженного состояния в исследуемом материале при его одноосном растяжении;
- задают одну из возможных пропорций между диаметром круга Мора D1, отображающего предельное плосконапряженное состояние в плоскости поверхности детали, и диаметром одного из кругов Мора, например, D2, отображающего напряженное состояние в плоскости одой из главных площадок, расположенной перпендикулярно поверхности детали. С учетом этой пропорции через D1 выражают диаметр D2. После этого, принимая во внимание связь между диаметрами D1, D2 и D3 трёх кругов Мора, представленных на фиг. 2 - 4, согласно которой крайние левая и правая точки двух внутренних, соприкасающихся между собой кругов, огибаются третьим кругом, через D1 и D2 выражают также диаметр третьего круга D3. Так на фиг. 2 и 4 диаметр третьего круга: D3=D2 - D1, а на фиг. 3: D3=D1 - D2;
- диаметр D1, а также, диаметры кругов Мора D2 и D3, выраженные через D1, подставляют в формулу (4). Далее, используя формулу (4), через диаметр D круга Мора (фиг. 2 - 4, 6), который соответствует пределу текучести или достижению предела статической прочности при одноосном растяжении материала и принят в качестве круга предельных допустимых эквивалентных напряжений σэкв энерг=σпред, определяют диаметр D1 круга Мора 6, отображающего предельно допустимое напряжение в плоскости поверхности детали. После этого, используя принятые пропорции между диаметрами трех кругов Мора D1, D2 и D3, определяют диаметр каждого из них;
- в соответствии с расположением кругов D1 и D2 представленным на фиг. 2 - 4 и масштаба, принятого при построении круга Мора диаметром D, определяют положение на оси Оσ системы координат Оστ (фиг. 6) центра круга Мора 6 диаметром D1. Через этот центр в направлении, параллельном оси Оτ проводят диаметр D1 указанного предельного круга Мора 6, отображающего предельно допустимое плосконапряженное состояние в плоскости поверхности детали, и наносят крайние точки этого диаметра. Через эти точки при предельно допустимом тензоре напряжений, который определён начально заданной пропорцией D1/D2, проходит граница области допускаемых напряжений, построенная по гипотезе энергии формоизменения;
- задавая другие пропорции между D1 и D2 можно рассчитать координаты и построить в системе координат Оστ любые другие точки границы области допускаемых плосконапряженных состояний. При ограниченном количестве построенных таким образом точек приближенное построение границы области предельных плосконапряженных состояний выполняют путем плавного соединения построенных указанным образом точек (фиг. 6).
Пропорции D1/D2, которые задавались при вычислении диаметров D1 кругов Мора, отображающих по гипотезе прочности энергии формоизменения различные предельно допустимые тензоры напряжений в плоскости плосконапряженного состояния, действующего на поверхности детали, а также полученные при этом значения D1 и номера точек, которые в плоскости плосконапряженного состояния определяют границу области статической прочности материала детали, приведены в таблице.
на фиг. 6
на фиг. 6
на фиг. 6
Граница области предельных плосконапряженных состояний материала детали, построенная по этим точкам, представлена на фиг. 6.
Полученные разными способами границы 1, 2, 3 областей предельных плосконапряженных состояний в поверхностном слое материала детали (фиг. 1) отличаются друг от друга. Наиболее точное представление о предельных плосконапряженных состояниях в поверхностном слое материала детали определяет граница 1, так как, в отличие от двух других, эта граница построена не по гипотезам прочности, а по данным экспериментального исследования по определению потери несущей способности материала при различных комбинациях компонентов тензора напряжений в испытываемых образцах из материала детали. Граница 1 в частности, позволяет учитывать различие статической прочности при одинаковых по модулю величинах напряжений растяжения и сжатия.
Сравнение границ статической прочности 2 и 3 (фиг. 1), построенных, соответственно, по гипотезе наибольших касательных напряжений Треска-Сен-Венана и по гипотезе энергии изменения формы Хубера-Мизеса показывает, что более жесткие, более консервативные требования к прочности устанавливает гипотеза наибольших касательных напряжений Треска - Сен-Венана. Максимальная разница предельных напряжений по двум указанным гипотезам достигает 13 % и наблюдается в том случае, когда в формуле (3) |σ1 - σ2|= |σ2 - σ3|, а в формуле (4) диаметры двух внутренних кругов Мора равны между собой: D1=D3 или D2=D3 (см. фиг. 2 - 4). Указанные плосконапряженные состояния на фиг. 6 и в таблице 1 обозначены номерами точек 1' (чистый сдвиг) и 13' (равномерное растяжение или сжатие поверхностного слоя материала по двум главным направлениям).
В настоящее время запас статической прочности n в исследуемой плосконапряженной зоне детали обычно вычисляют путем определения отношения величины предельно допустимых напряжений в материале детали к максимальным эквивалентным напряжениям, возникающим в исследуемой зоне детали в процессе её нагружения. Численную величину предельно допустимых напряжений при этом устанавливают на основе данных экспериментального исследования о разрушении или начале текучести образцов из материала детали при их одноосном растяжении. Численная величина эквивалентных напряжений, возникающих в исследуемой зоне детали, может быть определена путем пересчета значений компонентов тензора напряжений в этой зоне по соответствующей формуле (2 или 3) применяемой при этом гипотезы прочности.
Используя границы 2 и 3, построенные на фиг. 1 расчетным способом, запас статической прочности n в исследуемой зоне поверхности детали может также быть вычислен по формуле (1). При этом прямую ОА продолжают до пересечения с одной из указанных границ 2 или 3. Точку В переносят в точку пересечения указанных границ с прямой ОА. Расчет запаса n статической прочности по формуле (1) при этом выполняется с учетом изменившегося расстояния от точки О до точки В.
Для увеличения точности расчета запаса статической прочности n в исследуемой зоне поверхности детали с использованием гипотез прочности применяют ту из этих гипотез, согласно которой граница области предельных плосконапряженных состояний материала детали, построенная расчетным путем, в наибольшей мере повторяет границу предельных плосконапряженных состояний материала детали, построенную экспериментально. С целью снижения рисков получения при этом заниженного коэффициента запаса статической прочности n необходимо, чтобы граница области статической прочности, построенная по формулам применяемой гипотезы прочности, находилась внутри границы 1 (фиг. 1), построенной экспериментальным путем. В зонах плосконапряженного состояния, где такое условие не выполнено, определение коэффициента запаса статической прочности n по соответствующей гипотезе прочности приведет к завышенным результатам. Поэтому в таких зонах коэффициент запаса статической прочности необходимо уточнить, рассчитывая его по формуле (1), при этом точка В является точкой пересечения прямой ОА и границы, построенной на основе данных экспериментального исследования.
Таким образом, предложен способ определения статической прочности сложнонапряженной детали вне зон воздействия на неё внешних контактных сил, в котором в системе координат Оστ изображают границы тензоров предельных плосконапряженных состояний в поверхностном слое материала детали, построенные экспериментальным путем и по различным гипотезам прочности. При построении границы области статической прочности поверхностного слоя материала детали на основе экспериментальных данных выполняется учет влияния не двух, а трех главных напряжений, одно из которых всегда равно нулю. По сравнению со способом, применяемым в классической теории прочности Мора, это увеличивает точность построения такой границы и достоверность результатов расчета статической прочности детали с использованием такой границы.
Выполнить расчет статической прочности сложнонапряженной детали вне зон воздействия на неё контактных сил предлагаемым способом, проще, чем применяя для этих целей классическую теорию прочности Мора. Это обусловлено тем, что при использовании классической теории прочности Мора в исследуемой зоне детали необходимо экспериментальным или расчетным путем определить не два, а три главных напряжения σ1, σ2 и σ3, сравнить эти напряжения между собой, после чего учесть из них только максимальное σ1 и минимальное σ3, в то время как в предлагаемом способе выполняют учет только двух главных напряжений, действующих в плоскости плосконапряженного состояния. Возможность в предложенном способе наглядного сравнения границ области статической прочности, построенных по различным гипотезам прочности, с границей, построенной на основе данных эксперимента, позволяет подобрать для каждого материала детали наиболее подходящую гипотезу прочности, согласно которой граница области предельных допустимых плосконапряженных состояний этого материала точнее повторяет границу, построенную по данным эксперимента. Предложенный способ построения границы области статической прочности материала детали не в виде огибающей предельных кругов Мора, а в виде огибающей точек, отображающих максимальные касательные напряжения на этих кругах, позволит более точно построить указанную границу по сравнению с классическим методом Мора.
Список используемых источников:
1. Вахромеев, А.М. Определение циклической долговечности материалов и конструкций транспортных средств: методические указания - М.: МАДИ, 2015. - 64 с.
2. Патент на изобретение № 2697022. Способ графической записи изменения двухосных напряжений в рассматриваемой точке поверхности детали (варианты).
3. В. И. Феодосьев Сопротивление материалов. Издание седьмое, переработанное. М. Наука, 1974. - 560 с.
4. И.М. Беляев Сопротивление материалов. Издание двенадцатое. М.: Государственное издательство физико-математической литературы, 1959. - 856 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ графической записи изменения двухосных напряжений в рассматриваемой точке поверхности детали (варианты) | 2018 |
|
RU2697022C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕХАНИЧЕСКИХ СВОЙСТВ ГРУНТОВ | 2015 |
|
RU2600494C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРЕДЕЛЬНО МАКСИМАЛЬНОЙ КОНТАКТНОЙ ПРОЧНОСТИ ГРУНТОВОГО ОСНОВАНИЯ В УСЛОВИЯХ ПЛОСКОЙ ДЕФОРМАЦИИ | 2004 |
|
RU2265824C1 |
| МЕТОД ОЦЕНКИ НАПРЯЖЕННОГО СОСТОЯНИЯ МАТЕРИАЛОВ | 2015 |
|
RU2625360C2 |
| СПОСОБ ПОСТРОЕНИЯ ДИАГРАММЫ ПРЕДЕЛЬНЫХ ДЕФОРМАЦИЙ ЛИСТОВОГО МАТЕРИАЛА | 2015 |
|
RU2591294C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕХАНИЧЕСКИХ СВОЙСТВ ОБРАЗЦОВ ГОРНЫХ ПОРОД И МАТЕРИАЛОВ | 2013 |
|
RU2521116C1 |
| СПОСОБ ОЦЕНКИ ПРОЧНОСТИ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ | 1999 |
|
RU2186361C2 |
| Способ испытания листовых материалов на осесимметричную вытяжку | 2017 |
|
RU2659458C1 |
| Способ испытания листовых материалов на осесимметричную вытяжку | 2017 |
|
RU2655634C1 |
| Способ исследования напряжений и деформаций твердого материального тела поляризационно-оптическим методом на модели из пьезооптического материала при воздействии на нее локального теплового потока | 2015 |
|
RU2610219C1 |
Изобретение относится к способам определения прочности сложнонапряженных деталей, нагруженных системой сил, отдельные компоненты которых могут меняться несинхронно по отношению друг к другу, а количество циклов их нагружения не превышает предела квазистатической усталости. Сущность: в системе координат Оστ строят серию предельных кругов Мора, которые описывают различные тензоры предельных плосконапряженных состояний материала детали, предшествующих его пределу статической прочности или началу текучести. Прямыми, параллельными оси Оτ, проводят диаметры этих кругов и строят линию, огибающую точки пересечения этих диаметров с окружностями, ограничивающими указанные круги Мора. Эта линия является границей области предельных плосконапряженных состояний материала детали. При экспериментальном построении такой границы предельные круги Мора строят путем создания различных тензоров плосконапряженного состояния в образцах из материала детали, а при её расчетном построении - по формулам, принятым в качестве гипотез прочности. Тензоры плосконапряженных состояний, которые в процессе нагружения возникают в различных точках поверхностного слоя детали, изображают в системе координат Оστ в виде кругов Мора и отслеживают, чтобы проведенные в вертикальном направлении диаметры этих кругов не выходили за пределы границы области предельных плосконапряженных состояний материала детали. Дополнительно определяют уточненный запас статической прочности n в исследуемой зоне поверхности детали. Технический результат: увеличение точности определения статической прочности деталей на участках их поверхности, расположенных вне зон воздействия контактных сил. 2 н.п. ф-лы, 6 ил., 1 табл.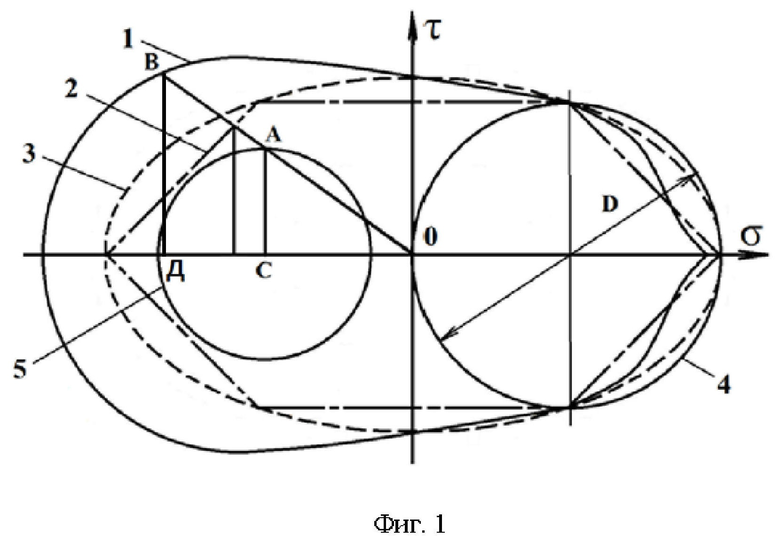
1. Способ определения статической прочности сложнонапряженной детали вне зон воздействия на неё контактных сил, включающий построение в прямоугольной системе координат Оστ графической записи малоцикловой смены тензоров двухосных напряжений в рассматриваемой точке поверхности детали в процессе её эксплуатации, выполняемой в виде серии кругов Мора, построенных на основе данных о двухосных напряжениях в этой точке в последовательно взятые моменты времени, с центрами кругов Мора, расположенными на оси Оσ, направление которой связано с выбранным направлением на поверхности исследуемой детали, также включающий построение в той же прямоугольной системе координат Оστ границы области предельных напряженных состояний материала детали, построенной путем обобщения отдельных экспериментальных данных, которые отображены в виде серии предельных кругов Мора, описывающих различные, доступные для получения при проведении испытаний тензоры предельных напряженных состояний в образцах из материала детали, отличающийся тем, что по данным экспериментального исследования, проводимого на образцах из материала детали, определяют точные величины различных сочетаний компонентов тензоров плосконапряженного состояния, при которых достигается предел текучести или предел статической прочности материала детали, указанные сочетания компонентов тензоров плосконапряженного состояния отображают в прямоугольной системе координат Оστ в виде серии предельных кругов Мора, затем путем проведения параллельно оси Оτ диаметров предельных кругов Мора и последующего построения линии, огибающей точки пересечения этих диаметров с окружностями, ограничивающими указанные предельные круги Мора, выполняют построение границы области предельных плосконапряженных состояний материала детали, при этом критерием обеспечения статической прочности исследуемой зоны детали является расположение точек пересечения диаметров, проведенных параллельно оси Оτ во всех кругах Мора, отображающих отдельные плосконапряженные состояния, возникающие в исследуемой зоне поверхностного слоя детали, с окружностями, ограничивающими эти круги, внутри границ области предельных плосконапряженных состояний, дополнительно определяют уточненный запас статической прочности n в исследуемой зоне поверхности детали путем выявления отношения максимально допустимых касательных напряжений в материале детали, выявленных по данным экспериментального исследования, к максимальным касательным напряжениям, возникающим в исследуемой зоне детали при одинаковом соотношении всех компонентов тензоров сравниваемых между собой плосконапряженных состояний.
2. Способ определения статической прочности сложнонапряженной детали вне зон воздействия на неё контактных сил, включающий построение в прямоугольной системе координат Оστ графической записи малоцикловой смены тензоров двухосных напряжений в рассматриваемой точке поверхности детали в процессе её эксплуатации, выполняемой в виде серии кругов Мора, построенных на основе данных о двухосных напряжениях в этой точке в последовательно взятые моменты времени, с центрами кругов Мора, расположенными на оси Оσ, направление которой связано с выбранным направлением на поверхности исследуемой детали, также включающий построение в той же прямоугольной системе координат Оστ границы области предельных напряженных состояний материала детали, построенной путем обобщения отдельных экспериментальных данных, которые отображены в виде серии предельных кругов Мора, описывающих различные, доступные для получения при проведении испытаний тензоры предельных напряженных состояний в образцах из материала детали, отличающийся тем, что построение границы области предельных плосконапряженных состояний материала детали в прямоугольной системе координат Оστ выполняют путем построения по каждой из гипотез прочности при различных тензорах напряжений серии предельных кругов Мора, параллельно оси Оτ проводят диаметры указанных предельных кругов Мора и строят линию, огибающую точки пересечения этих диаметров с окружностями, ограничивающими указанные предельные круги Мора, выбирают ту границу области предельных плосконапряженных состояний, которая в наибольшей мере повторяет границу, построенную экспериментальным путем, при этом критерием обеспечения статической прочности исследуемой зоны детали является расположение точек пересечения диаметров, проведенных параллельно оси Оτ, во всех кругах Мора, которые отображают отдельные плосконапряженные состояния, возникающие в исследуемой зоне поверхностного слоя детали, с окружностями, ограничивающими эти круги, внутри указанной границы области предельных плосконапряженных состояний, дополнительно определяют запас статической прочности n в исследуемой зоне поверхности детали путем выявления отношения максимально допустимых касательных напряжений в материале детали, полученных по формулам той гипотезы прочности, согласно которой построена граница области предельных плосконапряженных состояний, в наибольшей степени совпадающая с границей, построенной экспериментальным путем, к максимальным касательным напряжениям, возникающим в исследуемой зоне детали, при одинаковом соотношении всех компонентов тензоров сравниваемых между собой плосконапряженных состояний.
| Способ графической записи изменения двухосных напряжений в рассматриваемой точке поверхности детали (варианты) | 2018 |
|
RU2697022C1 |
| СПОСОБ ПРОГНОЗА ОСТАТОЧНОГО РЕСУРСА МЕТАЛЛА ДИАГНОСТИРУЕМОГО ОБЪЕКТА (ВАРИАНТЫ) | 2004 |
|
RU2267121C1 |
| МЕТОД ОЦЕНКИ НАПРЯЖЕННОГО СОСТОЯНИЯ МАТЕРИАЛОВ | 2015 |
|
RU2625360C2 |
| US 20200217730 A1, 09.07.2020. | |||
Авторы
Даты
2023-01-09—Публикация
2022-01-14—Подача