Изобретение относится к механическим испытаниям горных пород и материалов, имеющих хрупкий характер разрушения, и может быть использовано при инженерно-геологических изысканиях.
Известен способ определения напряженного состояния горных пород в массиве (авторское свидетельство СССР №1259005, кл. E21C 39/00, 1986), включающий вдавливание в горную породу (забой скважины) нагрузочного элемента в виде штампа до разрушения породы с образованием лунок выкола и определение глубин вдавливания штампа, равных глубинам лунок выкола.
Недостатками способа являются низкая точность относительного определения напряженного состояния породы без учета абсолютных значений предельной объемной прочности и действующих напряжений, а также сложность и трудоемкость испытаний из-за поэтапного бурения скважины и многократного вдавливания штампа.
Известен способ определения контактной динамической прочности (авторское свидетельство СССР №1346785, кл. E21C 39/00, 1987), включающий ударное внедрение нагрузочного элемента (наконечника мерного стержня) в породу, определение напряжений в нагрузочном элементе и геометрических параметров лунки разрушения (глубины лунки разрушения и ее диаметра).
Недостатками способа являются сложность испытательного и регистрирующего оборудования для определения максимальных напряжений в нагрузочном элементе и трудоемкость проведения испытаний, связанных с неоднократным ударным воздействием нагрузочного элемента и необходимостью его очистки от продуктов разрушения.
Известен способ определения коэффициента внутреннего трения горных пород (авторское свидетельство СССР №970197, кл. G01N 19/02, 1982), включающий приложение к образцу сферической формы раскалывающего усилия и определение в плоскости, проходящей через ось нагружения, геометрических параметров (радиуса основания и высоты) зон разрушенной породы на контакте с нагрузочными поверхностями.
Недостатками способа являются трудоемкость подготовки к испытаниям, связанная с изготовлением образца специальной сферической формы и низкая точность определения показателя прочности из-за сложности измерения размеров зон разрушенной породы в плоскости, проходящей через ось нагружения на неровных поверхностях обломков раздавленного образца.
Известен способ определения прочностных характеристик горных пород (авторское свидетельство СССР №473930, кл. G01N 3/12, E21C 39/00, 1975), включающий внедрение нагрузочного элемента (пуансона) в образец породы до разрушения с образованием сквозного отверстия и лунки выкола на противоположной свободной поверхности образца и определение геометрических параметров лунки выкола (диаметра и глубины лунки).
Недостатками способа являются низкая точность определения предельных прочностных характеристик с использованием обобщенных интегральных показателей по корреляционным зависимостям и трудоемкость испытаний из-за необходимости дополнительного определения одной из характеристик прочности (пределов прочности при растяжении, сжатии или сдвиге).
Известен способ определения механических свойств образцов горных пород (статья: Коршунов В.А. Определение показателей объемной прочности образцов горных пород при их нагружении сферическими инденторами. Горная геомеханика и маркшейдерское дело: Сборник научных трудов. - СПб.: ВНИМИ, 1999. - М-во топлива и энергетики РФ, РАН, - с.70-75), принимаемый за прототип и заключающийся в том, что образец нагружают двумя встречно направленными сферическими инденторами до его раскалывания, фиксируют разрушающую силу, определяют в разрушенном образце площадь поверхности трещины отрыва, проходящей через ось нагружения, и геометрические параметры разрушенных зон в областях контакта с обоими сферическими инденторами (глубину и максимальную ширину зон на поверхности трещины отрыва), вычисляют растягивающее напряжение разрыва образца и среднее сжимающее напряжение на границе большей из разрушенных зон и определяют в качестве механических свойств образца предел прочности (предел прочности при одноосном сжатии) и сопротивление срезу (предельное сопротивление срезу - сцепление).
Недостатком этого способа является трудоемкость и низкая точность определения механических свойств из-за значительной сложности и недостаточной точности определения геометрических параметров разрушенных зон на поверхности трещины отрыва расколотого образца, которая имеет, как правило, неудобную для измерений сложную рельефную форму. Другой недостаток способа заключается в его невысокой информативности. Возможности способа ограничены определением прочностных свойств в области «паспорта прочности», прилегающей к состоянию «чистого сдвига» и соответствующей разрушению от отрыва при действии растягивающих и сжимающих напряжений и разрушению сдвигом при действии неравномерных сжимающих невысокого уровня напряжений.
Технический результат изобретения заключается в упрощении испытаний и повышении точности определения механических свойств образцов за счет упрощения определения геометрических параметров разрушенных зон на торцах образцов в областях контакта с инденторами и повышении информативности испытаний за счет дополнительного определения прочностных характеристик «паспорта прочности» в областях растягивающих и сжимающих с высоким уровнем напряжений (предела прочности при всестороннем растяжении и максимального сопротивления срезу), а также коэффициента Пуассона.
Технический результат достигается тем, что в способе определения механических свойств образцов горных пород и материалов, включающем нагружение образца двумя встречно направленными сферическими инденторами до его раскалывания, фиксирование разрушающей силы, определение в разрушенном образце площади поверхности трещины отрыва, проходящей через ось нагружения, и геометрических параметров разрушенных зон в областях контакта с обоими сферическими инденторами, вычисление растягивающего напряжения разрыва образца и среднего сжимающего напряжения на границе большей из разрушенных зон и определение в качестве механических свойств образца предела прочности и сопротивления срезу, согласно изобретению, из обломков разрушенного образца собирают составной образец, на торцах которого определяют геометрические параметры разрушенных зон - диаметр остаточных отпечатков от инденторов и длину лунок выкола вдоль поверхности трещины отрыва, определяют площадь поверхности большей разрушенной зоны на контакте с инденторами по формуле:
F=π·Dотп·Lл,
где F - площадь поверхности большей разрушенной зоны;
Dотп - диаметр остаточного отпечатка от индентора;
Lл - длина лунки выкола вдоль поверхности трещины отрыва;
π=3,14,
а в качестве механических свойств образца определяют предел прочности при всестороннем растяжении 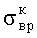
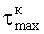
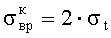
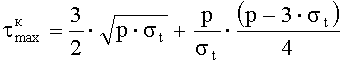
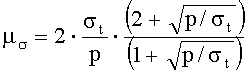
где σt - растягивающее напряжение разрыва образца;
p - среднее сжимающее напряжение на границе большей из разрушенных зон.
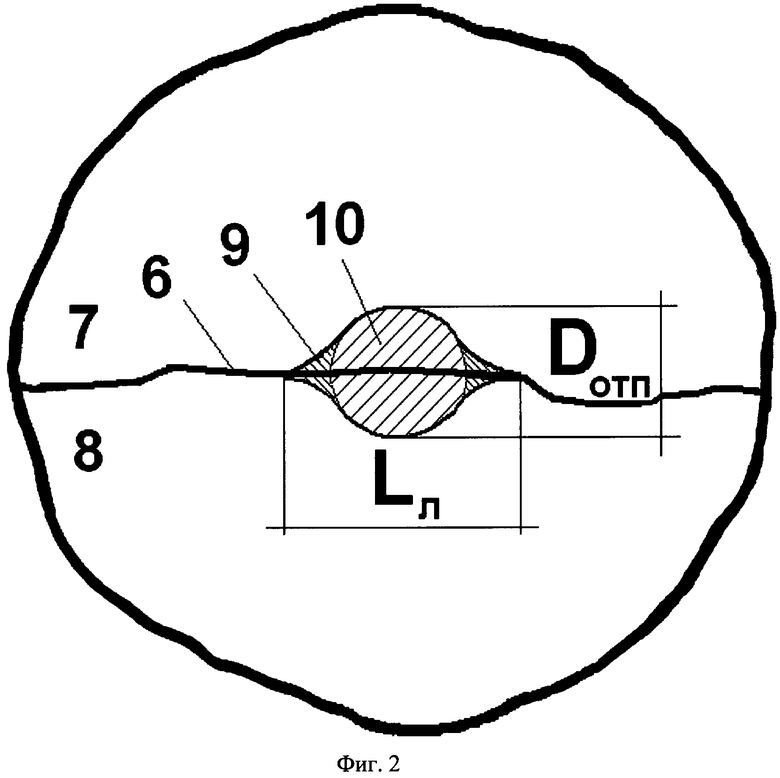
Способ поясняется фиг.1, на которой представлена схема нагрузочного устройства для реализации способа, и фиг.2, на которой представлена схема определения в составном разрушенном образце геометрических параметров разрушенной зоны в области контакта со сферическим индентором, где 1 - корпус устройства, 2 - штоки, 3 - вкладыши, 4 - сферические инденторы, 5 - образец, 6 - трещина отрыва, 7 и 8 - обломки разрушенного образца, 9 - лунка выкола, 10 - остаточный отпечаток от индентора.
Нагрузочное устройство должно обеспечивать приложение к образцу сжимающей силы двумя соосными встречно направленными сферическими инденторами. Корпус 1 устройства представляет собой жесткую раму, внутри которой на оси нагружения 00 размещается подвижная пара штоков 2 с вкладышами 3, содержащими стальные сферические инденторы 4 для передачи нагрузки на образец 5.
Способ осуществляют следующим образом.
Образец устанавливают между сферическими инденторами и равномерно нагружают с регистрацией сжимающей силы Р. Допускается испытание образцов произвольной, в том числе неправильной, формы с необработанными поверхностями.
С ростом нагрузки в образце в областях контакта со сферическими инденторами развиваются разрушенные зоны раздробленного, уплотняемого при сжатии материала. Зоны имеют форму усеченных эллипсоидов. Более интенсивно развивается зона в слабейшей по прочности области образца. При достижении предельного напряженного состояния на границе большей из разрушенных зон возникает трещина отрыва 6, которая, смыкаясь со второй зоной, раскалывает образец на обломки 7 и 8.
Фиксируют максимальную (разрушающую) силу P. После этого в обломках образца измеряют (например, штангенциркулем) характерные линейные размеры поверхности трещины отрыва, по которым вычисляют ее площадь S.
Затем из обломков образца собирают составной образец. Для этого обломки прикладывают друг к другу, обеспечивая плотный контакт вдоль трещины отрыва. В составном образце определяют геометрические параметры разрушенных зон - диаметр остаточных отпечатков от инденторов Dотп и длину лунок выкола вдоль поверхности трещины отрыва Lл. При этом границы лунки выкола выделяют по большему раскрытию берегов трещины в пределах выкола, а диаметр остаточного отпечатка предпочтительнее измерять в направлении, перпендикулярном трещине отрыва. Для упрощения и повышения точности измерений геометрические параметры разрушенных зон рекомендуется определять путем фотографирования образца совместно с измерительной линейкой и последующей обработки увеличенного на мониторе компьютера изображения.
Вычисляют площадь поверхностей разрушенных зон на контакте с обоими инденторами F1 и F2 как поверхностей тела в форме эллипсоида, по формуле:
F=π·Dотп·Lл.
Выбирают большее из двух значений F1 и F2-F.
Рассчитывают растягивающее напряжение разрыва образца σt и среднее сжимающее напряжение р на границе большей из разрушенных зон по формулам:
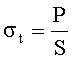
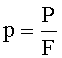
Определяют предел прочности при всестороннем растяжении 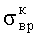
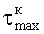
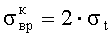
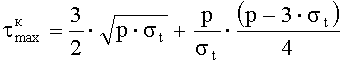
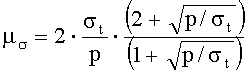
Экспериментальным обоснованием определения площади поверхности разрушенной зоны на контакте с индентором служат результаты сопоставления значений площади поверхности разрушенной зоны, определенной предлагаемым способом и в соответствии со способом-прототипом (через значения максимальной ширины D и глубины h зоны на поверхности трещины отрыва по формуле: F=π·D·h) для различных горных пород и хрупких материалов.
Установлено подобие формы и размеров зоны разрушения на поверхности трещины отрыва и на торце образца на контакте с индентором в расколотом образце. При этом геометрические параметры разрушенной зоны на торце образца (длина лунки выкола вдоль поверхности трещины отрыва Lл и диаметр остаточного отпечатка от индентора Dотп) весьма незначительно отличаются по величине от аналогичных параметров зоны на поверхности трещины отрыва (максимальной ширины D и глубины h зоны, соответственно).
В таблице 1 представлены примеры определения сравниваемыми способами геометрических параметров разрушенных зон и значений площади их поверхностей в образцах 22 проб горных пород и хрупких материалов. Отклонение результатов определений сравниваемыми способами колебалось в пределах от -8 до 11%, составило, в среднем, 6% и было связано со сложностью измерения нечетких границ зон на рельефных поверхностях трещины разрыва в расколотых образцах при использовании способа-прототипа. Определение предлагаемым способом параметров разрушенных зон на более ровной внешней поверхности образца существенно упрощает измерения и, соответственно, повышает точность определений. Положительный эффект еще более значителен в случае вдавливания инденторов в предварительно подготовленную поверхность (в отшлифованную плоскую поверхность образцов-дисков или боковую поверхность обломков кернов).
Теоретическим обоснованием определения величины предела прочности при всестороннем растяжении 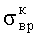
Известно, что в момент раскола образца на поверхности трещины отрыва на границе разрушенной зоны действуют касательные напряжения, равные величине предельного сопротивления срезу (сцепления) 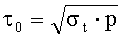
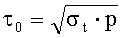

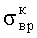
Экспериментальным обоснованием определения величины предела прочности при всестороннем растяжении 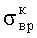
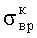
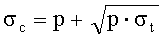
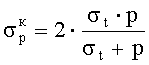
В таблице 2 представлены безразмерные значения прочности 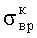
Теоретическим обоснованием определения величины максимального сопротивления срезу 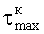
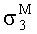
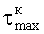
Если принять огибающую предельных кругов Мора в области разрушения сдвигом при действии неравномерных сжимающих невысокого уровня напряжений прямолинейной, что не противоречит опытным данным по испытанию хрупких горных пород и материалов, то установленная связь может быть выражена следующим образом:
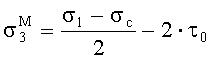
где (σ1-σc)/2 - радиус предельного круга Мора, соответствующего минимальному главному нормальному напряжению, равному σc.
После алгебраических преобразований 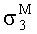
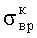
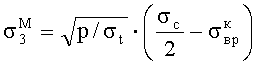
Величина 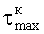
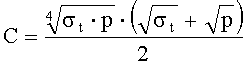
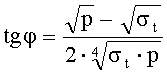
Вторым уравнением служило выражение для предельного круга Мора, пересекающего ось абсцисс «паспорта прочности» в точке 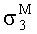
После алгебраических преобразований выражение относительно 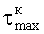
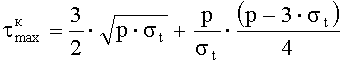
Экспериментальным обоснованием определения максимального сопротивления срезу 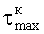
В таблице 3 представлены безразмерные значения максимального сопротивления срезу τmax (в долях от σt) для горных пород или хрупких материалов, характеризуемых показателем хрупкости Kxp (отношением σc/σp) в диапазоне от 5 до 20. Отклонение результатов определений колебалось в диапазоне от -6 до+6% с увеличением показателя хрупкости и составило, в среднем, менее 3,5%, что соизмеримо с точностью методов.
Теоретическим обоснованием определения коэффициента Пуассона µσ служит установленное экспериментально геомеханическое подобие коэффициента Пуассона и отношения диапазонов предельных напряжений на «паспорте прочности горной породы», соответствующих разрушению путем разрыва и сдвигом. Диапазон разрушения путем разрыва на паспорте прочности складывается из диапазона растягивающих минимальных главных нормальных напряжений, равного пределу прочности при всестороннем растяжении 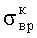
После алгебраических преобразований выражение относительно µσ приняло вид:
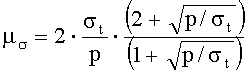
Экспериментальным обоснованием определения коэффициента Пуассона µσ служат результаты сопоставления значений, определенных предлагаемым способом, со значениями µк, определенными известным косвенным способом (патент РФ №2447284, кл. E21C 39/00, G01N 3/08, 2012) и с расчетными безразмерными параметрами метода построения паспорта прочности по данным определения пределов прочности при одноосном сжатии и растяжении (ГОСТ 21153.8-88 «Породы горные. Метод определения предела прочности при объемном сжатии. Приложение 2 обязательное. Методы построения паспорта прочности»). При этом в качестве исходных данных для расчетного метода были использованы значения пределов прочности при одноосном сжатии σc и растяжении σp, определенные методом нагружения сферическими инденторами, а в качестве аналога коэффициента Пуассона была использована сумма безразмерных параметров расчетного метода (K1+q1) и q2, по физическому смыслу подобная коэффициенту Пуассона µσ
В таблице 4 представлены значения коэффициентов Пуассона µσ и µк и суммы безразмерных параметров (K1+q1) и q2 для горных пород или хрупких материалов, характеризуемых показателем хрупкости Kxp (отношением σc/σp) в диапазоне от 5 до 20. Сравнение вычисленных значений коэффициента Пуассона свидетельствует о вполне приемлемой сходимости результатов. Отклонение значений µσ, определенных предлагаемым способом, как правило, не превышало 10% и по сравнению с результатами определения известным косвенным способом, в среднем, составило 8%.
В качестве примера эффективности использования способа в таблице 5 представлены результаты сопоставительных механических испытаний по определению комплекса механических характеристик кембрийской глины (Метрострой, Санкт-Петербург), выполненных согласно предлагаемому способу, а также расчетным методом по ГОСТ 21153.8-88 «Породы горные. Метод определения прочности при объемном сжатии. Приложение 2 обязательное. Методы построения паспорта прочности» и путем проведения объемных испытаний по ГОСТ 21153.8-88 «Породы горные. Метод определения прочности при объемном сжатии».
Показатели механических свойств кембрийской глины, вычисленные расчетным методом, были основаны на экспериментальных данных о пределах прочности при одноосном растяжении и сжатии, определенных способом-прототипом и составили 0,437 и 2,59 МПа, соответственно.
Испытания на объемное сжатие цилиндрических образцов кембрийской глины были выполнены в стабилометре запредельного деформирования БВ-21, подключенном к насосной станции, рассчитанной на создание давления рабочей жидкости до 60 МПа, и установленном на гидравлическом прессе ЦДМ-100, рассчитанном на создание сжимающего усилия до 100 тонн. Для построения паспорта прочности были использованы результаты определения пределов прочности σ1 при заданных величинах бокового гидростатического давления σ3 в диапазоне от 0,5 до 6,0 МПа. Величина максимального сопротивления срезу по данным определения пределов прочности при объемном сжатии была вычислена как максимальное (асимптотическое) значение предельных касательных напряжений, соответствующих предельным кругам напряжений Мора.
Сравнение вычисленных значений показателей механических свойств кембрийской глины различными способами свидетельствует о вполне приемлемой сходимости результатов. Отклонение значения 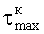
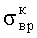
Отклонение значения коэффициента Пуассона µσ=0,36, определенного предлагаемым способом, от аналогичных значений µк=0,36 и (K1+q1)+q2=0,37, определенных известным косвенным способом (патент РФ №2447284, кл. E21C 39/00, G01N 3/08, 2012) и по данным ГОСТ 21153.8-88 «Породы горные. Метод определения предела прочности при объемном сжатии. Приложение 2 обязательное. Методы построения паспорта прочности», составило -0,9 и -4,5%, соответственно.
Реализация способа позволяет существенно упростить испытания, повысить точность и информативность определения механических свойств горных пород и материалов, имеющих хрупкий характер разрушения, доступным и весьма производительным методом нагружения образцов произвольной, в том числе неправильной, формы сферическими инденторами.
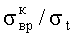
ГОСТ 21153.8-88)
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ОСТАТОЧНОЙ ПРОЧНОСТИ ГОРНЫХ ПОРОД | 2018 |
|
RU2684536C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ПУАССОНА ГОРНЫХ ПОРОД | 2010 |
|
RU2447284C2 |
| ПОРОДОРАЗРУШАЮЩИЙ ИНСТРУМЕНТ | 1997 |
|
RU2127349C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРЕДЕЛА ПРОЧНОСТИ ПРИ ОДНООСНОМ РАСТЯЖЕНИИ ГОРНЫХ ПОРОД | 2010 |
|
RU2435955C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРОЧНОСТИ ГОРНЫХ ПОРОД В ВОДОНАСЫЩЕННОМ СОСТОЯНИИ | 2018 |
|
RU2676046C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРОЧНОСТИ УГОЛЬНОГО ВЕЩЕСТВА | 2021 |
|
RU2790335C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ РАЗУПРОЧНЕНИЯ НАГРУЖЕННЫХ ГОРНЫХ ПОРОД | 2004 |
|
RU2261327C1 |
| СПОСОБ ВЗРЫВНОГО РАЗРУШЕНИЯ КРИСТАЛЛОСОДЕРЖАЩИХ ГОРНЫХ ПОРОД УДЛИНЕННЫМИ ЗАРЯДАМИ | 1998 |
|
RU2142610C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УСТОЙЧИВОСТИ СТВОЛА НАКЛОННЫХ СКВАЖИН | 2011 |
|
RU2472928C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УСТОЙЧИВОСТИ СТВОЛА ГОРИЗОНТАЛЬНЫХ СКВАЖИН | 2011 |
|
RU2473802C2 |
Изобретение относится к механическим испытаниям горных пород и материалов, имеющих хрупкий характер разрушения, и может быть использовано при инженерно-геологических изысканиях. Сущность: осуществляют нагружение образца двумя встречно направленными сферическими инденторами до его раскалывания, фиксируют разрушающую силу, определяют в разрушенном образце площадь поверхности трещины отрыва, проходящую через ось нагружения, и геометрические параметры разрушенных зон в областях контакта с обоими сферическими инденторами, вычисляют растягивающее напряжение разрыва образца и среднее сжимающее напряжение на границе большей из разрушенных зон и определяют в качестве механических свойств образца предел прочности и сопротивление срезу. Из обломков разрушенного образца собирают составной образец, на торцах которого определяют геометрические параметры разрушенных зон - диаметр остаточных отпечатков от инденторов и длину лунок выкола вдоль поверхности трещины отрыва. Определяют площадь поверхности большей разрушенной зоны на контакте с инденторами, предел прочности при всестороннем растяжении, максимальное сопротивление срезу и коэффициент Пуассона по формулам. Технический результат: упрощение испытаний, повышение точности определения механических свойств образцов и информативности испытаний. 5 табл., 2 ил.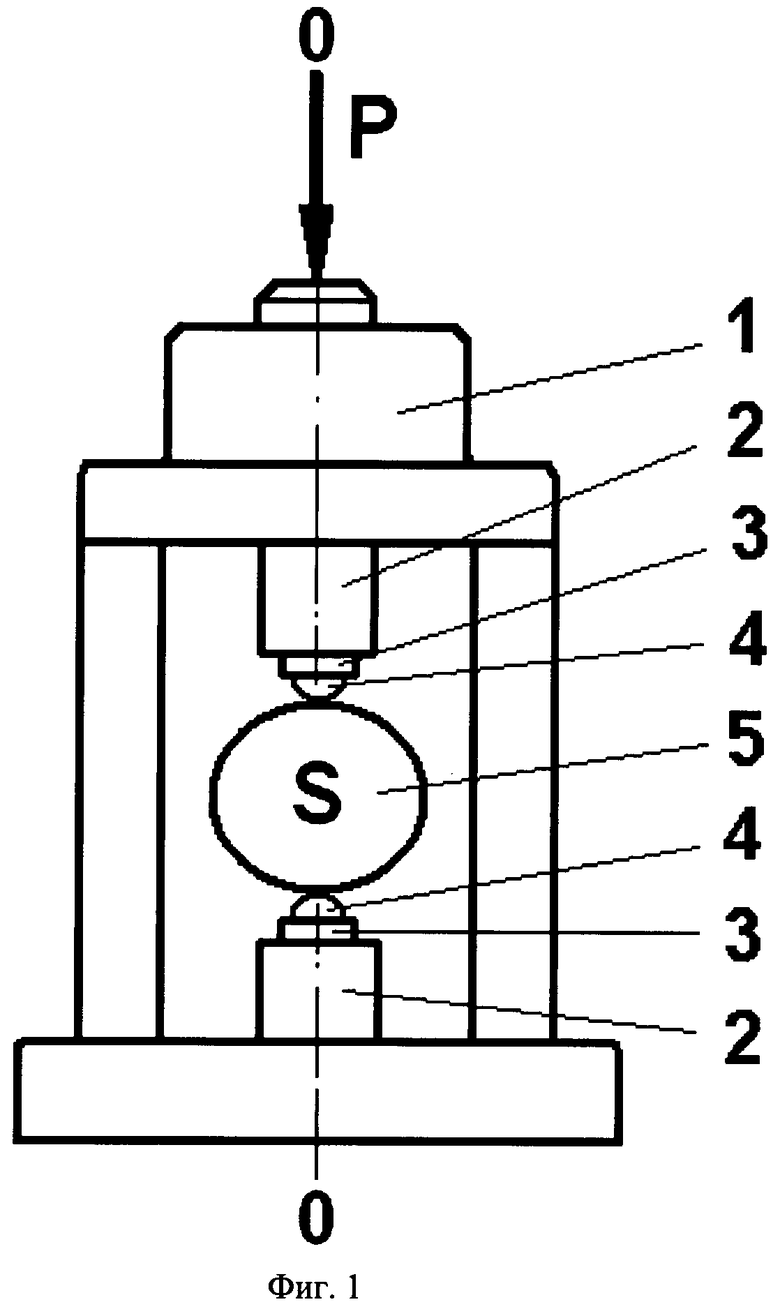
1. Способ определения механических свойств образцов горных пород и материалов, включающий нагружение образца двумя встречно направленными сферическими инденторами до его раскалывания, фиксирование разрушающей силы, определение в разрушенном образце площади поверхности трещины отрыва, проходящей через ось нагружения, и геометрических параметров разрушенных зон в областях контакта с обоими сферическими инденторами, вычисление растягивающего напряжения разрыва образца и среднего сжимающего напряжения на границе большей из разрушенных зон и определение в качестве механических свойств образца предела прочности и сопротивления срезу, отличающийся тем, что из обломков разрушенного образца собирают составной образец, на торцах которого определяют геометрические параметры разрушенных зон - диаметр остаточных отпечатков от инденторов и длину лунок выкола вдоль поверхности трещины отрыва, определяют площадь поверхности большей разрушенной зоны на контакте с инденторами по формуле:
F=π·Dотп·Lл,
где F - площадь поверхности большей разрушенной зоны;
Dотп - диаметр остаточного отпечатка от индентора;
Lл - длина лунки выкола вдоль поверхности трещины отрыва;
π=3,14,
а в качестве механических свойств образца определяют предел прочности при всестороннем растяжении 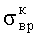
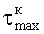
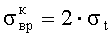
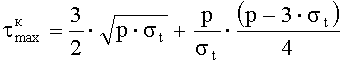
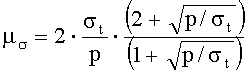
где σt - растягивающее напряжение разрыва образца;
p - среднее сжимающее напряжение на границе большей из разрушенных зон.
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРЕДЕЛА ПРОЧНОСТИ ПРИ ОДНООСНОМ РАСТЯЖЕНИИ ГОРНЫХ ПОРОД | 2010 |
|
RU2435955C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ПУАССОНА ГОРНЫХ ПОРОД | 2010 |
|
RU2447284C2 |
| ПРИБОР ДЛЯ ОПРЕДЕЛЕНИЯ ПРОЧНОСТИ ГОРН ПОРОД НА РАСТЯЖЕНИЕ,1х»СЕСою;П*ШТЙО-Тй;':ВИьЛ'--'^" • | 0 |
|
SU332223A1 |
| CN 102183410 A 14.09.2011 | |||
Авторы
Даты
2014-06-27—Публикация
2013-01-29—Подача