Изобретение относится к вычислительной технике и может быть использовано в цифровых вычислительных устройствах, а также в устройствах цифровой обработки сигналов, в криптографических приложениях и в системах управления.
Известен последовательный многоразрядный сумматор, который содержит n-разрядные сдвиговые регистры операндов X и Y, регистр результата, одноразрядный сумматор и двухступенчатый D-триггер для запоминания переноса [1].
Недостатком данного сумматора является ограниченные функциональные возможности, а именно невозможность суммирования по модулю.
Также известен многоразрядный параллельный сумматор с последовательным переносом, содержащий n одноразрядных параллельных сумматоров с соответствующими связями [2].
Недостатком данного сумматора является ограниченные функциональные возможности, а именно невозможность суммирования по модулю.
Наиболее близким по технической сущности к заявляемому изобретению является многоразрядный параллельный сумматор по модулю с последовательным переносом, содержащий (n+1) одноразрядных параллельных сумматоров по модулю с соответствующими связями, осуществляющий суммирование чисел A и B по произвольному модулю M [3].
Недостатком данного устройства является низкое быстродействие, вызванное последовательным поразрядным суммированием, а также наличием в каждом одноразрядном сумматоре по модулю двух последовательно соединенных параллельных одноразрядных сумматоров.
Техническим результатом изобретения является повышение быстродействия.
Для достижения технического результата в многоразрядный сумматор по модулю, содержащий n полных одноразрядных сумматоров, где n-разрядность устройства, RS-триггер, элемент «2И», элемент «НЕ», элемент задержки, входы первого числа суммирования, входы второго числа суммирования, вход модуля устройства, информационные выходы устройства, вход установки устройства в начальное состояние, причем входы первого числа суммирования соединены с первыми информационными входами n полных одноразрядных сумматоров, входы второго числа суммирования соединены со вторыми информационными входами n полных одноразрядных сумматоров, вход установки устройства в начальное состояние соединен со входом установки в единичное состояние RS-триггера, вход установки в нулевое состояние которого соединен с выходом элемента «2И», первый информационный вход которого соединен с выходом элемента «НЕ», а второй информационный вход соединен с выходом элемента задержки, введены n-разрядный ключи (n+1)-разрядный сумматор, первые информационные входы которого соединены с информационными выходами n полных одноразрядных сумматоров соответственно, (2…(n+1))-й разряды вторых информационных входов (n+1)-разрядного сумматора соединены с выходами переноса (1…n)-го одноразрядных сумматоров, первый разряд вторых информационных входов соединен с выходом RS-триггера и управляющим входом n-разрядного ключа, выход переноса соединён со входом элемента «НЕ», а информационные выходы являются информационными выходами устройства, информационные входы n-разрядного ключа соединены со входом модуля устройства, информационные выходы соединены со входами переноса n полных одноразрядных сумматоров, причём вход установки устройства в начальное состояние соединён со входом элемента задержки.
Сущность изобретения заключается в реализации следующего способа суммирования чисел A и B по модулю P.
Пусть 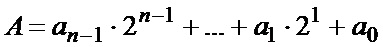 и
и  , где n-разрядность устройства, соответственно первый и второй операнды суммирования, причем
, где n-разрядность устройства, соответственно первый и второй операнды суммирования, причем  и
и  . Пусть
. Пусть  модуль, по которому проводится суммирование,
модуль, по которому проводится суммирование,  - сумма операндов A и B по модулю P.
- сумма операндов A и B по модулю P.
В результате выполнения операции необходимо получить сумму 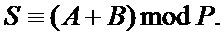
При сложении двух чисел, представленных в виде двоичных кодов A(an-1, …, a0) и B(bn-1, …, b0) образуется сумма С(сn, …, с0), равная 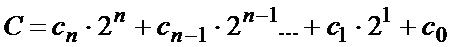 . Способ суммирования двух чисел A и Bпо модулю P заключается в том, что вначале находят решение разности С(сn, …, с0)–P(pn-1, …, p0). Если полученное значение больше или равно нулю, то оно и является искомой суммой S(sn-1,…, s0). Если же полученное значение меньше нуля, то осуществляется повторное суммирование чисел A и B и искомой суммой S является сумма этих чисел S(sn-1,…, s0)=A(an-1, …, a0) + B(bn-1, …, b0). В качестве индикатора превышения нуля используется выход переноса (n+1)-разрядного параллельного сумматора.
. Способ суммирования двух чисел A и Bпо модулю P заключается в том, что вначале находят решение разности С(сn, …, с0)–P(pn-1, …, p0). Если полученное значение больше или равно нулю, то оно и является искомой суммой S(sn-1,…, s0). Если же полученное значение меньше нуля, то осуществляется повторное суммирование чисел A и B и искомой суммой S является сумма этих чисел S(sn-1,…, s0)=A(an-1, …, a0) + B(bn-1, …, b0). В качестве индикатора превышения нуля используется выход переноса (n+1)-разрядного параллельного сумматора.
На фиг. 1 представлена схема многоразрядного сумматора по модулю. Многоразрядный сумматор по модулю содержит n-разрядный ключ 1, n полных одноразрядных сумматоров 2.1-2.n, RS-триггер 3, (n+1)-разрядный параллельный сумматор 4, где n-разрядность устройства, элемент «2И» 5, элемент «НЕ» 6, элемент задержки 7, вход 8 модуля устройства, входы 9 и 10 второго и первого чисел суммирования соответственно, информационные выходы 11 устройства, вход 12 установки устройства в начальное состояние.
На вход 10 и 9 устройства подают коды чисел A и B, поступающие далее на первый информационный вход A и второй информационный вход B соответствующего j-го полного одноразрядного сумматора 2.1-2.n, где j=1, …, n. Одновременно с этим на вход 8 устройства подается инверсный код модуля P, который поступает на информационные входы (X1…Xn) n-разрядного ключа 1. На вход 12 установки в начальное состояние, который соединён со входом элемента задержки 7 и S входом установки в единичное состояние RS-триггера 3, подаётся сигнал начала вычислений.
Многоразрядный сумматор по модулю работает следующим образом (см. Фиг. 1).
Перед началом работы устройство устанавливается в начальное состояние подачей на вход 12 управляющего сигнала. На выходе RS-триггера 3 устанавливается единичный сигнал. На информационные входы 10, 9 и 8 устройства подаются в двоичном виде коды операндов суммирования A(an-1, …,a0) и B(bn-1, …,b0) и инверсный код модуля P(pn-1, …, p0) соответственно. Для каждого разряда на выходах полных одноразрядных сумматоров 2.1-2.n формируется сигнал суммы S и сигналы переноса числа Pо. Так как, RS-триггер 3 находится в единичном состоянии, то ключ 1 пропускает на входы переноса Pi полных одноразрядных сумматоров 2.1-2.n инверсный код модуля P(pn-1, …, p0). В результате на информационных выходах полных одноразрядных сумматоров 2.1-2.n образуются поразрядные сигналы суммы, а на выходах переноса образуются поразрядные сигналы переноса. Сигналы с информационных выходов полных одноразрядных сумматоров 2.1-2.n поступают на первые информационные входы (n+1)-разрядного сумматора 4. Сигналы с выходов переноса полных одноразрядных сумматоров 2.1-2.n поступают на (2…(n+1))-й разряды вторых информационных входов (n+1)-разрядного сумматора 4. На первый разряд B1 вторых информационных входов (n+1)-разрядного сумматора 4 с выхода RS-триггера 3 поступает сигнал логической единицы. В результате на выходах (n+1)-разрядного сумматора 4 образуется значение S=
В случае если , то на выходе переноса Po(n+1)-разрядного сумматора 4 образуется сигнал логической единицы, который, проходя через элемент «НЕ» 6 закроет для прохождения на вход RRS-триггера 3 сигнала с выхода элемента задержки 7. Время задержки элемента задержки 7 выбирается не менее чем минимальное время прохождения входных сигналов через элементы 1, 2, 4. При этом на информационных выходах (n+1)-разрядного сумматора 4 образуется искомая сумма чисел A и B по модулю P.
, то на выходе переноса Po(n+1)-разрядного сумматора 4 образуется сигнал логической единицы, который, проходя через элемент «НЕ» 6 закроет для прохождения на вход RRS-триггера 3 сигнала с выхода элемента задержки 7. Время задержки элемента задержки 7 выбирается не менее чем минимальное время прохождения входных сигналов через элементы 1, 2, 4. При этом на информационных выходах (n+1)-разрядного сумматора 4 образуется искомая сумма чисел A и B по модулю P.
В случае если  , то на выходе переноса Po(n+1)-разрядного сумматора 4 остаётся нулевой сигнал, который, инвертируясь через элемент «НЕ» 6, открывает элемент «2И» 5 для прохождения сигнала с выхода элемента задержки 7. Далее сигнал поступает на R вход RS-триггера 3, переводя его в нулевое состояние. При этом закрывается n-разрядный ключ 1 и на вход B1 вторых информационных входов (n+1)-разрядного сумматора 4 поступает нулевой сигнал. В результате на его информационных выходах формируется сумма чисел A и B, которая и является искомой суммой
, то на выходе переноса Po(n+1)-разрядного сумматора 4 остаётся нулевой сигнал, который, инвертируясь через элемент «НЕ» 6, открывает элемент «2И» 5 для прохождения сигнала с выхода элемента задержки 7. Далее сигнал поступает на R вход RS-триггера 3, переводя его в нулевое состояние. При этом закрывается n-разрядный ключ 1 и на вход B1 вторых информационных входов (n+1)-разрядного сумматора 4 поступает нулевой сигнал. В результате на его информационных выходах формируется сумма чисел A и B, которая и является искомой суммой 
После получения результата суммирования чисел A и B по модулю P на выход с устройства, процесс суммирования может быть возобновлён с другими исходными данными.
Рассмотрим работу устройства на примере, когда  (см. фиг. 1).
(см. фиг. 1).
В исходном состоянии RS-триггер 3 находится в нулевом состоянии, на все входы устройства воздействуют логические нули.
Пусть A=610=01102, B=410=01002, P=910=10012,  =01102. Устройство для данного примера будет содержать четыре полных одноразрядных сумматора 2.1-2.4.
=01102. Устройство для данного примера будет содержать четыре полных одноразрядных сумматора 2.1-2.4.
На входы A, B и Pi четырех полных одноразрядных сумматоров 2.1-2.4 подаются коды чисел A=610=01102, B=410=01002, 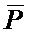 =01102. На вход 12 установки в начальное состояние, который соединён с S входом RS-триггера 3, подаётся единица, которая переводит RS-триггер 3 в единичное состояние. Сигнал с выхода RS-триггера 3 поступает на управляющий вход Wn-разрядного ключа 1 и первый разряд B1 вторых информационных входов (n+1)-разрядного сумматора 4. На выходах первого полного одноразрядного сумматора 2.1 получаем значения S=0, Pо=0. На выходах второго полного одноразрядного сумматора 2.2 получаем значения S=0, Pо=1. На выходах третьего полного одноразрядного сумматора 2.3 получаем значения S=1, Pо=1. На выходах четвёртого полного одноразрядного сумматора 2.4 получаем значения S=0, Pо=0. Сигналы суммы S и сигналы переноса числа Pо поступают на первые информационные входы (A1…An) и вторые информационные входы (B2…Bn+1)(n+1)-разрядного сумматора 4. Таким образом, на входах (n+1)-разрядного сумматора 4 образуются числа: С=001002 и D=011012. После суммирования на информационных выходах (n+1)-разрядного сумматора 4 (S1…Sn), а значит и на выходах устройства, формируется число E=00012=110, а на выходе переноса Po=1. При этом элемент «2И» 5 оказывается закрытым для прохождения сигнала с выхода элемента задержки 7.
=01102. На вход 12 установки в начальное состояние, который соединён с S входом RS-триггера 3, подаётся единица, которая переводит RS-триггер 3 в единичное состояние. Сигнал с выхода RS-триггера 3 поступает на управляющий вход Wn-разрядного ключа 1 и первый разряд B1 вторых информационных входов (n+1)-разрядного сумматора 4. На выходах первого полного одноразрядного сумматора 2.1 получаем значения S=0, Pо=0. На выходах второго полного одноразрядного сумматора 2.2 получаем значения S=0, Pо=1. На выходах третьего полного одноразрядного сумматора 2.3 получаем значения S=1, Pо=1. На выходах четвёртого полного одноразрядного сумматора 2.4 получаем значения S=0, Pо=0. Сигналы суммы S и сигналы переноса числа Pо поступают на первые информационные входы (A1…An) и вторые информационные входы (B2…Bn+1)(n+1)-разрядного сумматора 4. Таким образом, на входах (n+1)-разрядного сумматора 4 образуются числа: С=001002 и D=011012. После суммирования на информационных выходах (n+1)-разрядного сумматора 4 (S1…Sn), а значит и на выходах устройства, формируется число E=00012=110, а на выходе переноса Po=1. При этом элемент «2И» 5 оказывается закрытым для прохождения сигнала с выхода элемента задержки 7.
Непосредственной проверкой устанавливаем: 6+4=10, 10≡1 mod 9.
Рассмотрим работу устройства на примере, когда 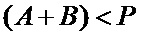 (см. фиг. 1).
(см. фиг. 1).
В исходном состоянии RS-триггер 3 находится в нулевом состоянии, на все входы устройства воздействуют логические нули.
Пусть A=310=00112, B=410=01002, P=910=10012, 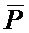 = 01102. Устройство для данного примера будет содержать четыре полных одноразрядных сумматора 2.1-2.4.
= 01102. Устройство для данного примера будет содержать четыре полных одноразрядных сумматора 2.1-2.4.
На входы A, B и Pi четырех одноразрядных сумматоров 2.1-2.4 подаются коды чисел A=310=00112, B=410=01002, 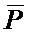 = 01102. На вход 12 установки в начальное состояние, который соединён с S-входом RS-триггера 3, подаётся единица, которая переводит RS-триггер 3 в единичное состояние. Сигнал с выхода RS-триггера 3 поступает на управляющий вход Wn-разрядного ключа 1 и первый разряд B1 вторых информационных входов (n+1)-разрядного сумматора 4. На выходах первого полного одноразрядного сумматора 2.1 получаем значения S=1, Po=0. На выходах второго полного одноразрядного сумматора 2.2 получаем значения S=0, Po=1. На выходах третьего полного одноразрядного сумматора 2.3 получаем значения S=0, Po=1. На выходах четвёртого полного одноразрядного сумматора 2.4 получаем значения S=0, Po=0. Сигналы суммы S и сигналы переноса числа Po поступают на первые информационные входы (A1…An)(n+1)-разрядного сумматора 4 и вторые информационные входы (B2…Bn+1). Таким образом, на входах сумматора образуются числа: С=000012 и D=011012. После суммирования на информационных выходах (n+1)-разрядного сумматора 4 (S1…Sn), а значит и на выходах устройства, формируется число E=01112=710, а на выходе переноса Sn+1=0. Поскольку значение на выходе переноса Po оказалось равно нулю, то на выходе элемента «НЕ» 6 окажется сигнал логической единицы, который откроет элемент «2И» 5 и сигнал с выхода элемента задержки 7 переведёт RS-триггер 3 в нулевое состояние. На управляющий вход Wn-разрядного ключа 1 поступит логический ноль, ключ закроется. Инверсный модуль в суммировании при этом не будет участвовать. Тогда, на выходе первого полного одноразрядного сумматора 2.1 получим значения S=1, Po=0. На выходе второго полного одноразрядного сумматора 2.2 получим значения S=1, Po=0. На выходе третьего полного одноразрядного сумматора 2.3 получим значения S=1, Po=0. На выходе четвёртого полного одноразрядного сумматора 2.4 получим значения S=0, Po=0.
= 01102. На вход 12 установки в начальное состояние, который соединён с S-входом RS-триггера 3, подаётся единица, которая переводит RS-триггер 3 в единичное состояние. Сигнал с выхода RS-триггера 3 поступает на управляющий вход Wn-разрядного ключа 1 и первый разряд B1 вторых информационных входов (n+1)-разрядного сумматора 4. На выходах первого полного одноразрядного сумматора 2.1 получаем значения S=1, Po=0. На выходах второго полного одноразрядного сумматора 2.2 получаем значения S=0, Po=1. На выходах третьего полного одноразрядного сумматора 2.3 получаем значения S=0, Po=1. На выходах четвёртого полного одноразрядного сумматора 2.4 получаем значения S=0, Po=0. Сигналы суммы S и сигналы переноса числа Po поступают на первые информационные входы (A1…An)(n+1)-разрядного сумматора 4 и вторые информационные входы (B2…Bn+1). Таким образом, на входах сумматора образуются числа: С=000012 и D=011012. После суммирования на информационных выходах (n+1)-разрядного сумматора 4 (S1…Sn), а значит и на выходах устройства, формируется число E=01112=710, а на выходе переноса Sn+1=0. Поскольку значение на выходе переноса Po оказалось равно нулю, то на выходе элемента «НЕ» 6 окажется сигнал логической единицы, который откроет элемент «2И» 5 и сигнал с выхода элемента задержки 7 переведёт RS-триггер 3 в нулевое состояние. На управляющий вход Wn-разрядного ключа 1 поступит логический ноль, ключ закроется. Инверсный модуль в суммировании при этом не будет участвовать. Тогда, на выходе первого полного одноразрядного сумматора 2.1 получим значения S=1, Po=0. На выходе второго полного одноразрядного сумматора 2.2 получим значения S=1, Po=0. На выходе третьего полного одноразрядного сумматора 2.3 получим значения S=1, Po=0. На выходе четвёртого полного одноразрядного сумматора 2.4 получим значения S=0, Po=0.
Таким образом, на входах (n+1)-разрядного сумматора 4 образуются числа: С=001112 и D=000002. После суммирования на информационных выходах (n+1)-разрядного сумматора (S1…Sn), а значит и на выходах устройства, формируется число E=01112=710, а на выходе переноса Po=0.
Непосредственной проверкой устанавливаем: 3+4=7, 7≡7 mod 9.
Оценим технический результат, достигаемый при использовании предлагаемого устройства по сравнению с устройством прототипом.
Оценим быстродействие Tпр устройства прототипа как:
T пр = 4ntзадSM1, где tзадSM1 – время задержки полного одноразрядного параллельного сумматора, n – разрядность устройства. Так как в каждом одноразрядном сумматоре по модулю содержится два последовательно соединенных одноразрядных параллельных сумматора и полное время суммирования выполняется за два цикла, то в выражение для Tпр входит коэффициент 4. Время задержки в логических цепях формирования управляющих сигналов учитывать не будем, так как оно будет существенно меньше основного времени суммирования и таким же, как и в предлагаемом устройстве.
Быстродействие Tиз предлагаемого устройства будет равно:
T из = tзадКл+2tзадSM1+2tзадSMn, где tзадКл – время задержки ключа 1, которым можно пренебречь, tзадSM1 – время задержки полного одноразрядного параллельного сумматора 2, tзадSMn – время задержки (n+1)-разрядного параллельного сумматора 4.
Если (n+1)-разрядный параллельный сумматор 4 выполнен по схеме с последовательным переносом, то тогда tзадSMn = ntзадSM1. Если же (n+1)-разрядный параллельный сумматор 4 выполнен в виде префиксного сумматора, то тогда tзадSMn = (logn)tзадSM1.
Тогда выигрыш B в быстродействии предлагаемого устройства по сравнению с устройством прототипом при выполнении сумматора 4 в виде сумматора с последовательным переносом составит
В = Tпр/Tиз = 4 ntзадSM1/(2tзадSM1+ 2ntзадSM1)=2n/(n+1).
Выигрыш B в быстродействии предлагаемого устройства по сравнению с устройством прототипом при выполнении сумматора 4 в виде префиксного сумматора составит
В= Tпр/Tиз = 4 ntзадSM1/(2tзадSM1+ 2logntзадSM1)=2n/(logn+1).
Источники информации
1. Бабич Н.П., Жуков И.А. Основы цифровой схемотехники: Учебное пособие. – М.: Издательский дом «Додэка–XXI», Киев: «МК-Пресс», 2007. – рисунок 4.45 с. 176.
2. Пухальский Г.И., Новосельцева Т.Я. Проектирование дискретных устройств на интегральных микросхемах: Справочник. – М.: Радио и связь, 1990. Рисунок 3.45, с.133.
3. Петренко В.И., Степанян Н.Э., Нелидин Ю.Р. Многоразрядный параллельный сумматор по модулю с последовательным переносом // Патент России № 2724597. Опубл. 25.06.2020. Бюл. № 18.
| название | год | авторы | номер документа |
|---|---|---|---|
| Многоразрядный сумматор по модулю | 2024 |
|
RU2831626C1 |
| МНОГОРАЗРЯДНЫЙ СУММАТОР ПО МОДУЛЮ | 2023 |
|
RU2804379C1 |
| Многоразрядный параллельный сумматор по модулю с последовательным переносом | 2019 |
|
RU2724597C1 |
| СУММАТОР ПО ПРОИЗВОЛЬНОМУ МОДУЛЮ | 2024 |
|
RU2835074C1 |
| СУММАТОР ГРУППОВОЙ СТРУКТУРЫ ПО ПРОИЗВОЛЬНОМУ МОДУЛЮ С ПОСЛЕДОВАТЕЛЬНЫМ ПЕРЕНОСОМ | 2024 |
|
RU2822292C1 |
| АРИФМЕТИКО-ЛОГИЧЕСКОЕ УСТРОЙСТВО ДЛЯ СЛОЖЕНИЯ, ВЫЧИТАНИЯ И УМНОЖЕНИЯ ЧИСЕЛ ПО МОДУЛЮ | 2019 |
|
RU2711051C1 |
| МНОГОРАЗРЯДНЫЙ ПАРАЛЛЕЛЬНЫЙ СУММАТОР ПО МОДУЛЮ С ПОСЛЕДОВАТЕЛЬНЫМ ПЕРЕНОСОМ | 2010 |
|
RU2439661C2 |
| УСТРОЙСТВО ДЛЯ КОНВЕЙЕРНОГО СУММИРОВАНИЯ ЧИСЕЛ ПО ПРОИЗВОЛЬНОМУ МОДУЛЮ | 2023 |
|
RU2805939C1 |
| Арифметико-логическое устройство для сложения чисел по модулю | 2016 |
|
RU2628180C1 |
| НАКАПЛИВАЮЩИЙ СУММАТОР ПО ПРОИЗВОЛЬНОМУ МОДУЛЮ | 2024 |
|
RU2829093C1 |

Изобретение относится к вычислительной технике и может быть использовано в цифровых вычислительных устройствах, а также в устройствах цифровой обработки сигналов, в криптографических приложениях и в системах управления. Техническим результатом является повышение быстродействия устройства. Технический результат достигается путем выполнения операции суммирования в одноразрядных параллельных сумматорах. Вначале определяется значение выражения  . Если полученное значение больше или равно нулю, т.е.
. Если полученное значение больше или равно нулю, т.е. 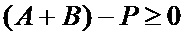 , то получено искомое значение. Если же полученное значение меньше нуля, т.е.
, то получено искомое значение. Если же полученное значение меньше нуля, т.е.  , то искомое значение получается повторным суммированием чисел A и B. Устройство содержит n полных одноразрядных сумматоров, (n+1)-разрядный сумматор, n-разрядный ключ, где n является разрядностью устройства, элемент задержки, RS-триггер, элемент «НЕ» и элемент «2И». 1 ил.
, то искомое значение получается повторным суммированием чисел A и B. Устройство содержит n полных одноразрядных сумматоров, (n+1)-разрядный сумматор, n-разрядный ключ, где n является разрядностью устройства, элемент задержки, RS-триггер, элемент «НЕ» и элемент «2И». 1 ил.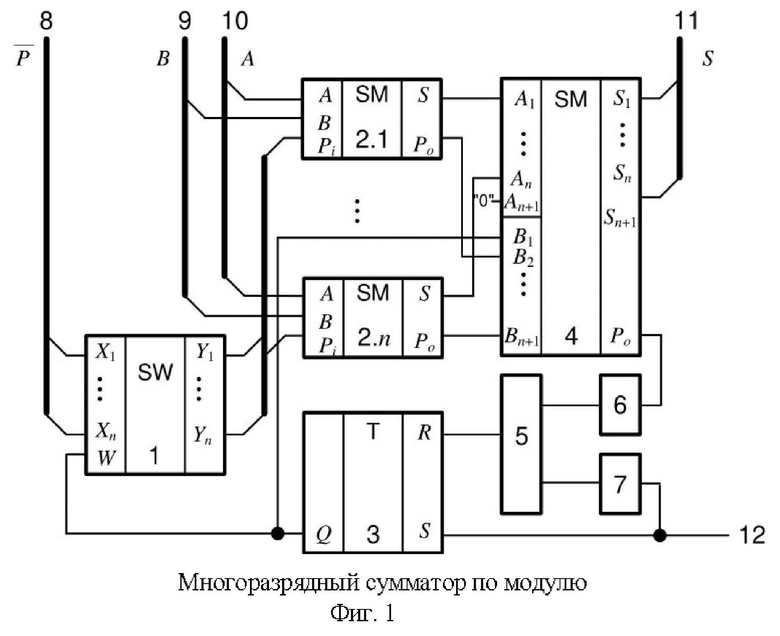
Многоразрядный сумматор по модулю, содержащий n полных одноразрядных сумматоров, где n – разрядность устройства, RS-триггер, элемент «2И», элемент «НЕ», элемент задержки, входы первого числа суммирования, входы второго числа суммирования, вход модуля устройства, информационные выходы устройства, вход установки устройства в начальное состояние, причем входы первого числа суммирования соединены с первыми информационными входами n полных одноразрядных сумматоров, входы второго числа суммирования соединены со вторыми информационными входами n полных одноразрядных сумматоров, вход установки устройства в начальное состояние соединен со входом установки в единичное состояние RS-триггера, вход установки в нулевое состояние которого соединен с выходом элемента «2И», первый информационный вход которого соединен с выходом элемента «НЕ», а второй информационный вход соединен с выходом элемента задержки, отличающийся тем, что в него введены n-разрядный ключ и (n+1)-разрядный сумматор, первые информационные входы которого соединены с информационными выходами n полных одноразрядных сумматоров соответственно, (2…(n+1))-й разряды вторых информационных входов (n+1)-разрядного сумматора соединены с выходами переноса (1…n)-го одноразрядных сумматоров, первый разряд вторых информационных входов соединен с выходом RS-триггера и управляющим входом n-разрядного ключа, выход переноса соединён со входом элемента «НЕ», а информационные выходы являются информационными выходами устройства, информационные входы n-разрядного ключа соединены со входом модуля устройства, информационные выходы соединены со входами переноса n полных одноразрядных сумматоров, причём вход установки устройства в начальное состояние соединён со входом элемента задержки.
| Многоразрядный параллельный сумматор по модулю с последовательным переносом | 2019 |
|
RU2724597C1 |
| НАКАПЛИВАЮЩИЙ СУММАТОР ПО МОДУЛЮ | 2012 |
|
RU2500017C1 |
| ПОЛНЫЙ ОДНОРАЗРЯДНЫЙ СУММАТОР ПО МОДУЛЮ | 2011 |
|
RU2484519C1 |
| US 4598266 A1, 01.07.1986. | |||
Авторы
Даты
2023-02-28—Публикация
2022-11-02—Подача