Предлагаемый способ относится к электрическим измерениям и может быть использован для точного измерения переменного напряжения. Способ позволяет получать значение измеряемого напряжения в комплексном виде, то есть вещественную и мнимую составляющие, по значениям которых можно вычислить амплитуду и фазу. Способ может применяться в тех случаях, когда необходимо обеспечить высокую чувствительность, высокую разрешающую способность, высокую точность измерения переменного напряжения.
Известен способ измерения эффективного значения переменного напряжения, включающий определение n выборок мгновенных значений напряжения, возведение этих значений в квадрат, суммирование, деление на число, извлечение квадратного корня [Шахов Э.К. Частотно- и времяимпульсные измерительные развертывающие преобразователи. Пенза: Изд-во Пензинского политех. института. 1978, стр. 72].
У этого способа есть недостатки.
Во-первых, сложность реализации и, как следствие, низкая надежность устройства, которое реализует способ. Это связано с тем, что для получения выборок требуется быстродействующий аналого-цифровой преобразователь (АЦП).
Во-вторых, этот способ не содержит усиления измеряемого напряжения, как результат - небольшой диапазон измеряемых переменных напряжений, так как напряжения с малой амплитудой, соизмеримой или меньшей шага квантования по уровню АЦП, не могут измеряться.
Наиболее близким по технической сущности к предлагаемому способу (прототипом) является способ измерения переменного напряжения, реализованный в прямоугольно-координатном потенциометре [Электрические измерения: Учебник для вузов / Байда Л.И., Добротворский Н.С., Душин Е.М. и др.; Под ред. А.В. Фремке и Е.М. Душина. – 5-е изд., перераб. и доп. – Л.: Энергия. Ленингр. отд-ние, 1980. стр. 209 - 212, рис. 5.16 а]. Способ заключается в том, что создают два рабочих тока в рабочих цепях А и Б, сдвинутых друг относительно друга на 90°. С помощью этих токов и калиброванной проволоки создают два регулируемых напряжения Ux1 и Ux2 сдвинутых друг относительно друга на 90°. Добиваются практически полного отсутствия тока в нуль-органе, при этом геометрическая сумма напряжений Ux1 и Ux2 соответствует измеряемому напряжению.
У прототипа есть недостатки.
Во-первых, подбирать значения вещественной и мнимой компенсирующих составляющих переменного напряжения приходится вручную, при этом время одного измерения очень большое.
Во-вторых, предполагается использовать стрелочный нуль-орган, что существенно ограничивает диапазон измеряемых переменных напряжений.
Задачей предлагаемого способа является повышение точности, разрешающей способности и чувствительности, уменьшение погрешности измерения вещественной и мнимой составляющих переменного напряжения, повышение надежности устройства, реализующего способ.
Технический результат заключается в том, что за счет предлагаемых отличительных признаков становится возможным использование нуль-органа с высокой чувствительностью, ограниченной только применяемыми техническими средствами. При этом становится возможным создавать компенсирующее переменное напряжение, соответствующее измеряемому напряжению с высокой точностью.
Поставленная задача достигается способом измерения вещественной и мнимой составляющих переменного напряжения, для выполнения которого используют следующие вспомогательные устройства:
- аналоговый сумматор, который имеет инвертирующий вход, неинвертирующий вход и выход, причем на инвертирующий вход подается измеряемое переменное напряжение, на неинвертирующий вход подается компенсирующее переменное напряжение;
- блок формирования компенсирующего напряжения (БФКН), который может формировать на своем выходе компенсирующее синусоидальное напряжение с заданными значениями вещественной и мнимой составляющих;
- усилитель, который может иметь неограниченно большой коэффициент усиления и ограниченную снизу и сверху полосу частот пропускания, на вход которого подается переменное напряжение с выхода аналогового сумматора;
- компаратор, на вход которого подается выходной сигнал усилителя, компаратор сравнивает его с нулевым напряжением и формирует выходные логические сигналы (прямоугольные импульсы), которые подаются на вход микроконтроллера;
- микроконтроллер, в котором программно реализован блок выделения основной гармоники (БВОГ);
- программно реализован блок выделения знаков (БВЗ) вещественной и мнимой составляющих основной гармоники.
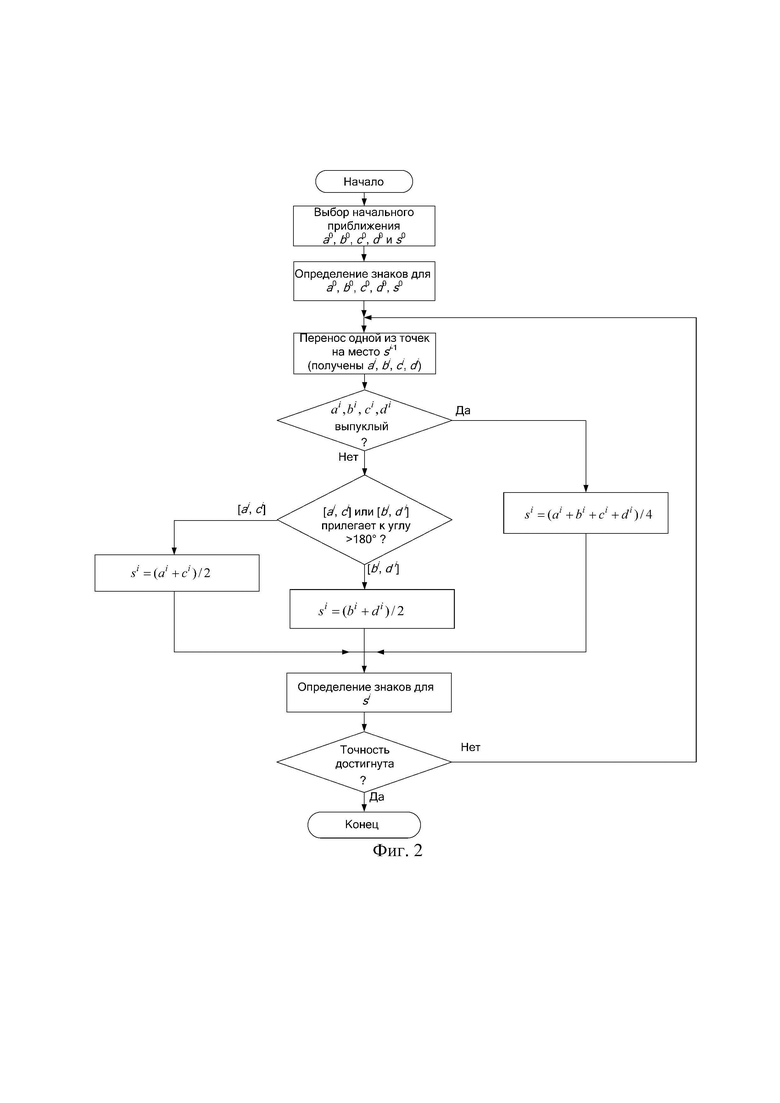
Выполняют шаги итерационной последовательности в соответствии с алгоритмом метода средних точек до тех пор, пока не будет достигнута заданная точность.
Алгоритм метода средних точек заключается в следующем. На комплексной плоскости выбирают четыре точки a0, b0, c0, d 0, названные «начальное приближение», причем у четырехугольника a0, b0, c0, d 0 углы a0 и c0 должны быть противоположными, углы b0 и d 0 должны быть противоположными, для каждой из точек выполняют шесть действий а, б, в, г, д, е:
а – «вещественную и мнимую составляющие комплексного числа, соответствующего точке, передают на БФКН»;
б – «подают переменное напряжение, сформированное БФКН, на неинвертирующий вход аналогового сумматора, на инвертирующий вход которого подано измеряемое переменное напряжение»;
в – «переменное напряжение, поступающее с выхода аналогового сумматора, усиливают с помощью усилителя»;
г – «выходной сигнал усилителя подают на вход компаратора, который сравнивает этот сигнал с нулевым напряжением и в результате формирует на своем выходе логические сигналы (прямоугольные импульсы)»;
д – «подают логические сигналы (прямоугольные импульсы) с выхода компаратора на БВОГ, выделяют основную гармонику»;
е – «с помощью блока выделения знаков (БВЗ) вещественной и мнимой составляющих основной гармоники определяют знаки вещественной и мнимой составляющих основной гармоники».
Точки a0, b0, c0, d 0 должны быть такими, что соответствующие этим точкам (то есть компенсирующим напряжениям) знаки основной гармоники были разные во всех сочетаниях, затем находят точку s 0 по формуле
s0=(a0+b0+c0+d 0)/4, для точки s0 выполняют шесть действий а, б, в, г, д, е, запоминают знаки вещественной и мнимой составляющих основной гармоники, соответствующие точкам a0, b0, c0, d 0, s0, затем выполняют шаги итерационной последовательности, каждый шаг состоит из следующих четырех действий ж, з, и, к:
ж – «находят из четырех точек ai-1, bi-1, ci-1, d i-1 (где i - номер шага) ту точку, для которой запомненные на предыдущем шаге знаки вещественной и мнимой составляющих основной гармоники равны знакам вещественной и мнимой составляющих основной гармоники, соответствующим точке si-1, затем найденную точку переносят на место точки si-1, остальные три точки оставляют на своих местах и, таким образом, находят четыре точки ai, bi, ci, d i»;
з – «находят пятую точку si по одному из трех вариантов следующим образом, если четырехугольник ai, bi, ci, d i выпуклый, то (первый вариант) точку si находят по формуле si=(ai+bi+ ci+di)/4, если же четырехугольник ai, bi, ci, d i не выпуклый, то есть один внутренний угол в одной из точек ai, bi, ci, d i более 1800, то из двух отрезков [ai, ci] или [bi, d i] выбирают один, который прилегает к углу более 1800, в соответствии с выбранным отрезком вычисляют si по одной из формул (второй вариант) si=(ai+ci)/2 или (третий вариант) si=(bi+di)/2»;
и – «для точки si выполняют шесть действий а, б, в, г, д, е, запоминают знаки вещественной и мнимой составляющих основной гармоники, соответствующей точке si»;
к – «проверяют условие окончания итерационного процесса, используя значение заданной погрешности Δз и следующие соотношения:
если │ai – ci│<Δз или │bi – d i│<Δз, то итерационный процесс необходимо заканчивать»;
шаги выполняют до тех пор, пока не будет выполнено условие окончания итерационного процесса, по окончании итерационного процесса в качестве результата измерения используют комплексное значение, соответствующее точке si. Вещественная составляющая Re(si) соответствует вещественной составляющей измеряемого переменного напряжения, а мнимая составляющая Im(si) соответствует мнимой составляющей измеряемого переменного напряжения.
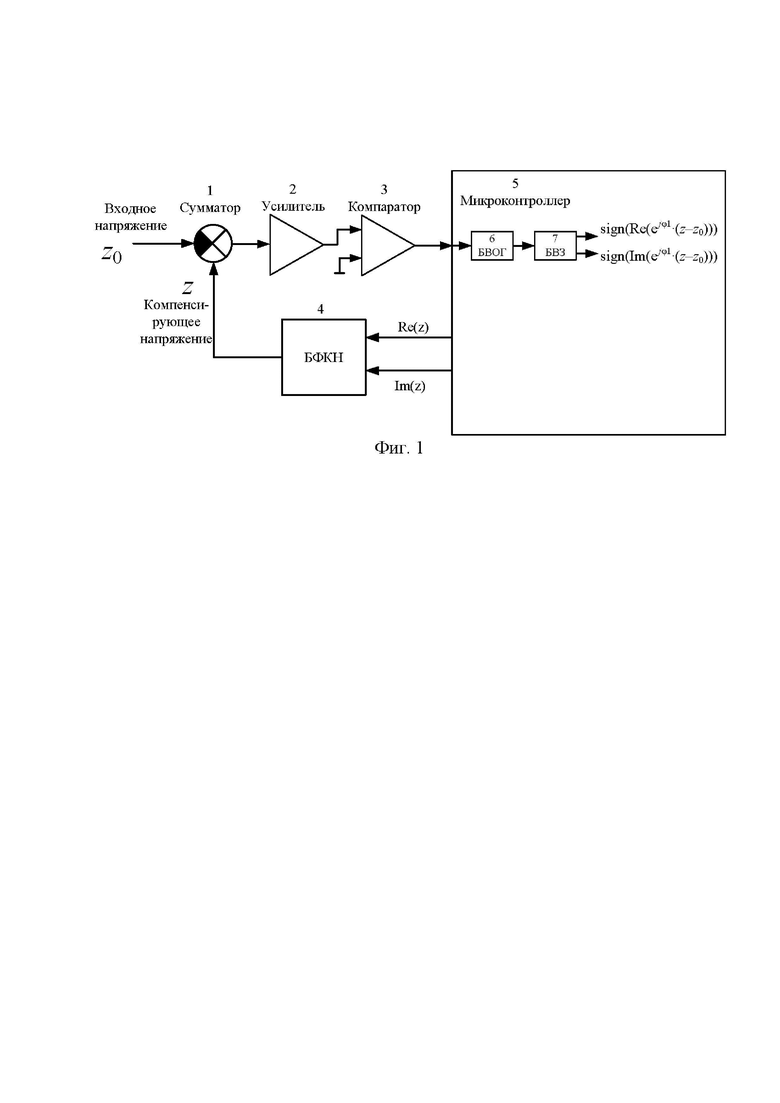
На фиг. 1 приведены вспомогательные устройства, объединенные в виде функциональной схемы устройства, реализующего предлагаемый способ. На фиг. 2 приведен алгоритм метода средних точек. На фиг. 3, фиг. 4, фиг. 5 приведен численный пример работы предлагаемого метода, состоящий из начального приближения и 13 шагов. На фиг. 6 и на фиг. 7 приведены случаи, когда в процессе выполнения шагов итерационного процесса может образоваться невыпуклый четырехугольник. На фиг. 8 приведен вектор, поясняющий связь точки si с амплитудой и фазой напряжения.
На фиг. 1. представлены сумматор 1, усилитель 2, компаратор 3, БФКН 4, микроконтроллер 5, в котором программно реализованы БВОГ 6 и БВЗ 7. Входное измеряемое переменное напряжение подается на инвертирующий вход сумматора 1, компенсирующее переменное напряжение от БФКН 4 подается на неинвертирующий вход сумматора 1, с выхода сумматора 1 переменное напряжение подается на вход усилителя 2. С выхода усилителя 2 переменное напряжение подается на первый вход компаратора 3, на второй вход которого подается нулевое напряжение. С выхода компаратора 3 логические сигналы (прямоугольные импульсы) подаются на вход микроконтроллера 5, в котором программно реализованы БВОГ 6 и БВЗ 7. Выход БВОГ 6 соединен со входом БВЗ 7. Используя знаки основной гармоники, в микроконтроллере реализуется алгоритм метода средних точек. В процессе реализации этого алгоритма многократно формируются вещественная Re(z) и мнимая Im(z) составляющие компенсирующего напряжения, которые передаются на БФКН 4.
Для описания работы устройства, реализующего предлагаемый способ, введем следующие обозначения.
j – мнимая единица, j 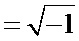 .
.
φ – угол, на который отличается измеряемое переменное напряжение от некоторого образцового переменного напряжения, например, если измеряется переменное напряжение на конденсаторе RC-цепочки, то за образцовое можно принять питающее переменное напряжение.
φ1 – угол, на который происходит сдвиг по фазе в канале измерения, то есть в сумматоре 1, усилителе 2, компараторе 3.
U(t) – измеряемое переменное напряжение, поступающее на инвертирующий вход сумматора 1, изменяющееся во времени t по синусоидальному закону U(t)=UA⋅sin(ω⋅t+φ).
UA – амплитудное значение измеряемого переменного напряжения.
z0 – измеряемое переменное напряжение, поступающее на инвертирующий вход сумматора 1, выраженное в комплексном виде, оно имеет вещественную составляющую Re(z0) и мнимую составляющую Im(z0).
Uк(t) – компенсирующее переменное напряжение, поступающее на неинвертирующий вход сумматора 1, изменяющееся во времени по синусоидальному закону.
z – компенсирующее переменное напряжение, поступающее на неинвертирующий вход сумматора 1, выраженное в комплексном виде, оно имеет вещественную составляющую Re(z) и мнимую составляющую Im(z).
Y – основная гармоника, выделенная из прямоугольных импульсов, действующих на выходе компаратора, выраженная в комплексном виде, она имеет вещественную составляющую Re(Y) и мнимую составляющую Im(Y).
Для реализации предлагаемого способа необходимо знать не только точное значение частоты измеряемого переменного напряжения, но и иметь синхронизирующий сигнал, связанный по фазе с некоторым образцовым переменным напряжением, фаза которого считается равной нулю. С помощью такого синхронизирующего сигнала можно создавать компенсирующее синусоидальное напряжение z с заданными параметрами - Re(z), Im(z), то есть с заданными значениями амплитуды и фазы.
Измеряемое переменное напряжение z0 поступает на инвертирующий вход сумматора 1. На неинвертирующий вход сумматора 1 поступает компенсирующее переменное напряжение z. Для формирования компенсирующего переменного напряжения используется БФКН 4.
Рассмотрим БФКН 7 более подробно. Он может быть реализован различными способами. Например, он может представлять собой управляемый RC-генератор синусоидального напряжения с подстройкой амплитуды и фазы таким образом, чтобы они соответствовали заданным значениям вещественной Re(z) и мнимой Im(z) составляющих требуемого синусоидального напряжения. Если частота измеряемого переменного напряжения низкая, то БФКН 4 может быть выполнен с помощью цифроаналогового преобразователя, на вход которого периодически подаются значения (поток) требуемых мгновенных значений напряжения, при этом соответствующая программа должна генерировать поток, обеспечивающий формирование синусоидального напряжения с заданным значениями вещественной Re(z) и мнимой Im(z) составляющих требуемого компенсирующего напряжения z. В этом случае микроконтроллер должен иметь цифровую синхронизацию с образцовым переменным напряжением, фаза которого считается равной нулю. Еще один возможный вариант - сформировать два сигнала, первый соответствует вещественной составляющей Re(z), второй соответствует мнимой составляющей Im(z) требуемого компенсирующего напряжения. Сигнал, соответствующий вещественной составляющей Re(z) можно сформировать непосредственно из синусоидального синхронизирующего сигнала. Сигнал, соответствующий мнимой составляющей Im(z) можно получить с помощью фазосдвигающего устройства. Суммируя эти два сигнала можно получить требуемое компенсирующее синусоидальное напряжение z. Такой способ предпочтительнее в том случае, если измеряемое переменное напряжение имеет сравнительно высокую частоту, например 1 МГц. На таких частотах затруднительно формировать сигнал «по точкам».
У БФКН 4 есть предельные значения, определяемые применяемой элементной базой. Это связано, прежде всего, с определенным значением напряжения питания, а также с допустимыми значениями тока и напряжения отдельных его элементов. Если попытаться превысить предельное значение, то устройство будет работать неправильно или выйдет из строя. Поэтому передаваемые на вход значения вещественной Re(z) и мнимой Im(z) составляющих не должны превышать этих предельных значений. Исходя из этого следует выбирать точки начального приближения a0, b0, c0, d 0.
Для анализа выходного напряжения сумматора 1 используются усилитель 2, компаратор 3, БВОГ 6, БВЗ 7. Результатом анализа являются знаки (+ или –) основной гармоники: знак вещественной составляющей и знак мнимой составляющей.
Рассмотрим анализ выходного напряжения сумматора 1 более подробно.
При реализации шагов итерационного процесса, каждый раз будет возникать некоторая разность входного переменного напряжения и компенсирующего переменного напряжения z–z0, назовем её разностный сигнал. Разностный сигнал усиливается с помощью усилителя 2. Любой усилитель имеет ограниченную полосу частот пропускания. Но при необходимости можно ограничить полосу пропускания снизу и сверху для подавления нежелательных высокочастотных и низкочастотных помех.
Следует отметить, что при традиционных способах измерения, например, как в приведенном аналоге, ограничение полосы частот пропускания может привести к фазовым искажениям полезного сигнала. В предлагаемом способе наличие фазовых искажений в канале усиления разностного сигнала не приводит к погрешности результата, так как при реализации алгоритма измерительного цикла разностный сигнал сводится практически к нулю, то есть значение z станет практически равно значению z0, у компенсирующего переменного напряжения z будут такие же амплитуда и фаза φ, как и у измеряемого переменного напряжения z0, независимо от того, как затем сдвигается разностный сигнал. Обозначим угол, на который сдвигается разностный сигнал, как φ1. Для хорошего подавления помех можно сделать верхнюю граничную частоту усилителя очень близкой к частоте измеряемого переменного напряжения, разумеется, при этом существенно изменится фаза разностного сигнала, то есть значение φ1 будет большим. Предлагаемый метод средних точек сходится при любом угле φ1.
Также следует отметить, что усилитель 1 может иметь большой коэффициент усиления, например такой, что при большом разностном сигнале усилитель 1 может выходить за пределы линейного режима, то есть на его выходе могут действовать прямоугольные импульсы, ограниченные питающими напряжениями. Предлагаемый способ остается работоспособным при измерении различных по амплитуде измеряемых напряжений, нет необходимости вводить несколько пределов измерения.
Сигнал с выхода усилителя поступает на первый вход компаратора 3, на второй вход которого подано нулевое напряжение. На выходе компаратора 3 образуются прямоугольные импульсы, которые поступают на вход микроконтроллера. Для предложенного способа информативной является только основная гармоника этих прямоугольных импульсов, обозначим её Y. Тогда:
Y=К⋅ejφ1⋅(z–z0)
где K - некоторый коэффициент.
Для выделения основной гармоники Y, импульсы с выхода компаратора 3 поступают на БВОГ 6, который входит в состав микроконтроллера 5. Реализация БВОГ 6 может быть различной. Например, это может быть аналого-цифровой преобразователь (АЦП) в совокупности с соответствующим программным обеспечением. В этом случае с помощью АЦП получают поток значений, соответствующий прямоугольным импульсам, а затем выделяют основную гармонику, например, с помощью преобразования Фурье. Но при сравнительно высокой частоте измеряемого переменного напряжения, например, 1 МГц, АЦП использовать затруднительно. Другой вариант - использовать не АЦП, а цифровой вход микроконтроллера, при этом выходные сигналы компаратора интерпретируются как логические сигналы, то есть нули и единицы. В этом случае БВОГ 6 также может выделить основную гармонику, применяя преобразование Фурье. В результате преобразования Фурье получаются гармонические составляющие. Для работы предлагаемого способа смысл имеет только основная гармоника. Большинство реализаций преобразования Фурье позволяют получить значения гармонических составляющих, в том числе и основную гармонику, в комплексном виде. Это означает, что в результате преобразования Фурье получаются две составляющие основной гармоники – вещественная Re(Y) и мнимая Im(Y). Каждая из них может иметь как положительный, так и отрицательный знак, то есть + или –. В БВЗ осуществляется выделение и запоминание этих знаков. Математически эти знаки можно получить по формулам sign(Re(e jφ1⋅(z–z0))) и sign(Im(e jφ1⋅(z–z0))).
В дальнейшем, для упрощения записи, условимся обозначать знаки основной гармоники следующим образом:
Re(Y) ≥ 0, Im(Y) ≥ 0 + +;
Re(Y) < 0, Im(Y) ≥ 0 – +;
Re(Y) ≥ 0, Im(Y) < 0 + –;
Re(Y) < 0, Im(Y) < 0 – –.
Всего существует четыре варианта знаков. Но с математической точки зрения есть случай, когда Re(Y) = 0, Im(Y) = 0. Этот случай рассматривать не будем, так как он крайне маловероятен.
Сумматор 1, усилитель 2, компаратор 3, БВОГ 6 и БВЗ 7 совместно образуют нуль-орган.
Для нахождения значения компенсирующего напряжения z, максимально приближенного к значению измеряемого напряжения z0, разработан итерационный метод, названный метод средних точек (см. фиг. 2). Метод позволяет решать уравнение вида:
sign(Re(e jφ1⋅(z–z0)))+j∙sign(Im(ejφ1⋅(z–z0)))=0,
где функция sign() определена следующим образом:
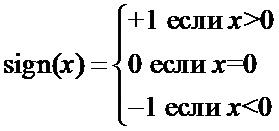
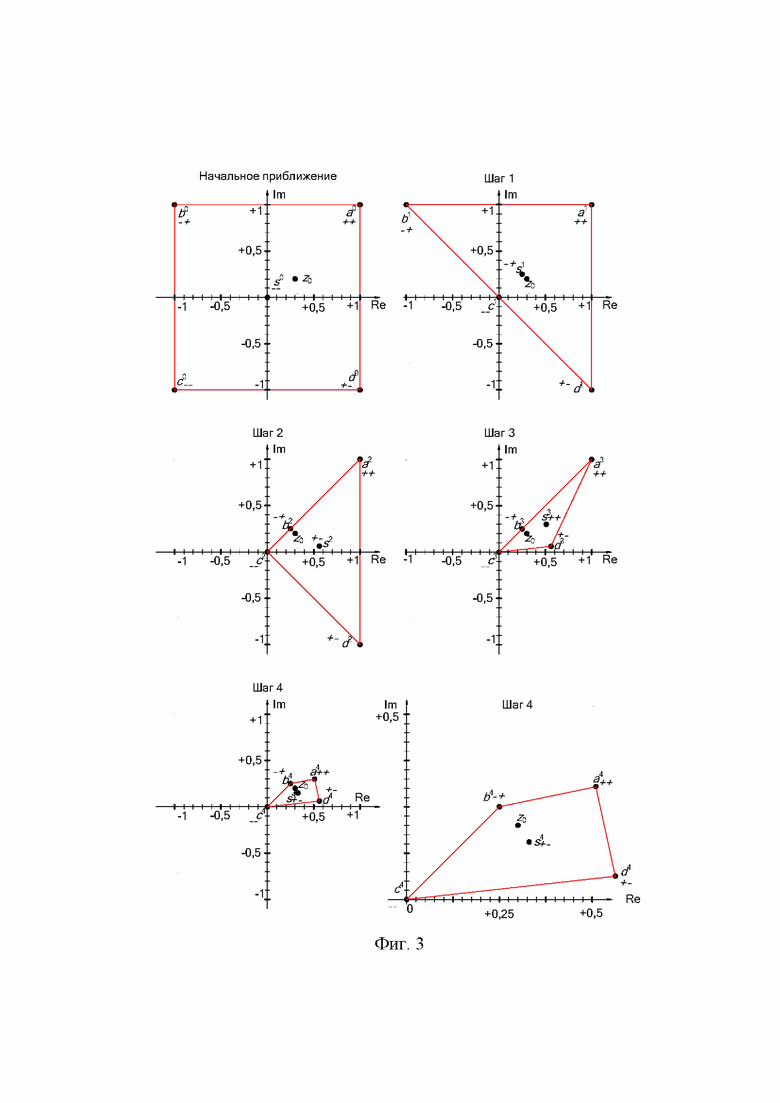
В начале итерационной последовательности выполняют действия, соответствующие начальному приближению. При этом на комплексной плоскости выбирают 4 точки, обозначаемые a0, b0, c0, d0. Один из возможных вариантов выбора этих точек следующий. У точки a0 предельная положительная вещественная и предельная положительная мнимая составляющие, у точки b0 предельная отрицательная вещественная и предельная положительная мнимая составляющие, у точки c0 предельная отрицательная вещественная и предельная отрицательная мнимая составляющие, у точки d0 предельная положительная вещественная и предельная отрицательная мнимая составляющие. Например, как начальное приближение, показанное на фиг. 3. Если знаки основной гармоники, соответствующие этим точкам, различные во всех сочетаниях, то есть ++, – +, + – и – –, то измеряемое значение z0 находится внутри этого прямоугольника. Для получения знаков основной гармоники для каждой из четырех точек a0, b0, c0, d0 выполняют шесть действий а, б, в, г, д, е.
Расположение точек начального приближения может быть любым другим, главное чтобы знаки основной гармоники Y, соответствующие этим четырем точкам были разными во всех сочетаниях.
Пятая точка s0 располагается в центре четырехугольника. Для неё также выполняются шесть действий а, б, в, г, д, е и запоминаются соответствующие знаки. На этом работа с начальным приближением заканчивается.
После этого начинают итерационный процесс, то есть циклическое выполнение следующих действий. Находят из четырех точек ai-1, bi-1, ci-1, di-1 (где i - номер шага) ту точку, для которой запомненные ранее знаки вещественной и мнимой составляющих основной гармоники Y равны знакам вещественной и мнимой составляющих основной гармоники, соответствующим точке si-1. Затем найденную точку переносят на место точки si-1, остальные три точки оставляют на своих местах и, таким образом, находят четыре точки ai, bi, ci, d i. Затем находят пятую точку si. При этом может быть три варианта. Первый вариант – когда четырехугольник ai, bi, ci, di выпуклый. В этом случае точку si необходимо находить по формуле:
si=(ai+bi+ci+di)/4.
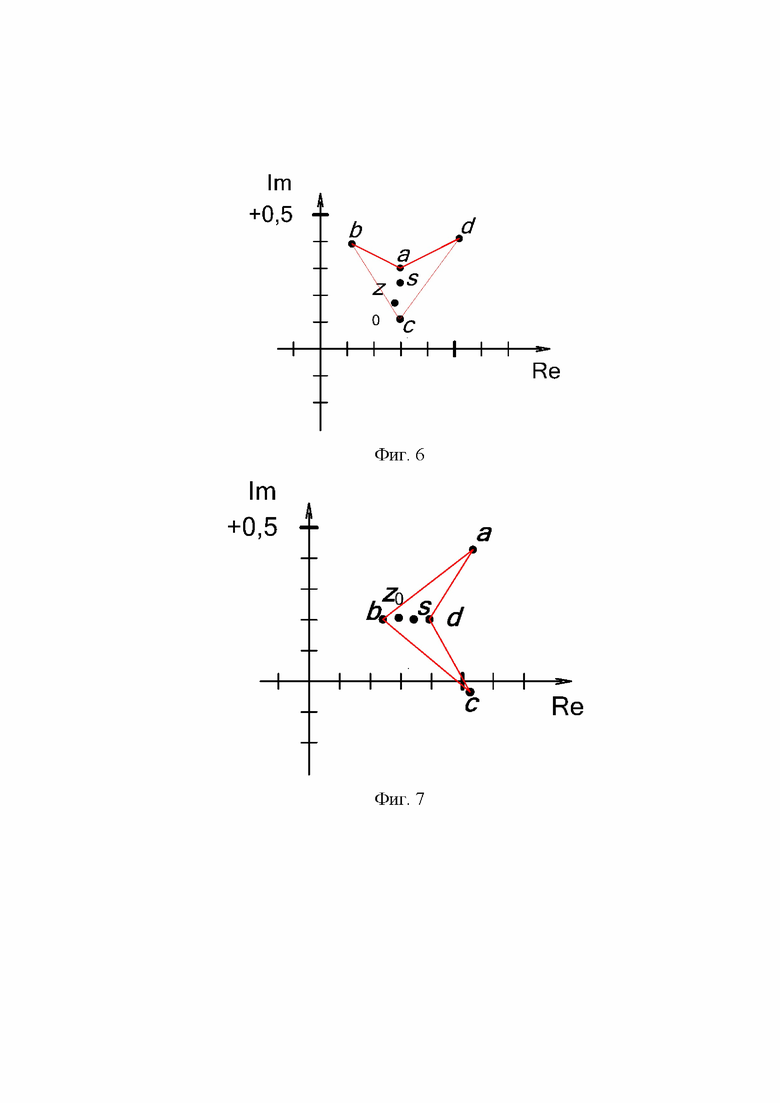
Второй вариант – когда четырехугольник не выпуклый, а внутренний угол, имеющий более 1800, принадлежит одной из точек ai или ci. Такой вариант приведен на фиг. 6. В этом случае точка si должна располагаться в середине отрезка [ai ci]:
si=(ai+ci)/2.
Третий вариант – когда четырехугольник не выпуклый, а внутренний угол, имеющий более 1800, принадлежит одной из точек bi или d i. Такой вариант приведен на фиг. 7. В этом случае точка si должна располагаться в середине отрезка [bi di]:
si=(bi+d i)/2.
Шаги итерационного процесса выполняют до тех пор, пока не будет достигнута заданная точность. Для этого необходимо задать необходимое значение допустимой погрешности Δз, которое не должно быть превышено по окончании итерационного процесса. Итерационный процесс заканчивают если
│ai – bi│<Δз или │ci – di│<Δз.
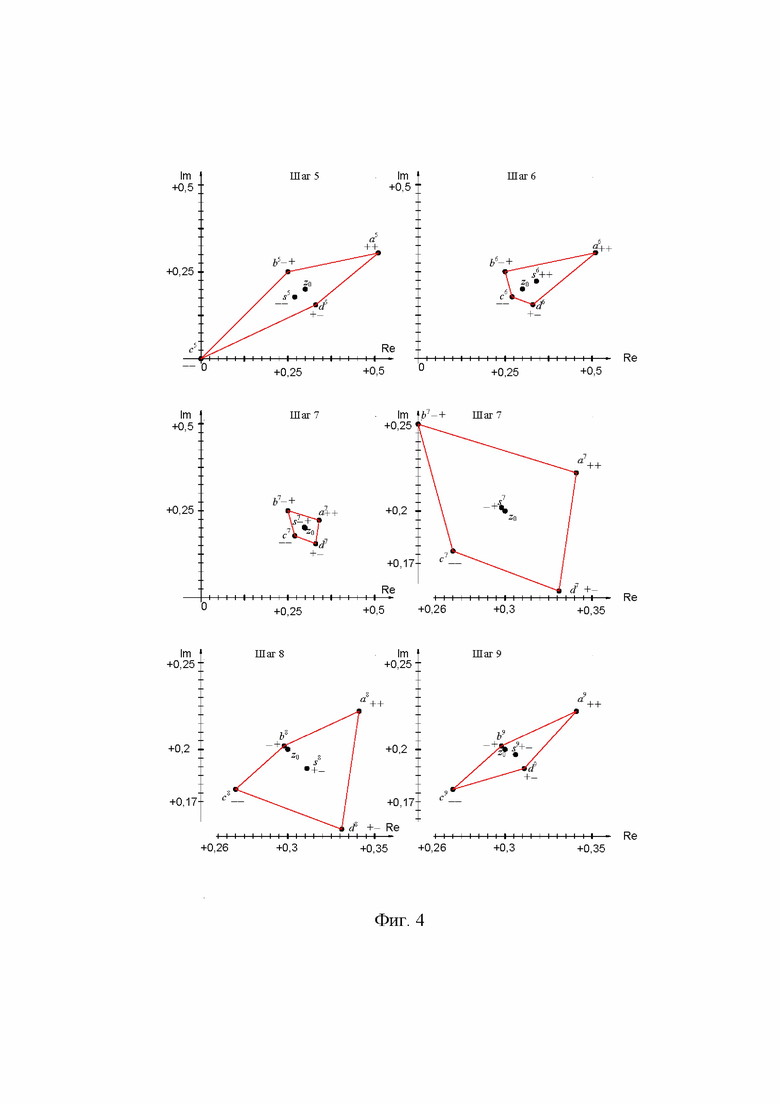
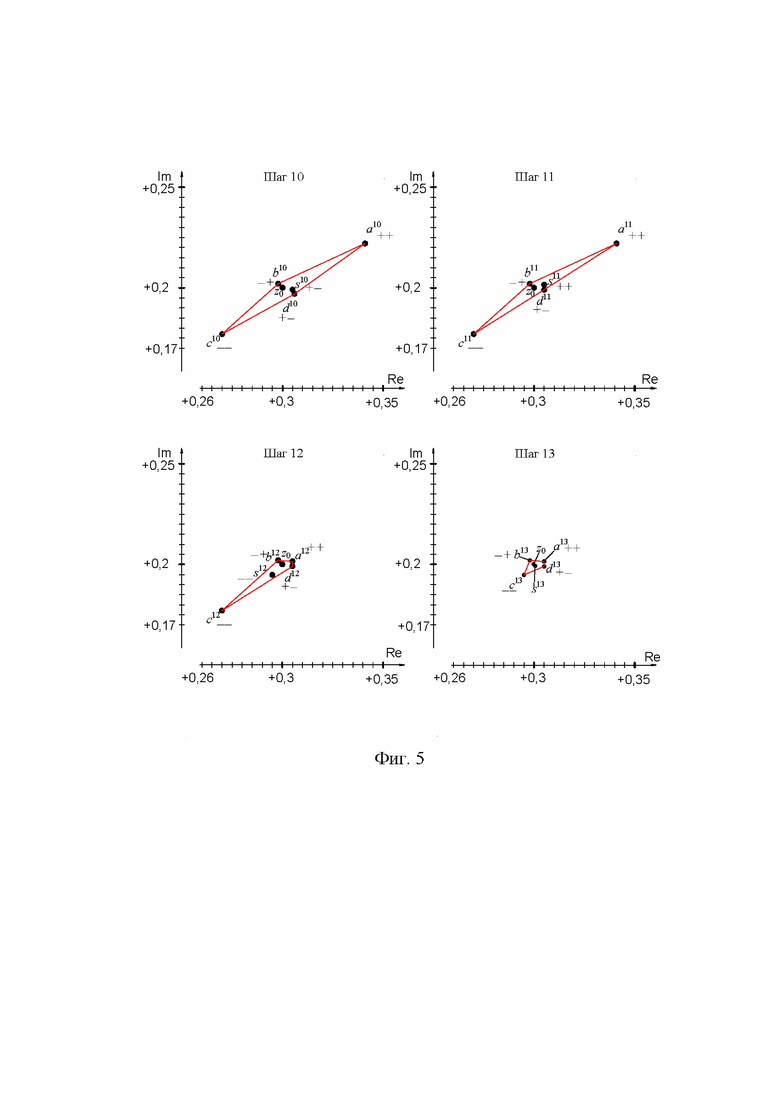
На фиг. 3, фиг. 4, фиг. 5 приведен численный пример работы предлагаемого метода. Для примера взято число z0=0,3+j0,2, угол φ1=0,1 рад. Визуально показано, что четырехугольник уменьшается, то есть точки ai, bi, ci, di стягиваются к точке решения. В этом примере, после выполнения шага 13 размеры четырехугольника не превышают 0,05 В. Это означает, что погрешность измеренного значения не превышает 0,05 В (амплитудное значение). Уменьшение погрешности при выполнении шагов итерационного процесса приблизительно соответствует уменьшению в 2 раза при выполнении двух шагов.
Теоретически у метода средних точек нет ограничений для уменьшения значения Δз, поэтому возможно достигнуть сколь угодно малую погрешность. Для получения меньшей погрешности просто увеличивается число шагов итерационного процесса. Погрешность может возникнуть из-за неидеальности сумматора и практически не зависит от неидеальности усилителя 2, компаратора 3.
По окончании итерационного процесса очередная точка si считается найденным значением. Вещественная составляющая Re(si) соответствует вещественной составляющей измеряемого напряжения, а мнимая составляющая Im(si) соответствует мнимой составляющей измеряемого напряжения.
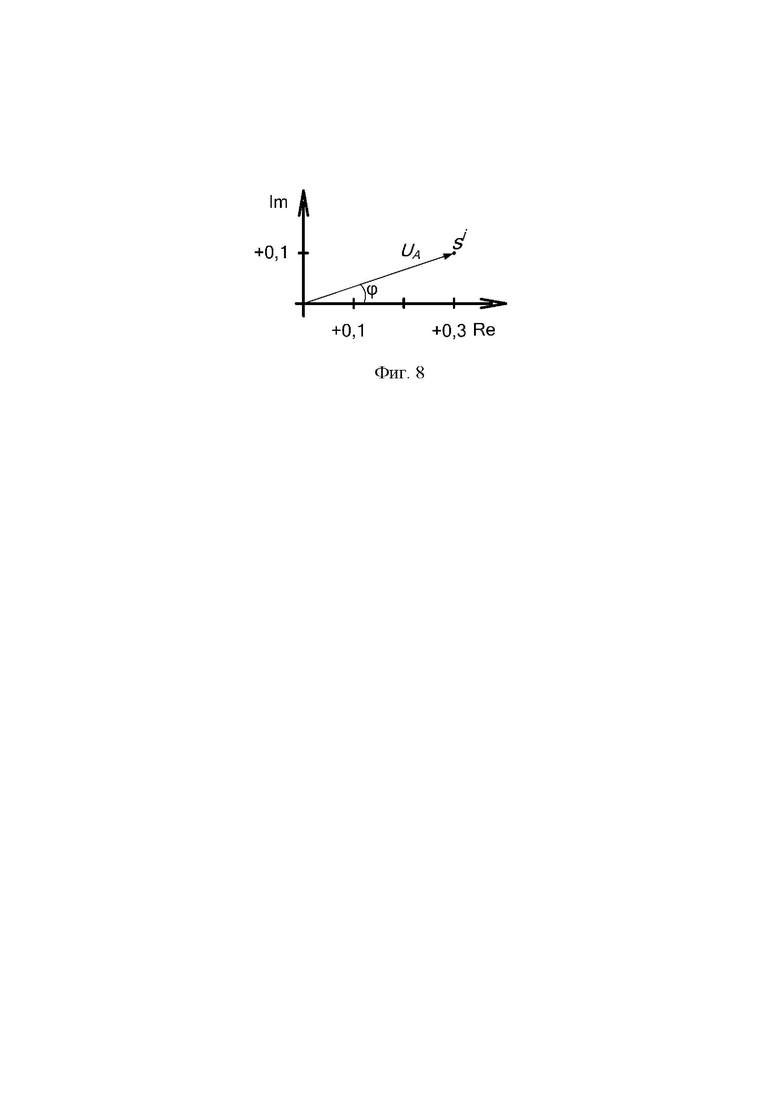
При необходимости можно определить амплитуду UA и фазу φ (фиг. 8) измеряемого переменного напряжения по формулам:
UA = 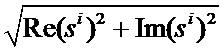 ;
;
φ=arctan(Im(si)/Re(si)).
Таким образом, за счет совокупности отличительных признаков появляется возможность предельно увеличить чувствительность нуль-органа не опасаясь того, что элементы выйдут за пределы линейного режима работы. Это позволяет сколь угодно уменьшать погрешность, то есть свести разностный сигнал практически к нулю. В результате повышается чувствительность, разрешающая способность и точность измерения, уменьшается погрешность измерения переменного напряжения. Причем результат сразу представлен в виде суммы вещественной и мнимой составляющих.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ измерения сопротивления изоляции с экстраполяцией тока абсорбции | 2022 |
|
RU2795369C1 |
| Устройство измерения сопротивления изоляции с ускоренным зарядом емкости сети | 2022 |
|
RU2792304C1 |
| СПОСОБ ГЕНЕРАЦИИ И ЧАСТОТНОЙ МОДУЛЯЦИИ ВЫСОКОЧАСТОТНЫХ СИГНАЛОВ И УСТРОЙСТВО ЕГО РЕАЛИЗАЦИИ | 2014 |
|
RU2568375C1 |
| УСТРОЙСТВО ДЕКОДИРОВАНИЯ КАСКАДНОГО КОДА РИДА-СОЛОМОНА | 1993 |
|
RU2036512C1 |
| СПОСОБ ГЕНЕРАЦИИ И ЧАСТОТНОЙ МОДУЛЯЦИИ ВЫСОКОЧАСТОТНЫХ СИГНАЛОВ И УСТРОЙСТВО ЕГО РЕАЛИЗАЦИИ | 2014 |
|
RU2568390C1 |
| СПОСОБ ГЕНЕРАЦИИ И ЧАСТОТНОЙ МОДУЛЯЦИИ ВЫСОКОЧАСТОТНЫХ СИГНАЛОВ И УСТРОЙСТВО ЕГО РЕАЛИЗАЦИИ | 2014 |
|
RU2568930C1 |
| СПОСОБ ГЕНЕРАЦИИ И ЧАСТОТНОЙ МОДУЛЯЦИИ ВЫСОКОЧАСТОТНЫХ СИГНАЛОВ И УСТРОЙСТВО ЕГО РЕАЛИЗАЦИИ | 2014 |
|
RU2595567C2 |
| КОМПЕНСАЦИЯ НА МЕСТЕ ПРИ АКУСТИЧЕСКИХ ИЗМЕРЕНИЯХ | 2017 |
|
RU2750093C2 |
| ЦИФРОВОЙ АВТОМАТИЧЕСКИЙ АНАЛИЗАТОР ЧАСТОТНЫХ | 1969 |
|
SU257579A1 |
| СПОСОБ ГЕНЕРАЦИИ И ЧАСТОТНОЙ МОДУЛЯЦИИ ВЫСОКОЧАСТОТНЫХ СИГНАЛОВ И УСТРОЙСТВО ЕГО РЕАЛИЗАЦИИ | 2014 |
|
RU2595571C2 |
Способ относится к электрическим измерениям и может быть использован для точного измерения вещественной и мнимой составляющих переменного напряжения. Способ измерения вещественной и мнимой составляющих переменного напряжения заключается в том, что измеряемое напряжение подают на инвертирующий вход сумматора, компенсирующее напряжение подают на неинвертирующий вход сумматора, разностный сигнал усиливают с предельно большим коэффициентом усиления, в результате чего получаются прямоугольные импульсы или последовательность логических сигналов, которые обрабатывают и выделяют основную гармонику. Выделяют знаки (+ или –) вещественной и мнимой составляющих основной гармоники. Анализируя эти знаки, реализуют шаги итерационной последовательности метода средних точек. Метод средних точек является двумерным аналогом метода половинного деления. Шаги выполняются до тех пор, пока не будет достигнута заданная точность. Метод позволяет найти компенсирующее переменное напряжение, максимально приближенное к измеряемому переменному напряжению. По окончании выполнения итерационной последовательности очередная точка s считается найденным значением. Вещественная составляющая Re(s) соответствует вещественной составляющей измеряемого тока, а мнимая составляющая Im(s) соответствует мнимой составляющей измеряемого тока. Техническим результатом при реализации заявленного решения является повышение точности, разрешающей способности и чувствительности, уменьшение погрешности измерения вещественной и мнимой составляющих переменного напряжения, повышение надежности устройства, реализующего способ. 8 ил.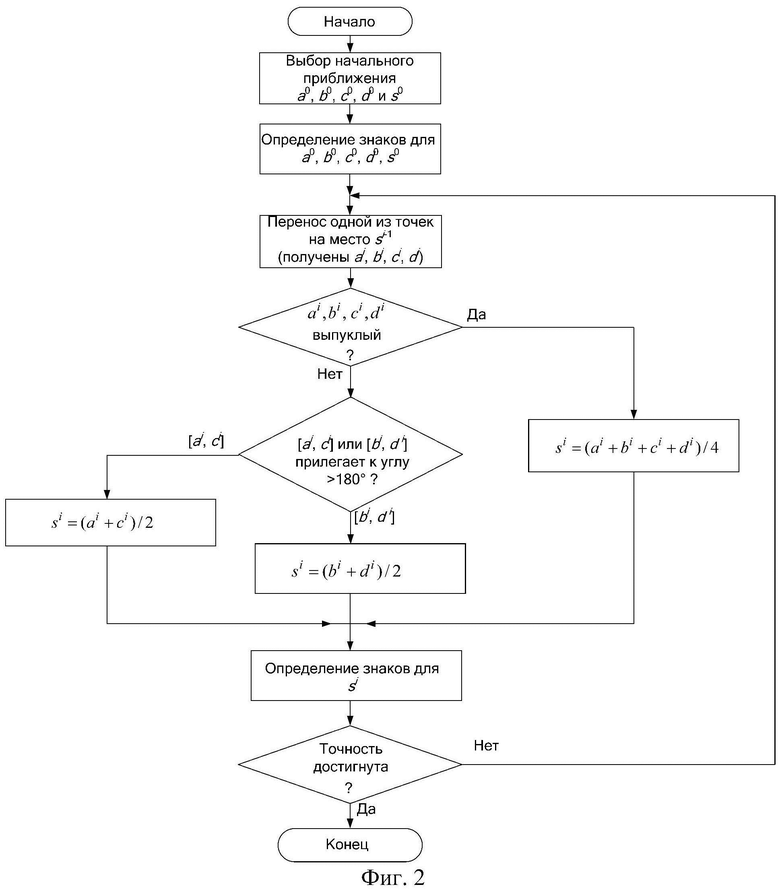
Способ измерения вещественной и мнимой составляющих переменного напряжения, для выполнения которого используют следующие вспомогательные устройства: аналоговый сумматор, который имеет инвертирующий вход, неинвертирующий вход и выход, причем на инвертирующий вход подается измеряемое переменное напряжение, на неинвертирующий вход подается компенсирующее переменное напряжение; блок формирования компенсирующего напряжения, который может формировать на своем выходе компенсирующее синусоидальное напряжение с заданными значениями вещественной и мнимой составляющих; усилитель, на вход которого подается переменное напряжение с выхода аналогового сумматора, который имеет предельно большой коэффициент усиления и ограниченную снизу и сверху полосу частот пропускания; компаратор, на вход которого подается выходной сигнал усилителя, компаратор сравнивает его с нулевым напряжением и формирует выходные прямоугольные импульсы, которые подаются на вход микроконтроллера; микроконтроллер, в котором программно реализован блок выделения основной гармоники; программно реализован блок выделения знаков вещественной и мнимой составляющих основной гармоники; выполняют шаги итерационной последовательности в соответствии с алгоритмом метода средних точек до тех пор, пока не будет достигнута заданная точность; алгоритм метода средних точек заключается в том, что на комплексной плоскости выбирают четыре точки a0, b0, c0, d0, названные «начальное приближение», причем у четырехугольника a0, b0, c0, d0 углы a0 и c0 должны быть противоположными, углы b0 и d0 должны быть противоположными, для каждой из точек выполняют шесть действий - а, б, в, г, д, е:
а – вещественную и мнимую составляющие комплексного числа, соответствующего точке, передают на блок формирования компенсирующего напряжения;
б – подают переменное напряжение, сформированное блоком формирования компенсирующего напряжения, на неинвертирующий вход аналогового сумматора, на инвертирующий вход которого подано измеряемое переменное напряжение;
в – переменное напряжение, поступающее с выхода аналогового сумматора, усиливают с помощью усилителя;
г – выходной сигнал усилителя подают на вход компаратора, который сравнивает этот сигнал с нулевым напряжением и в результате формирует на своем выходе прямоугольные импульсы;
д – подают прямоугольные импульсы с выхода компаратора на блок выделения основной гармоники, выделяют основную гармонику;
е – с помощью блока выделения знаков (БВЗ) вещественной и мнимой составляющих основной гармоники определяют знаки вещественной и мнимой составляющих основной гармоники;
точки a0, b0, c0, d0 должны быть такими, чтобы соответствующие этим точкам компенсирующие напряжения имели знаки основной гармоники, разные во всех сочетаниях, затем находят точку s0 по формуле
s0=(a0+b0+c0+d0)/4,
для точки s0 выполняют шесть действий - а, б, в, г, д, е, запоминают знаки вещественной и мнимой составляющих основной гармоники, соответствующие точкам a0, b0, c0, d0, s0, затем выполняют шаги итерационной последовательности, каждый шаг состоит из следующих четырех действий - ж, з, и, к:
ж – находят из четырех точек ai-1, bi-1, ci-1, di-1 , где i - номер шага, ту точку, для которой запомненные на предыдущем шаге знаки вещественной и мнимой составляющих основной гармоники равны знакам вещественной и мнимой составляющих основной гармоники, соответствующим точке si-1, затем найденную точку переносят на место точки si-1, остальные три точки оставляют на своих местах и, таким образом, находят четыре точки ai, bi, ci, di;
з – находят пятую точку si по одному из трех вариантов следующим образом, если четырехугольник ai, bi, ci, di выпуклый, то точку si находят по формуле si=(ai+bi+ ci+di)/4, если же четырехугольник ai, bi, ci, di не выпуклый, то есть один внутренний угол в одной из точек ai, bi, ci, di более 180°, то из двух отрезков [ai, ci] или [bi, di] выбирают один, который прилегает к углу более 180°, в соответствии с выбранным отрезком вычисляют si по одной из формул si=(ai+ci)/2 или (третий вариант) si=(bi+di)/2;
и – для точки si выполняют шесть действий - а, б, в, г, д, е, запоминают знаки вещественной и мнимой составляющих основной гармоники, соответствующей точке si;
к – проверяют условие окончания итерационного процесса, используя значение заданной погрешности Δз и следующие соотношения:
если │ai – ci│<Δз или │bi – di│<Δз, то итерационный процесс необходимо заканчивать;
шаги выполняют до тех пор, пока не будет выполнено условие окончания итерационного процесса, по окончании итерационного процесса в качестве результата измерения используют комплексное значение, соответствующее точке si, вещественная составляющая Re(si) соответствует вещественной составляющей измеряемого переменного напряжения, а мнимая составляющая Im(si) соответствует мнимой составляющей измеряемого переменного напряжения.
| Статья: "МЕТОД РЕШЕНИЯ УРАВНЕНИЙ ДЛЯ ВЫСОКОТОЧНЫХ СИСТЕМ ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН", Ж | |||
| Известия вузов | |||
| Электромеханика | |||
| Способ восстановления спиралей из вольфрамовой проволоки для электрических ламп накаливания, наполненных газом | 1924 |
|
SU2020A1 |
| Т | |||
| Способ приготовления сернистого красителя защитного цвета | 1915 |
|
SU63A1 |
| Очаг для массовой варки пищи, выпечки хлеба и кипячения воды | 1921 |
|
SU4A1 |
| СПОСОБ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ЭЛЕКТРИЧЕСКОЙ СЕТИ ОТНОСИТЕЛЬНО ЗЕМЛИ | 1995 |
|
RU2088947C1 |
| 0 |
|
SU250305A1 | |
| СПОСОБ ИЗМЕРЕНИЯ ДЕЙСТВУЮЩЕГО ЗНАЧЕНИЯ НАПРЯЖЕНИЯ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ ПЕРЕМЕННОГО ТОКА | 2006 |
|
RU2298194C1 |
| Статья: "Символический метод: двойственности в формуле определения комплексной мощности и знаке ее мнимой составляющей | |||
Авторы
Даты
2022-09-21—Публикация
2021-12-19—Подача