Изобретение относится к вычислительной технике и предназначено для генерации случайной последовательности значений из заданного множества значений с требуемыми характеристиками генерируемой последовательности.
Известен генератор случайной последовательности по Патенту РФ №2250489 «Генератор случайной последовательности» МПК G06F 7/58, H03K 3/84 опубликованный 20.04.2005 Бюл. №11, включающий источник случайных чисел, N-разрядный селектор-мультиплексор, оперативное запоминающее устройство, блок контроля интервалов, блок контроля количества генераций, J-входовый элемент ИЛИ, блок элементов И. Этот аналог обеспечивает формирование конечной последовательности заданных значений набора данных по заданному в интервальном виде закону распределения со случайной частостью появления значений в пределах интервалов.
Недостатком данного устройства является формирование ограниченной последовательности заданных значений набора данных, что обусловлено реализованным в устройстве подходе к заданию закона распределения, который предполагает указание абсолютных значений требуемого числа наблюдений элементов заданного набора данных на выходе устройства для каждого из интервалов.
Известен генератор случайной последовательности по Патенту РФ №2313125 «Генератор случайной последовательности» МПК G06F 7/58, H03K 3/84, G07C 15/00 опубликованный 20.12.2007, Бюл. №35. Это устройство содержит источник случайных чисел, оперативное запоминающее устройство, N-разрядный селектор-мультиплексор, K Р-разрядных регистров, K блоков сравнения, шифратор приоритетов, N инверторов. Устройство обеспечивает формирование неограниченной последовательности заданных значений набора данных, частность появления которых определяется только заданным законом распределения.
Однако данное устройство имеет недостаток - узкую область применения, ограниченную возможностью моделирования дискретных случайных процессов, характеризующихся отсутствием вероятностной связи между состояниями случайного процесса (между генерируемыми значениями заданного набора данных), отсутствием вероятностной зависимости каждого очередного состояния случайного процесса от предыдущего.
Из известных наиболее близким аналогом (прототипом), по своей технической сущности, заявленному устройству является генератор случайной последовательности по Патенту РФ №2542903 «Генератор случайной последовательности» МПК G06F 7/58, G06F 1/02, опубликованный 27.02.2015, Бюл. №6. Устройство-прототип содержит источник случайных чисел, оперативное запоминающее устройство, первый и второй селекторы-мультиплексоры, K блоков хранения границ интервалов, K блоков сравнения, шифратор приоритетов, N инверторов, первый и второй регистр. Устройство-прототип обеспечивает формирование значений элементов случайного процесса, учитывая вероятностные связи между состояниями этого процесса.
Однако прототип имеет недостаток - относительно низкую достоверность генерируемой последовательности заданных значений набора данных в условиях, характерных для случайных процессов, протекающих в реальных системах, в реальной вычислительной технике, когда состояния генерируемого случайного процесса зависят не только от количественно заданных значений границ интервалов этих состояний, но и от этих значений, задаваемых с учетом комплексной неопределенности, которая проявляется одновременно и совокупно в виде недостоверности и нечеткости информации.
Данное устройство позволяет получать текущие вероятностно-временные значения элементов заданного набора данных с учетом заданных количественно значений верхних границ интервалов, на которые разбивается множество адресов этого набора данных, определяемых на каждом последующем шаге работы устройства вероятностями переходов случайного процесса из состояния в состояние, в то время как при исследовании многих случайных процессов, протекающих в реальных системах, широкое применение находят нейро-нечеткие модели [1-6], объективно основанные на параллельной, комплексной обработке данных, задаваемых с учетом комплексной неопределенности значений границ интервалов для различных состояний случайного процесса, где эти значения носят не только количественный (достоверно идентифицируемый), но также одновременно недостоверный и нечеткий характер, традиционно описываемый с привлечением математики нейро-нечетких сетей (ННС), где нейросетевая компонента ННС отвечает за устранение аспекта комплексной неопределенности типа недостоверность данных, а функции устранения аспекта комплексной неопределенности типа нечеткость в рамках ННС реализуются в рамках компоненты, основанной на алгоритмах преобразования нечетких множеств.
Целью изобретения является разработка устройства, обеспечивающего повышение достоверности генерируемой последовательности за счет обеспечения возможности генерации заданного набора данных с учетом как количественно заданных значений верхних границ интервалов, на которые разбивается множество адресов этого набора данных, так и с учетом комплексной неопределенности значений этих границ интервалов для различных состояний генерируемого случайного процесса, создание генератора случайной последовательности, способного с высокой достоверностью формировать значения элементов случайного процесса, характеризующего реальное поведение сложной вычислительной системы, когда верхние границы интервалов для различных состояний этого случайного процесса имеют как количественно, так и качественно - одновременно недостоверно и нечетко выраженный физический смысл.
Указанная цель достигается тем, что в известный генератор случайной последовательности, содержащий K блоков сравнения, где K≥2 - максимально возможная мощность заданного множества генерируемых значений, первый селектор-мультиплексор, второй селектор-мультиплексор, оперативное запоминающее устройство, шифратор приоритетов, N инверторов, где N=[log2K] - число двоичных разрядов, достаточное для адресации элементов заданного множества генерируемых значений, K блоков хранения границ интервалов, выполненных в виде оперативных запоминающих устройств, первый регистр, второй регистр и источник случайных чисел, дополнительно включен блок нейро-нечеткой сети, предназначенный для проверки и выявления значений верхних границ интервалов (на которые разбивается множество адресов заданного набора данных, определяемых на каждом последующем шаге вероятностями переходов случайного процесса из состояния в состояние), задаваемых и идентифицируемых с учетом комплексной неопределенности этих значений, а также для обработки и трансформирования таких исходных данных, заданных одновременно в недостоверной и нечеткой форме к виду, позволяющему достоверно и однозначно идентифицировать и трактовать значения исходных данных о границах интервалов для различных состояний исследуемого процесса. При этом Р-разрядный, где Р>N, выход «Случайное число» источника случайных чисел соединен с Р-разрядными входами «Случайное число» K блоков сравнения, Р-разрядный выход k-го блока хранения границ интервалов, где k=1, 2, …, K, соединен с Р-разрядным входом «Верхняя граница» k-го блока сравнения, выход «Результат сравнения» k-го блока сравнения соединен с k-ым инверсным входом шифратора приоритетов, n-ый инверсный выход которого, где n=1, 2, …, N, соединен с входом n-го инвертора, вход выбора первого селектора-мультиплексора соединен с управляющим входом источника случайных чисел, с входом выбора второго селектора-мультиплексора и является управляющим входом генератора, первый N-разрядный информационный вход первого селектора-мультиплексора является первым N-разрядным адресным входом генератора, N-разрядный выход первого селектора-мультиплексора соединен с N-разрядным адресным входом оперативного запоминающего устройства, инверсные входы «Чтение/запись» и «Выбор кристалла» которого являются соответственно первым входом «Чтение/запись» и первым входом «Выбор кристалла» генератора, M-разрядный выход оперативного запоминающего устройства, где М≥2 - количество разрядов, достаточное для представления максимального значения из числа значений, входящих в состав заданного множества генерируемых значений, является M-разрядным выходом «Результат» генератора, М-разрядный информационный вход оперативного запоминающего устройства является М-разрядным информационным входом генератора. При этом P-разрядный информационный вход k-го блока хранения границ интервалов является k-ым Р-разрядным информационным входом генератора, n-ый разряд N-разрядного информационного входа второго регистра соединен с инверсным выходом n-го инвертора, а N-разрядный выход второго регистра подключен ко второму N-разрядному информационному входу первого селектора-мультиплексора и ко второму N-разрядному информационному входу второго селектора-мультиплексора, первый N-разрядный вход которого является вторым N-разрядным адресным входом генератора, а его N-разрядный выход соединен с N-разрядным прямым входом блока нейро-нечеткой сети, N-разрядный прямой выход которого соединен с N-разрядным информационным выходом этого блока и подключен к N-разрядному информационному входу первого регистра, N-разрядный нейро-нечеткий вход блока нейро-нечеткой сети является N-разрядным нейро-нечетким входом устройства, N-разрядный выход первого регистра соединен с N-разрядными адресными входами K блоков хранения границ интервалов, соответствующие инверсные входы «Выбор кристалла» и «Чтение/запись» которых объединены между собой и являются соответственно вторым входом «Выбор кристалла» и вторым входом «Чтение/запись» генератора, входы инициализации первого и второго регистров являются соответственно первым и вторым входом «Установка» генератора, а входы сброса первого и второго регистров объединены и являются входом «Обнуление» генератора.
Блок нейро-нечеткой сети, предназначенный для проверки и выявления значений верхних границ интервалов (на которые разбивается множество адресов заданного набора данных, определяемых на каждом последующем шаге вероятностями переходов случайного процесса из состояния в состояние), задаваемых и идентифицируемых с учетом комплексной неопределенности этих значений, а также для обработки и трансформирования таких исходных данных, заданных одновременно в недостоверной и нечеткой форме к виду, позволяющему достоверно и однозначно идентифицировать и трактовать значения исходных данных о границах интервалов для различных состояний исследуемого процесса, состоит из счетчика, регистра хранения, нейро-нечеткого программируемого вычислителя и запоминающего элемента, N-разрядный выход которого является N-разрядным информационным выходом блока нейро-нечеткой сети, N-разрядный вход нейро-нечеткого программируемого вычислителя соединен с N-разрядным информационным выходом регистра хранения и является N-разрядным нейро-нечетким входом блока нейро-нечеткой сети и N-разрядным нейро-нечетким входом устройства, вход разрешения выходов А нейро-нечеткого программируемого вычислителя соединен с разрешающим выходом регистра хранения, N выходов А нейро-нечеткого программируемого вычислителя соединены с соответствующими N входами запоминающего элемента, N-разрядный прямой выход регистра хранения является N-разрядным прямым выходом блока нейро-нечеткой сети, N-разрядный вход регистра хранения соединен с N-разрядным выходом счетчика, N-разрядный вход которого является N-разрядным прямым входом блока нейро-нечеткой сети.
Благодаря новой совокупности существенных признаков, за счет введения блока нейро-нечеткой сети, обеспечивающего предварительное выявление и селекцию значений верхних границ интервалов, идентифицируемых с учетом комплексной неопределенности этих значений и принятие решения об их математической природе, а также запись, хранение результатов анализа значений верхних границ интервалов, заданных одновременно в недостоверной и нечеткой форме, и математически корректное вычислительное преобразование и распознавание этих значений с использованием нейро-нечетких математических методов, в заявленном генераторе случайной последовательности достигается возможность повышения достоверности генерируемой последовательности заданных значений набора данных за счет обеспечения возможности их генерации с учетом наличия не только количественной меры идентификации состояний случайного процесса, но и качественной - комплексной неопределенности, т.е., одновременно недостоверно и нечетко заданных значений верхних границ интервалов состояний для конкретного шага моделирования этого дискретного случайного процесса.
Заявленное устройство поясняется чертежами, на которых:
на фиг. 1 - структурная схема генератора случайной последовательности;
на фиг. 2 - структурная схема блока нейро-нечеткой сети 11;
на фиг. 3 - схема построения нейро-нечеткой сети;
на фиг. 4 - структурная схема блока сравнения.
Генератор случайной последовательности (см. фиг. 1) состоит из первого селектора-мультиплексора 1, второго селектора-мультиплексора 2, первого регистра 3, источника случайных чисел 4, оперативного запоминающего устройства 5, K блоков хранения границ интервалов 61-6K, K блоков сравнения 71-7K, шифратора приоритетов 8, N инверторов 91-9N, второго регистра 10 и блока нейро-нечеткой сети 11.
Элементы соединены между собой следующим образом (см. фиг. 1). Р-разрядный выход «Случайное число» 42 источника случайных чисел 4 соединен с Р-разрядными входами «Случайное число» 711-71K K блоков сравнения 71-7K, Р-разрядный выход 65k k-го блока хранения границ интервалов 6k, где k=1, 2, …, K, соединен с Р-разрядным входом «Верхняя граница» 72k k-го блока сравнения 7k. Выход «Результат сравнения» 73k k-го блока сравнения 7k соединен с k-ым инверсным входом 81k шифратора приоритетов 8, n-ый инверсный выход 82n которого, где n=1, 2, …, N, соединен с входом 91n n-го инвертора 9n. Вход выбора 130 (вход SE) первого селектора-мультиплексора 1 соединен с управляющим входом 41 источника случайных чисел 4 с входом выбора 23 (входом SE) второго селектора-мультиплексора 2 и является управляющим входом 07 генератора, первый N-разрядный информационный вход 110 (вход для разрядов A1-AN) первого селектора-мультиплексора 1 является первым N-разрядным адресным входом 01 генератора, N-разрядный выход 140 (выход для разрядов Q1-QN) первого селектора-мультиплексора 1 соединен с N-разрядным адресным входом 52 (входом для разрядов A1-AN) оперативного запоминающего устройства 5, инверсные входы «Чтение/запись» 54 (вход  ) и «Выбор кристалла» 51 (вход
) и «Выбор кристалла» 51 (вход 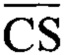 ) которого являются соответственно первым входом «Чтение/запись» 02 и первым входом «Выбор кристалла» 04 генератора. Причем М-разрядный выход 55 (выход для разрядов C1-CM) оперативного запоминающего устройства 5 является М-разрядным выходом «Результат» 013 генератора, М-разрядный информационный вход 53 (вход для разрядов D1-DM) оперативного запоминающего устройства 5 является М-разрядным информационным входом 03 генератора. При этом Р-разрядный информационный вход 63k (вход для разрядов D1-DP) k-го блока хранения границ интервалов 6k является k-ым Р-разрядным информационным входом 09k генератора, n-ый разряд N-разрядного информационного входа 101 второго регистра 10 соединен с инверсным выходом 92n n-го инвертора 9n, а N-разрядный выход 104 второго регистра 10 подключен ко второму N-разрядному информационному входу 120 (входу для разрядов B1-BN) первого селектора-мультиплексора 1 и ко второму N-разрядному информационному входу 22 (входу для разрядов B1-BN) второго селектора-мультиплексора 2, первый N-разрядный вход 21 которого является вторым N-разрядным адресным входом 05 генератора, а его N-разрядный выход 24 соединен с N-разрядным прямым входом 111 блока нейро-нечеткой сети 11, N-разрядный прямой выход 112 которого соединен с N-разрядным информационным выходом 113 блока нейро-нечеткой сети 11 и подключен к N-разрядному информационному входу 31 (входу для разрядов D1-DN) первого регистра 3, N-разрядный нейро-нечеткий вход 114 блока нейро-нечеткой сети 11 является N-разрядным нейро-нечетким входом 014 устройства, N-разрядный выход 34 первого регистра 3 соединен с N-разрядными адресными входами 621-62K K блоков хранения границ интервалов 61-6K, соответствующие инверсные входы «Выбор кристалла» 611-61K (входы
) которого являются соответственно первым входом «Чтение/запись» 02 и первым входом «Выбор кристалла» 04 генератора. Причем М-разрядный выход 55 (выход для разрядов C1-CM) оперативного запоминающего устройства 5 является М-разрядным выходом «Результат» 013 генератора, М-разрядный информационный вход 53 (вход для разрядов D1-DM) оперативного запоминающего устройства 5 является М-разрядным информационным входом 03 генератора. При этом Р-разрядный информационный вход 63k (вход для разрядов D1-DP) k-го блока хранения границ интервалов 6k является k-ым Р-разрядным информационным входом 09k генератора, n-ый разряд N-разрядного информационного входа 101 второго регистра 10 соединен с инверсным выходом 92n n-го инвертора 9n, а N-разрядный выход 104 второго регистра 10 подключен ко второму N-разрядному информационному входу 120 (входу для разрядов B1-BN) первого селектора-мультиплексора 1 и ко второму N-разрядному информационному входу 22 (входу для разрядов B1-BN) второго селектора-мультиплексора 2, первый N-разрядный вход 21 которого является вторым N-разрядным адресным входом 05 генератора, а его N-разрядный выход 24 соединен с N-разрядным прямым входом 111 блока нейро-нечеткой сети 11, N-разрядный прямой выход 112 которого соединен с N-разрядным информационным выходом 113 блока нейро-нечеткой сети 11 и подключен к N-разрядному информационному входу 31 (входу для разрядов D1-DN) первого регистра 3, N-разрядный нейро-нечеткий вход 114 блока нейро-нечеткой сети 11 является N-разрядным нейро-нечетким входом 014 устройства, N-разрядный выход 34 первого регистра 3 соединен с N-разрядными адресными входами 621-62K K блоков хранения границ интервалов 61-6K, соответствующие инверсные входы «Выбор кристалла» 611-61K (входы 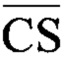 ) и «Чтение/запись» 641-64K (входы
) и «Чтение/запись» 641-64K (входы 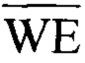 ) которых объединены между собой и являются соответственно вторым входом «Выбор кристалла» 08 и вторым входом «Чтение/запись» 010 генератора. Входы инициализации 33 и 103 (входы С) первого 3 и второго 10 регистров являются соответственно первым 06 и вторым 012 входом «Установка» генератора, а входы сброса 32 и 102 (входы R) первого 3 и второго 10 регистров объединены и являются входом «Обнуление» 011 генератора.
) которых объединены между собой и являются соответственно вторым входом «Выбор кристалла» 08 и вторым входом «Чтение/запись» 010 генератора. Входы инициализации 33 и 103 (входы С) первого 3 и второго 10 регистров являются соответственно первым 06 и вторым 012 входом «Установка» генератора, а входы сброса 32 и 102 (входы R) первого 3 и второго 10 регистров объединены и являются входом «Обнуление» 011 генератора.
Комплексная неопределенность представляет собой такой вид описания слабоструктурированных и трудно формализуемых данных, при котором недостаточность наших знаний о возможном состоянии среды и объекта исследований, а также тот факт, что мы полностью или частично не имеем информации о значениях границ интервалов для различных состояний генерируемого случайного процесса, одновременно и совокупно проявляются как недостоверность и нечеткость исходных данных о состояниях исследуемого процесса [7-10].
Физическая и математическая сущность значений границ интервалов - численные пределы границ состояний случайного процесса. Значения границ интервалов представляют собой набор двоичных кодов, определяющих пороговые, граничные значения вероятности появления соответствующих элементов заданного набора данных (набора данных в заданном интервале). Для задания интервалов указываются их верхние границы, значения верхних границ интервалов.
Число «N, (N=[log2K]; N≥1)» (блоков, разрядов, входов, выходов и т.п.) определяется в соответствии с количеством двоичных разрядов, достаточных для адресации элементов заданного множества генерируемых значений случайной последовательности (т.е, для адресации элементов набора данных), с количеством вычислителей (нейронов) в каждом слое ННС и, как правило, составляет от 2 (двух) до 10 (десяти).
Число «K, (K≥2)» характеризует максимально возможную мощность заданного множества генерируемых значений случайной последовательности (т.е., количество элементов в заданном наборе данных) и, как правило, составляет от 2 (двух) до 500 (пятисот).
Число «М, (М≥2)» характеризует количество двоичных разрядов, достаточное для представления максимального значения из числа значений, входящих в состав заданного множества генерируемых значений случайной последовательности (т.е, для представления значений элементов заданного набора данных) и, как правило, составляет от 2 (двух) до 10 (десяти).
Число «Р, (Р>N)» характеризует разрядность информационных входов генератора и определяется в соответствии с количеством, большим, чем количество двоичных разрядов, достаточных для адресации элементов заданного множества генерируемых значений случайной последовательности и, как правило, составляет от 3 (трех) до 11 (одиннадцати).
Блок нейро-нечеткой сети 11, изображенный на фиг. 2, предназначен для проверки и выявления значений верхних границ интервалов (на которые разбивается множество адресов заданного набора данных, определяемых на каждом последующем шаге вероятностями переходов случайного процесса из состояния в состояние), задаваемых и идентифицируемых с учетом комплексной неопределенности этих значений, а также для обработки и трансформирования таких исходных данных, заданных одновременно в недостоверной и нечеткой форме к виду, позволяющему достоверно и однозначно идентифицировать и трактовать значения исходных данных о границах интервалов для различных состояний исследуемого процесса.
Блок нейро-нечеткой сети 11 (фиг. 2) состоит из счетчика 11.1, регистра хранения 11.2, нейро-нечеткого программируемого вычислителя 11.3 и запоминающего элемента 11.4, N-разрядный выход 11.4-2 которого является N-разрядным информационным выходом 113 блока нейро-нечеткой сети 11, N-разрядный вход 11.3-1 (I1-IN) нейро-нечеткого программируемого вычислителя 11.3 соединен с N-разрядным информационным выходом 11.2-1 регистра хранения 11.2 и является N-разрядным нейро-нечетким входом 114 блока нейро-нечеткой сети 11 и N-разрядным нейро-нечетким входом 014 устройства, вход 11.3-2 (OEI) разрешения выходов А нейро-нечеткого программируемого вычислителя 11.3 соединен с разрешающим выходом 11.2-3 регистра хранения 11.2, N выходов A (A1-AN) нейро-нечеткого программируемого вычислителя 11.3 соединены с соответствующими N входами 11.4-11-11.4-1N запоминающего элемента 11.4, N-разрядный прямой выход 11.2-4 регистра хранения 11.2 является N-разрядным прямым выходом 112 блока нейро-нечеткой сети 11, N-разрядный вход 11.2-2 регистра хранения 11.2 соединен с N-разрядным выходом 11.1-2 счетчика 11.1, N-разрядный вход 11.1-1 которого является N-разрядным прямым входом 111 блока нейро-нечеткой сети 11.
Счетчик 11.1 блока нейро-нечеткой сети 11 предназначен для регистрации и последовательного сравнения, по количеству разрядов, поступающих в двоичном коде данных, характеризующих значения верхних границ интервалов, и преобразования этих данных из параллельного кода в последовательный. Техническая реализация счетчика 11.1 возможна на базе серийно выпускаемого программируемого суммирующего счетчика с функцией оперативного запоминающего устройства (ОЗУ) и управляемым сбросом, схема которого известна и описана, например, в [Угрюмов Е.П. Цифровая схемотехника: учеб. пособие для вузов. - 3-е изд., перераб. и доп. - СПб.: БХВ-Петербург, 2010. - 816 с., С. 246-247, рис. 3.46].
Регистр хранения 11.2 блока нейро-нечеткой сети 11 предназначен для принятия решения о математической природе исходных данных (пороговых, граничных значений вероятности появления генерируемого набора данных в заданном интервале), заданных в виде двоичного кода - значения верхних границ интервалов заданы количественно или с учетом комплексной неопределенности этих значений, т.е., заданы одновременно в недостоверной и нечеткой форме и нуждаются в дополнительной проверке и подтверждении. Регистр хранения 11.2 может быть технически реализован на базе серийно выпускаемого типового регистра хранения на триггерах, описанного в литературе [Основы электроники: учебник для СПО / О.В. Миловзоров, И.Г. Панков. - 5-е изд., перераб. и доп. - М.: Издательство Юрайт, 2016. - 407 с. С. 232-233, рис. 4.3.8].
Нейро-нечеткий программируемый вычислитель 11.3 блока нейро-нечеткой сети 11 предназначен для осуществления процедуры нейро-нечеткого преобразования исходных данных - значений верхних границ интервалов, заданных одновременно в недостоверной и нечеткой форме к виду, позволяющему достоверно идентифицировать и трактовать значения этих верхних границ интервалов для конкретного шага моделирования дискретных случайных процессов. Нейро-нечеткий программируемый вычислитель 11.3 блока нейро-нечеткой сети 11 с точки зрения теории ННС представляет собой программно-аппаратный аналог пятислойной нейро-нечеткой сети прямого распространения сигнала, такой, как ANFIS (Adaptive-Network-Based Fuzzy Inference System - адаптивная сеть нечеткого вывода) [1, 2]. Вариант такой ННС представлен на фиг. 3. С точки зрения теории ННС, нейро-нечеткий программируемый вычислитель 11.3 блока нейро-нечеткой сети 11 выполняет функции: фаззификации, т.е., преобразования численных входных значений в степени соответствия лингвистическим переменным (функции первого слоя ННС); записи и хранения нечетких правил, представляющих собой набор нечетких правил типа «Если-То» (функции второго слоя ННС); записи и хранения данных, определяющих функции принадлежности нечетких множеств, используемых в нечетких правилах (функции третьего слоя ННС); принятия решений, т.е., совершения операции вывода на основании имеющихся правил (функции четвертого слоя ННС) и функции дефаззификации, нацеленные на преобразование результатов вывода в численные значения исходных данных о границах интервалов для различных состояний исследуемого процесса (функции пятого, выходного слоя ННС). Нейро-нечеткий программируемый вычислитель 11.3 может быть технически реализован на базе серийно выпускаемой микропроцессорной секции (МПС или MPS - Micro-Processoring Section) типа MPS К1804ВС1, описанной, например, в [Угрюмов Е.П. Цифровая схемотехника: учеб. пособие для вузов. - 3-е изд., перераб. и доп. - СПб.: БХВ-Петербург, 2010. - 816 с., С. 371-376, рис. 6.14].
Запоминающий элемент 11.4 блока нейро-нечеткой сети 11 предназначен для записи и хранения проверенных и подтвержденных результатов анализа значений верхних границ интервалов, а также для преобразования этих данных из последовательного кода в параллельный. Запоминающий элемент 11.4 может быть технически реализован на базе серийно выпускаемого программируемого динамического оперативного запоминающего устройства с N входами и N-разрядным выходом, в соответствии с описанием, представленным в работе [Основы электроники: учебник для СПО / О.В. Миловзоров, И.Г. Панков. - 5-е изд., перераб. и доп. - М.: Издательство Юрайт, 2016. - 407 с. С. 229-231, рис. 4.3.2].
Первый селектор-мультиплексор 1, входящий в общую структурную схему генератора случайной последовательности, предназначен для коммутации на свой N-разрядный выход сигналов одной из двух групп: с первого N-разрядного информационного входа 110 (входа для разрядов A1-AN) либо со второго N-разрядного информационного входа 120 (входа для разрядов B1-BN). Схема построения первого селектора-мультиплексора 1 известна, он может быть технически реализован на базе серийно выпускаемого N-разрядного мультиплексора, как показано в [Угрюмов Е.П. Цифровая схемотехника: учеб. пособие для вузов. - 3-е изд., перер. и доп. - СПб.: БХВ-Петербург, 2010. - 816 с., С. 94-95].
Второй селектор-мультиплексор 2, входящий в общую структурную схему генератора случайной последовательности, предназначен для коммутации на свой N-разрядный выход сигналов одной из двух групп: с первого N-разрядного входа 21 (входа для разрядов A1-AN) либо со второго N-разрядного информационного входа 22 (входа для разрядов B1-BN). Он отвечает за запись значений верхних границ интервалов, величина которых может быть задана количественно либо одновременно недостоверно и нечетко, границ, на которые разбивается множество адресов заданного набора данных, определяемых на каждом последующем шаге заданными вероятностями переходов случайного процесса из состояния в состояние. Схема построения второго селектора-мультиплексора 2 известна и аналогична схеме первого селектора-мультиплексора 1. Он может быть технически реализован на базе серийно выпускаемого N-разрядного мультиплексора, как показано в [Угрюмов Е.П. Цифровая схемотехника: учеб. пособие для вузов. - 3-е изд., перераб. и доп. - СПб.: БХВ-Петербург, 2010. - 816 с., С. 94-95].
Первый регистр 3, входящий в общую структурную схему генератора случайной последовательности, предназначен для регистрации и хранения двоичных кодов, определяющих генерацию последовательности значений заданного набора данных, а также за регистрацию и хранение значений новых для каждого последующего шага, проверенных и подтвержденных (с помощью нейро-нечеткой сети) верхних границ интервалов, величина которых может быть задана количественно либо одновременно недостоверно и нечетко, и динамично изменяется по методам марковских цепей, зависит от вероятности перехода случайного процесса из состояния в состояние и соответствует значениям требуемых на данном шаге вероятностей наблюдения соответствующих элементов заданного набора данных. Описание работы и схема таких регистров известны и приведены, например, в книге [Аверченков О.Е. Схемотехника: аппаратура и программы. - М.: ДМК Пресс, 2012. - 588 с., С. 443-445].
Источник случайных чисел 4, входящий в общую структурную схему генератора случайной последовательности, предназначен для генерирования Р-разрядных случайных чисел, известен, и может быть технически реализован, как показано, например, в [Угрюмов Е.П. Цифровая схемотехника: учеб. пособие для вузов. - 3-е изд., перераб. и доп. - СПб.: БХВ-Петербург, 2010. - 816 с., С. 260-261].
Оперативное запоминающее устройство 5, входящее в общую структурную схему генератора случайной последовательности, предназначено для хранения значений элементов заданного набора данных. Схема построения оперативного запоминающего устройства известна, он может быть технически реализован на базе серийно выпускаемого оперативного запоминающего устройства, как показано в [Аверченков О.Е. Схемотехника: аппаратура и программы. - М: ДМК Пресс, 2012. - 588 с., С. 246-247].
Блоки хранения границ интервалов 61-6K, входящие в общую структурную схему генератора случайной последовательности, предназначены для хранения двоичных кодов, определяющих новые, проверенные и подтвержденные (с помощью нейро-нечеткой сети) верхние границы интервалов, т.е., граничные значения вероятности появления соответствующих элементов заданного набора данных (набора данных в заданном интервале). Они выполненных в виде оперативных запоминающих устройств, структура их построения известна, они могут быть технически реализованы на базе серийно выпускаемых оперативных запоминающих устройств, как показано в [Аверченков О.Е. Схемотехника: аппаратура и программы. - М.: ДМК Пресс, 2012. - 588 с., С. 246-247].
Блоки сравнения 71-7K, входящие в общую структурную схему генератора случайной последовательности, предназначены для сравнения случайного значения, генерируемого источником случайных чисел, и значения на выходе соответствующего регистра, а также для формирования результата сравнения. Принцип работы и структура любого k-го 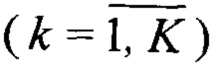 блока сравнения 7к известны, описаны в прототипе (см. патент РФ №2542903 «Генератор случайной последовательности» МПК G06F 7/58, G06F 1/02, опубликованный 27.02.2015, Бюл. №6, фиг. 4), структурная схема проиллюстрирована, на примере k-го блока сравнения 7k, на фиг. 4.
блока сравнения 7к известны, описаны в прототипе (см. патент РФ №2542903 «Генератор случайной последовательности» МПК G06F 7/58, G06F 1/02, опубликованный 27.02.2015, Бюл. №6, фиг. 4), структурная схема проиллюстрирована, на примере k-го блока сравнения 7k, на фиг. 4.
Шифратор приоритетов 8, входящий в общую схему генератора случайной последовательности, предназначен для преобразования значения логического нуля на одном из его входов в соответствующий двоичный код на его выходе, причем преобразование осуществляется с учетом приоритетов, определяемых номером входа. Схема реализации шифратора приоритетов известна и подробно описана, например, в [Аверченков О.Е. Схемотехника: аппаратура и программы. - М.: ДМК Пресс, 2012. - 588 с., С. 414-418].
Инверторы 91-9N, входящие в общую схему генератора случайной последовательности, предназначены для инвертирования сигналов с инверсных выходов шифратора приоритетов. Схема реализации инвертора известна и подробно описана, например, в [Аверченков О.Е. Схемотехника: аппаратура и программы. - М.: ДМК Пресс, 2012. - 588 с., С. 426].
Второй регистр 10, входящий в общую схему генератора случайной последовательности, предназначен для хранения двоичных кодов, определяющих вероятности появления соответствующих элементов заданного набора данных. Он отвечает за регистрацию и хранение значений предыдущих (для прошлого шага) проверенных и подтвержденных с помощью ННС верхних границ интервалов (полученных с учетом наличия не только количественно, но и одновременно недостоверно и нечетко заданных значений этих границ), величина которых динамично изменяется по методам марковских цепей, зависит от вероятности перехода случайного процесса из состояния в состояние и соответствует значениям требуемых на прошедшем шаге вероятностей наблюдения соответствующих элементов заданного набора данных. Он аналогичен первому регистру 3, описание работы и схема таких регистров известны и приведены, например, в книге [Аверченков О.Е. Схемотехника: аппаратура и программы. - М.: ДМК Пресс, 2012. - 588 с., С. 443-445].
В заявленном устройстве генерирование заданных значений набора данных с учетом как количественных значений границ между генерируемыми величинами этого набора данных (границ интервалов), так и с учетом комплексной неопределенности этих значений, осуществляется поэтапно. Первым этапом является генерирование заданных значений набора данных с учетом количественно заданных верхних границ интервалов, реализуемое на основе закона распределения, который задается путем указания требуемой вероятности появления соответствующего элемента заданного набора данных. При этом применяется подход [11], основанный на использовании источника случайных чисел, распределенных равномерно в диапазоне [0; 1). Данный диапазон разбивается на совокупность интервалов, количество которых соответствует количеству элементов в заданном наборе данных. Величины интервалов соответствуют значениям требуемых вероятностей наблюдения соответствующих элементов заданного набора данных. Вероятность попадания случайного числа, сформированного источником случайных чисел, внутрь каждого интервала равна его длине. Номер интервала используется в качестве адреса для извлечения элемента заданного набора данных из оперативного запоминающего устройства, а для задания интервалов указываются их верхние границы.
Исходное задание начальных вероятностей появления элементов заданного набора данных, на первом шаге - без учета комплексной неопределенности значений верхних границ интервалов, осуществляется следующим образом.
Пусть Н={h1, h2, …, hk, …, hK} - множество требуемых вероятностей появления элементов заданного набора данных, где  K - количество элементов заданного набора данных, а В={b1, b2, …, bk, …, bK} - множество количественно заданных соответствующих значений начальных верхних границ интервалов. Тогда начальное, количественно, полно, достоверно и однозначно заданное значение верхней границы k-го интервала будет равно сумме значений вероятностей появления элементов из заданного набора данных от 1-го до k-го:
K - количество элементов заданного набора данных, а В={b1, b2, …, bk, …, bK} - множество количественно заданных соответствующих значений начальных верхних границ интервалов. Тогда начальное, количественно, полно, достоверно и однозначно заданное значение верхней границы k-го интервала будет равно сумме значений вероятностей появления элементов из заданного набора данных от 1-го до k-го:

Таким образом, диапазон [0; 1) на первом шаге генерации будет разбит на следующие интервалы:

Используется Р-разрядный источник случайных чисел с равномерным законом распределения. При этом Р-разрядный двоичный код, формируемый на выходе источника случайных чисел, и Р-разрядный двоичный код, используемый для задания начальной (для первого шага) верхней границы интервала, рассматриваются количественно, как числа из диапазона [0; 1) без указания целой части.
Вместе с тем, либо в рамках генерации случайных чисел с равномерным законом распределения, либо извне, от оператора устройства могут быть заданы значения верхних границ интервалов, обладающие комплексной неопределенностью, т.е., заданные качественно, и имеющие одновременно недостоверно и нечетко выраженный физический смысл.
Если задано множество требуемых вероятностей появления элементов заданного набора данных Н={0,125; 0,125; 0,25; 0,5}, то количественно заданные значения верхних границ интервалов будут равны соответственно 0,125, 0,25, 0,5 и 1. В соответствии с правилами перевода [12] правильных десятичных дробей в двоичное представление данные значения в четырехразрядном коде представляются соответственно в виде чисел 0,0010, 0,0100, 0,1000, 0,1111. А в устройство заносятся только дробная часть этих чисел: соответственно значения 0010, 0100,1000 и 1111.
Аналогичным образом, если источник случайных чисел сформировал значение 1101 (в десятичном представлении 0,8125), то, представляя это значение как дробную часть числа из диапазона [0; 1), т.е. как 0,1101, и учитывая множество количественно заданных (для первого этапа) начальных верхних границ интервалов из предыдущего абзаца, видно, что случайное значение попало в интервал, ограниченный числами 0,1000 и 0,1111.
Для того, чтобы генератор случайной последовательности был способен моделировать дискретные случайные процессы, протекающие в реальных системах, с учетом значений границ интервалов для различных состояний случайного процесса, задаваемых как количественно, так и качественно - с учетом комплексной неопределенности значений этих границ между генерируемыми величинами заданного набора данных, в соответствии с теорией марковских процессов [13], сначала задают начальные значения вероятности переходов случайного процесса из состояния в состояние.
При этом, на каждом последующем шаге функционирования генератора, вероятности появления элементов заданного набора данных будут иметь новые, определяемые в соответствии с марковской моделью, значения верхних границ интервалов, и генерируемые случайные значения на каждом новом шаге будет попадать в новый (лишь для этого шага) интервал. Данное пошаговое уточнение, идентификация значений множества верхних границ интервалов позволяет получать значения элемента из заданного набора данных с учетом наличия количественных значений этих верхних границ интервалов для конкретного шага моделирования дискретных случайных процессов.
Помимо количественных пороговых величин, учет комплексной неопределенности значений верхних границ интервалов для конкретного шага, реализуемый в предложенном генераторе случайной последовательности, осуществляется в рамках процедур, основанных на известных результатах исследований в области теории нейро-нечетких сетей, изложенных в работах [1-6]. Анализ работ [1-6] позволяет сформировать математически корректный нейро-нечеткий алгоритм приведения заданных одновременно в недостоверной и нечеткой форме исходных данных - значений верхних границ интервалов для различных состояний марковской цепи, к ближайшему полному и однозначному заданному множеству.
Таким образом, в рамках моделирования дискретных случайных процессов, формируемых с учетом как количественно, так и качественно - одновременно недостоверно и нечетко идентифицированных значений верхних границ интервалов для различных состояний марковской цепи, ряд характеристик генерируемого процесса моделируется на основе параметрически заданных исходных данных, традиционными методами, а моделирование с учетом комплексной неопределенности значений этих границ интервалов (т.е., с учетом одновременно недостоверно и нечетко заданных пороговых значений состояний для конкретного шага моделирования дискретных случайных процессов) - путем последовательных преобразований с использованием методов теории ННС, сводится к возможности их относительно параметрического моделирования, т.е. осуществляется переход от одновременно недостоверно и нечетко поставленной задачи идентификации верхних границ интервалов, к параметрической.
Известно [1-6], что с точки зрения дополнительной проверки и подтверждения с помощью процедур нейро-нечеткой верификации значений верхних границ интервалов для конкретного шага с учетом комплексной неопределенности этих исходных данных для различных состояний марковской цепи, существует возможность определения этих значений, заданных как количественно, так и качественно - одновременно недостоверно и нечетко. Эта возможность реализуется с использованием нейро-нечетких вычислительных методов и алгоритмов, позволяющих путем последовательных математических нейро-нечетких преобразований, осуществить переход от недостоверно и нечетко определенных верхних пороговых значений состояний к виду, пригодному для однозначного принятия достоверного решения о значениях этих верхних границ интервалов для конкретного шага моделирования дискретных случайных процессов.
При этом значения верхних границ интервалов для различных состояний марковской цепи и для конкретного шага моделирования дискретных случайных процессов могут быть дополнительно проверенны и подтверждены на основе математических методов принятия решений в слабоструктурированных задачах - нейро-нечетких вычислительных методов и алгоритмов, которые достаточно просто могут быть аппаратно реализуемы в форме ННС. Нейро-нечеткие сети, основанные на них вычислительные методы и алгоритмы объединят в себе нейронные сети и нечеткую логику, собирают наилучшие свойства обоих методов, и в то же время освобождаются от их проблем. С одной стороны, такие структуры включают вычислительную мощность и способность к обучению нейронных сетей, а с другой стороны интеллектуальные возможности нейронных сетей усиливаются свойственными классическим способам «мышления» нечеткими правилами выработки решений [1, 2, 4].
Вычислительный нейро-нечеткий алгоритм такого класса состоит из пяти слоев по N вычислителей (нейронов) в каждом. При этом количество N вычислителей (нейронов) входного, промежуточных и выходного слоев соответствует коду адресации элементов набора данных, равно N=[log2K] и зависит от количества двоичных разрядов, достаточных для описания значений верхних границ интервалов для различных состояний марковской цепи, от количества экспертов и соответствующего количества входов устройств аппаратной реализации нейро-нечеткой сети. Причем N вычислителей (нейронов) в каждом слое ННС (в каждой ветви нейро-нечеткого алгоритма) отвечают за преобразование одновременно недостоверно и нечетко распознанных и определенных значений верхних пороговых значений состояний к виду, позволяющему однозначно и достоверно идентифицировать и трактовать значения этих верхних границ интервалов для конкретного шага моделирования дискретных случайных процессов.
В нашем случае N может принимать значения от 2 (двух) до 10 (десяти), соответствующие количеству входов микропроцессорной секции MPS К1804ВС1, на базе которой построен программируемый вычислитель 11.2 блока нейро-нечеткой сети 11.
Нейро-нечеткие сети позволяют осуществить дополнительную проверку и подтверждение истинности характеристик моделируемого генерируемого процесса, причем вывод этих характеристик - значений верхних границ интервалов, осуществляется на основе аппарата нечеткой логики, а параметры функций принадлежности настраиваются при помощи алгоритмов обучения нейронной сети. При этом модуль нечеткого управления представляется в форме многослойной сети, в которой слои выполняют функции элементов алгоритма нечеткого вывода [1, 2, 4].
Классический алгоритм нечеткого вывода в ННС состоит из пяти функциональных этапов: этап фаззификации, на котором преобразующий численные входные значения в степени соответствия лингвистическим переменным; этап получения, записи и хранения нечетких правил, содержащий набор нечетких правил типа «Если-То»; этап получения, записи и хранения данных, на котором определяются функции принадлежности нечетких множеств, используемых в нечетких правилах; этап принятия решений, в рамках которого осуществляются операции вывода на основании имеющихся правил, а также этап дефаз-зификации, на котором преобразуются результаты вывода в численные значения верхних границ интервалов [1, 2].
На вход нейро-нечеткой сети поступает входной образ - данные, характеризующие численные входные значения верхних границ интервалов и распознанные, определенные как количественно, так и качественно - одновременно недостоверно и нечетко. Определяется, какие из данных, характеризующих значения верхних границ интервалов, в данный момент времени распознаны количественно, а какие данные идентифицированы одновременно недостоверно и нечетко. В целях дополнительной проверки и подтверждения, с помощью процедур нейро-нечеткой верификации, значений верхних границ интервалов, необходимо математически корректно, используя ННС, преобразовать распознанные одновременно недостоверно и нечетко данные.
При этом первый (входной) слой ННС реализует первый этап, процедуру фаззификации - преобразования численных входных значений в степени соответствия лингвистическим переменным, характеризуемым функциями принадлежности для каждой входной переменной - значений верхних границ интервалов для каждого конкретного шага. На первый вход первого слоя поступают входные сигналы, характеризующие конкретное значение одновременно недостоверно и нечетко заданного значения верхней границы интервалов x1, на второй - мнения экспертов х2 о данном значении. На выходе слоя получаем значение функции принадлежности  для этих сигналов. Параметры функций принадлежности для конкретных значений верхних границ интервалов для каждого конкретного шага становятся весами связей для нейронов первого слоя ННС, и они могут модифицироваться в процессе обучения. В качестве функций принадлежностей входных и выходных переменных - значений верхних границ интервалов, используется функция Гаусса в виде
для этих сигналов. Параметры функций принадлежности для конкретных значений верхних границ интервалов для каждого конкретного шага становятся весами связей для нейронов первого слоя ННС, и они могут модифицироваться в процессе обучения. В качестве функций принадлежностей входных и выходных переменных - значений верхних границ интервалов, используется функция Гаусса в виде

где qi, wj - параметры функции принадлежности для конкретных значений верхних границ интервалов, требующие настройки в процессе обучения ННС, xn - значения верхних границ интервалов, поступающие на вход ННС.
Конфигурация связей второго слоя соответствует структуре правил:
Правило R1: если x1 есть 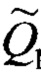 и х2 есть W1,
и х2 есть W1,
Правило R2: если x1 есть 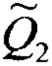 и х2 есть W2,
и х2 есть W2,
Правило Rn: если х1 есть  и х2 есть Wn,
и х2 есть Wn,
где  - нечеткие множества, элементы которых описывают одновременно не-
- нечеткие множества, элементы которых описывают одновременно не-
достоверно и нечетко заданные значения верхних границ интервалов.
Тогда правило (R1, R2, …, Rn) можно представить в виде нечеткой импликации (соединением двух высказываний в одно).

Второй слой реализует этап логического вывода. Число нейронов N во втором слое ННС равно количеству правил. Каждый узел слоя связан с предыдущим слоем таким образом, что узел второго слоя ННС, соответствующий k-му правилу, соединен со всеми нейронами первого слоя ННС, соответствующими нечетким множествам условий этого правила. Выходным значением второго слоя будет являться вес правила:


где 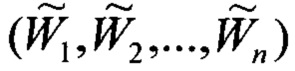 - нечеткие множества, элементы которых описывают функции принадлежности для конкретных одновременно недостоверно и нечетко заданных значений верхних границ интервалов.
- нечеткие множества, элементы которых описывают функции принадлежности для конкретных одновременно недостоверно и нечетко заданных значений верхних границ интервалов.
Элементы третьего слоя осуществляют нормализацию степеней выполнения правил и вычисляют нормализованные значения конкретных верхних границ интервалов


Четкие значения конкретных верхних границ интервалов, задающие заключение каждого правила, в четвертом слое рассматриваются как нечеткое множество с гауссов-ской функцией принадлежности. Адаптивные узлы четвертого слоя рассчитывают вклад каждого нечеткого правила в выход ННС по формуле

Пятый слой представляет собой реализацию функций дефазификации. На выходе пятого слоя формируется итоговые четкие значения верхних границ интервалов.
Этапы функционирования вычислительного нейро-нечеткого алгоритма, реализуемого ННС, подробно, алгоритмически и аналитически описаны в [1, 2]. На выходе вычислительного нейро-нечеткого алгоритма имеем выходной образ - данные, которые достоверно и однозначно характеризуют принадлежность значений верхних границах интервалов к пространству непротиворечивых, проверенных и подтвержденных значений.
Рассмотренный в [4-6] и детально описанный в [1, 2] вычислительный нейро-нечеткий алгоритм позволяет устранить комплексную неопределенность данных, характеризующих значения верхних границ интервалов для конкретного шага, позволяет однозначно распознать, проверить и подтвердить истинные значения этих верхних границ интервалов, а в конечном итоге, повысить достоверность формирования значения элементов случайного процесса, характеризующего реальное поведение сложной вычислительной системы - когда верхние границы интервалов для различных состояний этого случайного процесса имеют как количественно, так и качественно - одновременно недостоверно и нечетко выраженный физический смысл.
Иными словами, анализ рассмотренного в [4-6] и детально описанного в [1, 2] вычислительного нейро-нечеткого алгоритма позволяет сделать вывод о технической возможности реализации достоверной идентификации существенных параметров генерируемого потока данных с учетом как количественно заданных значений верхних границ интервалов, на которые разбивается множество адресов этого потока данных, так и с учетом комплексной неопределенности значений этих границ интервалов для различных состояний генерируемого случайного процесса. Это позволяет снизить неопределенность, а, следовательно, повысить достоверность генерируемой последовательности заданных значений набора данных.
С учетом этого в заявленном устройстве осуществляется генерирование заданных значений набора данных с учетом наличия не только количественной меры идентификации состояний случайного процесса, но и качественной - комплексной неопределенности, т.е., одновременно недостоверно и нечетко заданных значений верхних границ интервалов состояний для конкретного шага моделирования этого дискретного случайного процесса.
Техническая реализация принципа повышения достоверности распознавания значений верхних границ интервалов в заявленном устройстве осуществлена путем введения предварительного анализа и выявления этих значений верхних границ интервалов, задаваемых и идентифицируемых с учетом комплексной неопределенности данных значений, а также дополнительной проверки и подтверждения этих значений, заданных одновременно в недостоверной и нечеткой форме, с использованием нейро-нечетких методов к виду, позволяющему достоверно и однозначно идентифицировать и трактовать значения этих исходных данных о границах интервалов для различных состояний исследуемого процесса (в заявленном устройстве реализованы в рамках блока нейро-нечеткой сети 11).
Генератор случайной последовательности работает следующим образом.
В исходном положении на управляющем входе 07, перовом 06 и втором 012 входах «Установка» установлены значения логического нуля, а на первом 02 и втором 010 входах «Чтение/запись» и на первом 04 и втором 08 входах «Выбор кристалла» - значения логической единицы. Генератор работает в следующих режимах: режим подготовки к генерации; режим генерации.
Режим работы генератора с учетом не только количественно заданных значений верхних границ интервалов состояний, но и этих значений, задаваемых с учетом их комплексной неопределенности, определяется комбинацией сигналов на управляющем входе 07, первом 06 и втором 012 входах «Установка», первом 02 и втором 010 входах «Чтение/запись», а также на первом 04 и втором 08 входах «Выбор кристалла». Для перевода устройства в режим подготовки необходимо на управляющий вход 07 генератора, первый 04 и второй 08 входы «Выбор кристалла», первый 02 и второй 010 входы «Чтение/запись» подать значения логического нуля, а на первый 06 и второй 012 входы «Установка» - значение логической единицы.
В режиме генерации на управляющем входе генератора 07, первом 02 и втором 010 входах «Чтение/запись» устанавливаются значения логической единицы, а на первом 04 и втором 08 входах «Выбор кристалла» и первом 06 и втором 012 входах «Установка» - значения логического нуля.
В режиме подготовки генератора к работе выполняются следующие шаги.
Первый шаг - занесение множества А={а1, а2, …, aK} значений элементов заданного набора данных в оперативное запоминающее устройство, при этом:
0≤ak≤2M-1 - элемент заданного набора данных, где  ;
;
М≥2 - количество двоичных разрядов, достаточное для представления значений элементов заданного набора данных;
K≥2 - количество элементов в заданном наборе данных;
N≥1 - количество двоичных разрядов, достаточное для адресации элементов набора данных.
Второй шаг - установка множества В={b1, b2, …, bK} количественных значений начальных верхних границ интервалов, на которые разбивается все множество адресов заданного набора данных А.
Третий шаг - начальная установка множества количественно С={c1, c2, …, cK} или, через N-разрядный нейро-нечеткий вход 114 блока нейро-нечеткой сети 11, являющийся N-разрядным нейро-нечетким входом 014 устройства - одновременно в недостоверно и нечетко заданных значений новых (для данного шага) верхних границ интервалов, на которые разбивается множество адресов набора данных А, определяемых на каждом последующем шаге вероятностями переходов случайного процесса из состояния в состояние [13].
Первый шаг подготовки генератора к работе включает следующие действия. По первому N-разрядному адресному входу 01 генератора на первую группу информационных входов 110 (группу входов A1-AN) первого селектора мультиплексора 1 подается N-разрядный адрес, по которому должно быть записано значение первого элемента а1. На управляющем входе 07 генератора устанавливают значение логического нуля, который поступает на вход 130 (вход SE) первого селектора-мультиплексора 1, что приводит к коммутации адреса, установленного на входе 110 (входах A1-AN) первого селектора-мультиплексора 1, на N-разрядный адресный вход 52 (вход для разрядов A1-AN) оперативного запоминающего устройства 5. По М-разрядному информационному входу 03 генератора на информационные входы 53 (входы D1-DM) оперативного запоминающего устройства 5 подается значение первого элемента а1 заданного набора данных, которое записывается в оперативное запоминающее устройство 5 при поступлении на его входы 51  и 54
и 54 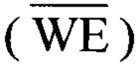 значений логического нуля по первым входам «Выбор кристалла» 04 и «Чтение/запись» 02 соответственно. Затем, по первому N-разрядному адресному входу 01 генератора на первую группу информационных входов 110 (группу входов A1-AN) первого селектора мультиплексора 1 подается N-разрядный адрес, по которому должно быть записано значение второго элемента а2, а по М-разрядному информационному входу 03 генератора на информационные входы 53 (входы D1-DM) оперативного запоминающего устройства 5 подают значение элемента а2 и, путем установки значений логического нуля на первых входах «Выбор кристалла» 04 и «Чтение/запись» 02, записывают значение а1 в оперативное запоминающее устройство 5. Аналогичным образом в оперативное запоминающее устройство 5 заносятся все K значений элементов заданного набора данных. После чего на первом входе «Чтение/запись» 02 генератора устанавливают значение логической единицы.
значений логического нуля по первым входам «Выбор кристалла» 04 и «Чтение/запись» 02 соответственно. Затем, по первому N-разрядному адресному входу 01 генератора на первую группу информационных входов 110 (группу входов A1-AN) первого селектора мультиплексора 1 подается N-разрядный адрес, по которому должно быть записано значение второго элемента а2, а по М-разрядному информационному входу 03 генератора на информационные входы 53 (входы D1-DM) оперативного запоминающего устройства 5 подают значение элемента а2 и, путем установки значений логического нуля на первых входах «Выбор кристалла» 04 и «Чтение/запись» 02, записывают значение а1 в оперативное запоминающее устройство 5. Аналогичным образом в оперативное запоминающее устройство 5 заносятся все K значений элементов заданного набора данных. После чего на первом входе «Чтение/запись» 02 генератора устанавливают значение логической единицы.
Второй шаг подготовки генератора к работе выполняется следующим образом. На K Р-разрядных информационных входах «Верхняя граница» 091-09K генератора устанавливают начальные количественные значения верхних границ интервалов. При этом, на вход 091 устанавливают значение b1, которое поступает на группу информационных входов 631 (группу D1-DP) блока хранения границ интервалов 61, на вход 092 - значение b2, которое поступает на группу информационных входов 632 блока хранения границ интервалов 62, на вход 09K - значение bK, которое поступает на группу информационных входов 63K блока хранения границ интервалов 6K. Для записи начальных количественных значений верхних границ интервалов в блоки хранения границ интервалов 61-6K на вторых входах «Выбор кристалла» 08 и «Чтение/запись» 010 устройства устанавливают значение логической единицы, которая поступает на входы 61k  и 64k
и 64k 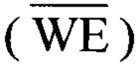 каждого k-ого блока хранения границ интервалов 6k. По окончании записи начальных количественных значений верхних границ интервалов в соответствующие блоки хранения границ интервалов, на вторых входах «Выбор кристалла» 08 и «Чтение/запись» 010 устройства устанавливают значение логического нуля.
каждого k-ого блока хранения границ интервалов 6k. По окончании записи начальных количественных значений верхних границ интервалов в соответствующие блоки хранения границ интервалов, на вторых входах «Выбор кристалла» 08 и «Чтение/запись» 010 устройства устанавливают значение логического нуля.
Третий шаг подготовки генератора к работе выполняется следующим образом. По второму N-разрядному адресному входу 05 генератора на первый N-разрядный вход 21 (входов разрядов A1-AN) второго селектора мультиплексора 2 подается N-разрядный адрес, по которому должно быть записано значение первого элемента, определяющее новое количественное значение верхней границы данного (первого) интервала. Аналогичным образом во второй селектор-мультиплексор 2 заносятся все K новых N-разрядных значений количественно (на первом этапе работы генератора) заданных верхних границ интервалов. На управляющем входе 07 генератора устанавливают значение логического нуля, который поступает на вход 23 (вход SE) второго селектора-мультиплексора 2, что приводит к коммутации адреса, записанного в двоичном коде и установленного на входе 21 второго селектора-мультиплексора 2 на N-разрядный информационный вход 31 (вход регистров D1-DN) первого регистра 3. В режиме подготовки генератора к работе на входы сброса 32 и 102 (входы R) первого 3 и второго 10 регистров соответственно поданы значения логической единицы.
На второй N-разрядный информационный вход 22 (вход для разрядов B1-BN) второго селектора-мультиплексора 2 с выхода 104 второго регистра 10 подается предыдущее (с прошлого шага) значение первого элемента с1 из множества значений вероятностей переходов случайного процесса из состояния в состояние, которое определяет новое, количественно заданное значение верхней границы данного интервала. Это значение первого элемента с1 записывается в первый регистр 3, причем для записи новых для данного шага количественных или проверенных и подтвержденных, преобразованных (с помощью ННС) значений верхних границ интервалов в первый регистр 3 на первом входе «Установка» 06 устройства устанавливают значение логической единицы, которая поступает на вход инициализации 33 (вход С) первого регистра 3. По окончании записи в первый регистр 3 новых (для данного шага) количественных или проверенных и подтвержденных (с помощью ННС) значений верхних границ интервалов в первый регистр 3 на первом входе «Установка» 06 устройства устанавливают значение логического нуля.
После вышеописанных действий генератор готов к работе.
В режиме генерации работа устройства с учетом не только количественно заданных значений границ интервалов состояний, но и этих значений, задаваемых с учетом комплексной неопределенности, которая проявляется одновременно и совокупно в виде недостоверности и нечеткости информации, происходит следующим образом (см. фиг. 1).
На управляющий вход 07 генератора подают значение логической единицы, которое поступает на вход выбора 13 (вход SE) первого селектора-мультиплексора 1, что обеспечивает коммутацию адреса, поступающего с выхода 104 второго регистра 10, на N-разрядный адресный вход 52 (вход для разрядов A1-AN) оперативного запоминающего устройства 5.
Источник случайных чисел 4 при наличии на управляющем входе 07 генератора значения логической единицы формирует Р-разрядное случайное значение адреса, которое поступает одновременно на Р-разрядные входы «Случайное число» 711-71K K блоков сравнения 71-7K, где происходит сравнение случайного значения адреса с начальными количественно заданными значениями верхних границ заданных интервалов В={b1, b2, …, bK} (см. фиг. 4). В случае если поступившее значение адреса принадлежит k-му интервалу, т.е. оно меньше либо равно количественно заданному значению верхней границы k-го интервала, то на выходе «Неравенство» (выходе А>В) компараторов 7.11-7.1k-1 формируются значения логической единицы, а на выходах «Неравенство» остальных компараторов значения логического нуля.
Сигналы с выходов «Неравенство» каждого компаратора 7.11-7.1K через элементы ИЛИ 7.31-7.3K и выходы «Результат сравнения» 731-73K K блоков сравнения 71-7K поступают на соответствующие инверсные входы 811-81K (входы регистров  ) шифратора приоритетов 8.
) шифратора приоритетов 8.
Таким образом (см. фиг. 1), при выполнении условия bk-1<ak<bk, на входах 811-81K (входах регистров  ) шифратора приоритетов 8 будут установлены значения логической единицы, а на входах 81k-1-81K (входах регистров
) шифратора приоритетов 8 будут установлены значения логической единицы, а на входах 81k-1-81K (входах регистров 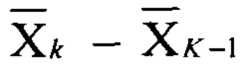 ) - значения логического нуля. В этом случае на N инверсных выходах 821-82N (выходах
) - значения логического нуля. В этом случае на N инверсных выходах 821-82N (выходах  ) шифратора приоритетов 8 будет сформирован двоичный код в инверсном представлении, соответствующий значению первого номера входа
) шифратора приоритетов 8 будет сформирован двоичный код в инверсном представлении, соответствующий значению первого номера входа 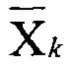 с установленным значением логического нуля, т.е. код соответствующий числу k - номеру интервала, которому принадлежит значение ak. Полученный код после инвертирования в элементах 91-9N поступает на N-разрядный информационный вход 101 второго регистра 10, здесь регистрируется как код предыдущего шага, затем поступает на второй N-разрядный информационный вход 120 (вход для разрядов B1-BN) первого селектора-мультиплексора 1 и второй N-разрядный информационный вход 22 (вход для разрядов B1-BN) второго селектора-мультиплексора 2.
с установленным значением логического нуля, т.е. код соответствующий числу k - номеру интервала, которому принадлежит значение ak. Полученный код после инвертирования в элементах 91-9N поступает на N-разрядный информационный вход 101 второго регистра 10, здесь регистрируется как код предыдущего шага, затем поступает на второй N-разрядный информационный вход 120 (вход для разрядов B1-BN) первого селектора-мультиплексора 1 и второй N-разрядный информационный вход 22 (вход для разрядов B1-BN) второго селектора-мультиплексора 2.
С N-разрядного выхода 24 второго селектора-мультиплексора 2 предыдущие (с прошлого шага), значения верхних границ интервалов, идентифицируемые как количественно, так и одновременно недостоверно и нечетко, поступают на N-разрядный прямой вход 111 блока нейро-нечеткой сети 11 для проверки и выявления значений этих верхних границ интервалов, задаваемых и идентифицируемых с учетом комплексной неопределенности, а также для обработки и трансформирования таких исходных данных, заданных одновременно в недостоверной и нечеткой форме к виду, позволяющему достоверно и однозначно идентифицировать и трактовать значения этих исходных данных о верхних границах интервалов для различных состояний исследуемого процесса.
Помимо данных о начальных и текущих значениях верхних границ интервалов, получаемых на N-разрядном выходе 24 второго селектора-мультиплексора 2 на основе Р-разрядного случайного значения адреса, генерируемого источником случайных чисел 4 (как предусмотрено в устройстве-прототипе), и которые могут быть идентифицированы как количественно, так и иногда недостоверно, в рамках динамического управления оператором устройства границами интервалов, возможно введение внешних управляющих воздействий, т.е., значений кода, характеризующих новые требуемые оператору значения верхних границ интервалов. Это происходит путем внешнего ввода N-разрядного кода, характеризующего эти, вновь вводимые в динамике управления, значения верхних границ интервалов через N-разрядный нейро-нечеткий вход 114 блока нейро-нечеткой сети 11 с N-разрядного нейро-нечеткого входа 014 устройства (см. фиг. 1).
При этом подразумевается, что вводимые оператором извне управления - новые значения верхних границ интервалов, гарантированно нуждаются в проверке и подтверждении, что эти значения априори обладают комплексной неопределенностью, что вводимые оператором новые пороговые значения состояний для конкретного шага моделирования дискретных случайных процессов заданы одновременно недостоверно и нечетко.
Реализация процедур проверки и подтверждения с помощью процедур нейро-нечеткой верификации значений верхних границ интервалов, задаваемых и идентифицируемых с учетом комплексной неопределенности, а также процедур математически корректной обработки и трансформирования таких исходных данных, заданных одновременно в недостоверной и нечеткой форме к виду, позволяющему достоверно и однозначно их идентифицировать и трактовать, осуществляется в блоке нейро-нечеткой сети 11 следующим образом.
С N-разрядного выхода 24 второго селектора-мультиплексора 2 предыдущие (с прошлого шага), значения верхних границ интервалов, идентифицируемые как количественно, так и одновременно недостоверно и нечетко, поступают и записываются в двоичном коде через N-разрядный прямой вход 111 на N-разрядный вход 11.1-1 счетчика 11.1 блока нейро-нечеткой сети 11.
Блок нейро-нечеткой сети 11 может быть реализован в соответствии со схемой, предложенной на фиг. 2. Последовательное сравнение по количеству разрядов поступающих в двоичном коде исходных данных - значений верхних границ интервалов, идентифицируемых как количественно, так и одновременно недостоверно и нечетко и принятие решения об их математической природе - значения верхних границ интервалов заданы параметрически, количественно или обладают комплексной неопределенностью и заданы, в нашем случае, весами связей для нейронов первого слоя ННС (выступающими как параметры функций принадлежности нечетких множеств для реализации правил ННС), осуществляется в счетчике 11.1 и регистре хранения 11.2 блока нейро-нечеткой сети 11 следующим образом.
Изначально информация, т.е., количественные данные и данные о начальных и текущих значениях верхних границ интервалов, задаваемые качественно - одновременно недостоверно и нечетко, поступающая с N-разрядного выхода 24 второго селектора-мультиплексора 2, различается по количеству разрядов: для записи в двоичном коде количественной информации достаточно 5 (пяти) разрядов двоичного кода, тогда как информация, обладающая комплексной неопределенностью несет в себе помимо обычного числа еще и характеристику весов связей для нейронов первого слоя ННС (параметров функций принадлежности), что объективно требует использования не менее 10 (десяти) разрядов двоичного кода для записи и хранения нейро-нечеткой информации - одновременно недостоверно и нечетко заданных значений верхних границ интервалов. С учетом этого факта построены счетчик 11.1 и регистр хранения 11.2 блока нейро-нечеткой сети 11.
Счетчик 11.1 и регистр хранения 11.2 блока нейро-нечеткой сети 11 рассчитаны на хранение пяти разрядов поступающей информации, если количество разрядов превышает данную цифру, значит, с точки зрения математики эта информация - начальные и текущие пошаговые значения верхних границ интервалов для состояний генерируемого случайного процесса, поступает в качественной форме - обладают одновременно недостоверностью и нечеткостью. В этом случае и счетчик 11.1 и регистр хранения 11.2 блока нейро-нечеткой сети 11 выполняют функции транзитного узла, причем, с N-разрядного информационного выхода 11.2-1 регистра хранения 11.2 эта информация в двоичном коде сразу поступает для дополнительной проверки и подтверждения с помощью процедур нейро-нечеткой верификации значений верхних границ интервалов, задаваемых и идентифицируемых с учетом комплексной неопределенности, на N-разрядный вход 11.3-1 (I1-IN) нейро-нечеткого программируемого вычислителя 11.3 (см. фиг. 2).
Также на N-разрядный вход 11.3-1 (I1-IN) нейро-нечеткого программируемого вычислителя 11.3 через N-разрядный нейро-нечеткий вход 114 блока нейро-нечеткой сети 11 с N-разрядного нейро-нечеткого входа 014 устройства в рамках динамического управления оператором устройства границами интервалов, поступают в двоичном коде внешние управляющие воздействия, т.е., значения кода, характеризующего новые требуемые оператору значения верхних границ интервалов. Эти значения (значения верхних границ интервалов) априори заданы с учетом комплексной неопределенности и нуждаются в дополнительной проверке и подтверждении с помощью процедур нейро-нечеткой верификации.
Если на N-разрядный прямой вход 111 и на N-разрядный вход 11.1-1 счетчика 11.1 блока нейро-нечеткой сети 11 поступает в двоичном коде информация (значения верхних границ интервалов состояний генерируемого случайного процесса) в количестве пяти разрядов, значит эта информация поступает в однозначной, достоверной форме, имеет количественный смысл и через N-разрядный выход 11.1-2 счетчика 11.1 поступает на N-разрядный вход 11.2-2 регистра хранения 11.2. Регистр хранения 11.2 записывает эту информацию и со своего N-разрядного прямого выхода 11.2-4 через N-разрядный прямой выход 112 блока нейро-нечеткой сети 11 направляет эти данные (заданные в однозначной, достоверной форме значения элементов генерируемого случайного процесса - количественно заданные, не требующие дополнительной проверки и подтверждения с помощью процедур нейро-нечеткой верификации значения верхних границ интервалов для конкретного шага) на N-разрядный информационный вход 31 (вход регистров D1-DN) первого регистра 3 (см. фиг. 1).
Данные, характеризующие значения верхних границ интервалов (для каждого последующего шага), определенные, распознанные в счетчике 11.1 и сохраненные в регистре хранения 11.2 блока 11 как одновременно недостоверные и нечеткие, и нуждающиеся в дополнительной проверке и подтверждении с помощью процедур нейро-нечеткой верификации с помощью ННС, поступают с N-разрядного информационного выхода 11.2-1 регистра хранения 11.2 на N-разрядный вход 11.3-1 (I1-IN) нейро-нечеткого программируемого вычислителя 11.3 блока нейро-нечеткой сети 11 (см. фиг. 2).
Нейро-нечеткий программируемый вычислитель 11.3 блока нейро-нечеткой сети 11 осуществляет запись, хранение результатов анализа кода, характеризующего значения верхних границ интервалов, и математически корректное нейро-нечеткое преобразование (верификацию) значений этого кода. Нейро-нечеткое преобразование, т.е. дополнительная проверка и подтверждение с помощью ННС истинных значений исходных данных - значений верхних границ интервалов, заданных одновременно в недостоверной и нечеткой форме к виду, позволяющему достоверно (полно, непротиворечиво) идентифицировать и трактовать значения этих верхних границ интервалов для конкретного шага моделирования дискретных случайных процессов, осуществляется в нейро-нечетком программируемом вычислителе 11.3 блока нейро-нечеткой сети 11 следующим образом (см. фиг. 2).
Нейро-нечеткий программируемый вычислитель 11.3 блока нейро-нечеткой сети 11 (см. фиг. 2) технически реализуется на базе программируемой (с точки зрения матрицы весов связей для нейронов первого слоя ННС, являющихся параметрами функций принадлежности, формулируемых экспертами) микропроцессорной секции (например, серийно выпускаемой MPS К1804ВС1), выполняющей роль программируемого параллельного арифметико-логического устройства (АЛУ), реализующего вычислительный нейро-нечеткий алгоритм работы пятислойной ННС прямого распространения сигнала, такой, как ANFIS (Adaptive-Network-Based Fuzzy Inference System - адаптивная сеть нечеткого вывода) и описанный в работах [1, 2].
Если информация с N-разрядного нейро-нечеткого входа 014 устройства, с N-разрядного нейро-нечеткого входа 114 блока нейро-нечеткой сети 11 и с N-разрядного информационного выхода 11.2-1 регистра хранения 11.2 блока нейро-нечеткой сети 11 на N-разрядный вход 11.3-1 (I1-IN) нейро-нечеткого программируемого вычислителя 11.3 блока нейро-нечеткой сети 11 не поступает, соответственно не поступает команда, инициирующая начало процедуры нейро-нечеткого преобразования значений верхних границ интервалов на вход 11.3-2 разрешения выходов A (OEI) нейро-нечеткого программируемого вычислителя 11.3.
В этом случае N выходов A (A1-AN) нейро-нечеткого программируемого вычислителя 11.3, а значит N-разрядный выход 11.4-2 запоминающего элемента 11.4 и N-разрядный информационный выход 113 блока нейро-нечеткой сети 11 заблокированы. В противном случае есть сигнал на входе 11.3-2 разрешения выходов A (OEI) нейро-нечеткого программируемого вычислителя 11.3 и одновременно недостоверные и нечеткие значения верхних границ интервалов (для каждого последующего шага), либо с N-разрядного информационного выхода 11.2-1 регистра хранения 11.2 блока нейро-нечеткой сети 11 либо с N-разрядного нейро-нечеткого входа 014 устройства через N-разрядный нейро-нечеткий вход 114 блока нейро-нечеткой сети 11 поступают на N-разрядный вход 11.3-1 (I1-IN) нейро-нечеткого программируемого вычислителя 11.3, выполняющего функции программируемого параллельного АЛУ и способного реализовать вычислительный нейро-нечеткий алгоритм работы пятислойной ННС прямого распространения сигнала.
Нейро-нечеткий программируемый вычислитель 11.3 блока нейро-нечеткой сети 11 (см. фиг. 2), реализующий функции программируемого параллельного АЛУ, опираясь на запрограммированные значения элементов матрицы весов связей для нейронов первого слоя ННС - аналитически описанные параметры функций принадлежности, формулируемые экспертами, осуществляет процедуру вычисления в соответствии с вычислительным нейро-нечетким алгоритмом работы пятислойной ННС прямого распространения сигнала, подробно описанным в работах [1, 2].
При этом входные разряды (ячейки) I1-In N-разрядного входа 11.3-1 (входа I) соответствуют разряду (1, …, N) последовательного кода, поступающего на N-разрядный вход 11.3-1 (вход I) нейро-нечеткого программируемого вычислителя 11.3 и являются равноправными N входами нейронов первого слоя ННС, на который подаются значения N разрядов кода, имеющего физический смысл одновременно недостоверно и нечетко определенных значений верхних границ интервалов. Набор прямых и обратных связей ННС (см. фиг. 3), программно реализованный в рамках нейро-нечеткого программируемого вычислителя 11.3, позволяет учитывать весовые коэффициенты для нейронов первого слоя ННС - аналитически описанных параметров функций принадлежности, формулируемых экспертами, и, на основе реализации нейро-нечеткого вычислительного алгоритма, описанного выражениями (3)-(9) данного описания, получать на N выходах А (А1-AN) нейро-нечеткого программируемого вычислителя 11.3 значения N разрядов параллельного кода, имеющего физический смысл дополнительно проверенного и подтвержденного, математически корректно верифицированного значения верхних границ интервалов, определенных на основе достоверных (полных) исходных данных.
При этом, реализуя нейро-нечеткий вычислительный алгоритм работы типовой пятислойной ННС прямого распространения сигнала (см. фиг. 3), подробно описанный в работах [1, 2] и иллюстрируемый выражениями (3)-(9) данного описания, с точки зрения теории ННС нейро-нечеткий программируемый вычислитель 11.3 блока нейро-нечеткой сети 11 выполняет арифметико-логические функции: фаззификации, т.е., преобразования численных входных значений в степени соответствия лингвистическим переменным (функции первого слоя ННС); записи и хранения нечетких правил, представляющих собой набор нечетких правил типа «Если-То» (функции второго слоя ННС); записи и хранения данных, определяющих функции принадлежности нечетких множеств, используемых в нечетких правилах (функции третьего слоя ННС); принятия решений, т.е., совершения операции вывода на основании имеющихся правил (функции четвертого слоя ННС) и функции дефаззификации, нацеленные на преобразование результатов вывода в численные значения исходных данных о границах интервалов для различных состояний исследуемого процесса (функции пятого, выходного слоя ННС). Причем подача на n-ый, где n=1, 2, …, N, вход (In) N-разрядного входа 11.3-1 (входа I) нейро-нечеткого программируемого вычислителя 11.3 значения разряда кода, характеризующего одновременно недостоверно и нечетко идентифицированные значения верхних границ интервалов (для каждого последующего шага), инициирует выдачу с соответствующего n-го выхода (An) нейро-нечеткого программируемого вычислителя 11.3 (с выхода суммирующего выходного нейрона пятого слоя ННС данных n-го нейрона четвертого, предпоследнего слоя) запрограммированного, согласно вычислительного нейро-нечеткого алгоритма, описанного в [1, 2], значения дополнительно проверенного и подтвержденного, математически корректно верифицированного значения верхних границ интервалов (фиг. 2).
В результате, на N выходах A (A1-AN) нейро-нечеткого программируемого вычислителя 11.3, на соответствующих разрядах N-разрядного выхода 11.4-2 запоминающего элемента 11.4 и на соответствующих разрядах N-разрядного информационного выхода 113 блока нейро-нечеткой сети 11 (см. фиг. 2), получаем информацию, характеризующую (на основе анализа, полученного в рамках работы ННС) дополнительно проверенные и подтвержденные, верифицированные, однозначные и истинные значения элементов генерируемого случайного процесса - значения верхних границ интервалов (для каждого последующего шага) в интересах повышения достоверности реализации генерируемой последовательности. Запоминающий элемент 11.4 блока нейро-нечеткой сети 11 (см. фиг. 2) записывает, хранит и выдает с соответствующих разрядов своего N-разрядного выхода 11.4-2 через соответствующие разряды N-разрядного информационного выхода 113 блока нейро-нечеткой сети 11 на соответствующие разряды N-разрядного информационного входа 31 (вход регистров D1-DN) первого регистра 3 (см. фиг. 1) код, содержащий дополнительно проверенные и подтвержденные, верифицированные результаты анализа значений верхних границ интервалов - код, однозначно (полно) и численно определяющий пороговые значения вероятности появления соответствующих элементов заданного набора данных.
Таким образом, на N-разрядном информационном входе 31 (входе регистров D1-DN) первого регистра 3, который отвечает за регистрацию и хранение значений как начальных и заданных количественно (поступающих с N-разрядного прямого выхода 112 блока нейро-нечеткой сети 11 (см. фиг. 1)), так и новых, дополнительно проверенных и подтвержденных, верифицированных с помощью ННС, значений верхних границ интервалов (поступающих с N-разрядного информационного выхода 113 блока нейро-нечеткой сети 11), имеем достоверно, однозначно и полно определенные верхние пороговые значения вероятности появления соответствующих элементов заданного набора данных для конкретного шага генерируемого случайного процесса.
Тем самым обеспечивается генерирование набора данных с учетом как количественно заданных значений верхних границ интервалов, на которые разбивается множество адресов этого набора данных, так и с учетом комплексной неопределенности значений этих границ интервалов для различных состояний генерируемого случайного процесса. Текущие (изменившиеся по сравнению с начальными) и дополнительно проверенные и подтвержденные с помощью ННС, достоверно, однозначно, полно определенные значения верхних границ интервалов для конкретного шага с N-разрядного выхода 34 первого регистра 3 поступают на N-разрядные адресные входы 621-62K K блоков хранения границ интервалов 61-6K и далее на Р-разрядные входы «Верхняя граница» 721-72K блоков сравнения 71-7K (см. фиг. 4).
На Р-разрядные входы «Случайное число» 711-71K блоков сравнения 71-7K по-прежнему поступает Р-разрядное случайное значение адреса от источника случайных чисел 4, вновь, но уже для данного конкретного шага происходит сравнение случайного значения адреса с текущими проверенными и подтвержденными, достоверно, однозначно и полно определенными значениями верхних границ заданных интервалов, полученных с учетом как количественной, так и качественной - одновременно недостоверной и нечеткой меры комплексной неопределенности пороговых значений вероятности появления соответствующих элементов заданного набора данных для конкретного шага генерируемого случайного процесса. Цикл повторяется, причем значения предыдущего адреса, поступающего с выхода 104 второго регистра 10 на второй N-разрядный информационный вход 120 (вход для разрядов B1-BN) первого селектора-мультиплексора 1, затем на N-разрядный адресный вход 52 (вход для разрядов A1-AN) оперативного запоминающего устройства 5, служат исходными данными для получения последующих значений элемента из заданного набора данных.
В итоге, в соответствии со случайными адресами, формируемыми источником случайных чисел и в соответствии с вводимыми извне (через N-разрядный нейро-нечеткий вход 014 устройства) и корректируемыми на каждом шаге проверенными и подтвержденными, достоверно, однозначно и полно определенными значениями верхних границ заданных интервалов, полученных с учетом как количественной, так и качественной - одновременно недостоверной и нечеткой меры комплексной неопределенности, происходит чтение текущих вероятностно-временных значений элементов А={а1, а2, …, aK] заданного набора данных из оперативного запоминающего устройства 5, которые через выход 55 поступают на М-разрядный выход «Результат» 013 генератора.
Генератор прекращает работу, когда на его управляющий вход 07 подается значение логического нуля, что соответствует прекращению формирования источником случайных чисел случайных адресов, либо когда по первому входу «Выбор кристалла» 04 генератора на вход 51 (вход  ) оперативного запоминающего устройства 5 подают значение логической единицы.
) оперативного запоминающего устройства 5 подают значение логической единицы.
Таким образом, заявленное устройство обеспечивает повышение достоверности генерируемой случайной последовательности за счет обеспечения возможности генерации заданного набора данных с учетом как количественно заданных значений верхних границ интервалов, на которые разбивается множество адресов этого набора данных, так и с учетом комплексной неопределенности значений этих границ интервалов для различных состояний генерируемого случайного процесса. Реализация возможности генерации случайной последовательности с учетом наличия не только количественно, но и одновременно недостоверно и нечетко заданных значений этих верхних границ интервалов происходит за счет реализуемых в блоке нейро-нечеткой сети 11 дополнительной проверки и подтверждения с помощью процедур нейро-нечеткой верификации значений верхних границ интервалов, задаваемых и идентифицируемых с учетом комплексной неопределенности, а также математически корректной обработки и трансформирования таких исходных данных, заданных одновременно в недостоверной и нечеткой форме к виду, позволяющему достоверно и однозначно их идентифицировать и трактовать в интересах осуществления процедуры параметрического моделирования (генерирования) случайных процессов.
Данный результат обусловлен, в итоге, получением на М-разрядном выходе «Результат» 013 генератора текущих вероятностно-временных значений элементов заданного набора данных с учетом наличия как количественно заданных значений верхних границ интервалов, на которые разбивается множество адресов этого набора данных, так и с учетом комплексной неопределенности значений этих границ интервалов для различных состояний генерируемого случайного процесса
Анализ принципа работы заявленного генератора случайной последовательности показывает очевидность того факта, что наряду с сохраненными и описанными в прототипе возможностями по генерации последовательности заданного набора данных, учитывая вероятностные связи между состояниями этого процесса, генератор случайной последовательности способен с высокой достоверностью формировать значения элементов случайного процесса, характеризующего реальное поведение сложной вычислительной системы -когда верхние границы интервалов для различных состояний этого случайного процесса имеют как количественно, так и качественно - одновременно недостоверно и нечетко выраженный физический смысл.
Данный генератор случайной последовательности обеспечивает повышение уровня достоверности моделирования (генерирования) случайных процессов, протекающих в реальных системах, где широкое применение находят как марковские модели, так и слабоформализуемые модели, наблюдаемые в условиях комплексной неопределенности, характеризуемые и описываемые одновременно недостоверно и нечетко заданными параметрами, что расширяет функциональные возможности универсальных генерирующих устройств в современной вычислительной технике, где заявленный генератор случайной последовательности будет использован.
ИСТОЧНИКИ ИНФОРМАЦИИ
1. R. Fuller. Introduction to Neuro-Fuzzy Systems. Advances in Soft Computing Series. Springer - Verlag, Berlin, 1999. - 289 p.;
2. Хижняков Ю.Н. Алгоритмы нечеткого, нейронного и нейро-нечеткого управления в системах реального времени. - Пермь: ПНИПУ, 2013. - 160 с.;
3. Паращук И.Б., Михайличенко Н.В. Особенности применения нейро-нечетких моделей для систем поддержки принятия решений в задачах оценки эффективности функционирования специализированных дата-центров // Информация и космос. №1, 2019. С. 84-88;
4. Андриевская Н.В., Резников А.С., Черанев А.А. Особенности применения нейро-нечетких моделей для задач синтеза систем автоматического управления. // Фундаментальные исследования. Технические науки. №11. - 2014. С. 1445-1449;
5. Рогозин О.В. Нейро-нечеткая адаптивная система поддержки принятия инновационного решения. // Образовательные технологии. №3. - 2011. С. 100-110;
6. Нестерук Г.Ф., Куприянов М.С., Елизаров С.И. К решению задачи нейро-нечеткой классификации. // Сборник трудов VI Междунар. конф. SCM'2003. - СПб.: СПГЭТУ, 2003. т. 1. С. 244-246;
7. Иваненко В.И., Лабковский В.А. Проблема неопределенности в задачах принятия решений. - Киев: Наукова думка. 1990. - 136 с.;
8. Паращук И.Б., Башкирцев А.С., Михайличенко Н.В. Анализ уровней и видов неопределенности, влияющей на принятие решений по управлению информационными системами // Информация и космос. №1, 2017. С. 112-120;
9. Баюк О.А., Браилов А.В., Денежкина И.Е. и др. Принятие финансовых решений в условиях сравнительной неопределенности. - М.: Вузовский учебник. 2014. - 106 с.;
10. Военная системотехника и системный анализ. Модели и методы подготовки и принятия решений в сложных организационно-технических комплексах в условиях неопределенности и многокритериальности. / Под ред. Б.В. Соколова. - СПб.: ВИКУ им. А.Ф. Можайского, 1999. - 496 с.;
11. Моделирование информационных систем. / Под ред. О.И. Шелухина. Учебное пособие. - М.: Радиотехника, 2005. - 368 с.;
12. Никитин Б.Я., Скребков В.Н. Теоретические основы вычислительной техники. Часть 2, - Л: ЛВВИУС, 1988, С. 9-11;
13. Тихонов В.И., Миронов М.А. Марковские процессы - М.: Советское радио, 1977. - 488 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| Генератор случайной последовательности | 2016 |
|
RU2635898C1 |
| ГЕНЕРАТОР СЛУЧАЙНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ | 2019 |
|
RU2717629C1 |
| УСТРОЙСТВО ДЛЯ ПРОГНОЗИРОВАНИЯ СЛУЧАЙНЫХ СОБЫТИЙ | 2024 |
|
RU2828686C1 |
| ВЕРОЯТНОСТНЫЙ АВТОМАТ | 2018 |
|
RU2718214C1 |
| ВЕРОЯТНОСТНЫЙ АВТОМАТ | 2021 |
|
RU2777531C1 |
| Устройство поиска информации | 2017 |
|
RU2656736C1 |
| ГЕНЕРАТОР СЛУЧАЙНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ | 2014 |
|
RU2542903C1 |
| ГЕНЕРАТОР СЛУЧАЙНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ | 2006 |
|
RU2313125C1 |
| УСТРОЙСТВО ДЛЯ ПРОГНОЗИРОВАНИЯ СЛУЧАЙНЫХ СОБЫТИЙ | 2020 |
|
RU2763126C1 |
| Устройство поиска информации | 2019 |
|
RU2724788C1 |
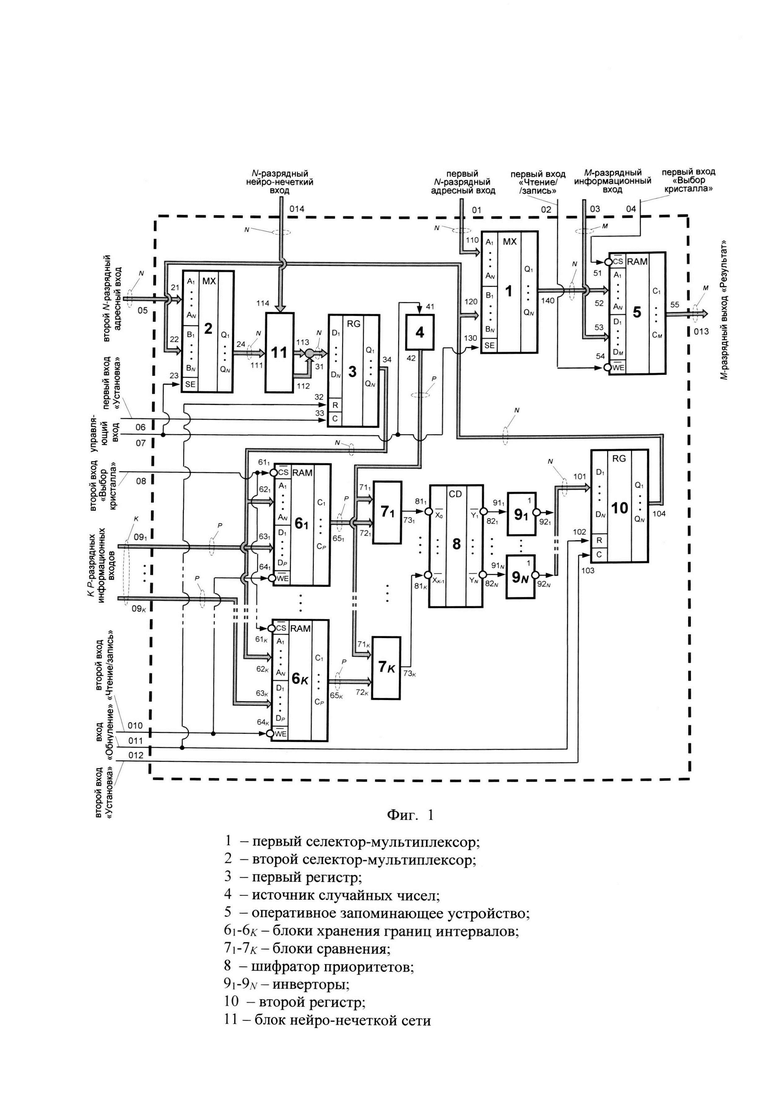
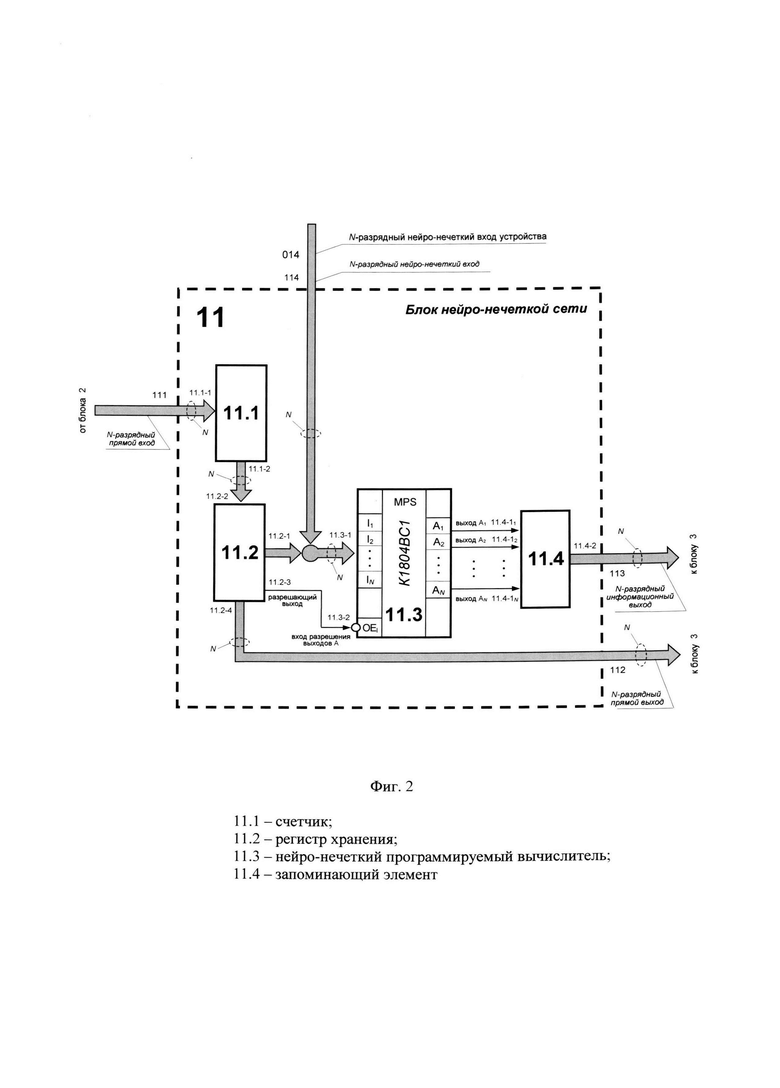
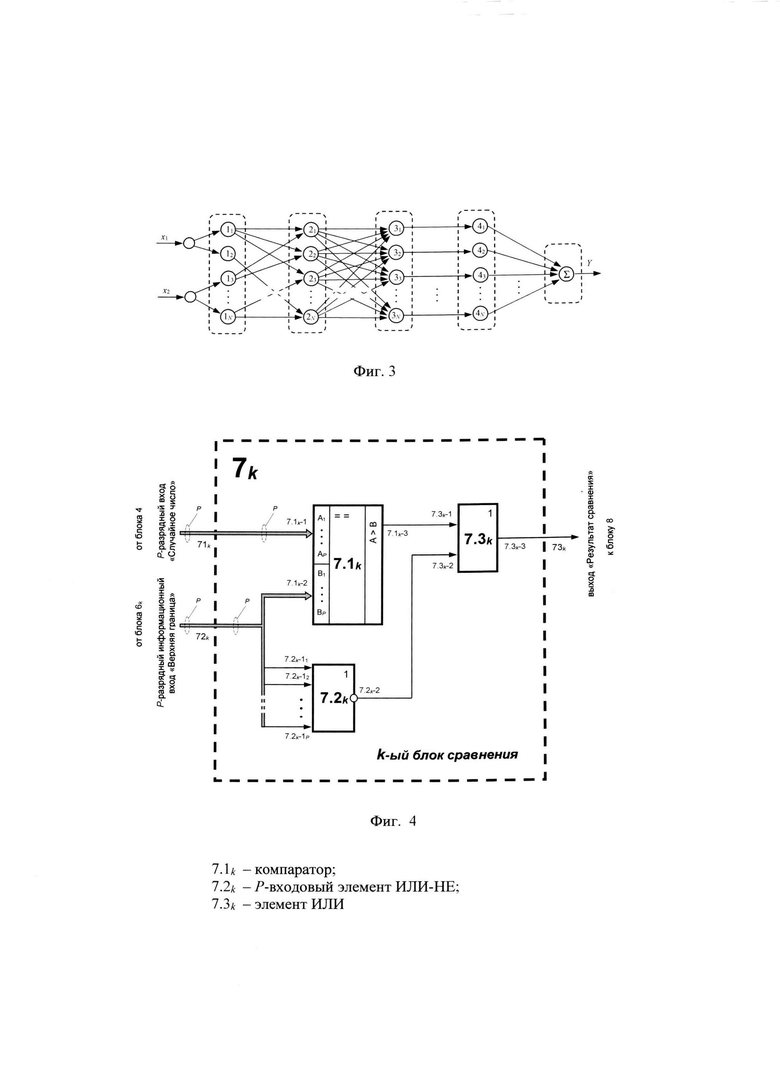
Изобретение относится к вычислительной технике. Технический результат заключается в повышении достоверности генерируемой последовательности. Генератор случайной последовательности содержит первый селектор-мультиплексор 1, второй селектор-мультиплексор 2, первый регистр 3, источник случайных чисел 4, оперативное запоминающее устройство 5, K≥2 блоков хранения границ интервалов 61-6K, K блоков сравнения 71-7K, шифратор приоритетов 8, N≥1 инверторов 91-9N, второй регистр 10 и блок нейро-нечеткой сети 11. 1 з.п. ф-лы, 4 ил.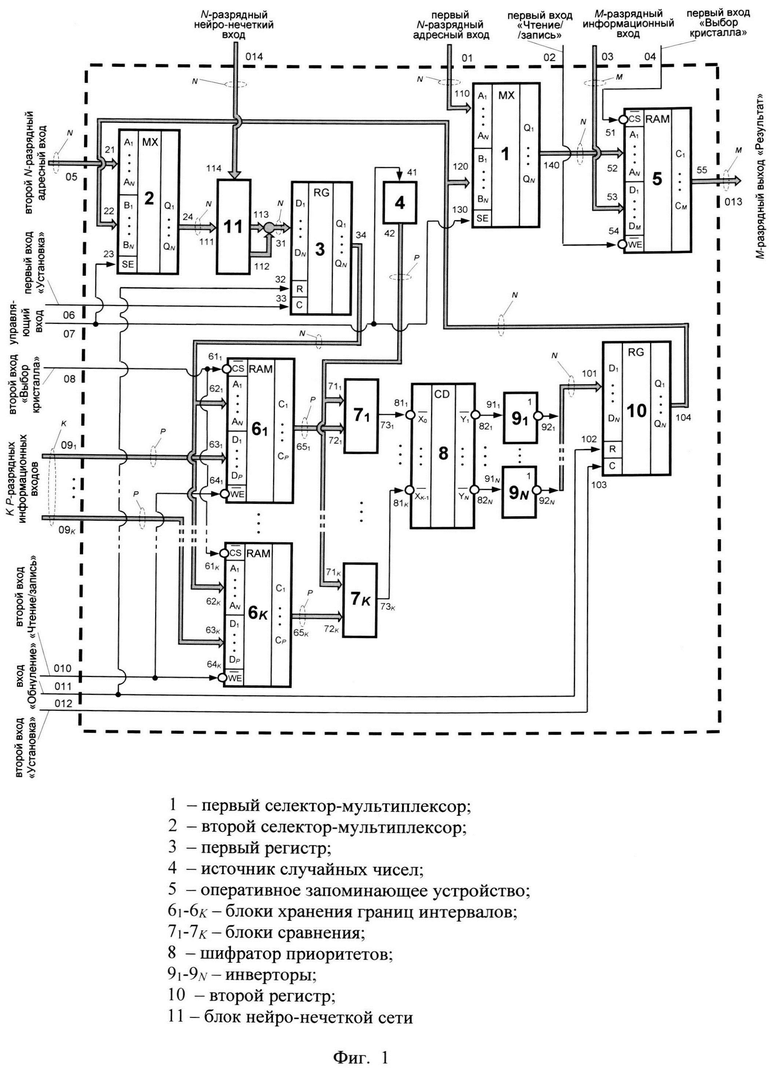
1. Генератор случайной последовательности, содержащий K блоков сравнения (71-7K), где K≥2 - максимально возможная мощность заданного множества генерируемых значений, первый селектор-мультиплексор (1), второй селектор-мультиплексор (2), первый регистр (3), оперативное запоминающее устройство (5), K блоков хранения границ интервалов (61-6K), шифратор приоритетов (8), N инверторов (91-9N), где N=[log2K] - число двоичных разрядов, достаточное для адресации элементов заданного множества генерируемых значений, второй регистр (10), источник случайных чисел (4), Р-разрядный, где Р>N - разрядность информационных входов генератора, выход «Случайное число» (42) которого соединен с Р-разрядными входами «Случайное число» (711-71K) K блоков сравнения (71-7K), Р-разрядный выход (65k) k-го блока хранения границ интервалов (6k), где k=1, 2, …, K, соединен с Р-разрядным входом «Верхняя граница» (72k) k-го блока сравнения (7k), выход «Результат сравнения» (73k) k-го блока сравнения (7k) соединен с k-м инверсным входом (81k) шифратора приоритетов (8), n-й инверсный выход (82n) которого, где n=1, 2, …, N, соединен с входом (91n) n-го инвертора (9n), вход выбора (130) первого селектора-мультиплексора (1) соединен с управляющим входом (41) источника случайных чисел (4) с входом выбора (23) второго селектора-мультиплексора (2) и является управляющим входом (07) генератора, первый N-разрядный информационный вход (110) первого селектора-мультиплексора (1) является первым N-разрядным адресным входом (01) генератора, N-разрядный выход (140) первого селектора-мультиплексора (1) соединен с N-разрядным адресным входом (52) оперативного запоминающего устройства (5), инверсные входы «Чтение/запись» (54) и «Выбор кристалла» (51) которого являются соответственно первым входом «Чтение/запись» (02) и первым входом «Выбор кристалла» (04) генератора, причем М-разрядный, где М≥2 - количество разрядов, достаточное для представления максимального значения из заданного множества генерируемых значений, выход (55) оперативного запоминающего устройства (5) является М-разрядным выходом «Результат» (013) генератора, М-разрядный информационный вход (53) оперативного запоминающего устройства (5) является М-разрядным информационным входом (03) генератора, при этом Р-разрядный информационный вход (63k) k-го блока хранения границ интервалов (6k) является k-м Р-разрядным информационным входом (09k) генератора, n-й разряд N-разрядного информационного входа (101) второго регистра (10) соединен с инверсным выходом (92n) n-го инвертора (9n), а N-разрядный выход (104) второго регистра (10) подключен ко второму N-разрядному информационному входу (120) первого селектора-мультиплексора (1) и ко второму N-разрядному информационному входу (22) второго селектора-мультиплексора (2), первый N-разрядный вход (21) которого является вторым N-разрядным адресным входом (05) генератора, N-разрядный выход (34) первого регистра (3) соединен с N-разрядными адресными входами (621-62K) K блоков хранения границ интервалов (61-6K), соответствующие инверсные входы «Выбор кристалла» (611-61K) и «Чтение/запись» (641-64K) которых объединены между собой и являются соответственно вторым входом «Выбор кристалла» (08) и вторым входом «Чтение/запись» (010) генератора, входы инициализации (33) и (103) первого (3) и второго (10) регистров являются соответственно первым (06) и вторым (012) входом «Установка» генератора, а входы сброса (32) и (102) первого (3) и второго (10) регистров объединены и являются входом «Обнуление» (011) генератора, отличающийся тем, что дополнительно введен блок нейро-нечеткой сети (11), предназначенный для осуществления процедур проверки и подтверждения с помощью процедур нейро-нечеткой верификации значений верхних границ интервалов состояний генерируемого случайного процесса, задаваемых и идентифицируемых с учетом комплексной неопределенности, а также математически корректной обработки и трансформирования таких исходных данных, заданных одновременно в недостоверной и нечеткой форме к виду, позволяющему достоверно и однозначно их идентифицировать и трактовать, причем N-разрядный выход (24) второго селектора-мультиплексора (2) соединен с N-разрядным прямым входом (111) блока нейро-нечеткой сети (11), N-разрядный прямой выход (112) которого соединен с N-разрядным информационным выходом (113) блока нейро-нечеткой сети (11) и подключен к N-разрядному информационному входу (31) первого регистра (3), N-разрядный нейро-нечеткий вход (114) блока нейро-нечеткой сети (11) является N-разрядным нейро-нечетким входом (014) генератора.
2. Генератор случайной последовательности по п. 1, отличающийся тем, что блок нейро-нечеткой сети (11) состоит из счетчика (11.1), регистра хранения (11.2), нейро-нечеткого программируемого вычислителя (11.3) и запоминающего элемента (11.4), N-разрядный выход (11.4-2) которого является N-разрядным информационным выходом (113) блока нейро-нечеткой сети (11), N-разрядный вход (11.3-1) нейро-нечеткого программируемого вычислителя (11.3) соединен с N-разрядным информационным выходом (11.2-1) регистра хранения (11.2) и является N-разрядным нейро-нечетким входом (114) блока нейро-нечеткой сети (11) и N-разрядным нейро-нечетким входом (014) генератора, вход (11.3-2) разрешения выходов А нейро-нечеткого программируемого вычислителя (11.3) соединен с разрешающим выходом (11.2-3) регистра хранения (11.2), N выходов A (A1-AN) нейро-нечеткого программируемого вычислителя (11.3) соединены с соответствующими N входами (11.4-11-11.4-1N) запоминающего элемента (11.4), N-разрядный прямой выход (11.2-4) регистра хранения (11.2) является N-разрядным прямым выходом (112) блока нейро-нечеткой сети (11), N-разрядный вход (11.2-2) регистра хранения (11.2) соединен с N-разрядным выходом (11.1-2) счетчика (11.1), N-разрядный вход (11.1-1) которого является N-разрядным прямым входом (111) блока нейро-нечеткой сети (11).
| ГЕНЕРАТОР СЛУЧАЙНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ | 2014 |
|
RU2542903C1 |
| ГЕНЕРАТОР СЛУЧАЙНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ | 2006 |
|
RU2313125C1 |
| ГЕНЕРАТОР СЛУЧАЙНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ | 2003 |
|
RU2250489C1 |
| Станок для придания концам круглых радиаторных трубок шестигранного сечения | 1924 |
|
SU2019A1 |
| Способ защиты переносных электрических установок от опасностей, связанных с заземлением одной из фаз | 1924 |
|
SU2014A1 |
| Пресс для выдавливания из деревянных дисков заготовок для ниточных катушек | 1923 |
|
SU2007A1 |
Авторы
Даты
2023-06-05—Публикация
2022-10-28—Подача